Abstract
We consider the spin-S ferromagnetic Heisenberg model in three dimensions, in the absence of an external field. Spin wave theory suggests that in a suitable temperature regime the system behaves effectively as a system of non-interacting bosons (magnons). We prove this fact at the level of the specific free energy: if S→∞ and the inverse temperature β→0 in such a way that βS stays constant, we rigorously show that the free energy per unit volume converges to the one suggested by spin wave theory. The proof is based on the localization of the system in small boxes and on upper and lower bounds on the local free energy, and it also provides explicit error bounds on the remainder.
Similar content being viewed by others
Notes
We use the convention of distinguishing (when needed) between operators and numbers or eigenvalues by means of a \(\hat{~} \) on top of the first ones. As usual we also denote vectors by bold letters.
This can be proved as follows. Let us indicate by \(\mathbf{x}_{1},\ldots , \mathbf{x}_{\ell^{3}}\) the sites of Λ 1 labeled in lexicographic order. By the theory of the composition of angular momenta, a bona fide basis for
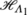 is provided by the common eigenvectors of \((\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\hat{\mathbf{S}}_{\mathbf {x}_{2}})^{2}\), \((\hat {\mathbf{S}}_{\mathbf{x}_{1}}+\hat{\mathbf{S}}_{\mathbf{x}_{2}}+\hat {\mathbf {S}}_{\mathbf{x}_{3}})^{2}, \ldots, (\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\cdots+\hat{\mathbf {S}}_{\mathbf{x}_{\ell ^{3}-1}})^{2}\), \(\hat{\mathbf{S}}_{T}^{2}\), \(\hat{S}^{3}_{T}\). In other words, the eigenvalues of \((\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\hat {\mathbf {S}}_{\mathbf{x}_{2}})^{2}\), \((\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\hat {\mathbf {S}}_{\mathbf{x}_{2}}+\hat{\mathbf{S}}_{\mathbf{x}_{3}})^{2}, \ldots, (\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\cdots+\hat{\mathbf {S}}_{\mathbf{x}_{\ell ^{3}-1}})^{2}\) can be used as good quantum numbers for classifying the states of
is provided by the common eigenvectors of \((\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\hat{\mathbf{S}}_{\mathbf {x}_{2}})^{2}\), \((\hat {\mathbf{S}}_{\mathbf{x}_{1}}+\hat{\mathbf{S}}_{\mathbf{x}_{2}}+\hat {\mathbf {S}}_{\mathbf{x}_{3}})^{2}, \ldots, (\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\cdots+\hat{\mathbf {S}}_{\mathbf{x}_{\ell ^{3}-1}})^{2}\), \(\hat{\mathbf{S}}_{T}^{2}\), \(\hat{S}^{3}_{T}\). In other words, the eigenvalues of \((\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\hat {\mathbf {S}}_{\mathbf{x}_{2}})^{2}\), \((\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\hat {\mathbf {S}}_{\mathbf{x}_{2}}+\hat{\mathbf{S}}_{\mathbf{x}_{3}})^{2}, \ldots, (\hat{\mathbf{S}}_{\mathbf{x}_{1}}+\cdots+\hat{\mathbf {S}}_{\mathbf{x}_{\ell ^{3}-1}})^{2}\) can be used as good quantum numbers for classifying the states of 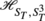 . Note that the operators associated with these quantum numbers are all scalars, i.e., they commute with the three components of \(\hat{\mathbf{S}}_{T}\): therefore, the eigenvectors of \(H_{\varLambda _{1}}^{N}\) on
. Note that the operators associated with these quantum numbers are all scalars, i.e., they commute with the three components of \(\hat{\mathbf{S}}_{T}\): therefore, the eigenvectors of \(H_{\varLambda _{1}}^{N}\) on 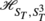 are invariant under the action of \(\hat{\mathbf{S}}_{T}\), which implies in particular that
are invariant under the action of \(\hat{\mathbf{S}}_{T}\), which implies in particular that 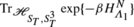 is independent of \(S^{3}_{T}\).
is independent of \(S^{3}_{T}\).
References
Bloch, F.: Zur Theorie des Ferromagnetismus. Z. Phys. 61, 206–219 (1930)
Bloch, F.: Zur Theorie des Austauschproblems und der Remanenzerscheinung der Ferromagnetika. Z. Phys. 74, 295–335 (1932)
Bricmont, J., Fontaine, J.-R., Lebowitz, J.L., Lieb, E.H., Spencer, T.: Lattice systems with a continuous symmetry III. Low temperature asymptotic expansion for the plane rotator model. Commun. Math. Phys. 78, 545–566 (1981)
Conlon, G.J., Solovej, J.P.: On asymptotic limits for the quantum Heisenberg model. J. Phys. A, Math. Gen. 23, 3199–3213 (1990)
Conlon, G.J., Solovej, J.P.: Upper bound on the free energy of the spin 1/2 Heisenberg ferromagnet. Lett. Math. Phys. 23, 223–231 (1991)
Conlon, G.J., Solovej, J.P.: Uniform convergence of the free energy of the classical Heisenberg model to that of the Gaussian model. J. Stat. Phys. 65, 235–245 (1991)
Cooke, J.F., Hahn, H.H.: Application of the hard-core boson formalism to the Heisenberg ferromagnet. Phys. Rev. B 1, 1243–1250 (1970)
Correggi, M., Giuliani, A., Seiringer, R.: in preparation
Dyson, F.J.: General theory of spin-waves interactions. Phys. Rev. 102, 1217–1230 (1956)
Dyson, F.J.: Thermodynamic behavior of an ideal ferromagnet. Phys. Rev. 102, 1230–1244 (1956)
Dyson, F.J., Lieb, E.H., Simon, B.: Phase transitions in the quantum Heisenberg model. Phys. Rev. Lett. 37, 120–123 (1976)
Dyson, F.J., Lieb, E.H., Simon, B.: Phase transitions in quantum spin systems with isotropic and nonisotropic interactions. J. Stat. Phys. 18, 335–383 (1978)
Fröhlich, J., Simon, B., Spencer, T.: Infrared bounds, phase transitions and continuous symmetry breaking. Commun. Math. Phys. 50, 79–85 (1976)
Garanin, D.A., Kladko, K., Fulde, P.: Quasiclassical Hamiltonians for large-spin systems. Eur. Phys. J. B 14, 293–300 (2000)
Herring, C., Kittel, C.: On the theory of spin waves in ferromagnetic media. Phys. Rev. 81, 869–880 (1951)
Hofmann, C.P.: Spontaneous magnetization of the O(3) ferromagnet at low temperatures. Phys. Rev. B 65, 094430 (2002)
Hofmann, C.P.: Spontaneous magnetization of an ideal ferromagnet: Beyond Dyson’s analysis. Phys. Rev. B 84, 064414 (2011)
Holstein, T., Primakoff, H.: Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098–1113 (1940)
Keffer, F.: Spin waves. In: Handbuch der Physik, vol. 18 (2), pp. 1–273. Springer, Berlin (1966)
Keffer, F., Loudon, R.: Simple physical theory of spin wave interactions. J. Appl. Phys. (Suppl.) 32, 2S (1961)
Kladko, K., Fulde, P., Garanin, D.A.: Cumulant expansion for systems with large spins. Europhys. Lett. 46, 425–430 (1999)
Kramers, H.A.: Commun. Kamerlingh Onnes Lab. Univ. Leiden (Suppl.) 22(83) (1936)
Lieb, E.H.: The classical limit of quantum spin systems. Commun. Math. Phys. 31, 327–340 (1973)
Lieb, E.H., Seiringer, R.: Proof of Bose–Einstein condensation for dilute trapped gases. Phys. Rev. Lett. 88, 170409 (2002)
Lieb, E.H., Seiringer, R., Yngvason, J.: A rigorous derivation of the Gross–Pitaevskii energy functional. Phys. Rev. A 61, 043602 (2000)
Lieb, E.H., Seiringer, R., Solovej, J.-P., Yngvason, J.: The mathematics of the Bose gas and its condensation. In: Oberwolfach Seminars, vol. 34. Birkhäuser, Basel (2005). Also available at arXiv:cond-mat/0610117 [cond-mat.stat-mech].
Lieb, E.H., Yngvason, J.: Ground state energy of the low density Bose gas. Phys. Rev. Lett. 80, 2504–2507 (1998)
Michoel, T., Nachtergaele, B.: Central limit theorems for the large-spin asymptotics of quantum spins. Prob. Theory Relat. Fields 130, 493–517 (2004)
Michoel, T., Nachtergaele, B.: The large-spin asymptotics of the ferromagnetic XXZ chain. Markov Process. Relat. Fields 11, 237–266 (2005)
Morita, T.: Bose–Einstein lattice gases equivalent to the Heisenberg model of ferro-, antiferro- and ferri-magnetism. Prog. Theor. Phys. 20, 614–624 (1958)
Oguchi, T.: Theory of spin-wave interactions in ferro- and antiferromagnetism. Phys. Rev. 117, 117–123 (1960)
Opechowski, W.: Über die temperaturabhängigkeit der magnetisierung eines ferromagnetikums bei tiefen temperaturen. Physica 4, 715–722 (1937)
Rastelli, E., Lindgard, P.A.: Exact results for spin-wave renormalisation in Heisenberg, and planar ferromagnets. J. Phys. C 12, 1899–1916 (1979)
Schafroth, M.R.: Self-consistent spin-wave theory for the ferromagnetic exchange problem. Proc. Phys. Soc. A 67, 33–38 (1954)
Szaniecki, J.: On certain divergences in the quantum spin wave theory of ferromagnetism. J. Phys. C 7, 4113–4125 (1974)
Toth, B.: Improved lower bound on the thermodynamic pressure of the spin 1/2 Heisenberg ferromagnet. Lett. Math. Phys. 28, 75–84 (1993)
Vaks, V.G., Larkin, A.I., Pikin, S.A.: Thermodynamics of an ideal ferromagnetic substance. Sov. Phys. JETP 26, 188–199 (1968)
van Hemmen, J.L., Brito, A.A.S., Wreszinski, W.F.: Spin waves in quantum ferromagnets. J. Stat. Phys. 37, 187–213 (1984)
Van Kranendonk, J.: Spin-deviation theory of ferromagnetism, I. Physica 21, 749–766 (1955)
Van Kranendonk, J.: Spin-deviation theory of ferromagnetism, II. Physica 21, 925–945 (1955)
Wallace, D.C.: Renormalized spin waves in the Heisenberg ferromagnet. Phys. Rev. 153, 547–558 (1967)
Yang, D.H., Wang, Y.: Green’s-function diagrammatic technique for complicated level systems. II. An application to the spin-1 Heisenberg ferromagnet with easy-axis single-ion anisotropy. Phys. Rev. B 12, 1057–1070 (1975)
Zittartz, J.: On the spin wave problem in the Heisenberg model of ferromagnetism. Z. Phys. 184, 506–520 (1965)
Acknowledgements
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme ERC Starting Grant CoMBoS (grant agreement No. 239694). We thank E.H. Lieb, B. Nachtergaele, R. Seiringer and J.-P. Solovej for useful comments and discussions.
Author information
Authors and Affiliations
Corresponding author
Appendix: Two Technical Bounds
Appendix: Two Technical Bounds
In this appendix we prove Propositions 2.2 and 2.3.
Proof of Proposition 2.2
Let us assume for definiteness that Λ
1={x∈ℤ3:x
i
=1,…,ℓ}. We rewrite \(H_{\varLambda _{1}}^{N} \) by applying the Fourier transform  , where \(\phi_{\mathbf{k}}(\mathbf{x})=\prod_{i=1}^{3}\phi_{k_{i}}(x_{i})\),
, where \(\phi_{\mathbf{k}}(\mathbf{x})=\prod_{i=1}^{3}\phi_{k_{i}}(x_{i})\),

and the set of momenta \(\varLambda^{*}_{1,N}\) is

Then a straightforward computation shows that, if \(\varepsilon (\mathbf{k})=\sum_{i=1}^{3}(1-\cos k_{i})\),

Now, for every k≠0, one has ε(k)≥c 0 ℓ −2, for a suitable c 0>0. Therefore,

where in the last inequality we used Plancherel’s identity  and the definition of total spin operator
and the definition of total spin operator  , from which
, from which  on
on  . Now, the expression in square brackets in the r.h.s. of Eq. (A.4) can be bounded from below by Sℓ
3(S−S
T
/ℓ
3), so that
. Now, the expression in square brackets in the r.h.s. of Eq. (A.4) can be bounded from below by Sℓ
3(S−S
T
/ℓ
3), so that

Therefore, for all S
T
such that \(S - \ell^{-3}S_{T} > 6c_{0}^{-1}\ell^{2} \), we get  , which proves the proposition with \(c : = \frac{1}{2}J c_{0} \). □
, which proves the proposition with \(c : = \frac{1}{2}J c_{0} \). □
Proof of Proposition 2.3
We start by investigating the part of \(\mathcal{K}^{N}_{\varLambda _{1}} \) associated with the square roots in the first term in (1.7). Using the fact that \(A_{\mathbf{x},\mathbf{y}}:= 1 - \sqrt{1 - \frac{\hat {n}_{\mathbf{x}}}{2S}} \sqrt{1 - \frac{\hat{n}_{\mathbf{y}}}{2S} } \) is a non-negative operator on the bosonic Hilbert space of interest, we get:

where in the first line we used the Cauchy–Schwarz inequality, while to go from the first to the second line we used the simple fact that \(1-\sqrt{1-x}\le x\), ∀x∈[0,1]. Finally, the remaining term in \(\mathcal{K}^{N}_{\varLambda _{1}} \) can be bounded trivially as \(J\vert \sum_{{ \langle\mathbf{x}, \mathbf{y} \rangle}\subset \varLambda _{1}} n_{\mathbf{x}}n_{\mathbf{y}}\vert \le(\mbox{const.}) ( \sum_{\mathbf{x}\in\varLambda_{1}} \hat{n}_{\mathbf {x}} )^{2}\), which implies the desired estimate. □
Rights and permissions
About this article
Cite this article
Correggi, M., Giuliani, A. The Free Energy of the Quantum Heisenberg Ferromagnet at Large Spin. J Stat Phys 149, 234–245 (2012). https://doi.org/10.1007/s10955-012-0589-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-012-0589-4



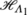 is provided by the common eigenvectors of
is provided by the common eigenvectors of 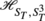 . Note that the operators associated with these quantum numbers are all scalars, i.e., they commute with the three components of
. Note that the operators associated with these quantum numbers are all scalars, i.e., they commute with the three components of 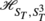 are invariant under the action of
are invariant under the action of 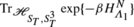 is independent of
is independent of