Abstract
Poly-parameter Linear Free Energy Relationships (PPLFERs) based on the Abraham solvation model are a useful tool for predicting and interpreting equilibrium partitioning of solutes in solvent systems. The focus of this work is neutral organic solutes partitioning in neutral organic liquid solvent-air systems. This is a follow-up to previous work (Brown, 2021) which developed predictive empirical correlations between solute descriptors and system parameters, allowing system parameters to be predicted from the solute descriptors of the solvent. A database of solute descriptors, and a database of system parameters supplemented by empirical predictions, form the basis for the development of new Quantitative Structure Property Relationships (QSPRs). A total of 11 QSPRs have been developed for the E, S, A, B and L solute descriptors, and the s, a, b, v, l, and c system parameters. The QSPRs were developed using a group-contribution method referred to as Iterative Fragment Selection. The method includes robust internal and external model validation and a well-defined Applicability Domain, including estimates of prediction uncertainty. System parameters can also be predicted by combining the solute descriptor QSPRs and the empirical correlations. The predictive power of PPLFERs applied using different combinations of experimental data, empirical correlations, and QSPRs are externally validated by predicting partition ratios between solvents and air. The uncertainty for predicting the log10 KSA of diverse solutes in diverse solvents using only the new QSPRs and empirical correlations is estimated to be one log10 unit or less.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Equilibrium partitioning of solutes between solvents, air, water, and other environmental or biological media are of fundamental importance in many fields of chemistry. Partitioning of solutes to solvents may be used in experimental design for chemical extraction or purification, as a part of process modelling in industrial applications, or as a proxy for more complex media in environmental and pharmacological chemistry [1,2,3,4,5]. Over the last several decades Abraham et al. have developed Linear Free Energy Relationships (LFERs) as an empirical method for predicting equilibrium partition ratios, or partition coefficients, from experimental descriptors [6, 7]. Here the term Poly-Parameter Linear Free Energy Relationships (PPLFERs) is used as opposed to Single-Parameter Linear Free Energy Relationships (SPLFERs) such as regressions versus log10 KOW, for example [8]. Partition ratios are a major chemical property required assessing chemicals for regulatory purposes [9, 10], and are major inputs for models used to assess human exposure to chemicals [11, 12]. However, experimental partition ratios even for well characterized solvent systems such as log10 KOW are missing for most chemicals that require assessment [2, 13], and PPLFERs can help to fill these data gaps [5, 14].
In this work equilibrium partitioning is expressed as the base-10 logarithm of partition ratios, Eq. 1 shows the general form. In Eq. 1 a solute k is in equilibrium between phase i and phase j, the concentrations Cik and Cjk are the molar concentrations of the solute in each phase, and log10 Kijk is the equilibrium partition ratio. Phase i is frequently a solvent S, and phase j is frequently either air A or water W, and the terms log10 KSAk and log10 KSWk will be used to refer to these partitioning systems, as was done in previous related work [15]. This corresponds to log10 K and log10 P, the terminology preferred by Abraham et al. [6]. Another commonly used partition ratio is the log10 KWAk, which Abraham et al. refer to as log10 KW, which is a unit conversion of the Henry’s Law constant for partitioning between water and air [6, 7, 16,17,18].
The two forms of PPLFERs developed by Abraham et al. are shown in Eq. 2, which is applied to log10 KSAk values, and Eq. 3 which is applied to log10 KSWk values [6, 7]. Equation 4 is a modification suggested by Goss which can be applied to both log10 KSAk and log10 KSWk [19]. In these equations the lower-case letters xij are the system parameters which must be calibrated for each pair of phases, and the upper-case letters Xk are the solute descriptors which must be calibrated for each solute. The solute descriptor E is the excess molar refractivity and the S solute descriptor is a combination of dipolarity and polarizability; for these two solute descriptors non-cyclic alkanes have a value of zero. The A and B solute descriptors are hydrogen bond acidity and basicity, with values equal to zero if no hydrogen bond donor or acceptor groups are present. The V solute descriptor is the McGowan volume [20], and L solute descriptor is the logarithm of the partition ratio between n-hexadecane and air. The system parameters are calibrated for each system, i.e. pair of phases i and j, by multiple linear regression (MLR) of the log10 Kijk values vs. the solute descriptors of the solutes with measured values. System parameters e, s, a, b, v, and l represent the relative propensity of solutes to partition to each phase contributed by each solute descriptor. The c system parameter is the MLR constant and has been mechanistically interpreted to be related to the difference in free volume [21] or packing density in the two phases [22]. The pairing of the system parameters and solute descriptors in the form of Eqs. 2, 3, and 4 is referred to as a PPLFER equation.
The main benefit of using PPLFER equations in the form of Eq. 4, and the reason it is used in this work and previous related work [15], is that it facilitates the application of thermodynamic cycles [19]. For example, Eq. 5 shows a thermodynamic cycle frequently applied in publications by Abraham et al., where log10 KSWk is calculated from log10 KSAk and log10 KWAk [17, 18]. If all three partition ratios are in the form of Eq. 4 then a new PPLFER equation for log10 KSWk can be calculated by applying Eq. 6 to the system parameters of the log10 KSAk and log10 KWAk PPLFER equations, where x is any of the six system parameters s, a, b, v, l, or c. This was leveraged in [15] when PPLFER equations were recalibrated into the form of Eq. 4 for 89 solvents based on data from almost 50 publications by Abraham et al. [15]. Values for log10 KSAk and log10 KWAk were pooled to calibrate a single PPLFER equation for log10 KSAk for each solvent, rather than a separate PPLFER equation calibrated on the data for each partition ratio. An additional benefit of using Eq. 4 instead of Eq. 2 for solvent air systems is that it includes only 4 experimentally determined solute descriptors, whereas Eq. 2 has 5; new values for V are derived by applying a simple Quantitative Structure Property Relationship (QSPR) to the chemical structure of the solute [20]. This means that fewer new predictive models need to be created for applying Eq. 4, which leads to less uncertainty in the predictions of log10 KSAk.
It is important to note that the log10 KSWk values and PPLFER equations derived from Eqs. 5 and 6, and the PPLFER equations calibrated in [15], are for hypothetical “dry” solvents. In an experimental determination of log10 KSWk the solvent and water will be in direct contact, and therefore the solvent will be saturated with water and “wet” [6, 23]. Abraham et al. have tested to see if including dry and wet data log10 KSWk data together affects the calibration PPLFER equations and found that in many cases the data can be pooled, either because the solubility of water in the solvent is so low [24], or because the presence of water does not appreciably alter the solvent’s partitioning properties [25]. There are exceptions, notably for log10 KOW the PPLFER equations for dry and wet octanol have different system parameters [23, 26]. In [15], the recalibrated PPLFER equations are specifically for pure phase, dry solvents. Wet solvents are mixtures and determining PPLFER equations for mixtures will be addressed in a follow-up publication based on the current work.
The work of determining new system parameters and solute descriptors is time and resource intensive. Five of the solute descriptors E, S, A, B, and L are originally derived from experimental data. New values of E can be calculated from molar refractivity [27], and new values of L can be measured directly or derived from retention times on non-polar GC columns [28]. New values for S, A, and B are derived by empirically fitting their values from log10 Kijk measurement in systems for which PPLFER equations have previously been calculated [27]. In [15] empirical relationships were derived to predict system parameters from solute descriptors, but experimentally determined solute descriptors are still not available for many chemicals. Calibrating system parameters is even more time and resource intensive, as evidenced by the far smaller number of solvents with system parameters, about 100, versus about 8000 solutes with descriptors. Publications calibrating system parameters for a new solvent typically include about 50 or more measured partition ratios for a diverse set of solutes to ensure that the MLR is stable and widely applicable.
QSPRs are a common tool for filling data gaps in the assessment of chemicals for regulatory purposes. QSPRs for solute descriptors already exist in the literature, some included in proprietary software [29] and others publicly available [30], most of them developed in collaboration with Michael Abraham. Some of these are group contribution MLR models [30] such as the QSPRs developed in this work, and others use different types of structural information and other statistical methods such as neural networks [29]. The QSPRs for solute descriptors developed here are an update of preliminary QSPRs, which are already publicly available and have been quite widely used [31]. Having multiple QSPRs available for a property is generally advantageous, because it allows for consensus modelling which generally increases predictive power. QSPRs for solute descriptors have immediate utility in environmental and pharmacological chemistry. PPLFERs have been calibrated for many environmental and biological media, and solvents, and the solute descriptor QSPRs can be used to apply the existing equations for novel solutes. Generally applicable QSPRs for system parameters of solvent–water systems have been published [32], but for solvent-air systems only simple QSPRs with narrow Applicability Domains (AD) are available [33, 34]. QSPRs for system parameters may be applied for predicting the partitioning of solvent systems without experimental data, assessment of chemical mixtures where the behaviour of chemicals as both solutes and solvents needs to be known, and for predicting vapor pressures where the solute and the solvent are the same chemical.
The goal of this paper is to develop robust and widely applicable QSPRs for solute descriptors and system parameters, so that PPLFER equations can be applied when either system parameters or solute descriptors or neither have been experimentally determined, which will allow for the prediction of partitioning for novel solute–solvent combinations. This builds on previous related work which developed methods to empirically predict system parameters for liquid solvents from measured solute descriptors [15] and applying these methods to solute descriptors predicted by QSPRs will also be explored. The QSPRs will have well-defined AD which will identify when their predictions will be most reliable, and an estimation of their prediction uncertainties [35, 36]. Methods for propagating AD and prediction uncertainties to the final predicted log10 Kijk are also defined. The preliminary QSPRs [31] have been recalibrated using updated algorithms and are based on more intensive curation of the experimental solute descriptors and chemical structures. The preliminary QSPRs for solute descriptors and those presented in this work draw from the extensive dataset of solute descriptors collected by Michael Abraham and shared with the author by personal communication ca. 2017, for which the author is grateful. The functionality and best practices described in this paper will be implemented in a Python package publicly available on GitHub (https://github.com/tnbrowncontam/ifsqsar) and integrated into the free and publicly available Exposure And Safety Estimation (EAS-E) Suite (www.eas-e-suite.com), which is an online platform for modelling chemical properties, environmental fate and risk estimation [37].
2 Methods
2.1 Data Collection and Curation
2.1.1 Solute Descriptors
The solute descriptor database compiled and curated by the author for previous related work [15] was used as the starting point for this work. In brief, two datasets were downloaded from the UFZ LSER database of solute descriptors [31]: the UFZ preselected and CompTox databases; and these were merged with a full version of the original database provided by Michael Abraham by personal communication (Abraham database). All solutes for which one or more descriptors were predicted by QSPRs were removed from the merged database. Any solutes missing one or more of the solute descriptors E, S, A, B, and L were also removed. Equilibrium partition ratios were collected from more than 40 papers in the primary literature, as cited in [15]; these papers also included solute descriptors which were used to update the merged database of solute descriptors if the publication dates were more recent than indicated for individual solutes in the three merged databases. All the papers are from Abraham et al., so changes to the solute descriptors represent continued refinement over time.
Additional data sources and curation steps were added to the python scripts used to curate the database of solute descriptors for [15]. This was not done in [15] because the focus was only on obtaining solute descriptors for 987 solutes with partitioning data. Solutes with equilibrium partition ratios in “wet” solvents were excluded from [15] which focused on pure phase “dry” solvents; solute descriptors for these solutes were included here. Some additional papers from the primary literature parameterizing PPLFER equations for systems excluded for other reasons were included as data sources here [38,39,40,41]. Literature sources which derive solute descriptors for specific solutes or groups of solutes were also included [27, 42,43,44]. Almost 200 additional solutes had their names standardized, which allowed them to be merged and checked for reliability based on their metadata in the Abraham database. More than 500 solutes in the CompTox dataset were found to have had their L values predicted with the preliminary QSPR available in the UFZ LSER database [31], these were removed from the merged database.
Molecular structures of the solutes database are included in the data downloaded from the UFZ LSER database as SMILES [45, 46]. These structures were standardized by first converting them to Inchified SMILES [47] using the Open Babel python package [48], which standardizes many functional groups that can be represented in different ways and selects a canonical tautomer if the structure has multiple tautomeric forms. Most dative bonds are converted to neutral forms in this step, for example nitro groups are converted from O=[N +]–[O–] to O=N=O. Isocyanide groups (–[N +]#[C–]) are not converted to a neutral form in this step and python code was written to manually convert them to a neutral form (–N=[C]). Elements in the “organic subset” automatically have their implicit hydrogen counts set when reading SMILES in Open Babel. However, silicon is not included in the built-in organic subset, so python code was written to manually set the number of implicit hydrogens so that silicon atoms had a total valence of four. Hydrogen atoms were deleted from the internal representation of all the structures in Open Babel (made implicit). These standardization steps are important so that the internal representations of structures in Open Babel are consistent and fragment counts determined by SMARTS substructure searches will also be consistent.
The accuracy of SMILES was checked by matching CAS registration numbers with two external databases and comparing the SMILES. The training datasets of the OPERA [49] suite of QSPRs were downloaded and merged into a single database. The NORMAN merged suspect list for non-target screening was downloaded from the NORMAN Network suspect list exchange (accessed May 2021) [50]. The molecular structures as SMILES in these databases were standardized as described above for the database of solutes to allow for comparison of the SMILES as strings. A little more than 4000 solutes had their structures confirmed using these external databases, with an error rate of about 1%. In the event of mismatched SMILES Pubchem [51] was consulted using the CAS registration number to look up the solute and the Pubchem SMILES was used and assumed correct. The SMILES errors identified in this process were generally minor, with misplaced double bonds or functional groups, or single atoms added or deleted from aliphatic carbon chains being the most common. About 1000 solutes could not be confirmed, many of these had no available CAS registration numbers. They were manually screened for egregious errors by comparing the solute names with the SMILES, for example to check for missing atom types.
The database of solutes was finally filtered to remove inorganic solutes and most organometallic solutes. Small inorganic structures are generally not amenable to group contribution QSPR methods such as the one applied in this work, so all solutes containing only two or three heavy atoms, and with no hydrogens attached were removed. Any solutes which contained no carbon atoms were removed. Any solutes which contained atoms that are not in the organic subset of elements [C, N, O, Si, P, S, F, Cl, Br, I] were removed, with two exceptions. Organometallics were accepted if there were three or more solutes which met the following criteria: the metal atoms have a full valence, metal atoms have bonds only to carbon atoms, and two or more carbon types (e.g. aromatic and aliphatic) were represented in the carbons bonded to metal atoms in the solutes. Only tin and mercury meet these criteria, and solutes that contain these elements and meet the above criteria are included in the database of solutes. The final database used for developing QSPRs contains 4974 solutes.
2.1.2 Experimental System Parameters
The first database of system parameters is from the PPLFER equations for solvent air systems recalibrated in the previous work [15]. Water as a solvent was removed from the database of system parameters because it falls under the definition of inorganic outlined in Sect. 2.1.1 and is not amenable to fragment-based prediction methods. A small number of solute descriptors used to calibrate the PPLFER equations in [15] were updated by the additional curation undertaken for this work. These updates were propagated through the workflow and the resulting recalibrated PPLFER equations were compared to the PPLFER equations of [15]. The difference between the two sets of system parameters is small, frequently less than two digits rounding error, and at most 0.02 absolute difference between them. Based on these small differences the PPLFER equations of the [15] are used for this work without any alteration, so that the literature is not confused with multiple versions of the recalibrated PPLFER equations.
Two additional solvent–air partitioning systems from one paper which should have been included in the [15] were discovered and included for this work: 1-hexadecene and 1,9-decadiene [41]. PPLFER equations were recalibrated using the same workflow as was applied in [15]. Solute descriptors were drawn from the database curated in Sect. 2.1.1 and equations were recalibrated into the form of Eq. 4. System parameter b was set to zero in both cases because A of both solvents is equal to zero i.e., there are no functional groups in the solvents that are hydrogen bond donors. The calibrated PPLFER equations and their regression statistics are shown in Eqs. 7 and 8. Including these two new solvents, and excluding water as described above, there are experimentally calibrated PPLFER equations for 90 solvents in the database.
2.1.3 Empirically Predicted System Parameters
The second database of system parameters includes the experimental system parameter database described in Sect. 2.1.2 as the starting point. This database is expanded by applying the empirical regressions developed in the [15] to predict system parameters for solutes acting as solvents, using the database described in Sect. 2.1.1. The experimental values of system parameters described in Sect. 2.1.2 were retained i.e., they were not replaced with the empirically predicted values. The solutes were checked to ensure that they were within the applicability domain (AD) of the empirical regressions using the leverage, as described in [15]. Borderline and out of domain solutes were found to have similar prediction errors in [15], so any solutes from the solute database defined as borderline or out of domain had their empirically predicted system parameters removed from the database. 3224 solutes out of 4974 were removed by this filter. As an additional AD check, solutes were filtered to ensure that only liquids were included in the database. Experimental melting points (MP) and boiling points (BP) were collected from the literature and used to identify the state of the solutes at room temperature. MP values were taken preferentially from the highly curated Bradley dataset [52], then the OPERA MP training dataset [49], and finally from Pubchem [51]. BP values were preferentially taken from the OPERA BP training dataset, and then from Pubchem. All solutes with BP greater than 25 °C and MP less than 25 °C were identified as liquids and retained in the dataset. Pubchem also frequently includes a description of each chemical’s state at room temperature, and if a solute could not be confirmed as liquid by MP and BP then this description was used to identify solutes as gases, liquids, or solids when available. Out of 1751 solutes which passed the first filter, 855 were identified as liquids, with another 754 which could not be identified as a gas or a solid, and which were retained for further filtering.
PPLFER equations were calibrated for MP and BP to identify additional solutes as liquids. The calibration datasets were all solutes with MP or BP values collected from the sources described above. For each calibration dataset the data were divided into a training and an external validation dataset by ordering the solutes by MP or BP and assigning every third solute to the external validation dataset. PPLFER models were selected by k-fold cross validation with k = 10, and the Akaike Information Criterion corrected for dataset size (AICC) was used to measure the goodness of fit. The pool of models considered was every combination of the solute descriptors in the set \(\left\{ {E,S,A,B,V,L,\left( {AB} \right)^{{0.5}} } \right\}\). (AB)0.5 was included because it correlates with the strength of hydrogen bonding between molecules of a chemical, such as could be expected for measurements of MP and BP for a pure chemical. Only A and B or (AB)0.5 were permitted to be in the models, but not both to avoid overfitting. The selected models along with the training and external validation statistics are shown in Eqs. 9 and 10.
The PPLFER equations for MP and BP were applied to the 754 solutes remaining from the second filtering step. Because the PPLFERs have a relatively large amount of uncertainty a margin of error was added to the predictions, equal to the 80% confidence interval calculated from the standard error of the predictions for the external validation. For MP predictions the margin of error was 77.5 °C and for BP the margin of error was 36.1 °C, meaning a solute was identified as a liquid if MPpred. + 77.5 < 25 °C and BPpred. − 36.1 > 25 °C. If an experimental value for either MP or BP was available, then that value was used instead of the PPLFER prediction. These strict filtering criteria remove many chemicals that might be liquids, but the goal is to expand the training dataset while still ensuring that it is consistent; because this will ensure that the QSPRs developed are reliable. An additional 184 solutes out of 754 were identified as liquids in this filtering step, and there are 1039 solvent-air partitioning systems in the final empirically predicted system parameter database.
2.1.4 External Validation Data
Experimental equilibrium partitioning data were used as an additional external validation dataset to test the combined predictive power of the solute descriptor and system parameter QSPRs. Two datasets from [15] were used for this: a dataset of log10 KSAK and log10 KSWK data collected from literature published by Abraham et al., and a dataset of vapor pressure (VPk) and water solubility (WSk) for pure chemicals collected from the training data of the OPERA QSAR software [49]. The log10 KSAk dataset has 3884 partitioning data (1922 log10 KSAk and 1962 log10 KSWk) in 23 solvents of the external validation dataset for experimental system parameters described in Sect. 2.1.2, see Sect. 2.2.2 for details on dataset splitting. This dataset has many structurally diverse solutes, but only a small number of solvents containing a limited number of functional groups.
VPk values were converted to log10 KSAK values and WSK values were converted to log10 KSWk values so that they are directly comparable to the values predicted by the QSPRs and PPLFER equations, and on the same scale as the other external validation data. They are converted by applying Eqs. 11 and 12 as described in [15], based on work by Abraham et al., e.g. [24, 33, 53].
For these equations the solvent is also the solute i.e., S = k, \({\gamma}_{\text{k}}^{\infty}\) is the infinite dilution activity coefficient of the solute, R is the ideal gas law constant, T is the temperature at which the VPk or WSK was measured, and VMk is the molar volume of the solute. A value of unity is assumed for \({\gamma}_{\text{k}}^{\infty}\), so the only additional experimental data required is the density of the solute to calculate VMk. There are 168 VPk values and 126 WSk values for solvents in the external validation dataset of the empirical system parameter database, which have been identified as liquids as described in Sect. 2.1.3. In addition to the VPK and WSK values from [15], 50 VPK values were added from a recent work by Abraham and Acree [54] bring the total number of VPk and WSk values in the dataset to 344. These added values were converted to log10 KSAk as described above; densities required to calculate VMk were manually collected from Pubchem [51]. If density was not available for a chemical in Pubchem then a value was obtained from the substance information sheet of a reputable chemical vendor such as Sigma-Aldrich (https://www.sigmaaldrich.com). These data contain structurally diverse solvents, but each solvent has partitioning measured for only one solute i.e., the solvent itself.
2.2 Model Building
2.2.1 Model Building Background for System Parameters
Previous work has shown that group contribution QSPRs can adequately predict PPLFER solute descriptors [29,30,31, 36]. Equation 13 shows the general relationship implied in these QSPRs, where X is a solute descriptor (E, S, A, B, L), and fi represents fragment counts in a group contribution QSPR. This is the method applied to generate QSPRs for solute descriptors in this work.
There has also been some work developing group contribution QSPRs to predict system parameters of solvent–water systems [33, 34], though the datasets used in this previous work were limited in size, and the solvents contained only a few different functional groups. This previous work generally followed the relationship shown in Eq. 14, where x is the system parameter (s, a, b, v, l, c) of a PPLFER equation. This direct relationship between system parameters and fragment counts was the first type of model building applied to the system parameters in this work. A QSPR that can predict system parameters has also been published for solvent–water systems but is not a group contribution method [32].
It was found in [15] that direct correlations between solute descriptors and system parameters worked poorly. The best correlations developed in [15] were between system parameters and solute descriptors normalized to molecular volume. The general relationship is shown in Eq. 15, where xSA is the system of a PPLFER equation for solvent-air (SA) partitioning, XS is a solute descriptor of a solvent as a solute, and VS is specifically the McGowan Volume descriptor of the solvent. XS may be any solute descriptor, for example the A solute descriptor correlates most closely with the b system parameter. In [15] the right hand side of Eq. 15 is a linear combination of several solute descriptors.
Combining Eqs. 15 and 13 implies that system parameters should be proportional to fragment counts normalized to molecular volume as shown in Eq. 16. The Iterative Fragment Selection (IFS) development code [35, 36, 55] was altered to facilitate generating this type of QSPR and was used to generate a second set of QSPRs for system parameters.
Equation 17 shows a rearrangement of the relationship from Eq. 16, which allowed for development of QSPRs for system descriptors without any alterations to the IFS QSPR development code. A third set of QSPRs for system parameters was developed using this method, with the results yielded by dividing the QSPR predictions by VS of the solvents.
The QSPRs developed using the relationships shown in Eqs. 16 and 17 do not produce equivalent results, because the right-hand side of the equations is a linear combination of fragments that are fitted with MLR. Using Eq. 16 the values for fi and VS are different for each chemical in the training dataset, so the MLR assigns different weights to the fragments than are assigned using Eq. 17.
2.2.2 Dataset Splitting
The datasets of solute descriptors and system parameters were split into training datasets used to develop the models and external validation datasets used to test the predictive power of the models. This ensures that the models meet principle 4 of the OECD guidance document on 5 principles for the development of validated QSARs for applications in regulatory decision making: appropriate measures of goodness of fit, robustness and predictive power [56, 57]. The dataset was split only once for each class of QSPR developed, and the QSPRs of each class for the individual solute descriptors and system parameters used the same training and external validation datasets.
The first class of QSPRs developed was trained on the experimental system parameters calibrated in [15]. The splitting of the experimental system parameters is the same as was defined in [15] with a few exceptions. Maintaining a consistent training and external validation datasets allows the results of this work to be more easily compared to the results of the empirical regressions developed in [15]. As noted in Sect. 2.1.2 water was removed from the database, which was in the training dataset. The two new solvents 1-hexadecene and 1,9-decadiene were assigned to the training and external validation datasets, respectively. In [15], the atoms contained in the solvents were not important, only the values of the solute descriptors and solvent parameters. However, representing each atom type in the training dataset is desirable for fragment-based QSPRs, so perfluoroheptane and tri-n-butyl phosphate were moved from the external validation to the training datasets, so that fluorine and phosphorus are represented in the training dataset. This left too few solvents in the external validation dataset to match the splitting ratio of 0.75:0.25 defined in [15]. There are 12 closely related nitrogen-containing solvents from a single literature source [58]; one of these solvents in the training dataset was randomly selected and assigned to the external validation dataset.
The second class of QSPRs developed were trained on the expanded database of empirically predicted system parameters described in Sect. 2.1.3. The assigned training and external validation datasets from the first class of QSPRs were retained without alteration and used as the seed for dataset splitting for the second class of QSPRs. The third class of QSPRs developed were trained on the database of solute descriptors described in Sect. 2.1.1. Again, the assignment of chemicals to the training or external validation datasets was retained from the second class of QSPRs and used to seed the dataset splitting for the third class of QSPRs. The dataset splitting ratio used for the second and third classes of QSPRs was 0.667:0.333 because more data were available, meaning a larger fraction could be used for external validation. The IFS QSPR model building algorithm has a defined method for splitting data into training and external validation datasets which is applied for this work with only one alteration [35, 36, 55]. Previously, the training dataset was seeded with the chemicals that had highest and lowest values of the property to be predicted, here the seed is the training and external validation datasets of the previous class of QSPRs as described above. The IFS splitting algorithm splits the dataset of chemicals so that as many structural features as possible are represented in both the training and external validation datasets.
The training datasets are further split so that k-fold cross validation can be applied with k = 10, which helps to ensure that the QSPRs are not over-fitted and have better predictive power. In previous work chemicals were assigned to folds by ordering them by the values of the property to be predicted and assigning the first n/k chemicals to the first fold, etc. where n is the number of chemicals in the training dataset. In this work, where multiple QSPRs will be generated for several different properties i.e., the system parameters and solute descriptors, the chemicals are instead ordered by the sum of the ranks of each chemical within each property. Then, the first chemical is assigned to the first fold, the second chemical to the second fold, etc. This was done because some of the system parameters and solute descriptors have a value of zero for many chemicals and following the previously used method would result in some folds having only zero values, which causes the cross validation to be ineffective.
2.2.3 IFS QSPR Fragment Pool Generation
The pool of chemical substructures (fragments) that IFS draws from during model selection is generated by fragmenting the structures of the training dataset. Various versions of the IFS fragment pool generation algorithm have been applied to generate QSARs for biotransformation rates in fish [35], biotransformation rates in humans [59], preliminary QSPRs for PPLFER solute descriptors [31], and QSPRs for entropy of fusion and melting point [55]. As in the most recent application of IFS [55] three pools of fragments are defined by the size of the fragment: first order fragments which contain a single atom, second order fragments which contain a central atom and some or all of the atoms bonded directly to it, and recursive fragments which may include any number of atoms in any configuration so long as the maximum distance between any pair atoms is five bonds or less. The fragments are generated by recursively adding atoms from the molecular structure to obtain all valid combinations of bonded atoms and formatted as very specific SMARTS search strings [55]. There are typically too many recursive fragments to be considered so the list is filtered by removing recursive fragments that have the lowest correlation to the property for which the QSPR is being generated, until the number of recursive fragments is equal to the sum of the other types of fragments. The SMARTS tokens included for every atom are atomic number (#), aromatic/aliphatic (aA), heavy atom connections (degree, D; hydrogens must be stripped from the structure as described in Sect. 2.1.1), number of hydrogens attached (H), total bond order (valence, v), number of ring bonds (x), number of rings that contain the atom (R), and formal charge (− +). The SMARTS tokens included for every bond are bond type (-: = #) and ring membership (@). The specific SMARTS are post-processed using string manipulation to remove tokens and generate more generalized SMARTS depending on the application.
Several alterations were made to the generation of the pool of fragments for this work to best construct models for solute descriptors and system parameters. The most important change is that a fourth pool of “element” fragments was added in which each first order SMARTS had all but one or two tokens stripped out. This pool contains more general SMARTS substructure searches that may match, for example, all carbons [#6], all atoms contained in only one ring with two ring connections [x2R1], or all aliphatic atoms [A]. All second order fragments with two atoms were also processed to add generalized bond SMARTS to element fragments pool, for example all bonds in a ring [!#1]@[!#1], or all triple bonds [!#1]#[!#1]. Generalized SMARTS for hydrogen bond donors [!H0;#7,#8,#9], hydrogen bond acceptors [#8,#7&!v5&!$([nX3])] and halogens [#9,#17,#35,#53] were also added to the element fragments pool.
Another alteration to the fragment pools is that a more general SMARTS with ring-matching tokens (x, R, @) stripped out was added for every first order, second order and recursive fragment to match substructures regardless of whether they were in a ring or not. The final alteration to the generation of the fragment pools was to add a new type of recursive fragment that can capture intramolecular hydrogen bonds. Linear fragments between 3 and 5 bonds in length with a hydrogen bond donor at one end and a hydrogen bond acceptor or a halogen at the other end were converted into several different types of intramolecular hydrogen bond fragments. The middle 2–4 atoms were converted to generic heavy atoms [!#1] and the bonds were converted to single bonds or not single bonds, - or !-, and ring information was stripped out of the end atoms. All 4 combinations of specific SMARTS and generalized SMARTS for the two end atoms were added as fragments.
After generating the fragment pools some of the fragments were excluded based on the solute descriptor or system parameter for which a QSPR was being generated. The most obvious example for why this is needed is A which represents the propensity of a solute to engage in hydrogen bonding. If there are no hydrogen bond donor groups, then the value of A is equal to zero. Fragments which contain hydrogen bond donors such as hydroxyl groups should obviously be included in the fragment pool. The molecular environment makes a big difference in the propensity for hydrogen bonding, for example if the hydroxyl group is an alcohol or a phenol. One way to capture this might be to add fragments for hydroxyl groups, aliphatic carbons, and aromatic carbons. But in this case the carbon fragments would also be present in chemicals where no hydrogen bond donors are present, causing the value of A to be non-zero in cases where it should be zero. A more appropriate method is to exclude the aliphatic and aromatic carbons from the fragment pool and capture the effect of molecular environment using fragments that include both the hydroxyl group and the attached carbon atom. In practice categorizing fragments correctly is not always unambiguous; for example, a functional group may usually be a hydrogen bond donor but due to a strong intramolecular hydrogen bond the A value of the solute is zero. A counterexample is that a functional group which is not typically a hydrogen bond donor may have a non-zero A value. For example, in chloroform the hydrogen in the CH group is a hydrogen bond donor due to the strong electron withdrawing effects of the three chlorines, chloroform has an A value of 0.15.
An algorithm was developed to choose a subset of fragments from the full fragment pool for E, S, A, B and s, a, b which may have values defined as zero for some chemicals. The basic aim is to compile a list of fragments that occur only in an “include” list of chemicals with non-zero values and a minimal number of chemicals with zero values. In each iteration the fragments in the chemical with the highest value solute descriptor or system parameter are considered. The fragments which occur in the minimum number of chemicals with zero values are selected. Ties are decided by selecting the fragments which occur in the maximum value of the number of chemicals with non-zero values minus the occurrences in chemicals with zero values. Remaining ties are decided by selecting fragments which occur in the maximum number of chemicals with non-zero values. All chemicals which contain the remaining fragments are added to the include list. This process continues until all chemicals with non-zero solute descriptor have been added to the include list. Finally, any fragments that occur in any chemicals that are not in the include list are removed from the fragment pool.
2.2.4 IFS QSPR Model Selection
The IFS QSPRs are a MLR of the property to be predicted versus counts of fragments within the chemicals of the training dataset. This simple model structure meets principle 2 of the OECD 5 principles for the development of QSARs: an unambiguous algorithm. It also allows the models to be easily interpretable, meeting principle 5 a mechanistic interpretation. During model selection the goodness of fit (GoF) is measured using the Akaike Information Criteria corrected for dataset size (AICC) [60], but with the predictive sum of squares (PRESS) from the k-fold cross validation used in place of the sum of squares. This helps avoid overfitting because the AICC penalizes adding more fragments to the MLR, and using the PRESS ensures the QSPRs have good predictive power. The QSPR regression coefficients are the average of the k individual MLR from the cross-validation.
The four pools of fragments are drawn from one at a time in the order: element fragments, first order fragments, second order fragments, and finally recursive fragments. Fragments are iteratively added to the MLR by forward selection, testing all the eligible fragments in the active pool each iteration and selecting the fragment which results in the largest improvement in GoF. Some fragments are considered “coincident”, meaning they occur in mostly the same chemicals, and are not included together in the MLR because this leads to overfitting and instability in the MLR. In each iteration of forward selection coincident fragments from the active pool may be selected to replace fragments in the MLR if this results in the largest improvement in GoF. After each iteration of forward selection all the fragments in the MLR are tested for backwards removal. Multiple fragments may be iteratively removed if this increases the GoF, always removing the fragment that increases the GoF by the most. Only fragments from the active pool are considered for removal. The MLR is done for all fragments from all the pools at once. Forward selection and backwards removal continue until the GoF cannot be improved any further, then the next pool of fragments becomes the active pool, or the model selection is complete if the active pool is recursive fragments.
2.2.5 IFS QSPR Applicability Domain
The IFS QSPRs have a well-defined Applicability Domain (AD) as required by principle 3 of the OECD 5 principles for the development of QSARs. Two complementary methods are used to assign an uncertainty level (UL) to each prediction, and the external validation data are used to estimate prediction uncertainties for each UL [35, 36, 55]. The first AD method is called Chemical Similarity Score (CSS), which quantifies the structural similarity of a chemical to the five nearest neighbors of the QSPR training dataset and how well those neighbors were fitted by the QSPR. Two CSS cutoffs are defined, and chemicals may be assigned a UL score of 0 if they do not exceed the first cutoff (in domain), 1 if they exceed the first cutoff (borderline), or 2 if they exceed the second cutoff (out of domain). The second AD method uses leverage which is calculated from the “hat matrix” of the training dataset and quantifies the amount of extrapolation from the training data [61, 62]. Two thresholds are again defined which assign chemicals a UL of 0, 1, or 2; and if leverage exceeds a value of 1, indicating egregious extrapolation, then a UL of 3 is assigned. The higher value of the UL from the two AD methods is taken as the overall UL for a prediction.
Some other domain checks are also applied, chemicals may be assigned a UL of 4 if they contain none of the fragments in the QSPR model, though as discussed in Sect. 2.2.3 these are not necessarily poor predictions. An additional “negative domain check” is applied to ensure that all the atoms in a chemical are represented in the training dataset. If a chemical contains an element that is not in the training dataset, or has an atom with a number of heavy atom connections, number of hydrogens, total valence, ring membership, etc. not included in the training data, then a UL of 5 is assigned. Some properties are bounded, for example A and B may not be lower than zero, and if a QSPR prediction exceeds the defined boundary then the prediction is set to the boundary value and a UL of 6 is assigned. A summary of the UL and their meanings is shown in Table 1.
Prediction errors for each UL are estimated by calculating the standard error of prediction for chemicals with each UL in the external validation dataset. This estimate relies on the assumption that the external validation dataset can represent the structural diversity of chemicals to which the QSPR may be applied, which may not be the case. The prediction errors have been observed to almost always be smallest for UL 0 and get progressively larger up to UL 3. If any of these UL is missing from the external validation dataset then a value is interpolated or extrapolated from other UL values. Prediction errors are similarly estimated for UL 4 and 5, with missing values filled in with the total dataset prediction error, or the UL 3 prediction error, respectively. Chemicals assigned a UL 6 because they exceeded a defined bounded value retain their originally assigned prediction error.
2.2.6 Additional External Model Validation
Statistics for robustness and GoF for the training and external validation datasets of all QSPRs have been calculated. Predicted system parameters and predicted solute descriptors were also combined with each other or with experimental solute descriptors and system parameters in PPLFER equations to predict solvent-air partitioning of solutes as partition ratios (log10 KSAk) and compared with the experimental log10 Kijk, VPk and WSk data. Where required the predicted log10 KSAk values were converted to solvent–water partition ratios (log10 KSWk) by thermodynamic cycle using the PLFER for water–air partitioning (Henry’s Law constant) calibrated in [15]. Statistics for the prediction of these additional external data have also been calculated. The three primary GoF statistics presented are the correlation between predicted and expected values (r2), the root mean squared error (RMSE), and the model bias (MB).
For log10 Kijk predictions aggregate UL are calculated which account for the UL of the solute descriptors and system parameters. UL 0 to UL 3 typically correlate with RMSE of chemicals in external validation datasets, so the integer values are averaged as the quadratic mean, roughly corresponding to propagation of uncertainty rules. This approach is invalid for UL 4 to UL 6, so these values are translated to an equivalent in the UL 0 to UL 3 range. UL 4 may be assigned to a UL 1 or UL 2 depending on whether this result is considered in or out of the AD for the solute descriptor or system parameter QSPR in question, as described in Sect. 3. UL 5 and UL 6 are assigned to UL 3, indicating results well out of the AD. When applying the empirical correlations from [15] the AD is defined by the leverage, similar to what is done for QSPRs as described in Sect. 2.2.5 where different thresholds translate the leverage into different UL. In cases where a prediction draws from multiple sources, e.g. solute descriptor QSPRs and system parameter QSPRs for predicting log10 Kijk, the aggregate UL is calculated as the quadratic mean and then rounded up to the nearest integer. An aggregate UL of 0 or 1 is in the AD, and aggregate UL of 2 or 3 is out of the AD.
Prediction uncertainties are estimated for QSPRs developed using the IFS algorithm, as described in Sect. 2.2.5, which will be propagated to log10 Kijk predictions. These are summed by applying propagation of uncertainty rules with the simplifying assumption that there is no covariance. In cases where the empirical correlations are used the standard error of the regression coefficients are used in the calculations. For experimentally determined system parameters the standard errors of the regression coefficients from the recalibrated PPLFER equations are used [15]. For experimentally determined solute descriptors the standard errors are estimated. The V descriptor is assumed to have a standard error of zero because it is calculated directly from the solute structure. In the original derivation of S Abraham et al. used several equations to calculate S and then took the average, reporting that the average error between the equations was 0.03 [63]. Stenzel et al. experimentally determined L values for large diverse dataset and estimated that the measurements had standard deviations equal to 0.15 and 0.17 [28]. Based on this limited data the E, S, A, and B solute descriptors standard error is conservatively estimated to be 0.05, and L 0.2.
3 Results and Discussion
3.1 New System Parameters and Re-evaluation of Empirical Correlations
The empirical correlations previously developed in [15] were applied to the two new solvents 1-hexadecene and 1,9-decadiene to predict their system parameters from their experimental solute descriptors. System parameters s and a were over-predicted by 0.7 to 1.6, which translates into significant prediction errors for the log10 K data in the additional model validation, where these two systems were significant outliers. The reason for this was determined to be that E, S and B for these solvents are much lower than for most other solvents in the dataset of experimental system parameters. As discussed in [15] the empirical correlations relate relative solute descriptors, e.g. Eri = Ei/Vi, etc. to the system parameters. Eri and Sri for 1-hexadecene and 1,9-decadiene are both less than 0.15, the only other solvents in the training dataset where this is true are the alkyl solvents where E and S are both equal to zero, and perfluoroheptane where both are negative. A rule was defined based on the alkyl solvents in [15] that for any solvent where Eri, Sri, Ari and Bri are all zero then s is set to a value of zero, overriding the prediction of the empirical correlation [15]. The data for perfluoroheptane were revisited, and it is hypothesized that s for this solvent should also be zero, although it does not meet the criteria because its Eri and Sri are negative rather than zero, and its Bri is greater than zero.
Perfluorinated alkyl chemicals such as perfluoroheptane are even less polar and polarizable than alkyl chemicals so the system parameter related to the effects of polarity and dipolarity should logically be equal to or less than that of alkyl chemicals. There is no evidence that s should be negative for solvent-air partitioning systems, the interactions of perfluorinated alkyl chemicals are weak but not repulsive, as discussed by Goss and Bronner [64]. Based on this the rule for when s should be set to a value of zero has been redefined to be when Eri and Sri are both equal to or less than zero. This has no effect on any of the solvents with experimentally determined system parameters other than perfluoroheptane. This rule also applies to the recalibration of the PPLFER equations that was done in [15], meaning that s should be left out of the regression equation for perfluoroheptane. Indeed, s in the PPLFER equation recalibrated in [15] is not significantly different than zero, with a value of 0.27 and a standard error of 0.15. Recalibrating the PPLFER for the log10 KSA of perfluoroheptane-air partitioning with s set to zero yields Eq. 18, which should be used in place of the equation presented in [15].
These new system parameters are used in developing the new QSPRs, and the redefined rule is applied to all empirically predicted system parameters. This change has no effect on the empirical correlations from [15] because perfluoroheptane was placed in the external validation dataset rather than the training dataset. Highly fluorinated chemicals are still considered to be out of the AD of the empirical correlations because these changes only slightly improve the prediction of log10 KSA data for perfluoroheptane.
Returning to the erroneously high s and a predicted for 1-hexadecene and 1,9-decadiene, it was initially hypothesized that because the Eri, Sri and Bri are small and dissimilar to other solvents they may be out of the AD of the empirical correlations developed in [15]. As a test, the empirical correlations of [15] were recalibrated including 1-hexadacene which was assigned to the training dataset in herein, however this did not significantly improve the predictions of s and a, or the prediction of the log10 Kijk data. It is instead hypothesized that because the Eri, Sri and Bri values are small that these properties of 1-hexadecene and 1,9-decadiene as solutes do not make significant contributions to their properties as solvents. Therefore, new rules have been defined to set s and a for chemicals with solute descriptors similar to 1-hexadecene and 1,9-decadiene to small but non-zero values, overriding the predictions of the empirical correlations. More complicated models were explored to relate relative solute descriptors to system parameters when the relative solute descriptors are small, but there are insufficient data to support these and they are not presented here. When Eri and Sri of a solvent are both less than or equal to 0.15 then s is set to a value of 0.26, the experimental value for 1-hexadecene which is the only solvent in the training dataset that meets these criteria. When the Bri is less than or equal to 0.1 then a is set to a value of 0.54, the mean of the experimental values of the two solvents in the training dataset which meet this criterion, 1-hexadecene and chlorobenzene. These rules are applied to empirically predicted system parameters including those in the training and validation datasets of the QSPRs, except that the experimentally determined s and a of 1-hexadecene, 1,9-decadiene, and chlorobenzene are used in the training dataset, as described in Sect. 2.1.3. The rules are superseded by the rules for setting the values of s and a to a value of zero. Applying these rules, the predictions for log10 Kijk values in the additional model validation data were significantly improved, not only for 1,9-decadiene, but also for some solvents with values derived from VPk and WSk data.
3.2 Solute Descriptor and System Parameter Predictions
3.2.1 Solute Descriptor QSPRs
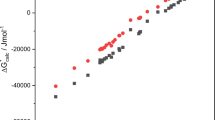
Training and external validation statistics for QSPRs for the five solute descriptors are shown in Table 2. Statistics for all solutes are shown, as well as for solutes that are in or out of the AD, and for the solutes within each UL. No solutes in the external validation dataset were assigned a UL of 5 by any of the QSPRs so the rows were omitted from Table 2. Solutes were identified as within the AD if their UL was 0 or 1. For E, S, A and B QSPRs solutes with UL 4 (no model fragments present in structure) were also considered to be within the AD, because these models were specifically constructed to give predictions of 0 for solutes without the correct functional groups. On average 85% of the solutes in the external validation datasets were within the AD, indicating that the QSPRs have wide applicability. The AD also does well at discriminating between solutes with high and low prediction errors, with solutes identified as out of the AD having lower r2, and RMSE values on average about 3 times higher than solutes identified as within the AD. E, A, and B have low total RMSE values in the range of 0.10 to 0.14 log10 units, with S and L having larger RMSE at 0.28 and 0.38. However, L has a much larger range than the others, so the prediction error is small in relative terms. The RMSE for all datapoints in the external validation dataset for the five QSPRS is 1–5% of the range of values in the external validation dataset. In these relative terms A has the highest prediction uncertainty followed by S, and L has the lowest prediction uncertainty. Figure 1 shows plots of predicted vs. expected values for solutes in the external validation dataset for solute descriptor QSPRs and includes the AD information of each data point. The slopes of linear fit between predicted and expected values are close to 1, and the model biases (MB) are all close to 0, indicating the QSPRs have no strong tendency to over- or under-predict relative to the expected values.
As shown in Table 2 there are about 300 fragments included in E, S, B, and L QSPRs, but this is only about 10% of the number of solutes in the training dataset, which is considered a reasonable ratio and similar to the ratio in previously developed QSPRs for chemical properties [36, 55]. The A QSPR has half as many fragments included as the others, however, A has far more solutes with a value of zero than the other solute descriptors. In the training dataset 1409 out of 3316 solutes have a non-zero A, which gives a similar ratio of fragments to training data of about 10%. All fragments as SMARTS and their regression coefficients have been included in the Supplemental Information and have been incorporated in a python package available as a GitHub repository (https://github.com/tnbrowncontam/ifsqsar).
As shown in Table 2E and A QSPRs have RMSE for solutes with UL 4 that are even lower than for solutes with UL 0, indicating that these QSPRs do very well at identifying solutes without the correct functional groups to give non-zero values. The QSPR for B does almost as well at identifying solutes that should have a value of zero with an RMSE for solutes with UL 4 comparable to the RMSE of solutes with UL 0. However, the QSPR for S only does adequately well at identifying solutes that should have a value of zero with an RMSE for solutes with UL 4 comparable to the RMSE of solutes with UL 1. All the solutes which should have a value of 0 for S were correctly predicted by the QSPR for S, the errors arise from QSPR predictions of 0 for solutes which should have non-zero values. Almost all these solutes were either highly fluorinated alkanes or alkyl siloxanes which had mostly negative values for S. The errors appear to be specifically related to the unusual properties of these solutes; solutes containing a small number of fluorine atoms or silicon atoms not bonded to oxygen were predicted with comparable accuracy to solutes containing no fluorine and silicon atoms. There was no generic fragment for fluorine atoms included in the QSPR for S indicating that the contribution to the S value has an average value of zero or is too variable to have predictive power and was therefore not included in the QSPR. There are several fragments which capture the effects of multiple fluorine atoms connected to aliphatic carbons included in S QSPR. These more specific fragments mean that S QSPR has a narrower AD with regards to highly fluorinated solutes relative to what could be expected if a generic fluorine atom fragment could be included.
A small number of solutes were assigned UL 6 for A or B QSPRs, meaning that their predicted values were negative, which violates the boundary condition that these solute descriptors must be greater than or equal to zero. The expected values for these solutes were low, with a range of 0.08 to 0.44 (median 0.25) for A and a range of 0.01 to 0.4 (median 0.07) for B. For the A QSPR these solutes all have a single hydrogen bond donor and contain other fragments that reduce the A value due to apparent steric effects or intramolecular hydrogen bonding. Many of the other fragments were present in solutes with multiple hydrogen bond donors in the training dataset, and possibly have regression coefficients that are too negative because of this. For the B QSPR four out of the nine solutes have only fragments with negative regression coefficients, meaning these fragments were added to reduce the B value of other functional groups, but the other functional groups are absent from these four solutes. The other solutes all contain fragments which reduce the B value of solutes with fluorine atoms attached to alkyl carbons. In summary, all the solutes with UL 6 are cases where fragments of the QSPRs interact with each other in unexpected ways, but the number of solutes where this occurs is very small in comparison to both the number of solutes in the external validation dataset and the number of fragments in the models.
Each solute descriptor QSPR has assigned a UL of 3 to about 1–2% of the solutes in the external validation dataset, meaning their predictions are an egregious extrapolation from the training dataset. These solutes are frequently outliers, as can be seen in Fig. 1. They are typically large; the median McGowan volume (V) of the full dataset of reliable solute descriptors is 1.3, the median V of solutes with a UL 3 in at least one solute descriptor QSPR is 2.1 and the median V of solutes with a UL 3 in two or more solute descriptor QSPRs is 2.5. Making predictions for large, complex chemicals is frequently challenging for QSPRs because they are usually out of the AD. As discussed in a previous paper about creating a QSPR for L this could only really be solved by adding even larger complex chemicals into the training data to pull the outliers within the AD [36]. However, measuring new solute descriptors for large solutes is experimentally challenging and many more would be needed to expand the AD, so QSPR predictions for large complex solutes will likely remain uncertain.
As discussed in the Introduction, preliminary unpublished QSPRs for the solute descriptors created by the author have been available for use on the UFZ LSER database since 2017 [31]. The QSPRs created in this work have been compared with the preliminary QSPRs and the statistics are shown in Table 3. The external validation dataset of 1137 solutes used for this comparison are solutes in the dataset of reliable solute descriptors described in Sect. 2.1.1 which are not in the training dataset of either of the sets of QSPRs. The S and A QSPRs have comparable r2 and RMSE for the dataset, and the E, B, and L QSPRs have notably lower RMSE values. The new QSPRs have a training dataset of 3300 solutes vs. 2400 solutes for the preliminary QSPRs so their AD will also be wider, and various improvements to the IFS algorithm have been made since 2017 so the new QSPRs should be preferred.
3.2.2 System Parameter QSPRs
QSPRs were developed for system parameters using the dataset of experimental values described in Sect. 2.1.2. However, the external validation statistics for these QSPRs were poor because there were insufficient data to calibrate reliable QSPRs, therefore the results are not shown. QSPRs were also developed using the dataset of experimental values supplemented with empirically predicted system parameters described in Sect. 2.1.3. The training and external validation statistics for the QSPRs developed using the standard method are shown in Table 4. As in Table 2 for solute descriptors, statistics are shown for all system parameters as well as system parameters in various subsets of the external validation dataset depending on the AD. As described in Sect. 2.2.1 QSPRs were developed for system parameters using three different strategies. First was the standard method which was also applied to developing QSPRs for solute descriptors and is shown in Eq. 14, and the second and third methods applied different methods for normalizing the fragment counts or the system parameters to the McGowan volume (Vk) and are shown in Eqs. 16 and 17. The standard method had the best external validation statistics, especially for the log10 Kijk data used as an additional external validation dataset. The results for the standard method are discussed in Sect. 3.3; the RMSE for log10 Kijk predictions using experimental solute descriptors and system parameters predicted by QSPR is 0.46. In comparison the RMSE for the second method shown in Eq. 16 was 0.72, and the RMSE for the second method shown in Eq. 17 was 0.65. Because of the poor predictive power, the QSPRs developed by the alternative methods are not recommended for use and are not presented here.
No solvents in the external validation dataset have UL 5, so these rows are excluded from the table. Any solvents with UL 4 for s, a, and b are considered within the AD because these QSPRs were specifically constructed to yield a value of zero for solvents without relevant functional groups to give non-zero values, as was done for E, S, A, and B. Any solvents with UL 4 for v, l or c are considered out of the AD of the QSPRs. About 85% of the external validation data are within the AD for all six QSPRs, although the external validation statistics for b are poor overall. Only 3 out of 353 solvents in the external validation dataset for b have UL 0 or UL 1, with most solvents having UL 4. The QSPR for b also has far fewer fragments than the other QSPRs; it is likely that there are too few data with non-zero b values in the training dataset (142 out of 706) to calibrate a robust QSPR. For the other five system parameters the AD does reasonably well at discriminating between good and poor predictions, with the RMSE for solvents out of the AD 1.2 to 2 times higher than the RMSE of solvents in the AD.
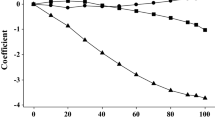
The system parameter QSPRs have less predictive power in relative terms than the solute descriptor QSPRs, with RMSE 6–13% of the range of values in the external validation datasets, compared to 1–5% of the range for the solute descriptor QSPRs. System parameter s is the most uncertain followed by a, with v, l and c all having RMSE about 6% of the range. Figure 2 shows predicted vs. expected values for external validation dataset of the system parameter QSPRs with the AD information denoted by the marker size and colour. The slopes of the plots for v, l, and c are all less than 1 and comparable to the r2, which means that the QSPR does not explain some of the variance in the properties; this is frequently because of uncertainty and errors in the expected values. This is not unexpected, because the empirical correlations for v and l are the most uncertain as discussed in [15], and the experimental calibration of c has more relative variability than the other system parameters because it includes any unexplained variability in the underlying log10 Kijk data. The slopes of the external validation plots for s and a are greater than their r2 values and close to 1. This suggests that although these QSPRs have greater relative variability they are trained on reliable data and do well at capturing the overall trends. The slope of the external validation plot for b is less than 1 because it is heavily influenced by the large number of predicted zero values.
There are far fewer solvents with UL 3 from one or more of the system parameter QSPRs, but the fraction is about 1% of the external validation dataset which is comparable to the fraction for the solute descriptor QSPRs. It is difficult to draw conclusions from so few data, but most of the structures appear to contain functional groups that are underrepresented in the training data. Only one solvent has UL 6 and is also underrepresented in the training data. The prediction of zero values by the QSPR for s is quite accurate, all the solvents in the external validation dataset with UL 4 are correctly predicted. Solvents with UL 4 for a and b have low RMSE and accurately predict zero values for all solvents which should have a value of zero. Some additional solvents have values of zero predicted when the expected values are greater than zero, which again appear to contain functional groups which are underrepresented in the training dataset.
For s, a, l, and c the number of fragments in the QSPRs are 9–14% of the number of solvents in the training dataset, comparable to the QSPRs for solute descriptors. The number of fragments in the QSPR for b is smaller but is 13% of the number of solvents with non-zero values in the training dataset, again comparable to what was observed for A. The number of fragments in the model for v seems anomalously low at only 5% of the number of solvents in the training dataset. System parameter v may be more easily predicted than the other system parameters because the effects on partitioning captured by v are very simple and are related only to molecular size, which is easily explained by a group contribution method such as IFS. The number of identical fragments contained in each system parameter QSPR and the closest corresponding solute descriptor QSPR is 20–37% of the number of fragments in the system descriptor QSPRs.
3.2.3 System Parameters from Empirical Correlations and Solute Descriptor QSPRs
Another method for predicting system parameters is to first make predictions with QSPRs for solute descriptors, and then use these values in the empirical correlations from [15] which relate the solute descriptors of a chemical to its system parameters for log10 KSA. This was done for all solvents in the external validation dataset for the system parameter QSPRs. The rules to determine when s, a, or b should be set to a value of zero overriding the predictions from the empirical correlations, as well as the additional rules outlined in Sect. 3.1, are also applied using the solute descriptors QSPR predictions. For solvents meeting any of these rules, UL 4 was assigned for the system parameter. In all other cases the AD of the empirical correlations is combined with the AD of the solute descriptor QSPR predictions to estimate an aggregate UL and determine if each prediction is in the overall AD. The estimation of aggregate UL and prediction uncertainties for this application and for log10 K predictions is discussed in detail in Sect. 2.2.6. The external validation statistics are shown in Table 5. None of the solvents in the external validation dataset are assigned UL 3 so these rows are omitted.
The external validation statistics for the predictions made with solute descriptor QSPRs and empirical correlations are about the same or better than those for the system parameter QSPRs described in Sect. 3.2.2. Values for r2 and RMSE for all solvents in the external validation dataset are almost identical for v and l. For b and c the r2 is a little better for the combined QSPR and empirical predictions and the RMSE is about the same. For s and a both r2 and RMSE are better. The separation of predictions into those that are in the AD and reliable vs. those that are out of the AD and less reliable is about the same as for the system parameter QSPRs.
3.3 Additional External Validation
The primary utility of PPLFERs is to predict partitioning properties, with applications in several fields of chemistry. The dataset of partition ratios for solvent-air systems (log10 KSAk) and solvent–water systems (log10 KSWk) compiled in this and previous work [15] is used as an additional external validation dataset to test the overall predictive power of the methods in the current work when used in combination. There are two sources of solute descriptors: experimental values and QSPR predictions; and four sources of system parameters: experimental, experimental solute descriptors + empirical correlations, system parameter QSPRs, and solute descriptor QSPRs + empirical correlations. External validation statistics vs. the dataset of log10 Kijk values are shown for all eight combinations of these solute descriptor and system parameter sources are shown in Table 6. A common dataset of 1453 log10 Kijk values was selected so that both the solute and the solvent of every datapoint were both in the external validation datasets of the solute descriptor and system parameter QSPRs. Experimental system parameters are not available for the log10 Kijk values which were calculated from VPk and WSk data as described in Sect. 2.1.4, so a smaller dataset of 1128 log10Kijk values which exclude these data was used in these cases. The predictions are divided into those which are in or out of the AD, which is based on the AD of both the solute and solvent, as described in Sect. 2.2.6. Experimental values and empirical predictions of system parameters using experimental solute descriptors are all considered to be in the AD. Example plots for the two cases where log10 Kijk predictions are based entirely on QSPRs are shown in Figs. 3 and 4. Plots for the other six combinations of solute descriptor and system parameter sources are included in the Supplemental Information as Figs. S1 to S6. External validation data in the figures is divided into log10 KSAk and log10 KSWk to show the differences in predictive power. As was observed in [15] predictive power for log10 KSWk is slightly lower, likely due to the extra steps required to make a prediction, i.e. thermodynamic cycle with log10 Kwak, and possibly more variability in the experimental data. However, the differences are minor considering the large range of expected values so only aggregate external validation statistics are shown in Table 6 and discussed.
As discussed in Sect. 2.1.4 and in [15] the additional external validation dataset of log10 Kijk values would ideally include diverse solutes partitioning to diverse solvent systems. However, the available data are limited to diverse solutes partitioning to a small number of solvent systems, and diverse solvent systems with only one solute each, i.e. the VPk and WSk data. An estimated standard error of prediction (ESE) was calculated to extrapolate to the real potential prediction uncertainty, which is included in Table 6. This value is estimated by calculating the variance of the log10 KSAk and log10 KSWk data for diverse solutes, calculating the variance of the log10 Kijk data sourced from VPk and WSk, and then summing these two variances. The prediction uncertainties for the two different types of log10 Kijk data are comparable, and the ESE is within 0.1 of double the overall variance in all cases, suggesting that the prediction uncertainties associated with diverse solutes are comparable to those associated with diverse solvents. This is further supported by the data in Table 6, the RMSE are almost identical for the case when solute descriptors are experimental and system parameters are predicted with QSPRs (0.46), and the opposite case when solute descriptors are predicted with QSPRs and system parameters are experimental (0.45). The second case neglects the VPk and WSk sourced data, but the case where solute descriptors are predicted with QSPRs and the system parameters were empirically predicted from experimental solute descriptors also has a very similar RMSE (0.51). The variances also appear to be nearly additive, estimating an RMSE as (0.462 + 0.452)0.5 = 0.64 gives a value nearly identical to the RMSE of the case when both solute descriptors and system parameters are predicted with QSPRs (0.62). The same is true when solute descriptors are predicted with QSPRs and system parameters are predicted with solute descriptor QSPRs and empirical correlations, where the estimated and actual RMSE values are 0.58 and 0.55. This near additivity gives some confidence to assigning AD and estimating prediction errors using simple additive propagation of uncertainty.
All the plots with solute descriptors predicted with QSPRs have a small group of obvious outliers below the 1:1 line at a log10 KSAk value between 3 and 4, see Figs. 3 and 4, S5 and S6. This group of outliers are all log10 KSAk values of nitromethane partitioning in various polar solvent systems. Nitromethane is a small molecule, which are poorly handled by group contribution methods in general, so this is not a surprising result. The error can be attributed primarily to the S value, which has an expected value of 0.95 but was predicted to be 0.19. Other nitro-containing solutes in the additional external validation dataset, including nitroethane and nitropropane have predicted S and log10 KSAk values that are close to expected values. The S QSPR assigns nitromethane UL 2, and the aggregate UL for all solute descriptors is also UL 2, so nitromethane is out of the AD.
Cases where system parameters are predicted with the combination of solute descriptor QSPRs and empirical correlations have consistently higher r2 and lower RMSE than cases where system parameters are predicted directly with system parameter QSPRs. Both of these strategies for predicting system parameters apply a combination of QSPRs and empirical correlations, with the major difference being whether the empirical correlations are applied before the QSPRs, i.e. in generating the training dataset, or after the QSPRs. The RMSE for solvents that are within the AD is the same for both strategies, the overall better predictive power is because many more solvents are in the AD when applying the combination of solute descriptor QSPRs and empirical correlations. Better predictive power when using the solute descriptor QSPRs combined with the empirical correlations is likely due to the solute descriptor QSPRs have more training data, which leads to QSPRs with a broader AD. Some caution must be exercised in interpreting these observations, because the additional external validation data is all within the AD of the empirical correlations. This is by design, as described in Sects. 2.1.3 and 2.1.4, so that the empirically predicted system parameters are reliable.
The QSPRs should have better predictive power for solvents that are explicitly out of the AD of the empirical correlations, highly fluorinated alkyl chemicals and siloxanes, but little data are available to examine this possibility. Data for the solvent perfluoroheptane is better explained by the system parameter QSPRs than the combination of solute descriptor QSPRs and empirical correlations, RMSE 0.70 vs. 1.10, but this solvent is in the training dataset so it does not constitute an external validation. The training dataset for system parameter QSPRs also contains other solvents with small numbers of fluorine and silicon, so it is possible that general trends of the system parameters with the number of these atoms can be predicted. Cases where the system parameter QSPRs may make more reliable predictions should be apparent by inspecting the AD of the two methods for predicting system parameters, perfluorinated solvents may be within the AD of the system parameter QSPRs but will always be out of the AD of the empirical correlations. There are only 34 datapoints in the additional external validation dataset where the UL of the system parameter QSPRs is lower than the UL of the solute descriptor QSPRs combined with the empirical correlations. The RMSE vs. expected values is slightly lower when applying system parameter QSPRs for these data, 0.43 vs. 0.49.
4 Conclusions
The QSPRs developed in this work have immediate utility in environmental and pharmacological chemistry. The new solute descriptor QSPRs have comparable or better external validation statistics as the preliminary QSPRs already in use [31]. Additional utility added by this work is the possibility to predict solvent-air partitioning as log10 KSAk for arbitrary pairs of solutes and solvents, including cases where the solute and solvent are the same, i.e. vapor pressure. These new models greatly expand the applicability of the property estimation methods pioneered and developed by Abraham.
The domain of the developed methods is explicitly liquid solvents at room temperature, so some care must be taken to ensure that the methods presented in this work are only applied to liquids. Future work will explore the possibility of applying the methods in this work to solid phases in some limited circumstances. Some domain checks are built into the developed methods; the empirical correlations were calibrated on a dataset of diverse liquid solvents [15], and the system parameter QSPRs are similarly calibrated on the same liquid solvents, and additional solvents which were identified as being liquids. If predictions from either of these methods are identified as within the AD, then the solvent is also likely a liquid due to its similarity to other known liquids. Predictions for solvents which are identified as out of the AD should be treated with more caution, confirming their phase with experimental data if possible, or at minimum predicting their MP and BP using the PPLFERs calibrated in this work.
If a solvent can be reasonably assumed to be a liquid, then the workflow shown Fig. 5 can be followed to select the appropriate combination of solute descriptor and system parameter predictions. The number of solvents with calibrated system parameters but no solute descriptors is small, so this possibility is neglected. The first step should be to search the UFZ LSER database [31] for experimental solute descriptors, and the previous work [15] and the UFZ database for system parameters. If these can be found, then experimental data should always be preferred. Lacking experimental data, both QSPR-based predictions should be applied to predict system parameters for the solvent. If the combination of solute descriptor QSPRs and empirical correlations has an assigned UL equal to or less than that assigned to the system parameter QSPR predictions, then the combination prediction should be used. In the remaining cases the system parameter QSPRs should be applied. Following this, thermodynamic cycles can be applied to predict log10 KSWk, for example, or partitioning in other solvent–solvent systems. It should be noted that the solvent phases will be “dry” in these applications, i.e. mutual solubility of solvents is assumed to be zero. Predicting partitioning to mixed solvent phases, including “wet” solvents will be the subject of future work.
References
Mackay, D.: Multimedia Environmental Models: The Fugacity Approach -, 2nd edn. Lewis Publishers, Boca Raton (2001)
Zhang, X., Brown, T.N., Wania, F., Heimstad, E.S., Goss, K.U.: Assessment of chemical screening outcomes based on different partitioning property estimation methods. Environ. Int. 36, 514–520 (2010)
Baskaran, S., Duan Lei, Y., Wania, F.: Reliable prediction of the octanol-air partition ratio. Environ. Toxicol. Chem. 40, 3166–3180 (2021)
Endo, S., Brown, T.N., Goss, K.U.: General model for estimating partition coefficients to organisms and their tissues using the biological compositions and polyparameter linear free energy relationships. Environ. Sci. Technol. 47, 6630–6639 (2013)
Endo, S., Goss, K.-U.: Applications of polyparameter linear free energy relationships in environmental chemistry. Environ. Sci. Technol. 48, 12477–12491 (2014)
Abraham, M.H., Smith, R.E., Luchtefeld, R., Boorem, A.J., Luo, R., Acree, W.E., Jr.: Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 99, 1500–1515 (2010)
Abraham, M.H.: Scales of solute hydrogen-bonding: their construction and application to physicochemical and biochemical processes. Chem. Soc. Rev. 22, 73 (1993)
Seth, R., Mackay, D., Muncke, J.: Estimating the organic carbon partition coefficient and its variability for hydrophobic chemicals. Environ. Sci. Technol. 33, 2390–2394 (1999)
Regulation (EC) No 1907/2006: Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH). L 136, pp. 3–280. European Commission, Official Journal of the European Union (2007)
Stockholm Convention on Persistent Organic Pollutants (POPs). In: Programme UNE (ed.) (2001)
Mackay, D., Paterson, G., Kicsi, G., Di Guardo, A., Cowan, C.E.: Assessing the fate of new and existing chemicals: a five stage process. Environ. Toxicol. Chem. 15, 1618–1626 (1996)
Arnot, J.A., Mackay, D.: Policies for chemical hazard and risk priority setting: can persistence, bioaccumulation, toxicity, and quantity information be combined? Environ. Sci. Technol. 42, 4648–4654 (2008)
Arnot, J.A., Brown, T.N., Wania, F., Breivik, K., McLachlan, M.S.: Prioritizing chemicals and data requirements for screening-level exposure and risk assessment. Environ. Health Perspect. 120, 1565–1570 (2012)
Goss, K.-U., Schwarzenbach, R.P.: Linear free energy relationships used to evaluate equilibrium partitioning of organic compounds. Environ. Sci. Technol. 35, 1–9 (2001)
Brown, T.N.: Empirical regressions between system parameters and solute descriptors of polyparameter linear free energy relationships (PPLFERs) for predicting solvent-air partitioning. Fluid Phase Equilib. 540, 113035 (2021)
Abraham, M.H., Andonian-Haftvan, J., Whiting, G.S., Leo, A., Taft, R.S.: Hydrogen bonding. Part 34. The factors that influence the solubility of gases and vapours in water at 298 K, and a new method for its determination. J. Chem. Soc. Perkins Trans. 2, 1777–1791 (1994)
Strickland, S., Ocon, L., Zhang, A., Wang, S., Eddula, S., Liu, G., Tirumala, P., Huang, J., Dai, J., Jiang, C., Acree, W.E., Abraham, M.H.: Abraham model correlations for describing dissolution of organic solutes and inorganic gases in dimethyl carbonate. Phys. Chem. Liq. 59, 181–195 (2019)
Qian, E., Gupta, A., Neal, R., Lee, G., Che, M., Wang, L., Yue, D., Wang, S., Liu, K., Zhang, A., Acree, W.E., Abraham, M.H.: Abraham model correlations for describing solute transfer into 4-methyl-2-pentanol from both water and the gas phase. J. Mol. Liq. 278, 335–341 (2019)
Goss, K.-U.: Predicting the equilibrium partitioning of organic compounds using just one linear solvation energy relationship (LSER). Fluid Phase Equilib. 233, 19–22 (2005)
Mcgowan, J.C.: The estimation of solubility parameters and related properties of liquids. J. Chem. Technol. Biotechnol. A 34, 38–42 (1984)
Goss, K.-U.: Free energy of transfer of a solute and its relation to the partition constant. J. Phys. Chem. B 107, 14025–14029 (2003)
van Noort, P.C.: Solvation thermodynamics and the physical-chemical meaning of the constant in Abraham solvation equations. Chemosphere 87, 125–131 (2012)
Abraham, M.H., Acree, W.E.: Comparison of solubility of gases and vapours in wet and dry alcohols, especially octan-1-ol. J. Phys. Org. Chem. 21, 823–832 (2008)
Stephens, T.W., Quay, A.N., Chou, V., Loera, M., Shen, C., Wilson, A., Acree, W.E., Jr.: Correlation of solute transfer into alkane solvents from water and from the gas phase with updated Abraham model equations. Glob. J. Phys. Chem. 3, 1–42 (2012)
Sprunger, L.M., Achi, S.S., Acree, W.E., Abraham, M.H., Leo, A.J., Hoekman, D.: Correlation and prediction of solute transfer to chloroalkanes from both water and the gas phase. Fluid Phase Equilib. 281, 144–162 (2009)
Abraham, M.H., Nasezadeh, A., Acree, W.E., Jr.: Correlation and prediction of partition coefficients from the gas phase and from water to alkan-1-ols. Ind. Eng. Chem. Res. 47, 3990–3995 (2008)
Abraham, M.H., Acree, W.E.: Descriptors for the prediction of partition coefficients and solubilities of organophosphorus compounds. Sep. Sci. Technol. 48, 884–897 (2013)
Stenzel, A., Endo, S., Goss, K.U.: Measurements and predictions of hexadecane/air partition coefficients for 387 environmentally relevant compounds. J. Chromatogr. A 1220, 132–142 (2012)
ABSOLV, part of ACD Percepta. Advanced Chemistry Development Inc.
Platts, J.A., Butina, D., Abraham, M.H., Hersey, A.: Estimation of molecular linear free energy relation descriptors using a group contribution approach. J. Chem. Inf. Comp. Sci. 39, 835–845 (1999)
Ulrich, N., Endo, S., Brown, T.N., Watanabe, N., Bronner, G., Abraham, M.H., Goss, K.U.: UFZ-LSER database v 3.2 [Internet] (2017)
Bradley, J.C., Abraham, M.H., Acree, W.E., Jr., Lang, A.S.: Predicting Abraham model solvent coefficients. Chem. Cent. J. 9, 12 (2015)
Grubbs, L.M., Saifullah, M., De La Rosa, N.E., Ye, S., Achi, S.S., Acree, W.E., Abraham, M.H.: Mathematical correlations for describing solute transfer into functionalized alkane solvents containing hydroxyl, ether, ester or ketone solvents. Fluid Phase Equilib. 298, 48–53 (2010)
Sprunger, L.M., Achi, S.S., Acree, W.E., Abraham, M.H.: Development of correlations for describing solute transfer into acyclic alcohol solvents based on the Abraham model and fragment-specific equation coefficients. Fluid Phase Equilib. 288, 139–144 (2010)
Brown, T.N., Arnot, J.A., Wania, F.: Iterative fragment selection: a group contribution approach to predicting fish biotransformation half-lives. Environ. Sci. Technol. 46, 8253–8260 (2012)
Brown, T.N.: Predicting hexadecane-air equilibrium partition coefficients (L) using a group contribution approach constructed from high quality data. SAR QSAR Environ. Res. 25, 51–71 (2014)
EAS-E Suite: Developed by ARC Arnot Research and Consulting Inc. www.eas-e-suite.com
Abraham, M.H., Ibrahim, A., Acree, W.E.: Partition of compounds from gas to water and from gas to physiological saline at 310K: linear free energy relationships. Fluid Phase Equilib. 251, 93–109 (2007)
Abraham, M.H., Sánchez-Moreno, R., Gil-Lostes, J., Acree, W.E., Enrique Cometto-Muñiz, J., Cain, W.S.: The biological and toxicological activity of gases and vapors. Toxicol. In Vitro 24, 357–362 (2010)
Abraham, M.H., Acree, W.E., Jr.: Equations for water–triolein partition coefficients for neutral species; comparison with other water-solvent partitions, and environmental and toxicological processes. Chemosphere 154, 48–54 (2016)
Abraham, M.H., Acree, W.E.: Linear free-energy relationships for water/hexadec-1-ene and water/deca-1, 9-diene partitions, and for permeation through lipid bilayers; comparison of permeation systems. New J. Chem. 36, 1798–1806 (2012)
Abraham, M.H., Gola, J.M.R., Cometto-Muñiz, J.E., Cain, W.S.: Solvation properties of refrigerants, and the estimation of their water–solvent and gas–solvent partitions. Fluid Phase Equilib. 180, 41–58 (2001)
Abraham, M.H., Acree, W.E.: Gas–solvent and water–solvent partition coefficients of the tetraphenyl compounds of group (IV). New J. Chem. 36, 626–631 (2012)
Green, C.E., Abraham, M.H., Acree, W.E., Jr., De Fina, K.M., Sharp, T.L.: Solvation descriptors for pesticides from the solubility of solids: diuron as an example. Pest Manag. Sci. 56, 1043–1053 (2000)
Weininger, D.: SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comp. Sci. 28, 31–36 (1988)
Weininger, D., Weininger, A., Weininger, J.L.: SMILES. 2. Algorithm for generation of unique SMILES notation. J. Chem. Inf. Comp. Sci. 29, 97–101 (1989)
O’Boyle, N.M.: Towards a Universal SMILES representation - A standard method to generate canonical SMILES based on the InChI. J. Cheminformatics 4, 22 (2012)
O’Boyle, N.M., Banck, M., James, C.A., Morley, C., Vandermeersch, T., Hutchison, G.R.: Open babel: an open chemical toolbox. J. Cheminformatics 3, 33 (2011)
Mansouri, K., Grulke, C.M., Judson, R.S., Williams, A.J.: OPERA models for predicting physicochemical properties and environmental fate endpoints. J. Cheminformatics 10, 1–19 (2018)
NORMAN Suspect List Exchange. NORMAN Network. https://www.norman-network.com/?q=suspect-list-exchange. Accessed 2021
Kim, S., Chen, J., Cheng, T., Gindulyte, A., He, J., He, S., Li, Q., Shoemaker, B.A., Thiessen, P.A., Yu, B., Zaslavsky, L., Zhang, J., Bolton, E.E.: PubChem 2019 update: improved access to chemical data. Nucleic Acids Res. 47, D1102–D1109 (2019)
Bradley, J.-C., Lang, A., Williams, A.: Jean-Claude Bradley Double Plus Good (Highly Curated and Validated) Melting Point Dataset (2014)
Stovall, D.M., Dai, C., Zhang, S., Acree, W.E., Abraham, M.H.: Abraham model correlations for describing solute transfer into anhydrous 1,2-propylene glycol for neutral and ionic species. Phys. Chem. Liq. 54, 1–13 (2015)
Abraham, M.H., Acree, W.E.: Estimation of vapor pressures of liquid and solid organic and organometallic compounds at 298.15 K. Fluid Phase Equilib. 519, 112595 (2020)
Brown, T.N., Armitage, J.M., Arnot, J.A.: Application of an iterative fragment selection (IFS) method to estimate entropies of fusion and melting points of organic chemicals. Mol. Inform. 38, e1800160 (2019)
OECD: OECD principles for the validation, for regulatory purposes, of (quantitative) structure-activity relationship models. OECD (2004)
OECD: Guidance document on the validation of (Quantitative) Structure-Activity Relationships (QSAR) models. OECD (2007)
Abraham, M.H., Acree, W.E., Cometto-Muniz, J.E.: Partition of compounds from water and from air into amides. New J. Chem. 33, 2034–2043 (2009)
Arnot, J.A., Brown, T.N., Wania, F.: Estimating screening-level organic chemical half-lives in humans. Environ. Sci. Technol. 48, 723–730 (2014)
Burnham, K.P., Anderson, D.R.: Multimodel inference. Sociol. Method. Res. 33, 261–304 (2004)
Gramatica, P.: Principles of QSAR models validation: internal and external. QSAR Comb. Sci. 26, 694–701 (2007)
Gramatica, P., Cassani, S., Roy, P.P., Kovarich, S., Yap, C.W., Papa, E.: QSAR modeling is not “push a button and find a correlation”: a case study of toxicity of (benzo-)triazoles on algae. Mol. Inform. 31, 817–835 (2012)
Abraham, M.H., Whiting, G.S., Doherty, R.M., Shuely, W.J.: Hydrogen bonding XVI. A new solute solvation parameter, S, from gas chromatographic data. J. Chromatogr. A 587, 213–228 (1991)
Goss, K.-U., Bronner, G.: What is so special about the sorption behavior of highly fluorinated compounds? J. Phys. Chem. A 110, 9518–9522 (2006)
Acknowledgements
We thank the European Chemical Industry Council Long-range Research Initiative (CEFIC-LRI), for financial support as part of the CEFIC-LRI B22 project, “Tiered Methods for Quantifying Exposure to Complex Substances (TMEX-Complex)” as well as the European Centre for Ecotoxicology and Toxicity of Chemicals (ECETOC) for project support. Dr. Alessandro Sangion is acknowledged for integrating the IFSQSAR code into EAS-E Suite. Dr. Jon Arnot and Prof. Dr. Frank Wania are acknowledged for providing comments on a draft of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
10953_2022_1162_MOESM1_ESM.docx
Supplementary file1 (DOCX 587 kb). Supplemental Information is provided in the form of additional Figs. S1-S15 referred to in the text. In addition, an Excel file is provided which contains for all 11 QSPRS the fragment SMARTS, regression coefficients, minimum and maximum counts of each fragment in any chemical, and the number of chemicals containing at least one of each fragment. Working versions of the models from this work are included in the python package IFSQSAR, which can be obtained from the author’s GitHub page at https://github.com/tnbrowncontam/ifsqsar
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brown, T.N. QSPRs for Predicting Equilibrium Partitioning in Solvent–Air Systems from the Chemical Structures of Solutes and Solvents. J Solution Chem 51, 1101–1132 (2022). https://doi.org/10.1007/s10953-022-01162-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10953-022-01162-2