Improving Superconductivity, Microstructure, and Mechanical Properties by Substituting Different Ionic Pb Elements to Bi and Ca Elements in Bi-2223 Superconductors

Abstract

In this detailed study, the changes of microstructural, mechanical, and superconducting features of bulk Bi_1.8Pb_0.2Sr_2.0Ca_1.8Pb_0.2Cu₃O_y materials prepared at different milling time intervals (0.5 h ≤ x ≤ 8 h) were investigated in the most precise manner. The measurements of X-ray powder diffraction (XRD) and Vickers microhardness (H_v) were designed to scrutinize the bulk BSCCO samples. All the results of the measurements and calculations show that the characteristics responsible for the applications of the technology, industry, and engineering are significantly improved up to the 3 h milling time beyond that they tend to deteriorate. The enhancement of the characters is generally related to the transition from underdoped level of the (Bi, Pb)-2223 to the optimum level with the milling duration and this event approves that sufficient Pb nanoparticles penetrate the crystal structure. On the other hand, some of the reasons for the suppression in the superconducting properties are the presence of the porosity, disorder, defects, and the localization problem in the Cu-O₂ consecutively stacked layers. In addition to those mentioned above, the other reasons are degradation in the crystallinity, reduction in the average crystallite size, and decrease in mobile hole concentration in the Cu-O₂ layers. Similarly, the Pb inclusion rises the artificial random dislocations and grain boundary weak-links in the (Bi, Pb)-2223 superconducting system. Vickers microhardness measurements show that (Bi, Pb)-2223 bulk superconducting specimens exhibit typical indentation size behavior depending on the presence of both elastic and plastic deformations in the system. The results obtained from the hardness measurements have been analyzed by using Meyer law, PRS model, MPRS model, elastic–plastic deformation model, and Hays-Kendall approach. As a result, the Hays-Kendall approach was identified as the most successful model in describing the mechanical properties of the samples.

1 Introduction

Investigations of high-temperature superconductivity have continued since 1986 with the aim of finding new superconducting materials with a higher transition temperature T_c. A ceramic high-temperature superconductor is almost an insulator at room temperature, since the electrons are only in contact with the solid lattice. When the superconducting ceramic is cooled below the critical temperature, the electrons come together and move with a vibrating lattice, balancing each other. High-temperature superconductors have strong anisotropic properties, very low charge density, very short coherence length, and wide penetration depth [1].

The superconducting compounds exhibit very low flexibility and high brittleness. As a result, these materials have limited poor mechanical properties for practical applications. In industrial applications of high-temperature superconductors, mechanical properties such as stiffness, fracture toughness, and hardness are as crucial as superconductivity properties such as critical temperature, critical current density, and critical magnetic field. Therefore, in studies on superconducting compounds, the development of mechanical characteristics of superconducting materials has become an important research area. Despite the hardness of a material can be found by scraping or cutting with a hard object, non-destructive indentation methods are preferred and frequently used because it is easy to apply and non-destructive. The hardness is a relative quantity and the hardness of a material is determined using known reference material (hardened steel, tungsten carbide, diamond). Hardness is a mechanical parameter strongly related to the structure and composition of the solid [2, 3]. One of the most common methods for determining mechanical properties is the Vickers microhardness test.

Load-dependent and load-independent hardness values of the Pb-doped Bi-2223 system were calculated using conventional methods and quasi-experimental theories [4, 5]. It could be said that if the porosity on the surface decreases with the addition of samples, the load-independent hardness values increase.

The paper contains extensive and novel experimental work with rigorous analysis and sound interpretation.

2 Experimental Procedure

Bi₂O₃, PbO, SrCO₃, CaCO₃, PbO₂, and CuO (Alfa Aesar Co., Ltd. with the purity of 99.99%) were weighed on a precision scale at the appropriate stoichiometric ratios to prepare the samples of (BiPb)₂Sr₂(CaPb)₂Cu₃O_y composition by the solid-state reaction method. Then, they were mixed in the agate mortar for half an hour to attain much smaller particle sizes of the chemicals. Next, the mixed powders were calcined in alumina crucible in the air at temperatures of 800 °C for 24 h in Protherm (Model PTF 12/75/200) programmable tube furnace with the heating and cooling rates of 5 °C/min. The foreign substances, oxide, and carbon dioxide separate from the powder mixture with the help of temperature in the calcining process. Then, the resultant powders are milled during the 0.5 h, 1 h, 2 h, 3 h, 4 h, and 8 h due to obtain a homogeneous mixture and are palletized into a rectangular bar of 1.5 × 0.5 × 0.2 cm³ at a constant load of 300 MPa. After that, the bulks are exposed to the annealing process (5 °C/min for heating and cooling rate) at 845 °C in the same Protherm furnace for 48 h. Since it is necessary to sinter the tablets to get the superconducting phase, to strengthen the bonds between the constituent atoms of the mixture, to create a polycrystalline structure, and to reduce the crystal defects. The bulk Bi_1.8Pb_0.2Sr₂Ca_1.8Pb_0.2Cu₃O_y superconducting ceramics produced by subjecting to grinding times of 0.5 h, 1 h, 2 h, 3 h, 4 h, and 8 h before sintering will hereafter be represented as Bi1, Bi2, Bi3, Bi4, Bi5, and Bi6, respectively.

Existing experimental measurement techniques such as powder X-ray diffraction and Vickers microhardness (H_v) were used to investigate the superconductivity and mechanical properties of Pb-doped Bi-2223 superconductor samples.

X-ray diffraction analysis is a very important technique when analyzing crystal structures such as the volume fractions, crystallite size, and lattice cell parameters (a and c lengths within an accuracy of ± 0.01 Å) for the Pb added Bi-2223 superconducting compounds. As is known, although crystalline materials give a sharp X-ray diffraction pattern, the glasses (amorphous materials) provide a relatively broad peak without sharp lines. Therefore, XRD analysis is essential for studying the crystallization of amorphous materials. A Rigaku Multiflex + XRD 2 kW computer-controlled diffractometer with CuK_α target including the monochromatic beam (λ = 1.5405 Å) was used during the study. Measurements were taken up the 2θ range from 3 to 70° at a scan speed of 3°/min with a step increase of 0.02. These diffractograms were analyzed using known indexing methods.

Furthermore, the mechanical features are scrutinized using the digital microhardness tester (SHIMADZU, HVM-2) at room temperature. The diagonal length of the indentation formed by immersing the Vickers pyramidal tip on the ceramic specimen for 10 s at different loads (0.245, 0.490, 0.980, 1.960, and 2.940 N) was measured with an accuracy of ± 0.1 μm. The indentations were made in different parts of the sample surface, such that the indentation would be at least twice as long as the diagonal. Average hardness values were calculated for each load value by taking averages of 5 different measurements taken from different parts of the ceramic surface. Vickers microhardness (relative stiffness), elastic modulus, fracture toughness, and yield strength values were calculated using the indentation diagonal length and loads.

3 Results and Discussion

First of all, the superconductivity of the produced materials can be easily seen, as shown in Fig. 1 that exhibits the normalized resistivity values depending on the temperature.

Fig. 1

Variation of dc resistivity normalization against temperature curves in the range from 70 to 130 K for the (BiPb)₂Sr_2.0(CaPb)₂Cu₃O_10+δ superconducting samples

3.1 XRD Measurement Evidences

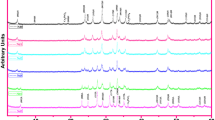
In this part of the study, the changes in the crystallinity, the crystal plane alignment (texturing), lattice constant, crystal structure, phase fracture, and grain size parameters of bulk Bi-2223 superconducting materials with Pb concentration level placed in the crystal lattice are investigated by using XRD measurements. In this regard, X-ray diffraction patterns are measured in the range of 2θ = 3–70° at room temperature. The characteristic peaks of the high phase and the low phase are determined by comparing the X-ray diffraction patterns given by Maeda et al. [6] and The International Centre for Diffraction Data (ICDD) as (hkl) H Miller indices and (hkl) L Miller indices as shown in Fig. 2, respectively. Although the peak of the high-temperature phase (Bi-2223) is dominant for all samples, the peak of the low-temperature phase (Bi-2212) is observed together with the peak of H(002) at 2θ = 4.7 and the peak of L(002) at 2θ = 5.7, which are characteristic peaks of the BSCCO system. Furthermore, the other well-known diffraction peaks of 008 and 0012 for the Bi-2223 (0012 for the Bi-2212) improve (worsen) steadily with the increment of the milling duration time up to 3 h beyond which the peaks degrade (upgrade) significantly as a consequence of the deterioration in crystal plane alignments and the crystallinity in the Bi-2223 structure. The volume fraction values of the low-temperature (2212) and high-temperature (2223) phases were calculated using the following correlations [7, 8].

Fig. 2

Experimental XRD patterns for the Bi1, Bi4, and Bi6 superconducting compounds

$${V}_{2223}=\frac{\sum {I}_{H}}{\sum {I}_{H}+\sum {I}_{L}}$$

(1)

and

$${V}_{2212}=\frac{\sum {I}_{L}}{\sum {I}_{L}+\sum {I}_{H}}$$

(2)

In the equations, I_H shows the intensities of the high-temperature phase peaks and I_L shows the intensity of the low-temperature phase peaks here, and the calculated results are given in Table 1. It can be seen from the table that the volume fraction ratio between the Bi-2223 phase and the Bi-2212 monotonically increases from 2.472 to 2.559 with increasing Pb concentration up to Δt = 3 h, after which the value begins to fall and falls to 2.311.

Table 1 Lattice cell parameters (a/c) and volume fractions of bulk Bi_1.8Pb_0.2Sr₂Ca_1.8Pb_0.2Cu₃O_y superconductors

The crystal sizes of the prepared samples were calculated using the Scherrer equation given below [9,10,11]:

$$t=\frac{0.941\lambda }{\beta {\text{cos}}{\theta }_{B}}$$

(3)

where t displays the average crystal size, λ corresponds to the wavelength of the X-ray source used, β is the full width at half maximum (FWHM) of the peaks in the X-ray patterns, and θ_B shows the peak angle (Bragg angle). The crystal sizes are given in Table 1. The crystal sizes directly provide information about the crystal quality and are inversely proportional to the FWHM of the diffraction peak obtained by XRD. The fact that the diffraction peak is too narrow suggests that the crystal size is large and in this case the crystal has a better-quality structure. As seen from Table 1, the average crystal sizes increase with increasing additive Pb up to the optimum level beyond which they decrease in the overdoped level of Pb inclusion owing to the worsening of the crystallinity and connection between the superconducting grains.

The variation of the Pb content level in the crystal lattice, the lattice cell parameters calculated by the least-squares method using the d, and (hkl) plane values for the tetragonal unit cell structure is a finding from the current study. The material’s crystal structure is tetragonal and the lattice constant parameter ratios are added in Table 1. It can be seen from this table that the increase in Pb concentration causes to expand the c-cell parameter up to the milling duration of 3 h, to shrink at over 3 h milling duration, and to increase the a lattice cell parameter for all durations as a result of the partial replacement of divalent of Pb inclusions for the trivalent Bi nanoparticles or tetravalent of Pb inclusions for the divalent Ca nanoparticles in the Bi-2223 system. Since divalent of Pb inclusions and tetravalent of Pb inclusions come from lead (II) oxide (Pb⁺²O) and lead (IV) oxide (Pb⁺⁴O₂) inorganic compounds, respectively. In other words, the existence of different aliovalent replacements into the Bi-2223 crystal structure leads to a positive charge in the Bi-O double layers with oxygen deficiency and the resulting positive charge must be balanced with valence/oxygen for charge neutrality [12,13,14,15,16]. Therefore, while the interlayer distances between the Cu-Ca-Cu and Ca-Sr sites in the layered structure increase, the interlayer spaces of the Sr-Bi, Bi-Bi, and Sr-Bi-Bi-Sr sites first expand and then contract automatically [17]. When the a/c ratio increases from 0.144 for Bi4 to 0.159 for Bi6, extra energy is naturally required for bond formation [18, 19]. At the same time, the decrease in the c-parameter is related to the reduction in the hole concentration in CuO₂ planes. It is also known that Cu–O bond lengths in repeatedly stacked layers of Cu-O₂ layers regulate the size of the base plane. Moreover, Pb foreign substances increase the a-axis length as a result of an increase in Cu–O bond length and effective Cu valance [20,21,22,23,24,25,26]. XRD measurements also provide information on impurity phases. For example, the Ca₂PbO₄ phase is observed at 2θ = 47.5° and 56° in all samples.

3.2 Vickers Microhardness Measurement Examination

Up to now, we have proved that Pb nanoparticles placed superconducting matrices improve the grain connectivity, surface morphology, and superconducting properties of bulk Bi-2223 materials with the help of experimental research. In this section of the study, we are interested in the change of mechanical performance about the Bi-2223 system, exposed to the different milling duration before sintering, using Vickers microhardness (H_v) measurements at different indentation loadings in the range of 0.245–2.940 N.

The Vickers hardness measurement method is one of the most sensitive methods with a long time taking, especially suitable for research and measuring hardness in micro and nano dimensions [27]. Vickers hardness value (H_v) is obtained by the equation given below:

$${H}_{v}=1854.4(\frac{F}{{d}^{2}})$$

(4)

In this relation, F is the applied load, and d ($d=\frac{{d}_{1}+{d}_{2}}{2}$) is the average diagonal length of the indentation impress. In Fig. 3, the H_v values obtained with precision can be easily seen. According to Fig. 3, each sample shows nonlinear microhardness behavior, and a rapid decrease in microhardness value is observed with an increasing amount of load at 0.245–2.940 N. The reason for this behavior may be related to the distribution of grain boundary weak connections. The calculated microhardness values decrease non-linearly up to 1.960 N with increasing applied load. Microhardness tends to reach saturation after this value and the change in microhardness value is very small. This region is referred to as the plateaued region and corresponds to independent (true) microhardness values of the samples. These plateaued zones are due to increased impurity phases, grain boundary weak connections, cracking/porosity, disorder, and irregular grain orientation distribution in the crystal lattice [28, 29].

Fig. 3

Variation of Vickers microhardness values as a function of applied indentation test loads for the superconducting materials

In this study, the true hardness values in the plateaued region are H_v = 0.304–0.273 GPa for the sample Bi1, H_v = 0.320–0.289 GPa for Bi2, H_v = 0.489–0.456 GPa for Bi3, H_v = 0.602–0.571 GPa for Bi4, H_v = 0.532–0.498 GPa for Bi5, and H_v = 0.420–0.388 GPa for Bi6. This nonlinear behavior of load-changing microhardness is a phenomenon observed in the literature for Bi-Pb-Sr-Ca-Cu–O superconductors and is referred to as an indentation size effect (ISE) [30, 31].

According to this effect, small microhardness values are obtained for large indentation forces and large microhardness values are obtained for small indentation forces. This behavior indicates that the weak grain boundaries in large indentation forces may have reduced the microhardness value. In contrast, with small indentation loads, the measured hardness is large and this condition is attributed as a single crystal state indicator without interference from grain boundaries. At the same time, elastic recovery is a dominant character in prepared samples at the lowest load of 0.245 N after which the plastic deformation plays the dominant character of the materials. That is, all prepared polycrystalline ceramic samples simultaneously exhibit both elastic (reversible) and plastic (irreversible) deformations.

In fact, the H_v parameters under the applied test load of 1.960 N are approximately consistent with those of the H_v parameters at the applied test load of 2.940 N, due to the purely dominant character of plastic deformation.

Furthermore, the H_v values for all test loads for the Bi4 sample were much higher than the others. This is attributed to the least sample cracking/porosity, irregular grain orientation distribution, and grain boundary weak-links [32] are observed in the preferred sample, as also supported by XRD results.

In detail, the reason for the rise in hardness value may be due to a plastic-flow zone that allows the undesirable forces caused by the particle anisotropy of superconductors to relax. Pb may induce pressure stresses in the superconductivity matrix due to a thermal expansion mismatch between superconductors and Pb particles. Thus, pressure stresses in the superconductivity matrix can compress cracks and prevent crack propagation [33].

When the grinding time is over 3 h, the Vickers microhardness (H_v) values tend to decrease considerably because of irregular grain orientation distribution and the increase in the specimen cracking/porosity in the inorganic Bi-2223 system [34,35,36,37]. Numerically, the H_v values are in a range of about 0.729–0.621 GPa and 0.723–0.567 GPa under the applied test load of 0.245–2.940 N for the Bi4 and Bi6 materials, respectively. Moreover, similar consequences, including the change in elastic features, were confirmed from the X-ray crystal structures of the inorganic compounds.

Theoretical calculations for the elastic (Young’s) modulus (E), the yield strength (Y), fracture toughness (K_IC) parameters, and brittleness index (B) are calculated from the Vickers measurement curves using the following equations:

$$E=81.9635{H}_{v}$$

(5)

$$Y\approx \frac{{H}_{v}}{3}$$

(6)

$$\begin{aligned}K_{IC}=\sqrt{2E\gamma}\;\;\;\;\;\;\;&(\gamma\text{displays surface en}\text{ergy and constant};\\&\gamma=0.000874787)\end{aligned}$$

(7)

$$B=\frac{{H}_{v}}{{K}_{IC}}$$

(8)

All calculated values are shown in Table 2 and it can be seen that the tendency of change in Young’s modulus, yield strength, fracture toughness, and brittleness index is like the tendency to change in the real (true) microhardness (H_v). In general, the more homogeneous structure of the material, the crystallinity, and the strength of interaction between grains develops up to the grinding time of Δt = 3 h, the excessive Pb impurities are formed over more than 3 h milling duration and damage the mechanical properties of the Pb-doped Bi-2223 superconducting materials due to weak bonds between the granules.

Table 2 The calculated load-dependent H_v, E, Y, K_IC, and B for the (Bi, Pb)-2223 samples

When the change in the crystallite size and the connection quality between the superconducting particles can be examined using Young’s modulus and yield strength versus volume density graphs as shown in Figs. 4 and 5, every graph shows a similar tendency due to the typical ISE behavior and the E and Y values improve parabolically with the enhancement of the bulk densities. Namely, the bulk samples with the higher densities have better crystallite size and interaction between the superconducting grains.

Fig. 4

Change of the elastic (Young’s) modulus against density curves for the Pb doped superconducting materials

Fig. 5

Change of the yield strength against density curves for the Pb doped superconducting materials

Some approaches and models have been proposed to describe the variation of the indentation size with the applied test load. Experimental and quasi-experimental equations such as Meyer’s law, Hays-Kendall approximation, elastic–plastic deformation model, energy-balance approximation, and proportional sample resistance model have been proposed. All approaches except Meyer’s law involve determining the actual hardness value (the value of the individual hardness of the load).

3.2.1 Meyer’s Law

Meyer’s law is one of the suitable commandments to describe the mechanical features of a solid and an empirical relationship between the size of the hardness test indentation and the load required to leave the indentation. It can be formulated as follows:

$$F={A}_{1}{d}^{n}$$

(9)

where F is applied load, A₁ is the resistance of the material to initial penetration, d is the diameter of the indentation, and n is Meyer’s number (or index) that is a measurement of the structural deformation on the material [38].

According to Meyer’s law, if the weight is reduced to a value of a quarter, the diameter of the indentation is approximately halved. For example, a 10 mm indentation that occurs at a 3000 kg test load creates a 5 mm diameter indentation when the test load is made at 750 kg [39].

If the value of n is less than 2, the microhardness values decrease with the increasing load value, and this is known as ISE, but if the value of n is greater than 2, the microhardness values increase with the increasing load value and this is known as RISE. When n is equal to 2, it is well known that Kick’s laws (F = A₁d²) are valid. The values of n and A₁ found from the linear fit all curves in the ln(d) versus ln(F) graph (Fig. 6) drawn for our samples are listed in Table 3. The results obtained were less than 2 for samples because of the ISE behavior [40].

Fig. 6

Variations of applied load ln F with diagonal ln d for the samples

Table 3 The calculated parameters according to Meyer’s law, PSR, and MPSR models for Bi-2223 system

Furthermore, Table 3 assures that the values of A₁ first decrease and then increase with increasing the Pb foreign impurities inserted in the Bi-2223 crystal texturing. This is in association with the fact that the mixing time is effective in ordering the Pb particles more uniformly in the compound. Therefore, while the mixing time is increased up to 3 h, the Pb distribution improves the Bi-2223 structure and the Pb distribution deteriorates it with increasing mixing time beyond 3 h.

3.2.2 Proportional Specimen Resistance (PSR) Model

The PSR model is an improved form of the Hays/Kendall approach, used to decide whether the materials have the property of the ISE or RISE properties and formulated by Eq. (10) [41,42,43]:

$$\frac{F}{d}={A}_{2}+{A}_{3}d$$

(10)

In this formula, although A₂ represents the surface energy or the elastic resistance and the friction resistance of the tested material interface [44, 45], A₃ is a measure of the true hardness that is associated with the plastic properties of the material. Parameters A₂ and A₃ can be evaluated through the graph F/d versus d in Fig. 7 and written in Table 3. The parameters A₂ are positive values, so all samples have the ISE feature, presenting that the elastic deformation is superior to the plastic deformation in all samples. Also, the harder materials with higher Young’s modulus are directly related to A₂ [46].

Fig. 7

Plots of F/d versus d for the samples studied

$${H}_{PSR}=1854.4{A}_{3}$$

(11)

3.2.3 Modified Proportional Specimen Resistance (MPSR) Model

As shown in Eq. 12, the MPSR model is a modification of the PSR model [47] to investigate the ISE or RISE behavior in tested bulk samples.

$$F={A}_{4}+{A}_{5}d+{A}_{6}{d}^{2}$$

(12)

where A₄ is the residual surface stresses composed of the surface grinding and polishing processes during sample preparation. A₆ shows resistance to uncracked plastic deformation and can estimate load-independent hardness in the absence of ISE (when A₅ = 0) [48]. As shown in Table 3, the decreasing/increasing trends of the parameters A₅ and A₆ are approximately the same as the decreasing/increasing trends for A₂ and A₃ in the PSR model, respectively. A₄, A₅, and A₆ parameters are calculated by using polynomial fit with second-order of F versus d graph in Fig. 8.

Fig. 8

Variations of applied loads with diagonal lengths for the bulk superconductors

$${H}_{MPSR}=1854.4{A}_{6}$$

(13)

ISE properties are seen in all samples as in the MPSR model. A ratio A₅/A₆ increases with increasing of the microhardness. At the same time, X-ray diffraction is used for explaining the correlation of the stress because all values such as a, c, and grain size found from X-ray measurement and correlation values in Hardness are the best values for the B4 sample.

3.2.4 Elastic/Plastic Deformation (EPD) Model

In this model, load-independent microhardness value is calculated from Eq. (14).

$$H_{EPD}=1854.4A_7$$

(14)

When this model is applied, as seen in Table 4, d_e value found from the point where the graph intersects the y axis is positive for all samples. Since there is no plastic deformation for the applied loads. This result is evidence of the ISE behavior of the material. In this model, the dependence of the indentation size on the applied load is given in the following Eq. (15) [49].

Table 4 The calculated parameters according to EPD, HK, and IIC models for Bi-2223 system

$$F={A}_{7}({d}_{p}+{d}_{e})$$

(15)

where A₇ is the load-independent microhardness constant when d_e is the elastic deformation and d_p is plastic deformation. According to the F^1/2 versus d_p graph shown in Fig. 9, the values of A₇ are calculated and labeled in Table 4. It is stated that the elastic deformation is more dominant than plastic deformation (every superconducting sample in this study has ISE behavior) due to be positive A₇ values. EPD model is not adequate for the determination of the real microhardness value. Because the values closest to the H_v plateaued values in Table 5 are the H_hk values. H_EPD values are not as close to H_v plateaued values as H_hk values.

Fig. 9

Plots of the square root of applied loads versus diagonal lengths for every material studied

Table 5 The calculated values of H_PSR, H_MPSR, H_EPD, H_HK, H_IIC, and H_v model for all bulk samples

3.2.5 Hays-Kendall (HK) Approach

In the hardness tests made for many different materials, while the only elastic deformation is observed below a specific limit of the applied load (F), plastic deformation begins to occur suddenly in the material above this limit value.

$$F={A}_{8}+{A}_{9}{d}^{2}$$

(16)

A₈ is a microhardness constant independent of the applied load. The A₈ and A₉ parameters are evaluated from the F-d² graph in Fig. 10 and tabulated in Table 4. Since the A₈ values seen in the table are positive, our superconducting ceramics exhibit ISE behavior. In other words, these positive values are adequate to create elastic (reversible) deformation as well as plastic (irreversible) deformation in superconducting materials [50].

Fig. 10

Applied load versus the square of the impression length for the samples

$${H}_{EPD}=1854.4{A}_{9}$$

(17)

According to the microhardness values shown in Table 5, it is seen that the microhardness values of the HK model are closer to the values in the plateaued area compared to the results found from other microhardness models. Therefore, it can be concluded that the Hays-Kendall approach is the most suitable model for both calculating microhardness and determining the mechanical properties of superconducting samples that show ISE behavior.

3.2.6 Indentation-Induced Cracking (IIC) Model

It is well known that hardness is the measurement of the effect of the indenter on the material in different shapes. When a load is applied, a material’s resistance is formed to prevent indentation deformation. It comprises four components: (1) friction in the indenter; (2) elastic deformation; (3) plastic deformation; and (4) sample cracking. The first two components are a cause of the ISE nature and others are the cause of the RISE behavior [51].

According to the IIC model, the microhardness of the samples are calculated by using the following formula:

$${\mathrm H}_{\mathrm v}={{\mathrm\lambda}_1{\mathrm A}_{10}\left(\mathrm F/\mathrm d^2\right)+{\mathrm A}_{11}\left(\mathrm F^{5/3}/\mathrm d^3\right)}^{\mathit m}$$

(18)

İn this formula, A₁₀ and A₁₁ depend on the indenter geometry and the applied load, respectively, whereas λ₁ is constant. If the samples are perfect plastic, the equation becomes like this due to λ₁ = 1 and ${A}_{11 }\left({F}^{5/3}/{d}^{3}\right)=0$:

$${\mathrm H}_{\mathrm v}={\mathrm\lambda}_1{\mathrm A}_{10}\left(\mathrm F/\mathrm d^2\right)$$

(19)

But, when the samples are perfect brittle, λ₁ = 0 and the equation becomes like following:

$${\mathrm H}_{\mathrm v}={\mathrm A}_{11}\left(\mathrm F^{5/3}/\mathrm d^3\right)$$

(20)

For Eq. 20, d = 7 h because of θ = 148° (h is the depth of the indentation, and θ is the angle between the opposite sides of the indenter). Thus, the equation is written as;

$${{\mathrm H}_{\mathrm v}={\mathrm A}_{12}\left(\mathrm F^{5/3}/\mathrm d^3\right)}^{\mathrm m}$$

(21)

where m is a constant that determines whether the material is ISE or RISE nature. A₁₂ and m are obtained using the graph of ln(H_v) with ln(F^5/3/d³) given in Fig. 11 and labeled in Table 5. Samples show ISE (RISE) behavior for m > 0.6 (m < 0.6). As seen in Table 5, all samples have ISE behavior due to m > 0.6.

Fig. 11

Variation of ln H_v with ln (F^5/3/d³) according to IIC model for every sample studied

As a result, the Pb inclusions inserted in the superconducting system for optimum level (underdoped/overdoped level) are adequate (inadequate) for the applications of the Bi-2223 materials in engineering areas.

Hardness surveys can provide a better understanding of the microstructures of superconducting materials and identify critical parameters such as heat treatment and mixing, which are very important for having single-phase material without much decomposition and porosity.

4 Conclusion

Throughout this study, XRD patterns and hardness measurements were performed for the analysis of the effect of the mixing duration on mechanical, microstructural, and superconducting features belonging to the (BiPb)₂Sr₂(CaPb)₂Cu₃O_y superconductor samples obtained after applying 48-h heat treatment at 845 °C using the solid-state method.

In addition, it was found from XRD measurements that the a/c ratio was constant until the milling time ∆t = 3 h, but above this period, there was a significant increase in the a/c ratio of the lattice cell parameters. It was determined that the a axis continued to increase while the c axis decreased due to the increase in the oxygen content in the unit cell at milling times longer than 3 h. It may be thought that the oxygen elements will settle in the bismuth oxide (Bi₂O₃) layer, causing an increase in the a-lattice parameter and a decrease in the c-lattice parameter. This shows a transition towards a multi-phase and complex structure. In other words, the decrease in the c-lattice parameter results from the extra valence in the oxygen-deficient in Bi-O planes and the extra energy required for bond formation. Conversely, the increase of the a-lattice parameter is due to the increase of effective Cu valence in CuO₂ successively stacked layers. As a result, the optimum mixing time is around 3 h.

It can be interpreted that superconductivity and hardness values, hole concentration in Cu–O planes, and charge balance change linearly with the mixing times.

Small hardness values are obtained at high load values for each ceramic sample, and large hardness values are obtained at small load values. The dependence of the microhardness on the load shows a nonlinear change. This behavior of the samples is called the indentation size effect (ISE). ISE behavior indicates that the weak grain boundaries in large indentation forces may have reduced the microhardness value, whereas in the case of small indent loads, the measured hardness is large and this condition is attributed as a single crystal state indicator without interference from grain boundaries [29]. ISE nature is also observed in our samples. Load-independent hardness (true hardness) values were calculated using the experimental and quasi-experimental models proposed to define the variation of the indentation size of the ceramic superconductor samples with the test load. The Hays-Kendall approach provides a meaningful definition of the measured indentation data. While examining the size effect of the indentation shown by the samples, the hardness values obtained from the Hays-Kendall approach gives the best results among other models for which we have calculated the microhardness values.

Moreover, when Pb was added to Bi_1.8Pb_0.2Sr_2.0Ca_1.8 Pb_0.2Cu₃O_y instead of Bi and Ca, the microhardness value, Young’s modulus, and yield strength were increased by increasing the amount of Pb to x = 0.3 h, and after that, the microhardness decreased. These increments are related to the strength of the intergranular bonds and the more homogeneous structure of the material. It is reported that the decrease in additions after x = 0.3 h was due to weak bonds between the granules. It could be said that the porosity on the surface decreases with the addition of Pb so the load-independent hardness values increase.