1 Introduction

Transition metal oxides have been the focus of intense interest over the past several years, a consequence of their displaying a wide range of unusual magnetic and electronic properties, aspects of which are not fully understood. To cite a specific example, such a description is currently applicable to colossal magnetoresistive (CMR) systems, viz., oxides with general formula A 1−x B x MnO3 where A is a rare-earth ion and B is a divalent alkaline earth cation [1], while the layered perovskite manganite Sr2MnO4 containing only Mn4+ ions crystallize in the K2NiF4-type structure [2, 3]. The feature of this structure is an insulating NaCl-type structural block separating two neighboring MnO2 layers [2, 3]. These structures are not much studied, mainly the magnetic study. The doped of Sr2+ by rare earth R3+= La3+ or Nd3+ provides a typical two-dimensional eg-electron system In these systems, a cascade of magnetic, structural, metal–insulator, and charge ordering phase transitions has been observed by change of doped level, temperature, applied magnetic field, and pressure [4, 5]. These properties were widely interpreted by means of the double-exchange (DE) mechanism, proposed by Zener [6], together with a strong electron–phonon interaction known as the Jahn–Teller effect [7]. However, the origin of the observed properties is still not fully understood. Particularly, it is unclear how the magnetic interactions are renormalized near the PM–FM transition range and what universality class governs the PM–FM transitions in these systems.

Among the fundamental questions which remain controversial is the universality class related to the paramagnetic (PM) to ferromagnetic (FM) transition in manganites [8–10]. The universality class does not depend on microscopic details of the system but only on global information such as the dimension of the order parameter and space. This practice has been extremely helpful in trying to discern the complexities of magnetic transitions in real systems [11]. Historically, the critical behavior in the DE model was described by long-range mean-field theory.

Many of the experimental studies of critical phenomena have been previously made on ferromagnetic manganites [12–16], with some controversial results concerning the critical exponents and even the order of the magnetic transitions. For example, Morrish et al. [13] had found a high value of β = 0.495 in a La0.65Pb0.44MnO3 crystal. This is in good agreement with later results from Lofland et al. [14] which yield β = 0.45 in La07Sr03MnO3, indicating a mean-field-like behavior at the magnetic phase transition. In contrast to this, neutron scattering experiments on La0.7Sr0.3MnO3 give a rather low β value, 0.295 [15]. Due to the drastic difference in the physical properties between La0.7Ca0.3MnO3 with a Curie temperature T C = 250 K and La0.7Sr0.3MnO3 (T C = 340 K), some authors distinguish the archetypical CMR compound La0.7Ca0.3MnO3 as a “low- T C” manganite. It has a higher resistivity, a sharper resistivity peak near T C and a larger CMR than La0.7Sr0.3MnO3 [17].

The continuous nature of the FM to PM transition has been investigated carefully for high-TC manganites such as the work of Tozri et al. for the compound La0.7Pb0.05Na0.25MnO3 (T C = 335 K) [9] and also Ghosh et al. for La0.7Sr0.3MnO3 (T C = 355 K) [20]. On the other hand, an unexpected dependence of the order of the ferromagnetic transition on doping has been reported for La1−x Ca x MnO3. The transition in La0.8Ca0.2MnO3 is continuous [18], while that for La0.7Ca0.3MnO3 was found to be of first order in various studies [19–21]. Quenched disorder in the Mn sublattice of La0.67Ca0.33MnO3 introduced by Ga doping leads to a rounded magnetic phase transition characterized by the critical properties of a Heisenberg-like ferromagnet [22]. This result implies a conventional behavior of the magnetic Mn sublattice in this manganite which is, however, impaired by additional effects in the undoped La0.67Ca0.33MnO3. There are still other conflicting results about the ferromagnetic transition in the series of compounds La1−x Ca x MnO3. From static magnetization studies, a tricritical behavior was found for x = 0.40 [23], while critical exponents close to those of the Heisenberg universality class have been found for x = 0.20 [18]. The same for work from Nasri et al. also found change for x = 0.2 in the compound La0.6Ca0.4−x Sr x MnO3.

Contrary to this, Rivadulla et al. [24] propose a heterogeneous magnetic ordering owing to intrinsic random fields or random anisotropies for the ranges x > 0.4 and x < 0.25 with a continuous phase transition. Finally, the experimental estimates are still controversial concerning the critical exponents and even the order of the magnetic transitions including three-dimensional 3D-Heisenberg interaction [25, 26], 3D-Ising values [27, 28], mean-field values [29], and those that cannot be classified into any universality class ever known [30]. To better understand the nature of the PM–FM transition, it is important to study in detail the critical exponents associated with the transition, based on a systematic investigation of the critical behavior in terms of the modified Arrot plot [31] and Kouvel–Fisher [32] methods.

The aim of this work is the studies of the critical behavior in Sr1.5Nd0.5MnO4 at its PM–FM transition via the detailed measurement of the dc magnetization. We find that the critical exponents for Sr1.5Nd0.5MnO4 are close to those theoretically predicted for the mean-field model.

Griffiths phases, associated with various forms of disorder, have also been reported in a number of other systems [33–37]. In this letter, we address the question of whether a Griffiths phase is always a precursor to the deference of values of critical exponent.

2 Experimental Details

The polycrystalline Sr1.5Nd0.5MnO4 compound is prepared from precursors of Sr2 O 3 (4N-purity), Nd2 O 3 (4N), and MnO2 by a solid-state reaction [38]. The raw powders were pre-heated before weighting and mixing by the following. These powders were mixed in a required atomic ratio with an agate mortar and pressed into pellets, which were put into a platinum boat. The pellets were fired at 1400 K for 6 h in air, followed by slowly cooling to room temperature. X-ray powder diffraction data of the sample were measured using a diffractometer system equipped with a single-crystal graphite monocromator (MAC MXP18 powder X-ray diffractometer). The diffraction patterns were collected with CuKα radiation over a 2 𝜃 range from 10 to 80∘ with a step width of 0.015∘ and counting time of 4.5–6.0 s (variable). The magnetization and susceptibility measurements were performed in a (BS2) magnetometer. The magnetization was measured as a function of field (H) and temperature (T), respectively. The field dependence of the magnetization (M) was carried out at 3 K in an applied field of 0.05 T.

3 Scaling Analysis

A second-order magnetic phase transition near the Curie point is characterized by a set of interrelated critical exponents, β (associated with the spontaneous magnetization), γ (relevant to the initial magnetic susceptibility), and δ (associated with the critical magnetization isotherm) [39] The mathematical definitions of the exponents from magnetization measurements can be described as follows [39–41]:

  • Below T C , the temperature dependence of the spontaneous magnetization \(M_{S} (T)=\lim \limits _{H\to 0} (M)\) is governed by β exponent through the relation

    $$ M_{S} (T)=M_{0} (-\varepsilon )^{\beta} ; \quad\varepsilon <0, \quad T< T_{\mathrm{C}} $$
    (1)

  • Above T C, the initial susceptibility \(\chi _{0}^{-1} (T)=\lim \limits _{H\to 0} \left (\frac {H}{M}\right )\) is given by

    $$ \chi_{0}^{-1} (T)=\left( \frac{h_{0}} {M_{0}} \right)\varepsilon^{\gamma} ; \quad \varepsilon >0, \quad T > T_{\mathrm{C}} $$
    (2)

  • At T C, M and H are related by the following equation:

    $$ M=DH^{\frac{1}{\delta} };\quad \varepsilon =0,\quad T=T_{\mathrm{C}} $$
    (3)

    where \(\varepsilon =\frac {T-T_{\mathrm {C}}} {T_{\mathrm {C}}}\) is the reduced temperature, M 0 as well as h 0 and D are critical amplitudes.

The magnetic equation of state is a relationship among the variables M (H,ε), H and T. From the scaling hypothesis this can be written as

$$ M(H,\varepsilon )=\varepsilon^{\beta} f_{\pm} (H/\varepsilon^{\beta +\gamma} ) $$
(4)

where f + for T > T C and f − for T < T C are regular analytic functions. Equation (4) implies that for true scaling relations and right choice of β, γ and δ values, the scaled M/|ε|β plotted as a function of H/|ε|β + γ reveals that the magnetic isotherms in the vicinity of T C fall on two individual branches, one for T < T C and the other for T > T C. However, exponents often show various systematic trends or crossover phenomena as one approaches T C [42, 43]. This occurs if a magnetic system is governed by various competing couplings and/or disorders. In that case, it is useful to generalize the power laws for the critical behavior by defining effective exponents for ε ≠ 0. It can be mentioned that effective exponents are nonuniversal properties and here we only analyze the effective exponent commonly used, γ eff, defined as

$$\gamma_{\text{eff}} =\frac{d\ln \chi_{0}^{-1} (\varepsilon )}{d\ln (\varepsilon )}. $$

  • In the asymptotic limit ε→0, the effective exponents approach the universal critical (asymptotic) exponent.

  • In the critical regime (asymptotic limit), where χ∝(T−T C )γ γ eff, defined as

    $$\begin{array}{l} \lim \gamma_{\text{eff}} =\gamma\\ \varepsilon \to 0 \\ \end{array} $$

  • At high temperatures (meanfield theory, T→∞), where we can establish the law of Curie–Weiss, χ = C (T−T c)−1, γ eff is defined by

    $$\begin{array}{l} \lim \gamma_{\text{eff}} =1 \\ \varepsilon \to \infty \\ \end{array} $$

4 Results and Discussion

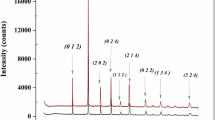
The structural analysis was carried out by X-ray diffraction (XRD) at room temperature. The data were analyzed by the Jana program [44]. This refinement of XRD shows that sample Sr1.5Nd0.5MnO4 crystallizes in the tetragonale structure with Pmmm space group [45].

4.1 Magnetic Properties

The magnetization presents a very sharp FM–PM transition at Curie temperature T C, which is near room temperature. The magnetic transition temperature (T C) is defined as the inflection point of dM/dT (Fig. 1). We have found that the transition temperature T C for the Sr1.5Nd0.5MnO4 compound is (245 K), followed by a decrease of spontaneous magnetization in the 300–100 K temperature range. This decrease of magnetization should be probably due to a spin canted state between manganese and neodymium spin systems. In fact, such type of canting due to rare-earth ion is indeed possible for manganites as also been reported in previous experimental results by Park et al. for Nd0.5Sr0.5MnO3 bulk material [45] and by Biswas et al. for Nd0.5Sr0.5MnO3 nanocrystalline material [46].

Fig. 1
figure 1

Variation of the magnetization and the dM/dT as a function of temperature in an applied field of 0.05 T for Sr1.5Nd0.5MnO4 compound

Full size image

This compound presented a Griffiths phase in form of FM cluster system within a PM matrix is indicated by macroscopic magnetization experiments [47–54]. The magnetic anomaly is more obvious in the inverse susceptibility and its derivative as a function of temperature [27].

4.2 Arrott–Noakes Plot

Figure 2 shows the M vs. H plots for Sr1.5Nd0.5MnO4. As can be seen, the magnetization curves indicate a gradual FM to PM transition, which were used to determine T C and the critical exponents β, γ, and δ.

Fig. 2
figure 2

Magnetization vs. applied magnetic field μ 0 H, measured at different temperatures, for the Sr1.5Nd0.5MnO4 sample

Full size image

The conventional method to determine the critical exponents and critical temperature involves the use of Arrott plot [55]. According to this method, isotherms plotted in the form of M 2 vs. H/M constitute a set of parallel straight lines around T C. It can be mentioned that the Arrott plot assumes the critical exponents following mean-field theory (β = 0.5, γ = 1, δ = 3). Hence, linear behavior of isotherms in a high field indicates the presence of mean-field interactions. The advantages of this plot are that (i) T C can be determined accurately, since the isotherm at T C will pass through the origin, (ii) it directly gives \(x_{0}^{-1}(T)\) as an intercept on the H/M axis, and (iii) the intercept on the positive M 2 axis gives M S (T) (Fig. 3).

Fig. 3
figure 3

The M 2 vs. H/M isotherms for Sr1.5Nd0.5MnO4 compound

Full size image

The curves obtained from the H/M vs M 2 plots of the sample are shown in Fig. 3. However, all curves in this plot show a linear behavior having a downward curvature even in a high field indicating a mean-field-like behavior. Moreover, the concave downward curvature clearly indicates a second-order phase transition according to the criterion suggested by Banerjee [56]; in addition, this curve indicates that a positive slope is clearly seen in the complete M 2 range, which means that a second-order ferromagnetic to paramagnetic phase transition happens.

The deeper insight of the magnetic phase transition may be checked by analyzing the critical phenomena. The exact values of the critical exponents and the Curie temperature T C were determined from the Arrott-Noakes plots (also called modified Arrott plots (MAP)).

In this technique, the M = f(H) data are converted into a series of isothermal (M 1/β = f((H/M))1/γ) depending on the following relationship [57, 58]:

$$ \left( {H/M} \right)^{1/\gamma} =\frac{\left( {T-T_{C}} \right)}{T_{1}} +\left( {M/M_{1}} \right)^{1/\beta} $$
(5)

A standard Arrott plot uses the critical exponents of the mean–field theory (β = 0.5, γ = 1, and δ = 3) characteristics of systems with long-range interactions. Thus, the relation (5) simplifies to a graph of M 2 vs. (H/M). In order to determine correctly the spontaneous magnetization and the initial susceptibility for our materials from the M−H isotherms, we constructed the Arrott plot M 2 vs. (H/M) (Fig. 3). Such curves in the mean-field theory near T C should form a progression of parallel straight lines for different temperatures and the line at T = T C should pass through the origin. However, the present curves were found to be non-linear at a low field and show a downward curvature suggesting that the mean-field theory cannot describe the critical behavior for this system. The MAP isotherms of M 1/β vs. (H/M)1/γ are plotted at different temperatures for this sample by using three models of critical exponents: the 3D-Heisenberg model (β = 0.365, γ = 1.336) (Fig. 4b), the tricritical mean-field model (β = 0.25, γ = 1) (Fig. 4a), and the 3D-Ising model (β = 0.325, γ = 1.24) (Fig. 4c).

Fig. 4
figure 4

Modified Arrott plots a tricritical mean-field model b using 3D-Heisenberg model and c 3D using model

Full size image

Based on these curves, all models render quasi straight lines and nearly parallel to the high-field region. Thus, it is somewhat difficult to distinguish which one of them is the best for the determination of critical exponents. In order to compare these results and select the better model describing this system, we calculated their relative slopes (RS) which are defined as Fig. 5 shows the RS vs. T curve for the three models, 3D-Heisenberg, Ising, and tricritical mean-field model. The most adequate model should be the one that possesses an RS value and is very close to the unit. Therefore, we can deduce that the mean-field model is the best model which can describe our system and for determination of critical exponents for this compound Sr1.5Nd0.5MnO4 [59].

Fig. 5
figure 5

Relative slope (RS) of Sr1.5Nd0.5MnO4 sample as a function of temperature defined as RS = S(T)/S (T C), using several methods

Full size image

As initial values, we have chosen (γ = 1 and β = 0.5) the critical exponents of the mean-field model based on the relative slopes (RS). Following a standard procedure, values of spontaneous magnetization M S (T) and \(x_{0}^{-1}(T)\) are obtained from a linear extrapolation of MAP at fields above 0.2 T to the intercept with the M 1/β and (H/M)1/γ axes, respectively. Only the high-field linear region is used for the analysis since MAP deviates from linearity at a low field, due to the mutually misaligned magnetic domains. Critical exponents of the mean field (δ = 3, γ = 1, and β = 0.5) [60] are used as trial critical exponents for this data (Fig. 6).

Fig. 6
figure 6

Variations of the spontaneous magnetization and the inverse of the initial susceptibility as a function of temperature deduced from the Arrott

Full size image

4.3 Kouvel–Fisher Plot

In order to obtain the accurate critical exponents, the Kouvel–Fisher (KF) method has been used based on the following relationship [61, 62]:

$$ \frac{M_{S} (T)}{dM_{S} (T)/dT}=\frac{T-T_{C}} {\beta} $$
(6)
$$ \frac{\chi_{0}^{-1} (T)}{d\chi_{0}^{-1} (T)/dT}=\frac{T-T_{C}} {\gamma} $$
(7)

To determine the critical exponents as well as T C more accurately, we have analyzed the M S (T) and \(x_{0}^{-1}(T)\) data by the Kouvel–Fisher (KF) plot [63]. According to this method, M S(T,0) (d M S(T,0)/dT)−1 vs. T and \(x_{0}^{-1} (T) (x_{0}^{-1}(T)/\textit {dT})^{\mathrm {-1}}\) vs. T yield straight lines with slopes 1/ β and 1/ γ, respectively. The KF plot has been presented in Fig. 6. We have listed the critical exponents obtained from the Arrott–Noakes plots as well as the KF method along with T C in Table 1. It is noticed that values of critical exponents as well as T C calculated using both methods match reasonably well. This suggests that the estimated values are self-consistent and unambiguous.

Table 1 Comparison of critical exponents of Sr0.5Nd0.5MnO4 compound with earlier reports
Full size table

4.4 Critical Isotherm Exponent

For the value of δ, it can be determined directly from the critical isotherm M (T C, H). Figure 7 shows the magnetic field dependence of magnetization at T = T C for our samples. In the insets of Fig. 7, we presented this critical isotherm on a log–log scale. According to (3), the log (M) vs. log (H) plot should be a straight line with slope 1/ δ. The exponent δ has also been calculated from the Widom scaling relation according to which critical exponents β, γ and δ are related in the following way [63]:

$$ \delta = 1 + \gamma /\beta. $$
(8)
Fig. 7
figure 7

Isothermal magnetic curves at T = T C. The insets show these plots in logarithmic scale along with the fitted data to (3)

Full size image

Using this scaling relation and the estimated values of β and γ we obtain a δ value which is very close to the estimates for δ from the critical isotherms at T C. Thus, the estimates of the critical exponents are consistent. In Table 1, we report some recent experiment results and we also include the theoretical values obtained for different models.

4.5 Scaling Law

In the critical region, magnetization and internal field should obey the universal scaling behavior. In Fig. 8, we show plots of M/|ε|B vs. H/|ε|β + γ for the considered sample. The two curves represent temperatures below and above T C. The inset shows the same data in the log–log scale. It can be clearly seen from Fig. 8 that the scaling is well obeyed, i.e., all the points fall on two curves; one for T < T C and the other for T > T C. As a consequence, the obtained values of the critical exponent and T C are reliable and in agreement with the scaling hypothesis.

Fig. 8
figure 8

Scaling plots indicating two universal curves below and above T C Sr1.5Nd0.5MnO4 sample. Inset shows the same plots on a log–log scale

Full size image

From Table 1, one can found that the critical exponent β typically has a value in the range of 0.5–0.6, similar to those of mean-field ferromagnets. Nevertheless, the reported value of γ is not close to the theoretical value of the mean-field model. In our case, analysis of critical exponents for Sr1.5Nd0.5MnO4 show that the β value is very close to the mean-field model value and the γ value lies very far from the 3D-Ising and 3D-Heisenberg models. The difference originates from β being calculated from fittings below T C, whereas γ is from above T C. Furthermore, the critical isotherm exponent δ is again very close to the mean-field model prediction. Even if T C is not stable, it varies from 230 to 225 K. The latter, incidentally, indicates—albeit indirectly—the existent of a Griffiths-type phase [27] in this specimen; in other time, the absence of a Griffiths-type phase gives a top δ (generally characterized by large δ values [39, 43].

One further interesting feature—we have determined the effective critical exponent γ eff according to (5), which describes the temperature dependence of χ −1 in the so-called intermediate range. This temperature range is limited by the critical regime for ε→0 and by the mean-field range for ε→∞.

4.6 Effective Critical Exponents

The effective exponent γ eff for this sample is plotted in Fig. 9. This latter shows that the compound exhibits a non-monotonic change with ε where γ eff shows two peaks: the first with the highest value (at ε = 0.127) and the second (at ε = 0162). It can be mentioned, when approaching the asymptotic regime (ε→0), that γ eff = 0.78 at ε min, where ε min is the lowest investigated ε and match very well with the mean-field universality class. As observed for this sample, γ eff shows a non-monotonic temperature dependence with a maximum which is attained at a reduced temperature. This behavior is considered as a characteristic feature of the disordered systems [64]. In contrast, for the crystalline FM, γ eff decreases monotonically with increasing ε [64]. Furthermore, it has been shown that chemical (site disorder) and structural disorders are sufficient to obtain the typical non-monotonic temperature dependence of γ eff [65]. A recent theoretical study [42], particularly for mean-field-like FM, has predicted that γ eff remains unaffected by disorder in the asymptotic regime but with the introduction of disorder; γ eff goes through a peak at higher ε. Thus, this study shows the presence of quenched disorder in this sample. The effect of weak quenched disorder on the critical behavior of magnetic systems is predicted by the Harris criterion [66]: If the critical exponent α pure > 0, disorder changes the critical exponents. While if the α pure is negative, the disorder is irrelevant. Using the Rushbrooke scaling relation expressed as α+2β + γ = 2, the exponent α is found to be positive for the system which implies that the disorder is relevant.

Fig. 9
figure 9

Effective exponent γ eff vs. ε = (T−T C)/T C above T C

Full size image

5 Conclusion

To summarize, for the effect of the Nd substitution on the A-site cation, we have made a comprehensive study in the phase transition PM–FM. The magnetic measurements show a PM–FM transition at T C = 228 K. The critical exponents δ, γ and β estimated from various techniques match reasonably well. It is significant that even with these critical exponents, magnetization, field, and temperature (M–H–T) data follow the scaling equation where they collapse into two distinct branches: one below T C and another above T C. Estimates of critical exponents yield δ = 2.212 ± 0.124, γ = 0.975 ± 0.0181, and β = 0.5029 ± 0.0129 with T C = 228.595 ± 0.1722 which are consistent with the nearest-neighbor mean field, model universality class. Indeed, these exponent values agree with the predictions for the universality class of the conventional DE model. The temperature variation in the effective exponent (γ eff) is similar to those for disordered ferromagnets.

Therefore, the answer to the question raised in the title of this paper is a GP and always a precursor to the deference of values of critical exponent and this sign and show by the effective critical exponents.