Abstract
The single-layer perovskite cobaltates have attracted enormous attention due to the recent observation of hour-glass shaped magnetic excitation spectra which resemble the ones of the famous high-temperature superconducting cuprates. Here, we present an overview of our most recent studies of the spin and charge correlations in floating-zone grown cobaltate single crystals. We find that frustration and a novel kind of electronic and magnetic nano phase separation are intimately connected to the appearance of the hour-glass shaped spin excitation spectra. We also point out the difference between nano phase separation and conventional phase separation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The hour-glass magnetic excitation spectrum has fascinated physicists over years. This spectrum has been observed in high-temperature superconducting cuprates, and it is widely believed that fluctuating charge stripes are involved in the physics of these intriguing materials [1, 2]. Besides, charge stripes also Fermi surface effects have been proposed for the emergence of these hour-glass spectra in cuprates [3]. Recently, Boothroyd et al. observed an hour-glass magnetic spectrum in the copper-free Co oxide material La 2−x Sr x CoO 4 implying that Fermi surface effects are not needed for the emergence of hour-glass spectra since this material is insulating [4]. The undoped parent material La 2CoO 4 is an antiferromagnetic insulator with a Néel-temperature of roughly 275 K [6]. In contrast to the high-temperature superconducting cuprates La 2−x Sr x CuO 4, the cobaltates remain insulating up to high hole-doping levels of x ∼ 1 [7]. Also, the antiferromagnetic correlations with La 2CoO 4-like character which are centered at the planar antiferromagnetic wavevector persist to very high hole-doping ranges [8], higher than in the cuprates where incommensurate magnetic satellites have been observed already above ∼2 % Sr-doping [9]. A clearly incommensurate antiferromagnetic regime with well-separated incommensurate antiferromagnetic peaks can be observed only above ∼33 % of hole-doping in the cobaltates [8]. At half-doping, a robust checkerboard charge order (CBCO) has been reported in these cobaltates (La 1.5Sr 0.5CoO 4) with a charge ordering temperature of the order of ∼800 K [10, 11]. It was shown that the Co 2+ and Co 3+ ions in La 1.5Sr 0.5CoO 4 are in the high spin and in the nonmagnetic low-spin state, respectively, [11, 12].
2 Results and Discussion
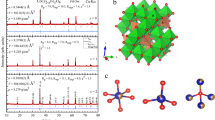
At one-third doping, i.e., in La 5/3Sr 1/3CoO 4, broad incommensurate magnetic peaks have been observed around third-integer positions in reciprocal space. Also, in the isostructural nickelates La 2−x Sr x NiO 4 [5], magnetic peaks can be observed at about the same positions in reciprocal space around 1/3-hole-doping, see Fig. 1a. These nickelates are known to exhibit a robust diagonal charge stripe phase [5]. Hence, it is natural to expect the existence of charge stripe ordered phases also in La 5/3Sr 1/3CoO 4, with the note that the correlation length of these diagonal charge stripes was thought to be very low in the cobaltate corresponding to the broadness of the magnetic peaks. However, using 100 keV hard X-rays at the synchrotron, we were able to show that in La 5/3Sr 1/3CoO 4 the charge correlations essentially occur with CBCO character only, see Fig. 1b [13, 14]. Also, in La 1.6Sr 0.4CoO 4, the charge ordering peaks were not observed at the incommensurate positions that correspond to the magnetic peak positions, but, instead at half-integer peak positions typical for CBCO [8, 14]. The CBCO character of the charge correlations in La 5/3Sr 1/3CoO 4 and La 1.6Sr 0.4CoO 4 is also reflected in the topmost Σ1 Co-O bond-stretching phonon dispersions that resemble the one in the half-doped CBCO ordered cobaltate La 1.5Sr 0.5CoO 4 where an anomalous phonon softening can be observed at half-integer propagation vectors, see magenta arrow in Fig. 2. This is unlike to the behaviour in the undoped parent material La 2CoO 4 and also unlike to the behaviour in charge stripe ordered nickelates [13].
a Polarization patterns for two high-frequency Σ1 Co-O bond-stretching phonon dispersions with propagation vectors of (1/3 1/3 0) and (1/2 1/2 0), respectively, are shown. As can be seen, one would expect a coupling of a phonon mode to charge correlations that have the same propagation vector as the phonon mode. b The Co-O bond-stretching phonon dispersions of La 2−x Sr x CoO 4 with x=0 (yellow), 1/3 (blue), 0.4 (red), and 1/2 (green) [8]. For a better comparison, the dispersion of La 2CoO 4 has been shifted to higher energies. The blue/red/green arrow marks the position of the propagation vector of a 1/3-doped and of a 40 % hole-doped charge stripe phase and of a CBCO phase. As can bee seen, La 5/3Sr 1/3CoO 4 exhibits absolutely no anomalies in the phonon dispersion at propagation vectors corresponding to a 1/3-hole-doped charge stripe phase (blue arrow). Instead, a phonon softening occurs at the zone boundary which is indicative for CBCO. Also, La 1.6Sr 0.4CoO 4 exhibits a similar phonon softening (magenta arrow) like the half-doped CBCO ordered cobaltate La 1.5Sr 0.5CoO 4
Interestingly, nickelates around half-doping also exhibit CBCO at high temperatures (∼480 K) and become charge stripe ordered on cooling to low temperatures (∼180 K) [14, 16]. This re-arrangement of charges into stripes at low temperatures seems to be hampered in the cobaltates which also have a much more robust CBCO with distinctly higher CBCO ordering temperatures than in the nickelates. An apparent difference between cobaltates and nickelates is the higher insulating properties of cobaltates according to the spin-blockade mechanism [12] as well as the stability of both Co 2+ and Co 3+ oxidation states (charges are localized at Co-sites and not at the oxygen ions) together with a very large difference in their ionic sizes (the ratio of the Co 2+ and Co 3+ ionic radii amounts to ∼1.367 [17]). All these effects together hamper the hopping of electrons from Co 2+ to Co 3+ sites and, thus, probably the re-arrangement of charges into stripes at low temperatures.
The absence of charge stripes and Fermi surfaces in La 5/3Sr 1/3CoO 4 and La 1.6Sr 0.4CoO 4 forced us to find an alternative mechanism for the emergence of the hour-glass spectrum [8, 13]. We proposed that frustration effects in disordered CBCO phases produce the incommensurabilities in La 2−x Sr x CoO 4 [8]. Even more intriguing is the microscopic origin behind this mechanism. For cobaltates below half-doping additional electrons have to be introduced into the Co-oxygen planes, i.e., Co 2+ ions have to be inserted at nonmagnetic Co 3+ sites. This electron doping of CBCO phases will create undoped La 2CoO 4-like islands on the nanometer scale. Within these undoped islands, large nearest-neighbour exchange interactions J occur, whereas the surrounding regions with CBCO character only contain much weaker exchange interactions \(J^{\prime }\) across the holes, see Fig. 3. This gives rise to a new situation—whereas nanometer-sized undoped islands can be excited to high energies the surrounding CBCO ordered regions are not able to follow these high-frequency oscillations. Hence, besides electronic (i.e. charge) also magnetic nano phase separation occurs in these cobaltates. The high energy excitations within the hour-glass shaped magnetic spectra appear to be basically hosted in nano phase separated undoped islands whereas the remaining hole-rich regions can be excited only at lower energies such that the so-called hour-glass spectrum is formed from the coupling of these two very different type of excitations.
The Co 2+ ions (green spheres with arrows symbolizing the spin) and the nonmagnetic Co 3+ ions (black spheres) within the ab-plane are schematically drawn for our nano phase separation scenario. By doping of electrons at Co 3+-sites in a checkerboard charge ordered matrix (blue) undoped islands (red) will be created. Within the undoped islands the nearest-neighbour exchange interactions J are quite large. However, in the surrounding CBCO regions, only weak exchange iteractions \(J^{\prime }\) across the holes exist [14]
The magnetic part of our nano phase separation scenario was corroborated by our study of the hole-doping dependence and the temperature dependence of the hour-glass spectra [13]. The charge part of our nano phase separation scenario was also verified by microdiffraction measurements on La 5/3Sr 1/3CoO 4 at the synchrotron, where we scanned a CBCO peak reflection intensity with a micro-focused beam across the surface. The domain size distribution exhibits islands with larger and islands with smaller domain sizes (correlation lengths). Using the statistical method developed in Ref. [18], we analyzed the probability density function (PDF) and observed an almost perfect power-law behaviour that reflects a scale-invariant (fractal-like) domain size distribution which nicely confirms our nano phase separation scenario in cobaltates [13]. Using these new tools, it has been possible to discover a common (structural) nano scale phase separation scenario characterized by the coexistence of competing granular networks of different striped orders [18–33]. However, so far, a rigorous study of the dynamical interplay among these multiple orders is still missing but a perspective might come from the use of the coherent x-ray beams available at the new generation synchrotron facilities and free electron lasers [34].
Here, we would like to emphasize that nano phase separation appears to be different from conventional phase separation as is schematically shown in Fig. 4. Whereas conventional phase separation will basically lead to a trivial superposition of magnetic excitation spectra of the contributing phases, electronic and magnetic nano phase separation is able to create new physical properties. As is shown schematically in Fig. 4, the energy scale and width of the magnetic excitations are altered and even the entire spectrum looks different from a simple superposition of the spectra of the contributing phases since the outwards-dispersing branches are suppressed in the low energy part of the spectrum. Whereas the bulk properties of a material are usually governed by the volume properties of the contributing phases if conventional phase separation occurs, it is this volume of the contributing phases which has almost vanished as soon as nano phase separation occurs. This is, then, responsible for new physical properties as is shown for the example of the hour-glass shaped magnetic excitation spectra in cobaltates.
The first two columns schematically show the magnetic excitation spectra of the undoped parent material La 2CoO 4 (phase A) and of the checkerboard charge ordered half-doped material La 1.5Sr 0.5CoO 4 (phase B). The reported [11] extremely weak optical mode in the spectrum of La 1.5Sr 0.5CoO 4 has been omitted since it could not be detected with a triple axis-spectrometer in Ref. [8] in the accessible Q-space and can be neglected for these reasons). The third column schematically shows the expected observations for conventional phase separation with any domain sizes down to the micro-meter scale very roughly. Finally, the last column schematically shows the situation for nano phase separation. When domain sizes shrink to the nano scale, the magnetic spectra are no longer a trivial superposition of the spectra of phases A and B. Instead, a novel spectrum with the characteristics of an hour-glass spectrum appears. Thus, nano phase separation is distinct from conventional phase separation and might induce new physical properties
References
Tranquada, J.M., Woo, H., Perring, T.G., Goka, H., Gu, G.D., Xu, G., Fujita, M., Yamada, K.: Nature 429, 534 (2004)
Vojta, M., Vojta, T., Kaul, R.K.: Phys. Rev. Lett. 97, 097001 (2006)
Eremin, I., Morr, D.K., Chubukov, A.V., Bennemann, K.H., Norman, M.R.: Phys. Rev. Lett. 94, 147001 (2005)
Boothroyd, A.T., Babkevich, P., Prabhakaran, D., Freeman, P.G.: Nature 471, 341–344 (2011)
Tranquada, J.M., Buttrey, D.J., Sachan, V., Lorenzo, J.E.: Phys. Rev. Lett. 73, 1003 (1994)
Babkevich, P., Prabhakaran, D., Frost, C.D., Boothroyd, A.T.: Phys. Rev. B 82, 184425 (2010)
Moritomo, Y., Higashi, K., Matsuda, K., Nakamura, A.: Phys. Rev. B 55, R14725 (1997)
Drees, Y., Lamago, D., Piovano, A., Komarek, A.C.: Nat. Commun. 4, 2449 (2013)
Matsuda, M., Fujita, M., Yamada, K., Birgeneau, R.J., Endoh, Y., Shirane, G.: Phys. Rev. B 65, 134515 (2002)
Zaliznyak, I.A., Hill, J.P., Tranquada, J.M., Erwin, R., Moritomo, Y.: Phys. Rev. Lett. 85, 4353 (2000)
Helme, L.M., Boothroyd, A.T., Coldea, R., Prabhakaran, D., Frost, C.D., Keen, D.A., Regnault, L.P., Freeman, P.G., Enderle, M., Kulda, J.: Phys. Rev. B 80, 134414 (2009)
Chang, C.F., Hu, Z., Hua, Wu, Burnus, T., Hollmann, N., Benomar, M., Lorenz, T., Tanaka, A., Lin, H.-J., Hsieh, H.H., Chen, C.T., Tjeng, L.H.: Phys. Rev. Lett. 102, 116401 (2009)
Drees, Y., Li, Z.W., Ricci, A., Rotter, M., Schmidt, W., Lamago, D., Sobolev, O., Rütt, U., Gutowski, O., Sprung, M., Piovano, A., Castellan, J.P., Komarek, A.C.: Nat. Commun. 5, 5731 (2014)
Guo, H., Schmidt, W., Tjeng, L.H., Komarek, A.C.: Phys. Status Solidi RRL 9, 580–582 (2015)
Kajimoto, R., Ishizaka, K., Yoshizawa, H., Tokura, Y.: Phys. Rev. B 67, 014511 (2003)
Ishizaka, K., Taguchi, Y., Kajimoto, R., Yoshizawa, H., Tokura, Y.: Phys. Rev. B 67, 184418 (2003)
Shannon, R.D. A32, 751 (1976)
Fratini, M., Poccia, N., Ricci, A., Campi, G., Burghammer, M., Aeppli, G., Bianconi, A.: Nature 466, 841 (2010)
Poccia, N., Fratini, M., Ricci, A., Campi, G., Barba, L., Vittorini-Orgeas, A., Bianconi, G., Aeppli, G., Bianconi, A.: Nat. Mater. 10, 733 (2011)
Poccia, N., Chorro, M., Ricci, A., Xu, W., Marcelli, A., Campi, G., Bianconi, A.: Appl. Phys. Lett. 104, 221903 (2014)
Poccia, N., Bianconi, A., Campi, G., Fratini, M., Ricci, A.: Supercond. Sci. Technol. 25, 124004 (2012)
Poccia, N., Campi, G., Fratini, M., Ricci, A., Saini, N.L., Bianconi, A.: Phys. Rev. B 84, 100504(R) (2011)
Ricci, A., Poccia, N., Campi, G., Joseph, B., Arrighetti, G., Barba, L., Reynolds, M., Burghammer, M., Takeya, H., Mizuguchi, Y., Takano, Y., Colapietro, M., Saini, N.L., Bianconi, A.: Phys. Rev. B 84, 060511(R) (2011)
Ricci, A., Poccia, N., Joseph, B., Innocenti, D., Campi, G., Zozulya, A., Westermeier, F., Schavkan, A., Coneri, F., Bianconi, A., Takeya, H., Mizuguchi, Y., Takano, Y., Mizokawa, T., Sprung, M., Saini, N.L.: Phys. Rev. B 91, 020503(R) (2015)
Innocenti, D., Ricci, A., Poccia, N., Campi, G., Fratini, M., Bianconi, A.: J. Supercond. Nov. Magn. 22, 529 (2009)
Ricci, A., Poccia, N., Joseph, B., Arrighetti, G., Barba, L., Plaisier, J., Campi, G., Mizuguchi, Y., Takeya, H., Takano, Y., Saini, N.L., Bianconi, A.: Supercond. Sci. Technol. 24, 082002 (2011)
Campi, G., Ricci, A., Poccia, N., Barba, L., Arrighetti, G., Burghammer, M., Caporale, A.S., Bianconi, A.: Phys. Rev. B 87, 014517 (2013)
Ricci, A., Poccia, N., Campi, G., Coneri, F., Caporale, A.S., Innocenti, D., Burghammer, M., Zimmermann, M.V., Bianconi, A.: Sci. Rep. 3, 2383 (2013)
Ricci, A., Poccia, N., Campi, G., Coneri, F., Barba, L., Arrighetti, G., Polentarutti, M., Burghammer, M., Sprung, M., Zimmermann, M., Bianconi, A.: New J. Phys. 16, 053030 (2014)
Poccia, N., Ricci, A., Campi, G., Fratini, M., Puri, A., Di Gioacchino, D.,Marcellif, A., Reynolds,M., Burghammer, M., Saini, N.L., Aeppli, G., Bianconi, A.: Proc. Natl. Acad. Sci. 109, 15685 (2012)
Poccia, N., Ricci, A., Bianconi, A.: Adv. Condens. Matter Phys. 2010, 261849 (2010)
Ricci, A., Poccia, N., Ciasca, G., Fratini, M., Bianconi, A.: J. Supercond. Nov. Magn. 22, 589 (2009)
Ricci, A., Fratini, M., Bianconi, A.: J. Supercond. Nov. Magn. 22, 305 (2009)
Ricci, A.: J. Supercond. Nov. Magn. 28, 1295 (2015)
Acknowledgments
A. C. K. thanks J. Zaanen and G. Seibold for valuable discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, Z.W., Drees, Y., Ricci, A. et al. Electronic and Magnetic Nano Phase Separation in Cobaltates La2−x Sr x CoO4 . J Supercond Nov Magn 29, 727–731 (2016). https://doi.org/10.1007/s10948-015-3302-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10948-015-3302-4