The thermodynamic properties of the superconducting state in cuprates can be determined on the basis of two characteristic types of temperature: T C (the critical temperature) and T ⋆ (the pseudogap temperature). The first temperature determines the disappearance of the superconducting state; the second one represents the value below which, in the normal state, the pseudogap appears in the electron density of states [1–3].

From the physical point of view, the values of the temperatures T C and T ⋆ depend, among other things, on the degree of the disorder occurring between CuO2 planes.

In the presented paper, the disorder induced by tin in the (Hg1−x Sn x )Ba2Ca2Cu3O8+y superconductor (Sn-doped Hg-1223) has been considered. In particular, for the selected values of tin content, the dependence of the average amplitude of the energy gap on the temperature and the dependence of the energy gap on the wave vector have been calculated. The numerical analysis has been conducted in the framework of the recently introduced model [4, 5].

We notice that the model is based on the following postulates:

  1. (i)

    In the superconductivity domain of the cuprates the fundamental role is played by the electrons on the CuO 2 planes.

  2. (ii)

    In the cuprates there exists the conventional electron–phonon interaction, which does not have to be strong.

  3. (iii)

    In the cuprates there exist strong electronic correlations, but the electron–electron scattering in the superconductivity domain is inseparably connected with absorption or emission of the vibrational quanta.

The postulate (i) underlines the importance of the quasi two-dimensionality of the electron system. The second one draws attention to the electron–phonon pairing mechanism given by Fröhlich [6, 7]. The third one postulates that the strong electron correlations in the cuprates are coupled with the phonon degrees of freedom. The first two postulates define the van Hove scenario [8–12]. The third postulate requires further discussion because it is far more subtle. In particular, it should be noted that the postulated electron correlations generalize the Hubbard approach [13]; the classical electron–electron interaction is replaced with the electron–electron–phonon coupling.

Based on approach presented in the papers [4] and [5], it is possible to prove that the critical temperature uniquely determines the value of the potential for the electron–phonon interaction. On the other hand, the temperature of the pseudogap depends on both the electron–phonon potential and the potential of the electron–electron–phonon interaction. Thus, having the experimental values of T C and T ⋆, it is possible to clearly determine the discussed potentials, and then calculate all relevant thermodynamic parameters of the superconducting state.

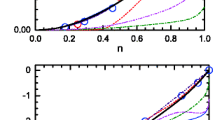
In Fig. 1, the experimental results for Sn-doped Hg-1223 obtained by Vyas and Lam are presented [14].

Fig. 1
figure 1

The influence of the tin-induced disorder on the value of the temperature T C and T ⋆ for Sn-doped Hg-1223 [14]

Full size image

Looking at Fig. 1, it is easy to notice that the growth of the parameter x causes a significant increase in the pseudogap temperature with a weak decrease of the critical temperature value at the same time.

Based on these observations, the averaged value of the amplitude of the energy gap G(T)≡2Δ(tot)(T) can be calculated on the basis of the following expression [4, 5]:

$$ \Delta^{ (\mathrm{tot} )} (T )\equiv \biggl(V+\frac {U}{6}\bigl\vert \Delta (T )\bigr\vert ^{2} \biggr)\bigl\vert \Delta (T ) \bigr\vert , $$
(1)

where V and U are the attractive electron–electron pairing potentials connected with the electron–phonon and electron–electron–phonon interactions, respectively. In the first approximation, we have:

$$ \frac{\omega_{0} |g^{ (1 )}_{\mathbf{k}} (\mathbf{q} )|^{2}}{ (\varepsilon_{\mathbf{k}}-\varepsilon_{\mathbf{k}+\mathbf {q}} )^{2}-\omega^{2}_{0}}\rightarrow-\frac{V}{2N_{0}} $$
(2)

and

$$ \frac{\omega_{0}|g^{ (2 )}_{\mathbf{k},\mathbf {k}^{'}} (\mathbf{q},\mathbf{l} )|^{2}}{ (\varepsilon_{\mathbf{k}}-\varepsilon_{\mathbf{k}-\mathbf {l}}+\varepsilon_{\mathbf{k}^{'}}- \varepsilon_{\mathbf{k}^{'}+\mathbf{l}+\mathbf{q}} )^{2}-\omega^{2}_{0}}\rightarrow-\frac{U}{24N_{0}^{3}}, $$
(3)

where \(N_{0}\equiv1/\sum^{\omega_{0}}_{\mathbf{k}}\) is the normalization constant; ω 0 represents the characteristic phonon frequency, which is of the order of the Debye frequency (ω 0=95 meV) [15]. The symbols \(g^{ (1 )}_{\mathbf{k}} (\mathbf{q} )\) and \(g^{ (2 )}_{\mathbf{k},\mathbf{k}^{'}} (\mathbf{q},\mathbf{l} )\) describe the matrix elements for the electron–phonon and electron–electron–phonon interactions, respectively. The function ε k denotes the band energy for the square lattice: ε k =−tγ(k); t is the nearest-neighbor hopping integral and γ(k)≡2[cos(k x )+cos(k y )]. In the paper, it has been assumed that t=450 meV [16].

The symbol Δ(T) in Eq. (1) denotes the averaged amplitude of the order parameter,

$$ \Delta (T )\equiv\frac{1}{N_{0}}\sum^{\omega _{0}}_{\mathbf{k}} \eta (\mathbf{k} )\langle c_{-\mathbf {k}\downarrow}c_{\mathbf{k}\uparrow} \rangle . $$
(4)

The function η(k) has the form η(k)≡2[cos(k x )−cos(k y )]. The anomalous thermodynamic average is given by 〈c −k↓ c k↑〉; c k σ is the annihilation operator of the electron state with the momentum k and the spin σ.

The amplitude Δ(T) should be calculated on the basis of the following equation [4]:

$$ 1= \biggl(V+\frac{U}{6}\big|\Delta (T )\big|^{2} \biggr) \frac {1}{N_{0}}\sum^{\omega_{0}}_{\mathbf{k}} \frac{\eta^{2}(\mathbf{k})}{2E_{\mathbf{k}}}\tanh\frac{\beta E_{\mathbf {k}}}{2}. $$
(5)

The function E k is given by the equation

$$ E_{\mathbf{k}}\equiv\sqrt{\varepsilon_{\mathbf{k}}^{2} + \biggl(V+\frac{U}{6}\big|\Delta (T )\big|^{2} \biggr)^{2} \bigl(\big|\Delta (T )\big|\eta (\mathbf{k} ) \bigr)^{2}}, $$
(6)

and the quantity β has been defined by the following: β≡1/k B T (k B is the Boltzmann constant).

From the mathematical point of view Eq. (5) can be solved only numerically. The summation of the wave vector has been approximated with the help of the integrals,

$$ \sum^{\omega_{0}}_{\mathbf{k}}\simeq\int ^{\pi}_{-\pi}\int^{\pi }_{-\pi}\,dk_{x}\,dk_{y} \theta \bigl(\omega_{0}-\vert \varepsilon _{ (\mathbf{k}_{x},\mathbf{k}_{y} )}\vert \bigr), $$
(7)

where θ denotes the Heaviside function.

The values of the pairing potentials V and U have been chosen on the basis of the temperatures T C and T ⋆ determined in the paper [14]. The obtained results have been presented in Table 1. It can be observed that the potential V is several times lower than the potential U. In addition, with the increase of tin content, the parameter V slightly decreases, whereas U significantly increases.

Table 1 The pairing potentials V and U for Sn-doped Hg-1223 superconductor
Full size table

Taking into consideration the calculated values of V and U, with the help of Eq. (5) one can determine the dependence of the averaged amplitude of the energy gap on the temperature for the selected concentrations of tin in Hg1223 superconductor. The achieved results are presented in Fig. 2.

Fig. 2
figure 2

The dependence of the averaged amplitude of the energy gap on the temperature for the selected values of tin doping. The vertical red line represents the value of the critical temperature. The vertical green line represents the temperature of the pseudogap

Full size image

On the basis of the plotted courses, it is clear that in the temperature range from 0 K to T C, the amplitude of the energy gap very weakly depends on the temperature. This result is independent of the value of the parameter x. However, with increasing tin concentration, the value of the energy gap noticeably increases.

Having the explicit form of the function G(T), it is possible to determine the influence of the concentration of tin on the value of the dimensionless ratio R G ≡G(0)/k B T C. In the case of Sn-doped Hg-1223, the growth of the parameter x causes the increase in R G from the value of 3.48 (this result is comparable with the result of the BCS theory [17, 18]) to the value of 4.88. The full course of the function R G (x) is presented in Fig. 3.

Fig. 3
figure 3

The dependence of the ratio R G on the value of the parameter x

Full size image

The results presented so far concern the properties of the energy gap, the amplitude values of which have been averaged in the vicinity of the Fermi surface. Below is the reasoning the purpose of which was to determine the dependence of the energy gap on the wave-vector with the non-averaged amplitude: G k (T)≡2Δ k (T)=2η k |ϕ k |[v+u|η k ||ϕ k |2], where ϕ k ≡〈c −k↓ c k↑〉.

In the first step, the anomalous thermodynamic average has been calculated. For this purpose, the following equation has been taken into account [19]:

$$\begin{aligned} \phi_{\mathbf{k}} =& \Biggl(\frac{1}{N_{0}}\sum ^{\omega_{0}}_{\mathbf{k}_{1}}\eta (\mathbf{k}_{1} ) \phi_{\mathbf{k}_{1}} \Biggr) \\ &{}\times \Biggl[v+u \Biggl(\frac{1}{N_{0}}\sum ^{\omega_{0}}_{\mathbf{k}_{2}}\eta (\mathbf{k}_{2} ) \phi_{\mathbf{k}_{2}} \Biggr) \Biggl(\frac{1}{N_{0}}\sum ^{\omega_{0}}_{\mathbf{k}_{3}}\eta (\mathbf{k}_{3} ) \phi^{\star}_{\mathbf{k}_{3}} \Biggr) \Biggr] \\ &{}\times \eta (\mathbf{k})\chi_{\mathbf{k}}, \end{aligned}$$
(8)

where

$$ \chi_{\mathbf{k}}\equiv\frac{\tan [\frac{i\beta}{2}\sqrt {\varepsilon^{2}_{\mathbf{k}}+M^{2}_{\mathbf{k}}} ]}{ 2i\sqrt{\varepsilon^{2}_{\mathbf{k}}+M^{2}_{\mathbf{k}}}}. $$
(9)

The function \(M^{2}_{\mathbf{k}}\) has been defined in the following way:

$$\begin{aligned} M^{2}_{\mathbf{k}} \equiv& \Biggl(\frac{1}{N_{0}} \sum^{\omega _{0}}_{\mathbf{k}_{1}}W_{\mathbf{k}_{1}\mathbf{k}} \phi^{\star }_{\mathbf{k}_{1}} \Biggr) \Biggl(\frac{1}{N_{0}}\sum ^{\omega_{0}}_{\mathbf{k}_{2}}W_{\mathbf {k}\mathbf{k}_{2}}\phi_{\mathbf{k}_{2}} \Biggr) \\ =& \eta^{2} (\mathbf{k} ) \Biggl(\frac{1}{N_{0}}\sum ^{\omega _{0}}_{\mathbf{k}_{1}}\eta_{\mathbf{k}_{1}} \phi^{\star}_{\mathbf {k}_{1}} \Biggr) \Biggl(\frac{1}{N_{0}}\sum ^{\omega_{0}}_{\mathbf{k}_{2}}\eta _{\mathbf{k}_{2}}\phi_{\mathbf{k}_{2}} \Biggr) \\ &{}\times \Biggl[v+u \Biggl(\frac{1}{N_{0}}\sum ^{\omega_{0}}_{\mathbf {k}_{3}}\eta_{\mathbf{k}_{3}}\phi_{\mathbf{k}_{3}} \Biggr) \Biggl(\frac{1}{N_{0}}\sum^{\omega_{0}}_{\mathbf{k}_{4}} \eta _{\mathbf{k}_{4}}\phi^{\star}_{\mathbf{k}_{4}} \Biggr) \Biggr]^{2}, \end{aligned}$$
(10)

where

$$ W_{\mathbf{k}_{1}\mathbf{k}_{2}}\equiv v_{\mathbf{k}_{1}\mathbf {k}_{2}}+\frac{1}{N^{2}_{0}}\sum ^{\omega_{0}}_{\mathbf {k}_{3}\mathbf{k}_{4}}u_{\mathbf{k}_{1}\sim\mathbf{k}_{4}} \phi_{\mathbf{k}_{3}} \phi^{\star}_{\mathbf{k}_{4}}. $$
(11)

Additionally, \(v_{\mathbf{k}_{1}\mathbf{k}_{2}}\equiv v\eta (\mathbf{k_{1}} )\eta (\mathbf{k_{2}} )\) and \(u_{\mathbf{k}_{1}\sim\mathbf{k}_{4}} \equiv u\eta (\mathbf{k_{1}} )\eta (\mathbf{k_{2}} )\eta (\mathbf{k_{3}} )\eta (\mathbf{k_{4}} )\).

Equation (8) has been solved for 7000 points placed close to the Fermi level. The numerical procedures discussed and tested in the works have been applied (see [19–23]).

Figure 4 presents the full dependence of the energy gap on the angle α, where α≡arctan(k y /k x ). The calculations have been made for x=0.25 and for the few selected values of the temperature.

Fig. 4
figure 4

The circles show the dependence of the energy gap on the angle for the selected values of the temperature. The red line represents the average values of the energy gap. It has been assumed that x=0.25

Full size image

Based on the presented results, it can be noted that in the anti-nodal region (α∼0 deg) the G(α) values are weakly dependent on the temperature. On the other hand, the values of the energy gap from the nodal region (α∼45 deg) are very low for T>T C. Note that the obtained results are consistent with the results of the ARPES experiments conducted for cuprates [24, 25].

In summary, in the presented work we have determined the dependence of the energy gap averaged amplitude on the temperature for the (Hg1−x Sn x )Ba2Ca2Cu3O8+y superconductor. The selected values of the x parameter, taken from the range of 0 to 0.25, have been considered. It has been found that higher concentration of tin forces the dimensionless ratio R G to increase and reach the values far beyond the value predicted by the BCS theory. In particular, R G ∈(3.48,4.88). It should be noted that this result is related to the strong growth of the electron–electron–phonon potential with an increase in the parameter x.

When conducting the studies of the superconducting properties in Sn-doped Hg-1223, the dependence of the energy gap on the angle α has been additionally determined. The rate of the concentration of tin equal to 0.25 and some selected values of the temperature have been taken into account. It has been found that in the nodal area the energy gap disappears with the increasing temperature. On the other hand, in the anti-nodal area its values are weakly dependent on the temperature. This proves the existence of the pseudogap in the electron density of states above the critical temperature.