Drug structure–transport relationships

Abstract

Malcolm Rowland has greatly facilitated an understanding of drug structure–pharmacokinetic relationships using a physiological perspective. His view points, covering a wide range of activities, have impacted on my own work and on my appreciation and understanding of our science. This overview summarises some of our parallel activities, beginning with Malcolm’s work on the pH control of amphetamine excretion, his work on the disposition of aspirin and on the application of clearance concepts in describing the disposition of lidocaine. Malcolm also spent a considerable amount of time developing principles that define solute structure and transport/pharmacokinetic relationships using in situ organ studies, which he then extended to involve the whole body. Together, we developed a physiological approach to studying hepatic clearance, introducing the convection–dispersion model in which there was a spread in blood transit times through the liver accompanied by permeation into hepatocytes and removal by metabolism or excretion into the bile. With a range of colleagues, we then further developed the model and applied it to various organs in the body. One of Malcolm’s special interests was in being able to apply this knowledge, together with an understanding of physiological differences in scaling up pharmacokinetics from animals to man. The description of his many other activities, such as the development of clearance concepts, application of pharmacokinetics to the clinical situation and using pharmacokinetics to develop new compounds and delivery systems, has been left to others.

“Write for the reader – not for oneself” Malcolm Rowland, personal communication, 1983

Introduction

I would like to acknowledge from the outset that I have been privileged to be an invited speaker at the 70th birthday of one of my mentors, Malcolm Rowland, who has greatly assisted in the development of my views about science and life. There are a number of other Australians, including Felix Bochner, Garry Graham, Andrew McLachlan, Allan Evans and Lloyd Sansom, who have also worked with Malcolm and would like to have been here. There are many others who have been influenced by your many sojourns “Down Under”. Malcolm was successful in attracting one of us, Leon Aarons, to work with him at Manchester from postdoctoral studies to today, a collaboration that has resulted in many pivotal papers in our discipline. In this paper, I highlight the influence Malcolm has had on my own research, especially the role of solute structure on pharmacokinetics. I begin with the physiological perspective Malcolm brought to pharmacokinetics and how he used that knowledge to define solute structure pharmacokinetic relationships. My perspective is an intensely personal one in that I started in membrane transport and was influenced by Malcolm’s thinking early on, I had the pleasure to work with Malcolm whilst on my only sabbatical leave, to watch Malcolm’s continuing journey but, at the same time, working independently to reach where I think we are now.

Physiological pharmacokinetics

Malcolm’s early studies were concerned with the assay of a number of drugs but three “stand out” in my mind, perhaps because I have also worked on them. The first is amphetamine/methylamphetamine which Malcolm analysed in urine by gas chromatography and showed that their excretion was highly dependent on urine pH [1, 2] (Fig. 1a). Malcolm’s future focus on physiological pharmacokinetics is undoubtedly nurtured by these studies showing that amphetamine renal excretion is dependent on both urine flow rate and urine pH and this can change greatly over a 24 h period. Less well known is my work on the percutaneous absorption of phenol in the rat, mainly because it was published in a local journal that was not in Current Contents or Index Medicus, the Australian Journal of Pharmaceutical Science. Phenol was widely used in Calamine Lotion and had a similar assay problem to amphetamine—it was volatile and poor recovery resulted if evaporated to dryness before reconstitution and injection into a gas chromatograph. The “secret” to avoid such losses was to apply the technique used by Malcolm for amphetamine. In my case, this involved extraction of phenol from blood using diethyl ether and evaporation to 20 μl in a 100 μl nipple at the end of a tube and injecting 10 μl. I found that phenol displayed bi-exponential kinetics after intravenous administration and, importantly, that the anaesthetic greatly affected phenol’s intravenous disposition and percutaneous absorption. As shown in Fig. 1b, there are much higher phenol plasma levels for urethane than for ethyl ether. There are two effects induced by the anaesthetics—alterations in blood flow at the absorption site and alterations in phenol clearance. Urethane is a dermal vasodilator whereas ethyl ether is a vasoconstrictor [3]. Phenol is rapidly metabolised by conjugation through the sulphate and glucuronide pathways and these are inhibited by diethyl ether but not by urethane [4], explaining the continued accumulation over time for ether.

Fig. 1

a Effect of urine pH and urine output on the urinary excretion of amphetamine in man, after oral administration of 10 mg (+)-amphetamine sulphate (reprinted by permission from Macmillan Publishers Ltd: Nature [1], copyright 1965). b Blood levels of phenol in the rat observed during the cutaneous application of phenol (1%) under different anaesthetics [169]. c Plasma aspirin concentrations after 650 mg aspirin as a solution on two separate occasions. On the second occasion (open circle), the subject felt nervous and faint while the 10 min blood sample was being taken. It is apparent that there is impairment in absorption on this occasion, probably “due to decreased motility of, and circulation to, the GIT” (adapted from [17]). d Plasma and synovial fluid aspirin concentrations in one patient after oral ingestion of aspirin, ASA, 20 grains (1,296 mg). Time zero corresponds to 2.5 h after the patient had inadvertently taken 10 grains (648 mg) of aspirin (adapted from [18]). e Plasma levels of lidocaine (±SD, n = 7) after 50 mg intravenous bolus to control and heart failure (adapted from [24]). f Plasma levels of lidocaine after infusion to a normal patient and in a patient of same size with heart failure (adapted from [24]). g Effect of heart failure, liver disease, and renal failure on lidocaine disposition parameters in man (adapted from [24])

The second “stand-out” drug that Malcolm studied during his postdoctoral studies at the University of San Francisco with Sid Riegelman was aspirin [5], a compound that I also did a number of studies on, including defining its disposition in elderly and alcoholic subjects [6], extrahepatic metabolism [7], its effects on platelets [8] and in describing the apparent autoinduction of the salicyluric acid pathway on chronic ingestion of high doses [9, 10]. We also followed up on Tom Tozer and colleagues’ steady state work on salicylate clearance being determined by saturable protein binding and metabolism [11] to model these effects during a single dose [12]. Perhaps, one of the most fulfilling aspects of our work on aspirin is that a dose form we helped to develop [8] as a prophylaxis for heart attacks and stroke, Cartia^® (Glaxo-Smith-Kline) is still on the market today. Malcolm, Leon Aarons and others also showed that aspirin absorption was faster in women after oral administration but slower after intramuscular administration [13]. They also defined the kinetics of aspirin hydrolysis by albumin [14]. These early studies, many of which we conducted on ourselves naive in terms of today’s ethics requirements, have not all been without problems. One of my colleagues suffered from a most profound, long and sustained Arthus reaction (i.e. a rare but rather severe and immediate nonatopic hypersensitivity reaction) when we each injected each other with diluted wasp venom to see if topical aspirin and other products lessened the resulting inflammatory response [15]. Another Australian colleague, Felix Bochner, obtained his tinnitus in taking high doses of salicylate whilst on sabbatical with Malcolm [16].

Figure 1c and d shows two illustrations of Malcolm’s work with aspirin. Figure 1c shows the importance of blood flow in oral absorption. Here, blood sampling continued to be undertaken in one of their subjects who felt faint. It is clear that there is impairment of aspirin absorption in this situation [17]. The second example shows that there may be a delay in reaching a target site of action is distant from the plasma, contributing to a delay in response. Here, the peaking of aspirin in synovial fluid occurs some time after that in plasma (Fig. 1d) [18]. One of the “follow-up” questions that I studied was how did posture and sleep affect pharmacokinetics and, if the changes observed meant a need to change dosing regimens? The first drug we studied, amoxicillin, showed the most pronounced postural effect with the plasma AUC being significantly greater in the upright position than in the lying down position or during sleep [19]. I feel certain that exercise (subjects were allowed to walk whilst in the upright position) possibly added to the postural effect of an increase in real blood flow and higher active renal secretion of amoxicillin. We did not find differences when we examined benzyl penicillin given intramuscularly [20] or intravenously [21]. Lying down and sleeping had the effect of delaying the absorption of paracetamol [22].

The third “stand out” compound is lidocaine. Here, Malcolm and colleagues showed that an altered clearance can lead to enhanced plasma levels and, in heart failure, disposition effects further compounds lidocaine pharmacokinetics. Figure 1e and f shows the altered disposition of lidocaine in heart failure after intravenous bolus and infusion administration, examples I have often used in my teaching. Here, the reduced body perfusion in cardiac failure leads to reduction in the apparent distribution volume by about one third. Lidocaine clearance in heart failure is also reduced by about one third. An important finding is that the dependent variable half life (= 0.693 × apparent distribution volume/clearance) is effectively unchanged in heart failure [23, 24]. A reduced dosing is indicated with both a reduced clearance (target steady state plasma concentration = infusion rate/clearance) and a reduced volume of distribution (initial plasma concentration = dose/apparent distribution volume), whereas the lack of change in half life would predict that no change in lidocaine dosing was necessary. It is noted that physiological pharmacokinetic principles does not predict a reduced volume of distribution at steady state in heart failure for all drugs. For example, cardiac failure leads to a reduction in the clearance of midazolam but not in its steady state distribution volume [25]. In contrast to the significant changes in lidocaine pharmacokinetics in cardiac failure, no significant changes in lidocaine pharmacokinetics are observed in renal failure; whereas, in liver disease, only lidocaine clearance is impaired, leading in turn to an increased half life (Fig. 1g).

Structure transport relationships in absorption and distribution

Most target tissues contain vasculature, interstitium, and cells, and representing them as a single compartment is physiologically naive. [26].

In my view, one of Malcolm’s key contributions was his work with Rene Levy in which he explored structure penetration relationships for the subcutaneous absorption kinetics of local anaesthetics [27]. Here, lidocaine was the lead compound. Malcolm and Rene used a relatively simple pharmacokinetic model involving uptake from a subcutaneous solution into a membrane and thence clearance into the systemic circulation (Fig. 2a). He showed that for a series of synthesised lidocaine derivatives disappearance was characterised by increased membrane uptake and uptake into the systemic circulation with lipophilicity (Fig. 2b). We used this model to show that solute lipophilicity and surface area also defined the uptake of preservatives into plastic containers and loss into the atmosphere during storage [28] (Fig. 2c). We also used Levy and Rowland’s experimental approach [27] to study the deep tissue penetration of a number of compounds after dermal application, including salicylate, and showed that direct penetration to deeper tissues occurred early on but that levels at longer times were mainly due to recirculatory events [29]. Later, we became interested in using subcutaneous infusions to manage rehydration of elderly subjects and had the opportunity to use radiolabelled tracers and imaging to better define the kinetics of subcutaneous absorption in man [30, 31].

Fig. 2

a Compartmental model representation of drug loss from solutions at subcutaneous site and stored in plastic containers (adapted from [27]). b In vivo biphasic disappearance curves of lidocaine and compound I(F) (pH 7.95) and compound III (CH₃) (pH 7.95) after subcutaneous application (adapted from [27]). c Representative plots of fraction of solute remaining in aqueous solution in polyethylene containers stored at 37 ± 1°C [28]. d In vivo and postmortem lidocaine disappearance curves from subcutaneous solutions in the rat (adapted from [27]). e Vasoconstriction and penetration: salicylic acid 2 h after dermal application [170]. f Fraction remaining versus time plot for paracetamol, salicylate, diclofenac and albumin after injection of a mixture of all solutes into the knee effusions of the five subjects studied [35]. (P and K are octanol-water and hexane-water partition coefficients)

An elegant part of Malcolm and Rene’s subcutaneous absorption kinetics studies was to show that blood flow and ionisation were components in the subcutaneous absorption kinetics. As shown in Fig. 2d, there was negligible absorption for lidocaine from subcutaneous solutions with no blood flow (post-mortem studies) and when the lidocaine was in an ionised form (pH 5.42). On the other hand, initial uptake an unionised lidocaine (pH 7.95) was faster than the partially ionised lidocaine in vivo and the later disappearance from a pH 7.95 solution in vivo was greater than for post-mortem studies showing the importance of subcutaneous blood flow in determining clearance from the site into the systemic circulation. We used a similar approach to show that vasoconstrictors modified the salicylate concentrations in deeper tissues after dermal application to be intermediate between in vivo and post-mortem tissues (Fig. 2e). We also used the lack of blood flow induced changes in interferon disappearance from dermal sites to show that the dermal absorption of larger molecules, like interferon, was most likely absorbed via the lymphatics [32]. The role of lymphatics in solute disposition has been extensively studied by my Australian colleagues [33, 34]. Finally, in contrast to the absorption findings shown for subcutaneous and dermal administration of aqueous solutions, the uptake of compounds from synovial fluid in man decreases with increasing lipophilicity. Here, binding to synovial fluid protein dominates and, indeed, for diclofenac about half its clearance occurs as diclofenac bound to albumin (Fig. 2f) [35]. A similar finding was reported by Malcolm’s group but this time using an air pouch in the rat [36]. They concluded that a perfusion rate limitation probably applied to the uptake of NSAIDs into the pouch during the first 2 h when albumin flux into the pouch is not enough to affect the permeability of the NSAIDs. The effective flux of the NSAIDs is lowered when the albumin concentration in the pouch increases after 5 h. In a later paper, they suggested that drug transport into the site cannot be based on unbound drug only and must also include the simultaneous flux of drug bound to albumin, which enters the target site due to increased vascular permeability associated with the inflammatory response [37].

The famous German writer Goethe is said to have remarked “Whatever you can do or dream you can, begin it. Boldness has genius, power and magic in it.” [180]. Looking back, this certainly applies in my own studies of absorption and pharmacokinetics of drugs and toxins across the skin and the uptake of drugs into plastics. My own scientific journey into transport-structure relationships began during an undergraduate pharmacy research project. One of our objectives was to quantify the uptake of drugs and preservatives into the plastic surface of eye dropper bottles that had been sterilised in the autoclave. We showed that solute properties, the nature of the container and the role of the area:solution volume ratio were determinants of drug loss [38]. My PhD studies in topical absorption was driven by an interest in making topical creams and a 1942 publication by Zondek [181], that showed topical chloroxylenol could be effective in treating urinary tract infections. It was during this time that Les Benet introduced me to Laplace Transforms in pharmacokinetics, John Wagner interested me in the modelling of nonlinear processes and one of Malcolm’s younger PhD colleagues from Arnold Beckett’s laboratory in London, Ted Triggs, taught me nonlinear regression with NonLin, leading in part to a paper we published in Nature [39]. A key finding, in our work on the percutaneous absorption of different phenolic compounds, was that penetration of phenolic compounds increased in a parabolic fashion with lipophilicity (Fig. 3a) [40]. At that time, I had used thermodynamic studies to argue that the non-parabolic behaviour was due to the more polar “aqueous” layers below the skin providing an additional resistance to the penetration of the more lipophilic solutes. Russ Potts and Richard Guy subsequently reanalysed my data with others and concluded that the parabolic behaviour was most likely due to these more lipid solutes also being larger in size [41]. We then showed that molecular size is the dominant determinant for the maximum flux of solutes through the skin (Fig. 3b) [42]. Hence, when we re-examined the percutaneous absorption of a series of phenolic compounds with almost identical size and hydrogen bonding, we found that the permeability coefficient is linearly related to lipophilicity (Fig. 3c) [43]. An important outcome of this work was the observation of a parabolic relationship between maximum flux and lipophilicity for solutes of approximately the same size (Fig. 3d) but that the estimated diffusivity was independent of lipophilicity (Fig. 3e) and the maximum flux was directly related to the solubility in the stratum corneum (Fig. 3f). Thus, parabolic relationship between maximum flux and lipophilicity reflects a maximum solubility that exists for solutes in the stratum corneum lipids [43]. Our finding differs from conventional thinking that polar solutes cannot partition into a membrane while lipid solutes partition out of a membrane when a solute crosses several membranes and aqueous interstitial fluids. This conventional view has long been advocated by many [44–46]. Figure 3 illustrates the overturning of a long held scientific paradigm through a key experiment. It also reinforces advice given to me as a young PhD student by a then faculty member, Jack Thomas. His advice was that all quality data can help, even if the interpretation is incorrect—as that data may enable others or yourself to come up with better models. This wise advice has proven to be so correct, particularly in pharmacokinetic modelling where George Box, the industrial statistician, is frequently quoted as having said ‘all models are wrong, some are useful’. One of my other mentors, Gordon Flynn, with whom I also have the privilege of writing a textbook soon to be published [47], has also pointed out that perhaps a particular model is never really wrong, it just applies to a different jurisdiction. Hence, the dependence of skin maximum flux on skin solubility probably dominates for the low to moderately lipophilic compounds (0 < log P < 4) that we studied. Other mechanisms are more likely to dominate for very polar solutes (e.g. via appendages or polar head group pathway [48]) and very lipophilic solutes (significant additional barrier resistance from the more polar epidermis [49], dermis [50] and aqueous layer [40, 44]. As Gordon Flynn, points out [47]: ‘This (latest work) seems to be the first clear demonstration of how biological permeability, at its maximum, is directly dependent on solubility.’

Fig. 3

a Relationship between permeability of phenolic compounds through human epidermis and their lipophilicity as defined by their logarithm of octanol-water partition coefficient, log P (adapted from [40]). b Relationship between maximum flux, J_max and solute size, as defined by molecular weight MW, for solutes from aqueous solution through human epidermal membranes [42]. c Variation in permeability coefficient (kp), with experimental log octanol-water partition coefficient (log P) (r² = 0.81) [43]. d Dependence of maximum flux J_max on log P for penetration of phenolic compounds through excised human epidermal membranes using Franz cells [43]. e Variation of diffusivity (D) with experimental log P [43]. f Dependence of maximum flux J_max on stratum corneum solubility Sc for penetration of phenolic compounds through excised human epidermal membranes [43]

However, as is often the case, the real clinical outcomes occur by serendipity. In other words, one normally finds the unexpected in trying to understand something else. One of my more profound experiences occurred in early 1975, when our hospital clinicians began infusions of nitroglycerin as a treatment for cardiac failure. Initially the infusions appeared successful but, within 30 min, efficacy was lost. Some efficacy could be regained if the infusion rate was increased but never as much as the clinicians anticipated. When studies were repeated a week later no response at all was obtained. The question became: what was happening? We deduced that one of two possibilities were possible. Either the drug was not getting to the patient as anticipated or there was something happening in the body to the nitroglycerin. We therefore did some simulated infusions and measured what came out of the infusion system at different flow rates. The results obtained are shown in Fig. 4a. It is evident that 100% was delivered initially but then became very low when low flow rates were used and somewhat higher when higher flow rates were employed. Hence, clearly, there was uptake of nitroglycerin into the plastic of the infusion sets [51]. Later studies showed that uptake was occurring into both the polyvinyl chloride infusion bag and into the giving set [182]. Indeed, the reason why there was no delivery a week later was that the hospital’s pharmacy had decided to make up the nitroglycerin infusions in the infusion bags 24 h earlier to have stock on hand as needed—without realising this would effectively deactivate the nitroglycerin as it enabled it even more time to diffuse into the plastic infusion bag. The importance of this finding is that we then went on to show that a number of other drugs including isosorbide dinitrate [52], diazepam, various phenothiazines etc. [53, 54] are also lost into these systems and that diffusion in the plastic was a major mechanism for loss [55]. Importantly, our work paralleled Levy and Rowland’s [27], in that we found it was the unionised and not ionised solutes that were lost into infusion bags on storage [56]. Thus, the pH of the infusion solution and pK _a of the solute are key determinants for loss on storage. But, returning to the earlier story, the cardiologists were not happy in just knowing the reason. They wanted to know how to give nitroglycerin without such problems. The solution turned out to be the same one we know needs to be applied in minimising lipophilic drug loss for solutes stored in aqueous solutions in plastic containers—the plastic should be high density and relatively inert. For nitroglycerin infusions, this equated to using a polyolefin system, later commercialised by Tridil^®, where there was negligible loss on infusion (Fig. 4b).

Fig. 4

a Effect of flow rate on percentage of nitroglycerin in solutions emerging from plastic infusion sets (adapted from [51]). b Percentage of nitroglycerin emerging after passage through 80 cm polyethylene tubing attached to glass syringe (adapted from [51])

Malcolm and a then young postdoc Andrew MacLachlan, also ventured into the area of using regional administration to more effectively target drugs by applying pharmacokinetic principles [26]. Earlier studies had initially used a well-stirred pharmacokinetic models and transport by blood flow. Later studies included a permeability barrier as well as a tissue partition coefficient. Together, they showed that a positive Drug Targeting Index (DTI), or Selective Advantage could be achieved using intra-arterial administration. They showed that DTI depended on the relative permeability of unbound drug across the vascular and cellular membranes in the target tissue relative to the tissue blood flow rate and that the flux of bound drug between the vascular and interstitial spaces of the target could also affect the DTI [26].

Whole body physiological pharmacokinetics

“An overall objective of physiological modelling is to simulate the complete system through a fundamental study of its component parts.” [57]

Malcolm also had a particular interest in defining solute structure pharmacokinetic relationships in terms of the underlying tissue volumes, blood flows and clearances. Using lidocaine again as the reference compound, Malcolm and colleagues used a physiological pharmacokinetic model (Fig. 5a) to describe the effect of haemorrhage on lidocaine blood levels (Fig. 5b) and predicted tissue disposition (Fig. 5c) [58, 59]. Our work possibly adds another dimension, in that we showed for both aspirin and the organic nitrates that breakdown occurs in the blood [60–62] and in extravascular tissues [62, 63], resulting in extraction across various organs [64, 65], as illustrated in Fig. 5d. Malcolm and Steve Toon also conducted a seminal drug structure pharmacokinetic study in which they described the physiological pharmacokinetics for a series of barbiturates [66]. This work showed that total barbiturate volume of distribution was relatively constant but that protein binding and unbound barbiturate volume of distribution increased with lipophilicity (Fig. 5e), consistent with an underlying increased tissue affinity [66]. In contrast, the relationship for clearance was complex and mainly due to renal and hepatic elimination for low and high lipophilicity, respectively (Fig. 5f). A hepatic blood flow limitation applied for the highest homologs, whereas metabolism of the lowest homologs was determined by the stereochemistry of position 5 on the barbituric acid ring. Renal clearance decreased with increasing lipophilicity as a consequence of increased tubular reabsorption (Fig. 5f) [66].

Fig. 5

a A blood perfusion model used to describe the disposition kinetics of lidocaine in the monkey and man (reprinted by permission from Macmillan Publishers Ltd: Clinical Pharmacology and Therapeutics [59], copyright 1974). b Arterial blood concentrations of lidocaine in a normal and subsequently bled rhesus monkey, with superimposed perfusion model simulation following a bolus (10 mg) and a constant infusion (100 μg/kg/min) (reprinted by permission from Macmillan Publishers Ltd:[58] Clinical Pharmacology and Therapeutics, copyright 1974). c Perfusion model simulation of the distribution of lidocaine in various tissues in man after a 1 min injection of 100 mg in a 70 kg man (reprinted by permission from Macmillan Publishers Ltd: [58] Clinical Pharmacology and Therapeutics, copyright 1974). d Extraction of nitroglycerin across various organs of the sheep after intravenous infusion (adapted from [65]). e Semilogarithmic plot of barbiturate total and unbound volume of distribution at steady state against lipophilicity, as defined by the logarithm of the octanol water partition coefficient (log P) (adapted from [66]). f Relationship between barbiturate total blood and renal clearance and lipophilicity, as defined by the logarithm of the octanol water partition coefficient (log P) (adapted from [66])

Pharmacokinetics in the perfused rat liver

The manner in which alterations in physiological states, such as organ blood flow, degree of drug binding within blood, and hepatocellular enzymatic activity, influence the hepatic handling of drugs and hence their oral availability is poorly understood [67]

Malcolm also saw the wisdom of studying solute disposition in isolated organs so as to excluding varying blood flow, systemic feedback and recirculation effects. His work on lidocaine in isolated perfused livers with Sandy Pang is in some ways an extension of his work at the subcutaneous site, if both are seen as isolated organs. Malcolm and Sandy had shown the disposition of lidocaine and its metabolite MEGX was better described by a “well-stirred” than by a “tube” model [67–69].

The question of what was the most appropriate physiological clearance model for the liver was also a topic that I embarked on during my time at Manchester with Malcolm. This occurred during the years 1983 to 1984 and were an eventful time for my family and I as it was our first time out of Australia and I was taking my first (and as it has proved to be so far, only) sabbatical leave. I had organised to spend most of my time with Malcolm but had also organised to spend some time in Clinical Pharmacology at Guy’s Hospital in London and to also visit various institutions in Europe. It was during my time with Malcolm that I met and spent time with Dawn and a fellow Australian Leon Aarons and his family as well as others in Malcolm’s team. During my family’s sojourn to Europe in the middle of this leave, we ventured behind the then Iron Curtin to meet Michael Weiss and his family (a separate ‘mystical’ story), and one also leading to a long term collaboration.

Malcolm had originally planned for me to do a series of experiments on protein flux from the blood into tissues across the capillaries but soon realised that my interest lay in modelling. He therefore raised with me the controversial question of what model should we be using to describe extraction in the liver. The experimental steady state extraction data, in general, supported a well stirred (also called venous equilibrium) model, whereas pragmatically, the liver physiology was more consistent with a series of hepatic blood vessels (sinusoids) being described by a tube model. One of the important first steps Malcolm made was in giving me every relevant American Journal of Physiology article on solute disposition in the liver he came across. This was a crucial first step as it encouraged me to read outside my usual area of the pharmaceutical sciences. I know that I tried every modelling ‘trick’ I knew and got to a ‘desperation’ stage when I left for my scheduled trip to Europe. It was then on the way back that the ‘obvious’ occurred to me. Maybe the distribution of blood flows was not exponential as assumed by the well stirred model, nor a single value as assumed by the tube model nor a normal distribution as assumed by a distributed form of the model introduced by Luxon and Forker [70]? Could it be a log normal distribution? Koo et al. [71] had published blood cell velocities in 515 sinusoids. When we analysed this data as a cumulative probability distribution, we found that the data was better described by a log-normal than a normal plot [72]. Further, we also found that the outflow concentration response–time data for labelled red blood cells and albumin injected into a perfused liver as a bolus by one of Malcolm’s PhD students (Anis Ahmad) was a skewed distribution [72]. This led us on a chase looking for all models that may be applicable to such phenomena and could also describe the outflow concentration–time profiles for extracted drugs in organs. I ended up in the University of Manchester Institute for Science Technology (UMIST) library, housed in a ‘grimy red-brick gothic structure’ in the centre of the city. I learned that the most widely used models in chemical reaction engineering was the convection–dispersion model, often just called the dispersion model, and the tank-in-series model [73, 74]. The dispersion model generated an inverse Gaussian distribution of residence times–a similar skewed shape to a log normal distribution. As shown in Fig. 6, this model gives a skewed to the right outflow distribution after an impulse-response or bolus input. This, to me, was an important insight as almost all studies seeking to discriminate between physiological clearance models had been using a steady state input and steady state outflow concentrations. The other contemplated tank-in-series model generates a gamma distribution, which is also a skewed distribution. The important realisation was that one should not be assuming a model but rather letting the physiology define the model. Again, the Box quote (op. cit.) is applicable.

Fig. 6

Comparison of different models of hepatic elimination (adapted from [72, 82, 90, 109–117, 171])

One of the other realisations for me is that other disciplines often providing a platform that can be used to develop our science. The convection–dispersion model has its origins from the Chemistry Nobel Laureate Irving Langmuir’s second paper in 1908 [75] and has been used in a wide range of areas including chemical reaction engineering [76], meteorology [77], oceanography [78], soil science [79] and so on. In addition, as had been realised for many years by the physiologists and chemical engineers, one also needed to inject non-extracted markers as a bolus input to a system to describe the various spaces in an individual organ such as the heart, liver and kidney [80] or chemical reactor [76]. Indeed, Goresky had elegantly shown that the impulse-response profiles for various markers can be superimposed if the differences in their volumes can be corrected for [81]. As shown in Fig. 7a, the convection–dispersion model describes that data very closely. One of the major lessons that I learned from Malcolm was “to write for one’s reader and not for oneself”. It is this insight that led to Malcolm’s suggested dispersion and efficiency numbers so that the dispersion model was characterised and readily understood in physiological pharmacokinetic terms.

Fig. 7

a Output fraction versus time data of Goresky and the line of best fit for mixed boundary model (adapted from [81]). b Availability of colloidal chromic phosphate across the isolated perfused rat liver as a function of blood perfusate flow rate (data of Brauer et al. [172]) [83]. c Availability of diazepam across the isolated perfused rat liver against fraction diazepam unbound (data of Rowland et al. [173]) [83]. d Residual plot for (filled diamond) well stirred model, (filled square) parallel-tube and (open circle) dispersion models for apparent availability of the metabolite (acetaminophen) generated from its precursor (phenacetin) [84]. e Availabilities (F) observed after perfusion of drugs through rat isolated perfused livers versus the estimated efficiency number (RN) determined from in vitro microsomal data. (adapted from [85]

The dispersion number derived from Goresky’s data was 0.12 (Fig. 7a), intermediate between the well stirred model value of infinity and tube model value of zero [82]. Thus, the dispersion model was an intermediate model and the work to date had been on comparing the extremes of this model. Importantly, when one fits steady state data and allows the dispersion number to vary, one obtains an intermediate, if not a precise a value. For instance, the dependence of chromic phosphate hepatic availability on liver flow rate has a dispersion number of 0.35 ± 0.24 (Fig. 7b) whereas the hepatic availability for diazepam varies with fraction unbound in plasma with a dispersion number of 0.29 ± 0.23 (Fig. 7c) [83]. In addition, the formation of metabolites [84] (Fig. 7d) and the correspondence of perfused liver availability and in vitro microsomal enzyme activity [85] (Fig. 7e) are consistent with intermediate dispersion numbers. The importance of the latter is in scaling up human microsomal and hepatocyte data to predict hepatic extraction in vivo as exemplified by Sugiyama’s group [86, 87] and others [88]. It should also be noted that the well stirred and parallel-tube models are the asymptotic solutions for the dispersion model and that, when the availability in the liver is high (F > 0.6), one can show that the predicted availability for all models is similar [72].

It would be remiss of me not to acknowledge also the extensive and continuing work on modelling of drug disposition in the liver undertaken by Sandy Pang, Carl Goresky, Yuichi Sugiyama, Frank Burzynski, Andreas Schwab, Ludvik Bass, Tony Bracken, Yuri Anissimov, Peter Robinson, Bruce Luxon, Leigh Forker, Denis Morgan and colleagues using a physiological ‘segregated” transit time approach that contrasts with the micromixing that is assumed for the convection–dispersion model in the liver and the “tank-in-series” model described by Dick Weisiger, Gray and Tam and by us. As Malcolm, John Donaldson (great applied mathematician and, incidentially, father of Princess Mary of Denmark) and I showed, the choice of an overall micromixing or segregated transit time does not affect outflow predictions for linear kinetics [183]. It does however, matter for non-linear kinetics as can be seen by comparing inflow into a tank in series with a tube with inflow into a tube in series with a tank. Notably, also, the morphological organisation of the liver is characterised by high intervascular mixing in the periportal (zone 1) region but mainly segregated vascular flow in the central (zone 3 region). One possible pharmacokinetic hypothesis for the arrangement is that an efficient “flattening” of plasma concentrations brought about by well-stirred conditions (Fig. 6) is needed in the periportal region to limit exposure of the cells to drug and metabolite, especially as much drug metabolism occurs in zone 3 [89]. The segregated “tube” arrangement would allow more efficient extraction in zone 3.

Our work on heterogeneity in liver kinetics [183] as well as nonlinear models [90] is an area developed greatly and contributed to by Sugiyama’s group [86, 87] and others [88]. There has been some controversy on what boundary conditions are the most appropriate for use with the dispersion model [91, 92]. Malcolm and his colleagues have made the last comment on this issue and, in noting the pros and cons of the closed conditions (favoured in providing mass conservation at the boundary) and mixed conditions (ease of its analytical form), suggest that the two models give essentially equivalent fits and dispersion numbers [93]. My group has moved, influenced by Michael Weiss, to using an empirical dual inverse Gaussian function that best describes the outflow profiles after bolus injections into the liver [94] combined with a two compartment model that enables the relative importance of permeability, diffusion and binding in the cells to be dissected out [95]. With Yuri Anissimov, we have also developed a compartmental model for hepatic elimination that accurately describes the observed vascular dispersion [96], but our application of this model has, to this stage been limited [97].

Over the last two decades, both Malcolm’s and my group have had a major emphasis on gathering data using the impulse-response technique in the in situ perfused liver and in analysing data using the two compartment dispersion or related vascular residence time model, taking into account the effects of catheter transit times (Fig. 8a). The use of a bolus input has enabled the effect of vascular dispersion and two compartment distribution in the liver (Fig. 8b) to be dissected out using a vascular reference to define the vascular space and vascular dispersion (Fig. 8c). To my knowledge this is the only effective way to separate out the role of hepatocyte permeability as a determinant in hepatic pharmacokinetics. Malcolm’s group has shown, for instance, that the hepatocyte permeability surface area product increases with lipophilicity but that the dispersion number is independent of the compound studied [98, 99]. This finding confirms that the dispersion number is a measure of the variation in residence times of solutes in the hepatic vasculature. In other studies, Malcolm’s group has examined hepatic disposition of salicylate [100], the effect of varying plasma [101, 102] and hepatic tissue binding [103], as well as the role of the dual liver blood supply [104] and erythrocyte binding [105] on hepatic disposition kinetics. My group’s work has taken a slightly different track and concentrated on solute structure-hepatic disposition relationships in normal and in diseased livers. We have added to Malcolm’s work to show in our latest analysis with 38 compounds that the permeability surface area product was dependent on both lipophilicity and either the number of hydrogen bonding groups or the polar surface area, but not the molecular size of the solutes (Fig. 8d) [106]. The lack of solute dependency on size contrasts with transport of solutes through skin where solute size is dominating [42]. Other studies include protein binding [107], interspecies scaling [108], liver regeneration [109], metabolite kinetics [110, 111], binding, ion trapping and disease [112–117]. In addition, we have examined saturable uptake of digoxin and its inhibition by rifampicin [118]. Our work in the diseased liver suggests that the hepatic permeability surface area product depends both on the solute properties, defined mainly by lipophilicity, and the liver pathophysiology, as defined by a computerised fibrosis index derived from histology slides (Fig. 8e). More recently, Tony Hunt has worked with us to apply his group’s in silico autonomous software object models that allow the hepatic morphology and transported events to be simulated in a physiologically based, mechanistically realistic, in silico liver. We have been able to then use this in silico model to describe their disposition in normal and diseased livers [119–121].

Fig. 8

a Impulse-response technique showing the change in the shape of the impulse on passage through catheters and a perfused organ. b Outflow profile of a vascular reference (sucrose) and the drug atenolol in a perfused rat liver (adapted from [113]). c Convection–dispersion model showing the processes of vascular dispersion in hepatic sinusoids, distribution into and from, binding and clearance in hepatocytes [171]. d Permeability surface area product (log PS)_predicted for 38 drugs entering hepatocytes in perfused livers can be related to observed values log PS_observed using (filled diamond) solute lipophilicity (log P_app) alone (r² = 0.62) or, even better, (filled square) both solute lipophilicity and number of hydrogen bonding groups (r² = 0.76), or (open circle) solute lipophilicity and polar surface area (r² = 0.75) (adapted from [106]). e In diseased livers both lipophilicity (defined by log P_app) and liver fibrosis (defined by a computerised fibrosis index (FI) derived from histology slides) define permeability surface area products (PS) in the perfused rat liver: open circle normal group; filled diamond CCl₄ treated group, filled square alcohol treated group (log PS = 1.647 − 0.028FI + 0.08 log P_app: p = 0.001, r² = 0.844, n = 30) (adapted from [113])

Let us return to the original question that led to the development of the dispersion model, the ability to predict the extraction of highly extracted drugs. Currently, two approaches are being taken. One is to ignore that a substantial difference exists between the predicted and observed values using the well stirred model [122]. In the end, it is about changing paradigms as Malcolm has most recently pointed out [123].

Pharmacokinetics in other perfused organs

Physiologically-based pharmacokinetics: academic curiosity or the holy grail to prediction? Why do we get the profiles we see? Can we predict quantitatively events in humans from in vitro, animal and other information? Can we explain differences across compounds? Can we predict likely variability in target patient population under clinically realistic conditions?

Malcolm Rowland 2009

Three different models described in 1968 set the scene for seeking to better understand physiological pharmacokinetics at a more basic level.

Malcolm along with Sid Riegelman started questioning the one compartment pharmacokinetic model [124]. Ken Bischoff and Bob Dedrick suggested that the pharmacokinetics for thiopental could be described by an a priori mathematical pharmacokinetic model that included blood flows, tissue volumes, lipid solubility, protein binding and metabolism [125]. Perl and Chinard described a convection–diffusion model to describe solute disposition in the kidney in 1968 [126]. This model is identical to the convection–dispersion model we described for the liver, except that the terminology is different. The need to apply a convection dispersion model in describing renal clearance of drugs has yet to be established. It could be argued that, for most drugs, the well stirred model is adequate in describing renal clearance. Indeed, Malcolm’s group used a simple physiologically based model of tubular reabsorption to relate the renal clearances of a homologous series of six 5-substituted barbituric acids, of varying lipophilicity, in a recirculating isolated perfused rat kidney preparation [127]. In addition, Malcolm, with Stephen Hall, has also conducted a number of studies in the perfused kidney, emphasising the role of protein binding [128, 129].

We began looking at the application of the dispersion model to other organs and began by defining the physiological spaces in the perfused leg under differing physiological conditions [130] and recognising the combined importance of vascular dispersion, tissue partitioning and tissue diffusion [95]. Figure 9a shows that the model we used involved blood flow to the organ, vascular dispersion of blood in the organ, permeation from the blood into tissue and diffusion in tissue. We then applied this information to describe the disposition of diazepam, lidocaine and antipyrine in the isolated perfused rat hindlimb [131]. We later showed that a similar dispersion existed in the perfused human leg [132]. One practical application was in trying to estimate the optimal perfusion conditions for administering and washing out a cytotoxic agent whilst the limb bearing the melanoma(s) was separated from the rest of the body [133]. In a second application, we also measured drug levels in the tumour and tissue using microdialysis [134, 135]. We also applied this perfused limb model to study the uptake of solutes of different protein binding into underlying tissue after topical application [136]. Our data suggests that transport into tissues is both perfusion and tissue binding limited, the latter being most evident for the highly bound diclofenac where significant diclofenac was eluted in albumin containing but not dextran containing perfusate. In general, the outflow profile for a solute bound to perfusate correlates with its uptake into muscle, the site for most uptake, and not into fat or skin (Fig. 9b) [137]. However, consistent with events shown in Fig. 8a, Anne Heatherington and Malcolm showed that intravascular distribution in the hindlimb after bolus administration can be overshadowed by events in the connecting tubing and cannulas, resulting in discrepancies between bolus and infusion pharmacokinetics [138]. Malcolm’s group has also applied the dispersion model to describe the disposition of markers and a series of barbiturates in the perfused hind leg [139].

Fig. 9

a Vascular dispersion in a muscle capillary bed and drug distribution from the capillaries into the tissue (adapted from [95, 131, 137, 174, 175]). b Using the stochastic two-phase model fit (dashed line) for perfusate outflow concentration–time profile (open circle) for propranolol to show that the resulting predicted amount of propranolol in muscle tissue (solid line) is similar to that measured directly in muscle (filled diamond) (adapted from [137]). c Predicted human venous concentration–time profiles after intravenous administration based on the rat whole body dispersion model, showing an oscillation in the initial 15 min (adapted from [145]). d Excellent linear relationship between predicted and experimentally determined unbound partition coefficients Kpu between tissue and plasma for disparate compounds (7 very weak bases, 20 acids, 4 neutral drugs, 2 group 2 zwitterions and 6 group 1 zwitterions in 13 rat tissues). The dashed lines represent 82% of 314 predictions (adapted from [154]). e In vivo imaging of fluorescein uptake into rat liver cells by multiphoton tomography [156]

We also investigated the importance of dispersion in the human placenta [140]. The perfused head proved to be a more challenging organ as we were unable to distinguish uptake between the brain and other parts of the head [141, 142]. Recently, we have described disposition in the pancreas [143]. Most recently, we have described the disposition of solutes in the perfused rat lung [144]. The eventual outcome of bringing these various organs together is a whole-body physiologically based pharmacokinetic model based on dispersion concepts and to scale it to man in vivo [145]. The human venous outflow profiles were characterised by the oscillation in venous and arterial blood flow at early times as reported in the anaesthesiology literature, as illustrated in Fig. 9c. At longer times there was a build up of drugs in the skeletal muscle, skin, and fat and was better able to accurately predict the distribution of drugs in the body than the conventional well-stirred organ whole-body PBPK model. In our experience, similar profiles, with much less computation, can be achieved by representing each organ with a three compartment in series model and interlinking the organs as in the classical physiological PBPK model. It is possible, however, that the dispersion generated by the varying flows to individual organs will prove to be the major determinant of whole body dispersion [146] rather than the vascular dispersion in individual organs. Indeed, Michael Weiss has generated a similar profile to that in Fig. 9c for the whole body based on cardiac output and systemic transit time dispersion [147].

Sampling body organs

The alternative to trying to understand what happens in the individual organs of the body and resynthesising them back into the body is to study drug disposition in organs directly in vivo. This latter approach was reported by Malcolm’s group in 1998 as basis for evaluating the contribution of structural and physicochemical properties to pharmacokinetics. They studied the distribution kinetics of nine 5-alkyl-5-ethyl barbituric acids in arterial blood and 14 tissues (lung, liver, kidney, stomach, pancreas, spleen, gut, muscle, adipose, skin, bone, heart, brain, testes) after i.v. bolus administration in rats using well-stirred organ compartments and assuming that either permeability rate limitation or perfusion rate limitation may be involved in the distribution processes [148]. Muscle accounted for ~ 50% of the total unbound volume of distribution for all compounds. This data was then analysed using tissue-to-unbound plasma distribution coefficients for each of the 14 rat tissues in terms of their octanol to water partition ratio, P, binding capacity of each tissue and its water content [149]. Confounders include albumin diffusion [150] and lipophilic solutes [151]. Later work included the benzodiazepines [152]. This work was then extended to the predictability of tissue-to-plasma water partition coefficients for 7 very weak bases, 20 acids, 4 neutral drugs and 8 zwitterions in rat adipose, bone, brain, gut, heart, kidney, liver, lung, muscle, pancreas, skin, spleen and thymus [153, 154]. Expressions were developed that recognise solubility in tissue water, partitioning into neutral lipids, neutral phospholipids and other sites as well as drug ionisation). Interestingly, in their latest paper in the series, Trudy Rodgers and Malcolm found a prediction for binding restricted to muscle was similar to that using individual tissues and was high in rats and humans [155]. Figure 9d shows that their modelling has provided an excellent description of unbound partitioning coefficients for a series of heterogeneous compounds.

The dilemma remains—what is the best way forward. My group is adopting three key approaches. One is to image events as they occur in individual organs in space and time in vivo [156] (Fig. 9e). The second is to sample those organs with time. Our group has used blood and destructive tissue sampling (Fig. 9b) as well as cutaneous microdialysis [134, 135] to define the time course of drugs in organs. Data analysis involves using either a mechanistic physiological pharmacokinetic model [64, 65, 137] or to use simulation spatiotemporal processing of solutes in individual organs [119]. Interestingly, the convection–dispersion developed with Malcolm underpins each approach. For instance, the dispersion process is seen on the direct imaging of the liver. Unpublished work on the transport of solutes into deeper tissues of human skin after topical application in vivo measured by microdialysis suggests that a convection dispersion process is partly responsible for the carriage of highly albumin bound drugs to deeper tissues. Finally, all of our in vivo simulations include an empirical gamma function that mimics the dispersion process.

Comments made by Malcolm in 2009 at the American Society of Clinical Pharmacology and Therapeutics contextualises our work in the way that drugs may be developed in the future. In brief, the physiological pharmacokinetic model structure is common to all mammals and includes both physiological parameters, such as blood flow, tissue size, composition etc. that are independent of drug (system properties) and compound specific parameters that must be overlaid onto this system such as clearance, tissue affinity, membrane permeability etc. Much is now known about pharmacokinetic variability with intrinsic factors such as age, genetics, gender, and extrinsic factors such as formulation, disease, co-medication, environment, diet and nutrition) affecting tissue weight, composition, blood flow, enzyme and transporter activity as well as hepatic metabolism, biliary, renal, gastrointestinal and lung function. Building mechanistic physiological pharmacokinetic models by this approach, as emphasised by this overview, is essentially a bottom up synthetic approach in which parameter variability is defined by determinants such as enzyme activity, organ size, age etc. I would suggest that a futuristic opportunity is a combination of the synthetic in silico approach that Tony Hunt has led [119–121, 157] and The Simcyp Population-based ADME Simulator [158] led by Geoff Tucker and Amin Rostami to predict drug-drug interactions and pharmacokinetics in clinical populations. Simcyp integrates existing human physiological, genetic and epidemiological data base information with supplied in vitro data to predict ‘real-world’ pharmacokinetics.

Malcolm also commented that population pharmacokinetics has been essentially a parallel but top down approach. Population pharmacokinetics has its origins in applying statistical methodology to refine dosage regimens for individual patients [159]. Today, population pharmacokinetics continues to apply a statistical approach in analysing observed data with usually a simple compartmental empirical but, sometimes, with semi-physiologic, pharmacokinetic model. Appropriate covariates are used to account for the variability in parameters. The approach, now called pharmacometrics, has become a standard component in drug development, in defining exposure-responses in Phase II/III studies and in satisfying regulatory agencies, such as the FDA and TGA, that a product is sufficiently efficacious and safe to be approved for release into the general human population. A major limitation in the approach is that Phase III studies rarely have the statistical power required to confidently assess the quantitative significance of potential covariates, and their correlations. Malcolm concluded his talk with a future vision advocating a middle out approach, in which physiologically-based PK models into all phases of clinical drug development. Models defined by animal and human physiological pharmacokinetic data should be refined by preclinical pharmacokinetic parameters from early experimental human/patient (Phase 0, I and II) data. Phase III then becomes a confirmation phase where the emphasis is on whether observed concentration–time data are within expectations, instead of searching for covariates and relationships. I have attempted to summarise the three approaches in Fig. 10. Similar principles should apply to pharmacodynamics. The eventual outcome should be a move to a better model-based drug development paradigm.

Fig. 10

Diagrammatic comparison of the bottom up synthesised physiological pharmacokinetic models approach to drug development, including microdosing, with the top down population pharmacokinetic approach and the middle out approach that seeks to bring the bottom up and top down approaches together. Similar principles are applied in extension to pharmacokinetic–pharmacodynamic relationships [176–179] (broader population histogram redrawn from [176]; events at steady state redrawn from [179])

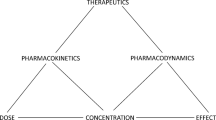
Pharmacokinetics and pharmacodynamics

The idea of applying the concept of clearance, well established in renal physiology, to drug kinetics was of singular importance and one to which Malcolm Rowland and Grant Wilkinson made the major contribution. [160].

The story I have presented to date represents only a small fraction of the total impact Malcolm has had on our discipline and on me, in particular. There are many other stories to tell about Malcolm’s contribution to the broader discipline of pharmacokinetics and pharmacodynamics, including the development of clearance concepts [161], the application of pharmacokinetics to the clinical situation [162, 163], understanding toxicokinetic principles [164] and using pharmacokinetics in drug development [165–167] and making pharmacokinetics easier to understand [168]. I will leave it to others to tell those stories!