The Helmholtz Equation with Uncertainties in the Wavenumber

Abstract

We investigate the Helmholtz equation with suitable boundary conditions and uncertainties in the wavenumber. Thus the wavenumber is modeled as a random variable or a random field. We discretize the Helmholtz equation using finite differences in space, which leads to a linear system of algebraic equations including random variables. A stochastic Galerkin method yields a deterministic linear system of algebraic equations. This linear system is high-dimensional, sparse and complex symmetric but, in general, not hermitian. We therefore solve this system iteratively with GMRES and propose two preconditioners: a complex shifted Laplace preconditioner and a mean value preconditioner. Both preconditioners reduce the number of iteration steps as well as the computation time in our numerical experiments.

1 Introduction

The Helmholtz equation is a linear partial differential equation (PDE), whose solutions are time-harmonic states of the wave equation, see [15, 20]. Important applications of this model are given in acoustics and electromagnetics [2]. The Helmholtz equation includes a wavenumber, which is either a constant parameter or a space-dependent function. Furthermore, boundary conditions are imposed on the spatial domain.

We consider uncertainties in the wavenumber. Thus the wavenumber is replaced by a random variable or a spatial random field to quantify the uncertainties. The solution of the Helmholtz equation changes into a random field, which can be expanded into the (generalized) polynomial chaos, see [31]. We employ the stochastic Galerkin method to compute approximations of the unknown coefficient functions. Stochastic Galerkin methods were used for linear PDEs of different types including random variables, for example, see [13, 33] on elliptic type, [14, 24] on hyperbolic type, and [22, 32] on parabolic type. Wang et al. [30] applied a multi-element stochastic Galerkin method to solve the Helmholtz equation including random variables. We investigate the ordinary stochastic Galerkin method, which is efficient if the wavenumbers are not close to resonance.

The stochastic Galerkin method transforms the random-dependent Helmholtz equation into a deterministic system of linear PDEs. Likewise, the original boundary conditions yield boundary conditions for this system. We examine the system of PDEs in one and two space dimensions. A finite difference method, see [16], produces a high-dimensional linear system of algebraic equations. When considering absorbing boundary conditions, the coefficient matrices are complex-valued and non-hermitian.

We focus on the numerical solution of the linear systems of algebraic equations. The dimension of these linear systems rapidly grows for increasing numbers of random variables. Hence we use iterative methods like GMRES [27] in the numerical solution. The efficiency of an iterative method strongly depends on an appropriate preconditioning of the linear systems. We propose two preconditioners in the general case where the wavenumber can depend on space and on multiple random variables: a complex shifted Laplace preconditioner, see [6, 8], and a mean value preconditioner, see [10, 30]. Statements on the location of spectra and estimates of matrix norms are shown. Furthermore, results of numerical computations are presented for both settings.

The article is organized as follows. The stochastic Helmholtz equation is introduced in Sect. 2 and discretized in Sect. 3. We discuss the complex shifted Laplace preconditioner in Sect. 4 and the mean value preconditioner in Sect. 5. Sections 6 and 7 contain numerical experiments in one and two spatial dimensions, respectively, which show the effectiveness of the preconditioners.

2 Problem Definition

We illustrate the stochastic problem associated to the Helmholtz equation.

2.1 Helmholtz Equation

The Helmholtz equation is a PDE of the form

$$\begin{aligned} - \Delta u - k^2 u = f \quad \text {in } Q \end{aligned}$$

(1)

with an (open) spatial domain $Q \subseteq \mathbb {R}^d$ and given source term $f: Q \rightarrow \mathbb {R}$. The wavenumber k is either a positive constant or a function $k: \overline{Q} \rightarrow \mathbb {R}_+$. The unknown solution is $u: \overline{Q} \rightarrow \mathbb {K}$ with either $\mathbb {K} = \mathbb {R}$ or $\mathbb {K} = \mathbb {C}$. Here $\Delta = \sum _{j=1}^d \frac{\partial ^2}{\partial x_j^2}$ denotes the Laplace operator with respect to $x = [x_1, \ldots , x_d]^\top \in \mathbb {R}^d$.

Often homogeneous Dirichlet boundary conditions, i.e.,

$$\begin{aligned} u = 0 \quad \text {on } \partial Q , \end{aligned}$$

(2)

are applied for simplicity. Alternatively, absorbing boundary conditions read as

$$\begin{aligned} \partial _n u - {{\text {i}}}k u = 0 \quad \text {on } \partial Q , \end{aligned}$$

(3)

where $\partial _n$ denotes the derivative with respect to the outward normal of Q and ${{\text {i}}}= \sqrt{-1}$ is the imaginary unit.

2.2 Stochastic Modeling

We consider uncertainties in the wavenumber. A simple model to include a variation of the wavenumber is to replace the constant k by a random variable on a probability space $(\Omega ,\mathcal {A},P)$. We write $k=k(\xi )$, where $\xi : \Omega \rightarrow \mathbb {R}$ is some random variable with a traditional probability distribution. More generally, the wavenumber can be a space-dependent function on $\overline{Q}$ including a multidimensional random variable $\xi : \Omega \rightarrow \Xi$ with $\Xi \subseteq \mathbb {R}^s$. We assume $\xi = (\xi _1,\ldots ,\xi _s)^\top$ with independent random variables $\xi _{\ell }$ for $\ell =1,\ldots ,s$. Now the wavenumber becomes a random field

$$\begin{aligned} k(x,\xi ) = k_0(x) + \sum _{\ell =1}^s \xi _{\ell } k_{\ell }(x) \end{aligned}$$

(4)

with given functions $k_{\ell }: \overline{Q} \rightarrow \mathbb {R}$ for $\ell =0,1,\ldots ,s$, as in [30]. A truncation of a Karhunen-Loève expansion, see [11, p. 17], also yields a random input of the form (4). Consequently, the solution of the deterministic Helmholtz equation (1) changes into a random field $u: \overline{Q} \times \Xi \rightarrow \mathbb {K}$. We write $u(x,\xi )$ to indicate the dependence of the solution on space as well as the random variables.

We assume that each random variable $\xi _{\ell }$ has a probability density function $\rho _{\ell }$. Since the random variables are independent, the product $\rho = \rho _1 \cdots \rho _s$ is the joint probability density function. Without loss of generality, let $\rho (\xi ) > 0$ for almost all $\xi \in \Xi$. The expected value of a measurable function $f: \Xi \rightarrow \mathbb {K}$ depending on the random variables is

$$\begin{aligned} \mathbb {E}(f) = \int _{\Omega } f(\xi (\omega )) \; \text {d}P(\omega ) = \int _{\Xi } f(\xi ) \, \rho (\xi ) \, \text {d}\xi , \end{aligned}$$

if the integral is finite. The inner product of two square-integrable functions f, g is

$$\begin{aligned} \langle f,g\rangle = \int _{\Xi } f(\xi ) \, \overline{g(\xi )} \, \rho (\xi ) \, \text {d}\xi . \end{aligned}$$

(5)

In the following, $\mathcal {L}^2(\Xi ,\rho )$ denotes the Hilbert space of square-integrable functions. The associated norm is $\Vert f\Vert _{\mathcal {L}^2(\Xi ,\rho )} = \sqrt{\langle f,f\rangle }$.

Later we will focus on uniformly distributed random variables $\xi _{\ell }: \Omega \rightarrow [-1,1]$. In this case, the joint probability density function is constant, i.e., $\Xi = [-1,1]^s$ and $\rho \equiv 2^{-s}$.

2.3 Polynomial Chaos Expansions

We assume that there is an orthonormal polynomial basis $(\phi _i)_{i \in \mathbb {N}_0}$ in $\mathcal {L}^2(\Xi ,\rho )$. Thus it holds that

$$\begin{aligned} \langle \phi _{i} , \phi _{j}\rangle = \delta _{i,j} = {\left\{ \begin{array}{ll} 1 &{} \text {for } i = j \\ 0 &{} \text {for } i \ne j \\ \end{array}\right. } \end{aligned}$$

with the inner product (5). In the case of uniform probability distributions, the multivariate functions $\phi _i$ are products of the (univariate) Legendre polynomials. We assume that $\phi _0 \equiv 1$. The number $m+1$ of multivariate polynomials in s variables up to a total degree r is

$$\begin{aligned} m+1 = \frac{(s+r)!}{s! \, r!}, \end{aligned}$$

(6)

see [31, p. 65]. This number grows fast for increasing r or s.

Let $u(x,\cdot ) \in \mathcal {L}^2(\Xi ,\rho )$ for each $x \in \overline{Q}$. The polynomial chaos (PC) expansion is

$$\begin{aligned} u(x, \xi ) = \sum _{i=0}^\infty v_i(x) \phi _i(\xi ) \end{aligned}$$

(7)

with (a priori unknown) coefficient functions

$$\begin{aligned} v_i(x) = \langle u(x, \xi ), \phi _i(\xi )\rangle \quad \text {for } i \in \mathbb {N}_0. \end{aligned}$$

(8)

The series (7) converges in $\mathcal {L}^2(\Xi ,\rho )$ pointwise for $x \in \overline{Q}$. If the wavenumber k is an analytic function of the random variables, then the rate of convergence is exponentially fast for traditional probability distributions.

3 Discretization of the Stochastic Helmholtz Equation

We consider the stochastic Helmholtz equation

$$\begin{aligned} - \Delta u(x, \xi ) - k(x, \xi )^2 u(x, \xi ) = f(x), \quad x \in Q \subseteq \mathbb {R}^d, \end{aligned}$$

(9)

with given source term $f: Q \rightarrow \mathbb {R}$ and random wavenumber $k: \overline{Q} \times \Xi \rightarrow \mathbb {R}_+$, together with either homogeneous Dirichlet boundary conditions

$$\begin{aligned} u(x, \xi ) = 0, \quad x \in \partial Q, \quad \xi \in \Xi , \end{aligned}$$

(10)

or with absorbing boundary conditions

$$\begin{aligned} \partial _n u(x, \xi ) - {{\text {i}}}k(x, \xi ) u(x, \xi ) = 0, \quad x \in \partial Q, \quad \xi \in \Xi . \end{aligned}$$

(11)

All derivatives are taken with respect to x. We discretize this boundary value problem in two steps, with a finite difference method (FDM) in space and the stochastic Galerkin method in the random-dependent part. The steps can be done in any order. We first give an overview of the procedure when beginning with the FDM in Sect. 3.1. In Sect. 3.2, we discuss the discretization when beginning with the stochastic Galerkin method.

3.1 FDM and Stochastic Galerkin Method

A spatial discretization of the boundary value problem with a second order FDM on an equispaced grid leads to a (stochastic) linear algebraic system

$$\begin{aligned} S(\xi ) U(\xi ) = F_0 \end{aligned}$$

(12)

with constant vector $F_0 \in \mathbb {R}^n$ and stochastic matrix $S(\xi ) \in \mathbb {K}^{n,n}$ for $\xi \in \Xi$, depending on the boundary conditions. In the case of homogeneous Dirichlet boundary conditions, it follows that

$$\begin{aligned} S(\xi ) = T - D_2(\xi ), \end{aligned}$$

(13)

with T and $D_2(\xi )$ symmetric positive definite, and in case of absorbing boundary conditions,

$$\begin{aligned} S(\xi ) = T - {{\text {i}}}D_1(\xi ) - D_2(\xi ), \end{aligned}$$

(14)

with T and $D_1(\xi )$ symmetric positive semidefinite and $D_2(\xi )$ symmetric positive definite. (For details of this discretization, see the appendix of [23].) In a second step, we consider a PC approximation of $U(\xi )$ of the form

$$\begin{aligned} \widetilde{U}_m(\xi ) = \sum _{i=0}^m \phi _i(\xi ) V_i, \quad \text {where } V_i = \begin{bmatrix} v_{\ell , i} \end{bmatrix}_{\ell =1}^n \in \mathbb {R}^n \text { for } i = 0, 1, \ldots , m, \end{aligned}$$

(15)

and $\phi _i$ are polynomials as in Sect. 2.3. The coefficient vectors $V_i$ are determined by the orthogonality of the residual

$$\begin{aligned} R_m(\xi ) = S(\xi ) \widetilde{U}_m(\xi ) - F_0. \end{aligned}$$

(16)

to the subspace ${{\,\textrm{span}\,}}\{ \phi _0, \phi _1, \ldots , \phi _m \}$ with respect to the inner product $\langle \cdot , \cdot \rangle$ in (5), i.e., by $\langle R_m(\xi ), \phi _i(\xi )\rangle = 0$ for $i = 0, 1, \ldots , m$. Here the inner product is taken component-wise. The orthogonality condition is equivalent to

$$\begin{aligned} \langle S(\xi ) \widetilde{U}_m(\xi ), \phi _i(\xi )\rangle = \langle 1, \phi _i(\xi )\rangle F_0 = \delta _{i,0} F_0, \quad i = 0, 1, \ldots , m, \end{aligned}$$

(17)

due to $\phi _0 \equiv 1$. This leads to a (deterministic) linear algebraic system

$$\begin{aligned} A V = F, \quad V = \begin{bmatrix} V_0 \\ \vdots \\ V_m \end{bmatrix}, \quad F = \begin{bmatrix} F_0 \\ \vdots \\ F_m \end{bmatrix}, \end{aligned}$$

(18)

where the stochastic Galerkin projection $A \in \mathbb {K}^{(m+1)n, (m+1)n}$ is a block matrix with $m+1$ blocks of size $n \times n$, and $F_i = 0 \in \mathbb {R}^n$ for $i = 1, \ldots , m$.

Remark 1

The Galerkin approximation (15) can be interpreted as a spatial discretization of a Galerkin approximation $\widetilde{u}_m(x, \xi ) = \sum _{i=0}^m v_i(x) \phi _i(\xi )$ of $u(x, \xi )$. Evaluating $\widetilde{u}_m$ at discretization points $x_1, \ldots , x_n$ yields

$$\begin{aligned} \begin{bmatrix} \widetilde{u}_m(x_1, \xi ) \\ \vdots \\ \widetilde{u}_m(x_n, \xi ) \end{bmatrix} = \sum _{i=0}^m \phi _i(\xi ) \begin{bmatrix} v_i(x_1) \\ \vdots \\ v_i(x_n) \end{bmatrix}. \end{aligned}$$

(19)

Hence $V_i$ in (15) can be interpreted as a discretization of $v_i(x)$ by $v_{\ell ,i} = v_i(x_\ell )$.

The matrix $S(\xi )$ in (13) and (14) is a (complex) linear combination of real symmetric positive (semi-)definite matrices. The following lemma shows that this structure is preserved in the stochastic Galerkin method; see [21, Lem. 1] and its proof. These properties of the matrix S and thus A will be essential for our analysis of shifted Laplace preconditioners in Sect. 4.

Lemma 2

Let $A(\xi ) = \begin{bmatrix} a_{\mu , \nu }(\xi ) \end{bmatrix}_{\mu ,\nu } \in \mathbb {R}^{n,n}$ with $a_{\mu ,\nu } \in \mathcal {L}^2(\Xi , \rho )$, and $V \in \mathbb {R}^n$. Define

$$\begin{aligned} A_{ij} :=\begin{bmatrix} \langle a_{\mu , \nu }(\xi ) \phi _i(\xi ), \phi _j(\xi )\rangle \end{bmatrix}_{\mu ,\nu } \in \mathbb {R}^{n,n}, \quad i, j = 0, 1, \ldots , m, \end{aligned}$$

(20)

and the stochastic Galerkin projection

$$\begin{aligned} A :=\begin{bmatrix} A_{ij} \end{bmatrix}_{i,j} \in \mathbb {R}^{(m+1)n, (m+1)n}. \end{aligned}$$

(21)

We then obtain for $i, j = 0, 1, \ldots , m$

$$\begin{aligned} \langle A(\xi ) \phi _i(\xi ) V, \phi _j(\xi )\rangle = A_{ij} V, \end{aligned}$$

(22)

where the inner product is taken component-wise. Additionally, $A_{ij} = A_{ji}$. Moreover, if $A(\xi )$ is symmetric, then A is symmetric, and if $A(\xi )$ is symmetric positive (semi-)definite for almost all $\xi \in \Xi$, then A is symmetric positive (semi-)definite.

Corollary 3

In the notation of Lemma 2, if $A(\xi ) = A_0$ is independent of $\xi$, then $A_{ij} = \delta _{ij} A_0$ and $A = I_{m+1} \otimes A_0$, with the identity matrix $I_{m+1} \in \mathbb {K}^{m+1, m+1}$ and the Kronecker product.

Finally, we obtain the following result on the structure of the matrix A in (18).

Theorem 4

Let the spatial dimension be $d \in \{ 1, 2 \}$. A finite difference and stochastic Galerkin approximation of the Helmholtz equation (9) on $Q = ]0, 1[^d$ with either homogeneous Dirichlet or absorbing boundary conditions leads to a linear system (18) with coefficient matrix

$$\begin{aligned} A = L - {{\text {i}}}B - K \end{aligned}$$

(23)

and real-valued matrices L, B, K. The matrix K is symmetric positive definite, B, L are symmetric positive semidefinite. In case of homogeneous Dirichlet boundary conditions, L is symmetric positive definite and $B = 0$.

Proof

The statement of the theorem follows in each case by applying the stochastic Galerkin approximation as described above to (12) and using Lemma 2 as well as Corollary 3 separately for each term composing $S(\xi )$; see (13) and (14). $\square$

The matrix L results essentially from the discretization of the Laplacian, B from the (absorbing) boundary conditions, and K is the discretization of the term including the wavenumber.

3.2 Stochastic Galerkin Method and FDM

Alternatively, we can begin with the stochastic Galerkin method. This leads to a system of deterministic PDEs, which are subsequently discretized by a FDM. The PC expansion (7) suggests a stochastic Galerkin approximation of $u(x, \xi )$ of the form

$$\begin{aligned} \widetilde{u}_m(x, \xi ) = \sum _{i=0}^m v_{i, m}(x) \phi _i(\xi ). \end{aligned}$$

(24)

The coefficient functions $v_{i,m}$ in the stochastic Galerkin method are in general distinct from the coefficients $v_i$ in (8). Nevertheless, we will usually write $v_i$ instead of $v_{i, m}$ in the sequel for notational convenience. The coefficients in the Galerkin approach are determined by the orthogonality of the residual

$$\begin{aligned} R_m(x,\xi )&= - \Delta \widetilde{u}_m(x, \xi ) - k(x,\xi )^2 \widetilde{u}_m(x, \xi ) - f(x) \\&= - \sum _{i=0}^m \Delta v_i(x) \phi _i(\xi ) - k(x,\xi )^2 \sum _{i=0}^m v_i(x) \phi _i(\xi ) - f(x) \end{aligned}$$

to the subspace ${{\,\textrm{span}\,}}\{ \phi _0, \phi _1, \ldots , \phi _m \}$, i.e., by $\langle R_m(x,\xi ), \phi _j(\xi ) \rangle = 0$ for $j = 0,1,\ldots , m$ and each $x \in Q$. The latter is equivalent to

$$\begin{aligned} - \Delta v_j(x) - \sum _{i=0}^m \langle k(x,\xi )^2 \phi _i(\xi ), \phi _j(\xi )\rangle v_i(x) = \langle 1, \phi _j(\xi )\rangle f(x) = \delta _{j,0} f(x) \end{aligned}$$

(25)

for $j=0,1,\ldots ,m$ in Q. Thus we obtain a system of PDEs for the unknown coefficient functions $v_0,v_1,\ldots ,v_m$. Define $C(x) = [c_{ij}(x)] \in \mathbb {R}^{m+1, m+1}$ for $x \in Q$ by

$$\begin{aligned} c_{ij}(x) = \langle k(x, \xi )^2 \phi _i(\xi ), \phi _j(\xi )\rangle = \int _\Xi \phi _i(\xi ) \phi _j(\xi ) k(x, \xi )^2 \rho (\xi ) \, \text {d}\xi , \quad i, j = 0, 1, \ldots , m. \end{aligned}$$

(26)

Since by assumption $k(x,\xi ) > 0$ for all x and $\xi$, the matrix C(x) is symmetric positive definite (as Gramian of an inner product with weight function $k(x, \xi )^2 \rho (\xi )$). Setting

$$\begin{aligned} v(x) = \begin{bmatrix} v_0(x)&v_1(x)&\cdots&v_m(x) \end{bmatrix}^\top , \quad F(x) = \begin{bmatrix} f(x)&0&\cdots&0 \end{bmatrix}^\top , \end{aligned}$$

(27)

we write the system of PDEs (25) as

$$\begin{aligned} - \Delta v(x) - C(x) v(x) = F(x) \quad \text {in } Q, \end{aligned}$$

(28)

which is a larger deterministic system of linear PDEs. Still we require boundary conditions for the system (28).

The homogeneous Dirichlet boundary condition (10) implies $v_j(x) = 0$ for $x \in \partial Q$ and $j = 0, 1, \ldots , m$, hence

$$\begin{aligned} v(x) = 0 \quad \text {on } \partial Q. \end{aligned}$$

(29)

Inserting the Galerkin approximation (24) into the absorbing boundary conditions (11) yields the residual

$$\begin{aligned} R_m(x,\xi )&= \sum _{i=0}^m (\partial _n v_i)(x) \phi _i(\xi ) - {{\text {i}}}k(x, \xi ) \sum _{i=0}^m v_i(x) \phi _i(\xi ). \end{aligned}$$

(30)

By the orthogonality $\langle R_m(x, \xi ), \phi _j(\xi )\rangle = 0$ in the Galerkin approach, we obtain

$$\begin{aligned} \partial _n v_j(x) - {{\text {i}}}\sum _{i=0}^m \langle k(x, \xi ) \phi _i(\xi ), \phi _j(\xi )\rangle v_i(x) = 0, \quad j = 0, 1, \ldots , m. \end{aligned}$$

(31)

The matrix $B(x) = [b_{ij}(x)] \in \mathbb {R}^{m+1, m+1}$ with

$$\begin{aligned} b_{ij}(x) = \langle k(x, \xi ) \phi _i(\xi ), \phi _j(\xi )\rangle = \int _\Xi \phi _i(\xi ) \phi _j(\xi ) k(x, \xi ) \rho (\xi ) \, \text {d}\xi , \quad i, j = 0, 1, \ldots , m, \end{aligned}$$

(32)

is symmetric and positive definite (since $k(x, \xi ) > 0$ by assumption). The boundary condition (31) can be written with B(x) as

$$\begin{aligned} (\partial _n v)(x) - {{\text {i}}}B(x) v(x) = 0 \quad \text {on } \partial Q. \end{aligned}$$

(33)

Discretizing the boundary value problem (28) with (29) or (33) with a second order FDM yields the same linear algebraic system as in Sect. 3.1.

4 Complex Shifted Laplace Preconditioner

Following the investigation in [9], we consider the Helmholtz equation (9) with a complex shift in the wavenumber

$$\begin{aligned} - \Delta u(x, \xi ) - (1 + {{\text {i}}}\beta ) k(x, \xi )^2 u(x, \xi ) = f(x), \quad x \in Q, \end{aligned}$$

(34)

with $\beta \in \mathbb {R}$, together with either homogeneous Dirichlet boundary conditions (10) or absorbing boundary conditions (11). We discretize this boundary value problem as described in Sect. 3.1. For $\beta = 0$, we have the matrix (23) in Theorem 4, and for $\beta \in \mathbb {R}$ we obtain

$$\begin{aligned} M :=M(\beta ) :=L - {{\text {i}}}B - (1 + {{\text {i}}}\beta ) K = A - {{\text {i}}}\beta K, \end{aligned}$$

(35)

since only the term with the wavenumber is multiplied by $1 + {{\text {i}}}\beta$. Motivated by [12, p. 1945], we call M a complex shifted Laplace preconditioner (CSL preconditioner).

For the deterministic Helmholtz equation, preconditioning with the CSL preconditioner is a widely studied and successful technique for solving the discretized Helmholtz equation; see, e.g., [1, 3, 6, 7, 25] and [9], as well as references therein. See also [5] for a survey and [18] for recent developments. In the deterministic case, the spectrum of the preconditioned matrix $A M^{-1}$ lies in the disk (36), and the improved localization of the spectrum typically leads to a faster convergence of Krylov solvers. The CSL preconditioner M can be approximately inverted efficiently, for example, by multigrid techniques.

Here, we focus on locating the spectrum of the preconditioned matrix in the stochastic case, in analogy to [8, 9, 12] for the deterministic Helmholtz equation.

Theorem 5

Let the notation be as in Theorem 4, let $\beta > 0$, let A be the discretization (23) of the stochastic Helmholtz equation (9) and M be the discretization (35) of the shifted Helmholtz equation (34).

• 1. In the case of absorbing boundary conditions (11), the spectrum of the preconditioned matrix $A M^{-1}$ is contained in the closed disk

  $$\begin{aligned} \mathcal {D} = \{ z \in \mathbb {C}: |z - 1/2| \le 1/2 \}. \end{aligned}$$

  (36)

• 2. In the case of homogeneous Dirichlet boundary conditions (10), the spectrum of the preconditioned matrix $A M^{-1}$ lies on the circle

  $$\begin{aligned} \mathcal {C}= \{ z \in \mathbb {C}: |z - 1/2| = 1/2 \}. \end{aligned}$$

  (37)

Proof

We begin with the case of absorbing boundary conditions. The proof closely follows [12, Sect. 3] with minor modifications. We have

$$\begin{aligned} A = L - {{\text {i}}}B - z_1 K, \quad M = L - {{\text {i}}}B - z_2 K \end{aligned}$$

(38)

with $z_1 = 1$ and $z_2 = 1 + {{\text {i}}}\beta$ and where L, B, K are symmetric, K is positive definite and L, B are positive semidefinite; see Theorem 4. Then A and M are of the form in [12, Sect. 3], except for the opposite sign of B. The opposite sign affects the positive semidefiniteness, but not the overall strategy of the proof. Nevertheless, we give a full proof here.

Step 1: Observe first that $A M^{-1}$ and $M^{-1} A$ have the same spectrum, and that $M^{-1} A x = \sigma x$ is equivalent to the generalized eigenproblem $A x = \sigma M x$.

Step 2: x is an eigenvector of $A x = \sigma M x$ if and only if $(L - {{\text {i}}}B) x = \lambda K x$, which can be seen as follows:

$$\begin{aligned} (L - {{\text {i}}}B - z_1 K) x = \sigma (L - {{\text {i}}}B - z_2 K) x \Leftrightarrow (1 - \sigma ) (L - {{\text {i}}}B) x = (z_1 - \sigma z_2) K x. \end{aligned}$$

(39)

For $\sigma \ne 1$, we obtain $(L - {{\text {i}}}B) x = \lambda K x$ with $\lambda = (z_1 - \sigma z_2)/(1 - \sigma )$. (Note that $\sigma = 1$ is equivalent to $z_1 = z_2$, i.e., to $A = M$, which is excluded since $\beta > 0$.) Conversely, if $(L - {{\text {i}}}B) x = \lambda K x$, then $(L - {{\text {i}}}B - z_1 K) x = (\lambda - z_1) K x = \frac{\lambda - z_1}{\lambda - z_2} (L - {{\text {i}}}B - z_2 K) x$ and $\sigma = \frac{\lambda - z_1}{\lambda - z_2}$, provided that $\lambda \ne z_2$. (Note that $(L - {{\text {i}}}B) x = z_2 K x$, i.e., $\lambda = z_2$, implies that M is singular and thus not eligible as preconditioner.)

Step 3: Location of $\lambda$ in the generalized eigenvalue problem $(L - {{\text {i}}}B) x = \lambda K x$. Since K is real, symmetric positive definite, it has a Cholesky factorization $K = U U^\top = U U^{{\text {H}}}$ and the generalized eigenvalue problem is equivalent to

$$\begin{aligned} U^{-1} (L - {{\text {i}}}B) U^{-{{\text {H}}}} y = \lambda y, \end{aligned}$$

(40)

where $y = U^{{\text {H}}}x$. Multiplication of (40) by $y^{{\text {H}}}$ and division by $y^{{\text {H}}}y$ yields

$$\begin{aligned} \lambda = \frac{y^{{\text {H}}}U^{-1} L U^{-{{\text {H}}}} y}{y^{{\text {H}}}y} - {{\text {i}}}\frac{y^{{\text {H}}}U^{-1} B U^{-{{\text {H}}}} y}{y^{{\text {H}}}y}. \end{aligned}$$

(41)

This shows ${{\,\textrm{Re}\,}}(\lambda ) \ge 0$ and ${{\,\textrm{Im}\,}}(\lambda ) \le 0$ since L and B are symmetric positive semidefinite.

Step 4: Estimate of the eigenvalues $\sigma$ of $M^{-1} A$. Since it holds that $z_1 \ne z_2$,

$$\begin{aligned} \mu (z) = \frac{z - z_1}{z - z_2} \end{aligned}$$

(42)

is a Möbius transformation. By step 2, $\sigma = \mu (\lambda )$ where $\lambda$ is an eigenvalue of the generalized eigenvalue problem $(L - {{\text {i}}}B) x = \lambda K x$ which satisfies ${{\,\textrm{Im}\,}}(\lambda ) \le 0$. To determine $\mu (\mathbb {R})$, we compute

$$\begin{aligned} \mu (0) = \frac{z_1}{z_2} = \frac{1}{1 + {{\text {i}}}\beta } = \frac{1 - {{\text {i}}}\beta }{1 + \beta ^2}, \quad \mu (z_1) = 0, \quad \mu (\infty ) = 1 \end{aligned}$$

(43)

and

$$\begin{aligned} |*|{\mu (0) - \frac{1}{2}}^2 = |*|{\frac{1}{1 + \beta ^2} - \frac{1}{2} - {{\text {i}}}\frac{\beta }{1 + \beta ^2}} = \frac{(1 - \beta ^2)^2}{4 (1 + \beta ^2)^2} + \frac{\beta ^2}{(1 + \beta ^2)^2} = \frac{1}{4}. \end{aligned}$$

(44)

Hence $\mu$ maps the real line onto the circle $\mathcal {C}$ in (37) (for any $\beta \ne 0$). For $\beta > 0$, the lower half-plane is mapped by $\mu$ onto the interior of $\mathcal {C}$ (for $\beta < 0$ onto the exterior); see Fig. 1. This completes the proof in case of absorbing boundary conditions.

The proof in the case of Dirichlet boundary conditions is very similar. The only difference is in the location of the eigenvalues $\lambda$ in step 3. Since L is symmetric positive definite and $B = 0$, (40) implies $\lambda > 0$, hence $\sigma = \mu (\lambda )$ lies on the circle (37). $\square$

Fig. 1

Images under $\mu$ of the real and imaginary axis (solid and dashed circles, respectively) and of the four quadrants; see Remark 6 and the proof of Theorem 5

Remark 6

In the proof of Theorem 5, we additionally have ${{\,\textrm{Re}\,}}(\lambda ) \ge 0$. Hence $\sigma$ is located in the image of the (closed) fourth quadrant under $\mu$ in (42). To determine this image, note that $\mu$ maps the imaginary axis onto the circle

$$\begin{aligned} \mathcal {C}_\beta = \{ z \in \mathbb {C}: |z - (1 - {{\text {i}}}(\beta /2))| = |\beta |/2 \}, \end{aligned}$$

(45)

which intersects $\mu (\mathbb {R}) = \mathcal {C}$ perpendicularly in $\mu (0)$ and $\mu (\infty ) = 1$. Considering the orientations shows that $\mu$ maps the right half-plane onto the exterior of $\mathcal {C}_\beta$; see Fig. 1. Thus the spectrum satisfies

$$\begin{aligned} \sigma (A M^{-1}) \subseteq \{ z \in \mathbb {C}: |z - 1/2| \le 1/2 \} \setminus \{ z \in \mathbb {C}: |z - (1 - {{\text {i}}}(\beta /2))| < |\beta |/2 \}. \end{aligned}$$

(46)

In case of Dirichlet boundary conditions, the eigenvalues of $A M^{-1}$ lie on the arc of the circle $\mathcal {C}$ from $\mu (0)$ to $\mu (\infty ) = 1$ that contains the origin.

This observation further tightens the inclusion set of $\sigma (A M^{-1})$, also in the case of a deterministic wavenumber. This tighter inclusion set is already visible in [8, Figs. 1, 2] and [9, Fig. 2.1] but we are not aware of a proof in the literature.

5 Mean Value Preconditioner

We consider the discretization from Sect. 3.1. Let $S(\xi ) \in \mathbb {K}^{n,n}$ be the coefficient matrix of a linear system resulting from a spatial discretization of the Helmholtz equation (1) including boundary conditions and wavenumber $k(x,\xi )$. We assume that $S(\xi )$ is non-singular for almost all realizations $\xi \in \Xi$. Let $\bar{\xi } \in \Xi$ be the expected value of the multidimensional random variable $\xi$. It holds that

$$\begin{aligned} S(\xi ) = S(\bar{\xi }) + (S(\xi ) - S(\bar{\xi })) =:S(\bar{\xi }) + \Delta S (\xi ). \end{aligned}$$

The stochastic Galerkin method applied to $S(\xi )$ yields a matrix $A \in \mathbb {K}^{(m+1)n,(m+1)n}$ as shown in Sect. 3.1. Furthermore, we define the constant matrix

$$\begin{aligned} \bar{A} = I_{m+1} \otimes S(\bar{\xi }). \end{aligned}$$

(47)

This matrix allows for the construction

$$\begin{aligned} A = \bar{A} + (A-\bar{A}) =:\bar{A} + \Delta A. \end{aligned}$$

(48)

We employ the Frobenius matrix norm $\Vert \cdot \Vert _\textrm{F}$ in the following.

Theorem 7

Using the Frobenius norm, it holds that

$$\begin{aligned} \Vert \bar{A}^{-1} A - I_{(m+1)n} \Vert _\textrm{F} \le C_m \, \Vert S(\bar{\xi })^{-1} \Vert _\textrm{F} \, \big \Vert \Vert \Delta S(\xi ) \Vert _\textrm{F} \big \Vert _{\mathcal {L}^2(\Xi ,\rho )} \end{aligned}$$

(49)

with the constants

$$\begin{aligned} C_m = \sqrt{m+1} \, \bigg ( \sum _{i,j=0}^m \Vert \phi _i(\xi ) \phi _j(\xi ) \Vert _{\mathcal {L}^2(\Xi ,\rho )}^2 \bigg )^{\frac{1}{2}} \end{aligned}$$

provided that the $\mathcal {L}^2$-norm of the matrix norm is finite.

Proof

The definition (48) directly yields

$$\begin{aligned} \bar{A}^{-1} A - I_{(m+1)n} = I_{(m+1)n} + \bar{A}^{-1} \Delta A - I_{(m+1)n} = \bar{A}^{-1} \Delta A. \end{aligned}$$

We obtain $\Vert \bar{A}^{-1} \Delta A \Vert _\textrm{F} \le \Vert \bar{A}^{-1} \Vert _\textrm{F} \, \Vert \Delta A \Vert _\textrm{F}$. The properties of the Kronecker product and (47) imply $\Vert \bar{A}^{-1} \Vert _\textrm{F}^2 = (m+1) \Vert S(\bar{\xi })^{-1} \Vert _\textrm{F}^2$. We estimate $\Vert \Delta A\Vert _\textrm{F}$ using the Cauchy-Schwarz inequality with respect to the inner product (5)

$$\begin{aligned} \Vert \Delta A \Vert _\textrm{F}^2&= \sum _{i,j=0}^{m} \sum _{\mu ,\nu =1}^n \left| \langle \phi _i(\xi ) \phi _j(\xi ) , \Delta S_{\mu ,\nu }(\xi ) \rangle \right| ^2 \\&\le \sum _{i,j=0}^{m} \sum _{\mu ,\nu =1}^n \Vert \phi _i(\xi ) \phi _j(\xi ) \Vert _{\mathcal {L}^2(\Xi ,\rho )}^2 \, \Vert \Delta S_{\mu ,\nu }(\xi ) \Vert _{\mathcal {L}^2(\Xi ,\rho )}^2 \\&= \bigg ( \sum _{i,j=0}^{m} \Vert \phi _i(\xi ) \phi _j(\xi ) \Vert _{\mathcal {L}^2(\Xi ,\rho )}^2 \bigg ) \, \big \Vert \Vert \Delta S(\xi ) \Vert _\textrm{F} \big \Vert _{\mathcal {L}^2(\Xi ,\rho )}^2 . \end{aligned}$$

In the last step, we used that the square of an $\mathcal {L}^2$-norm is an integral and thus summation (with respect to $\mu ,\nu$) and integration can be interchanged. Applying the square root to the above estimate yields the statement (49). $\square$

Remark 8

Rough estimates are used in the proof of Theorem 7. Thus the true matrix norms of $\bar{A}^{-1} A - I_{(m+1)n}$ are often much smaller than the upper bounds in (49).

Remark 9

If the random variable $\Delta S(\xi )$ is essentially bounded, then it follows that

$$\begin{aligned} \big \Vert \Vert \Delta S(\xi ) \Vert _\textrm{F} \big \Vert _{\mathcal {L}^2(\Xi ,\rho )} \le \sup _{\xi \in \Xi \backslash \Upsilon } \Vert \Delta S(\xi ) \Vert _\textrm{F} < \infty \end{aligned}$$

with a set $\Upsilon \subseteq \Xi$ of measure zero due to the normalization $\Vert 1 \Vert _{\mathcal {L}^2(\Xi ,\rho )} = 1$.

Remark 10

The bound of Theorem 7 also holds true for the Frobenius norm of $A \bar{A}^{-1} - I_{(m+1)n}$.

Theorem 7 together with Remark 8 demonstrate that the matrix $\bar{A}$ is a good preconditioner for solving linear systems with coefficient matrix A. In this context, $\bar{A}$ is called the mean value preconditioner, as in [30] for the multi-element method. When $\bar{A}$ is used as a preconditioner (left-hand or right-hand), linear systems with coefficient matrix $\bar{A}$ have to be solved. The matrix $\bar{A}$ from (47) is block-diagonal with $m+1$ identical blocks in this application. Thus just a single LU-decomposition of the matrix $S(\bar{\xi })$ is required. Many linear systems with different right-hand sides are solved using this LU-decomposition in an iterative method like GMRES, for example.

Theorem 11

Let $S(\xi ) = S_0 + \theta T(\xi )$ with a non-singular constant matrix $S_0$, a matrix $T= \begin{bmatrix} t_{\mu ,\nu } \end{bmatrix}_{\mu ,\nu }$ depending on a random variable $\xi$ with components $t_{\mu ,\nu }\in \mathcal {L}^2(\Xi ,\rho )$ and a real parameter $\theta > 0$. Using $A_0 = I_{m+1} \otimes S_0$, the Frobenius norm exhibits the asymptotic behavior

$$\begin{aligned} \Vert A_0^{-1} A - I_{(m+1)n} \Vert _\textrm{F} = O(\theta ) . \end{aligned}$$

(50)

Proof

Since the entries of $T(\xi )$ are assumed to be square-integrable, also the expected values are finite. Let $\bar{T}$ be the constant matrix containing the expected values of $T(\xi )$. We apply the decomposition

$$\begin{aligned} S(\xi ) = (S_0 + \theta \bar{T}) + \theta (T(\xi ) - \bar{T}). \end{aligned}$$

The matrix $S_0 + \theta \bar{T}$ is non-singular for sufficiently small $\theta$. Moreover, we obtain the relation $(S_0 + \theta \bar{T})^{-1} = S_0^{-1} + O(\theta )$. Theorem 7 yields

$$\begin{aligned} \Vert \bar{A}^{-1} A - I_{(m+1)n} \Vert _\textrm{F} \le C_m \, \Vert (S_0 + \theta \bar{T})^{-1} \Vert _\textrm{F} \, \big \Vert \Vert \theta (T - \bar{T}) \Vert _\textrm{F} \big \Vert _{\mathcal {L}^2(\Xi ,\rho )} \end{aligned}$$

with $\bar{A} = I_{m+1} \otimes (S_0+\theta \bar{T})$. It holds that $\bar{A} = A_0 + O(\theta )$ and thus $\bar{A}^{-1} = A_0^{-1} + O(\theta )$. We conclude

$$\begin{aligned} \Vert {A}_0^{-1} A - I_{(m+1)n} \Vert _\textrm{F} \le \left( C_m \, \left( \Vert S_0^{-1} \Vert _\textrm{F} + O(\theta ) \right) \, \theta \, \big \Vert \Vert T - \bar{T} \Vert _\textrm{F} \big \Vert _{\mathcal {L}^2(\Xi ,\rho )} \right) + O(\theta ) = O(\theta ), \end{aligned}$$

which confirms (50). $\square$

An important case of Theorem 11 is $\bar{T} = 0$, i.e., these expected values are zero. Then $A_0 = \bar{A}$ is the mean value preconditioner.

Corollary 12

Under the assumptions of Theorem 7, the Frobenius norm satisfies the estimate

$$\begin{aligned} \Vert \bar{A}^{-1} A - I_{(m+1)n} \Vert _\textrm{F} < 1 \end{aligned}$$

(51)

for all sufficiently small $\Delta S$.

Likewise, the Frobenius norm using $A_0$ instead of $\bar{A}$ is smaller than one if the parameter $\theta$ is sufficiently small in the context of Theorem 11.

A stationary iterative scheme for solving a linear system $A x = b$ reads as

$$\begin{aligned} B x^{(i+1)} = b - (A-B) x^{(i)} \qquad \text{ for } \; i=0,1,2, \ldots \end{aligned}$$

(52)

with a non-singular matrix B which should approximate A, see [29, p. 621]. In each iteration step, we have to solve a linear system with coefficient matrix B. The property (51) is sufficient for the global convergence of the iteration (52) using $B = \bar{A}$. The computational costs of an iteration step are much less than the steps in GMRES using $\bar{A}$ as preconditioner, because the construction of Krylov subspaces is avoided. In practice, we do not know if $\Delta S$ is sufficiently small such that the bound (51) is guaranteed. Nevertheless, it is worth to try this stationary iteration, as we will observe in Sect. 7.

6 Numerical Experiments in 1D

Our model problem in one space dimension is the stochastic Helmholtz equation (9) on $Q = ]0, 1[$ with absorbing boundary conditions. The right-hand side is the point source $f(x) = \delta (x - \frac{1}{2})$, similarly to, e.g., [9, 12, 19, 28], where the right-hand side is a (possibly scaled) point source. We consider a random wavenumber $k(x, \xi ) = k(\xi )$ constant in space, which is uniformly distributed in some interval $[k_{\min }, k_{\max }]$ with $0< k_{\min } < k_{\max }$. Equivalently, we define

$$\begin{aligned} k(\xi ) = (1 + \theta \xi ) \overline{k} \end{aligned}$$

(53)

with a random variable $\xi$ that is uniformly distributed in $[-1, 1]$, a mean value $\overline{k}$, and a real parameter $\theta \in ]0, 1[$. It follows that $k_{\min } = (1-\theta )\overline{k}$ and $k_{\max } = (1+\theta )\overline{k}$.

In our numerical experiments in one and two spatial dimensions, we compute the mesh-size $h = \frac{1}{q + 1}$ in the FD discretization by

$$\begin{aligned} q = 2^\ell - 1, \quad \text {where } \ell = \max \biggl \{ \biggl \lceil \log _2 \biggl ( \frac{15}{2 \pi } k_{\max } \biggr ) \biggr \rceil , 1 \biggr \}. \end{aligned}$$

(54)

Then the relation $\frac{2 \pi }{k h} \approx \text {constant}$, advocated in [17, Sect. 4.4.1], is satisfied. Indeed, the estimate $x \le \lceil x \rceil \le x + 1$ for $x \in \mathbb {R}$ implies $\frac{15k}{2 \pi } \le q+1 \le 2 \frac{15 k}{2 \pi }$ for large k. In particular, q grows linearly with k and thus the size of the matrix A grows with k; see, e.g., Fig. 3. Our choice for q can be adapted for a future use of a multigrid method (as in [9]).

Discretizing the model problem yields the linear algebraic system of equations

$$\begin{aligned} A x = b \end{aligned}$$

(55)

in Theorem 4. This one-dimensional problem can be solved by a direct method, since the computational work is not too large. Nevertheless we also consider its solution with the GMRES method [27] and investigate the application of CSL and mean value preconditioners introduced in Sects. 4 and 5, respectively.

The matrix A in (55) has the form

$$\begin{aligned} A = I_{m+1} \otimes T - {{\text {i}}}[B_{ij}] - [C_{ij}]. \end{aligned}$$

(56)

If needed, we write $A_\theta$ to indicate the dependence of A on $\theta$, and in particular $A_0$ for $\theta = 0$, which corresponds to the mean value preconditioner. Since the wavenumber in (53) is constant in space, the matrices $[B_{ij}]$ and $[C_{ij}]$ have the form

$$\begin{aligned}{}[B_{ij}]&= \begin{bmatrix} \langle k(\xi ) \phi _j(\xi ), \phi _i(\xi )\rangle \end{bmatrix}_{ij} \otimes D_1,&D_1&= \frac{1}{h} {{\,\textrm{diag}\,}}(1, 0, \ldots , 0, 1), \end{aligned}$$

(57)

$$\begin{aligned}&= \begin{bmatrix} \langle k(\xi )^2 \phi _j(\xi ), \phi _i(\xi )\rangle \end{bmatrix}_{ij} \otimes D_2,&D_2&= {{\,\textrm{diag}\,}}\Bigl ( \frac{1}{2}, 1, \ldots , 1, \frac{1}{2} \Bigr ), \end{aligned}$$

(58)

and, moreover, $B_{ij} = 0$ for $|i-j| > 1$ and $C_{ij} = 0$ for $|i-j| > 2$. In other words, the matrices $\begin{bmatrix} \langle k(\xi ) \phi _j(\xi ), \phi _i(\xi )\rangle \end{bmatrix}_{ij}$ and $\begin{bmatrix} \langle k(\xi )^2 \phi _j(\xi ), \phi _i(\xi )\rangle \end{bmatrix}_{ij}$ are tridiagonal and pentadiagonal, respectively, due to the orthogonality properties of the polynomials $\phi _i(\xi )$, $i = 0, 1, \ldots$.

Remark 13

In the deterministic case $k(\xi ) = \overline{k}$ in (53), i.e., $\theta = 0$, the matrices $[B_{ij}] = \overline{k} I_{m+1} \otimes D_1$ and $[C_{ij}] = \overline{k}^2 I_{m+1} \otimes D_2$ are diagonal, and

$$\begin{aligned} A_0 = I_{m+1} \otimes (T - {{\text {i}}}\overline{k} D_1 - \overline{k}^2 D_2) = I_{m+1} \otimes S(0) \end{aligned}$$

(59)

with S from (14). This shows that the mean value preconditioner $A_0$ is block-diagonal with $m+1$ identical diagonal blocks. The latter are the FD-discretization of the deterministic Helmholtz equation with wavenumber $\overline{k}$ (associated to $\xi = 0$).

If not specified otherwise, we use $m = 3$ in the stochastic Galerkin method and $\theta = 0.1$ in (53). Finally, we also consider the shifted Helmholtz equation (34) with shift $\beta = \frac{1}{2}$ and denote the CSL preconditioner by $M = M(\frac{1}{2})$, see (35). As for A, we write $M_\theta$ if we wish to emphasize the dependence on $\theta$. Table 1 summarizes the four kinds of matrices involved in our computations in Sect. 6 and Sect. 7.

Table 1 Different discretizations of the Helmholtz and shifted Helmholtz equation, with or without uncertainties

The numerical experiments have been performed in the software package MATLAB R2020b on an i7-7500U @ 2.70GHz CPU with 16 GB RAM.

6.1 Spectra

By Theorem 5, the eigenvalues of the CSL preconditioned matrix $A M^{-1}$ lie in the closed disk (36). This is illustrated in the left panel of Fig. 2, which displays the spectra of $A M^{-1}$ with $\theta = 0.1$ and of $A_0 M_0^{-1}$, i.e., with $\theta = 0$ (without uncertainties); see also Table 1 for an overview of the different matrices. Each eigenvalue of $A_0 M_0^{-1}$ is $(m+1)$-fold, since $A_0 = I_{m+1} \otimes S(0)$ is block-diagonal with identical diagonal blocks, see Remark 13, and similarly for $M_0$. For $\theta \ne 0$, the matrix $A M^{-1}$ is not block-diagonal, and $A M^{-1}$ has clusters of $m+1$ eigenvalues close to each $(m+1)$-fold eigenvalue of $A_0 M_0^{-1}$. This can be observed in the figure with $m + 1 = 4$. The right panel in Fig. 2 displays the spectrum of $A A_0^{-1}$ with the mean value preconditioner $A_0$. The eigenvalues are clustered at 1, which suggests a fast convergence of GMRES. If the eigenvalues satisfy $|\lambda - 1| < 1$, then the stationary method (52) with $B = A_0$ converges.

Fig. 2

Left: Spectrum of $A M^{-1}$ for $\overline{k} = 50$, $m = 3$, $\theta = 0.1$ (crosses) and $\theta = 0$ (circles). The large solid circle illustrates (37). Right: Spectrum of $A A_0^{-1}$

6.2 Condition Numbers

Recall that A, M, $A_0$ and $M_0$ denote the discretizations of the (shifted) Helmholtz equation wiht or without uncertainties; see Table 1. Figure 3 displays the 2-norm condition numbers of A, M, $A M^{-1}$, $A_0$ and $A A_0^{-1}$ as functions of $\overline{k}$ (with $\theta = 0.1$). Clearly, the condition numbers of M and $A M^{-1}$ are much smaller than the condition number of A. A smaller condition number is beneficial when solving linear systems, since then a small relative residual of an approximate solution implies a small relative error of the approximate solution. (This follows from the following well-known residual-based forward error bound: Let $A \in \mathbb {C}^{n,n}$ be non-singular, $b \in \mathbb {C}^n {\setminus } \{ 0 \}$, $x = A^{-1} b$, and let $\hat{x}$ be an approximate solution of the linear algebraic system $A x = b$. Then the relative error satisfies $\Vert x - \hat{x}\Vert _2 / \Vert x\Vert _2 \le \kappa _2(A) \Vert r\Vert _2 / \Vert b\Vert _2$ with the residual $r = b - A \hat{x}$.) In this example, $\kappa _2(M) \le 205$ for all $\overline{k}$, which is very moderate, and $\kappa _2(A M^{-1})$ grows linearly in $\overline{k}$ from 2.6485 when $\overline{k} = 10$ to only 36.5190 when $\overline{k} = 200$. In contrast, $\kappa _2(A)$ is roughly 50 to 160 times larger than $\kappa _2(A M^{-1})$. The observed spikes of $\kappa _2(A)$ occur when more discretization points are used which leads to a larger size of A, compare the curve of |size(A)|. The condition number of the mean value preconditioned matrix $A A_0^{-1}$ is also moderate, growing from 2 to 141, which is beneficial for solving the preconditioned linear system, while $\kappa _2(A_0)$ is of the order of $\kappa _2(A)$.

Fig. 3

2-norm condition numbers as functions of $\overline{k}$ (left) and zoom-in (right). The matrices A and $A_0$ arise from the Helmholtz equation with and without uncertainties, respectively, and M and $M_0$ from the shifted Helmholtz equation; see also Table 1

6.3 GMRES

We solve the unpreconditioned system (55) and the right and left preconditioned systems

$$\begin{aligned} A M^{-1} y = b, \quad x = M^{-1} y, \qquad \text {and} \qquad M^{-1} A x = M^{-1} b \end{aligned}$$

(60)

with full GMRES (no restarts), using MATLAB’s built-in |gmres| command. The residual in the ith step is $r^{(i)} = b - A x^{(i)}$ for unpreconditioned and right preconditioned GMRES, and $M^{-1} r^{(i)}$ for left preconditioned GMRES. The stopping criterion is that the relative residual norm is less than $10^{-12}$, i.e., $\Vert r^{(i)}\Vert _2 / \Vert r^{(0)}\Vert _2 < 10^{-12}$ for unpreconditioned and right preconditioned GMRES, and $\Vert M^{-1} r^{(i)}\Vert _2 / \Vert M^{-1} r^{(0)}\Vert _2 < 10^{-12}$ for left preconditioned GMRES. In particular, the stopping criterion is in general different for left and right preconditioning; see [26, Ch. 9.3] for a detailed discussion. We will consider the following three preconditioners:

• 1. the CSL preconditioner M,

• 2. the mean value preconditioner $A_0$,

• 3. the mean value CSL preconditioner $M_0$.

In preconditioned GMRES, we need to solve linear systems with the preconditioner, for which we use an LU-decomposition. In one spatial dimension, this is not competitive with the direct solution (see the end of Sect. 6.3), but in two spatial dimensions the block structure of the preconditioners $A_0$ and $M_0$ leads to a competitive method. In MATLAB, the LU-decomposition of the sparse matrix M calls the associated routine from UMFPACK; see [4]. The decomposition has the form

$$\begin{aligned} P M Q = L U \end{aligned}$$

(61)

with a lower triangular matrix L, upper triangular matrix U, and two permutation matrices P, Q. By Remark 13, $A_0 = I_{m+1} \otimes S(0) \in \mathbb {K}^{(m+1)n, (m+1)n}$ is block-diagonal with equal diagonal blocks so that, for fixed $\overline{k}$, only a single LU-decomposition of $S(0) \in \mathbb {K}^{n,n}$ is necessary to compute $A_0^{-1} x$ for any vector $x \in \mathbb {K}^{(m+1)n}$. In our implementation, we partition and reshape x so that only one linear system with S(0) (using the LU-factors) is solved. The preconditioner $M_0$ is implemented in the same way.

Fig. 4

Relative residual norms when solving (55) with GMRES with various preconditioners, $m = 3$, $\overline{k} = 50$, and $\theta = 0.1$ (left) or $\theta = 0.2$ (right). The matrices A and $A_0$ arise from the Helmholtz equation with and without uncertainties, respectively, and M and $M_0$ from the shifted Helmholtz equation; see also Table 1

In a first experiment, we fix $\overline{k} = 50$, $\theta = 0.1$ and $m = 3$. Solving the unpreconditioned system (55) with GMRES suffers from a long delay of convergence; see Fig. 4. In contrast, all three preconditioners M, $M_0$, and $A_0$ lead to a significant decrease in the number of iteration steps from about 250 to 50 for M and $M_0$ (factor 5), and to about 25 for $A_0$ (factor 10); see Fig. 4 (left panel). The differences between computed solutions are very small: $\Vert x - x'\Vert _\infty \le 1.7 \cdot 10^{-14}$ (and typically of order $10^{-15}$), where x is the computed direct solution and $x'$ is a solution computed with GMRES (unpreconditioned or with one of the preconditioners). Left and right preconditioning lead to very similar relative residual norms and timings for each preconditioner. A heuristic explanation why $A_0$ performs better than M and $M_0$, is that A is closer to $A_0$ than to M or $M_0$. Indeed, we have $\Vert A - A_0\Vert _\infty< \Vert A - M\Vert _\infty < \Vert A - M_0\Vert _\infty$ in this example. Repeating this experiment with $\theta = 0.2$ leads to very similar results, see Fig. 4, so we focus on $\theta = 0.1$.

Fig. 5

Number of GMRES iteration steps (top) and computation time in seconds (bottom) as functions of $\overline{k}$ for different left and right preconditioners (see Table 1) with fixed $\theta = 0.1$ and $m = 3$. The right panels are zoom-ins

In a second experiment, we let $\overline{k}$ vary while $\theta = 0.1$ and $m = 3$ are fixed. Figure 5 displays the number of GMRES iteration steps (top) and the computation time (bottom), measured as wall clock time with MATLAB’s |tic toc| command, as functions of $\overline{k}$. For small $\overline{k} \in [10, 50]$, the difference between unpreconditioned and preconditioned GMRES is not so pronounced, since the linear systems are rather small. For $60 \le \overline{k} \le 200$, the three preconditioners significantly reduce the number of iteration steps and the computation time compared to unpreconditioned GMRES. The number of iteration steps is reduced to 8–15% of the number of iteration steps in unpreconditioned GMRES when using M, to 9–16% when using $M_0$ and to only 3–6% when using $A_0$ as preconditioner. GMRES preconditioned with M or $M_0$ needs only 1–4% of the computation time of unpreconditioned GMRES, and the computation time of GMRES preconditioned with $A_0$ is reduced to 0.5–1.1% of the computation time of unpreconditoned GMRES. The mean value preconditioner $A_0$ leads to the smallest number of GMRES iteration steps and computation time, which is likely due to the fact that A is closer to $A_0$ than to M or $M_0$. Note, however, that the condition number of $A_0$ (and A) is much larger than that of M and $M_0$. For $\overline{k} = 150$, we have (rounded to the nearest integer) $\kappa _2(A) = 2428$, $\kappa _2(A_0) = 2220$, $\kappa _2(M) = 109$, $\kappa _2(M_0) = 91$; see also Fig. 3. Thus, if accuracy is an issue, it is preferable to work with the CSL preconditioners M or $M_0$.

Finally, we note that the direct solution using the ‘backslash’ command with a sparse matrix in MATLAB calls an efficient algorithm from UMFPACK; see [4]. In the above test example, solving the linear system (55) by GMRES (with or without preconditioner) is not competitive with this direct solution, as it is much faster; see the bottom right panel in Fig. 5.

6.4 Solutions

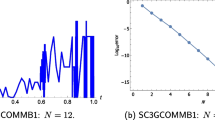
Figure 6 displays the real and imaginary parts of the computed coefficients $v_0$, $v_1$, $v_2$, $v_3$ in the Galerkin approximation for $\overline{k}=50$ and $\theta = 0.1$ in (53). We recognize an effect of the point source at $x=\frac{1}{2}$ in the real part of $v_0$.

Fig. 6

Plots of the coefficients $v_0, v_1, v_2, v_3$ for $\overline{k} = 50$ and $\theta = 0.1$

Fig. 7

Maximum-norms $\Vert v_i\Vert _\infty$ as a function of $i = \deg (\phi _i)$. Left: For fixed $\theta = 0.1$ and different values of $\overline{k}$. Right: For fixed $\overline{k} = 100$ and different values of $\theta$

We compute the solution for total polynomial degree $m = 100$. Figure 7 shows $\Vert v_i\Vert _\infty$ as a function of the polynomial degree i. In the left panel, $\theta = 0.1$ is fixed and $\overline{k}$ varies, while in the right panel $\theta$ varies and $\overline{k} = 100$ is fixed. We observe an exponential decay of the coefficients in all cases, which is related to the exponential convergence of the PC expansion (7). Larger wavenumbers and larger values of $\theta$ lead to a slower decay of the maximum-norm of the coefficients. The effect of larger $\theta$ on the convergence/decay is more pronounced, compare, for example, the curve for $(\overline{k}, \theta ) = (150, 0.1)$ in the left panel with the curve for (100, 0.5) in the right panel.

Fig. 8

Norms $\Vert x_m - x_{m+1}\Vert _2$ as a function of the maximal degree m in the stochastic Galerkin method. Left: For fixed $\theta = 0.1$ and different values of $\overline{k}$. Right: For fixed $\overline{k} = 100$ and different values of $\theta$

Next, we vary m (the maximal degree of the polynomials in the stochastic Galerkin method) and denote by $x_m$ the solution of (55), which consists of a discretization of the coefficients $v_{0,m}, \ldots , v_{m,m}$ in a Galerkin approximation (24) of the solution u of the Helmholtz equation; see also Remark 1. The convergence of the stochastic Galerkin method is illustrated by the exponential decay of the norms $\Vert x_m - x_{m+1}\Vert _2$ in Fig. 8.

7 Numerical Experiments in 2D

Next, we consider the stochastic Helmholtz equation in two space dimensions, where the wavenumber depends on random variables and on the spatial variables.

7.1 Modeling

We consider the stochastic Helmholtz equation (9) in $Q = ]0, 1[^2$ with absorbing boundary conditions (11), the point source $f(x,y) = \delta ( (x,y) - (\frac{1}{2}, \frac{1}{2}))$ as right-hand side, and space-dependent random wavenumber

$$\begin{aligned} k(x, y, \xi _1, \xi _2, \xi _3) = {\left\{ \begin{array}{ll} (1 + \theta \xi _1) k_1, &{} y \le 0.2 + 0.1 x, \\ (1 + \theta \xi _2) k_2, &{} 0.2 + 0.1 x< y < 0.6 -0.2 x, \\ (1 + \theta \xi _3) k_3, &{} 0.6 -0.2 x \le y. \end{array}\right. } \end{aligned}$$

(62)

on the wedge-shaped domain from [19, p. 146]; similar domains have been examined in [6, Sect. 6.3] and [8, Sect. 4.4]. The modeling (62) can also be written in the form (4) using spatial indicator functions. The random variables $\xi _1, \xi _2, \xi _3$ are independent and uniformly distributed in $[-1, 1]$. The mean value of the wavenumber is

$$\begin{aligned} \overline{k}(x, y) = {\left\{ \begin{array}{ll} k_1, &{} y \le 0.2 + 0.1 x, \\ k_2, &{} 0.2 + 0.1 x< y < 0.6 - 0.2 x, \\ k_3, &{} 0.6 - 0.2 x \le y. \end{array}\right. } \end{aligned}$$

(63)

We discretize the boundary value problem as described in Sect. 3.1 and obtain the linear algebraic system $A x = b$ in Theorem 4. The number of polynomials in the three random variables $\xi _1, \xi _2, \xi _3$ with total degree at most r is, see (6),

$$\begin{aligned} m + 1 = \textstyle \frac{(r+3)!}{r! \, 3!} = \tfrac{1}{6} (r+1) (r+2) (r+3). \end{aligned}$$

(64)

Table 2 includes the number of basis polynomials for degrees $r = 0, 1, \ldots , 8$.

Table 2 For different total degrees r, number of basis polynomials (n.basis), size of the matrix A, number of non-zero elements in A (nnz), and time to generate A

Let $k_1 = 30$, $k_2 = 15$, $k_3 = 20$, and $\theta = 0.1$. Table 2 shows the size of A and the time (in seconds) for constructing the matrix A for polynomial degrees up to $r = 0, 1, \ldots , 8$ in the stochastic Galerkin method. As a function of r, the computation time when solving $A x = b$ directly in MATLAB grows much faster than for the iterative solvers; see Fig. 9 (left panel).

7.2 Iterative Solvers

We solve the linear algebraic system $A x = b$ with GMRES using the mean value preconditioner $A_0 = I_{m+1} \otimes S_0$ from (47) as right preconditioner, that is, we solve

$$\begin{aligned} A A_0^{-1} y = b, \quad A_0 x = y. \end{aligned}$$

(65)

Here $S_0$ denotes the FD discretization of the Helmholtz equation with absorbing boundary conditions and deterministic wavenumber (63). The solution of linear systems with the preconditioner $A_0$ is implemented as described in Sect. 6.3. We solve (65) with full GMRES (no restarts), |tol=1e-8| and |maxit=200| for polynomial degrees up to $r = 1, \ldots , 8$ in the stochastic Galerkin method. In contrast to the experiments in 1D in Sect. 6, preconditioned GMRES is significantly faster than the direct solution with MATLAB’s ‘backslash’ command; see Fig. 9 (left panel). The computation times for preconditioned GMRES include the computation of the LU-decomposition of a diagonal block of $A_0$. Furthermore, the relative residual norms in GMRES for polynomial degree $r = 8$ are shown in Fig. 9 (right panel). The mean value CSL preconditioner $M_0$ has a similar block-diagonal structure to $A_0$, which we denote again by $M_0 = I_{m+1} \otimes S_0$, and performs similarly well; see Fig. 9. Here $S_0$ denotes the FD discretization of the Helmholtz equation with absorbing boundary conditions and deterministic wavenumber (63) with a complex shift. Tables 3 and 4 contain the number of operations performed until preconditioned GMRES converges to the prescribed tolerance.

Fig. 9

Solving the linear system directly and with GMRES preconditioned by $A_0$ and $M_0$; see Sect. 7. Left: Computation time (in seconds) as a function of the polynomial degree r in the stochastic Galerkin method. Right: Relative residual norms in preconditioned GMRES for polynomial degree $r = 8$

Table 3 Total operation count until convergence of preconditioned GMRES with the mean value preconditioner $A_0 = I_{m+1} \otimes S_0$ for polynomial degrees $r = 1, \ldots , 8$, as described in Sect. 7.2

Table 4 Total operation count until convergence of preconditioned GMRES with the mean value CSL preconditioner $M_0 = I_{m+1} \otimes S_0$ for polynomial degrees $r = 1, \ldots , 8$, as described in Sect. 7.2

Fig. 10

Relative error norms in the stationary iteration (66) for different polynomial degrees r in the stochastic Galerkin method

Alternatively to GMRES or a direct solution of the linear system, we also investigate the stationary iteration (52) with $B = A_0$, i.e.,

$$\begin{aligned} A_0 x^{(i+1)} = b - (A-A_0) x^{(i)} \quad \text {for } i = 0,1,2, \ldots \, . \end{aligned}$$

(66)

We take the starting vector $x^{(0)} = A_0^{-1} b$. Linear systems with the matrix $A_0$ are solved as described above. For $\theta = 0.1$, this iteration converges. Figure 10 displays the relative error norms in the maximum-norm for polynomial degrees $r=2,4,6$, where we take the direct solution as the ‘exact’ solution. The slower convergence for larger degree r in the stochastic Galerkin method is expected, since the matrix size also grows causing higher condition numbers. For $\theta = 0.2$, the stationary iteration diverges. This behavior is in agreement to Theorem 11 and Corollary 12.

7.3 Solutions

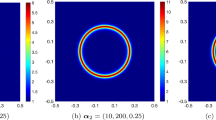
In Fig. 11, the top row displays the expected value of the real and imaginary part of the computed stochastic Galerkin approximation $\widetilde{u}_m$ (with polynomial degree $r = 5$). The variance is displayed in the bottom row of the figure.

Fig. 11

Expected value (top) and variance (bottom) of ${{\,\textrm{Re}\,}}(\widetilde{u}_m)$ and ${{\,\textrm{Im}\,}}(\widetilde{u}_m)$

Fig. 12

Left: Euclidean norms $\Vert x_{r-1} - x_r\Vert _2$ as a function of the polynomial degree $r = 2, \ldots , 8$, where $x_r$ is the solution of $A x = b$ using total degree r in the stochastic Galerkin method. Right: Magnitudes (67) as a function of the degree j

Denote by $x_r$ the solution of $A x = b$ when using polynomials of degree up to r in the stochastic Galerkin method, where the number of basis polynomials is given in (64). The left panel of Fig. 12 displays the differences $\Vert x_{r-1} - x_r\Vert _2$ as a function of r (the vector $x_{r-1}$ is padded with zeros at the end to match the size of $x_r$). The observed exponential decay suggests convergence of the stochastic Galerkin method.

Next, we fix the degree $r = 8$ in the stochastic Galerkin method. Recall from (15) and (18) that the solution of $A x = b$ contains the coefficient vectors $V_0, \ldots , V_m$ of the polynomials $\phi _0, \ldots , \phi _m$ in the stochastic Galerkin method. We also examine the largest maximum norm of the coefficients associated to polynomials of total degree (exactly) j, i.e., the values

$$\begin{aligned} \gamma _j = \max \left\{ \Vert V_i\Vert _{\infty } : \, \deg (\phi _i) = j \right\} . \end{aligned}$$

(67)

The right panel of Fig. 12 shows the magnitudes (67) for $j=0,1,\ldots ,8$. The observed exponential decay stems from the exponential convergence of (7), since the wavenumber in (62) is an analytic function of $\xi _1, \xi _2, \xi _3$.

We repeat this experiment with $\theta = 0.2$ instead of $\theta = 0.1$. Overall, the behavior is similar as for $\theta = 0.1$, but convergence is slower: the relative residual norms reach the prescribed tolerance in 60 instead of 20 iteration steps, and also $\Vert x_{r-1} - x_r\Vert _2$ as well as the magnitudes (67) converge more slowly.

8 Conclusions

We investigated the Helmholtz equation including a random wavenumber. The combination of a stochastic Galerkin method and a finite difference method yielded a high-dimensional linear system of algebraic equations. We examined the iterative solution of these linear systems using three types of preconditioners: a complex shifted Laplace preconditioner, a mean value preconditioner, and a combined variant. Theoretical properties of the preconditioned linear systems were shown. In our numerical experiments, the straightforward mean value preconditioner leads to a more efficient iterative solution of the linear system than the other preconditioners considered here.