1 Introduction

Solving the Boltzmann equation numerically is an area of ongoing research. There are already existing results based on Spectral-Fourier Approach by Pareschi and Russo [1] and Gamba and Tharkabhushanam [2], with recent work improving some of its shortcomings such as [3] on the preservation of conservations or [4] on the stability of such methods. Another ansatz is based on the spectral Hermite ansatz introduced by Grad (1949) [5] with early work [6] and more recent work such as [7, 8] on linearising the collision operator. Wang and Cai were recently [9] able to calculate the bilinear collision operator based on the spectral Hermite ansatz. However, their method is computationally expensive. In response, Cai et al. [10] developed and implemented a more efficient algorithm based on the spectral Burnett ansatz. This ansatz has also been looked into analytically [11] and numerically [12]. Inspired by Struchtrup’s (2005) tensorial approach to the collision operator in Equation 6.35 in [13], we chose a different approach for calculating the Spectral-Burnett approximation of the Boltzmann collision operator. The main difference lies in the exploitation of features of the basis set, which is adapted to the irreducible subspaces with respect to the orthogonal group of the polynomial space as it consists of real solid spherical harmonics multiplied with Laguerre polynomials. While we also implemented the mostly analytical calculation of collision coefficients for a variety of potentials, the focus of this paper is the algorithm and corresponding numerical code, which uses these coefficients to solve the space-homogeneous Boltzmann equation for any distribution. Utilizing the properties of the irreducible subspaces, compared to the previous works we are able to significantly reduce the memory and computation time required for calculating the numerical solution. We could achieve this by virtue of the uniqueness up to a constant of linear maps between the irreducible subspaces. Representation theory allowed us to isolate each bilinear map, the constant for each map that encodes particle collisions and identify all bilinear maps, that evaluate to zero due to the mathematical properties of the irreducible subspaces in question. Our method provides a deep understanding of the underlying structure of the bilinear collision operator, allows for a very flexible setup for numerical computations and therefore is ideal for a purposeful reduction of computational effort.

The structure of this paper is as follows: The next section provides an overview of the collision operator and the potentials used in this paper. Sections 3 and 4 describe the application of representation theory to the collision operator, while Sect. 5 explains the representation theoretically inspired algorithm and its implementation. In Sect. 6 we apply our algorithm and also compare the results with [9]. For an overview of the applied representation theory refer to the “Appendix”.

2 Boltzmann’s Collision Operator

To describe gas flows, the Boltzmann equation is known to be valid for a wide range of situations. In particular, it describes non-equilibrium gas flows accurately for Knudsen numbers in the transition regime between the range of Navier–Stokes–Fourier equations and the kinetic regime. The Boltzmann equation describes the evolution of the gas distribution function f, which in general depends on seven variables—time t, position space \(\textbf{x}\) and velocity space \(\textbf{c}\).

As done in previous papers we look at the space-homogenous Boltzmann equation to be able to focus solely on the collision operator:

$$\begin{aligned} \frac{\partial f}{\partial t} = \mathcal {S}(f,f) \end{aligned}$$
(1)

where f gives the time-dependent velocity distribution of particles,

$$\begin{aligned} f: [0,T]\times \mathbb {R}^3&\rightarrow \mathbb {R}\nonumber \\ f(t,\textbf{c})\,\text {d}{\textbf{c}}&= \text {density of particles with velocity in }[\textbf{c},\textbf{c}+\,\text {d}{\textbf{c}}] \text { at }t, \end{aligned}$$
(2)

and \(\mathcal {S}(f,f)\) is the bilinear collision operator, see e.g. the textbooks [14, 15], modelling the binary collisions of the particles in the gas:

$$\begin{aligned} \mathcal {S}\left( f,f\right) =\int \limits _{R^{3}}\int \limits _{\textbf{n}\perp \textbf{g}}\int \limits _{0}^{\infty }\left( f(t,\textbf{c}^{\prime })f(t,\textbf{c}_{1}^{\prime })-f(t,\textbf{c})\,f(t,\textbf{c}_{1})\right) B(|\textbf{g}|,\chi )\,\text {d}{\chi }\,\text {d}{\textbf{n}}\,\text {d}{\textbf{c}_1} \end{aligned}$$
(3)

where \(\textbf{n}\) is the unit vector orthogonal to the collisional plane, the relative velocity \(\textbf{g}=\textbf{c}-\mathbf {c_1}\), the average velocity \(\textbf{h}=\frac{1}{2}(\textbf{c}+\mathbf {c_1})\), and the primed velocities \(\textbf{c}', \textbf{c}_1'\), \(\mathbf {g'}=\mathbf {c'}-\mathbf {c_1'}\) with \(||\mathbf {g'}||=||\textbf{g}||\), \(\mathbf {h'}=\textbf{h}\) are the velocities after the collision. Additionally, we assume the initial average velocity of the gas to be 0, and as this is one of the conserved moments it will always be 0. The solution of (1) converges to a Gaussian centered around the average velocity. Our assumption will allow us to exactly represent this solution with our numerical ansatz.

As discussed in several textbooks, [14, 15], they are given by

$$\begin{aligned} \mathbf {g'}&=R_{\textbf{n},\chi }(\textbf{g})=\cos {(\chi )}\textbf{g} + \sin {(\chi )} \textbf{n}\times \textbf{g}&\textbf{c}'&= \textbf{h} + \frac{1}{2}\mathbf {g'}&\textbf{c}_1'&= \textbf{h} - \frac{1}{2}\mathbf {g'}, \end{aligned}$$
(4)

where \(\mathbf {g'}\) is the result of rotating \(\textbf{g}\) around \(\textbf{n}\) by the angle \(\chi \). According to Cercignani’s work [14], the kernel \(B(|\textbf{g}|,\chi )\) depends on the assumed potential between the colliding particles. Following [14, 15], different choices are possible and common models [7,8,9,10] include

  • The hard spheres model, i.e.

    $$\begin{aligned} B(|\textbf{g}|,\chi )&= |\textbf{g}| \frac{d^2}{4}&\text {with }&d \text { a constant for the diameter of the colliding particles}. \end{aligned}$$
    (5)

  • Its generalization given by the variational hard spheres (VHS) model,

    $$\begin{aligned} B(|\textbf{g}|,\chi )&= |\textbf{g}|^{\frac{\eta -5}{\eta -1}} \frac{d^2}{4}. \end{aligned}$$
    (6)

  • The inverse power law potentials (IPL), i.e. with \(\eta >3\) determining the power law exponent

    $$\begin{aligned} B(|\textbf{g}|,\chi )&= |\textbf{g}|^{\frac{\eta -5}{\eta -1}} W_0 \frac{\,\text {d}W_0}{\,\text {d}\chi }{} & {} \text {with}&\chi&= \pi - 2 \int _0^{W_1} \left( 1-W^2 -\frac{2}{\eta -1}\left( \frac{W}{W_0}\right) ^{\eta -1}\right) ^{-\frac{1}{2}}\,\text {d}W \end{aligned}$$
    (7)
    $$\begin{aligned} \text {and } W_1&\text { the positive root of }{} & {} {} & {} 1-W_1^2 -\frac{2}{\eta -1}\left( \frac{W_1}{W_0}\right) ^{\eta -1}. \end{aligned}$$
    (8)

    We use the change of variables given in [7] to evaluate \(W_0(\chi )\).

We identify two types of assumed potentials corresponding to whether or not B depends on the angle \(\chi \). Additionally, \(\eta \) can be chosen from \((3,\infty )\). Note that the IPL potential models can be derived from assuming a specific potential between the colliding particles, whereas the VHS model only allows that for \(\eta =\infty \), in which case the two models correspond to each other. In this sense, the power potentials can be seen as more realistic models and the VHS models as a simplified version.

In this paper we will work with different examples of these models and compare them. In particular, we work with the classical \(\chi \)-dependent Maxwell Potential with \(\eta =5\), the \(\chi \)-independent and hence simplified Maxwell potential, as well as the hard power potential with \(\eta =10\). As we will explore in Sect. 4.2.2, these choices reflect different levels of computational difficulty both in a priori calculations as well as in the numerical evaluation.

3 Irreducible Burnett Ansatz

3.1 Traditional Setup

3.1.1 Expansion of the Distribution Function

To solve the space homogeneous Boltzmann equation numerically, we follow [16] to expand the distribution function with an orthonormal basis set \(\Upsilon _\alpha (\textbf{c})\),

$$\begin{aligned} f(t,\textbf{c})&= \sum _{\alpha } w_\alpha (t) \Upsilon _\alpha (\textbf{c}){} & {} \text {with}&\Upsilon _\alpha (\textbf{c})&:= \Psi _\alpha (\textbf{c}) \cdot f^{(\text {eq})}(\textbf{c}) \end{aligned}$$
(9)

where \(\alpha \) is typically a multi-index in three indices determining the basis polynomial \(\Psi _\alpha \), \( f^{(\text {eq})}(\textbf{c})\) is the global equilibrium or Maxwellian function and the scalar product is chosen for the weighted function space \(W_{\text {eq}}:L^2(\mathbb {R}^3,\mathbb {R}, \frac{1}{f^{(\text {eq})}} \,\text {d}{\textbf{c}})\), see e.g. [16]:

$$\begin{aligned} \langle \cdot , \cdot \rangle :&\, W_{\text {eq}} \times W_{\text {eq}} \rightarrow \mathbb {R}\nonumber \\ \langle g,h \rangle :=&\int _{\mathbb {R}^3} g h \frac{1}{f^{(\text {eq})}} \,\text {d}{\textbf{c}}, \end{aligned}$$
(10)

to allow us to identify the weights \(w_\alpha \) as moments of the distribution function. Here, we shift the velocity-coordinates such that the medium velocity is zero and rescale the variables so that the temperature is 1, giving us

$$\begin{aligned} f^{(\text {eq})} := \frac{1}{\left( \sqrt{2\pi }\right) ^3} \exp {\left( -\frac{\textbf{c}^2}{2}\right) }. \end{aligned}$$
(11)

Generalizing this approach, the distribution function \(f(t,\textbf{c})\) is approximated as a time-dependent polynomial in \(\textbf{c}\) of degree \(M\in \mathbb {N}\) or less, multiplied by the global Maxwellian,

$$\begin{aligned} f(t,\textbf{c}) = \underbrace{p_t(\textbf{c})}_{\begin{array}{c}\text {time-dependent,}\\ \text {real valued} \\ \text { polynomial in} \textbf{c} \text {of degree } \le M\end{array}} \underbrace{f^{(\text {eq})}(\textbf{c})}_{\begin{array}{c}\text {global Maxwellian,}\\ \text {Gaussian-like}\\ \text {equilibrium distribution}\end{array}}, \end{aligned}$$

implicitly choosing the approximation space for the distribution function \(f(t,\textbf{c})\in V_{\text {eq}}\) with

$$\begin{aligned} V_{\text {eq}}&:= P^M\cdot f^{(\text {eq})}(\textbf{c}),&P^M&\subset \mathbb {R}[c_x,c_y,c_z],&P^M&:= \left\{ p\in \mathbb {R}[c_x,c_y,c_z] | \text {degree of } p \le M\right\} \cong \mathbb {R}^N, \end{aligned}$$
(12)

where \(\mathbb {R}[c_x,c_y,c_z]\) is the space of all real polynomials in three variables and \(N=\frac{1}{6}(M+1)(M+2)(M+3)\) the dimension of \(P^M\). We can equip the polynomial space with a scalar product corresponding to the setup (10):

$$\begin{aligned} \langle \cdot , \cdot \rangle _P :&\mathbb {R}[c_x,c_y,c_z] \times \mathbb {R}[c_x,c_y,c_z] \rightarrow \mathbb {R}\nonumber \\ \langle p,q \rangle _P :=&\int _{\mathbb {R}^3} p q {f^{(\text {eq})}} \,\text {d}{\textbf{c}}. \end{aligned}$$
(13)

3.1.2 Expansion of the Collision Operator

Inserting the expansion of the distribution function (9) into the space homogeneous Boltzmann equation (1) and using the linearity of the bilinear collision operator yields:

$$\begin{aligned} \sum _{\alpha '} \Upsilon _{\alpha '}(\textbf{c}) \frac{\partial w_{\alpha '}(t)}{\partial t} = \sum _{\beta \gamma }\mathcal {S}\left( \Upsilon _{\beta }, \Upsilon _{\gamma }\right) w_\beta w_{\gamma }. \end{aligned}$$
(14)

We now project this expression onto \(V_{\text {eq}}\) spanned by orthonormal basis functions \( \Upsilon _{\alpha }\). The left hand side leads to

$$\begin{aligned} \left\langle \Upsilon _{\alpha }, \sum _{\alpha '} \Upsilon _{\alpha '} \frac{\partial w_{\alpha '}(t)}{\partial t}\right\rangle&= \sum _{\alpha '} \underbrace{\left\langle \Upsilon _{\alpha }, \Upsilon _{\alpha '}\right\rangle }_{\delta _{\alpha '\alpha }} \frac{\partial w_{\alpha '}(t)}{\partial t} \nonumber = \frac{\partial w_{\alpha }(t)}{\partial t}, \end{aligned}$$

while the right hand side evaluates to

$$\begin{aligned} \sum _{\beta ,\gamma } \underbrace{\left\langle \Upsilon _{\alpha },\mathcal {S}\left( \Upsilon _{\beta }, \Upsilon _{\gamma }\right) \right\rangle }_{C_{\alpha \beta \gamma }^{(\Psi )}} w_\beta w_\gamma =: s_{\alpha } . \end{aligned}$$
(15)

Overall, we find that the rate of change of the distribution function’s weights depends on the collision vector \(s_{\alpha }\),

$$\begin{aligned} \frac{\partial w_\alpha (t)}{\partial t} = s_\alpha . \end{aligned}$$
(16)

The collision vector in turn is determined by the bilinear operation (15) between the weights \(w_\alpha \) of the distribution function and a basis-dependent collision tensor

$$\begin{aligned} C_{\alpha \beta \gamma }^{(\Psi )} :&= \langle \Psi _\alpha f^{(\text {eq})},\mathcal {S}(\Psi _\beta f^{(\text {eq})}, \Psi _\gamma f^{(\text {eq})}) \rangle . \end{aligned}$$
(17)

3.2 Structure of the Approximation Space

The remaining choice are the N basis polynomials \(\Psi _\alpha (\textbf{c})\), with which we span \(P^M\), which has great influence on the structure and sparsity of the collision tensor and hence on the required computational time and memory to obtain \(s_\alpha \).

For example Grad [5] or more recently Cai [9] choose Hermite polynomials in three coordinates, since these are known to be orthogonal with respect to the corresponding scalar product \(\langle \cdot ,\cdot \rangle _P\). However, structure and sparsity of the resulting collision tensor can still be improved.

We want to use a basis that exploits a key feature of the collision operator: It describes a physical process in the three dimensional velocity space, requiring it to be, like all physical processes, compatible with isometric transformations of the coordinate system, i.e. with \(\mathscr {O}_3\) the group of orthogonal matrices from \(\mathbb {R}^{3\times 3}\):

$$\begin{aligned} \forall r\in \mathscr {O}_3: r\left( S(f)(\textbf{c})\right) = S\left( r(f)\right) . \end{aligned}$$
(18)

While this identity is often accepted, we included a proof in the “Appendix” for completeness, as this statement is central for this paper. This restriction allows us to employ results from the representation theory of \(\mathscr {O}_3\) and reduce the bilinear maps with which we express \(s_\alpha \) to only those bilinear maps between the \(\mathscr {O}_3\)-irreducible subspaces of \(P^M\).

3.2.1 Decomposition of \(P^M\) into Its Irreducible Subspaces

With the space of homogeneous and harmonic polynomials of degree \(n\in \{0,1,\cdots , M\}\) and dimension \(2n+1\)

$$\begin{aligned} \mathscr {H}^n := \left\{ p \in \mathbb {R}[c_x,c_y,c_z] | \left. \begin{array}{c} \forall \lambda \in \mathbb {R}: p(\lambda c_x, \lambda c_y, \lambda c_z) = \lambda ^n p(c_x, c_y, c_z) \\ \Delta p := (\partial _x^2 +\partial _y^2 +\partial _z^2)p= 0\end{array}\right. \right\} \cong \mathbb {R}^{2n+1} \end{aligned}$$
(19)

we have the building blocks for the irreducible subspaces of \(P^M\) [17]. To make it clear when an index describes the degree of a harmonic polynomial, we call n the anisotropic index. We also define the one-dimensional space of homogeneous isotropic polynomials of second degree

$$\begin{aligned} \Omega := \left\{ p(c_x,c_y,c_z)=\lambda (c_x^2 + c_y^2 + c_z^2) | \lambda \in \mathbb {R}\right\} \in P^M, \end{aligned}$$
(20)

and denote with \(c^2\) its element where \(\lambda =1\). Ignoring the chosen scalar product from Eq. (13) for now allows us to decompose \(P^M\) into a direct sum of homogeneous polynomials with respect to some corresponding scalar product,

$$\begin{aligned} P^M = \bigoplus _{a = 0}^{\left\lfloor \frac{M}{2}\right\rfloor } \bigoplus _{n=0}^{M-2a} (c^2)^a \cdot \mathscr {H}^{n}. \end{aligned}$$
(21)

We can check that this decomposition is complete by counting dimensions:

$$\begin{aligned} \sum _{a=0}^{\left\lfloor \frac{M}{2}\right\rfloor } \sum _{n=0}^{M-2a} \dim \left( (c^2)^a\mathscr {H}^n\right) =\sum _{a=0}^{\left\lfloor \frac{M}{2}\right\rfloor } \sum _{n=0}^{M-2a} 2n+1=\frac{1}{6}(M+1)(M+2)(M+3) = \dim \left( P^M\right) . \end{aligned}$$
(22)
Fig. 1
figure 1

Decomposition of \(P^1, P^2, P^3\) to \(P^M\) into their homogeneous irreducible subspaces. The irreducible subspaces are sorted column-wise by their homogeneous degree \(\text {deg}=2a+n\) and row-wise by the degree n of the harmonic spaces \(\mathscr {H}^n\). Those that share a row are isomorphic, subspaces that are from different rows are pairwise non-isomorphic. The decomposition is not unique within each row, linear combinations of different orders of \(c^2\) are possible. Here we chose the homogeneous polynomials of \(c^2\) for visual clarity. All non-isomorphic irreducible subspaces are orthogonal to each other for every \(\mathscr {O}_3\) invariant scalar product. To achieve orthogonality with respect to our chosen scalar product within each row of isomorphic irreducible subspaces, we use the linear combinations given by associated Laguerre polynomials of \(c^2\), \(L_a^{\left( n+\nicefrac {1}{2}\right) }\left( \nicefrac {{c}^2}{2}\right) \)

Full size image

Figure 1 sorts these subspaces column-wise according to their homogeneous degree \(\text {deg}=2a+n\) and row-wise according to their anisotropic index n. Subspaces with same anisotropic index n are isomorphic to each other and the decomposition is not unique within each set of isomorphic subspaces. Subspaces with different anisotropic indices are non-isomorphic to each other and therefore necessarily pairwise orthogonal with respect to any \(\mathscr {O}_3\) invariant scalar product, see Remark 9.5 in this paper’s “Appendix”.

Now we come back to the chosen scalar product in (13). The isomorphic subspaces shown in Fig. 1 are not orthogonal with respect to \(\langle \cdot ,\cdot \rangle _P\). We therefore orthogonalize each set of isomorphic subspaces with a linear combination of suitable powers of \((c^2)\) determined by associated Laguerre polynomials:

$$\begin{aligned} P^M = \bigoplus _{a = 0}^{\left\lfloor \frac{M}{2}\right\rfloor } \bigoplus _{n=0}^{M-2a} \underbrace{L_a^{\left( n+\frac{1}{2}\right) }\left( \frac{{c}^2}{2}\right) \cdot \mathscr {H}^{n}}_{=:{^{a}\mathscr {H}^{n}}}, \end{aligned}$$
(23)

where \({^{a}\mathscr {H}^{n}}\) are the orthogonalized irreducible subspaces. We call a the isotropic index and are left with the basis choice for \(\mathscr {H}^{n}\).

3.2.2 Basis Choice Adapted to the Irreducible Subspaces

Here we employ the real-valued solid spherical harmonics \(Y_n^l: \mathbb {R}^3 \rightarrow \mathbb {R}\) of n-th degree with the directional index \(l\in \{-n, -n+1, \cdots , n-1, n\}\), related to the real spherical harmonics \(\mathscr {Y}_n^l: S^2 \rightarrow \mathbb {R}\) by extension \(S^2 \rightarrow \mathbb {R}^3\) via

$$\begin{aligned} Y_n^l (\textbf{c}) = \Vert {\textbf{c}} \Vert ^n \cdot \mathscr {Y}_n^l\left( \frac{\textbf{c}}{\Vert {\textbf{c}} \Vert }\right) . \end{aligned}$$
(24)

Note, that we can draw parallels to indices in quantum mechanics where the spherical harmonics are complex, and the principal, azimuthal and magnetic quantum numbers have similar mathematical roles to the isotropic index a, anisotropic index n and directional index l, respectively.

This leads to the following choice for \(\Psi _\alpha \):

$$\begin{aligned} \Psi _{\alpha }=\Psi _{anl}= \underbrace{\frac{1}{\mathscr {N}_{anl}}}_{ \begin{array}{c} \text {normalization}\\ \text {coefficient} \end{array} } \underbrace{Y_n^l(\textbf{c})}_{ \begin{array}{c} \text {real solid} \\ \text {spherical} \\ \text {harmonic}\end{array} } \underbrace{L_a^{\left( n+\frac{1}{2}\right) }\left( \frac{c^2}{2}\right) }_{ \begin{array}{c}\text {associated} \\ \text {Laguerre} \\ \text {polynomials} \end{array} }, \end{aligned}$$
(25)

with \((a,n,l)\in \mathbb {N}_0 \times \mathbb {N}_0 \times \{-n,\cdots ,n\}\) specifying the multi-index \(\alpha \), and the normalization coefficient given by

$$\begin{aligned} \mathscr {N}_{anl} := \sqrt{\left\langle Y_n^l L_a^{\left( n+\frac{1}{2}\right) },Y_n^l L_a^{\left( n+\frac{1}{2}\right) }\right\rangle _P}. \end{aligned}$$

3.3 Discussion of the Basis Set and Irreducibility

Instead of immediately choosing a basis set, we first looked at the irreducible subspaces of \(P^M\) with respect to \(\mathscr {O}_3\) and collected them as spaces of homogeneous polynomials in Fig. 1. Upon finding that we have multiple isomorphic subspaces, all row-wise collected in Fig. 1, we linearly combined them via Laguerre polynomials to obtain \({^{a}\mathscr {H}^{n}}\), the orthogonalized irreducible subspaces. Then we chose basis polynomials for each \({^{a}\mathscr {H}^{n}}\), but again using the isomorphism between spaces within one row, it was enough to choose a set of basis polynomials for each lowest degree irreducible subspace per row, i.e. for the spaces \(\mathscr {H}^{n}\) of harmonic polynomials of degree n.

We have chosen real solid spherical harmonics, since they are easily accessible, orthogonal and adapted to the chain of subgroups \(\mathscr {O}_3 \ge \mathscr {O}_2 \ge \mathscr {O}_1\) with \(c_z\) the special symmetry direction, i.e. for an \(\mathscr {O}_2\)-invariant problem rotated so that \(c_z\) is the rotation axis for \(\mathscr {O}_2\), all coefficients with \(l\ne 0\) are zero.

The basis set containing all basis polynomials with \(2a +n \le M\) spans the full space \(P^M\). Note, that only basis polynomials with \(n=0\) are rotationally invariant. However, similar to the decomposition of a natural number into its prime factors, this basis is adapted to the decomposition of \(P^M\) into its smallest invariant subspaces. Here “smallest” is defined as an invariant subspace U, that cannot be further decomposed into invariant subspaces other than U itself and the zero space, similar to a prime number only being devisable by itself and 1. These subspaces are called irreducible. Figure 1 shows the decomposition of \(P^M\) into its homogeneous irreducible subspaces, while we use orthogonalized subspaces with respect to \(\langle \cdot ,\cdot \rangle _P\) given for a pair of chosen isotropic index a and anisotropic index n by

$$\begin{aligned} {{\,\textrm{span}\,}}\left\{ \Psi _{anl} | -n \le l \le n \right\} \end{aligned}$$

with a dimension of \(2n+1\).

Note that we have recovered the spectral Burnett ansatz with real spherical harmonics. First results with the spectral Burnett basis have been developed previously in [10,11,12, 18], but we are the first to exploit the underlying structure of the collision operator in our implementation. We also implement the nearly fully analytic calculation of the tensor coefficients and carry out numerical tests for large M.

4 Implications of Representation Theory

4.1 Decomposing the Collision Operator

Equation (15) is the orthogonal projection of \(\mathcal {S}(f,f)\) onto the approximation space \(V_{\text {eq}}\). Equivalently we can identify the bilinear map \(\mathcal {C}: P^{M} \times P^{M} \rightarrow P^{M}\) with coefficients given by the collision tensor in terms of the basis functions of \(P^{M}\), now defined as

$$\begin{aligned} {C}_{\alpha \beta \gamma }&= {C}_{anl, b\hat{n}\hat{l}, c\tilde{n}\tilde{l}}:=\langle \Psi _{anl},\mathcal {S}(\Psi _{b\hat{n}\hat{l}} f^{(\text {eq})}, \Psi _{c\tilde{n}\tilde{l}} f^{(\text {eq})}) \rangle _P, \end{aligned}$$
(26)

i.e. with \(p,q \in P^{M}\) and their respective expansion coefficients \(w_{anl},u_{anl}\) we can express the map \(\mathcal {C}\) via

$$\begin{aligned} \mathcal {C} (p,q) = \sum _{anl}\sum _{b\hat{n}\hat{l}}\sum _{c\tilde{n}\tilde{l}}{C}_{anl, b\hat{n}\hat{l}, c\tilde{n}\tilde{l}} w_{b\hat{n}\hat{l}} u_{c\tilde{n}\tilde{l}} \Psi _{anl}. \end{aligned}$$
(27)

Not only is \(\mathcal {C}\) a bilinear map, it inherits the property of the collision operator \(\mathcal {S}\) that it is linear with respect to \(\mathscr {O}_3\), compare to Eq. (18):

$$\begin{aligned} \forall r\in \mathscr {O}_3: r\left( \mathcal {C}(p,q)\right) = \mathcal {C}\left( r(p),r(q)\right) . \end{aligned}$$
(28)

Such a map is called natural. This restriction has been studied in representation theory and implies a decomposition of \(\mathcal {C}\) into a sum over isotropic and anisotropic indices

$$\begin{aligned} \mathcal {C}&: P^M\times P^M\rightarrow P^M =\sum _{abc}\sum _{n\tilde{n}\hat{n}} S_{abc}^{n\hat{n}\tilde{n}} \cdot \Phi _{abc}^{n\hat{n}\tilde{n}}, \end{aligned}$$
(29)

with \(S_{abc}^{n\hat{n}\tilde{n}}\in \mathbb {R}\) some constants that, given a set of maps \(\Phi _{abc}^{n\hat{n}\tilde{n}}\), distinguish between different maps \(\mathcal {C}\). Each \(\Phi _{abc}^{n\hat{n}\tilde{n}}: P^M \times P^M \rightarrow P^M\) is a non-zero natural bilinear map given by

(30)

with orthogonal projections \(\mathscr {P}_{(n,a)}: P^M \rightarrow {^{a}\mathscr {H}^{n}}\), isomorphisms \(\psi _{(n,a)}: {^{a}\mathscr {H}^{n}} \rightarrow \mathscr {H}^n\), embedding \(\mathscr {E}_{(n,a)}: {^{a}\mathscr {H}^{n}}\rightarrow P^M\), and the universal natural bilinear map

$$\begin{aligned} Q^{n\hat{n}\tilde{n}}: \mathscr {H}^{\hat{n}} \times \mathscr {H}^{\tilde{n}} \rightarrow \mathscr {H}^n. \end{aligned}$$
(31)

This map \(Q^{n\hat{n}\tilde{n}}\) is either zero or unique up to a constant, depending on the combination of anisotropic indices:

$$\begin{aligned} Q^{n\hat{n}\tilde{n}} \text {is zero unless } \left\{ \begin{aligned} {\hat{n}} + \tilde{n} - n&\in 2\mathbb {N}_0, \text {and}\\ 0 \le {\hat{n}} + \tilde{n} - n&\le 2 \min ({\hat{n}},\tilde{n}). \end{aligned}\right. \end{aligned}$$
(32)

Note, that a decomposition of a (multi-) linear map between vector spaces into a sum of maps between subspaces as done in Eq. (29) by itself is generally possible. Equation (28) is crucial for the decomposition of \(\mathcal {C}\) in (29), requiring \(\Phi _{abc}^{n\hat{n}\tilde{n}}\) and \(Q^{n\hat{n}\tilde{n}}\) to be natural as well, and ultimately restricting all possible bilinear and natural maps \(\mathscr {H}^{\hat{n}} \times \mathscr {H}^{\tilde{n}} \rightarrow \mathscr {H}^n\) to be the same up to a constant with the additional condition (32).

4.2 Decoding the Structure of the Collision Tensor

Overall, the previous result implies the decomposition of the collision tensor into two tensors:

$$\begin{aligned} {C}_{anl, b\hat{n}\hat{l}, c\tilde{n}\tilde{l}}&= \mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc} Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}, \end{aligned}$$
(33)

mirroring the structure of irreducible subspaces of \(P^M\). \(Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}\) and \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) have two distinct roles for the overall collision tensor. The coupling tensor \(Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}\) collects the coefficients of the map \(Q^{n\hat{n}\tilde{n}}\). It is independent of the potential and encodes the purely mathematical coupling of \(Y_{\hat{n}}^{\hat{l}}\) and \(Y_{\tilde{n}}^{\tilde{l}}\) to \(Y_n^l\). The impact tensor \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) encodes the physics of the particle collisions.

4.2.1 The Coupling Tensor

The coupling tensor \(Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}\) encodes the natural bilinear map, unique up to a constant factor, from two harmonic polynomial spaces of degrees \(\hat{n}\) and \(\tilde{n}\) to a third harmonic polynomial space of degree n, see Eq. (31). Crucially, two natural bilinear maps between different, but isomorphic irreducible subspaces are identical up to a constant factor and hence all can be expressed in terms of one \(Q^{n \hat{n} \tilde{n}}\). Referring to Fig. 1 and knowing that all subspaces of the same row are isomorphic to each other, we can also picture \(Q^{n \hat{n} \tilde{n}}\) as the bilinear map between three rows. This universality is the key in our algorithm, allowing us to achieve high efficiency both in terms of computational time and memory usage. We can calculate the values of the coupling tensor for example with

$$\begin{aligned} Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}} = \langle Y_n^l, Y_{\hat{n}}^{\hat{l}} \cdot Y_{\tilde{n}}^{\tilde{l}} \rangle _P = \int _{\mathbb {R}^3} Y_n^l \cdot Y_{\hat{n}}^{\hat{l}} \cdot Y_{\tilde{n}}^{\tilde{l}} f^{(\text {eq})} \,\text {d}\textbf{c}. \end{aligned}$$
(34)

The coupling tensor is related to the Clebsch–Gordon-Coefficients [19]. While the Clebsch–Gordon-Coefficients are more common in quantum physics, where they are usually used for three harmonic spaces of complex polynomials, the coupling tensor is the equivalent for real harmonic polynomials. It shares the property that it is zero for most combinations of anisotropic and directional indices \((n,\hat{n},\tilde{n},l,\hat{l},\tilde{l})\), but does not have as many restrictions as its complex counterpart. In particular, the conditions in Eq. (32) hold for \(Q_{l\hat{l}\tilde{l}}^{n \hat{n}\tilde{n}}\), and if they are met, then \(Q_{000}^{n \hat{n}\tilde{n}}\) is unequal to zero. Keeping in mind the uniqueness up to a constant of the coupling tensor for each triple of anisotropic indices \((\hat{n},\tilde{n},n)\), we choose one instance of \(Q^{n \hat{n} \tilde{n}}\) for each triple \((n, \hat{n}, \tilde{n})\), calculate the values of the coupling tensor once and hard-code them in the implementation as function

figure a

.

4.2.2 The Impact Tensor

In contrast to \(Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}\), the impact tensor \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) contains all information about the physics of the collision. While from the mathematical point of view the constant factor distinguishing two maps \(Q^{n \hat{n} \tilde{n}}\) with same anisotropic indices \((n, \hat{n}, \tilde{n})\) may seem irrelevant, it is clear that in the physical application these factors are the main interest. Here the conservation rules come into play as zeroes for particular combinations of anisotropic and isotropic indices \((n,{\hat{n}},\tilde{n},a,b,c)\), but this is also where different potentials lead to different values in the coefficients of the impact tensor. Notice, that the impact tensor is independent of the directional indices \((l,\hat{l},\tilde{l})\), so with our chosen map \(Q^{n \hat{n} \tilde{n}}\) we can compute its coefficients with

$$\begin{aligned} \mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc} =\frac{\langle \Psi _{an0} f^{(\text {eq})},\mathcal {S}(\Psi _{b\hat{n}0} f^{(\text {eq})}, \Psi _{c\tilde{n}0} f^{(\text {eq})}) \rangle }{Q_{000}^{n \hat{n} \tilde{n}}} \end{aligned}$$
(35)

for combinations of anisotropic indices \((n,{\hat{n}},\tilde{n})\) fulfilling the conditions in (32). Depending on the potential, we can solve the integration in (35) fully or almost fully analytically with a computer algebra system, see the git-repository [20] for further details.

Table 1 Overview of a few choices for \(\eta \) and \(\chi \)-dependence in \(B(|\textbf{g}|,\chi )\) and their corresponding potential models
Full size table

Referring to Table 1, we can now see where each chosen potential falls on the spectrum of high and low computational difficulty of both a priori evaluation, i.e. the calculation of the impact tensor itself, and runtime evaluation of the collision vector.

Note, that there is some relation between these two types of difficulty. The a priori evaluation only determines a set of numbers that make up the impact tensor, whereas the runtime evaluation mostly depends on the number of non-zero impact tensor entries and not on the specific non-zero entry \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\). As already noted by Grad [5], for the potentials with \(\eta =5\) the additional condition

$$\begin{aligned} 2a+n \ne 2b+\tilde{n}+2c+{c} \implies \mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc} = 0 \end{aligned}$$
(36)

applies, which stems from the orthogonality of the basis functions and the independence of the kernel from \(\textbf{c}\) and \(\mathbf {c_1}\). This significantly reduces the amount of non-zero impact tensor coefficients, leading to comparatively low computational difficulty both a priori and during runtime.

The a priori computational difficulty of the impact tensor coefficients additionally is determined by the \(\chi \)-dependency of the kernel B. All \(\chi \)-independent models are of lower difficulty, with the simplified Maxwell model the lowest difficulty due to (36). On the other side of the spectrum lies the hard power potential with \(\eta =10\), since it is \(\chi \)-dependent and condition (36) does not apply, requiring the evaluation of the full set of \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\). This potential also has high runtime computational difficulty, since almost all impact tensor coefficients are non-zero.

4.3 Full Generalization of the Collision Operator

Notice, that the decomposition of the collision tensor into the impact and coupling tensor not only implies a particular implementation to calculate the collision vector, but it also gives us a unique understanding of the role of each coefficient. In particular, we can now generalize the collision operator to any symmetric, bilinear map between real polynomials in three variables with physical meaning, i.e. invariance under transformation of the coordinate system: Such a map would not necessarily follow the conservation laws but still follow the decomposition into coupling and impact tensor. To obtain an upper limit for the computational cost of calculating the collision vector, we can assign the impact tensor random numbers for all combinations of anisotropic and isotropic indices that fulfil Eq. (32). When testing the performance with this setup, we shall call such a potential general.

5 Implementation

The task is to implement the tensor-vector multiplication between the expansion coefficients of the collision tensor in the form of \({S}_{n{\hat{n}}\tilde{n}}^{abc} Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}\) and the expansion coefficients \(w_{anl}\) of the distribution function. The result is saved as a vector with expansion coefficients \(s_{anl}\), so we want to find an efficient algorithm to compute the collision vector s, i.e.

(37)

5.1 Custom Implementation Adapted to the Given Tensor Structure

Looking at the calculation task in (37), we can separate it into operations that need to be carried out for all combinations of anisotropic and isotropic indices. Beginning by setting the collision vector s to zero, we can rewrite the task as

(38)

Note, how the impact tensor is now outside of the sum, only remaining as a constant factor.

5.1.1 Implementing the Coupling Tensor

In fact, we can now isolate the map between the irreducible subspaces of different anisotropic and isotropic indices in terms of an operation that only involves the coupling tensors and the directional indices:

(39)

Here the anisotropic indices are only relevant to indicate the degree of the harmonic subspaces and hence the length of the involved vectors. Note, that we changed the positions of the indices and font of the coefficients of the distribution function and collision vector to indicate that this is an operation on a small subsection of the overall vectors.

Fig. 2
figure 2

Schematic showing the operation of

figure b
on the specifically structured arrays of the distribution function f determined by the weights w and the collision operator determined by the weights s

Full size image

Apart from the constant factor determined by the impact tensor, this operation is independent of the isotropic indices (a, b, c), so we can give it as a general operation between three generic vectors \(\varsigma ^{n},u^{\hat{n}},v^{\tilde{n}}\) of lengths \(2n+1, 2\hat{n}+1,2\tilde{n}+1\), respectively:

$$\begin{aligned} \varsigma ^{n}_l \mathrel {+}=\beta \cdot \sum _{\hat{l} \tilde{l}} Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}} u^{\hat{n}}_{\hat{l}} v^{\tilde{n}}_{\tilde{l}}. \end{aligned}$$
(40)

We obtain Eq. (39) by replacing \(\beta \) with the corresponding value of \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\).

Since \(Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}\) are constants, the above operation (40) can be hard-coded without loss of generality of the overall implementation. We do so by giving each triple of anisotropic indices \((n, \hat{n}, \tilde{n})\) a unique case numer q and saving the expansion coefficients of both the distribution function \(w_{anl}\) and the collision vector \(s_{anl}\) in a specific order, so that we seperate it into coherent \(2n+1\) long sections, or sub-vectors, \(\text {w}^{an}\). We also order the \(w_{anl}\) such that the directional index l starts at \(-n\) and ends at n, see Fig. 2. This reflects the splitting of the polynomial space into its irreducible subspaces: Each section \(\text {w}^{an}\) contains the coordinates of w in one particular irreducible subspace characterized by the anisotropic and isotropic indices a and n. The position of each section \(\text {w}^{an}\) is given by a corresponding pointer \(p_{an}\), which locates the first of the \(2n+1\) entries. The collision vector is ordered similarly.

Furthermore, we know that the following symmetry relations must hold:

$$\begin{aligned} \mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}&= \mathcal {S}_{n\tilde{n}{\hat{n}}}^{acb}&Q_{l\hat{l}\tilde{l}}^{n \hat{n} \tilde{n}}&=Q_{l\tilde{l}\hat{l}}^{n \tilde{n} \hat{n}} \end{aligned}$$
(41)

Therefore, we used Mathematica to generate the C++ function

figure c

that implements Eq. (40) for all combinations of anisotropic indices \((n, \hat{n}, \tilde{n})\) with \(\hat{n} \le \tilde{n}\). Input for this method is \(\beta \) as double

figure d

, q as integer

figure e

and the three vectors \(\xi ^{n},\zeta ^{\hat{n}},\varsigma ^{\tilde{n}}\) as three double pointers

figure f

,

figure g

,

figure h

. The method switches between all relevant triplets of anisotropic indices \((n, \hat{n}, \tilde{n})\), where q indicates the triplet and is thus used in the case distinction. For each case C++-code corresponding to the operation in (40) was generated. Here the three pointers are used as starting positions for the three vectors.

Fig. 3
figure 3

Extract from the C++ code for the function

Full size image

Note, that this code does not check, whether the three vectors actually have been allocated, all input is assumed to be valid in order for the computation to be as time-efficient as possible. Furthermore, it is always assumed that \(\hat{n}\le \tilde{n}\), the input vectors should be ordered accordingly (Fig. 3).

5.1.2 Implementing the Impact Tensor

Fig. 4
figure 4

Extract from the impact tensor file, each line containing all necessary information for

figure j
. These are the first 20 lines corresponding to the Maxwellian potential and \(M=20\)

Full size image

In contrast to Q, the coefficients \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) can vary depending on the potential. We therefore give the impact tensor in a text file as input for the code. Each line of this text file is an input list containing the necessary information for

figure k

, compare to Eq. (40) and see Fig. 4:

$$\begin{aligned}&\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}&\quad \quad&q&\quad \quad&p_{an}&\quad \quad&p_{b\hat{n}}&\quad \quad&p_{c\tilde{n}} \end{aligned}$$

To calculate the collision vector, i.e. to compute (38), the C++-code iterates through each line of the impact tensor file and applies

figure l

with the case q, \(\beta =\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) and the three vectors determined by \(p_{an}, p_{b\hat{n}}, p_{c\tilde{n}}\). Utilizing (41), we can shorten the input list by stating twice the value of \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) when \((b,\hat{n}) \ne (c,\tilde{n} )\), leaving the line with \(\hat{n}<\tilde{n}\) and omitting the corresponding line of \(\mathcal {S}_{n\tilde{n}{\hat{n}}}^{acb}\).

5.1.3 Discussion of the Implementation

Effectively, we have now implemented the map \(\Phi _{abc}^{n\hat{n}\tilde{n}}\) from Eq. (30): Structuring the array of moments \(w_{anl}\) into subsections corresponding to the irreducible subspaces and using the positions given by the pointers \(p_{b\hat{n}}\) and \(p_{c\tilde{n}}\) as starting positions for the operation

figure m

corresponds to \(\phi _{(\hat{n},b)}\circ \mathscr {P}_{(\hat{n},b)}\) and \(\phi _{(\tilde{n},c)}\circ \mathscr {P}_{(\tilde{n},c)}\).

figure n

itself is the implementation of the map \( Q^{n\hat{n}\tilde{n}}\), only that it operates on the section of the vector \(s_{anl}\) indicated by the pointer \(p_{an}\), implementing \(\mathscr {E}_{(n,a)} \circ \phi ^{-1}_{(n,a)}\).

This setup is very flexible. It is easily adapted to different potentials, theories and initial conditions, i.e. the initial occupancy of \(w_{anl}\) of the distribution function. Omitting lines belonging to irrelevant combinations of \((a,b,c,n,{\hat{n}},\tilde{n})\) for the given setup, we can build calculation-specific input files for the collision operator. In Table 2 we have listed the required memory space for the impact tensor and the average calculation time of one time step for a selection of different potentials and theories. All computation is done sequentially on a CPU model Intel(R) Core(TM) i7-8650U. We note that the hard power potential with \(\eta =10\) is very close to the general potential in terms of computational requirements. In Table 3 we have listed the number of coupling coefficients for different M and the corresponding sizes of the compiled program. We note, that the memory requirement for the compiled program is much larger than that for the text file of the impact tensor.

Table 2 Overview of the computational requirements to calculate the collision operator with our implementation of the irreducible Burnett ansatz depending on the computational setups
Full size table
Table 3 Overview of the computational requirements for the coupling tensor depending on the computational setups
Full size table

5.2 Comparison to an Algorithm for General Tensor-Vector Multiplications and Current State of the Art

Given that the ultimate goal of this work is to produce an implementation of the evaluation of \(\mathcal {S}(f,f)\) within a numerical code, that is as fast as possible, the question is, whether the above described implementation is better than an algorithm developed specifically for the computation of tensor-vector multiplications. The efficient implementation of tensor operations is a field of on-going research in high performance computing and currently there are many different options available.

To check how the algorithm we developed compares to other algorithms, we chose the Tensor Algebra Compiler (TACO) [21] as a case study, as it provides code generation in C++ and seems to perform similarly well to other libraries. Here we found that TACO performed best when given the full collision tensor \(C_{\alpha \beta \gamma }\) with every triple of indices (a, n, l) mapped to one counter index. We found the computational times comparable but slightly slower than our implementation. We also compare memory requirements for the full tensor \(C_{\alpha \beta \gamma }\) with the irreducible Burnett approach and found that for a general potential, the full tensor \(C_{\alpha \beta \gamma }\) is much more demanding than what is needed for the impact tensor and

figure o

together. However, when measuring the memory requirements for the Maxwell potential, we initially found that the memory requirements for the full tensor \(C_{\alpha \beta \gamma }\) are less than the requirements for

figure p

. This is because saving

figure q

as compiled program is more memory intensive than a file with only numbers, and because we still compared to the general coupling tensor which has many more cases than actually necessary—for \(M=20\) out of the 1331 possible cases only 505 are actually required for the Maxwell potential, leading to a significantly smaller program of only 6.6MB. This reduction is due to the additional condition on the indices (36).

Assessing the performance of the irreducible Burnett algorithm would be incomplete without looking at the performance of the Burnett spectral method in [10] obtained from a single thread computation on a CPU model Intel Xeon E5-2697A V4. In Table 4 we can compare the three algorithms for the Maxwell potential. Additionally, for the hard Maxwell potential with \(\eta =10\) and \(M=M_0=20\), we find from Figure 15 in [10], that one evaluation of the collision operator takes about 90ms, whereas our algorithm takes about 50ms. Note however, that a different computational setup with different CPU models was used for each computation. We therefore conclude, that the computational time of both methods is similar for the IPL potential with \(\eta =10\), while the memory cost is greatly reduced with the irreducible Burnett method, which requires about 51MB, whereas the spectral Burnett method needs 784MB for just the sparse Maxwell potential. Table 4 also allows us to compare performance for the Maxwell potential of both methods and here we can see a significant difference both in computational time and memory usage.

Overall, we are satisfied to conclude that our implementation utilizes the underlying structure of the collision operator well enough to outperform the current state of the art.

Table 4 Comparison between total runtimes of different algorithms for the Maxwell Potential (top), and a general potential (bottom)
Full size table

5.3 Comparison to the Spectral Burnett Method in [10]

The spectral Burnett method used in the ansatz in [10] is based on complex solid harmonics. Here the presented algorithm exploits the relation for the directional indices—the collision tensor’s entries can only be non-zero if \(l=\hat{l}+\tilde{l}\) holds. By contrast, the irreducible Burnett ansatz uses real solid harmonics, for which this condition does not apply. Instead, we find a sparse coupling tensor with band structures, since the real solid harmonics are a simple linear combination of their complex counterparts. Crucially, the main difference between the two approaches lies in the decomposition of the collision tensor into the impact and coupling tensor. The algorithm of the irreducible Burnett ansatz exploits both this decomposition and the sparsity of the coupling tensor. It is possible, that the performance can still be improved by applying the decomposition to the basis with complex spherical harmonics.

5.4 Comparison to the Spectral Fourier Approach

The irreducible and the spectral Burnett ansatz share a similar approach to discretize the velocity space through moments. This method is based on picking a finite polynomial degree and using a finite-dimensional approximation space for the velocity-dependency of the distribution function. In contrast, the spectral Fourier approach discretizes the velocity space by choosing some finite 3-dimensional velocity domain and representing that with a grid of equally distant points. The collision operator is a weighted convolution. [2] and [10] compared its computational costs to the presented algorithm and found comparable performance. Fixing the velocity domain introduces problems in the form of aliasing effects, choice of cut off and conservation properties. On the other hand, moment methods have difficulty in approximating some distributions, an example for this will be demonstrated in Sect. 6.3.

Notably, the spectral Fourier approach is connected to the representation theory of abelian groups, such as \(\mathscr {O}_2\) or the group of translations. In fact, the functions \(e^{2\pi i \theta _k}\) used for the expansion each span a one-dimensional irreducible subspace [22].

5.5 Using the Irreducible Burnett Ansatz

As we will see in the numerical application, not all initial conditions are computable in the Burnett basis. However, moment equations allow a relatively low number of numerical degrees of freedom to describe physically relevant situations. Moments as variables encode physical quantities, usually those of low order are the most interesting, allowing us to interpret a subset of the numbers representing the distribution function in a meaningful way.

Moment equations come with a level of complexity, and the irreducible Burnett ansatz is no exception. Its implementation is challenging compared to other numerical methods for the Boltzmann equation such as direct simulation monte carlo methods [23] or the aforementioned spectral Fourier approaches. This is due to the low level C++ code of the coupling tensor, which needs to be generated using scripts or similar for a high polynomial degree M due to the large number of different cases. We generated the function

figure r

with Mathematica, and while the generating code can be checked, the overall code of

figure s

cannot be verified by a human, only tested for plausibility in a small number of cases. However, this paper must be seen in the context of moment approximations for the Boltzmann equation, see e.g. [13, 24, 25]. In this context, via one way or the other, the collision operator will always be implemented as some matrix–vector product in the linear case, or a tensor-vector-vector product in the bilinear case. While the implementation of such a (bi-) linear operation can be verified by a human, for large degree M the matrix or tensor entries themselves similarly cannot be checked due to their number.

Solving just the spatially homogeneous Boltzmann equation is incomplete, the overall goal is to provide a method, with which the collision operator can be evaluated efficiently. However, the application of the irreducible Burnett ansatz to the inhomogeneous Boltzmann equation is out of the scope of this paper and we refer to [26] for further details.

6 Numerical Application

The irreducible Burnett ansatz is the real pendant to the spectral Burnett ansatz, additionally mathematically decomposing the collision tensor. While the spectral Burnett ansatz in [10] uses complex solid harmonics, the distribution function is real for their method as well. Therefore we expect its properties to be inherited from the spectral Burnett ansatz, including the rate of convergence. All differences between results of both methods must stem from purely numerical effects resulting from computational accuracy. This section aims to ensure the correct implementation of the method. To do so, we will roughly estimate spectral convergence by comparing lower orders of approximation to the numerical solution with \(M=20\) for all cases and times. Additionally we compare to the analytical solution where possible.

Let f denote the exact distribution, \(\hat{f}\) the numerical solution with degree \(M=20\) and moments \(\hat{w}\), \(\tilde{f}\) any other numerical solution with smaller degree and moments \(\tilde{w}\), \(\Delta f:= \hat{f}-\tilde{f}\) and their difference. Using the \(L^2\)-norm implied by the scalar product on \(V_\text {eq}\) from Eq. (10),

$$\begin{aligned} \Vert {f} \Vert = \sqrt{\left\langle f,f\right\rangle } = \sqrt{\int _{\mathbb {R}^3} f^2 \frac{1}{f^{(\text {eq})}} \,\text {d}\textbf{c}}, \end{aligned}$$

\(\Vert {\Delta f} \Vert \) is simply given by the standard vector norm of the difference between their moments,

$$\begin{aligned}\Vert {\Delta f} \Vert = \Vert {\hat{w}-\tilde{w}} \Vert .\end{aligned}$$

Unlike the exact solution f, which we can only access in the first test case, \(\Delta f\) is available for all times. It is also a good indicator for spectral convergence, as we find for the residual

$$\begin{aligned} \Vert {f-\tilde{f}} \Vert = \Vert {f-\hat{f} - (\hat{f}-\tilde{f})} \Vert \le \Vert {f-\hat{f}} \Vert + \Vert {\Delta f} \Vert . \end{aligned}$$

Note that for \(t=0\), \(\hat{f}\) is the result of the orthogonal projection of f and therefore \(f-\hat{f}\) is in the orthogonal complement of \(V_{\text {eq}}\), implying that \(\Delta f \perp (f-\hat{f})\). Therefore, at \(t=0\)

$$\begin{aligned}\Vert {f-\tilde{f}} \Vert ^2 = \Vert {f-\hat{f}} \Vert ^2 + \Vert {\Delta f} \Vert ^2\end{aligned}$$

holds, so when \(\Vert {\Delta f} \Vert \) decreases, so does \(\Vert {f-\tilde{f}} \Vert \). We will calculate \(\Vert {f-\hat{f}} \Vert \) at \(t=0\) to find the difference’s order of magnitude, but show plots of \(\Vert {\Delta f} \Vert \) for both \(t=0\) and \(t\ne 0\), as we are mostly interested in the evolution of the coefficients calculated by the irreducible Burnett ansatz.

We consider three initial distributions to demonstrate the range of numerical application of our method:

  • BKW-Solution, where the initial function can be visualized as a 3-dimensional hollow sphere.

  • Bi-Gaussian distribution, where the initial function consists of two overlapping Gaussians.

  • Discontinuous distribution, where the initial function consists of two different states that are seperated at a flat plane in velocity space and that haven’t interacted with each other yet.

We will look both at the effect of the choice of potential, as well as the difference between various numerical approximations, mainly given by the choice of different maximal polynomial degrees M. The equilibrium solution to the Boltzmann equation, the Gaussian distribution, lies in the chosen approximation space \(V_\text {eq}\) for any M. With the our basis the Gaussian distribution corresponds to the state \(w_{000}=1\) and all other moments equal to zero. Note, that all presented initial distributions evolve towards the Gaussian distribution with time for all presented potentials. Therefore, for large times we expect no difference between any two solutions, regardless of their initial distribution. This also implies that the residual between any two solutions decreases with increasing time. As a result, the focus should be on early time scales, because differences show up in early times and decrease with large time.

Additionally, conservation of mass, momentum and energy imply constraints on the first coefficients, making them irrelevant for further consideration:

$$\begin{aligned} \forall t&\in \mathbb {R}^+:&w_{000}&= 1&w_{01-1}&=0&w_{010}&=0&w_{011}&=0&w_{100}&=0. \end{aligned}$$
(42)

6.1 BKW Solution

Fig. 5
figure 5

Graphs of the initial distribution of the BKW solution

Full size image
Fig. 6
figure 6

BKW solution: Analytical (solid lines) vs. numerical (dots) evolution of coefficients \(w_{a00}\). Numerical coefficients were calculated with the bilinear Maxwell potential

Full size image

The BKW solution is one of the few analytical solutions to the homogeneous Boltzmann Equation with Maxwell-potential and has been originally developed by Krupp (1967); Bobylev et al. (1976) [27]. As done in [9], we use the dimensionless formulation from Ernst [27]:

$$\begin{aligned} f(t,\textbf{c}) = \left( 2\pi \tau (t)\right) ^{\frac{3}{2}} \exp \left( -\frac{|\textbf{c}|^2}{2\tau (t)}\right) \left[ 1+\frac{1-\tau (t)}{\tau (t)} \left( \frac{|\textbf{c}|^2}{2\tau (t)}-\frac{3}{2}\right) \right] , \end{aligned}$$
(43)

where

$$\begin{aligned} \tau (t)&= 1 - \exp \left( \frac{\pi }{3} B t-T_0\right)&\text {with}{} & {} B&=-0.6542926411560946`&T_0&= 0.92 \end{aligned}$$
(44)

The initial distribution \(f(0,\textbf{c})\) can be envisioned as a 3D hollow sphere. In particular, it is obvious, that this distribution is rotationally invariant, allowing us to plot it in cylindrical coordinates without loosing information. Since our basis is adapted to \(\mathscr {O}_3\), we can reduce the degrees of freedom to only those coefficients that correspond to rotationally invariant basis functions, i.e. only weights \(w_{anl}\) with \((a,n,l) = (a,0,0)\) can be non-zero (Fig. 5).

Choosing a maximal degree of \(M=20\), we only have 11 relevant coefficients:

$$\begin{aligned} a&\in \{0,1,2,3,4,5,6,7,8,9,10\}{} & {} \text { and }&n=l=0&: \end{aligned}$$
$$\begin{aligned} w_{000}{} & {} w_{100}{} & {} w_{200}{} & {} w_{300}{} & {} w_{400}{} & {} w_{500} \\ w_{600}{} & {} w_{700}{} & {} w_{800}{} & {} w_{900}{} & {} w_{10\,00}. \end{aligned}$$

Combined with the restraints from Eq. (42), this allows us to take a look at the remaining nine time-dependent moments, all of higher order with \(w_{200}\) the lowest one, to judge how well the analytical and numerical solutions match without loosing any information.

Fig. 7
figure 7

Spectral Convergence of the solution for the BKW distribution. The y-Axis shows \(\Vert {\Delta f} \Vert \), i.e. the \(L^2\)-Norm given by the weighted scalar product of the difference between the projection of the analytical solution onto the approximation space with \(M=20\) and the numerical solution with different maximal polynomial degrees M, the x-Axis shows this degree. The plots are shown for times between 0 (top graph) and 1 (bottom graph) in steps of 0.1 (in order from top to bottom) and the evolution is calculated with the Maxwell potential

Full size image

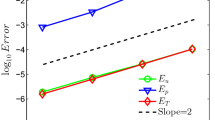
Given that Cai et al. observed very good correspondence in [9, 10], and that the approximations differ in basis choice at most, we expect to obtain similar results. Looking at Fig. 6, we observe that this expectation is met. We can also see spectral convergence of our method in Fig. 7 by comparing results of lower polynomial degrees

$$\begin{aligned}M\in \left\{ 4,6,8,10,12,14,16,18\right\} \end{aligned}$$

to the projection of the analytical solution onto the approximation space with \(M=20\) for different times \(t\in [0, 1]\). We observe faster than exponential convergence, which is demonstrated by the downward sloping curves on the semi-log scale. However, there is no reason to expect that this behaviour translates from the very special BKW test case to the approximation of a general distribution.

Note, that for various M the difference between the evolution of the lowest order time-dependent moment \(w_{200}\), which all compared theories share, is in the order of \(10^{-14}\). This is due to the restriction in Eq. (36) imposed by the Maxwell potential, which for this particular case simplifies to

$$\begin{aligned}a=b+c.\end{aligned}$$

With \(a=2\), the only possible contributions can come from \((b,c)\in \left\{ (0,2),(1,1)\right\} \), which are already taken into account by the lowest order ansatz with \(M=4\). A corresponding argument applies to any higher moment—in this specific test case the increase of polynomial degree cannot have an influence on the lower moments, but it does add accuracy to the overall distribution, as shown in Fig. 7.

While the difference in basis choice and understanding of the underlying representation theory seems benign, in this particular case it means we have reduced the roughly 1700 perceived degrees of freedom to just 9. This also affects the number of relevant impact coefficients: For a rotationally invariant distribution and \(M=20\) we only need 34 impact coefficients \(\mathcal {S}_{n{\hat{n}}\tilde{n}}^{abc}\) and hence the evaluation time for one time step is only a few ms.

Fig. 8
figure 8

BKW solution: Analytical (solid lines) vs. numerical (dots) evolution of coefficients for different potentials

Full size image

Figure 8 compares the evolution of the moments for different potentials. By omitting any line in the impact tensor file where \(b\ne 0\), we generated the linear collision operator. In Fig. 8a we can clearly see a difference between the linear Maxwell potential and the analytical solution, in particular in the higher moments. We also calculated the evolution of the coefficients for the simplified Maxwell model and found that it corresponds well to the analytical solution. Figure 8b compares the residual between the moments obtained from the numerical solution with \(M=20\) and the moments given by projecting the analytical solution onto the approximation space \(V_{\text {eq}}\) with \(M=20\) for the three different potentials. We can see that both the Maxwell and the simplified Maxwell potential produce very accurate moments with error in the order of \(10^{-13}\), while the linear potential differs significantly from the analytical solution. The plot also shows \(\Vert {f-\hat{f}} \Vert \), i.e. the difference between the analytical and numerical solution obtained with the Maxwell potential for the ansatz with \(M=20\) in the full function space equipped with the same scalar product as \(V_{\text {eq}}\). The residual starts at 8.9e\(-\)4 for \(t=0\) and we can see it steadily decreasing with time, as the solutions converge to the same Gaussian.

We conclude, that for rotationally invariant cases, the simplified Maxwell model produces similar results as the exact Maxwell model, and linearising the collision operator introduces a noticeable error. We also see even in this simple example the limit of spectral Burnett ansatz—moments can be accurately calculated, but the actual distribution function can only be approximated with some error depending on the degree M.

We also calculated the evolution of the coefficients for the simplified Maxwellian model and found that it corresponds to the analytical solution as well. The linearised simplified Maxwell model differs to the analytical solution similarly to the linearised Maxwell model. We conclude, that for rotationally invariant cases, the simplified Maxwell model is as good as the exact Maxwell model, and linearising the collision operator introduces a small but noticeable error (Fig. 9).

6.2 Bi-Gaussian Distribution

Fig. 9
figure 9

Bi-Gaussian distribution: Exact and with \(M=20\) approximated inital distribution function together with two views of their difference in cylindric coordinates

Full size image

Again we take the initial distribution from [9]

$$\begin{aligned} f(0,\textbf{c}) = \frac{1}{{2 \pi ^{3/2}}} \left( e^{-{c_x}^2-{c_y}^2-\left( {c_z}-\sqrt{\frac{3}{2}}\right) ^2}+e^{-{c_x}^2-{c_y}^2-\left( {c_z}+\sqrt{\frac{3}{2}}\right) ^2}\right) . \end{aligned}$$
(45)

Due to the distribution’s mirror symmetry w.r.t the x, y-plane, only even anisotropic indices n can result in non-zero projection coefficients in our basis. This is reflected in the projection of a monomial. Using the computer algebra system Mathematica, the projection of a monomial leads to a product from which it is easy to find a corresponding condition—any uneven degree leads to 0:

$$\begin{aligned} \langle c_x^a c_y^b c_z^c, f(0,\textbf{c}) \rangle =&\left( (-1)^a+1\right) \left( (-1)^b+1\right) \left( (-1)^c+1\right) K_1(a,b,c), \end{aligned}$$

with some additional function \(K_1(a,b,c)\). We further see, that the distribution is \(\mathscr {O}_2\)-invariant for rotations around the z-axis, resulting in the additional constraint that unless the directional index \(l=0\), the coefficients are zero. Overall, with \(M=20\) we find 66 relevant coefficients from combinations of

$$\begin{aligned} \text {isotropic index } a&\in \{0,1,2,3,4,5,6,7,8,9,10\} \text { , }\\ \text {anisotropic index } n&\in \{0,2,4,6,8,10,12,14,16,18,20\}, \text { with }2a+n\le M \text { and } l=0. \end{aligned}$$
Fig. 10
figure 10

Bi-Gaussian distribution: Snapshots of the evolution of the approximation with \(M=10\), \(M=20\) and their difference in cylindrical coordinates for \(t\in \{0,0.3,0.6,1\}\) calculated with the Maxwell potential

Full size image

We note, that with all the coefficients of uneven anisotropic indices being zero in the beginning and due to the conditions (32), we again may drop many lines from the impact tensor file, albeit not as many as in the BKW case. Figure 11 shows the residual between the ansatz with \(M=20\) and lower order approximations with the maximal polynomial degrees \(M\in \left\{ 10,12,14,16,18\right\} \).

Here we again see spectral convergence of the solution, indicating that this test case can also be well approximated by the spectral Burnett basis. Figure 10 indicates that the smallest and largest orders \(M=10\) and \(M=20\) both have similar looking distributions, with their largest difference located at the tips and overlap of the two Gaussians. We can further see from both Figs. 10 and 11 that the difference between approximations decreases with time as discussed in the beginning of this chapter. \(\Vert {f-\hat{f}} \Vert \) at \(t=0\) evaluates to 1.6e\(-\)3, the same order of magnitude as the first case. Overall, this indicates that the initial distribution is well approximated.

Fig. 11
figure 11

Spectral convergence of the solution for the bi-Gaussian distribution. The y-Axis shows \(\Vert {\Delta f} \Vert \), i.e. the \(L^2\)-Norm given by the weighted scalar product of the difference between the two solutions of different M and \(M=20\) as indicated by the x-Axis. The plots are shown for times between 0 (top graph) and 1 (bottom graph) in steps of 0.1 (in order from top to bottom) and the evolution is calculated with the Maxwell potential

Full size image
Fig. 12
figure 12

Bi-Gaussian distribution: Comparison of the evolution of the coefficients \(w_{an0}\) of the bi-Gaussian distribution function for the Maxwell (MX, solid lines) and simplified Maxwell (SMX, dots) potential

Full size image

Lastly, we compare the simplified and actual Maxwell potential in Fig. 12, where we look at the evolution of 19 out of the 66 coefficients as examples to demonstrate the range of possibilities. We note that for some moments the Maxwell and simplified Maxwell potential correspond to each other well, while for other moments those calculated with the Maxwell potential converge faster to 0. This trend is observed for most of the not displayed coefficients as well. However, we also note that some coefficients grow first, before converging to zero. Here we see, that the coefficients of the Maxwell potential remain closer to zero than those of the simplified Maxwell potential. Overall, we conclude that the simplified Maxwell potential can lead to a significantly different solution than the Maxwell potential in setups that are not rotationally invariant.

6.3 Discontinuous Distribution

Fig. 13
figure 13

Discontinuous distribution: Exact and with \(M=20\) approximated inital distribution function together with two views of their difference in cylindric coordinates

Full size image

Using the dimensionless formulation from [9] for this case we have

$$\begin{aligned} f(0,\textbf{c}) = {\left\{ \begin{array}{ll}\frac{\root 4 \of {2} \left( 2-\sqrt{2}\right) }{\pi ^{3/2}} \cdot \exp \left( -\frac{c^2}{\sqrt{2}}\right) &{} c_z >0\\ \frac{\root 4 \of {2} \left( 2-\sqrt{2}\right) }{4\pi ^{3/2}} \cdot \exp \left( -\frac{c^2}{2\sqrt{2}}\right) &{} \text {else}\end{array}\right. } \end{aligned}$$
(46)

Projection of a monomial, evaluated by Mathematica, again leads to a product from which we can infer that certain index combinations lead to zero:

$$\begin{aligned} \langle c_x^a c_y^b c_z^c, f(0,\textbf{c}) \rangle =&\left( (-1)^a+1\right) \left( (-1)^b+1\right) \left( (-1)^c \, 2^{\frac{1}{2} (a+b+c)}+\sqrt{2}\right) K_2(a,b,c), \end{aligned}$$

again with some additional function \(K_2(a,b,c)\) However, finding exclusion rules for the projection coefficients is less obvious here. They can only be non-zero if n is uneven or zero. We again find that the distribution function is \(\mathscr {O}_2\)-symmetric, requiring the projection coefficients to be zero unless \(l=0\). Note in contrast to the bi-Gaussian case, that even though at the beginning the relevant coefficients have an uneven or zero anisotropic index, two uneven anisotropic indices can couple to an even anisotropic index, see (32). So the total set of relevant coefficients \(w_{anl}\) for \(M=20\) is given by:

$$\begin{aligned} \text {isotropic index } a&\in \{0,1,2,3,4,5,6,7,8,9,10\} \text { , }\\ \text {anisotropic index } n&\in \{x| x\in \mathbb {N}_0 \wedge 0\le x \le M\}, \text { with }2a+n\le M \text {and } l=0. \end{aligned}$$

i.e. one coefficient per irreducible subspace, which makes 121 coefficients in total for \(M=20\). However, because all combinations of isotropic and anisotropic indices are possible, this case requires the full impact tensor and basis set, which has 1771 moments. Due to the \(\mathscr {O}_2\)-symmetry, most of them are zero and will always be zero for this test case. Looking at Fig. 13, we can clearly see that the discontinuity at \(t=0\) is not well approximated, even with a large degree of \(M=20\). This is reflected in \(\Vert {f-\hat{f}} \Vert \), which at \(t=0\) evaluates to 1.7e\(-\)1, a much larger value than in the other two cases.

Comparing the evolution of the distribution function in Fig. 14 for approximations of degree \(M=10\) and \(M=20\), we again find that the two approximations get closer to each other with time, as both converge to the same Gaussian.

Fig. 14
figure 14

Snapshots of the evolution of the approximation of the discontinuous distribution function with \(M=10\), \(M=20\) and their difference in cylindrical coordinates for \(t\in \{0,0.3,0.6,1\}\) calculated with the Maxwell potential

Full size image
Fig. 15
figure 15

Convergence of the solution for the discontinuous distribution. The y-Axis shows \(\Vert {\Delta f} \Vert \), i.e. the \(L^2\)-Norm given by the weighted scalar product of the difference between the two solutions of different \(M=20\) and M as indicated by the x-Axis. The plots are shown for times between 0 (top graph) and 1 (bottom graph) in steps of 0.1 (in order from top to bottom) and the evolution is calculated with the Maxwell potential

Full size image
Fig. 16
figure 16

Discontinuous distribution: Comparison of the evolution of the coefficients \(w_{an0}\) for the Maxwell (MX, solid lines) and simplified Maxwell (SMX, dots) potential

Full size image
Fig. 17
figure 17

Discontinuous distribution: Evolution of the stress tensor entries \(\sigma _{11}\) and \(\sigma _{22}\) and the heat flux entry \(q_1\) for the hard IPL potential with \(\eta =10\). The results of the irreducible Burnett ansatz (irreducible, dots) are compared to those from [9] (reference, solid lines), with values kindly provided by the authors. Note, that we transformed our coordinates to match the orientation of the reference values for this plot

Full size image

Figure 15 shows the residual between the ansatz with \(M=20\) and lower order approximations, each denoted by their maximal polynomial degree

$$\begin{aligned}M\in \left\{ 10,11,12,13,14,15,16,17,18\right\} .\end{aligned}$$

Here we see a rather slow spectral convergence and that there is little gain of accuracy when increasing M from an uneven to an even degree, which is also why \(M=19\) was omitted. We propose that this is due to the initial condition, in which most of the coefficients with even \(2a+n\) are zero. Together with the badly approximated discontinuity shown in Fig. 13, this shows one of the limits of the approximation space. This is the first test case where all lines of the impact tensor file are contributing to the overall evolution of the distribution function and as with the previous example we can see clear differences in the evolution of coefficients between the simplified Maxwell and Maxwell potential in Fig. 16.

When looking at the heat flux and stress tensor, we find good correspondence to previously published results in [9] in Fig. 17, with an absolute difference in the order of \(10^{-6}\). Note, that the approximation space for this comparison is not the same. Referring to the method demonstrated in [9], our ansatz corresponds to \(M_0 = M = 20\), while the values provided by the authors have been calculated with \(M_0=15, M=60\). The good correspondence suggests that this difference has little influence on the moments of this low order and that the irreducible Burnett ansatz produces results very similar to the spectral Burnett ansatz. This should be the case, since the difference between the spectral and the irreducible Burnett ansatz lies solely in the exploitation of the collision tensor’s decomposition.

7 Summary

With the irreducible Burnett ansatz we were able to reduce the computational effort of calculating Boltzmann’s collision operator in the spectral Burnett ansatz both in computational time and memory by implementing an algorithm inspired by the representation theoretical decomposition of the collision operator. This decomposition relies on the fact that the used basis is adapted to the irreducible subspaces of the approximation space.

This decomposition not only allowed us to find an efficient algorithm, but also provides an understanding behind the structure of the collision tensor by separating factors that depend on the underlying physics from those that are of pure mathematical nature: The bilinear collision tensor can be expressed as product of the impact tensor with coefficients depending on the potential between the colliding particles and the coupling tensor with coefficients only depending on the basis choice of the irreducible subspaces.

With spherical harmonics as basis, further structure of the coupling tensor could be exploited by looking at \(\mathscr {O}_2\)-irreducible subspaces. For example, the coupling tensor could be split into the case where all anisotropic indices are zero and everything else. This is not necessarily generally applicable, but there may exist interesting use-cases.

Applying the method of this paper to collision operators of different kind, such as polyatomic gases [28] or the Landau operator [29], looks like a promising next step.