Unconditional Convergence of Conservative Spectral Galerkin Methods for the Coupled Fractional Nonlinear Klein–Gordon–Schrödinger Equations

Abstract

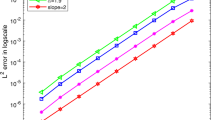
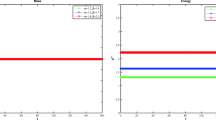
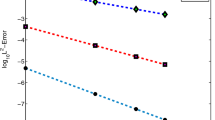
In this work, two novel classes of structure-preserving spectral Galerkin methods are proposed which based on the Crank–Nicolson scheme and the exponential scalar auxiliary variable method respectively, for solving the coupled fractional nonlinear Klein–Gordon–Schrödinger equation. The paper focuses on the theoretical analyses and computational efficiency of the proposed schemes, the Crank–Nicoloson scheme is proved to be unconditionally convergent and has maximum-norm boundness of numerical solutions. The exponential scalar auxiliary variable scheme is linearly implicit and decoupled, but lack of the maximum-norm boundness, also, the energy structure is modified. Subsequently, the efficient implementations of the proposed schemes are introduced in detail. Both the theoretical analyses and the numerical comparisons show that the proposed spectral Galerkin methods have high efficiency in long-time computations.

Appendices

A Appendix: Proof of (3.11)

Proof

Utilizing the Taylor’s expansion for $\phi$ and $\psi$ of (3.5) at $t=t_{n+1/2}$, we have

$$\begin{aligned} \widehat{\mathscr {R}}^{n}_2=\phi _t(\cdot ,t_{n+1/2})-\delta _t \phi ^{n+1/2}+\psi ^{n+1/2}-\psi (\cdot ,t_{n+1/2})=\mathcal {T}_1+\mathcal {T}_2, \end{aligned}$$

in which

$$\begin{aligned} \mathcal {T}_1&=\phi _t(\cdot ,t_{n+1/2})-\delta _t \phi ^{n+1/2}\\&=-\frac{\tau ^2}{16}\int _0^1 \left[ \phi _{ttt}\left( \cdot ,t_{n+1/2}+\frac{\tau }{2}s\right) +\phi _{ttt}\left( \cdot ,t_{n+1/2}-\frac{\tau }{2}s\right) \right] (1-s)^2ds \end{aligned}$$

and

$$\begin{aligned} \mathcal {T}_2&=\psi ^{n+1/2}-\psi (\cdot ,t_{n+1/2})=\frac{\tau ^2}{8}\int _0^1 \left[ \psi _{tt}\left( \cdot ,t_{n+1/2}+\frac{\tau }{2}s\right) +\psi _{tt}\left( \cdot ,t_{n+1/2}-\frac{\tau }{2}s\right) \right] (1-s)ds\\&=\frac{\tau ^2}{8}\int _0^1 \left[ \phi _{ttt}\left( \cdot ,t_{n+1/2}+\frac{\tau }{2}s\right) +\phi _{ttt}\left( \cdot ,t_{n+1/2}-\frac{\tau }{2}s\right) \right] (1-s)ds. \end{aligned}$$

Assume that $\phi (\cdot ,t)\in C^3([0,T])$. We deduce

$$\begin{aligned} \Big | \widehat{\mathscr {R}}_2^{n} \Big |\le \mathcal {C}\tau ^2,\quad n=0,1,\ldots ,N_t-1. \end{aligned}$$

Simultaneously,

$$\begin{aligned} \delta _t \widehat{\mathscr {R}}_2^{n+1/2} =&-\frac{\tau ^2}{16}\int _0^1 \left[ \delta _t \phi _{ttt}\left( \cdot ,t_{n+1/2}+\frac{\tau }{2}s\right) + \delta _t \phi _{ttt}\left( \cdot ,t_{n+1/2}-\frac{\tau }{2}s\right) \right] (1-s)^2ds\\&+\frac{\tau ^2}{8}\int _0^1 \left[ \delta _t \phi _{ttt}\left( \cdot ,t_{n+1/2}+\frac{\tau }{2}s\right) + \delta _t \phi _{ttt}\left( \cdot ,t_{n+1/2}-\frac{\tau }{2}s\right) \right] (1-s)ds. \end{aligned}$$

Employing the Lagrange’s mean value theorem, we obtain

$$\begin{aligned}&\phi _{ttt}\left( \cdot ,t_{n+3/2}+\frac{\tau }{2}s\right) -\phi _{ttt}\left( \cdot ,t_{n+1/2}+\frac{\tau }{2}s\right) =\tau \phi ^{(4)}(\cdot ,\xi _1),\\&\quad t_{n+1/2}+\frac{\tau }{2}s<\xi _1<t_{n+3/2}+\frac{\tau }{2}s, \end{aligned}$$

and

$$\begin{aligned}&\phi _{ttt}\left( \cdot ,t_{n+3/2}-\frac{\tau }{2}s\right) -\phi _{ttt} \left( \cdot ,t_{n+1/2}-\frac{\tau }{2}s\right) \\&\quad =\tau \phi ^{(4)}(\cdot ,\xi _2),\quad t_{n+1/2}-\frac{\tau }{2}s<\xi _2<t_{n+3/2}-\frac{\tau }{2}s. \end{aligned}$$

Suppose that $\phi (\cdot ,t)\in C^4([0,T])$. We get

$$\begin{aligned} \Big | \delta _t \widehat{\mathscr {R}}_2^{n+1/2} \Big |\le \mathcal {C}\tau ^2,\quad n=0,1,\ldots ,N_t-1. \end{aligned}$$

This completes the proof of (3.11). $\square$

B Appendix: Proof of Theorem 3.3

The proof of Theorem 3.3 is divided into two parts, including the existence and uniqueness.

(I) Existence:

Proof

It is worth noting that $U_N^{n+1}=2U_N^{n+1/2}-U_N^{n}$ and $\delta _t\Phi _N^{n+1/2}=\Psi _N^{n+1/2}$. We reformulate the spectral Galerkin scheme (3.12)–(3.14) into the following form

$$\begin{aligned}&\left( U_N^{n+1/2}-U_N^{n},w_N\right) +\frac{\lambda \tau }{4}\text {i}\mathcal {B}\left( U_N^{n+1/2},w_N\right) -\frac{\kappa _1\tau }{2}\text {i} \left( U_N^{n+1/2}\Phi _N^{n+1/2},w_N\right) \nonumber \\&\qquad -\frac{\kappa _2\tau }{2} \text {i}\Big (\left( |2U_N^{n+1/2}-U_N^{n}|^2+|U_N^{n}|^2\right) U_N^{n+1/2}\Phi _N^{n+1/2},w_N\Big )=0, \end{aligned}$$

(B.1)

$$\begin{aligned}&\left( 2\Phi _N^{n+1/2}-2\Phi _N^{n} -\tau \Psi _N^{n},w_N\right) +\frac{\gamma \tau ^2}{2}\mathcal {B}\left( \Phi _N^{n+1/2},w_N\right) +\frac{\eta ^2\tau ^2}{2} \left( \Phi _N^{n+1/2},w_N\right) \nonumber \\&\qquad -\frac{\kappa _1\tau ^2}{4} \Big (\left( |2U_N^{n+1/2}-U_N^{n}|^2+|U_N^{n}|^2\right) ,w_N\Big )-\frac{\kappa _2\tau ^2}{4} \Big (\left( |2U_N^{n+1/2}-U_N^{n}|^4+|U_N^{n}|^4\right) ,w_N\Big )=0. \end{aligned}$$

(B.2)

Now, we carry out proving the existence of $U_N^{n+1/2}$ and $\Phi _N^{n+1/2}$. For convenience, we define the map ${\textbf {s}}=(s_1,s_2)$, $\mathscr {F}=(\mathscr {F}_1,\mathscr {F}_2):$ $(X_N^0(\Omega ),X_N^0(\Omega ))\rightarrow (X_N^0(\Omega ),X_N^0(\Omega ))$, such that

$$\begin{aligned} \left( \mathscr {F}_1({\textbf {s}}),w_N\right) =&(s_1-U_N^n,w_N)+\frac{\lambda \tau }{4}\text {i}\mathcal {B}( s_1,w_N )-\frac{\kappa _1\tau }{2}\text {i}(s_1s_2,w_N)\nonumber \\&-\frac{\kappa _2\tau }{2}\text {i}\Big ( \left( |2s_1-U_N^n|^2+|U_N^n|^2 \right) s_1s_2,w_N\Big ),\quad \forall w_N\in X_N^0(\Omega ) \end{aligned}$$

(B.3)

and

$$\begin{aligned} (\mathscr {F}_2({\textbf {s}}),w_N)=\,&(2s_2-2\Phi _N^{n}-\tau \Psi _N^{n},w_N)+\frac{\gamma \tau ^2}{2}\mathcal {B}( s_2,w_N )+\frac{\eta ^2\tau ^2}{2}( s_2,w_N)\nonumber \\&-\frac{\kappa _1\tau ^2}{4} \Big (|2s_1-U_N^n|^2+|U_N^{n}|^2,w_N \Big )\nonumber \\&-\frac{\kappa _2\tau ^2}{4} \Big (|2s_1-U_N^n|^4+|U_N^{n}|^4,w_N \Big ),\quad \forall w_N\in X_N^0(\Omega ). \end{aligned}$$

(B.4)

Choosing $w_N=s_1$ in (B.3) and taking the real part, from the Young’s inequality, we derive

$$\begin{aligned} \text {Re}(\mathscr {F}_1({\textbf {s}}),s_1)&=\text {Re}(s_1-U_N^n,s_1)\}=\Vert s_1\Vert ^2-\text {Re}( U_N^n,s_1 )\ge \frac{1}{2}\Vert s_1\Vert ^2-\frac{1}{2} \Vert U_N^n\Vert ^2\\&\ge \frac{1}{2}\Vert s_1\Vert ^2-\mathcal {C}. \end{aligned}$$

Setting $w_N=s_2$ in (B.4), by utilizing the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} (\mathscr {F}_2({\textbf {s}}),s_2)&\ge (2s_2-2\Phi _N^{n}-\tau \Psi _N^{n},s_2)-\frac{\kappa _1\tau ^2}{4} \Big (|2s_1-U_N^n|^2+|U_N^{n}|^2,s_2 \Big )\nonumber \\&\qquad -\frac{\kappa _2\tau ^2}{4} \Big (|2s_1-U_N^n|^4+|U_N^{n}|^4,s_2 \Big )\nonumber \\&=2\Big \Vert s_2\Big \Vert ^2-(2\Phi _N^{n}+\tau \Psi _N^{n},s_2)-\frac{\kappa _1\tau ^2}{4} \Big (|2s_1-U_N^n|^2+|U_N^{n}|^2,s_2 \Big )\nonumber \\&\qquad -\frac{\kappa _2\tau ^2}{4} \Big (|2s_1-U_N^n|^4+|U_N^{n}|^4,s_2 \Big ). \end{aligned}$$

(B.5)

By employing the boundness of the numerical solutions (see Theorem 3.2) and the Young’s inequality, for sufficient small $\tau$, we conclude

$$\begin{aligned}&\left( 2\Phi _N^{n}+\tau \Psi _N^{n},s_2\right) \le \Big \Vert 2\Phi _N^{n}+\tau \Psi _N^{n} \Big \Vert \Big \Vert s_2 \Big \Vert \le \frac{1}{2}\Big \Vert 2\Phi _N^{n}+\tau \Psi _N^{n} \Big \Vert ^2 +\frac{1}{2} \Big \Vert s_2 \Big \Vert ^2, \end{aligned}$$

(B.6)

$$\begin{aligned}&\frac{\kappa _1\tau ^2}{4}\Big (|2s_1-U_N^n|^2+|U_N^{n}|^2,s_2 \Big )\le \frac{\kappa _1^2\tau ^4}{32} \Big \Vert |2s_1-U_N^n|^2+|U_N^{n}|^2 \Big \Vert ^2 + \frac{1}{2} \Big \Vert s_2 \Big \Vert ^2\le \mathcal {C}+\frac{1}{2} \Big \Vert s_2 \Big \Vert ^2 \end{aligned}$$

(B.7)

and

$$\begin{aligned} \frac{\kappa _2\tau ^2}{2}\Big (|2s_1-U_N^n|^4+|U_N^{n}|^4,s_2 \Big )\le \mathcal {C}+\frac{1}{2} \Big \Vert s_2 \Big \Vert ^2. \end{aligned}$$

(B.8)

Substituting (B.6)–(B.8) into (B.5), we arrive at

$$\begin{aligned} (\mathscr {F}_2({\textbf {s}}),s_2)\ge \frac{1}{2} \Big \Vert s_2 \Big \Vert ^2-\frac{1}{2}\Big \Vert 2\Phi _N^{n}+\tau \Psi _N^{n} \Big \Vert ^2-\mathcal {C}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \text {Re} (\mathscr {F}({\textbf {s}}),s_1)&=\text {Re} (\mathscr {F}_1({\textbf {s}}),s_2)+\text {Re} (\mathscr {F}_2({\textbf {s}}),s)\\&\ge \frac{1}{2} \Big \Vert {\textbf {s}} \Big \Vert ^2-\frac{1}{2}\Big \Vert 2\Phi _N^{n}+\tau \Psi _N^{n} \Big \Vert ^2-\mathcal {C} =\frac{1}{2}\Big ( \Big \Vert {\textbf {s}} \Big \Vert ^2 - \Big \Vert \Big ( 2\Phi _N^{n}+\tau \Psi _N^{n}, \sqrt{2\mathcal {C}}\Big ) \Big \Vert ^2 \Big ). \end{aligned}$$

Taking $\delta =\Big \Vert \Big ( 2\Phi _N^{n}+\tau \Psi _N^{n}, \sqrt{2\mathcal {C}}\Big ) \Big \Vert$, which satisfies the condition of Lemma 3.5, we derive

$$\begin{aligned} \text {Re}( \mathscr {F}({\textbf {s}}),{\textbf {s}}) \ge 0,\quad \forall {\textbf {s}}:~~\Vert {\textbf {s}}\Vert =\delta . \end{aligned}$$

This proves the existence of the numerical solution of (3.12)–(3.14). $\square$

Next, we prove the uniqueness of the numerical solution.

(II) Uniqueness:

Proof

We prove the theorem by introduction. It is obvious to find from (3.15) that the numerical solution $(U_N^0,\Phi ^0_N,\Psi _N^0)\in (X_N^0(\Omega ),X_N^0(\Omega ),X_N^0(\Omega ))$ exists and is unique. Assume that $(U_N^n,\Phi ^n_N,\Psi _N^n)$ is the unique solution of (3.12)–(3.14) for $n=0,1,\ldots ,N_t-1$. Next, we prove the uniqueness of the solution $(U_N^{n+1/2},\Phi ^{n+1/2}_N)$. Assume there are two solutions $X^{n+1/2}=(X_1^{n+1/2},X_2^{n+1/2})$ and $Y^{n+1/2}=(Y_1^{n+1/2},Y_2^{n+1/2})$ for scheme (3.12)–(3.14). Then $X_1^{n+1/2}-Y_1^{n+1/2}$ and $X_2^{n+1/2}-Y_2^{n+1/2}$ satisfy (B.3) and (B.4) as follows

$$\begin{aligned} \big (\mathscr {F}_1\big ({X}^{n+1/2}\big )-\mathscr {F}_1\big ({Y}^{n+1/2}\big ),X_1^{n+1/2}-Y_1^{n+1/2}\big )&=0,\\ \big (\mathscr {F}_2\big ({X}^{n+1/2}\big )-\mathscr {F}_2\big ({Y}^{n+1/2}\big ),X_2^{n+1/2}-Y_2^{n+1/2}\big )&=0. \end{aligned}$$

By the definition of $\mathscr {F}_1$, we have

$$\begin{aligned}&\Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2+\frac{\lambda \tau }{4} \text {i}\mathcal {B}\big (X_1^{n+1/2}-Y_1^{n+1/2},X_1^{n+1/2}-Y_1^{n+1/2}\big )\nonumber \\&\quad -\frac{\kappa _1\tau }{2}\text {i}\big (X_1^{n+1/2}X_2^{n+1/2} -Y_1^{n+1/2}Y_2^{n+1/2},X_1^{n+1/2}-Y_1^{n+1/2}\big )\nonumber \\&\quad -\frac{\kappa _2\tau }{2}\text {i}\Big ( \big ( |2X_1^{n+1/2}-U_N^n|^2+|U_N^n|^2 \big )X_1^{n+1/2}X_2^{n+1/2}\nonumber \\&\quad -\big ( |2Y_1^{n+1/2}-U_N^n|^2+|U_N^n|^2 \big )Y_1^{n+1/2}Y_2^{n+1/2},X_1^{n+1/2}-Y_1^{n+1/2}\Big )=0. \end{aligned}$$

(B.9)

Taking the real part of (B.9), by admitting the boundness of the numerical solutions (see Theorem 3.2), Lemma 3.4 and the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2&=-\frac{\kappa _1\tau }{2}\text {Im}\big (X_1^{n+1/2}X_2^{n+1/2}-Y_1^{n+1/2}Y_2^{n+1/2},X_1^{n+1/2}-Y_1^{n+1/2}\big )\nonumber \\&\quad +\frac{\kappa _2\tau }{2}\text {Im}\Big ( \big ( |2X_1^{n+1/2}-U_N^n|^2+|U_N^n|^2 \big )X_1^{n+1/2}X_2^{n+1/2}\nonumber \\&\quad -\big ( |2Y_1^{n+1/2}-U_N^n|^2+|U_N^n|^2 \big )Y_1^{n+1/2}Y_2^{n+1/2},X_1^{n+1/2}-Y_1^{n+1/2}\Big )\nonumber \\&\le \mathcal {C}\tau \Big (\Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2+\Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2 \Big ). \end{aligned}$$

(B.10)

Taking into account of the definition of $\mathscr {F}_2$, we get

$$\begin{aligned}&\Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2+\frac{\gamma \tau ^2}{4}\mathcal {B}\big (X_2^{n+1/2}-Y_2^{n+1/2},X_2^{n+1/2}-Y_2^{n+1/2}\big )\\&\quad +\frac{\eta ^2\tau ^2}{4} \big (X_2^{n+1/2}-Y_2^{n+1/2},X_2^{n+1/2}-Y_2^{n+1/2}\big )\\&\quad -\frac{\kappa _1\tau ^2}{8} \Big (\big (|2X_2^{n+1/2}-U_N^{n}|^2\big )-\big (|2Y_2^{n+1/2}-U_N^{n}|^2\big ),X_2^{n+1/2}-Y_2^{n+1/2}\Big )\\&\quad -\frac{\kappa _2\tau ^2}{8} \Big (\big (|2X_2^{n+1/2}-U_N^{n}|^4\big )-\big (|2Y_2^{n+1/2}-U_N^{n}|^4\big ),X_2^{n+1/2}-Y_2^{n+1/2}\Big )=0. \end{aligned}$$

By employing Theorem 3.2, Lemma 3.4 and the Cauchy–Schwarz inequality, we deduce

$$\begin{aligned} \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2&\le \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2\nonumber \\&\quad +\frac{\gamma \tau ^2}{4}\Big |X_2^{n+1/2}-Y_2^{n+1/2}\Big |^2_{\alpha /2}+\frac{\eta ^2\tau ^2}{4} \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2}\Big \Vert ^2\nonumber \\&=\frac{\kappa _1\tau ^2}{8} \Big (\big (|2X_2^{n+1/2}-U_N^{n}|^2\big )-\big (|2Y_2^{n+1/2}-U_N^{n}|^2\big ),X_2^{n+1/2}-Y_2^{n+1/2}\Big )\nonumber \\&\quad +\frac{\kappa _2\tau ^2}{8} \Big (\big (|2X_2^{n+1/2}-U_N^{n}|^4\big )-\big (|2Y_2^{n+1/2}-U_N^{n}|^4\big ),X_2^{n+1/2}-Y_2^{n+1/2}\Big )\nonumber \\&\le \mathcal {C}\tau ^2 \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2. \end{aligned}$$

(B.11)

Summing up (B.10) and (B.11), for a sufficient small $\tau$, we arrive at

$$\begin{aligned} \Big \Vert X^{n+1/2}-Y^{n+1/2} \Big \Vert ^2&=\Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2+\Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2\\&\le \mathcal {C}\tau \Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2+\mathcal {C}\tau \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2\\&\quad +\mathcal {C}\tau ^2 \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2\\&\le \mathcal {C}\tau \Big \Vert X_1^{n+1/2}-Y_1^{n+1/2} \Big \Vert ^2+\mathcal {C}\tau \Big \Vert X_2^{n+1/2}-Y_2^{n+1/2} \Big \Vert ^2\\&= \mathcal {C}\tau \Big \Vert X^{n+1/2}-Y^{n+1/2} \Big \Vert ^2. \end{aligned}$$

By assuming $\mathcal {C}\tau <1$, it leads to $\Big \Vert X^{n+1/2}-Y^{n+1/2} \Big \Vert =0$, which implies $X_1^{n+1/2}=Y_1^{n+1/2}$ and $X_2^{n+1/2}=Y_2^{n+1/2}$. This ends the proof of the uniqueness. $\square$