Skip to main content
SpringerLink
Log in

Stability analysis and error estimates of local discontinuous Galerkin method for nonlinear fractional Ginzburg–Landau equation with the fractional Laplacian

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

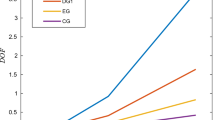
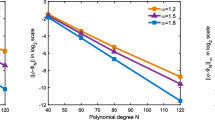
In this paper, we present and analyze local discontinuous Galerkin (LDG) method to solve nonlinear fractional Ginzburg–Landau equation (FGLE) with the fractional Laplacian. This method transforms the nonlinear FGLE with fractional Laplacian of order \(\sigma \) into a system of first-order equations and approximates the solution of the equation by selecting the appropriate basis functions. The stability analysis for FGLE has been investigated, and the optimal convergence rates \(O(h^{N+1})\) of the semi-discrete scheme have been established. Finally, numerical examples are displayed to verify the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. T. Aboelenen. A direct discontinuous galerkin method for fractional convection-diffusion and schrödinger type equations. arXiv:1708.04546 (2017)

  2. T. Aboelenen, A high-order nodal discontinuous Galerkin method for nonlinear fractional Schrödinger type equations. Commun. Nonlinear Sci. Numer. Simul. 54, 428–452 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. T. Aboelenen, Stability analysis and error estimates of implicit-explicit Runge–Kutta local discontinuous galerkin methods for nonlinear fractional convection-diffusion problems. Comput. Appl. Math. 41(6), 256 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  4. T. Aboelenen, H. El-Hawary, A high-order nodal discontinuous Galerkin method for a linearized fractional Cahn–Hilliard equation. Comput. Math. Appl. 73(6), 1197–1217 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  5. M. Ahmadinia, Z. Safari, Convergence analysis of a LDG method for tempered fractional convection-diffusion equations. ESAIM Math. Model. Numer. Anal. 54(1), 59–78 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  6. I.S. Aranson, L. Kramer, The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 74(1), 99 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. D.N. Arnold, F. Brezzi, B. Cockburn, L.D. Marini, Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  8. C.-W. S. Bernardo Cockburn, G. E. Karniadakis. Discontinuous Galerkin Methods: Theory, Computation and Applications, 1st edn. Springer (2000)

  9. P.G. Ciarlet, Finite Element Method for Elliptic Problems (Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 2002)

    Book  MATH  Google Scholar 

  10. B. Cockburn, G. E. Karniadakis, and C.-W. Shu. Discontinuous Galerkin Methods: Theory, Computation and Applications, vol. 11. Springer Science & Business Media (2012)

  11. B. Cockburn, C.-W. Shu, The local discontinuous galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35(6), 2440–2463 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  12. W. Deng, J.S. Hesthaven, Local discontinuous Galerkin methods for fractional diffusion equations. ESAIM Math. Model. Numer. Anal. 47(6), 1845–1864 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  13. H. Ding and C. Li. High-order numerical algorithm and error analysis for the two-dimensional nonlinear spatial fractional complex Ginzburg–Landau equation. Commun. Nonlinear Sci. Numer. Simul. 107160 (2023)

  14. A. El-Sayed, M. Gaber, On the finite Caputo and finite Riesz derivatives. Electron. J. Theor. Phys. 3(12), 81–95 (2006)

    Google Scholar 

  15. S. El-Tantawy, T. Aboelenen, Simulation study of planar and nonplanar super rogue waves in an electronegative plasma: Local discontinuous Galerkin method. Phys. Plasmas 24(5), 052118, (2017)

    Article  ADS  Google Scholar 

  16. V.J. Ervin, J.P. Roop, Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Eq. 22(3), 558–576 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. B. Guo, Z. Huo, Well-posedness for the nonlinear fractional Schrödinger equation and inviscid limit behavior of solution for the fractional Ginzburg-Landau equation. Fract. Calculus Appl. Anal. 16(1), 226–242 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Z.-P. Hao, Z.-Z. Sun, A linearized high-order difference scheme for the fractional Ginzburg–Landau equation. Numer. Methods Part. Differ. Eq. 33(1), 105–124 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Z.-P. Hao, Z.-Z. Sun, W.-R. Cao, A three-level linearized compact difference scheme for the Ginzburg–Landau equation. Numer. Methods Part. Differ. Eq. 31(3), 876–899 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. J.S. Hesthaven, T. Warburton, Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications, 1st edn. (Springer Publishing Company, Incorporated, 2007)

    MATH  Google Scholar 

  21. R. Jan, Z. Shah, W. Deebani, E. Alzahrani, Analysis and dynamical behavior of a novel dengue model via fractional calculus. Int. J. Biomath. 15(06), 2250036 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  22. J. Li, L. Xia, Well-posedness of fractional Ginzburg–Landau equation in sobolev spaces. Appl. Anal. 92(5), 1074–1084 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. H. Lu, S. Lü, Z. Feng, Asymptotic dynamics of 2D fractional complex Ginzburg–Landau equation. Int. J. Bifurc. Chaos 23(12), 1350202 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  24. S. Lü, Q. Lu, Fourier spectral approximation to long-time behavior of three dimensional Ginzburg–Landau type equation. Adv. Comput. Math. 27(3), 293–318 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  25. V. Millot and Y. Sire. On a fractional Ginzburg-Landau equation and 1/2-harmonic maps into spheres. arXiv preprint arXiv:1307.7015 (2013)

  26. V. Millot, Y. Sire, On a fractional Ginzburg–Landau equation and 1/2-harmonic maps into spheres. Arch. Ration. Mech. Anal. 215, 125–210 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  27. S.I. Muslih, O.P. Agrawal, Riesz fractional derivatives and fractional dimensional space. Int. J. Theor. Phys. 49(2), 270–275 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. A. Mvogo, A. Tambue, G.H. Ben-Bolie, T.C. Kofané, Localized numerical impulse solutions in diffuse neural networks modeled by the complex fractional Ginzburg-Landau equation. Commun. Nonlinear Sci. Numer. Simul. 39, 396–410 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. X. Pu, B. Guo, Well-posedness and dynamics for the fractional Ginzburg–Landau equation. Appl. Anal. 92(2), 318–334 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. W. H. Reed and T. R. Hill. Triangular mesh methods for the neutron transport equation. Technical report, Los Alamos Scientific Lab., N. Mex (USA) (1973)

  31. V.E. Tarasov, Psi-series solution of fractional Ginzburg–Landau equation. J. Phys. A Math. Gen. 39(26), 8395 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. V.E. Tarasov, G.M. Zaslavsky, Fractional Ginzburg–Landau equation for fractal media. Phys. A Stat. Mech. Appl. 354, 249–261 (2005)

    Article  Google Scholar 

  33. P. Wang, C. Huang, An implicit midpoint difference scheme for the fractional Ginzburg–Landau equation. J. Comput. Phys. 312, 31–49 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. T. Wang, B. Guo, Analysis of some finite difference schemes for two-dimensional Ginzburg–Landau equation. Numer. Methods Partial Differ. Eq. 27(5), 1340–1363 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  35. L. Wei, H. Dai, D. Zhang, Z. Si, Fully discrete local discontinuous galerkin method for solving the fractional telegraph equation. Calcolo 51(1), 175–192 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. L. Wei, Y. He, X. Zhang, S. Wang, Analysis of an implicit fully discrete local discontinuous Galerkin method for the time-fractional Schrödinger equation. Finite Elem. Anal. Des. 59, 28–34 (2012)

    Article  MathSciNet  Google Scholar 

  37. H. Weitzner, G. Zaslavsky, Some applications of fractional equations. Commun. Nonlinear Sci. Numer. Simul. 8(3), 273–281 (2003)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Q. Xu, J.S. Hesthaven, Discontinuous Galerkin method for fractional convection–diffusion equations. SIAM J. Numer. Anal. 52(1), 405–423 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  39. J. Yan, C.-W. Shu, Local discontinuous Galerkin methods for partial differential equations with higher order derivatives. J. Sci. Comput. 17(1), 27–47 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  40. Q. Yang, F. Liu, I. Turner, Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 34(1), 200–218 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  41. S. Zeng, S. Migórski, A.A. Khan, Nonlinear quasi-hemivariational inequalities: existence and optimal control. SIAM J. Control Optim. 59(2), 1246–1274 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  42. L. Zhang, Long time behavior of difference approximations for the two-dimensional complex Ginzburg–Landau equation. Numer. Funct. Anal. Optim. 31(10), 1190–1211 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  43. L. Zhang, Y. Xu, Y. Tao, and L. Chen. Preconditioned iterative solver for 2d complex fractional ginzburg-landau equation. In 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), vol. 5, pp. 1736–1741. IEEE (2022)

  44. L. Zhang, Q. Zhang, H.-W. Sun, Exponential Runge–Kutta method for two-dimensional nonlinear fractional complex ginzburg-landau equations. J. Sci. Comput. 83(3), 59 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  45. Y.-N. Zhang, Z.-Z. Sun, T.-C. Wang, Convergence analysis of a linearized Crank–Nicolson scheme for the two-dimensional complex Ginzburg-Landau equation. Numer. Methods Part. Differ. Eq. 29(5), 1487–1503 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to express special thanks to anonymous referees for their valuable comments and suggestions, which significantly improved the quality of this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Unaizah College of Sciences and Arts, Qassim University, Qassim, Saudi Arabia

    Tarek Aboelenen

  2. Department of Mathematics, College of Science and Arts, Qassim University, Ar Rass, Saudi Arabia

    Mohammed Alqawba

  3. Department of Mathematics, Assiut University, Assiut, 71516, Egypt

    Tarek Aboelenen

Authors
  1. Tarek Aboelenen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammed Alqawba
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tarek Aboelenen.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aboelenen, T., Alqawba, M. Stability analysis and error estimates of local discontinuous Galerkin method for nonlinear fractional Ginzburg–Landau equation with the fractional Laplacian. Eur. Phys. J. Spec. Top. 232, 2607–2617 (2023). https://doi.org/10.1140/epjs/s11734-023-00921-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjs/s11734-023-00921-6

Search

Navigation