Global Stabilization of BBM–Burgers’ Type Equations by Nonlinear Boundary Feedback Control Laws: Theory and Finite Element Error Analysis

Abstract

In this article, global stabilization results for the Benjamin–Bona–Mahony–Burgers’ (BBM–B) type equations are obtained using nonlinear Neumann boundary feedback control laws. Based on the $C^0$-conforming finite element method, global stabilization results for the semidiscrete solution are also discussed. Optimal error estimates in $L^\infty (L^2)$, $L^\infty (H^1)$ and $L^\infty (L^\infty )$-norms for the state variable are derived, which preserve exponential stabilization property. Moreover, for the first time in the literature, superconvergence results for the boundary feedback control laws are established. Finally, several numerical experiments are conducted to confirm our theoretical findings.

1 Introduction

Consider the Benjamin–Bona–Mahony–Burgers’ (BBM–B) equations of the following type: seek $u=u(x,t),\, x\in I=(0,1)$ and $t>0$ which satisfies

$$\begin{aligned}&u_t-\mu u_{xxt}-\nu u_{xx}+u_x+uu_x=0,\qquad (x,t)\in (0,1)\times (0,\infty ), \end{aligned}$$

(1.1)

$$\begin{aligned}&u_x(0,t)=v_0(t), \qquad t\in (0,\infty ), \end{aligned}$$

(1.2)

$$\begin{aligned}&u_x(1,t)=v_1(t), \qquad t\in (0,\infty ), \end{aligned}$$

(1.3)

$$\begin{aligned}&u(x,0)=u_0(x),\qquad x\in (0,1), \end{aligned}$$

(1.4)

where, the dispersion coefficient $\mu >0$ and the dissipative coefficient $\nu >0$ are constants; $v_0$ and $v_1$ are scalar control inputs. The problem (1.1) describes the unidirectional propagation of nonlinear dispersive long waves with dissipative effect. In case, $\nu =0$ and $\mu >0,$ the equation (1.1) is known as Benjamin–Bona–Mahony (BBM) equation. When $\mu =0$ and $\nu >0$ in (1.1), then it is called Burgers’ equation. For mathematical modeling and physical applications of (1.1), see [2, 3, 21] and references, therein.

Based on distributed and Dirichlet boundary control in feedback form through Riccati operator, local stabilization results for the Burgers’ equation with sufficiently small initial data are established in [4, 5]. Moreover, for local stabilization results using Neumann boundary control, we refer to [7, 8, 11, 12]. For different behavior of steady state solution with anti-symmetric initial condition, see [6]. It is to be noted that for viscous Burgers’ equation, global existence and uniqueness results with Dirichlet and Neumann boundary conditions are derived for any initial data in $L^2$ in [18]. Subsequently, based on nonlinear Neumann and Dirichlet boundary control laws, global stabilization results for the Burgers’ equation are proved using a suitable application Lyapunov type functional in Krstic [14], Balogh and Krstic [1]. Later on, adaptive (when $\nu$ is unknown) and nonadaptive (when $\nu$ is known) stabilization results for generalized Burgers’ equations are established in [17, 24, 25] with different types of boundary conditions. For existence of solution to the problem (1.1)–(1.4), when $\mu =0$, we refer to [1, 17].

For stabilization of the BBM–B equation, the authors in [10] have shown global stabilization results corresponding to $\mu =1$ with zero Dirichlet boundary condition at one end and Neumann boundary control on the other end. Using a reduced order model, distributed feedback control for the BBM–B equation is discussed in [22]. Also, quadratic B-spline finite element method followed by linear quadratic regulator theory to design feedback control, is used to stabilize in [23] without any convergence analysis. In [15], we have shown that, under the uniqueness assumption of the steady state solution, the steady state solution of the problem (1.1) with zero Dirichlet boundary condition is exponentially stable.

In this paper, we discuss global stabilization results using nonlinear Neumann feedback control law. Our second objective is to apply $C^0$-finite element method to the stabilization problem (1.1)–(1.4) using nonlinear Neumann boundary control laws and discuss convergence analysis. Since to the best of our knowledge, there is hardly any discussion in the literature on the rate of convergence, hence, in this paper, an effort has been made to prove optimal order of convergence of the state variable along with superconvergence result for the feedback control laws. The main contributions of this article are summarized as:

• Global stabilization for problem (1.1)–(1.4), that is, convergence of the unsteady solution to the problem (1.1) to its constant steady state solution under nonlinear Neumann boundary control laws (1.2)–(1.3) is proved (see Theorem 2.1).

• Based on the $C^0$-conforming finite element method, global stabilization results for the semidiscrete solution are discussed and optimal error estimates are established in $L^\infty (L^2)$, $L^\infty (H^1(0,1))$, and $L^\infty (L^\infty )$ norms for the state variable. Moreover, superconvergence results are derived for the nonlinear Neumann feedback control laws (see Theorems 3.1 and 3.2).

• Finally, some numerical experiments are conducted to confirm our theoretical results.

For related issues of finite element analysis of the viscous Burgers’ equation using nonlinear Neumann boundary feedback control law, we refer to our recent article [16]. Compared to [16], special care has been taken to establish global stabilization results in $L^\infty (H^i(0,1)) (i=0, 1, 2)$ norms as $\mu \rightarrow 0.$ It is further observed that the decay rate for the BBM–B type equation is less than the decay rate for the viscous Burgers’ equation and as the dispersion coefficient $\mu$ approaches zero, the decay rate also converges to the decay rate for the Burgers’ equation. Finite element error analysis holds for fixed $\mu$.

For the rest of this article, we denote $H^m$ by $H^m(0,1)$ the standard Sobolev spaces with norm $\left\| \cdot \right\| _m$ and for $m=0$, $\left\| \cdot \right\|$ denotes the corresponding $L^2$ norm. For more details, see e.g. [13]. The space $L^p((0,T);X)$$1\le p\le \infty ,$ consists of all strongly measurable functions $v:(0,T) \rightarrow X$ with norm

$$\begin{aligned} \left\| v\right\| _{L^p((0,T);X)}:=\left( \int _{0}^{T}\left\| v(t)\right\| _X^p dt\right) ^\frac{1}{p}<\infty \quad \text {for} \quad 1\le p<\infty , \end{aligned}$$

and

$$\begin{aligned} \left\| v\right\| _{L^\infty ((0,T);X)}:=\mathop {\text {ess sup}}\limits _{0\le t\le T}\left\| v(t)\right\| _X<\infty . \end{aligned}$$

When there is no confusion, $L^p((0,T);X)$ is simply denoted by $L^p(X)$. Throughout the paper, we use the following norm which is equivalent to the usual $H^1$-norm for $z\in H^1(0,1)$:

$$\begin{aligned} \left| \! \left| \! \left| z \right| \! \right| \! \right| =\sqrt{z^2(0)+z^2(1)+\left\| z_x\right\| ^2}. \end{aligned}$$

(1.5)

We now recall some results to be use in our subsequent sections.

Lemma 1.1

Poincaré–Wirtinger’s inequality For any $z\in H^1(0,1)$, the following inequality holds:

$$\begin{aligned} \left\| z\right\| ^2\le 2z^2(i)+\left\| z_x\right\| ^2, \quad \text {for} \, i=0 \,\text{ or } \, 1. \end{aligned}$$

Using Agmon’s and Poincaré inequality, the following inequality holds

$$\begin{aligned} \left\| z\right\| _{L^\infty }\le \sqrt{2}\left| \! \left| \! \left| z \right| \! \right| \! \right| , \end{aligned}$$

(1.6)

where $\left| \! \left| \! \left| \cdot \right| \! \right| \! \right|$ is given in (1.5).

The equilibrium or steady state solution $u^\infty$ of (1.1)–(1.3) satisfies

$$\begin{aligned}&-\nu u^\infty _{xx}+u^\infty _x+u^\infty u^\infty _{x}=0 \qquad \text {in} \quad (0,1) , \end{aligned}$$

(1.7)

$$\begin{aligned}&u^\infty _x(0)=u^\infty _x(1)=0 . \end{aligned}$$

(1.8)

Note that any constant $w_d$ is a solution of the steady state problem (1.7)–(1.8). Without loss of generality, we assume that $w_d\ge 0$.

Set $w=u-w_d,$ which satisfies

$$\begin{aligned}&w_t-\mu w_{xxt}-\nu w_{xx}+(1+w_d)w_x+ww_x=0 \qquad \text {in} \quad (0,1)\times (0,\infty ) , \end{aligned}$$

(1.9)

$$\begin{aligned}&w_x(0,t)=v_0(t) \quad t\in (0,\infty ), \end{aligned}$$

(1.10)

$$\begin{aligned}&w_x(1,t)=v_1(t) \quad t\in (0,\infty ), \end{aligned}$$

(1.11)

$$\begin{aligned}&w(x,0)=w_0(x), \quad x\in (0,1), \end{aligned}$$

(1.12)

where, w is the state variable and $v_0$ and $v_1$ are feedback control variables. Since for the problem with zero Neumann boundary condition, the steady state constant solution $w_d$ is not asymptotically stable, we plan to achieve stabilization result through boundary feedback law. The present analysis can be easily extended to the problem with one side control law say for example: when $w(0,t)=0$, $w_x(1,t)=v_1(t)$, see [10]. For motivation to choose the control laws $v_{0}(t)$ and $v_{1}(t)$ using construction of Lyapunov functional, see [14].

Based on the nonlinear Neumann control law propose in our earlier article for Burgers’ equation, see [16], which is a modification of control law in [14], we now choose the feedback control law as

$$\begin{aligned} w_x(0,t)=v_0(t)=:\frac{1}{\nu }\Big ((c_0+1+w_d)w(0,t)+\frac{2}{9c_0}w^3(0,t)\Big )\equiv : K_0(w(0,t)),\nonumber \\ \end{aligned}$$

(1.13)

and

$$\begin{aligned} w_x(1,t)=v_1(t)=:-\frac{1}{\nu }\Big ((c_1+1+w_d)w(1,t)+\frac{2}{9c_1}w^3(1,t)\Big )\equiv :K_1(w(1,t)),\nonumber \\ \end{aligned}$$

(1.14)

where $K_0$ and $K_1$ represent feedback control laws, and $c_0$ and $c_1$ are positive constants.

The variational formulation of the problem (1.9)–(1.12) is to seek $w\in L^\infty (H^1),$$w_t \in L^2(L^2)$ and $\mu w_t\in L^2(H^1)$ such that for almost all $t>0$

$$\begin{aligned}&(w_t,\chi )+\mu (w_{xt},\chi _x)+\nu (w_x,\chi _x)+(1+w_d)(w_x,\chi )+(ww_x,\chi )-\mu \Big (v_{1t}(t)\chi (1)\nonumber \\&\quad -v_{0t}(t)\chi (0)\Big )-\nu \Big (v_1(t)\chi (1)-v_0(t)\chi (0)\Big )=0 \qquad \forall ~ \chi \in H^1 \end{aligned}$$

(1.15)

with $w(x,0)=w_0(x).$

Using (1.13)–(1.14), we obtain a typical nonlinear problem (1.9)–(1.12) with boundary conditions (1.13)–(1.14). Its weak formulation (1.15) becomes

$$\begin{aligned}&(w_t,\chi )+\mu (w_{xt},\chi _x)+\nu (w_x,\chi _x)+(1+w_d)(w_x,\chi )+(ww_x,\chi )\nonumber \\&\quad +\frac{\mu }{\nu }\Big (\big ((c_0+1+w_d)w_t(0,t)+\frac{2}{3c_0}w^2(0,t)w_t(0,t)\big )\chi (0)+\big ((c_1+1+w_d)w_t(1,t)\nonumber \\&\quad +\frac{2}{3c_1}w^2(1,t)w_t(1,t)\big )\chi (1)\Big )+\Big (\big ((c_0+1+w_d)w(0,t)\nonumber \\&\quad +\frac{2}{9c_0}w^3(0,t))\chi (0)+\big ((c_1+1+w_d)w(1,t)+\frac{2}{9c_1}w^3(1,t)\big )\chi (1)\Big )=0 \quad \forall ~ \chi \in H^1,\, t>0 . \end{aligned}$$

(1.16)

Throughout the paper $C=C(\left\| w_0\right\| _2,\nu ,\mu )$ is a generic positive constant. Bellow, we make the following assumptions

Assumption ${\mathbf{(A1)}}$

Compatibility conditions at $t=0$ ($w_{0x}(0)=v_0(0)$, $w_{0x}(1)=v_1(0)$, $w_{0xt}(0)=v_{0t}(0)$, $w_{0xt}(1)=v_{1t}(0)$) with $w_0(\cdot )\in H^2$ are satisfied.

Assumption ${\mathbf{(A2)}}$

There exist unique weak solution w of (1.9)–(1.12) satisfying the following regularity result

$$\begin{aligned} \left\| w(t)\right\| ^2_2+ \left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\int _{0}^{t} \Big (\left| \! \left| \! \left| w_t(s) \right| \! \right| \! \right| ^2+\mu \left\| w_{xxt}(s)\right\| ^2\Big )\;ds\le C. \end{aligned}$$

(1.17)

Subsequently for our error estimates in $L^\infty (L^\infty )$ norm, we further assumed that $w(t)\in W^{2,\infty }$ with its norm denoted by $\left\| \cdot \right\| _{2,\infty }$.

Regarding assumption $\mathbf{(A2)}$ on existence, uniqueness and regularity results, the proof of existence and uniqueness result can be easily modeled on the lines of proof of Theorems 1.1 and 2.1 of [19], but the constants appeared there may depend on $1/\mu ^r,\;r\ge 1.$ Therefore, using Bubnov-Galerkin methods and similar a priori bounds as in Theorems 2.1 and 2.2 for the weak solution u of (1.9)–(1.12) with compactness arguments of J.L. Lions, it is possible to rewrite the existential proof so that the constants involved are valid uniformly in $\mu$ as $\mu \mapsto 0.$ We also observe that as a consequence of Lemma 2.6, we obtain easily uniqueness result. Further, we note that using eigenfunction expansion, Galerkin approximation and taking limit as in the regularity Theorem 2.1 of [19], proper meaning can be attached to regularity estimates in Lemmas 2.2–2.5. For more details, see, the appendix. Note that we need compatibility conditions in (A1) in the proofs of regularity results for Lemmas 2.4–2.5.

The rest of the article is organized as follows. Section 2 deals with global stabilization results and the existence and uniqueness of strong solution. Section 3 is devoted to optimal error estimates for the semidiscrete solution with superconvergence results for feedback controllers. Finally in Sect. 4, some numerical examples are considered to confirm our theoretical results.

2 Stabilization and Continuous Dependence Result

In this subsection, we discuss a priori bounds for the problem (1.16) and derive stabilization results and its main Theorem 2.1. In addition, these estimates are needed to prove optimal error estimates for the state variable and feedback controllers. All estimates throughout the paper are valid for the same $\alpha$ with

$$\begin{aligned} 0\le \alpha \le \frac{1}{2}\min \Bigg \{\frac{\nu }{(\mu +1)}, \frac{\nu }{(2\mu +\nu )}, \frac{\nu (1+c_i+w_d)}{(\nu +(1+c_i+w_d)\mu )} (i=0,1)\Bigg \}. \end{aligned}$$

(2.1)

Lemma 2.1

Under assumptions $\mathbf{(A1)}$–$\mathbf{(A2)},$ there holds for $t>0$

$$\begin{aligned}&\left\| w(t)\right\| ^2+\mu \left\| w_{x}(t)\right\| ^2+\frac{\mu }{\nu }E_1(w)(t)+\beta e^{-2\alpha t}\int _{0}^{t} e^{2\alpha s}\Big (E_1(w)(s)+\left\| w_x(s)\right\| ^2\Big ) ds\\&\quad \le e^{-2\alpha t}\big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big ), \end{aligned}$$

where $\alpha$ is given in (2.1),

$$\begin{aligned} \beta= & {} \min \Bigg \{2\big (\nu -\alpha (\mu +1)\big ), \big (1-2\alpha \frac{\mu }{\nu }\big ), \Big ((1+c_i+w_d)\nonumber \\&-\,2\alpha \big ((1+c_i+w_d)\frac{\mu }{\nu }+1\big )\Big ),i=0,1 \Bigg \}, \end{aligned}$$

(2.2)

and

$$\begin{aligned} E_1(w)(t)=\sum _{i=0}^{1}\Big ((c_i+1+w_d)+\frac{1}{3c_i}w^2(i,t)\Big )w^2(i,t). \end{aligned}$$

(2.3)

Proof

Set $\chi =w$ in the weak formulation (1.16) to obtain

$$\begin{aligned}&\frac{d}{dt}\Big ( \left\| w(t)\right\| ^2+\mu \left\| w_x(t)\right\| ^2 +\frac{\mu }{\nu }E_1(w)(t)\Big )+2\nu \left\| w_x(t)\right\| ^2+E_1(w)(t)\nonumber \\&\quad +\Big (c_0w^2(0,t)+\frac{1}{9c_0}w^4(0,t)\nonumber \\&\quad +\big (c_1+2(1+w_d)\big )w^2(1,t)+\frac{1}{9c_1}w^4(1,t)\Big )=\frac{2}{3}\Big (w^3(0,t)-w^3(1,t)\Big ), \end{aligned}$$

(2.4)

where $E_1(w)(t)$ is given in (2.3). A use of Young’s inequality for the right hand side term shows

$$\begin{aligned} \frac{2}{3}w^3(i,t)\le c_i w^2(i,t)+\frac{1}{9c_i}w^4(i,t), \quad i=0,1. \end{aligned}$$

(2.5)

Therefore, using (2.5) and (2.3), we obtain from (2.4)

$$\begin{aligned}&\frac{d}{dt}\Big (\left\| w(t)\right\| ^2+\mu \left\| w_x(t)\right\| ^2+\frac{\mu }{\nu }E_1(w)(t)\Big )\nonumber \\&\qquad +E_1(w)(t)+2(1+w_d)w^2(1,t)+2\nu \left\| w_x\right\| ^2\le 0. \end{aligned}$$

(2.6)

Multiply (2.6) by $e^{2\alpha t}$ to arrive at

$$\begin{aligned}&\frac{d}{dt}\Big (e^{2\alpha t}\big (\left\| w(t)\right\| ^2+\mu \left\| w_x(t)\right\| ^2+\frac{\mu }{\nu }E_1(w)(t)\big )\Big )\nonumber \\&\quad -2\alpha e^{2\alpha t}\big (\left\| w(t)\right\| ^2+\mu \left\| w_x(t)\right\| ^2+\frac{\mu }{\nu }E_1(w)(t)\big )\nonumber \\&\quad +e^{2\alpha t}\Big (E_1(w)(t)+2\nu \left\| w_x(t)\right\| ^2+2(1+w_d)w^2(1,t)\Big )\le 0. \end{aligned}$$

(2.7)

A use of Poincaré-Wirtinger’s inequality yields

$$\begin{aligned} \left\| w(t)\right\| ^2\le w^2(0,t)+w^2(1,t)+\left\| w_x(t)\right\| ^2. \end{aligned}$$

(2.8)

Substitute (2.8) in (2.7) and expanding $E_1(w)(t)$ to find that

$$\begin{aligned}&\frac{d}{dt}\Big (e^{2\alpha t}\big (\left\| w(t)\right\| ^2+\mu \left\| w_x(t)\right\| ^2+\frac{\mu }{\nu }E_1(w)(t)\big )\Big )\nonumber \\&\quad +e^{2\alpha t} \Bigg (\sum _{i=0}^{1}\Big ((1+c_i+w_d)-2\alpha \big ((1+c_i+w_d)\frac{\mu }{\nu }+1\big )\Big )w^2(i,t)\nonumber \\&\quad +\Big (1-2\alpha \frac{\mu }{\nu }\Big )\sum _{i=0}^{1}\frac{1}{3c_0}w^4(i,t)\Bigg )+2\big (\nu -\alpha (\mu +1)\big )e^{2\alpha t}\left\| w_x(t)\right\| ^2 \le 0 . \end{aligned}$$

(2.9)

Now choose $\alpha$ as in (2.1), so that all the coefficients on the left hand side are positive. Then integrating the above inequality from 0 to t and multiplying the resulting inequality by $e^{-2\alpha t},$ we obtain

$$\begin{aligned}&\left\| w(t)\right\| ^2+\mu \left\| w_x(t)\right\| ^2+\frac{\mu }{\nu }E_1(w)(t) +\beta e^{-2\alpha t}\int _{0}^{t} e^{2\alpha s}\Big (E_1(w)(s)+\left\| w_x(s)\right\| ^2\Big )\; ds\\&\quad \le e^{-2\alpha t}\big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big ). \end{aligned}$$

This completes the proof. $\square$

Remark 2.1

Since

$$\begin{aligned} E_1(w)(t)+\left\| w_x(t)\right\| ^2\ge \left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2, \end{aligned}$$

we obtain from Lemma 2.1

$$\begin{aligned} \beta e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left| \! \left| \! \left| w(s) \right| \! \right| \! \right| ^2\; ds\le e^{-2\alpha t}\Big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\Big ). \end{aligned}$$

When $\alpha =0,$ Lemma 2.1 holds for all $t>0$, that is,

$$\begin{aligned} \int _{0}^{t}\left| \! \left| \! \left| w(s) \right| \! \right| \! \right| ^2 \;ds \le \Big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+E_1(w)(0)\Big )\le C. \end{aligned}$$

Lemma 2.2

Under assumptions $\mathbf{(A1)}$–$\mathbf{(A2)}$, there is a positive constant C such that for $t>0$

$$\begin{aligned}&\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\Big )+\beta e^{-2\alpha t}\int _{0}^{t} e^{2\alpha s}\left\| w_{xx}(s)\right\| ^2 ds\\&\quad \le Ce^{-2\alpha t}\big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{1}{\nu }E_1(w)(0)\big )e^C, \end{aligned}$$

where $E_2(w)(t)=\Big ((c_0+1+w_d)+\frac{1}{9c_0}w^2(0,t)\Big )w^2(0,t)+\Big ((c_1+1+w_d) +\frac{1}{9c_1}w^2(1,t)\Big )w^2(1,t).$

Proof

Forming the $L^2$- inner product between (1.9) and $-w_{xx},$ we obtain

$$\begin{aligned}&\frac{d}{dt}\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2\Big )+2\nu \left\| w_{xx}(t)\right\| ^2-2\big (v_1(t)w_t(1,t)-v_0(t)w_t(0,t)\big )\nonumber \\&\quad =2(ww_x,w_{xx})+2(1+w_d)(w_x,w_{xx}). \end{aligned}$$

(2.10)

After substituting (1.13)–(1.14) in (2.10), the contributions of the boundary terms in (2.10) are

$$\begin{aligned}&-2\big (w_t(1,t)w_x(1,t)-w_t(0,t)w_x(0,t)\big )\nonumber \\&\quad =\frac{1}{\nu }\frac{d}{dt}\Big ((c_0+1+w_d)w^2(0,t)+(c_1+1+w_d)w^2(1,t)\nonumber \\&\qquad +\frac{1}{9c_0}w^4(0,t)+\frac{1}{9c_1}w^4(1,t)\Big )=\frac{1}{\nu }\frac{d}{dt}(E_2(w)(t)). \end{aligned}$$

(2.11)

The terms on the right hand side of (2.10) are now bounded by

$$\begin{aligned} 2(1+w_d)(w_x,w_{xx})\le \frac{\nu }{2}\left\| w_{xx}(t)\right\| ^2+\frac{2}{\nu }(1+w_d)^2\left\| w_{x}(t)\right\| ^2, \end{aligned}$$

and

$$\begin{aligned} 2(ww_x,w_{xx})\le \left\| w(t)\right\| _{L^\infty }\left\| w_x(t)\right\| \left\| w_{xx}(t)\right\| \le \frac{\nu }{2}\left\| w_{xx}(t)\right\| ^2+C\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\left\| w_x(t)\right\| ^2. \end{aligned}$$

Using (2.10) we arrive at

$$\begin{aligned}&\frac{d}{dt}\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\Big )+\nu \left\| w_{xx}(t)\right\| ^2\nonumber \\&\quad \le C\left\| w_x(t)\right\| ^2 +C\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\left\| w_x(t)\right\| ^2. \end{aligned}$$

(2.12)

Multiplying the above inequality by $e^{2\alpha t},$ and using

$$\begin{aligned} \left\| w_x(t)\right\| ^2\le & {} w_x^2(0,t)+w_x^2(1,t)+\left\| w_{xx}(t)\right\| ^2\\\le & {} C\Big (1+w^2(0,t)+w^2(1,t)\Big )E_2(w)(t)+\left\| w_{xx}(t)\right\| ^2, \end{aligned}$$

and $E_2(w)(t)\le E_1(w)(t)$ we obtain

$$\begin{aligned}&\frac{d}{dt}\Big (e^{2\alpha t}\big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\big )\Big )+\Big (\nu -2\alpha (\mu +1)\Big ) e^{2\alpha t}\left\| w_{xx}(t)\right\| ^2\\&\quad \le C e^{2\alpha t}\big (\left\| w_x(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\big )\\&\qquad +Ce^{2\alpha t}\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\Big )\\&\quad \le Ce^{2\alpha t}(\left\| w_x(t)\right\| ^2+E_1(w)(t))\\&\qquad +C\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2e^{2\alpha t}\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\Big ). \end{aligned}$$

A use of Gronwall’s inequality now yields

$$\begin{aligned}&e^{2\alpha t}\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\Big )+\Big (\nu -2\alpha (\mu +1)\Big )\int _{0}^{t} e^{2\alpha s}\left\| w_{xx}(s)\right\| ^2 ds\nonumber \\&\quad \le \Big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{1}{\nu }E_2(w)(0)+C\int _{0}^{t}e^{2\alpha s}\big (\left\| w_x(t)\right\| ^2+E_1(w)(s)\big ) ds\Big )\nonumber \\&\qquad \times \exp \Big (C\int _{0}^{t}\left| \! \left| \! \left| w(s) \right| \! \right| \! \right| ^2 ds\Big ). \end{aligned}$$

(2.13)

From Remark 2.1 and Lemma 2.1, we bound the right hand side term of (2.13). Therefore, after multiplying (2.13) by $e^{-2\alpha t},$ we obtain

$$\begin{aligned}&\Big (\left\| w_x(t)\right\| ^2+\mu \left\| w_{xx}(t)\right\| ^2+\frac{1}{\nu }E_2(w)(t)\Big )+\beta e^{-2\alpha t}\int _{0}^{t} e^{2\alpha s}\left\| w_{xx}(s)\right\| ^2 ds\\&\quad \le Ce^{-2\alpha t}\big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{1}{\nu }E_1(w)(0)\big )\\&\qquad \times \exp \Big (C(\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0))\Big ). \end{aligned}$$

Since the terms in the bracket in the exponential form are bounded, this completes the rest of the proof. $\square$

Lemma 2.3

Let assumptions $\mathbf{(A1)}$–$\mathbf{(A2)}$ hold true. Then, there exists a positive constant C such that for $t>0$

$$\begin{aligned}&\nu \big (\left\| w_x(t)\right\| ^2+E_2(w)(t)\big )+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(s)\Big ) ds\\&\quad \le C e^Ce^{-2\alpha t}\big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{1}{\nu }E_1(w)(0)\big ), \end{aligned}$$

where

$$\begin{aligned} E_3(w)(t)&=\Big ((1+c_0+w_d)+\frac{2}{3c_0}w^2(0,t)\Big )w_t^2(0,t)+\Big ((1+c_1+w_d)\nonumber \\&\quad +\frac{2}{3c_1}w^2(1,t)\Big )w_t^2(1,t). \end{aligned}$$

(2.14)

Proof

Set $\chi =w_t$ in the weak formulation (1.16) to obtain

$$\begin{aligned}&\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{1}{2}\frac{d}{dt}\Big (\nu \left\| w_x(t)\right\| ^2+E_2(w)(t)\Big )+\frac{\mu }{\nu }E_3(w)(t)\nonumber \\&\quad =(1+w_d)(w_x,-w_t)+(ww_x,-w_t), \end{aligned}$$

(2.15)

where $E_3(w)(t)$ is given in (2.14). Note that

$$\begin{aligned} (1+w_d)(w_x,-w_t)\le \frac{1}{4}\left\| w_t(t)\right\| ^2+(1+w_d)^2\left\| w_x(t)\right\| ^2, \end{aligned}$$

and

$$\begin{aligned} (ww_x,-w_t)\le C\left\| w(t)\right\| _{L^\infty }\left\| w_x(t)\right\| \left\| w_t(t)\right\| \le \frac{1}{4}\left\| w_t(t)\right\| ^2+C\left\| w_x(t)\right\| ^2\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2. \end{aligned}$$

Therefore, from (2.15), we arrive at

$$\begin{aligned}&\frac{d}{dt}\Big (\nu \left\| w_x(t)\right\| ^2+E_2(w)(t)\Big )+\left\| w_t(t)\right\| ^2+2\mu \left\| w_{xt}(t)\right\| ^2+\frac{2\mu }{\nu }E_3(w)(t)\\&\quad \le C\left\| w_x(t)\right\| ^2\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2+C\left\| w_x(t)\right\| ^2. \end{aligned}$$

Multiply the above inequality by $e^{2\alpha t}$. Now, a use of the Gronwall’s inequality and Lemma 2.1 completes the rest of the proof. $\square$

Lemma 2.4

Under assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)},$ there holds for $t>0$

$$\begin{aligned}&\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big )+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\nu \left\| w_{xt}(s)\right\| ^2+E_3(w)(s)\Big ) ds\\&\quad \le Ce^Ce^{-2\alpha t}\Big (\big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big ), \end{aligned}$$

where $E_3(w)(t)$ is as in (2.14).

Proof

Differentiating (1.9) with respect to t and then taking the inner product with $\chi =w_t$, we obtain

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big )+\nu \left\| w_{xt}(t)\right\| ^2\nonumber \\&\quad +(1+w_d)(w_{xt},w_t)+(w_tw_x+ww_{xt},w_t)\nonumber \\&\quad +2\frac{\mu }{\nu }\Big (\frac{1}{3c_0}w(0,t)w_t^3(0,t)+\frac{1}{3c_1}w(1,t)w_t^3(1,t)\Big )+E_3(w)(t)=0. \end{aligned}$$

(2.16)

The other terms in (2.16) are bounded by

$$\begin{aligned} (1+w_d)(w_{xt},w_t)&\le \frac{\nu }{4}\left\| w_{xt}(t)\right\| ^2+\frac{2(1+w_d^2)}{\nu }\left\| w_t(t)\right\| ^2,\\ (w_tw_x+ww_{xt},w_t)&\le \left\| w_t(t)\right\| _{L^\infty }\left\| w_x(t)\right\| \left\| w_t(t)\right\| +\left\| w(t)\right\| _{L^\infty }\left\| w_{xt}(t)\right\| \left\| w_t(t)\right\| \\&\le (|{w_t(0,t)}|+\left\| w_{xt}(t)\right\| )\left\| w_x(t)\right\| \left\| w_t(t)\right\| \\&\quad +\sqrt{2}\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| \left\| w_{xt}(t)\right\| \left\| w_t(t)\right\| \\&\le \frac{1+c_0+w_d}{2}w_t^2(0,t)+\frac{\nu }{4}\left\| w_{xt}(t)\right\| ^2+C\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\left\| w_t(t)\right\| ^2, \end{aligned}$$

and

$$\begin{aligned} \frac{2\mu }{\nu }\frac{1}{3c_0}w(0,t)w_t^3(0,t)\le \frac{1}{3c_0}w^2(0,t)w_t^2(0,t)+\frac{\mu ^2}{\nu ^2}\frac{1}{3c_0}w_t^4(0,t). \end{aligned}$$

Therefore, from (2.16), we arrive at

$$\begin{aligned}&\frac{d}{dt}\Big (\left\| w_t\right\| ^2+\mu \left\| w_{xt}\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big )+\nu \left\| w_{xt}(t)\right\| ^2+\Big ((1+c_0+w_d)w_t^2(0,t)\\&\qquad +2(1+c_1+w_d)w_t^2(1,t)+\frac{2}{3c_0}w^2(0,t)w_t^2(0,t)+\frac{2}{3c_1}w^2(1,t)w_t^2(1,t)\Big )\\&\quad \le 2\frac{\mu ^2}{\nu ^2}\Big (\frac{1}{3c_0}w_t^4(0,t)+\frac{1}{3c_1}w_t^4(1,t)\Big ) +C\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\left\| w_t(t)\right\| ^2+C\left\| w_t(t)\right\| ^2. \end{aligned}$$

Now multiply the above inequality by $e^{2\alpha t}$ to obtain

$$\begin{aligned}&\frac{d}{dt}\Big (e^{2\alpha t}\big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\big )\Big )+\nu e^{2\alpha t}\left\| w_{xt}(t)\right\| ^2+e^{2\alpha t}E_3(w)(t)\\&\quad \le C e^{2\alpha t}\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\left\| w_t(t)\right\| ^2+C(\alpha ) e^{2\alpha t}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big )\\&\qquad +C\frac{\mu }{\nu }e^{2\alpha t}E_3(w)(t)\Big (w_t^2(0,t)+w_t^2(1,t)\Big )\\&\quad \le Ce^{2\alpha t}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big ) \big (\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2+\frac{\mu }{\nu }(w_t^2(0,t)+w_t^2(1,t)\big )\\&\qquad +Ce^{2\alpha t}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big ). \end{aligned}$$

By the Gronwall’s inequality, it follows from above with a use of Lemmas 2.1 and 2.3 that

$$\begin{aligned}&e^{2\alpha t}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big )+\int _{0}^{t}e^{2\alpha s}\big (\nu \left\| w_{xt}(s)\right\| ^2+E_3(w)(s)\big ) ds\\&\quad \le \Big (\left\| w_t(0)\right\| ^2+\mu \left\| w_{xt}(0)\right\| ^2+\frac{\mu }{\nu }E_3(w)(0)+C\int _{0}^{t}e^{2\alpha s} \Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2\\&\qquad +\frac{\mu }{\nu }E_3(w)(s)\Big )ds\Big )\exp \Big (C\int _{0}^{t}\big (\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2+\frac{\mu }{\nu }(w_t^2(0,s)+w_t^2(1,s)) \big )ds\Big )\\&\quad \le C\Big (\left\| w_t(0)\right\| ^2+\mu \left\| w_{xt}(0)\right\| ^2+\frac{\mu }{\nu }E_3(w)(0)+\big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{1}{\nu }E_1(w)(0)\big )\\&\qquad \quad \times \exp \Big (C\big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big ). \end{aligned}$$

Also after putting $\chi =w_t$ in the weak formulation (1.16), we arrive at

$$\begin{aligned} \left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\le 3\nu \left\| w_{xx}(t)\right\| ^2+C\left\| w_x(t)\right\| ^2+C\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\left\| w_x(t)\right\| ^2. \end{aligned}$$

Therefore, we can find the value of $\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)$ at $t=0$ as

$$\begin{aligned}&\left\| w_t(0)\right\| ^2+\mu \left\| w_{xt}(0)\right\| ^2+\frac{\mu }{\nu }E_3(w)(0)\\&\quad \le C\Big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{1}{\nu }E_1(w)(0)\Big )\exp \Big (C\big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big ). \end{aligned}$$

Hence, we arrive at

$$\begin{aligned}&e^{2\alpha t}\Big (\left\| w_t(t)\right\| ^2+\mu \left\| w_{xt}(t)\right\| ^2+\frac{\mu }{\nu }E_3(w)(t)\Big )+\int _{0}^{t}e^{2\alpha s}\big (\nu \left\| w_{xt}(s)\right\| ^2+E_3(w)(s)\big ) ds\\&\quad \le \Big (C\big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big )\\&\qquad \times \exp \Big (C\big (\left\| w_{0x}\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big ). \end{aligned}$$

Multiply the above inequality by $e^{-2\alpha t}$ to complete the proof. $\square$

Lemma 2.5

Let assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)}$ hold. Then, there is a positive constant C such that for $t>0$

$$\begin{aligned}&\nu \left\| w_{xx}(t)\right\| ^2+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| w_{xt}(t)\right\| ^2+\mu \left\| w_{xxt}(t)\right\| ^2+\frac{2}{\nu }E_3(w)(s)\Big )\;ds\\&\quad \le Ce^Ce^{-2\alpha t}\Big (C(1+\mu )\big (\left\| w_0\right\| ^2_2+E_1(w)(0)\big )\Big ). \end{aligned}$$

Proof

Form the $L^2$-inner product between (1.9) and $-w_{xxt}$ to obtain

$$\begin{aligned}&\left\| w_{xt}(t)\right\| ^2+2\mu \left\| w_{xxt}(t)\right\| ^2+\frac{2}{\nu }E_3(w)(t)+\nu \frac{d}{dt}\left\| w_{xx}(t)\right\| ^2\nonumber \\&\quad \le C\Big (1+\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2\Big )\left\| w_{xx}(t)\right\| ^2+CE_1(w)(t)\left\| w_x(t)\right\| ^2+C\Big (E_1(w)(t)+E_3(w)(t)\Big ), \end{aligned}$$

(2.17)

where we use the bound of $w^2(i,t)$ and $w^4(i,t)$ for $i=0,\,1$ from Lemma 2.2.

Multiply (2.17) by $e^{2\alpha t}$ to obtain

$$\begin{aligned}&\frac{d}{dt}\Big (e^{2\alpha t}\big (\nu \left\| w_{xx}(t)\right\| ^2\big )\Big )+e^{2\alpha t}\Big (\left\| w_{xt}(t)\right\| ^2+2\mu \left\| w_{xxt}(t)\right\| ^2+\frac{2}{\nu }E_3(w)(t)\Big )\\&\quad \le Ce^{2\alpha t}\Big (1+\left| \! \left| \! \left| w_x(t) \right| \! \right| \! \right| ^2\Big )\left\| w_{xx}(t)\right\| ^2+Ce^{2\alpha t}E_1(w)(t)\left\| w_x(t)\right\| ^2\\&\qquad +Ce^{2\alpha t}\Big (E_1(w)(t)+E_3(w)(t)\Big ). \end{aligned}$$

Integrate from 0 to t and then multiply the resulting inequality by $e^{-2\alpha t}$ with a use of Lemmas 2.2 and 2.4 to arrive at

$$\begin{aligned}&\nu \left\| w_{xx}(t)\right\| ^2+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| w_{xt}(t)\right\| ^2+\mu \left\| w_{xxt}(t)\right\| ^2+\frac{2}{\nu }E_3(w)(s)\Big )\;ds\\&\quad \le Ce^{-2\alpha t}\Big (\big (\left\| w_0\right\| ^2+\mu \left\| w_{0x}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big )\\&\quad \qquad \times \exp \Big (C\big ((1+\mu )\left\| w_{0x}\right\| ^2+\mu \left\| w_{0xx}\right\| ^2+\frac{\mu }{\nu }E_1(w)(0)\big )\Big ). \end{aligned}$$

This completes the proof. $\square$

Now combining the above lemmas, we get the global stabilization result in the following theorem.

Theorem 2.1

Under assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)},$ there holds for $t>0$

$$\begin{aligned} \left\| w(t)\right\| ^2_2+\left\| w_t(t)\right\| ^2_1&+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| w_{t}(t)\right\| ^2_2+E_3(w)(s)\Big )\;ds\le Ce^Ce^{-2\alpha t}. \end{aligned}$$

Proof

Proof follows from Lemmas 2.1–2.5. $\square$

2.1 Continuous Dependence Property

Below, we show a continuous dependence property from which uniqueness follows.

Lemma 2.6

For two different initial conditions $w_{10}(\cdot )$ and $w_{20}(\cdot )$$\in H^1(0,1),$ the following continuous dependence property holds for $t>0$

$$\begin{aligned} \left\| z(t)\right\| ^2+\mu \left\| z_x(t)\right\| ^2+E_4(t)&\le Ce^C\big (\left\| z_0\right\| ^2+\mu \left\| z_{0x}\right\| ^2+E_4(0)\big ), \end{aligned}$$

where $z=w_1-w_2$ satisfies (2.19)–(2.22); $w_1$ and $w_2$ be two solutions of (1.9) with boundary conditions (1.13), (1.14) and initial conditions $w_{10}$ and $w_{20}$, and

$$\begin{aligned} E_4(t)=&\frac{\mu }{\nu }\Big ((1+c_0+w_d)z^2(0,t)+(1+c_1+w_d)z^2(1,t)\nonumber \\&\quad +\frac{1}{3c_0}w_1^2(0,t)z^2(0,t) +\frac{1}{3c_1}w_1^2(1,t)z^2(1,t)\Big ). \end{aligned}$$

(2.18)

Proof

Since $z=w_1-w_2$, z satisfies

$$\begin{aligned}&z_t-\mu z_{xxt}-\nu z_{xx}+(1+w_d)z_x+w_1w_{1x}-w_2w_{2x}=0 , \end{aligned}$$

(2.19)

$$\begin{aligned}&z_x(0,t)=\frac{1}{\nu }\Big ((1+c_0+w_d)z(0,t)+\frac{2}{9c_0}(w^3_1(0,t)-w^3_2(0,t))\Big ), \end{aligned}$$

(2.20)

$$\begin{aligned}&z_x(1,t)=-\frac{1}{\nu }\Big ((1+c_1+w_d)z(0,t)+\frac{2}{9c_1}(w^3_1(1,t)-w^3_2(1,t))\Big ), \end{aligned}$$

(2.21)

$$\begin{aligned}&z(x,0)=w_{10}(x)-w_{20}(x). \end{aligned}$$

(2.22)

In its weak formulation, seek $z\in H^1$ such that

$$\begin{aligned}&(z_t,v)+\mu (z_{xt},v_x)+\nu (z_x,v_x)+(1+w_d)(z_x,v)+(w_1w_{1x}-w_2w_{2x},v)\nonumber \\&\quad +\frac{\mu }{\nu }\bigg (\Big ((1+c_0+w_d)z_t(0,t)\nonumber \\&\quad +\frac{2}{9c_0}\frac{d}{dt}\big (w^3_1(0,t)-w^3_2(0,t)\big )\Big )v(0)+\Big ((1+c_1+w_d)z_t(1,t)\nonumber \\&\quad +\frac{2}{9c_1}\frac{d}{dt}\big (w^3_1(1,t)-w^3_2(1,t)\big )\Big )v(1)\bigg ) +\Big ((1+c_0+w_d)z(0,t)v(0)\nonumber \\&\quad +(1+c_1+w_d)z(1,t)v(1)+\frac{2}{9c_0}\Big (\big (w^3_1(0,t)-w^3_2(0,t)\big )v(0)\nonumber \\&\quad +\frac{2}{9c_1}\big (w^3_1(1,t)-w^3_2(1,t\big )v(1)\Big )=0. \end{aligned}$$

(2.23)

Set $v=z$ in (2.23), and bound the fourth and fifth terms on the left hand side, respectively, as

$$\begin{aligned} (1+w_d)(z_x,z)=\frac{(1+w_d)}{2}(z^2(1,t)-z^2(0,t)), \end{aligned}$$

and

$$\begin{aligned}&(w_1w_{1x}-w_2w_{2x},z)\\&\quad =(w_1z_x,z)+(zw_{2x},z)\\&\quad \le \left\| w_1(t)\right\| _{L^\infty }\left\| z_x(t)\right\| \left\| z(t)\right\| +\left\| z(t)\right\| _{L^\infty }\left\| w_{2x}(t)\right\| \left\| z(t)\right\| \\&\quad \le \sqrt{2}\left| \! \left| \! \left| w_1(t) \right| \! \right| \! \right| \left\| z_x(t)\right\| \left\| z(t)\right\| +(|z(0,t)|+\left\| z_x(t)\right\| )\left\| w_{2x}(t)\right\| \left\| z(t)\right\| \\&\quad \le \frac{\nu }{4}\left\| z_x(t)\right\| ^2+\frac{1+c_0+w_d}{2}z^2(0,t)+C(\left| \! \left| \! \left| w_{1}(t) \right| \! \right| \! \right| ^2+\left| \! \left| \! \left| w_{2}(t) \right| \! \right| \! \right| ^2)\left\| z(t)\right\| ^2. \end{aligned}$$

Now to bound the other terms on the left hand side of (2.23), we rewrite the following terms as for $i=0,\,1$

$$\begin{aligned} \big (w^3_1(i,t)-w^3_2(i,t)\big )z(i,t)&=z^2(i,t)\big (w^2_1(i,t)+w_1(i,t)w_2(i,t)+w_2^2(i,t)\big )\\&\ge z^2(i,t)\big (w^2_1(i,t)-|w_1(i,t)||w_2(i,t)|+w_2^2(i,t)\big ) \\&\ge \frac{1}{2}z^2(i,t)(w_1^2(i,t)+w_2^2(i,t))\ge 0, \end{aligned}$$

and

$$\begin{aligned} \frac{d}{dt}\big (w^3_1(i,t)-w^3_2(i,t)\big )z(i,t)&=\frac{3}{2}\frac{d}{dt}\Big (w_1^2(i,t)z^2(i,t)\Big )-3w_1(i,t)w_{1t}(i,t)z^2(i,t)\\&\quad +3z^2(i,t)\big (w_1(i,t)+w_2(i,t)\big )w_{2t}(i,t)\\&\le \frac{3}{2}\frac{d}{dt}\Big (w_1^2(i,t)z^2(i,t)\Big )+Cz^2(i,t)\Big (w_1^2(i,t)+w_{1t}^2(i,t)\\&\qquad +w_2^2(i,t)+w_{2t}^2(i,t)\Big ). \end{aligned}$$

Therefore, from (2.23), we arrive at

$$\begin{aligned}&\frac{d}{dt}\Bigg (\left\| z(t)\right\| ^2+\mu \left\| z_x(t)\right\| ^2+\frac{\mu }{\nu }\Big ((1+c_0+w_d)z^2(0,t)+(1+c_1+w_d)z^2(1,t)\\&\qquad +\frac{1}{3c_0}w_1^2(0,t)z^2(0,t) \\&\qquad +\frac{1}{3c_1}w_1^2(1,t)z^2(1,t)\Big )\Bigg )+\nu \left\| z_x(t)\right\| ^2\\&\quad \le C(\left| \! \left| \! \left| w_{1} \right| \! \right| \! \right| ^2+\left| \! \left| \! \left| w_{2} \right| \! \right| \! \right| ^2)\left\| z\right\| ^2 +C\frac{\mu }{\nu }z^2(0,t)\Big (w_1^2(0,t)+w_{1t}^2(0,t)+w_2^2(0,t)\\&\qquad +w_{2t}^2(0,t)\Big )+C\frac{\mu }{\nu }z^2(1,t)\Big (w_1^2(1,t)+w_{1t}^2(1,t)+w_2^(1,t)+w_{2t}^2(1,t)\Big ). \end{aligned}$$

Using (2.18), we obtain

$$\begin{aligned}&\frac{d}{dt}\Big (\left\| z(t)\right\| ^2+\mu \left\| z_x(t)\right\| ^2+E_4(t)\Big )+\nu \left\| z_x(t)\right\| ^2\\&\quad \le C\Big (\left\| z(t)\right\| ^2+\mu \left\| z_x(t)\right\| ^2+E_4(t)\Big )\Big (w_{1t}^2(0,t)+w_{2t}^2(0,t)\\&\qquad +w_{1t}^2(1,t)+w_{2t}^2(1,t)+\left| \! \left| \! \left| w_{1}(t) \right| \! \right| \! \right| ^2+\left| \! \left| \! \left| w_{2}(t) \right| \! \right| \! \right| ^2\Big ). \end{aligned}$$

Applying Gronwall’s inequality to the above inequality yields

$$\begin{aligned}&\left\| z(t)\right\| ^2+\mu \left\| z_x(t)\right\| ^2+E_4(t)\\&\quad \le \big (\left\| z_0\right\| ^2+\mu \left\| z_{0x}\right\| ^2+E_4(0)\big )\exp \Bigg (C\int _{0}^{t}\Big (w_{1t}^2(0,s)+w_{2t}^2(0,s) \\&\qquad +w_{1t}^2(1,s)+w_{2t}^2(1,s)+\left| \! \left| \! \left| w_{1}(t) \right| \! \right| \! \right| ^2+\left| \! \left| \! \left| w_{2}(t) \right| \! \right| \! \right| ^2\Big )\; ds\Bigg ). \end{aligned}$$

A use of Lemmas 2.2–2.4 gives the desired result. $\square$

As a consequence, when $w_{10}=w_{20},$ it follows that $w_1(t)=w_2(t)$ for all $t>0$. Hence, the solution is unique.

3 Finite Element Approximation

In this section, we discuss semidiscrete Galerkin approximation keeping the time variable continuous. Moreover, optimal error estimates for the state variable and superconvergence results for feedback controllers are established.

For any positive integer N,  let $\Pi =\left\{ 0 = x_0< x_1<\cdots < x_{N} = 1\right\}$ be a partition of ${\overline{I}}$ into subintervals $I_j = (x_{j-1} , x_j ),\, 1\le j \le N$ with $h_j = x_j-x_{j-1}$ and mesh parameter $h = \max \limits _{1\le j\le N }h_j$. We define a finite dimensional subspace $V_h$ of $H^1$ as follows

$$\begin{aligned} V_h=\left\{ v_h\in C^0\big ({\overline{I}} \big ):\, v_h\Big |_{I_j} \in {\mathcal {P}}_{1}(I_j) \quad 1\le j\le N\right\} , \end{aligned}$$

where ${\mathcal {P}}_{1}(I_j)$ is the set of linear polynomials in $I_j$.

Now, the corresponding semidiscrete formulation for the problem (3.3)–(3.6) is to seek $w_h\in H^1(V_h)$ such that

$$\begin{aligned}&(w_{ht},\chi )+\mu (w_{hxt},\chi _x)+\nu (w_{hx},\chi _x)+(1+w_d)(w_{hx},\chi )+(w_hw_{hx},\chi )\nonumber \\&\quad +\Big (\big ((1+c_0+w_d)w_h(0,t)\nonumber \\&\quad +\frac{2}{9c_0}w_h^3(0,t)\big )\chi (0) +\big ((1+c_1+w_d)w_h(1,t)+\frac{2}{9c_1}w_h^3(1,t)\big )\chi (1)\Big )\nonumber \\&\quad +\frac{\mu }{\nu }\Big (\big ((c_0+1+w_d)w_{ht}(0,t)+\frac{2}{3c_0}w_h^2(0,t)w_{ht}(0,t)\big )\chi (0)+\big ((c_1+1+w_d)w_{ht}(1,t)\nonumber \\&\quad +\frac{2}{3c_1}w_h^2(1,t)w_{ht}(1,t)\big )\chi (1)\Big ) =0 \qquad \forall ~ \chi \in V_h \end{aligned}$$

(3.1)

with $w_h(x,0)=w_{0h}(x),$ an approximation of $w_0$. For our analysis, we assume that $w_{0h}$ is the $H^1$ projection of $w_0$ onto $V_h$.

Now since $V_h$ is finite dimensional, the semidiscrete problem (3.1) leads to a system of nonlinear ODEs. Then an appeal to the Picard’s theorem yields the existence of a unique solution $w_h(t)$ in $t\in (0,t^*)$ for some $t>0$. Since from Lemma 3.1, $w_h(t)$ is bounded for all $t>0,$ using a continuation argument, the global existence of $w_h(t)$ is established.

Below, we state four Lemmas for the semidiscrete problem (1.9)–(1.12), which imply global stabilization result for the semidiscrete solution.

Lemma 3.1

Under the assumptions $\mathbf{(A1)}$–$\mathbf{(A1)}$ and $\alpha$ as in (2.1), there holds for $t>0$

$$\begin{aligned}&\left\| w_h(t)\right\| ^2+\mu \left\| w_{hxt}(t)\right\| ^2+\frac{\mu }{\nu }E_{1h}(w_h)(t)+\beta e^{-2\alpha t}\int _{0}^{t} e^{2\alpha s}\left| \! \left| \! \left| w_h(t) \right| \! \right| \! \right| ^2 ds\\&\quad \le Ce^{-2\alpha t}\big (\left\| w_{0h}\right\| ^2+\mu \left\| w_{0hx}\right\| ^2+\frac{\mu }{\nu }E_{1h}(w_h)(0)\big ), \end{aligned}$$

where

$$\begin{aligned} E_{1h}(w_h)(t)= & {} \Big ((c_0+1+w_d)w_h^2(0,t)+(c_1+1+w_d)w_h^2(1,t)\\&+\,\frac{1}{3c_0}w_h^4(0,t)+\frac{1}{3c_1}w_h^4(1,t)\Big ), \end{aligned}$$

and $\beta$ is the same as in (2.2).

Proof

For the proof we can proceed as in continuous case. $\square$

One dimensional discrete Laplacian$\Delta _h:V_h\longrightarrow V_h$ is defined by

$$\begin{aligned} (-\Delta _hv_h,w_h)=(v_{hx},w_{hx})+v_{hx}(0)w_h(0)-v_{hx}(1)w_h(1) \qquad \forall ~ v_h, w_h\in V_h. \end{aligned}$$

(3.2)

The semidiscrete version of the control problem (1.9)–(1.12) satisfies

$$\begin{aligned}&w_{ht}-\mu \Delta _hw_{ht}+\nu \Delta _hw_h+(1+w_d)w_{hx}+w_hw_{hx}=0 , \end{aligned}$$

(3.3)

$$\begin{aligned}&w_{hx}(0,t)=:v_{0h}(t)=\frac{1}{\nu }\Big ((1+c_0+w_d)w_h(0,t)+\frac{2}{9c_0}w_h^3(0,t)\Big ) , \end{aligned}$$

(3.4)

$$\begin{aligned}&w_{hx}(1,t)=:v_{1h}(t)=-\frac{1}{\nu }\Big ((1+c_1+w_d)w_h(1,t)+\frac{2}{9c_1}w_h^3(1,t)\Big ) , \end{aligned}$$

(3.5)

$$\begin{aligned}&w_h(x,0)=w_{0h}(x)\,(\text {say}) , \end{aligned}$$

(3.6)

where following estimates hold:

$$\begin{aligned} \Vert w_0- w_{0h}\Vert _j \le C h^{2-j} \Vert w_0\Vert _2, \quad j=0,1. \end{aligned}$$

(3.7)

Using (3.7), we can show that $\left\| w_{0h}\right\| \le \left\| w_{0}\right\|$ and $\left\| w_{0hx}\right\| \le \left\| w_{0x}\right\|$. For showing the bound of $\left\| \Delta _h w_{0h}\right\| ,$ we rewrite

$$\begin{aligned} \Big (-\Delta _h w_{0h},\phi _{h}\Big )&=(w_{0hx},\phi _{hx})+w_{0hx}(0)\phi _{h}(0)-w_{0hx}(1)\phi _{h}(1)\\&=(-w_{0xx},\phi _{h})-\Big ((w_{0x}-w_{0hx},\phi _{hx})+(w_{0x}(0)-w_{0hx}(0))\phi _{h}(0)\\&\quad -(w_{0x}(1)-w_{0hx}(1))\phi _{h}(1)\Big ). \end{aligned}$$

Choose ${{\tilde{w}}}_h(0)=w_{0h}$ so that from Lemma 3.5, we obtain the bound of $|w_{0x}(0)-w_{0hx}(0)|$ and $|w_{0x}(1)-w_{0hx}(1)|$. Now a use of inverse inequality yields $\left\| \Delta _h w_{0h}\right\| \le C\left\| w_{0xx}\right\|$ easily.

Lemma 3.2

Under the assumptions $\mathbf{(A1)}$–$\mathbf{(A2)}$, there exists a positive constant C such that for $t>0$

$$\begin{aligned}&\Big (\left\| w_{hx}(t)\right\| ^2+\mu \left\| \Delta _hw_h(t)\right\| ^2+\frac{1}{\nu }E_{2h}(w_h)(t)\Big )+\beta e^{-2\alpha t}\int _{0}^{t} e^{2\alpha s}\left\| \Delta _hw_h(s)\right\| ^2 ds\\&\quad \le C(1+\mu )e^{-2\alpha t}\big (\left\| w_{0}\right\| ^2_1\big )\exp \Big (C(1+\mu )\left\| w_0\right\| ^2_1\Big ), \end{aligned}$$

where

$$\begin{aligned} E_{2h}(w_h)(t)= & {} \Big ((c_0+1+w_d)w_h^2(0,t)+(c_1+1+w_d)w_h^2(1,t)\\&+\,\frac{1}{9c_0}w_h^4(0,t)+\frac{1}{9c_1}w_h^4(1,t)\Big ). \end{aligned}$$

Lemma 3.3

Let assumptions $\mathbf{(A1)}$- $\mathbf{(A2)}$ hold. Then, there is a positive constant C such that for $t>0$

$$\begin{aligned}&\nu \big (\left\| w_{hx}(t)\right\| ^2+E_{2h}(w_h)(t)\big )+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| w_{ht}\right\| ^2+\mu \left\| w_{hxt}\right\| ^2+\frac{\mu }{\nu }E_{3h}(w_h)(s)\Big ) ds\\&\quad \le C(1+\mu )e^{-2\alpha t}\big (\left\| w_{0}\right\| ^2_2\big )\exp \Big (C(1+\mu )\left\| w_0\right\| ^2_1\Big ), \end{aligned}$$

where

$$\begin{aligned} E_{3h}(w_h)(t)&=\Big ((1+c_0+w_d)w_{ht}^2(0,t)+(1+c_1+w_d)w_{ht}^2(1,t)+\frac{2}{3c_0}w_h^2(0,t)w_{ht}^2(0,t)\\&\quad +\frac{2}{3c_1}w_h^2(1,t)w_{ht}^2(1,t)\Big ). \end{aligned}$$

Lemma 3.4

Under the assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)},$ there holds for $t>0$

$$\begin{aligned}&\Big (\left\| w_{ht}(t)\right\| ^2+\mu \left\| w_{hxt}(t)\right\| ^2+\frac{\mu }{\nu }E_{3h}(w_h)(t)\Big )\\&\qquad +e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\nu \left\| w_{hxt}(s)\right\| ^2+E_{3h}(w_h)(s)\Big ) ds\\&\quad \le C(1+\mu )e^{-2\alpha t}\big (\left\| w_{0}\right\| ^2_1\big )\exp \Big (C(1+\mu )\left\| w_0\right\| ^2_1\Big ), \end{aligned}$$

where $E_{3h}(w_h)(t)$ is as in previous Lemma 3.3.

Remark 3.1

The proofs of the above Lemmas 3.2–3.4 follows in a similar fashion as in continuous case. Also for $\alpha =0,$ all results in these lemmas hold.

3.1 Error Estimates

To bound the error, we first introduce an auxiliary projection ${{\tilde{w}}}_h(t) \in V_h$ of w(t) through the following form

$$\begin{aligned} (w_x-{\tilde{w}}_{hx},\chi _x)+\lambda (w-{{\tilde{w}}}_h,\chi )=0 \quad \chi \in V_h, \end{aligned}$$

(3.8)

where $\lambda$ is some fixed positive number. For a given $w(t)\in H^1,$ the existence of a unique ${{\tilde{w}}}_h(t)$ follows from the Lax–Milgram Lemma. Let $\eta :=w-{{\tilde{w}}}_h$ be the error involved in the auxiliary projection. Then, the following standard error estimates hold

$$\begin{aligned} \left\| \eta (t)\right\| _j&\le C h^{\min (2,m)-j}\;\left\| w(t)\right\| _m, \;\text {and} \;\left\| \eta _t(t)\right\| _j\nonumber \\&\le C h^{\min (2,m)-j}\left\| w_t(t)\right\| _m,\;\; j=0,1 \; \text{ and } \; m=1,2. \end{aligned}$$

(3.9)

and

$$\begin{aligned} \left\| \eta (t)\right\| _{L^\infty }\le Ch^2\left\| w(t)\right\| _{2,\infty }. \end{aligned}$$

(3.10)

For a proof, we refer to Thomée [26]. In addition, for proving optimal error estimates, we need the following estimates of $\eta$ and $\eta _t$ at the boundary points $x=0,1$ whose proof can be found in [9, 16, 20].

Lemma 3.5

For $x=0,1,$ there holds for $t>0$

$$\begin{aligned} |\eta (x,t)|\le C h^2\left\| w(t)\right\| _2 \text{ and } \qquad |\eta _t(x,t)|\le C h^2\left\| w_t(t)\right\| _2. \end{aligned}$$

Using elliptic projection, write

$$\begin{aligned}e:=w-w_h=(w-\tilde{w}_h)-(w_h-{{\tilde{w}}}_h)=:\eta -\theta .\end{aligned}$$

Choose ${{\tilde{w}}}_h(0)=w_{0h}$ so that $\theta (0)=0$.

Since estimates of $\eta$ are known, it is enough to estimate $\theta$. Subtracting (3.1) from (1.16) and using (3.8), we arrive at

$$\begin{aligned}&(\theta _t,\chi )+\mu (\theta _{xt},\chi _x)+\nu (\theta _x,\chi _x)+\sum _{i=0}^{1}(1+c_i+w_d)\theta (i,t)\chi (i)\nonumber \\&\qquad +\frac{\mu }{\nu }\sum _{i=0}^{1}(1+c_i+w_d)\theta _t(i,t)\chi (i)\nonumber \\&\quad =\Big ((\eta _t,\chi )-\mu \lambda (\eta _t,\chi )-\nu \lambda (\eta ,\chi )\Big )+(1+w_d)(\eta _x-\theta _x,\chi )+(ww_x-w_hw_{hx},\chi )\nonumber \\&\qquad +\sum _{i=0}^{1}\Big ((1+c_i+w_d)\eta (i,t)\chi (i)+\frac{2}{9c_i}\big (w^3(i,t)-w^3_h(i,t)\big )\chi (i)\Big )\nonumber \\&\qquad +\frac{\mu }{\nu }\sum _{i=0}^{1}\Big ((1+c_i+w_d)\eta _t(i,t)\chi (i)+\frac{2}{9c_i}\frac{d}{dt}\big (w^3(i,t)-w_h^3(i,t)\big )\chi (i)\Big ) , \end{aligned}$$

(3.11)

where $w^3(i,t)-w_h^3(i,t)$ for $i=0,\,1$ can be rewritten as

$$\begin{aligned} w^3(i,t)-w_h^3(i,t)&=\eta ^3(i,t)-\theta ^3(i,t)+3w(i,t)\eta (i,t)\big (w(i,t)-\eta (i,t)\big )\\&\quad -3w_h(i,t)\theta (i,t)\big (w_h(i,t)-\theta (i,t)\big ). \end{aligned}$$

Lemma 3.6

Let assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)}$ hold true. Then, there exists a positive constant C independent of h such that for $t>0$

$$\begin{aligned}&\Big (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2+\frac{1}{9}\frac{\mu }{\nu }E_1(\theta )(t)\Big )+ \frac{\beta _1}{2}e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| \theta _x(s)\right\| ^2+E_1(\theta )(s)\Big ) \;ds\\&\quad \le C\frac{1}{\mu }(\left\| w_0\right\| _2) (1+\mu )h^4e^{-2\alpha t} \exp \Big (C\left\| w_0\right\| _2\Big ), \end{aligned}$$

where $\beta _1=\min \Bigg \{(\frac{3\nu }{2}-2\alpha (\mu +1)), \Big (1-2\alpha \big (\frac{2\mu }{\nu }+1\big )\Big )\Bigg \}>0$.

Proof

Set $\chi =\theta$ in (3.11) to obtain

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\big (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2)+\nu \left\| \theta _x(t)\right\| ^2+\sum _{i=0}^{1}(c_i+(1+w_d))\theta ^2(i,t)\nonumber \\&\qquad +\frac{\mu }{2\nu }\frac{d}{dt}\Big (\sum _{i=0}^{1}(1+c_i+w_d)\theta ^2(i,t)\Big )\nonumber \\&\quad =\Big ((\eta _t,\theta )-\mu \lambda (\eta _t,\theta )-\nu \lambda (\eta ,\theta )\Big )+(1+w_d)(\eta _x-\theta _x,\theta )\nonumber \\&\qquad +\Big (w(\eta _x-\theta _x)+(\eta -\theta )w_{hx},\theta \Big )\nonumber \\&\qquad +\sum _{i=0}^{1}\Big ((1+c_i+w_d)\eta (i,t)\theta (i,t)+\frac{2}{9c_i}\big (w^3(i,t)-w_h^3(i,t)\big )\theta (i,t)\Big )\nonumber \\&\qquad +\frac{\mu }{\nu }\sum _{i=0}^{1}\Bigg ((1+c_i+w_d)\eta _t(i,t)\theta (i,t)+\frac{2}{9c_i} \frac{d}{dt}\big (w^3(i,t)-w_h^3(i,t)\big )\theta (i,t)\Bigg )\nonumber \\&\quad = \sum _{j=1}^{5}I_j(\theta ), \end{aligned}$$

(3.12)

where $I_4(\theta )$ and $I_5(\theta )$ are last two summation term respectively. The first term on the right hand side of (3.12) is bounded using the Cauchy-Schwarz inequality and the Young’s inequality in

$$\begin{aligned} I_1(\theta )=(\eta _t,\theta ) -\mu \lambda (\eta _t,\theta )-\nu \lambda (\eta ,\theta )&\le \frac{\epsilon }{4}\left\| \theta (t)\right\| ^2+C(1+\mu ^2)\left\| \eta _t(t)\right\| ^2+C\left\| \eta (t)\right\| ^2, \end{aligned}$$

where constant $\epsilon >0$ we choose later. For the second term on the right hand side of (3.12), integration by parts, the Cauchy-Schwarz inequality, and Young’s inequality yield

$$\begin{aligned} I_2(\theta )=(1+w_d)(\eta _x-\theta _x,\theta )&=-(1+w_d)\Big ((\eta ,\theta _x)+\eta (1,t)\theta (1,t)-\eta (0,t)\theta (0,t)\Big )\\&\quad -\frac{(1+w_d)}{2}\Big (\theta ^2(1,t)-\theta ^2(0,t)\Big )\\&\le \frac{\nu }{8}\left\| \theta _x(t)\right\| ^2+\frac{c_0}{8}\theta ^2(0,t)+\frac{c_1}{8}\theta ^2(1,t)+C\left\| \eta (t)\right\| ^2 \\&\quad +C(\eta ^2(0,t)+\eta ^2(1,t)) -\frac{(1+w_d)}{2}\Big (\theta ^2(1,t)-\theta ^2(0,t)\Big ). \end{aligned}$$

For the third term, we note that

$$\begin{aligned} I_3(\theta )&=\big (w(\eta _x-\theta _x)+(\eta -\theta )w_{hx},\theta )\\&=-(w\eta ,\theta _x)-(w_x\eta ,\theta )-(w\theta _x,\theta )+\big ((\eta -\theta )w_{hx},\theta \big )\\&\quad +w(1,t)\eta (1,t)\theta (1,t)-w(0,t)\eta (0,t)\theta (0,t) \\&\le \frac{\nu }{8}\left\| \theta _x(t)\right\| ^2+C\left\| w(t)\right\| ^2_{L^\infty }\left\| \eta (t)\right\| ^2+C\left\| \eta (t)\right\| ^2 +\frac{c_0}{8}\theta ^2(0,t)\\&\quad +\frac{c_1}{8}\theta ^2(1,t)+C\big (\left\| w_x(t)\right\| ^2_{L^\infty }+\left\| w_{hx}(t)\right\| ^2_{L^\infty }+\left\| w(t)\right\| ^2_{L^\infty }\big )\left\| \theta (t)\right\| ^2\\&\quad +\frac{\epsilon }{4}\left\| \theta (t)\right\| ^2+C(w^2(0,t)\eta ^2(0,t)+w^2(1,t)\eta ^2(1,t)). \end{aligned}$$

First subterms of the fourth and fifth term on the right hand side of (3.12) are bounded by

$$\begin{aligned}&(1+c_0+w_d)\eta (0,t)\theta (0,t)+(1+c_1+w_d)\eta (1,t)\theta (1,t)\\&\qquad +\frac{\mu }{\nu }\Big ((1+c_0+w_d)\eta _t(0,t)\theta (0,t)+(1+c_1+w_d)\eta _t(1,t)\theta (1,t)\Big )\\&\quad \le \frac{c_0}{8}\theta ^2(0,t)+ \frac{c_1}{8}\theta ^2(1,t)+C\Big (\eta ^2(0,t)+\eta ^2(1,t)\\&\qquad +\mu ^2\big (\eta _t^2(0,t)+\eta _t^2(1,t)\big )\Big ). \end{aligned}$$

For second subterm of the fourth term on the right hand side, we note that for $i=0,\,1$

$$\begin{aligned}&\frac{2}{9c_i}\Big (w^3(i,t)-w_h^3(i,t)\Big )\theta (i,t)\\&\quad =-\frac{2}{9c_i}\theta ^4(i,t)-\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)-\frac{2}{9c_i}\eta ^3(i,t)\theta (i,t)\\&\qquad +\frac{2}{3c_i}\Big (w^2(i,t)\eta (i,t)-w(i,t)\eta ^2(i,t)+w_h(i,t)\theta ^2(i,t)\Big )\theta (i,t). \end{aligned}$$

Using Young’s inequality, implies that for $i=0,\,1$

$$\begin{aligned} \frac{2}{9c_i}\eta ^3(i,t)\theta (i,t)\le & {} \frac{2}{9c_i}\frac{1}{16}\theta ^4(i,t)+C\eta ^4(i,t),\\ \frac{2}{3c_i}w^2(i,t)\eta (i,t)\theta (i,t)\le & {} \frac{c_i}{8}\theta ^2(i,t)+Cw^4(i,t)\eta ^2(i,t) \end{aligned}$$

and

$$\begin{aligned} \frac{2}{3c_i}w(i,t)\eta ^2(i,t)\theta (i,t)\le \frac{2}{9c_i}\frac{1}{16}\theta ^4(i,t)+C(w(i,t)\eta ^2(i,t))^\frac{4}{3}. \end{aligned}$$

Again, a use of Young’s inequality yields

$$\begin{aligned} \frac{2}{3c_i}w_h(i,t)\theta ^3(i,t)\le \frac{2}{3c_i}12w_h^2(i,t)\theta ^2(i,t)+\frac{2}{9c_i}\frac{1}{16}\theta ^4(i,t). \end{aligned}$$

Hence, the contribution of the second subterm of the fourth term on the right hand side of (3.12) after applying Lemmas 2.2, 2.4 and 3.5, can be bounded as

$$\begin{aligned} \sum _{i=0}^{1}&\frac{2}{9c_i}\Big (w^3(i,t)-w_h^3(i,t)\Big )\theta (i,t)\\&\le -\frac{2}{9c_0}\frac{13}{16}\theta ^4(0,t)+\frac{c_0}{8}\theta ^2(0,t)+C\eta ^2(0,t) \\&\quad -\frac{2}{9c_1}\frac{13}{16}\theta ^4(1,t)+\frac{c_1}{8}\theta ^2(1,t)+C\eta ^2(1,t)+8\sum _{i=0}^{1}\frac{1}{c_i}w_h^2(i,t)\theta ^2(i,t). \end{aligned}$$

Expanding the second subterm of the fifth term, we note that for $i=0,\,1$

$$\begin{aligned} \frac{2}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\big (\eta ^3(i,t)\big )\theta (i,t)\le & {} \frac{\mu }{\nu }C\theta ^2(i,t)\eta ^2(i,t)+C\frac{\mu }{\nu }\eta ^2(i,t)\eta _t^2(i,t),\\ \frac{2}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\big (\theta ^3(i,t)\big )\theta (i,t)= & {} -\frac{1}{6c_i}\frac{\mu }{\nu }\frac{d}{dt}\big (\theta ^4(i,t)\big ), \end{aligned}$$

and using Lemmas 2.2 and 2.4, we obtain

$$\begin{aligned} \frac{2}{3c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (w^2(i,t)\eta (i,t)\Big )\theta (i,t)\le \frac{\mu }{\nu }C\theta ^2(i,t)w^2(i,t)+C\frac{\mu }{\nu }\eta ^2(i,t)+C\frac{\mu }{\nu }\eta _t^2(i,t). \end{aligned}$$

Also, it holds that

$$\begin{aligned} -\frac{2}{3c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (w(i,t)\eta ^2(i,t)\Big )\theta (i,t)&\le \frac{\mu }{\nu }C\theta ^2(i,t)\big (w^2(i,t)+w_t^2(i,t)\big )+C\frac{\mu }{\nu }\eta ^4(i,t)\\&\quad +C\frac{\mu }{\nu }\eta ^2(i,t)\eta _t^2(i,t). \end{aligned}$$

Rewrite and use the Young’s inequality to obtain

$$\begin{aligned} -\frac{2}{3c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (w_h^2(i,t)\theta (i,t)\Big )\theta (i,t)&\le -\frac{1}{3c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (w_h^2(i,t)\theta ^2(i,t)\Big )\\&\quad +C\theta ^2(i,t)\Big (w_h^2(i,t)+\mu ^2 w_{ht}^2(i,t)\Big ). \end{aligned}$$

Similarly,

$$\begin{aligned} \frac{2}{3c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (w_h(i,t)\theta ^2(i,t)\Big )\theta (i,t)&\le \frac{4}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\big (w_h(i,t)\theta ^3(i,t)\big )+\frac{2}{9c_i}\frac{1}{16}\theta ^4(i,t)\\&\quad +C\frac{\mu ^2}{\nu ^2}w_{ht}^2(i,t)\theta ^2(i,t). \end{aligned}$$

Hence, from (3.12), we arrive using Lemmas 2.2, 2.4, 3.2, 3.4 and 3.5 at

$$\begin{aligned}&\frac{d}{dt}\big (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2)+\frac{3\nu }{2}\left\| \theta _x(t)\right\| ^2+\sum _{i=0}^{1}\frac{4}{3c_i}w_h^2(i,t)\theta ^2(i,t)+E_1(\theta )(t)\\&\qquad +\frac{\mu }{\nu }\frac{d}{dt}\Big (E_1(\theta )(t)+\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)\Big )\\&\quad \le C((1+\mu ^2)\left\| \eta _t(t)\right\| ^2+\left\| \eta (t)\right\| ^2)+C\Big (\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2+\left\| w_{xx}(t)\right\| ^2+\left\| \Delta _hw_h(t)\right\| ^2+w_x^2(0,t)\\&\qquad +w_{hx}^2(0,t)\Big )\left\| \theta \right\| ^2+\epsilon \left\| \theta \right\| ^2+C(1+\mu )\Big (\sum _{i=0}^{1}\eta ^2(i,t)\Big )+16\sum _{i=0}^{1}\frac{1}{c_i}w_h^2(i,t)\theta ^2(i,t) \\&\qquad +\frac{\mu }{\nu }\frac{d}{dt}\Big (\sum _{i=0}^{1}\frac{8}{9c_i}w_h(i,t)\theta ^3(i,t)\Big )+C(\mu +\mu ^2)\Big (\sum _{i=0}^{1}\eta _t^2(i,t)\Big ) \\&\qquad +C\sum _{i=0}^{1}\frac{\mu }{\nu }\theta ^2(i,t)\Big (w^2(i,t)+w_t^2(i,t)+w_h^2(i,t)+\mu w_{ht}^2(i,t)\Big ). \end{aligned}$$

Multiply the above inequality by $e^{2\alpha t}$. Use Poincaré–Wirtinger’s inequality

$$\begin{aligned} \left\| \theta (t)\right\| ^2\le \theta ^2(0,t)+\theta ^2(1,t)+\left\| \theta _x(t)\right\| ^2 \le E_1(\theta )(t)+\left\| \theta _x(t)\right\| ^2 \end{aligned}$$

with

$$\begin{aligned} 2\alpha \frac{\mu }{\nu }\sum _{i=0}^{1}\frac{8}{9c_i}w_h(i,t)\theta ^3(i,t)&\ge -2\alpha \frac{\mu }{\nu }\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)-2\alpha \frac{\mu }{\nu }E_1(\theta )(t) \end{aligned}$$

This yields

$$\begin{aligned}&\frac{d}{dt}\Bigg (e^{2\alpha t}\Big (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2+\frac{\mu }{\nu }\big (E_1(\theta )(t)+\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)\big )\Big )\Bigg )\\&\qquad +e^{2\alpha t}\sum _{i=0}^{1}\frac{4}{3c_i}w_h^2(i,t)\theta ^2(i,t)+e^{2\alpha t}\Big (1-2\alpha \big (\frac{2\mu }{\nu }+1\big )\Big )E_1(\theta )(t)\\&\qquad +\Big (\frac{3\nu }{2}-2\alpha (1+\mu )\Big ) e^{2\alpha t}\left\| \theta _x(t)\right\| ^2\\&\quad \le Ce^{2\alpha t}\big ((1+\mu ^2)\left\| \eta _t\right\| ^2+\left\| w(t)\right\| ^2_1\left\| \eta (t)\right\| ^2\big )\\&\qquad +Ce^{2\alpha t}\Big (\phi (t)+w_x^2(0,t)+w_{hx}^2(0,t)\Big )\left\| \theta \right\| ^2 \\&\qquad +C\frac{\mu }{\nu }\sum _{i=0}^{1}\theta ^2(i,t)\Big (w^2(i,t)+w_t^2(i,t)+w_h^2(i,t)+\mu w_{ht}^2(i,t)\Big )\\&\qquad +\epsilon e^{2\alpha t}\Big (E_1(\theta )(t)+\left\| \theta _x(t)\right\| ^2\Big )\\&\qquad +\frac{\mu }{\nu }\frac{d}{dt}\Bigg (e^{2\alpha t}\sum _{i=0}^{1}\Big (\frac{8}{9c_i}w_h(i,t)\theta ^3(i,t)\Big )\Bigg )+e^{2\alpha t}(4\alpha \frac{\mu }{\nu }+24)\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)\\&\qquad +C(1+\mu )e^{2\alpha t}\big (\sum _{i=0}^{1}\eta ^2(i,t)\big )+C(\mu +\mu ^2)e^{2\alpha t}\Big (\sum _{i=0}^{1}\eta _t^2(i,t)\Big ), \end{aligned}$$

where $\phi (t)=\left| \! \left| \! \left| w(t) \right| \! \right| \! \right| ^2+\left\| w_{xx}(t)\right\| ^2+\left\| \Delta _hw_h(t)\right\| ^2$. Now integrate from 0 to t and choose $\epsilon =\frac{\beta _1}{2}$ with

$$\begin{aligned} 2\alpha \frac{\mu }{\nu }\frac{8}{9c_i}w_h(i,t)\theta ^3(i,t)&\ge -2\alpha \frac{\mu }{\nu }\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)-2\alpha \frac{\mu }{\nu }\frac{8}{27c_i}\theta ^4(i,t) , \quad i=0,1. \end{aligned}$$

to find that

$$\begin{aligned}&e^{2\alpha t}\Bigg (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2+\frac{1}{9}\frac{\mu }{\nu }E_1(\theta )(t)\Bigg )+\frac{\beta _1}{2}\int _{0}^{t}e^{2\alpha s}\Bigg (\left\| \theta _x(t)\right\| ^2+E_1(\theta )(s)\Bigg )\;ds\nonumber \\&\qquad +\int _{0}^{t}e^{2\alpha s}\Big (\sum _{i=0}^{1}\frac{4}{3c_i}w_h^2(i,s)\theta ^2(i,s)\Big ) ds \end{aligned}$$

(3.13)

$$\begin{aligned}&\quad \le Ch^4\int _{0}^{t}e^{2\alpha s}\Big ((1+\mu +\mu ^2)\left\| w_t(t)\right\| ^2_2+(1+\mu )\left\| w(t)\right\| _2^2\Big )\; ds\nonumber \\&\qquad +C\int _{0}^{t}e^{2\alpha s}\Big (\phi (t)+w_x^2(0,t)+w_{hx}^2(0,t)\Big )\left\| \theta (t)\right\| ^2 ds\nonumber \\&\qquad +C(\frac{\mu }{\nu }+1)\int _{0}^{t}e^{2\alpha s}E_1(\theta )(s)\psi (s)\;ds, \end{aligned}$$

(3.14)

where $\psi (t)=\sum _{i=0}^{1}\Big (w^2(i,t)+w_t^2(i,t)+w_h^2(i,t)+\mu w_{ht}^2(i,t)\Big )$. Then, an application of Gronwall’s inequality to (3.14) shows

$$\begin{aligned}&e^{2\alpha t}\Bigg (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2+\frac{1}{9}\frac{\mu }{\nu }E_1(\theta )(t)\Bigg )+\frac{\beta _1}{2}\int _{0}^{t}e^{2\alpha s}\Bigg (\left\| \theta _x(t)\right\| ^2+E_1(\theta )(s)\Bigg )\;ds\nonumber \\&\qquad +\int _{0}^{t}e^{2\alpha s}\Big (\sum _{i=0}^{1}\frac{4}{3c_i}w_h^2(i,s)\theta ^2(i,s)\Big ) ds\nonumber \\&\quad \le Ch^4\int _{0}^{t}e^{2\alpha s}\Bigg ((1+\mu )\left\| w(t)\right\| ^2_2+(1+\mu +\mu ^2)\left\| w_t(s)\right\| ^2_2\Bigg )\; ds\nonumber \\&\qquad \times \exp \Bigg (\int _{0}^{t}\Big ({\phi }(s)+{\psi }(s)+(w^4(0,s))^2+(w^4_h(0,s))^2\Big ) ds\Bigg ). \end{aligned}$$

(3.15)

Multiplying (3.15) by $e^{-2\alpha t}$ and using Lemmas 2.2, 2.4, 3.2 and 3.4 with $\alpha =0,$ it follows that

$$\begin{aligned}&\Bigg (\left\| \theta (t)\right\| ^2+\mu \left\| \theta _x(t)\right\| ^2+\frac{1}{9}\frac{\mu }{\nu }E_1(\theta )(t)\Bigg )+\frac{\beta _1}{2}e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Bigg (\left\| \theta _x(t)\right\| ^2+E_1(\theta )(s)\Bigg )\;ds\\&\quad +e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\sum _{i=0}^{1}\frac{4}{3c_i}w_h^2(i,s)\theta ^2(i,s)\Big ) ds\le C\frac{1}{\mu }(\left\| w_0\right\| _2)h^4e^{-2\alpha t} \exp \Big (C\left\| w_0\right\| _2\Big ). \end{aligned}$$

This completes the proof. $\square$

Lemma 3.7

Under assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)},$ there exists a positive constant C independent of h such that for $t>0$

$$\begin{aligned}&\nu \left\| \theta _x(t)\right\| ^2+\frac{1}{3}E_2(\theta )(t)+2e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| \theta _t(t)\right\| ^2+\mu \left\| \theta _{xt}(t)\right\| ^2\Big )\; ds\\&\qquad +\frac{\mu }{\nu }e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big ((1+c_0+w_d)\theta _t^2(0,s)+(1+c_1+w_d)\theta _t^2(1,s)\Big )\; ds\\&\quad \le C\frac{1}{\mu }(\left\| w_0\right\| _2)(1+\mu )h^4e^{-2\alpha t}\exp \big (C(\left\| w_0\right\| _2)\big ). \end{aligned}$$

Proof

Set $\chi =\theta _t$ in (3.11) to obtain

$$\begin{aligned}&\left\| \theta _t(t)\right\| ^2+\mu \left\| \theta _{xt}(t)\right\| ^2+\frac{1}{2}\frac{d}{dt}\Bigg (\nu \left\| \theta _x(t)\right\| ^2+\sum _{i=0}^{1}(1+c_i+w_d)\theta ^2(i,t)\Bigg )\nonumber \\&\qquad +\frac{\mu }{\nu }\Big (\sum _{i=0}^{1}(1+c_i+w_d)\theta _t^2(i,t)\Big )\nonumber \\&\quad =\sum _{{i=1}}^{5}I_i(\theta _t). \end{aligned}$$

(3.16)

The first term on the right hand side of (3.16) is bounded by

$$\begin{aligned} I_1(\theta _t)=(\eta _t,\theta _t)-\mu \lambda (\eta _t,\theta _t)+\nu \lambda (\eta ,\theta _t)&\le \frac{1}{4}\left\| \theta _t(t)\right\| ^2+C(1+\mu ^2)\left\| \eta _t(t)\right\| ^2+C\left\| \eta (t)\right\| ^2. \end{aligned}$$

For the second term $I_2(\theta _t),$ first rewrite it as

$$\begin{aligned} I_2(\theta _t)&=(1+w_d)(\eta _x-\theta _x,\theta _t)\\&=-(1+w_d)\frac{d}{dt}(\eta ,\theta _x)+(1+w_d)(\eta _t,\theta _x)\\&\quad +(1+w_d)\frac{d}{dt}\Big (\eta (1,t)\theta (1,t)-\eta (0,t)\theta (0,t)\Big )\\&\quad -(1+w_d)\big (\eta _t(1,t)\theta (1,t)-\eta _t(0,t)\theta (0,t)\big )-(1+w_d)(\theta _x,\theta _t). \end{aligned}$$

A use of Young’s inequality shows

$$\begin{aligned} I_2(\theta _t)&\le (1+w_d)\frac{d}{dt}\Big (\eta (1,t)\theta (1,t)-\eta (0,t)\theta (0,t)\Big )-(1+w_d)\frac{d}{dt}(\eta ,\theta _x)\\&\quad +C\Big (\left\| \eta _t(t)\right\| ^2+\left| \! \left| \! \left| \theta (t) \right| \! \right| \! \right| ^2+\eta _t^2(1,t)+\eta _t^2(0,t)\Big )+\frac{1}{8}\left\| \theta _t(t)\right\| ^2. \end{aligned}$$

For the third term $I_3(\theta _t)$ on the right hand side of (3.16), we first rewrite it as

$$\begin{aligned} I_3(\theta _t)&= \big (w(\eta _x-\theta _x)+(\eta -\theta )w_{hx},\theta _t\big )\\&=-\frac{d}{dt}\big ((w\eta ),\theta _x\big )+\frac{d}{dt}\Big (w(1,t)\eta (1,t)\theta (1,t)-w(0,t)\eta (0,t)\theta (0,t)\Big )\\&\quad +\big ((w\eta )_t,\theta _x\big )-\big (w_x\eta ,\theta _t\big )-\Big (\big (w(1,t)\eta (1,t)\big )_t\theta (1,t)-\big (w(0,t)\eta (0,t)\big )_t\theta (0,t)\Big )\\&\quad -(w\theta _x,\theta _t)+\big ((\eta -\theta )w_{hx},\theta _t\big ). \end{aligned}$$

and then an application of Young’s inequality with Lemmas 2.2, 2.4 and 3.2 yields

$$\begin{aligned} I_3(\theta _t)&\le -\frac{d}{dt}\big ((w\eta ),\theta _x\big )+\frac{d}{dt}\Big (w(1,t)\eta (1,t)\theta (1,t)-w(0,t)\eta (0,t)\theta (0,t)\Big )\\&\quad +C\Big (\left\| \eta _t(t)\right\| ^2+\left\| \eta (t)\right\| ^2+\eta ^2(1,t)+\eta ^2(0,t)+\eta _t^2(0,t)+\eta _t^2(1,t) +\left| \! \left| \! \left| \theta (t) \right| \! \right| \! \right| ^2\Big )\\&\quad +C\left\| \theta (t)\right\| ^2\Big (w_h^2(0,t)+w_h^4(0,t)+\left\| \Delta _h w_h(t)\right\| ^2\Big )+\frac{1}{8}\left\| \theta _t(t)\right\| ^2. \end{aligned}$$

The first subterm of the fourth term $I_4(\theta _t)$ on the right hand side of (3.16) can be rewritten for $i=0,\,1$ as

$$\begin{aligned} (1+c_i+w_d)\eta (i,t)\theta _t(i,t)&=(1+c_i+w_d)\frac{d}{dt}\big (\eta (i,t)\theta (i,t)\big )-(1+c_i+w_d)\eta _t(i,t)\theta (i,t)\\&\le (1+c_i+w_d)\frac{d}{dt}\big (\eta (i,t)\theta (i,t)\big )+C\Big (\eta _t^2(i,t)+\eta _t^2(i,t)\Big ). \end{aligned}$$

For second subterm of the fourth term on the right hand side, we note that for $i=0,\,1$

$$\begin{aligned}&\frac{2}{9c_i}\Big (w^3(i,t)-w_h^3(i,t)\Big )\theta _t(i,t)\\&\quad =-\frac{1}{18c_i}\frac{d}{dt}\theta ^4(i,t)-\frac{1}{3c_i}\frac{d}{dt}\Big (w_h^2(i,t)\theta ^2(i,t)\Big )+\frac{2}{9c_i}\eta ^3(i,t)\theta _t(i,t)\\&\qquad +\frac{2}{3c_i}\Big (w^2(i,t)\eta (i,t)-w(i,t)\eta ^2(i,t)+w_h(i,t)\theta ^2(i,t)\Big )\theta _t(i,t)\\&\qquad +\frac{2}{3c_i}w_h(i,t)w_{ht}(i,t)\theta ^2(i,t). \end{aligned}$$

Using Lemma 2.2, it follows that for $i=0,\,1$

$$\begin{aligned}&\frac{2}{9c_i}\eta ^3(i,t)\theta _t(i,t)-\frac{2}{9c_i}\frac{d}{dt}\big (\eta ^3(i,t)\theta (i,t)\big )\le C\eta ^2(i,t)\theta ^2(i,t)+C\eta ^2(i,t)\eta _t^2(i,t),\\&\frac{2}{3c_i}w^2(i,t)\eta (i,t)\theta _t(i,t)-\frac{2}{3c_i}\frac{d}{dt}\Big (w^2(i,t)\eta (i,t)\theta (i,t)\Big )\\&\quad \le C\Big (\theta ^2(i,t)+\eta ^2(i,t)+\eta _t^2(i,t)\Big ), \end{aligned}$$

and

$$\begin{aligned}&-\frac{2}{3c_i}w(i,t)\eta ^2(i,t)\theta _t(i,t)+\frac{2}{3c_i}\frac{d}{dt}\Big (w(i,t)\eta ^2(i,t)\theta (i,t)\Big )\\&\quad \le C\Big (\theta ^2(i,t)+\eta ^2(i,t)+\eta _t^2(i,t)\Big ). \end{aligned}$$

Also, we obtain for $i=0,\,1$

$$\begin{aligned} \frac{2}{9c_i}3w_h(i,t)\theta ^2(i,t)\theta _t(i,t)\le \frac{2}{9c_i}\frac{d}{dt}\big (w_h(i,t)\theta ^3(i,t)\big )+ C\big (w_{ht}^2(i,t)\theta ^2(i,t)+\theta ^4(i,t)\big ). \end{aligned}$$

We note that for $i=0,\,1$

$$\begin{aligned} \frac{2}{3c_i}w_h(i,t)&w_{ht}(i,t)\theta ^2(i,t) \le C\Big (w_h^2(i,t)+w_{ht}^2(i,t)\Big )\theta ^2(i,t)\Big ). \end{aligned}$$

The first subterm of the fifth term $I_5(\theta _t)$ on the right hand side is bounded by

$$\begin{aligned}&\frac{\mu }{\nu }(1+c_0+w_d)\eta _t(0,t)\theta _t(0,t)+\frac{\mu }{\nu }(1+c_1+w_d)\eta _t(1,t)\theta _t(1,t)\\&\quad \le \frac{\mu }{\nu }\Big (\frac{c_0}{10}+\frac{1}{2}(1+w_d)\Big )\theta _t^2(0,t) +\frac{\mu }{\nu }\Big (\frac{c_1}{10}+\frac{1}{2}(1+w_d)\Big )\theta _t^2(1,t)\\&\qquad +\frac{\mu }{\nu }C\Big (\eta _t^2(0,t)+\eta _t^2(1,t)\Big ), \end{aligned}$$

For the second subterm of the fifth term $I_5(\theta _t),$ we note that for $i=0,\,1$

$$\begin{aligned} \frac{2}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\eta ^3(i,t)\theta _t(i,t)\le & {} \frac{\mu }{\nu }\frac{c_i}{10}\theta ^2_t(i,t)+C\frac{\mu }{\nu }\eta ^4(i,t)\eta _t^2(i,t),\\ -\frac{\mu }{\nu }\frac{2}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\theta ^3(i, t)\theta _t(i,t)= & {} -\frac{\mu }{\nu }\frac{2}{3c_i}\theta ^2(i,t)\theta _t^2(i,t). \end{aligned}$$

Using Lemmas 2.2 and 3.5, it follows that for $i=0,\,1$

$$\begin{aligned}&\frac{2}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (w^2(i,t)\eta (i,t)-w(i,t)\eta ^2(i,t)\Big )\theta _t(i,t)\\&\quad \le \frac{\mu }{\nu }\frac{c_i}{10}\theta _t^2(i,t)+C\frac{\mu }{\nu }\Big (\eta ^2(i,t)+\eta _t^2(i,t)\Big ). \end{aligned}$$

Also, it is valid using Young’s inequality that for $i=0,\,1$

$$\begin{aligned} \frac{2}{9c_i}\frac{\mu }{\nu }\frac{d}{dt}\Big (3w_h(i,t)\theta ^2(i,t)\Big )\theta _t(i,t)&\le \frac{\mu }{\nu }\frac{c_i}{10}\theta _t^2(i,t)\\&\quad +\frac{2\mu }{3\nu c_i}\Big (w_h^2(i,t)\theta _t^2(i,t)+\theta ^2(i,t)\theta _t^2(i,t)\Big )\\&\quad +C\frac{\mu }{\nu }w_{ht}^2(i,t)\theta ^4(i,t),\\ -\frac{\mu }{\nu }\frac{2}{3c_i}\frac{d}{dt}\Big (w_h^2(i,t)\theta (i,t)\Big )\theta _t(i,t)&=-\frac{2\mu }{3\nu c_i}w_h^2(i,t)\theta _t^2(i,t)\\&\quad -\frac{4\mu }{3\nu c_i}w_h(i,t)w_{ht}(i,t)\theta (i,t)\theta _t(i,t). \end{aligned}$$

Applying Lemma 3.2, it follows that for $i=0,\,1$

$$\begin{aligned} -\frac{4\mu }{3\nu c_i}&w_h(i,t)w_{ht}(i,t)\theta (i,t)\theta _t(i,t) \le \frac{\mu }{\nu }\frac{c_i}{10}\theta _t^2(i,t)+C\frac{\mu }{\nu }w_{ht}^2(i,t)\theta ^2(i,t). \end{aligned}$$

Hence, from (3.16), we obtain using Lemmas 2.4 and 3.5

$$\begin{aligned}&\big (\left\| \theta _t(t)\right\| ^2+\mu \left\| \theta _{xt}(t)\right\| ^2\big )+\frac{d}{dt}\Big (\nu \left\| \theta _x(t)\right\| ^2+E_2(\theta )(t)+\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)\Big )\\&\qquad +\frac{\mu }{\nu }\Big (\sum _{i=0}^{1}(1+c_i+w_d)\theta _t^2(i,t)\Big )\\&\quad \le C\Big (\left\| \eta (t)\right\| ^2+(1+\mu )\left\| \eta _t(t)\right\| ^2\Big )+C(1+\mu )\Big (\left\| \theta _x(t)\right\| ^2+\sum _{i=0}^{1}\big (\eta ^2(i,t)+\eta _t^2(i,t)\\&\qquad +w_{ht}^2(i,t)\theta ^2(i,t)\big )\Big )+C\left\| \theta (t)\right\| ^2\left\| \Delta _hw_h(t)\right\| ^2+C(1+\mu )\big (\sum _{i=0}^{1}\theta ^4(i,t)\big )\\&\qquad -2(1+w_d)\frac{d}{dt}(\eta ,\theta _x)+2(1+w_d)\frac{d}{dt}\Big (\sum _{i=0}^{1}(-1)^{i+1}\eta (i,t)\theta (i,t)\Big )\\&\qquad -2\frac{d}{dt}\big ((w\eta ),\theta _x\big )+2\frac{d}{dt}\Big (\sum _{i=0}^{1}(-1)^{i+1}w(i,t)\eta (i,t)\theta (i,t)\Big ) \\&\qquad +2\sum _{i=0}^{1}(1+c_i+w_d)\frac{d}{dt}\big (\eta (i,t)\theta (i,t)\big )+\frac{d}{dt}\Big (\sum _{i=0}^{1}E_5(i,t)\Big ), \end{aligned}$$

where

$$\begin{aligned} E_5(i,t)=&\frac{4}{9c_i}\Big (\big (\eta ^3(0,t)+w^2(0,t)\eta (0,t)-w(0,t)\eta ^2(0,t)\\&+w_h(0,t)\theta ^2(0,t)\big )\theta (0,t)\Big )\quad i=0,1. \end{aligned}$$

Multiply the above inequality by $e^{2\alpha t}$ and use Lemmas 2.2–2.3, 3.2 and 3.5 with bounds of nonlinear boundary terms as in Lemma 3.6 to arrive at

$$\begin{aligned}&e^{2\alpha t}\big (\left\| \theta _t(t)\right\| ^2+\mu \left\| \theta _{xt}(t)\right\| ^2\big )+\frac{d}{dt}\Bigg (e^{2\alpha t}\Big (\nu \left\| \theta _x(t)\right\| ^2+E_2(\theta )(t)\\&\qquad +\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)\Big )\Bigg )\\&\qquad +\frac{\mu }{\nu }e^{2\alpha t}\Big (\sum _{i=0}^{1}(1+c_i+w_d)\theta _t^2(i,t)\Big )\\&\quad \le Ch^4e^{2\alpha t}(1+\mu )\Big (\big (\left\| w(t)\right\| ^2_2+\left\| w_t\right\| ^2_2\big )\Big )+C(1+\mu )e^{2\alpha t}\Big (\left\| \theta _x(t)\right\| ^2\\&\qquad +\sum _{i=0}^{1}\big (w_{ht}^2(i,t)\theta ^2(i,t)\\&\qquad +\theta ^4(i,t)\big )\Big )+2c_0\frac{d}{dt}\Big (e^{2\alpha t}\eta (0,t)\theta (0,t)\Big )+2(2+c_1+2w_d)\frac{d}{dt}\Big (e^{2\alpha t}\eta (1,t)\theta (1,t)\Big )\\&\qquad -2\frac{d}{dt}\Big (e^{2\alpha t}\big ((w+1+w_d)\eta ,\theta _x\big )\Big )+2\frac{d}{dt}\Big (e^{2\alpha t}\big (\sum _{i=0}^{1}(-1)^{i+1}w(i,t)\eta (i,t)\theta (i,t)\big )\Big )\\&\qquad +Ce^{2\alpha t}\left\| \theta (t)\right\| ^2\left\| \Delta _h w_h(t)\right\| ^2+\frac{d}{dt}\Big (e^{2\alpha t}\big (E_5(0,t)+E_5(1,t)\big )\Big ). \end{aligned}$$

Integrate from 0 to t and then multiply the resulting inequality by $e^{-2\alpha t}$ to obtain

$$\begin{aligned}&\Big (\nu \left\| \theta _x(t)\right\| ^2+E_2(\theta )(t)+\sum _{i=0}^{1}\frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)\Big )\nonumber \\&\qquad +e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| \theta _t(t)\right\| ^2+\mu \left\| \theta _{xt}(t)\right\| ^2\Big )\; ds\nonumber \\&\qquad +\frac{\mu }{\nu }e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\sum _{i=0}^{1}(1+c_i+w_d)\theta _t^2(i,s)\Big )\; ds \nonumber \\&\quad \le C(1+\mu )h^4e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\big (\left\| w(t)\right\| ^2_2+\left\| w_t(t)\right\| ^2_2\big )\Big )\; ds\nonumber \\&\qquad +Ce^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\| \theta (t)\right\| ^2\left\| \Delta _hw_h(t)\right\| ^2 ds+C(1+\mu ) e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| \theta _x(t)\right\| ^2\nonumber \\&\qquad +w_{ht}^2(0,s)\theta ^2(0,s)+w_{ht}^2(1,s)\theta ^2(1,s)+\theta ^4(0,s)+\theta ^4(1,s)\Big ) ds\nonumber \\&\qquad +\Big (\big ((2c_0-2w(0,t))\big )\eta (0,t)\theta (0,t)+\big ((4+2c_1+4w_d+2w(1,t))\big )\nonumber \nonumber \\&\qquad \eta (1,t)\theta (1,t)\Big )-2\Big ((w+1+w_d)\eta ,\theta _x\Big )+E_5(0,t)+E_5(1,t). \end{aligned}$$

(3.17)

A use of the Young’s inequality with Lemma 2.2 shows

$$\begin{aligned} -2\Big ((w+1+w_d)\eta ,\theta _x\Big )\le \frac{\nu }{2}\left\| \theta _x(t)\right\| ^2+C\left\| \eta (t)\right\| ^2. \end{aligned}$$

Again using the Young’s inequality and Lemma 2.2, we arrive at

$$\begin{aligned}&\Big ((2c_0-2w(0,t))\eta (0,t)\theta (0,t)+(4+2c_1+4w_d+2w(1,t))\eta (1,t)\theta (1,t)\Big )\\&\quad \le \frac{c_0}{4}\theta ^2(0,t)+\frac{(c_1+2(1+w_d))}{4}\theta ^2(1,t) +C\big (\eta ^2(0,t)+\eta ^2(1,t)\big ). \end{aligned}$$

Bounding in a similar fashion as in Lemma 3.6, we obtain a bound for the nonlinear boundary terms as follows

$$\begin{aligned} E_5(i,t)\le \frac{2}{3c_i}w_h^2(i,t)\theta ^2(i,t)+\frac{1}{9c_i}\frac{5}{6}\theta ^4(i,t)+\frac{c_i}{4}\theta ^2(i,t)+C\eta ^2(i,t)\quad i=0,1. \end{aligned}$$

Finally, apply Grönwall’s inequality to (3.17) to arrive using Lemmas 2.2, 2.4, 3.1–3.3 and 3.6 at

$$\begin{aligned}&\nu \left\| \theta _x(t)\right\| ^2+\sum _{i=0}^{1}\Big ((c_i+1+w_d)\theta ^2(i,t)+\frac{1}{27c_i}\theta ^4(i,t)\\&\qquad +2e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\| \theta _t(t)\right\| ^2+\mu \left\| \theta _{xt}(t)\right\| ^2\Big )\; ds\\&\qquad +\frac{\mu }{\nu }e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\sum _{i=0}^{1}(1+c_i+w_d)\theta _t^2(i,s)\Big )\; ds\\&\quad \le C\frac{1}{\mu }(\left\| w_0\right\| _2)(1+\mu )h^4e^{-2\alpha t}\exp \big (C(\left\| w_0\right\| _2)\big ). \end{aligned}$$

This completes the proof. $\square$

Remark 3.2

As a consequence of Lemma 3.7, we obtain superconvergence result for $\left| \! \left| \! \left| \theta (t) \right| \! \right| \! \right|$ which depends on $\frac{1}{\sqrt{\mu }}$. However, for proving optimal estimate, only one modification may be made to compute $\int _{0}^{t}\left\| \eta _t(t)\right\| ^2\;ds\le Ch^2\int _{0}^{t}\left\| w_{xt}(t)\right\| ^2 \;ds$. Hence, we obtain

$$\begin{aligned} \left| \! \left| \! \left| \theta (t) \right| \! \right| \! \right| =O(h), \end{aligned}$$

(3.18)

which does not depend on $\frac{1}{\sqrt{\mu }}$. Now using triangle inequality with Lemmas 3.6 and 3.7 and (3.18), we obtain the following result.

Theorem 3.1

Let assumptions $\mathbf{(A1)}$ and $\mathbf{(A2)}$ be satisfied. Then, the following error estimates hold for both state and control variables and for $t>0$

$$\begin{aligned} \left\| (w-w_h)(t)\right\| ^2_r= O\Big (\frac{1}{\sqrt{\mu }}h^{2-2r}e^{-\alpha t}\Big ), \end{aligned}$$

(3.19)

where $r=0,1$ and

$$\begin{aligned} \left| \! \left| \! \left| (w-w_h)(t) \right| \! \right| \! \right| =O\Big (he^{-\alpha t}\Big ). \end{aligned}$$

Proof

The proof follows from Lemmas 2.4, 3.6 and 3.7 with a use of triangle inequality and (3.9). $\square$

Theorem 3.2

For $w_0(\cdot )\in H^2(0,1),$ there exists a constant $C>0$ such that for $t>0$

$$\begin{aligned} \left\| (w-w_h)(t)\right\| _{L^\infty }= O\Big (\frac{h^2}{\sqrt{\mu }}e^{-\alpha t}\Big ) \end{aligned}$$

(3.20)

and

$$\begin{aligned} |v_i(t)-v_{ih}(t)|&:=|K_i(w(i,t))-K_i(w_h(i,t))|= O\Big (\frac{h^2}{\sqrt{\mu }}e^{-\alpha t}\Big ), \end{aligned}$$

(3.21)

where $i=0,$ 1.

Proof

From Lemma 3.7, we obtain a superconvergence result for $\left| \! \left| \! \left| \theta (t) \right| \! \right| \! \right|$. Using the Poincaré–Wirtinger’s inequality, it follows that

$$\begin{aligned} \left\| \theta (t)\right\| _{{L^\infty }(I)}\le C\left| \! \left| \! \left| \theta (t) \right| \! \right| \! \right| . \end{aligned}$$

Now a use of triangle inequality with estimates of $\left\| \eta (t)\right\| _{L^\infty }$ and$\left\| \theta (t)\right\| _{L^\infty },$ we arrive at the estimate (3.20). To find (3.21), we note that the error in the control law is given by

$$\begin{aligned} |v_0(t)-v_{0h}(t)|&:=|K_0(w(0,t))-K_0(w_h(0,t))|\\&=|\frac{1}{\nu }\Big ((1+c_0+w_d)(\eta (0,t)-\theta (0,t))+\frac{2}{9c_0}(w^3(0,t)-{{\tilde{w}}}_h^3(0,t))\\&\quad -\frac{2}{9c_0}(w_h^3(0,t)-{{\tilde{w}}}_h^3(0,t))\Big )|\\&\le C\big (|\eta (0,t)|+|\theta (0,t)|\big )+\frac{C}{c_0}|\eta (0,t)|(w^2(0,t)+\eta ^2(0,t))\\&\quad +\frac{C}{c_0}|\theta (0,t)|(w_h^2(0,t)+\eta ^2(0,t))\\&\le C\frac{h^2}{\sqrt{\mu }}\left\| w\right\| _2\big (1+w^2(0,t)+\left\| w\right\| ^2_2\big )+C|\theta (0,t)|(1+w_h^2(0,t)+\left\| w\right\| ^2_2)\\&\le C\frac{h^2}{\sqrt{\mu }}e^{-\alpha t}\exp \big (C\left\| w_0\right\| _2\big ). \end{aligned}$$

Similarly, it follows that

$$\begin{aligned} |v_1(t)-v_{1h}(t)|&:=|K_1(w(1,t))-K_1(w_h(1,t))|\\&\quad \le C\frac{h^2}{\sqrt{\mu }}e^{-\alpha t}\exp \big (C\left\| w_0\right\| _2\big ). \end{aligned}$$

This completes the proof. $\square$

4 Numerical Experiments

In this section, we discuss the fully discrete finite element formulation of (1.9) using backward Euler method with Neumann boundary control laws. Here, the time variable is discretized by replacing the time derivative by difference quotient. Let $W^n$ be the approximation of w(t) in $V_h$ at $t=t_n=nk,$ where $0<k<1$ denote the time step size and $t_n=nk,$ and n is nonnegative integer. For smooth function $\phi$ defined on $[0,\infty ),$ set $\phi ^n=\phi (t_n)$ and ${\bar{\partial }}_t\phi ^n=\frac{(\phi ^n-\phi ^{n-1})}{k}$.

Using backward Euler method, the fully discrete scheme corresponding $\{{W^n}\}_{n\ge 1}\in V_h$ is a solution of

$$\begin{aligned}&({\bar{\partial }}_tW^n,\varphi _h)+\mu ({\bar{\partial }}_tW^n_x,\varphi _{hx})+\nu (W^n_x,\varphi _{hx})+(1+w_d)(W^n_x,\varphi _h)\nonumber \\&\qquad +(W^nW^n_x,\varphi _h)+\Big ((c_0+w_d)W^n(0)\nonumber \\&\qquad +\frac{2}{9c_0}(W^n(0))^3\Big )\varphi _h(0)+\Big ((c_1+w_d)W^n(1)+\frac{2}{9c_1}(W^n(1))^3\Big )\varphi _h(1)\nonumber \\&\qquad +\frac{\mu }{\nu }\Bigg (\Big ((c_0+w_d){\bar{\partial }}_tW^n(0)\varphi _h(0)+\frac{2}{9c_0}{\bar{\partial }}_t\big (W^n(0)\big )^3\varphi _h(0)\Big )+\Big ((c_1+w_d){\bar{\partial }}_tW^n(1)\nonumber \\&\quad \qquad +\frac{2}{9c_1}{\bar{\partial }}_t\big (W^n(1)\big )^3\Big )\varphi _h(1)\Bigg )=0 \quad \forall \varphi _h \in V_h \end{aligned}$$

(4.1)

with $W^0=w_{0h}.$ At each time level $t_n$, the nonlinear algebraic system (4.1) is solved by Newton’s method with initial guess $W^{n-1}$. For implicit scheme (4.1) in our case, CFL condition is not needed. We take time step $k=0.0001$ and mesh size $h=1/60$.

Example 4.1

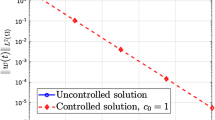
Here, we have taken the initial guess (exact solution at $t=0$) $w_0=20(0.5-x)^3-3,$ where $w_d=3$ is a constant steady solution for the original problem. We do not know the exact solution w(t). Choose $t=[0,3.5]$. We consider zero Neumann boundary condition, which is without control and mark it as uncontrolled solution. Then to check whether constant steady state solution $w_d=3$ is asymptotically stable, we take nonlinear Neumann boundary feedback controllers which are given in (1.10)–(1.11) for different values of $c_0$ and $c_1$ with $\mu =0.5$ and $\nu =0.5$.

From the line denoted as ‘Uncontrolled solution’ in Fig. 1, we can clearly observe that $W^n$ does not go to zero, that is, constant steady state solution $w_d=3$ is not asymptotically stable with zero Neumann boundaries. We now observe that for various combination of $c_0$ and $c_1$, the discrete solution goes to zero exponentially, see Fig. 1. Moreover from Fig. 1, we can see that the optimal decay rate $\alpha$ (with $w_d=3$), $0<\alpha \le \frac{1}{2}\min \Big \{\frac{\nu }{\mu +1}, \frac{\nu }{2\mu +\nu }, \frac{\nu (4+c_i)}{\nu +(4+c_i)\mu } (i=0,1)\Big \}$ happens when $c_0=1=c_1$, which verify our theoretical result in Lemma 2.1. When $c_i(i=0,1)<1$, then decay rate for the state is slow compare to the case when $c_i(i=0,1)\ge 1$.

Fig. 1

Both uncontrolled and controlled solution

Fig. 2

Order of convergence plot in $L^2$ norm for state w

Fig. 3

Order of convergence plot in $L^\infty$ norm for state w

Fig. 4

Convergence plot for feedback control error at $x=0$

Fig. 5

Convergence plot for feedback control error at $x=1$

Fig. 6

Control plot at $x=0$

Fig. 7

Control plot at $x=1$

Now, we present order of convergence for the error in state variable w(t) in $L^2$ and $L^\infty$ norms ($\left\| w(t_n)-W^N\right\| _{L^2}$ and $\left\| w(t_n)-W^N\right\| _{L^\infty }$ respectively) and also for the feedback controllers $v_0(t)$ and $v_1(t)$ ($|{v_0(t_n)-v_{0h}(t_n)}|$ and $|{v_1(t_n)-v_{1h}(t_n)}|$ ) in $L^\infty$ norm at $t=1$. Exact solution is obtained through refined mesh solution.

For Figures 2, 3, 4 and 5, in each plot we have also added reference curve for theoretical convergence rate to compare with the numerical rate of convergence. Figures 2 and 3 indicate the error plot for the state variable w in $L^2$ and $L^\infty$ norms respectively, for various values of $c_0$ and $c_1$. We can easily observe from Figure 2 that the convergence rate in the $L^2$- norm for error in state variable is of order 2 as predicted by Theorem 3.1. From Figure 3, it is also noticeable that the order of convergence for error in state variable in $L^\infty$ norm is 2 as expected from Theorem 3.2.

For error in feedback controllers at $x=0$ and $x=1,$ it is observed from Figures 4 and 5 that for various values of $c_0$ and $c_1,$ the order of convergence is 2 which confirms the result in Theorem 3.2. In Figures 6 and 7, we present the behavior of the feedback controllers at $x=0$ and $x=1$ with respect to time for various positive values of $c_0$ and $c_1$. Absolute value of the feedback controllers go to zero as time increases. So for $c_i(i=0,1)<1$ in the feedback control law, it will take more time for the control and state to settle down to zero (See Figs. 1, 6,  7).

The next example consists of different type feedback control which is stated below. In the following example, we consider the solution of (1.9) with one part zero Dirichlet boundary and another part different Neumann conditions.

Example 4.2

In this example, we consider the solution of (1.9) with different boundary conditions. Take initial condition as $w_0=15\sin (\pi x)-5$, where 5 is the steady state solution. We choose time $t=[0,10]$ and the time step $k=0.0001$ and $\mu =0.1$ and $\nu =0.1$.

For the uncontrolled solution, we take $w(0,t)=0$ and $w_x(1,t)=0$. The uncontrolled solution is denoted by ‘Uncontrolled solution’ in Figure 8.

For the controlled solution we consider $w(0,t)=0$ and $w_x(1,t)=v_1(t)=-\frac{1}{\nu }\Big ((c_1+1+w_d)w(1,t)+\frac{2}{9c_1}w^3(1,t)\Big )$ with $c_1=0.1, 1 \hbox { and } 10$. Denote the controlled solutions by ‘Controlled solution $c_1=1$’, ‘Controlled solution with $c_1=10$’, and ‘Controlled solution with $c_1=0.1$’ in Fig. 8.

Fig. 8

Controlled and Uncontrolled solution plot in $L^2$ norm

First draw line in Fig. 8 shows that solution with zero boundary conditions ($w(0,t)=0$ and $w_x(1,t)=0$) oscillate. But using above mentioned type of control with different values of $c_1$, solution goes to zero. With the initial condition of Example 4.2, decay of the state w in $L^2$- norm varying $\mu$ with fixed $\nu =0.1$, $c_0=1=c_1$ is shown in Fig. 9. We observe that as $\mu$ decreases, $L^2$- norm of the state w for BBM–B equation converges to the $L^2$- norm of the state w with $\mu =0$ that is to the $L^2$- norm of the state of Burgers’ equation.

Fig. 9

Decay of state w in $L^2$ norm as $\mu \rightarrow 0$

5 Conclusion

In this article, under the assumption of the existence of solution, we show stabilization estimate in higher order norms which is crucial to obtain optimal error estimates in the context of $C^0$- conforming finite element analysis. Optimal error estimates for the state variable w in $L^\infty (L^2)$, $L^\infty (H^1)$ and $L^\infty (L^\infty )$ norms are established. Furthermore, superconvergence results for error in feedback controllers are also proved. Following points which are itemized below will be addressed in a separate paper.

• When the coefficient of viscosity is unknown (in the case of adaptive control), we believe that the control law as in Smaoui [24] will also work for BBM–B equation. Also when $\nu =0$, it is interesting to extend the analysis modifying the control law appropriately.

• In addition, for the fully discrete scheme (4.1), it is interesting to know the large time behavior of the solution and how the corresponding time step size k behaves in error estimates for fully discrete solution in addition to the space step size h.

Appendix

Regarding the proof of assumption (A2) on existence and uniqueness of solution w to the problem (1.9) with boundary conditions:

$$\begin{aligned} w_x(0,t)-\kappa _0 w(0,t)&=\frac{2}{9c_0\nu }w^3(0,t) , \end{aligned}$$

(1)

$$\begin{aligned} w_x(1,t)+\kappa _1 w(1,t)&=-\frac{2}{9c_1\nu }w^3(1,t) , \end{aligned}$$

(2)

where $\kappa _i=\frac{1}{\nu }(c_i+1+w_d)>0$ for $i=0$ and 1, and the initial condition (1.12), we apply Bubnov Galerkin method as follows: Set $A=-\frac{d^2}{dx^2}$ with dense domain D(A) in $L^2(0,1)$, where

$$\begin{aligned} D(A)=\Big \{\phi \in H^2(0,1):\quad \phi _x(0)-\kappa _0\phi (0)=0 \quad \text {and} \quad \phi _x(1)+\kappa _1\phi (1)=0\Big \}. \end{aligned}$$

As $\kappa _0+\kappa _1>0$, A is linear selfadjoint positive definite with a compact inverse, and hence, it has a discrete spectrum with $0<\lambda _1<\lambda _2<\ldots<\lambda _l<\ldots$ and $\underset{l\rightarrow \infty }{\lim }\lambda _l=\infty$. The corresponding eigenvectors $\{\phi _l(x)\}_{l=1}$ forms an orthonormal basis in $L^2(0,1).$ For $s\ge 0$, let ${\mathcal {H}}^s$ consist of vector $\phi \in L^2(0,1)$ such that $\left\| \phi \right\| _{\mathcal {H}^s}=\Big (\sum _{j=1}^{\infty }\lambda _j^s(\phi ,\phi _j)^2\Big )^{1/2}<\infty$. On ${\mathcal {H}}^s$, we define an innerproduct

$$\begin{aligned} (\phi ,\psi )_s=(A^{s/2}\phi ,A^{s/2}\psi ). \end{aligned}$$

(3)

When $s=1$, the norm on ${\mathcal {H}}^1$ can be written as

$$\begin{aligned} \left\| \phi \right\| _1=\Big (\int _{0}^{1}|\phi _x|^2 dx+\kappa _0|\phi (0)|^2+\kappa _1|\phi (1)|^2\Big )^{1/2}. \end{aligned}$$

(4)

Since for $\phi \in {\mathcal {H}}^1$, $\left\| \phi \right\| ^2\le \lambda _1^{-1}\left\| \phi \right\| ^2_1$, where $0<\lambda _1<\pi ^2$ is the first eigenvalue of A. Then, ${\mathcal {H}}^1$-norm is equivalent to the standard $H^1$-norm. Let ${\mathcal {H}}^{-s}$ be denoted by the dual space of ${\mathcal {H}}^s$.

Let $V_m=span\{\phi _1,\ldots ,\phi _m\}\subset {\mathcal {H}}^1(0,1)$. Now seek a Galerkin approximation $w^m$ to w which is of the form $w^m(x,t)=\sum _{j=1}^{m}\alpha _{jm}(t)\phi _j(x)$ satisfying

$$\begin{aligned}&(w^m_t,\phi _k)+\mu (w^m_t,\phi _k)_1+\nu (w^m,\phi _k)_1+(w^mw^m_{x},\phi _k)\nonumber \\&\quad +\sum _{i=0}^{1}\frac{2\mu }{3c_i\nu }({w^m})^2(i,t)w^m_t(i,t)\phi _k(i)\nonumber \\&\quad +\sum _{i=0}^{1}\frac{2}{9c_i}({w^m})^3(i,t)\phi _k(i)=0,\quad k=1,2,\ldots \end{aligned}$$

(5)

with $\alpha _{jm}(0)=(w_0,\phi _j)$, $j=1,2,\ldots ,m$. Since $V_m$ is finite dimensional, (5) gives rise to a system of nonlinear ODEs. Therefore, an application of the Picard’s existence theorem yields a local existence of a unique solution $\alpha _{jm}(t)$ and hence, the existence of a unique $w^m(t)$ for $t\in [0,t_m^*)$ with $t_m^*<T$. In order to prove global existence, we need a priori bound to continue the solution to the whole of [0, T). Multiply (5) by $\alpha _{km}$ and then, sum up to obtain

$$\begin{aligned}&(w^m_t,w^m)+\mu (w^m_t,w^m)_1+\nu (w^m,w^m)_1+(w^mw^m_x,w^m)+\sum _{i=0}^{1}\frac{2\mu }{3c_i\nu }({w^m})^3(i,t)w^m_t(i,t)\nonumber \\&\quad +\sum _{i=0}^{1}\frac{2}{9c_i}({w^m})^4(i,t)=0. \end{aligned}$$

(6)

As in Lemmas 2.1, 2.3 and 2.4, we can easily obtain with $\alpha =0$ that the sequences $\{w^m\}$, $\{w^m_x\}$, $\{w^m_t\}$ are bounded uniformly in $L^\infty (0,T;L^2)$. Moreover, the sequences $\{\mu w^m\}$, $\{w^m\}$ are also uniformly bounded in $L^\infty (0,T;\mathcal {H}^1)$ and $\{E_1(w^m)\}$, $\{E_2(w^m)\}$, $\{\mu E_2(w^m)\}$ are bounded uniformly in $L^\infty (0,1)$. Finally, to obtain uniform boundedness of $\{w_{xx}^m\}$, we modify the proof in the Lemma 2.2 with $\alpha =0$ as follows. Multiply (5) by $\lambda _k\alpha _m$ and then, sum over $k=1,\ldots ,m$, we obtain after integration by parts with respect to x

$$\begin{aligned} \sum _{k=1}^{m}(w^m_t,\lambda _k\alpha _{km}\phi _k)&=\sum _{k=1}^{m}(w^m_t,\alpha _{km}A\phi _k) =\frac{1}{2\nu }\frac{d}{dt}\Big (\left\| w^m(t)\right\| ^2_1+\sum _{i=0}^{1}\frac{1}{9c_i}({w^m})^4(i,t)\Big )\\&=\frac{1}{2\nu }\frac{d}{dt}\Big (\left\| w^m_x(t)\right\| ^2+E_2(w^m)(t)\Big ),\\ \mu \sum _{k=1}^{m}(w^m_t,\lambda _k\alpha _{km}\phi _k)_1&=\mu \sum _{k=1}^{m}(w^m_{tx},\lambda _k\alpha _{km}\phi _{kx})\\&\quad +\frac{\mu }{\nu }\sum _{k=1}^{m}\Big (w^m_t(i,t)+\frac{2}{3c_i}({w^m})^2(i,t)w^m_t(i,t)\Big )\lambda _k\alpha _{km}\phi _k\\&=-\mu \sum _{k=1}^{m}(w^m_{txx},\lambda _k\alpha _{km}\phi _k)=\mu \sum _{k=1}^{m}(w^m_{txx},\alpha _{km}\phi _k'')\\&=\mu \sum _{k=1}^{m}(w^m_{txx},w^m_{xx})=\frac{\mu }{2}\frac{d}{dt}\left\| w^m_{txx}\right\| ^2 \end{aligned}$$

and similarly,

$$\begin{aligned} \nu \sum _{k=1}^{m}(w^m,\lambda _k\alpha _{km}\phi _k)_1=\frac{\nu }{2}\frac{d}{dt}\left\| w^m_{xx}\right\| ^2. \end{aligned}$$

Further, use rest of the analysis in the proof of Lemma 2.2 to derive that the sequences $\{w^m_x\}$, $\{\mu w^m_{xx}\}$ are uniformly bounded in $L^\infty (0,T;L^2)$ and $\{E_2(w^m)(t)\}$ is uniformly bounded in $L^\infty (0,T;L^2)$. Then, using weak * compactness argument, there exists subsequence, say, $\{w^{m_n}\}$ of $\{w^m\}$ such that for $w^l\subset V_l\subset V_m$ with $l<m$ and as $m_n\rightarrow \infty$.

$$\begin{aligned}&(w_t^{m_n},w^l)\quad \text {converges to} \quad (w_t,w^l) \quad \text {weak * in} \quad L^\infty (0,T), \\&\mu (w_t^{m_n},w^l)_1 \quad \text {converges to} \quad (w_t,w^l)_1\quad \text {weak * in} \quad L^\infty (0,T), \\&\nu (w^{m_n},w^l)_1\quad \text {converges to}\quad \nu (w,w^l)_1\quad \text {weak * in} \quad L^\infty (0,T). \end{aligned}$$

Since ${\mathcal {H}}^1$ is compactly embedded in $L^2$, there is a subsequence, say again $\{w^{m_n}\}$ such that $\{w^{m_n}\}\rightarrow w$ strongly in $L^2(0,1)$ a.e. $t\in (0,T)$. Thus

$$\begin{aligned} (w^{m_n}w^{m_n}_x,w^l)\rightarrow \quad (ww_x,w^l)\quad \text {weak * in}\quad L^\infty (0,T). \end{aligned}$$

In a similar spirit,

$$\begin{aligned} \frac{2\mu }{3\nu }\sum _{i=0}^{1}\frac{1}{c_i}({w^{m_n}})^2(i,t)w^{m_n}_t(i,t) \quad \text {converges weak * in } \quad L^\infty (0,T), \end{aligned}$$

and

$$\begin{aligned} \frac{2}{9}\sum _{i=0}^{1}\frac{1}{c_i}({w^{m_n}})^3(i,t)w^{l}(i,t)\quad \text {converges weak * in } \quad L^\infty (0,T). \end{aligned}$$

Therefore, as $m_n\rightarrow \infty$ we obtain

$$\begin{aligned}&(w_t,w^l)+\mu (w_t,w^l)_1+\nu (w,w^l)_1+(ww_x,w^l)\\&\quad +\sum _{i=0}^{1}\Big (\frac{2\mu }{3\nu c_i}w^2(i,t)w_t(i,t)+\frac{2}{9c_i}w^3(i,t)\Big )w^l(i)=0, \end{aligned}$$

for all l. Since the set of finite linear combinations of $w^l$ is dense in ${\mathcal {H}}^1$, we arrive for any $v\in {\mathcal {H}}^1$ at

$$\begin{aligned}&(w_t,v)+\mu (w_t,v)_1+\nu (w,v)_1+(ww_x,v)\nonumber \\&\quad +\sum _{i=0}^{1}\Big (\frac{2\mu }{3\nu c_i}w^2(i,t)w_t(i,t)+\frac{2}{9c_i}w^3(i,t)\Big )v(i)=0 \end{aligned}$$

(7)

To verify that w satisfies the initial data, let us observe that as $\{w^{m_n}\}$, $\{w^{m_n}_t\}$ converging to w, $w_t$, respectively weak * in $L^\infty (0,T;L^2)$, then

$$\begin{aligned}&\int _{0}^{T}(w^{m_n},v)\; dt\rightarrow \int _{0}^{T}(w,v)\; dt \quad \forall v\in L^1(0,T;L^2) \end{aligned}$$

(8)

$$\begin{aligned}&\int _{0}^{T}(w^{m_n}_t,v)\; dt\rightarrow \int _{0}^{T}(w_t,v)\; dt \quad \forall v\in L^1(0,T;L^2) \end{aligned}$$

(9)

Let $\phi \in C^1(0,T)$ with $\phi (T)=0$ and $\phi (0)=1$. Now, choose $v=\phi 'z$ in (8) and $v=\phi z$ in (9). Then, sum both to obtain $\underset{m_n\rightarrow \infty }{\lim }( w^{m_n}(0),z)=(w(0),z) \quad \forall z\in L^2$. Therefore $w(0)=w_0.$ The part of the uniqueness follows from Lemma 2.6.

For the proof of Lemma 2.5 with $\alpha =0$, we now multiply (5) by $\lambda _k\alpha '_{km}$ and sum over $k=1,\ldots ,m$. We derive in similar way the estimate (2.17) and then, the rest of the estimates follows as in the proof of Lemma 2.5 with $\alpha =0.$ Thus, we obtain the uniform boundedness of the sequence $\{w^m_{xx}\}$ and then, passing to the limit, we derive the regularity result (1.17).