Global Stabilization of Two Dimensional Viscous Burgers’ Equation by Nonlinear Neumann Boundary Feedback Control and Its Finite Element Analysis

Abstract

In this article, global stabilization results for the two dimensional viscous Burgers’ equation, that is, convergence of unsteady solution to its constant steady state solution with any initial data, are established using a nonlinear Neumann boundary feedback control law. Then, applying $C^0$-conforming finite element method in spatial direction, optimal error estimates in $L^\infty (L^2)$ and in $L^\infty (H^1)$-norms for the state variable and convergence result for the boundary feedback control law are derived. All the results preserve exponential stabilization property. Finally, several numerical experiments are conducted to confirm our theoretical findings.

1 Introduction

We consider the following Neumann boundary control problem for the two-dimensional viscous Burgers’ or Bateman–Burgers equation: seek $u=u(x,t),$$t>0$ which satisfies

$$\begin{aligned}&u_t-\nu \Delta u+u(\nabla u\cdot \mathbf{{1}})=0\qquad \text {in}\quad (x,t)\in \Omega \times (0,\infty ), \end{aligned}$$

(1.1)

$$\begin{aligned}&\frac{\partial u}{\partial n}(x,t)=v_2(x,t)\qquad \text {on} \quad (x,t)\in \partial \Omega \times (0,\infty ), \end{aligned}$$

(1.2)

$$\begin{aligned}&u(x,0)=u_0(x)\qquad \text {in}\quad x\in \Omega , \end{aligned}$$

(1.3)

where $\Omega \subset {\mathbb {R}}^2$ is a bounded domain with smooth boundary $\partial \Omega ,$$\nu >0$ is the diffusion constant with the diffusion term $\nu \Delta u$, $v_2$ is scalar control input, $\mathbf{{1}}=(1,1),$$u(\nabla u\cdot \mathbf{{1}})=u\sum _{i=1}^{2}u_{x_i}$ is the nonlinear convection term and $u_0$ is a given function. Application of (1.1) in the area of fluid mechanics is significant to study turbulence behavior, where u is denoted as flow speed of fluid media, $\nu >0$ is the viscosity parameter which is analogous to the inverse of Reynolds number in the Navier Stokes system. The rate of flow or flux through the boundary is $v_2$ which is our control. When $\nu$ tends to zero in (1.1), it models nonlinear wave propagation.

In literature, several local stabilization results for one dimensional Burgers’ equation are available, say for example, see, [5, 6] for distributed and Dirichlet boundary control, and [7] for Neumann boundary control under sufficiently smallness assumption on the initial data. We refer to [16, 17] and [23] for further references on local stabilization results including results on existence and uniqueness. Related to instantaneous control of 1D Burgers’ equation, we refer to [15].

Local stabilization result for 2D viscous Burgers’ equation is available in [29] where a nonlinear feedback control law is applied which is obtained through solving Hamilton–Jacobi–Bellman (HJB) equation and using Riccati based optimal feedback control. For instance, authors first formulate the two dimensional Burgers’ equation in abstract form as

$$\begin{aligned} w_t=Aw+F(w)+Bv, \quad w(0)=w_0, \end{aligned}$$

where A, with domain D(A), is the infinitesimal generator of an analytic semigroup on a Hilbert space W, F(w) is the nonlinear term, B is the operator from a control space V into W. With corresponding cost functional of the form

$$\begin{aligned} J(w_v,v)<\infty \quad \text {where}\quad J(w_v,v)=\frac{1}{2}\int _{0}^{\infty }\Big (\left\Vert w_v\right\Vert ^2_{W}+\left\Vert v\right\Vert ^2_V\Big )\;dt, \end{aligned}$$

the associated linear feedback control law becomes $v=-B^*Pw$, where P is the solution to the algebraic Riccati equation for the linear quadratic regulator (LQR) problem. Through solving HJB equation using Taylor series expansion, one can obtain the nonlinear feedback control law as

$$\begin{aligned} v=-B^*Pw+B^*(A-BB^*P)^{-*}PF(w), \end{aligned}$$

where $(A-BB^*P)^{-*}$ is the inverse of $(A-BB^*P)^{*}$ (see [29] for more details). Later on, Buchot et al. [4] have discussed local stabilization result in the case of partial information for the two dimensional Burgers’ type equation. Subsequently in [25], author has shown local stabilization results for the Navier–Stokes system around a nonconstant steady state solution by constructing a linear feedback control law for the corresponding linearized equation. This, in turn, locally stabilizes the original nonlinear system. All the above mentioned stabilization results are local in nature and are valid under smallness assumption on the data.

Our attempt in this paper is to establish global stabilization result without smallness assumption on the data through the nonlinear Neumann control law using Lyapunov type functional. Such global stabilization results for one dimensional Burgers’ equation was earlier studied in [3, 18] for both Dirichlet and Neumann boundary control laws. When the coefficient of viscosity is unknown, an adaptive control for one dimensional Burgers’ equation is discussed in [22, 26, 27]. Although, effect of these control laws to their state are shown computationally using finite difference method and Chebychev collocation method, but convergence of numerical solution posses some serious difficulty because of the typical nonlinearity present in the system through nonlinear feedback laws. Also in [5, 6], authors have considered finite element method to solve numerically local stabilization problem for 1D Burgers’ equation without any convergence analysis. Subsequently in [19], optimal error estimates in the context of finite element method for the state variable and superconvergence result for the feedback control laws are derived. For related analysis on Benjamin Bona Mahony Burgers’ (BBM-Burgers’) type equations, we refer to [20]. Concerning extensive literature for one dimensional Burgers’ and BBM-Burgers’ problem, see the references in [19, 20].

To the best of our knowledge, there is hardly any result on global stabilization for the two dimensional Burgers’ equation. Further to continue our investigation keeping an eye on the Navier–Stokes system, finite element method is applied to 2D Burgers’ equation, that is, the Eq. (1.1).

The major contributions of this article are summarized as follows:

• With the help of Lyapunov functional, a nonlinear Neumann feedback control law for the problem (1.1)–(1.3) is derived and global stabilization results in $L^\infty (H^i)$$(i=0,1,2)$ norms are established.

• Based on $C^0$-conforming finite element method in spatial direction, optimal error estimates, (optimality with respect to approximation property) for the state variable and for the feedback control law are derived keeping time variable continuous.

• Several numerical examples including an example in which a part of boundary is with Neumann control and other part is with Dirichlet boundary condition are given to illustrate our theoretical findings.

For the rest of the article, denote $H^m(\Omega )=W^{m,2}(\Omega )$ to be the standard Sobolev space with norm $\left\Vert \cdot \right\Vert _m,$ and seminorm $|\cdot |_m$. For $m=0,$ it corresponds to the usual $L^2$ norm and is denoted by $\left\Vert \cdot \right\Vert$. The space $L^p((0,T);X)$$1\le p\le \infty ,$ consists of all strongly measurable functions $v:[0,T] \rightarrow X$ with norm

$$\begin{aligned} \left\Vert v\right\Vert _{L^p((0,T);X)}:=\left( \int _{0}^{T}\left\Vert v(t)\right\Vert ^p_X dt\right) ^\frac{1}{p}<\infty \quad \text {for} \quad 1\le p<\infty , \end{aligned}$$

and

$$\begin{aligned} \left\Vert v\right\Vert _{L^\infty ((0,T);X)}:=\mathop {\hbox {ess sup}}\limits _{0\le t\le T}\left\Vert v(t)\right\Vert _X<\infty . \end{aligned}$$

The rest of the paper is organized as follows. While Sect. 2 is on problem formulation and preliminaries, Sect. 3 focuses on global stabilization results using a nonlinear feedback control law. Section 4 deals with finite element approximation for the semidiscrete system. Further, optimal error estimates are obtained for the state variable and convergence result is derived for the feedback control law. Finally, Sect. 5 concludes with some numerical experiments.

2 Preliminaries and Problem Formulation

This section focuses on some preliminary results to be used in our subsequent sections. Further, it deals with the Neumann control law using Lyapunov functional and with problem formulation for our global stabilizability and finite element analysis on our latter sections.

The following trace embedding result holds for 2D.

Boundary Trace Imbedding Theorem (p. 164, [1]): There exists a bounded linear map

$$\begin{aligned} T: H^1(\Omega )\hookrightarrow L^q(\partial \Omega ) \quad \text {for}\quad 2\le q<\infty \end{aligned}$$

such that

$$\begin{aligned} \left\Vert Ty\right\Vert _{L^q(\partial \Omega )}\le C\left\Vert y\right\Vert _{H^1(\Omega )}, \end{aligned}$$

(2.1)

for each $y\in H^1(\Omega )$, with the constant C depend on q and $\Omega$. Also the following trace result holds

Trace inequality [21]:

$$\begin{aligned} \left\Vert Ty\right\Vert _{H^s(\partial \Omega )}\le C\left\Vert y\right\Vert _{H^{s+\frac{1}{2}}(\Omega )}, \quad s\ne 1,\quad 0<s\le \frac{3}{2}. \end{aligned}$$

(2.2)

Below, we recall the following inequalities for our subsequent use:

Friedrichs’s inequality: For $y\in H^1(\Omega ),$ there holds

$$\begin{aligned} \left\Vert y\right\Vert ^2\le C_F\Big (\left\Vert \nabla y\right\Vert ^2+\left\Vert y\right\Vert ^2_{L^2(\partial \Omega )}\Big ), \end{aligned}$$

(2.3)

where $C_F>0$ is the Friedrichs’s constant.

More precisely, in 2D we have

$$\begin{aligned} \int _{\Omega } y^2dx=\int _{\Omega }y^2\Delta \phi dx, \end{aligned}$$

where $\phi (x)=\frac{1}{4}|x|^2$ so that $\Delta \phi =1$. Now integrate by parts to obtain

$$\begin{aligned} \int _{\Omega } y^2dx&=-2\int _{\Omega } y\nabla y\nabla \phi dx+\frac{1}{2}\int _{\partial \Omega }y^2(x\cdot n)\; d\Gamma \\&=-\int _{\Omega } y\nabla y x dx+\frac{1}{2}\int _{\partial \Omega }y^2(x\cdot n)\; d\Gamma \\&\le \frac{1}{2}\int _{\Omega } y^2 dx+\frac{1}{2}\sup _{x\in \partial \Omega }|x|^2\int _{\Omega } |\nabla y|^2 dx+\frac{1}{2}\sup _{x\in \partial \Omega }|x|\int _{\partial \Omega }y^2\; d\Gamma . \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} \int _{\Omega } y^2dx\le \sup _{x\in \partial \Omega }|x|^2\int _{\Omega } |\nabla y|^2 dx+\sup _{x\in \partial \Omega }|x|\int _{\partial \Omega }y^2\; d\Gamma . \end{aligned}$$

Hence, the Friedrichs’s inequality constant can be taken as $C_F=\max \{\sup _{x\in \partial \Omega }|x|^2,\sup _{x\in \partial \Omega }|x|\}$. Gagliardo–Nirenberg inequality (see [24]): For $w\in H^1(\Omega )$, we have

$$\begin{aligned} \left\Vert w\right\Vert _{L^4}&\le C\Big (\left\Vert w\right\Vert ^{1/2}\left\Vert \nabla w\right\Vert ^{1/2}+\left\Vert w\right\Vert \Big ), \quad \hbox { and for}\ w\in H^2(\Omega ),\quad \text {we have}\\ \left\Vert \nabla w\right\Vert _{L^4}&\le C\Big (\left\Vert w\right\Vert ^{1/4}\left\Vert \Delta w\right\Vert ^{3/4}+\left\Vert w\right\Vert \Big ). \end{aligned}$$

Agmon’s inequality (see [2]): For $z\in H^2(\Omega ),$ there holds

$$\begin{aligned} \left\Vert z\right\Vert _{L^\infty }\le C\Big (\left\Vert z\right\Vert ^\frac{1}{2}\left\Vert \Delta z\right\Vert ^\frac{1}{2}+\left\Vert z\right\Vert \Big ). \end{aligned}$$

Now the corresponding equilibrium or steady state problem of (1.1)–(1.3) becomes: find $u^\infty$ as a solution of

$$\begin{aligned} -\nu \Delta u^\infty +u^\infty (\nabla u^\infty \cdot \mathbf{{1}})&=0 \qquad \text {in} \quad \Omega , \end{aligned}$$

(2.4)

$$\begin{aligned} \frac{\partial u^\infty }{\partial n}&=0 \quad \text {on} \quad \partial \Omega . \end{aligned}$$

(2.5)

Note that any constant $w_d$ satisfies (2.4)–(2.5). Without loss of generality, we assume that $w_d\ge 0$. When $\nu$ is sufficiently small and initial condition $u_0$ is antisymmetric, the numerical solution of (1.1)–(1.3) with $\frac{\partial u}{\partial n}=0$ may converge to a nonconstant steady state solution for which related references are given in [19]. We do not consider such cases here. To achieve

$$\begin{aligned} \lim _{t\rightarrow \infty } u(x,t)=w_d\quad \forall ~ x\in \Omega , \end{aligned}$$

it is enough to consider $\lim _{t\rightarrow \infty }w=0,$ where $w=u-w_d$ and w satisfies

$$\begin{aligned}&w_t-\nu \Delta w+w_d(\nabla w\cdot \mathbf{{1}})+w(\nabla w\cdot \mathbf{{1}})=0 \qquad \text {in}\quad (x,t)\in \Omega \times (0,\infty ), \end{aligned}$$

(2.6)

$$\begin{aligned}&\frac{\partial w}{\partial n}(x,t)=v_2(x,t),\quad \text {on} \quad \partial \Omega \times (0,\infty ), \end{aligned}$$

(2.7)

$$\begin{aligned}&w(0)=u_0-w_d=w_0(\text {say})\quad \text {in}\quad \Omega . \end{aligned}$$

(2.8)

The motivation behind choosing the Neumann boundary control comes from the physical situation. Say for example, in thermal problem, one cannot actuate the temperature w on the boundary, but the heat flux $\frac{\partial w}{\partial n}$. This makes the stabilization problem nontrivial because $w_d$ is not asymptotically stable with zero Neumann boundary data. Concerning Dirichlet boundary control unlike in 1D [18], it is not easy to get a concrete useful form of the control law. Although the control law $v_2$ derived in (2.13), is in invertible form so we can obtain w in terms of $\frac{\partial w}{\partial n}$ on the boundary by solving cubic equation using Cardan’s method, but that form is not useful for the stabilizability analysis.

For our analysis, the following compatibility conditions for $w_0$ on the boundary are required, namely;

$$\begin{aligned} \frac{\partial w_0}{\partial n}=v_2(x,0) \quad \text {and} \quad \frac{\partial w_t}{\partial n}(x,0)=v_{2t}(x,0), \end{aligned}$$

(2.9)

where $v_2(x,\cdot )$ is continuously differentiable at $t=0$ for almost all x. These conditions are required for the proof of Lemmas 3.4 and 3.5.

Now, the motivation for choosing the control law comes from the construction of a Lyapunov functional of the following form $V(t)=\frac{1}{2}\int _{\Omega }w(x,t)^2\; dx$. Hence, on taking derivative with respect to time, we arrive at

$$\begin{aligned} \frac{dV}{dt}&=\int _{\Omega }w\Big (\nu \Delta w-w_d(\nabla w\cdot \mathbf{{1}})-w(\nabla w\cdot \mathbf{{1}})\Big )\;dx\\&=-\nu \left\Vert \nabla w\right\Vert ^2+\nu \int _{\partial \Omega }\frac{\partial w}{\partial n}w\;d\Gamma -\int _{\Omega }w_d(\nabla w\cdot \mathbf{{1}})w\; dx-\int _{\Omega }w(\nabla w\cdot \mathbf{{1}})w\; dx. \end{aligned}$$

Using the Young’s inequality, it follows that

$$\begin{aligned} w_d\Big (\big (\nabla w\cdot \mathbf{{1}}\big ),w\Big )&=\frac{w_d}{2}\int _{\Omega }\Big ((w^2)_{x_1}+(w^2)_{x_2}\Big )\;dx =\frac{w_d}{2}\sum _{j=1}^{2}\int _{\partial \Omega }w^2\cdot \nu _j\; d\Gamma \nonumber \\&\le \frac{w_d}{\sqrt{2}} \int _{\partial \Omega } w^2 \;d\Gamma \le w_d\int _{\partial \Omega } w^2\; d\Gamma , \end{aligned}$$

(2.10)

and

$$\begin{aligned} \int _{\Omega }w(\nabla w\cdot \mathbf{{1}})w\; dx&\le \frac{1}{3}\sum _{j=1}^{2}\int _{\partial \Omega }w^3\cdot \nu _j\; d\Gamma \le \frac{1}{3}\sqrt{2}\int _{\partial \Omega }|w|^3\; d\Gamma \nonumber \\&\le {c_0}\int _{\partial \Omega }w^2\; d\Gamma +\frac{1}{18 c_0}\int _{\partial \Omega }w^4\; d\Gamma , \end{aligned}$$

(2.11)

where $c_0$ is a positive constant. Therefore, it follows that

$$\begin{aligned} \frac{dV}{dt}\le -\nu \left\Vert \nabla w\right\Vert ^2+\int _{\partial \Omega }\Big (\nu \frac{\partial w}{\partial n}+(w_d+{c_0}) w+\frac{1}{18 c_0}w^3\Big )w\;d\Gamma . \end{aligned}$$

(2.12)

Now, choose the Neumann boundary feedback control law as

$$\begin{aligned} v_2(x,t)=-\frac{1}{\nu }\Big (2(c_0+w_d)w+\frac{2}{9c_0}w^3\Big ) \quad \text {on} \quad \partial \Omega , \end{aligned}$$

(2.13)

to obtain

$$\begin{aligned} \frac{dV}{dt}&\le -\nu \left\Vert \nabla w\right\Vert ^2-\big ({c_0}+w_d\big )\int _{\partial \Omega }w^2\;d\Gamma -\frac{1}{6 c_0}\int _{\partial \Omega }w^4\;d\Gamma \\&\le -\min \Big \{\nu ,\big ({c_0} +w_d\big )\Big \}\Big (\left\Vert \nabla w\right\Vert ^2+\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}\Big )\\&\le -\frac{2}{C_F}\min \Big \{\nu ,\big ({c_0}+w_d\big )\Big \}(\frac{1}{2}\left\Vert w\right\Vert ^2) \le -C_{Lyp}V, \end{aligned}$$

where $C_{Lyp}=\frac{2}{C_F}\min \Big \{\nu ,\big ({c_0}+w_d\big )\Big \}>0$.

Setting $B\big (v;w,\phi \big )$ as $B\big (v;w,\phi \big )=\Big (v\big (\nabla w\cdot \mathbf{{1}}\big ),\phi \Big ),$w satisfies a weak form of (2.6)–(2.8) as

$$\begin{aligned} (w_t,v)+&\nu (\nabla w,\nabla v)+w_d\big (\nabla w\cdot \mathbf{{1}}, v\big )+B\big (w;w,v\big )\nonumber \\&+\Big \langle (2 c_0+2w_d)w+\frac{2}{9c_0}w^3,v\Big \rangle _{\partial \Omega }\; =0\quad \forall ~v\in H^1(\Omega ), \end{aligned}$$

(2.14)

with $w(0)=w_0,$ where $\langle v,w\rangle _{\partial \Omega }:=\int _{\partial \Omega }vw \;d\Gamma$.

For our subsequent analysis, we assume that there exists a unique weak solution w of (2.14) satisfying the following regularity results

$$\begin{aligned} \left\Vert w(t)\right\Vert ^2_2+\left\Vert w_t(t)\right\Vert ^2_1+\int _{0}^{t}\left\Vert w_t(s)\right\Vert ^2_2 ds\le C. \end{aligned}$$

(2.15)

For existence and uniqueness with continuous dependence property of one dimensional Burgers’ equation with similar type nonlinearity, see, [17, 22] and their arguments can be modified to prove the wellposedness of the problem (2.14). For regularity results, the energy method applied in our Sect. 3 can be appropriately modified to prove (2.15). Therefore, we shall not pursue it further in this article.

Throughout the paper C is a generic positive constant.

3 Stabilization Results

In this section, we establish global stabilization results of the continuous problem (1.1)–(1.3). More precisely, exponential stabilization results for the state variable w(t) are shown for the modified problem (2.6)–(2.8), where feedback control $v_2$ is given in (2.13). Moreover, additional regularity results are established assuming compatibility conditions, which are crucial for proving optimal error estimates for the state variable.

Our results of this section are based on energy arguments using exponential weight functions. For similar analysis, see, [8, 11, 12, 14, 28, 30].

Throughout this section, all the results hold with the same decay rate $\alpha$:

$$\begin{aligned} 0\le \alpha \le \frac{1}{C_F}\min \Big \{{\nu },(c_0+w_d)\Big \}. \end{aligned}$$

(3.1)

Lemma 3.1

Let $w_0\in L^2(\Omega )$. Then, there holds

$$\begin{aligned} \left\Vert w(t)\right\Vert ^2+\beta e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\Vert \nabla w(s)\right\Vert ^2+\left\Vert w(s)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{ 3\beta c_0}\left\Vert w(s)\right\Vert ^4_{L^4(\partial \Omega )} \Big )ds\le e^{-2\alpha t}\left\Vert w_0\right\Vert ^2, \end{aligned}$$

where $\beta = 2\min \{(\nu -\alpha C_F), (c_0+w_d-\alpha C_F)\}>0$, and $C_F>0$ is the constant in the Friedrichs’s inequality (2.3).

Proof

Set $v=e^{2\alpha t}w$ in (2.14) to obtain

$$\begin{aligned} \frac{d}{dt}\left\Vert e^{\alpha t}w\right\Vert ^2-&2\alpha \left\Vert e^{\alpha t}w\right\Vert ^2+2\nu \left\Vert e^{\alpha t}\nabla w\right\Vert ^2+2e^{2\alpha t}\int _{\partial \Omega }\Big (( 2 c_0+2w_d)w^2+\frac{2}{9c_0}w^4\Big )\; d\Gamma \nonumber \\&=-2w_de^{2\alpha t}\Big (\big (\nabla w\cdot \mathbf{{1}}\big ),w\Big )-2e^{2\alpha t}B\big (w;w,w\big ) . \end{aligned}$$

(3.2)

For the first term on the right hand side of (3.2), we use (2.10) to bound it as

$$\begin{aligned} 2w_de^{2\alpha t}\Big (\big (\nabla w\cdot \mathbf{{1}}\big ),w\Big ) \le \sqrt{2} w_de^{2\alpha t}\int _{\partial \Omega } w^2 d\Gamma \le 2 w_de^{2\alpha t}\int _{\partial \Omega } w^2 d\Gamma . \end{aligned}$$

(3.3)

For the second term on the right hand side of (3.2), a use of (2.11) with the Young’s inequality yields

$$\begin{aligned} 2e^{2\alpha t}B\big (w;w,w\big ) \le \frac{2}{3}e^{2\alpha t}\sqrt{2}\int _{\partial \Omega }|w|^3\; d\Gamma \le 2 c_0 e^{2\alpha t}\int _{\partial \Omega }w^2\; d\Gamma +\frac{1}{9c_0}e^{2\alpha t}\int _{\partial \Omega }w^4 \;d\Gamma . \end{aligned}$$

(3.4)

Now, using the Friedrichs’s inequality (2.3), it follows that

$$\begin{aligned} -2\alpha e^{2\alpha t}\left\Vert w\right\Vert ^2 \ge -2\alpha e^{2\alpha t}C_F\Big (\left\Vert \nabla w\right\Vert ^2+\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}\Big ). \end{aligned}$$

(3.5)

Hence, from (3.2), we arrive using (3.3)- (3.5) at

$$\begin{aligned} \frac{d}{dt}\left\Vert e^{\alpha t}w\right\Vert ^2&+2(\nu -\alpha C_F)\left\Vert e^{\alpha t}\nabla w\right\Vert ^2+2 e^{2\alpha t}\Big (\big (c_0+w_d- \alpha C_F\big )\int _{\partial \Omega }w^2\; d\Gamma \nonumber \\&+\frac{1}{6 c_0}\int _{\partial \Omega }w^4\; d\Gamma \Big ) \le 0. \end{aligned}$$

(3.6)

Since decay rate satisfy (3.1), the coefficients on the left hand side of (3.6) are non-negative. Integrate (3.6) with respect to time from 0 to t,  and then, multiply the resulting inequality by $e^{-2\alpha t}$ to obtain

$$\begin{aligned} \left\Vert w(t)\right\Vert ^2+2(\nu -\alpha C_F)e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\Vert \nabla w(s)\right\Vert ^2 ds&+2 e^{-2\alpha t}\int _{o}^{t}e^{2\alpha s}\Big (\big (c_0+w_d- \alpha C_F\big )\left\Vert w(s)\right\Vert ^2_{L^2(\partial \Omega )}\\&+\frac{1}{6 c_0}\left\Vert w(s)\right\Vert ^4_{L^4(\partial \Omega )}\Big ) \;ds\le e^{-2\alpha t}\left\Vert w_0\right\Vert ^2. \end{aligned}$$

This completes the proof. $\square$

Remark 3.1

The above Lemma also holds for $\alpha =0,$ that is,

$$\begin{aligned} \left\Vert w(t)\right\Vert ^2+2\nu \int _{0}^{t}\left\Vert \nabla w(s)\right\Vert ^2 ds+2 \int _{0}^{t}\Bigg (\int _{\partial \Omega }\Big (\big (c_0+ w_d\big )w(s)^2+\frac{1}{6c_0}w(s)^4\Big ) \;d\Gamma \Bigg ) ds\le \left\Vert w_0\right\Vert ^2.\nonumber \\ \end{aligned}$$

(3.7)

Moreover, by the Friedrichs’s inequality, it follows that

$$\begin{aligned} e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\Vert w(s)\right\Vert ^2 ds\le Ce^{-2\alpha t}\left\Vert w_0\right\Vert ^2. \end{aligned}$$

Remark 3.2

Now instead of taking the control on the whole boundary, if we take the above mentioned Neumann control on some part of the boundary ($\Gamma _N$) where $\Gamma _N$ has nonzero measure with remaining part zero Dirichlet boundary condition, still the stabilization result holds. For instance, consider $\partial \Omega =\Gamma _D\cup \Gamma _N$ with $\Gamma _D\cap \Gamma _N=\phi$, where $\Gamma _D$ and $\Gamma _N$ are sufficiently smooth. With this setting, from (3.2), we arrive at

$$\begin{aligned} \frac{d}{dt}\left\Vert e^{\alpha t}w\right\Vert ^2-&2\alpha \left\Vert e^{\alpha t}w\right\Vert ^2+2\nu \left\Vert e^{\alpha t}\nabla w\right\Vert ^2+2e^{2\alpha t}\int _{\Gamma _N}\Big ((2 c_0+2w_d)w^2+\frac{2}{9c_0}w^4\Big )\; d\Gamma \nonumber \\&=-2w_de^{2\alpha t}\Big (\big (\nabla w\cdot \mathbf{{1}}\big ),w\Big )-2e^{2\alpha t}B\big (w;w,w\big )\nonumber \\&\le 2 w_de^{2\alpha t}\int _{\Gamma _N} w^2 d\Gamma +2 c_0 e^{2\alpha t}\int _{\Gamma _N}w^2 d\Gamma +\frac{1}{9c_0}e^{2\alpha t}\int _{\Gamma _N}w^4 d\Gamma . \end{aligned}$$

(3.8)

Using Friedrichs’s inequality $\left\Vert v\right\Vert ^2\le C_F\Big (\left\Vert \nabla v\right\Vert ^2+\left\Vert v\right\Vert ^2_{L^2(\Gamma _N)}\Big )$, we obtain

$$\begin{aligned} \frac{d}{dt}\left\Vert e^{\alpha t}w\right\Vert ^2&+2(\nu -\alpha C_F)\left\Vert e^{\alpha t}\nabla w\right\Vert ^2+2 e^{2\alpha t}\Big (\big (c_0+w_d-2\alpha C_F\big )\int _{\Gamma _N}w^2 d\Gamma \\&+\frac{1}{6 c_0}\int _{\Gamma _N}w^4 d\Gamma \Big ) \le 0. \end{aligned}$$

Proceed as before to complete the rest of the proof for $L^2$- stabilization result. In higher order norm, stabilization result also holds similarly when control works on some part of the boundary.

Lemma 3.2

Let $w_0\in H^1(\Omega ).$ Then, for $C=C(\left\Vert w_0\right\Vert _1)$ there holds

$$\begin{aligned} \Big (\left\Vert \nabla w(t)\right\Vert ^2&+\frac{2(c_0+w_d)}{\nu }\left\Vert w(t)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9\nu c_0}\left\Vert w(t)\right\Vert ^4_{L^4(\partial \Omega )}\Big )+\nu e^{-2\alpha t}\int _{0}^{t}\left\Vert e^{\alpha s}\Delta w(s)\right\Vert ^2\; ds\\ {}&\le Ce^Ce^{-2\alpha t}. \end{aligned}$$

Proof

Form an $L^2$-inner product between (2.6) and $-e^{2\alpha t}\Delta w$ to obtain

$$\begin{aligned} \frac{d}{dt}\left\Vert e^{\alpha t}\nabla w\right\Vert ^2-&2\alpha e^{2\alpha t}\left\Vert \nabla w\right\Vert ^2+2\nu \left\Vert e^{\alpha t}\Delta w\right\Vert ^2+\frac{2}{\nu }\int _{\partial \Omega }e^{2\alpha t}\Big (2(c_0+w_d)w+\frac{2}{9c_0}w^3\Big )w_t\; d\Gamma \nonumber \\&=2e^{2\alpha t}w_d(\nabla w\cdot \mathbf{{1}},\Delta w)+2e^{2\alpha t}B(w;w,\Delta w). \end{aligned}$$

(3.9)

The fourth term on the left hand side of (3.9) can be rewritten as

$$\begin{aligned} \frac{2}{\nu }\int _{\partial \Omega }&e^{2\alpha t}\Big (2(c_0+w_d)w+\frac{2}{9c_0}w^3\Big )w_t\; d\Gamma \\&= \frac{d}{dt}\Big (\frac{2(c_0+w_d)}{\nu }\left\Vert e^{\alpha t}w\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9\nu c_0}\big (e^{2\alpha t}\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}\big )\Big )\\&\qquad -2\alpha e^{2\alpha t}\Big (\frac{2(c_0+w_d)}{\nu }\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9\nu c_0}\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}\Big ). \end{aligned}$$

The terms on the right hand side of (3.9) are bounded by

$$\begin{aligned} 2e^{2\alpha t}w_d(\nabla w\cdot \mathbf{{1}},\Delta w)\le \frac{\nu }{2}\left\Vert e^{\alpha t}\Delta w\right\Vert ^2+\frac{2}{\nu }e^{2\alpha t}w_d^2\left\Vert \nabla w\right\Vert ^2, \end{aligned}$$

and using Gagliardo–Nirenberg inequality and Lemma 3.1, by

$$\begin{aligned} 2e^{2\alpha t}B(w;w,\Delta w)&\le Ce^{2\alpha t}\left\Vert w\right\Vert _{L^4}\left\Vert \nabla w\right\Vert _{L^4}\left\Vert \Delta w\right\Vert \\&\le Ce^{2\alpha t}\Big (\left\Vert w\right\Vert ^\frac{1}{2}\left\Vert \nabla w\right\Vert ^\frac{1}{2}+\left\Vert w\right\Vert \Big )\Big (\left\Vert w\right\Vert ^\frac{1}{4}\left\Vert \Delta w\right\Vert ^\frac{3}{4}+\left\Vert w\right\Vert \Big )\left\Vert \Delta w\right\Vert \\&\le Ce^{2\alpha t}\Big (\left\Vert w\right\Vert ^\frac{3}{4}\left\Vert \nabla w\right\Vert ^\frac{1}{2}\left\Vert \Delta w\right\Vert ^\frac{7}{4}+\left\Vert w\right\Vert ^\frac{5}{4}\left\Vert \Delta w\right\Vert ^\frac{7}{4}+\left\Vert w\right\Vert ^\frac{3}{2}\left\Vert \nabla w \right\Vert ^\frac{1}{2}\left\Vert \Delta w\right\Vert \\&\qquad +\left\Vert w\right\Vert ^2\left\Vert \Delta w\right\Vert \Big )\\&\le \frac{\nu }{2}\left\Vert e^{\alpha t}\Delta w\right\Vert ^2+Ce^{2\alpha t}\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^4+Ce^{2\alpha t}\left\Vert w\right\Vert ^2+Ce^{2\alpha t}\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2. \end{aligned}$$

Finally, from (3.9), we arrive at

$$\begin{aligned} \frac{d}{dt}\Big (e^{2\alpha t}\big (\left\Vert \nabla w\right\Vert ^2&+\frac{2(c_0+w_d)}{\nu }\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9\nu c_0}\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}\big )\Big )+\nu \left\Vert e^{\alpha t}\Delta w\right\Vert ^2\nonumber \\&\le 2\alpha e^{2\alpha t}\Big (\frac{2(c_0+w_d)}{\nu }\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}+ \frac{1}{9\nu c_0}\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}\Big )+\frac{2}{\nu }e^{2\alpha t}w_d^2\left\Vert \nabla w\right\Vert ^2\nonumber \\&\qquad +Ce^{2\alpha t}\left\Vert w\right\Vert ^2+Ce^{2\alpha t}\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2 +Ce^{2\alpha t}\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^4. \end{aligned}$$

(3.10)

Integrate the above inequality from 0 to t,  and then use the Grönwall’s inequality with Lemma 3.1 to obtain

$$\begin{aligned} e^{2\alpha t}\Big (\left\Vert \nabla w(t)\right\Vert ^2&+\frac{2(c_0+w_d)}{\nu }\left\Vert w(t)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9\nu c_0}\left\Vert w(t)\right\Vert ^4_{L^4(\partial \Omega )}\Big )+\nu \int _{0}^{t}\left\Vert e^{\alpha s}\Delta w(s)\right\Vert ^2\; ds\\ {}&\le C\Big (\left\Vert w_0\right\Vert ^2_1+\left\Vert w_0\right\Vert ^2_{L^2(\partial \Omega )}+\left\Vert w_0\right\Vert ^4_{L^4(\partial \Omega )}\Big )\exp \Big (C\int _{0}^{t}\left\Vert w\right\Vert ^2\big (1+\left\Vert \nabla w\right\Vert ^2\big ) ds\Big ). \end{aligned}$$

Use Remark 3.1 for the integral term under the exponential sign, and then multiply the resulting inequality by $e^{-2\alpha t}$ to complete the rest of the proof. $\square$

Lemma 3.3

Let $w_0\in H^1(\Omega )$. Then, there exists a positive constant $C=C\Big (\left\Vert w_0\right\Vert _1\Big )$ such that the following estimate holds.

$$\begin{aligned} \Big (\nu \left\Vert \nabla w(t)\right\Vert ^2&+2(c_0+w_d)\left\Vert w(t)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9c_0}\left\Vert w(t)\right\Vert ^4_{L^4(\partial \Omega )}\Big )\\&+\,e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\Vert w_t(s)\right\Vert ^2 ds\le Ce^Ce^{-2\alpha t}. \end{aligned}$$

Proof

Choose $v=e^{2\alpha t}w_t$ in (2.14) to obtain

$$\begin{aligned} 2\left\Vert e^{\alpha t}w_t\right\Vert ^2+\nu \frac{d}{dt}\left\Vert e^{\alpha t}\nabla w\right\Vert ^2&-2\nu \alpha \left\Vert e^{\alpha t}\nabla w\right\Vert ^2+2\int _{\partial \Omega }\Big (2(c_0+w_d)w+\frac{2}{9c_0}w^3\Big )e^{2\alpha t}w_t \;d\Gamma \nonumber \\&=-2w_de^{2\alpha t}\big (\nabla w\cdot \mathbf{{1}},w_t\big )-2e^{2\alpha t}B\big (w;w,w_t\big ). \end{aligned}$$

(3.11)

The terms on the right hand side of (3.11) are bounded by

$$\begin{aligned} 2w_de^{2\alpha t}\big (\nabla w\cdot \mathbf{{1}},w_t\big )\le \frac{1}{2}e^{2\alpha t}\left\Vert w_t\right\Vert ^2+4e^{2\alpha t}w_d^2\left\Vert \nabla w\right\Vert ^2, \end{aligned}$$

and using Gagliardo–Nirenberg inequality and Lemma 3.1, by

$$\begin{aligned} 2e^{2\alpha t}B\big (w;w,w_t\big )&\le Ce^{2\alpha t}\left\Vert w\right\Vert _{L^4}\left\Vert \nabla w\right\Vert _{L^4}\left\Vert w_t\right\Vert \\&\le Ce^{2\alpha t}\Big (\left\Vert w\right\Vert ^\frac{1}{2}\left\Vert \nabla w\right\Vert ^\frac{1}{2}+\left\Vert w\right\Vert \Big )\Big (\left\Vert w\right\Vert ^\frac{1}{4}\left\Vert \Delta w\right\Vert ^\frac{3}{4}+\left\Vert w\right\Vert \Big )\left\Vert w_t\right\Vert \\&\le Ce^{2\alpha t}\Big (\left\Vert w\right\Vert ^\frac{3}{4}\left\Vert \nabla w\right\Vert ^\frac{1}{2}\left\Vert \Delta w\right\Vert ^\frac{3}{4}\left\Vert w_t\right\Vert +\left\Vert w\right\Vert ^\frac{5}{4}\left\Vert \Delta w\right\Vert ^\frac{3}{4}\left\Vert w_t\right\Vert \\&\qquad +\left\Vert w\right\Vert ^\frac{3}{2}\left\Vert \nabla w\right\Vert ^\frac{1}{2}\left\Vert w_t\right\Vert +\left\Vert w\right\Vert ^2\left\Vert w_t\right\Vert \Big )\\&\le \frac{1}{2}e^{2\alpha t}\left\Vert w_t\right\Vert ^2+Ce^{2\alpha t}\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^4+Ce^{2\alpha t}\left\Vert \Delta w\right\Vert ^2+Ce^{2\alpha t}\left\Vert w\right\Vert ^2\\&\qquad +Ce^{2\alpha t}\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2. \end{aligned}$$

Hence, rewriting the boundary integral term in (3.11) as in previous Lemma 3.2, we arrive from (3.11) at

$$\begin{aligned} \frac{d}{dt}\Big (e^{2\alpha t}\big (\nu \left\Vert \nabla w\right\Vert ^2&+2(c_0+w_d)\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9c_0}\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}\big )\Big )+\left\Vert e^{\alpha t}w_t\right\Vert ^2\\&\le Ce^{2\alpha t}\Big (\left\Vert w\right\Vert ^2_{L^2(\partial \Omega )}+\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}+\left\Vert \nabla w\right\Vert ^2+\left\Vert \Delta w\right\Vert ^2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2\\&+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^4+\left\Vert w\right\Vert ^2\Big ). \end{aligned}$$

Apply Lemmas 3.1 and 3.2, and the Grönwall’s inequality to the above inequality to complete the rest of the proof. $\square$

Lemma 3.4

Let $w_0\in H^2(\Omega )$. Then there exists a positive constant $C=C\Big (\left\Vert w_0\right\Vert _2\Big )$ such that

$$\begin{aligned} \left\Vert w_t(t)\right\Vert ^2+\left\Vert \Delta w(t)\right\Vert ^2&+\nu e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\Vert \nabla w_t(s)\right\Vert ^2 ds +2e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (2(c_0+w_d)\left\Vert w_t(s)\right\Vert ^2_{L^2(\partial \Omega )}\\&+\frac{2}{3c_0}\left\Vert w(s)w_t(s)\right\Vert ^2_{L^2(\partial \Omega )}\Big ) ds\le Ce^Ce^{-2\alpha t}. \end{aligned}$$

Proof

Differentiate (2.6) with respect to t and then take the inner product with $e^{2\alpha t}w_t$ to obtain

$$\begin{aligned} \frac{d}{dt}\big (&\left\Vert e^{\alpha t}w_t\right\Vert ^2\big )-2\alpha \left\Vert e^{\alpha t}w_t\right\Vert ^2+2\nu \left\Vert e^{\alpha t}\nabla w_t\right\Vert ^2+2\int _{\partial \Omega }\big (2(c_0+w_d)w_t^2+\frac{2}{3c_0}w^2w_t^2\big )e^{2\alpha t}\;d\Gamma \nonumber \\&= -2e^{2\alpha t}\Big (B\big (w_t;w,w_t\big )+B\big (w;w_t,w_t\big )\Big )-2w_de^{2\alpha t}\big (\nabla w_t\cdot \mathbf{{1}},w_t\big ). \end{aligned}$$

(3.12)

The right hand side terms in (3.12) are bounded by

$$\begin{aligned} -2e^{2\alpha t}&\Big (\big (\nabla w_t\cdot \mathbf{{1}},w_t\big )+B\big (w_t;w,w_t\big )+B\big (w;w_t,w_t\big )\Big )\\&\le 2w_de^{2\alpha t}\left\Vert \nabla w_t\right\Vert \left\Vert w_t\right\Vert +Ce^{2\alpha t}\left\Vert w_t\right\Vert _{L^4}\left\Vert \nabla w\right\Vert \left\Vert w_t\right\Vert _{L^4}+Ce^{2\alpha t}\left\Vert w\right\Vert _{L^4}\left\Vert \nabla w_t\right\Vert \left\Vert w_t\right\Vert _{L^4}\\&\le Ce^{2\alpha t}\left\Vert \nabla w_t\right\Vert \left\Vert w_t\right\Vert +Ce^{2\alpha t}\Big (\left\Vert w_t\right\Vert ^\frac{1}{2}\left\Vert \nabla w_t\right\Vert ^\frac{1}{2}+\left\Vert w_t\right\Vert \Big )^2\left\Vert \nabla w\right\Vert \\&\qquad +C\Big (\left\Vert w\right\Vert ^\frac{1}{2}\left\Vert \nabla w\right\Vert ^\frac{1}{2}+\left\Vert w\right\Vert \Big )\Big (\left\Vert w_t\right\Vert ^\frac{1}{2}\left\Vert \nabla w_t\right\Vert ^\frac{1}{2}+\left\Vert w_t\right\Vert \Big )\left\Vert \nabla w_t\right\Vert \\&\le \nu \left\Vert e^{\alpha t}\nabla w_t\right\Vert ^2+Ce^{2\alpha t}\Big (\left\Vert w_t\right\Vert ^2+\left\Vert w_t\right\Vert ^2\left\Vert \nabla w\right\Vert ^2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2\left\Vert w_t\right\Vert ^2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2\\&\qquad +\left\Vert w_t\right\Vert ^2\left\Vert w\right\Vert ^2+\left\Vert w_t\right\Vert ^2\left\Vert w\right\Vert ^4+\left\Vert w\right\Vert ^2\Big ). \end{aligned}$$

Hence, from (3.12), we arrive at

$$\begin{aligned} \frac{d}{dt}(\left\Vert e^{\alpha t}w_t\right\Vert ^2)+&\nu \left\Vert e^{\alpha t}\nabla w_t\right\Vert ^2+2e^{2\alpha t} \Big (2(c_0+w_d)\left\Vert w_t\right\Vert ^2_{L^2(\partial \Omega )}+\frac{2}{3c_0}\left\Vert ww_t\right\Vert ^2_{L^2(\partial \Omega )}\Big )\nonumber \\&\le Ce^{2\alpha t}\Big (\left\Vert w_t\right\Vert ^2+\left\Vert w_t\right\Vert ^2\left\Vert \nabla w\right\Vert ^2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2\left\Vert w_t\right\Vert ^2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^2\nonumber \\&\quad +\left\Vert w_t\right\Vert ^2\left\Vert w\right\Vert ^2+\left\Vert w_t\right\Vert ^2\left\Vert w\right\Vert ^4+\left\Vert w\right\Vert ^2\Big ). \end{aligned}$$

(3.13)

To calculate $\left\Vert w_t(0)\right\Vert ,$ take the inner product between (2.6) and $w_t$; and use compatibility condition to obtain

$$\begin{aligned} \left\Vert w_t(0)\right\Vert ^2\le C\Big (\left\Vert \nabla w_0\right\Vert ^2+\left\Vert \Delta w_0\right\Vert ^2+\left\Vert w_0\right\Vert ^2\left\Vert \nabla w_0\right\Vert ^4\Big ). \end{aligned}$$

Integrate the inequality (3.13) from 0 to t and then use Lemmas 3.1-3.3 to complete the proof of $\left\Vert w_t(t)\right\Vert .$ From this the estimate of $\left\Vert \Delta w(t)\right\Vert$ follows. Altogether it completes the rest of the proof. $\square$

Lemma 3.5

Let $w_0\in H^3(\Omega ).$ Then there exists a positive constant $C=C\Big (\left\Vert w_0\right\Vert _3\Big )$ such that

$$\begin{aligned} \left\Vert \nabla w_t(t)\right\Vert ^2+\big (2(c_0+w_d)\left\Vert w_t(t)\right\Vert ^2_{L^2(\partial \Omega )}&+\frac{2}{3c_0}\left\Vert w(t)w_t(t)\right\Vert ^2_{L^2(\partial \Omega )}\big )+\nu e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\Vert \Delta w_t(s)\right\Vert ^2 ds\\&\le Ce^{C(\left\Vert w_0\right\Vert _2)}e^{-2\alpha t}. \end{aligned}$$

Proof

Differentiate (2.6) with respect to t and then take inner product with $-e^{2\alpha t}\Delta w_t$ to obtain

$$\begin{aligned} \frac{d}{dt}\left\Vert e^{\alpha t}\nabla w_t\right\Vert ^2&-2\alpha \left\Vert e^{\alpha t}\nabla w_t\right\Vert ^2+2\nu \left\Vert e^{\alpha t}\Delta w_t\right\Vert ^2+\frac{d}{dt}\int _{\partial \Omega }e^{2\alpha t}\Big (2(c_0+w_d)w_t^2+\frac{2}{3c_0}w^2w_t^2\Big ) d\Gamma \nonumber \\&\le 2e^{2\alpha t}w_d(\nabla w_t\cdot \mathbf{{1}},\Delta w_t)+2e^{2\alpha t}B\big (w_t,w,\Delta w_t\big )+2e^{2\alpha t}B\big (w;w_t,\Delta w_t\big )\nonumber \\&\qquad +C\int _{\partial \Omega }e^{2\alpha t}\Big (w_t^2+ww_t^3+w^2w_t^2\Big )\;d\Gamma . \end{aligned}$$

(3.14)

The first three terms on the right hand side of (3.14) are bounded by

$$\begin{aligned} 2e^{2\alpha t}w_d(\nabla w_t\cdot \mathbf{{1}},\Delta w_t)\le \frac{\nu }{3}\left\Vert e^{\alpha t}\Delta w_t\right\Vert ^2+Ce^{2\alpha t}\left\Vert \nabla w_t\right\Vert ^2, \end{aligned}$$

and using Gagliardo–Nirenberg inequality and Lemma 3.1, by

$$\begin{aligned} 2e^{2\alpha t}&\Big (B\big (w_t;w,\Delta w_t\big )+ B\big (w;w_t,\Delta w_t\big )\Big )\\&\le Ce^{2\alpha t}\Big (\left\Vert w_t\right\Vert _{L^4}\left\Vert \nabla w\right\Vert _{L^4}\left\Vert \Delta w_t\right\Vert +\left\Vert w\right\Vert _{L^4}\left\Vert w_t\right\Vert _{L^4}\left\Vert \Delta w_t\right\Vert \Big )\\&\le \frac{2\nu }{3}\left\Vert e^{\alpha t}\Delta w_t\right\Vert ^2+Ce^{2\alpha t}\left\Vert w_t\right\Vert ^2\Big (\left\Vert w\right\Vert ^2_2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^4\Big )\\ {}&\quad +Ce^{2\alpha t}\left\Vert \nabla w_t\right\Vert ^2\Big (\left\Vert w\right\Vert ^2+\left\Vert \Delta w\right\Vert ^2\Big ). \end{aligned}$$

The boundary terms on the right hand side of (3.14) are bounded by

$$\begin{aligned} C\int _{\partial \Omega }e^{2\alpha t}\Big (w_t^2{+}ww_t^3+w^2w_t^2\Big )\;d\Gamma&\le C\int _{\partial \Omega }e^{2\alpha t}\Big (w_t^2{+}w^2w_t^2\Big )\;d\Gamma +Ce^{2\alpha t}\left\Vert w_t\right\Vert ^4_{L^4(\partial \Omega )}. \end{aligned}$$

Therefore, from (3.14), we arrive at

$$\begin{aligned} \frac{d}{dt}\Big (\left\Vert e^{\alpha t}\nabla w_t\right\Vert ^2&+2(c_0+w_d)\left\Vert e^{\alpha t}w_t\right\Vert ^2_{L^2(\partial \Omega )}+\frac{2}{3c_0}\int _{\partial \Omega }e^{2\alpha t}w^2w_t^2\;d\Gamma \Big )+\nu \left\Vert e^{\alpha t}\Delta w_t\right\Vert ^2\\&\le Ce^{2\alpha t}\left\Vert w_t\right\Vert ^2\Big (\left\Vert w\right\Vert ^2_2+\left\Vert w\right\Vert ^2\left\Vert \nabla w\right\Vert ^4\Big )+Ce^{2\alpha t}\left\Vert \nabla w_t\right\Vert ^2\Big (1+\left\Vert w\right\Vert ^2+\left\Vert \Delta w\right\Vert ^2\Big )\\&+\int _{\partial \Omega }e^{2\alpha t}\Big (w_t^2+w^2w_t^2\Big )\;ds+Ce^{2\alpha t}\Big (\left\Vert w_t\right\Vert ^4+\left\Vert \nabla w_t\right\Vert ^4\Big ). \end{aligned}$$

Integrate the above inequality from 0 to t and then apply the Grönwall’s inequality along with Lemmas 3.1–3.4 to obtain

$$\begin{aligned} \Big (\left\Vert e^{\alpha t}\nabla w_t(t)\right\Vert ^2&+2(c_0+w_d)\left\Vert e^{\alpha t}w_t(t)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{2}{3c_0}\int _{\partial \Omega }e^{2\alpha t}w(t)^2w_t(t)^2\;d\Gamma \Big )\nonumber \\ {}&+\nu \int _{0}^{t}\left\Vert e^{\alpha s}\Delta w_t(s)\right\Vert ^2 ds\nonumber \\&\le C\Big (\left\Vert \nabla w_t(0)\right\Vert ^2+\left\Vert w_t(0)\right\Vert _{L^2(\partial \Omega )}+\left\Vert w(0)w_t(0)\right\Vert ^2_{L^2(\partial \Omega )}\Big )\nonumber \\&\qquad \exp \Big (C\int _{0}^{t}\big (\left\Vert w(s)\right\Vert ^2+\left\Vert \Delta w(s)\right\Vert ^2+\left\Vert \nabla w_t(s)\right\Vert ^2\big )\;ds\Big ). \end{aligned}$$

(3.15)

Differentiate (2.6) with respect to $x_1$ and $x_2$ and applying compatibility condition to arrive at $\left\Vert \nabla w_t(0)\right\Vert \le C\left\Vert w_0\right\Vert _3$. Also, by (2.1), $\left\Vert w_t(0)\right\Vert _{L^2(\partial \Omega )}\le C\left\Vert w_t(0)\right\Vert ^2_1$ and $\left\Vert w(0)w_t(0)\right\Vert ^2_{L^2(\partial \Omega )}\le C\left\Vert w(0)\right\Vert _{L^4(\partial \Omega )}\left\Vert w_t(0)\right\Vert ^2_1.$

Again, use of Lemmas 3.1, 3.2 and 3.4 for the above inequality (3.15) completes the proof. $\square$

4 Finite Element Method

In this section, we discuss semidiscrete Galerkin approximation keeping the time variable continuous and show global stabilization result for the spatially discrete or semidiscrete solution. Further optimal error estimates ( optimality with respect to approximation property) for both state variable and feedback controller are derived. With respect to $H^s$ regularity of w, the optimal error estimate satisfy $\left\Vert w(t)-w_h(t)\right\Vert _{H^m(\Omega )}\le Ch^{\min (s,k+1)-m}\left\Vert w(t)\right\Vert _{H^s(\Omega )}$, where m, s ( $0\le m<s$) are integers and k is the degree of polynomial used, Here $m=0$ or 1, $k=1$ and $s=2$.

For our semidiscrete analysis we assume $\Omega$ is a convex polygonal domain with boundary $\partial \Omega$, otherwise we can always get a polygonal domain $\Omega _h\subset \Omega$, where union of quasi-uniform triangulation determines $\Omega _h$ with boundary vertices on $\partial \Omega$. For more details see [31]. Given a regular triangulation ${\mathcal {T}}_h$ of ${\overline{\Omega }}$, let $h_K=\text {diam}(K)$ for all $K\in {\mathcal {T}}_h$ and $h=\displaystyle \max _{ K\in {\mathcal {T}}_h} h_K$.

Set

$$\begin{aligned} V_h=\left\{ v_h\in C^0({\overline{\Omega }} ): v_h\Big |_K \in {\mathcal {P}}_{1}(K) \quad \forall K\in {\mathcal {T}}_{h}\right\} . \end{aligned}$$

We shall assume further that the following inverse property hold for each $v_h\in V_h$ and $p\in [2,\infty ],$ see, [9]

$$\begin{aligned} \left\Vert v_h\right\Vert _{L^p(\Omega )} \le C \;h^{2(\frac{1}{p}-\frac{1}{2})} \;\left\Vert v_h\right\Vert . \end{aligned}$$

(4.1)

The semidiscrete approximation corresponding to the problem (2.14) is to seek $w_h(t)=w_h(\cdot ,t)\in V_h$ such that

$$\begin{aligned} (w_{ht},\chi )+&\nu (\nabla w_h,\nabla \chi )+w_d\big (\nabla w_h\cdot \mathbf{{1}},\chi \big )+B\big (w_h;w_h,\chi \big )\nonumber \\&\qquad +\int _{\partial \Omega }\Big (2(c_0+w_d)w_h+\frac{2}{9c_0}w_h^3\Big )\chi \; d\Gamma =0,\quad \forall ~ \chi \in V_h \end{aligned}$$

(4.2)

with $w_h(0)=P_h u_0-w_d=w_{0h}$ (say), an approximation of $w_0,$ where, $P_hu_0$ is the $H^1$ projection of $u_0$ onto $V_h$ such that

$$\begin{aligned} \left\Vert u_0-u_{0h}\right\Vert _j\le Ch^{2-j}\left\Vert u_0\right\Vert _2\quad j=0,1. \end{aligned}$$

(4.3)

Since $V_h$ is finite dimensional, (4.2) leads to a system of nonlinear ODEs. Hence, an application of Picard’s theorem ensures the existence of a unique solution locally, that is, there exists an interval $(0,t_h)$ such that $w_h$ exists for $t\in (0,t_h)$. Then, using the boundedness of the discrete solution from Lemma 4.1 below, the continuation arguments yields existence of a unique solution for all $t>0$.

In a similar fashion as in continuous case, the following stabilization result holds for the semidiscrete solution.

Lemma 4.1

Let $w_0\in L^2(\Omega )$.Then, there holds

$$\begin{aligned}&\left\Vert w_h(t)\right\Vert ^2+\beta e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\big (\left\Vert \nabla w_h(s)\right\Vert ^2+\left\Vert w_h(s)\right\Vert ^2_{L^2(\partial \Omega )}\big )ds+\frac{1}{3c_0}e^{-2\alpha t}\\&\qquad \times \int _{0}^{t}e^{2\alpha s}\left\Vert w_h(s)\right\Vert ^4_{L^4(\partial \Omega )} ds\\&\quad \le e^{-2\alpha t}\left\Vert w_{0h}\right\Vert ^2. \end{aligned}$$

4.1 Error Estimates

Define an auxiliary projection ${{\tilde{w}}}_h\in V_h$ of w through the following form

$$\begin{aligned} \Big (\nabla (w-{{\tilde{w}}}_h),\nabla \chi \Big )+\lambda \Big (w-\tilde{w}_h,\chi \Big )=0\quad \forall ~ \chi \in V_h, \end{aligned}$$

(4.4)

where $\lambda \ge 1$ is some fixed positive number. For a given w,  the existence of a unique ${{\tilde{w}}}_h$ follows by the Lax-Milgram Lemma. Let $\eta :=w-{{\tilde{w}}}_h$ be the error involved in the auxiliary projection. Then, the following error estimates hold:

$$\begin{aligned} \left\Vert \eta \right\Vert _j&\le C h^{\min (2,m)-j}\;\left\Vert w\right\Vert _m, \;\text {and}\nonumber \\ \left\Vert \eta _t\right\Vert _j&\le C h^{\min (2,m)-j}\left\Vert w_t\right\Vert _m,\;\; j=0,1 \; \text{ and } \; m=1,2. \end{aligned}$$

(4.5)

For a proof, we refer to Thomée [9, 31]. Following Lemma 4.2 is needed to establish error estimates.

Lemma 4.2

Let $F\in H^{3/2+\epsilon }(\Omega )$, for some $\epsilon >0$, and $G\in H^{1/2}(\partial \Omega ).$ Then $FG\in H^{1/2}(\partial \Omega )$ and

$$\begin{aligned} \left\Vert FG\right\Vert _{H^{1/2}(\partial \Omega )}\le C\left\Vert F\right\Vert _{H^{3/2+\epsilon }(\Omega )}\left\Vert G\right\Vert _{H^{1/2}(\partial \Omega )}. \end{aligned}$$

Proof

For a proof see [10]. $\square$

In addition, for proving error estimates for state variable and feedback controllers, we need the following estimates of $\eta$ and $\eta _t$ at boundary.

Lemma 4.3

For smooth $\partial \Omega ,$ there holds

$$\begin{aligned}&\left\Vert \eta \right\Vert _{L^2(\partial \Omega )}\le Ch^{3/2}\left\Vert w\right\Vert _2, \quad \left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\le Ch^2\left\Vert w\right\Vert _2, \quad \left\Vert \eta _t\right\Vert _{H^{-1/2}(\partial \Omega )}\le Ch^2\left\Vert w_t\right\Vert _2,\\&\left\Vert \eta \right\Vert _{L^q(\partial \Omega )}\le Ch\left\Vert w\right\Vert _2, \quad \text {and} \quad \left\Vert \eta _t\right\Vert _{L^q(\partial \Omega )}\le Ch\left\Vert w_t\right\Vert _{2},\;\; 2\le q <\infty . \end{aligned}$$

Proof

Consider an auxiliary function $\phi$ satisfying the following problem

$$\begin{aligned} -\Delta \phi +\lambda \phi&=0 \quad \text {in} \quad \Omega ,\nonumber \\ \frac{\partial \phi }{\partial \nu }&=\eta \quad \text {on} \quad \partial \Omega , \end{aligned}$$

(4.6)

with $\left\Vert \phi \right\Vert _2\le C\left\Vert \eta \right\Vert _{H^\frac{1}{2}(\partial \Omega )}$. For a proof of this regularity result see [21].

Take the inner product between (4.6) and $\eta$ to obtain

$$\begin{aligned} \left\Vert \eta \right\Vert ^2_{L^2(\partial \Omega )}=(\nabla \phi ,\nabla \eta )+\lambda (\phi ,\eta )&=(\nabla \phi -\nabla \tilde{\phi _h},\nabla \eta )+\lambda (\phi -\tilde{\phi _h},\eta )\\&\le ch^2\left\Vert \phi \right\Vert _2\left\Vert w\right\Vert _2+Ch^4\left\Vert \phi \right\Vert _2\left\Vert w\right\Vert _2\le Ch^2\left\Vert w\right\Vert _2\left\Vert \eta \right\Vert _{H^\frac{1}{2}(\partial \Omega )}. \end{aligned}$$

Using the Trace inequality (2.2) for $s=1/2$, we arrive at

$$\begin{aligned} \left\Vert \eta \right\Vert ^2_{L^2(\partial \Omega )}\le Ch^2\left\Vert w\right\Vert ^2_2\left\Vert \eta \right\Vert _{H^1(\Omega )}\le Ch^3\left\Vert w\right\Vert ^2_2. \end{aligned}$$

Hence, $\left\Vert \eta \right\Vert _{L^2(\partial \Omega )}\le Ch^\frac{3}{2}\left\Vert w\right\Vert _2$.

The idea for showing estimate $\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}$ using variant of the Aubin-Nitsche technique can be found in [10]. For completeness, we provide a brief proof here. Let $\beta =\beta (t)$ be the solution of

$$\begin{aligned} (\nabla \beta ,\nabla \chi )+\lambda (\beta ,\chi )=\langle \delta ,\chi \rangle _{\partial \Omega }, \end{aligned}$$

(4.7)

where $\delta \in H^{1/2}(\partial \Omega )$ is such that

$$\begin{aligned} \left\Vert \delta \right\Vert _{H^{1/2}(\partial \Omega )}=\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}, \quad \langle \delta ,\eta \rangle _{\partial \Omega }=\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}, \end{aligned}$$

where the existence of $\delta$ follows from the Hahn-Banach theorem. Set $\chi =\eta$ and use (4.4) to obtain

$$\begin{aligned} \left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}&=(\nabla \eta , \nabla \beta )+\lambda (\eta ,\beta )\\&=(\nabla \eta , \nabla (\beta -\phi ))+\lambda (\eta ,\beta -\phi )\le C\left\Vert \eta \right\Vert _{1}\left\Vert \beta -\phi \right\Vert _1 \quad \forall \phi \in V_h. \end{aligned}$$

Therefore using $\inf _{\chi \in V_h}\left\Vert v-\chi \right\Vert _i\le Ch^{2-i}\left\Vert v\right\Vert _2, \quad i=0,1$ and (4.6), it follows that

$$\begin{aligned} \left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}&\le Ch\left\Vert \eta \right\Vert _1\left\Vert \beta \right\Vert _2\le Ch\left\Vert \eta \right\Vert _1\left\Vert \delta \right\Vert _{H^{1/2}(\partial \Omega )}\le Ch\left\Vert \eta \right\Vert _1\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}. \end{aligned}$$

Hence $\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\le Ch^2\left\Vert w\right\Vert _2.$

Consider an auxiliary function $\phi$ satisfying the following problem

$$\begin{aligned} -\Delta \phi +\lambda \phi&=0 \quad \text {in} \quad \Omega ,\nonumber \\ \frac{\partial \phi }{\partial \nu }&=\eta _t \quad \text {on} \quad \partial \Omega , \end{aligned}$$

(4.8)

where $\left\Vert \phi \right\Vert _2\le C\left\Vert \eta _t\right\Vert _{H^\frac{1}{2}(\partial \Omega )}$. For a proof of this regularity result see [21].

Similarly we can show that $\left\Vert \eta _t\right\Vert _{H^{-1/2}(\partial \Omega )}\le Ch^2\left\Vert w_t\right\Vert _2.$

Using (2.1), it follows for $q \in [2,\infty )$ that

$$\begin{aligned} \left\Vert \eta \right\Vert _{L^q(\partial \Omega )}\le C\left\Vert \eta \right\Vert _1\le Ch\left\Vert w\right\Vert _2, \end{aligned}$$

and

$$\begin{aligned} \left\Vert \eta _t\right\Vert _{L^q(\partial \Omega )}\le C\left\Vert \eta _t\right\Vert _1\le Ch\left\Vert w_t\right\Vert _2. \end{aligned}$$

This completes the proof. $\square$

With $e:=w-w_h,$ decompose $e:=(w-{{\tilde{w}}}_h)- (w_h-{{\tilde{w}}}_h)=:\eta -\theta ,$ where $\eta =w-{{\tilde{w}}}_h$ and $\theta =w_h-{{\tilde{w}}}_h$.

Since estimates of $\eta$ are known from (4.5) and Lemma 4.3, it is sufficient to estimate $\theta$. Subtracting the weak formulation (2.14) from (4.2) and a use of (4.4) yields

$$\begin{aligned} (\theta _t,\chi )&+\nu (\nabla \theta , \nabla \chi )+\int _{\partial \Omega } \Big ( 2 (c_0+w_d) \theta +\frac{2}{9c_0} \theta ^3+ \frac{2}{3c_0} w_h^2 \theta \Big ) \chi \,\;d\Gamma \nonumber \\&=(\eta _t -\nu \lambda \eta ,\chi ) +w_d\big (\nabla (\eta -\theta )\cdot \mathbf{{1}},\chi \big )+\int _{\partial \Omega } 2 (c_0+w_d)\;\eta \;\chi \;d\Gamma \nonumber \\&\qquad +\big ((\eta -\theta )\nabla w\cdot \mathbf{{1}}+w_h(\nabla \eta -\nabla \theta )\cdot \mathbf{{1}},\chi \big ) +\frac{2}{9c_0}\int _{\partial \Omega }\big (\eta ^3 +3w\eta (w-\eta )+3 w_h \theta ^2 \big ) \chi \;d\Gamma \nonumber \\&= \sum _{i=1}^{5}I_i(\chi ). \end{aligned}$$

(4.9)

Hence forward, we like to restrict the range of $\alpha$, that is,

$$\begin{aligned} 0 \le \alpha \le \frac{1}{C_F}\min \{ 3\nu /4, ((c_0/2)+ w_d)\}. \end{aligned}$$

For such $\alpha$, the results of Sect. 3 are also valid.

In the following theorem, we estimate $\left\Vert \theta (t)\right\Vert$.

Theorem 4.1

Let $w_0\in H^3(\Omega )$. Then, there exists a positive constant $C=C(\left\Vert w_0\right\Vert _3)$ such that there holds

$$\begin{aligned} \left\Vert \theta (t)\right\Vert ^2&+ \beta _1\;e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\Big (\left\Vert \nabla \theta (s)\right\Vert ^2+ \left\Vert \theta (s)\right\Vert ^2_{L^2(\partial \Omega )} +\left\Vert \theta (s)\right\Vert ^4_{L^4(\partial \Omega )} \Big )\;ds\\&\qquad \qquad \le C\Big (\left\Vert w_0\right\Vert _3\Big )\exp \Big (\left\Vert w_0\right\Vert _2\Big )h^4e^{-2\alpha t}, \end{aligned}$$

where $\beta _1= \min \Big (\big (\frac{3\nu }{2}-2\alpha C_F\big ), \big ((c_0+2w_d)- 2\alpha C_F\big ), \frac{1}{27 c_0} \Big )>0$.

Proof

Set $\chi =\theta$ in (4.9) to obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\left\Vert \theta \right\Vert ^2+\nu \left\Vert \nabla \theta \right\Vert ^2 +2 (c_0+ w_d) \Vert \theta \Vert ^2_{L^2(\Omega )} + \frac{2}{9c_0} \Vert \theta \Vert ^4_{L^4(\Omega )} + \frac{2}{3c_0} \int _{\partial \Omega } w_h^2\;\theta ^2\;d\Gamma =\sum _{i=1}^{5}I_i(\theta ). \end{aligned}$$

(4.10)

The first term $I_1(\theta )$ on the right hand side of (4.10) is bounded by

$$\begin{aligned} I_1(\theta )=(\eta _t -\nu \lambda \eta ,\theta )\le C\big (\left\Vert \eta \right\Vert ^2+\left\Vert \eta _t\right\Vert ^2\big )+\frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2, \end{aligned}$$

where $\epsilon >0$ is a positive number which we choose later. For the second term $I_2(\theta )$ on the right hand side of (4.10), a use of the Cauchy-Schwarz inequality with Young’s inequality and $\left\Vert \theta \right\Vert _{H^{1/2}(\partial \Omega )}\le C\left\Vert \theta \right\Vert _1$ yields

$$\begin{aligned} I_2(\theta )&=w_d\Big (\nabla (\eta -\theta )\cdot \mathbf{{1}},\theta \Big )\\&=-w_d\big (\eta ,\nabla \theta \cdot \mathbf{{1}}\big )+w_d\sum _{i=1}^{2}\int _{\partial \Omega }\eta \nu _i\theta d\Gamma -\frac{w_d}{2}\sum _{i=1}^{2}\int _{\partial \Omega }\theta ^2 \nu _i d\Gamma \\&\le C\left\Vert \eta \right\Vert \left\Vert \nabla \theta \right\Vert +C\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert \theta \right\Vert _{H^{1/2}(\partial \Omega )}+w_d\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}\\&\le \frac{\nu }{24}\left\Vert \nabla \theta \right\Vert ^2+\frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2+C\left\Vert \eta \right\Vert ^2+w_d\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}+C\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}. \end{aligned}$$

The third term $I_3(\theta )$ on the right hand side is bounded by

$$\begin{aligned} 2(c_0+ w_d)\langle \eta ,\theta \rangle _{(\partial \Omega )}&\le C\;\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\;\left\Vert \theta \right\Vert _{H^{1/2}(\partial \Omega )} \le C \left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\; (\left\Vert \nabla \theta \right\Vert + \left\Vert \theta \right\Vert ) \\& \le \frac{\nu }{24}\left\Vert \nabla \theta \right\Vert ^2+\frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2+C\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}. \end{aligned}$$

For the fourth term $I_4(\theta ),$ first we use the Gagliardo–Nirenberg inequality for $H^1$ function to bound the following sub-terms as

$$\begin{aligned} \big ((\eta -\theta )&\nabla w\cdot \mathbf{{1}},\theta \big ) \le C\left\Vert \eta \right\Vert \left\Vert \nabla w\right\Vert _{L^4}\left\Vert \theta \right\Vert _{L^4}+C\left\Vert \theta \right\Vert \left\Vert \theta \right\Vert _{L^4}\left\Vert \nabla w\right\Vert _{L^4} \\&\le \frac{\nu }{48}\left\Vert \nabla \theta \right\Vert ^2+\frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2+C\left\Vert \theta \right\Vert ^2 \left\Vert w\right\Vert ^2_2 +C\left\Vert \eta \right\Vert ^2\Big (1+\left\Vert w\right\Vert ^2+\left\Vert \Delta w\right\Vert ^2\Big ) \end{aligned}$$

and apply $w_h= \theta + {\tilde{w}}_h$ with integration by parts and $\Vert {\tilde{w}}_h\Vert _{L^{\infty }} \le C \Vert w\Vert _2$ to obtain a bound

$$\begin{aligned} -(w_h\nabla \theta \cdot \mathbf{{1}},\theta )&= -( \theta \nabla \theta \cdot \mathbf{{1}},\theta )-({\tilde{w}}_h\nabla \theta \cdot \mathbf{{1}},\theta ) =-\frac{1}{3} \sum _{j=1}^2 \int _{\partial \Omega } \theta ^3\; n_j \;d\Gamma -({\tilde{w}}_h\nabla \theta \cdot \mathbf{{1}},\theta )\\&\le \frac{\sqrt{2}}{3} \int _{\partial \Omega } |\theta |^3 \;d\Gamma + \Vert {\tilde{w}}_h\Vert _{L^{\infty }} \left\Vert \nabla \theta \right\Vert \;\left\Vert \theta \right\Vert \\&\le \frac{3c_0}{2} \int _{\partial \Omega } |\theta |^2 \;d\Gamma + \frac{1}{27 c_0} \int _{\partial \Omega } |\theta |^4 \;d\Gamma +\frac{\nu }{48} \left\Vert \nabla \theta \right\Vert ^2 +C\left\Vert \theta \right\Vert ^2 \left\Vert w\right\Vert ^2_2. \end{aligned}$$

Using the Sobolev inequality $\left\Vert \theta \right\Vert _{L^4} \le C \left\Vert \theta \right\Vert _1$ and $\left\Vert {\tilde{w}}_h\theta \right\Vert _{H^{1/2}(\partial \Omega )}\le C \left\Vert w\right\Vert _2 \; \left\Vert \theta \right\Vert _1$, the other sub-term in $I_4(\theta )$ can be bounded by

$$\begin{aligned} \big (w_h\nabla \eta \cdot \mathbf{{1}},\theta \big )&=\big (\theta \nabla \eta \cdot \mathbf{{1}},\theta \big )-\big ({\tilde{w}}_h\nabla \theta \cdot \mathbf{{1}},\eta \big )-\big (\eta \nabla {\tilde{w}}_h\cdot \mathbf{{1}},\theta \big )+\sum _{i=1}^{2}\int _{\partial \Omega }{\tilde{w}}_h\eta \nu _i\theta \; d\Gamma \\&\le \left\Vert \theta \right\Vert \left\Vert \nabla \eta \right\Vert _{L^4} \;\left\Vert \theta \right\Vert _{L^4} + \left\Vert \eta \right\Vert \left\Vert \nabla \theta \right\Vert \left\Vert {\tilde{w}}_h\right\Vert _{L^\infty }+ \left\Vert \eta \right\Vert \left\Vert \nabla {\tilde{w}}_h\right\Vert _{L^4}\left\Vert \theta \right\Vert _{L^4}\\&\quad +\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert {\tilde{w}}_h\theta \right\Vert _{H^{1/2}(\partial \Omega )}\\&\le \frac{\nu }{24}\left\Vert \nabla \theta \right\Vert ^2+\frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2+C\; \big (\left\Vert w\right\Vert ^2_2\;\left\Vert \eta \right\Vert ^2 + \left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}\big ) +C\left\Vert \theta \right\Vert ^2\big (\left\Vert w\right\Vert ^2+\left\Vert \nabla \eta \right\Vert ^2_{L^4}\big ). \end{aligned}$$

For $I_5(\theta ),$ we note that

$$\begin{aligned} \frac{2}{9c_0}\int _{\partial \Omega }\eta ^3\theta d\Gamma&\le C\; \left\Vert \eta \right\Vert ^3_{L^6(\partial \Omega )}\left\Vert \theta \right\Vert _{L^2(\partial \Omega )} \le C \;\left\Vert \eta \right\Vert ^3_{L^6(\partial \Omega )}\;(\left\Vert \nabla \theta \right\Vert + \left\Vert \theta \right\Vert )\\&\le \frac{\nu }{48}\left\Vert \nabla \theta \right\Vert ^2 + \frac{\epsilon }{16} \left\Vert \theta \right\Vert ^2 + C \;\left\Vert \eta \right\Vert ^6_{L^6(\partial \Omega )}, \\ \frac{2}{9c_0}\int _{\partial \Omega }3w^2\eta \theta d\Gamma&\le C\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert w^2\theta \right\Vert _{H^{1/2}(\partial \Omega )}\\&\le C\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert w\right\Vert _2\left\Vert w\theta \right\Vert _{H^{1/2}(\partial \Omega )}\\&\le C\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert w\right\Vert ^2_2\left\Vert \theta \right\Vert _1\\&\le \frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2+\frac{\nu }{48}\left\Vert \nabla \theta \right\Vert ^2+C\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}\left\Vert w\right\Vert ^4_2, \\ \frac{2}{9c_0}\int _{\partial \Omega }3w\eta ^2\theta d\Gamma&\le \frac{\epsilon }{16}\left\Vert \theta \right\Vert ^2+\frac{\nu }{24}\left\Vert \nabla \theta \right\Vert ^2+C\left\Vert w\right\Vert ^2_{L^4(\partial \Omega )}\left\Vert \eta \right\Vert ^4_{L^4(\partial \Omega )}, \end{aligned}$$

and

$$\begin{aligned} \frac{2}{9c_0}\int _{\partial \Omega }3w_h\theta ^3 d\Gamma \le \frac{2}{3c_0}\Bigg (\int _{\partial \Omega } w_h^2\theta ^2 d\Gamma +\frac{1}{4}\int _{\partial \Omega }\theta ^4 d\Gamma \bigg ). \end{aligned}$$

Finally, using Lemmas 3.1-3.4, 4.1 and 4.3, we arrive from (4.10) at

$$\begin{aligned} \frac{d}{dt}\left\Vert \theta \right\Vert ^2&+\frac{3}{2}\nu \left\Vert \nabla \theta \right\Vert ^2+(c_0+2w_d)\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{27c_0}\left\Vert \theta \right\Vert ^4_{L^4(\partial \Omega )}\nonumber \\&\le \epsilon \left\Vert \theta \right\Vert ^2+C\left\Vert \eta \right\Vert ^2(1+\left\Vert w\right\Vert ^2+\left\Vert \Delta w\right\Vert ^2)+C\left\Vert \eta \right\Vert ^6_{L^6(\partial \Omega )}+C\left\Vert \theta \right\Vert ^2(1+h^2)\left\Vert w\right\Vert ^2_2\nonumber \\&\qquad +C\Big (\left\Vert \eta \right\Vert ^4_{L^4(\partial \Omega )}+\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}\Big )\Big (1+\left\Vert w\right\Vert ^2_2+\left\Vert w\right\Vert ^4_{L^4(\partial \Omega )}\Big ). \end{aligned}$$

(4.11)

Multiply (4.11) by $e^{2\alpha t}$ and use Friedrichs’s inequality

$$\begin{aligned} -2\alpha e^{2\alpha t}\left\Vert \theta \right\Vert ^2\ge -2\alpha C_F e^{2\alpha t}\left\Vert \nabla \theta \right\Vert ^2-2\alpha C_Fe^{2\alpha t}\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}. \end{aligned}$$

Then a use of Lemmas 3.1, 3.2, and 4.3in (4.11) yields

$$\begin{aligned} \frac{d}{dt}&\big (\left\Vert e^{\alpha t}\theta \right\Vert ^2\big )+e^{2\alpha t}\Bigg (\Big (\frac{3\nu }{2}-2\alpha C_F\Big )\left\Vert \nabla \theta \right\Vert ^2 +\Big ((c_0+2w_d)-2\alpha C_F\Big )\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{27c_0}\left\Vert \theta \right\Vert ^4_{L^4(\partial \Omega )} \Bigg )\\&\le Ce^{2\alpha t}\Big (\left\Vert \eta \right\Vert ^2+\left\Vert \eta _t\right\Vert ^2 +\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}+C\left\Vert \eta \right\Vert ^4_{L^4(\partial \Omega )}\\&\quad +\left\Vert \eta \right\Vert ^6_{L^6(\partial \Omega )} \Big ) +Ce^{2\alpha t}\left\Vert \theta \right\Vert ^2\;\big ((1+h^2)\left\Vert w\right\Vert ^2_2\big ) \\&\quad +\epsilon C_Fe^{2\alpha t}\Big (\left\Vert \nabla \theta \right\Vert ^2+\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}\Big ). \end{aligned}$$

Integrate the above inequality from 0 to t and choose $\epsilon =\frac{\beta _1}{2C_F}$. Then use the Grönwall’s inequality to obtain

$$\begin{aligned}&\left\Vert e^{\alpha t}\theta (t)\right\Vert ^2+ \beta _1\int _{0}^{t}e^{2\alpha s}\Big (\left\Vert \nabla \theta (s)\right\Vert ^2+\left\Vert \theta (s)\right\Vert ^2_{L^2(\partial \Omega )}+\left\Vert \theta (s)\right\Vert ^4_{L^4(\partial \Omega )}\Big )\;ds\\&\quad \le Ch^4\Big (\int _{0}^{t}\big (\left\Vert w(s)\right\Vert ^2_2+\left\Vert w_t(s)\right\Vert ^2_2\big )\;ds\Big )\exp \Bigg (\int _{0}^{t}\Big ((1+h^2)\left\Vert w(s)\right\Vert ^2_2\Big )\;ds\Bigg ). \end{aligned}$$

A use of Lemmas 3.1–3.5, and 4.1to the above inequality with a multiplication of $e^{-2\alpha t}$ completes the proof. $\square$

Remark 4.1

As a consequence of Theorem  4.1, we use inverse property (4.1) to arrive for $p\in [2,\infty ]$ at

$$\begin{aligned} \left\Vert w_h(t)\right\Vert _{L^p(\Omega )}&\le \left\Vert {\tilde{w}}_h(t)\right\Vert _{L^p(\Omega )} + \left\Vert \theta (t)\right\Vert _{L^p(\Omega )}\nonumber \\&\le C\; \left\Vert w(t)\right\Vert _2 + C\; h^{2(\frac{1}{p}-\frac{1}{2})}\; \left\Vert \theta (t)\right\Vert \le C e^{-\alpha t} \le C. \end{aligned}$$

(4.12)

Theorem 4.2

Let $w_0\in H^3(\Omega )$. Then, there is a positive constant C independent of h such that

$$\begin{aligned} \nu \left\Vert \nabla \theta (t)\right\Vert ^2+&2 (c_0+ w_d)\left\Vert \theta (t)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9c_0}\left\Vert \theta (t)\right\Vert ^4_{L^4(\partial \Omega )}+e^{-2\alpha t}\int _{0}^{t}e^{2\alpha s}\left\Vert \theta _t(s)\right\Vert ^2\;ds\\&\le C\Big (\left\Vert w_0\right\Vert _3\Big )\exp \Big (C\left\Vert w_0\right\Vert _2\Big )h^4e^{-2\alpha t}. \end{aligned}$$

Proof

Set $\chi =\theta _t$ in (4.9) to obtain

$$\begin{aligned} \left\Vert \theta _t\right\Vert ^2+\frac{1}{2}\frac{d}{dt}\Big (\nu \left\Vert \nabla \theta \right\Vert ^2&+ 2(c_0+w_d) \left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )} + \frac{1}{9c_0} \left\Vert \theta \right\Vert ^4_{L^4(\partial \Omega )} + \frac{2}{3c_0} \left\Vert w_h \theta \right\Vert ^2_{L^2(\partial \Omega )}\Big )\nonumber \\&\quad \quad =\sum _{i=1}^{4}I_i(\theta _t) + \Big ( I_5(\theta _t) +\frac{2}{3c_0} \big \langle w_h\;w_{ht}\; \theta ,\theta \big \rangle _{\partial \Omega }\Big ). \end{aligned}$$

(4.13)

The first term $I_1(\theta _t)$ on the right hand side of (4.9) is bounded by

$$\begin{aligned} I_1(\theta _t)=(\eta _t-\lambda \nu \eta ,\theta _t) \le \frac{1}{6}\left\Vert \theta _t\right\Vert ^2+C\Big (\left\Vert \eta \right\Vert ^2+\left\Vert \eta _t\right\Vert ^2\Big ). \end{aligned}$$

The second term $I_2(\theta _t)$ on the right hand side of (4.9) can be rewritten as

$$\begin{aligned} I_2(\theta _t)&=w_d\Big ((\nabla \eta -\nabla \theta )\cdot \mathbf{{1}},\theta _t\Big )\\&=-w_d\frac{d}{dt}\Big (\eta ,\nabla \theta \cdot \mathbf{{1}}\Big )+w_d(\eta _t,\nabla \theta \cdot \mathbf{{1}})+w_d\frac{d}{dt}\Big (\sum _{i=1}^{2}\int _{\partial \Omega }\eta \nu _i\theta \;d\Gamma \Big )\\&\quad -w_d\sum _{i=1}^{2}\int _{\partial \Omega }\eta _t\nu _i\theta \;d\Gamma -w_d(\nabla \theta \cdot \mathbf{{1}},\theta _t), \end{aligned}$$

and hence, we get

$$\begin{aligned} I_2(\theta _t)&=w_d\Big ((\nabla \eta -\nabla \theta )\cdot \mathbf{{1}},\theta _t\Big )\\&\le -w_d\frac{d}{dt}\Big (\eta ,\nabla \theta \cdot \mathbf{{1}}\Big )+ w_d\frac{d}{dt}\Big (\sum _{i=1}^{2}\int _{\partial \Omega }\eta \nu _i\theta d\Gamma \Big )\\&\quad + \frac{1}{12}\left\Vert \theta _t\right\Vert ^2+C\Big (\left\Vert \theta \right\Vert ^2+\left\Vert \nabla \theta \right\Vert ^2\Big )+C\Big (\left\Vert \eta _t\right\Vert ^2+\left\Vert \eta _t\right\Vert ^2_{H^{-1/2}(\partial \Omega )}\Big ). \end{aligned}$$

The third term $I_3(\theta _t)$ on the right hand side of (4.9) is bounded by

$$\begin{aligned} I_3(\theta _t)&=\Big \langle 2(c_0+w_d)\eta ,\theta _t\Big \rangle _{\partial \Omega } = \frac{d}{dt}\Big \langle 2(c_0+w_d)\eta ,\theta \Big \rangle - 2(c_0+w_d)\langle \eta _t,\theta \rangle \\&\le \frac{d}{dt}\Big \langle 2(c_0+ w_d)\eta ,\theta \Big \rangle +C\Big (\left\Vert \theta \right\Vert ^2+\left\Vert \nabla \theta \right\Vert ^2\Big )+C\left\Vert \eta _t\right\Vert ^2_{H^{-1/2}(\partial \Omega )}. \end{aligned}$$

For the fourth term $I_4(\theta _t)$ on the right hand side of (4.9), first we rewrite the sub terms as

$$\begin{aligned} (\eta \nabla w\cdot \mathbf{{1}},\theta _t)=\frac{d}{dt}\Big ((\eta \nabla w\cdot \mathbf{{1}},\theta )\Big )-(\eta _t\nabla w\cdot \mathbf{{1}},\theta )-\Big (\eta (\nabla w\cdot \mathbf{{1}})_t,\theta \Big ), \end{aligned}$$

and bound it using the Gagliardo–Nirenberg inequality for $H^2$ function

$$\begin{aligned} (\eta \nabla w\cdot \mathbf{{1}},\theta _t)&\le \frac{d}{dt}\Big ((\eta \nabla w\cdot \mathbf{{1}},\theta )\Big )+ C\left\Vert \eta _t\right\Vert ^2\Big (1+\left\Vert w\right\Vert ^2_2\Big )+C\left\Vert \theta \right\Vert ^2\Big (1+\left\Vert \Delta w\right\Vert ^2+\left\Vert \Delta w_t\right\Vert ^2\Big )\\&\qquad +C\left\Vert \nabla \theta \right\Vert ^2\Big (\left\Vert w\right\Vert ^2+\left\Vert w_t\right\Vert ^2\Big )+C\left\Vert \eta \right\Vert ^2\left\Vert \Delta w_t\right\Vert ^2. \end{aligned}$$

For the other sub-term of $I_4(\theta _t)$, apply $w_h= \theta + {\tilde{w}}_h$ with and then use integration by parts to obtain

$$\begin{aligned} (w_h\nabla \eta \cdot \mathbf{{1}},\theta _t)&=(\theta \nabla \eta \cdot \mathbf{{1}},\theta _t) -\frac{d}{dt} \Big ((\eta \nabla \theta \cdot \mathbf{{1}}, {\tilde{w}}_h)+\big (\eta (\nabla {\tilde{w}}_h \cdot \mathbf{{1}}),\theta \big )-\sum _{i=1}^{2}\int _{\partial \Omega }\eta {\tilde{w}}_h\nu _i\theta \; d\Gamma \Big )\\&\qquad +\Big ((\eta {\tilde{w}}_h)_t,\nabla \theta \cdot \mathbf{{1}}\Big )+\Big ((\eta \nabla {\tilde{w}}_h\cdot \mathbf{{1}})_t,\theta \Big )-\sum _{i=1}^{2}\int _{\partial \Omega }(\eta {\tilde{w}}_h)_t\nu _i\theta \;d\Gamma , \end{aligned}$$

and hence, from $\left\Vert \theta \right\Vert _{L^4(\Omega )} \le C (\left\Vert \nabla \theta \right\Vert + \left\Vert \theta \right\Vert )$ and $\left\Vert {\tilde{w}}_h\right\Vert _{L^{\infty }}\le C (1+h)\; \left\Vert w\right\Vert _2,$ (see, Ciarlet [9, page 168]), it follows that

$$\begin{aligned} \Big (w_h\nabla \eta \cdot \mathbf{{1}},\theta _t\Big )&\le -\frac{d}{dt}\Big ((\eta \nabla \theta \cdot \mathbf{{1}}, {\tilde{w}}_h)+\big (\eta (\nabla {\tilde{w}}_h \cdot \mathbf{{1}}),\theta \big )-\sum _{i=1}^{2}\int _{\partial \Omega }\eta {\tilde{w}}_h\nu _i\theta \; d\Gamma \Big )\\&\quad + C\left\Vert \eta _t\right\Vert ^2\Big (1+\left\Vert w\right\Vert ^2_2\Big )+C\left\Vert \eta \right\Vert ^2\Big (1+\left\Vert w_{t}\right\Vert ^2_2\Big )\\&\quad +C \big (\left\Vert \theta \right\Vert ^2 +\left\Vert \nabla \theta \right\Vert ^2\big )\; \Big (\left\Vert \nabla \eta \right\Vert _{L^4}^2+\left\Vert \nabla \eta _t\right\Vert ^2_{L^4}+\left\Vert w\right\Vert ^2_2+\left\Vert w_{t}\right\Vert ^2_2\Big )\\&\quad +C\Big (\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}+\left\Vert \eta _t\right\Vert ^2_{H^{-1/2}(\partial \Omega )}\Big ) + \frac{1}{12} \left\Vert \theta _t\right\Vert ^2. \end{aligned}$$

For the remaining other two sub-terms of $I_4(\theta _t),$ a use of $\left\Vert \theta (t)\right\Vert _{L^{\infty }} \le C\;h e^{-\alpha t}\le C$ now leads to

$$\begin{aligned} -\Big (\theta (\nabla w\cdot \mathbf{{1}}),\theta _t\Big )&-\Big (w_h(\nabla \theta \cdot \mathbf{{1}}),\theta _t\Big )= -\Big (\theta (\nabla w\cdot \mathbf{{1}}),\theta _t\Big )-\Big ( (\theta + {\tilde{w}}_h)\;\nabla \theta \cdot \mathbf{{1}},\theta _t\Big )\\&\le \Big (\left\Vert \nabla w\right\Vert _{L^4}\; \left\Vert \theta \right\Vert _{L^4} + (\left\Vert \theta \right\Vert _{L^{\infty } }+ \left\Vert {\tilde{w}}_h\right\Vert _{L^{\infty }}) \left\Vert \nabla \theta \right\Vert \Big )\;\left\Vert \theta _t\right\Vert \\&\le \frac{1}{12}\left\Vert \theta _t\right\Vert ^2+C\;\left\Vert \theta \right\Vert ^2 \;\left\Vert w\right\Vert _2^2+ \left\Vert \nabla \theta \right\Vert ^2\;\big (\left\Vert w\right\Vert ^2_2+ 1\big ). \end{aligned}$$

For the last term on the right hand side of (4.9), the first sub-term is bounded by

$$\begin{aligned} \frac{2}{9c_0}\int _{\partial \Omega }\eta ^3\theta _t \;d\Gamma&=\frac{2}{9c_0}\frac{d}{dt}\Big (\int _{\partial \Omega }\eta ^3\theta \;d\Gamma \Big )-\frac{2}{3c_0}\int _{\partial \Omega }\eta ^2\eta _t\theta \;d\Gamma \\&\le \frac{2}{9c_0}\frac{d}{dt}\Big (\int _{\partial \Omega }\eta ^3\theta \;d\Gamma \Big )+C\Big (\left\Vert \eta \right\Vert ^4_{L^4(\partial \Omega )}+\left\Vert \eta _t\right\Vert ^2_{L^4(\partial \Omega )}\left\Vert \theta \right\Vert ^2_1\Big ). \end{aligned}$$

Similarly, the other sub-terms are bounded by

$$\begin{aligned} \frac{2}{9c_0}\int _{\partial \Omega }3w^2\eta \theta _t\;d\Gamma&\le \frac{2}{3c_0}\frac{d}{dt}\Big (\int _{\partial \Omega }w^2\eta \theta \;d\Gamma \Big )+C\left\Vert \eta _t\right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert w\right\Vert ^2_2\left\Vert \theta \right\Vert _1\\&\quad +C\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\left\Vert w\right\Vert _2\left\Vert w_t\right\Vert _2\left\Vert \theta \right\Vert _1\\ {}&\le \frac{2}{3c_0}\frac{d}{dt}\Big (\int _{\partial \Omega }w^2\eta \theta \;d\Gamma \Big )+C\left\Vert w\right\Vert ^2_2\Big (\left\Vert \theta \right\Vert ^2+\left\Vert \nabla \theta \right\Vert ^2\Big )\\&\quad +C\left\Vert \eta _t\right\Vert ^2_{H^{-1/2}(\partial \Omega )}+C\left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )}\left\Vert w_t\right\Vert ^2_2, \\ -\frac{2}{9c_0}3\int _{\partial \Omega }w\eta ^2\theta _t\;d\Gamma&\le -\frac{2}{3c_0}\frac{d}{dt}\Big (\int _{\partial \Omega }w\eta ^2\theta \;d\Gamma \Big )+C\left\Vert \eta \right\Vert ^4_{L^4(\partial \Omega )}\\&\quad +C\left\Vert \eta \right\Vert ^2_{L^4(\partial \Omega )}\left\Vert \eta _t\right\Vert ^2_{L^4(\partial \Omega )}+C\left\Vert \theta \right\Vert ^2_1\Big (\left\Vert w\right\Vert ^2_1+\left\Vert w_t\right\Vert ^2_1\Big ). \end{aligned}$$

Trace inequality for fractional Sobolev norm yields

$$\begin{aligned} \left\Vert v_h\right\Vert _{L^\infty (\partial K)} \le C( \left\Vert v_h\right\Vert _{L^{\infty }(K)} + h_{K}^{\delta } \left\Vert v_h\right\Vert _{W^{\delta ,\infty }(K)}). \end{aligned}$$

Using inverse inequality $\left\Vert v_h\right\Vert _{W^{\delta ,\infty }(K)} \le C h^{-\delta } \left\Vert v_h\right\Vert _{L^{\infty }(K)}$, we obtain $\left\Vert v_h\right\Vert _{L^\infty (\partial K)} \le C \left\Vert v_h\right\Vert _{L^{\infty }(K)}$.

A use of $\Vert \theta (t)\Vert _{L^{\infty }} \le C \;h e^{-\alpha t}$ with $w_{ht}= \theta _t + {\tilde{w}}_{ht}$, $\left\Vert v_h\right\Vert _{L^\infty (\partial K\cap \partial \Omega )}\le \left\Vert v_h\right\Vert _{L^\infty (\Omega )}$, and inverse inequality $\Vert \theta \Vert _1\le C h^{-1} \Vert \theta \Vert$ yields

$$\begin{aligned} \frac{2}{3c_0} \int _{\partial \Omega } \Big ( w_h \theta ^2 \;\theta _t&+ w_h\;w_{ht}\;\theta ^2\Big )\;d\Gamma = \frac{2}{3c_0} \int _{\partial \Omega } \Big ( 2 w_h \theta ^2 \;\theta _t + w_h\;{\tilde{w}}_{ht}\;\theta ^2\Big )\;d\Gamma \\&\le C\;\Vert w_h\Vert _{L^{\infty }}\Big (\left\Vert \theta \right\Vert _{L^{\infty }} \;\left\Vert \theta \right\Vert _{L^2(\partial \Omega )}\;\left\Vert \theta _t\right\Vert _{L^2(\partial \Omega )} + \big (\left\Vert w_h\right\Vert ^2_{L^{\infty }} +\left\Vert {\tilde{w}}_{ht}\right\Vert ^2_{L^{\infty }}\big )\;\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}\Big )\\&\le C\;\Big ( h\;\left\Vert w\right\Vert _2\;\left\Vert \theta \right\Vert _{L^2(\partial \Omega )}\;\left\Vert \theta _t\right\Vert _1 + \big (\left\Vert w_t\right\Vert _2^2+\left\Vert w\right\Vert _2^2\big )\; \left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )}\Big )\\&\le C\; \big (\left\Vert w_t\right\Vert _2^2+\left\Vert w\right\Vert _2^2\big )\;\left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )} + \frac{1}{12} \left\Vert \theta _t\right\Vert ^2. \end{aligned}$$

Substitute all the above estimates in (4.13), apply kickback argument and then multiply the resulting ones by $e^{2\alpha t}$ with using Lemmas 3.1, 3.4, 4.1 and 4.2 to obtain after setting

$$\begin{aligned} \Vert |\theta (t)\Vert | := \Big (\nu \left\Vert \nabla \theta \right\Vert ^2 + 2(c_0+w_d) \left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )} + \frac{1}{9c_0} \left\Vert \theta \right\Vert ^4_{L^4(\partial \Omega )} + \frac{2}{3c_0} \left\Vert w_h \theta \right\Vert ^2_{L^2(\partial \Omega )}\Big )^{1/2} \end{aligned}$$

and

$$\begin{aligned} F(\eta ,w_h)(\theta )&:= \Bigg (\big (\eta (\nabla w_h\cdot \mathbf{{1}}),\theta \big ) +\big (\eta (\nabla \theta \cdot \mathbf{{1}}),w_h \big ) -\big (\eta (\nabla w\cdot \mathbf{{1}}),\theta \big )\\&\qquad -\sum _{i=1}^{2}\int _{\partial \Omega }\eta w_h\nu _i\theta \;d\Gamma -(2c_0+2w_d)<\eta ,\theta >_{\partial \Omega }\Bigg ) \end{aligned}$$

as

$$\begin{aligned} \frac{d}{dt}\Bigg (e^{2\alpha t} \Vert |\theta (t) \Vert |^2 \Bigg )&+e^{2\alpha t}\left\Vert \theta _t\right\Vert ^2 \le 2\alpha e^{2\alpha t} \Vert |\theta (t)\Vert |^2 -\frac{d}{dt} \Big (e^{2\alpha t} \;F(\eta ,w_h)(\theta )\Big ) + 2\alpha e^{2\alpha t} \;F(\eta ,w_h)(\theta )\\&+C\;e^{2\alpha t} \Big (\left\Vert \eta \right\Vert ^2+\left\Vert \eta _t\right\Vert ^2 +\left\Vert \eta \right\Vert ^2_{L^{4}(\partial \Omega )} + \left\Vert \eta \right\Vert ^2_{H^{-1/2}(\partial \Omega )} + \left\Vert \eta _t\right\Vert ^2_{H^{-1/2}(\partial \Omega )}\Big )\\&+Ce^{2\alpha t}\left\Vert \theta \right\Vert ^2 \Big (1+ \left\Vert w\right\Vert ^2_2+\left\Vert w_t\right\Vert ^2_2 +\left\Vert \eta _t\right\Vert ^2_{L^{4}(\partial \Omega )} \Big ) + C\;e^{2\alpha t}\left\Vert \theta \right\Vert ^4_{L^4(\partial \Omega )}\;\left\Vert w_{t}\right\Vert _2^2 \\&+ C\;e^{2\alpha t} \left\Vert \nabla \theta \right\Vert ^2 \Big ( \left\Vert w\right\Vert _2^2+ \left\Vert w_t\right\Vert _2^2 + \left\Vert \eta _t\right\Vert ^2_{L^4(\partial \Omega )}\Big )+Ce^{2\alpha t}\left\Vert \nabla \theta \right\Vert ^2. \end{aligned}$$

Integrate the above inequality from 0 to t. Note that using the bound $\left\Vert w_h\right\Vert _{L^{\infty }} \le C \;\left\Vert w\right\Vert _2$, we obtain

$$\begin{aligned} 2\alpha \int _{0}^{t} e^{2\alpha s} \Vert |\theta (s)\Vert |^2\;ds \le C\,\int _{0}^{t} e^{2\alpha s} \Big (\left\Vert \nabla \theta \right\Vert ^2 + \left\Vert \theta \right\Vert ^2_{L^2(\partial \Omega )} + \left\Vert \theta \right\Vert ^4_{L^4(\partial \Omega )}\Big )\;ds \end{aligned}$$

and using the splitting $w_h=\theta + {\tilde{w}}_h$ for first term of F, we bound F as

$$\begin{aligned} F(\eta ,w_h)(\theta )&\le C \;\Big (\left\Vert \eta \right\Vert _{L^4(\Omega )}\;\left\Vert \theta \right\Vert +\left\Vert \eta \right\Vert \;\left\Vert w\right\Vert _2 + \left\Vert w\right\Vert _2\;\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\Big ) \;(\left\Vert \theta \right\Vert +\left\Vert \nabla \theta \right\Vert )\\&\le \frac{\nu }{2}\left\Vert \nabla \theta (t)\right\Vert ^2 + C \Big ( (1+\left\Vert w\right\Vert _2^2 )\;\left\Vert \theta \right\Vert ^2 +\left\Vert \eta \right\Vert ^2\;\left\Vert w\right\Vert _2^2 + \left\Vert w\right\Vert _2^2\;\left\Vert \eta \right\Vert _{H^{-1/2}(\partial \Omega )}\Big ). \end{aligned}$$

Then use kickback argument and apply estimate (4.5), Lemmas 3.2, 3.4, 3.5, 4.3 and Theorem 4.1 to arrive at

$$\begin{aligned}&e^{2\alpha t} \Big (\frac{\nu }{2} \left\Vert \nabla \theta (t)\right\Vert ^2+ 2(c_0+ w_d)\left\Vert \theta (t)\right\Vert ^2_{L^2(\partial \Omega )}+\frac{1}{9c_0}\left\Vert \theta (t)\right\Vert ^2_{L^4(\partial \Omega )}+\frac{2}{3c_0}\int _{\partial \Omega }w_h(t)^2\theta (t)^2\;d\Gamma \Big )\\&\quad + \int _{0}^{t}e^{2\alpha s}\left\Vert \theta _t(s)\right\Vert ^2\;ds \le Ch^4 \;\Big (\left\Vert w_0\right\Vert _3\Big )\exp \Big (C\left\Vert w_0\right\Vert _2\Big ) \\&\quad + C \int _{0}^{t} e^{2\alpha s} \;\left\Vert w_t\right\Vert ^2_2 \;e^{2\alpha s} \left\Vert \nabla \theta (t)\right\Vert ^2\;ds. \end{aligned}$$

Now a use of Gronwall’s Lemma with a multiplication of $e^{-2\alpha t}$ completes the rest of the proof. $\square$

As a consequence of Theorem  4.2, we obtain a super convergence result $\left\Vert \nabla (w_h(t)-{{\tilde{w}}}_h(t))\right\Vert$. This, in turn, provides an optimal order of convergence result for feedback control law. Finally, the main theorem of this section, which provides optimal error estimates (optimality with respect to approximation property) in the state variable as well as feedback control law is given below.

Theorem 4.3

There is a positive constant $C=C(\left\Vert w_0\right\Vert _3)$ independent of h such that

$$\begin{aligned} \left\Vert w-w_h\right\Vert _{L^\infty (H^i)}\le Ch^{2-i}e^{-\alpha t}\exp \Big (\left\Vert w_0\right\Vert _2\Big ),\quad i=0,1 \end{aligned}$$

and

$$\begin{aligned} \left\Vert v_{2t}-v_{2ht}\right\Vert _{L^\infty (L^2(\partial \Omega ))}\le Ch^{3/2}e^{-\alpha t}\exp \Big (\left\Vert w_0\right\Vert _2\Big ). \end{aligned}$$

Proof

First part of the proof follows from estimates of $\eta$ in (4.5) and Theorems 4.1 and 4.2with a use of triangle inequality.

For the second part, we note that

$$\begin{aligned} v_{2t}-v_{2ht}=-\frac{1}{\nu }\Big (2(c_0+w_d)(\eta -\theta )+\frac{2}{9c_0}(\eta -\theta )(w^2+ww_h+w_h^2)\Big ). \end{aligned}$$

Hence, using $w_h=\theta +{{\tilde{w}}}_h$ we get

$$\begin{aligned}&\left\Vert v_{2t}-v_{2ht}\right\Vert _{L^\infty (L^2(\partial \Omega ))}\\&\le C\Big (\left\Vert \eta \right\Vert _{L^\infty (L^2(\partial \Omega ))}+\left\Vert \theta \right\Vert _{L^\infty (L^2(\partial \Omega ))}\Big )\Big (1+\left\Vert w\right\Vert ^2_{L^\infty (L^4(\partial \Omega ))}+\left\Vert \tilde{w}_h\right\Vert ^2_{L^\infty (L^4(\partial \Omega ))}+\left\Vert \theta \right\Vert ^2_{L^\infty (L^4(\partial \Omega ))}\Big ). \end{aligned}$$

A use of Lemmas 3.2, 4.3 and Theorem 4.2 completes the proof. $\square$

5 Numerical Experiments

In this section, we conduct several numerical experiments to observe stabilizability of the system (2.6)–(2.8). More precisely, the convergence of the unsteady solution to its constant steady state solution using nonlinear Neumann feedback control law are shown. Moreover, we show the order of convergence for both state variable and feedback control law by solving (2.14). Finally, our last example concerns with the stabilization of solution for the forced viscous Burgers’ equation applying linear control law in which case steady state solution is nonconstant.

For a complete discrete scheme, we use a semi-implicit Characteristic-Galerkin method as follows: Let $0<k<1$ denote the time step size and $t_n=nk,$ where n is nonnegative integer. For smooth function $\phi$ defined on $[0,\infty ),$ set $\phi ^n=\phi (t_n).$ We now apply the Characteristic-Galerkin method to approximate

$$\begin{aligned} (w_t,\varphi _h)+\Big (w\big (\nabla w\cdot \mathbf{{1}}\big ),\varphi _h\Big )\approx (\frac{W^{n}-W^{n-1}(X^{n-1}(x))}{k},\varphi _h), \end{aligned}$$

where $X^{n-1}(x)$ is an approximation of the solution at $t=(n-1)k$ of the ordinary differential equation $\frac{d\mathbf{X}(t)}{dt}=\mathbf{W}^{n-1}(\mathbf{X}(t))$, $\mathbf{X}(nk)=x$, where $\mathbf{W}^{n-1}(x)=(w(x,(n-1)k), w(x,(n-1)k))$ and $\mathbf{X}=(X_1,X_2)$. Now this can be easily solve by Freefem++ ’convect’ operator command. Hence, finally we seek $\{{W^n}\}_{n\ge 1}\in V_h$ as a solution of

$$\begin{aligned} \frac{(W^n,\varphi _h)}{k}&-\frac{1}{k}\Big ((convect([W^{n-1}, W^{n-1}],-k,W^{n-1}),\varphi _h)\Big )+\nu (\nabla W^n,\nabla \varphi _{h})+w_d\big (\nabla W^n\cdot \mathbf{{1}},\varphi _h\big )\nonumber \\&+\Big \langle 2(c_0+w_d)W^n+(\frac{2}{9c_0}(W^{n-1})^2)W^n,\varphi _h\Big \rangle =0 \quad \forall ~ \varphi _h \in V_h, \end{aligned}$$

(5.1)

with $W^0=w_{0h}$. For more details see [13]. For state and control trajectories final plot, we use Matlab.

Example 5.1

We choose initial condition $w_0$ as $w_0=x_1(x_1-1)x_2(x_2-1)-3,$ where $w_d=3$ is the steady state solution and $\nu =1$ with $\Omega =[0,1]\times [0,1]$. For uncontrolled solution, we take zero Neumann boundary condition in (2.14) and corresponding solution is denoted as “Uncontrolled solution” in Fig. 1. For controlled solution, we choose the Neumann control (2.13) with $c_0=1$ and corresponding solution is denoted as “Controlled solution, $c_0=1$” in Fig. 1.

Fig. 1

State, Example 5.1

Table 1 Errors and convergence rate of w when $c_0=1$, $k=0.0001$ and $t=1$ for Example 5.1

Table 2 Errors and convergence rate of $v_2$ when $c_0=1$ and $t=1$ for Example 5.1

From Fig. 1, we can easily see that without any control i.e. with zero Neumann boundary, solution of (2.14) does not settle at zero, whereas applying the control (2.13), the solution for the problem (2.14) in $L^2$- norm goes to zero. Also it is observed that for other values of $c_0>0$, the system (2.14) is stabilizable. From Table 1, it follows that $L^2$ and $H^1$ orders of convergence for state variable w(t) are 2 and 1, respectively, which confirms our theoretical results established in Theorem 4.3. Since the exact solution is unknown in this case, we have taken very refined mesh solution as exact solution to compute the order of convergence. In Table 2, it is noted that the order of convergence of feedback control law (2.13) is 2, while theoretically it is proved to be 3/2 in Theorem 4.3. Behavior of the trajectory of the control law (2.13) which tends to zero, is shown in Fig. 2.

Example 5.2

In this example, take the initial condition $w_0=\sin (\pi x_1)\sin (\pi x_2)$ and $\nu =0.05$, $c_0=1$ with 0 as the steady state solution in $\Omega =[0,1]\times [0,1]$.

Fig. 2

Control, Example 5.1

Fig. 3

State, Example 5.2

Fig. 4

Control, Example 5.2

From Fig. 3, it is observed that steady state solution $w_d=0$ is unstable in the first case denoted as “Uncontrolled solution”. But using the control law (2.13), it is shown that state w in $L^2$- norm goes to zero exponentially. Figure 4 indicates how control law (2.13) behave with time and tends to settle at zero after some time.

Now the following example is related to the Remark 3.2 where the control law is applied to some part of the boundary. In the remaining part, either zero Dirichlet or zero Neumann condition is considered.

Example 5.3

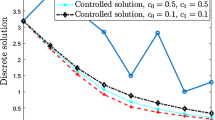
We take the initial condition $w_0=\cos (\pi x_1)\cos (\pi x_2)-5$, where $w_d=5$ is the steady state solution with $\nu =0.01$ and $\Omega =[0,1]\times [0,1]$. We consider two cases.

Case 1:

Take zero Dirichlet boundary $\Gamma _D={1}\times [0,1]$ and on the remaining parts Neumann boundary control $\Gamma _N$. For controlled solution, we take (2.13) with $c_0=10$ on $\Gamma _N$ i.e. on 3 parts of the boundary. We then compare the trajectories with another case which is given below.

Case 2:

We consider zero Dirichlet boundary $\Gamma _D={1}\times [0,1]$, put the Neumann boundary control on ${0}\times [0,1]$ and put zero Neumann boundary condition on other 2 parts. So, in Case 2 control works only on one part of the boundary. For uncontrolled solution, we take zero Neumann boundary condition on $\Gamma _N$ and zero Dirichlet on $\Gamma _D={1}\times [0,1]$.

Fig. 5

State, Example 5.3

Fig. 6

Control, Example 5.3

From Fig. 5, it is clear that with homogeneous mixed boundary condition, uncontrolled solution does not change its state to zero whereas in presence of control on $\Gamma _N$ only, state and control trajectories go to zero both in Case 1 and Case 2. Since in Case 2, control works only in one part of the boundary, so control needs more time compare to Case 1 to settle its state to zero, which is also visible in Fig. 5. The $L^2$- norm of feedback control has a tendency to settle at zero faster in the Case 2 compare to Case 1 which is documented in Fig. 6. Also we have not observed much differences in the trajectories if we change the zero Dirichlet by zero Neumann condition in Case 1. Concerning zero Dirichlet boundary on more parts of the boundary e.g. if we take $w=0$ on 3 parts of the boundary with Neumann control on remaining one part, corresponding state tends to settle at zero even within $t<1$ since with zero Dirichlet boundary, the system is already stable.

Below we discuss another example, where steady state solution is not a constant for the forced Burgers’ equation. It will be shown that, even with the linear control law, system can be stabilizable numerically.

Example 5.4

We now consider a case when the steady state solution is not constant:

$$\begin{aligned}&u_t-\nu \Delta u+u(\nabla u\cdot \mathbf{{1}})=f^\infty \qquad \text {in}\quad (x,t)\in \Omega \times (0,\infty ), \nonumber \\&\frac{\partial u}{\partial n}(x,t)=g^\infty +v_2(x,t)\qquad \text {on} \quad (x,t)\in \partial \Omega \times (0,\infty ),\nonumber \\&u(x,0)=u_0(x)\qquad x\in \Omega , \end{aligned}$$

(5.2)

where, $f^\infty$ and $g^\infty$, independent of t are functions of $x_1$ and $x_2$ only. Corresponding equilibrium or steady state solution $u^\infty$ of the unsteady state problem satisfies

$$\begin{aligned} -\nu \Delta u^\infty +u^\infty (\nabla u^\infty \cdot \mathbf{{1}})&=f^\infty \qquad \text {in} \quad \Omega ,\nonumber \\ \frac{\partial u^\infty }{\partial n}&=g^\infty \quad \text {on} \quad \partial \Omega . \end{aligned}$$

(5.3)

Let $w=u-u^\infty$. Then, w satisfies

$$\begin{aligned}&w_t-\nu \Delta w+u^\infty (\nabla w\cdot \mathbf{{1}})+w(\nabla u^\infty \cdot \mathbf{{1}})+w(\nabla w\cdot \mathbf{{1}})=0 \qquad \text {in}\quad (x,t)\in \Omega \times (0,\infty ),\nonumber \\&\frac{\partial w}{\partial n}(.,t)=v_2(x,t),\quad \text {on} \quad \partial \Omega \times (0,\infty ),\nonumber \\&w(0)=u_0-u^\infty =w_0(\text {say})\quad \text {in}\quad \Omega . \end{aligned}$$

(5.4)

Similarly as before we solve (5.4) using Freefem++ as in (5.1) with linear control law $v_2=-\frac{1}{\nu }c_0W^n$.

For the numerical experiment, we choose viscosity parameter $\nu =0.1$, steady state solution $u^\infty =-0.2x_1$, forcing function $f^\infty =0.04x_1$ and $g^\infty = -0.2n_1$, control parameter $c_0=10$ with initial condition $w_0=\sin (\pi x_1)\sin (\pi x_2)+0.2x_1$ in $\Omega =[0,1]\times [0,1]$.

Fig. 7

State, Example 5.4

Fig. 8

Control, Example 5.4

From the first draw line in Fig. 7, we observe that nonconstant steady state solution is not asymptotically stable with zero Neumann boundary condition. But, using the linear control law $-\frac{1}{\nu }c_0W^n$, system (5.4) is stabilizable which is also documented in Fig. 7. Figure 8 shows that the linear control law $-\frac{1}{\nu }c_0W^n$ decays to zero as time increases. However, we do not have a theoretical result to substantiate this observation. We believe that the system is locally stabilizable with this linear control law.

6 Concluding Remarks

In this paper, global stabilization results for the two dimensional viscous Burgers’ equation are established in $L^\infty (H^i)$, $i=0,1,2$ norms, when the steady state solution is constant. Optimal error estimates in $L^\infty (L^2)$ and in $L^\infty (H^1)$ for the state variable are established. Further, error estimate for the feedback controller is also shown. All the results are verified by numerical examples. Now under addition of forcing function in the two dimensional viscous Burgers’ equation, the steady state solution is no more constant and as such the present analysis does not hold for nonconstant steady state case. Hence, the analysis for two dimensional generalized forced viscous Burgers’ equation will be addressed in future.