In vitro proton magnetic resonance spectroscopy at 14T for benign and malignant ovary: Part I, signal processing by the nonparametric fast Padé transform

Abstract

The present study deals with two different kinds of time signals, encoded by in vitro proton magnetic resonance spectroscopy (MRS) with a high external static magnetic field, 14.1T (Bruker 600 MHz spectrometer). These time signals originate from the specific biofluid samples taken from two patients, one with benign and the other with malignant ovarian cysts. The latter two diagnoses have been made by histopathologic analyses of the samples. Histopathology is the diagnostic gold standard in medicine. The obtained results from signal processing by the nonparametric derivative fast Padé transform (dFPT) show that a number of resonances assignable to known metabolites are considerably more intense in the malignant than in the benign specimens. Such conclusions from the dFPT include the recognized cancer biomarkers, lactic acid and choline-containing compounds. For example, the peak height ratio for the malignant-to-benign samples is about 18 for lactate, Lac. This applies equally to doublet Lac(d) and quartet Lac(q) resonating near 1.41 and 4.36 ppm (parts per million), respectively. For the choline-containing conglomerate (3.19-3.23 ppm), the dFPT with already low-derivative orders (2nd, 3rd) succeeds in clearly separating the three singlet component resonances, free choline Cho(s), phosphocholine PC(s) and glycerophosphocholine GPC(s). These constituents of total choline, tCho, are of critical diagnostic relevance because the increased levels, particularly of PC(s) and GPC(s), are an indicator of a malignant transformation. It is gratifying that signal processing by the dFPT, as a shape estimator, coheres with the mentioned histopathology findings of the two samples. A very large number of resonances is identifiable and quantifiable by the nonparametric dFPT, including those associated with the diagnostically most important low molecular weight metabolites. This is expediently feasible by the automated sequential visualization and quantification that separate and isolate sharp resonances first and subsequently tackle broad macromolecular lineshape profiles. Such a stepwise workflow is not based on subtracting nor annulling any part of the spectrum, in sharp contrast to controversial customary practice in the MRS literature. Rather, sequential estimation exploits the chief derivative feature, which is a faster peak height increase of the thin than of the wide resonances. This is how the dFPT simultaneously improves resolution (linewidth narrowing) and reduces noise (background flattening). Such a twofold achievement makes the dFPT-based proton MRS a high throughput strategy in tumor diagnostics as hundreds of metabolites can be visualized/quantified to offer the opportunity for a possible expansion of the existing list of a handful of cancer biomarkers.

1 Introduction

The main interest of cancer medicine in proton magnetic resonance spectroscopy ($\mathrm{{}^1H\,MRS}$) is largely driven by a twofold noninvasive procedure: monitoring metabolic processes and differentiating between normal and malignant tissues. Such a strategy encompasses both the initial differential diagnoses of primary tumors (benign versus cancerous) and post-therapeutic follow-up management of malignancies. Both purposes are of utmost importance, given that the ultimate goal of the physician is to bring the disease under control.

Here, the key word ’control’ intervenes at the primary diagnoses and post-treatment levels. Malignant transformations occur first on a molecular level and their early detection by $\mathrm{{}^1H\,MRS}$ enhances the possibility for the patient survival. Likewise, the usage of $\mathrm{{}^1H\,MRS},$ while following patients treated for cancers, is an opportunity to noninvasively evaluate efficiency of different therapies. The principal results of such evaluations, the response of primary cancers to therapy, as a measurable quantity, should be an integral part of clinical trials.

To make a further progress in $\mathrm{{}^1H\,MRS}$ towards this goal, it is necessary to identify certain characteristic metabolic disorders or derangements associated with malignant transformations. This is an extremely challenging task given that there are many different kinds of cancers and, of course, metabolism varies from organ to organ. Thus, one cancer biomarker can be synthesized through unequal metabolic pathways in different human organs. Yet, numerous clinical studies have shown that even for several vital organs (brain [1,2,3], prostate [4,5,6], breast [7,8,9,10,11], ovary [12,13,14,15,16,17,18,19], cervix [20,21,22,23,24]), some metabolites, particularly the choline-containing compound and lactic acid, systematically exhibit significantly higher concentration levels in malignant than in benign lesions.

Importantly, in prostate, such a relationship for cholines and lactate coexists with the opposite trend for a concurrent cancer biomarker. This is citrate (Cit) whose concentration levels have consistently been found to be considerably lower in malignant than in normal tissue [4,5,6]¹. That these crucial metabolic distinctions of carcinomas in the mentioned five organs are spectroscopically detectable in a noninvasive way by $\mathrm{{}^1H\,MRS}$ is all the more remarkable.

Nevertheless, the usefulness of either in vivo or in vitro $\mathrm{{}^1H\,MRS}$ is not directly provided by clinical scanners nor spectrometers. These may only visually identify some recognized cancer biomarkers, even with high magnetic field spectrometers with or without the so-called magic angle spinning of specimens excised from a human organ. However, this is utterly insufficient for medical diagnostics for which metabolites must be reliably quantified to obtain molar concentrations. More precisely, the key sought spectral information (accurate resonance peak parameters) for malignant and benign samples ought to be significantly dissimilar to allow adequate distinction between the diseased and normal tissues.

For decades now, because of various reasons (both technical in encodings and analytical in reconstructions), these conditions were hard to fulfill with time signals encoded both by in vivo and in vitro $\mathrm{{}^1H\,MRS},$ operating at low and high magnetic field strengths, respectively. This is due to the most frequently employed, yet wholly unsuitable approach to signal processing, the fast Fourier transform (FFT), post-processed by various fitting recipes that are all but forgotten long ago in basic sciences, including physics and chemistry.

The present study is on in vitro $\mathrm{{}^1H\,MRS}$ with a Bruker 600 MHz spectrometer ($B_0\approx 14.1\,{\mathrm{T}}$) used in Ref. [15] to encode time signals from ovarian cyst fluids of patients. This high magnetic field strength $B_0$ is about 9.4 and 4.7 times stronger than $B_0=$1.5 and 3T in our most recent studies on in vivo $\mathrm{{}^1H\,MRS}$ with clinical scanners using time signals encoded from the malignant brain and ovary of the patients [25, 26], respectively. The particular manner in which we tackle this subject is through helping decision making in diagnostics by providing the clinically reliable signal processing methods. Such mathematical methods can give adequate interpretation of the encoded time signals or free induction decay (FID) curves, and the corresponding spectra reconstructed by computation.

Invaluable information about the disease state in patients with cancer can be obtained from the metabolic fingerprints generated by means of the properly designed quantification of FIDs, encoded utilizing $\mathrm{{}^1H\,MRS}$ from biofluids [27,28,29,30,31]. As we have done previously [25, 26], here too, we will carry out signal processing through shape estimation by using the derivative fast Padé transform (dFPT) [32,33,34,35,36,37]. In other words, of primary interest and focus is again the nonparametric version of the dFPT. This is an upgrade of the nonderivative nonparametric fast Padé transform (FPT) [38,39,40,41,42,43,44,45,46,47]. The nonparametric dFPT begins as a purely shape estimator, which after only 2–4 derivatives, becomes de facto the parameter estimator. Thus, the dFPT as a shape estimator can, in fact, quantify on its own without resorting to any fitting procedures.

Usually, shape estimators have no capability to autonomously quantify, i.e. to provide the key clinical information through the signatures of the reconstructed physical resonances, the peak positions, widths, heights (and, hence, the peak areas that are proportional to the metabolite concentrations). In particular, the full width at half maximum (FWHM) for an absorptive Lorentzian resonance lineshape is equal to $1/(\pi T^\star _2).$ Here, $T^\star _2$ is an effective spin-spin relaxation time constant, $T^\star _2=T_2/(1+T_2\gamma \mathrm{\Delta }B_0),$ where $\gamma \mathrm{\Delta }B_0>0.$ Here, constant $\gamma$ is the gyromagnetic ratio (the quotient of the angular and magnetic moments of a spin-active nucleus). The $T^\star _2$ parameter is smaller than the intrinsic transverse relaxation time constant $T_2.$ This occurs because of the presence of the local, shielding magnetic field $\mathrm{\Delta }B_0,$ which stems from the paramagnetism of the surrounding electrons bound in atoms, ions or molecules in the examined sample.

In our most recent mentioned studies on in vivo $\mathrm{{}^1H\,MRS}$ [25, 26], we employed time signals of short lengths $N=512$ and 1024. Therein, the dFPT reconstructed many physical resonances of metabolites present in the human tissues (>50 [25] and >150 [26]) in a relatively small frequency band of the main diagnostic interest, 1-4 ppm (parts per million). All the resonances, reconstructed by the third or fourth derivatives in the dFPT, were sharp and fully resolved down to the completely flat background baselines. The separations between any two adjacent resonances were sufficient to unambiguously define the integration limits for application of any standard quadrature (Gauss-Legendre, ...) to determine the peak areas and, therefore, the concentrations of metabolites.

From the clinical standpoints, one of the main foci in Refs. [25, 26] was unequivocal detection and quantification of the recognized cancer biomarkers, such as lactate (Lac), free choline (Cho) and phosphocholine (PC). The perennial diagnostic challenge for in vivo $\mathrm{{}^1H\,MRS}$ with low magnetic field clinical scanners (1.5, 3T) is the inability to detect Cho and PC (resonating around 3.20 ppm) as two separate resonances instead of their usual spectral amalgamation within a single compound peak, the total choline (tCho). Another diagnostic dilemma is caused by the lack of separation of the peaks for the lactate and lipids that resonate in a close proximity of each other, near 1.4 ppm. In both studies [25, 26], for the first time within purely shape estimations, Cho and PC were fully delineated by the nonparametric dFPT.

Broader resonances for macromolecules (lipids, fatty acids, proteins, ...) cluster beneath narrower peaks for metabolites of the main diagnostic relevance, e.g. isoleucine (Iso), leucine (Leu), valine (Val), $\beta -$hydroxybutyric acid ($\beta -$HB or 3-HB), threonine (Thr), alanine (Ala), lactate Lac, lysine (Lys), nitrogen acetyl aspartate (NAA), methionine (Met), glutamine (Gln), glutamate (Glu), creatine (Cr), creatinine (Crn), {5,6}-dihydrothymine (DHT), choline Cho, phosphocholine PC, glycerophosphocholine (GPC), ethanolamine (Eth), phosphoethanolamine (PE), glycerophosphoethanolamine (GPE), taurine (Tau), myo-inositol (m-Ins), glucose (Glc), etc. In this way macromolecular resonances lift the background baselines on which the main metabolite resonances are superimposed.

Expectedly then, such hills of macromolecules (together with the long multiple tails of the residuals after water suppression in the process of encoding) may appreciably enhance the peak areas (and, thus, the concentrations) of the diagnostically informative metabolites. This could cause considerable confusion and ambiguities in attempting to make differential diagnoses (benign versus malignant). This obstacle is further exacerbated by the occurrence that most data analyses rely upon the FFT (the lowest resolution estimator), which is post-processed by fitting, as stated, in attempts to assess the main metabolite concentrations.

It is well-documented on multiple counts that the FFT is inadequate for MRS [40, 41, 44,45,46,47,48]. The main task of MRS is to provide the quantitative data for the metabolites present in the examined tissue (chemical shifts, relaxation times, concentrations), not to yield merely the often clinically unusable FFT-based lineshape profiles. The FFT cannot quantify on its own as it necessitates post-processing by various fitting techniques. Any fitting technique is the least-square adjustment of a set of free parameters in a mathematical function chosen to describe the given spectrum. None of the available fitting recipes in the MRS literature is reliable as they invariably fail to detect some physical (genuine) resonances and yield some unphysical (spurious) resonances that spoil the output data. This makes all fitting recipes invalid for clinical diagnostic purposes. Moreover, the FFT as a linear mapping cannot suppress noise from encodings.

Further, the common practice in the MRS literature is to fit the rolling background baseline using some low-degree (2nd-4th) spline polynomials and subtract the obtained result from the full FFT envelope. This arbitrary and dubious procedure can uncontrollably change the true concentrations of many metabolites by the unknown amount. Similarly, the customary FFT-based treatments of macromolecules are also mired with arbitrariness [49,50,51,52,53,54,55,56,57,58,59,60]. This is the case because first, a fitting of the visible main metabolites is made to roughly determine the peak parameters. Then, a model spectrum made up from such estimated peak parameters is subtracted from the full FFT envelope. The residual, believed to be comprised solely of macromolecules, is fitted again. The outcome is treated as if it were an estimation of the true concentration of macromolecules.

In reality, however, this is altogether untenable. Firstly, the residual spectra would invariably contain some resonances other than those assignable to macromolecules. This occurs because the so-called ’visible’ main metabolites are often invisibly structured, as they may contain the underlying, overlapped components. Secondly, this double fitting is prone to exacerbate the nonuniqueness of the whole procedure of adjusting the freely chosen parameters to the investigated lineshape profiles.

We adopt an entirely different strategy, the nonparametric shape estimation by the dFPT. This versatile methodology is at every stage automatically controlled by its self-correcting procedures with a twofold benefit, the tandem improvements of resolution and signal-to-noise ratio (SNR). Such an achievement is accomplished by systematically narrowing the linewidths of resonances and flattening the background baselines. Linewidth narrowings translate into the resolution improvement in spectra. Moreover, by definition, narrower peaks are taller. This fact and the flattened baseline translate into a higher SNR. These are the prime advantages of derivative over nonderivative estimations of envelopes within the dFPT.

By contrast, the derivative fast Fourier transform (dFFT) flagrantly fails as it simultaneously deteriorates both resolution and SNR. This occurs because the derivative operator within the Fourier processing emphasizes the FID data points encoded at later times at which noise prevails. Low resolution and poor SNR are the two main bottlenecks of MRS, when it is accompanied by the FFT, which is used in all scanners. It is then the FFT that slowed down the entry of MRS into the routine clinic practice. The derivative Padé methodology by shape estimations alone overcomes all the FFT-type obstacles as has recently been demonstrated in a comprehensive and compelling manner by way of different types of time signals: synthesized (noiseless, noisy) [32,33,34] and encoded (from a dedicated phantom [35,36,37] and from patients [25, 26, 61]).

Traditionally, the term ’high-resolution’ for usual (nonderivative) signal processing in MRS is reserved exclusively to parametric estimations, such as the FPT, etc. The parametric FPT achieves high resolution by reconstructing all the components underlying the given envelope. Especially for the clinically most needed in vivo MRS at 1.5 and 3T, the clause ’high-resolution shape estimation’ was for a long time considered as unachievable. The reason is in the abundance of overlapping resonances that no customary shape estimator from the nonderivative signal processing category could resolve.

Of late, however, the derivative signal processing in MRS by the nonparametric dFPT extended the notion of high-resolution to encompass shape estimations, as well. This method solves the overlapping resonance problem for in vivo MRS at 1.5 and 3T through linewidth narrowings and baseline flattenings, as stated [25, 26, 35,36,37]. Such a tandem effect succeeds in splitting apart the most intense resonances first by the derivatives of low orders (2nd-4th). Subsequently, the remaining weaker resonances can also be isolated by application of some higher-order derivatives through shape estimations by the dFPT. This is the concept of sequential derivative shape estimations.

Eventually, all the resonances, even the weakest, can be isolated in this manner by being sequentially separated out without any subtraction procedure. In other words, there is no need to subtract the first isolated strongest resonances from the given shape-estimated envelope in the dFPT. Instead, all that is needed to make the smaller peaks more approachable for the analysis is to reduce the display of the dynamic range on the ordinates for the spectral intensities. With the increased derivative orders, this would narrow and sharpen the formerly broad resonances, including those associated with macromolecules. As a result, the sequential shape estimation by the dFPT would bring closure on the overlapping resonance problem (’spectral crowding’) [27, 31] for in vivo MRS by offering the component spectra for all the isolated resonances. Once separated from the immediate neighbors, each such resonance can be perfectly quantified. This is done with no fitting. Instead, for determination of e.g. the peak areas, a numerical quadrature can be used due to clarity of definition of the integration limits about the separated resonances.

Recently, in Refs. [25, 26], the concept of sequential visualization and quantification through shape estimations by the nonparametric dFPT has been proposed using time signals encoded by in vivo MRS at clinical scanners with $B_0=$1.5T and 3T, respectively.² In the meantime, we implemented this strategy on several FIDs from different in vivo $\mathrm{{}^1H\,MRS}$ encodings at 1.5 and 3T and it worked precisely according to the theoretical anticipation. Presently, we perform sequential quantification for in vitro $\mathrm{{}^1\,H\,MRS}$ at 14.1T using a long time signal ($N=16384$) encoded from the samples of two patients, one with benign and the other with malignant ovarian cyst fluid.

Ordinarily, one would think that high magnetic field strengths (e.g. 14.1T) at spectrometers could provide all the needed diagnostic information from in vitro $\mathrm{{}^1H\,MRS}.$ This would imply that the FFT should suffice for signal processing. However, even a cursory look at spectra provided by in vitro $\mathrm{{}^1H\,MRS}$ encoded with e.g. Bruker 600 MHz spectrometer in Ref. [15] on ovarian tumors would at once place doubt on this contemplation. A similar doubt would persist even when the samples are rotated, as in the case with the high-resolution magic angle spinning (HRMAS) in vitro $\mathrm{{}^1H\,MRS}$ in e.g. Ref. [24] on cervical cancer. With or without sample spinning, the Fourier envelope spectra at such high $B_0$ are not fully resolved as the main metabolites are seen as lying superimposed on bumpy macromolecular hills across a number of frequency bands of diagnostic interest throughout the Nyquist range [15, 24].

This fact cannot be mitigated by the usual practice of showing relatively abundant metabolite maps with about 30-50 or more metabolite acronyms placed on top of peaks and/or listed in tables. Such assignments of metabolites to resonances are based mostly on the resonance locations alone extracted by extrapolating the peak tops down to the chemical shift axis. The provided tables show only the metabolite acronyms and resonance frequencies. No other peak parameters nor metabolite concentrations have been reported for the complete set of these numerous resonances. Eventually, merely 12 metabolites are accompanied with their concentrations in e.g. Ref. [15]. The reason is in the fact that ’spectral crowding’ and bumpy backgrounds prevented quantification. In such circumstances, determining the peak areas by numerical quadratures is unfeasible due to the impossibility to unambiguously determine the integration limits with overlapping resonances. Fitting these spectral structures by e.g. Lorentzian, Gaussians or Voigtians would not help either because of arbitrariness in subjectively choosing the number of resonances.

Such a situation leads to the conclusion that there is definitely room for improvement in data analyses of FIDs for in vitro $\mathrm{{}^1H\,MRS}$ at high magnetic fields, e.g. 14.1T. This is necessary since the principal task of MRS (be it in vivo or in vitro) is to yield the quantitative spectral information (peak positions, widths, heights, areas) of most (if not all) of large numbers of resonances, so that the concentrations of the sought metabolites can reliably be found. Our earlier studies on the nonparametric dFPT [32,33,34] used synthesized time signals (noise-free, noise-corrupted), reminiscent of those with in vitro $\mathrm{{}^1H\,MRS}$ encodings [8] from malignant breast at 14.1T. Presently, the focus is also on in vitro $\mathrm{{}^1H\,MRS}$ at 14.1T, but this time the employed FIDs have been encoded in Ref. [15], using samples from patients with benign and malignant ovary. It is, therefore, expected that the challenge will be greater with measured than with theoretical, synthesized FIDs. We are prepared to meet this challenge as we proceed to the section with the presentation of the results, including their analysis and discussion.

In our previous investigations on $\mathrm{{}^1H\,MRS}$ for breast [67,68,69,70,71,72,73] and ovary [74,75,76,77,78,79,80], applying the nonderivative FPT, time signals have been synthesized using the metabolite concentrations estimated in Refs. [8] (breast) and [15] (ovary), both at 14.1T. While many metabolites have been identified in Refs. [15] (thirty six) and [8] (thirty seven) only a very small number (twelve, ten), respectively were reported as being quantified. Here, the clause ’identified metabolites’ means ’detected peaks (in Fourier envelopes) assigned to known metabolites’ by referring to the available chemical shift databases. In Ref. [15], the chemical shifts of an additional set of some sixteen resonances have been listed as ’unassigned metabolites’ (denoted by $\mathrm{U_1,...,U_{16}}$).

By contrast, the goal of shape estimation by the nonparametric dFPT is richer and broader in its drive to meet the actual needs of $\mathrm{{}^1H\,MRS}.$ This is put into practice by an en route autonomous and automatic full quantification of all the reconstructed resonances. The net result is the comprehensive linelist of the peak parameters even though the nonparametric dFPT is employed. This linelist includes the exact number of physical resonances, their chemical shifts (peak positions), the spin-spin relaxation times $T^\star _2$ (reciprocals of the full widths at half maxima) and the number of the spin-active nuclei (proportional to the metabolite concentrations). It is this output linelist from the dFPT, as a shape estimator, that unravels the hidden inner structure of metabolites with no envelope fitting nor solving the explicit quantification problem (polynomial rooting, data matrix diagonalizing, etc.). Presently, the lineshape profiles of isolated resonances from the dFPT will be displayed, whereas their detailed peak parameters will be reported elsewhere due to abundance of spectroscopic data.

2 Theory

Let the set $\{c_n\}\, (0\le n\le N-1)$ be the given FID or time signal of full length N (finite or infinite) and total duration T,  sampled with the equidistant rate $\tau =T/N.$ The corresponding exact spectrum, as a function of complex linear frequency $\nu ,$ is the $z-$transform or the Green function $G_N(z^{-1}),$ defined by the MacLaurin series (a development in powers of $z^{-1}):$

$$\begin{aligned} G_N(z^{-1})=\sum _{n=0}^{N-1}c_nz^{-n},\quad z=\mathrm{e}^{2\pi i\nu \tau }, \quad \mathrm{Im}(\nu )>0, \quad |z|>1. \end{aligned}$$

(1)

Hereafter, no specific form of the FID is assumed. The standard, nonderivative, nonparametric diagonal FPT proceeds through approximating the exact spectrum $G_N(z^{-1})$ by the Padé rational function. The latter function is the unique ratio of the polynomials $P_K(z^{-1})$ and $Q_K(z^{-1})$ of the same degree K : 

$$\begin{aligned}&G_N(z^{-1})\approx R_K(z^{-1}), \,\,R_K(z^{-1})=\frac{P_K(z^{-1})}{Q_K(z^{-1})}, \end{aligned}$$

(2)

$$\begin{aligned}&\,\,P_K(z^{-1})=\sum _{r=0}^Kp_rz^{-r},\,\,Q_K(z^{-1})=\sum _{s=0}^Kq_sz^{-s}. \end{aligned}$$

(3)

The expansion coefficients $\{p_r,q_s\}\,(0\le r,s\le K)$ are determined from the relation $G_N(z^{-1})Q_K(z^{-1})=P_K(z^{-1}).$ This is done through multiplying by $Q_K(z^{-1})$ the definition $G_N(z^{-1})=P_K(z^{-1})/Q_K(z^{-1})$ of the FPT from Eq. (1). The results of this multiplication (convolution) are the following two systems of linear equations, one for $\{q_s\}$ and the other for $\{p_r\}:$

$$\begin{aligned}&\sum _{s=1}^K q_s c_{K + s-s'}=-c_{K+s'},\,\,q_0\equiv 1,\,\,1\le s'\le N-K-1, \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{r=0}^{r'}c_rq_{r'-r}=p_{r'},\,\,0\le r'\le K. \end{aligned}$$

(5)

In practice, only the system (4) is necessary to solve for obtaining the set $\{q_s\}\,(0\le s\le K).$ Then, the available coefficients $\{q_s\}\,(0\le s\le K)$ make the system (5) an analytical formula for $\{p_r\}\,(0\le r\le K).$ Systems of linear equations are the workforce of computer-based linear algebra. They are solvable with machine accuracy. Moreover, their solution can be refined by singular value decomposition (SVD), as always done in our usage of the Padé processing. As such, the numerical algorithm for the nonparametric FPT is robust, stable and machine accurate.

Once the polynomial coefficients $\{p_r,q_s\}\,(0\le r,s\le K)$ have been generated, the nonparametric derivative dFPT of any order m (positive integer), with respect to frequency $\nu ,$ can be generated by:

$$\begin{aligned} R^{(m)}_{K,\nu }(z^{-1})=\mathrm{D}^m_\nu R_K(z^{-1}),\,\,\mathrm{D}_\nu =\frac{\text{ d }}{\text{ d }\nu } \quad (m=1,2,3,...). \end{aligned}$$

(6)

Function $R_K(z^{-1})$ is a composite function because it depends on variable $\nu$ by way of another variable u,  which is $u\equiv z^{-1} =\mathrm{e}^{-2\pi i\nu \tau }.$ Thus, the $m\,$th derivative $\mathrm{D}^m_\nu \equiv (\text{ d }/\text{d }\nu )^m$ of $R_K(z^{-1}),$ with respect to $\nu ,$ is a derivative of a composite function. Therefore, we first need the $m\,$th derivative $\mathrm{D}^m_u\equiv (\text{ d }/\text{d }u)^m$ of $R_K(z^{-1}),$ with respect to u: 

$$\begin{aligned} R^{(m)}_{K,u}(u)=\mathrm{D}^m_uR_K(u),\,\,\mathrm{D}_u=\frac{\text{ d }}{\text{ d }u} \quad (m=1,2,3,...). \end{aligned}$$

(7)

Subsequently, $R^{(m)}_{K,\nu }(u)$ is to be expressed in terms of $R^{(m)}_{K,u}(u),$ or more precisely, as a linear combination of $R^{(\ell )}_{K,u}(u),$ where $0\le \ell \le m.$ Such a passage is made by using the connection formula between the two general-order derivatives with respect to u and $\nu :$

$$\begin{aligned} \mathrm{D}^m_\nu =\alpha ^m\sum _{\ell =0}^mS(m,\ell )u^\ell \mathrm{D}^\ell _u,\,\,\alpha =-2\pi i\tau . \end{aligned}$$

(8)

Here, quantity $S(m,\ell )$ designates the Stirling number of the second kind [81, 82]:

$$\begin{aligned} S(m,\ell )=\frac{1}{\ell !}\sum _{\lambda =0}^\ell (-1)^{\ell -\lambda }\left( {\begin{array}{c}\ell \\ \lambda \end{array}}\right) \lambda ^m, \end{aligned}$$

(9)

where $\left( {\begin{array}{c}\ell \\ \lambda \end{array}}\right) =\ell !/[\lambda !(\ell -\lambda )!]$ is the standard symbol for the binomial coefficient. Therefore, once the function $R^{(\ell )}_{K,u}(u)$ becomes available, the sought $m\,$th derivative function $R^{(m)}_{K,\nu }(u)$ for the dFPT would acquire the form:

$$\begin{aligned} R^{(m)}_{K,\nu }(u)=\alpha ^m\sum _{\ell =0}^mS(m,\ell )u^\ell R^{(\ell )}_{K,u}(u). \end{aligned}$$

(10)

In all our previous as well as in the present applications of the nonparametric dFPT for the general $m\,$th derivative order, we compute $R^{(m)}_{K,u}(u)$ by using the following accurate, stable and expedient recursion [25, 37]:

$$\begin{aligned} {\displaystyle {R^{(\ell )}_{K,u}(u)= \frac{P^{(\ell )}_{K,u}(u)-\sum \limits _{j=0}^{\ell -1}\left( {\begin{array}{c}\ell \\ j\end{array}}\right) R^{(j)}_{K,u}(u)Q^{(\ell -j)}_{K,u}(u)}{Q_K(u)} }},\,\,\ell \ge 0, \end{aligned}$$

(11)

where $\sum _{j=0}^{-1}(\cdots )\equiv 0.$ The recursion (11) is initialized by the relationship:

$$\begin{aligned} {\displaystyle {R^{(1)}_{K,u}(u)=\frac{P^{(1)}_{K,u}(u)-R_K(u)Q^{(1)}_{K,u}(u)}{Q_K(u)} }}. \end{aligned}$$

(12)

The functions denoted by $P^{(m)}_{K,u}(u)=\mathrm{D}^m_uP_K(u)$ and $Q^{(m)}_{K,u}(u)=\mathrm{D}^m_uQ_K(u)$ are the $m\,$th order derivatives of the polynomials $P_K(u)=\sum _{r=0}^Kp_ru^{r}$ and $Q_K(u)=\sum _{s=0}^Kq_su^{s}$, respectively. Their explicit expressions read as:

$$\begin{aligned} P^{(m)}_{K,u}(u)=\sum _{r=m}^K[m]_rp_ru^{r-m},\,\,Q^{(m)}_{K,u}(u)=\sum _{s=m}^K[m]_sq_su^{s-m}, \end{aligned}$$

(13)

where $[m]_n=n!\left( {\begin{array}{c}m\\ n\end{array}}\right) .$

Next, we pass to the dFFT by giving mainly the working formula. As detailed in Ref. [35], this formula is obtained by applying the derivative operator $\mathrm{D}_m=(\text{ d }/\text{d }\nu )^m$ to the continuous Fourier transform $F(\nu ),$ which is the standard finite integral over time t in the interval $0\le t\le T$ of the product of the analogue time signal c(t) and the harmonic function $\mathrm{e}^{-2\pi i\nu t},$ divided by T. Therefore, the $m\,$th derivative $\mathrm{D}_mF(\nu )$ is a new integral with an altered integrand, $\mathrm{e}^{-2\pi i\nu t}w_m(t)c(t),$ where $w_m(t)$ is a weight function, $w_m(t)=(-2\pi it)^m.$ The use of function $\mathrm{D}_mF(\nu ),$ alongside discretization of both continuous variables (t and $\nu$), yields the result $F^{(m)}_k,$ which is the derivative discrete Fourier transform (dDFT) [35]:

$$\begin{aligned} F^{(m)}_k=\frac{1}{N}\sum _{n=0}^{N-1}\mathrm{e}^{-2\pi ink/N}(-2\pi in\tau )^mc_n\,, \end{aligned}$$

(14)

where $0\le k\le N-1.$ Finally, when a numerical computation of the dDFT from Eq. (14) is carried out by the Cooley-Tukey fast algorithm [44], the outcome $F^{(m)}_k$ is the dFFT.

For noise-contaminated time signals, as is always the case for encoded FIDs, the weight function $(-2\pi in\tau )^m$ in Eq. (14) emphasizes heavily the data points acquired at later times, near the tail of $\{c_n\}\, (0\le n\le N-1),$ where noise prevails. Thus, the theory predicts that derivative spectra due to the dFFT will have worse SNR than the corresponding nonderivative spectra from the FFT.

Increased noise in a spectrum from the dFFT would fill out the space between adjacent resonances and lift the background baseline. The outcome is resolution deterioration. Overall, within the dFFT, it is theoretically anticipated that both resolution and SNR will be decreased relative to the FFT. This has indeed been confirmed by a number of detailed computations, as thoroughly documented in Refs. [25, 26, 32,33,34,35,36,37, 61].

In the rest of the presentation, whenever we mention the $m\,$th derivative operator, we will always refer to $\mathrm{D}^m_\nu$ which, for simplicity shall be denoted by $\mathrm{D}_m\equiv \mathrm{D}^m_\nu .$ The present convention for the magnitude mode envelope (total shape spectra) will be as follows:

$$ {\text{Pad}}{\acute{\text{e}}}{:}\, \left| {{\text{D}}_{m} {\text{FPT}}} \right|,\, {\text{Fourier}}{:}\, \left| {{\text{D}}_{m} {\text{FFT}}} \right|,\, \left( {m = 0,1,2,...} \right). $$

(15)

Here, $\mathrm{D}_m\mathrm{FPT}=R^{(m)}_{K,\nu }(z^{-1})$ and $\mathrm{D}_m\mathrm{FFT}=F^{(m)}_k$ are complex-mode envelopes given by Eqs. (6) and (14), respectively.

3 Results and discussion

3.1 Encoded time signals

The time signals analyzed here have been encoded with in vitro $\mathrm{{}^1H\,MRS}$ by the authors of Ref. [15] who kindly provided to us some of their FID data. For a group of 40 patients, they used a Bruker 600 MHz spectrometer to encode the time signals from the ovary (excized samples were in the D₂O solvent). We were given the FIDs encoded from two patients with the histopathologic diagnoses, benign and malignant ovarian cysts. The present main emphasis is on the findings for the malignant ovarian cyst fluid (serous cystadenocarcinoma). Nevertheless, for very important clinical comparisons, some of our results are also given for the benign ovarian cyst fluid (serous cystadenoma).

During the process of encoding, the content of water has significantly been reduced. Moreover, the residual water peak resonance was presaturated during the relaxation delay (12s). The encoding parameters are: the static magnetic field strength $B_0\approx 14.1$T for the Larmor frequency $\nu _{\mathrm{L}}=600\,\mathrm{MHz},$ repetition time $T_{\mathrm{R}}=1200$ ms, the bandwidth BW=6667 Hz, the full length of each of the FIDs, $N=16384,$ the sampling time $\tau =1/\mathrm{BW}\approx$ 0.15 ms, the number of excitations $N_{\mathrm{EX}}=128.$ The total acquisition time of every transient or FID is $T=N\tau =2.46\,\mathrm{s}.$ In order to improve SNR, these 128 encoded FIDs were averaged.

In Ref. [15], for calibration (chemical shifts, molar concentrations), as an internal standard, trimethylsilyl {2,2,3,3}-tetradeuteropropionic (TSP) acid was used. Chemical shifts of metabolites of interest are counted from the exact location of the TSP resonance (0 ppm) in the spectrum. Metabolite concentrations (with the allowance for the number of resonating protons), expressed in biophysical units (micro-mol per gram, $\mu$M/g), were obtained from the fitted peak areas and the reference TSP concentration [15]. Thus, the TSP resonance had a twofold purpose, referencing of both chemical shifts and concentrations of metabolites.

For signal processing, the phase-and-baseline-corrected real parts of the complex envelopes in the FFT were used [15]. Quantification consisted in estimating the peak areas by fitting the semi-absorptive Lorentzian lineshapes to the Fourier envelopes. The same linewidth of all the resonances was employed and assessed to be about 1.0 Hz. It was found in Ref. [15] that the concentration levels of several metabolites are notably higher in malignant compared to benign ovarian cyst fluids: isoleucine Iso, valine Val, threonine Thr, lactate Lac, lysine Lys, methionine Met, glutamine Glu and total choline tCho. These biomolecules participate to various pathways of ovarian cyst metabolism. Therefore, their identification and quantification by $\mathrm{{}^1H\,MRS}$ can give invaluable information on the metabolic status of ovarian cysts with the hints about the metabolism of the surrounding tissue, as well.

3.2 Reconstructed spectra

All the spectra to be shown are based on the mentioned averaged FIDs from Ref. [15]. In the present investigation, only the shape estimations of magnitude envelopes by the nonparametric versions of the nonderivative FPT and derivative dFPT are employed. For the same time signals, the parametric variants of the FPT and dFPT are the subject of the accompanying study [83].

Figure 1 shows the average values of the encoded time signals or FIDs (a-d) and the computed Padé magnitude envelope spectra (e-h). The FIDs for the benign (a,b) and malignant (c,d) cases are seen to be largely symmetric around the abscissae confirming that both shimming and water suppression were appropriate. Also, the decays of these FIDs to zero are observed very well, as especially pronounced for the malignant case (c,d). The dense thickness of the FID waveforms (a-d) indicates that the samples contain a huge number of exponentially damped harmonic oscillations associated with abundant metabolites. Namely, each such time signal component, especially those oscillating with appreciable intensities at the given fundamental frequencies, corresponds to a metabolite present in the scanned specimen.

Fig. 1

In vitro $\mathrm{{}^1H\,MRS}$ for two patients with different ovarian cyst fluids: benign (serous cystadenoma) and malignant (serous cystadenocarcinoma). Acronym dMRS refers to derivative MRS. The time signals or FIDs have been encoded with a Bruker 600 MHz ($\approx 14.1$T) spectrometer [15]. For the FIDs, abscissae are in time signal numbers n and ordinates in arbitrary units (au). The first row, the real and imaginary parts of the complex averaged FIDs: benign (a,b) and malignant (c,d). The Padé magnitude envelopes from shape estimations by the nonparametric variants of the FPT and dFPT. Spectral intensities on the ordinates in au and abscissae as chemical shifts in ppm (parts per million). Frequency window of interest: 0.85–4.85 ppm. Nonderivative spectra ($m=0$), FPT (benign: e, malignant: f,g). First derivative spectrum ($m=1$), dFPT (malignant: h). Spectral intensities reduced on (g,h) for the doublet and quartet of lactate, Lac. For details, see the main text (color online)

Regarding the Padé envelopes in Fig. 1 at frequencies 0.85–4.85 ppm, panel (e) is on the benign case, whereas panels (f-h) deal with the malignant ovarian cyst fluid alone. The nonderivative spectra in the FPT are on panels (e–g), while the first derivative envelope in the dFPT is on panel (h). A comparison between panels (e: benign) and (f: malignant) shows the two strikingly unlike envelopes. Their visual dissimilarity stems from a smaller (e) and a larger (f) span of the weakest and strongest peak heights.

This is reflected on the discrepancy in the dynamic range of the spectral intensities on the ordinates on panels (e) and (f). Thus, the spectrum on panel (e: benign) is seen to be abundant with many resonances. On the other hand, the spectrum on panel (f: malignant) appears as if it were almost empty (with the exception of lactate and water) in most of the displayed range, 0.85–4.85 ppm.

The tallest resonance structure on panels (e) and (f) is the lactate doublet Lac(d) around 1.41 ppm. Moreover, the lactate quartet Lac(q) near 4.36 ppm is the second tallest resonance only on panel (f: malignant), but not on panel (e: benign). There is also a notable difference in the lactate resonance intensities for the malignant and benign ovarian cyst fluids. More precisely, the peak heights of Lac(d), as seen on panels (e: benign) and (f: malignant), are about 326 and 6041 au, respectively. A similar discrepancy persists in the peak heights of Lac(q), about 88 and 1597 au, when comparing panels (e: benign) and (f: malignant), respectively.

It then follows that the peak height ratios, malignant/benign, for Lac(d) and Lac(q) are about 18.54 and 18.06, respectively. Such significantly elevated levels of lactate in the nonderivative spectrum $\mathrm{|FPT|}$ (f) usually indicate a malignant transformation. This finding on panel (f: malignant) coheres with the corresponding histopathologic diagnosis of cancer, serous cystadenocarcinoma [15]. Among the recognized cancer biomarkers, the most prominent metabolites are lactates and cholines. The status of lactates, as a cancer biomarker is solidly confirmed by the just effected comparison between panels (e: benign) and (f: malignant). Nothing of this sort can directly be checked for cholines from panels (e: benign) and (f: malignant). This occurs because, on both panels (e,f), the choline-containing compounds are buried in the background baseline, when viewing the full dynamic range of intensities displayed on the ordinates.

One of the possibilities to eventually visualize the resonances other than Lac(d) and Lac(q) also for the malignant case is to have either a comparable or exactly the same span of the spectral intensities on the ordinates for the two spectra (benign, malignant). This can be done simply by shrinking (scaling down) the ordinate on panel (f: malignant) by a factor of 20, namely from 8000 to 400 au. The result is seen on panel (g: malignant) whose layout for $\mathrm{|FPT|}$ can now be more usefully compared to that from panel (e: benign). The maximal value on the ordinates on both panels, (e: benign) and (g: malignant), is the same: 400 au. The net outcome of such an ordinate reduction or scaling (amounting to cutting off a large upper fraction of the lactate doublet), is especially appreciable for the choline-containing compounds. These compounds are encapsulated in the joint name, total choline tCho, comprised of three components each appearing as a singlet resonance, free choline Cho(s), phosphocholine PC(s) and glycerophosphocholine GPC(s), as mentioned.

In particular, Cho(s) and PC(s) are seen on panel (g: malignant) to emerge from their former complete invisibility in panel (f: malignant). This is especially important in view of the fact that, on the same ordinate scale on panels (e: benign) and (g: malignant), only Cho(s) and PC(s) in the latter, malignant case, become clearly visible. Thus, Cho(s) and PC(s) also confirm their standing as metabolites belonging to the clinically most critical category of recognized cancer biomarkers. However, at least on the level of the scale of the ordinate on panel (g: malignant), the third tCho component, namely GPC, cannot be discerned, if present at all. Thus, zooming into a chemical shift region of particular relevance to the choline-bearing compounds, e.g. 3.17–3.30 ppm, would deserve a special attention. This issue will, therefore, be revisited later (Fig. 4) through a comparison of spectra for the benign and malignant cases, using the nonderivative FPT $(m=0)$ and derivative dFPT of orders $1\le m\le 3.$

Thus far, all the three panels (e)–(g) of Fig. 1 on spectra are concerned with the nonderivative estimations by the FPT. This is further complemented on panel (h: malignant) of the same figure by the first derivative spectrum $|\mathrm{D_1FPT}|$ in the dFPT. Herein, a twofold benefit is achieved by passing from $|\mathrm{FPT}|$ (g) to $|\mathrm{D_1FPT}|$ (h), both for the malignant case. The benefit consists of simultaneously improved resolution and SNR in $|\mathrm{D_1FPT}|$ (h) relative to $|\mathrm{FPT}|$ (g). Such an accomplishment is manifested in the emergence of narrower peak widths and flatter background baseline in $|\mathrm{D_1FPT}|$ (h) compared with $|\mathrm{FPT}|$ (g). Note that the ordinate reduction device is also applied to $|\mathrm{D_1FPT}|$ (h). The maximal ordinate is 800 au for $|\mathrm{D_1FPT}|$ (h) compared to 400 au for $|\mathrm{FPT}|$ (g). We have not descended to 400 au for the intensities of $|\mathrm{D_1FPT}|$ (h) to match the maximal ordinate for $|\mathrm{FPT}|$ (g) because the aim here is to avoid cutting off the tops of the resonances surrounding Lac(d), notably Ala(d) near 1.51 ppm on the left of Lac(d). With the ordinate for $|\mathrm{D_1FPT}|$ (h) maximized at 800 au, the tops of the derivative versions of the Lac(d) and Lac(q) resonances have to be cut off.

The width narrowing and background flattening is most pronounced around the three strongest resonances, Lac(d), Lac(q) and the $\mathrm{H_2O}$ residual. The bottoms (bases) of these resonances in $|\mathrm{FPT}|$ (g) are wide and considerably lifted from the chemical shift axis. The tails of Lac(d), Lac(q) and the water remnant extend far from their resonance frequencies in $|\mathrm{FPT}|$ (g). This causes significant distortions of the surrounding resonances. Such marked deformations by these intense peaks are seen in the nonderivative spectrum $|\mathrm{FPT}|$ (g) to erroneously increase the actual levels of other resonances, especially those in the close neighborhood of Lac(d) and Lac(q).

By comparison, the first derivative spectrum $|\mathrm{D_1FPT}|$ (h) has much better delineated individual resonances, displaying their distinct inter-separations across the nearly entire frequency band, 0.85-4.85 ppm and beyond (not shown). A dramatic suppression of the long tails from Lac(d), Lac(q) and $\mathrm{H_2O}$ accomplished by the action of the $\mathrm{D_1}=\text{ d }/\text{d }\nu$ operator in $|\mathrm{D_1FPT}|$ (h), yields a hugely lowered background level. This gives an opportunity to all the resonances around Lac(d), Lac(q) and $\mathrm{H_2O}$ to show much of their full intrinsic intensities. The almost perfect clarity by which this is exhibited in $|\mathrm{D_1FPT}|$ (h) is best illustrated by several resonances (doublets d, double doublets dd, triplets t) via Iso(d,t), Leu(d,t), Val(dd), $\beta -$HB(d), Thr(d) and Ala(d) around Lac(d) in the frequency band 0.9-1.6 ppm.

Note that the acronyms for the just listed small sequence of metabolites around Lac(d) are intentionally not marked in Fig. 1h. The reason is twofold. Firstly, our principal emphasis in this figure is placed upon the tandem of the recognized cancer biomarkers, lactates and cholines. Thus, drawing the acronyms of several other metabolites would introduce some clutter and might drive the reader’s attention away from the main focus in Fig. 1. Secondly, the stated chemical shift interval around Lac(d) will be revisited in depth later (Figs. 2 and 3), giving the graphs with the acronyms of the main resonances of diagnostic interest.

Fig. 2

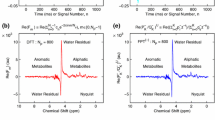
In vitro $\mathrm{{}^1H\,MRS}$ for a patient with malignant ovarian cyst fluid: serous cystadenocarcinoma. Acronym dMRS refers to derivative MRS. The FIDs from panels (c,d) of Fig. 1 are used to compute the Padé magnitude envelopes in the band 0.9–1.6 ppm by shape estimations with the nonparametric versions of the FPT and dFPT. Spectral intensities on the ordinates in au and the abscissae as chemical shifts in ppm. Nonderivative spectra $(m=0),$ FPT (a,c). Second derivative spectra $(m=2),$ dFPT (b, d–f). Spectral intensities reduced on (c,d) for the doublet of lactate, Lac. Two ordinate axes on (e): right for Lac, left for the remaining metabolites. Intensities from the Lac lineshape divided by 25: (f). For details, see the main text (color online)

Fig. 3

In vitro $\mathrm{{}^1H\,MRS}$ for a patient with malignant ovarian cyst fluid: serous cystadenocarcinoma. Acronym dMRS refers to derivative MRS. The FIDs from panels (c,d) of Fig. 1 are used to compute the Padé magnitude envelopes in the band 0.9–1.6 ppm by shape estimations with the nonparametric versions of the FPT and dFPT. Spectral intensities on the ordinates in au and the abscissae as chemical shifts in ppm. Nonderivative spectra $(m=0),$ FPT (a,b). Derivative spectra, dFPT (c: $m=1,$ d: $m=2,$ e: $m=3$). Spectral intensities reduced on (b–e) for the doublet of lactate, Lac. For details, see the main text (color online)

In the Introduction, by reference to the literature, we mentioned the presence of some bumpy hills beneath diagnostically relevant metabolites in customary, nonderivative spectra from FIDs encoded by in vitro $\mathrm{{}^1H\, MRS}$ even at strong magnetic fields (e.g. 14.1T). This can also be seen in Fig. 1g even outside the dominant resonances Lac(d) and Lac(q), i.e. at chemical shifts 1.6–4.25 ppm. The situation is somewhat mitigated if, instead of the magnitude mode, the phased real part of the corresponding complex spectrum is employed. Nevertheless, the latter semi-absorption-type spectra would still have the main resonances superimposed on the bumpy macromolecular background baselines. Such spectral deformations would impact adversely on the efforts aimed at quantification of resonance lineshapes of the diagnostically most relevant metabolites.

However, regarding the bumpy macromolecular background baselines, a substantial improvement is obtained by resorting to derivative shape estimations with the dFPT. Thus, already the first derivative order $(m=1)$ in the dFPT, by way of the spectrum $|\mathrm{D_1FPT}|$ (h), appears to substantially outperform its nonderivative counterpart, $|\mathrm{FPT}|$ (g). This is most evidenced beneath Lac(d), Lac(q) and $\mathrm{H_2O},$ as stated. Moreover, the bumpy hills are hugely diminished also at several chemical shift regions containing multiplet resonances, e.g. within 1.67-1.78 ppm for lysine Lys, 2.42-2.52 ppm for glutamine Glu, 3.18-3.87 ppm for glucose Glc, etc.

Such an encouraging prelude via Fig. 1 is an invitation to the reader to pose a question: what happens next when passing to $|\mathrm{D}_m\mathrm{FPT}|$ for some higher derivative orders, $m>1$?

We will cope with this question in a step-wise manner. To this end, in principle, we could again consider the wider frequency range 0.85-4.85 ppm, as done in Fig. 1. However, since this whole range is tightly packed with many resonances, to attain a better transparency, it is deemed advisable to zoom into the two clinically most relevant sub-bands, hosting cancer biomarkers, 0.9–1.6 ppm around Lac(d) and 3.17–3.30 ppm for tCho. This would facilitate much more detailed comparisons between the nonderivative FPT and derivative dFPT $(m>1)$ than what is done in the introductory confrontations on Fig. 1. Specifically, Figs. 2 and 3 deal only with the malignant case at chemical shifts 0.9–1.6 ppm surrounding Lac(d). On the other hand, as announced, Fig. 4 is concerned with both the benign and malignant cases of the ovarian cyst fluids, analyzed in a narrow vicinity of Cho(s) at resonance frequencies 3.17–3.30 ppm. Finally, Fig. 5 compares the Padé and Fourier spectra using the pairs {FPT,FFT} and {dFPT,dFFT} for the malignant cyst fluid.

Fig. 4

In vitro $\mathrm{{}^1H\,MRS}$ for two patients with different ovarian cyst fluids: benign (serous cystadenoma) and malignant (serous cystadenocarcinoma). Acronym dMRS refers to derivative MRS. The FIDs from panels (a–d) of Fig. 1 are used to compute the Padé magnitude envelopes in the band of cholines, 3.17–3.30 ppm, by shape estimations with the nonparametric versions of the FPT and dFPT. Left and right column for the benign and malignant cases, respectively. Spectral intensities on the ordinates in au and the abscissae as chemical shifts in ppm. Nonderivative spectra $(m=0),$ FPT (a,e). Derivative spectra, dFPT, $m=1$ (b,f), $m=2$ (c,g), $m=3$ (d,h). Spectral intensities with no reduction (a–h). For details, see the main text (color online)

We now continue the analysis by referring to Fig. 2 for an illustration of the concept of sequential visualization of stronger and weaker resonances. Already the passage from panels (f) to (g) in Fig. 1 may be thought as an initialization of sequential visualization. However, the real power of such a concept is not just in stopping at visualizations alone. Quite the contrary, sequential visualization also allows quantification of both the stronger and weaker resonances in two (or more) goes. This gives the notion of sequential quantification. The whole quantification process of this kind relies exclusively on shape estimations. Yet, its usefulness and attractiveness rest upon the fact that no spectral lineshape fitting is needed whatsoever. This avoids altogether the troublesome ambiguities and nonuniqueness of all fitting approaches for quantifying the given lineshape profiles. In other words, sequential quantification permits autonomous extraction of the resonance signatures (peak positions, widths, heights, areas) solely through nonparametric means, i.e. only by shape estimations. This is a brand new quantification alternative to parametric signal processing.

To gradually accustom the reader to the novelties offered by derivative signal processing, we pass from $m=1$ (Fig. 1) to $m=2$ (Fig. 2). Here, the envelope $|\mathrm{FPT}|,$ as the reference nonderivative spectrum $(m=0),$ is shown on panels (a,c), whereas $|\mathrm{D_2FPT}|$ is on panels (b,d–f). In Fig. 2, we first compare $|\mathrm{FPT}|$ (a) and $|\mathrm{D_2FPT}|$ (b) by using the whole sizes of the ordinates (no shrinking/scaling). In other words, in panels (a,b), we encompass the full dynamic range of intensities of all the resonances present at chemical shifts 0.9-1.6 ppm. Therein, it is seen that $|\mathrm{D_2FPT}|$ (b) hugely improves both resolution and SNR with respect to $|\mathrm{FPT}|$ (a). Frequency resolution is enhanced by virtue of the narrower peak widths of Lac(d) in $|\mathrm{D_2FPT}|$ (b) with respect to $|\mathrm{FPT}|$ (a). Narrower peaks, in turn, produce taller (more intense) resonances. This is observed through the intensities $\sim 75000$ au in $|\mathrm{D_2FPT}|$ (b) versus $\sim 6000$ au in $|\mathrm{FPT}|$ (a), around 1.41 ppm at the location of Lac(d). The ratio of these latter two peak heights is 12.5 (75000/6000).

Linewidth narrowing is coupled with tightening the bottom part or base of Lac(d) in $|\mathrm{D_2FPT}|$ (b) relative to that in $|\mathrm{FPT}|$ (a). The increased intensity of the lactate doublet resonance Lac(d) and the concomitant lower level of the accompanying background around 1.41 ppm, automatically translate into an improved SNR for this particular cancer biomarker metabolite. Hence, all the facets of derivative estimation superiority (over its corresponding nonderivative counterpart), in a nut shell, are present in plain view already in comparing panels (a) and (b) of Fig. 2.

Most importantly, quantification of Lac(d) would be more accurate from $|\mathrm{D_2FPT}|$ (b) than from $|\mathrm{FPT}|$ (a). The reason for this (especially regarding, e.g. determination of the peak area and the concentration), is not merely in an obviously better definition of the integration limits around the Lac(d) resonances in $|\mathrm{D_2FPT}|$ (b) than in $|\mathrm{FPT}|$ (a). The wider base (bottom) of Lac(d) in $|\mathrm{FPT}|$ (a) hides the invisible, broader macromolecular spectral structures (lipids, proteins,...) that co-resonate with the lactate doublet at very close or nearly the same chemical shifts, as explicitly shown in Ref. [83].

Such a ’spectral crowding’ [15, 27] or spectral congesting artificially elevates the true concentration level of Lac(d). This would impact adversely on the ability to make the correct diagnostic decision. Such an obstruction is largely reduced in $|\mathrm{D_2FPT}|$ (b) because the second-order derivative operator $\mathrm{D}_2=(\text{ d }/\text{d }\nu )^2$ makes the wider resonances, beneath Lac(d), temporarily disappear from the display, thus allowing the lactate doublet to come up with its truer intensity. Of course, the third or fourth derivatives $|\mathrm{D_3FPT}|$ or $|\mathrm{D_4FPT}|,$ respectively (not shown here) would give the more accurate peak area and concentration of Lac(d) on account of further suppression of the broader resonances underneath Lac(d).

Theoretically, it is expected that the two lactate resonances in Lac(d) have the identical intensities. Indeed, by the naked eye, the two peak heights are nearly the same in $|\mathrm{FPT}|$ (a). Moreover, also by a visual inspection, they seem to be almost identical in $|\mathrm{D_2FPT}|$ (b). This itself indicates that the widths of the two peaks in Lac(d) are very close to each other. If there were a difference between the two linewidths in Lac(d), the operator $\mathrm{D_2}$ would produce the two unequal peak heights in $|\mathrm{D_2FPT}|$ (b). This would be the case because the pace of the peak height increases slower with augmentation of the derivative order m for a wider than for a narrower peak. In fact, both wider and narrower peaks are simultaneously enhanced with increased derivatives, but the former lag behind the latter. As a result, after a certain derivative order m,  only the narrower peaks ’survive’ on the display, whereas the broader resonances become embedded into the chemical shift axis (i.e. they disappear from the view). However, the broader resonances are not washed out for good. Rather, they temporarily vanish from the spectrum only to return (pop out) by a further convenient reduction of the ordinate for intensities.

To find the peak area of Lac(d) by a numerical quadrature, the integration limits should approximately be 1.34 and 1.50 ppm in $|\mathrm{FPT}|$ (a), i.e. notably wider than in $|\mathrm{D_2FPT}|$ (b). One of the reasons for this is the presence of the background baseline in $|\mathrm{FPT}|$ (a). The elevated background baseline in $|\mathrm{FPT}|$ (a) superficially enhances the concentration of Lac(d), as emphasized. By contrast, the background contribution to Lac(d) is almost completely suppressed in $|\mathrm{D_2FPT}|$ (b), as seen by the flattened baseline around 1.41 ppm. The disparity between the intensities of Lac(d) and the surrounding resonances makes the latter peaks barely noticeable. Albeit poorly visible, these minuscule resonances are observed to be deformed in $|\mathrm{FPT}|$ (a), compared to the corresponding perfect stick spectrum (the bar spectrum) in $|\mathrm{D_2FPT}|$ (b).

The Fourier envelopes can be computed only at a limited number of the equidistant frequency grid points $(k/T, k=0,1,...,N-1)$ predetermined by the total acquisition time T,  or equivalently, the full signal length N. However, the Padé spectra are computable at any desired mesh of sweep frequencies (equidistant or nonequidistant alike). This is handy because by choosing a very dense set of the sweep or running linear frequencies, the same computer algorithm for $\mathrm{D}_m\mathrm{FPT}$ can automatically give the precise values of the given peak height $\mathrm{max}|\mathrm{D}_m\mathrm{FPT}|$ as well as the associated chemical shift (peak position), $\nu _{\mathrm{R}}.$

Likewise, the FWHM, as the difference between the two frequencies (left and right of the peak center $\nu _{\mathrm{R}}$), are automatically provided by the same program at the two chemical shifts of the halved peak height $\mathrm{max}|\mathrm{D}_m\mathrm{FPT}|/2.$ This gives an alternative computation of the peak area as the product of the peak height and the FWHM. Such a possibility can be used in practice even with encoded FIDs because the magnitude derivative lineshapes $|\mathrm{D}_m\mathrm{FPT}|$ in the dFPT for $m\ge 2$ are quite symmetric and fairly close to bell-shaped absorptive-like Lorentzian profiles. The nonderivative magnitude spectra $|\mathrm{FPT}|$ in the FPT (or $|\mathrm{FFT}|$ in the FFT) are not of an absorptive Lorentzian form.

The outlined automatic procedure should begin with the internal standard, the TSP singlet resonance, TSP(s). Its peak area can be converted to the TSP concentration (in units of e.g. micro-mol per gram, $\mu$M/g) by using the known molecular mass of the TSP molecule and the given amount of the TSP acid added to the analyzed sample.

The outlined automatic and autonomous determination of the peak position, height and width amounts to quantification from a shape-estimated spectrum in the dFPT with no fitting nor numerical integration (for the peak area). The selected derivative order m should guarantee that the specific peak subjected to quantification in the explained way is a reasonably well-isolated resonance. This is undoubtedly the case with the TSP(s) peak at 0 ppm as no other, interfering resonances are observed nearby in $|\mathrm{D_2FPT}|.$ Therefore, the peak area of TSP can be computed almost perfectly [83]. The same can also be said for Lac(d) using $m=2$ via $|\mathrm{D_2FPT}|$ (b). Repeating the above procedure for each of the two peaks in Lac(d), an important additional spectral parameter can also be extracted, the J-coupling constant as the distance between the center frequencies of each component peak in the lactate doublet.

The peak area of the two Lac(d) resonances in $|\mathrm{D_2FPT}|$ (b) is the sum of its two component peak areas. Using the latter compound peak area, the Lac(d) concentration is expressed in the proper biophysical units (e.g. $\mu$M/g) by referring it to the internal standard. This means that the Lac(d) concentration is given as the percentage of the already available accurate TSP concentration. Finally, using the available correspondence expressions (from derivatives to the nonderivative) [34], all the peak parameters due to the expounded quantification by means of $|\mathrm{D}_m\mathrm{FPT}|\, (m>1)$ should be scaled back to deduce their counterparts attributable to $|\mathrm{FPT}|.$ The linewidth of a Lorentzian resonance in the magnitude envelope $|\mathrm{FPT}|$ is wider by $\sqrt{3}$ than that of the associated purely absorptive spectrum. This additional scaling could also be used since an absorptive Lorentzian lineshape profile is interpretable in the most direct way.

We now see how the dFPT as an initially defined shape estimator (nonparametric processing) turned out, in the end, to be a quantifier with no fitting. As discussed, quantification signifies determining the peak parameters (positions, widths, heights). Thus, by employing the nonparametric dFPT, at the onset of the analysis, we end up with a parametric signal processor without ever adjusting (fitting) the given derivative lineshapes to any mathematical model function and without rooting the Padé polynomials.

To peer into the Lac(d) surroundings, a scale reduction on the ordinate for the spectral intensity can also be used in Fig. 2, in the spirit of panels (g,h) of Fig. 1. This is done on panel (c) of Fig. 2 by shrinking the former ordinate from $\sim 6000$ au (a) to 420 au (c), i.e. by using the reduction factor $\sim 19.05$ (8000/420). This makes in evidence the existence of the elevated background baseline in $|\mathrm{FPT}|$ (c). It is seen in $|\mathrm{FPT}|$ (c) that the bottom or base of Lac(d) is distorted by the background and macromolecules. This would diminish the accuracy of the concentration of Lac(d), if estimated from $|\mathrm{FPT}|$ (a). The asymmetry of Lac(d) in its base proves that the lineshape of the nonderivative magnitude spectrum $|\mathrm{FPT}|$ (c) is not a bell-shaped absorptive Lorentzian, the fact mentioned earlier.

Also directly observed in $|\mathrm{FPT}|$ (c) is the extent of the severity of distortion of the Lac(d) surrounding by the long tail of the lactate doublet resonance. Thus Ala(d), Thr(d), $\beta -$HB(d), Val(dd), Iso(d,t) and Leu(d,t) appear as deformed and twisted, riding on the lifted tail of Lac(d). They are simultaneously superimposed on the background baseline, which is indiscernibly immersed into the Lac(d) tail. Critically, no metabolite from the assembly {Ala(d), Thr(d), $\beta -$HB(d), Iso(d,t), Val(dd), Leu(d,t)} in $|\mathrm{FPT}|$ (c) is quantifiable.

On the other hand, the situation seen in $|\mathrm{D_2FPT}|$ (d) is in sharp contrast with $|\mathrm{FPT}|$ (c). The second derivative spectrum $|\mathrm{D_2FPT}|$ (d) is also shown on a reduced ordinate. The ordinate reduction factor is $\sim 21.43$ (75000/3500), after shortening the intensity axis on panel (b) to match that on panel (d). The benefit brought by $|\mathrm{D_2FPT}|$ (d) in comparison with $|\mathrm{FPT}|$ (c) is truly astounding. The main contributor to the mega success of $|\mathrm{D_2FPT}|$ (d) is the high quality of the second derivative lineshape profile of the Lac(d) resonance. The Lac(d) resonance is enormously narrowed in panel (d) relative to (c). Moreover, the formerly long tail of the lactate doublet is effectively cut off by the action of the $\mathrm{D_2}$ operator in $|\mathrm{D_2FPT}|$ (d).

With the totally flattened background baseline in $|\mathrm{D_2FPT}|$ (d), all the surrounding resonances are straightened up and symmetrized. In particular, the resonances Ala(d), Thr(d), $\beta -$HB(d) and Leu(d) are seen on panel (d) as lying on the chemical shift axis, i.e on the zero-valued background baseline. A very slight overlap (near the chemical shift axis) exists between one peak from Iso(d) and the other from the nearby left peak of Val(d). In the most congested region (leucine/isoleucine) within 0.9-0.95 ppm, when going upfield (i.e. as usual from the right to the left of the chemical shift axis), first comes the isoleucine triplet resonance, Iso(t). This is followed by the leucine triplet Leu(t) and then leucine doublet Leu(d) appears. Here too, the peak separation is very good for Iso(t) and Leu(d), whereas to attain the same status, Leu(t) needs a further refinement to bring all its three components straight to the chemical shift axis.

The two peaks in one doublet taken at a time from the set {Ala(d), Thr(d), $\beta -$HB(d), Val(dd)} are of almost the same height. This also means that the linewidths of the two peaks in e.g. Ala(d) are basically coincident. The same holds true for Thr(d), $\beta -$HB(d) and Val(dd), as well, when considering one doublet at a time. To the right of the spectrum in Fig. 2, around 1 ppm, there are two doublets, the taller is Val(d) and the shorter is Iso(d). In contrast to $|\mathrm{FPT}|$ (c), the spectrum $|\mathrm{D_2FPT}|$ (d) has no background. This permits quantification of all the structured resonances {Ala(d), Thr(d), $\beta -$HB(d), Iso(d), Val(dd), Leu(d), Iso(t)} in $|\mathrm{D_2FPT}|$ (d) with no fitting in the same way as explained for the Lac(d) in $|\mathrm{D_2FPT}|$ (b).

To recapitulate panels (a–d) in Fig. 2, we note first that after quantifying the TSP reference peak, the Lac(d) resonance came next to quantify. Both resonances are visualized and then quantified using $|\mathrm{D_2FPT}|$ on the full size of their respective ordinates for the spectral intensity around the chemical shifts 0 and 1.41 ppm for TSP and Lac(d), respectively. The TSP peak is located outside the band from Fig. 2, but this internal standard resonance will be shown in Fig. 5. We mentioned that in Fig. 2b, the peaks {Ala(d), Thr(d), $\beta -$HB(d), Iso(d,t), Val(dd), Leu(d,t)} around Lac(d) are poorly visible (if at all) due to a large span of intensities on the ordinate. To expand the view around Lac(d), the dynamic range of the intensities on the ordinate needed to be reduced, as done in Fig. 2c. Such a reduction allowed these doublets and triplets to pop out from the background baseline, as seen in $|\mathrm{FPT}|$ (c). Therein, the said doublet and triplet resonances are visible, but not quantifiable, due to spectral distortions caused by their interference with the intense Lac(d) tail and the background baseline.

Fig. 5

In vitro $\mathrm{{}^1H\,MRS}$ for a patient with malignant ovarian cyst fluid: serous cystadenocarcinoma. Acronym dMRS refers to derivative MRS. The FIDs from panels (c,d) of Fig. 1 are used to compute the Fourier and Padé magnitude envelopes by shape estimations (both nonderivative and derivative). Spectral intensities on the ordinates in au and the abscissae as chemical shifts in ppm. Nonderivative spectra $(m=0):$ $|\mathrm{FFT}|$ (a,c,e) and $|\mathrm{FPT}|$ (b,d,f). Derivative spectra $(m=3):$ $|\mathrm{D_3FFT}|$ (g) and $|\mathrm{D_3FPT}|$ (h). Spectral intensities without and with reductions on the ordinates: a–d and e–h , respectively. For details, see the main text (color online)

In other words, zooming into the nonderivative lineshape $|\mathrm{FPT}|$ (c) helped only visualization of resonances Ala(d), Thr(d), $\beta -$HB(d), Iso(d,t) Val(dd) and Leu(d,t). Therefore, such an analysis is qualitative, at best, as it exhibits a lineshape profile alone, i.e. it shows a variation of the spectrum as a function of sweep frequency. However, this is only the initial step in data analysis for MRS, which is aimed at extraction of quantitative information from the spectrum built on encoded FIDs. To make the key passage, from qualitative to quantitative, we resort to derivative signal processing within shape estimation by the dFPT. The situation is then salvaged by $|\mathrm{D_2FPT}|$ (d), where the resonances Ala(d), Thr(d), $\beta -$HB(d), Iso(d,t), Val(dd) and Leu(d) are also quantifiable in the same fashion as for Lac(d) in $|\mathrm{D_2FPT}|$ (b). This summarizes the sequential derivative dFPT with visualization and quantification performed in concert, firstly with the dominant peaks on the full ordinate (Fig. 2b) and secondly with the weaker resonances on the reduced dynamic range of intensities (Fig. 2d). Of course, to double check the stability of quantification of resonances in $|\mathrm{D_2FPT}|$ (b), the third $|\mathrm{D_3FPT}|$ derivative should also be used, as this would represent no computational burden at all.

In illustrating sequential visualization/quantification, we could have introduced two separate frequency sub-bands, one around Ala(d) to the left of Lac(d) and the other to the right of Lac(d) for housing Thr(d), $\beta -$HB(d), Iso(d,t), Val(dd) and Leu(d,t). Instead, we opted to keep the whole original band 0.9–1.6 ppm, similarly to Fig. 1. With such an option, a truncation of the upper part of the tall Lac(d) peak was necessary, as done in $|\mathrm{FPT}|$ (c) and $|\mathrm{D_2FPT}|$ (d). However, this is not the only way to hold onto the entire frequency range 0.9-1.6 ppm, while simultaneously displaying the Lac(d) resonance.

Instead, an even more advantageous option exists. Namely, together with preservation of the complete band 0.9-1.6 ppm on the chemical shift axis, the entire size of the Lac(d) peak can be shown, while still keeping the full visibility of the doublet resonances Ala(d), Thr(d), $\beta -$HB(d), Iso(d,t), Val(dd) and Leu(d,t). This is depicted in $|\mathrm{D_2FPT}|$ (e) by using two sets of axes, one (upper chemical shifts, right ordinate) for Lac(d) and the other (lower chemical shifts, left ordinate) for all the remaining resonances. The Lac(d) lineshape and its axes are drawn in red color, while the rest is drawn in blue color. The upper (red) and lower (blue) abscissae for chemical shifts are identically configured. That is to say, they have the coincident ticks for all the indicated frequencies, e.g. 1.05 (lower) versus 1.05 ppm (upper),..., etc. The ticks on the upper chemical shift axis are not numbered to avoid clutter.

The maximum 3500 au on the left (blue) ordinate is chosen to make fully visible all the resonances drawn in blue: Ala(d), Thr(d), $\beta -$HB(d), Iso(d,t), Val(dd) and Leu(d,t). The maximum 87500 au on the right (red) ordinate is chosen to fulfill these two conditions: to display the full size of Lac(d) and to vertically align the ticks on the left and right ordinates in the fixed proportion, e.g. 1000 (left) versus 25000 au (right), ..., etc. Technically, the Lac(d) lineshape together with its small vicinity is extracted from $|\mathrm{D_2FPT}|$ (b) and ’glued’ into $|\mathrm{D_2FPT}|$ (e) in red color.

Alternatively, the same idea of preserving the full visibility for all the resonances in sequential quantification (yet within the complete band 0.9-1.6 ppm) can also be implemented through division of the extracted Lac(d) lineshape by a numerical factor. That factor is 25 as dictated by the ratio of the maximal values on the right (red) and left (blue) ordinates from $|\mathrm{D_2FPT}|$ (e), i.e. 87500/3500=25. Thus, division by 25 of the red Lac(q) extract from $|\mathrm{D_2FPT}|$ (b) makes it possible to have panel (f) for $|\mathrm{D_2FPT}|$ with the common abscissa (chemical shift) as well as ordinate (intensity) for all the resonances, including Lac(d), from the full range 0.9–1.6 ppm.

Illustration of the sequential visualization/quantification in Fig. 2 for the dFPT deals with a fixed derivative order $(m=2)$ for the representative band 0.9-1.6 ppm. It would also be instructive to see how this special quantification develops as the derivative order m is varied. This is the theme of Fig. 3, which shows $|\mathrm{D}_m\mathrm{FPT}|$ at the same frequencies 0.9–1.6 ppm, but with $0\le m\le 3.$ Therein, the seed spectrum, the nonderivative envelope $|\mathrm{FPT}|\, (m=0),$ is included again to monitor the behavioral trend $|\mathrm{D}_m\mathrm{FPT}|$ as m is gradually increased from 0 (panels a, b) through 1 (panel c) to 2 (panel d) and 3 (panel e).

The acronyms for some of the metabolites other than Lac(d) are formally marked in Fig. 3a, just for orientation, although their lineshape profiles remain barely visible for the employed full scale on the ordinate. However, these acronyms become more useful in Fig. 3b with the truncated ordinate, which allows the formerly smaller metabolites to become prominently present in the spectrum. Figure 3b is the same as Fig. 2c. In Fig. 2, three different, but equivalent layouts (d-f) are given, while presenting sequential visualization/quantification for a single, fixed derivative order, $m=2.$ For panels (c-e) in Fig. 3 ($1\le m\le 3$), we adopt the representation with the reduced dynamic range for intensities on the ordinates, as in Fig. 2d.

The first derivative spectrum $\mathrm{D_1FPT}|$ (Fig. 3c) is a zoom (through the window 0.9–1.6 ppm) from Fig. 1h. Because of a wider frequency range 0.85-4.85 ppm in Fig. 1h, many resonances therein appeared as too heavily congested and this diminished the overall visibility of the layout. Comparing $|\mathrm{FPT}|$ (Fig. 3b) with $|\mathrm{D_1FPT}|$ (Fig. 3c), a quantum leap is obtained already by the first derivative $(m=1)$ in the dFPT. This is true in every regard, including the most critical aspects: simultaneous improvement of resolution and SNR.

The mechanism for this twofold achievement is in linewidth narrowing and background flattening, both coupled with huge cutting off the resonance tails of every peak. The cutting off in the resonance tails (i.e. lineshape localization) is seen in $\mathrm{D_1FPT}|$ (Fig. 3c) to be gigantic for the Lac(d) resonance. As a result, in Fig. 3c, most of the formerly lifted resonances, on both sides of Lac(d) are brought down almost to the level of the chemical shift axis. Such an effect amounts to zeroing or near-zeroing the background baseline and the tails of the majority of all the peaks throughout the band 0.9–1.6 ppm. This shows that even the first derivative in the dFPT fulfills, at least partially, the long awaited promise in signal processing: robust noise elimination from spectra due to encoded time signals. Nevertheless, it should be noted that the bottom of Iso(d) has not completely descended to the chemical shift axis and it is partially overlapping with one of the neighboring peaks in Val(d), as mentioned for Fig. 2d. Moreover, the tightly packed peaks of Leu(d,t) and Iso(t), within the narrow sub-band 0.9-0.95 ppm reside on a slight background and, as such, are not yet amenable to quantification either.

Resolution improvement in $|\mathrm{D_1FPT}|$ (Fig. 3c) over that in $|\mathrm{FPT}|$ (Fig. 3b) is stunning. Thus, e.g. the resonances Ala(d), Thr(d), $\beta -$HB(d) and Val(dd) progressed immensely from $m=0$ (Fig. 3b) to $m=1$ (Fig. 3c) in terms of their shapes as well as with respect to paving the road toward quantification. The two individual peaks in Ala(d), Thr(d), $\beta -$HB(d) and Val(dd) in $|\mathrm{D_1FPT}|$ (Fig. 3c) are almost of the same heights. Moreover, the peak heights of Thr(d), $\beta -$HB(d) and Val(dd), taken together, are nearly equal to each other. Nevertheless, there is still room for improvement. The lacunae in $|\mathrm{D_1FPT}|$ (Fig. 3c) are chiefly due to Lac(d) whose base (bottom) is still relatively broad and, hence, it necessitates a further localization. The two peaks of the Lac(d) doublet are not fully separated. In fact, their dividing line is too high, as it stops near 400 au, which is about 60% of the peak height of the Ala(d) doublet from the left of Lac(d).

The encouraging prospect by the dFPT, present already at the onset of derivative estimation by way of $|\mathrm{D_1FPT}|$ (Fig. 3c), is observed to be further solidified with all the main resonances in $|\mathrm{D_2FPT}|$ (Fig. 3d) and even more so in $|\mathrm{D_3FPT}|$ (Fig. 3e). In particular, each of the two peaks in the Lac(d) doublet independently descended to the chemical shift axis as did their dividing lines in $|\mathrm{D_2FPT}|$ (Fig. 3d) and $|\mathrm{D_3FPT}|$ (Fig. 3e). This signifies disappearance of presumably most spectral structures co-resonating with Lac(d) around 1.41 ppm, pointing to the possibility of accurate quantification of Lac(d) for $m=2$ and $m=3.$

Such an opportunity was announced first in $|\mathrm{D_2FPT}|$ (Fig. 2b), then seen again in $|\mathrm{D_2FPT}|$ (Fig. 3d) and further reinforced in $|\mathrm{D_3FPT}|$ (Fig. 3e). Note that the individual peaks in Lac(d) are thinner in $|\mathrm{D_3FPT}|$ (Fig. 3e) than in $|\mathrm{D_2FPT}|$ (Fig. 3d), as it should be with the increased derivative order m from 2 to 3. Moreover, the base (bottom) of Lac(d) is more localized/narrowed in $|\mathrm{D_3FPT}|$ (Fig. 3e) than in $|\mathrm{D_2FPT}|$ (Fig. 3d). This points to an improved SNR in panel (e) relative to panel (d) of Fig. 3.

In Fig. 3, the ’spectral crowding’ at 0.9-0.95 ppm seen in $|\mathrm{FPT}|$ (b) and $|\mathrm{D_1FPT}|$ (c) is cleared up in $|\mathrm{D_2FPT}|$ (d) and $|\mathrm{D_3FPT}|$ (e). We saw that, in spite of some small overlaps, the first derivative spectrum $|\mathrm{D_1FPT}|$ (c) offers a notably better spectral clarity relative to it nonderivative counterpart $|\mathrm{FPT}|$ (b). This is partially facilitated by a large suppression of the background in $|\mathrm{D_1FPT}|$ (c). The said slight overlap is further minimized in $|\mathrm{D_2FPT}|$ (d), whereas a complete separation of all resonances is attained in $|\mathrm{D_3FPT}|$ (e). Hence, quantification becomes possible in $|\mathrm{D_3FPT}|$ (e) even in the very congested leucine/isoleucine band 0.9-0.95 ppm. By comparison, in Ref. [15] it has been stated that ’spectral crowding’ prevented quantifying the resonances from the leucine/isoleucine range 0.9–0.95 ppm. As mentioned, Ref. [15] used the phase and baseline corrected real part of the complex spectrum in the FFT which despite lowering the background, could not reduce the strong overlap of resonances.

Apart from Lac(d), the tallest resonances are the two peaks in the Ala(d) doublet, as per panels (c–e) in Fig. 3. Herein, for a fixed derivative order m,  the doublets Thr(d) and $\beta -$HB(d) are of equal strength and their intensity is about 45% of that in Ala(d). Such a peak height ratio is quite well maintained when the derivative order m is augmented from 1 to 3, as seen in $|\mathrm{D_1FPT}|$ (c), $|\mathrm{D_2FPT}|$ (d) and $|\mathrm{D_3FPT}|$ (e). This indicates that the linewidths of all the individual peaks in Ala(d), Thr(d) and $\beta -$HB(d) are almost the same.

Regarding the double doublet Val(dd), the following observation is made. These two doublets are of comparable intensity for one derivative order considered at a time. As to their intensities, the peak heights of Val(dd) in $|\mathrm{D_1FPT}|$ (c) are about 90% of the strength of Thr(d) or $\beta -$HB(d). However, this ratio is not preserved for higher derivative orders. Rather, it is notably smaller, about 70% in $|\mathrm{D_2FPT}|$ (d) and close to 50% in $|\mathrm{D_3FPT}|$ (e). This implies that the peak widths of either of the doublets in Val(dd) are not the same as those in Thr(d) or $\beta -$HB(d). If they were the same, then the peak heights in Val(dd) would also be $\sim 90\%$ of the intensity of Thr(d) or $\beta -$HB(d) in $|\mathrm{D_2FPT}|$ (d) and $|\mathrm{D_3FPT}|$ (e) as it is in $|\mathrm{D_1FPT}|$ (c).

The moral of this story is clear and important: it is not advisable to assume that the peak widths of all the resonances in a given spectrum are equal, since such an approximation runs the risk of making errors in estimations of metabolite concentrations. It is here too where derivative estimation by the dFPT can be of great practical help since, even prior to explicit quantification by shape estimation, it can be decided whether there are differences among linewidths of the resonances in a spectrum. In the MRS literature, it is often assumed that the linewidths of all the resonances in an entire spectrum are equal. Such an assumption in quantification has also been made in Ref. [15], where 1.0 Hz was taken as the common linewidth of all resonances, as stated. If the resonance linewidths for any two given peaks are not the same, the ratio of the peak heights becomes misleading. In such a case, valid biophysical information is obtained from comparing the corresponding areas of the two peaks.

Figure 4 continues the theme of Fig. 1 by comparing the spectra for the benign and malignant cyst fluids. More precisely, Fig. 4 is a specific zoom of Fig. 1 as, this time, the focus is on the narrow window 3.17-3.30 ppm, which is the band of another recognized cancer biomarker, the set of cholines. As to derivative estimations, Fig. 1 considers only the first derivative $(m=1)$ for the malignant case. However, for completeness, Fig. 4 includes the three derivatives $(1\le m\le 3)$ and, moreover, it does so for both the benign and malignant cases. The nonderivative spectra are also given in Fig. 4, as the starters to which the derivative envelope should always refer for visualizing the extent of the lineshape alteration as the order m is gradually enhanced.

Regarding the first row in Fig. 4, with the nonderivative FPT ($m=0:$ a,e) versus the derivative dFPT ($1\le m\le 3:$ b-d,f-h) estimations, there are spectral features that are shared by the benign and malignant cases. For example, the nonderivative lineshape profiles in $|\mathrm{FPT}|$ (a,e) are broad, asymmetric and visibly elevated above the chemical shift axis. This is due to interference of the real and imaginary parts in the magnitude mode of the complex lineshapes, exacerbated with the contribution from the macromolecular background. However, such interference effects are observed in Fig. 4 to be diminished in derivative lineshapes on the second, third and fourth rows for $m=1,\, 2$ and 3, respectively. As a result, the derivative lineshapes become narrower and, by implication, taller, i.e. more intense.

Simultaneously, the derivative operator $\mathrm{D}_m$ in $|\mathrm{D}_m\mathrm{FPT}|$ for $1\le m\le 3$ is seen to progressively reduce more and more noise as the order m is increased. A gradual background flattening can be noted when scrolling down from panels (a) to (d) on the left and, likewise, from panels (e) to (h) on the right column of Fig. 4. This synergism of synchronized resolution and SNR improvements, starting from its promising trajectory already with the first derivatives $|\mathrm{D_1FPT}|$ (b,f) is consistently followed by further significant ameliorations in $|\mathrm{D_2FPT}|$ (c,g) and $|\mathrm{D_3FPT}|$ (d,h).

The dominant resonance throughout Fig. 4, i.e. for both the benign and malignant cases, is the peak assigned to taurine, Tau. Herein, the Tau resonance should be a triplet, Tau(t). This is not materialized yet in Fig. 4 because the derivative orders $1\le m\le 3$ are insufficiently high. However, we checked in the benign case that already the spectrum $|\mathrm{D}_4\mathrm{FPT}|$ (not shown) begins to distinctly exhibit the three Tau peaks. Comparing the left and the right columns in Fig. 4, it is seen that the intensities of the Tau resonance on different panels are systematically stronger (nearly twice) for the benign (a-d) than for the malignant (e-h) cases.

For the benign cyst fluid, panels (a-d) of Fig. 4 show that the m-Ins and $\beta -\mathrm{Glc}$ peaks are the second and third strongest resonances at 3.17-3.30 ppm. The $\beta -\mathrm{Glc}$ resonance complex is theoretically expected to be a double doublet, $\beta -$Glc(dd). It is clear that no such a spectral structure is visible in either of the two nonderivative spectra (a,e) for $|\mathrm{FPT}|.$ In $|\mathrm{FPT}|$ (a:benign), near 3.248 ppm, there is pronounced peak in $\beta -$Glc with a visible and smaller right shoulder close to 3.245 ppm. The opposite occurs in $|\mathrm{FPT}|$ (e:malignant), where a wider and taller peak shows up near 3.245 ppm with a left smaller shoulder at 3.248 ppm.

On the other hand, derivative estimations greatly improve the situation for $\beta -$Glc in $|\mathrm{D}_m\mathrm{FPT}|\, (1\le m\le 3).$ Thus, a triplet appears on the location of $\beta -$Glc in $|\mathrm{D_1FPT}|$ (b,f). Finally, the two doublets in $\beta -$Glc(dd) are visible in $|\mathrm{D_2FPT}|$ (c,g) and $|\mathrm{D_3FPT}|$ (d,h). The middle two peaks are of approximately equal heights only in $|\mathrm{D_2FPT}|$ (g). Therein, however, the right peak of these two middle resonances from $\beta -$Glc(dd) is slightly wider than its left companion. As a consequence, already in $|\mathrm{D_3FPT}|$ (h), the right peak in the middle of $\beta -$Glc(dd) becomes shorter than its left neighbor. This illustrates the characteristic results of the action of the derivative operator $\mathrm{D}_m$ for increasing order m :  a different pace of the peak height increase for narrower and broader resonances.

The third derivative spectra (d,h) via $|\mathrm{D_3FPT}|$ show that the average peak heights of the four peaks in $\beta -$Glc(dd) are very close on these two panels. Also, for the nonderivative envelope $|\mathrm{FPT}|,$ the tallest peak within $\beta -$Glc is of nearly the same height on panels (a: benign) and (e: malignant) in Fig. 4.

As to myo-inositol, also according to the theory, this resonance should be a triplet, m-Ins(t). Such a multiplicity is not observed in the nonderivative spectra (a,e) for $|\mathrm{FPT}|.$ However, for the malignant case, in all the three derivative envelopes $|\mathrm{D}_m\mathrm{FPT}|\, (1\le m\le 3:$ f-h), the myo-inositol triplet m-Ins(t) is detected. Using e.g. $|\mathrm{D_3FPT}|$ to compare the average peak heights in m-Ins(t) for the benign (Fig. 4d) and malignant (Fig. 4h) ovarian cyst fluids, it is seen that the former is stronger than the latter by a factor of about 3.

These insights, although limited to the two compound resonances, $\beta -$Glc and m-Ins, still give a hint on the relative peak intensity variations when attempting to assess the potential qualification of various metabolites as cancer biomarkers. Of course, for clinical practice, such qualification must undergo a more stringent scrutiny by considering a sufficiently large number of patients with a particular cancer type in different human organs. However, when it comes to the choline-containing compounds, they are already well established as the recognized cancer biomarkers for several human organs, as stated (brain [1,2,3], prostate [4,5,6], breast [7,8,9,10,11], ovary [12,13,14,15,16,17,18,19], cervix [20,21,22,23,24]).

Therefore, we can now check how this status of the choline-bearing compounds is represented in Fig. 4. Therein, it is immediately seen on panels (e–h) for the malignant case that there is a clear detection of the three separate resonances assigned to the Cho, PC and GPC metabolites. Moreover, on panels (e–h), the PC and Cho resonances are the second and third strongest peaks within the band 3.17–3.30 ppm. This is opposed to the benign case (a–d) for which, as mentioned, after the tallest Tau peak, the $\beta -$Glc and m-Ins resonances are the most intense. Further, for the benign case, the Cho and GPC resonances are barely identifiable from the ondulatory background baselines on any of the panels (a-d) in Fig. 4. Herein, for the benign cyst fluid, the PC peak is about twice more intense than the Cho and GPC components of tCho. However, the lineshape tops of the Cho, PC and GPC resonances (a-d: benign) are markedly smaller than their counterparts (e-h: malignant) in Fig. 4.

Quantitatively, in $|\mathrm{FPT}|$ (a,e), the malignant-to-benign (M/B) ratios of the maxima of the lineshape profiles of the components of tCho are given by: $\mathrm{(M/B)_{Cho}\approx 5.0,}$ $\mathrm{(M/B)_{PC}\approx 1.9}$ and $\mathrm{(M/B)_{GPC}\approx 1.9}.$ In other words, the peak heights of all the three components Cho, PC and GPC of tCho are stronger in the malignant (e-h) than in the benign (a-d) case. This is consistent with the cancer biomarker status of these cholines under the provision of the same linewidths of the Cho, PC and GPC. For unequal linewidths, the corresponding ratios of the peak areas should be estimated to make a more appropriate comparison (malignant versus benign) for Cho, PC as well as GPC and then for tCho.

There is a both interesting and important occurrence around 3.19 ppm, which is the known chemical shift of free choline, assigned to a singlet resonance, Cho(s). When cholines are a part of the information for making a differential diagnosis (benign versus malignant), the conventional, nonderivative total shape spectra in the FFT are used in practice. In such envelopes (irrespective of the employed mode, e.g. the magnitude or the phase-and-baseline-corrected real part of a complex lineshape), the free choline has invariably been treated as if it were unquestionably a singlet, Cho(s). This occurred because a single peak of Cho usually appears at 3.19 ppm in the nonderivative spectrum from the FFT.

The appropriate question to ask, however, regarding Fig. 4e would seem to be: is the single lineshape profile for free choline, Cho, near 3.19 ppm sufficiently representative of the actual level of this metabolite assessed by either the FPT or FFT?

The answer to this critical question is in the negative, as testified by the derivative spectra on panels (f–h) of Fig. 4 for the malignant cyst fluid. The reason is in the fact that the spectral portion in $|\mathrm{FPT}|$ (e) centered at 3.19 ppm is, in fact, structured. Precisely at 3.19 ppm, already the first derivative spectrum $|\mathrm{D_1FPT}|$ (f) shows a splitting. Subsequently, two adjacent and distinct co-resonating peaks near 3.19 ppm are generated in $|\mathrm{D_2FPT}|$ (g) and $|\mathrm{D_3FPT}|$ (h). There is no trace whatsoever of such a splitting in the benign case from the left column (a-d) of Fig. 4, where free choline is hardly detectable.

Near 3.19 ppm on panels (f-h) of Fig. 4, the left peak is assigned to Cho(s), whereas the right peak, marked by a red star and letter U, is presently left unassigned, as it needs a biochemical analysis for a proper interpretation. There might be several potential competitors for assigning a known metabolite to the U-resonance. The narrow band 3.17–3.30 ppm of the choline-containing compounds is populated by the ethanolamine-containing compounds (ethanolamine Eth, phosphoethanolamine PE and glycerophosphoethanolamine GPE), amino-acid-based taurine as well as $\alpha -$ and $\beta -$glucose [5, 84].

The levels of the unassigned metabolite U and free choline in Fig. 4 resemble each other as they are both hardly detectable in the benign case (a-d) and significantly enhanced for the malignant case (e-h). Therefore, a well-qualified metabolite, which might be considered for assignment to the U-resonance, could also be a cancer biomarker. This might be the {5,6}-dihydrothymine metabolite, which resonates precisely at 3.19 ppm [31, 85]. Synthesized by epithelial cells of various human organs, within thymine-containing metabolism, the {5,6}-DHT molecules are the intermediate products of the thymine degradations. Changes in the concentration levels of the {5,6}-DHT metabolites are caused by cellular malignant transformations and cancer proliferation. By contrast, normal cells hardly exhibit any appreciable level of the {5,6}-DHT molecules.

In vitro spectroscopic studies have identified the strikingly high level of the thymine breakdown through the DHT pathway, leading to e.g. breast and lung adenocarcinomas [86,87,88,89]. Thus, it appears as tempting in Fig. 4 to assign the {5,6}-DHT metabolite to the unknown U-peak which is located near 3.19 ppm. In fact, a double rationale for such a choice would be the tumor marker feature of {5,6}-DHT and its resonance frequency (close to 3.19 ppm). Nevertheless, for the time being, we will leave this question open for a further and more detailed interpretation. However, what matters the most here, even prior to an explicit assignment of the U-resonance to a known metabolite, is that, contrary to the common practice, free choline Cho(s) cannot be viewed as the only peak near 3.19 ppm.

It is this previously unreported finding that calls into question the results of the usual quantification of the choline-containing compounds employing any nonderivative spectrum. Such a procedure would erroneously double the level of free choline Cho(s), thus yielding significant overestimations of the true concentration of total choline, tCho. This could influence the values of the cut-points in the concentration ratios (malignant/benign) and alter the diagnostic decision.

The spectral findings from envelopes due to the nonparametric FPT and dFPT are checked against the parametrically computed components from the FPT and dFPT [83]. It is found that the splitting at 3.19 ppm is genuine and already the components in the nonderivative parametric FPT show two clear peaks tightly positioned at each side of chemical shift 3.19 ppm. Moreover, as it is now the standard, the components in the parametric derivative dFPT gradually collapse into the corresponding envelopes from shape estimations by the nonparametric derivative dFPT. In any case, whichever metabolite is to be assigned to the U-resonance in Fig. 4, the key information is that near 3.19 ppm in the nonderivative envelope $\mathrm{|FPT|}$ (e), a wider resonance conventionally perceived as a free choline Cho(s), is definitely not a lone peak.

The implication of these findings is that the concentration level of free choline at 3.19 ppm could easily be overestimated, if assessed by nonderivative envelopes in any processor, including the FPT and FFT. This conclusion holds true for both the magnitude mode and the phase-and-baseline-corrected real part of the complex-mode spectra. Hence, if Cho(s) is to be trusted as one of the key recognized cancer biomarkers in tumor diagnostics by MRS, its concentration level must unequivocally be estimated. For this to occur, one should not count at all on customary, nonderivative nonparametric signal processing because of its inability to uncover the sub-structure of the apparent singlet lineshape profile of Cho(s) near 3.19 ppm. Here too, derivative shape estimations by the dFPT come to the rescue by peering into the possible sub-structure of an apparent single resonance.

Figure 5 juxtaposes the Padé and Fourier estimations of envelopes on the level of both nonderivative ($m=0:$ FPT, FFT) and derivative ($m=3:$ dFPT, dFFT) reconstructions in the magnitude mode. The nonderivative spectra ($m=0$) are on panels (a-f), whereas panels (g,h) are on the two envelopes from the third derivative $(m=3).$ Specifically, the Fourier results are on panels (a,c,e) for the FFT $(m=0)$ and (g) for the dFFT $(m=3).$ On the other hand, the Padé findings are on panels (b,d,f) for the FPT $(m=0)$ and (h) for the dFPT $(m=3).$ The first row (a-d) uses the full scale on the ordinates for the spectral intensities. From the 2nd to the 5th rows, employed are the reduced ranges of the spectral intensities on the ordinates.

The internal standard, the singlet resonance TSP(s), is shown on panels (a,b) at frequencies [–0.05,0.05] ppm. The remaining panels (c-h), within the band [0.9, 1.6] ppm, are on the Lac(d) resonance and its main close surrounding, Ala(d), Thr(d), $\beta -$HB, Val(dd), Iso(d,t) and Leu(d,t). It is seen that the standard nonderivative variant of signal processing ($m=0$) gives the same results in the FFT (a,c,e) and FPT (b,d,f). Panels (d,f) for the FPT, dealing with the Lac(d) surrounding, have already been presented in Fig. 3 and the pertinent analysis need not be repeated here. Moreover, due to the coincidence of the spectra $|\mathrm{FFT}|$ (c,e) with $|\mathrm{FPT}|$ (d,f) at the displayed frequencies [0.9, 1.6] ppm around Lac(d), it is not necessary either to discuss the nonderivative Fourier estimation.

The complete agreement also exists between the Fourier $|\mathrm{FFT}|$ (a) and Padé $|\mathrm{FPT}|$ (b) envelopes around the TSP(s) resonance. The internal standard TSP(s), centered at 0 ppm, is seen not to be a lone resonance. Firstly, it hides the two nearby satellites whose tops can be observed as the slight shoulders to TSP(s). The peak heights of each of the two satellites are $\sim 220$ au, compared to the peak height $\sim 1750$ au of the TSP(s) resonance. The satellite on the right is slightly taller than that on the left of 0 ppm. This lifts somewhat the right wing of the TSP(s) tail, on the side of negative frequencies, as perceivable on panels (a,b).

In the MRS literature, it is a common stance that the TSP(s) peak area can perfectly be computed from the FFT spectrum because this internal standard is unquestionably assumed to be a lone resonance with no contribution whatsoever from its immediate neighbors, as if there were none. This is misleading even without reference to the mentioned two satellites around TSP(s). The reason is in the lack of any guarantee to support the assumption that the TSP(s) base (bottom) is void of some other peaks located in a close vicinity of 0 ppm. As a matter of fact, the contrary is true, as revealed in Ref. [83], where the component spectra from the parametric nonderivative FPT show some hidden wider nonnegligible resonances beneath TSP(s).

Therefore, it is not advisable to compute even the peak area of the reference resonance, TSP(s), by relying upon a nonderivative spectrum, be it $|\mathrm{FFT}|$ (a) or $|\mathrm{FPT}|$ (b) or any other nonderivative magnitude of absorptive-type envelope. The argument for this statement runs as follows. One role of an internal standard is in referencing the chemical shifts of other resonances relative to 0 ppm, where presently the TSP(s) peak resides. However, the other role is also on the calibration kind and it refers to quantification, as stated. This is done when expressing the concentrations of all the other metabolites as the percentages of the TSP(s) molar concentration. Evidently, if the TSP(s) peak area is prone to be unreliable, so will be the TSP(s) concentration. This would impact adversely on the estimates of the concentrations of all the other metabolites.

By contrast, derivative estimation, particularly with the dFPT, does not encounter such obstacles. This occurs because already the low-order derivatives (e.g. $m=2$ or 3) in the dFPT can push the hidden resonances from the bottom of TSP(s) into the baseline which, in turn, would coincide with the chemical shift axis. With such a procedure at the disposal, the true peak area of the TSP(s) resonances can be obtained perfectly to give the correct molar concentration of this internal standard. The implication is that the concentrations of all the other metabolites can also be trusted when the dFPT is used as a shape estimator.

The Fourier and Padé derivative estimations, yielding the spectra $\mathrm{|D_3FFT}|$ (g) and $\mathrm{|D_3FPT}|$ (h), respectively, are observed to be in a stark contrast. The high quality of the Padé envelope $\mathrm{|D_3FPT}|$ (h) was the subject of the analysis for Fig. 3 and this gains its further importance by reference to the Fourier prediction $\mathrm{|D_3FFT}|$ (g). It is clear from panel (g) that the breakdown of the dFFT is complete as both resolution and SNR are worsened in the third derivative $\mathrm{|D_3FFT}|$ relative even to its nonderivative counterpart $\mathrm{|FFT}|$ (e). This is a marked deterioration of Fourier processing, especially when compared to simultaneous huge resolution and SNR improvements in the corresponding Padé analysis when passing from the nonderivative $\mathrm{|FPT}|$ (f) to the derivative $\mathrm{|D_3FPT}|$ (h) envelopes.

In the Fourier spectrum $\mathrm{|D_3FFT}|$ (g), all the resonances at 0.9-1.6 ppm are severely distorted. In particular, some resonances, e.g. Leu(d,t) and Iso(d,t), that should be seen at 0.9–1.025 ppm, are practically unrecognizable. Further, at 1.025–1.6 ppm, some severe spectral deformations also occur in the main resonances, Val(dd), $\beta -$HB(d), Thr(d), Lac(d) and Ala(d). Thus, e.g. Val(dd), $\beta -$HB(d), Thr(d) and Ala(d) have significant intensity losses. This is reflected not only in their reduced peak heights, compared to the Padé envelope $\mathrm{|D_3FPT}|$ (h), but also in unequal intensities of the individual resonances in each of these doublets, viewed separately. Moreover, the Lac(d) resonance is wider in $\mathrm{|D_3FFT}|$ (g) than in $\mathrm{|D_3FPT}|$ (h). Further, in $\mathrm{|D_3FFT}|$ (g), the background has filled the spacing between the two individual peaks from Lac(d) to a high level, reaching about 50% of the Ala(d) intensity. Overall, the result $\mathrm{|D_3FFT}|$ (g) is utterly unsatisfactory, even relative to $|\mathrm{FFT}|$ (e), let alone with respect to $\mathrm{|D_3FPT}|$ (h).

The breakdown of the Fourier derivative estimations (deteriorated resolution and SNR) is due to processing modified FIDs that weigh heavily the noisy part of the encoded time signals. This dramatic failure of the dFFT, as seen in Fig. 5g, is due to the action of the derivative operator $\mathrm{D}_m=(\text{ d }/\text{d }\nu )^m,$ which emphasizes the later parts of the measured FIDs, where noise dominates. Such a deleterious effect of the same operator $\mathrm{D}_m$ is completely absent from the corresponding Padé derivative estimations whose results $|\mathrm{D}_m\mathrm{FPT}|$ systematically improve both resolution and SNR even for low orders m.

3.3 Broader inferences for ovarian cancer detection

The present findings are indeed relevant for advancing efforts to achieve effective and timely ovarian cancer detection. This goal is still unrealized and, as a consequence, most cases of ovarian cancer are identified late with poor survival rates [90, 91]. The key motivation for pursuing further these efforts is to achieve early ovarian cancer detection, i.e. when the malignancy is confined to within the ovary itself without further spread (stage 1a). This stage is associated with well over 90% five-year survival [43, 92]. The inability of noninvasive methods to provide clear distinction between benign and cancerous ovarian lesions remains a key stumbling block for achieving this goal.

As extensively reviewed previously on the ovary diagnostics [26, 63], in vivo MRS, with its reliance upon the FFT, is inadequate for distinguishing cancerous from benign ovarian lesions. Coupled with the technical problems entailed with attempts to encode time signals from this small, moving pelvic organ, the potential of effective noninvasive, timely ovarian cancer detection by MRS has remained unfulfilled.

In sharp contrast, studies applying the parametric, nonparametric, nonderivative FPT as well as its derivative variant dFPT to in vivo MRS time signals encoded from borderline ovarian cyst, have provided encouraging data [26, 63]. These findings point to a rich store of metabolic information, with some 150 resonances that were unequivocally resolved and quantified. Particularly in Ref. [26], the reconstruction data were presented through the graphs in a readily interpretable manner for clinicians.

Comparison between such results for the ovary using the derivative version of in vivo MRS [26] at clinical scanners (3T) and in vitro MRS (spectrometers with larger $B_0,$ above 10T) is clearly needed. Previously, it was assumed that the latter MRS would represent the “gold standard” due to the application of much stronger static magnetic fields. This was particularly considered to be the case with the application of HRMAS MRS, by which the tissue architecture is preserved, so that subsequent histology and molecular pathology can be analyzed [93]. Using HRMAS MRS, otherwise wide resonances become substantially narrowed, yielding spectra with much better resolution of metabolites.

However, as already discussed in the present study, a closer examination of results from in vitro MRS, including its HRMAS variant (both based on data analysis by the FFT, with or without post-processing), indicates that these in vitro methods also need to be optimized. Namely, without derivative processing, macromolecules and other resonances that underlie the “hills” can be missed, especially in regions of ’spectral crowding’. Accurate quantification, insofar as it is carried out nonparametrically, also requires maximally flattened baseline, with each resonance being resolved down to that baseline. It is only thereby that the peak areas can be correctly computed e.g. by a numerical quadrature method due to the possibility to clearly define the integration limits.

Notwithstanding these considerations, there appears to be substantial coherence between the present results and in vitro studies of benign and cancerous ovarian lesions. Notably, elevated levels of alanine Ala, whose main resonance was at approximately 1.5 ppm, were reported in serous ovarian tumor biopsies in the HRMAS MRS study of Ref. [94]. Moreover, in the latter examination, the findings from benign ovary were characterized by higher levels of taurine Tau (resonating near 3.26 and 3.42 ppm). This is also consistent with our Padé-reconstructed data.

In Ref. [94], three different histological types of epithelial ovarian carcinomas were included, endometrioid, mucinous and serous. Substantial differences in the findings among these three tumor types have been reported [94]. This is not surprising, given the heterogeneity of ovarian pathology. Also for these different kinds of MRS data, the precision provided by the dFPT (with its sequential visualization and quantification) would be particularly welcome.

Considerable MRS-detectable differences have previously been reported between the metabolic characteristics of cystic and solid ovarian lesions [16, 63]. In the present study, we used the high-field MRS time signals (14.1T) encoded from ovarian cysts, that had histologically been diagnosed as serous cystadenoma and serous cystadenocarcinoma [15]. We found that a number of resonances in different chemical shift bands were significantly more intense for the malignant than for the benign cyst, in agreement with the observation from Ref. [15] for encoded FIDs associated with other patients.

Two such frequency bands have been exemplified in the current investigation. One is 0.9-1.6 ppm (Ala, Lac, Thr, $\beta -$HB, Val, Leu, Iso) and the other is 3.17-3.30 ppm (Cho, PE, PC, GPC, $\beta -$Glc, Tau, m-Ins). Sequential visualization/quantification by the dFPT was shown to be especially practical when there is at least one dominant peak which overwhelms all the other resonances. At 0.9-1.6 ppm, this the lactate double peak, Lac(d). Once quantified, a large portion of the upper part of Lac(d) can safely be cut-off. This allows the other weaker resonances to show up so that they too can be visualized/quantified in the same manner as Lac(d), i.e. by linewidth narrowing and background flattening.

In Ref. [15], despite using a strong magnetic field (Bruker 600 MHz spectrometer) for encoding of FIDs, the treatment of e.g. the choline-containing recognized cancer biomarkers was limited only to total choline tCho using a rough quantification by fitting the FFT spectra with the Lorentzian lineshape profiles. Here too, the usefulness of the dFPT was presently evidenced by visualizing/quantifying free Cho, PC and GPC as the three components of tCho. This is of a notable importance given that often it is precisely the elevated levels of PC and/or GPC that are critical in enabling the physician to make differential diagnosis, benign versus malignant.

There is more to the choline-bearing compounds within 3.17–3.30 ppm. Namely, besides separating the three constituents of tCho, we detected a previously unobserved resonance at $\sim 3.19$ ppm. The dFPT finds that at $\sim 3.19$ ppm, free Cho has an immediate neighbor, a co-resonating metabolite (left unassigned) of similar intensity. Without this information, which was absent from Ref. [15], the level of tCho is surely over-estimated. The feature of unraveling a hidden resonance lying within another resonance, while analyzing MRS data by shape estimation, is the strongest argument in favor of derivative signal processing. This advantage gains its full diagnostic significance when such a sub-structured resonance (ordinarily taken as a singlet) is assigned to a cancer biomarker (recognized and/or potential alike).

However, to accordingly improve the overall diagnostic interpretation of MRS data, a replacement of the nonderivative FFT by its derivative counterpart, dFFT, would not be the road to undertake. The reason is in the well-documented complete inadequacy of the dFFT [25, 26]. Rather, the dFPT as a shape estimator is an optimal candidate for the said improvement because this method, even without an explicit quantification, can inform the physician about the hidden resonances so as to avoid misdiagnoses.

4 Conclusion

The problem area of this study is diagnostics of human tumors by means of proton magnetic resonance spectroscopy, $\mathrm{{}^1H\,MRS}.$ This is one of the most powerful, noninvasive methods for metabolic profiling. Such profiling consists of identification and quantification of known and unknown metabolites. Metabolites are molecules that participate in many different pathways of metabolism in various organs of the human body. The usage of MRS offers the opportunity to expand understanding of a myriad of processes and to monitor structural, dynamical, functional and physiological changes in biological systems.

Such an added value is of paramount importance for early tumor diagnostics because the detected changes occur on a molecular level and, as such, precede their anatomical/morphological manifestations on scans by e.g. magnetic resonance imaging, MRI. The prime advantage of MRS over other methods is in providing the possibility to extract abundant information about the metabolic composition of the examined samples by identification and quantification of structurally vastly different metabolites. However, this possibility would remain entirely unexplored, if not for the pivotal role of mathematical methods through signal processing. The reason is that time signals (encoded by either spectrometers or clinical scanners), being heavily packed exponentially attenuated harmonic functions, are totally uninterpretable in a direct way. This drawback can be surmounted by the mathematical transformations (Fourier, Padé, ...) for mapping the measured time signals into the computed frequency spectra that show a number of more manageable resonance peaks assignable to metabolites.

It is these resonance peaks whose description constitute metabolic profiling. To accurately represent these spectral structures, it is necessary to identify and extract the resonance peak parameters (position, widths, heights, phases). Such quantitative information about the resonance peaks allows their assignments to known and unknown metabolites. This is how identification and quantification of metabolites, contained in the given sample, are carried out. Physical and biochemical information conveyed by the resonance peak parameters is multifacetedly rich.

Thus, the peak position informs about the electron surroundings of the resonating proton. Circulating electrons (bound to molecules, atoms or ions) create a small local magnetic field $\mathrm{\Delta }B_0\ll B_0,$ which screens the much stronger external static magnetic field $B_0$ at the position of the resonating proton. It is this minuscule shielding that allows MRS to differentiate among various metabolites in a sample. The peak width, or more frequently employed the full width at half maximum, FWHM, is proportional to the rate $1/T^\star _2$ of the decay of the metabolite response to an external excitation by a radio-frequency or RF pulse, $\mathrm{FWHM}=1/(\pi T^\star _2).$

Quantity $T^\star _2$ is the effective transverse (or spin-spin) relaxation time constant, $1/T^\star _2=1/T_2+\gamma \mathrm{\Delta }B_0,$ where $\gamma$ is the gyromagnetic ratio and $T _2$ is the intrinsic spin-spin relaxation time constant. An RF pulse excites the protons in the sample. After cessation of that pulse, the protons undergo de-excitation (recovering or relaxing) to regain their Boltzmann equilibrium distribution. This recovery time is $T^\star _2$ which differs across the sample because both $T_2$ and $\mathrm{\Delta }B_0$ vary from one to another metabolite. Such an occurrence permits MRS to identify diverse metabolites in a sample.

In the absence of $\mathrm{\Delta }B_0,$ the resonance is sharp in liquids because it is determined by its natural full width at half maximum $1/(\pi T_2).$ However, the inhomogeneity $\mathrm{\Delta }B_0$ of $B_0$ broadens the peak width according to $\mathrm{FWHM}=1/(\pi T_2)+ (\gamma /\pi )\mathrm{\Delta }B_0.$ The sharper the resonance, the taller the peak height. Metabolites with larger/smaller transverse relaxation time constants correspond to narrower/broader resonance peaks, respectively.

The number of resonating protons is given by the peak area (ratio of the peak height and its FWHM). Metabolite concentration (proportional to the peak area) is of primary diagnostic relevance. Detecting an abnormal abundance of certain metabolites in a specimen can help differential diagnosis (benign versus malignant tumor). Some metabolites (choline, lactate, ...) are categorized as the recognized cancer biomarkers.

In particular, the spectral structure of total choline tCho is comprised of three singlet resonances, free choline Cho(s), phosphocholine PC(s) and glycerophosphocholine GPC(s). Their resonance frequencies are close to each other, lying in the proximity of chemical shift 3.20 ppm. Because of this ’spectral crowding’, total shape spectra or envelopes from the fast Fourier transform, FFT, are of poor resolution. They do not show separate resonances of Cho, PC and GPC, even for patients with cancer, when using time signals encoded by in vivo $\mathrm{{}^1H\, MRS}$ at clinical scanners (1.5, 3T). Instead, the FFT may provide only the amalgamated peak of tCho as the unresolved sum of the three components, Cho, PC and GPC.

While still staying within shape estimations, this situation changed to the better with derivative signal processing. Thus, it has recently been shown that e.g. tCho can unequivocally be separated into Cho, PC and GPC by applying the nonparametric derivative fast Padé transform, dFPT, to time signals encoded by in vivo $\mathrm{{}^1H\, MRS}$ at 1.5 and 3T [25, 26]. Moreover, the same variant of the dFPT succeeded in splitting apart myriad of other resonances that appear as single peaks in envelopes from the FFT. These outcomes from the dFPT were due to the systematic and simultaneous improvements in resolution and signal-to-noise ratio, SNR. Moreover, such a twofold accomplishment can be monitored by visualizing gradual linewidth narrowing and flattening of the background baseline.

Most importantly, once isolated with a sufficient derivative order in shape estimations by the dFPT, any given resonance can accurately be quantified. This is done most conveniently in the phase-insensitive magnitude mode for total shape spectra or envelopes. The same program in the dFPT, which reconstructs these envelopes, can automatically quantify by determining the peak positions, widths and heights of all the well-isolated resonances. This is enabled by the fact that any Padé spectrum can be computed at an arbitrarily large number of sweep frequencies by employing the desired mesh (equidistant or with variable sampling rates) without zero-filling of time signals. With the abundant frequency grid points, the program in the nonparametric dFPT can instantly find and print out the peak position, height and FWHM of all the isolated resonances. Each corresponding peak area is also automatically available as the product of the peak height and FWHM since the magnitude derivative envelopes in the dFPT are bell-shaped, similarly to absorptive nonderivative Lorentzians. Finally, the existing conversion expressions, established in Ref. [34], are used to map the derivative to the corresponding nonderivative peak parameters. This is how quantification by the nonparametric dFPT works in a nut shell.

For in vitro $\mathrm{{}^1H\, MRS},$ aimed at resolution and noise improvements, much stronger magnetic fields are used, e.g. 14.1T as in Bruker spectrometers operating at the Larmor frequency of 600 MHz. Still, in e.g. Ref. [15] on in vitro $\mathrm{{}^1H\, MRS}$ for benign and malignant ovarian cyst fluids, despite the employed strong magnetic field $(B_0=14.1\,{\mathrm{T}}),$ the concentration listed under designation “choline” has not detailed the separate abundances of free Cho, PC nor GPC. In Ref. [15], some 36 and 16 resonances were assigned to known and unknown metabolites, respectively. Therein, the ’spectral crowding’ (peak overlaps in congested frequency bands) permitted only 12 assigned resonances to be quantified using the FFT followed by fitting the lineshape profiles to Lorentzians.

The time signals from two samples of ovarian cysts, benign (serous cystadenoma) and malignant (serous cystadenocarcinoma) encoded by the authors of Ref. [15] were presently subjected to the Padé and Fourier spectral estimations (both nonderivative and derivative). In the effected comparisons, the dFPT completely outperformed the FFT in both resolution and SNR throughout the entire exemplified spectrum (0.9–4.85 ppm) and beyond. Within merely the third derivative order in the dFPT, a huge number of resonances were separated from each other, so that they became amenable to highly accurate quantifications. On the other hand, while the FFT and FPT (both nonderivative) are found to be in full coherence with each other, their derivative variants, dFPT and dFFT, are in complete disagreement. In sharp contrast to a remarkable success of the dFPT, it is observed that the dFFT worsens the resolution and SNR even relative to the FFT.

The usefulness of the concept of sequential visualization and quantification is illustrated in three different and equivalent graphical layouts within the band 0.9–1.6 ppm which, besides the recognized cancer biomarker, lactate doublet Lac(d), also contains some other doublets, double doublets and triplets like isoleucine Iso(t), leucine Leu(d,t), valine Val(dd), $\beta -$hydroxybutyric acid $\beta -$HB (d), threonine Thr(d) and alanine Ala(d). All these resonances as well as those assigned to a number of other metabolites at 1.60–4.85 ppm, including Cho(s), PC(s) and GPC(s), are notably more intense in the malignant than in the benign ovarian cyst fluids.

For the malignant case, the conventional nonderivative envelopes from the FPT give the same peak heights of the singlet-appearing resonances for free choline Cho and phosphocholine PC, with the former being slightly broader than the latter. However, the first three derivatives from the dFPT exhibit two clear peaks (on each side of chemical shift 3.19 ppm) of comparable heights, one is assigned to Cho(s), whereas the other is temporarily left unassigned, but some potential known metabolite candidates are contemplated. This shows that it is not advisable to estimate the concentration level of Cho(s) based only on customary nonderivative shape estimators. Yet, thus far, the nonderivative FFT has predominantly been used to assess the abundance of the choline-containing compounds to make the benign-versus-malignant diagnoses in tumorous tissues from several human organs (e.g. brain, prostate, breast, ovary). In this context of making critical decisions, the role of derivative signal processing by the dFPT becomes all the more necessary.