In vitro proton magnetic resonance spectroscopy at 14T for benign and malignant ovary: Part II, Signal processing by the parametric fast Padé transform

Abstract

The topic of this study is in vitro proton magnetic resonance spectroscopy (MRS). The theme is on theoretical analysis of time signals encoded at a high magnetic field 14.1T, using a Bruker spectrometer, operating at a Larmor frequency of 600 MHz. The samples, dissolved in a D${}_2$O buffer, are from histopathologically analyzed ovarian cyst fluid from two patients. The benign and malignant diagnoses were serous cystadenoma and serous cystadenocarcinoma, respectively. It is of vital clinical importance to determine whether certain specific patterns, inferred from the analyzed/interpreted MRS data could be correlated with this and similar histopathologic findings for other patients. Encoded time signals contain the fingerprint of the examined sample, its metabolic content. Therefore, to detect the sought patterns from MRS data, the salient characteristics of a malignant tumor, implied by the diagnostically most relevant metabolites (including recognized cancer biomarkers, e.g. lactic acids, cholines, ...), need to be unambiguously identified by their significant departures from the associated control data of benign biomaterial, ovarian cyst fluid (serous cystadenoma) in the diagnostic problem under the present consideration. Such identifications are unfeasible by visualization in the domain of encoding (time domain). A direct inspection of the graphed waveforms of an encoded time signal would give no clue about its structure nor about the sample content. However, merely visualizing the plots of the equivalent, information-preserving spectral lineshape profiles in the frequency domain would make transparent at least some of clinically useful, discernible features of MRS data, a number of resonances assignable to the known and unknown metabolites. For instance, the size of each resonance (peak area) is proportional to the concentration of the given metabolite. This is a key quantitative measure, which could help differentiate a malignant from a benign specimen by reference to the normal standards. A number of metabolites (choline, alanine, lactate, threonine, $\beta$-hydroxybuturate, valine, isolecine, leucine, ...) have substantially different concentrations in the malignant compared with normal samples. Time signals can be processed by two substantially different categories of mathematical transforms, shape and parameter estimators. The former processors are alternatively called nonparametric estimators. They have been employed for envelopes in our recent study on this problem, which will presently be addressed with the prime focus on reconstructions of the corresponding components. Components and envelopes are partial and total shape spectra, respectively. The sum of all the component lineshapes (one per metabolite) yields the envelope nondegenerate spectrum representation of the entire sample. Presently, a deeper diagnostically valid insight is gained about the metabolic content of the scanned sample through the reported exact component spectra. The employed parameter estimators are the high-resolution, noise-suppressing nonderivative and derivative fast Padé transforms. Detailed are several critical achievements by the parametric Padé processing of direct clinical relevance. Importantly, all the accomplishments are shared by the nonparametric derivative Padé estimations. Three examples are highlighted here as follows.

• (i) Confirmation of our recent nonparametric derivative detection of an unassigned metabolite (a singlet peak) co-resonating with free choline near chemical shift 3.19 ppm (parts per million). Therein, with the nonderivative envelope, only one compound peak usually appears and is conventionally assigned to a free choline singlet. However, such an oversight would yield about twice larger value of the true concentration of this key cancer biomarker.

• (ii) The concentration level of another cancer biomarker (lactate) is also overestimated by any nonparametric nonderivative envelope. In sharp contrast, the parametric nonderivative Padé estimation unequivocally detects six usually invisible resonances (assignable to other metabolites) beneath the lactate doublet, around chemical shift 1.41 ppm. At least two of the strongest among these invisible six resonances can be also identified in the nonparametric fourth derivative Padé envelope.

• (iii) Regularization of the spectral compound for the water residual (4.71 ppm), which deforms the neighboring resonance lineshapes and impacts adversely on the concentration assessments of other nearby metabolites. This is accomplished by the fourth derivative envelope (coincident with the components) whose narrowing of the widths, cutting off the long tails and the background flattening generate a quantifiable singlet of water. This can serve as a reliable calibration reference resonance. After such a localization, no distortion appears around water, so that even very near 4.71 ppm, several smaller resonances are detected (assignable to a multiplet of nitrogen acetyl asparate), totally invisible in the nonparametric nonderivative envelope.

1 Introduction

In magnetic resonance spectroscopy (MRS),¹ the two main objects of studies are time signals (extracted by measurements/encodings) and frequency spectra (predicted/reconstructed by theory through computations). The principal interest of cancer medicine within MRS is in a potential establishment of diagnostically informative correlations between the reconstructed metabolic profiling and the functional/pathophysiological status of the scanned tissues/biofluids from patients. This brings metabolites into the mainstream of MRS as the key content of encoded time signals, or free induction decay (FID) curves from samples/specimens stemming from human organs.

Metabolites are of utmost importance for the timely differential diagnosis (malignant versus benign). The reason is that metabolites (being molecules participating in many pathways of cellular metabolism and functioning differently in healthy and diseased cells), are of a key help to early tumor detection. This is the case because malignant transformations first develop on a molecular level, much before their manifestations on anatomical/morphological scans from e.g. magnetic resonance imaging (MRI) or computerized tomography (CT). Early tumor diagnoses increase the chance for success of treatment, cure and overall disease management.

Diagnostics by MRS uses nonionizing radiation, which is from the electromagnetic field spectrum of energies far below the degradation thresholds of molecules in the living cells. Thus, advantageously, MRS can be employed for repeated monitoring and surveillance/screening of the same patient during the primary diagnosis, treatment and post-therapeutic follow-up. By way of MRS, detailed information about hundreds or thousands of metabolites, including cancer biomarkers (lactic acids, cholines, etc.) could become available to critically aid vital decision making for the patient.

Such an information depth about metabolites provided by MRS encompasses both the static characteristics (i.e. structures) and the dynamical features (e.g. transition probabilities or rates for underlying biochemical processes). These two aspects are strongly coupled together. The static properties represent the motionally averaged structures of metabolites. They are the essential prerequisite for the vital biochemical reactions/processes to occur. The reason is in the fact, that the dynamics develop through various molecular motions. Description of every motion involves difference and/or differential equations that could faithfully reconstruct the true state of the system only for the known initial conditions and these are provided by the static structures of metabolites. The generators of the dynamics are the kinetic and potential energy operators of the system. Potential energies play the determinant role since they exhibit the interactions among the constituents of the system (e.g. protein-protein interactions in heavy metabolites, macromolecules).

The basis on which MRS has a potential to perform the stated comprehensive task in diagnostic cancer medicine stems from the following three main physical properties of the magnetic resonance phenomenon:

• (a) Almost unlimited spatial resolution. The explanation is that a spin assembly, as the principal sensor of MRS visible nuclei, is detectable at minute localizations through distances of the order of $\sim$ 2 fm or less (1 fermi, $10^{-13}\,\mathrm{cm},$ the diameter of a nucleus).

• (b) Nearly perturbation-free peering into the chemical environment of spin-active nuclei. This is reasoned by the fact that interactions of spin-active nuclei with their environment are extremely weak, of the order of $\sim$ 0.2 J/M (joule per mol) or less. Yet, these interactions are highly sensitive to the nuclear and electronic configurations of molecules from the chemical surroundings of the given resonating nucleus. The interaction sensitivity is also affected by the spatial orientation of the nuclear dipole moments relative to the axis of the externally applied static magnetic field.²

• (c) Detectability of myriad of light molecules in minuscule concentrations of a few $\mu \mathrm{M/g}$ (micromol per gram) by a single encoding. The rationale is that an encoded time signal or FID contains the entire information about the interactive spin system for any number of resonating nuclei and for any molecular weight as well as abundance. A time response function of the spin system to external excitations is weak since only a tiny fraction of nuclei actually make the state-to-state transitions. Nevertheless, this time signal keeps the intact information about the evolution of the spin system irrespective of its size and no matter how small or large the host molecule could be.

The features (a–c) exhibit the causal relationships. For example, energy and distance obey their inverse proportionality. The higher the impact energy, the smaller the probed distance. A high spatial resolution in e.g. particle scattering modalities for investigating the structure of matter, such as neutron diffraction, needs very high primary beam energies that, in turn, are destructive and cause severe damage of the targeted specimen. A great advantage relative to such a particle scattering method is provided by MRS which probes the matter by fully nondestructive/noninvasive means because of the usage of very low energies of radio-frequency (RF) pulses and the two magnetic fields (static, gradient).

Probing small distances with high energies (as in the scattering method) is in accord with the anticipation from the quantum-mechanical uncertainty principle. At first, it might seem that this Heisenberg principle is disobeyed by NMR, which probes small distances of the size of a nucleus by low energies. However, the limitation imposed by the uncertainty principle does not apply to NMR in either of its two measurement options, originated by Bloch [3,4,5] (the nuclear induction method) and Purcell [6, 7] (the energy absorption method). In the nuclear induction method [3,4,5], it is not the energy, but rather the time signal that is measured, after being induced in a coil surrounding a sample placed in a static magnetic field. The energy absorption method [6, 7] uses the fact that the cause for the observed effect in NMR is stored in the spacing of spin discrete energy levels. This would permit measurements of the frequencies of transitions among such levels with unlimited precision, if sufficient time has been allocated.

Nevertheless, these arguments should not be interpreted to mean that e.g. the Heisenberg energy-time uncertainty relation is never a limiting factor in encodings by MRS. It is, albeit in disguised form. The spin-spin interactions cause the transversal relaxation times $T_2$ of metabolites to be finite, and this puts a limit on the duration of the total acquisition time T which then impacts on the accuracy of the measured energy by the Purcell’s method [6, 7]. Hence, the uncertainty relation exists between the measured energy and the total observation time. However, generally, care must be exercised with the uncertainty relations that apply only to the two observables (experimentally measured quantities) assigned to the corresponding pair of the conjugate variables. In NMR observations by the Bloch’s method [3,4,5], the time signal is measured, whereas the frequency spectrum is computed, not encoded/acquired.

Therefore, two resonances separated by 1/T can be resolved (depending on the employed signal processor) because the frequency spectrum is computed, while the associated FID is measured. However, the fast Fourier transform (FFT) cannot resolve two resonances that are less than 1/T apart. This occurs because the separation between any two adjacent linear frequencies in the equidistantly sampled FFT spectrum is 1/T. On the other hand, resolution in the fast Padé transform (FPT) is not predetermined solely by T so that, in principle, it may be possible to separate at least some of the overlapped resonances from the given envelope spectrum. Resolving power in a total shape spectrum or envelope computed with the FPT is determined by the average frequency spacing $({\Delta }\nu )_{\mathrm{av}}$ among the adjacent resonances in a fixed band.

If a frequency band is overly congested (over-crowded), the resulting value of $({\Delta }\nu )_{\mathrm{av}}$ may prevent resolving the individual resonances in the envelope from the nonparametric FPT. In such situations, the derivative fast Padé transform (dFPT), as a shape estimator, can be used to separate any two adjacent resonances, provided that a sufficiently high derivative order is taken, no matter how closely these resonances might be located.

The research area of the present work is within the realm of cancer medicine, employing a high magnetic field for in vitro proton MRS (or $\mathrm{{}^1H\,MRS}$) with a Bruker 600 MHz ($B_0\approx 14.1\,\mathrm{T}$) spectrometer to analyze the time signals encoded using the benign and malignant samples of the ovarian cyst fluid from two patients. We approach this topic by aiding diagnostics through the suitable signal processing methodology for accurate evaluation and interpretation of the encoded FID data. This is the versatile Padé-based methodology in its several variants, including nonparametric, parametric, nonderivative and derivative estimations.

The use of the FFT, a low-resolution method for exclusively shape estimation (nonparametric signal processing), is of a limited clinical value for both in vitro and in vivo $\mathrm{{}^1H\,MRS}.$ The FFT cannot quantify MRS data without fitting the given Fourier spectral envelope through post-processing, which is invariably equivocal. This is prone to cause uncontrollable ambiguities in diagnoses. Due to such circumstances, persistent doubts exist in practice about the overall clinical utility and performance of in vivo $\mathrm{{}^1H\,MRS}.$ In reality, however, it is not necessarily in vivo $\mathrm{{}^1H\,MRS}$ that should be doubted. Rather, it is more prudent to question the suitability of the Fourier-based data analyses employed for in vivo $\mathrm{{}^1H\,MRS}.$

The FPT comes to the rescue by putting signal processing on a firm mathematical basis and elevating the usage of in vivo MRS in the clinic to a rigorous, scientific platform [31, 32]. Moreover, we have recently demonstrated that the Fourier analysis (using the standard FFT or its derivative counterpart, dFFT) cannot be trusted for in vitro MRS time signals either, even when encoded at the magnetic field strengths as high as 14.1T [33]. By contrast, in the same study [33], it has been shown that the nonparametric dFPT performed with a remarkable versatility.

In the present investigation, we want to determine whether such a versatility of the nonparametric dFPT [33] could also imply high accuracy. To proceed, we subject the nonparametric dFPT to the most stringent scrutiny by comparing its envelope to the spectra from the parametric FPT and dFPT. The main focus will be on comparisons between the envelopes from the nonparametric dFPT and the component spectra due to the parametric dFPT. The eventual compatibility of two such differently conceived spectra would prove that lone shape estimations by the nonparametric dFPT could autonomously perform quantification (exact determination of the resonance peak positions, widths, heights), as the main signal processing task of both in vivo and in vitro MRS.

Having in mind the important medical diagnostic context of the problem under study, and following Ref. [33], here too the principal focus shall be on metabolites that are either recognized or potential/new cancer biomarkers. Lactates and cholines are among recognized cancer biomarkers for several organs (brain [34,35,36], prostate [37,38,39,40,41,42,43,44], breast [45,46,47,48,49], ovary [50,51,52,53,54,55,56,57], cervix [58,59,60,61,62]). Additionally, a number of other metabolites resonating e.g. at chemical shifts around the lactate doublet (such as leucine, isoleucine, valine, $\beta -$hydroxybuturate, threonine, alanine) have their molar concentration levels markedly different for malignant compared to benign lesions [33, 53]. These could be qualified as potential cancer biomarkers, as has been suggested in Refs. [50, 53] and, therefore, they too deserve particular attention in the present report.

2 Theory

In MRS, the encoded time signal $\{c_n\}\, (0\le n\le N-1)$ of length N is given and the main task is determine its composition. This is the harmonic inversion problem [63]. The unknown structure of this FID reflects the sought constituents of the scanned specimen. It is the number K of metabolites and their fundamental parameters that are needed to quantify the content of the sample. The diagnostically most relevant fundamental parameters of metabolites include their chemical shifts, transversal relaxation times, spectral intensity (resonance strength) and concentrations. Finding these parameters amounts to performing quantification of the encoded MRS data.

In the Padé methodologies, the quantification problem can be solved exactly by both the nonparametric and parametric estimations. To this end, the nonparametric Padé processing requires a supplementary operation, derivative estimation (which, in turn, yields the dFPT). On the other hand, the parametric Padé processing quantifies by the usual nonderivative FPT, with no need for any additional operation.

A frequency spectrum is the Green function. It represents the frequency-domain response function of the sample to the external triple excitation (RF pulse, static and gradient magnetic fields). The finite-rank Green function is the finite $z-$transform (ZT), defined by the $N-$term MacLaurin polynomial. Its expansion coefficients represent a set of length N containing the encoded discrete time signal points, $\{c_n\}\, (0\le n\le N-1),$ sampled at rate $\tau =T/N,$ where as before T is the total acquisition time (the full duration of one FID):

$${\text{ZT}}:\begin{aligned} Z(\nu )=\sum _{n=0}^{N-1}c_nz^{-n},\,\,z^{-1}=\mathrm{e}^{-2\pi i\nu \tau }. \end{aligned}$$

(1)

Here, $\nu$ is linear frequency, connected to the corresponding angular frequency $\omega$ by $\omega =2\pi \nu .$ In Eq. (1), frequency $\nu$ is a continuous variable, real or complex. The quantity $Z(\nu )/N$ is the Riemann sum. Alternatively stated, the sum $Z(\nu )/N=(1/N)\sum _{n=0}^{N-1}c_nz^{-n},$ where $Z(\nu )$ is from Eq. (1), is the trapezoidal quadrature rule for the corresponding finite Fourier integral $F(\nu )\equiv (1/T)\int _0^T\text{ d }t\mathrm{e}^{-2\pi i\nu t}c(t)$ with the continuous (analog) time signal c(t). In Eq. (1), after discretizing the continuous time variable t by $t=t_n=n\tau ,$ the digitized FID, $c_n,$ is linked to c(t) by $c_n=c(n\tau ).$ The sampling time (the dwell time) $\tau$ is the inverse of the bandwidth (BW) or sweepwidth (SW), i.e. $\tau =1/\mathrm{BW}.$

To include the possibility $N\rightarrow \infty ,$ it must be ensured that the ZT will be convergent. Convergence of the ZT will be secured outside the unit circle in the complex $z-$plane $(\left| z\right| >1),$ provided that $\mathrm{Im}(\nu )>0.$ The spectrum $Z(\nu )$ is model-independent, meaning that no specific representation is assumed for the time signal $\{c_n\}$ in Eq. (1).

A simplification of $Z(\nu )/N$ can be obtained by discretizing frequency $\nu ,$ as well, according to $\nu =k/T\, (0\le k\le N-1).$ The result, denoted by $Z (k/T)/N \equiv{ F_k},$ is the discrete Fourier transform (DFT):

$$\begin{aligned} \mathrm{DFT}: \qquad F_k=\frac{1}{N} \sum _{n=0}^{N-1}\mathrm{e}^{-2\pi ink/N}c_n,\,\,0\le k\le N-1, \end{aligned}$$

(2)

where the relation $\tau /T=1/N$ is utilized. Here, for any time signal $\{c_n\}\, (n=0,1,...,N-1),$ the Fourier grid frequencies $k/T\, (k=0,1,...,N-1)$ are fixed for the given total acquisition time T. The Fourier resolution is 1/T and the envelope in the DFT is a stick spectrum (a bar code spectrum). The continuous line drawn for the spectrum $F_k\, (k=0,1,2,...,N-1)$ in the DFT connects the tops of the sticks.

The FFT is a fast Cooley–Tukey algorithm (a rediscovery of the Gauss algorithm [63]), which accelerates the numerical computation of the DFT. The computational complexity of the DFT involves some $N^2$ multiplications. This occurs because the multiplying sequences $\{c_n\}$ and $\mathrm{e}^{-2\pi ik/N}$ in (2) are of length N,  counting the running indices n and k,  respectively. Taking N to be a composed positive integer, e.g. $N=2^M\, (M=1,2,3,...),$ computations are speeded up by the FFT which has $N\mathrm{log}_2N$ multiplications that, relative to the DFT, yield an enormously faster algorithm for large values of N.

In the FFT, adding zeros after the N encoded FID data points is always practiced to artificially increase the number of the sampled frequencies. Such a zero-filling or zero-padding in the time domain leads to a trigonometric interpolation in the frequency domain [64,65,66,67]. This procedure might yield somewhat nicer looking envelope lineshapes in the FFT, but cannot lead to resolution improvement. The reason is that the entire information is already contained in the encoded $N-$data points in the time domain. Thus, extending superficially the FID of the original length N beyond the actual end of encoding at $t=T=N\tau$ by appending some unmeasured time signal points of the zero-valued intensities cannot produce any additional information in either domain (time, frequency).

In derivative signal processing, a given spectrum is subjected to a derivative operator $\mathrm{D}_m$ of order $m\ge 1$ with respect to frequency $\nu :$

$$\begin{aligned} \mathrm{D}_m=\left( \frac{\text{ d }}{\text{ d }\nu }\right) ^m\,\,(m=1,2,3,...). \end{aligned}$$

(3)

Applying $\mathrm{D}_m$ to $Z(\nu )$ and $F_k$ gives the derivative $z-$transform (dZT) and the derivative discrete Fourier transform (dDFT), respectively:

$$\begin{aligned}&\mathrm{D}_m\mathrm{ZT}=\sum _{n=0}^{N-1}(\alpha n)^mc_nz^{-n},\,\,\alpha =-2\pi i\tau , \end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{D}_mF_k=\frac{1}{N}\sum _{n=0}^{N-1}\mathrm{e}^{-2\pi ink/N}(\alpha n)^mc_n,\,\,0\le k\le N-1. \end{aligned}$$

(5)

The derivative fast Fourier transform, dFFT, is obtained by computing the dDFT with the Cooley–Tukey algorithm [63] for the modified time signal $(\alpha n)^mc_n.$ Here, the power function $(\alpha n)^m$ puts emphasis on the later encoded FID data points at which noise prevails. Thus, for noisy time signals (as is always the case with all encoded FIDs), the dFFT is bound to fail. It is only the matter of detecting (by numerical computations) at which derivative order m, the theoretically predicted breakdown will occur.

A viable alternative to Fourier processing, the superior Padé analysis can be used. For instance, the paradiagonal $P_{K-1}/Q_K$ or diagonal $P_K/Q_K$ nonparametric nonderivative FPT is a rational function specification of the ZT. For the given ZT from Eq. (1), the said rational function is the unique ratio of two polynomials in either the $z^{-1}$ or z variable, known as the Padé approximant (PA). Presently, for the input MacLaurin polynomial $Z(\nu ),$ the diagonal FPT uses the numerator $P_K(z^{-1})$ and denominator $Q_K(z^{-1})$ polynomials of degree K,  both in terms of the same expansion variable $z^{-1}$ as in the ZT from Eq. (1):

$$\begin{aligned} \sum _{n=0}^{N-1}c_nz^{-n}=\frac{P_K(z^{-1})}{Q_K(z^{-1})}. \end{aligned}$$

(6)

Of course, a single polynomial on the left, $\sum _{n=0}^{N-1}c_nz^{-n},$ cannot be equal exactly to a quotient of two polynomials, $P_K(z^{-1})/Q_K(z^{-1}),$ on the right of Eq. (6). Strictly speaking, we should have an approximate equality in (6), $\sum _{n=0}^{N-1}c_nz^{-n}\approx P_K(z^{-1})/Q_K(z^{-1}).$ Or, we can keep the equality sign provided that a modeling error estimate is introduced:

$$\begin{aligned} \left\{ \sum _{n=0}^{N-1}c_nz^{-n}\right\} _{\mathrm{Input}}-\left\{ \frac{P_K(z^{-1})}{Q_K(z^{-1})}\right\} _{\mathrm{Model}} =\left\{ {{\mathcal {O}}}(z^{-2K-1})\right\} _{\mathrm{Error}}. \end{aligned}$$

(7)

The error estimate ${{\mathcal {O}}}(z^{-2K-1})$ of modeling the general ZT by the FPT represents a series in powers of $z^{-1}$ beginning with $z^{-2K-1}.$ This series is obtained by making an expansion of $P_K(z^{-1})/Q_K(z^{-1})$ in powers of $z^{-1}.$ The meaning of the definition (7) is in the extremely important extrapolation feature of the FPT. Let us continue to keep the full record $\{c_n\}\, (0\le n\le N-1)$ of all the N encoded FID points, but temporarily stop using the subset $\{c_n\}\, (K\le n\le N-1)$ for $2K<N.$ This would lead to a truncation of the ZT from the lhs of Eq. (7) at $n=K-1.$ In the ensuing spectrum $\sum _{n=0}^{K-1}c_nz^{-n},$ the remainder of $\{c_n\}\, (K\le n\le N-1)$ is completely ignored as if this part of the encoded FID were unavailable, i.e. as if encoding stopped at $K\tau$ instead of $N\tau =T.$

Suppose now that we model this truncated ZT by the $K\,$th order FPT via $\sum _{n=0}^{K-1}c_nz^{-n}\approx P_K(z^{-1})/Q_K(z^{-1}).$ The model function $P_K(z^{-1})/Q_K(z^{-1})$ can be generated only by the K input FID data points $\{c_n\}\, (0\le n\le K-1)$ since, for this purpose, the encoded subset $\{c_K, c_{K+1}, ..., c_{N-1}\}$ is nonexistent. Such a model has an error ${{\mathcal {O}}}(z^{-2K-1}).$ As stated, this means that, if the spectrum $P_K(z^{-1})/Q_K(z^{-1})$ is developed as a series in powers of $z^{-1},$ its first 2K expansions coefficients from the generated infinite set will be $\{c_0, c_1, ..., c_{2K-1}\}.$ The implication is that the model $P_K(z^{-1})/Q_K(z^{-1})$ for $\sum _{n=0}^{K-1}c_nz^{-n}$ would reconstruct exactly the set $\{c_K, c_{K+1}, ..., c_{2K-1}\},$ which is absent from the input $\sum _{n=0}^{K-1}c_nz^{-n}.$ Thus, the FPT found the extrapolation $\{c_K, c_{K+1}, ..., c_{2K-1}\}$ to the employed subset $\{c_0, c_1, ..., c_{K-1}\}.$

The extrapolated ensemble $\{c_n\}\, (K\le n\le 2K-1)$ is precisely within the intentionally ’forgotten’ part $\{c_K, c_{K+1}, ..., c_{2K-1}, c_{2K},...,c_{N-1}\}$ of the encoded full time signal, $\{c_0, c_1, ..., c_{K-1}, c_K, c_{K+1}, ..., c_{2K-1}, c_{2K},...,c_{N-1}\}.$ Extrapolation amounts to prediction. This shows that the FPT is a prediction model. The selected example illustrates prediction of the known subset $\{c_n\}\, (K\le n\le 2K-1)$ of the available full encoded FID record contained in the set $\{c_0, c_1, ..., c_{K-1}, c_K, c_{K+1}, ..., c_{2K-1}, c_{2K},...,c_{N-1}\}.$

Importantly, the same extrapolation feature of the FPT also remains in place for $2K=N,$ i.e. when the entire encoded time signal $\{c_n\}\, (0\le n\le N-1)$ is exhausted in the input MacLaurin polynomial, $\sum _{n=0}^{N-1}c_nz^{-n}\approx P_K(z^{-1})/Q_K(z^{-1}).$ For this case, the error of the model $P_K(z^{-1})/Q_K(z^{-1})$ or $P_{N/2}(z^{-1})/Q_{N/2}(z^{-1})$ is ${{\mathcal {O}}}(z^{-2N-1})$ showing that the FPT is able to predict the extra N time signal points $\{c_n\}\, (N\le n\le 2N-1),$ as if the total encoding time were 2T instead of the corresponding original value T.

This theoretical finding explains the systematically encountered empirical outcome of computations that the FPT has at least twice better resolution than that in the FFT for the same number of the employed FID data points, $\{c_n\}.$ Alternatively, resolution in the FFT might occasionally be comparable to that of the FPT, provided that Fourier analysis employs twice more input time signal points. Such features of the FPT can be traced back to the extrapolation virtue. By comparison, the FFT cannot extrapolate. Moreover, as to the frequency grid points, the FPT is not restricted at all to the Fourier equidistant mesh $k/T\, (0\le k\le N-1).$ The FPT can use any frequency sampling (equidistant, nonequidistant) with an arbitrary number of the sampled frequency grid points.

The outcome of the latter property is recognized as interpolation. It is a rational function interpolation which occurs in the FPT. This is why there is no need for zero filling of the FID envisaged to be subjected to the FPT. Suppose that the envelope $P_K(z^{-1})/Q_K(z^{-1})$ in the FPT, retrieved from an encoded FID of length N,  is computed at e.g. 4N equidistant grid frequencies. An inversion of this Padé spectrum produces a reconstructed FID of the quadrupled length compared to the originally encoded FID. The extra 3N time signal points are the Padé-extrapolated FID data as an optimal prediction of the time signal points that would have been encoded had the acquisition time lasted until 4T in lieu of T. These supplementary 3N time signal points are based upon nonlinear combinations of the encoded N values of the original FID. In contrast, when the FFT is applied, a triple zero filling of the same encoded FID would not have any relation whatsoever with the measured data points.

The expansion coefficients $\{p_r,q_s\}$ $(r,s=1,2,...,K)$ of the polynomials $P_K(u)=\sum _{r=0}^Kp_ru^r$ and $Q_K(u)=\sum _{s=0}^Kq_su^s,$ respectively, are extracted from the definition of the nonparametric nonderivative FPT in Eq. (6) with $u=z^{-1}.$ This amounts to solving only one system of linear equations that are for $\{q_s\},$ whereas the set $\{p_r\}$ is obtained from the exact analytical formula, a convolution of $\{q_s\}$ and $\{c_n\}.$ In computations, alterations of $P_K/Q_K$ are monitored for a sequence of the values of K until a converged (stabilized) envelope has been attained. Prior to convergence, the expansion coefficients $\{p_r,q_s\}$ may vary widely, in contrast to the corresponding milder changes of $P_K/Q_K.$ The reason is that inaccuracies in the numerator $P_K$ and denominator $Q_K$ polynomials are largely canceled in the ratio $P_K/Q_K,$ which eventually reaches a plateau. This is a familiar situation encountered in most experiments in which errors in two measured quantities are significantly compensated in their quotient.

The nonparametric derivative dFPT of the $m\,$th order is produced by applying the operator $\mathrm{D}_m$ from Eq. (3) to the nonparametric nonderivative FPT and denoting the result by $R^{(m)}_{K,\nu }(u):$

$$\begin{aligned} R^{(m)}_{K,\nu }(u)=\mathrm{D}_mR_K(u), \,\,R_K(u)=\frac{P_K(u)}{Q_K(u)}. \end{aligned}$$

(8)

The explicit analytical expression for $R^{(m)}_{K,\nu }(u)$ is taken from Ref. [33]:

$$\begin{aligned} R^{(m)}_{K,\nu }(u)=\alpha ^m\sum _{\ell =0}^mS(m,\ell )u^\ell R^{(\ell )}_{K,u}(u),\,\,u=z^{-1}=\mathrm{e}^{\alpha \nu }, \end{aligned}$$

(9)

where $S(m,\ell )$ is the Stirling number of the second kind given in e.g. Refs [68] (# 9.746/1, p. 1037) and [69] (Eq. 24a, p. 34). One of the ways of generating quantity $R^{(\ell )}_{K,u}(u),$ as the $\ell \,$th derivative of $R_K(u)$ with respect to variable u,  is to utilize a robust recursion, which is very fast and highly accurate [33]:

$$\begin{aligned} R^{(\ell )}_{K,u}(u)= \frac{P^{(\ell )}_{K,u}(u)-\sum \limits _{j=0}^{\ell -1}\left( {\begin{array}{c}\ell \\ j\end{array}}\right) R^{(j)}_{K,u}(u)Q^{(\ell -j)}_{K,u}(u)}{Q_K(u)},\,\,\ell \ge 0, \end{aligned}$$

(10)

where $\sum _{j=0}^{-1}(\cdots )\equiv 0,$ $\left( {\begin{array}{c}\ell \\ j\end{array}}\right)$ is the binomial coefficient, $P^{(m)}_{K,u}(u)=(\text{ d }/\text{d }u)^mP_K(u)$ and $Q^{(m)}_{K,u}(u)=(\text{ d }/\text{d }u)^mQ_K(u)$ with $m\ge 1.$ The initialization to the recurrence (10) is given by the first derivative of $P_K(u)/Q_K(u):$

$$\begin{aligned} R^{(1)}_{K,u}(u)\equiv \frac{\text{ d }}{\text{ d }u}\frac{P_K(u)}{Q_K(u)}=\frac{P^{(1)}_{K,u}(u)-Q^{(1)}_{K,u}(u)R_K(u)}{Q_K(u)}. \end{aligned}$$

(11)

The parametric nonderivative FPT begins with the envelope $P_K/Q_K$ obtained by the nonparametric nonderivative FPT. The task of the parametric nonderivative FPT in the frequency domain is to determine the structure of the envelope $P_K/Q_K.$ The structure of $P_K/Q_K$ is mostly invisible. To make it transparent, the envelope $P_K/Q_K$ should be decomposed, which is a synonym for quantification. It should be recalled that this decomposition is encountered in the standard calculus, which contains a general integration rule of a rational function given by a quotient of two polynomials. For example, in the ’Tables of Integrals, Series and Products’ of Gradshteyn and Ryzhik [68] (# 2.101, p. 56), the pertinent rule for evaluating the indeterminate integral of the quotient of two polynomials, $\int \text{ d }xA_L(x)/B_K(x),$ consists of first decomposing $A_L(x)/B_K(x)$ into the sum of its K building blocks called partial fractions $C_k/(x-x_k).$ Here, $x_k$ is the $k\,$th simple roots (no multiplicities) of equation $B_K(x)=0,$ so that the sought decomposition becomes:

$$\begin{aligned} \frac{A_L(x)}{B_K(x)}=\sum _{k=1}^K\frac{C_k}{x-x_k},\,\,C_k=\frac{A_L(x_k)}{B'_K(x_k)},\,\,B'_K(x)=\frac{\text{ d }}{\text{ d }x}B_K(x). \end{aligned}$$

(12)

With this decomposition of $A_L(x)/B_K(x),$ the remaining integral over the $k\,$th partial fraction, $\int \text{ d }x/(x-x_k),$ is elementary, i.e. $\int \text{ d }xA_L(x)/B_K(x)=\sum _{k=1}^KC_k\int \text{ d }x/(x-x_k)= \sum _{k=1}^KC_k\ln (x-x_k)+C,$ where C is an integration constant.

This reminder of a well-known rule can immediately be exploited to cast the polynomial ratio $P_K(u)/Q_K(u)$ from the FPT into its appropriate Heaviside partial fraction representation:

$$\begin{aligned} \frac{P_K(u)}{Q_K(u)}=\frac{p_0}{q_0}+\sum _{k=1}^K\frac{d_ku}{u-u_k}, \end{aligned}$$

(13)

where $u_k$ is the $k\,$th simple zero of $Q_K(u),$ i.e. $Q_K(u_k)=0.$ Further, similarly to the numerator $C_k$ of the partial fraction $C_k/(x-x_k)$ from Eq. (12), quantity $d_k$ is the corresponding $k\,$th Cauchy residue of $P_K(u)/Q_K(u),$ taken at $u_k:$

$$\begin{aligned} d_k=\frac{P_K(u_k)}{Q'_K(u_k)},\,\,Q'_K(u)=\frac{\text{ d }}{\text{ d }u}Q_K(u), \,\,Q'_K(u_k)\ne 0. \end{aligned}$$

(14)

Thus, in the parametric nonderivative FPT, the envelope $P_K(u)/Q_K(u)$ is the sum of the baseline constant $p_0/q_0$ and the K partial shape spectra (components), each recognized as a partial fraction, $d_ku/(u-u_k).$ This is how the parametric nonderivative FPT determines the hidden structure, i.e. the components of the envelope $P_K(u)/Q_K(u)$ from the nonparametric nonderivative FPT. Overall, in the parametric nonderivative FPT, only one more numerical step is needed relative to the nonparametric nonderivative FPT.

That closing step is rooting the characteristic/secular polynomial, $Q_K(u)=0.$ In practice, even this last remaining nonlinear operation is replaced by solving the equivalent linear eigenvalue problem of the Hessenberg (companion) matrix. This is an exceptionally sparse $K\times K$ matrix with the coefficients $\{q_s\}$ of $Q_K(u)$ lying on the first row, unity on the main diagonal and zero elsewhere. Such a structure is convenient for exhaustive computations as it permits extremely large values of K. As such, even though the FPT is a nonlinear transform, its nonparametric and parametric variants involve only linear numerical operations.

Decomposition (12) for the simple poles of $A_K(x)$ can readily be extended to include the poles with any multiplicity as quoted in e.g. the same ’Tables of Gradshteyn and Ryzhik’ [68] (# 2.101, p. 56). In the FPT, for the zeros of $Q_K$ with multiplicity, a similar generalization of (13) has been reported earlier in e.g. Refs. [70] and need not be repeated here. For any encoded FIDs, no two zeros of $Q_K$ are numerically identical to the last decimal place. Therefore, in practice with measured time signals, the envelope (13) for simple roots of $Q_K$ would suffice. In Ref. [71], a synthesized FID has been constructed with some 25 complex damped harmonics, two of which were with the resonance frequencies differing by one unit in the 11th decimal places. Therein, the input data consisted of some 100 parameters (4 real 12-digit numbers per peak). The reconstruction in double precision (12 digit accuracy) determined exactly all the 100 input parameters, including the said ’quasi-degeneracy’. This remarkable example shows that the FPT is extremely robust even against all possible round-off errors.

We can give now the mathematical meaning of the recovered parameters $\{u_k,d_k\}$ in the context of the resonance component $d_ku/(u-u_k).$ This component spectrum is a Lorentzian lineshape profile in its complex mode. Its equivalent name is the Cauchy distribution of frequencies. The magnitude mode $\left| d_ku/(u-u_k)\right|$ appears as a resonance peak (symmetric or quasi-symmetric), which is fully quantified by the fundamental or characteristic/eigen parameters $\{u_k,d_k\}.$ The complex root $u_k$ of $Q_K$ is the pole of the component spectrum $d_ku/(u-u_k).$ This is the case because the partial fraction $d_ku/(u-u_k)$ is a meromorphic function (a function whose only singularities are its poles, i.e. no branch cuts, etc.). The complex number $d_k$ is the Cauchy residue of the same component lineshape $d_ku/(u-u_k).$ Mathematically, this residue describes the behavior of the complex function $d_ku/(u-u_k)$ around its sole singularity, which occurs at $u=u_k.$ Note that $d_ku/(u-u_k)$ never blows up to infinity since, in practice, $u\ne u_k$ for $\mathrm{Im}(\nu _k)\ne 0.$ In FID encodings by MRS, quantity $\nu$ in the harmonic variable $u=\exp {(-2\pi i\nu \tau )}$ is always a real-valued sweep frequency.

The physical interpretation of the fundamental/characteristic/eigen parameters $\{K,u_k,d_k\}$ can also be described. As outlined, they are explicitly determined in the frequency domain. Nevertheless, their transportation to the time domain can be made at once by taking the inverse transform of the total shape spectrum (13) in the parametric nonderivative FPT. The result is the FID given by:

$$\begin{aligned} c_n=\frac{p_0}{q_0}\delta _{n,0}+\sum _{k=1}^K d_k\mathrm{e}^{2\pi i\nu _k\tau },\,\,\mathrm{Im}(\nu _k)>0, \end{aligned}$$

(15)

where $\delta _{n,n'}$ is the Kronecker delta-symbol. Number K is unknown prior to processing of any FID encoded by MRS from human tissues or biofluids. This number is guessed in the MRS literature. In the FPT, number K is treated as yet another parameter to be reconstructed, just like the fundamental pair $\{u_k,d_k\}.$ However, to find K,  it is sufficient to use the nonparametric FPT as follows. A set of the nonparametric Padé envelopes $\{P_{K_j}/Q_{K_j}\}\, (j=1,2,...)$ is computed first, beginning with an initial value $K_1$ (taken as e.g. the number of the visible peaks in the corresponding FFT spectrum, evaluated with the full encoded FID). Then a specific value $K_{j'}$ for which the nonparametric envelope $P_{K_{j'}}/Q_{K_{j'}}$ is stabilized would represent the sought number K,  i.e. $K=K_{j'}.$

Thus, number K,  as the first critical parameter in quantification, is retrievable by the nonparametric FPT. This is very important as it gives credence to the notion that determination of spectral parameters is not a privilege of parametric methods alone. Such a hint is encouraging as it is rooted already in nonparametric nonderivative estimations. It gives hope that perhaps the peak parameters (resonance position, width, height) might also be reconstructed by nonparametric derivative estimations. Mathematically, K is the model order and also the common degree of the numerator and denominator polynomials in the diagonal FPT, $P_K/Q_K.$ Physically, K is the number of resonances (in the reconstructed spectrum $P_K/Q_K$), assignable to the K metabolites (known, unknown) in the scanned sample.

In medical diagnostics by MRS, number K is as essential as metabolite concentrations. For the physician, it is anathema to have to deal with analyses of MRS data ’detecting’ spurious and missing genuine metabolites. This is precisely what invariably occurs with all the fitting recipes that have no guard against these severe drawbacks. For such a reason, the clinical potential of MRS, as a diagnostic modality, is often undeservedly questioned.

The FPT puts these doubts at rest by determining K exactly in full coherence with the examined sample. Inevitably, spurious resonances are also encountered in the FPT, as in every other processor, but they are eliminated altogether from the spectrum $P_K/Q_K$ by pole-zero cancellations [70, 72]. Pole-zero cancellations stem from pole-zero coincidences (Froissart doublet), i.e. from the fact that there is an equipartition of spuriousness among the zeros (roots of $P_K$) and poles (roots of $Q_K$) of the spectrum $P_K/Q_K$ [70, 72]. This again testifies to the usefulness of representing a spectrum in the quotient form $P_K/Q_K,$ where spuriousness (as a noisy part of the reconstruction output) in $P_K$ is compensated by the like ’pollution’ of $Q_K.$

Parameter $u_k$ has a twofold role, as a simple pole in the frequency spectrum $d_ku/(u-u_k)$ and a complex damped harmonic in the time signal, $c_n.$ The complex resonance frequency $\nu _k$ is extracted from harmonic $u_k$ as $\nu _k=(1/\alpha )\ln {u_k}.$ The real and imaginary parts of complex $\nu _k$ are the chemical shift and the reciprocal of the spin-spin relaxation time constant $T^\star _{2,k}$ of the $k\,$th metabolite. The intensity of the response of this metabolite to the external excitation is defined by the magnitude (absolute value, modulus) $\left| d_k\right|$ of the complex amplitude $d_k=\left| d_k\right| \exp {(i\phi _k)}$ in $c_n.$ Thus, intensity $\left| d_k\right|$ also has a twofold role, as the strength of the resonance lineshape profile $d_ku/(u-u_k)$ in the frequency domain, and as the strength of the harmonic $\exp {(2\pi i\nu _k\tau )}$ from $c_n$ in the time domain. Likewise, the angle $\phi _k$ in $d_k$ has its two roles, as a phase of a harmonic oscillation in $c_n$ in the time domain and as a factor which influences the shape of the component profile $d_ku/(u-u_k)$ in the frequency domain.

The parametric dFPT of the $m\,$th order is obtained by applying the derivative operator $\mathrm{D}_m$ from Eq. (3) to either the envelope or the component spectra. In the case of the $k\,$th component $d_ku/(u-u_k),$ the result is:

$$\begin{aligned} \mathrm{D}_m\frac{d_ku}{u-u_k}=d_k(-\alpha )^m\frac{A_m(\xi _k)}{(\xi _k-1)^{m+1}},\,\,\xi _k=\frac{u}{u_k},\,\,m\ge 1, \end{aligned}$$

(16)

where $A_m(\xi _k)$ is the Eulerian polynomial [33, 73]. Using this expression and Eq. (13), the formula for the general derivative envelope spectrum in the parametric dFPT becomes:

$$\begin{aligned} \mathrm{D}_m\left( \frac{p_0}{q_0}+\sum _{k=1}^K\frac{d_ku}{u-u_k}\right) =(-\alpha )^m\sum _{k=1}^Kd_k\frac{A_m(\xi _k)}{(\xi _k-1)^{m+1}},\,\,m\ge 1. \end{aligned}$$

(17)

It is seen in Eq. (16) for the $m\,$th derivative component spectrum in the parametric dFPT that the behavior of the resonance part $d_k[u/(u-u_k)]^{m+1}$ has the sought prerequisite for simultaneous improvements of resolution and signal to noise ratio (SNR), relative to the corresponding nonderivative counterpart, $d_ku/(u-u_k).$ For $m\ge 1,$ the derivative resonance function $d_k[u/(u-u_k)]^{m+1}$ falls off faster than $d_ku/(u-u_k).$ Consequently, the derivative operator $\mathrm{D}_m$ would split apart the overlapping component resonances and flatten (localize) their tails. Thus, in derivative spectra from the parametric dFPT, resonance linewidths will be narrowed, the peak heights increased and the background contribution diminished. These three features are automatically shared by the nonparametric dFPT. Taller physical peaks and a lower noise-like background baseline translate to better SNR. Hence, the theory predicts that derivative estimations by the nonparametric dFPT will enhance both resolution and SNR.

This conclusion is drawn on theoretical grounds for the general $k\,$th component spectrum due to the parametric dFPT using the analytical expression $d_k[u/(u-u_k)]^{m+1}$ from Eq. (16), i.e. without any numerical computation. Would this conclusion also hold true for the associated envelope spectrum (17) from the same parametric dFPT? The nonderivative envelope (13) in the parametric FPT could, in principle, possess many overlapping resonances whose interference could blend together some adjacent peaks into certain compound spectral structures. However, such interferences will be considerably reduced with every increased derivative order m in the derivative envelope (17). This should occur because the derivative envelope (17) is explicitly built from the derivative components $\{d_k[u/(u-u_k)]^{m+1}\}\, (1\le k\le K).$ Therefore, resolution and SNR improvements of $d_k[u/(u-u_k)]^{m+1}$ from (16) are inherited by the parametric derivative envelope (17). For a sufficiently high derivative order m,  the derivative envelope (17) should collapse onto its derivative components (16).

The main concern, however, is whether the nonparametric derivative envelope (9) would also exhibit the same or similar resolution and SNR improvements (linewidth narrowing, peak height increase and background diminishing) as that just anticipated from the parametric derivative envelope (17). This is a relevant issue given that the nonparametric dFPT computes the derivative envelope (9) directly as its component spectra are unavailable. Here, it is pertinent to recall that in the envelope $P_K/Q_K$ for any K,  the nonparametric and parametric variants of the FPT, of course, share the same expansion coefficients $\{p_r,q_s\}\, (0\le r,s\le K)$ of the polynomials $\{P_K(u),Q_K(u)\},$ respectively. It is from these polynomial expansion coefficients $\{p_r,q_s\},$ extracted from the encoded data $\{c_n\}\, (0\le n\le N-1),$ that the peak parameters $\{u_k,d_k\}$ are reconstructed and incorporated into the components $\{d_ku/(u-u_k)\}\, (1\le k\le K)$ that, in turn, build the envelope (17) in the parametric nonderivative FPT.

Therefore, since the principal set $\{p_r,q_s\}\, (0\le r,s\le K)$ is common to the nonparametric and parametric FPT, these processors should give the same envelope $P_K/Q_K$ (upon convergence relative to K), computed with or without the explicit allowance for the components $\{d_ku/(u-u_k)\}\, (1\le k\le K),$ i.e. by using either Eq. (9) or (17), respectively. This nonderivative envelope $P_K/Q_K,$ common to the nonparametric and parametric FPT, is subjected to the same derivative operator $\mathrm{D}_m$ to yield the two derivative envelopes. The resulting two expressions (9) and (17) are formally dissimilar. Nevertheless the numerical results from these derivative envelopes ought to coincide for the nonparametric and parametric dFPT. This implies that for a sufficiently high derivative order m,  the derivative envelope (9) in the nonparametric dFPT should also collapse onto the derivative components (16) from the parametric dFPT, as was the anticipation for the derivative envelope (17) in the parametric dFPT.

In retrospect, the outlined argument means that, similarly to the envelope in the parametric FPT, also the envelope in the nonparametric FPT implicitly contains the same K true components $\{d_ku/(u-u_k)\}\, (1\le k\le K)$ that should become deconvolved in derivative estimations by the nonparametric dFPT. Despite the plausibility of these theoretical predictions, numerical computations are needed for their verifications because noise in spectra computed using the encoded FIDs can be a limiting factor. Moreover, such verifications, followed by the plotted graphs, would provide a convenient way to visually inspect the spectral lineshapes. This would check whether an envelope from the nonparametric derivative dFPT can indeed contain all the true components generated with the explicit solution of the quantification problem by the parametric nonderivative FPT.

In the Result Section, all the spectra will be presented in the phase-insensitive magnitude mode alone. Therein, the total shape spectra in the nonderivative FPT and derivative dFPT will be denoted by:

$$\begin{aligned} \left| {\mathrm{FPT}}\right| _{\mathrm{Tot}}\equiv \left| \frac{P_K(u)}{Q_K(u)}\right| ,\,\,\left| \mathrm{D}_m{\mathrm{FPT}}\right| _{\mathrm{Tot}}\equiv \left| \mathrm{D}_m\frac{P_K(u)}{Q_K(u)}\right| ,\,\,m\ge 1. \end{aligned}$$

(18)

To avoid a double indexing by adding e.g. a superscript, the same convention (18) will refer to both nonparametric and parametric Padé estimations. It will be clear from the context to which of these two variants a particular reference is made. In the case of the parametric FPT and dFPT, the component spectra will be labeled as:

$$\begin{aligned} \left| \mathrm{FPT}\right| _{\mathrm{Comp}}\equiv \left| \frac{d_ku}{u-u_k}\right| ,\,\,\left| \mathrm{D}_m\mathrm{FPT}\right| _{\mathrm{Comp}}\equiv \left| \mathrm{D}_m\frac{d_ku}{u-u_k}\right| ,\,\,m\ge 1. \end{aligned}$$

(19)

Regarding the FFT and dFFT, total shape spectra are the only option. Therefore, in the envelopes $\left| \mathrm{FFT}\right| _{\mathrm{Tot}}$ and $\left| \mathrm{D}_m\mathrm{FFT}\right| _{\mathrm{Tot}}\, (m\ne 0),$ the subscript ’Tot’ would be superfluous. Neverheless, in the Fourier envelopes too, we shall keep the subscript ’Tot’ so as to have a parallel presentation with respect to $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ and $\left| \mathrm{D}_m\mathrm{FPT}\right| _{\mathrm{Tot}}\, (m\ne 0)$ by reference to (18). Thus, we shall write:

$$\begin{aligned} \left| \mathrm{FFT}\right| _{\mathrm{Tot}}\equiv \left| F_k\right| ,\,\,\left| \mathrm{D}_m\mathrm{FFT}\right| _{\mathrm{Tot}}\equiv \left| \mathrm{D}_mF_k\right| ,\,\,m\ge 1. \end{aligned}$$

(20)

3 Results

3.1 Encoded time signals

A study reported in Ref. [53] included 40 patients with ovarian tumors (28 benign and 12 malignant). Such diagnoses resulted from the standard histopathological classifications of the examined ovarian cysts. The task for Ref. [53] was to see whether these diagnoses could correlate to the pertinent findings by in vitro ${}^1\mathrm{H\,MRS}.$ With this goal, a Bruker 600 MHz ($B_0\approx$14.1T) spectrometer for in vitro ${}^1\mathrm{H\,MRS}$ was used to encode time signals from the ovarian cyst fluid specimens dissolved in the $\mathrm{D_2O}$ buffer [53]. For each patient, some 128 time signals have been encoded with water suppression in the process of measurements. Subsequently, to improve SNR, an average FID is generated per patient by means of the usual arithmetic average values of the encoded 128 time signals.

The acquisition parameters of each transient time signal from Ref. [53] were: the full FID length $N=32768,$ the bandwidth $\mathrm{BW=6667\, Hz},$ the sampling time $\tau =1/\mathrm{BW\approx \,0.15\, ms},$ the repetition time $T_{\mathrm{R}}=1200\,\mathrm{ms}$ and the echo times $T_{\mathrm{E}}=30$ and 136 ms. Trimethylsilyl-2-2-3-3-tetradeuteropropionic (TSP) acid (sodium salt) was added to each sample as an internal reference substance for calibration of chemical shifts and metabolite concentrations. One zero filling is applied to have the extended FID length $N=65536,$ which in Ref. [53] was deemed sufficient in applications of the FFT aimed at resolving a number of resonances of interest.

The authors of Ref. [53] have kindly given to us two averaged FIDs, each of length $N=16384,$ encoded at $T_{\mathrm{E}}=30\,\mathrm{ms},$ corresponding to two patients, one with the benign (serous cystadenoma) and the other with malignant (serous cystadenocarcinoma) ovarian cyst fluid. The remaining acquisition parameters of these FIDs to be processed here were the same as those just listed by reference to study [53].

3.2 Computed spectra: general remarks

In Ref. [33], shape estimations alone have been considered. Presently, both shape and parameter estimations will be investigated. One of our chief goals is to see which new and/or complementary insights of the scientific and clinical merits can be offered by the parametric relative to the nonparametric versions of the FPT and dFPT [33]. Component lineshapes can alternatively be referred to as partial lineshapes (partial lines) in order to make a link with the corresponding total shape spectra (total line) or envelope. A sum line is the sum of all the partial lines, irrespective of whether these are known (parametric FPT) or unknown (nonparametric FPT). In the nonparametric FPT (nonderivative), the partial lines or components are explicitly unavailable, but they are implicitly contained (in a folded form) in the total or sum line (envelope). In the parametric FPT, the explicitly reconstructed partial fraction $d_ku/(u-u_k)$ is one of the summed K components of envelope $P_K(u)/Q_K(u).$ Therefore, the ’partial shape spectra’ for the components $\{d_ku/(u-u_k)\}\, (1\le k\le K)$ and the corresponding ’total shape spectrum’ for the envelope $P_K(u)/Q_K(u)$ is a convenient parallel structure terminology in the Padé-based signal processings.

The presentation of the reconstructed spectra in the nonparametric and parametric Padé estimations will cover the nonderivative and derivative signal processings. On the other hand, the nonderivative and derivative Fourier spectra can be given in their only possible form, the default nonparametric processing. Both the Padé and Fourier spectra will be shown in the magnitude mode. The magnitude mode is much more convenient than the real part of the corresponding complex mode. The reason is that the magnitude mode is positive-definite and, therefore, does not need any phase correction. Moreover, in the real part mode of derivative spectra, the side satellite lobes around the resonances of interest are a burden to interpretation. Such side lobes are pushed down to the background baseline using the magnitude mode of derivative spectra. This makes the overall layout transparent and more amenable to adequate identification, quantification and clinical interpretation of the main resonances [74,75,76,77,78,79,80].

For both the benign and malignant samples, all the present spectra are computed using the complex-valued FIDs (encoded in the quadrature mode) [53]. As in Ref. [53], where only the FFT was used, we shall also zero fill the encoded 16384 FID data points so as to have the total length extended to 65536. Generally, zero-filling of time signals is regularly used for the FFT, but this is optional for the FPT.

Throughout the computation, as in Ref. [33], the model order K in the Padé nonparametric and parametric processing is taken to be $K=3000$ for which the full stabilization of the peak parameters and the ensuing spectra is achieved. The Padé derivative estimation by the dFPT is generated from the nonderivative FPT for both nonparametric and parametric signal processings. Hence, in the dFPT, the same model order $K=3000$ is also used, as in the corresponding FPT for both nonparametric and parametric data analyses.

Among the reconstructed 3000 poles of the spectrum $P_K(u)/Q_K(u),$ some belong to the genuine (physical, stable), whereas the remainders are associated with the spurious (unphysical, unstable) resonances. Unphysical, noisy resonances in the spectrum $P_K(u)/Q_K(u)$ have their poles (roots of $Q_K$) and zeros (roots of $P_K$) coincident, i.e. they are Froissart doublets. Therefore, they are washed out from the spectrum $P_K(u)/Q_K(u)$ on account of pole-zero cancellations [70, 72]. As such, only the physical resonances remain in the final, denoised spectrum $P_{K_{\mathrm{g}}}(u)/Q_{K_{\mathrm{g}}}(u),$ where $K_{\mathrm{g}}$ is the number of genuine poles (the difference between the total number of poles K and the number of the unphysical, spurious poles).

Fig. 1

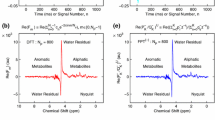
In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Envelopes (nonparametric FPT, dFPT): (a–h), Components (parametric FPT, dFPT): (i–l). Nonderivative $(m=0):$ (a, c, i), derivatives: (b, d–h, j–l). Abscissae are chemical shifts in parts per million, ppm. Ordinates are spectral intensities in arbitrary units, au. Wider band, 0.87–5.125 ppm (a, b). Narrower band, 4.65–4.75 ppm (c–l): optimal treatment of the residual water spectra. For a discussion, see the main text. (Color online)

Fig. 2

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé spectra (a–l) by the nonderivative FPT ($m=0)$ and derivative dFPT ($m=1-2$) at 5.0-5.1 ppm, near the water residual. Unassigned quartet U’(q) in (a–f) and unassigned triplet U”(t) in (g–l). Components by the parametric FPT and dFPT: (a–c, g–i). Envelopes by the nonparametric FPT and dFPT: (d–f, j–l). For a discussion, see the main text. (Color online)

Fig. 3

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. In Ref. [53], internal reference TSP at 0.0 ppm has been used for calibration of chemical shifts and metabolite concentrations. Padé spectra (a–j) by the nonderivative FPT ($m=0)$ and derivative dFPT ($m=1-20$) at [− 0.01,0.01] ppm. Components by the parametric FPT: (a). Envelopes by the nonparametric FPT and dFPT: (b–j). For a discussion, see the main text. (Color online)

Fig. 4

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé nonderivative $(m=0)$ spectra in the FPT (a–d) at 1.21–1.54 ppm, involving Ala(d), Lac(d), Thr(d) and $\beta -$HB(d). Components by the parametric FPT: (a, c). Envelopes by the nonparametric FPT: (b, d). Dynamic range of spectral intensities on the ordinates: unrestricted (a, b) and reduced (c, d). For a discussion, see the main text. (Color online)

Fig. 5

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé derivative spectra ($m=1-3$) by the dFPT (a–f) at 1.21–1.54 ppm, involving Ala(d), Lac(d), Thr(d) and $\beta -$HB(d). Components by the parametric dFPT: (a, c, e). Envelopes by the nonparametric dFPT: (b, d, f). For a discussion, see the main text. (Color online)

We will now present altogether eleven figures. Each of these figures contains the results of the FPT and dFPT. The Fourier data are given in Fig. 6. The reconstructions for the malignant case are in Figs. 1–9 and 11, whereas those for the benign case are in Fig. 10. First shown will be a wider frequency band in a part of Fig. 1. This will be followed by zooming into the various smaller windows of interest in Figs. 2–11 with certain particular themes (e.g. a proper treatment of the water residual, detection of unassigned resonances, calibrating resonance, resonances of branched-chain amino acids, spectra of recognized cancer biomarkers, etc).³

Fig. 6

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé and Fourier estimations: spectral crowding of branched-chain amino acids at 0.91–1.12 ppm, involving Leu(d,t) and Iso(d,t). Padé nonderivative spectra ($m=0$): components (a parametric FPT) and envelope (b nonparametric FPT). Padé 4th derivative spectra ($m=4$): components by the parametric dFPT (c) and envelope by the nonparametric dFPT (d). Fourier 4th derivative dFFT ($m=4$): (e). For a discussion, see the main text. (Color online)

Fig. 7

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé derivative estimations by the dFPT ($m=1-3$): spectral crowding of branched-chain amino acids at 0.91–1.12 ppm, involving Leu(d,t) and Iso(d,t). Components by the parametric dFPT: (a, c, e). Envelopes by the nonparametric dFPT: (b, d, f). For a discussion, see the main text. (Color online)

Fig. 8

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Derivative shape estimation for detecting hidden resonances beneath Lac(d) at 1.39-1.43 ppm. Padé nonderivative $(m=0)$ and derivative $(m=1-4)$ spectra. Components by the parametric FPT and dFPT: (a–e). Envelopes by the nonparametric FPT and dFPT: (f–j). For a discussion, see the main text. (Color online)

Fig. 9

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Derivative shape estimation for detecting hidden resonances beneath Lac(q) at 4.34-4.39 ppm. Padé nonderivative $(m=0)$ and derivative $(m=1-4)$ spectra. Components by the parametric FPT and dFPT: (a–e). Envelopes by the nonparametric FPT and dFPT: (f–j). For a discussion, see the main text. (Color online)

Fig. 10

In vitro $\mathrm{{}^1H\,MRS}$ for benign ovarian cyst fluid (serous cystadenoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé nonderivative $(m=0)$ and derivative $(m=1-4)$ spectra at 3.17-3.30 ppm. Components by the parametric FPT and dFPT: (a–e). Envelopes by the nonparametric FPT and dFPT: (f–j). For a discussion, see the main text. (Color online)

Fig. 11

In vitro $\mathrm{{}^1H\,MRS}$ for malignant ovarian cyst fluid (serous cystadenocarcinoma) from a patient. Encodings of time signals or FIDs from Ref. [53] have been made with a Bruker 600 MHz ($\approx 14.1$T) spectrometer. Padé nonderivative $(m=0)$ and derivative $(m=1-3)$ spectra at 3.17-3.30 ppm encompassing the choline-containing compounds. Components by the parametric FPT and dFPT: (a–d). Envelopes by the nonparametric FPT and dFPT: (f–h). For a discussion, see the main text. (Color online)

In Fig. 1, the respective results of the nonparametric (panels a–h) and parametric (panels i–l) variants of the FPT and dFPT are given. Therein, the nonderivative (a, $m=0$) and first derivative (b, $m=1$) envelopes cover a wider frequency band (0.87-5.125 ppm), which includes the water residual. Panels (c-l) deal with the derivative orders $m\le 5$ in a much smaller sub-band 4.65–4.75 ppm around the $\mathrm{H_2O}$ residual. Therein, panels (c-h) are on the nonparametric FPT and dFPT, whereas panels (i–l) are concerned with the parametric FPT and dFPT.

The part (drawn in red) on panels (a, b), containing the lactate doublet Lac(d) with its small surrounding, is divided by a factor of 3.5. Additionally, the red part on panel (a, $m=0$) is scaled upward by 0.1 au (arbitrary units). This allows a smooth joining of the red and blue parts. The blue part represents the remainder of the entire envelope within the shown frequency window, 0.87-5.125 ppm. On panel (b, $m=1$), the red and blue parts of the spectrum merge smoothly together without any supplementary lifting upward of Lac(d) and its immediate neighborhood.

On the displayed scale, despite the said reduction of the size of the originally dominant Lac(d) resonance, the nonderivative envelope (a, $m=0$) does not appear to be too abundant with other metabolites between the lactate doublet and quartet. Namely, except for Lac(d) at 1.41 ppm and the lactate quartet Lac(q) at 4.36 ppm as well as the water residual at 4.71 ppm, only a limited number of smaller resonances are noticeable on panel (a). Therein, the $\mathrm{H_2O}$ residual is seen as a still intense double-structured broad bump. Moreover, around Lac(d) from 0.87 to 1.52 ppm, several smaller resonances can be seen, lined up in a spectrally crowded way from lower to higher frequencies, as follows: isoleucine Iso(d,t), leucine Leu(d,t), valine Val(dd), $\beta -$hydroxybuturate $\beta -$HB(d), threonine Thr(d) and alanine Ala(d).

In the first derivative envelope from panel (b, $m=1$), dominance of Lac(d) and Lac(q) also obscures the majority of the remaining resonances. Despite an apparent similarity of the envelopes for $m=0$ and $m=1,$ it is clear that there are several critical differences between the nonderivative FPT (a) and the first derivative dFPT (b), respectively. These are:

• (i) A near-disappearance of the water residual from panel (b, $m=1$).

• (ii) A narrower bottom (base) of Lac(d) and Lac(q) for $m=1$ (b) than for $m=0$ (a).

• (iii) A markedly better resolution for $m=1$ (b) than for $m=0$ (a), especially in e.g. the mentioned sub-band 0.87–1.52 around Lac(d).

This can readily be understood by the arguments that run as follows:

• (i’) Narrowing of resonances in a derivative envelope spectrum increases the intensity gap between the thin and wide resonances. With increasing derivative order m,  the peak heights grow faster for sharper than for broader resonances. Consequently, the broad water residual on $\mathrm{\left| FPT\right| }_{\mathrm{Tot}}$ (a, $m=0$) becomes significantly reduced on $\mathrm{\left| D_1FPT\right| _{Tot}}$ (b, $m=1$), as stated in (i).

• (ii’) The derivative operator $\mathrm{D}_m=(\text{ d }/\text{d }\nu )^m \, (m=1,2,3,...)$ effectively cuts off the long tails of resonances. Such a “wave-packet-type” localizing effect produces well-tightened lineshapes. For e.g. $m=1$ (b), the net result is observed in narrowing the bottom parts of spectral peaks. This is most clearly manifested in the strong Lac(d) resonance, as indicated in (ii).

• (iii’) The linewidth narrowing phenomenon, as the prime feature of derivative signal processing, leads to overlap splitting and/or to a better delineation of the neighboring peaks, most notably for Ala(d), Thr(d), $\beta -$HB(d) and Val(dd), the five doublets in the close proximity (1.0–1.52 ppm) of Lac(d), as noticed in (iii).

In the magnitude mode, the $m\,$th derivative lineshape $(m=1,2,3,...)$ of a complex Lorentzian frequency distribution is narrower than the corresponding nonderivative profile $(m=0)$ [75]. Concomitantly, the derivative peak heights are taller than their associated nonderivative counterparts. In other words, the narrower the peak width, the taller the peak height. This causal connection is directly prescribed by the definition of the peak height as the ratio of the FID intensity $\left| d_k\right|$ and the peak width, which is, according to Refs. [75, 76], proportional to the imaginary part of the resonance frequency, $\mathrm{Im}(\nu _k).$

In MRS with encoded FIDs, some rolling background baselines are always encountered in computed envelopes. These background lineshapes are comprised mainly of noise, wide spectral hills (heavy macromolecules, e.g. lipids, proteins) and long tails of the water and other stronger resonances. Noise and these wider spectral structures are diminished in derivative spectra, resulting in flatter background baselines. Such an achievement also exists in Fig. 1 for $\mathrm{\left| D_1FPT\right| }$ (b, $m=1$).

Overall, an improved delineation and splitting of overlapping resonances point to the frequency resolution enhancement. Moreover, a stronger content of physical resonances and simultaneously a weaker noisy background baseline signify a higher SNR. As such, these advantages, emanating from Fig. 1, establish the fact that already the first derivative envelope $\mathrm{\left| D_1FPT\right| _{Tot}}$ (b, $m=1$) significantly outperforms its nonderivative counterpart $\mathrm{\left| FPT\right| _{Tot}}$ (a, $m=0$) in what matters the most for MRS, resolution and SNR. Nevertheless, this by no means implies that the first derivative spectra would qualify to be the end point of signal processing. Quite the contrary, it is to be expected that spectra for higher derivative orders $(m\ge 2)$ should be superior to the case with $m=1.$ It only remains to determine the extent of some further improvements and, most importantly, to find out whether that would be of notable clinical relevance.

On panels (a, b), a very small band 3.18-3.24 ppm, near the mid-point between Lac(d) and Lac(q), is extremely important because it houses the choline-containing compounds (recognized cancer biomarkers). They consist of three singlet resonances, free choline Cho(s), phosphocholine PC(s), and glycerophosphocholine GPC(s). On the scale of panels (a, b) only Cho(s) and PC(s) can be spotted as the two minuscule peaks. Many other poorly visible, weak resonances are present on panels (a, b). To enhance their visibility, sequential signal processing is needed. This can be achieved by either a further truncation of most of the upper part of Lac(d) or by zooming into certain particular sub-intervals [33]. A similar procedure can also be used for other derivatives $(m\ge 2).$ Such a step-wise analysis will be carried out for several sub-bands, including 0.91–1.12, 1.21–1.54, 1.39–1.43, 3.17–3.30, 4.34–4.39, 4.65–4.75, 5.00–5.10 and 5.07–5.10 ppm.

The main reason for selecting several of these chemical shift bands is in their diagnostic relevance (differentiating between benign and malignant samples) [50, 53]. Namely, for this purpose, it has initially been suggested in Ref. [50] and later supported by Ref. [53], that future studies should focus on metabolites resonating near chemical shifts 1.5, 1.7, 2.8, 3.0, 3.2. 3.3 ppm, where possibly some new cancer biomarkers could be found. For example, it has been found in Refs. [33, 53] for the range 0.9–1.6 ppm that besides Lac(d), several other resonances, e.g. Val(dd), $\beta -$HB(d), Thr(d) and Ala(d), are significantly more intense for malignant (serous cystadenocarcinoma) than for benign (serous cystadenoma) samples.

The step-wise band-by-band approach is illustrated already in Fig. 1 through panels (c-l) for the frequency interval 4.65–4.75 ppm around the water residual (4.71 ppm). Therein, one of the essential issues of practical relevance is addressed through the problem of localization of the water residual. Due to dominance of water in human tissues and biofluids, the original, unsuppressed $\mathrm{H_2O}$ peak in spectra is gigantic, as its intensity is generally about 10000 times stronger than those of resonances for all the other metabolites. This can significantly be mitigated by a partial water suppression in the course of FID encodings, as done in many studies including Ref. [53]. The effect of such a procedure from Ref. [53] is seen in the spectrum $\mathrm{\left| FPT\right| _{Tot}}$ (a, $m=0$) which has a relatively small water residual. On panel (a), despite division of the red part by 3.5, the Lac(d) resonance remains stronger (by a factor of about 4.3) than the $\mathrm{H_2O}$ residual. Still, there is always room for a further improvement since any water residual, including the one on panel (a), could distort the neighboring and remote resonances alike.

The usual practice in the MRS literature is to fit the water residual structure by e.g. 3–10 arbitrary Lorentzians. Afterward, the local spectrum (around $\mathrm{H_2O}$), generated by using the fitted peak parameters, is subtracted from the given full envelope. However, the ensuing difference spectrum is always modified introducing possibly significant changes (by an unknown amount) in the assessments of the true concentrations of metabolites. This would defeat the purpose of MRS.

Instead, we propose an alternative novel method. It is based on derivative processing by the nonparametric dFPT (d–h, $1\le m\le 5$), which can tackle the water residual (c, $m=0$) without any arbitrariness. The derivative envelopes from panels (d–h) need to be scrutinized by the components from the parametric derivative dFPT. For such a purpose, we give panels (i–l) for nonderivative and derivative component lineshapes.

Regarding the nonparametric Padé processings around the water residual, we first show the nonderivative envelope $\mathrm{\left| FPT\right| _{Tot}}$ (c, $m=0$). This is followed by the nonparametric derivative envelopes: $\mathrm{\left| D_1FPT\right| _{Tot}}$ (d, $m=1$), $\mathrm{\left| D_2FPT\right| _{Tot}}$ (e, $m=2$), $\mathrm{\left| D_3FPT\right| _{Tot}}$ (f, $m=3$), $\mathrm{\left| D_4FPT\right| _{Tot}}$ (g, $m=4$) and $\mathrm{\left| D_5FPT\right| _{Tot}}$ (h, $m=5$). Finally, the components from the parametric Padé processings near the $\mathrm{H_2O}$ residual are displayed through the nonderivative FPT (i, $m=0$) as well as via the derivative dFPT (j, $m=1$), (k, $m=2$) and (l, $m=4$).

The $\mathrm{H_2O}$ residual is seen on the nonderivative envelope $\mathrm{\left| FPT\right| _{Tot}}$ (c, $m=0$) to be an asymmetric ‘doublet’ of unequal peak widths and heights. The right peak is notably wider and taller than its companion on the left. The dip in between these two wings is located near 4.71 ppm. Such a twofold spectral configuration is very instructive for analysis since it represents an excellent opportunity to verify the veracity of the foregoing reasonings (i’–iii’) that are the heart of derivative signal processing. In particular, we stated in (i’) that, with augmentation of the derivative order m,  there is a different pace of change of the peak width and height for narrower and wider resonances.

In fact, the difference begins to show up already from comparing $\mathrm{\left| FPT\right| _{Tot}}$ (c, $m=0$) with the first derivative spectrum $\mathrm{\left| D_1FPT\right| _{Tot}}$ (d, $m=1$). Namely, the right wider peak, which is dominant in $\mathrm{\left| FPT\right| _{Tot}}$ (c, $m=0$), turns out in $\mathrm{\left| D_1FPT\right| _{Tot}}$ (d, $m=1$) to be smaller than the left thinner peak. This trend is further accentuated for the increased value of the derivative order when m passes from 2 (e) to 5 (h). For instance, by the time m has reached the value 5 on panel (h), the right wing has completely disappeared, whereas the left peak still remained as a visible resonance.

Specifically, the dip at 4.71 ppm in $\mathrm{\left| FPT\right| _{Tot}}$ (c, $m=0$) has undergone some marked alterations. Viewed in isolation from the left and the right peaks, this dip can be considered as a narrow negative peak (directed downward) in $\mathrm{\left| FPT\right| _{Tot}}$ (c, $m=0$). Alternatively, the width of the dip can be taken as the separation distance between the centers of the left and right positive peaks (those directed upward). A rough visual assessment indicates that the dip width is $\sim$ 2.7 and $\sim$ 7.5 times smaller than the widths of the left and right positive peaks. With the first derivative $\mathrm{\left| D_1FPT\right| }$ (d, $m=1$), the dip at 4.71 ppm, becomes a positive peak. Moreover, this new positive peak is seen on panel (d, $m=1$) to be dominant, on account on its smallest width.

This dominance of the peak at 4.71 ppm on panel (d) is maintained throughout the remaining envelopes om panels (e–h). The exact location of this peak, which was formerly negative (on panel c) and subsequently positive (on panels d–h), is 4.70755 ppm which coincides precisely with the chemical shift of the water molecule resonance. Presently and in Ref. [33], the position of the water resonance is defined to be at 4.70755 ppm. We then see how sequential processing through zooming into the narrow frequency band 4.65–4.75 ppm, around the $\mathrm{H_2O}$ residual, can enable the derivative transform within the nonparametric dFPT to illuminate the two main achievements of clinical relevance to MRS, resolution and SNR improvements:

• Resolution improvement The $\mathrm{H_2O}$ residual is split into its constituents. One of these components is due to the water molecule itself (4.70755 ppm) and the rest can be assigned to some other metabolites. For instance, a set of smaller resonances located a bit upfield of 4.71 ppm, i.e. almost co-resonating with $\mathrm{H_2O},$ is a multiplet of nitrogen acetyl aspartatic (NAA) acid. This can be followed through the panels (d–h), where e.g. two such small peaks are visible at the positions slightly to the left of the chemical shift of water, 4.70755 ppm.

• SNR improvement Background baseline is notably elevated on panel (c, $m=0$), where it attains its maximal value of about 0.95 au, which is roughly a quarter of the intensity of the right tall peak in $\mathrm{\left| FPT\right| _{Tot}}$ therein. This high background is vastly reduced on panel (d, $m=1$) and, basically, all but gone on panels (e, $m=2$), (f, $m=3$), (g, $m=4$) and (h, $m=5$).

Isolation of the clean singlet resonance of the water molecule at 4.70755 ppm is best accomplished on panels (g, $m=4$) and (h, $m=5$). Thus, using the nonparametric dFPT, the $\mathrm{H_2O}$ peak area can be perfectly determined by any means, including the use of a numerical quadrature method since the integration limits are optimally well defined on panels (g, h). The same applies to the neighboring small peaks on each side of 4.70755 ppm $(\mathrm{H_2O})$ that can be made more visible on panels (g, h) by e.g. truncating most of the upper part of the central water peak, in the spirit of sequential visualization [33].

To complement the envelopes (a–h) from the nonparametric FPT and dFPT, we now pass onto panels (i–l) for the components from the parametric FPT and dFPT. The nonderivative components on panel (i, $m=0$) provide an illustrative and instructive insight into the $\mathrm{H_2O}$ residual. Therein, several broader and narrower lineshapes are seen. The narrowest lineshape appears at 4.70755 ppm. This is the singlet of the $\mathrm{H_2O}$ molecule. Its top is at an intensity level of about 1.0 au, which coincides with the bottom of the dip in the corresponding envelope (c, $m=0$). Moreover, there are three other peaks on panel (i, $m=0$) that are extremely close to the chemical shift 4.70755 ppm of the water molecule. Two of them are very small. The third peak is an example of near-degeneracy as it is lying infinitesimally near the chemical shift of water (4.70755 ppm) and, moreover, it is of the same height as the $\mathrm{H_2O}$ resonance, albeit slightly broader.

The four widest resonance components on panel (i, $m=0$) are the lineshapes that actually build the two broad peaks in the envelope (c, $m=0$). These four broad resonances on panel (i, $m=0$) are significantly reduced in the first derivative components (j, $m=1$). Only one of them is visible (and barely so) in the second derivative components (k, $m=2$). However, none of these initially broad resonances on panel (i, $m=0$) can be seen in the fourth derivative components (l, $m=4$). The peak of the unknown molecule, which co-resonates with $\mathrm{H_2O},$ is clearly visible on panel (j, $m=1$). However, its strength on panels (j, $m=1$) and (k, $m=2$) is only about one 1/3 and 1/9 respectively of the intensity of the $\mathrm{H_2O}$ peak on account of being broader than the water resonance on panel (i, $m=0$). Finally, this near-degenerate peak practically disappears from the fourth derivative components (l, $m=4$).

Similarly, the origin of the spectral structures in the first (d, $m=1$) and second (e, $m=2$) derivative envelopes can be identified and its development monitored by reference to the associated component spectra on panels (j, $m=1$) and (k, $m=2$), respectively. At last, the fourth derivative envelope (g, $m=4$) from the nonparametric dFPT is coincident with its fourth derivative component counterpart (l, $m=4$) from the parametric dFPT. This confirms the trustworthiness of the nonparametric dFPT in uniquely unraveling the exact, true components from the given envelope.

A specimen of perfectly pure water subjected to proton MRS would produce an ideal singlet resonance in an envelope spectrum. Water is present to within 60–70% by weight in living cells, tissues or biofluids. Consequently, computation of envelopes using time signals encoded from such samples without water suppression would generate a dominant, singlet-appearing resonance. However, this is deceptive. The reason is that, despite its appearance, such a water peak is structured. In proton MRS for biomedical samples (e.g. organ biopsies, glandular secretions, cell suspensions, colloidal protein solutions, etc.), the single aqueous lineshape at the expected chemical shift of pure water molecules must be interpreted as a composite or total or sum lineshape, i.e. an interactive superposition of a number of partial lineshapes.

Hence, the partial lineshapes in a sum or composite lineshape have their biomedical origin and can be assigned to protons contained in various chemical environments (nucleotides, lipids, proteins, carbohydrates and other chemical compounds). They might be poorly visible (if at all) in an envelope from FIDs encoded without water suppression. Nevertheless, some sub-structure invariably appears in an envelope computed from FIDs with partially suppressed water during the process of encoding. In the case of the water residual, a rough representation of such a sub-structure is seen in the envelope on panel (c, $m=0$). The corresponding refinement is provided by the explicit components on panel (i, $m=0$). The parametric nonderivative FPT ($m=0$) would also find some partial lineshapes, i.e. the components by employing FIDs encoded without water suppression. This is presently verified to be true for in vivo $\mathrm{{}^1H\, MRS}$ at a 3T clinical used without water suppression to encode FIDs from a patient with the borderline serous cystic ovarian tumor [54].

The unsuppressed and/or partially suppressed water resonance in the MRS literature is often viewed as a nuisance to be discarded. However, even if some spectral structures (e.g. water residual, background baseline, etc.) are considered as a burden to signal processing for MRS, they still must be treated with due care. Fitting such resonances to remove them from the given envelope spectrum would inevitably take away some of the information provided by weaker physical resonances that might be of useful diagnostic significance. This problem, which is encountered with an improper dealing with the so-called ’nuisance’ resonances, does not exist in the derivative transform implemented by the nonparametric dFPT.

As the case in point, it can be seen on panels (d–h) that, without any fitting, the nonparametric dFPT is able not only to unambiguously single out the water peak and quantify it, but also to do likewise with some other smaller resonances (such as an NAA multiplet) that were completely hidden in the nonderivative spectrum $\mathrm{\left| FPT\right| }_{\mathrm{Tot}}$ (c, $m=0$). The NAA metabolites are usually found in large concentrations in healthy neuronal cells. These molecules are either absent away from the brain or present in minute concentrations. However, some notable concentrations of N-acetylated metabolites have been detected outside the human brain, not only in ovarian cyst fluid [54, 55], but also in the lens of the eye [81] and peritoneal mast cells [82].

In the mentioned Ref. [54] on a borderline serous cystic ovarian tumor in a patient, certain resonances assignable to NAA or nitrogen acetyl neuraminic (Neu) acid have been identified at 2.06 ppm (singlet) and 2.95 ppm (multiplet). In this case, the computed envelope spectra from the FFT have been reported only up to 4.0 ppm [54]. The sole reason for such an abrupt cut-off was to avoid dealing with the severely distorted part of the Fourier spectrum above 4.0 ppm containing a large water residual. In the aliphatic region (below 5 ppm), the $\mathrm{H_2O}$ residual was about ten times stronger than the tallest resonance therein, the NAA-containing peaks near 2.0 ppm [54]. However, such an avoidance is wholly unnecessary, when using an adequate estimator. The proof has recently been provided within the dFPT [32] by employing the same FID used in Ref. [54].

In Ref. [32], the N-acetylated metabolites were quantifiably detected in the derivative Padé envelope $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ ($m=3$), not only around 2.06 and 2.95 ppm as in Ref. [54], but also slightly to the right of the sharply narrowed leftover of the formerly broad water residual, similarly to e.g. panel (f, $m=3$) of the present Fig. 1. By contrast, the derivative Fourier processing with the dFFT failed completely as it was worse than even its nonderivative counterpart, FFT [32].

It is then obviously highly advantageous for clinical purposes (and beyond) to use an adequate processor for treating all the resonances on the same footing. This invalidates the usual practice in the MRS literature to deliberately avoid some ’inconvenient’ spectral regions containing the ’nuisance’ resonances (lipids, ...) as e.g. in Ref. [62], just because of the inherent inability of the Fourier-based processing to perform the proper analysis of encoded FID data points. Such a ’pick and choose’ approach to resonances would influence the estimated concentrations of the retained metabolites and could impact adversely also on the tissue classification (benign versus malignant).

The main task in addressing the water residual by the explained manner on panels (c–l) of Fig. 1 is to optimally localize this initially broad spectral structure. The derivative shape estimation by the nonparametric dFPT succeeds in solving such an important problem by drastically narrowing the wide bottom/base of the water residual. The dFPT achieves this by effectively cutting-off the previously long-extending tails of the $\mathrm{H_2O}$ resonance. With this result, as optimally provided by panels (g, $m=4$) and (h, $m=5$), we can be sure that quantification of the entire remaining metabolite set from the envelope spectrum can proceed with no distortion whatsoever from the $\mathrm{H_2O}$ residual.

Advantageously, once confidently quantified, as becomes feasible on panels (g, h), the water peak itself may find its own useful applications. For instance, it can be employed as a convenient internal reference metabolite which is, unlike e.g. the commercially available TSP, naturally present in biomedical samples. This applies not only to the present problem, but also to the entire field of MRS since the expounded procedure is general for handling the $\mathrm{H_2O}$ resonance region (corresponding to FIDs encoded with and without water suppression). Thus, as opposed to various fitting and subtraction recipes (that could impact deleteriously on approximating the true concentrations of all the other metabolites), we turn this ‘nuisance’ problem with the water residual into a practical and verifiable device for establishing an internal reference. Practical, because it is done with the nonparametric dFPT. Verifiable, because it is corroborated by the parametric dFPT.

The residual water resonance conglomerate, centered close to 4.71 ppm, and shown on panels (c–l) of Fig. 1, covers a narrow frequency band, 4.65–4.75 ppm. This region is chosen to avoid clutter with the neighboring resonances as the main focus is on isolating the $\mathrm{H_2O}$ singlet. Throughout both in vitro and in vivo proton $\mathrm{{}^1H\, MRS}$ literature, in nonderivative envelopes, any closer neighborhood of the residual water resonance ensemble has always and systematically been skipped. The reason was in severe lineshape distortions of all the nearby resonances by the still elevated long tails coming out from the water residual. However, as per Fig. 1, such limitations, leading unavoidably to information loss, are foreign to derivative spectra by the nonparametric dFPT, where a strong localization of the $\mathrm{H_2O}$ spectral cluster de facto cuts off its tails, as stated. In other words, for derivative envelopes in the nonparametric dFPT, we could have afforded to work with a window wider than 4.65–4.75 ppm on panels (c–h) of Fig. 1 and still accomplish the same goal, which is a complete isolation of the water singlet resonance.

Besides uncovering e.g. the NAA multiplet near 4.71 ppm, there other advantages of the just outlined strong localization of the water residual. For example, at 5.0–5.1 ppm, the flattened tail of the water residual uncovers the two new resonances of some unknown metabolites, a quartet and a triplet denoted by U’(q) and U”(t) centered near 5.05 and 5.092, respectively. Although weak, the quartet U’(q) can nevertheless be spotted on panels (a) and (b) of Fig. 1. Therein, the triplet U”(t) is invisible. However, visibility can be tremendously improved by zooming into the narrow range 5.0–5.1 ppm, as illustrated in Fig. 2. For both U’(q) and U”(t), this figure shows the spectra from the nonderivative FPT ($m=0$) and derivative dFPT ($m=1,\, 2$).

The spectra from Fig. 2 include the components (parametric FPT, dFPT) on the left column and envelopes (nonparametric FPT, dFPT) on the right column. The three top and three bottom rows are for U’(q) and U”(t), respectively. The nonderivative spectra are on panels (a: components, d: envelope) for U’(q) and on panels (g: components, j: envelope) for U”(t). The derivative spectra for U’(q) include $m=1$ (b: components, e: envelope) and $m=2$ (c: components, f: envelope). Similarly, the derivative spectra for U”(t) refer to $m=1$ (h: components, k: envelope) and $m=2$ (i: components, l: envelope).

The nonderivative components of U’(q) are all symmetric in the magnitude mode (a, $m=0$), even though they are not Lorentzians. Moreover, to a reasonable approximation, their peak heights satisfy the ratio relationships 1:3:3:1 from the Pascal triangle for a $J-$coupled triplet [78, 79]. Note, however, that on panel (a), the inner two peaks of U’(q) are of slightly different heights. Moreover, the heights of the two outer peaks of U’(q) do not seem to be identical either. The peak height ratios 1:3:3:1 are indicative of the theoretically predicted relations of the like strengths (intensities) of the individual resonances only if all four of them are of equal widths. If this condition is not fulfilled, the peak areas should be used for the peak intensities to verify e.g. the ratios 1:3:3:1 [78, 79, 83, 84]. On the other hand, it is virtually impossible to tell, by way of the naked eye, whether or not the widths of the four peaks in U’(q) are the same in the nonderivative components from panel (a, $m=0$).

By comparison, the associated four peaks in the magnitude lineshape of the nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}\equiv \sqrt{\mathrm{Re^2(FPT)_{Tot}+Im^2(FPT)_{Tot}}}$ (d, $m=0$) look more like being an asymmetric profile in a typical dispersion mode. This means that the squared imaginary part $\mathrm{Im^2(FPT)_{Tot}}$ contributes more heavily to $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ than the corresponding squared real part $\mathrm{Re^2(FPT)_{Tot}}$ of the complex nonderivative envelope, $\mathrm{FPT}_{\mathrm{Tot}}=P_K/Q_K.$

A better insight into the linewidth issue within U’(q) is provided by the derivative component spectra (b, c). Herein, it is seen that the widths of the central two component peaks in U’(q) are very similar since their height relations may have changed only mildly with the increasing derivative order. By reading off the heights of the left and right central peaks, the ratios 1.05, 1.05 and 1.03 are obtained from the component spectra $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (a), $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (b) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (c), respectively. For the two outer peaks in U’(q), a like reading off from the plots gives quite different height ratios of the left to the right peaks, 1.27, 1.33 and 1.57 by reference to the components $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (a), $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (b) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (c), respectively. Thus, the derivative components (b, c) imply that the two outer peaks in U’(q) are of unequal widths, the finding which could not be deduced by looking at the nonderivative component spectra (a), as mentioned.

It should be emphasized that the just made conclusions are based upon visually inspecting only the lineshapes of the component spectra (a–c), without looking at the available tables of the numerical results from the explicit quantification by the Padé parametric estimations. This remark is important since we presently use the results of the parametric FPT and dFPT exclusively to peruse the plots for the spectra due to these estimators, without referring to the tabular numerical data of the performed quantification.

Similar conclusions can be drawn also from the corresponding envelopes (d–f), computed by the nonparametric dFPT. Namely, the heavily distorted nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d) is greatly improved already in the first derivative envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (e). For instance, the background baseline in $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d) is very high, nearly one third of the heights of the two central peaks in the U’ quartet. However, such an elevated background is pushed down straight to the chemical shift axis in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (e).

Furthermore, it can be seen that the envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (e) actually represents an excellent match, all around, to the corresponding first derivative component $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (b). In the derivative envelopes (e,f) for U’(q), the background baselines exhibit a marked straightening. Simultaneously, the four peaks in U’(q) are narrowed. The combined benefit of these two outcomes of the derivative estimation, within the nonparametric dFPT ($m=1$), is SNR and resolution enhancements. The background is likewise flattened in the derivative component spectra (b,c) relative to their nonderivative counterpart on panel (a).

In addition to the U’ quartet, the nonderivative component spectra on panel (a) have some other resonances, two of which are visible and both centered at about 5.076 ppm (hence, degenerate). However, as to derivative component spectra, these resonances are poorly visible on panel (b, $m=1$) and practically absent from panel (c, $m=2$). As such, the components from panel (c) and the envelope (f) become largely coincident in the second derivative spectra throughout the interval 5.0–5.1 ppm.

In the nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d), some ’spectral bifurcations’ are seen as being superimposed on the tails of the U’ quartet. These structures are gradually lessened due to the reduced background baselines in the derivative envelopes (e, f). In fact, except for one tiny structure toward the end of the band at 5.1 ppm, they are all washed out from the second derivative envelope $\left| \mathrm{D_2FPT}\right| _{\mathrm{Tot}}$ (f). This tiny spectral structure, the unassigned triplet U”(t), is partially noticeable in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (e) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Tot}}$ (f).

However, zooming into the sub-range 5.07–5.10 ppm can help also with the U” triplet, as done on panels (g–i: components) and (j–l: envelopes). The nonderivative components in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g) are over-crowded. Therein, besides the three peaks of U”(t) of roughly similar heights, equidistantly separated (5.0875, 5.0925, 5.0975 ppm), there are six other peaks. These include the two degenerate peaks at 5.076 ppm, discussed with panels (a–c) for U’(q), regarding the wider interval 5.0–5.1 ppm. The two confluent resonances at 5.076 ppm are of unequal widths, where the taller peak is more spread out. Around the degenerate doublet (5.076 ppm), there are three resonances, one narrower at 5.070, two wider at 5.082 and 5.084. The former two peaks are completely covered by the degenerate doublet. Furthermore, a part of a wider singlet resonance can be seen in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g) near the very end of the band at about 5.099 ppm.

The widths of the individual resonances of the U” triplet are different in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g). Herein, the middle peak (5.0925 ppm) is narrower than the two side peaks (5.0975, 5.0875 ppm) that themselves are of almost of the same width. The middle peak (5.0925 ppm) on panel (g) is about 3 times shorter and 4 times narrower than the corresponding average values of the two degenerate resonances at 5.076 ppm.

On top of the mentioned nine resonances in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g), there are also four elevated tails from the neighboring U’ quartet as well as some other low-lying tails. In the nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (j), these tails are seen to hugely lift upward the background baseline on which all the highly deformed resonances are superimposed. Earlier, we referred to such distorted resonances as some ’spectral bifurcations’ in the nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d) for U’(q) within the wider interval 5.0–5.1 ppm.

For U”(t), most of these tails in the nonderivative component spectra in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g) are absent from the first derivative components in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h). On panel (g), we could have plotted only those lineshapes whose peak heights appear in the interval 5.07–5.10 ppm. We intentionally did not do that as we wanted to give a chance to the dFPT on panels (h, i) to demonstrate its ability of suppressing the elevated extended tails of resonances whose maxima are located outside the range 5.07–5.10 ppm. The opportunity is seized and maximally realized already by the first derivative in the dFPT on panel (h). This cleared the way for a more visible emergence of the nine derivative resonances in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h).

Such a situation can now be related to the observations made about the heights and widths of the two groups of resonances, one being the components of U”(t) at 5.0875, 5.0925 and 5.0975 ppm and the other comprised of the two degenerate peaks (5.076 ppm). The taller (also broader) of the two degenerate peaks in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g) at 5.076 ppm is seen in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) to be shorter. Moreover, in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h), the middle resonance (5.0925 ppm) from U”(t) is about the same height as the taller of the two degenerate resonances (5.076 ppm) therein.

This circumstance in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) is reversed relative to $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g), where the peak at 5.0925 ppm from U”(t) was 3 times shorter than the average height of the two confluent peaks at 5.076 ppm. Such a height ratio reversal in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) occurs because, as emphasized, in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g) the peak at 5.0925 ppm from U”(t) is 4 times narrower than the average height of the two degenerate peaks at 5.076 ppm. Subsequently, this is advantageously exploited by the first-order derivative operator $\mathrm{D}_1,$ which in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h), increases the height of a narrower peak at a faster pace than that of a broader resonance. In the same vein, among the three constituents of U”(t) at 5.0875, 5.0925 and 5.0975 ppm, the middle peak (5.0925 ppm) in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) is significantly taller than its two neighbors (5.0875, 5.0975 ppm) on account of being narrower than these latter two resonances in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (g).

The effect of the $\mathrm{D}_1$ operator in the first-derivative envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (k) is seen to be striking, especially by reference to the nonderivative spectrum $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (j). The background baseline is reduced from $\sim$ 21.5 au in $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (j) to $\sim$ 0.25 au in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (k). Furthermore, the three constituents of U”(t) at 5.0875, 5.0925 and 5.0975 ppm are sharply delineated in the envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (k). Their peak height ratios are reasonably close to those in the associated component spectra in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h).

Note that from panels (g–i) for the component spectra, one can approximately read off the peak height ratios for the discussed two groups of resonances (three centered at 5.0925 ppm within U” and two co-resonating at 5.076 ppm). For the group within the U” triplet, the ratios of the central to the two outer peak heights are 1.6 and 2.5 in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (i), respectively. Moreover, the widths of the two outer peaks (5.0875, 5.0975 ppm) in U”(t) are very close to each other. In the case of the two degenerate resonances at 5.076 ppm, their derivative peak height ratios are 1.4 and 2.0 in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (i), respectively. The three resonances at 5.070, 5.082 and 5.084 ppm, formerly hidden beneath the degenerate doublet (5.076 ppm), become unfolded in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (h) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (i). Among these latter three resonances, only the narrowest peak at 5.070 remains visible in $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp}}$ (not shown), where the wider of the two confluent peaks at 5.076 ppm are buried in the chemical shift axis. Altogether, five well-delineated resonances remain visible in $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp}},$ the three of them are the peaks from the U”(t) triplet (5.0875, 5.0925, 5.0975 ppm), the narrower degenerate peak (5.076 ppm) and the singlet centered at 5.070 ppm.

Regarding the envelopes from the nonparametric FPT and dFPT, the superiority of already the first derivative spectrum $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (k) relative to its nonderivative counterpart $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (j) is overwhelmingly self-evident. This is of practical usefulness because the envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (k) has a clear physical content, whereas $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (j) is uninterpretable. Such an encouraging trend is systematically continued for higher derivative spectra. Thus, a further significant improvement of concordance between the parametric and nonparametric dFPT in the second derivatives is recorded with $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (i) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Tot}}$ (l), respectively. Eventually, full coincidence is attained between all the five remaining resonances in $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp}}$ and $\left| \mathrm{D_4FPT}\right| _{\mathrm{Tot}}$ (not shown). Broader resonances that become invisible by the application of the derivative operator $\mathrm{D}_m$ are not lost from the analysis. These only temporarily vanished into the chemical shift axis from which they can pop out for visualization and quantification by truncating the neighboring narrower and more intense peaks.

Figure 3 displays the internal reference spectra assigned to the TSP molecule. As stated, the twofold purpose of adding this commercially available substance to the studied samples is to calibrate the chemical shifts and concentrations of metabolites. Especially, the latter task cannot be done before the peak area of the TSP is known as accurately as possible. It is here that there is an obstacle to achieve such a key goal, as elucidated in Fig. 3. Regarding chemical shifts there is, of course, no problem as the location of the TSP resonance is taken by default to be at 0.0 ppm. Then, the positions of all the other resonances in the spectrum are counted with respect to the chemical shift 0.0 ppm of the TSP molecule. On the other hand, finding the peak area is less straightforward. Ordinarily, this is a priori considered to be also an obstacle-free step in signal processing from the MRS literature. The supposed reason for such a stance is that, in a standard nonparametric nonderivative envelope (from the FFT or due to any other estimator), the TSP resonance is viewed as a symmetric, unobstructed singlet, which is, thus, easy to integrate and find its peak area.

However, it has been shown in Ref. [33] that even in the standard nonderivative FFT and FPT processors, the TSP peak is not a lone symmetric resonance. It exhibits the two visible low-lying shoulder satellites around $0.005\, \mathrm{ppm}$ [33]. In order to have a more detailed insight into this matter of practical significance, we present Fig. 3 by giving the spectra in the band [− 0.01,0.01] ppm, surrounding the chemical shift 0.0 ppm of TSP. Herein, panel (a) for $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ shows four visible component spectra reconstructed by the parametric nonderivative FPT. The tallest peak is the TSP resonance at 0.0 ppm. The remaining three resonances are totally covered by the TSP peak. The smaller two of these peaks are nearly symmetric relative to 0.0 ppm and they are very close to $\pm \, 0.005\, \mathrm{ppm}.$ The satellite peak at $0.005\, \mathrm{ppm}$ is wider than its neighbor at $-0.005\, \mathrm{ppm}.$ The third masked peak is broader than these two satellites and it is positioned at about $0.00125\, \mathrm{ppm}.$

All the other lineshapes on panels (b–j) are for the envelope spectra from the nonparametric FPT: nonderivative (b, $m=0$) and derivative (c–j, $1\le m\le 20$). Already the nonderivative envelope (b, $m=0$) is slightly asymmetric and it exhibits the tops of the two side satellites, as in Ref. [33]. However, there is no hint whatsoever about the presence of the third broader and taller peak, which is completely swamped by the much larger TSP resonance. This gives the reason for which the TSP peak area cannot be trusted when computed by means of any of the existing nonparametric nonderivative estimations.

To overcome this hurdle and perform the correct quantification of the TSP resonance by employing shape estimations alone, the reference peak should be fully separated from the underlying three lineshapes. This can be tried with the nonparametric derivative dFPT. In the just analyzed similar case of the water residual, such an approach through $\left| \mathrm{D}_m\mathrm{FPT}\right| _{\mathrm{Tot}}$ met with success in Fig. 1 for $m=4,\, 5$ on panels (g, h), respectively. A similar success is seen to be also recorded for the TSP resonance in $\left| \mathrm{D}_{10,15,20}\mathrm{FPT}\right| _{\mathrm{Tot}}$ in Fig. 3 on panels (h, i, j), respectively. Therefore, perfect quantification of the TSP resonance is possible in Fig. 3 on any of the panels (h–j).

In the nonderivative component spectra from Fig. 3a, the linewidths of the two small hidden satellites are unequal, as noted. Such an occurrence should influence the pace of the peak height enhancements of these two resonances with the increased derivative order m,  according to the experience from Figs. 1 and 2. On panels (c, $m=1$) and (d, $m=2$), the visibility of both satellites is still comparable. However, starting with $m=4$ (e), the broader satellite at 0.005 ppm begins to rapidly fade away, such that it disappears altogether at $m\ge 8,$ e.g. at panels (h–j). On the other hand, the traces of the narrower satellite near − 0.005 ppm can be observed even at $m\le 15$ (i) but, eventually, this peak too vanishes at higher derivatives, as can be observed on panel (j, $m=20$).

As to the wider resonance at 0.00125 ppm, it is clearly delineated at $m\ge 4$ and it persists (albeit as a minuscule peak) even at derivative orders as high as $m=15$ (i) and $m=20$ (j). Above $m=20$ (not shown), this last remainder of the three formerly hidden resonances is completely washed out so that only the TSP peak survives. On panel (c, $m=1$), the broader resonance at 0.00125 ppm is merely a slight shoulder. Subsequently, it develops into an asymmetric peak on panels (d, $m=2$) and (e, $m=4$).

What is important to retain from this analysis is that Fig. 3 illustrates the systematics in the ability of shape estimations by the nonparametric dFPT to tease out the entirely hidden resonances beneath the TSP peak (0.0 ppm), even those from its extremely close neighborhood (0.00125 and ±0.005 ppm). In such situations of very close proximity of resonances, higher-order derivatives in the dFPT are needed, according to Fig. 3, as has also been previously found in our study on $\mathrm{{}^1H\,MRS}$ for breast cancer [74,75,76].

Thus far, we highlight the possibility to use the nonparametric dFPT to deconvolve the compound spectral structures into their constituents, as done in Fig. 1 (the residual water conglomerate), Fig. 2 (the two unassigned peaks, triplet U”(t) and quartet U’(q) near $\mathrm{H_2O}$) as well as in Fig. 3 (the TSP reference resonance). In other words, Figs. 1–3 deal with the most stringent cross-validation of the discussed findings by the nonparametric dFPT. Such a stringency consists of showing that, for the given amalgamated spectral structure, its actual (true, genuine) component lineshapes from the parametric dFPT coincide with the constituents unfolded from the envelopes by the nonparametric dFPT. More such in-depth cross-validations will be reported in the illustrations that follow.

In so doing, the main attention will be devoted to the two recognized cancer biomarkers, lactic acids (1.41, 4.36 ppm) and choline-containing compounds (near 3.20 ppm), alongside their close surroundings, comprised of a number of metabolites that are also of diagnostic relevance. In this vein, let us then analyze Fig. 4 within the band 1.21–1.54 ppm, which includes Lac(d) at 1.41 ppm. Herein, only nonderivative spectra are shown as the components (a, c, parametric FPT) and envelopes (b, d, nonparametric FPT). On the ordinates in panels (a, b), we give the full dynamic range of intensities. On the other hand, the reduced ordinates are on panels (c, d). Since the lactate doublet Lac(d) is enormously dominant, the other resonances are seen to be very small on panels (a, b). Throughout the interval 1.21–1.54 ppm, the components and envelope look quite similar on panels (a, b). The only exception, which is visible even with the nontruncated ordinates, is the presence of some small resonances underneath Lac(d) in the component spectra on panel (a).

To peer into the spectral configuration for searching further information, the ordinates on panels (c, d) are scaled down to 420 au from 8000 au (a, b). Such a scaling amounts to cutting-off most of the top part of Lac(d) to allow the other resonances to pop out. This time, however, the difference between the components on panel (c) and envelope on panel (d) becomes striking. While on panel (b), the doublet Lac(d) appears as completely symmetric, its zoomed version on panel (d) is highly asymmetric, especially on the bottom/base. Moreover, the apparently flat background baseline on panel (b) is markedly elevated on panel (d).

The component spectra from panel (c) indicate that it is the high as well as long tails of Lac(d) that disturb the shape and size of Ala(d), Thr(d) and $\beta -$HB(d) in the envelope from panel (d). This is also true for a smaller unassigned doublet (of an unknown metabolite) centered at 1.3 ppm beneath the Lac(d) tail. On panel (c) for component spectra, this latter doublet is perfectly symmetric and its two peaks are of the same width and height. They are deformed and appear as asymmetric on panel (d), where their lineshapes are of a dispersive-type. On panel (c), the tail heights on both sides of Lac(d) are so strong that they reach $\sim$ 50% and $\sim$ 20% of the intensities of the doublets of Thr(d) and Ala(d), respectively. The tails of Lac(d) contribute heavily to the buildup of the background baseline on panel (d). This background baseline is additionally configured by all the other wide resonances whose existence is hinted by the envelope spectrum on panel (d). Broad spectral structures are usually assigned to macromolecules (lipids, proteins, peptides, fatty acids, etc.). They lift considerably the background baseline, as seen in the envelope on panel (d).

Viewing e.g. one doublet at a time in the set Ala(d), Thr(d) and $\beta -$HB(d) from $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (c), it is obvious that the bottoms of each of the two constituent peaks therein overlap considerably. Of course, this is most pronounced for Lac(d). Depending on the extent of the constructive and/or destructive interference effects, such overlaps among the components can have varied influence on the envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d). Since the magnitude mode is used on panels (c, d), it is the real and imaginary parts of the complex spectra that produce the interference effects. The intensities of the individual peaks from the doublets Ala(d) and $\beta -$HB(d) are approximately comparable when confronting $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (c) with $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d).

This implies that the interference effects are weak. The exception is Thr(d) which is higher on panel (d) than on panel (c). However, this is not necessarily due to a much different interference effect. In $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d), the closeness to Lac(d) surely causes a strong lineshape change of Thr(d). This may cause Thr(d) to be more uplifted than Ala(d) and $\beta -$HB(d) on panel (d). As a result, the top parts of Thr(d) in $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d) and $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (c) are at notably different heights $\sim$ 200 and $\sim$140 au, respectively.

It is especially interesting to consider the two individual peaks from Lac(d) centered near 1.41 ppm. Their bottom parts have a wide overlap in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (c). This overlap is such that the two individual peaks are hardly distinguishable from each other even up to the maximum (420 au) of the scale on the ordinate on panel (c). By contrast, the left and the right peaks in Lac(d) are clearly discerned in $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d) even at $\sim$ 150 au. This testifies to a high degree of destructive interference in formation of the Lac(d) envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d) around 1.41 ppm. The depth of a dip between the two peaks in a doublet can serve as a qualitative measure of the extent of the destructive interference effects. The more notable the destructive interference, the deeper the inter-peak separation in Lac(d) as well as in other doublets.

Panel (c) also reveals that there are some six clearly visible unassigned resonances (lipids and other macromolecules) beneath Lac(d), clustered very near 1.41 ppm. Therein, two sharp doublets and two broad peaks can be seen. The taller doublet is intense. It has about 80% of the strength of Ala(d), which is located near 1.51 ppm. The shorter doublet beneath Lac(d) is twice stronger than the unknown doublet at 1.30 ppm. The two broad and shorter resonances below Lac(d) in the component spectra on panel (c) are observed to occupy quite a significant area. Thus, the six peaks, positioned extremely close to the location of Lac(d), cannot be ignored when assessing the concentration of Lac(d). Being completely swamped by Lac(d) in the envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (d), these six resonances would yield a non-negligible contribution to the peak area of the lactate doublet. This would invalidate quantification of Lac(d) using any nonderivative shape estimators because these cannot separate the six hidden peaks. As such, the ensuing concentration of Lac(d), obtained by nonderivative shape estimations, cannot be taken as a reliable estimate of the true abundance of this recognized cancer biomarker metabolite.

This resembles precisely the circumstances with the water residual (Fig. 1) and the reference TSP molecule (Fig. 3). Therefore, the optimal way out is to rid Lac(d) of its hidden resonances, if the correct quantification is sought not only for this, but also for any other metabolite in a similar situation. For instance, Ala(d) from Fig. 4d hides three other resonances located very near 1.51 ppm, as seen in the overlying component spectra in Fig. 4c. Similarly to Figs. 1–3, derivative signal processing comes to the rescue, when performed by the dFPT as a shape estimator. This important issue of detecting and separating out the hidden resonances beneath e.g. Lac(d) and Lac(q) in derivative envelopes $1\le m\le 4,$ reconstructed by the nonparametric dFPT, will be tackled in Figs. 8 and 9 at 1.39–1.43 and 4.34–4.39 ppm, respectively.

Prior to that, however, we shall consider again the wider band 1.21–1.54 ppm (Fig. 5), but this time for derivative estimations by the parametric and nonparametric dFPT $(1\le m\le 3).$ This will be followed by the Padé-based parametric and nonparametric FPT ($m=0,$ Fig. 6) and dFPT ($1\le m\le 3,$ Fig. 7) focused on the resonant frequencies 0.9–1.12 ppm with the important group of branched-chain amino acids, valine Val(dd), leucine Leu(d,t) and isoleucine Iso(d,t). Finally, the Result Section will be devoted to the choline-containing compounds at 3.17–3.30 ppm, where comparisons are made between the components (parametric FPT, dFPT) and envelopes (nonparametric FPT, dFPT). This part addresses the benign and malignant samples on Figs. 10 ($1\le m\le 4$) and 11 ($1\le m\le 3$), respectively.

Figure 5 compares the components (a, c, e, parametric dFPT) and envelopes (b, d, f, nonparametric dFPT) at 1.21–1.54 ppm for $1\le m\le 3.$ Here, one of the three variants of sequential signal processing from Ref. [33] is explored by scaling only the derivative lineshapes of the dominant resonance Lac(d) with its close proximity. Expectedly, the scaling factors are considerable, as they follow divisions by 25 (a, b, $m=1)$ by 30 (c, d, $m=2$) and by 35 (e, f, $m=3$). This is convenient since the full lineshape of Lac(d), without any truncation, is directly visualized alongside all the other much smaller resonances with their intact (i.e. unscaled) spectral intensities on the ordinates. For the varying derivative order m,  the reduced Lac(d) lineshapes with their close surroundings are drawn in two different colors: green for the components (a, c, e) and cyan for the envelope (b, d, f). The indicated multiplicative factors are sufficient to smoothly merge the Lac(d) lineshapes with the remaining spectra on panels (a–f).

Already with $m=1,$ we see a high level of concordance between components $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (a) and envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (b). This is a beneficial consequence of the background baseline flattening at the onset of derivative estimations, i.e. with the first-order derivative operator, $\mathrm{D_1}.$ As seen in Fig. 4d, the dispersive-like lineshapes of Ala(d), Thr(d) and $\beta -$HB(d) in the nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ are riding high on the elevated tails of Lac(d). However, such severe spectral distortions in Fig. 4d are completely rectified in Fig. 5b by the sole action of the $\mathrm{D_1}$ operator, which brings down the tails of Ala(d), Thr(d) and $\beta -$HB(d) straight to the chemical shift axis. The same occurs with the doublet resonance of the unknown metabolite located at 1.3 ppm.

The component-envelope concordance is further improved by higher derivative orders, as seen in $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (c) and $\left| \mathrm{D_2FPT}\right| _{\mathrm{Tot}}$ (d) as well as in $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp}}$ (e) and $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ (f). In fact, at 1.21–1.54 ppm, the third derivative components $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp}}$ (e, parametric dFPT) and their envelope counterpart $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ (f, nonparametric dFPT) are identical.

The proximity of Ala(d) to Lac(d) points to the possibility of a strong interference of these two doublets. This is indeed confirmed by the nonderivative envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (Fig. 4d) through the considerably deformed lineshape of Ala(d). Such an obstacle is significantly mitigated in the derivative envelopes from Fig. 5. The effect is so striking that the small sharp mini doublet centered at 1.515 ppm, appearing as completely overlaid by Ala(d) in the component spectra from $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (Fig. 4c), is distinctly separated out in the envelopes $\left| \mathrm{D_2FPT}\right| _{\mathrm{Tot}}$ (Fig. 5d) and $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ (Fig. 5f). This was made possible by the derivative-induced localization of the bottoms of not only Lac(d), but also of Ala(d). A narrower base or bottom of Ala(d) itself facilitated much of the pulling out of the smaller doublet near 1.515 ppm in $\left| \mathrm{D_{2,3}FPT}\right| _{\mathrm{Tot}}$ (Figs. 5d, f), respectively.

The mini doublet at 1.515 ppm is also masked by Ala(d) in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (Fig. 5b). The peak heights of the two resonances in the mini doublet seem to be equal in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (Fig. 5a). Nevertheless, this does not necessarily mean that their linewidths are identical. In fact, the contrary is true. The evidence is in $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp,\,Tot}}$ (Figs. 5c, d) and $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp,\, Tot}}$ (Figs. 5e, f). For example, in $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp,\, Tot}}$ (Figs. 5e, f), the right peak in the mini doublet near Ala(d) is about twice taller than its left neighbor.

Hence, there is no linewidth uniformity in this particular example nor among many other resonances across the entire Nyquist range. This invalidates the usual practice in the MRS literature, where many reported studies assume the same linewidths for all resonances in analyzed spectra. Thus, in e.g. Ref. [53], at variance with the present exact signal processing, the uniform linewidth of 1 Hz has roughly been assessed for all the resonances in the Fourier spectra computed with the same type of FIDs considered in the present work.

It is interesting that in Ref. [85], the same two small doublets, one at 1.30 ppm near Thr(d) and the other at 1.515 ppm near Ala(d), have been detected in samples of cerebrospinal fluid (CSF) and assigned to the $[\mathrm{{}^{13}C}]$Lactic acid molecules. This assignment has not presently been extrapolated from the CSF to the ovarian cyst fluid. The reason is the lack of knowledge about a possible metabolic pathway producing the $[\mathrm{{}^{13}C}]$Lactic acid molecules in the ovarian cyst fluid.

As discussed, the components in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (Fig. 4c) clearly show six resonances beneath Lac(d), the two sharp doublets (one taller, the other shorter) and the two broader, lower peaks. They were all distinctly visible because the Lac(d) lineshape was cut-off at 420 au in Fig. 4c. However, by retaining the full Lac(d) profile, up to its intact peak height at about 6000 au, among these six peaks only the taller sharp doublet shows up in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (Fig. 4a).

In Fig. 5, we opted to keep the whole lineshape of Lac(d). Therefore, here too, it is expected to have considerable masking for the six resonances clustered very near 1.41 ppm. This indeed occurs since out of these six components only the said taller sharp doublet can be clearly seen in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (a) as lying on the bottom of Lac(d). In $\left| \mathrm{D_{2,3}FPT}\right| _{\mathrm{Comp}}$ (c, e), respectively, this doublet becomes narrower and taller relative to panel (a), so that its lineshape is glued to the sides of the Lac(d) profile and, hence, poorly visible. It would then be instructive to separately zoom into a small band around 1.41 ppm to better visualize some of the masked sub-peaks of Lac(d), as shall be done in Fig. 8 for $0\le m\le 4.$

In Fig. 5, we discussed the background baseline, peak heights and the bottom parts of the resonances at 1.21–1.54 ppm. It now remains to explicitly spell out the pertinent interpretation and usefulness of the analyzed results. Relative to the nonderivative spectra $\left| \mathrm{FPT}\right| _{\mathrm{Comp, \,Tot}}$ (Figs. 4c, d), the observed flattened background baseline, tightened bottoms of resonances and their enhanced peak heights in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp,\, Tot}}$ (Figs. 5a, b), respectively, indicate that both resolution and SNR are greatly improved in this frequency band already by the application of the first derivative operator $\mathrm{D}_1.$ Moreover, these accomplishments are further consolidated in $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp,\, Tot}}$ (Figs. 5c, d) and $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp,\, Tot}}$ (Figs. 5e, f), respectively. It is pertinent to recall here that the magnitude first derivative envelope and the real (absorptive) part of a complex pure Lorentzian profile have the same linewidth [76].

Overall, the nonparametrically reconstructed envelope $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ (Fig. 5f) is found to completely collapse onto the corresponding component spectra in $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp}}$ (Fig. 5e), predicted by the parametric dFPT. This confirms the quantification capabilities of the nonparametric dFPT. Such a type of perfect agreement between the parametric and nonparametric dFPT persists at frequency bands other than the illustrative range 1.21–1.54 ppm from Fig. 5. Thus, as another important example, a further analysis presented on Figs. 6 and 7 will deal with band 0.91–1.12 ppm, which contains the branched-chain amino acids Val(dd), Leu(d,t) and Iso(d,t).

Comparisons of the Padé-based “parameter” and “shape” estimations can be made using the parametric and nonparametric versions, respectively, for either the nonderivative or derivative signal processings or both. Moreover, such comparisons can be performed on two levels. One is using the components (parametric FPT, dFPT) and envelopes (nonparametric FPT, dFPT), as in Figs. 2–5. The other involves only the envelopes reconstructed by the nonparametric as well as the parametric FPT and dFPT. We explicitly verified within the derivative orders $0\le m\le 3,$ that the envelopes by the parametric dFPT are identical (down to the slightest spectral detail) to the envelopes by the nonparametric dFPT. Therefore, there is no need for presenting separate graphs comparing only shape estimations by the parametric and nonparametric FPT and dFPT since the parametric envelopes would repeat the nonparametric envelopes for $m=0$ (Figs. 4b, d) and $1\le m\le 3$ (Figs. 5b, d, f).

This finding is yet another useful internal level of cross-validation. Such a test is important because the presently reconstructed envelopes stem from the two different Padé algorithms. Namely, the envelope $P_K/Q_K$ in the nonparametric nonderivative FPT becomes available as soon as the expansion coefficients $\{p_r,q_s\}\, (0\le r,s\le K)$ of the numerator and denominator polynomials $\{P_K,Q_K\},$ respectively, are extracted from the input FID data points. Then, subjecting such an envelope $P_K/Q_K$ to the $\mathrm{D}_m$ operator yields the $m\,$th derivative envelope $\mathrm{D}_mP_K/Q_K=(\text{ d }/\text{d }\nu )^mP_K/Q_K$ in the nonparametric dFPT.

In the parametric FPT, the explicit solution of the quantification problem (finding the peak positions, heights, weights, phases) of all the K resonances is found first. Afterward, using these peak parameters, the K component spectra are generated. Summing all such components and adding the baseline constant $p_0/q_0$ produces the nonderivative envelope (13) in the parametric FPT. Its transformation by means of the $\mathrm{D}_m$ operator yields the $m\,$th parametric derivative envelope. The application of the derivative transform $\mathrm{D}_m$ within the nonparametric and parametric dFPT proceeds through the usage of the two entirely dissimilar mathematical expressions in Eqs. (9) and (17), respectively.

Demonstration of the exact agreement between the nonparametric and parametric dFPT (Figs. 1–5) boosts confidence in the reliability (accuracy, robustness) of the versatile Padé-performed estimations not only throughout MRS, but also in the whole field of signal processing. Moreover, the found identical envelopes from the nonparametric and parametric dFPT retroactively confirm, after the appropriate scaling [76], the exactness of all the K peak parameters (position, width, height of each peak) reconstructed by the parametric nonderivative FPT.

By definition, the nonparametric nonderivative FPT for envelope $P_K/Q_K$ can estimate only the lineshape profiles of resonances, but not their peak parameters in an autonomous manner. In principle, such a nonparametric envelope implicitly contains all the K resonances. In practice, however, often many of these resonances are tightly overlapped when using any encoded FID. This makes them partially or completely invisible. What the derivative transform does in the envelope $(\text{ d }/\text{d }\nu )^mP_K/Q_K$ from the nonparametric dFPT is to split apart these overlaps by separating out the K individual resonances. Eventually, for certain values of m (mostly of lower orders), all the K constituent resonances from the envelope in the nonparametric derivative dFPT become not only visible (throughout their lineshapes, from the bottom to the top), but also coincident with the K component spectra due to the parametric derivative dFPT.

Such a coincidence means that the nonparametric derivative dFPT (a shape estimator at the onset of the analysis) converts itself (at the analysis end) to a parameter estimator. It finishes its work by unfolding all the true components from the processed nonparametric envelope without explicitly solving the quantification problem per se (and without fitting either). Hence, in the Padé-conceived signal processing, besides the parametric nonderivative FPT, there are two more equivalent and conceptually as well as algorithmically very different quantification-equipped strategies: the nonparametric and parametric derivative dFPT. Proofs, through Figs. 1–5, that their reconstructions of all the physical resonances are identical for an encoded FID represents the most stringent scrutiny in cross-disciplinary signal processing aimed at super-high resolution. By way of examples, the illustrations in Figs. 1–5 refer to the chosen specific frequency intervals. However, the same benefit from the nonparametric dFPT is also gained for any other frequency band throughout the entire Nyquist interval.

Up to now, we made several exhaustive comparisons, all within the versatile Padé signal processings. We shall continue with this type of internal comparisons in the Padé-based methodologies in Figs. 7–11. In the meantime, we will confront the Padé and Fourier processings in Fig. 6 with the prime focus on derivative estimations. Since, by default, the Fourier envelopes rely upon shape estimations alone, the main emphasis in Fig. 6 for 0.91–1.12 ppm $(m=0,\, 4)$ is on the matching competitor, the Padé nonparametric processor. Additionally, also plotted in this figure for m = 0 and $m=4$ are the corresponding gold standard components spectra from the parametric FPT and dFPT, respectively. The panels to be scrolled down are configured according to the scheme: components by the parametric FPT (a, $m=0)$ and dFPT (c, $m=4$), envelopes by the nonparametric FPT (b, $m=0$) and dFPT (d, $m=4$). The envelope by the derivative Fourier transform dFFT is on panel (e, $m=4$). The nonderivative FFT is verified to give the same envelope as the nonderivative FPT at any sweep frequency. Therefore, there is no need to plot the envelope of the nonderivative FFT in Fig. 6 nor elsewhere.

We chose the interval 0.91–1.12 ppm here because the ’spectral crowding’ problem was quoted in Ref. [53] as the main reason for not being able to quantify (through fitting the FFT envelope by some adjustable Lorentzians) the resonances containing the leucine and isoleucine metabolites at 0.9125–0.975 ppm. This minuscule frequency range is congested with a dozen of tightly overlapped resonances, including Leu(d,t) and Iso(t). Such an obstacle with the leucine and isoleucine metabolites is also seen in Fig. 6b, where the resonances at 0.9125–0.975 ppm cannot be quantified by the nonderivative estimation $(m=0)$ of any nonparametric signal processor.

The spectral content displayed on Fig. 6, in the upfield direction (0.975–1.12 ppm), is metabolite-rich, as well. It is filled with several resonances, including those assigned to the known metabolites: 2-hydroxyisovaleric acid 2-HV(d), valine Val(dd), isoleucine Iso(d), 3-methyl-2-oxovaleric acid 3-Met-2-OV(d) and 2-oxoisovaleric acid 2-OV(d) [86]. However, in $\left| \mathrm{FPT}\right| _{\mathrm{Comp}}$ (a), the doublets 2-HV(d), 3-Met-2-OV(d) and 2-OV(d) near 0.98, 1.09 and 1.12 ppm, respectively, are completely masked. Such a masking is due to the tails of broad and low-lying resonances as clear from the thick ensemble of the almost horizontal lineshapes beneath Val(dd), Iso(d,t) and Leu(d,t). One of these wide resonances on panel (a) is centered at about 1.05 ppm and extended over the entire range 0.9–1.12 ppm (as well as beyond, up to 1.6 ppm).

In $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (b), at the mentioned chemical shifts 0.98, 1.09 and 1.12 ppm, barely some faint hints can be surmised about the presence of 2-HV(d), 3-Met-2-OV(d) and 2-OV(d), respectively. Insufficient resolution by nonderivative estimations is caused by the overlap of resonances as well as by an elevated background baseline. The intense and far-extending tail of Lac(d) also contributes heavily to the high background baseline in $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (b).

However, as per panels (b, d, f) of Fig. 5, in the nonparametric envelopes $\left| \mathrm{D}_m\mathrm{FPT}\right| _{\mathrm{Tot}}$ for $1\le m\le 3,$ the Lac(d) tail is flattened and the underlying resonance overlaps are considerably reduced. Such simultaneous improvement of resolution and SNR is further refined in the nonparametric envelope $\left| \mathrm{D_4FPT}\right| _{\mathrm{Tot}}$ (Fig. 6d). Crucially, in Fig. 6, the individual resonance lineshapes in the envelope $\left| \mathrm{D_4FPT}\right| _{\mathrm{Tot}}$ (d) from the nonparametric dFPT are identical to the true component spectra $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp}}$ (c) reconstructed by the parametric dFPT. However, the Padé and Fourier estimations by the dFPT and dFFT, respectively, are in total disharmony. Specifically, for the fourth order derivative, the Fourier envelope $\left| \mathrm{D_4FFT}\right| _{\mathrm{Tot}}$ (e) flagrantly fails to reproduce the corresponding exact prediction provided by the Padé result $\left| \mathrm{D_4FPT}\right| _{\mathrm{Tot}}$ (d, nonparametric dFPT), which is confirmed by $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp}}$ (c, parametric dFPT).

The obstacle with the dFFT is in an unfavorable result of the application of the derivative operator $\mathrm{D}_m\, (m\ge 1),$ which introduces a time-dependent power function $\sim \, t^m$ multiplying the given FID as seen in Eq. (5). Such a weight function accentuates noise from the encoded FIDs and this causes severe information loss. The consequence of such a fundamental failure is also reflected in $\left| \mathrm{D_4FFT}\right| _{\mathrm{Tot}}$ (Fig. 6e) through drastically decreased resolution and SNR, a diametrically opposite direction of the expectation from proper derivative signal processing, such as the dFPT.

Figure 7, while also dealing with the band 0.9–1.12, uses the dFPT for $1\le m\le 3$ to verify the validity of the nonparametric envelopes by means of comparisons with the corresponding parametrically reconstructed component spectra. The components (parametric dFPT) are on panels (a, $m=1$), (c, $m=2$) and (e, $m=3$), whereas the envelopes (nonparametric dFPT) are on panels (b, $m=1$), (d, $m=2$) and (f, $m=3$). Unrestricted spectral intensities are employed on all the ordinates. This figure is a complement to Fig. 6, where only $m=0$ and $m=4$ are considered in the nonparametric and parametric nonderivative and derivative Padé estimations.

In terms of visibility of the totality of the resonances, the first derivative components from $|\mathrm{D_1FPT}|_{\mathrm{Comp}}$ (Fig. 7a) are by far more transparent than their nonderivative counterparts in $|\mathrm{FPT}|_{\mathrm{Comp}}$ (Fig. 6a). As discussed with Fig. 6a, the background lineshape therein completely covers several resonances, including 2-HV(d), 3-Met-2-OV(d) as well as 2-OV(d) and significantly blurs some other resonances within 0.9-0.975 ppm. All that strong masking is totally erased from $|\mathrm{D_1FPT}|_{\mathrm{Comp}}$ (Fig. 7a), where none of the visible resonances appear to be obstructed by the background baseline, which is glued to the chemical shift axis. In particular, in $|\mathrm{D_1FPT}|_{\mathrm{Comp}}$ (Fig. 7a), the formerly hidden doublets 3-Met-2-OV(d) and 2-OV(d) now appear distinctly. Therein, a tiny hint points to the presence of 2-HV(d), as well.

This situation is reflected directly in the first derivative envelope despite its nonparametric reconstruction via $|\mathrm{D_1FPT}|_{\mathrm{Tot}}$ (Fig. 7b), which progressed enormously with respect to $|\mathrm{FPT}|_{\mathrm{Tot}}$ (Fig. 6b). The level of the background baseline is high in the envelope $|\mathrm{FPT}|_{\mathrm{Tot}}$ (Fig. 6b), where all the resonances are deformed. By contrast, the background baseline of the envelope $|\mathrm{D_1FPT}|_{\mathrm{Tot}}$ (Fig. 7b) is very near the chemical shift axis and, moreover, all the resonances therein are straightened upward. In $|\mathrm{D_1FPT}|_{\mathrm{Tot}}$ (Fig. 7b), some resonances within the sub-band 0.91–1.12 ppm are slightly elevated above the chemical shift axis because of the tight overlaps of the associated components from $|\mathrm{D_1FPT}|_{\mathrm{Comp}}$ (Fig. 7a).

These overlaps from $|\mathrm{D_1FPT}|_{\mathrm{Tot}}$ (Fig. 7b) are reduced in $|\mathrm{D_2FPT}|_{\mathrm{Tot}}$ (Fig. 7d) and $|\mathrm{D_3FPT}|_{\mathrm{Tot}}$ (Fig. 7f), where most resonances are sharply separated, including 2-HV(d), 3-Met-2-OV(d) and 2-OV(d). Crucially, the envelopes $|\mathrm{D_2FPT}|_{\mathrm{Tot}}$ (Fig. 7d) and $|\mathrm{D_3FPT}|_{\mathrm{Tot}}$ (Fig. 7f) are in excellent agreement with the components in $|\mathrm{D_2FPT}|_{\mathrm{Comp}}$ (Fig. 7c) and $|\mathrm{D_3FPT}|_{\mathrm{Comp}}$ (Fig. 7e), respectively. This finding confirms the veracity of the predictions of the exact components by the nonparametric dFPT.

Next, using the FPT and dFPT with $0\le m\le 4,$ we will zoom into the very narrow frequency bands of the groups of recognized cancer biomarkers, lactates in Figs. 8 (1.39–1.43 ppm) as well as Fig. 9 (4.34–4.39 ppm) for the malignant sample and cholines (3.17–3.30 ppm) in Figs. 10 (benign) and 11 (malignant). Here too, the derivative signal processing is tasked with separating the overlapped peaks and unraveling the resonances that are potentially present albeit invisible in the associated nonparametric nonderivative envelopes. The general theme of Figs. 8–11 is validation of the envelopes predicted by the nonparametric dFPT through their comparisons with the component spectra from the parametric dFPT. In these four figures, the components and envelopes are on the left and right columns, respectively.

As discussed with the nonderivative component spectra from Fig. 4c, the scaled ordinate (truncated at 420 au) made six peaks (lipids and other macromolecules) plainly visible below the very wide lineshape of the lactate doublet, Lac(d). On the other hand, for the full scale on the ordinate (extended up to 8000 au) in Fig. 4a, among these six peaks, only the two tallest resonances could be seen beneath the two nonderivative component peaks of Lac(d). Keeping the intact (non-shortened) ordinates for intensities on the ordinate in Fig. 5, it was hard to follow the development of the overlapping doublets hidden within Lac(d) in derivative spectra for $1\le m\le 3$ at 1.21–1.54 ppm. This was experienced for the components and envelope alike. However, even with the full dynamic range of intensity on the ordinates, spectral visibility could still be judiciously ameliorated by considering e.g. a smaller spectral window, as just announced.

This is exemplified in Fig. 8 for Lac(d) by using a narrow frequency band 1.39–1.43 ppm of length 0.04 ppm, shown in a layout which is, however, widely elongated on the chemical shift axis. Figure 5 used the same allocated physical space across the full page for the chemical shift axis as does Fig. 8, but for more than eight times wider window (1.21–1.54 ppm) of length 0.33 ppm. The layout in Fig. 8 leads to a clear visualization for the derivative lineshapes $(1\le m\le 4)$ of the components (a–e) and envelopes (f–j). The nonderivative spectra $(m=0)$ are on panels (a, f), whereas their derivative counterparts are for $m=1$ (b, g), $m=2$ (c, h), $m=3$ (d, i) and $m=4$ (e, j).

In the nonderivative components $(m=0),$ the two constituent peaks of the lineshape for Lac(d) on panel (a) are wide and, thus, heavily overlapped. Their interference and long tails notably lift the background baseline in the nonderivative envelope (f). This latter envelope has no trace whatsoever from the two small peaks under the umbrella of Lac(d) in the nonderivative components on panel (a). However, the situation is visibly changed already with the first derivative spectra (b, g). The manifestations of the changes in the components and envelopes $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (b) and $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (g), respectively, are multi-layered.

The peak widths in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp,Tot}}$ (b, g, $m=1$) are narrowed and the peak heights are concomitantly enhanced relative to $\left| \mathrm{FPT}\right| _{\mathrm{Comp,Tot}}$ (a, f, $m=0$). Moreover, the Lac(d) tails elevated on panels (a, f) are now significantly lowered in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp,Tot}}$ (b, g). This implies a reduced background baseline in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp,Tot}}$ (b, g). Combined together, these achievements of the $\mathrm{D}_1$ operator translate into improved resolution and SNR in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp,Tot}}$ (b, g, $m=1$) with respect to $\left| \mathrm{FPT}\right| _{\mathrm{Comp,Tot}}$ (a, f, $m=0$). Nevertheless, the two small peaks are still fully covered by the large resonances of Lac(d) in $\left| \mathrm{D_1FPT}\right| _{\mathrm{Comp}}$ (b, $m=1$). In particular, their lineshapes are not touching either of the two Lac(d) component peaks. Despite this circumstance, these two small peaks still appear in the envelope $\left| \mathrm{D_1FPT}\right| _{\mathrm{Tot}}$ (g, $m=1$) as the clear shoulders on the bottoms of each of the two Lac(d) peaks, in sharp contrast to $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}$ (f, $m=0$).

Lineshape changes are continued to be manifested in the second derivative spectra $(m=2)$ in the direction of gradual, systematic and simultaneous narrowing of the peak widths and the consequent increasing of the peak heights. As a result, the lineshapes of the two small peaks and Lac(d) are partially intertwined in the component spectra $\left| \mathrm{D_2FPT}\right| _{\mathrm{Comp}}$ (c, $m=2$). This closeness of the lineshape profiles produced a slightly better delineation of the two small shouldered peaks in the envelope $\left| \mathrm{D_2FPT}\right| _{\mathrm{Tot}}$ (h, $m=2$).

Such a progressive trend is further pursued by the third and fourth derivative spectra $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp,Tot}}$ (d, i, $m=3$) and $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp,Tot}}$ (e, j, $m=4$), respectively. Thus, the component lineshapes of the upper parts of both of the two small peaks become separated from Lac(d) in $\left| \mathrm{D_3FPT}\right| _{\mathrm{Comp}}$ (d, $m=3$). The right small peak in the associated envelope from $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ (i, $m=3$) also begins its sharper delineation relative to Lac(d). However, in $\left| \mathrm{D_3FPT}\right| _{\mathrm{Tot}}$ (i, $m=3$) the corresponding smaller left peak is still only a shoulder to Lac(d). The split between each of the two Lac(d) resonances and the two smaller peaks is widened in the fourth derivative spectra $\left| \mathrm{D_4FPT}\right| _{\mathrm{Comp,Tot}}$ (e, j, $m=4$). This allows a clearer distinction of most of the upper parts of both smaller peaks, not only in the components on panel (e), but also in the envelope on panel (j). As a matter of fact, the envelope on panel (j) and the components on panel (e) are coincident in the major parts of their lineshape profiles. With derivatives of the order $m>4$ (not shown), all the four peaks are completely separated down to the chemical shift axis in a similar manner as explicitly demonstrated in e.g. Figs. 1 and 3.

The evolution of the linewidths and heights of the component spectra (a–e) from the two small peaks in Fig. 8 is in itself important to follow and interpret since this too transcends the basic principle of derivative signal processing. On panel (a) of Fig. 8 for the nonderivative components $(m=0),$ these two small peaks appear as if they were of the nearly equal size (area) with almost the same widths and heights, as far as such an observation can be made by the naked eye. This is also very closely the case with the corresponding first derivative components (b, $m=1$), since one cannot tell the difference between the lineshapes for the two small peaks. However, already their second derivative components (c, $m=2$) indicate that the small right peak is slightly taller than its left neighbor. This discrepancy is further enhanced in the third derivative components (d, $m=3$).

Finally, in the fourth derivative components (e, $m=4$) in Fig. 8, the left peak is roughly about 40% shorter than the right peak. Such a large difference in the peak heights on panel (e, $m=4$) retrospectively shows that the visual impression of the nearly equal nonderivative peak widths (a, $m=0$) was deceptive. However, as the derivative order is gradually augmented from $m=0$ (a) to $m=4$ (e), the existent initial tiny difference in the nonderivative peak widths became most obvious in the third (d) and fourth (e) derivative components of the two small unassigned peaks. They are faithfully replicated in the nonparametrically computed envelope on panel (j).

This shows that the derivative transform $\mathrm{D}_m$ within the nonparametric dFPT can act, depending on the value of m,  as an unprecedentedly sensitive detector of even the slightest differences in the peak widths of resonances (i.e. in the spin-spin relaxation times of the associated metabolites). It is like a specially designed “instrument” or a probe, which is able to ’visit’ and detect the sub-structures that are otherwise invisible to other tools. Here too, the components due to the parametric dFPT approve the correctness of the findings though the envelopes from the nonparametric dFPT.

It should be noted that, despite the clearer emergence of the two smaller peaks with the increased value of the derivative order m,  the two individual peaks in the lactate doublet Lac(d) have the same intensity in the components and the corresponding envelope for one given row of Fig. 8 taken at a time. Of course, these two peaks grow with augmented m,  but they maintain almost the same height implying that they are of the nearly equal widths.

Figure 9 is on the lactate quartet Lac(q) around 4.34–4.39 ppm of length 0.05 ppm. Therein, the two middle large peaks and the two smaller outermost peaks constitute the lactate quartet, Lac(q). Here too there are two small peaks (possibly lipids) beneath the two central peaks of Lac(q). Theoretically, the intensities of the four peaks in Lac(q) should be 1:3:3:1 (the Pascal rule) [78, 79]. This is only approximately true in the nonderivative spectra of both the components from panel (a) and envelope (f). Therein, the four peaks of Lac(q) have the height ratios 500:1625:1625:500 au. The same height of the middle two peaks of Lac(q) exceeds the theoretically expected value 1500 au by 125 au. Interestingly, the heights of the two small non-lactate peaks beneath the two central peaks of Lac(q) are also about 125 au in the nonderivative components from panel (a, $m=0$).

It is also seen that the two small non-lactate peaks are of unequal widths. Here, the left peak is wider than the right peak and such a relation should dictate an unequal growth pace of their peak heights. This is already clear in the first derivative components from panel (b), where the right non-lactate peak is taller, but neither peak touches the walls of the two central Lac(q) resonances. In the second, third and fourth derivative non-lactate components from panels (c, d, e), the height of the right peak relative to that of the left peak is larger by a factor of 2, 6 and 10, respectively. During the development of these two component resonances for $0\le m\le 4$ (a–e), the smaller non-lactate peak remained always fully covered by the left central peak of Lac(q) from which it eventually gets separated for higher-order derivatives, $m\ge 5$ (not shown).

On the other hand, the right taller non-lactate component peak kept getting closer to the wall of the right central peak of the lactate quartet for $m=2$ (c) and $m=3$ (d) such that, finally, it begins to separate itself from the nearest Lac(q) peak for $m=4$ (e). This is also directly evidenced in the fourth derivative envelope (j) for the right taller non-lactate peak, which is seen to clearly emerge therein. However, for $0\le m\le 3,$ the right non-lactate peak remained masked by Lac(q) in the envelope spectra (f–i). At the same time, the left non-lactate peak is invisible on the right column for the envelopes in all the panels (f–j, $0\le m\le 4$). For this particular peak to show up in envelope spectra, higher derivatives are needed, as we checked. By comparison, the left non-lactate peak in Fig. 8 for Lac(d) showed up in the fourth derivative. This occurred because of more favorable linewidth relations in Fig. 8 that allowed the left non-lactate peak to escape the lineshape umbrella of Lac(d).

Scrolling down the components (a–e) and envelopes (f–j) in Fig. 9, it is seen that the heights of the two outermost smaller peaks of Lac(q) very well maintained their equality in both the components and envelopes for one row considered at a time. In the case of the two inner taller peaks of Lac(q), their peak heights are only slightly different for $m=0$ (a, f) and $m=1$ (b, g), but notably unequal for $m=2$ (c, h), $m=3$ (d, i) and $m=4$ (e, j). It might be that the presence of the taller non-lactate peak, through destructive interference, weakens the right central resonance of Lac(q). This is one potential explanation. The other possibility could be that in the two inner resonances of Lac(q), the right peak is slightly wider than the left peak already in the nonderivative spectra (a, f). This then could exacerbate the difference between the peak heights of the two central resonances of Lac(q) with increase in the derivative order m. The sought intensity ratio 1:3:3:1 assumes equal peak widths, but for unequal peak widths, the corresponding peak area ratios should be used to check the Pascal rule, as mentioned [78, 79, 83, 84].

It should, however, be emphasized that these and other similar theoretically expected spectral intensity ratios, contained in the Pascal triangular table, could be confirmed with NMR spectrometers in chemical laboratories using a set of the purchased pure metabolite samples. However, in medical diagnostics, due to various uncertainties in FID encodings by MRS, and because of very complex interplay among many metabolites (thousands) present in samples from human tissues/biofluids, deviations from such anticipated ratios occur regularly, as is presently the case.

Finally, at 3.17–3.30 ppm, we consider the choline-containing compounds comprised of free choline Cho, phosphocholine PC and glycerophosphocholine GPC. For this purpose, we show the nonparametric and parametric FPT and dFPT for the benign (Fig. 10, $1\le m\le 4$) and malignant (Fig. 11, $1\le m\le 3$) samples. Both cases have also been analyzed in Ref. [33] by using only the nonparametric FPT and dFPT. It would be important to see how the findings from Ref. [33] fare with the present results, especially on the parametric dFPT. This is the subject of Figs. 10 and 11.

Despite the narrowness of this frequency band of length 0.13 ppm, besides the three cholines, there should be some other known metabolites, including phosphoethanolamine PE, beta-glucose $\beta -$Glc, taurine Tau, myo-inositol m-Ins, etc. [33]. Moreover, very near Cho(s), there is also an unassigned singlet peak U(s) at 3.19 ppm in the derivative envelopes for $m\ge 1$ (absent for $m=0$) from the nonparametric dFPT found in Ref. [33] with the same presently used FID (malignant sample). However, for the benign sample, the Padé nonparametric envelopes (nonderivative and derivative alike) from Ref. [33] do not contain this unknown U(s) peak and, moreover, none of the three cholines therein is appreciable. By contrast, for the malignant sample, the intensities of the Cho(s), PC(s) and GPC(s) resonances are considerable as has been detected in Ref. [33].

It would be important to try to assign U(s) to a known metabolite. In Ref. [33], it has been argued that this metabolite could be e.g. {5,6}-dihydrothymine (DHT), which as a doublet or a multiplet resonates at 1.19, 2.80, 3.19 and 3.50 ppm [86]. Another potential candidate for U(s) could be carnitine ester, which is a singlet resonance at 3.19 ppm [87] (for the significance of the pioneering study [87], see the Editorial comment [88]). Note that within the band 3.17–3.30 ppm from Figs. 10 and 11, carnitine has been reported to resonate as a singlet in ovarian cyst fluid (3.23 ppm [53]), in serum and blood plasma (3.21 ppm [87]) as well as in cerebrospinal fluid (3.22 ppm [85]). A biochemical analysis is needed to determine whether the ovarian epithelial cells could synthesize the DHT and/or carnitine metabolites, resonating in the nearest proximity of 3.19 ppm, so that the unknown singlet resonance U(s) could have an assignment with certainty.

Over the decades now, the in vivo $\mathrm{{}^1H\, MRS}$ literature with clinical scanners (1.5, 3T) reported mostly the total choline compound (tCho), with the unresolved contributions from the Cho, PC and GPC resonances. Yet, e.g. the PC resonance has been, and still is, considered as one of the recognized cancer biomarkers for brain [34,35,36], prostate [37,38,39,40,41,42,43,44], breast [45,46,47,48,49], ovary [50,51,52,53,54,55,56,57] and cervix [58,59,60,61,62]. There are two main reasons for this unenviable situation regarding tCho. First, FIDs encoded by in vivo $\mathrm{{}^1H\, MRS}$ at clinical low-field scanners are noisy and the corresponding spectra are congested with many tightly overlapping resonances. Second, for analyses and interpretations of such measured data in the great majority of the reported studies, a low-resolution-noise-preserving estimator, the customary linear nonderivative FFT has been employed. The FFT describes only the forms of the spectral lineshapes with no autonomous capability to quantify resonances in the examined envelopes. To attempt to quantify the uninformative Fourier envelope, some ambiguous and subjective fitting techniques are utilized for decades throughout the MRS literature [89,90,91,92,93,94,95,96,97].

However, there ought to be some other more appropriate mathematical methods, still within shape estimations alone for FIDs encoded by either in vivo or in vitro $\mathrm{{}^1H\, MRS}$ at low or high magnetic fields with clinical scanner or spectrometers, respectively. The most adequate example for such sought signal processors is the nonparametric derivative dFPT. This super high-resolution, noise-suppressing, quantification-capable estimator has recently been used to objectively and unequivocally process the FIDs encoded by $\mathrm{{}^1H\, MRS},$ both in vivo (1.5, 3T) [31, 32] and in vitro (14.1T) [33]. Therein, the nonparametric dFPT has robustly and accurately visualized and quantified a large number of resonances, including the clearly separated Cho, PC and GPC peaks.

Presently, the usage of the parametric dFPT complements and builds on the past work with the nonparametric dFPT [33] for processing the same FIDs encoded by in vitro $\mathrm{{}^1H\, MRS}$ at a Bruker spectrometer operating at 600 MHz ($B_0\approx 14.1$T) [53]. As emphasized, the goal of using the parametric dFPT in the problem under study is to cross-validate the associated reconstructions by nonparametric dFPT reported in Ref. [33]. In the preceding nine figures, when dealing with e.g. the lactate biomarker, such abundant cross-validations have successfully passed the test of checking whether the envelopes from the nonparametric dFPT could collapse onto the associated components due to the parametric dFPT for some low derivative orders $(m\le 4).$ It remains now to check in Figs. 10 and 11 whether a matching type of accord between components (parametric dFPT) and envelopes (nonparametric dFPT) might be feasible for the choline-containing compounds also for some low-order derivatives, e.g. $m\le 4.$

In Fig. 10 for the benign sample, the Cho(s) and GPC(s) peaks are very weak in both the components (a–e) and envelopes (f–j) from the parametric and nonparametric Padé estimations, respectively. Moreover, the size of the PC(s) resonance is also very small. On the other hand, it is seen throughout Fig. 10 that the three strongest resonances are those assigned to Tau(t), m-Ins(t) and $\beta -$Glc(dd). Here, the stated multiplicity of these three resonances are the theoretical predictions. Such predictions are only partially visualized in the nonderivative components on panel (a, $m=0$). For example, the three peaks within Tau(t) can be spotted in the entire left column for the component spectra on panels (b, $m=1$), (c, $m=2$), (d, $m=3$) and (e, $m=4$).

In the nonderivative envelope on panel (f), the taurine triplet is not resolved and only a single peak appears therein with a broad base and a slight shoulder on the right hand side. On panel (j, $m=4$) for the fourth derivative envelope, the mentioned shoulder develops into a well-delineated peak, one of the three constituents of Tau(t). A gradual progress of this shoulder in the derivative envelopes can be followed though the three preceding panels (g, $m=1$), (h, $m=2$) and (i, $m=3$). In the derivative envelopes, the left shoulder of the central peak in Tau(t) is slightly hinted first on panel (i, $m=3$). This latter shoulder eventually becomes a clear peak as the third constituent of Tau(t) in the derivative envelope on panel (j, $m=4$).

The double doublet resonance $\beta -$Glc(dd) begins its delineation with two clear singlets in the nonderivative envelope on panel (f, $m=0$). Gradually, it develops into two doublets on panels (g, $m=1$), (h, $m=2$), (i, $m=3$) and (j, $m=4$). A similar delineation within $\beta -$Glc(dd) proceeds with the component spectra on panels (b, $m=1$), (c, $m=2$), (d, $m=3$) and (e, $m=4$). With the m-Ins(t) resonance, the central peak is clearly visualized in the components from (a–e) and envelopes (f–j), but therein the two smaller side peaks are barely noticeable.

One of the reasons for the distortions of the lineshape for the nonderivative envelope (f, $m=0$), especially near $\beta -$Glc(dd), GPC and PC, is rooted in the nonderivative components on panel (a). Such spectral deformations are caused by interference of densely packed resonances that include two broad low-lying peaks (lipids) centered near 3.23 and 3.24 ppm. These two broad peaks completely overlay the PC(s) and GPC(s) resonances in the nonderivative component spectra from panel (a, $m=0$). The fact that the PC(s) and GPC(s) peaks are clearly visible in the nonderivative envelope (f, $m=0$) can be attributed to destructive interference.

The two spread-out peaks, around 3.23 and 3.24 ppm are strongly reduced in the first-derivative components on panel (b, $m=1$) and this allowed the PC(s) and GPC(s) resonances to pop out from their hiding. On panels (c-e) for the component spectra, there is no trace whatsoever of the mentioned two broad resonances. The nonparametric envelopes on panels (f–j) are, of course, not built from any explicit set of the components given on the left column of Fig. 10. Nevertheless, the envelopes (f–j) implicitly contain the true components and it is the derivative transform of a certain order m that can make them emerge explicitly.

This fact is beginning to show up already by the first derivative spectra on panels (b) and (g). Specifically, a huge suppression on the two broad components at 3.23 and 3.24 ppm on panel (b) is directly sensed by the envelope on panel (g) through the lineshape narrowing and background flattening. This powerful and practical mechanism is gradually and systematically enforced by higher-order derivatives until eventually the entire envelope (nonparametric dFPT) collapses into the true genuine components (parametric dFPT). Once the components become available from an envelope (which itself is due to derivative shape estimation alone), the peak parameters of the obtained individual resonance can be extracted. Such estimated derivative peak parameters can be related to the exact nonderivative peak parameters (from the parametric nonderivative FPT) by using the known connection analytical formulae [76], as discussed. This is a veritable paradigm shift consisting of starting with a shape estimator and ending with a parameter estimator.

Figure 11 for the choline-containing compounds (malignant sample) closes the Result Section. Within this figure, in the nonderivative component spectra from panel (a), besides the mentioned resonances (U, Cho, PE, PC, GPC, $\beta -$Glc, Tau and m-Ins), there are also several unmarked peaks. Among these, one can see some broad lineshape profiles very near chemical shifts 3.229, 3.245, 3.269 and 3.280 ppm in the immediate neighborhood of the sharper PC, $\beta -$Glc, Tau and m-Ins resonances, respectively. The wide peaks either overwhelm the nearby resonances (e.g. close to $\beta -$Glc and m-Ins) or are centered below the taller peaks (e.g. near PC and Tau). Such wide macromolecular-type peaks alongside the densely packed tails of thinner resonances, generate the elevated background baseline, as seen in the nonderivative envelope (e).

The most intense resonances on panel (e) are Tau, PC and Cho in that order. Herein, Tau is supposed to be a triplet, whereas both PC and Cho should be singlets. The lineshapes of Tau, PC and Cho are asymmetrical in the envelope (e). It is the interference of real and imaginary parts of the complex spectrum $P_K/Q_K$ that leads to asymmetry in the nonderivative magnitude envelope $\left| \mathrm{FPT}\right| _{\mathrm{Tot}}\equiv \left| P_K/Q_K\right|$ (e). Furthermore, another origin of this asymmetry could stem from the possibility that the envelope (e) hides some invisible peaks. This is impossible to know from any nonderivative envelope due to shape estimations alone. However, in the nonderivative components from the parameter estimation employing the FPT on panel (a), there are several resonances that are not visible in the corresponding envelope on panel (e).

There is also a special situation with Fig. 11. It occurs at the chemical shift 3.19 ppm, which separates the two resonances, free choline Cho(s) on the left and the unassigned peak U(s) on the right. These two singlet peaks are so similar that, by the naked eye, one would be hard pressed to decisively say which of them is narrower in the nonderivative component spectra from panel (a). However, what matters the most in this regard is that the hidden U(s) resonance in the nonderivative envelope (e) is, in fact, the reason for the skewness of the compound peak at 3.19 ppm therein. Provisionally, only the label Cho is used at 3.19 ppm on panel (e), disregarding the prior knowledge from Ref. [33] about the presence of the U(s) peak.

The $\mathrm{{}^1H\, MRS}$ databases contain spectral information on specimens with free choline alone dissolved in the $\mathrm{D_2O}$ buffer. Therein, free choline appears as a singlet resonance Cho(s) at 3.19 ppm. Small fluctuations around the anticipated chemical shift 3.19 ppm for Cho(s) can happen when, besides free choline, some other chemicals are present in the sample. This is due to interactions of protons from different molecules and the situation becomes very involved for specimens with human tissues or biofluids. Care must be exercised to first identify Cho(s) properly and then to perform quantification, e.g. by a shape estimator. Presently, because the Cho(s) peak near 3.19 ppm is co-resonating with the U(s) peak, such a quantification of free choline cannot be done in panel (e) by using the nonderivative nonparametric envelope.

Comparing the two resonances denoted by Cho and PC in the envelope (e), it follows that the former peak is wider than the latter. The limitation of such a comparison, relying only upon panel (e), is the lack of information about the possible substructures of these resonances. By being unaware, as in Ref. [53], that in the envelope (e), the peak at 3.19 ppm assigned to Cho at the start is a composite resonance (Cho+U), one would overestimate the peak area and concentration of free choline Cho(s) and tCho. Such type of inaccuracies, common to any nonderivative shape estimator, is prone to be harmful particularly to differential diagnosis (benign versus malignant) in the clinic, where cholines are considered to be in the category of recognized cancer biomarkers.

The stated warning, doubting any nonderivative shape estimator in the quantification context with overlapping resonances, paves the road to derivative signal processing. The benefit of this latter approach on the level of nonparametric envelopes can be appreciated already with the first derivative (f), which represents a dramatic improvement over its nonderivative counterpart (e). The improvement is in both resolution and SNR, on account of lineshape narrowing and the background diminishing. Such a pattern is further significantly accelerated by the second (g) and third (h) derivative envelopes. The co-resonating peaks, the free choline Cho(s) and the U (s) unassigned metabolite, begin to split apart in the first derivative (f). Such a delineation trend is sharpened and more pronounced in the second (g) and third (h) derivative envelopes from the nonparametric dFPT.

The explicit reason for the considerably lowered background baseline in the first derivative envelope (f) can now be understood by reference to the corresponding first derivative component spectra from panel (b). Relative to the nonderivative components on panel (a), the resonance tails are strongly reduced on panel (b) and they are basically lying on the chemical shift axis. A similar occurrence is noticed on panel (b) with the unmarked wide macromolecular resonances at 3.229, 3.245, 3.269 and 3.28 ppm. Namely, the widest peak centered at 3.28 ppm near m-Ins, immersed into the background baseline on panel (a), vanished completely from panel (b). The other three broad peaks at 3.229, 3.245 and 3.269 ppm on panel (b) are significantly weakened with respect to the neighboring sharp resonances PC, $\beta -$Glc and Tau, respectively. For example, on panel (b), the $\beta -$Glc peak is stronger than the broad resonance centered at 3.229 ppm, as opposed to panel (a). These three broader resonances are further suppressed in the second derivative components (c). Finally, they are almost washed out from the third derivative components on panel (d). Basically, the only noticeable exception is a small bump beneath the $\beta -$Glc peak on panel (d).

The Cho(s)-U(s) tandem near 3.19 ppm has its own interesting and intriguing development in the derivative components (b–d). This can explain the corresponding evolution around 3.19 ppm in the envelopes (f–h). We said earlier that one cannot tell the difference between the widths of the Cho(s) and U(s) resonances by looking merely at their nonderivative component lineshape profiles on panel (a). It is seen on panel (a) that the U(s) peak is slightly taller than the Cho(s) peak. This, nevertheless, does not necessarily mean that the U(s) peak is narrower than the Cho(s) peak. The reason is that the peak height is not determined only by the peak width, but rather by the quotient of the FID intensity $\left| d_k\right|$ and the peak width, as discussed.

The $m\,$th order derivative operator $\mathrm{D}_m=(\text{ d }/\text{d }\nu )^m$ reduces the resonance width, but it leaves the FID intensity $\left| d_k\right|$ unaltered. Thus, by following the peak heights of the derivative components, it is seen that the Cho(s) peak is actually taller than the U(s) peak, implying that the former is narrower than the latter, the fact which could hardly be inferred from panel (a). On the right column (f–h), the derivative envelope lineshapes for increasing m gradually converge to the spectra from the left column (b–d), row-by-row-wise. For $1\le m\le 3,$ the best matching between the spectra on the two columns (components versus envelopes) is achieved by the third derivative $(m=3)$ on panels (d) and (h). Hence, the envelope (h) nearly collapses onto the component spectra from panel (d). Some remaining small differences disappear with higher derivatives (not shown).

Overall, for the third derivative spectra in Fig. 11, the envelopes from the nonparametric dFPT are found to practically coincide with the corresponding components due to the parametric dFPT. Further, the separation of the three components Cho(s), PC(s) and GPC(s) of tCho reported earlier using the nonparametric dFPT [33], is presently confirmed by the parametric dFPT. Moreover, in Fig. 11, the parametric dFPT provided assurance about the unassigned singlet resonance U(s) near 3.19 ppm, co-resonating with the free choline Cho(s). The U(s) peak, first detected in the envelops from the nonparametric dFPT in Ref. [33], is genuine as it is detected here in the components due to both nonderivative (a) and derivative (b–d) estimations by the FPT and dFPT, respectively. Here too, for Fig. 11, similarly to Figs. 1–10, the parametric dFPT is shown to explain the simultaneous improvement of resolution and SNR by evoking the step-by-step mechanism, linewidth narrowing and background flattening.

This, in retrospect, validates the previous findings from the nonparametric dFPT [33] and consolidates its status of a shape estimator, which can autonomously quantify any number of the physical resonances in the given spectrum. The tandem improvement of achieving superior resolution and SNR by the nonparametric derivative dFPT relative to the nonparametric nonderivative FPT, offers an opportunity not only to separate the overlapped peak resonances, but also to detect the previously unreported resonances, some of which might be new potential cancer biomarkers.

4 Discussion and Conclusion

This study is on magnetic resonance spectroscopy, MRS. In modern laboratory spectrometers and clinical scanners based on MRS, time signals are measured first and subsequently the frequency spectra are computed. The time and frequency domains are equivalent since they contain the same amount of information. However, despite this equivalence, the transparency of the data displayed on graphs is not the same when it comes to the possibility of reading off some clinically useful information.

Absolutely nothing diagnostically interpretable can be deduced by merely looking at a plot of an average value of many encoded time signals. All that such a graph could show is a densely packed attenuated oscillatory waveform. This gives no hint about the structure of the time signal and, by implication, no insight into the content of the investigated specimen, i.e. no quantifiable specifics viz the number of metabolites, their chemical shifts, relaxation times and abundance.

In the frequency domain, the corresponding total shape spectrum (envelope), made out of such a time signal, looks much sparser, as it exhibits fewer discernible lineshape profiles. Yet, advantageously, such an envelope might potentially be diagnostically more informative in a provisional way, at least for the well-isolated resonance peaks. For these peaks, their positions, widths and heights could roughly be read off from the given plot as an approximate initial information on the detected singlet resonances assignable to some of the known or unknown metabolites. Nevertheless, this peak-picking procedure, commonly practiced in the MRS literature, could easily be deceptive since even a perfectly symmetric single peak might hide one or more invisible smaller resonances.

Suppose, for example, that a vastly simplified time signal contains some 100 damped oscillatory waveforms, while the associated total shape spectrum or envelope lineshape shows only about 30 apparently single resonance peaks. At first, this might seem to be at odds with the information preservation when passing from the time to the frequency domain. Ideally, for a nondegenerate spectrum, each complex attenuated harmonic from the time domain should yield one resonance in the frequency domain. Nevertheless, regarding the information preservation when passing from the time to the frequency domain, there might not be any contradiction as the remaining 70 peaks could well be swamped by the apparent singlets and thus became invisible.

A spectrum originates from integrating the given time signal. Integration is an averaging procedure which, being basically a smoothing operator, can amalgamate smaller to the larger adjacent spectral constituents. This does not mean that the smaller peaks are washed out from the spectrum. Quite the contrary, they are still present, but might be unrecognizably glued to the larger resonances in an envelope spectrum. Still, for the purpose of interpreting the given envelope, such finer spectral structures are irretrievably lost. However, since smaller resonances might also be diagnostically relevant, there is every interest to unravel these peaks, as well. Then, within signal processing in the frequency domain, a considerable benefit would be gained to mitigate, as much as feasible, the smoothing effect of the integration operator in envelopes.

The derivative operator is an anti-smoother. It exploits even the mildest slope changes in the given curve and maps them into a more structured lineshape with maxima and minima. Derivatives with respect to frequency and integrations over time are the two opposite operations. Also, an integration operator can be considered as an anti-derivative operator. Therefore, in the frequency domain, the most natural way to unfold the hidden peaks from the compound overlapping resonances would be to apply the derivative operator to the given envelope. Strictly speaking, the obtained derivative spectra would still represent only the envelopes. However, it might be possible that after only a few derivatives, the derivative envelope may actually reconstruct most (if not all) of the true physical components. This could also include some of the mentioned smaller peaks that were completely invisible in the given nonderivative envelope.

Such a concept of derivative shape estimations works as per theory in the derivative fast Padé transform, dFPT. This processor applies the derivative operator to the given envelope from the nonderivative fast Padé transform, FPT. Here, both the FPT and dFPT act as the shape estimators (nonparametric processings). The nonparametric dFPT succeeds in unfolding the hidden peaks from an envelope. Nevertheless, it remains to be seen whether such a deconvolution could yield the separate individual peaks that would coincide with the actual, true components. This challenging verification is the topic of the present study. The ultimate check is made by comparing the component spectra from the parametric dFPT with the envelopes from the nonparametric dFPT.

With this goal, the main emphasis is presently placed onto the parametric dFPT while processing the time signals encoded with samples of ovarian cyst fluid (benign, malignant) from two patients. Processed recently by the nonparametric dFPT [33], these time signals have originally been encoded by in vitro $\mathrm{{}^1H\,MRS}$ at a Bruker 600 MHz ($\approx 14.1$T) spectrometer [53]. Regarding data interpretation in Ref. [53], the nonderivative fast Fourier transform, FFT, has been employed, alongside the envelope fitting with some adjustable Lorentzian lineshapes, to yield certain approximate concentrations of only 12 resonances, assigned to 12 known metabolites. Therein, not counting the internal reference peak, altogether 52 resonances were visually identified and assigned to some 32 known and 16 unknown metabolites [53]. However, the remaining 40 visually spotted resonances could not be quantified and this has been attributed in Ref. [53] to to the so-called ’spectral crowding’ problem (tight overlaps of several congested resonances within a very small frequency band).

Using the frequency domain spectral analysis, the parametric nonderivative FPT explicitly finds the exact solution of the posed quantification problem by reconstructing the peak position, width, height and phase of every physical resonance. These four peak parameters give the component spectrum. The sum of all the reconstructed component spectra represents the parametrically reconstructed envelope. The peak position is the chemical shift (resonance frequency) and the peak width is proportional to the reciprocal of the effective spin-spin relaxation time. The peak height is the ratio of the intensity of the time signal and the peak width. This intensity is the absolute value (magnitude or modulus) of the complex amplitude of the encoded time signal. The peak phase is the phase of the complex amplitude of the time signal. The peak area is the product of the peak height and the full width at half maximum. Thus, the peak area is given by the halved intensity of the time signal. In medical diagnostics by MRS, the peak area is the most relevant quantity since it is directly proportional to the concentration of the metabolite assigned to the given resonance.

The advantage of the outlined procedure is in simultaneously encompassing both the frequency and time domain representations. Although the outlined procedure for quantification in the FPT refers explicitly to the frequency domain, it also applies directly to the time domain. It automatically parametrizes the encoded time signal without fitting the encoded FID data. This is done by summing up all the found attenuated complex harmonics. Each such harmonic is the product of the signal intensity and the damped complex exponential whose variable is the complex frequency given by the pair of the retrieved peak position and the peak width. Such a construct leads to a damped sinusoidal and cosinusoidal oscillatory waveform of the time signal. The same waveform is also observed for time signals encoded by MRS.

The present results for nonderivative envelopes computed by the parametric and nonparametric FPT are identical throughout the entire Nyquist range. Nevertheless, the most stringent level of comparisons is to confront the nonderivative envelopes from the nonparametric FPT with the components from the parametric nonderivative FPT. Expectedly, the two nonderivative plots are substantially different. Here, the word ’comparison’ should not be taken literally because there are many component lineshapes from the parametric FPT and only a single envelope lineshape from the nonparametric FPT. Nevertheless, it makes sense to juxtapose these components and the envelope in order to realize what actually the latter spectrum is lacking in a visual inspection. An alternative view is that the envelope from the nonparametric FPT is not missing anything judging upon its coincidence with the envelope from the parametric FPT. In principle, this coincidence should mean that the envelope from the nonparametric FPT could contain all the true components that became opaque due to interference.

For this to be true, there ought to be a way of teasing out all the genuine components from an envelope computed nonparametrically (i.e. by shape estimation alone). In general, no system would spontaneously disclose its inner structure. An external action onto the system is needed. Then, the inner structure could be inferred from the system’s response (signal) to the external perturbation. The same reasoning applies also to an envelope, which is a frequency representation of the system (a scanned sample). The examined specimen conveyed its structure to the encoded time signal, albeit in a convolved way. It is this convolution (folding) that disables both the encoded time signal and the computed nonderivative envelope to unravel the inner working of the sample. To extract the components from a conventional envelope, we should “perturb” it by one or more additional actions.

For example, the sought action could be a derivative operator applied to this envelope. The answer of the ’perturbed’ envelope might give a hint about some of its building elements, the components. Using the first derivative operator, the response function of the standard, conventional envelope is the first derivative envelope. Some components might be revealed already by the first derivative envelope. If this leaves some compound resonances unresolved, higher derivative envelopes can be generated by further applications of the derivative operator. Eventually, all the components could be teased out from the initial (nonderivative) envelope. In such a case, for a sufficient derivative order, the corresponding derivative envelope from the nonparametric dFPT would collapse onto all the true components from the parametric dFPT. This is the concept of exact derivative signal processing, exemplified within the nonparametric dFPT.

To proceed in this direction, we presently compare the envelopes from the nonparametric dFPT with the components as well as the envelopes from the parametric dFPT. The outcome is that all the computed derivative envelopes are exactly the same (to the slightest spectral detail) irrespective of whether the nonparametric or parametric dFPT is utilized. This is important since the nonparametric and parametric dFPT employ two completely different analytical formulae for derivative envelopes.

Comparisons of the components from the parametric dFPT with the corresponding envelope from the nonparametric dFPT begin to gradually make fuller sense when the derivative order is augmented. Already the first derivative spectra make a remarkable progress. In particular, all the wide resonances in the first derivative components (parametric dFPT) are either hugely reduced or completely pushed into the background baseline, whereas the sharp resonances are narrowed and their tails lowered. This is partially matched by the first derivative envelope (nonparametric dFPT), depending on the spectral density (some overlaps persist in the over-crowded bands, e.g. with the leucine and isoleucine downfield of the lactate doublet). In the nonparametric processing, the reconstructed nonderivative envelope has a considerably elevated background baseline, which is in the first derivative envelope flattened down to the level of the chemical shift axis. Subsequently, a further substantial advance is achieved by the second and third derivative spectra. In particular, the third or fourth derivative envelopes from the nonparametric dFPT are often confluent with the third or fourth derivative components from the parametric dFPT.

This is achieved by the systematic action of the derivative operator through the simultaneous improvements of signal to noise ratio, SNR, and spectral resolution. Derivative envelopes in the nonparametric dFPT have increased resolution (thanks to linewidth narrowing) and SNR (because of the reduced contributions from broad macromolecular resonances and due to cutting off the peak tails). Linewidth narrowing of sharp resonances enhances their peak heights, especially relative to the broad macromolecular spectral structures. This translates into a higher SNR. Such mechanisms for arriving at the superior resolution and SNR in the derivative envelopes from the nonparametric dFPT are elucidated in plain view by the availability of the explicitly reconstructed components from the parametric dFPT. The stated reasons for a steady progress of the derivative envelopes (nonparametric dFPT) with the gradual augmentation of the derivative order could be transparently identified and followed step-wise by reference to the juxtaposed component spectra (parametric dFPT).

We devoted special attention to detection of hidden resonances in nonparametric envelopes by way of three conceptually different scenarios. The first includes the visible and apparently unstructured lineshape profiles (examples: the calibrating internal standard and lactates as well as cholines, where the former two are seemingly bell-shaped, nearly perfectly symmetric). The second involves the residual water (examples: uncovered nearly co-resonating sub-structures, a multiplet of nitrogen acetyl aspartate, NAA). The third incorporates the background baseline full of some ondulatory “bifurcations” that are uninterpretable by any means (examples: unfolding a triplet and a quartet of the unknown metabolites).

As a rule, the conventionally conceived unobstructed resonances are, in fact, rarely free of some underlying peaks, completely invisible in standard, nonderivative envelopes. This is found out here to be true even for the resonance representing the internal reference standard, let alone for other numerous peaks, including the recognized cancer biomarkers (lactic acids, choline-containing compounds, ...). Among the most consequential examples is the resonance assigned to free choline (located very near 3.19 parts per million, ppm), which is theoretically predicted to be a singlet spectral profile.

Indeed, this resonance appears roughly as a singlet (albeit slightly skewed) in the customary, nonderivative envelope. However, the first, second and third nonparametric derivative envelopes from Ref. [33] and the parametric components (present computations) clearly show two singlet peaks of comparable intensities, positioned exceedingly close to the expected location of free choline (3.19 ppm). One of these two resonances is assigned to free choline, Cho(s), and the other is unassigned, as denoted by U(s). Consequently, this would raise serious concerns about the actual meaning of the concentration estimates of the free choline metabolite when using conventional nonderivative envelope from any estimator. More specifically, the concentration of free choline evaluated by e.g. a Lorentzian fit to the usual Fourier envelope would be over-estimated by about 50%. This large error bar is intolerable for any cut-point chosen to make the sought vital differential diagnosis (malignant versus benign) using the examined sample from the two patients in the present case.

Free choline, phosphocholine and glycerophosphocholine appear separated even in the usual nonderivative envelope from Ref. [33]. Therein, however, none of these three cholines is quantifiable by any means, including numerical quadratures since the integration limits cannot be determined with certainty. Another obstacle is the presence of some underlying hidden peaks and the elevated background baseline contribution to every resonance in the nonderivative envelope. The derivative Padé-conceived shape estimations simultaneously overcome all these limitations and furnish exact quantification by way of a veritable conversion of the given derivative envelope into the underlying derivative components. These derivative components from the nonparametric dFPT turn out to be consistently coincident with the derivative components from the parametric dFPT.

The two lactate bell-shaped resonances appear at 1.41 and 4.36 ppm through a doublet and a quartet, Lac(d) and Lac(q), respectively. Beneath Lac(d), there are some six non-negligible resonances of unequal widths (two sharp doublets and two broader resonances), visible in the components (parametric nonderivative FPT). However, they are totally invisible, i.e. swamped by Lac(d) in the corresponding envelope (nonderivative FPT). Nevertheless, e.g. the strongest two among these hidden resonances are visualized in the nonparametric fourth derivative envelope. In the case of the lactate quartet, the nonparametric fourth derivative envelope singles out one of the two completely invisible resonances underneath Lac(q). Crucially, around Lac(d) and Lac(q), the fourth derivative components (parametric dFPT) are nearly coincident with the associated fourth derivative envelopes (nonparametric dFPT). For both Lac(d) and Lac(q), the remaining four and one opaque resonances, respectively, could also be made more visible in the envelopes of some higher-order derivatives in the nonparametric dFPT.

Upfield of Lac(q), the water residual is located at 4.71 ppm. Originally, water is about 10000 times more abundant than any of the other metabolites in human tissuses or biofluids. Their peaks are invisible relative to the giant water resonance. However, a partial suppression of water in the process of encoding [53] results in an incomparably better transparency of most of the formerly opaque resonances. Still, after Lac(d) and Lac(q), the residual water content is the third strongest resonance compound in the entire envelope spectrum. Prior to a partial suppression, the water peak appeared as an almost perfect singlet resonance. Afterward, the water residual became a broad spectral structure with two bumpy hills whose long tails deform the surrounding resonances in the nonderivative envelope. However, the nonparametric fourth or fifth derivative envelopes succeed in fully isolating the single water resonance, precisely at its exact chemical shift, 4.71 ppm. The same success by the nonparametric dFPT is also achievable for envelopes reconstructed using encoded water-unsuppressed time signals, as has recently been shown in Ref. [79] in a different context.

The presently obtained singlet of the residual water resonance can be most accurately quantified and eventually used as an independent calibration standard. Therefore, derivative estimations by the nonparametric dFPT are an optimal way of treating the water residual. This is opposed to the customary practice in the MRS literature, where the water residual is fitted by some 3-10 freely adjustable Lorentzians and the result is subtracted from the full envelope. The ensuing problem is twofold. The neighboring resonances are still distorted. And, most critically, a subtraction technique (partial annulling of the water residual) can unknowingly wash out some of other nearby metabolites of a potential diagnostic relevance.

The present treating all the resonances on the same footing (be they the water residual, lactic acids, cholines, etc.) should be contrasted to a common practice in the MRS literature, where some resonances are often intentionally ignored at the onset of computations as ’nuisance’. Suffice it to quote Ref. [62], which employs in vitro $\mathrm{{}^1H\,MRS}$ with high-resolution magic angle spinning, HRMAS, for encoding time signals from cervical biopsies (normal, malignant). Therein, the frequency range downfield of the water residual was omitted. The cited reason was that due to partial water suppression by saturation in the process of spin-echo encoding of time signals, “the peaks in this area have intensity variations” [62] (p. 178). Moreover, herein, even a recognized cancer biomarker, Lac(d), was excluded from the principal component analysis of spectra because “the remaining lipid signals influence the intensity of the lactate peak” [62] (p. 178).

Derivative spectra are not sparser because of intentionally discarding some allegedly obstructing broader resonances assignable to macromolecular metabolites (lipids, proteins, ...). The sparseness of derivative spectra is due to the fact that the pace of the peak height increase is slower for wider than for narrower resonances. In other words, the derivative operator visualizes and quantifies first the narrower resonances. Simultaneously, the broader resonances are pushed into the background baseline. They are not gone for good as it is possible to retrieve them for visualization and quantification by sequential processing through e.g. truncating the top of the tall and sharp resonances that have already been quantified.

Figuratively, the derivative operator acts on resonances as if it were ’a pencil sharpener’. However, the derivative operator is not ’a resonance sharpener’, which uses some artifices to make spectra appear superficially sparser and better resolved. Quite the contrary, resolution and SNR are simultaneously and synchronously improved by the well-identifiable/controllable three mechanisms. These mechanisms are at work synergistically and consist of line narrowing, the implied peak height enhancing and the background baseline flattening systematically with increased derivative order. Such a pattern is predicted first and foremost by the theoretically derived expressions [76] and then confirmed by the explicit numerical computations.

There is yet another bonus from the remarkable narrowing/sharpening with concomitant intensifying of the water singlet from the broad water residual. Namely, some other resonances pop out right around the water singlet center, 4.71 ppm. For instance, a metabolite possibly based on NAA is detected therein. Ordinarily, neuronal metabolites, such as NAA, are rarely present in non-negligible concentrations outside the human brain tissue or cerebral fluid. However, some NAA-related metabolites have earlier been identified at 2.06 and 2.95 ppm in the borderline ovarian cyst fluid, using in vitro and in vivo $\mathrm{{}^1H\,MRS}$ [54, 55]. The ’molecular pump mechanism’ [98] has been evoked in trying to understand the traces of NAA in the ovarian samples investigated in Refs. [54, 55].

That the intact water residual adversely impacts on the lineshapes of the neighboring resonances is illustrated within the range 5.0-5.1 ppm. Herein, the envelope in the nonderivative FPT shows a small and notably deformed unassigned quartet U’(q), centered near 5.05 ppm, in a quasi-dispersive mode. However, such a distortion is quickly rectified/straightened/symmetrized by the first nonparametric derivative envelope. This bell-shaped quartet is further perfected by higher-order derivative envelopes (nonparametric dFPT). Moreover, they are found to be identical to the corresponding 2nd-4th derivative components in the parametric dFPT.

On the upfield side of the tail of the unassigned quartet U’(q), only some minuscule irregular undulations are present in the envelope from the nonderivative FPT. However, from these spectral ’bifurcations’ a clear unassigned triplet U”(t) centered near 5.0925 ppm emerges in the 1st-4th derivative envelope of the nonparametric dFPT. In particular, the fourth derivative envelope (nonparametric dFPT) is identical to the fourth derivative components (parametric dFPT). This illustrates how the dFPT can pull out some well-structured physical resonances out of a seemingly information-void stochastic-appearing background baseline.

The Padé estimation is demonstrated to be able to successfully handle a large dynamic range of spectral intensities. It detects, visualizes and quantifies resonances whose peak heights differ within a factor 3000 au or less. One such example is the set of the peak heights of the lactate doublet Lac(d) {1.41 ppm, 6000 au}, alanine doublet Ala(d) {1.51 ppm, 300 au}, lactate quartet Lac(q) {4.36 ppm, 1600 au}, unassigned quartet U’(q) {5.05 ppm, 70 au} and unassigned triplet U”(t) {5.0925 ppm, 2 au}. The implication is that the sought metabolite concentrations, accessible to the Padé reconstruction, might vary within three or more orders of magnitude, from e.g. $\le \mu \mathrm{M/g}$ to $\ge \mathrm{mM/g}$ or even for a wider range. A quantifiable detection of the minuscule concentrations of metabolites directly translates to an essential quality for medical diagnostics by MRS, the considerably increased detection sensitivity and specificity.

This is very significant, especially in the light of the intrinsically low sensitivity of MRS due to an exceedingly small number of spin-active nuclei participating to the resonance event (about 10 or 20 out of a million at 1.5 or 3T, respectively, at room temperature). Added to this drawback are very weak interactions of resonating nuclei with their environment. How can then such a twofold obstacle be surmounted to achieve a high detection precision by MRS? More concretely, what would be a physical basis of enhanced sensitivity of MRS by three or more orders of magnitude?

The answer is in the occurrence that the resonance signature (peak parameters) are very sensitive to even the weakest alterations in the nuclei-environment interactions. If this could judiciously be probed, the outcome would inform about the minute abundance of resonating nuclei and, hence, about the minuscule molecular concentrations. For this purpose, regarding in vitro MRS, the first measuring device which comes to mind is HRMAS. While the HRMAS variant of in vitro MRS for rotating samples significantly improves resolution (by reducing or nearly eliminating the line broadening due to magnetic dipolar coupling), it still offers an incomplete framework as the ensuing envelopes exhibit many overlapped resonances superimposed on bumpy macromolecular baselines [62]. And, most critically, HRMAS is not applicable to patients when using in vivo MRS which is needed in the clinic.

One then wonders whether perhaps theory by some advanced signal processings of the time-domain data points encoded by MRS could provide a wider platform in this realm? The possibility that even many minuscule metabolite concentrations might be detectable (first visualized and then quantified) is amply exploited by the nonparametric dFPT to greatly enhance sensitivity of both in vitro and in vivo MRS by a huge margin [31,32,33]. Moreover, a comparable success of this versatile Padé-based estimation methodology for time signals encoded by in vitro MRS is achievable with and without sample rotations.

From the derivative components obtained exclusively with the help of shape estimation by the dFPT, the peak parameters can unequivocally be extracted. Afterward, they can be scaled back (using the known connecting formulae from Ref. [76]) to the nonderivative components identical to those from the parametric FPT. This is how the same true components are teased out (in the fashion of an inverse problem) from the given nonderivative envelope, computed either by the nonparametric or parametric dFPT. For the parametric dFPT, such a procedure is optional as a confirmation of the correctness of derivative estimations for the peak parameters. We say ’optional’ because this processor already produces the components from the onset by explicitly solving the quantification problem.

However, for the nonparametric dFPT, where quantification is not even mentioned at the onset, the same inverse problem is essential. It begins with a nonderivative envelope in the nonparametric FPT, with no hint about its components. And it ends up with the genuine components and their peak parameters. This amounts to solving the quantification problem without tackling any usual prescription (diagonalization of the data matrix, rooting the characteristic, secular, eigen polynomial, etc.). No fitting is used either to extract the peak parameters from any derivative lineshapes. In fact, all that is needed to quantify the reconstructed well-isolated derivative resonances is to use a dense frequency grid so that the position, width and height of every such peak can simply be printed out from the same computer program which generates these spectral profiles.

We presently confirmed that this strategy in the nonparametric Padé estimations produces exactly the same peak parameters (position, width, height) of all the physical resonances as those in the parametric Padé processings. Especially significant is that the mentioned unassigned peak U(s), almost co-resonating with free choline Cho(s) near 3.19 ppm and reported earlier using the nonparametric dFPT [33], is reproduced exactly by the present solution of the spectral analysis problem (or equivalently, the quantification problem) in the parametric dFPT. As a matter of fact, already the nonderivative component spectra in the parametric FPT clearly show two peaks of similar strengths, tightly positioned on each side of 3.19 ppm. Here lies the usefulness of this cross-validation since quantification by the nonparametric dFPT can be checked by the parametric dFPT and vice verse.

It is precisely this type of rigorous, double scrutiny of quantitative data analysis which is lacking in signal processing for MRS and beyond. We cannot think of a more needy beneficiary of the precision certainty of the presented quantitative estimations than diagnostics by MRS. Within ’precision medicine’ and ’system medicine’ this is of the prime relevance to cancer medicine, where accuracy of data analyses and interpretation could mean the difference between life and death. The current study on ovarian cancer detection uses time signals encoded by in vitro MRS at a high field (14.1T). Similar conclusions have also been drawn for time signals encoded by in vivo MRS at clinical scanners of much lower magnetic field strengths (1.5, 3T) in our recent studies on brain tumor [31] and borderline ovarian tumor [32], respectively.

How the confidence in data analysis for MRS matters in the clinic is profoundly illustrated in the case of ovary. Ovarian cancer is a frequent cause of death among women worldwide with many thousands of lost lives every year primarily due to late detection. Early detection of ovarian tumor is of critical importance as timely treatments would dramatically increase chances for the five year survival above 90%. Regrettably, within the last decades, astonishingly small number of studies using MRS were on ovarian cancer compared to other human organs. One of the main reasons is the lack of adequate data analyses to make proper clinical interpretations of spectra even for time signals encoded by in vitro MRS with a Bruker 600 MHz spectrometer (14.1T) [99]. It is high time that the situation changes to the better. For processing time signals encoded by in vitro and in vivo MRS data, we offer our practical proposals (present and recent [31,32,33]) to employ the superior Padé-based versatile methodology of the proven intrinsic validity and clinically highest reliability.