1 Introduction

This paper focuses on the advantageous properties of rational polynomials for handling functions containing resonances. Magnetic resonance spectroscopy (MRS) falls into this latter category. The fast Padé transform (FPT) is particularly amenable for processing MRS time signals. We presently investigate certain unexplored features of the non-parametric FPT prior to quantification. This is applied to a clinical problem of particular saliency. Namely, we examine the possibilities to more efficiently detect the presence of a breast cancer biomarker. We begin by briefly presenting the conventional Fourier-based methodology for processing MRS time signals, and the drawbacks inherent therein.

1.1 The fast Fourier transform: generator of spectra as a single polynomial

The current practice in MRS is to convert the encoded time signal or the free induction decay (FID) curve into its spectral representation in the frequency domain by the fast Fourier transform (FFT). The Fourier spectrum is conveyed as a single polynomial:

$$\begin{aligned} \hbox {FFT}: F_{m} =\sum \limits _{n=0}^{N-1} c_{n}\mathrm {exp}(-2\pi imn/N) , 0\le m\le N-1. \end{aligned}$$
(1)

Here, the fixed \(m^{\mathrm {th}}\) Fourier grid frequency is \(2\pi m/T\) and the set of complex-valued time signal points is \(\left\{ c_{n} \right\} \). The total signal duration or total acquisition time T is \( T=N\tau \), where N is the total signal length and \(\tau \) is the sampling time, which is the reciprocal of the bandwidth (BW). The variables \( \mathrm {exp}(\pm 2\pi imn/N)\) are the undamped sinusoids and cosinusoids \((nm\tau /T = nm/N)\).

One of the main rationales for employing the FFT is its capability to rapidly process signals whenever their length is of the composite form, \(N=2^{m}(m= 1, 2, 3,\ldots )\). Besides this computational efficiency, the other favorable property of the FFT is its relatively steady convergence as a function of increasing signal length [1].

Notwithstanding these advantages, the FFT has a number of major drawbacks. Firstly is its poor resolution capability which has a number of causes. One is the lack of possibility to interpolate. Namely, the FFT envelope spectrum is generated from the pre-assigned frequencies whose minimal separation is predetermined by the total acquisition time, T. Since any truthful interpolation is precluded, attempting to improve resolution requires the use of longer T. However, since the FID rapidly decays over time, mainly noise is recorded at longer T. This is especially problematic at low magnetic field strength \(B_{0}\) such as in clinical scanners (1.5 and 3 T). Thus, attempts to enhance resolution with the FFT, unavoidably lead to deterioration of signal-noise ratio (SNR) [1]. Another reason for the poor resolution of the FFT is the absence of any genuine extrapolation capabilities. In other words, there is no possibility to predict information beyond the final encoded signal point, \(c_{N-1}\). Attempts to circumvent this latter obstacle consist of using the periodic extensions of the time signals. This is unsatisfactory since time signals encoded in MRS are not periodic. Contrary to the common misconception, zero-filling cannot augment resolution since the original N data points in the encoded time signal already contain the entire information. Further contributing to poor resolution and SNR is the linearity of the FFT.

The FFT is solely a non-parametric estimator. No further information beyond the total shape spectrum can be generated via Fourier analysis alone. No trustworthy information whatsoever can be ascertained concerning the number and abundance of the components underlying the envelope spectrum. Common practice has often been to subsequently perform post-processing via fitting. However, this practice is highly speculative and entirely non-unique. Consequently, inaccuracies abound in the reports of metabolite concentrations based upon this approach for handling MRS data [2].

Overall, the inadequacy of processing MRS data by the FFT is related to its mathematical structure as a single polynomial. Its inadequacy in representing functions with peaks is primarily due to the lack of polar structure [2, 3].

1.2 The fast Padé transform: generator of spectra via the unique ratio of two polynomials

In contrast to the FFT, the fast Padé transform, FPT, produces a spectrum as a non-linear response function via the unique ratio of two polynomials [2]. This spectrum is \(P_{K} / Q_{K}\) in the diagonal form, with K being the polynomial degree or model order.

The exact response function is given by the infinite-rank Green function \(G(z^{-1})\), which is defined by the Maclaurin series:

$$\begin{aligned} G(z^{-1}) =\sum \limits _{n=0}^\infty {c_{n} } z^{-n}, z=\text{ e }^{i\tau \omega } (\text {Exact Green series}), \end{aligned}$$
(2)

where the time signal points \(\left\{ c_{n} \right\} \) are the expansion coefficients. Whenever only a finite number \(N(\textit{N} <\infty )\) of signal points \(\{c_{n}\}\) is available, as is always the case in reality, a truncated response function is given. This is the finite-rank Green function or the Green polynomial \(G_{N} (z^{-1})\):

$$\begin{aligned} G_{N} (z^{-1}) =\sum \limits _{n=0}^{N-1} {c_{n} } z^{-n} \;(\text {Exact Green polynomial}). \end{aligned}$$
(3)

Alternatively, as per discrete time series nomenclature, these infinite- and finite-rank Green functions are called the infinite and finite \(z- \)transform, respectively [2].

1.2.1 The two variants the FPT

With respect to the complex harmonic variable z, there are two variants of the FPT, defined inside \((\left| z \right| <1)\) and outside \((\left| z \right| >1)\) the unit circle for the causal and anti-causal representations, respectively. These are acronymed as \({\mathrm {FPT}}^{(+)}\) and \({\mathrm {FPT}}^{(-)}\), respectively, and are both frequency-dependent polynomial quotients extracted from the common exact Green polynomial (3) in powers of \(z^{-1}\) [2, 4]. Thus, in the \({\mathrm {FPT}}^{\left( \pm \right) },\) the input response function \(G_{N} (z^{-1})\) from (3) is approximated by the Green-Padé functions \(G_{K}^{\pm } (z^{\pm 1})\), as the diagonal rational polynomials in the harmonic variables \(z^{\pm 1}\):

$$\begin{aligned}&\text{ FPT }^{(-)}: G_{N} (z^{-1})\approx G_{K}^{-} (z^{-1})=\frac{P_{K}^{-} (z^{-1})}{Q_{K}^{-} (z^{-1})}\equiv \frac{{\sum }_{r=0}^K {p_{r}^{-} z^{-r}} }{{\sum }_{s=0}^K {q_{r}^{-} z^{-r}} }, \end{aligned}$$
(4)
$$\begin{aligned}&\text{ FPT }^{(+)}: G_{N} (z^{-1})\approx G_{K}^{(+)} (z)=\frac{P_{K}^{+} (z)}{Q_{K}^{+} (z)}\equiv \frac{{\sum }_{r=1}^K {p_{r}^{+} z^{r}} }{{\sum }_{s=0}^K {q_{r}^{+} z^{r}}}. \end{aligned}$$
(5)

For the same input \(G_{N} (z^{-1})\), the two equivalent Green-Padé representations (4) and (5) for spectra \(P_{K}^{-} (z^{-1})/Q_{K}^{-} (z^{-1})\) and \(P_{K}^{+} (z)/Q_{K}^{+} (z)\) are the mentioned anti-causal and causal response functions in the \({\mathrm {FPT}}^{(-)}\) and \({\mathrm {FPT}}^{(+)}\), respectively. The expansion coefficients of the numerators \(P_{K}^{\pm } (z^{\pm 1})\) and denominators \(Q_{K}^{\pm } (z^{\pm 1})\) are \(\left\{ p_{r}^{\pm } \right\} \) and \(\left\{ q_{s}^{\pm } \right\} ,\) respectively. They are extracted uniquely from the time signal points \(\{c_{n}\}\) by solving a single system of linear equations from definitions (4) and (5).

Since it operates with the reciprocal variable 1 / z, the \({\mathrm {FPT}}^{(-)}\) is an accelerator of convergence of the input slowly converging expansion in powers of \(z^{-1}\) [1, 2]. On the other hand, the \({\mathrm {FPT}}^{(+)}\) works directly with variable z and, thus, performs analytical continuation of the same input development (3) which is in powers of \(z^{-1}\). The \({\mathrm {FPT}}^{(+)}\) is more difficult algorithmically, as it requires induction of convergence into divergent series [2, 5]. For that reason, to achieve convergence, the \({\mathrm {FPT}}^{(+)}\) generally needs more signal points than the \({\mathrm {FPT}}^{(-)}\).

Internal cross-validation is provided by the \({\mathrm {FPT}}^{(+)}\) and \({\mathrm {FPT}}^{(-)}\) against each other within the same Padé methodology, but using different algorithms [2, 4, 6]. Once convergence has been achieved by both of these two variants of the FPT, the final joint output list is produced from the spectral parameters that are generated by the \({\mathrm {FPT}}^{(+)}\) and the \({\mathrm {FPT}}^{(-)}\). This self-contained checking requires no further comparison with any other signal processor for verification.

1.2.2 High resolution of the FPT

The two approximations of the Green function \(G_{N} (z^{-1})\) are provided by the expressions for \(G_{K}^{(-)} (z^{-1})\) and \(G_{K}^{(+)} (z)\) from (4) and (5), respectively. From (2), the input Green function \(G(z^{-1})\) is convergent outside the unit circle \((\left| z \right| >1)\), and divergent inside the unit circle \((\left| z \right| <1)\). For the \({\mathrm {FPT}}^{(-)}\), using (2) and truncating the entire N-point set \(\{c_{n}\}\) to its first half, would generate the Padé spectrum \(P_{K}^{-} (z^{-1})/Q_{K}^{-} (z^{-1})\) by (4) which is twice more informative than the truncated version \(G_{N/2} (z^{-1})\) of \(G_{N} (z^{-1})\). Namely, the quotient \(P_{K}^{-} (z^{-1})/Q_{K}^{-} (z^{-1})\) includes the information from the complete non-truncated set \(\{c_{n}\}\;(0\le n\le N -1)\). This is because expanding \(P_{K}^{-} (z^{-1})/Q_{K}^{-} (z^{-1})\) in its Maclaurin series (in powers of \(z^{-1})\) would exactly reconstruct the entire input N time signal points \(\{c_{n}\}\; (0\le n\le N -1)\). This feature of rational Padé polynomials reveals why the \({\mathrm {FPT}}^{(-)}\) can attain superior resolution compared to the FFT by using the same number of time signal points. This has been demonstrated exhaustively with both synthesized FIDs [4, 7,8,9,10,11,12,13,14,15] and in vivo encoded MRS time signals [1, 4, 6, 16,17,18]. Conversely, the \({\mathrm {FPT}}^{(-)}\) attains the same resolution as that of the FFT by using fewer signal points, e.g. N / 2 or so [6, 16].

1.2.2.1 Extrapolation capabilities of the FPT

As noted, with the FFT, there is a sharp cut-off of the time signal at the end of T. In contradistinction, via the unique polynomial quotient \(P_{K} /Q_{K}\), extracted directly from the investigated time signal, the FPT can extrapolate beyond the acquisition time T. Namely, through the FPT, it is possible to utilize the first available half \((M=N/2)\) of the input data. The extracted polynomial quotient \(P_{K} /Q_{K}\) will have an expansion whose first 2M terms coincide with the first N terms of the input data from (3). In this way, the FPT will have predicted the missing second half \((>N/2)\) of the expansion coefficients in the truncated input Green polynomial of length \(M=N/2.\) This extrapolation improves resolution, since the N terms of a convergent power series (2) are more accurate than its truncation to N / 2. Moreover, the total length of the FID reconstructed by the \({\mathrm {FPT}}^{(\pm )}\) and denoted by \(\{c_{n}^{\pm }\}\) need not stop at \(N\;( \mathrm {i.e.}\; n\; \mathrm {in}\;{\{c}_{n}^{\pm }\}\,\mathrm {can\; run\;through}\; n=0,1,\ldots ,N-1, N,N+1,\ldots ).\) Additional data points for \(n\ge N\) in the full set \(\{c_{n}^{\pm }\}\) relative to \(\left\{ c_{n} \right\} \) are the Padé-based extrapolations that would have been available had the encoding continued after \(c_{N-1}\) beyond the total acquisition time T, i.e. at times \(n\tau >T\) [19]. Hence, the predictive feature of the \({\mathrm {FPT}}^{(\pm )}\).

1.2.2.2 Interpolation capabilities of the FPT

In the FPT, the fixed Fourier mesh \(2\pi m \tau /T\;(m= 0, 1,2,\ldots )\) is not required. As soon as the Padé polynomials \(P_{K}\) and \(Q_{K}\) are extracted from the input time signal \(\{c_{n}\}\), the non-parametric envelopes can be generated by the FPT. The total shape spectrum \(P_{K} /Q_{K}\) can be computed at any sweep frequency and these do not need to correspond to any preassigned grid. Thus, unlike the FFT, there is no conundrum in the FPT between the need to increase T in order to enhance resolution with worsening SNR. In other words, Padé-based resolution is not limited by the total acquisition time, T. Through the FPT, interpolation can be carried out relying exclusively upon the actual features of the encoded time signal, as opposed to zero-padding in the FFT. Interpolation is also a benefit of the extrapolation features of the FPT, namely, that a finer grid becomes available based on the time signal data predicted for \(t>T\) [19].

1.2.2.3 Noise suppression via numerator and denominator polynomials in the FPT

Further enhancing its high resolution properties is the non-linearity of the FPT, as a ratio of two polynomials, whereby noise is suppressed and SNR augmented [1, 2, 4]. Namely, with the numerator \({(P}_{K})\) and denominator \({(Q}_{K})\) polynomials, there is cancellation in the Padé spectrum \({(P}_{K}/Q_{K})\). A similar amount of noise or noise-like content is present in \(P_{K} \) and \(Q_{K}\) because these two polynomials are correlated (they are constrained by the relation \(G_{N}Q_{K}=P_{K})\). This noise is imported from \(\left\{ c_{n} \right\} \) by the expansion coefficients of \(P_{K}\) and \(Q_{K}.\) Even if the input time signal \(\left\{ c_{n} \right\} \) is a noiseless, synthesized FID, there will necessarily be some spurious (noise-like) parts of the solution of an over-determined system of linear equations for the expansion coefficients of \(Q_{K}\). As to \(P_{K},\) its polynomial coefficients are available from an analytical expression. This expression is given in terms of \(\left\{ c_{n} \right\} \) and the already extracted expansion coefficients of \(Q_{K}\), as is clear from \(G_{N}Q_{K}=P_{K}\). Regarding noise cancellation in the Padé spectrum \(P_{K}/Q_{K}\), it should be recalled that, generally, when e.g. two observables A and B are experimentally measured, or generated through numerical computations with finite precision, the errors in A and B are considerably canceled in their ratio A / B [18].

1.2.3 The non-parametric FPT

Non-parametric analysis via the \({\mathrm {FPT}}^{(\pm )}\) is automatically carried out as soon as the expansion coefficients \(\left\{ p_{r}^{\pm } \right\} \) and \(\left\{ q_{s}^{\pm } \right\} \) of the polynomials \(P_{K}^{\pm }\) and \(Q_{K}^{\pm }\) , respectively, are extracted using only the input time signal \(\{c_{n}\}\). The results are the non-parametrically generated Padé total shape spectra or envelopes, \(P_{K}^{\pm } /Q_{K}^{\pm }.\) If the input time signal \(\left\{ c_{n} \right\} \) were completely free of dephasing, the real and imaginary parts \({\mathrm {Re}}(P_{K}^{\pm } /Q_{K}^{\pm })\) and \({\mathrm {Im}}(P_{K}^{\pm } /Q_{K}^{\pm })\) would be purely absorptive and dispersive spectral lineshapes, respectively. In practice, this idealization would only be feasible with synthesized time signals having the input real amplitudes (i.e. those with zero-valued phases of the amplitudes of the fundamental harmonics). On the other hand, for encoded MRS time signals, the phases of the amplitudes of such FIDs are predominantly non-zero due to various sources, including a delay between the end of the excitation pulse and the beginning of the encoding. As a consequence, for encoded FIDs, absorption and dispersion lineshapes are inevitably mixed in \({\mathrm {Re}}(P_{K}^{\pm } /Q_{K}^{\pm })\) as well as in \({\mathrm {Im}}(P_{K}^{\pm } / Q_{K}^{\pm })\).

1.2.4 The parametric FPT (quantification)

Via a single numerical procedure consisting of polynomial rooting, the parametric variants \({\mathrm {FPT}}^{(\pm )}\) provide quantification of MRS time signal data. The roots of the characteristic equations of the numerator \(P_{K}^{\pm }\) and the denominator \(Q_{K}^{\pm }\) polynomials generate the zeros and poles of the Padé spectra \(P_{K}^{\pm } / Q_{K}^{\pm }\). Since the rational functions \(P_{K}^{\pm } / Q_{K}^{\pm }\) are meromorphic functions whose only singularities are poles, the roots of \(P_{K}^{\pm }\) and \(Q_{K}^{\pm }\) are the zeros and poles of \(P_{K}^{\pm } /Q_{K}^{\pm }\), respectively.

The roots \(z_{k}^{\pm 1} \) of equation \(Q_{K}^{\pm }(z^{\pm 1})=0\) yield the fundamental frequencies \(\omega _{k}^{\pm }\), where \(\omega _{k}^{\pm }=\mp (i/\tau ) \ln (z_{k}^{\pm 1})\). The corresponding amplitudes \(d_{k}^{\pm }\) in the \({\mathrm {FPT}}^{(\pm )}\) are automatically provided by the analytical expressions for the Cauchy residues of \({P_{K}^{\pm }(z^{\pm 1})} / Q_{K}^{\pm }(z^{\pm 1})\) taken at the \(k^{\mathrm {th}}\) pole \(z^{\pm 1}=z_{k}^{\pm 1} =z_{k,Q}^{\pm 1} \) :

$$\begin{aligned} d_{k}^{\pm } =\frac{P_{K}^{\pm } (z_{k,Q}^{\pm 1} )}{Q_{K}^{\pm '} (z_{k,Q}^{\pm 1} )} , Q_{K}^{\pm '} (z^{\pm 1} )=\frac{{\hbox {d}}Q_{K}^{\pm } (z^{\pm 1})}{{\hbox {d}}z^{\pm 1}}, Q_{K}^{\pm } (z_{k,Q}^{\pm 1} )=0, Q_{K}^{\pm '} (z_{k,Q}^{\pm 1} )\ne 0. \end{aligned}$$
(6)

Once the spectral frequencies and amplitudes become reconstructed, the parametric total shape spectra \(P_{K}^{\pm } /Q_{K}^{\pm }\) can be computed from either the Heaviside partial fractions:

$$\begin{aligned} \frac{P_{K}^{\pm } }{Q_{K}^{\pm } }=\frac{p_{0}^{\pm } }{q_{0}^{\pm } }+\sum \limits _{k=1}^K {\frac{d_{k}^{\pm } z^{\pm 1} }{z^{\pm 1} -z_{k,Q}^{\pm 1} }} , \end{aligned}$$
(7)

or from the equivalent canonical representations:

$$\begin{aligned} \frac{P_{K}^{\pm } }{Q_{K}^{\pm } }=\frac{p_{K}^{\pm } }{q_{K}^{\pm } }\prod \limits _{k=1}^K {\frac{z^{\pm 1}-z_{k,P}^{\pm 1} }{z^{\pm 1}-z_{k,Q}^{\pm 1} }} , P_{K }^{\pm } (z_{k,P}^{\pm 1} )=0. \end{aligned}$$
(8)

Coincidences \(z_{k,Q}^{\pm 1} =z_{k,P}^{\pm 1} \) of poles \(z_{k,Q}^{\pm 1} \) and zeros \(z_{k,P}^{\pm 1} \) lead to pole–zero cancellation, as especially evident in (8). Such an occurrence results in a smaller degree \({\textit{K}}\) of the polynomials in \(P_{K}^{\pm } /Q_{K}^{\pm }\), and this effectively reduces the dimensionality of the over-determined problem. Pole–zero coincidences yield zero-valued amplitudes \((d_{k}^{\pm }=0)\), as per (6), because in this particular case with \(z_{k,Q}^{\pm 1} =z_{k,P}^{\pm 1} \), we have \(P_{K}^{\pm } (z_{k,Q}^{\pm 1} )=0.\) Resonances with pole–zero coincidences (or near-zero coincidences) and the concomitant zero (or near zero) amplitudes are markedly unstable relative to any perturbation. They are classified as spurious or unphysical. This particular coupling of poles and zeros in spurious resonances is known as the phenomenon or Froissart doublets [2]. Their elimination from the \({\mathrm {FPT}}^{(\pm )}\) through pole–zero cancellation in spectra constitutes the powerful concept of Padé-based signal-noise separation (SNS) [4].

1.2.5 Stabilization of Padé-reconstructed envelopes

With a gradual augmentation of the degree of the Padé polynomials, the computation is carried out, such that the reconstructed spectra fluctuate until stabilization occurs. At that stage, all the terms in the Padé numerator and denominator polynomials cancel insofar as the computation is continued after the stabilized value of degree K in the \({\mathrm {FPT}}^{(\pm )}\) has been reached. Such a stabilization occurs in both the non-parametric and parametric generation of the envelopes \(P_{K}^{\pm } /Q_{K}^{\pm }\). The converged non-parametric and parametric Padé envelopes fully coincide with each other.

We proceed now to link the briefly outlined considerations about signal processing to a well-defined clinical problem in MRS, for which the highlighted features are very relevant. Specifically, by way of an illustration within the \({\mathrm {FPT}}^{(+)}\), we want to demonstrate how to non-parametrically and, hence, most effectively visually identify the presence of a molecular marker associated with breast cancer.

1.3 Phosphocholine: a breast cancer biomarker heretofore undetected with in vivo MRS

1.3.1 Importance and challenges in breast cancer diagnostics

Breast cancer is the most frequently diagnosed malignancy and the leading cause of cancer-related deaths among women worldwide [20, 21]. Timely breast cancer detection is vital and has been consistently associated with improved survival [20, 22, 23]. Screening aimed at early breast cancer detection is currently carried out via morphologic imaging techniques: mammography as the mainstay and magnetic resonance imaging (MRI) with its very high sensitivity applied among women at increased risk. However, these anatomic imaging methods, MRI in particular, are associated with a large percentage of false positive findings, i.e. they have poor specificity. False positive findings can engender various deleterious consequences [20, 24]. Hence, the need to go beyond anatomy, to assess the metabolic features of breast and other tissues has been emphasized: namely, to detect the molecular changes reflecting the cancer process [25], termed the “hallmarks of cancer” [26].

1.3.1.1 In vivo MRS for detecting breast cancer: reliance upon total choline

By revealing the metabolic features of breast tissue, both MRS (single-voxels) and its multi-voxel counterpart termed magnetic resonance spectroscopic imaging (MRSI) have been shown to enhance the specificity of MRI in distinguishing breast cancer from non-malignant breast lesions [27,28,29,30,31,32,33]. Nearly all the in vivo MRS studies aimed at characterizing breast lesion have focused upon the peak of total choline (tCho), located at chemical shift \(\sim \)3.2 parts per million (ppm). In the spectral envelope, the tCho peak, considered to reflect cell membrane turnover, has therefore been linked to breast cancer [28]. However, for the several hundred breast lesions evaluated in investigations using clinical (1.5 or 3T) scanners with FFT-based data processing, the diagnostic accuracy of MRS based upon estimates of tCho is insufficient (pooled estimates of sensitivity ranging from 71 to 88%, and specificity from 76 to 88% [27, 29, 30, 33], with the likelihood of publication bias considered to lower the actual diagnostic accuracy even further [29, 30, 33]). Namely, on the basis of lack of detected tCho, breast cancers, especially if small, were sometimes missed and benign lesions such as fibroadenomas were sometimes misdiagnosed as malignant, if tCho was detected.

In vivo MRS studies have been carried out on breast lesions using higher field (4 or 7T) scanners [34,35,36,37], for which it was anticipated that a smaller voxel size could be used, since SNR increases with magnetic field strength. However, tCho was still not detected in several breast cancers. In a number of benign breast lesions and in normal breast, tCho was reported as being present [35]. With the regard to the latter, further challenges arise in the normal breast during lactation. Namely, tCho is generally detected during that time, but breast cancer can occur during lactation and when it does, it is usually detected late [38]. Overall, it is seen that many different cut-points have been used for tCho in attempts to distinguish cancerous breast lesions from benign breast tissue. On the basis of tCho assessments through in vivo MRS, there are no reliable standards for adequately identifying breast cancer.

1.3.2 Components of tCho detected via in vitro MRS: Implications for breast cancer diagnostics

By in vitro MRS, much stronger static magnetic fields can be utilized, and the methods of analytical chemistry can also be applied to the excised specimens. Accordingly, through in vitro nuclear magnetic resonance (NMR), much richer metabolic information has been gleaned when employed to extracted specimens from the breast [39]. It was shown in these NMR studies of breast tissue that within tCho there are three components that aid in identifying breast cancer as opposed to benign or normal breast tissue. Namely, these are free choline (Cho) resonating at \(\sim \)3.21 ppm, phosphocholine (PC) at \(\sim \)3.22 ppm and glycerophosphocholine (GPC) at \(\sim \)3.23 ppm [40]. A “GPC to PC switch” occurs with malignant transformation in the breast. This switch is related to over-expression of choline kinase, the enzyme responsible for PC synthesis [40,41,42]. Two pathways, phosphorylation and oxidation of Cho, are favored with cancerous transformation of mammary cells [40]. Consequently, PC levels rise, whereas choline-derived ether lipids are diminished. High concentrations of PC and an elevated PC to GPC concentration ratio are interpreted as indications of malignant transformation of the breast [42, 43]. More abundant PC may also reflect a loss of the tumor suppressor p53 function [44]. Elevated PC is not only an indicator of breast cancer, but it is reportedly associated with other malignancies, as well [45, 46], and is thus considered a cancer biomarker [43].

Not only are the resonant frequencies of PC, GPC and free Cho very close to one another, but according to the NMR data from Ref. [39], phosphoethanolamine (PE) resonating at \(\sim \)3.22 ppm is also identified in extracted breast specimens. Phosphoethanolamine is not a cancer biomarker. Due to its abundance, the PE peak completely obfuscates the underlying PC resonance which is also located at \(\sim \)3.22 ppm in total shape spectra. Through the FFT, the overlapping resonances contained within the tCho peak cannot be resolved or quantified.

1.3.3 Non-parametric FPT compared to the FFT applied to the synthesized data associated with breast

In Refs. [12,13,14,15], detailed comparisons were made between the performance of the non-parametric FPT and the FFT on the controlled, i.e. synthesized noise-corrupted data (\(\sigma =0.0289\) RMS, where RMS is the root-mean-square of the noise-free MRS time signal) associated with normal breast, fibroadenoma and breast cancer reminiscent of those encoded in vitro in Ref. [39]. The FPT consistently showed a far superior resolution capability, generating converged total shape spectra at a partial signal length (\(N_{\mathrm {P}}=1700\)), whereas even at the full signal length \(\left( N=2048 \right) ,\) the FFT could produce only rough, uninformative envelopes. On the other hand, through the standard non-parametric computation of the absorption total shape spectrum in the FPT, the prominent peak centered at \(\sim \)3.22 ppm was a pure Lorentzian, with no indication whatsoever that a PC resonance was underlying PE. It was only through the parametric FPT that this was ascertained.

1.3.4 The parametric FPT: PC detected and quantified for the synthesized data related to breast

The parametric \({\mathrm {FPT}}^{(-)}\) was initially applied to synthesized noise-free MRS time signals with input parameters akin to those reconstructed from in vitro MRS data encoded for normal breast, fibroadenoma and breast cancer [39]. Both PC and PE, as well as the seven other input resonances were all exactly reconstructed by the \({\mathrm {FPT}}^{(-)}\) after convergence was attained [47, 48] for all three types of breast tissue. Subsequent controlled studies with simulated FIDs were performed with the addition of various levels of noise for normal breast, fibroadenoma and breast cancer [12,13,14,15]. At much higher noise levels (\(\sigma =2.89\) RMS), the parametric \({\mathrm {FPT}}^{(+)}\) was particularly effective in identifying and quantifying PC, PE and the other seven resonances, despite the presence of far more abundant spurious resonances [15].

1.4 Further exploration of the capabilities of the non-parametric FPT: the aim of the present study

Thus far, in all the cited studies applying the FPT to process MRS data associated with breast cancer, it was exclusively through parametric processing that the PC resonance could be identified. The complex–valued total shape spectrum was generated directly through \(P_{K} /Q_{K}\) , with the absorption spectrum being \(\mathrm {Re}(\hbox {P}_{K} /Q_{K}).\) As stated, from an inspection of the absorption spectrum provided by the non-parametric FPT via the ratio of two polynomials \(P_{K} /Q_{K}\) , the smooth, symmetric Lorentzian at \(\sim \)3.22 ppm, gave no hint whatsoever that there might be a PC peak beneath the far more abundant PE resonance [14].

It has been noted that a key advantage of rational polynomials as a quotient of two polynomials is their automatically built-in polar representation [3]. Consequently, rational polynomials are the most appropriate for describing functions with peaks, such as MR spectra. Among the rational polynomials, the Padé approximant is the most important because of its uniqueness for the power series expansion of the given function. The leading role of the Padé approximant is well-recognized in a wide range of disciplines incorporating spectral analysis. Among these are: mathematics (theory of approximations, extrapolations, series resummation), physics (quantum-mechanical eigenvalue problems), chemistry (ion-cyclotron resonance mass spectrometry ICRMS), in NMR, engineering (response functions) and technology (water leakage). In our research, we have used the Padé approximant in physics (particle collisions and spectroscopy) [49, 50] and chemistry (ICRMS, NMR) [51,52,53]. Subsequently, we brought this multi-purpose method of rational polynomials to MRS with a focus on early cancer diagnostics, where we incorporated the term “fast” to indicate a quasi-linear scaling of the computational complexity with the total signal length N, using the Euclid algorithm for extracting the numerator and denominator polynomials.

Non-parametric analysis through the \({\mathrm {FPT}}^{(\pm )}\) is a convenient initial step for processing MRS time signals, since, as noted, it can be carried out once the expansion coefficients \(\left\{ p_{r}^{\pm } \right\} \;\mathrm {and}\; \left\{ q_{s}^{\pm } \right\} \) of the polynomials \(P_{K}^{\pm }\) and \(Q_{K}^{\pm }\) , respectively, are generated from the input time signal \(\{c_{n}\}\). No polynomial rooting is required. As the spectral parameters have not yet been reconstructed, quantification is obviously not performed. The question arises as to whether more information could be gleaned via the non-parametric FPT applied to MRS time signals than has heretofore been the case. Namely, would it be possible to further explore the additional degree of freedom via the two polynomials of the FPT relative to the single polynomial of the FFT vis-à-vis reconstruction of spectral envelopes? To this end, we will compute absorptive \(\mathrm {Re}(P_{K}^{+} / Q_{K}^{+})\) and dispersive \(\mathrm {Im}(P_{K}^{+} / Q_{K}^{+})\) spectra directly and also from their corresponding partitioned analytical expressions to be given in Sect. 2.

From a practical standpoint, we would inquire as to whether a clear indication of the presence of underlying resonances in some composite spectral structures could be ascertained from these alternative, non-parametric representations. In the present study, the first on this particular sub-topic, we will carry out this investigation with a focus on the spectral region between 3.2 and 3.3 ppm for synthesized, noise-free MRS time signals associated with breast cancer according to the in vitro data of Ref. [39]. Thus, in concert with this general strategic inquiry, the direct clinical relevance will be addressed.

2 Methods

2.1 The MRS time signal based on in vitro encoding from cancerous breast: The input data

The MRS time signal was synthesized as the sum of complex-valued attenuated exponentials, according to the quantum-mechanical form:

$$\begin{aligned} c_{n} =\sum \limits _{k=1}^K {d_{k} z_{k}^{n} } , z_{k} =\text{ e }^{i\tau \omega _{k} }, 0\le n\le N-1, \text {Im}(\omega _{k} )>0,\omega _{k} =2\pi \nu _{k} , \end{aligned}$$
(9)

where as before, N denotes the total signal length. These theoretical data are based upon encoded FIDs from cancerous breast, as reported in Ref. [39]. Every signal point \(c_{n}\) from the presently used formula (9) is the sum of \(K= 9\) damped complex exponentials \(\exp \left( in\tau \omega _{k} \right) \;(1\le k\le 9)\). In general, the amplitudes \(d_{k}\) are complex. The angular frequencies \(\omega _{k}\) are also complex, such that there is an exponential decrease in \(c_{n}\) over time \(n\tau \left( n=0,1,2,\ldots ,N-1 \right) .\)

The corresponding MRS time signals of length \(N=65536\) in Ref. [39] were encoded at a Larmor frequency \((\nu _{\mathrm {L}}\) ) of 600 MHz. The static magnetic field strength was \(B_{0}\approx 14.1T\). The bandwidth, BW, was 6 MHz, where the inverse of this bandwidth is the sampling time \(\tau \). Herein, within the \({\mathrm {FPT}}^{(+)}\) we use only a quarter of the above, i.e. \(N/4=16384\) of the total signal length. Two of the nine resonances reconstructed in Ref. [39] were located in the frequency band between 1.3 and 1.5 ppm. These were lactate (Lac) at 1.332 ppm and alanine (Ala) at 1.471 ppm. The remaining seven resonances from the same Ref. [39] were in the frequency band between 3.2 to 3.3 ppm. Included therein were PC and PE, respectively resonating at 3.220 and 3.221 ppm, i.e. separated by a mere 0.001 ppm.

With two exceptions, the median metabolite concentrations were based upon 14 samples taken from twelve patients (2 samples were taken from two of the patients). The two exceptions were for \(\beta \)-glucose (\(\beta \)-Glc) and myoinositol (m-Ins), for which metabolite concentrations were available for only 6 and 9 samples, respectively [39].

These median concentrations were used to derive the values of \(\left| d_{k} \right| \) employed for the breast cancer input data, with \(\left| d_{k} \right| =2\mathrm {C}_{\mathrm {met}}/\mathrm {C}_{\mathrm {ref}}\) (\(\mathrm {C}_{\mathrm {ref}}= 0.05\) mM/g). The mean metabolite concentration is denoted by \(\mathrm {C}_{\mathrm {met}} \). Among these, the largest concentration is that of taurine (Tau). The internal reference (ref) was TSP (3-(trimethylsilyl-) 3,3,2,2-tetradeutero-propionic acid), a molecule which is not present in the tissue. Thus, \(\left| d_{k} \right| =\mathrm {C}_{\mathrm {met}}/(\mathrm {25}\mu \mathrm {M/g})\) of wet weight (ww). Since the \(T_{2}^{*}\) relaxation times were not reported in Ref. [39], we set the line widths (full-widths at half-maximum, FWHM) as 0.0008 ppm. The peaks are all Lorentzian, consistent with the time signal from (9). The phases \(\varphi _{k}\, (1\le k\le 9)\) from generally complex-valued \(d_{k}\) were all set to zero, such that all the input amplitudes are real, \(d_{k}=\left| d_{k} \right| \).

Specifically, the string of input metabolites and their fundamental parameters are as follows:

$$\begin{aligned} \left. \begin{array}{l} \text{ Met }_{k} =\{\text{ Lac }, \text{ Ala }, \text{ Cho }, \text{ PC }, \text{ PE }, \text{ GPC },\beta \text{-Glc }, \text{ Tau }, \text{ m-Ins }\}, \\ \text{ Re }(\nu _{k} )=\{1.332,1.471,3.212,3.220,3.221,3.232,3.251,3.273,3.281\}\;\hbox {ppm},\\ \text{ Im }(\nu _{k} )=0.0008 \hbox { ppm } (1\le k\le 9) \\ d_{k} =\left| {d_{k} } \right| =\{0.325,0.032,0.004,0.012,0.090,0.009,0.029,0.112,0.036\} \text{ au }, \\ \end{array}\right\} \nonumber \\ \end{aligned}$$
(10)

where the acronym au denotes arbitrary units. As stated, the \({\mathrm {FPT}}^{(+)}\) is presently applied to the noise-free MRS time signal.

2.2 Two ways of computing the envelopes

The envelopes will be computed first, as common practice, by directly feeding the set of the extracted complex numbers \(P_{K}^{+} /Q_{K}^{+}\) into the computer to generate the pure absorption, \({\mathrm {Re}}({P}_{K}^{+} / Q_{K}^{+})\) and pure dispersion, \({\mathrm {Im}}(P_{K}^{+} / Q_{K}^{+}),\) spectral lineshapes. Alternatively, the same absorption and dispersion envelopes can be computed from the explicit expressions for the real and imaginary parts, respectively, of the complex spectrum \(P_{K}^{+} /Q_{K}^{+}\).

2.2.1 Why partitioning of the total shape spectra?

The mentioned explicit expressions for \({\mathrm {Re}(P}_{K}^{+} /Q_{K}^{+})\) and \({\mathrm {Im}(P}_{K}^{+} / Q_{K}^{+})\) taken “by hand” from \(P_{K}^{+} /Q_{K}^{+}\) constitute the presently introduced “partitioned envelopes”. The motivation for this is, in fact, suggested by the polynomial quotient form of the complex spectrum \(P_{K}^{+} /Q_{K}^{+}\) in the \({\mathrm {FPT}}^{(+)}\). Namely, this latter Padé spectrum is, already by its definition, subdivided into two compartments: the numerator \(P_{K}^{+}\) and denominator \(Q_{K}^{+}\) polynomials. Polynomials \(P_{K}^{+}\) and \(Q_{K}^{+}\) can respectively produce only zeros and poles in the Padé complete spectrum given by the meromorphic complex function \(P_{K}^{+} /Q_{K}^{+}.\) Part \(P_{K}^{+}\) is recognized as the moving average (MA), whereas part \(Q_{K}^{+}\) is the auto-regression (AR). The spectrum \(P_{K}^{+} /Q_{K}^{+}\) of the combined AR and MA processes represents the ARMA (auto-regressive moving average) model whose \(z-\)transform is equivalent to the \({\mathrm {FPT}}^{(+)}\) [2, 4]. In fact, the expansion coefficients \({\{q}_{s}^{+}\} \;(1\le s\le K)\) of polynomial \(Q_{K}^{+}\) coincide with the backward prediction coefficients in the AR process.

Spectra generated by using \(P_{K}^{+}\) alone are also known as an “All-zero model”. Similarly, spectra built by employing only \(Q_{K}^{+}\) go under the name of an “All-pole model”. In other words, the reciprocal \({1/Q}_{K}^{+}\) would contain only poles and these are determined by the roots of the characteristic or secular equation \(Q_{K}^{+}=0\). Thus, if the quotient \(P_{K}^{+} /Q_{K}^{+}\) is alternatively viewed as the product \({[P}_{K}^{+}]\cdot {[1/Q}_{K}^{+}]\), it would be possible to determine, and then visualize separate contributions to \({\mathrm {Re}(P}_{K}^{+} / Q_{K}^{+})\) and \({\mathrm {Im}(P}_{K}^{+} /Q_{K}^{+})\) stemming from the various products of the real and imaginary parts of \(P_{K}^{+}\) (MA) and \({[1/Q}_{K}^{+}]\) (AR).

Such separate products follow automatically from the general formula for the ratio of any two complex numbers \(z_{1} \) and \(z_{2} \) as \(z_{1} /z_{2} =z_{1} z_{2}^{*} /\left| {z_{2} } \right| ^{2}\), where the star superscript indicates the operation of complex conjugation. Using this straightforward rule for the case of \(P_{K}^{+} /Q_{K}^{+}\) immediately gives the mentioned separate products in the form of the below-listed quantities \({A}_{K}^{+},{B}_{K}^{+},{C}_{K}^{+}\) and \({D}_{K}^{+}\) for the partitioned envelopes:

$$\begin{aligned} \frac{P_{K}^{+}}{Q_{K}^{+}}={\mathrm {Re}(P}_{K}^{+} / Q_{K}^{+}) \quad +{i\mathrm {Im}(P}_{K}^{+} / Q_{K}^{+}), \end{aligned}$$
(11)

with \(i=\sqrt{-1} \) being imaginary unity,

$$\begin{aligned} {\mathrm {Re}(P}_{K}^{+} /Q_{K}^{+}) ={A}_{K}^{+}+B_{K}^{+},\quad {\mathrm {Im}}(P_{K}^{+} /Q_{K}^{+}) =C_{K}^{+}+D_{K}^{+}, \end{aligned}$$
(12)

where,

$$\begin{aligned} A_{K}^{+}= & {} {\mathrm {[Re}(P}_{K}^{+})]{\mathrm {[Re}(Q}_{K}^{+})]/\left| Q_{K}^{+} \right| ^{2}={\mathrm {[Re}(P}_{K}^{+})]{\mathrm {Re}(1/Q}_{K}^{+}), \end{aligned}$$
(13)
$$\begin{aligned} B_{K}^{+}= & {} {\mathrm {[Im}(P}_{K}^{+})]{\mathrm {[Im}(Q}_{K}^{+})]/\left| Q_{K}^{+} \right| ^{2}={\mathrm {[Im}(P}_{K}^{+})]{\mathrm {Im}(1/Q}_{K}^{+}), \end{aligned}$$
(14)

and

$$\begin{aligned} C_{K}^{+}= & {} {\mathrm {-[Re}(P}_{K}^{+})]{\mathrm {[Im}(Q}_{K}^{+})]/\left| Q_{K}^{+} \right| ^{2}={\mathrm {-[Re}(P}_{K}^{+})]{\mathrm {Im}(1/Q}_{K}^{+}), \end{aligned}$$
(15)
$$\begin{aligned} D_{K}^{+}= & {} {\mathrm {[Im}(P}_{K}^{+})]{\mathrm {[Re}(Q}_{K}^{+})]/\left| Q_{K}^{+} \right| ^{2}={\mathrm {[Im}(P}_{K}^{+})]{\mathrm {Re}(1/Q}_{K}^{+}). \end{aligned}$$
(16)

The part \(1/\left| Q_{K}^{+} \right| ^{2}\) in \(A_{K}^{+}\), \(B_{K}^{+}\), \(C_{K}^{+}\) and \(D_{K}^{+}\) is the so-called power spectrum in an “All pole model”. When \(P_{K}^{+}\) and \(Q_{K}^{+}\) are divided and the resulting numbers directly programmed as \(P_{K}^{+} /Q_{K}^{+},\) the computer would give the complete contributions \(\mathrm {Re}(P_{K}^{+} /{Q_{K}^{+}})\) and \(\mathrm {Im}(P_{K}^{+} /{Q_{K}^{+}})\) as in (11), without the specifics (12)–(16). This standard procedure includes all the intact interference effects, with no insight whatsoever into the separate influence of the constituent parts of \(P_{K}^{+} /Q_{K}^{+}\). However, when \(\mathrm {Re}(P_{K}^{+} /{Q_{K}^{+}})\) and \(\mathrm {Im}(P_{K}^{+} /{Q_{K}^{+}})\) are identified by (12)–(16), prior to any numerical computations, the possibility emerges to peer into the inner structure of the overall envelope \(P_{K}^{+} /Q_{K}^{+}.\)

This inner structure appears in the partitioned envelopes \(A_{K}^{+}\), \(B_{K}^{+}\), \(C_{K}^{+}\) and \(D_{K}^{+}\) that are built from the pertinent products of the two spectra (at a time) in the MA and AR sequences. Thus, the absorption \(\mathrm {Re}(P_{K}^{+} /{Q_{K}^{+}})\) of the complete spectrum \(P_{K}^{+} /Q_{K}^{+}\) is the sum \(A_{K}^{+} + B_{K}^{+}\) of the absorption-absorption \({(A}_{K}^{+})\) and dispersion-dispersion \({(B}_{K}^{+})\) products via \(A_{K}^{+}={\mathrm {[Re}(P}_{K}^{+})]{\mathrm {Re}(1/Q}_{K}^{+})\) and \({B_{K}^{+}=\mathrm {[Im}(P}_{K}^{+})]{\mathrm {Im}(1/Q}_{K}^{+}), \) as per (13) and (14), respectively. Analogously, the dispersion \(\mathrm {Im}(P_{K}^{+} / {Q_{K}^{+})}\) of \(P_{K}^{+} /Q_{K}^{+}\) is the sum \(C_{K}^{+} + D_{K}^{+}\) of the cross-products (or mixed products) through absorptive-dispersive \(C_{K}^{+}={\mathrm {-[Re}(P}_{K}^{+})]{\mathrm {Im}(1/Q}_{K}^{+})\) and dispersive-absorptive \(D_{K}^{+}={\mathrm {[Im}(P}_{K}^{+})]{\mathrm {Re}(1/Q}_{K}^{+})\) lineshapes according to (15) and (16), respectively.

The described compartmentalization of \(\mathrm {Re}(P_{K}^{+} / {Q_{K}^{+}})\) and \(\mathrm {Im}{(P_{K}^{+}} / {Q_{K}^{+}})\) is, in fact, a redistribution of the full interference between the two partitioned envelopes. Therefore, a smaller interference effect in \(A_{K}^{+}\) and \(B_{K}^{+}\), when these are viewed separately, could unfold certain hidden resonances in compound peaks. A similar remark also applies to \(C_{K}^{+}\) and \(D_{K}^{+}\) taken as individual, partitioned envelopes. As a check of the correctness of the expressions (11)–(16), the spectra \(\mathrm {Re}(P_{K}^{+} / {Q_{K}^{+})}\) computed directly or via \(A_{K}^{+}+ B_{K}^{+}\) must coincide with each other. The same ought to hold true also for a direct computation of \(\mathrm {Im}(P_{K}^{+} / {Q_{K}^{+})}\) and by way of the sum \(C_{K}^{+} +D_{K}^{+}\).

For single, isolated resonances either way of these two computations would yield mere superpositions of peaks with their minimal interference due to lack of overlap. By contrast, overlapped resonances may interact strongly depending on the extent of overlap. This would result in enhanced interference which is, in turn, able to mask the individual lineshapes of the closely spaced resonances. It is in this case that the partitioned envelopes are expected to be especially useful in disentangling the hidden spectral content of the compound peaks. We emphasize that such an anticipation is based on the reduced interference in \(A_{K}^{+}\) and \(B_{K}^{+}\) relative to \(A_{K}^{+}+B_{K}^{+},\) with a similar outcome in \(C_{K}^{+}\) and \(D_{K}^{+}\) with respect to \(C_{K}^{+} + D_{K}^{+}\). In other words, interference reduction by spectra partitioning should lead to a narrower localization of the overlapped resonances with potential dips or “windows” in between the adjacent, tightly packed peaks. This framework is tested in the Results Section, with a particular focus on the possibility of using the partitioned envelopes to visualize the separate PC and PE resonances. Recall that the PC peak is buried in the PC \(+\) PE compound resonance obtained by conventionally computed, non-partitioned envelopes.

3 Results

All the reconstructions are performed using a partial signal length \(N_{\mathrm {P}} = 6000\, (K= 3000)\) of full signal length \(N=16384\), which itself is only a quarter of its encoded counterpart for Ref. [39]. Figure 1 displays the partitioned and non-partitioned absorption envelopes computed non-parametrically in the \({\mathrm {FPT}}^{(+)}\). Along the abscissae of each panel are the input chemical shifts in the spectral region between 3.205 and 3.290 ppm. These are symbolized by circles that are mainly open and shown in black. The two exceptions with the filled green and magenta circles relate to PC and PE, respectively. The colored filling is shown only when the PC and PE lineshapes are peaked practically at their correct locations 3.220 and 3.221 ppm, respectively. This is the case in panels (a) and (b) where PC and PE are separately visualized, although both circles are not simultaneously filled. Therein, the PC and PE peaks are centered almost precisely at 3.220 and 3.221 ppm only on panels (a) and (b), respectively. For this reason, panels (a) and (b) each have only one filled circle.

Fig. 1
figure 1

The partitioned and non-partitioned absorption envelopes computed non-parametrically in the \({\mathrm {FPT}}^{(+)}\) by using the noiseless FID, sampled at \(N=16384\) and truncated at \(N_{\mathrm {P}}=6000\, (K = 3000)\). Along the abscissae of each panel are the input chemical shifts. The definitions of the displayed spectra \(A_{K}^{+}\) and \(B_{K}^{+}\) are on the titles of the panels (a) and (b), respectively. Panel (c) repeats the top 2 panels alongside \(A_{K}^{+}+B_{K}^{+}\) . Panel (d) shows 2 identical curves for \(\mathrm {Re}\left( P_{K}^{+}/Q_{K}^{+} \right) \) computed with (black) and without (blue) partitioning. For a discussion and the meaning of color-coding, see the main text. (color online)

Full size image

On panel (a), the PE peak is slightly shifted to the left from the associated input fundamental frequency 3.221 ppm and its circle if left unfilled. Similarly, on panel (b), the PC peak is slightly shifted to the right of its exact location at 3.220 ppm, and the open circle is seen therein. However, on panel (c), both circles for PC and PE are filled, since therein the entire partitioned spectra from panels (a) and (b) are displayed together. Panel (a) shows the partitioned envelope spectrum for \(A_{K}^{+}=\left[ \mathrm {Re}\left( P_{K}^{+} \right) \right] \;\mathrm {Re}\left( 1/Q_{K}^{+} \right) \). Therein, PC and PE are clearly distinguished as two separate peaks of fairly comparable heights, and the five other resonances are also identified. Panel (b) exhibits the partitioned envelope spectrum for \(B_{K}^{+}=\left[ \mathrm {Im}\left( P_{K}^{+} \right) \right] \;\mathrm {Im}\left( 1/Q_{K}^{+} \right) \). Once again, PC and PE are clearly seen to be two separate, adjacent peaks, with PE being more prominent than PC.

Fig. 2
figure 2

The partitioned and non-partitioned dispersion envelopes computed non-parametrically in the \({\mathrm {FPT}}^{(+)}\) by using the noiseless FID, sampled at \(N=16384\) and truncated to \(N_P = 6000\, (K = 3000)\): Along the abscissae of each panel are the input chemical shifts. The definitions of the displayed spectra \(C_{K}^{+}\) and for \(D_{K}^{+}\) are on the titles of the panels (a) and (b), respectively. Panel (c) repeats the top 2 panels alongside \(C_{K}^{+}+D_{K}^{+}\). Panel (d) shows 2 identical curves for Im \(\mathrm {Re}\left( P_{K}^{+}/Q_{K}^{+} \right) \) computed with (black) and without (blue) partitioning. For a discussion and the meaning of color-coding, see the main text. (color online)

Full size image

Taurine and \(\beta \)-Glc show much smaller peak heights in the partitioned envelope spectrum for \(B_{K}^{+}\) compared to that for \(A_{K}^{+}\). These latter two partitioned envelope spectra are displayed jointly in panel (c), with the same color coding as in panels (a) and (b): green for \(A_{K}^{+}\) and magenta for \(B_{K}^{+}\). In addition, on panel (c) is the summed envelope \(A_{K}^{+}+ B_{K}^{+}\), indicated in black, where only a single compound peak PC \(+\) PE can be identified in the interval [3.220, 3.221] ppm. It can be seen on panel (d), that the complete absorption envelope: \(A_{K}^{+}+B_{K}^{+}=\left\{ \left[ \mathrm {Re}\left( P_{K}^{+} \right) \right] \mathrm {Re}\left( {1/Q}_{K}^{+} \right) \right\} +\left\{ \left[ \mathrm {Im}\left( P_{K}^{+} \right) \right] \mathrm {Im}\left( {1/Q}_{K}^{+} \right) \right\} \) is indistinguishable from the related non-partitioned absorption envelope \(\mathrm {Re}\left( P_{K}^{+}/Q_{K}^{+} \right) \), both of which display a symmetrical smooth single Lorentzian peak in the range [3.220, 3.221] ppm, without any indication whatsoever that more than one peak may be present therein.

The most notable feature of the absorption spectra displayed in Fig. 1 is that the PC and PE peaks appearing in both partitions \(A_{K}^{+}\) and \(B_{K}^{+}\) are so well delineated that the dips (or “windows”) between them descend all the way down to the background or baseline of zero-values ordinates. On panel (a), it appears as if \(A_{K}^{+}\) needs to push PE a bit upstream in order to place PC at its correct position, 3.220 ppm. Likewise, on panel (b), it is seen that \(B_{K}^{+}\) acts as if it were necessary to push PC a bit downstream so that PE could be centered at the corresponding correct location, 3.221 ppm. These slight dislocations in PE or PC within \(A_{K}^{+}\) or \(B_{K}^{+}\) on panels (a) or (b) are due to the minimal distance of merely 0.001 ppm between the input chemical shifts of 3.220 and 3.221 ppm of PC and PE, respectively. Moreover, this incremental separation of 0.001 ppm between the chemical shifts, or equivalently, Re\({(\nu }_{k}),\) of PC and PE is smaller than the sum 0.0016 ppm of their associated individual values of Im\((\nu _{k})\). By reference to the input parameters in (10), all the resonances have the same exceedingly small values for Im(\(\nu _{k})\) that are Im(\(\nu _{k})= 0.0008\) ppm. Given that the imaginary frequency Im(\(\nu _{k})\) is the measure of the breadth of an absorptive Lorentzian resonance, it is understandable why the individuality of PC and PE is masked under the combined PC and PE peak on panel (d) of Fig. 1.

When it comes to the background baseline, panel (c) is the most illustrative not only regarding PC and PE, but also with respect to the remaining five resonances (Cho, GPC, \(\beta \)-Glc, Tau and m-Ins) throughout the displayed spectral region of interest (SRI), which is 3.205–3.290 ppm. Namely, on panel (c), the black curve for \(A_{K}^{+} + B_{K}^{+}\) just like the blue curve for the non-partitioned counterpart \(\mathrm {Re}(P_{K}^{+} / {Q_{K}^{+})}\) on panel (d), is entirely positive-definite, and exhibits a perfectly smooth background immersed into the near-zero level of the ordinate. Such an ideal smoothness of the black curve on panel (c) comes after mutual exact compensations of the background undulations present in the green and magenta curves for \(A_{K}^{+}\) and \(B_{K}^{+}.\) The partitioned envelopes \(A_{K}^{+}\) and \(B_{K}^{+}\) display rolling backgrounds that are seen on panel (c) as being almost perfectly symmetrical around the black curve for \(A_{K}^{+} + B_{K}^{+}\) . Hence, the mentioned compensation of whichever deviations \(A_{K}^{+}\) and \(B_{K}^{+}\) might individually have with respect to the non-rolling background in \(A_{K}^{+} + B_{K}^{+}.\)

The reason for which the rolling backgrounds appear in the green and magenta curves on panel (c) is in only a partial suppression of spurious resonances in \(A_{K}^{+}\) and \(B_{K}^{+}\), respectively. Conversely, a full suppression of all the spurious resonances is behind the totally smooth background in the black curve for \(A_{K}^{+} +B_{K}^{+}\) on panel (c). When \(\mathrm {Re}(P_{K}^{+} / {Q_{K}^{+})}\) is conceived as \(A_{K}^{+} + B_{K}^{+}\), suppression of spurious resonances is necessarily only partial in either \(A_{K}^{+}\) or \(B_{K}^{+}.\) Suppression of spurious resonances is mediated by pole–zero cancellations, as discussed with the parametric fast Padé transform. Quantification to explicitly determine poles and zeros is not performed in the non-parametric processing whose results are depicted on Fig. 1. Nevertheless, the information on the implicit presence of spurious poles and zeros is still felt by \(P_{K}^{+}\) and \(Q_{K}^{+}\) in the envelope \(P_{K}^{+}/Q_{K}^{+}\) through the expansion coefficients \(\{p_{r}^{+}\}\) and \(\{q_{s}^{+}\}\). In other words, regardless of whether or not we quantify via \(P_{K}^{+}=0\) and \(Q_{K}^{+}=0\) to find the explicit zeros \(z_{k,P}^{+} \) and \(z_{k,Q}^{+} \) , respectively, the nearly equal amount of spuriousness in \(P_{K}^{+}\) and \(Q_{K}^{+}\) will cancel out in the Padé spectral ratio \(P_{K}^{+}/Q_{K}^{+}\).

The corresponding partitioned and non-partitioned dispersion envelopes are presented in Fig. 2, with the input chemical shift parameters along the abscissae. The partitioned dispersion envelope for \(C_{K}^{+}\) is shown in panel (a), where \(C_{K}^{+}=-\left[ \mathrm {Re}\left( P_{K}^{+} \right) \right] \;\mathrm {Im}\left( 1/Q_{K}^{+} \right) \). Both PC and PE are identified in the chemical shift region [3.220, 3.221] ppm. The five other resonances are of quite low amplitude, but can still be visualized. Panel (b) displays the partitioned dispersion envelope for \(D_{K}^{+}=\left[ \mathrm {Im}\left( P_{K}^{+} \right) \right] \;\mathrm {Re}\left( 1/Q_{K}^{+} \right) \). Here also, PC and PE are clearly separated from each other. The negative dispersion component of Tau is also very prominent in panel (b). The smaller downward pointed branches or lobes are also seen for \(\beta \)-Glc and GPC. The partitioned dispersion spectra for \(C_{K}^{+}\) and \(D_{K}^{+}\) are juxtaposed in panel (c), with the same color-coding as previously: green and magenta, respectively, alongside the black colored complete dispersion spectrum for \(C_{K}^{+} + D_{K}^{+}\). For \(C_{K}^{+} +D_{K}^{+}\), there is a prominent negative lobe at 3.22 ppm, but no indication at all that there are actually two resonances, i.e. PC and PE at that chemical shift site. It can be seen in panel (d) that the complete dispersion spectrum for \(C_{K}^{+} +D_{K}^{+}=\left\{ \left[ \mathrm {Im}\left( P_{K}^{+} \right) \right] \mathrm {Re}\left( {1/Q}_{K}^{+} \right) \right\} -\left\{ \left[ \mathrm {Re}\left( P_{K}^{+} \right) \right] \mathrm {Im}\left( {1/Q}_{K}^{+} \right) \right\} \) is identical to that for the non-partitioned absorption envelope \(\mathrm {Im}\left( P_{K}^{+}/Q_{K}^{+} \right) \).

Fig. 3
figure 3

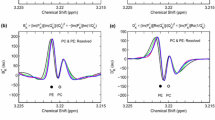
The partitioned and non-partitioned absorption (left) and dispersion (right) envelopes computed non-parametrically in the FPT\(^{(+)}\): A zoomed view of Figs. 1 and 2 into the critical frequency window [3.215,3.225] ppm containing the overlapping PC and PE resonances. Along the abscissae of each panel are the input chemical shifts of PC and PE. The definitions of the displayed spectra \(A_{K}^{+}, \,B_{K}^{+}, \,C_{K}^{+} \,\mathrm{and} \,D_{K}^{+}\) are on the titles of the panels (a), (b), (e), (f), respectively. Panels (c) and (g) join together the top 2 panels. Panels (d) and (h) show the partitioned spectra alongside \(A_{K}^{+}+ \,B_{K}^{+}\,\mathrm{and} \,C_{K}^{+} + D_{K}^{+}\), respectively. For a discussion and the meaning of color-coding, see the main text. (color online)

Full size image
Fig. 4
figure 4

Non-parametrically reconstructed total shape spectra and the parametric processing (quantification) for the component shape spectra in the \({\mathrm {FPT}}^{(+)}\) using the noiseless FID sampled at \(N=16384\) and truncated at \(N_{\mathrm {P}}=6000\, (K = 3000)\). The input chemical shift parameters are along the abscissae. Left column absorption spectra, right column dispersion spectra. The component absorption and dispersion spectra generated via the parametric \({\mathrm {FPT}}^{(+)}\) in panels (a) and (e), respectively. Panels (b) and (f), respectively: partitioned envelope spectra \(A_{K}^{+}\) (absorption) and \(C_{K}^{+}\) (dispersion). Panels (c) and (g): the partitioned envelope spectra \(B_{K}^{+}\) (absorption) and \(D_{K}^{+}\) (dispersion), respectively. Non-partitioned absorption and dispersion envelopes are shown in panels (d) and (h), respectively. (color online)

Full size image

Figure 3 zooms into the critical frequency window [3.215, 3.225] ppm containing the overlapping PC and PE resonances. The left column shows absorption spectra and the right column presents the dispersion spectra. In panel (a) is the partitioned absorption envelope spectrum for \(A_{K}^{+}.\) Resonance PC at 3.220 ppm is a filled green circle. Panel (b) exhibits the partitioned absorption envelope spectrum for \(B_{K}^{+}\) . Resonance PE at 3.221 ppm is a filled magenta circle. In panel (c), the two partitioned envelope spectra are jointly shown (green for \(A_{K}^{+}\), magenta for \(B_{K}^{+})\). Therein, both PC and PE are filled circles. In panel (d), the two partitioned envelope spectra are displayed (green for \(A_{K}^{+}\), magenta for \(B_{K}^{+})\) alongside the complete envelope \((A_{K}^{+}+ B_{K}^{+})\), indicated in black. Here, both PC and PE are filled circles. Panel (e) is the partitioned dispersion envelope spectrum for \(C_{K}^{+}.\) The PC peak at 3.220 ppm is a filled green circle. Panel (f) exhibits the partitioned dispersion envelope spectrum for \({D}_{K}^{+}\), where PE at 3.221 ppm is a filled magenta circle. In panel (g), the two partitioned envelope spectra are plotted together (green for \(C_{K}^{+}\), magenta for \(D_{K}^{+})\). Both PC and PE are filled circles. In panel (h), the two partitioned envelope spectra are presented together (green for \(C_{K}^{+}\), magenta for \(D_{K}^{+})\) alongside the complete envelope \((C_{K}^{+}+ D_{K}^{+})\), indicated in black. Both PC and PE are filled circles.

A comparison between the non-parametrically reconstructed total shape spectra and the component shape spectra (parametric estimation) is provided in Fig. 4. Here too, the input chemical shift parameters are given along the abscissae. On the left column are the various absorption spectra and on the right column are the related dispersion spectra. The component spectra, as reconstructed by the parametric \({\mathrm {FPT}}^{(+)}\), are displayed in panels (a) and (e). These are the standard absorption \({\mathrm {Re}(P_{K}^{+} / Q_{K}^{+})}_{k}\) and dispersion \({\mathrm {Im}(P_{K}^{+} /Q_{K}^{+})}_{k}\) component spectra without partitioning, where the subscript k refers to the \(k^{\mathrm {th}}\) resonance. In the absorption component spectra, it is clearly seen that at 3.220 ppm, there is a PC peak which completely underlies the much larger and wider PE at 3.221 ppm. Two separate, bi-lobed peaks, one the larger PE and the other the smaller PC are also well delineated on the dispersion component spectrum of panel (e). In panels (b) and (f), respectively, juxtaposed are the partitioned envelope spectra for \(A_{K}^{+}\) (absorption) and \(C_{K}^{+}(\)dispersion), wherein PE and PC are resolved. This is also the case in panels (c) and (g) in the partitioned envelope spectra for the \(B_{K}^{+}\) (absorption) and \(D_{K}^{+}\) (dispersion), where PE and PC are readily identified. Each of the panels (d) and (h) for absorptive \({\mathrm {Re}(P}_{K}^{+} / Q_{K}^{+})\) and dispersive \({\mathrm {Im}(P}_{K}^{+} / Q_{K}^{+})\) envelopes, respectively, shows two indistinguishable curves with (black) and without (blue) partitioning. Therein, for either way of computations, there is no hint of any kind that PC and PE are present at 3.22 ppm, i.e. they appear as unresolved.

4 Discussion and conclusions

The present paper is the first time that the non-parametric FPT has been applied in the partitioned manner with the aim of identifying underlying components, without quantification. The most striking finding is that indeed such analysis is not only fruitful, but also trustworthy. The latter was confirmed by subsequent comparison with the component shape spectra computed via \({\mathrm {Re}(P_{K}^{+} /Q_{K}^{+})}_{k}\) and \({\mathrm {Im}(P_{K}^{+} / Q_{K}^{+})}_{k}\) after quantification (parametric processing).

The key is to examine the interference mechanism which is present in \(A_{K}^{+}\) and in \(B_{K}^{+}\) for the partitioned absorption envelopes and in \(C_{K}^{+}\) and in \(D_{K}^{+}\) for the partitioned dispersion envelopes. Thus, in all four of these cases, PC and PE were clearly resolved. However, with the sums \(A_{K}^{+} \quad +\) \(B_{K}^{+}\) for the real part, \(\mathrm {Re}\left( P_{K}^{+}/Q_{K}^{+} \right) ,\) or \(C_{K}^{+} + D_{K}^{+}\) for the imaginary part, \(\mathrm {Im}\left( P_{K}^{+}/Q_{K}^{+} \right) \), these effects were washed out. Thus, the absorption and dispersion spectra for \(A_{K}^{+} + B_{K}^{+}\) and \(C_{K}^{+} + D_{K}^{+}\) are identical, respectively to the standard, non-partitioned total shape spectra \(\mathrm {Re}\left( P_{K}^{+}/Q_{K}^{+} \right) \) and \(\mathrm {Im}\left( P_{K}^{+}/Q_{K}^{+} \right) \), and neither of these two representations resolved PC and PE.

The findings in this paper have clear fundamental implications. At the same time, their practical importance, which also motivated this investigation, is emphasized, especially for the specific clinical problem under study. Namely, it would now appear to be feasible to first apply the non-parametric FPT, explicitly extracting the analytical expressions for the real and imaginary parts of complex \(P_{K}/Q_{K}\) by way of (15)–(16). This would be a convenient initial “screening” step to assess whether or not the particular cancer biomarker PC is present. Further, the quantification procedure through the parametric FPT (which reconstructs all the metabolites from the SRI), might have a special focus upon those cases in which PC was identified firstly by non-parametric processing. Such an approach has heretofore been entirely untenable with the conventional, low resolution, single polynomial FFT, which does not quantify at all. Rather, as outlined, because of the insufficient accuracy of Fourier-based in vivo MRS with clinical (1.5 or 3T) MR scanners for identifying breast cancers and distinguishing these from benign breast lesions, investigations have been made using higher field scanners. Not only were these attempts sub-optimal, but the enormous costs [54] would preclude such an approach for widespread applications in breast cancer diagnostics, including and especially screening/surveillance. Rather, on the basis of the present study, it can now be recommended that this step-wise, multi-faceted Padé-based approach be tested in vivo, aimed at validation on clinical MR scanners for breast cancer diagnostics, and beyond.