1 Introduction

The information theory (IT) [1–8] is one of the youngest branches of the applied probability theory in which the probability ideas have been introduced into the field of communication, control, and data processing. These classical information concepts have been also successfully applied to explore the molecular electron probabilities and the system chemical bonds, e.g., [9–20]. Both the electron density or its shape factor, the probability distribution determined by the wave-function modulus, and the system current distribution, related to the gradient of the wave-function phase, ultimately contribute to the resultant information content of molecular states. The particle density reveals the classical information content, while the probability current generates its non-classical complement in the overall (quantum) information measure [9, 10, 21, 22]. The latter introduces a non-vanishing information source into the associated entropy/information continuity equation, which expresses a local balance in the time evolution of the resultant information density [10, 13].

The IT perspective on molecular systems introduces into the theory of electronic structure the novel entropy-representation, which complements the familiar energy-representation of the molecular quantum mechanics. Such a dual representation parallels that known from the ordinary thermodynamics. It establishes the equivalent energy and entropy/information principles governing the system equilibrium states and provides a new, unifying perspective on molecular states, extends the variety of tools for probing chemical processes, and enriches the range of available descriptors of the bonding patterns in molecules.

Many classical problems of theoretical chemistry can be approached afresh using the IT perspective. For example, the displacements of the classical information distribution in molecules, relative to the promolecular reference consisting of the molecularly placed non-bonded constituent atoms, have been investigated [11–13] and the least-biased partition of the molecular electron distributions into subsystem contributions, e.g., densities of bonded atoms, has been examined [11–13, 23–33]. This IT approach has been shown to lead to the “stockholder” atoms-in molecules (AIM) of Hirshfeld [34]. These optimum density pieces have been derived from alternative global and local variational principles of IT. This way of dividing the one-electron distributions has been subsequently generalized in a related problem of the AIM partitioning of two-electron densities [11, 30–32]. The non-additive Fisher information in the atomic orbital (AO) resolution has been used as the contra-gradience (CG) criterion for localizing bonding regions in molecules [11–16, 35–38], while the related information (kinetic energy) density in the molecular orbital (MO) resolution has been shown [11, 38] to determine the vital ingredient of the electron-localization function (ELF) [39–41].

The communication theory of the chemical bond (CTCB) has been developed [11–13, 42–59], using the basic entropy/information descriptors of the molecular communication channels in the AIM, orbital or local levels of resolving the electron probability distributions. The conditional probabilities of these information systems have been generated from the bond-projected superposition principle of quantum mechanics [60, 61]. The same bond descriptors have been used to provide the information-scattering perspective on the intermediate stages in the electron redistribution processes [62], including the atom promotion via the orbital hybridization [63], and the communication theory for excited electron configurations has been developed [64]. Moreover, the phenomenological description of equilibria in molecular subsystems has been proposed [11, 65–67], which formally resembles that developed in the ordinary thermodynamics [68].

Entropic probes of the molecular electronic structure have provided attractive tools for describing the chemical bond phenomenon in information terms [11–13, 69–78]. The importance of the non-additive effects in the chemical-bond phenomena has been emphasized and the information-cascade (bridge) propagation of electronic probabilities in molecular information systems, which generates the indirect bond contributions due to orbital intermediaries, has been examined [13, 74–78].

All these local and AO/MO-resolved entropic tools were classical (probability-based). Of similar character were the communication descriptors derived from the classical information channels, which use the conditional probabilities of AO events of the real basis states describing the assumed stationary (non-degenerate) molecular state, for which the spatial phase components and hence also the associated currents identically vanish. A truly quantum channel, exhibiting the interference effects, calls for the amplitude scattering system, with the amplitudes of the underlying conditional probabilities then explicitly depending on phases of the emitting and monitoring event-states.

The extremum principles of the quantum information measures, possibly constrained by the extra requirements of conserving some “geometric” (normalization) and/or physical constraints, ultimately determines the associated quantum equilibria in molecules. In this work we shall first focus on the vertical information principles, for the fixed electron density, and then examine the horizontal (energy/probability unconstrained) entropic rules, examining the relation between the phase and probability distributions. Selected physical descriptors of the resulting phase-equilibrium states will be explored. It will be argued that the density-constrained (vertical) energy and entropy/information rules in quantum mechanics, for the conserved system entropy/information and energy, respectively, resemble the complementary energy and entropy principles of the ordinary thermodynamics. The horizontal phase equilibria will be shown to exhibit spatial phase related to electron density, and hence also a non-vanishing probability current related to the gradient of electron density.

Throughout the article the following tensor notation is used: \(A\) denotes a scalar quantity, A stands for the row-or column-vector, and A represents a square or rectangular matrix. The logarithm of the Shannon-type information measure is taken to an arbitrary but fixed base. In keeping with the custom in works on IT the logarithm taken to base 2, \(\hbox {log} = \hbox {log}_{2}\), corresponds to the information measured in bits (binary digits), while selecting log = ln expresses the amount of information in nats (natural units): 1 nat = 1.44 bits.

2 Entropy/information contributions due to probability and current densities

Consider the electron density \(\rho ({{\varvec{r}}}) = Np({{\varvec{r}}})\), or its shape (probability) factor \(p({{\varvec{r}}}) = [A({{\varvec{r}}})]^{2 }\) and the current density j(r) in the given (“frozen”-nuclei) molecular system, at the initial time \(t_{0}\) = 0. In the simplest case of a single electron in the variational state

$$\begin{aligned} \varphi ({{\varvec{r}}}) =R({{\varvec{r}}})\hbox {exp}[\hbox {i}\phi ({{\varvec{r}}})] =\varphi [p,\phi ;{{\varvec{r}}}] \end{aligned}$$
(1)

the modulus part \(R\)(r) of the latter represents the classical amplitude \(A\)(r) of the particle spatial probability distribution,

$$\begin{aligned}&p({{\varvec{r}}})=\langle \varphi |\hat{{\uprho }}({{\varvec{r}}})|\varphi \rangle =\varphi ^{*}({{\varvec{r}}})\varphi ({{\varvec{r}}}) =R({{\varvec{r}}})^{2}=\rho ({{\varvec{r}}}),\quad \int p({{\varvec{r}}})\,d{{\varvec{r}}}=1,\nonumber \\&\hat{{\uprho }}({{\varvec{r}}})=\delta ({{\varvec{r}}}^{\prime }-{{\varvec{r}}}), \end{aligned}$$
(2)

while the gradient of its (spatial) phase component \(\phi \)(r) generates the associated current density:

$$\begin{aligned} {{\varvec{j}}}({{\varvec{r}}})&= \langle \varphi | \hat{\mathbf{j}}({{\varvec{r}}})|\varphi \rangle =\frac{\hbar }{2mi}[\varphi ^{*}({{\varvec{r}}})\nabla \varphi ({{\varvec{r}}})-\varphi ({{\varvec{r}}})\nabla \varphi ^{*}({{\varvec{r}}})] \nonumber \\&= \frac{\hbar }{m}\hbox {Im}[\varphi ^{*}({{\varvec{r}}})\nabla \varphi ({{\varvec{r}}})] = \frac{\hbar p({{\varvec{r}}})}{m}\nabla \phi ({{\varvec{r}}}), \nonumber \\ \hat{\mathbf{j}}({{\varvec{r}}})&= \frac{\hbar }{2mi}[\delta ({{\varvec{r}}}^{\prime }-{{\varvec{r}}})\nabla _{{{\varvec{r}}}^{\prime }} +\nabla _{{{\varvec{r}}}^{\prime }} \delta ({{\varvec{r}}}^{\prime }-{{\varvec{r}}})]. \end{aligned}$$
(3)

In the molecular scenario, one envisages a single particle moving in an external potential \(v\)(r) due to the fixed nuclei (Born–Oppenheimer approximation) described by the Hamiltonian

$$\begin{aligned} \hat{\hbox {H}}({{\varvec{r}}}) =-\left( {\hbar ^{2}/2m} \right) \nabla ^{2}+v({{\varvec{r}}}). \end{aligned}$$
(4)

Its eigensolutions, the stationary states \(\{\varphi _{i}({{\varvec{r}}})\}\),

$$\begin{aligned} \hat{\hbox {H}}({{\varvec{r}}})\varphi _i ({{\varvec{r}}}) =E_i\,\varphi _i ({{\varvec{r}}}),\quad i= 0,1,2\ldots , \end{aligned}$$
(5)

correspond to the sharply specified energies \(\{E_{i}\}\), with the lowest eigenvalue for \(i\) = 0 corresponding to the system ground state, and the stationary (time-independent) probability distribution \(p_{i}({{\varvec{r}}}) = [R_{i}({{\varvec{r}}})]^{2}\). The non-degenerate states correspond to the vanishing spatial phase, \(\phi _{i}({{\varvec{r}}}) = 0 \equiv \phi _{0}({{\varvec{r}}})\) or \(\varphi _{i}({{\varvec{r}}}) = R_{i}({{\varvec{r}}})\), and hence also to \({{\varvec{j}}}_{i}({{\varvec{r}}}) = {{\varvec{0}}}\).

When examining the dynamics of such quantum states one allows the time dependence of both components of the full quantum state

$$\begin{aligned} \psi ({{{\varvec{r}}},t}) =R({{{\varvec{r}}},t}) \hbox {exp}[\hbox {i}\phi ({{{\varvec{r}}},t})]\equiv \langle {{\varvec{r}}}|\psi \!\left( t\right) \rangle . \end{aligned}$$
(6)

Its time evolution is described by the Schrödinger equation,

$$\begin{aligned} \hat{\hbox {H}}\psi =\hbox {i}\hbar \,\partial \psi /\partial t, \end{aligned}$$
(7)

which marks the stationary quantum action:

$$\begin{aligned} A[\psi ] =\langle \psi (t)|\hat{\hbox {A}}({{\varvec{r}}}, t)|\psi \!\left( t \right) \rangle ,\quad \hat{\hbox {A}}({{\varvec{r}}}, t) =\hbox {i}\hbar \,\partial /\partial t-\hat{\hbox {H}}({{\varvec{r}}}). \end{aligned}$$
(8)

One also recalls that the stationary state exhibits a purely time-dependent phase:

$$\begin{aligned} \varphi _i\!\left( {{{\varvec{r}}},t} \right)&= \langle {{\varvec{r}}}|\varphi _i(t)\rangle =\varphi _i ({{\varvec{r}}}) \;\hbox {exp}\left[ {-\hbox {i}\left( {E_i /\hbar } \right) t} \right] \nonumber \\&\equiv R_i ({{\varvec{r}}}) \;\hbox {exp}[-\hbox {i}\omega _i t]\equiv R_i ({{\varvec{r}}})\;\hbox {exp}[\hbox {i}\phi _i\!\left( t \right) ], \end{aligned}$$
(9)

and thus the vanishing current density of Eq. (3).

It should be stressed that both the probability distribution and its phase/current density contribute to the resultant information content of quantum states [9, 10, 21, 22]. Therefore, the wave-function modulus (amplitude of the particle probability function) and its phase (or phase-gradient, i.e., the current density) constitute two fundamental “degrees-of-freedom” in the quantum IT description of electronic states:

$$\begin{aligned} \psi \Leftrightarrow (R,\phi )\Leftrightarrow \left( {p,{{\varvec{j}}}} \right) . \end{aligned}$$
(10)

One also recalls that the Schrödinger equation gives rise to the probability-continuity equation,

$$\begin{aligned} \partial p/\partial t=-\nabla \cdot {{\varvec{j}}}\quad \hbox {or}\quad dp/dt\equiv \dot{{{\varvec{p}}}} =\sigma _p =\partial p/{\partial } t+\nabla \cdot {{\varvec{j}}}= 0, \end{aligned}$$
(11)

which expresses the local balance in electron redistributions from the system probability angle, of the wave-function modulus. It shows that the local change in the probability density (l.h.s) is solely due to the probability outflow (r.h.s.) measured by the negative divergence of the probability current density. It thus signifies the sourceless probability redistributions, with the vanishing total time derivative (the particle probability source), \(\dot{p}=\sigma _{p}\) = 0, which expresses the time rate of change of the particle density in an infinitesimal “monitoring” volume element flowing with the particle. One can also examine the continuity in the phase aspect of the quantum state of Eq. (6), alternatively phrased in terms of the phase-density and the associated phase-current, with the resulting equation then exhibiting a non-vanishing phase-source [9, 10, 12, 13, 21, 22]. It also follows from the preceding equation that the probability (wave function) norm remains conserved in time,

$$\begin{aligned} \partial /\partial t \left[ \int p({{{\varvec{r}}},t})\,d{{\varvec{r}}}\right] ={\partial /\partial t} \left[ \int \psi ^{*}({{{\varvec{r}}},t})\psi ({{{\varvec{r}}},t})\,d{{\varvec{r}}}\right] =\int [{\partial p({{{\varvec{r}}},t})/\partial t}]\,d{{\varvec{r}}}= 0,\nonumber \\ \end{aligned}$$
(12)

with the probability current-per-particle, \(({{\varvec{j}}}/p) \equiv {{\varvec{V}}}\), measuring the local speed V of this probability “fluid”, being completely determined by the gradient of the phase part of the system wave function:

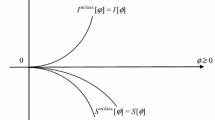
$$\begin{aligned} \nabla \phi = \left( {m/\hbar } \right) (~{{{\varvec{j}}}/p} ) = \left( {m/\hbar } \right) {{\varvec{V}}}=p^{-1}\hbox {Im}\left[ \psi ^{*}\nabla \psi \right] . \end{aligned}$$
(13)

We further recall that the density \(S^{nclass.}\)(r) \(= S_\phi ({{\varvec{r}}})\) of the non-classical, (phase/current)-related complement

$$\begin{aligned} S^{nclass.}[\varphi ]&= \langle \varphi |\hat{\hbox {S}}_\phi |\varphi \rangle = -2\int p({{\varvec{r}}}) [\phi ^{2}({{\varvec{r}}})]^{1/2}d{{\varvec{r}}}\nonumber \\&= -2\langle |\phi |\rangle \equiv S[p,\phi ]\equiv \int p({{\varvec{r}}})S^{nclass.}({{\varvec{r}}})\,d{{\varvec{r}}},\nonumber \\ \hat{\hbox {S}}_\phi ({{\varvec{r}}})&= -2[\phi ^{2}({{\varvec{r}}})]^{1/2}= -2|\phi ({{\varvec{r}}})| =S_{\phi } ({{\varvec{r}}}), \end{aligned}$$
(14)

of the Shannon entropy [3, 4] of the classical, probability-based IT,

$$\begin{aligned} S^{class.}[\varphi ]&= \langle \varphi |\hat{\hbox {S}}_p |\varphi \rangle = -\int p({{\varvec{r}}})\,\hbox {log}p({{\varvec{r}}})\,d{{\varvec{r}}}\equiv S[p]\equiv \int p({{\varvec{r}}})\,S^{class.}({{\varvec{r}}})\,d{{\varvec{r}}},\nonumber \\ \hat{\hbox {S}}_p ({{\varvec{r}}})&= -\hbox {log}p({{\varvec{r}}}) =S_p ({{\varvec{r}}}), \end{aligned}$$
(15)

is proportional to the local magnitude of the phase function, \(|\phi | = [\phi ^{2}]^{1/2}\), the square root of the phase-density \(\pi =\phi ^{2}\), with the particle probability \(p\) providing the local “weighting” factor. Together the two components generate the overall Shannon measure of the quantum indeterminicity content of both the probability and current distributions in a generally complex state \(\varphi \):

$$\begin{aligned} S[\varphi ]&= S^{class.} [\varphi ] +{S^{nclass.}} [\varphi ] =\langle \varphi |\hat{\hbox {S}}|\varphi \rangle , \nonumber \\ \hat{\hbox {S}}({{\varvec{r}}})&= \hat{\hbox {S}}_p ({{\varvec{r}}})+\hat{\hbox {S}}_\phi ({{\varvec{r}}}) =S_p ({{\varvec{r}}}) +S_\phi ({{\varvec{r}}}) =S({{\varvec{r}}}). \end{aligned}$$
(16)

The Fisher information for locality events [1, 2], called the intrinsic accuracy, provides the classical gradient measure of the information content in the quantum state \(\varphi \)(r):

$$\begin{aligned} I^{class.}[\mathbf{\varphi }]&= \langle \varphi |\hat{\hbox {I}}_p | \varphi \rangle =\int p({{\varvec{r}}})[\nabla \hbox {ln } p({{\varvec{r}}})]^{2}d{{\varvec{r}}}=\int {[\nabla p({{\varvec{r}}})]}^{2}/p({{\varvec{r}}})~d{{\varvec{r}}}=I[p] \nonumber \\&= 4\int [\nabla A({{\varvec{r}}})]^{2}d{{\varvec{r}}}\equiv I[A], \nonumber \\ \hat{\hbox {I}}_{p} ({{\varvec{r}}})&= [\nabla \hbox {ln} p({{\varvec{r}}})]^{2}= [\nabla p({{\varvec{r}}})/p({{\varvec{r}}})]^{2}=I_{p} ({{\varvec{r}}})= 4[\nabla R({{\varvec{r}}})]^{2}, \end{aligned}$$
(17)

where \(A({{\varvec{r}}}) =\sqrt{p({{\varvec{r}}})}\) denotes the associated classical (real) amplitude of the probability distribution. This amplitude form is then naturally generalized into the domain of quantum probability amplitudes, i.e., the complex wave-functions of quantum mechanics [35]. For the one-electron system [see Eqs. (1) and (2)], when \(A({{\varvec{r}}}) = R({{\varvec{r}}})\), this generalized measure is given by the overall gradient functional,

$$\begin{aligned} I [\varphi ] =4\int \mid \!\nabla \varphi ({{\varvec{r}}})\!\mid ^{2} d{{\varvec{r}}}={\frac{8m}{\hbar ^{2}}}T[\varphi ], \end{aligned}$$
(18)

related to the expectation value of the kinetic energy:

$$\begin{aligned} T[\varphi ] \equiv \left\langle \varphi \right| \hat{\hbox {T}}\left| \varphi \right\rangle =-\frac{\hbar ^{2}}{2m}\int {\varphi ^{*}({{\varvec{r}}})\Delta \varphi ({{\varvec{r}}}) } \,d{{\varvec{r}}}=\frac{\hbar ^{2}}{2m}\int {\left| {\nabla \varphi ({{\varvec{r}}})} \right| ^{2}}\,d{{\varvec{r}}}. \end{aligned}$$
(19)

This quantum expression for the kinetic energy consists of the classical, von Weizsäcker type [79] contribution,

$$\begin{aligned} T[p]&= \frac{\hbar ^{2}}{8m}\int {\frac{[\nabla p({{\varvec{r}}})]^{2}}{p({{\varvec{r}}})}} \,d{{\varvec{r}}}=\frac{\hbar ^{2}}{2m}\int {[\nabla R({{\varvec{r}}})]^{2}}\,d{{\varvec{r}}}=T^{class.}[\varphi ] =\langle \varphi |T_p |\varphi \rangle , \nonumber \\ T_p ({{\varvec{r}}})&= \frac{\hbar ^{2}}{8m} [\nabla p({{\varvec{r}}})/p({{\varvec{r}}})]^{2}=\frac{\hbar ^{2}}{2m}[\nabla R({{\varvec{r}}})/R({{\varvec{r}}})]^{2}, \end{aligned}$$
(20)

depending solely upon the electron probability density, and the non-classical, (phase/current)-related term

$$\begin{aligned} T[ {p,{{\varvec{j}}}} ]&= \frac{m}{2}\int {\frac{j({{\varvec{r}}})^{2}}{p({{\varvec{r}}})} } \,d{{\varvec{r}}}=\frac{\hbar ^{2}}{2m}\int {p({{\varvec{r}}})[\nabla \phi ({{\varvec{r}}})]^{2}}\,d{{\varvec{r}}}=T[p,\phi ]\nonumber \\&= {T^{nclass.}} [\varphi ] =\langle \varphi |T_{\phi } |\varphi \rangle ,\nonumber \\ T_{\phi } ({{\varvec{r}}})&= \frac{\hbar ^{2}}{2m}[\nabla \phi ({{\varvec{r}}})]^{2}. \end{aligned}$$
(21)

This separation gives a transparent partition of the kinetic energy functional of Eq. (19):

$$\begin{aligned} T[\varphi ]&= \langle \varphi |\hat{\hbox {T}}|\varphi \rangle =T[ p ] +T[p,\phi ] ={T^{class.}} [\varphi ] +{T^{nclass.}} [\varphi ] =\int p({{\varvec{r}}})T({{\varvec{r}}})\,d{{\varvec{r}}} \nonumber \\ T({{\varvec{r}}})&= T_{p} ({{\varvec{r}}})+T_{\phi } ({{\varvec{r}}}). \end{aligned}$$
(22)

Notice, however, that the effective (multiplicative, real) “operator” \(T({{\varvec{r}}})\), derived from equality of the quantum expectation values,

$$\begin{aligned} \langle \varphi |\hat{\hbox {T}}|\varphi \rangle =\langle \varphi |T|\varphi \rangle =\int T({{\varvec{r}}})p({{\varvec{r}}})\,d{{\varvec{r}}}=T[ p ], \end{aligned}$$
(23)

differs from the true (differential) kinetic energy operator \(\hat{\hbox {T}}(r)= -(\hbar ^{2}/2m)\nabla ^{2}\) and measures the density-per-electron of the functional \(T[p]\) for the system kinetic energy.

A similar division applies to the overall Fisher information of Eq. (18):

$$\begin{aligned} I[\varphi ]&= I [p] + 4\int p({{\varvec{r}}}) [\nabla \phi ({{\varvec{r}}})]^{2}\,d{{\varvec{r}}}\equiv I[p] +I[p,\phi ] \nonumber \\&= I[ p ] +4\left( {\frac{m}{\hbar }} \right) ^{2}\int {{{\varvec{j}}}^{\,2}({{\varvec{r}}})} /p({{\varvec{r}}})\,d{{\varvec{r}}}\equiv I[ p ] +I[p,{\varvec{j}}]\nonumber \\&\equiv I^{class.}[\varphi ] {+I^{nclass.}} [\varphi ] \equiv \int p({{\varvec{r}}}) [I^{class.}({{\varvec{r}}}) +I^{nclass.}({\varvec{r}})]~d{{\varvec{r}}}, \end{aligned}$$
(24)

where the two information densities-per-electron read:

$$\begin{aligned} I^{class.}({{\varvec{r}}})&= [\nabla p({{\varvec{r}}})/p({{\varvec{r}}})]^{2}=4[\nabla R({{\varvec{r}}})]^{2},\nonumber \\ I^{nclass.}({{\varvec{r}}})&= 4[\nabla \phi ({{\varvec{r}}})]^{2}=4\left( {m/\hbar } \right) ^{2}[\,{\varvec{j}}({{\varvec{r}}})/p({{\varvec{r}}})]^{2}. \end{aligned}$$
(25)

The two Fisher information components can be thus expreassed as the quantum mechanical expectation values of the related (multiplicative) “operators” in the position representation, \(I^{class.}[\varphi ] = \langle \varphi |\hat{\hbox {I}}_p |\varphi \rangle \) [see Eq. (17)] and

$$\begin{aligned} I^{nclass.}[\varphi ] =\langle \varphi |\hat{\hbox {I}}_{\phi } |\varphi \rangle ,\quad \hat{\hbox {I}}_{\phi } ({{\varvec{r}}}) =4 [\nabla \phi ({{\varvec{r}}})]^{2}=I_{\phi } ({{\varvec{r}}}), \end{aligned}$$

thus giving the associated expression for the overall quantum measure of Eq. (24):

$$\begin{aligned} I[\varphi ]&= I [p] {\,+\, I} [p,\phi ] { =I^{class.}} [\varphi ] + { I^{nclass.}} [\varphi ] =\langle \varphi |\hat{\hbox {I}}|\varphi \rangle ,\nonumber \\ \hat{\hbox {I}}({{\varvec{r}}})&= \hat{\hbox {I}}_p ({{\varvec{r}}})+\hat{\hbox {I}}_{\phi } ({{\varvec{r}}}) =I_p ({{\varvec{r}}})+I_{\phi } ({{\varvec{r}}}) =I({{\varvec{r}}}). \end{aligned}$$
(26)

Both the classical and non-classical densities-per-electron of these complementary measures of information content are mutually related via the common-type dependence [9, 10]:

$$\begin{aligned} I^{class.}({{\varvec{r}}})&= [\nabla \hbox {ln}p\left( {{\varvec{r}}}\right) ]^{2}= [\nabla S^{class.}({{\varvec{r}}})]^{2}\quad \hbox {and} \nonumber \\ I^{nclass.}({{\varvec{r}}})&= \left( {\frac{2m\,{\varvec{j}}({{\varvec{r}}})}{\hbar p({{\varvec{r}}})}} \right) ^{2}\equiv [\nabla S^{nclass.}({{\varvec{r}}})]^{2}. \end{aligned}$$
(27)

Thus, the square of the gradient of the local Shannon probe of the state resultant quantum “indeterminicity” (disorder) generates the density of the corresponding Fisher measure of the state quantum “determinicity” (order).

The classical Fisher information is reminiscent of von Weizsäcker’s [79] inhomogeneity correction to the density functional for the electronic kinetic energy in the Thomas–Fermi theory. It characterizes the compactness of the probability density \(p\)(r). For example, the Fisher information in the normal distribution measures the inverse of its variance, called the invariance, while the complementary Shannon entropy is proportional to the logarithm of variance, thus monotonically increasing with the spread of the Gaussian distribution. Therefore, the Shannon entropy and intrinsic accuracy describe complementary facets of the probability density: the former reflects distribution’s spread (delocalization, “disorder”), while the latter measures its narrowness (localization, “order”).

To summarize, the system electron distribution, related to the wave-function modulus, reveals the probability (classical) aspect of the molecular information content [1–6], while the phase(current) facet of the molecular state gives rise to the specifically quantum (non-classical) entropy/information terms [9, 10, 21, 22]. Together these two contributions allow one to monitor the full information content of the non-equilibrium (variational) quantum states, thus providing the complete information description of their evolution towards the final equilibrium.

3 Molecular equilibria

In this section we reexamine the equilibrium states of electrons in general atomic or molecular systems [21, 22]. The combined classical and non-classical entropy/information contributions determine the resultant measure of the information content in quantum states. In DFT [80, 81] one often refers to the density-constrained (vertical) principles [9, 10, 82] and states [83–86], corresponding to the fixed probability distribution of electrons. They give rise to the so called vertical equilibria, which are determined solely by the non-classical entropy/information functionals [9, 10, 21, 22]. The density-unrestricted variational principles associated with the resultant information measure similarly determine the horizontal (unconstrained) equilibria in molecules [9–11]. The vertical entropy-information principles, for the constrained ground-state energy, have been shown to recover the (stationary) ground-state solution [21, 22]. In what follows we examine the associated solutions of the complementary energy-unconstrained entropy/information principles for the system equilibrium (stationary) phase.

Let us again consider the simplest, one-electron case of the preceding section. We explore the vertical equilibrium principles, for the fixed ground-state probability distribution \(p_{0 }=R_{0}^{2}\). The optimum solutions are then derived from the extrema of the non-classical entropy/information functionals \(S[p_{0},\,\phi ]\hbox { and }I[p_{0},\,\phi ]\), for the fixed classical contributions \(S[p_{0}]\hbox { and }I[p_{0}]\), respectively. These vertical extrema,

$$\begin{aligned} \hbox {max}_\phi S[p_0 ,\phi ]\quad \hbox {or}\quad \hbox {min}_\phi I[p_0 ,\phi ], \end{aligned}$$
(28)

give rise to the associated Euler equations for the optimum phase \(\phi =\phi ^{opt}\). in the trial state \(\varphi ^{0}({{\varvec{r}}}) = \varphi [p_{0},\,\phi ; {{\varvec{r}}}]\):

$$\begin{aligned}&\delta \langle \varphi ^{0}|\hat{\hbox {S}}_{\phi } |\varphi ^{0}\rangle /\delta \varphi ^{0}({{\varvec{r}}})^{*}\left| {_{\phi =\phi ^{opt.}} } \right. = 0 \quad \hbox {or}\quad \hat{\hbox {S}}_{\phi ^{opt.}} ({{\varvec{r}}}) \varphi _0 ({{\varvec{r}}}) = -2|\phi ^{opt.}({{\varvec{r}}})|\varphi _0 ({{\varvec{r}}}) = 0 \nonumber \\&\qquad \Rightarrow \phi ^{opt.}({{\varvec{r}}}) = 0\equiv \phi _0 ({{\varvec{r}}}), \nonumber \\&\delta \langle \varphi ^{0}|\hat{\hbox {I}}_{\phi } |\varphi ^{0}\rangle /\delta \varphi ^{0}({{\varvec{r}}})^{*}\left| {_{\phi =\phi ^{opt.}} } \right. = 0 \quad \hbox {or} \quad \hat{\hbox {I}}_{\phi ^{opt.}} ({{\varvec{r}}})\varphi _0 ({{\varvec{r}}}) =4[\nabla \phi ^{opt.}({{\varvec{r}}})]^{2}\varphi _0 ({{\varvec{r}}}) = 0\nonumber \\&\qquad \Rightarrow \phi ^{opt.}({{\varvec{r}}}) =\phi _0 ({{\varvec{r}}}). \end{aligned}$$
(29)

Hence, they both properly identify the stationary, ground-state solution, for \(\phi ^{opt.}\)(r) \(=\phi _{0}\)(r) \(=\) 0, as the vertical equilibrium state \(\varphi _{0}\)(r) = \(\varphi [p_{0},\,\phi _{0}\); r] of this model system (see also Fig. 1). We thus conclude, that these non-classical, (phase/current)-related extreme information principles (EPI) [2] properly predict this lowest eigenstate of the electronic Hamiltonian as the vertical equilibrium state of the molecule for the ground-state probability distribution, in which all physical quantities become functionals of the system electron density alone, in accordance with the first Hohenberg–Kohn theorem [80].

Fig. 1
figure 1

Schematic diagram of the average electronic energy surface \(E[p,\phi ] = \langle \varphi |\hat{\hbox {H}}|\varphi \rangle \) of the one-electron system described by the Hamiltonian \(\hat{\hbox {H}}(r) = -(\hbar ^{2}/2{m})\nabla ^{2}+v({{\varvec{r}}})\) in the variational equilibrium state \(\varphi ({{\varvec{r}}}) = R({{\varvec{r}}})\hbox {exp}\{\hbox {i}\phi ({{\varvec{r}}})]= [p({{\varvec{r}}})]^{1/2}\hbox {exp}\{\hbox {i}\phi ({{\varvec{r}}})] \equiv \varphi [p,\,\phi ; {{\varvec{r}}}]\), corresponding to the particle-probability density \(p({{\varvec{r}}}) = |\varphi ({{\varvec{r}}})|^{2}=R^{2}({{\varvec{r}}})\) and the phase distribution \(\phi ({{\varvec{r}}})\). Its lowest value \(E[p_{0},\phi _{0}]=E_{0}=E_{v}[p_{0}]\) corresponds to the ground-state \(\varphi _{0}({{\varvec{r}}}) = R_{0}({{\varvec{r}}}) = \varphi [p_{0},\phi _{0}; {{\varvec{r}}}]\), for \(p=p_{0}\hbox { and }\phi _{0 }=0\). The zero-energy contour, \(E[p,\phi ]=0\), includes the ground-state related points \(E[p_{0},\phi _{eq.}[p_{0}]]\hbox { and }E[p_{s},\phi _{0}]\), in the “frozen” probability \((p = p_{0})\) and the stationary-phase \((\phi =\phi _{0})\) cross sections \(E[p_{0},\phi ]\hbox { and }E[p,\phi _{0}]\), respectively; they accordingly correspond to the equilibrium-phase, \(\phi _{eq.}[p_{0}]= - (1/2)\hbox {ln}p_{0}\), and the uniformly-scaled probability distribution, \(p_{s}({{\varvec{r}}}) =s^{3}p_{0}(s{{\varvec{r}}})\), for \(s = 2\)

Full size image

Next, let us examine the implications of the horizontal extrema of the quantum measures of the overall (resultant) entropy/information content, subject only to the constraint of the wave function/probability normalization. Since in quantum mechanics the phase of wave functions is determined only up to the constant, its sign is physically irrelevant. In what follows, we thus assume \(\phi \)(r) = |\(\phi \)(r)| \(\ge \) 0. The functional derivatives with respect to \(\varphi ^{*}\)(r) of the corresponding auxiliary functionals including the information terms of Eqs. (16) and (28) and the constraint \(\langle \varphi \)|\(\varphi \rangle \) = 1 multiplied by the Lagrange multiplier \(\mu \) enforcing this unit norm of the wave function, i.e., the normalization of probability density,

$$\begin{aligned} \Omega _S [\varphi ] =\langle \varphi |\hat{\hbox {S}}|\varphi \rangle -\mu \langle \varphi |\varphi \rangle \quad \hbox {and}\quad \Omega _I [\varphi ] =\langle \varphi |\hat{\hbox {I}}|\varphi \rangle -\mu \langle \varphi |\varphi \rangle , \end{aligned}$$
(30)

give the associated Euler equations for the horizontal equilibrium states \(\varphi _{eq.} [p,\phi _{eq.}[p\)]; r] \(\equiv \varphi _{eq.}[p\); r], determining the the system equilibrium phase in terms of its probability density:

$$\begin{aligned}&\delta \Omega _S [\varphi ]/\delta \varphi ^{*}({{\varvec{r}}})\left| {_{\varphi =\varphi _{eq.} } } \right. = \{\hat{\hbox {S}}[p, \phi _{eq.} [p]; {{\varvec{r}}}]-\mu \}\varphi _{eq.} ({{\varvec{r}}}) = 0\quad \hbox {or}\nonumber \\&\qquad \{-\hbox {log}p({{\varvec{r}}}) -2\phi _{eq.}\!\left[ {p;{{\varvec{r}}}} \right] -\mu \}\varphi _{eq.} ({{\varvec{r}}}) = 0,\nonumber \\&\delta \Omega _I [\varphi ]/\delta \varphi ^{*}({{\varvec{r}}})\left| {_{\varphi =\varphi _{eq.} } } \right. = \{\hat{\hbox {I}}[p, \phi _{eq.} [p]; {{\varvec{r}}}]-\mu \}\varphi _{eq.} ({{\varvec{r}}}) = 0\quad \hbox {or}\nonumber \\&\qquad \{[\nabla p({{\varvec{r}}})/p({{\varvec{r}}})]^{2}+4[\nabla \phi _{eq.} ({{\varvec{r}}})]^{2}-\mu \}\varphi _{eq.} ({{\varvec{r}}}) = 0. \end{aligned}$$
(31)

Therefore, these two horizontal principles consistently predict a non-vanishing spatial phase related to the current probability distribution [9]:

$$\begin{aligned} \phi _{eq.} ({{\varvec{r}}}) = -(1/2)\,\hbox {ln}p({{\varvec{r}}}) +const., \end{aligned}$$
(32)

and hence:

$$\begin{aligned} \varphi _{eq.}\!\left[ {p;{{\varvec{r}}}}\right] =R({{\varvec{r}}})\,\hbox {exp}[\hbox {i}\phi _{eq.}\! ({{\varvec{r}}})] { =R({{\varvec{r}}})\hbox {exp}} [-(1/2)\,\hbox {ln}p({{\varvec{r}}})]\equiv \varphi _{eq.}\!\left( {{\varvec{r}}}\right) . \end{aligned}$$
(33)

We call such (energy-unconstrained) horizontal-equilibrium states, which correspond to the unconstrained extrema of the resultant quantum entropy/information measures, the phase-equilibria of the system under consideration, with the phase then reflecting the molecular probability distribution.

Clearly, these equilibrium states yield the prescribed probability distribution, \(|\varphi _{eq.}[p; {{\varvec{r}}}]|^{2} \equiv R^{2}({{\varvec{r}}}) = p({{\varvec{r}}})\). Another distinct property of such states is that the classical and non-classical entropies and their densities are equal, e.g.,

$$\begin{aligned} S^{class.}[\varphi _{eq.} ] =S^{nclass.} [\varphi _{eq.}] \quad \hbox {or} \quad S [\varphi _{eq.} [p]] =2S [p]. \end{aligned}$$
(34)

The same is true for the Fisher information (kinetic energy) contributions:

$$\begin{aligned} I^{class.}[\varphi _{eq.} ] =I^{nclass.} [\varphi _{eq.} ] \quad \hbox {or}\quad I [\varphi _{eq.} [ p ]] =2I [p],\end{aligned}$$
(35)
$$\begin{aligned} T^{class.}[\varphi _{eq.} ] =T^{nclass.} [\varphi _{eq.} ]\quad \hbox {or}\quad T [\varphi _{eq.} [ p ]] { =2T} [p]. \end{aligned}$$
(36)

We further recall that for the equilibrium molecular geometry the ground-state probability distribution \(p_{0 }=R_{0}^{2}\) and the exact wave function \(\varphi _{0}=\varphi [p_{0},\,\phi _{0}\)] = \(R_{0}\) correspond to the atomic-like virial relations between the expectation values \(T_{0}\) and \(V_{0}\) of the system kinetic and potential energies, respectively,

$$\begin{aligned} \langle \varphi _0 |\hat{\hbox {T}}|\varphi _0 \rangle&= T[p_0 ,\phi _0 ] =T_0 \nonumber \\&= -E\!\left[ {p_0 } \right] = -\langle \varphi _0 |\hat{\hbox {H}}|\varphi _0 \rangle = -E[p_0 ,\phi _0 ] { = -E_v } [p_0 ] = -E_0 \nonumber \\&= -(1/2)V\!\left[ {p_0 } \right] = -(1/2)\langle \varphi _0 \left| v \right| \varphi _0 \rangle \nonumber \\&= -(1/2)V[p_0 ,\phi _0 ] { = -(1/2)V_v }[p_0 ] = -(1/2)V_0 , \end{aligned}$$
(37)

where \(E_{0}=T_{0}+V_{0}\) stands for the system ground-state energy. In the equilibrium state \(\varphi _{eq.}[p_{0}\)] the potential component remains unchanged,

$$\begin{aligned} \langle \varphi _{eq.}\!\left[ {p_0 } \right] \left| v \right| \varphi _{eq.}\!\left[ {p_0 }\right] \rangle =V[p_0 ,\phi _{eq.}\!\left[ {p_0 } \right] ] =\int p_0 \!\left( {{\varvec{r}}}\right) v({{\varvec{r}}})d{{\varvec{r}}}=V_0 , \end{aligned}$$
(38)

while the kinetic energy is doubled [see Eq. (35)]:

$$\begin{aligned} \langle \varphi _{eq.}\!\left[ {p_0 }\right] |\hat{\hbox {T}}|\varphi _{eq.}\!\left[ {p_0 }\right] \rangle =T[p_0 ,\phi _{eq.}\!\left[ {p_0 } \right] ] =2T_0 . \end{aligned}$$
(39)

Therefore, the virial relation in the phase-equilibrium state \(\varphi _{eq.}[p_{0}]\) reads

$$\begin{aligned} T[p_0 ,\phi _{eq.} [ {p_0 } ]] { = -V} [p_0 ,\phi _{eq.} [{ p_0 } ]] \end{aligned}$$
(40)

and hence its average electronic energy exactly vanishes (see Fig. 1):

$$\begin{aligned} \langle \varphi _{eq.} [ {p_0 }] |\hat{\hbox {H}}|\varphi _{eq.} [ {p_0 } ]\rangle =T[p_0 ,\phi _{eq.} [{p_0 } ]] { +V} [p_0 ,\phi _{eq.} [ {p_0 } ]] = 0. \end{aligned}$$
(41)

As also shown in the figure, this level of electronic energy can be also reached by scaling the probability distribution alone, by uniformly contracting (\(s >\) 0) the ground-state density:

$$\begin{aligned} p_s ({{\varvec{r}}}) =s^{3}p_0 \!\left( {s{{\varvec{r}}}} \right) . \end{aligned}$$
(42)

Such manipulation of the electronic state modifies both energy components of the system ground state, \(T_{s=1}=T_{0}\hbox { and }V_{s=1}=T_{0}\),

$$\begin{aligned} T_s =s^{2}T_0\quad \hbox {and}\quad V_s =sV_0 . \end{aligned}$$
(43)

The requirement \(E_{s}=T_{s}+V_{s}\) = 0 thus implies \(s\) = 2, for which

$$\begin{aligned} T_{s=2} =4T_0 = -4E_0 = -V_{s=2} =-2V_0 . \end{aligned}$$
(44)

The zero-energy contour \(E[p,\phi \)] \(=\) 0, including points \(E[p_{0},\,\phi _{eq.}[p_{0}\)]] and \(E[p_{s=2},\,\phi _{0}\)], is also qualitatively depicted on the energy surface of Fig. 1.

Let us next examine other properties of the phase-equilibrium solutions. One first obseves that these states are not stationary, since their phase gradient does not vanish,

$$\begin{aligned} \nabla \varphi _{eq.}\!\left[ {p_0 } \right] = -(1/2)\,(\nabla p_0 /p_0 ) = -(\nabla R_0 /R_0 ), \end{aligned}$$
(45)

thus giving a finite probability current of Eq. (3):

$$\begin{aligned} {\varvec{j}}[\varphi _{eq.}\!\left[ {p_0 }\right] ;{{\varvec{r}}}]&= \langle \varphi _{eq.}\!\left[ {p_0 }\right] | \hat{\mathbf{j}}({{\varvec{r}}})|\varphi _{eq.}\!\left[ {p_0 } \right] \rangle =\frac{\hbar p_0 ({{\varvec{r}}})}{m}\nabla \phi _{eq.}\![p_0 ;{{\varvec{r}}}]\nonumber \\&= -\frac{\hbar }{2m}\nabla p_0 ({{\varvec{r}}})=\frac{\hbar }{m}R_0 ({{\varvec{r}}})\nabla R_0 ({{\varvec{r}}}). \end{aligned}$$
(46)

Indeed, the direct action of the Hamiltonian of Eq. (4) on \(\varphi _{eq.}\![p_{0}\)] gives:

$$\begin{aligned} \hat{\hbox {H}}\,\varphi _{eq.}\!\left[ {p_0 } \right]&= \left\{ (1-\hbox {i})\left( {\frac{-\hbar ^{2}}{2m}} \right) [\Delta R_0 /R_0 -\hbox {i}(\nabla R_0 /R_0 )^{2}] +v\right\} \varphi _{eq.}\!\left[ {p_0 }\right] \nonumber \\&\equiv [\mathcal {J}\!\left( {R_0 } \right) +v]\varphi _{eq.}\!\left[ {p_0 }\right] . \end{aligned}$$
(47)

Replacing the complex (multiplicative) operator \(\mathcal {J}(R_{0})\) by its Hermitian (real) analog,

$$\begin{aligned} T\!\left( {R_{0} } \right)&= (1/2) [\mathcal {J}\!\left( {R_{0}} \right) +\mathcal {J}\!\left( {R_{0}} \right) ^{*}] =\left( {\frac{-\hbar ^{2}}{2m}} \right) [\Delta R_{0} /R_{0} - (\nabla R_{0} /R_{0})^{2}]\nonumber \\&= \left( {\frac{-\hbar ^{2}}{2m}} \right) \Delta \hbox {ln}R_0 , \end{aligned}$$
(48)

then finally gives

$$\begin{aligned} \hat{\hbox {H}}\,\varphi _{eq.}\!\left[ {p_0 } \right] = \left[ \left( {\frac{-\hbar ^{2}}{2m}} \right) \Delta \hbox {ln}R_0 +v\right] \varphi _{eq.}\!\left[ {p_0 } \right] . \end{aligned}$$
(49)

Using next the energy eigenvalue problem for the ground-state [see Eq. (5)],

$$\begin{aligned} \hat{\hbox {H}}\,R_{0} = (\hat{\hbox {T}}+v)R_{0} =\left( {\frac{-\hbar ^{2}}{2m}} \right) \Delta R_{0} +vR_{0} =E_{0}\,R_{0} , \end{aligned}$$
(50)

identifies the above local kinetic energy as \(E_{0}-v\):

$$\begin{aligned} \left( {\frac{-\hbar ^{2}}{2m}} \right) (\Delta R_0 /R_0 ) =E_0 -v. \end{aligned}$$
(51)

Therefore, Eq. (49) reads [see Eq. (21)]:

$$\begin{aligned} \hat{\hbox {H}}\,\varphi _{eq.}\!\left[ {p_0 } \right] = \{E_0 +T_{\phi } [\phi _{eq.}({{\varvec{r}}})]\}\varphi _{eq.}\!\left[ {p_0 } \right] . \end{aligned}$$
(52)

The preceding equation thus explicitly confirms, that the equilibrium state \(\varphi _{eq.}[p_{0}\)] is not one of the eigenstates of the Hamiltonian.

One further observes that in the ground state [see Eqs. (20) and (50)]

$$\begin{aligned} \hat{\hbox {H}}\,R_{0} = (\hat{\hbox {T}}+v)R_0 = \left[ {T_p +v} \right] R_{0} =E_{0}\,R_{0} . \end{aligned}$$
(53)

We further recall that, for the purpose of calculating the expectation values of the electronic energy and its components, the action of the Hamiltonian on the equilibrium state can be effectively replaced by the multiplicative kinetic energy densities of Eqs. (20)–(22):

$$\begin{aligned} \hat{\hbox {H}}\,\varphi _{eq.}\!\left[ {p_{0} } \right]&= (\hat{\hbox {T}}+v)R_{0}\,\hbox {exp}\left[ {(-1/2)\hbox {ln}p_{0}} \right] \nonumber \\&= [\left( {T_{p} + v} \right) +T_{\phi } ]R_{0}\,\hbox {exp}\left[ {(-1/2)\hbox {ln}p_0 } \right] \nonumber \\&= (E_0 +T_\phi )\varphi _{eq.}\!\left[ {p_0 } \right] , \end{aligned}$$
(54)

thus again arriving at Eq. (52).

For examining the time evolution of \(\varphi _{eq.}[p_{0}\)] one expands this lowest phase-equilibrium state at the specified time \(t_{0}\) = 0 in terms of the complete set of eigenfunctions of Eq. (5),

$$\begin{aligned}&\{\varphi _{\alpha } ({{\varvec{r}}}) =\langle {{\varvec{r}}}|\varphi _\alpha \rangle =R_{\alpha } ({{\varvec{r}}})\; \hbox {exp}[\hbox {i}\phi _\alpha ({{\varvec{r}}})],\quad \alpha = 0,1,2, \ldots \},\nonumber \\&\qquad \sum \limits _{\alpha } |\varphi _{\alpha } \rangle \langle \varphi _{\alpha } | =1, \end{aligned}$$
(55)

which determine the basis of the energy representation of \(\varphi _{eq.}[p_{0}]\):

$$\begin{aligned} |\varphi _{eq.} [ {p_0 ;t_0 = 0} ]\rangle&= \sum \limits _{\alpha } |\varphi _{\alpha } \rangle \langle \varphi _{\alpha } |\varphi _{eq.} [{p_0 } ]\rangle \equiv \sum \limits _{\alpha } |\varphi _{\alpha } \rangle C_{\alpha } \!\left( {t_0 = 0} \right) , \nonumber \\ C_{\alpha }\! \left( {t_0 = 0} \right)&= \int \varphi _{\alpha } \!\left( r \right) ^{*}\varphi _{eq.} [ {p_0 ;{{\varvec{r}}}}] d{{\varvec{r}}}\nonumber \\&= \int [R_{\alpha }({{\varvec{r}}})R_{0} ({{\varvec{r}}})] \;{\hbox {exp}\{-\hbox {i}} [\phi _\alpha ({{\varvec{r}}}) +(1/2)\hbox {ln}p_0 ({{\varvec{r}}})]\}\,d{{\varvec{r}}}.\quad \end{aligned}$$
(56)

By the superposition principle of quantum mechanics [60], the squares of these expansion coefficients deftermine the associated conditional probabilities of observing at \(t_{0}\) = 0 the stationary state \(\varphi _{\alpha }\) in the equilibrium state \(\varphi _{eq.}[p_{0}\); \(t_{0}\)]:

$$\begin{aligned} P(\varphi _\alpha |\varphi _{eq.}\!\left[ {p_0 ;t_0 } \right] ) = |C_\alpha ({t_0})|^{2},\quad \sum \limits _{\alpha } P(\varphi _\alpha |\varphi _{eq.}\!\left[ {p_0 ;t_0 } \right] ) =1. \end{aligned}$$
(57)

The normalization condition of the preceding equation can be directly verified using the completeness of the energy basis [Eq. (55)],

$$\begin{aligned} \sum \limits _\alpha \varphi _\alpha ({{\varvec{r}}})\varphi _\alpha \!\left( {{{\varvec{r}}}^{\prime }} \right) ^{*}=\sum \limits _\alpha \langle {{\varvec{r}}}|\varphi _\alpha \rangle \langle \varphi _\alpha |{{\varvec{r}}}^{\prime }\rangle =\langle {{\varvec{r}}}|{{\varvec{r}}}^{\prime }\rangle =\delta \!\left( {{{\varvec{r}}}^{\prime }-{{\varvec{r}}}} \right) , \end{aligned}$$
(58)
$$\begin{aligned} \sum \limits _\alpha |C_\alpha |^{2}&= \int \int \varphi _\alpha \! \left( {{{\varvec{r}}}^{\prime }} \right) ^{*}\varphi _{eq.}\!\left[ {p_0 ;{{\varvec{r}}}^{\prime }} \right] \varphi _{eq.}\!\left[ {p_0 ;{{\varvec{r}}}} \right] ^{*}\varphi _\alpha ({{\varvec{r}}})\,d{{\varvec{r}}}^{\prime }d{{\varvec{r}}}\nonumber \\&= \int \int \delta \!\left( {{{\varvec{r}}}^{\prime }\!-{{\varvec{r}}}} \right) \left[ {R_0 ({{\varvec{r}}})R_0\!\left( {{{\varvec{r}}}^{\prime }} \right) } \right] \hbox {exp}(-\hbox {i}\{[\phi _\alpha ({{\varvec{r}}})\!-\phi _\alpha \!\left( {{{\varvec{r}}}^{\prime }} \right) ] \nonumber \\&\quad +(1/2)\hbox {ln} [p_0 ({{\varvec{r}}})/p_0\!\left( {{{\varvec{r}}}^{\prime }} \right) ]\})\,d{{\varvec{r}}}^{\prime }d{{\varvec{r}}}\nonumber \\&= \int R_0 ({{\varvec{r}}})^{2}d{{\varvec{r}}}=\int p_0 ({{\varvec{r}}})\,d{{\varvec{r}}}=1. \end{aligned}$$
(59)

Finally, using Eq. (9) gives the time-dependent equilibrium state at \(t >\) 0:

$$\begin{aligned} |\varphi _{eq.}\!\left[ {p_0 ;t} \right] \rangle&= \sum \limits _\alpha C_\alpha ({t_0})|\varphi _\alpha \!\left( t \right) \rangle =\sum \limits _\alpha C_\alpha ({t_0}) |\varphi _\alpha ({t_0})\rangle \hbox {exp}[-\hbox {i}\omega _\alpha t]\nonumber \\&= \sum \limits _\alpha C_\alpha ({t_0}) |\varphi _\alpha ({{{\varvec{r}}},t})\rangle . \end{aligned}$$
(60)

4 \(N\)-electron extension

In DFT one often explores the density-constrained, “entropic” variational principles, e.g., in Levy’s [82] construction of the universal density functional for the sum of the electron kinetic and repulsion energies. They are also called the “vertical” [11] or “thermodynamic” [9, 10] searches, by analogy to the maximum-entropy equilibrium principle in the ordinary thermodynamics [68]. A related problem of constructing the antisymmetric wave functions of \(N\) fermions yielding the prescribed density \(\rho \)(r), vital for solving the familiar \(N\)-representability problem of DFT, has been tackled by Harriman [85] using crucial insights due to Macke [83] and Gilbert [84]. Its three-dimensional generalization by Zumbach and Maschke [86] introduces the complete set of the density-conserving Slater determinants. They are build using the plane–wave-type equidensity orbitals \(\{\varphi _{k}({{\varvec{r}}})= R({{\varvec{r}}})\hbox {exp}[\hbox {i}\varPhi _{k}({{\varvec{r}}})]\}\), which offer a convenient framework for an extension of the present analysis to general, \(N\)-electron systems [21, 22]. In constructing the orthogonal Slater determinants, that generate the specified electron density [84–86], these orbitals adopt equal, density-dependent modulus \(R({{\varvec{r}}}) = p({{\varvec{r}}})^{1/2}\) and the space-dependent phase \(\varPhi _{k}({{\varvec{r}}}) = {{\varvec{k}}}\cdot {{\varvec{f}}}({{\varvec{r}}}) + \phi ({{\varvec{r}}}) \equiv F_{k}({{\varvec{r}}}) + \phi ({{\varvec{r}}})\), with the density dependent vector function \({{\varvec{f}}}({{\varvec{r}}}) = {{\varvec{f}}}[\rho ; {{\varvec{r}}}]\) common to all equidensity orbitals and linked to the Jacobian of the \({{\varvec{r}}}\rightarrow {{\varvec{f}}}({{\varvec{r}}})\) transformation [21, 22].

To summarize, the (orthonormal) Harriman–Zumbach–Maschke (HZM) orbitals [85, 86] for the ground-state probability distribution \(p_{0}({{\varvec{r}}}) = [R_{0}({{\varvec{r}}})]^{2}\),

$$\begin{aligned} \varphi _{{\varvec{k}}} \left( {{\varvec{r}}} \right)&= \left[ {p_0 ({{\varvec{r}}})} \right] ^{1/2}\hbox {exp}\{\hbox {i}[{{\varvec{k}}}\cdot {{\varvec{f}}}\!\left[ {p_0 ;{{\varvec{r}}}} \right] +\phi ({{\varvec{r}}})]\}\nonumber \\&\equiv R_0 ({{\varvec{r}}})\hbox {exp}(\hbox {i}\varPhi _{{\varvec{k}}}\!\left[ {p_0 ;{{\varvec{r}}}} \right] ) \equiv \varphi _{{\varvec{k}}}\!\left[ {p_0 ;{{\varvec{r}}}} \right] , \end{aligned}$$
(61)

define the so called Harriman representation of electronic states [22]. The optimum HZM orbitals are determined by the “orthogonality” phase \(F_{{\varvec{k}}}({{\varvec{r}}}) = {{\varvec{k}}}\cdot {{\varvec{f}}}[p_{0}; {{\varvec{r}}}]\), with the wave-vector (reduced momentum) k and the the density-dependent, spatial vector field \({{\varvec{f}}}_{0}({{\varvec{r}}}) = {{\varvec{f}}}[p_{0}; {{\varvec{r}}}]\), both resulting from the ordinary variational principle for the system minimum electronic energy. The optimum shape of the remaining part \(\phi \)(r) of \(\varPhi _{{\varvec{k}}}\)(r), called the thermodynamic phase [22], results from the quantum Extreme Physical Information (EPI) rule, for the given ground-state density \(\rho =\rho _{0}\) or the associated probability distribution \(p=p_{0}\) determined at the energy optimization stage, which gives \(\phi \)(r)\(^{opt.}=\phi _{eq.}[p_{0}\); r] and hence j[\(\varphi _{eq.}[p_{0}\)]; r] \(\ne \) 0 [Eq. (46)]. Therefore, the horizontal equilibrium state of \(N\) electrons again implies the non-vanishing phase-gradient and hence also a presence of a finite probability current.

The overall phase \(\varPhi _{{\varvec{k}}}\)(r) of such equidensity orbitals thus involves the orbital-specific orthogonality (geometric) contribution \({{\varvec{k}}}\cdot {{\varvec{f}}}({{\varvec{r}}}) \equiv F_{{\varvec{k}}}({{\varvec{r}}})\), which enforces the independence of these one-particle states, and a “thermodynamic” term \(\phi \)(r) representing the phase common to all orbitals. The Slater determinants build from the specific selection of \(N\) different equidensity orbitals,

$$\begin{aligned} \Psi _{{\varvec{k}}_1 ,{\varvec{k}}_1 ,\ldots ,{\varvec{k}}_N } (N)&= (1/\sqrt{N!}) \det (\varphi _{{\varvec{k}}_1 } ,\varphi _{{\varvec{k}}_2 } , \ldots , \varphi _{{\varvec{k}}_N } )\nonumber \\&\equiv \Psi _\mathbf{k } (N),\quad {{\varvec{k}}}_i \ne {{\varvec{k}}}_j\quad \hbox {for} \quad i\ne j, \end{aligned}$$
(62)

then by construction generate the prescribed electron density \(\rho \)(r),

$$\begin{aligned} \left\langle {{\Psi }_\mathbf{k}} \right| \hat{\uprho }({{\varvec{r}}})\left| {{\Psi }_\mathbf{k} } \right\rangle =\sum \limits _{i=1}^N {\left| {\varphi _{{\varvec{k}}_i } ({{\varvec{r}}})} \right| ^{2}} =\rho ({{\varvec{r}}}). \end{aligned}$$
(63)

They constitute the complete orthonormal system of \(N\)-particle functions capable of representing any molecular state of \(N\) electrons for this specific electron distribution, in the HZM Configuration–Interaction (CI) type expansion:

$$\begin{aligned} \Psi _0 \!\left( N \right) =\int C_0 \!\left( \mathbf{k} \right) \,\Psi _{{\varvec{k}}}\! \left( N \right) \,d\mathbf{k}. \end{aligned}$$
(64)

Both parts of the orbital phase in Harriman’s construction contribute to the probability current in such a representative (trial) Slater determinant yielding the prescribed electron density. A given (occupied) equidensity orbital \(\varphi _{{\varvec{k}}}\)(r) generates the associated probability-current contribution

$$\begin{aligned} {{\varvec{j}}}_{{\varvec{k}}} ({{\varvec{r}}}) =\langle \varphi _{{\varvec{k}}} | \hat{\mathbf{j}}({{\varvec{r}}})|\varphi _{{\varvec{k}}} \rangle =\frac{\hbar \rho ({{\varvec{r}}})}{mN}\nabla \varPhi _{{\varvec{k}}} ({{\varvec{r}}})\equiv \frac{\hbar p({{\varvec{r}}})}{m} \{\nabla [{{\varvec{k}}} \cdot {{\varvec{f}}}({{\varvec{r}}})]+\nabla \phi ({{\varvec{r}}})\}. \end{aligned}$$
(65)

Hence, the overall current j(r) = \(\langle \Psi _\mathbf{k} (N)\)|\(\hat{\mathbf{j}}({\varvec{r}};N)\)|\(\Psi _\mathbf{k} (N)\rangle \) = j[\(\Psi _\mathbf{k}\); r] corresponding to the \(N\)-electron current operator \(\hat{\mathbf{j}}({\varvec{r}};N)=\sum \limits _{l=1}^N {\hat{\mathbf{j}}_l ({\varvec{r}})} \) in the trial Slater determinant \(\Psi _\mathbf{k} (N)\)reads:

$$\begin{aligned} {{\varvec{j}}}_\mathbf{k}({{\varvec{r}}}) \!&= \!\langle \Psi _\mathbf{k} (N)| \hat{\mathbf{j}}({\varvec{r}};N)|\Psi _\mathbf{k} (N)\rangle \!=\!\sum \limits _{l=1}^N {{{\varvec{j}}}_{{\varvec{k}}_l } ({{\varvec{r}}})} \!=\!\frac{\hbar \rho ({{\varvec{r}}})}{mN}\left( {\sum _{l=1}^N \{{\nabla [{{\varvec{k}}}_l \cdot {{\varvec{f}}}({{\varvec{r}}})]+\nabla } \phi ({{\varvec{r}}})}\} \right) \nonumber \\&= \frac{\hbar }{m}\rho ({{\varvec{r}}})\left( {\frac{1}{N}\sum \limits _{l=1}^N {{{\varvec{k}}}_l } } \right) \nabla \cdot {{\varvec{f}}}({{\varvec{r}}})+\frac{\hbar }{m}p({{\varvec{r}}})\nabla \phi ({{\varvec{r}}})\nonumber \\&\equiv \frac{\hbar }{m}\{\rho ({{\varvec{r}}})\nabla [{\varvec{K}} \cdot {\varvec{f}}({{\varvec{r}}})]+p({{\varvec{r}}})\nabla \phi ({{\varvec{r}}})\}, \end{aligned}$$
(66)

where the average “wave-number” vector of \(\Psi _\mathbf{k} (N)\), independent of the spatial position r,

$$\begin{aligned} {{\varvec{K}}}=\frac{1}{N}\sum \limits _{l=1}^N {{{\varvec{k}}}_l } . \end{aligned}$$

The phase side of the molecular electronic structure reflects its “entropic” aspect, which still remains largely unexplored. The complex wave function of the equilibrium state, generally exhibits a non-vanishing probability current, hence qualitatively differing from the lowest eigenstate (assumed non-degenerate) of the \(N\)-electron Hamiltonian,

$$\begin{aligned} \hat{\hbox {H}}(N)=\hat{\hbox {V}}_{ne}(N)+[\hat{\hbox {T}}(N)+\hat{\hbox {V}}_{ee}(N)]\equiv \sum \limits _{i=1}^{N}v(i)+\hat{\hbox {F}}(N), \end{aligned}$$
(67)

in which the particle current identically vanishes. Here, \(\hat{\hbox {F}}(N)\)combines the electron kinetic (\(\hat{\hbox {T}})\) and repulsion (\(\hat{\hbox {V}}_{ee})\) energy operators. Such an “entropic” interpretation has been also attributed [10–13] to the density-constrained principles in modern DFT, in the so called “vertical” (entropic) searches performed for the specified electron density \(\rho \), e.g., in Levy’s [82] constrained-search construction of the universal part of the energy density functional,

$$\begin{aligned} F[\rho ]=T[\rho ]+V_{ee}[\rho ]=\hbox {inf}_{\Psi \rightarrow \rho }\langle \Psi |\hat{\hbox {F}}|\Psi \rangle \end{aligned}$$
(68)

In this variational procedure one searches over the wave functions \(\Psi (N)\) of \(N\) electrons, which yield the given electron density \(\rho \), symbolically denoted by \(\Psi \rightarrow \rho \), and calculates the \(v\)-independent part \(F[\rho \)] of the density functional for the system electronic energy,

$$\begin{aligned} E_{v}[\rho ]=F[\rho ]+\int v({{\varvec{r}}})\,\rho ({{\varvec{r}}})\,d{{\varvec{r}}}, \end{aligned}$$
(69)

as the lowest value (infimum) of the expectation value of \(\hat{\hbox {F}}(N)\). When this search is performed for the fixed ground-state density, \(\rho =\rho _{0}\), it also implies the fixed DFT value of the system electronic energy, by the first Hohenberg–Kohn (HK) theorem [80].

This feature is reminiscent of the criterion for the equilibrium state formulated in the entropy representation, viz., the maximum-entropy principle for constant internal energy in ordinary thermodynamics. Indeed, the familiar variational principle for determining the ground-state wave-function, involving a search for the minimum of the system energy, can be interpreted as the DFT optimization over all admissible densities, in accordance with the second HK theorem [80], which then involves the “internal” (entropic) search over functions of \(N\) fermions that yield the current trial density:

$$\begin{aligned} \hbox {min}_{\Psi }\langle \Psi |\hat{\hbox {H}}|\Psi \rangle =\hbox {min}_{\rho }\,E_{v}[\rho ]=\hbox {min}_{\rho }\left\{ \int v({{\varvec{r}}})\rho ({{\varvec{r}}})d{{\varvec{r}}}+\hbox {inf}_{\Psi \rightarrow \rho }\langle \Psi |\hat{\hbox {F}}|\Psi \rangle \right\} .\qquad \end{aligned}$$
(70)

Consider the equilibrium principles for the extrema of the system entropy/information, corresponding to the fixed ground-state electron density, \(\rho =\rho _{0}\) or its probability factor \(p=\rho \)/\(N = \rho _{0}\)/\(N =p_{0}\), determined in the external search of the preceding equation. In DFT this internal, entropic principle involves the search for the optimum wave function \(\Psi (N)\) of \(N\)-fermions, corresponding to the fixed external potential \(v\) due to the system nuclei:

$$\begin{aligned} E[\Psi (N)\rightarrow \rho _{0}]=E_{v}[\rho _{0}]&= \int v({{\varvec{r}}})\rho _{0}({{\varvec{r}}})\,d{{\varvec{r}}}+\hbox {inf}_{\Psi \rightarrow \rho _{0}}\langle \Psi |\hat{\hbox {F}}|\Psi \rangle \nonumber \\&= \int v({{\varvec{r}}})\rho _{0}({{\varvec{r}}})\,d{{\varvec{r}}}+F[\rho _{0}]\nonumber \\&= \int v({{\varvec{r}}})\rho _{0}({{\varvec{r}}})\,d{{\varvec{r}}}+V_{ee}[\rho _{0}]+\hbox {inf}_{\Psi \rightarrow \rho _{0}}\langle \Psi |\hat{\hbox {T}}|\Psi \rangle .\nonumber \\ \end{aligned}$$
(71)

One observes the presence of the Levy universal functional \(F[\rho \)] as the crucial (entropic) part of this EPI rule [10–13, 22]. Notice, that in DFT the external potential and electron-repulsion energies are fixed by the frozen density constraint, so that the optimum state also marks the infimum of the Fisher measure of the information content, related to the system average kinetic energy.

Consider the quantum Fisher information in the electronic state approximated by the Harriman determinant of Eq. (62), \(\Psi (N) \approx \Psi _\mathbf{k}(N)\),

$$\begin{aligned} I[\Psi _\mathbf{k}]&= 4\sum \limits _{i=1}^{N}\int |\nabla \varphi _{{\varvec{k}}_{i}}\!({{\varvec{r}}})|^{2}\,d{{\varvec{r}}}={\frac{8m}{\hbar ^{2}}}T[\Psi _\mathbf{k }]\equiv \int p({{\varvec{r}}})I\!({{\varvec{r}}})\,d{{\varvec{r}}}\nonumber \\&= \int p({{\varvec{r}}})[I^{class.}({{\varvec{r}}})+I^{nclass.}({{\varvec{r}}})]\,d{{\varvec{r}}}=I[p]+I[p,\mathbf{k},\phi ], \end{aligned}$$
(72)

proportional to the system average kinetic energy

$$\begin{aligned} I[\Psi _\mathbf{k}]&\equiv \langle \Psi _\mathbf{k}|\hat{\hbox {T}}|\Psi _\mathbf{k}\rangle ={\frac{\hbar ^{2}}{2m}}\sum \limits _{i=1}^{N}\int |\nabla \varphi _{{\varvec{k}}_{i}}\!({{\varvec{r}}})|^{2}d{{\varvec{r}}}\nonumber \\&\equiv T^{class.}[\Psi _\mathbf{k }]+T^{nclass.}[\Psi _\mathbf{k }]\equiv T[p]+T[p,{\mathbf{k}},\phi ]. \end{aligned}$$
(73)

The latter consists of the “classical”, von Weizsäcker density functional \(T[p\)], depending solely upon the particle distribution,

$$\begin{aligned} T^{class.}[\Psi _\mathbf{k}]={\frac{\hbar ^{2}N}{8m}}\int {\frac{|\nabla p({{\varvec{r}}})|^{2}}{p({{\varvec{r}}})}}d{{\varvec{r}}}=T[p], \end{aligned}$$
(74)

and the “non-classical”, (phase/current)-dependent contribution,

$$\begin{aligned} T^{nclass.}[\Psi _\mathbf{k}]&= {\frac{\hbar ^{2}}{2m}}\int p({{\varvec{r}}})\sum _{l=1}^{N}(\nabla [{{\varvec{k}}}_{l}\cdot {{\varvec{f}}}({{\varvec{r}}}+\phi ({{\varvec{r}}})])^{2}d{{\varvec{r}}}=T[p,\mathbf{k},\phi ],\end{aligned}$$
(75)
$$\begin{aligned} T[\Psi _\mathbf{k}]&= T[p]+T[p,\mathbf{k},\phi ], \end{aligned}$$
(76)

related to the corresponding quantum information terms [Eq. (72)]:

$$\begin{aligned} I[\Psi _\mathbf{k} ] {=I} [p] { +I} [p,\mathbf{k},\phi ]. \end{aligned}$$
(77)

In the vertical ground-state search, for \(p = p_{0}=\rho _{0}\)/\(N\), it is the phase component of the quantum state which is being optimized. The condition of the extremum (minimum) Fisher information \(I[{\varvec{\Psi }}_\mathbf{{k}}[p_{0}\)]],

$$\begin{aligned} \delta I[\Psi _\mathrm{k} [p_0 ]]/\delta \phi \left( {{\varvec{r}}} \right) \!=\!\partial I[p_0 ,\phi ]/\partial \phi \left( {{\varvec{r}}} \right) \!=\! 0 \quad \hbox {or}\quad \sum \limits _{l=1}^N {\{\mathbf{k}_l } \cdot {\varvec{f}}[p_0 ;{{\varvec{r}}}]\!+\!\phi _{eq.} [p_0 ;{{\varvec{r}}}]\} \!=\! 0,\nonumber \\ \end{aligned}$$
(78)

then determines the orthogonality thermodynamic phase \(\phi ^{eq.}[p_{0}\); r] that minimizes \(I[p_{0},\,\phi \)] [22]:

$$\begin{aligned} \phi _{eq.}\!\left[ {p_0 ;{{\varvec{r}}}} \right] =-\left( {\frac{1}{N}\sum \limits _{l=1}^N {{{\varvec{k}}}_l } } \right) \cdot {{\varvec{f}}}[p_0 ;{{\varvec{r}}}]\equiv -{\varvec{K}}(\mathbf{k})\cdot {{\varvec{f}}}[p_0 ;{{\varvec{r}}}]. \end{aligned}$$
(79)

Therefore, the equilibrium phase is determined by the average “wave-number” vector K in \({\varvec{\Psi }}_{k}={\varvec{\Psi }}_{k_1 ,k_1 ,\ldots ,k_N } \), for which the density of \(I^{nclass. }\)exhibits the least structure, i.e., the maximum indeterminacy. Hence the equilibrium equidensity orbitals

$$\begin{aligned} \varphi _{k_l } [p_0 ;{{\varvec{r}}}]&= \left[ {p_0 \left( {{\varvec{r}}} \right) } \right] ^{1/2}\hbox {exp}\left( \hbox {i}\left\{ ({\varvec{k}}_l -{\varvec{K}})\cdot {{\varvec{f}}}\left[ {p_0 ;{{\varvec{r}}}} \right] \right\} \right) \nonumber \\&\equiv \left[ {p_0 \left( {{\varvec{r}}} \right) } \right] ^{1/2}\hbox {exp}\{\hbox {i}\delta {{\varvec{k}}}_l \cdot {{\varvec{f}}}\left[ {p_0 ;{{\varvec{r}}}} \right] \},\nonumber \\&\equiv \left[ {p_0 \left( {{\varvec{r}}} \right) } \right] ^{1/2}\hbox {exp}\{\hbox {i}F_{{{\varvec{k}}_{l}}} \left[ {p_0 ;{{\varvec{r}}}} \right] \}, \end{aligned}$$
(80)

determine the equilibrium level of the non-classical kinetic energy:

$$\begin{aligned} T^{nclass.}[p_0 ,\phi ^{eq.}\!\left[ {p_0 } \right] ]&= \frac{\hbar ^{2}}{2m}\int {p_0 ({{\varvec{r}}})\sum \limits _{l=1}^N {\left( {\nabla \{\delta {{\varvec{k}}}_l \cdot {{\varvec{f}}}[p_0 ;{{\varvec{r}}}]\}} \right) ^{2}} } d{{\varvec{r}}}\nonumber \\&\equiv T^{eq.} [p_0 ,{{\varvec{K}}},\phi ^{eq.}\!\left[ {p_0 } \right] ] \nonumber \\&= \frac{\hbar ^{2}}{2m}\int {p({{\varvec{r}}})\sum \limits _{l=1}^N {\left( {\nabla \{\delta {{\varvec{k}}}_l \cdot {\varvec{f}}[p_0 ;{{\varvec{r}}}]\}} \right) ^{2}} } d{{\varvec{r}}}. \end{aligned}$$
(81)

This vertical “thermodynamic” state exhibits the vanishing resultant probability current

$$\begin{aligned} {{\varvec{j}}}\!\left[ {p_0 ;{{\varvec{r}}}} \right] =\frac{\hbar }{m}p_0 ({{\varvec{r}}})\left\{ \left( {\frac{1}{N}\sum \limits _{l=1}^N {\delta {{\varvec{k}}}_l } } \right) \nabla \cdot {{\varvec{f}}}[p_0 ;{{\varvec{r}}}]\right\} \equiv \frac{\hbar }{m}p_0 ({{\varvec{r}}}) \nabla (\delta {\varvec{K}} \cdot {{\varvec{f}}}[p_0 ;{{\varvec{r}}}])=0,\nonumber \\ \end{aligned}$$
(82)

since \(\sum _l\!\delta {{{\varvec{k}}}_l} = N \delta {\varvec{K}} = 0.\)

Therefore, in this one-determinant, vertical approximation of the ground-state wave function \(\Psi _{0}(N)=\Psi [N,\,v\)], for the vanishing thermodynanmic phase \(\phi \) = 0 \(\equiv \phi _{0}\),

$$\begin{aligned} \Psi _0\!\left( N \right) \cong \Psi _{\mathbf{k}_0}\![N,\phi _0 ] \equiv \Psi _{\mathbf{k}_0 } (N) \rightarrow \rho _0 =Np_0 , \end{aligned}$$
(83)

e.g., in the Kohn–Sham (KS) [81] or Hartree–Fock (HF) [87, 88] Self-Consistent Field (SCF) theories, the optimum (real) reduced-momentum vectors \(\mathbf{k}_{0}[p_{0}] = \{{{\varvec{k}}}_{l}^{0}[p_{0}]\}\) result from the (vertical) minimum energy principle for determining the best (orthonormal) equidensity orbitals \(\varphi _{{\varvec{k}}}[p_{0}\); r] that minimize the average value of the system electronic energy:

$$\begin{aligned} \hbox {min}_{\Psi _\mathbf{k} \rightarrow \rho _0 } \left\langle {\Psi _\mathbf{k} (N)} \right| \hat{\hbox {H}}(N) \left| {\Psi _\mathbf{k} (N)} \right\rangle&= \left\langle {\Psi _{\mathbf{k}_0 } (N)} \right| \hat{\hbox {H}}(N)\left| {\Psi _{\mathbf{k}_0 } (N)} \right\rangle = E_{\mathbf{k}_0 } (N)\nonumber \\&\Rightarrow \Psi _{\mathbf{k}_0 } (N). \end{aligned}$$
(84)

This optimum stationary-state determinant \(\Psi _{\mathbf{k}_{0} } (N)\) generates the best estimate \(E_{\mathbf{k}_{0} } (N)\) of the ground-state energy \(E_{0}=E_{v}[\rho _{0}\)] in the HZM representation. This variational procedure implies the Euler–Lagrange problem of the auxiliary energy functional absorbing the orbital orthonormality constraints, enforced by the relevant Lagrange multipliers. The associated equilibrium function \(\Psi _{\mathbf{k}_0 } [N,\varphi ^{eq.} [p_0 ]]\) results from the extra (Fisher) EPI [8, 13, 22]:

$$\begin{aligned} \hbox {inf}_{{\Psi }\rightarrow \rho _{0}}I[\Psi ]=I^{class.}[p_{0}]+\hbox {inf}_{{\Psi }\rightarrow \rho _0 } I^{nclass.}[p_0 ,\mathbf{k}_0 ,\phi ]\quad \Rightarrow \Psi _{\mathbf{k}_0 } [N,\varphi ^{eq.} [p_0 ]].\nonumber \\ \end{aligned}$$
(85)

In the HZM construction the lowest equilibrium state is thus determined by the best SCF values of the “wave-number” vectors k = k \(_{0}\) = {k \(_{l}^{0}\)} of the energy variational principle of Eq. (84) and the optimum spatial-phase function of Eq. (79):

$$\begin{aligned} \phi ({{\varvec{r}}}) =\phi ^{eq.}\!\left[ {p_0 ;{{\varvec{r}}}} \right] =-\left( {\frac{1}{N}\sum _{l=1}^N {{\varvec{k}}_l^0 } } \right) \cdot {{\varvec{f}}}_0 ({{\varvec{r}}})\equiv -{{\varvec{K}}}(\mathbf{k}_0 )\cdot {{\varvec{f}}}_0 ({{\varvec{r}}}),\quad {{\varvec{f}}}_0 \equiv {{\varvec{f}}}[p_0 ].\nonumber \\ \end{aligned}$$
(86)

Together they uniquely specify the \(N\) lowest, singly-occupied (complex) spin-orbitals of the “thermodynamic” Slater determinant \(\Psi _{\mathbf{k}_0 } [N,\phi ^{eq.} [p_0 ]]\) corresponding to the system phase-equilibrium. The minimum Fisher information principle of Eqs. (71) and (85) thus involves a search for the optimum equidensity orbitals of \(N\) electrons in the ground-state electron distribution \(\rho _{0} = { Np}_{0}\), determined by the energy-optimum “wave-number” vectors \(\mathbf{k}_{0}[p_{0}]\) of Eq. (84) and the (entropy/information)-optimum, “equilibrium” phase of Eq. (79).

Let us further explore the relation between the equilibrium (horizontal) phases of orbitals and the molecular probability distributions. In the single-determinant approximation \(\Psi (N) = (N!)^{-1/2}\hbox {det}(\{\varphi _{l}\})\) using the equidensity orbitals \(\{\varphi _{l} = [p({{\varvec{r}}})]^{1/2}\hbox {exp}[\hbox {i}\varPhi _{l}({{\varvec{r}}})]\}\) the quantum entropy or gradient measures of the information content are given by the sums of the corresponding orbital contributions:

$$\begin{aligned} S[\Psi ] =\sum \limits _{l} \langle \varphi _{l} |\hat{\hbox {S}}({{\varvec{r}}})|\varphi _{l} \rangle =\sum \limits _{l} S[\varphi _{l} ] \quad \hbox {and} \quad I [\Psi ] =\sum \limits _{l} \langle \varphi _{l}|\hat{\hbox {I}}({{\varvec{r}}})|\varphi _{l} \rangle =\sum \limits _{l} I[\varphi _{l}].\nonumber \\ \end{aligned}$$
(87)

The horizontal equilibria now mark the extrema of the auxiliary entropy/information functionals

$$\begin{aligned} \delta \{S[\Psi ] -\mu \langle \Psi |\Psi \rangle \} = 0\quad \hbox {or}\quad \delta \{I[\Psi ] -\mu \langle \Psi |\Psi \rangle \} = 0,\quad \langle \Psi |\Psi \rangle =\prod \limits _l \langle \varphi _l |\varphi _l \rangle =1.\nonumber \\ \end{aligned}$$
(88)

By performing the unconstrained variations of the complex conjugate orbitals these principles give, for the optimum (normalized) orbitals,

$$\begin{aligned} \sum \limits _l \langle \delta \varphi _l |\hat{\hbox {S}}({\varvec{r}})-\mu |\varphi _l \rangle = 0\quad \hbox {or}\quad \sum \limits _l \langle \delta \varphi _l |\hat{\hbox {I}}({\varvec{r}})-\mu |\varphi _l \rangle = 0. \end{aligned}$$
(89)

For arbitrary variations {\(\delta \varphi _{l}^{*}\)} the preceding relations thus imply the following Euler equations for the optimum orbitals:

$$\begin{aligned}{}[\hat{\hbox {S}}({\varvec{r}})-\mu ]\varphi _l = 0\quad \hbox {or}\quad [\hat{\hbox {I}}({\varvec{r}})-\mu ]\varphi _l = 0,\quad l=1,2, \ldots ,N, \end{aligned}$$
(90)

which again imply the relation of Eq. (32) [see also Eq. (80)]:

$$\begin{aligned} \varPhi _l ({\varvec{r}})_{eq.}&= -\, (1/2)\,\hbox {ln}p({\varvec{r}}) + F_{{\varvec{k}}_l}[p_0;{\varvec{r}}] +const.\nonumber \\&\equiv -\, (1/2)\,\hbox {ln}p({\varvec{r}}) + F_{{\varvec{k}}_l}[p_0;{\varvec{r}}],\quad l=1,2, \ldots ,N, \end{aligned}$$
(91)

where we have again absorbed the constant phase, irrelevant in quantum mechanics, by the appropriate choice of the zero value of orbital phases.

Therefore, the horizontal equilibrium marks the resultant orbital phases, determined by the electron probability distribution alone. For \(p=p_{0}\) this is a manifestation of the Hohenberg–Kohn theorem: the electron density uniquely determines the equilibrium equidensity orbitals:

$$\begin{aligned} \mathbf{k}_{eq.} =\mathbf{k}\!\left[ {p_0 } \right] ,\quad {\varvec{f}}_{eq.} ={\varvec{f}}\!\left[ {p_0}\right] ,\quad \phi _{eq.} =\phi _{eq.}\!\left[ {p_0 } \right] . \end{aligned}$$
(92)

The phases of Eq. (91) imply the following orbital contributions to the equilibrium current:

$$\begin{aligned} {\varvec{j}}[\varphi _l ;{\varvec{r}}]_{eq.}&= {\varvec{j}}_l ({\varvec{r}})_{eq.} =-\frac{\hbar }{2m}\nabla p({\varvec{r}}) + \frac{\hbar }{m} p({\varvec{r}})\nabla (\delta {\varvec{k}}_l[p_0] \cdot {\varvec{f}}[p_0;{\varvec{r}}])\nonumber \\&\equiv -\frac{\hbar }{2m}\nabla p({\varvec{r}}) + \frac{\hbar }{m}p({\varvec{r}})\nabla ({\varvec{F}}_l[p_0;{\varvec{r}}]), \end{aligned}$$
(93)

shaped by the system probability distribution, and hence the resultant equilibrium current of \(N\) electrons:

$$\begin{aligned} {\varvec{j}}[{\Psi }_\mathbf{k} ;{\varvec{r}}] =N{\varvec{j}}_l ({\varvec{r}})_{eq.} =-\frac{\hbar }{2m}\nabla \rho ({{\varvec{r}}}). \end{aligned}$$
(94)

Therefore, in the phase-equilibrium the overall current is also fully determined by the gradient of the molecular electron density.

As argued elsewhere [9, 10], both the classical and non-classical parts of the densities-per-electron of the quantum measures of the resultant Fisher and Shannon information descriptors are mutually related, with the former being determined by the squared gradient of the latter [Eq. (27)]. One further observes that for the fixed electron distribution in the internal (vertical) search only the non-classical components depend upon the “wave-number” vectors \(\mathbf{k}_{0}\) and the phase function \(\phi \)(r), which together determine the resultant phase in Harriman’s construction, to be optimized in the adopted energy or EPI principle. Thus the infimum of the Fisher measure implies the supremum of the average gradient of the wave function and hence its lowest degree of structure (“order”). This further implies the highest admissible degree of the wave-function indeterminacy (“disorder”) marked by the supremum of the complementary measure, the quantum Shannon entropy:

$$\begin{aligned} \hbox {sup}_{\Psi _{{\mathbf{k}}_{0}} \rightarrow p_{0}} S[\Psi ] =S [p_0 ] +\hbox {sup}_{\Psi _{{\mathbf{k}}_{0} } \rightarrow p_{0} } S[p_0 ,\mathbf{k}_0 ,\phi ]\quad \Rightarrow \quad \Psi _{{{\mathbf{k}}_{0}} [p_{0} ]} [N,\phi _{eq.} [p_0 ]].\nonumber \\ \end{aligned}$$
(95)

Therefore, the two generalized measures of the information content of the complex wave-function in the Harriman-type construction are complementary in character: the ground-state density/energy constrained EPI of the lowest quantum Fisher information is synonymous with the related principle of the highest quantum Shannon entropy. This is again reminiscent of the complementary equilibrium criteria of the minimum energy and the maximum entropy in phenomenological thermodynamics.

To further illustrate this point we again refer to the one-electron example. As in ordinary thermodynamics, the lowest equilibrium state alternatively results either from the (ground-state) entropy-constrained minimum-energy principle, or from the (ground-state) energy-constrained maximum of the non-classical Shannon entropy or the minimum of the quantum Fisher information [7, 8]. Consider the illustrative example of a single particle described by the Hamiltonian of Eq. (5) in the variational state \(\varphi ({{\varvec{r}}})\) [Eq. (1)]. The minimum principle of the expectation value of the system electronic energy

$$\begin{aligned} E_v [\varphi ^{0}] =\left\langle {\varphi ^{0}} \right| \hat{\hbox {H}}\left| {\varphi ^{0}} \right\rangle =(\hbar ^{2}\hbox {/2}m)\int {[(\nabla R_{0} )^{2}} +R_{0}^{2} (\nabla \phi )^{2}]\,d{\varvec{r}}+\int {R_{0}^{2} v}\,d{\varvec{r}}\equiv E_{v}^{0} [\phi ]\nonumber \\ \end{aligned}$$
(96)

in the modulus-constrained trial state \(\varphi ^{0}({{\varvec{r}}}) = R_{0}({{\varvec{r}}}) \hbox {exp}[\hbox {i}\Phi ({{\varvec{r}}})]\), where \(R_{0}({{\varvec{r}}}) = [\rho _{0}({{\varvec{r}}})]^{1/2}\), for the conserved (phase-independent) entropy \(S_{0}[\varphi _{0}] = S^{class.}[p_{0}]\) in the system ground-state \(\varphi _{0}({{\varvec{r}}}) = R_{0}({{\varvec{r}}})\) which marks the vanishing spatial phase \(\phi ({{\varvec{r}}}) = \phi _{0}= {\varvec{0}}\), its gradient \(\nabla \phi _{0} = {{\varvec{0}}}\), and the probability current \({{\varvec{j}}}({{\varvec{r}}}) = {{\varvec{j}}}_{0}({{\varvec{r}}})= {{\varvec{0}}}\), gives:

$$\begin{aligned} \mathop {\min }\limits _{\phi } E_{v}^{0} [\phi ]&= \left\langle {\varphi _{0} }\right| \hat{\hbox {H}}\left| {\varphi _{0} } \right\rangle =(\hbar ^{2}\hbox {/2}m)\int {(\nabla R_{0} )^{2}}\,d{\varvec{r}}+\int {R_{0}^{2} v}\,d{{\varvec{r}}} \equiv E_{v}^{0} [\phi _0] \nonumber \\&= \left( {\frac{\hbar ^{2}}{8m}} \right) \int {\frac{(\nabla p_{0} )^{2}}{p_{0} }}\,d{{\varvec{r}}}+\int {p_{0}\,{v}}\,d{{\varvec{r}}} =E_{v} [p_{0} ]. \end{aligned}$$
(97)

This optimum solution also identifies the maximum of the non-classical entropy \(S[p_{0},\,\phi ]\),

$$\begin{aligned} \hbox {max}_{\phi } S[p_{0} ,\phi ] =S [p_{0} ,\phi _{0} ]= 0, \end{aligned}$$

which also implies the minimum of the associated density-constrained quantum Fisher information \( I[p_{0},\,\phi ]\):

$$\begin{aligned} \hbox {min}_\phi I[p_{0} ,\phi ] =I[p_{0} ,\phi _{0} ]= 0. \end{aligned}$$

Therefore, we have arrived at a remarkable parallelism with the ordinary thermodynamics: the ground-state solution alternatively results from the equivalent density-constrained (vertical) variational principles: of the system minimum electronic energy or the extremum of the quantum entropy/information.

5 Conclusion

In this article we have emphasized a need for the quantum extensions of the classical information concepts, in order to accommodate the complex wave functions (probability amplitudes) of the quantum-mechanical description of molecular electronic states. The appropriate non-classical generalization of the gradient (Fisher) measure of the information content introduces the contribution due to the probability current, giving rise to a non-vanishing information source. The quantum-generalized Shannon entropy similarly includes the additive phase contribution. This extension has been accomplished by postulating that the relation between the classical Shannon and Fisher information densities-per-electron extends into the non-classical (quantum) domain, between entropy/information densities due to the state phase/current. These quantum information contributions complement the classical Fisher and Shannon information measures, functionals of the particle probability distribution alone. The resultant descriptors extract the full information content of the complex probability amplitudes (wave functions) of the quantum mechanical description, due to both the probability and current distributions.

The phase-equilibria of molecular systems have been explored. They correspond to the unconstrained (horizontal) extrema of the quantum information measures for the given probability distribution. This optimum phase has been shown to be related to the logarithm of the electron probability distribution, thus generating a non-vanishing current and non-classical entropy/information contributions. Selected properties of such equilibrium states have been examined. In particular, in one-electron systems the equalization of the classical and non-classical information contributions is observed. Such states were also shown to correspond to the vanishing expectation value of the electronic energy, while their currents are shaped by the gradient of the electron probability distribution.