1 Introduction

The classical information theory (CIT) [1–8], using measures of the entropy/information content of molecular probability distributions, has been remarkably successfull in addressing many classical issues in the theory of electronic structure and reactivity, e.g., [9–12]. It fails, however, to account for the structural information contained in the phase or current distributions of complex quantum states, being designed to probe solely the particle density. The electronic current, generated by the phase gradient, ultimately contributes to the resultant information content and quantum communications between bonded atoms in molecules. Such a quantum extension of information concepts, which recognizes the entropic contributions generated by the state phase density or electronic current, calls for the nonclassical complements to the familiar classical measures of the information content [13–20]. This quantum information theory (QIT) distinguishes states exhibiting the same electron distribution but differing in composition of electronic currents, which CIT fails to do.

In QIT an adequate measure of the resultant information content of molecular electronic states must reflect their complete “structure” aspect, accounting for the entropy/information characteristics of the spatial distributions of both the probability and phase components of the system wavefunction. The electron density, related to the wavefunction modulus, reveals the classical (probability) aspect of the state information content, while the phase/current facet gives rise to the nonclassical entropy/information terms. Together these two contributions allow one to monitor the full (resultant) information content of, say, degenerate, non-equilibrium or general (variational) states, thus providing the complete information description of their evolution towards the ground-state equilibrium.

Such a combined perspective also applies to the cross-entropy (information-distance) quantities and electronic communications in molecules, which generate the entropic descriptors of chemical bonds. In QIT the classical information channel reflects the probability-scattering from the “input” to “output” events relevant for the adopted resolution level. Its nonclassical supplement involves the associated networks of elementary phase- and current-propagations in the molecular bond system [19]. Such phase/current networks generate the nonclassical supplements to classical entropic descriptors of molecular bond multiplicities and their covalent/ionic composition [19, 20].

A conservation in time of the overall classical measures of the entropy/information content in the position-probability density, due to the sourceless character of the continuity equation for the quantum distribution of electrons, has been stressed [11] and the continuity equations for the resultant Shannon and Fisher type measures have been explored [21, 22]. These full measures exhibit finite source terms due to the nonclassical information terms. The phenomenological description of equilibria in molecular systems has been proposed [17, 18, 21], which resembles that developed in the ordinary irreversible thermodynamics [23]. This nonequilibrium treatment of the time evolution of entropic probes of molecular electronic states has introduced a new framework for describing in information terms the dynamics of chemical processes [20]. The relevant entropy current and source concepts have been identified in the continuity equation for the resultant entropy density, and the local sources of the overall Shannon (global) and Fisher (gradient) type entropies have been interpreted [22].

The sourceless character of the continuity equation for the quantum probability density in position representation implies a conservation of the classical information measures in time. This is no longer the case, when the information contributions due to the phase/current distributions are taken into account. Indeed, the continuity equations for these nonclassical degrees-of-freedom of molecular electronic states exhibit finite sources [11, 14, 17, 18, 24], which ultimately contribute to the time dependence of the resultant entropy measures. These nonclassical state-variables also introduce a nonvanishing source term into the associated continuity equation for the resultant entropy, which expresses a local balance between the flow and source contributions in the time evolution of the resultant information density [22]. However, specific forms of this continuity relation for the Fisher or Shannon type of the overall measure of the entropy/information content is phase-current dependent, with different flux definitions only reshuffling the local probability and phase rates, known from molecular Schrödinger equation, between the inflow and source parts of the underlying phase-continuity equation.

The molecular phase-equilibria are determined by the extremum information principles involving either the nonclassical or resultant entropy/information concepts [15–18, 25, 26]. The latter determines the so called horizontal-equilibrium state, which represents the phase-transformed quantum state of a molecule, corresponding to the optimum, density-dependent “thermodynamic” phase. This manipulation of the electronic state, without an accompanying change of quantum observables, preserves the electron probability distribution but modifies its current. It is the main purpose of this work to examine how this “thermodynamic” transformation affects the continuity equations for the electron probability, phase and entropy densities.

2 Probability and phase continuity

Let us consider a general one-electron state \(\varphi ({\varvec{ r}}, t)=R({{\varvec{r}}}, t)\) exp[i\(\phi ({\varvec{ r}}, t)\)], with \(R({\varvec{ r}}, t)\) and \(\phi ({\varvec{ r}}, t)\) representing its modulus and phase components, respectively. We adopt the usual Born-Oppenheimer (BO) approximation of the fixed nuclear positions. In this prototype molecular scenario one envisages a single electron moving in the external potential \(v({\varvec{ r}})\) due to the “frozen” nuclei, described by the Hamiltonian

$$\begin{aligned} {\hat{\mathrm{H}}}({\varvec{ r}})=-\left( {\hbar ^{2}/2m} \right) \nabla ^{2}+v({\varvec{ r}}) ={\hat{\mathrm{T}}}({\varvec{ r}})+v({\varvec{ r}}). \end{aligned}$$
(1)

The state probability distribution and its current density read:

$$\begin{aligned} p\left( {{\varvec{r}},t} \right)= & {} |\varphi \left( {{\varvec{r}},t} \right) |^{2}=R\left( {{\varvec{r}},t} \right) ^{2}, \nonumber \\ {\varvec{j}}\left( {{\varvec{r}},t} \right)= & {} \frac{\hbar }{2mi}[\varphi ^{*}({\varvec{r}},t)\nabla \varphi ({\varvec{r}},t)-\varphi ({\varvec{r}},t)\nabla \varphi ^{*}({\varvec{r}},t)] =\frac{\hbar }{m}p({\varvec{r}},t)\nabla \phi ({\varvec{r}},t). \end{aligned}$$
(2)

These principal distributions reflect the state two independent components: its modulus and the phase or its gradient determining the current density \(\mathbf {\varvec{j}} \equiv {\mathbf {\varvec{j}}}_{p}\). The wave-function modulus factor R, the classical amplitude of the particle probability distribution \(p = R^{2}\), and the state phase \(\phi \) or its gradient \(\nabla \phi \) thus constitute two fundamental “degrees-of-freedom” of electronic states:

$$\begin{aligned} \varphi \Leftrightarrow (R,\phi )\Leftrightarrow \left( {p,{\varvec{j}}} \right) . \end{aligned}$$
(3)

They both contribute to the resultant entropy/information descriptors of molecular quantum states, which combine both the classical contributions, due the the particle probability distribution, and the nonclassical terms, related to the state phase/current [13–20].

The dynamics of this quantum state in wave mechanics is determined by the Schrödinger equation (SE):

$$\begin{aligned} {\hat{\mathrm{H}}}({\varvec{r}}) \varphi ({\varvec{r}},t)=\hbox {i}{\hbar \partial }\varphi \left( {{\varvec{r}},t} \right) /\partial t. \end{aligned}$$
(4)

One further recalls that the weighted sum of this equation and its Hermitian conjugate gives rise to the sourceless form of the continuity equation for the particle probability distribution \(p({\varvec{ r}}, t)\):

$$\begin{aligned} \partial p\left( {{\varvec{r}},t} \right) /\partial t= & {} -\nabla \cdot {\varvec{j}}\left( {{\varvec{r}},t} \right) \hbox { or } \nonumber \\ dp\left( {{\varvec{r}},t} \right) /dt\equiv \sigma _p\left( {{\varvec{r}},t} \right)= & {} \partial p\left( {{\varvec{r}},t} \right) /\partial t+\nabla \cdot {\varvec{j}}\left( {{\varvec{r}},t} \right) = 0. \end{aligned}$$
(5)

This continuity relation for the position-space probability expresses a local balance in electron redistributions from the angle of the wave-function modulus: the local rate of the probability density in the fixed “monitoring” volume element, \(\partial p({\varvec{ r}}, t)/\partial t\), is solely due to the probability outflow measured by the negative divergence of the probability current density, \(-\nabla \cdot {{\varvec{j}}}({\varvec{ r}}, t)\), while its rate in the volume element moving with the particle, \({dp}({\varvec{ r}}, t)/{dt}\), i.e., the probability source, identically vanishes: \(\sigma _{p}({\varvec{ r}}, t) = 0\).

The weighted difference of SE and its conjugate,

$$\begin{aligned} (\hbox {i}\hbar )^{-1}(\psi ^{*} {\hat{\mathrm{T}}}\psi +\psi {\hat{\mathrm{T}}}\psi ^{{*}} + 2pv)= & {} -\left[ {\hbar /\left( {m\hbox {i}} \right) } \right] [R\Delta R-p(\nabla \phi )^{2}] +(\hbox {i}\hbar )^{-1}2pv \\= & {} \psi ^{*}(\partial \psi /\partial t)-\psi (\partial \psi ^{*}/\partial t)= 2\hbox {i}p(\partial \phi /\partial t), \end{aligned}$$

similarly determines the time derivative of the state phase \(\phi ({\varvec{ r}}, t)\) [14],

$$\begin{aligned} \partial \phi ( {{\varvec{r}},t} )/\partial t= \left[ {\hbar /\left( {2m} \right) } \right] \{R( {{\varvec{r}},t} )^{-1} \Delta R( {{\varvec{r}},t} )-[\nabla \phi ( {{\varvec{r}},t} )]^{2}\}-v( {\varvec{r}} )/\hbar , \end{aligned}$$
(6)

or the associated rate of the phase-density \(f({\varvec{ r}}, t)=\phi ({\varvec{ r}}, t)^{2} \ge 0\):

$$\begin{aligned} \partial f({{\varvec{r}},t} )/\partial t= 2 \phi ( {{\varvec{r}},t} )\partial \phi ( {{\varvec{r}},t} )/\partial t. \end{aligned}$$
(7)

Ascribing the flux concept to phase component of molecular states is not unique [14, 20, 25, 26]. Alternative phase-flow concepts \({\varvec{ J}}_{f}({{\varvec{r}}}, t)\) only reshuffle the known rate of the state phase-density between the outflow, \(-\nabla \cdot {\varvec{ J}}_{f }({{\varvec{r}}}, t)\), and the source, \(\varSigma _{f}({\varvec{ r}}, t)\), contributions in the underlying phase-continuity equation:

$$\begin{aligned} df({{\varvec{r}},t} )/dt\equiv \varSigma _f ({{\varvec{r}},t} ) =\partial f( {{\varvec{r}},t} )/\partial t+\nabla \cdot {\varvec{J}}_{f} ( {{\varvec{r}},t} ). \end{aligned}$$
(8)

Therefore, for definiteness, one ascribes the whole derivative of Eq. (7) exclusively to the absolute (abs.) phase-source, for the identically vanishing phase-current [20, 22, 25, 26],

(9)

3 Classical entropy/information measures nad their nonclassical complements

At specified time t, which for simplicity we temporarily leave out from the list of the state arguments, the Fisher measure [1, 2] of the gradient information in \(p({\varvec{ r}})\), reflecting the average determinicity-information content in this probability density, is reminiscent of the von Weizsäcker [27] inhomogeneity correction to the kinetic energy functional in Thomas–Fermi–Dirac (TFD) theory:

$$\begin{aligned} I[ p ] =\smallint [\nabla p({\varvec{r}})]^{2}/p({\varvec{r}}) d{\varvec{r}}\equiv \smallint p({\varvec{r}}) I_{p} ({\varvec{r}}) d{\varvec{r}}\equiv \smallint g_{p} ({\varvec{r}}) d{\varvec{r}}\equiv I^{class.}[\varphi ], \end{aligned}$$
(10)

where

$$\begin{aligned} I_{p} ({\varvec{r}}) = [\nabla p({\varvec{r}})/p({\varvec{r}})] ^{2}=[\nabla \hbox {ln}p({\varvec{r}})]^{2}\equiv I^{class.}\left( {\varvec{r}} \right) \end{aligned}$$
(11)

stands for the functional density-per-electron. This intrinsic accuracy descriptor measures an effective localization (compactness, narrowness, “order”) of the probability distribution. It simplifies, when expressed in terms of its classical probability aplitude \(R({\varvec{r}})\),

$$\begin{aligned} I[ p ] = 4\smallint [\nabla R({\varvec{r}})]^{2} d{\varvec{r}}\equiv I[ R ], \end{aligned}$$
(12)

thus revealing that it effectively measures the average length of the gradient of the state modulus factor \(R({\varvec{ r}})\).

The complementary CIT descriptor, the classical entropy of Shannon [3, 4],

$$\begin{aligned} S[ p ]=-\smallint p({\varvec{r}}) \hbox {ln}p({\varvec{r}}) d{\varvec{r}}\equiv \smallint p({\varvec{r}})S_p ({\varvec{r}}) d{\varvec{r}}\equiv \smallint h_p ({\varvec{r}}) d{\varvec{r}}\equiv S^{class.}[\varphi ], \end{aligned}$$
(13)

where the associated density-per-electron, \( S_{p}({\varvec{ r}}) \equiv \, S^{class.}({\varvec{ r}}) = -\hbox {ln} p({\varvec{ r}})\), reflects the average indeterminacy-information content in \(p({\varvec{ r}})\). This functional measures the average uncertainty (diffuseness, spread, “disorder”) in the probability distribution. It also provides the average amount of the information received, when this uncertainty is removed by the particle-localization experiment: \(I^\mathrm{S}[p] \equiv \, S[p]\). One further observes that densities of these complementary gradient and global entropy/information probes are mutually related:

$$\begin{aligned} I_p \left( {\varvec{r}} \right) =[\nabla \hbox {ln}p({\varvec{r}})]^{2}= [\nabla S_p \left( {\varvec{r}}\right) ]^{2}. \end{aligned}$$
(14)

The amplitude form of the Fisher information renders its natural, resultant generalization in terms of the system complex probability amplitude, i.e., the wavefunction \(\varphi ({{\varvec{r}}})\) itself:

$$\begin{aligned} I[\varphi ]= & {} 4\smallint |\nabla \varphi ({\varvec{r}})|^{2} d{\varvec{r}}=\hbox { }4\{\smallint [\nabla R({\varvec{r}})]^{2} d{\varvec{r}}+\smallint R({\varvec{r}})^{2} [\nabla \phi ({\varvec{r}})]^{2} d{\varvec{r}}\}\nonumber \\&\equiv I^{class.}[\varphi ] {\,+\,I^{nclass.}} [\varphi ] \nonumber \\= & {} I[ p ] + 4\smallint p({\varvec{r}}) [\nabla \phi ({\varvec{r}})]^{2} d{\varvec{r}}\equiv \smallint p({\varvec{r}}) [I_p ({\varvec{r}}) +I_\phi ({\varvec{r}})] d{\varvec{r}}\nonumber \\&\equiv I[ p ]+I[\phi ]\equiv I[p,\phi ] \nonumber \\= & {} I[ p ] +(2m/\hbar )^{2}\smallint {\varvec{j}}({\varvec{r}})^{2}/p({\varvec{r}}) d{\varvec{r}}\equiv I[ p ] +I[{\varvec{j}}]\equiv I[p,{\varvec{j}}]. \end{aligned}$$
(15)

It is proportional to the state overall kinetic energy \(T[\varphi ], I[\varphi ] = (8{m/\hbar }^{2})T[\varphi ]\), and introduces the nonclassical supplement to the classical gradient information due to phase/current:

$$\begin{aligned} I^{nclass.}[\varphi ]\hbox { }=4 \smallint p({\varvec{r}}) [\nabla \phi ({\varvec{r}})]^{2} d{\varvec{r}}\equiv I[\phi ] =(2m/\hbar )^{2} \smallint {\varvec{j}}({\varvec{r}})^{2}/p({\varvec{r}}) d{\varvec{r}}\equiv I[{\varvec{j}}]. \end{aligned}$$
(16)

One conjectures the nonclassical complement \(S^{nclass.}[\varphi ]\) to \(S^{class.}[\varphi ]\) by applying the classical equation (14) to the nonclassical entropy/information densities [15–20, 25, 26]:

$$\begin{aligned} I_\phi ({\varvec{r}}) =[2\nabla \phi ({\varvec{r}})] ^{2}= [\nabla S_\phi ({\varvec{r}})]^{2}. \end{aligned}$$
(17)

It follows from Eqs. (14) and (17) that the square of the gradient of the Shannon probe, of the state indeterminicity (disorder), generates the density of the complementary Fisher measure, of the state determinicity (order). For the positive phase convention, \(\phi = {\vert } \phi {\vert } = (f)^{1/2} \, \ge \) 0, this relation finally gives:

$$\begin{aligned} S^{nclass.}[\varphi ] = -2\smallint p({\varvec{r}}) \phi ({\varvec{r}}) d{\varvec{r}}=\smallint p({\varvec{r}}) S_\phi ({\varvec{r}}) d{\varvec{r}}\equiv -2\langle \phi \rangle . \end{aligned}$$
(18)

The nonclassical entropy \(S^{nclass.}[\varphi ]\) thus reflects the state average phase \(\langle \phi \rangle \). The relevant densities-per-electron of the nonclassical entropy/information contributions thus read:

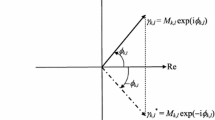
$$\begin{aligned} S_\phi ({\varvec{ r}})= & {} -2 \phi ({\varvec{ r}}) \equiv \quad S^{nclass.}({\varvec{ r}}) \quad \hbox { and }\nonumber \\ I_\phi ({\varvec{r}})= & {} 4[\nabla \phi ({\varvec{r}})]^{2}=\left( {2m/\hbar } \right) ^{2}[{\varvec{j}}({\varvec{r}})/p({\varvec{r}})]^{2}\equiv I^{nclass.}({\varvec{r}}). \end{aligned}$$
(19)

For the specified probability density p and the adopted phase convention, its negative sign signifies the maximum entropy in the strong-stationary molecular state, when \(\phi ({\varvec{ r}}) = 0\) and \({\varvec{ j}}({{\varvec{r}}}) = {\mathbf {0}}\). One thus predicts that the probability-constrained (vertical) displacements \(\Delta \phi ({\varvec{ r}}) = \phi ({\varvec{ r}}) \ge \) 0 from this strong-stationary, vertical-equilibrium state \(\varphi \), for which the nonclassical entropy/information terms exactly vanish, result in lowering the resultant entropy \(S[\varphi \)], the overall information-indeterminicity measure, compared to the initial phase-maximum level \(S^{class.}[\varphi ] = S[p]\). Therefore, in close analogy to the maximum entropy principle of the ordinary thermodynamics [23], such transitions of the state spatial phase, \(0\rightarrow \phi ({\varvec{ r}})\), diminish the nonclassical entropy component, \(\Delta S^{nclass.}[\varphi ] \equiv S[\phi ] \le \) 0, with \(\delta S^{nclass.}[\varphi ] \equiv -S[\phi ] \ge \) 0 then measuring the entropy change corresponding to the reverse displacement \(\phi ({\varvec{ r}})\rightarrow 0\), which restores back the system vertical equilibrium (see Fig. 1).

A complementary picture emerges, when one examines the Fisher-type, gradient measure of the state information-determinicity. For the specified probability distribution \(p({\varvec{ r}})\), the vertical equilibrium \(\phi ({\varvec{ r}}) = 0\) now represents the phase-minimum of the resultant information content. Thus, a finite displacement of the spatial phase, \(\Delta \phi =\phi \, >\) 0, increases the gradient information content by \(\Delta I^{nclass.}[\phi ] \equiv \, I[\phi ] \ge 0\), with the relaxational quantity \(\delta I^{nclass.}[\phi ] \equiv -I[\phi ] \le 0\) measuring the change in the information content corresponding to the reverse displacement, \(\phi ({\varvec{ r}})\rightarrow ~0\), which restores back the vertical equilibrium marking the vanishing nonclassical information.

Fig. 1
figure 1

Qualitative plots of the nonclassical measures of the entropy/information content in the trial state \(\varphi ^{0}({\varvec{ r}}) = \varphi [p_{0}\), \(\phi ; {\varvec{ r}}] = R_{0}({\varvec{ r}})\) exp[i\(\phi ({\varvec{ r}})\)]

Full size image

Therefore, a presence of a finite spatial phase, i.e., of a nonvanishing electronic current, signifies a displacement from the system strong stationarity. It introduces an additional “structure” element of quantum systems, which is not recognized in CIT. The current pattern implies less “uncertainty” (more “order”) in the molecular electronic state, compared to its classical information content. The CIT approach formally corresponds to the vanishing local currents, i.e., to the “standing-wave” solution representing our total “ignorance” of the current direction, when the “forward” and “backward” currents have exactly the same probability. Thus, the state with a definite current direction and its (finite) magnitude exhibits a higher information content, i.e., a lower entropy descriptor, compared to the strong-stationary state, in which the direction of the current remains undefined, with the “forward” and “backward” contributions exactly cancelling each other.

Indeed, since higher information content implies less state uncertainty, one predicts the negative sign of the nonclassical phase entropy (indeterminicity) supplement \(S^{nclass.}[\varphi \)], and the positive sign of the nonclassical current information (determinicity) term \(I^{nclass.}[\varphi \)]. The complex quantum state exhibiting a nonvanishing spatial phase thus exhibits less resultant entropy compared to its maximum value in the strong-stationary state of the same probability distribution, and hence relatively more resultant information. Indeed, a close relation of the classical gradient measure to the kinetic energy suggests a similar relation between its nonclassical supplement and the kinetic energy due to electronic current, thus suggesting a positive sign of the current contribution to the resultant Fisher-type information. The negative nonclassical entropy contribution, which lowers the resultant entropy relative to its classical value, further implies less resultant information received, when this current “order” is removed in the strong-stationary state of the same density.

To summarize, the average resultant entropy is determined by the sum of the classical, \(S^{class.}[\varphi ] =S[p]\), and nonclassical, \(S^{nclass.}[\varphi ] = S[\phi ]\), entropy components:

$$\begin{aligned} S[\varphi ]\equiv & {} S^{class.}[\varphi ] +S^{nclass.}[\varphi ] \equiv \smallint p ({\varvec{ r}}) S({{\varvec{r}}}) d {\varvec{ r}} \equiv \smallint h ({\varvec{ r}}) d{{\varvec{r}}}\nonumber \\= & {} \smallint p({\varvec{ r}}) S_{p} ({\varvec{ r}}) d {{\varvec{r}}} +\smallint p({\varvec{ r}}) S_\phi ({{\varvec{r}}})d{\varvec{ r}} = S[p] +S[\phi ] \equiv S[p, \phi ], \end{aligned}$$
(20)

each separately related [see Eqs. (14), (17)] to the corresponding gradient information contributions, \(I^{class.}[\varphi ] =I[p]\) and \(I^{nclass.}[\varphi ] = I[\phi ] = I[{\varvec{ j}}]\), in the average resultant Fisher information:

$$\begin{aligned} I[\varphi ]\equiv & {} I^{class.}[\varphi ]+I^{nclass.}[\varphi ] \equiv \, \smallint p({\varvec{ r}}) I({{\varvec{r}}}) d{\varvec{ r}} \equiv \, \smallint g({\varvec{ r}}) d {{\varvec{r}}}\nonumber \\= & {} \smallint p ({\varvec{ r}}) I_{p}({{\varvec{r}}}) d{\varvec{ r}} +\smallint p ({\varvec{ r}}) I_\phi ({\varvec{ r}}) d{{\varvec{r}}} = I[p]+I[\phi ] = I[p, \phi ] \nonumber \\= & {} I[p] +I[{\varvec{ j}}]= I[p, {\varvec{ j}}]. \end{aligned}$$
(21)

Of interest also is the state resultant gradient entropy [25], a local indeterminicity descriptor

$$\begin{aligned} {\tilde{I}}[\varphi ]= \tilde{I}^{class.}[\varphi ] + {\tilde{I}}^{nclass.}[\varphi ] = \tilde{I}[p] + {\tilde{I}}[\phi ] \equiv \tilde{I}[p,\phi ]. \end{aligned}$$
(22)

Since the classical Shannon entropy also measures the information content in the probability distribution, \(S[p] = I^{\mathrm{S}}[p]\), one similarly attributes the classical Fisher functional to the classical part of this gradient entropy:

$$\begin{aligned} \tilde{I}^{class.}[\varphi ]= \tilde{I}[p] = I^{\mathrm{F}}[p] = I[p] > 0. \end{aligned}$$
(23)

Moreover, since the presence of a finite current diminishes the state resultant uncertainty, we ascribe the negative nonclassical gradient term \(I^{nclass.}[\varphi ]\) to the nonclassical gradient entropy:

$$\begin{aligned} \tilde{I}^{nclass.}[\varphi ] = \tilde{I}[\phi ] = -I^{nclass.}[\varphi ] = - I[\phi ] \le 0. \end{aligned}$$
(24)

One also observes that the density-per-electron of this nonclassical gradient entropy is now related to its Shannon-type analog by the modified variant of Eq. (17):

$$\begin{aligned} \tilde{I}^{nclass.}({\varvec{r}}) \equiv \tilde{I}_\phi ({\varvec{r}}) = - [\nabla S_\phi ({\varvec{ r}})]^{2 }\equiv -[\nabla S^{nclass.}({\varvec{ r}})]^{2}. \end{aligned}$$
(25)

The nonpositive character of the nonclassical entropy \(S^{nclass.}[\varphi ] = S[\phi ]\) and a similar character of the associated gradient measure \({\tilde{I}}^{nclass.}[\varphi ]={\tilde{I}}[\phi ]\) manifest that a presence of a finite electronic current decreases the uncertainty (“disorder”) level in electronic state. This is also in accord with the nonnegative kinetic-energy type Fisher measure \(I[{\varvec{ j}}] = I[\phi ]\), which reflects a degree of the state nonclassical determinicity (“order”).

4 Molecular phase-equilibria

The maxima of generalized measures of quantum entropy content determine the associated molecular phase-equilibria [15–18, 25, 26]. Let us first summarize the vertical equilibrium principles, for the fixed probability distribution \(p=p_{0 }=R_{0}^{2}\) of the nondegenerate ground-state \(\varphi _{0}= R_{0}\), which determines the trial (variational) states \(\varphi ^{0}({\varvec{ r}}) = \varphi [p_{0}\), \(\phi ; {\varvec{ r}}] = R_{0}({\varvec{ r}})\) exp \([\hbox {i}\phi ({{\varvec{r}}})]\), where the real functions \(R_{0}({\varvec{ r}})\) and \(\phi ({\varvec{ r}})\) stand for the (fixed) state modulus and (variational) phase components, respectively. The optimum, vertical-equilibrium solutions are then derived from the extrema of the nonclassical entropy/information functionals \(S[\phi ]\) or \(I[\phi ]\) alone, for the fixed classical contributions \(S[p_{0}\)] and \(I[p_{0}]\), respectively. The optimum phase \(\phi =\phi ^{opt.}\) of such trial states in the vertical extremum is then determined by the Euler equations resulting from the nonclassical entropy/information principles,

$$\begin{aligned}&\hbox {max}_ \phi S[\phi ]\quad \hbox { or\quad max}_\phi \, {\tilde{I}}[\phi ],\quad \hbox { and\quad min }_{\phi } I[\phi ], \end{aligned}$$
(26a)
$$\begin{aligned}&\delta S^{nclass.}[\varphi ^{ 0}]/ \delta \varphi ^{0}({{\varvec{r}}})^{*}\left| {_{\phi =\phi ^{opt.}} } \right. = 0 \Rightarrow \quad \hat{\mathrm{S}}_{\phi ^{opt.}} ({\varvec{r}})\varphi _{0}({\varvec{ r}}) = 2 \phi ^{opt.} ({\varvec{ r}}) \varphi _{0}({\varvec{ r}}) = 0,\nonumber \\&\delta \tilde{I}^{nclass.}[\varphi ^{0}]/\delta \varphi ^{0}({{\varvec{r}}})^{*}\left| {_{\phi =\phi ^{opt.}} } \right. = 0 \nonumber \\&\quad \Rightarrow \quad -\hat{\mathrm{I}}_{\phi ^{opt.}} ({\varvec{r}})\varphi _{0}({\varvec{ r}}) = -4[\nabla \phi ^{opt.} ({\varvec{ r}})]^{2} \varphi _{0}({\varvec{ r}}) = 0,\nonumber \\&\delta I^{nclass.}[\varphi ^{ 0}]/\delta \varphi ^{0}({{\varvec{r}}})^{*}\left| {_{\phi =\phi ^{opt.}} } \right. = 0 \nonumber \\&\quad \Rightarrow \quad \hat{\mathrm{I}}_{\phi ^{opt.}} ({\varvec{r}})\varphi _{0}({\varvec{ r}}) = 4[\nabla \phi ^{opt.}({\varvec{ r}})]^{2} \varphi _{0}({\varvec{ r}}) = 0. \end{aligned}$$
(26b)

They consistently predict the strong-stationary ground-state solution \(\phi ^{opt.}({\varvec{ r}}) = \phi _{0}({\varvec{ r}}) = 0\) as the system vertical equilibrium \(({}^{eq.})\), for which the electronic current exactly vanishes:

$$\begin{aligned} \varphi ^{eq.}[p_{0}; {\varvec{ r}}] \equiv \, \varphi _{0} ({{\varvec{r}}}) = \varphi [p_{0}, \phi _{0}; {\varvec{ r}}] = R_{0}({{\varvec{r}}}). \end{aligned}$$
(27)

Thus, the nonclassical, (phase/current)-related information principles (26a) all identify the lowest eigenstate of the electronic Hamiltonian,

$$\begin{aligned} {\hat{\mathrm{H}}}({\varvec{r}})\varphi _{0}({\varvec{ r}}) = E_{0 }\varphi _{0}({\varvec{ r}}), \end{aligned}$$
(28)

as the vertical equilibrium state of this one-electron system. The ground-state probability distribution \(p_{0}\) then determines all physical properties of the system, functionals of the electron density alone, in accordance with the first Hohenberg-Kohn theorem of the modern density functional theory (DFT) [28, 29].

The vanishing spatial phase in the nondegenerate ground state thus signifies the complete absence of the current aspect in the molecular electronic structure. Any displacement from this extreme, strong-stationary situation is manifested by the presence of a finite nonclassical entropy/information contribution, reflecting the average magnitude of either the state spatial phase (in Shannon’s measure) or of its gradient (in Fisher’s descriptor). These nonclassical terms reflect the extra current “disorder” or “order” in the quantum state under consideration: increased presence of currents implies more overall “structure” (order) in the system and hence less overall electronic “uncertainty” (disorder). This expectation is reflected by the negative signs of the nonclassical complements \(S^{nclass.}[\varphi ^{0}]\) or \(\tilde{I}^{nclass.}[\phi ^{0}]\), of the classical Shannon or gradient entropy terms. Therefore, any finite displacement \(\Delta \phi ({\varvec{ r}}) = \phi ({\varvec{ r}}) \ne 0\) in the spatial phase from the \(\phi _{0}({\varvec{ r}}) = 0\) reference level generates the negative entropy displacements from the relevant classical entropy values, \(S[p_{0}]\) or \(\tilde{I}[p_0 ]=I[p_{0}]\) (see Fig. 1):

$$\begin{aligned} \Delta S[\Delta \phi ] = S^{nclass.}[\varphi ^{0}] < 0\quad \hbox { and }\quad \Delta {\tilde{I}}^{nclass.}[\Delta \phi ]={\tilde{I}}^{nclass.}[\varphi ^{0}] < 0. \end{aligned}$$
(29a)

The vertical equilibrium state for \({\varvec{ j}}_{0} = {\mathbf {0}}\) also marks the minimum value \(I[p_{0}]\) of the resultant gradient information \(I[\varphi ^{0}\)], and hence the vanishing nonclassical term \(I^{nclass.}[\varphi _{0}] = I[{\varvec{ j}}_{0}] = 0\). It implies the positive change in this information measure due to a displacement from the vertical equilibrium, reflected by a finite current in a trial state \(\varphi ^{0}\), \(\Delta {{\varvec{j}}} = {\varvec{ j}} \ne {\mathbf {0}}\),

$$\begin{aligned} \Delta I[\Delta {\varvec{ j}}] = I^{nclass.}[\varphi ^{0}] = I[{\varvec{ j}}] > 0. \end{aligned}$$
(29b)

Therefore, the nonpositive gradient entropy \({\tilde{I}}^{nclass.}[\varphi ^{0}]\) behaves very much like the nonclassical entropy \(S^{nclass.}[\varphi ^{0}]\), reaching the maximum (zero) value in the system lowest stationary state. Obviously, the same is true for the associated resultant measure

$$\begin{aligned} \tilde{I}[\varphi [p_0 ]] = I^{class.}[\varphi [p_{0}]] + {\tilde{I}}^{nclass.}[\varphi [p_0 ]]=I[p_{0}] + {\tilde{I}}^{nclass.}[\varphi ^{0}], \end{aligned}$$

which also reaches its phase-maximum value \(I[p_{0}]\) for the lowest equilibrium state \(\varphi _{0}\) (Fig. 1).

We now put these measures to a consistency test by exploring the horizontal phase-equilibria (\(_{eq.}\)), \(\phi _{eq.}[p; {\varvec{ r}}]\), which mark extrema of the resultant global and gradient entropies:

$$\begin{aligned} \hbox {max } S[p, \phi ]\quad \hbox { or\quad max } \tilde{I}[p,\phi ]. \end{aligned}$$

The associated Euler equations determine the optimum phase \(\phi _{eq.}\) of such equilibrium states,

$$\begin{aligned} \varphi _{eq.}[p,{\varvec{ r}}]\equiv \varphi _{eq.}[p, \phi _{eq.}[p];{\varvec{ r}}], \end{aligned}$$

in terms of the state probability distribution: \(\phi _{eq.}=\phi _{eq.}[p]\). One expects that predictions resulting from these complementary Shannon-type and gradient resultant entropy measures should have common solutions.

Let us first examine implications of the maximum principle of the resultant Shannon-type (global) entropy. The functional derivative, with respect to \(\varphi ^{*}({\varvec{ r}})\), of the resultant entropy functional \(S[\varphi ] = \langle \varphi {\vert }{\hat{\mathrm{S}}}{\vert }\varphi \rangle \), where the multiplicative operator \(\hat{\mathrm{S}}({\varvec{r}})=S({\varvec{r}})\), ultimately determines the horizontal-equilibrium state \(\varphi _{eq.}\) corresponding to “thermodynamic” phase \(\phi _{eq.}[p]\):

$$\begin{aligned} \varphi _{eq.}({\varvec{ r}}) = \varphi _{eq.}[p,\phi _{eq.}[p];{\varvec{ r}}] \equiv \varphi _{eq.}[p;{\varvec{ r}}]. \end{aligned}$$

The relevant Euler equations determining this equilibrium phase in terms of the probability density p, \(\phi _{eq.}=\phi _{eq.}[p]\), read:

$$\begin{aligned}&\delta S[\varphi ]/\delta \varphi ^{*}({\varvec{ r}})\left| {_{\varphi =\varphi _{eq.} } } \right. ={\hat{\mathrm{S}}}[p, \phi _{eq.} [p]; {\varvec{r}}]\varphi _{eq.}({\varvec{ r}}) = 0 \quad \hbox {or}\nonumber \\&\quad S({\varvec{ r}})\varphi _{eq.}({\varvec{ r}}) = \{- \hbox {log} p ({\varvec{ r}}) - 2\phi _{eq.}[p; {{\varvec{r}}}]\}\varphi _{eq.}({\varvec{ r}}) = 0. \end{aligned}$$
(30)

This entropic rule thus predicts the equilibrium thermodynamic phase related to electron probability distribution,

$$\begin{aligned} \phi _{eq.}({\varvec{ r}}) = -(1/2) \hbox {ln}p({\varvec{ r}}). \end{aligned}$$
(31)

For the ground-state probability distribution \(p=p_{0}\) this prediction is in spirit of the Hohenberg-Kohn theorem of modern DFT, that the ground-state density or the associated probability distribution uniquely identify the system electronic state.

The same prediction follows from the maximum of the resultant gradient entropy \(\tilde{I}[\varphi ]\),

$$\begin{aligned} \tilde{I}[\varphi ]= & {} \langle \varphi {\vert } {\hat{{\tilde{\mathrm{I}}}}}{\vert }\varphi \rangle =I^{class.}[\varphi ]+{\tilde{I}}^{nclass.}[\varphi ] \quad \equiv \int {p({\varvec{r}})} {\tilde{I}}({\varvec{r}})d{\varvec{r}}, \nonumber \\&\tilde{I}({\varvec{r}})=I_p ({\varvec{r}})-I_\phi ({\varvec{r}}). \end{aligned}$$
(32)

The optimum phase \(\phi _{eq.}=\phi _{eq.}[p]\) of the resulting Euler equation,

$$\begin{aligned} \delta {\tilde{I}}[\varphi ]/\delta \varphi ^{*}({\varvec{ r}})\left| {_{\varphi =\varphi _{eq.} } } \right.= & {} \tilde{I}({\varvec{r}})\varphi _{eq.}({\varvec{ r}}) = 0 \quad \hbox { or }\nonumber \\ \{\nabla \phi _{eq.}[p; {\varvec{ r}}]\}^{2}= & {} \{\nabla [(1/2) \hbox { ln}p({\varvec{ r}})]\}^{2}, \end{aligned}$$
(33)

indeed recovers the solution of Eq. (31).

Thus, the maximum entropy principles derived from the quantum-generalized global and gradient entropies predict the same horizontal equilibrium state corresponding to the spatial phase determined by the negative logarithm of the system electron probability density:

$$\begin{aligned} \varphi _{eq.}({\varvec{ r}}) = R({{\varvec{r}}})\hbox { exp }\{\hbox {i}[\phi ({\varvec{ r}}) + \phi _{eq.}({\varvec{ r}})]\} \equiv R({\varvec{ r}}) \hbox {exp}[\hbox {i}\Phi _{eq.}({\varvec{ r}})] \equiv \varphi _{eq.}[p; {\varvec{ r}}].\nonumber \\ \end{aligned}$$
(34)

It represents the result of the (unitary) phase-transformation of the original quantum state

$$\begin{aligned} \varphi ({\varvec{ r}}) = R({{\varvec{r}}}) \hbox { exp} [\hbox {i}\phi ({\varvec{ r}})], \end{aligned}$$
(35)

giving rise to the resultant phase component

$$\begin{aligned} \Phi _{eq.}({\varvec{ r}}) = \phi ({\varvec{ r}}) + \phi _{eq.}({\varvec{ r}}). \end{aligned}$$
(36)

5 Continuity equations in equilibrium states

We have shown above that the extremum of the resultant entropy content in a general quantum state at time t, \(\varphi ({{\varvec{r}}},t)=\langle {\varvec{ r}}{\vert }\varphi (t) \rangle \) [Eq. (35)], determines the equilibrium thermodynamic phase of Eq. (31), which specifies the equilibrium state \(\varphi _{eq.}({\varvec{ r}},t)=\langle {{\varvec{r}}}{\vert }\varphi _{eq.}(t)\rangle \) [Eq. (34)]. While preserving the state probability distribution,

$$\begin{aligned} p({\varvec{ r}}, t) = {\vert }\varphi _{eq.}({\varvec{ r}}, t){\vert }^{2} = {\vert } \varphi ({\varvec{ r}}, t){\vert }^{2}=R ({\varvec{ r}}, t) ^{2}, \end{aligned}$$
(37)

this unitary transformation of the system wavefunction \(\varphi ({\varvec{ r}}, t)\) modifies the initial probability current in \(\varphi \),

$$\begin{aligned} {\varvec{ j}}_\varphi ({\varvec{ r}}, t)=\langle \varphi {\vert }{\hat{{\mathbf{j}}}}({\varvec{r}}){\vert }\varphi \rangle = ({\hbar }/m) p({\varvec{ r}}, t) \nabla \phi ({\varvec{ r}}, t), \end{aligned}$$
(38)

into the equilibrium current:

$$\begin{aligned} {\varvec{ j}}_{eq.}({{\varvec{r}}}, t)= & {} \langle \varphi _{eq.}(t){\vert }{\hat{{\mathbf{j}}}}({\varvec{r}}){\vert }\varphi _{eq.}(t) \rangle =\frac{\eta p({\varvec{r}},t)}{m}\nabla \Phi _{eq.} ({\varvec{r}},t)\nonumber \\= & {} \frac{\eta p({\varvec{r}},t)}{m}\{\nabla \phi ({\varvec{r}},t)+\nabla \phi _{eq.} ({\varvec{r}},t)\}\nonumber \\= & {} {\varvec{j}}_\varphi ({\varvec{r}},t)-\frac{\eta }{2m}\nabla p({\varvec{r}},t)= {\varvec{j}}_\varphi ({\varvec{r}},t)-\frac{\eta }{m}R({\varvec{r}},t)\nabla R({\varvec{r}},t). \end{aligned}$$
(39)

Let us now examine how this unitary equilibrium transformation of the initial wavefunction influences the continuity equations of the probability and phase distributions. Multiplying both sides of SE (4) from the left by exp[i\(\phi _{eq.}({\varvec{ r}})\)] and inserting the trivial factor

$$\begin{aligned} \hbox {exp}[-\hbox {i}\phi _{eq.}({\varvec{ r}}, t)] \hbox {exp}[\hbox {i}\phi _{eq.}({\varvec{ r}}, t)] = \hbox {exp}(0) = 1 \end{aligned}$$
(40)

between the Hamiltonian and the wavefunction express this equation in terms of the equilibrium state and the phase-transformed (equilibrium) Hamiltonian \({\hat{\mathrm{H}}}^{eq.}({\varvec{r}},t)\)

$$\begin{aligned}&\{\hbox {exp}[\hbox {i}\phi _{eq.}({\varvec{ r}}, t)]{\hat{\mathrm{H}}}({\varvec{r}}) \hbox {exp}[-\hbox {i}\phi _{eq.}({\varvec{ r}}, t)]\}\{\hbox {exp}[\hbox {i}\phi _{eq.}({\varvec{ r}}, t)]\varphi ({\varvec{ r}}, t)\}\nonumber \\&\quad \equiv {\hat{\mathrm{H}}}^{eq.}({\varvec{r}},t)\varphi _{eq.}({\varvec{ r}},t)\nonumber \\&\quad = \hbox {i}{\hbar } \hbox { exp}[\hbox {i}\phi _{eq.}({{\varvec{r}}}, t)]{\partial }\varphi ({\varvec{ r}}, t)/\partial t. \end{aligned}$$
(41)

One further observes that

$$\begin{aligned} {\partial }\varphi _{eq.}/\partial t =\hbox { exp}(\hbox {i}\phi _{eq.}) {\partial }\varphi /\partial t + \hbox {i } \varphi _{eq. }({\partial }\phi _{eq.}/\partial t), \end{aligned}$$
(42)

where using the probability continuity relation \({\partial p}/ \partial t = -\nabla \cdot {\varvec{ j}}\) gives

$$\begin{aligned} {\partial }\phi _{eq.}/\partial t = [{\partial }\phi _{eq.}/\partial p] [{\partial p}/\partial t] = (2p)^{-1 }\nabla \cdot {\varvec{ j}}. \end{aligned}$$
(43)

Therefore, the transformed SE finally reads:

$$\begin{aligned} {\hat{\mathrm{H}}}^{eq.}\varphi _{eq.} = \hbox {i}{\hbar }[{\partial }\varphi _{eq.}/\partial t - \hbox {i}\varphi _{eq.} {\partial }\phi _{eq.}/\partial t] = \hbox {i}{\hbar }({\partial }\varphi _{eq.}/\partial t) + {\hbar }\varphi _{eq.}({\partial }\phi _{eq.}/\partial t).\quad \quad \end{aligned}$$
(44)

In particular, for an eigenstate of the Hamiltonian,

$$\begin{aligned} \varphi _{s}({\varvec{ r}}, t)=R_{s}({{\varvec{r}}})\hbox {exp}(-\hbox {i}\omega _{s }t),\quad \omega _{s}=E_{s}/{\hbar }, \end{aligned}$$
(45)

when \(p_{s}({\varvec{ r}},t)=p_{s}({\varvec{ r}}) = R_{s}({{\varvec{r}}})^{2}\), \({\partial p}_{s}/\partial t = 0, \phi _{eq.}({{\varvec{r}}}, t)=\phi _{s}({\varvec{ r}})\) and \({\partial }\phi _{eq.}/\partial t = 0\), Eq. (44) reads:

$$\begin{aligned} {\hat{\mathrm{H}}}^{eq.}({\varvec{r}})\varphi _{s,eq.}({\varvec{ r}},t) = \hbox {i}{\hbar }{\partial }\varphi _{s,eq.}({\varvec{ r}}, t)/\partial t. \end{aligned}$$
(46)

We recall, that the stationary-probability condition \(p_{s}({\varvec{ r}},t)=p({{\varvec{r}}})\) covers both the plane-wave, weak-stationary \({\varvec{ j}} = {const.}\), and the strong-stationary \({\varvec{ j}} = {{\mathbf { 0}}}\) states.

It can be now explicitly demonstrated that the phase transformation of the wavefunction, which generates the horizontal equilibrium state, does not affect the local time derivative in the continuity equation for the particle probability distribution. It indeed follows from Eq. (44) and its Hermitian conjugate that their weighted difference gives:

$$\begin{aligned}&(\hbox {i}{\hbar })^{-1}[\varphi _{eq.}{}^{*}{\hat{\mathrm{H}}}^{eq.}\varphi _{eq.}-\varphi _{eq. }{\hat{\mathrm{H}}}^{eq.}\varphi _{eq.}{}^{*}]\nonumber \\&= -{\hbar }/(2m\hbox {i})[\varphi _{ eq.}^{*}\Delta \varphi _{eq.}-\varphi _{eq.}\Delta \varphi _{eq.}{}^{*}] = -\nabla \cdot {\varvec{ j}}_{eq.}+\sigma _{p,eq.}\nonumber \\&= (\hbox {i}{\hbar })^{-1}[\varphi ^{*}{\hat{\mathrm{H}}}\varphi -\varphi {\hat{\mathrm{H}}}\varphi ^{*}] = -{\hbar }/(2m\hbox {i})[\varphi ^{*}\Delta \varphi -\varphi \Delta \varphi ^{*}] = -\nabla \cdot {\varvec{ j}}\nonumber \\&= \varphi _{eq.}^{*}({\partial }\varphi _{ eq.}/\partial t)+\varphi _{eq.}({\partial }\varphi _{eq.}^{*}/\partial t) = ({\partial p}_{eq.}/\partial t)\nonumber \\&= \varphi ^{*}({\partial }\varphi /\partial t)+\varphi ({\partial }\varphi ^{*}/\partial t) = ({\partial p}/\partial t). \end{aligned}$$
(47)

Therefore, the probability source \(\sigma _{p,eq. }\) in the horizontal equilibrium state \(\varphi _{eq.}\) is modified relative to \(\sigma _{p} = 0\) [Eq. (5)] in the initial state \(\varphi \):

$$\begin{aligned} \sigma _{p,eq.}= & {} ({\partial p}_{eq.}/\partial t)+\nabla \cdot {\varvec{ j}}_{eq.} = [({\partial p}/\partial t)+\nabla \cdot {\varvec{ j}}] - [{\hbar }/(2m)]\Delta p\nonumber \\= & {} \sigma _{p} - [{\hbar }/(2m)]\Delta p = - [{\hbar }/(2m)]\Delta p. \end{aligned}$$
(48)

It should be observed, however, that—by the Gauss theorem—this equilibrium local source of the probability density does not affect its overall normalization, since the particles are neither produced nor destroyed:

$$\begin{aligned} \smallint \sigma _{p,eq.}({\varvec{ r}})d{{\varvec{r}}}= & {} - [{\hbar }/(2m)] \smallint \nabla \cdot \nabla p({\varvec{ r}})d{{\varvec{r}}}\nonumber \\= & {} - [{\hbar }/(2m)] {\mathop {\smallint \smallint }\nolimits _{{S}\rightarrow {\infty }}}[\nabla p({\varvec{ r}})]_{n }{} { dS} = 0. \end{aligned}$$
(49)

One similarly recovers in the equilibrium state the phase-derivative equations (6) and (7). From the weighted sum of Eq. (44) and its Hermitian conjugate one again finds:

$$\begin{aligned}&[\varphi _{eq.}^{*}{\hat{\mathrm{H}}}^{eq.}\varphi _{eq.}+\varphi _{eq.}{\hat{\mathrm{H}}}^{eq.}\varphi _{eq.}^{*}]\nonumber \\&\quad =(\varphi ^{*}{\hat{\mathrm{T}}}\varphi +\varphi {\hat{\mathrm{T}}}\varphi ^{*} + 2{ p}v) = -[{\hbar }^{2}/(2m)][\varphi ^{*}\Delta \varphi +\varphi \Delta \varphi ^{*}] + 2{ p}v\nonumber \\&\quad = -({\hbar }^{2}/m) \hbox {Re}(\varphi \Delta \varphi ) + 2{ p}v = -({\hbar }^{2}/m)[R\Delta R-p(\nabla \phi )^{2}] + 2{ p}v\nonumber \\&\quad = (\hbox {i}{\hbar })[\varphi _{eq.}^{*}({\partial }\varphi _{eq.}/\partial t)-\varphi _{eq.}({\partial }\varphi _{eq.}^{*}/\partial t) + 2{\hbar p}(\partial \phi _{eq.}/\partial t)\nonumber \\&\quad = -2{\hbar p} [\partial (\Phi _{eq.}-\phi _{eq.})/\partial t] =-2{\hbar p}(\partial \phi /\partial t)]\quad \hbox { or } \nonumber \\ {\partial }\phi /\partial t= & {} [{\hbar }/(2m)][R^{-1}\Delta R - (\nabla \phi )^{2}] - v/{\hbar }. \end{aligned}$$
(50)

Thus, at the specified particle location the partial time-derivative of the original phase distribution \(f=\phi ^{2}\) also remains unaffected by the equilibrium phase transformation. However, in this equilibrium state the time derivative of the resultant phase

$$\begin{aligned} \Phi _{eq.}=\phi +\phi _{eq.},\quad \phi _{eq.} = -(1/2)\hbox {ln}p, \end{aligned}$$
(51)

reads:

$$\begin{aligned} {\partial }\Phi _{eq.}/\partial t= & {} {\partial }\phi /\partial t + {\partial }\phi _{eq.}/\partial t = {\partial }\phi /\partial t - [1/(2p)] ({\partial p}/\partial t)\nonumber \\= & {} {\partial }\phi /\partial t + [1/(2p)] \nabla \cdot {\varvec{ j}}_{p}, \end{aligned}$$
(52)

where we have used the probability continuity equation. In the absolute source scale of Eq. (9) the equilibrium phase-source is determined by the partial time derivative of the equilibrium phase density \(f_{eq.}=\Phi _{eq.}^{2}\):

$$\begin{aligned} {\partial f}_{eq.}/\partial t= & {} 2\Phi _{eq. }({\partial }\Phi _{eq.}/\partial t) = {\varSigma }_{f}^{abs.} - (\hbox {ln}p)({\partial }\phi /\partial t)\nonumber \\&+ (2p)^{-1}(2\phi - \hbox {ln}p) \nabla \cdot {\varvec{ j}}_{p} \quad \equiv {\varSigma }_{f.eq.}^{abs.}. \end{aligned}$$
(53)

This equation also identifies the displacement of \({\varSigma }_{f.eq.}^{abs.}\) relative to the original phase-source of Eq. (9), \({\varSigma }_{f}^{abs.}= {\partial f}/ \partial t\). We thus conclude that the equilibrium phase transformation of electronic states while preserving the molecular probability distribution introduces finite displacements in sources of both the probability and phase distributions

6 Harriman representation

This single-electron development can be readily extended into general N-electron systems by using the Harriman-Zumbach-Maschke (HZM) [30, 31] construction of the antisymmetric wave functions of N fermions yielding the specified particle distribution. In this section we briefly summarize the equilibrium one-determinantal states of molecular systems, e.g., in the familiar Kohn-Sham (KS) or Hartree-Fock (HF) self-consistent field (SCF) theories, which result from extrema of the resultant entropy/information functionals including the nonclassical contributions due to the current/phase components of molecular orbitals (MO) defining the electron configuration in question.

The density-conserving Slater determinants generated in the HZM construction provide natural variational functions for the vertical thermodynamic searches in the IT principles of electronic structure theory. These trial N-electron functions are constructed using the complex, plane-wave type equidensity MO \(\{\varphi _{{\varvec{k}}}({\varvec{ r}})=R({{\varvec{r}}})\hbox { exp}[\hbox {i}\varPhi _{{\varvec{k}}}({\varvec{ r}})]\}\). They offer a convenient framework for an extension of the present analysis into the general N-electron case. In constructing the mutually orthogonal Slater determinants generating the specified electron density \(\rho ({\varvec{ r}}) = N p({{\varvec{r}}})\) these MO adopt the equal, density-dependent modulus \(R({\varvec{ r}}) = [\rho ({\varvec{ r}})/N]^{1/2 }=p({\varvec{ r}})^{1/2}\) and the resultant spatial phase,

$$\begin{aligned} \varPhi _{{\varvec{k}}}({\varvec{ r}}) = {{\varvec{k}}}\cdot {{\varvec{f}}}({\varvec{ r}}) + \phi ({\varvec{ r}}) \equiv F_{{\varvec{k}}}({\varvec{ r}}) + \phi ({\varvec{ r}}), \end{aligned}$$
(54)

defined by the orbital reduced momentum \({\varvec{ k}}\), the density-dependent vector function \({\varvec{ f}}({{\varvec{r}}}) = {\varvec{ f}}[\rho ; {{\varvec{r}}}]\), common to all orbitals and linked to the Jacobian of the \({\varvec{ r}}\rightarrow {{\varvec{f}}}({\varvec{ r}})\) transformation, and the system “thermodynamic” phase \(\phi ({\varvec{ r}})\), identicall in all occupied orbitals. The “orthogonality” phases \(\{F_{{\varvec{k}}}({\varvec{ r}})\}\) assure the independence of these single-particle states.

The optimum wave-number vectors \(\mathbf{k}_{0 }=\{{{\varvec{k}}}_{l}^{0}\}\) and the associated density \(\rho _{0}({\varvec{ r}})\) are determined at the SCF MO stage, i.e., from the energy-minimization principle using the HZM determinant as variational wavefunction. The thermodynamic phase \(\phi _{0}({\varvec{ r}})\) is subsequently determined from the resultant entropic rule. The equilibrium HZM determinant is thus defined by N-lowest equidensity MO for the prescribed ground-state probability distribution \(p_{0}({\varvec{ r}}) = [R_{0}({{\varvec{r}}})]^{2}=\rho _{0}({\varvec{ r}})/N\), for which \({{\varvec{f}}}[p_{0}; {\varvec{ r}}] \equiv {\varvec{ f}}_{0}({{\varvec{r}}})\) and

$$\begin{aligned} \varphi _{{\varvec{k}}}({\varvec{ r}})= & {} [p_{0}({\varvec{ r}})]^{1/2 }\hbox {exp}\{\hbox {i}[{\varvec{ k}}_{0}\cdot {{\varvec{f}}}_{0}({\varvec{ r}}) + \phi ({\varvec{ r}})]\}\nonumber \\\equiv & {} R_{0}({\varvec{ r}}) \hbox {exp}(\hbox {i}\varPhi _{{\varvec{k}}}[p_{0}; {\varvec{ r}}]) \equiv \varphi _{{\varvec{k}}}[p_{0}; {\varvec{ r}}]. \end{aligned}$$
(55)

The overall phase \(\varPhi _{{\varvec{k}}}[p_{0}; {\varvec{ r}}]\) of the (ground-state occupied) equidensity orbital determines its electronic current,

$$\begin{aligned} {\varvec{ j}}_{{\varvec{k}}}({\varvec{ r}}) = \langle \varphi _{{\varvec{k}}}{\vert }{\hat{{\mathbf{j}}}}({\varvec{r}}){\vert }\varphi _{{\varvec{k}}}\rangle =\frac{\hbar p_0 ({\varvec{r}})}{m} \{\nabla [{\varvec{k}}_0 \cdot \mathbf {{\mathbf {f}}}_0 ({\varvec{r}})]+\nabla \phi ({\varvec{r}})\}. \end{aligned}$$
(56)

The configuration overall flow measure of all N electrons, \({\varvec{ j}}({{\varvec{r}}}; N) \quad \equiv {\varvec{ j}}({{\varvec{r}}})\), is now determined by the expectation value of the N-electron current operator,

$$\begin{aligned} {\hat{{\mathbf{j}}}}({\varvec{r}};N)=\sum _{l=1}^N {{\hat{{\mathbf{j}}}}_l ({\varvec{r}})} , \end{aligned}$$
(57)

in the ground-state HZM determinant,

$$\begin{aligned} \Psi _{\mathbf{k}_0 } (N)\equiv & {} \Psi _{{\varvec{k}}_1 ,{\varvec{k}}_1 ,\ldots ,{\varvec{k}}_N } (N)=(1/\sqrt{N!}) \det (\varphi _{{\varvec{k}}_1 } ,\varphi _{{\varvec{k}}_2 } , \ldots , \varphi _{{\varvec{k}}_{N}} ) \nonumber \\\equiv & {} {\vert }\varphi _{{\varvec{k}}_1 } ,\varphi _{{\varvec{k}}_2 } , \ldots , \varphi _{{\varvec{k}}_N } {\vert } \equiv {\vert }\{\varphi _{{\varvec{k}}_l }\}{\vert },\end{aligned}$$
(58)
$$\begin{aligned} {\varvec{ j}}({{\varvec{r}}}; N)= & {} \langle \Psi _{\mathbf{k}_0 } (N){\vert }{\hat{{\mathbf{j}}}}({\varvec{r}};N){\vert }\Psi _{\mathbf{k}_0} (N)\rangle \nonumber \\= & {} \sum _{l=1}^N {{\varvec{j}}_{{\varvec{k}}_l } ({\varvec{r}})} \equiv \frac{\hbar }{m}\{\rho ({\varvec{r}})\nabla [{\varvec{K}}(\mathbf{k}_0 )\cdot {\varvec{f}}_0 ({\varvec{r}})+\phi ({\varvec{r}})]\}. \end{aligned}$$
(59)

It is determined by the average “wave-number” vector in \(\Psi _{\mathbf{k}_0 } (N)\), \(\mathbf{k}_{0} = ({{\varvec{k}}}_{1}^{0}, {\varvec{ k}}_{2}^{0}, {\ldots }, {{\varvec{k}}}_{N}^{0})\),

$$\begin{aligned} {\varvec{ K}}(\mathbf{k}_{0})=\frac{1}{N}\sum _{l=1}^N {{\varvec{k}}_l^0 } \equiv {\varvec{ K}}_{0}. \end{aligned}$$
(60)

For the fixed electron distribution in the vertical entropy principle only the nonclassical components depend upon the MO “wave-number” vectors \(\mathbf{k}_{0}\) and their thermodynamic phase \(\phi ({\varvec{ r}})\), which together determine the resultant phase in Harriman’s construction. In the vertical search only \(\phi ({\varvec{ r}})\) is varied for the fixed \(\mathbf{k}_{0}\). The maximum principle of the average nonclassical entropies \(S^{nclass.}[\Psi _{\mathbf{k}_0 } [p_0 ]]\) or \({\tilde{I}}^{nclass.}[\Psi _{\mathbf{k}_0 } [p_0 ]]\) determines the optimum thermodynamic phase of the vertical-equilibrium, labeled by the upper index “\(^{eq.}\)”,

$$\begin{aligned} \phi ^{eq.}[p_{0}; {\varvec{ r}}] = -{\varvec{K}}_0 \cdot {\varvec{f}}_0 ({\varvec{r}}), \end{aligned}$$
(61)

that also minimizes \(I[(p_{0},\mathbf{k}_{0}), \phi ]\). The associated equidensity orbitals are shaped by the displacements \(\{\delta {\varvec{ k}}_{l} = {{\varvec{k}}}_{l} -{{\varvec{K}}}_{0}\}\) of the orbital wave-number vector from the average value \({\varvec{ K}}_{0}\),

(62)
$$\begin{aligned} \varphi _{{\varvec{k}}_l }^{eq.} [p_0 ;{\varvec{r}}]= & {} [p_{0}({{\varvec{r}}})]^{1/2}\hbox {exp}\{\hbox {i}\delta {\varvec{ k}}_{l }\cdot {\varvec{ f}}[p_{0}; {{\varvec{r}}}]\},\quad l = 1, 2, {\ldots }, N. \end{aligned}$$
(63)

Therefore, in this equilibrium state the overall current [Eq. (59)] exactly vanishes:

(64)

Let us now examine the horizontal-equilibrium phases of the occupied equidensity orbitals. In a general HZM determinant \(\Psi (N) = (N!)^{-1/2 } \hbox {det}(\{\varphi _{l}\})\) constructed from equidensity orbitals \(\{\varphi _{l}({\varvec{ r}}) = [p({{\varvec{r}}})]^{1/2} \hbox {exp}[\hbox {i}\varPhi _{l}({\varvec{ r}})]\}\), the resultant entropy or the overall gradient measure of the information content are both given by the sums of the corresponding orbital contributions,

$$\begin{aligned} S[\Psi ] = \Sigma _{l }\langle \varphi _{l}{\vert }{\hat{\mathrm{S}}}_l ({\varvec{r}}){\vert }\varphi _{l}\rangle =\Sigma _{l} S[\varphi _{l}],\quad {\hat{\mathrm{S}}}_l ({\varvec{r}})=S_{l}({\varvec{ r}}) = -\hbox {log}p({\varvec{ r}}) -2\varPhi _{l}({\varvec{ r}}). \end{aligned}$$
(65)

The vertical energy principle fixes the MO orthogonality phases in the resultant phases \(\{\varPhi _{l}({\varvec{ r}}) =\delta {{\varvec{k}}}_{l}\cdot {\varvec{f}}_0 ({\varvec{r}})+\phi ({\varvec{r}})\}\), which remain conserved at the final, “thermodynamic” optimization stage determining their missing thermodynamic contribution \(\phi ({\varvec{ r}})\), equal in all occupied MO of \(\Psi (N)\). This assures the orthonormality of the equilibrium orbitals and the normalization of \(\Psi (N)\): \(\langle \Psi (N){\vert }\Psi (N)\rangle =\prod _{l}\langle \varphi _{l}{\vert }\varphi _{l}\rangle = 1\).

For the prescribed ground-state probability distribution \(p_{0}\), determined at an earlier SCF energy minimization stage, in the associated horizontal principle for the resultant-entropy one thus manipulates only the thermodynamic phase component \(\phi ({{\varvec{r}}})\) of all MO phases \(\{\varPhi _{l}({\varvec{ r}})\}\). The relevant variation of \(\varphi _{l}^{*}\) in this variational search reads:

$$\begin{aligned} \delta \varphi _{l}^{*}[\delta \phi ; {\varvec{ r}}]= & {} [p_{0}({\varvec{ r}})]^{1/2 }\hbox {exp}\{\hbox {i}[{{\varvec{k}}}_{l}^{0}\cdot {\varvec{ f}}[p_{0}; {{\varvec{r}}}] +\delta \phi ({\varvec{ r}})]\}\nonumber \\\equiv & {} [p_{0}({\varvec{ r}})]^{1/2 }\hbox {exp}\{\hbox {i}[F_{l}^{0}({\varvec{ r}}) +\delta \phi ({\varvec{ r}})]\} \equiv R_{0}({\varvec{ r}}) \hbox {exp}(-\hbox {i}\varPhi _{l}[\delta \phi ; {\varvec{ r}}]).\nonumber \\ \end{aligned}$$
(66)

The horizontal phase-equilibrium extremizes the functional of the resultant entropy or information:

$$\begin{aligned} \delta S[\Psi _\mathbf{k}(N)] = 0 \quad \hbox { or }\quad \delta {\tilde{I}}[\Psi _\mathbf {k} (N)] = 0,\quad \hbox { and }\quad \delta I[\Psi _\mathbf{k}(N)] = 0. \end{aligned}$$
(67)

Performing variations (66) of the complex-conjugate orbitals gives the associated Euler equation for determining the optimum equilibrium phase \(\phi _{eq.}({\varvec{ r}})\) of “thermodynamic” orbitals in a general N-electron case,

$$\begin{aligned}&\Sigma _{l}[-\hbox {ln}p_{0}({\varvec{ r}}) - 2\varPhi _{l}({{\varvec{r}}})_{eq.}]\nonumber \\&\quad = -N\hbox {ln}p_{0}({\varvec{ r}}) - 2\Sigma _{l} F_{l}^{0}({\varvec{ r}}) - 2N\phi _{eq.}({\varvec{ r}})]\nonumber \\&\quad = -N\hbox {ln}p_{0}({{\varvec{r}}}) - 2N\phi _{eq.}({\varvec{ r}}) = 0, \end{aligned}$$
(68)

which finally gives

$$\begin{aligned} \phi _{eq.}({\varvec{ r}}) = - (1/2)\hbox {ln}p_{0}({\varvec{ r}}) = \phi _{eq.}[p_{0}; {\varvec{ r}}]. \end{aligned}$$
(69)

Therefore, the horizontal equilibrium state marks the resultant orbital phases determined by the electron probability distribution alone. For \(p=p_{0}\) this is again a manifestation of the Hohenberg-Kohn theorem of DFT [28], that the ground-state electron density uniquely determines the equilibrium equidensity orbitals in HZM construction:

$$\begin{aligned} \mathbf{k}_{eq.} = \mathbf{k}[p_{0}] = \mathbf{k}_{0 }= \{{{\varvec{k}}}_{l}^{0}\},\,\,\, {\varvec{ f}}_{eq.} = {\varvec{ f}}[p_{0}] = {\varvec{ f}}_{0},\,\,\, \phi _{eq. }=\phi _{eq.}[p_{0}]. \end{aligned}$$
(70)

The associated equilibrium orbital,

$$\begin{aligned} \varphi _{l,eq.}({\varvec{ r}})= & {} [p_{0}({\varvec{ r}})]^{1/2 }\hbox {exp}\{\hbox {i}[({\varvec{ k}}_{l}^{ }- {\varvec{ K}}_{0}) \cdot {\varvec{ f}}_{0}({{\varvec{r}}}) - (1/2)\hbox {ln}p_{0}({\varvec{ r}})]\}\nonumber \\\equiv & {} [p_{0}({\varvec{ r}})]^{1/2 }\hbox {exp}\{\hbox {i}[\delta {\varvec{ k}}_{l }\cdot {{\varvec{f}}}_{0}({\varvec{ r}}) - (1/2)\hbox {ln}p_{0}({\varvec{ r}})]\}, \end{aligned}$$
(71)

now generates the following MO current contribution,

$$\begin{aligned} {\varvec{ j}}_{l}({{\varvec{r}}})_{eq}=\frac{\hbar }{m}p_0 ({\varvec{r}})\left[ {\delta {\varvec{k}}_l^0 \nabla \cdot {\varvec{f}}_0 ({\varvec{r}})-\frac{\nabla p_0 ({\varvec{r}})}{2p_0 ({\varvec{r}})}} \right] , \end{aligned}$$
(72)

and hence the resultant equilibrium current of N electrons:

$$\begin{aligned} {\varvec{ j}}_{eq.}({{\varvec{r}}}) = \Sigma _{l}{{\varvec{j}}}_{l}({\varvec{ r}})_{eq.}=-\frac{\hbar }{2m}\nabla \rho _0 ({\varvec{r}}), \end{aligned}$$
(73)

where we have again observed that \(\Sigma _{l}\delta {{\varvec{k}}}_{l}=N\delta {\varvec{ K}}_{0} = {{\varvec{0}}}\). In the horizontal ground phase-equilibrium the overall current of N electrons is thus also determined by the gradient of the molecular electron density \(\rho _{0} = {Np}_{0}\).

It can be also directly verified that the same equilibrium thermodynamic phase of Eq. (69) results from the extremum of the gradient entropy:

$$\begin{aligned} \tilde{I}[\Psi (N)]= & {} \Sigma _{l }\langle \varphi _{l}{\vert }{\hat{{\tilde{\mathrm{I}}}}}_l ({\varvec{r}}){\vert }\varphi _{l}\rangle =\Sigma _{l}\tilde{I}[\phi _l ],\nonumber \\ {\hat{{\tilde{\mathrm{I}}}}}_l ({\varvec{r}})= & {} \tilde{I}_l ({\varvec{r}}) = [\nabla p_{0}({\varvec{ r}})/p_{0}({{\varvec{r}}})]^{2} - 4\{\nabla \varPhi _{l}[p_{0}; {\varvec{ r}}]\}^{2}. \end{aligned}$$
(74)

From the associated Euler equation,

$$\begin{aligned}&\Sigma _{l} \{[\nabla \hbox {ln} p_{0}({\varvec{ r}})]^{2} - (2\nabla \varPhi _{l}[p_{0}; {\varvec{ r}}])^{2}\}\\&\quad = \Sigma _{l }\nabla \{\hbox {ln}p_{0}({\varvec{ r}}) - 2\varPhi _{l}[p_{0}; {\varvec{ r}}]\}\cdot \nabla \{\hbox {ln}p_{0}({\varvec{ r}}) + 2\varPhi _{l}[p_{0}; {{\varvec{r}}}]\} = 0, \end{aligned}$$

one obtains:

$$\begin{aligned} \nabla \hbox {ln}p_{0}({\varvec{ r}}) = \pm 2\nabla \varPhi _{l}[p_{0}; {\varvec{ r}}] = \pm 2\{[\delta {\varvec{ k}}_{l}^{0 }\nabla \cdot {\varvec{ f}}_{0}({{\varvec{r}}}) + \nabla \phi _{eq.}({{\varvec{r}}})]\}, l = 1, 2, {\ldots }, N.\quad \quad \end{aligned}$$
(75)

Therefore, for the positive phase convention the summation of these equations gives

$$\begin{aligned} N\nabla \hbox {ln}p_{0}({\varvec{ r}}) = \pm 2\{[\Sigma _{l}\delta {\varvec{ k}}_{l}]\nabla \cdot {\varvec{ f}}_{0}({{\varvec{r}}}) + N\nabla \phi _{eq.}({\varvec{ r}})]\} = - 2N\nabla \phi _{eq.}({\varvec{ r}}), \end{aligned}$$
(76)

which again identifies the equilibrium resultant phase of Eq. (69) as the optimum solution.

7 Elements of nonequilibrium thermodynamic description

Consider again the simplest one-electron case. The resultant entropy \(S[\varphi \)] combines the (positive) classical contribution of the Shannon entropy \(S^{class.}[\varphi ] = S[p]\), reflecting the “wideness” (uncertainty) in p, and the (negative) nonclassical supplement \(S^{nclass.}[\varphi ] = S[p, \phi ] \equiv \quad S[f]\), measuring the average magnitude of the phase-distribution \(f=\phi ^{2}\),

$$\begin{aligned} S[\varphi ]= & {} S^{class.}[\varphi ] + S^{nclass.}[\varphi ]\nonumber \\= & {} -\smallint p({\varvec{ r}}, t) \hbox {ln}p({\varvec{ r}}, t)d{{\varvec{r}}}{} \mathbf{- }2\smallint p({\varvec{ r}}, t)f({{\varvec{r}}}, t)^{1/2}d{\varvec{ r}} \equiv \smallint h({\varvec{ r}}, t)d{{\varvec{r}}}. \end{aligned}$$
(77)

As in the ordinary thermodynamics [23], we now identify the entropy (“intensive”) conjugates of the two independent density variables \(p = {\vert }\varphi {\vert }^{2}=R^{2}\) and \(f=\phi ^{2}\):

$$\begin{aligned}&\theta _{p}({\varvec{ r}}, t)=\delta S[\varphi ]/\delta p({{\varvec{r}}}, t)=\frac{\partial h(r\hbox {, }t)}{\partial p({\varvec{r}},t)}\quad \hbox { and }\nonumber \\&\theta _{f }({\varvec{ r}}, t)=\delta S[\varphi ]/\delta f({{\varvec{r}}}, t)=\frac{\partial h({\varvec{r}},t)}{\partial f({\varvec{r}},t)}. \end{aligned}$$
(78)

For the adopted convention \(\phi \ge ~ 0\), when \(f^{1/2}={\vert }\phi {\vert } = \phi \), one finds:

$$\begin{aligned} \theta _{p}({\varvec{ r}}, t)= & {} [-\hbox {ln}p({\varvec{ r}}, t)- 1] - 2\phi ({\varvec{ r}}, t) \equiv \theta _{p}^{class.}({\varvec{ r}}, t) + \theta _{p}^{nclass.}({\varvec{ r}}, t)\quad \hbox { and }\nonumber \\ \theta _{f }({\varvec{ r}}, t)= & {} - p({\varvec{ r}}, t)/f({{\varvec{r}}}, t)^{1/2} = - p({\varvec{ r}}, t)/\phi ({\varvec{ r}}, t) \equiv \theta _{f}^{nclass.}({\varvec{ r}}, t). \end{aligned}$$
(79)

These conjugates determine the associated affinities, the QIT “thermodynamic” forces defined by gradients of these intensities,

$$\begin{aligned} {\varvec{ G}}_{p }= & {} \nabla \theta _{p} = -[p^{-1}\nabla p+f^{-1/2 }\nabla f] = -2[R^{-1}\nabla R+\nabla \phi ]\nonumber \\&\quad \equiv {\varvec{ G}}_{p}^{class.}({\varvec{ r}}) + {{\varvec{G}}}_{p}^{nclass.}({\varvec{ r}})\quad \hbox { and }\nonumber \\ {\varvec{ G}}_{f}= & {} \nabla \theta _{f}=f^{-1/2}\{[p/(2f)]\nabla f-\nabla p\} = (R/\phi ) [(R/\phi )\nabla \phi - 2\nabla R]\nonumber \\&\quad \equiv {\varvec{ G}}_{f}^{nclass.}({\varvec{ r}}). \end{aligned}$$
(80)

Next, one introduces the current of the resultant entropy density for the adopted choice of the phase-flux \({\varvec{ J}}_{f }({{\varvec{r}}}, t)\):

$$\begin{aligned} {\varvec{ J}}_{h}({{\varvec{r}}}, t) = \theta _{p}({\varvec{ r}}, t){{\varvec{j}}}_{p}({\varvec{ r}}, t)+ \theta _{f}({\varvec{ r}}, t){{\varvec{J}}}_{f }({\varvec{ r}}, t). \end{aligned}$$
(81)

Its divergence \(\nabla \cdot {\varvec{ J}}_{h}({{\varvec{r}}}, t)\) in an associated expression for the entropy-source,

$$\begin{aligned} { dh}({\varvec{ r}}, t)/{ dt} \equiv \sigma _{h}({\varvec{ r}}, t)=\partial h({\varvec{ r}}, t)/\partial t+\nabla \cdot {\varvec{ J}}_{h}({{\varvec{r}}}, t), \end{aligned}$$
(82)

determines the corresponding entropy inflow to the infinitesimal volume \(d{\varvec{ r}}\) around \({\varvec{ r}}\). The first term in the right-hand side of the preceding equation is suggested by the entropy differential,

$$\begin{aligned} { dS}= & {} \int {\frac{\partial h({\varvec{r}},t)}{\partial p({\varvec{r}},t)} dp({\varvec{r}},t)} d{\varvec{r}} +\int {\frac{\partial h({\varvec{r}},t)}{\partial f({\varvec{r}},t)} df({\varvec{r}},t)}d{\varvec{r}}\nonumber \\= & {} \int {[\theta _p ({\varvec{r}},t) dp({\varvec{r}},t) +} \theta _f ({\varvec{r}},t) df({\varvec{r}},t)]d{\varvec{r}}, \end{aligned}$$
(83)
$$\begin{aligned} \partial h({\varvec{ r}}, t)/\partial t= & {} \theta _p ({\varvec{r}},t)\frac{\partial p({\varvec{r}},t)}{\partial t} + \theta _f ({\varvec{r}},t)\frac{\partial f({\varvec{r}},t)}{\partial t}, \end{aligned}$$
(84)

while the divergence of the entropy current gives:

$$\begin{aligned} \nabla {\cdot }{\varvec{ J}}_{h}= & {} {\varvec{ j}}_{p} \cdot \nabla \theta _{p }+ {\varvec{ J}}_{f} \cdot \nabla \theta _{f }+ \theta _{p }\nabla \cdot {{\varvec{j}}}_{p} + \theta _{f }\nabla \cdot {\varvec{ J}}_{f}\nonumber \\= & {} {\varvec{ G}}_{p }\cdot {\varvec{ j}}_{p }+ {{\varvec{G}}}_{f }\cdot {\varvec{ J}}_{f }+ \theta _{p }\nabla \cdot {\varvec{ j}}_{p} + \theta _{f }\nabla \cdot {\varvec{ J}}_{f}. \end{aligned}$$
(85)

When combined with the probability- and phase-continuity equations these two relations give the following thermodynamic-like expression for the rate of the local production of the resultant entropy,

$$\begin{aligned} \sigma _{h}({\varvec{ r}},t) = {{\varvec{G}}}_{p}({\varvec{ r}},t) \cdot {\varvec{ j}}_{p}({{\varvec{r}}},t) + {\varvec{ G}}_{f }({{\varvec{r}}},t) \cdot {\varvec{ J}}_{f }({{\varvec{r}}},t)+ \theta _{f }({\varvec{ r}})\varSigma _{f}({\varvec{ r}},t), \end{aligned}$$
(86)

where the second term vanishes in the absolute-source scale of Eq. (9):

$$\begin{aligned} \sigma _{h}({\varvec{ r}},t) = {{\varvec{G}}}_{p}({{\varvec{r}}},t)\cdot {\varvec{ j}}_{p}({{\varvec{r}}},t) + \theta _{f }({\varvec{ r}},t)\varSigma _{f}^{abs.}({\varvec{ r}},t). \end{aligned}$$
(87)

Therefore, besides the thermodynamic-like product of the probability affinity and its flux the above expression also involves a product of the affinity and (absolute) source of the the phase distribution. Elsewhere we have explored expressions for the corresponding sources of the resultant entropies in the position and momentum spaces, in terms of the state QIT intensities, affinities and currents [22, 24, 32]. They predict that the vanishing intensities give rise to vanishing sources of the quantum Shannon- and Fisher-type entropies. A generalization of this one-electron analysis to general N-electron systems would again involve the wave functions in the HZM construction of the modern DFT.

Let us finally examine the extra information-source contributions generated by the equilibrium phase transformation of the electronic wavefunction. It modifies the initial phase \(\phi ({\varvec{ r}},t)\) of the complex quantum state

$$\begin{aligned} \varphi ({\varvec{ r}},t)=R({{\varvec{r}}},t)\hbox {exp}[\hbox {i}\phi ({\varvec{ r}},t)], \end{aligned}$$
(88)

by the equilibrium “thermodynamic” phase component \(\phi _{eq.}({\varvec{ r}}, t) = - (1/2)\hbox {ln}p({\varvec{ r}},t)\) [Eqs. (31), (69)], which extremizes the resultant measure of the state entropy content, into the resultant phase \(\Phi _{eq.}({\varvec{ r}},t)\) of the associated equilibrium state

$$\begin{aligned} \varphi _{eq.}({\varvec{ r}},t)=R({{\varvec{r}}},t)\hbox {exp}\{\hbox {i}[\phi ({{\varvec{r}}},t)+\phi _{eq.}({\varvec{ r}},t)]\} \equiv R({{\varvec{r}}},t)\hbox {exp}[\hbox {i}\Phi _{eq.}({\varvec{ r}},t)]. \end{aligned}$$
(89)

The initial probability current in \(\varphi \),

$$\begin{aligned} {\varvec{ j}}_\varphi ({\varvec{ r}},t)=\langle \varphi {\vert }{\hat{\mathbf{j}}}({\varvec{r}}){\vert }\varphi \rangle = ({\hbar }/m) p({\varvec{ r}},t)\nabla \phi ({\varvec{ r}}, t) \equiv {\varvec{ j}}({{\varvec{r}}},t), \end{aligned}$$
(90)

is thus modified by the correction term proportional to the negative gradient of the conserved probability distribution,

$$\begin{aligned} p({\varvec{ r}},t)= & {} {\vert }\varphi _{eq.}({{\varvec{r}}},t){\vert }^{2} = {\vert }\varphi ({{\varvec{r}}},t){\vert }^{2}=R({\varvec{ r}},t)^{2}, \end{aligned}$$
(91)
$$\begin{aligned} {{\varvec{j}}}_{eq.}({\varvec{ r}},t)= & {} \langle \varphi _{eq.}{\vert }{\hat{\mathbf{j}}}({\varvec{r}}){\vert }\varphi _{eq.}\rangle \equiv {{\varvec{j}}}_{p}[\varphi _{eq.}]=({\hbar }/m) p({{\varvec{r}}},t)\nabla [\phi ({\varvec{ r}}, t)+\phi _{eq.}({\varvec{ r}}, t)]\nonumber \\= & {} {\varvec{ j}}({{\varvec{r}}},t) - [{\hbar }/(2m)]\nabla p({\varvec{ r}},t). \end{aligned}$$
(92)

We have also demonstrated in Sect. 5 that this change in the state phase/current affects sources of both the probability and phase distributions in the position representation:

$$\begin{aligned} \sigma _{p}[\varphi _{eq.}]= & {} \sigma _{p}[\varphi ] - [{\hbar }/(2m)]\Delta p = - [{\hbar }/(2m)]\Delta p \quad \hbox { and}\nonumber \\ {\varSigma }_{f}^{abs.}[\varphi _{eq.}]= & {} \varSigma _f^{abs.} [\varphi ]+(2p)^{-1}(2\phi -\ln p)\nabla \cdot {\mathbf {j}}_{p} -(\ln p)(\partial \phi /\partial t). \end{aligned}$$
(93)

The nonvanishing probability source \(\sigma _{p}[\varphi _{eq.}]\) modifies the relevant expression for the equilibrium source of the resultant entropy [compare Eq. (87)]:

$$\begin{aligned} \sigma _{h}[\varphi _{eq.}]= & {} \partial h[\varphi _{eq.}]/\partial t+\nabla \cdot {{\varvec{J}}}_{h}[\varphi _{eq.}]\nonumber \\= & {} \theta _{p}[\varphi _{eq.}](\partial p[\varphi _{eq.}]/\partial t+\nabla \cdot {{\varvec{j}}}_{p}[\varphi _{eq.}]) \nonumber \\&+ \theta _{f }[\varphi _{eq.}]\varSigma _{f}^{abs.}[\varphi _{eq.}] + {{\varvec{G}}}_{p}[\varphi _{eq.}] \cdot {{\varvec{j}}}_{p}[\varphi _{eq.}]\nonumber \\= & {} \theta _{p}[\varphi _{eq.}]\sigma _{p}[\varphi _{eq.}] + \theta _{f }[\varphi _{eq.}]\varSigma _{f}^{abs.}[\varphi _{eq.}] + {{\varvec{G}}}_{p}[\varphi _{eq.}] \cdot {{\varvec{j}}}_{p}[\varphi _{eq.}]. \end{aligned}$$
(94)

A reference to the preceding equation indicates that the remaining quantities determining the entropy source \(\sigma _{h}[\varphi _{eq.}]\) are also modified by the thermodynamic phase-shift in the equilibrium state \(\varphi _{eq.}\), compared to their values in the original state \(\varphi \):

$$\begin{aligned}&{\varvec{ G}}_\rho [\varphi _{eq.}] = {\varvec{ G}}_\rho [\varphi ] - 2\nabla \phi _{eq. }= {\varvec{ G}}_\rho [\varphi ] + (\nabla p)/p,\nonumber \\&\quad \theta _{p}[\varphi _{eq.}]= - \hbox {lnp} - 1 - 2\Phi _{eq.},\quad \theta _{f }[\varphi _{eq.}] = -p/\Phi _{eq.}. \end{aligned}$$
(95)

Finally, these modified state parameters and the probability source of Eq. (93) give rise to the modified source of the resultant entropy in the horizontal equilibrium state [Eq. (94)].

8 Conclusion

Elsewhere we have explored in a more detail the densities, currents, information measures, and continuity relations in the p-space [22, 24, 32]. The composition of the probability and current distributions in the position (r) and momentum (p) spaces are quite different [33]. For example, the chemically most important external (large r, valence) region of the position-density corresponds to the internal (low p) region of the momentum-density. The former gives rise to a sourceles continuity relation, while the latter exhibits a finite source term, conditional on the adopted flux definition [22, 24, 32]. Indeed, the Fourier transforms of the strong-stationary (zero-current) states in the position representation generally give rise to the weak-stationary (finite-current) states in the momentum space. This observation strengthens the need for the nonclassical information supplements in the QIT treatments of molecular electronic states.

One recalls that the change of the position representation of the present analysis into its canonical, momentum analog involves the simultaneous unitary operation performed on both the vavefunctions and operators. Therefore, from the known properties of such unitary transformations one predicts that the above position-space conclusions remain generally valid also in the momentum space. Indeed, the unitary canonical transformations between these two representations change the form of the system wavefunction without affecting its independent variables. Thus the quantum mechanical operators related by the unitary transformations represent the same physical quantity, preserve their linear and Hermitian character and algebraic relations between observables, e.g., commutation rules, the spectrum of eigenvalues, and the matrix elements, e.g., the expectation values

$$\begin{aligned} E= & {} \langle \varphi {\vert }{\hat{\mathrm{H}}}{\vert }\varphi \rangle =\langle \varphi _{eq.}{\vert }{\hat{\mathrm{H}}}^{eq.}{\vert }\varphi _{eq.}\rangle ,\,\, {\varvec{ j}}({{\varvec{r}}},t)=\langle \varphi {\vert }{\hat{\mathbf{j}}}({\varvec{r}}){\vert }\varphi \rangle =\langle \varphi _{eq.}{\vert }{\hat{\mathbf{j}}}^{eq.}({\varvec{r}}){\vert }\varphi _{eq.}\rangle , \hbox { etc }.\nonumber \\&{\vert }\varphi _{eq.}\rangle ={\hat{\mathrm{U}}}{\vert }\varphi \rangle , \,\,{\hat{\mathrm{H}}}^{eq.}={\hat{\mathrm{U}}{\hat{\mathrm{H}}}{\hat{\mathrm{U}}}}^{-{1}},\quad {\hat{\mathbf{j}}}^{eq.}({\varvec{r}})={\hat{\mathrm{U}}}{ \hat{\mathbf{j}}}^{eq.}({\varvec{r}}){\hat{\mathrm{U}}}^{-{1}}. \end{aligned}$$
(96)

One further observes that, due to the nonvanishing equilibrium source of the probability density in r-space, the densities of classical information contributions exhibit the nonvanishing sources in the associated r-space entropy/information continuity equations in such phase-optimized states. The nonclassical information terms also introduce finite information sources due to the modified probability current in the equilibrium molecular state. Moreover, a generally nonvanishing source of the momentum density generates finite information-source contributions in p-space, due to both the classical and nonclassical information/entropy terms. In the momentum representation a nonvanishing momentum-probability current, due to a finite p-phase component of the momentum wavefunction, and the current-dependent terms of the resultant measures of the entropic content of molecular states should have a profound influence on the time-evolution of the resultant entropy/information functionals.