Abstract
We report on a novel technique to measure quartz tuning forks, and possibly other vibrating objects, in a quantum fluid using a multifrequency lock-in amplifier. The multifrequency technique allows to measure the resonance curve of a vibrating object much faster than a conventional single frequency lock-in amplifier technique. Forks with resonance frequencies of 12 kHz and 16 kHz were excited and measured electro-mechanically either at a single frequency or at up to 40 different frequencies simultaneously around the same mechanical mode. The response of each fork was identical for both methods and validates the use of the multifrequency lock-in technique to probe properties of liquid helium at low fork velocities. Using both methods we measured the resonance frequency and drag of two 25-\(\upmu \)m-wide quartz tuning forks immersed in liquid \(^4\)He in the temperature range from 4.2 K to 1.5 K at saturated vapour pressure. The damping and shift of resonance frequency experienced by both tuning forks at low velocities are well described by hydrodynamic contributions in the framework of the two-fluid model. The sensitivity of the 25-\(\upmu \)m-wide tuning forks is larger compared to similar 75-\(\upmu \)m-wide forks and in combination with the faster multifrequency lock-in technique could be used to improve thermometry in liquid \(^4\)He. The multifrequency technique could also be used for studies of the onset of non-linear phenomena such as quantum turbulence and cavitation in superfluids.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quartz tuning forks were relatively recently introduced for probing quantum liquids [1] and were quickly adopted for low temperature thermometry [2–4], the generation and detection of quantum turbulence [5–8] and studies of acoustic emission [9–11] and cavitation [12]. The popularity of quartz tuning forks is driven by their availability, high quality factor and ease of use. The majority of tuning forks studied so far in quantum fluids research have been common off-the-shelf electronic components and depending on the manufacturer had different physical dimensions, length, width and thickness, even though the resonance frequencies are the same. Previously, to investigate the frequency dependence of acoustic emission and the critical velocity for the generation of turbulence in superfluid \(^4\)He [7, 10], we had manufactured custom-designed tuning forks on a 75-micron quartz waferFootnote 1 and used the length of the forks to control resonance frequencies. Here we present the temperature dependence of damping experienced by two forks manufactured on a \(25\,\upmu \)m thick wafer. The miniaturisation of the forks was driven by a desire to probe local properties of helium and to boost the fork’s sensitivity to temperature.
Conventional measurements of the resonant properties of an oscillating object use a continual sweep of the excitation frequency using a signal generator and detection of the object’s response using a lock-in amplifier. While this technique is well established for linear systems, mapping out the complete resonant curve can be quite slow. The single frequency lock-in technique is also used to capture the resonance properties in non-linear systems and has successfully characterised Duffing-like oscillators [13]. Furthermore, the presence of strong non-linear interactions in a system brings new opportunities to probe such systems using various modes of multifrequency excitation and detection. For example, the strong non-linearities between the different mechanical resonance modes of an oscillator are utilised to study nano-electromechanical structures [14, 15]. Atomic force microscopy community also has developed multifrequency techniques for scanning the surface of a sample using a cantilever [16, 17]. One such technique excites the fundamental mechanical mode of a resonator using two frequencies and detects intermodulation (mixing) products created by strong non-linear interactions of the system [18].
We adapted the intermodulation approach and have observed that at low oscillation velocities the tuning forks only respond at the excitation frequencies. The absence of frequency mixing implies that our tuning forks are extremely linear and have no visible intrinsic non-linear effects. As a result, we devised a new linear multifrequency technique that excites a tuning fork in the vicinity of the lowest mode resonance at 40 separate frequencies simultaneously and measures its resonance curve without frequency sweeping. In this paper, we compare the measurements of the tuning forks by the conventional technique, using a Stanford Research Systems SR830 Lock-in Amplifier, with the multifrequency approach using an Intermodulation Products Multifrequency Lock-in Analyser (MLA) [19].Footnote 2 We demonstrate that new technique is applicable even when the fork is immersed in liquid helium as the interactions of the fork with the fluid remain linear at small fork velocities. In the future, if non-linear effects are observed at high fork velocities the mixing effects can be attributed solely to the interaction of the fork with the fluid and should help to understand the nature of arising non-linearities.
2 Experimental Details
All measurements on the tuning forks were conducted in a simple \(^{4}\)He immersion cryostat that operates in the temperature range from 4.2 K down to a base temperature of \(\sim \)1.5 K using the evaporative cooling technique. The temperature of the liquid helium was deduced from the vapour pressure [20]. Both tuning forks were mounted directly in the helium bath and immersed in liquid helium.
The studied tuning forks were fabricated on a single quartz wafer with a thickness of 25 \(\upmu \)m using the same lengths and thicknesses as the previously reported 75-\(\upmu \)m-wide forks [10]. The prong lengths of the forks were L = 2600 \(\upmu \)m and L = 2200 \(\upmu \)m, resulting in resonance frequencies of approximately 12 kHz and 16 kHz, respectively. Both forks have an identical prong width of W = 25 \(\upmu \)m, prong thickness of T = 90 \(\upmu \)m and inter-prong distance of D = 75 \(\upmu \)m. The right side of Fig. 1 shows a photograph of the 12 kHz fork with the corresponding dimensions.
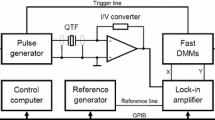
In our measurements, forks were driven and detected electro-mechanically. The left side of Figure 1 shows a diagram of the electrical circuit used. The fork motion was excited by applying an alternating voltage from a signal generator that was attenuated by 20 dB. The motion of the fork induces a current, which was amplified by a custom-built IV-converter [21] with a gain of 10\(^6\) V A\(^{-1}\) and the voltage was measured by a lock-in amplifier. Due to the presence of a summation amplifier, we can measure the fork’s response using conventional lock-in technique either with an Agilent 33521 signal generator and SR830 lock-in amplifier or with a Intermodulation Products MLA and its internal generator. Furthermore, the multifrequency lock-in technique can be operated with the MLA on up to 42 frequencies simultaneously. We direct the interested reader to the paper by Tholén et al. [19] for details behind the operating principles of the MLA. We have measured the resonance curve of each fork using both sets of lock-in amplifiers in order to compare them.
The physical parameters of the fork such as force and velocity can be determined from the applied voltage and measured current [2]. The force experienced by the fork prong is determined by the applied voltage V and is given by \(F = {aV}/{2}\), where the coefficient a is termed the fork constant. The resulting motion of the fork induces current \(I = av\), where v is the velocity of the tip of the prong. The experimental value of the fork constant is given by
The resonant current I, and the damping width of the resonance \(\Delta {f_{2}}\) can be obtained from a measurement of a single frequency sweep around the resonance at excitation voltage V. The only parameter still required to deduce the experimental fork constant is the effective mass of the prong \(m_\mathrm{eff}\), assumed to be a quarter of the actual mass of the fork prong, \(\rho _{q}WTL/4\) [10], where \(\rho _{q}\) = 2659 kg m\(^{-3}\) is the density of quartz. Previous measurements show that the experimental fork constant determined electro-mechanically agrees with a direct optical detection to within 10 % [7].
3 Experimental Results
After the cryostat was filled with \(^4\)He and left to settle for a period of about 20 minutes, the temperature of the cryostat was reduced from 4.2 K down to the base temperature of about 1.5 K by pumping the helium bath over a period of approximately 3–4 h. The frequency response of the 12 kHz tuning fork near resonance was measured continually during cooling by alternating between the conventional lock-in technique using the SR830 and the multifrequency mode using the MLA.
3.1 Comparison Between SR830 and MLA
Frequency response of the 12 kHz tuning fork in superfluid \(^4\)He at 1.45 K and saturated vapour pressure. Left Frequency dependence of the in-phase component. Right Frequency dependence of the quadrature component. Filled and open symbols correspond to SR830 and MLA measurements, respectively. The solid red line is a Lorentzian fit of the data. See text for details (Colour figure online)
Figure 2 shows the frequency dependence of the 12 kHz fork response normalised by the excitation voltage at the base temperature of the cryostat, 1.45 K at saturated vapour pressure. The left and right sides of the figure correspond to the in-phase and quadrature responses, while filled and open symbols denote the SR830 and MLA measurements, respectively. The difference between the measurements is negligible and the red solid line shows the expected Lorentzian lineshape for a driven damped harmonic oscillator in a fluid [10]
Here \(f_0\) is the vacuum frequency of the oscillator, and \(\gamma =\gamma _2 + i\gamma _1\) describes the complex drag force, where the real component \(\gamma _2\) corresponds to the dissipative drag forces, and the non-dissipative imaginary component \(\gamma _1\) arises from the backflow of fluid around the oscillator and the mass enhancement due to the normal component clamped around the oscillator. The least-squares fit yields a resonance width of \(\Delta f_2 = \gamma _2/2\pi =8.3\) Hz, and resonance frequency of 11597.6 Hz in superfluid \(^4\)He at 1.45 K. The fork constants deduced from the resonance curves are \((9.12\pm 0.02)\times 10^{-8}\) N V\(^{-1}\) and \((9.04\pm 0.03)\times 10^{-8}\) N V\(^{-1}\) correspondingly for SR830 and MLA measurements. The non-zero quadrature component at resonance frequency is due to the intrinsic capacitance of the fork and can be used to verify that the current amplifier and our electronic circuit are working as expected even in the absence of the resonance.
The SR830 data presented in Fig. 2 were obtained by performing a conventional frequency sweep and comprises 60 data points. The time interval between acquisition of each data point was 1 s. The generator excitation was constant and equal to 50 mV before being reduced by the 20dB attenuator. The peak velocity of the top of the fork prong was 1.2 mm s\(^{-1}\) at the resonance frequency. The MLA data were obtained by exciting the fork with a frequency comb of 40 discrete, equally spaced tones with peak amplitude of 20 mV each and detected by the phase-sensitive lock-in technique at 40 different frequencies. In the present measurements, the frequency comb had identical phases on all excitation frequencies, but it would be interesting in the future to alter the relative phases in order to cancel the overall motion of the fork and only have a low-frequency beatingFootnote 3. We have used a reduced amplitude for the multifrequency lock-in measurements compared with the single frequency lock-in measurements since for correct operation the MLA’s amplitude of the generated voltage signal combined across all frequencies should not exceed 2 V, to avoid clipping of the lock-in amplifier. The peak velocity of the fork was 0.46 mm s\(^{-1}\) at the resonance frequency. It is very instructive to compare the power injected into the system using both methods. The power injected into the fluid at a single excitation frequency is IV or 2Fv and for a conventional frequency sweep has the largest value at the resonance frequency and equals 0.4 pW. To deduce the power applied in the multifrequency approach, the sum of power injected at each frequency needs to be calculated and equals 0.6 pW. The power injected into the system using the frequency comb was only 50% higher than in a single frequency technique due to nearly 3 times lower excitation and hence \(\sim \)3 times lower peak velocity at the resonance.
The observed response of the fork to a multifrequency excitation is observed to be nearly identical to that from a single frequency excitation due to the small velocity of the fork and of the surrounding liquid. This result suggests that the velocity fields of different modes do not interact and the equations of motion for each frequency can be separated. The resulting velocity field is then simply the superposition of the fields of the individual modes. In this case, the quadratic (\(v \nabla v\)) term in Euler’s equation is negligible, and the total mass of the system “oscillator plus moving fluid liquid” does not depend on the amplitude of the oscillationsFootnote 4. Hence the Lorentzian shape described by Eq. 2 can be observed. At much higher peak fork velocities, on the order of \(\sim \)8 cm s\(^{-1}\), the quantum turbulence is expected to be generated by a tuning fork [7], and the shape of resonance curve should look completely different for the single frequency sweep and multifrequency excitation. To reach this velocity, the generator voltage should be on the order of the 330 mV and the multifrequency lock-in amplifier will need to be excited at a fewer number of frequencies in order to avoid saturation of the MLA. We have not carried out such turbulence measurements yet, but are planning to do them in the near future.
The acquisition time of the presented MLA data in Fig. 2 was about 40 s and could be reduced by nearly an order of magnitude. We have not tried to minimise the measurement time in this instance as we wanted to keep the time for acquiring the full spectrum roughly the same for both methods during the evaporative cooling. The measurement time is limited by the resolution of the frequency comb and the signal-to-noise ratio. The measurement frequencies of the MLA in multifrequency mode are not arbitrary, but have to form a frequency comb where all frequencies are integer multiples of some base frequency \(\Delta f_\mathrm{comb}\) [19]. The base frequency is used as a reference frequency in the lock-in amplifier calculations, and in our measurements its value is determined by the quality factor of the fork or the width of the fork resonance. For example, a base frequency of 1 Hz would allow for a frequency comb that contains frequencies which are integer multiples of 1 Hz a minimal frequency coverage/span of 40 Hz. Such a comb is nearly ideal for a fork in liquid \(^4\)He with a 10 Hz wide resonance and a quality factor of \(\sim \)10\(^3\). The shortest measurement time \(t_\mathrm{min} = 1/\Delta f_\mathrm{comb}\) is inversely proportional to the base frequency and so should be on the order of 1 s for the 1 Hz base frequency.
Figure 3 shows the in-phase component of the resonance curve of the 16 kHz fork as a function of MLA’s measurement time at room temperature acquired using a comb of 40 frequencies. The comb had frequency separation of 0.5 Hz and was identical in all of these measurements. The shortest total measurement time needed for this frequency comb is thus 2 s. While the 2 s data are clearly noisier than the rest of the measurements, it is impressive that a complete resonance curve of the tuning fork can be acquired in such a short time. Increasing the measurement time to 5 s makes the resonance curve much better defined, while further time increases to 15 s and 60 s do not improve the quality of the fit significantly enough to warrant longer waiting times. Tripling the shortest possible measurement time \(t_\mathrm{min}\) of the MLA is a good compromise between the quality of experimental data and the acquisition time. The multifrequency measurement time increases as the frequency comb narrows, but the requirement to have a smaller frequency spacing usually correlates with an increase in the quality factor of an oscillator. In this situation, the single frequency lock-in technique also requires longer acquisition times to account for the increased ringdown time between frequency steps.
3.2 Temperature Dependence of Resonance Properties
Temperature dependence of resonance frequency (top) and resonance width (bottom) of the 12 kHz fork, obtained from the same measurements. The filled and opened symbols are measured using the frequency sweep method with the SR830 and the frequency comb approach with the MLA correspondingly. The solid lines are fits to the data using Eqs. 3 and 4 for the top and bottom parts of the figure, respectively. See text for details (Colour figure online)
We measured the temperature dependence of the resonance frequency and resonance width of the forks immersed in liquid helium in the temperature range from 4.2 K down to \(\sim \)1.5 K. The top part of Fig. 4 presents the temperature dependence of the square of the ratio of resonant frequency in vacuum \(f_{0}\) and in liquid helium \(f_\mathrm{H}\) of the 12 kHz fork. The bottom part of Fig. 4 shows the temperature dependence of the resonance damping width of the fork \(\Delta f_2\). The filled and open symbols correspond to SR830 and MLA measurements respectively, and are in an excellent agreement. Each point of Fig. 4 was obtained by acquiring a resonance curve for the fork, and measurements were taken alternatively using the frequency sweep method with the SR830 and the frequency comb approach with the MLA.
To quantitatively explain our results, we follow the approach and annotation described by Blaauwgeers et al. [2] and Bradley et al. [10] by assuming that the viscous penetration depth (\(\sim \)1 \(\upmu \)m for both forks) is much smaller than the fork dimensions and that acoustic damping is negligible at resonance frequencies below 100 kHz. In such case, it is possible to employ the two-fluid model of the superfluid and to obtain the fork resonance frequency and resonance width using the hydrodynamic contributions to the effective mass and Stokes’ drag. The dependence of the resonance frequency in superfluid helium is given by the following expression:
Here the second term describes the fluid backflow around the fork and is related to the prong volume \(V = TWL\) via a geometric parameter \(\beta \), while the third term arises from the normal component being viscously clamped around the fork. The thickness of normal fluid clamped to the surface of a prong, \(S = 2L(T+W)\), is approximately equal to the viscous penetration depth and warrants the introduction of another geometrical factor B. These terms are governed by the densities of the whole fluid \(\rho _{H}\) and normal fluid \(\rho _\mathrm{nf}\), respectively. The viscosity \(\eta \) also gives rise to the Stokes’ drag [2]
where C is another geometrical factor of the order of unity.
We treated all three geometrical factors \(\beta \), B and C as fitting parameters to compare our measurements and the hydrodynamic two-fluid model described above. Solid lines on Fig. 4 are least-square fits using Eqs. 3 and 4 and show good agreement between the data and the model. We found that the values of geometric parameters were almost identical for the SR830 and MLA measurements and are summarised as follows: \(\beta =0.1030\pm 0.0004\), \(B=0.236\pm 0.006\) and \(C=0.410\pm 0.002\).
The frequency fit on the top part of Fig. 4 shows a slight discrepancy at high and low temperatures. This disagreement can be eliminated by allowing the vacuum frequency of the fork to become a fitting parameter. In our measurements, the vacuum frequency \(f_{0}\)=11.730 kHz was measured in saturated vapour pressure of helium at 1.45 K by allowing the superfluid helium level to drop below the fork location. The fitted vacuum frequency yielded a value of 11.749 kHz while the values of \(\beta \), B and C were largely unchanged. The observed discrepancy of the vacuum frequencies is almost certainly due to conducting experiments in the main bath of the cryostat, and not in a dedicated cell filled with clean helium. Any impurities contained in helium transport dewar: water, oil or air molecules would reduce the measured fork frequency as they would be deposited on a fork and possibly change their position on a fork with helium level. It is worth noting here that subsequent cooldowns typically showed slightly different results and the fitting parameters changed on the order of 5–10% between cooldowns. For identical results and reproducible thermometry, the vibrating object needs to be placed in a cell that is linked to the main bath of the cryostat via a filter and the purity of the liquid helium should be controlled.
The results of measurements obtained using the 16 kHz fork are nearly identical to the results of the 12 kHz fork. Table 1 summarises the parameters of both forks and contrasts them with the parameters of two 75-\(\upmu \)m-wide forks that have similar fork length, the same prong separation and thickness [10].
The value of B, linked to clamping of the normal component, is almost identical for both types of forks. The geometrical factor associated with the fluid backflow, \(\beta \), is reduced by a factor of 2.6–2.8 compared to the wider forks, which roughly agrees with a factor of three expected from the theoretical expression of \(\beta = \pi W / 16T\) for a cantilever beam [2, 22]. Our definition of \(\beta \) is a quarter of the conventional definition due to our introduction of the effective mass of the fork. The experimental values of the \(\beta \) are \(\sim \)50 % larger than the expected theoretical values for a single beam, which is not unreasonable as forks have a more complicated flow geometry due to the presence of two prongs that oscillate in anti-phase [2].
The value of constant C is slightly smaller than for larger forks and analysis of Eq. 4 leads to the conclusion that thinner forks have a higher sensitivity in terms of the magnitude of the change in resonance width as temperature changes. Let us consider two forks A and B that have different widths \(W_A\) and \(W_B\), while all other physical parameters, the length, thickness and distance between prongs, are identical. The resonance frequency of the fork in vacuum is a function of prong length and its thickness, and does not depend on the width of the fork [2]. The ratio of the vacuum and helium frequencies is on the order of unity for both forks and consequently the ratio of resonance widths of these forks is given below
The right side of this equation shows that the main difference between sensitivities of two considered forks is governed by a ratio of the fork thickness and width \(1+T/W\). For the 75-\(\upmu \)m-wide fork this ratio is 2.2, while for 25-\(\upmu \)m-wide fork it is 4.6. Substitution of values of the ratios and of parameter C explains the near doubling of resonance width change with the temperature of the present forks. To further enhance sensitivity, we would recommend using the thinnest available forks with shortest lengths or highest resonance frequencies; however, care should be taken to keep the acoustic damping of forks negligible [10].
4 Conclusions
We have probed properties of liquid \(^4\)He using custom-manufactured quartz tuning forks in the temperature range from 4.2 K down to \(\sim \)1.5 K. The tuning forks were excited and detected electro-mechanically simultaneously at 40 frequencies. Our results show that at low fork velocities the multifrequency and conventional single frequency lock-in techniques produce identical resonance curves, and suggest that tuning forks behave as linear oscillators at low excitation. We find the identical fork response for both methods fascinating as the fluid flow around the fork is the superposition of fluid motion at all possible frequencies. The multifrequency lock-in technique has many applications and benefits: it requires shorter measurement time; it could be used to study the response of an oscillating object at various harmonics and the interplay between them and offers the possibility to study more than one vibrating object at the same time. Furthermore, at high oscillation velocities, the response in superfluid should become non-linear due to the development of quantum turbulence or cavitation, and the multifrequency lock-in technique will be useful to study the origins of these phenomena. The temperature dependence of the resonance width of 25-\(\upmu \)m-wide tuning forks shows that the fork damping at low velocities is well described by a hydrodynamic contribution in the framework of the two-fluid model. The \(^4\)He liquid temperature sensitivity of the 25-\(\upmu \)m-wide tuning forks is larger compared to similar 75-\(\upmu \)m-wide forks and in combination with the faster multifrequency lock-in technique could be used to improve thermometry in liquid \(^4\)He by probing fluid directly and locally. Localised thermometry should be useful in studies of second sound, co-flow, counterflow turbulence and cavitation.
Notes
Manufactured by the Statek Corporation, 512, N. Main Street, Orange, CA 92868, USA.
Intermodulation Products AB, Landa Landav\(\ddot{\mathrm{a}}\)gen 4193, SE - 823 93 Segersta, Sweden.
We thank one of the referees for this suggestion.
We thank one of the referees for the suggested theoretical justification.
References
D.O. Clubb, O.V.L. Buu, R.M. Bowley, R. Nyman, J.R. Owers-Bradley, J. Low Temp. Phys. 136(1), 1 (2004)
R. Blaauwgeers, M. Blažkova, M. Človečko, V.B. Eltsov, R. de Graaf, J. Hosio, M. Krusius, D. Schmoranzer, W. Schoepe, L. Skrbek, P. Skyba, R.E. Solntsev, D.E. Zmeev, J. Low Temp. Phys. 146, 537 (2007)
D.I. Bradley, M. Clovecko, S.N. Fisher, D. Garg, A.M. Guénault, E. Guise, R.P. Haley, G.R. Pickett, M. Poole, V. Tsepelin, J. Low Temp. Phys. 171, 750 (2013)
I. Todoshchenko, J.-P. Kaikkonen, R. Blaauwgeers, P.J. Hakonen, A. Savin, Rev. Sci. Instrum. 85, 085106 (2014)
M. Blažkova, M. Človečko, E. Gažo, L. Skrbek, P. Skyba, J. Low Temp. Phys. 148, 305 (2007)
D.I. Bradley, M.J. Fear, S. Fisher, A.M. Guénault, R.P. Haley, C.R. Lawson, G.R. Pickett, R. Schanen, V. Tsepelin, L.A. Wheatland, Phys. Rev. B 89, 21 (2014)
S.L. Ahlstrom, D.I. Bradley, M. Človečko, S.N. Fisher, A.M. Guénault, E.A. Guise, R.P. Haley, O. Kolosov, P.V.E. McClintock, G.R. Pickett, M. Poole, V. Tsepelin, A.J. Woods, Phys. Rev. B 89, 014515 (2014)
M.J. Jackson, O. Kolosov, D. Schmoranzer, L. Skrbek, V. Tsepelin, A.J. Woods, J. Low Temp. Phys. 183, 208 (2016)
D. Schmoranzer, M. La Mantia, G. Sheshin, I. Gritsenko, A. Zadorozhko, M. Rotter, L. Skrbek, J. Low Temp. Phys. 163, 317 (2011)
D.I. Bradley, M. Človečko, S.N. Fisher, D. Garg, E. Guise, R.P. Haley, O. Kolosov, G.R. Pickett, V. Tsepelin, D. Schmoranzer, L. Skrbek, Phys. Rev. B 85, 014501 (2012)
J. Rysti, J. Tuoriniemi, J. Low Temp. Phys. 177, 3-4133-150 (2014)
M. Blažkova, T.V. Chagovets, M. Rotter, D. Schmoranzer, L. Skrbek, J. Low Temp. Phys. 150, 194 (2008)
E. Collin, Yu.M. Bunkov, H. Godfrin, Phys. Rev. B 82, 235416 (2010)
K.J. Lulla, R.B. Cousins, A. Venkatesan, M.J. Patton, A.D. Armour, C.J. Mellor, J.R. Owers-Bradley, New J. Phys. 14, 113040 (2012)
A. Castellanos-Gomez, H.B. Meerwaldt, W.J. Venstra, H.S.J. van der Zant, G.A. Steele, Phys. Rev. B 86, 041402 (2012)
R. Garcia, E.T. Herruzo, Nat. Nano 7, 217 (2012)
D. Platz, D. Forchheimer, E.A. Tholén, D.B. Haviland, Nanotechnology 23, 265705 (2012)
D. Platz, E.A. Tholén, D. Pesen, D.B. Haviland, Appl. Phys. Lett. 92, 153106 (2008)
E.A. Tholén, D. Platz, D. Forchheimer, V. Schuler, M.O. Tholén, C. Hutter, D.B. Haviland, Rev. Sci. Instrum. 82, 026109 (2011)
R.J. Donnelly, C.F. Barenghi, J. Phys. Chem. Ref. Data 27, 1217 (1998)
S. Holt, P. Skyba, Rev. Sci. Instrum. 83, 064703 (2012)
J.E. Sader, J. Appl. Phys. 84, 64 (1998)
Acknowledgments
We thank S.M. Holt, A. Stokes and M.G. Ward for excellent technical support. We would like to thank D. Forchheimer, E. Tholén and D. Haviland for their help with MLA and useful discussions. This paper significantly benefitted from supportive and very thorough referees. This research was supported by the UK EPSRC Grants Nos. EP/L000016/1 and EP/I028285/1. Underlying data can be found from the Lancaster University research portal at http://dx.doi.org/10.17635/lancaster/researchdata/69.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bradley, D.I., Haley, R.P., Kafanov, S. et al. Probing Liquid \(^4\)He with Quartz Tuning Forks Using a Novel Multifrequency Lock-in Technique. J Low Temp Phys 184, 1080–1091 (2016). https://doi.org/10.1007/s10909-016-1634-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10909-016-1634-5