1 Introduction

The production and consumption of energy today are closely linked to several environmental issues, including air pollution, climate change, water pollution, and the collection of solid refuse [1]. Among the many useful, viable options, energy can be produced electrochemically and kept in batteries and supercapacitors (SCs) [2, 3]. The charging and discharging processes used by batteries and supercapacitors, as well as the materials used to construct their components, are very distinct [4]. Because they can store a significant amount of energy in a comparatively small volume and weight and provide suitable power levels for a variety of uses, batteries are the technology of choice for the majority of users [5,6,7]. However, batteries have several issues including poor power density and a constrained number of charging/discharging cycles. On the other hand, supercapacitors are energy storage systems that have a high capacity and minimal internal resistance [8].

Their energy storage mechanism involves physically storing charges in an electric double layer at the interface between a surface and an electrolyte, which allows them to save and create energy at significantly higher rates than batteries. The charge condition does not significantly alter the material’s structure [9]. Therefore, batteries are required for equipment with long-lasting energy needs and low power output [10]. Capacitors are recommended for applications requiring high-power energy delivery. Due to their distinct advantages over batteries, such as higher power density, long cycling life, and improved cycle stability, supercapacitors are thus seen as a more useful energy storage technology. Supercapacitors can be divided into two types based on how they store charge: electric double-layer capacitors (EDLCs) or pseudocapacitors. In EDLCs, energy is stored through reversible charge collection at the electrode–electrolyte interface by fast electrolyte ion adsorption and desorption. In contrast, pseudocapacitors store energy by fast and reversed redox reactions on the electrode surface of conducting polymers or metal oxides.

Generally, in energy storage devices, the mechanism of electrochemical electrodes is detected by their physicochemical properties, like chemical structure, particle size, crystallinity, and morphology [11, 12]. The inverse spinel- Li4Ti5O12 (LTO) is one of the electrode materials that can be used for high-power energy devices. Li+ ions take up residence in sites 8a and 16d of the original LTO crystal structure, whereas O2− ions occupy sites 32e. When LTO is lithiated, the extra Li ions that were inserted occupy the octahedral 16c sites, and other Li atoms change the cubic structure's 8a to 16c vacancies. In the end, Li4+xTi5O12 only has all 16c sites filled at the Li content of (x = 3), indicating the creation of stable Li7Ti5O12 and electron transport between Ti3+ and Ti4+. [13].

The Li4Ti5O12 spinel is a marvelous electrode due to its safety, long cycling life, high Li+ mobility, effective Li+ intercalation, structural stability throughout cycling, and broad temperature work range. However, low electrical conductivity (σ < 10–13 S/cm) [14] and low Li-ion diffusion coefficient ((10–8 cm2/s) of Li4Ti5O12 significantly limit its rate performance [15] are considered a disadvantage. Nowadays, several attempts to resolve these issues, including 1- nanoscale particle preparation to decrease the Li+ pathway and increase the diffusion coefficient [16,17,18,19,20]. 2- conductive phase surface covering, such as carbon-based materials coating [21]. 3- Ions doping in the Ti4+ or Li+ octahedral sites [17, 22,23,24]. These tactics may also be used to increase LTO intrinsic conductivity [16, 25,26,27,28,29].

PANI is a conducting polymer for various applications, including supercapacitor applications, owing to its magnificent thermal and chemical stability, high electrical conductivity, great flexibility, cheapness, and various redox state. Although it has a high theoretical capacitance, its limited cycle stability reduced its energy storage application [30, 31].

Composite materials can be created by distributing transition metal oxides in conductive polymers. Due to the synergistic interaction of the two elements, they exhibit great surprising hybrid properties [32]. This suggests that a hybrid EDL/Faradaic pseudocapacitive material may be suitable for supercapacitor devices with a high energy density and specific capacitance [33,34,35].

In this work, we used a solid-state method to produce pure LTO and Mg, Mn, and V-doped LTO nanoparticles, as well as a chemical polymerization method to synthesize PANI and composites of pure and doped LTO@PANI nanoparticles. The addition of a BaSO4 seed with low percent (< 5%) during polymerization gives oriented assembled PANI showing a higher AC conductivity and enhancing the capacitive parameters of PANI [36, 37]. The samples were characterized using XRD and SEM methods, and their electrical and electrochemical characteristics were examined using the electrochemical instruments EIS, CV, and GCD. How doping and surface modification affect the electrical conductivity and electrochemical properties of LTO materials has been documented and discussed. Of all the materials under investigation, the doped LTO@PANI composite had the highest specific capacitance and the best cycle life.

2 Experimental

2.1 Materials

All chemicals were reagent grade. (Li2CO3) 98%, (TiO2) 98%, (C6H5-NH2) 98.5%, (K2S2O8) 98%, (MnO2), (MgO), (V2O5) 99%, Poly (vinylidene fluoride) 99.5% (M.wt = 543,000 g/mole), (HCl) 35%, (C2H5OH) 99%, BaCl2.2H2O, and Carbon black were supplied from Alfa Aesar.

2.2 Preparation Methods

2.2.1 Preparation of Pure Li4Ti5O12 (LTO) and Doped LTO (V-LTO)

Pure Li4Ti5O12 (LTO) and Mn, V, Mg-doped LTO were prepared through a modified solid-state method [38]. The TiO2: Li2CO3 molar ratio of 5:2.3 was used to synthesize the LTO in a stoichiometric formula of Li4Ti5O12 [39]. TiO2 and Li2CO3 were completely mixed with the necessary amounts of MgO, MnO2, and V2O5 dopants to create samples of Li3.9Mg0.1Ti5O12, Li3.9Mn0.1Ti5O12, and Li3.9V0.1Ti5O12 as seen in Table 1. The combined powders were treated in a vigorous ball mill for a week, then autoclaved in ethanol for 24 h at 150 °C. Absolute ethanol was used to wet the particles during this process. The remaining slurry was then dried for an hour at 80 °C to remove the ethanol. LTO samples were then calcined at 750 °C in the air for two hours.

Table 1 Stoichiometric ratios of the prepared materials
Full size table

2.2.2 Preparation of Polyaniline Composites (LTO@PANI)

PANI composites were prepared by in-situ oxidation-polymerization [37]. In the standard processes, aniline hydrochloride was created by ultrasonically combining 1 g of the produced LTO (pure or doped) with 2 ml of aniline monomer dissolved in 100 ml of 1 M HCl, and 0.01 g of BaCl2.6H2O was added during the sonication process. K2S2O8 was used as the oxidant, and 50 ml of 0.1 M was carefully added while continuously stirring for three hours in an ice bath. To remove any extra oxidant and unreacted monomers, the solution was washed with 250 ml of distilled water after being left in the solution for 24 h to finish polymerization. Finally, the produced polymer was filtered and dried in air at 60 °C to get a consistent weight.

2.3 Materials Characterizations and Measurements

Cu-K with λ = 0.154 nm and a diffraction angle between 15 and 80º was used in an X-ray diffractometer (Philips XL 40) to record the XRD patterns of the materials. The morphology of the materials was analyzed with a scanning electron microscope (SEM) (JEOL-JSM-6510 LV). Rietveld refinement approach was used to confirm the crystalline structures of LTO and doped LTO samples, employing the GSAS program with the EXPGUI interface. X-ray Photoelectron Spectroscopy (XPS) studies were performed using a KRATOS XSAM-800 and calibrated by adventitious carbon.

2.3.1 Electrochemical and Dielectrics Measurements

2.3.1.1 Preparation of Working Electrodes

To make the electrodes, a paste was made by blending LTO materials, carbon black, polyvinylidene fluoride in the proportions 75:15:10, and a few drops of ethanol. The paste was created on FTO glass using the doctor blade method and allowed to dry at 80 °C for two hours to evaporate the solvent for the optimum adhesion to the substrate surface.

2.3.1.2 Electrochemical and Electrical Measurements

Cyclic voltammetry (CV) and galvanostatic charge–discharge (GCD) techniques were used using the Digi-Ivy 2116 B instrument to determine the studied electrodes' energy storage capacity. EIS was measured by (Metrohm Auto Lab PGSTAT 204), Netherlands, between 0.1 Hz and 100 kHz at a constant voltage of 10 mV. A cell with three electrodes was used to determine the electrochemical characteristics in a published worldwide. The examined materials were used to make working electrodes on FTO glass, whereas the reference and counter electrodes were saturated calomel electrodes (SCE), Pt foil, and 1 M LiNO3 aqueous solution, respectively. CVs were run between − 1.1 and 1.1 V at scan rates between 1 and 100 mV/s. GCD was measured between 0.5 and 3 A/g of current density. GW Instek 8110G LCR meter, Taiwan, was used to measure the dielectric properties of AC conductivity (AC), dielectric constant, and dielectric loss across the frequency range of 103–107 Hz. Samples were pressed as pellets, then connected to a 4-port LCR bridge via a conductive cell.

3 Results and Discussions

3.1 Chemical Characterizations

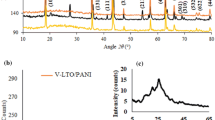
Figure 1a shows the XRD patterns of the pure and doped LTO samples. The diffraction peaks for the pure LTO sample are at 2θ = 18°, 37°, 43°,49°, 58°, 63°, 66°, 75°, 76°, and 79°, corresponding to (111), (311), (400), (331), (511), (440), (531), (532), (622), (444) planes, respectively. They correspond to the LTO cubic spinel phase structure (JCPDS card no. 49–0207). The spinel structure was also seen in the XRD of the LTO-doped samples. All of the observed diffraction peaks have indicated the formation of pure and highly crystalline LTO materials. Additionally, it was noted that the introduction of dopant ions into the LTO lattice caused the diffraction peak of the (111) crystal plan to move noticeably to the right. This shift is due to the presence of atoms with smaller substituted ionic radii (The ionic radius of Mg2+, Mn4+, and V5+ are 72, 53, and 46 pm), which are smaller than Ti4+ and Li+ (60 pm) [40, 41]. These results suggest that the dopant was effectively generated in the (111) plane of Li4Ti5O12’s spinel lattice. In conclusion, The XRD results confirm no modification in the structure but a change in the cubic parameter.

Fig. 1
figure 1

XRD of a LTO samples, b LTO@PANI samples, Rietveld Refinement of c LTO, d Mg-LTO, e Mn-LTO, f V-LTO

Full size image

The XRD of the LTO@PANI composites, as shown in Fig. 1b, displays peaks associated with the orthorhombic phase structure of BaSO4 in addition to the peaks of the LTO spinel structure. The peaks of the orthorhombic structure of BaSO4 appeared at 2θ = 20.6°, 22.8°, 25°, 25.9°, 27°, 28.8°, 31.7°, and 32.8° corresponding to (011), (111), (002), (210), (120), (211), (112), and (020) planes, respectively,(JCPDS No. 24–1035) [39, 42], The BaSO4 was formed during the polymerization of PANI, as shown in the following equation [37].

figure a

The presence of BaSO4 planes on XRD occurred because of the oriented assembling of PANI on the surface of BaSO4 seed owing to the similarity of crystal structure between PANI and BaSO4 [36].

The XRD reveals the presence of some interactions between LTO and PANI in the composite samples, as seen by the small changes in the peak locations of LTO in the LTO@PANI composite samples compared to those seen for the pure LTO [36].

The texture coefficient (Tc) was derived from XRD data using Eq. 1 [43] to identify the relative degree of preferred orientation among crystal planes of examined materials.

$$ {\text{T}}_{{\text{c}}} \left( {{\text{hkl}}} \right)\, = \,\frac{{\frac{{I \left( {hkl} \right)}}{{I_{o} \left( {hkl} \right)}}}}{{\frac{1}{N} \mathop \sum \nolimits_{N} \frac{{I \left( {hkl} \right)}}{{I_{o} \left( {hkl} \right)}} }} $$
(1)

where (hkl) are the Miller indices, I(hkl) is the measured intensity of X-ray reflection, Io (hkl) is the equivalent standard intensity from the JCPDS card (49–0207), and N is the number of reflections seen in the XRD pattern. The variation in Tc with 2θ for different hkl values is listed in Table 2. The more excellent Tc value refers to the abundance of grains oriented along a given hkl plane. Table 2 shows that the greatest Tc values were observed for plans (111) and (400), indicating that the crystallites were more oriented along these planes.

Table 2 Surface and structural data of samples
Full size table

Because Li4Ti5O12 exhibits a face-centered cubic structure, the lattice constant (a) is computed by using lattice space dhkl using Eq. (2) [44]

$$ d_{hkl} \, = \,a/\sqrt {\left( {h^{2} \, + \,k^{2} \, + l^{2} } \right)} $$
(2)

The results obtained are also listed in Table 2, which shows a decrease in the lattice parameter (a) of all doped materials, except that containing Mg, compared with that of pure LTO. Because Mg2+’s ionic radius (72 pm) is larger than Li+ (60 pm), Mg ions were easily incorporated into the Li sites of the Mg-doped LTO. This substitution can promote the reduction of Ti4+ to Ti3+ to balance the charge [29]. This may be the reason for the increase in the lattice constant parameter of the Mg-LTO specimen because the ionic radius of Ti3+ (67 pm) is larger than that of Ti4+ (60 pm) [41].

The average crystallite size of the investigated samples was calculated using two different equations (Scherrer-Debye Eq. (3) and Williamson-Hall Eq. (4)) [44]

$$ D\, = \,\frac{0.9 \lambda }{{\beta \cos \theta }} $$
(3)
$$ {\upbeta }_{hkl} \,{\text{cos }}\,{\uptheta }\,{ = }\,\frac{K\lambda }{D}\,{ + }\,{4}\,{\upvarepsilon }\,{\text{sin}}\,{\theta } $$
(4)

where λ is the X-ray wavelength employed, and β denotes full width of half maximum peak (FWHM). The results obtained are also reported in Table 2, which illustrates that all the samples lie on the nanometer scale and that their sizes decrease by adding dopants.

The strain (ε) induced in the samples was calculated using Eqs. (5, 6) [45]

$$ \beta_{{\text{s}}} \, = \,{4}\varepsilon \,{\text{tan }}\theta $$
(5)
$$ {\upvarepsilon }\,{ = }\,\frac{{{\upbeta }\,{\text{cos}}\,{\uptheta }}}{4} $$
(6)

The results are listed in Table 2, which shows an increase in the strain of the pure LTO due to the addition of dopants. This is explained by the fact that dopant ionic radii are lower than Ti4+ (60 pm) and Li+ (68 pm), hence replacing Ti4+ or Li+ ions with Mg2+, Mn4+, and V5+ ions will enhance the strain of LTO crystals [46]. Dopant addition increases strain because the Lattice constant decreases as compared to pure LTO. That is, the dopant causes mechanical strain on the lattice's surface, causing it to shrink.

The dislocation density (ρD), which denotes the number of defects in the prepared materials, defines the length of the dislocation line per unit volume of the crystals and is calculated by using the Eqs. (7, 8) [43]

$$ {\uprho }_{D} \,{ = }\,\frac{{1}}{{D^{2} }} $$
(7)
$$ {\uprho }_{D} \,{ = }\,\frac{{{15}\,{\upvarepsilon }}}{a\,D} $$
(8)

The results obtained are given in Table 2, which shows that the addition of dopants leads to a change in ρD value due to the dissimilarity of either ionic radii or valency charges between the substituted dopants (Mg, Mn, V) and the host elements (Li, Ti). That increases the bulk deformation of crystals [46], and in turn, the ρD value increases.

To identify the nature of the doping site in the LTO Fd-3 m lattice, Rietveld refinement of the synchrotron X-ray diffraction data for the studied samples was performed. The Rietveld patterns for pure and doped materials were shown in Fig. 1c–f and compared to the experimental patterns. The acquired outcomes from a model with Li1 atoms in the 8a (1/8, 1/8, 1/8) position, Li2/Ti atoms in the 16d (1/2, 1/2, 1/2), and O atoms in the 32e (x, x, x) position are enumerated in Table 3, which displays good values for profile (Rp), weighted profile residuals (Rwp), and goodness of fit (χ2). However, some significant structural changes occurred across the doped LTO and pure LTO samples. The oxygen coordinate (x), the lattice parameter (a), the lattice volume (V), the Li1-O bond distance, and the Li1-Li1 bond distance are all less in the doped LTO samples, although the Li2/Ti–O bond distance is bigger. These variations indicate that both the pure and doped LTO include larger tetrahedrons and smaller octahedrons. The number of accessible octahedral cavities determined the Li-insertion capacity [47], and the low value of x implied structural distortion [20]. As a result, when Li-ion diffuses in the < 111 > direction, the doped LTO electrode is anticipated to perform electrochemically better than the LTO electrode.

Table 3 Rietveld mathematical data of the pure and doped LTO samples
Full size table

The SEM micrographs of the investigated samples are given in Fig. 2a–h. The images of the pure and doped LTO, Fig. 2a–d, illustrate a cubic morphology with an average length of 0.08–0.15 μm, distorted by dopants addition. The SEM images of the composite samples, Fig. 2e–h, show core–shell structures of the pure and doped LTO as cores wrapped in polymer matrix shells that form agglomerates of 50–80 μm. The agglomerates are due to polymer matrix formation, which makes a core–shell structure beside the metal bridge with polymer skeletons that increase polymer stacking on the surface of LTO. The agglomerated particles in the composites form different domains for conducting and insulating areas, influencing the electrical characteristics as seen in our conductivity data.

Fig. 2
figure 2

SEM of a LTO, b Mg-LTO, c Mn-LTO, d V-LTO, e LTO@PANI, f Mg-LTO@PANI, g Mn-LTO@PANI, h V-LTO@PANI,

Full size image

As shown later, the electrochemical performance and dielectric studies demonstrated that binary systems offer better behaviors than pure ones. This might be connected to the kind of bonds and valence state fluctuation in doped binary materials, which can be studied using the XPS method. The results obtained are shown in Fig. 3. The scanner spectrum shows that the sample contains only the main elements: Ti, O, Mn, V, and N. The high-resolution XPS spectra of Mn (2p3/2), Ti (2p3/2), N (1 s), O (1 s), and V(2p3/2) peaks. Ti (2p3/2) bands are observed at 455.2 eV and 456.5 eV are assigned for Ti+2 (2p1/2) level, and Ti+3 (2p3/2) level, respectively, it's also observed 2 peaks at 457.7, and 458.8 which they are related to Ti+4-O (2p1/2) level, and O-Ti+4-N (2p3/2) level, respectively [48]. V (2p3/2) spectrum shows 4 peaks with binding energies of 513.7, 514.4, 516.3, and 517.8 eV which are related to V+2, V+3, V+4, and V+5, respectively [49,50,51,52,53], and referring to the presence of various oxidation states of V ion. This might be attributed to the reduction of V+5 → V+4 → V+3 → V+2 during the polymerization process of PANI. Mn (2p3/2) spectrum shows 3 peaks at 640.6, 641.7, 642, and 644.9 eV related to Mn+2, Mn+3, Mn+4, and Mn–N [54], which is attributed to reduction of Mn+4 → Mn+3 → Mn+2 during the polymerization process of PANI. These results refer to the formation of different interaction types between individual components in binary composite samples [55]. XPS of N (1 s) peaks illustrate peaks at 397.9, 398.4, 399, 399.8 400.6, and 401.8 eV referring to N–M–N, C=N, –NH, M–N+H, –NH+●–and –N+H (M is Mn, Ti, and/or V). The probability of M bridging is V and Mn due to their oxidative property which helps the formation of N–M–N, which proves that N has various bonding arrangements [24, 56, 57] [58]. O(1 s) shows peaks at 530.8 eV, 532, 532.9 eV, and 535.3 eV related to Ti–O, M–O, M–OH, and H2O respectively [48, 50, 59].

Fig. 3
figure 3

XPS of elements in LTO@PANI samples

Full size image

For further consideration of surface parameters to illustrate the electrochemical performance of the prepared samples (LTO samples and their composites), N2 adsorption–desorption isotherms are studied and revealed in Fig. 4.The isotherm of LTO samples is classified (according to IUPAC classification) as Type IV isotherms with hysteresis loops, which shows the mesoporous nature of the material. Adding a dopant doesn’t change the isotherm type, but variation happens in surface parameters like specific surface area (SSA) and pore volume (Vp). The addition of PANI in composite samples improves surface characteristics due to chemical composition branching, which increases the pores and active sites in the binary system structure. The results are listed in Table 2.

Fig. 4
figure 4

N2 Adsorption/desorption isotherm of the prepared samples

Full size image

3.2 Electrical Studies

The results of analyzing pure and doped LTO, PANI, and their composites for AC conductivity at room temperature and frequencies between 103 and 107 Hz are displayed in Fig. 5. For all samples, the AC increases almost linearly with frequencies up to 5 × 105 Hz. At this point, it rises sharply in the following order: LTO > Mn-LTO > Mg-LTO > V-LTO.

Fig. 5
figure 5

AC conductivity of a LTO samples, b LTO binary samples, EIS of c LTO samples, d LTO binary samples

Full size image

The results further showed that at all applied frequencies, the AC values of LTO were greater than those of doped LTO. This could be explained by the fact that the electronic charge transfers in the doped LTO lattice will be more diffused in the doped LTO lattice because doped LTO samples have lower lattice constants than LTO [60].

The conductivity studies further demonstrated that the PANI addition to the LTO materials causes an increase in the σac. This may be attributed to the formation of additional interfacial phases in the binary system [61], which leads to a rise in the polarization of samples in following order: LTO < Mg-LTO < V-LTO < Mn-LTO. The formation of the M–N bond during in-situ polymerization by the chemical interaction between LTO and PANI may also explain the increase in conductivity in binary systems. The new M–N bonds aid in electrical conductivity through the highly branched polymer matrix via -bond resonance [53]. As seen in the PANI composite diagram and validated by XPS data, the addition of PANI as a conducting polymer is dependent on the π–π* transition, which forms a bridge between the two polymer skeletons via a metal-N connection [63]. Furthermore, the inclusion of BaCl2 during the polymerization process causes BaSO4 seed formation, which assembles PANI on its surface and promotes the stacking of polymer layers, resulting in the facilitation of charge transfer between LTO and a polymer shell. As a result, conductivity rises. Table 4 displays the acquired results.

Table 4 Frequency effect on dielectric properties of the investigated materials
Full size table
figure b

Figure 6 depicts the frequency impact on dielectric loss (ε″), and dielectric constant (ε′) for the studied materials. In the low-frequency domain, ε′ and ε″ values rapidly decrease with rising frequency for all samples, and at higher frequencies, they nearly adopt a frequency-independent pattern. This was explained because dipole polarization decreases when the electric field reaches higher frequencies [64].

Fig. 6
figure 6

Dielectric studies of investigated samples

Full size image

In other words, interfaces with significant volume fractions in nanostructured dielectric materials contain many defects, including vacancies, dangling bonds, and micro-porosities. After an electric field is applied, space charges move, and when imperfections catch them, multiple dipole moments are created [65]. These dipole moments ease tracking changes in the electric field at lower frequencies. The ε′- and ε″- values are consequently noticeably high at low frequencies, as seen in Table 4.

The electrical characteristics of the samples under investigation were further explored using electrical impedance (EI) measurements at frequencies ranging from 103 to 107 Hz. The acquired data are represented as a Cole–Cole diagram in Fig. 5. The plots show a single semicircular form as it approaches the origin. This pattern reveals a parallel grain boundary capacitance and resistance in the materials. It's important to observe that each arc’s center is quite close to the true axis, meaning that the dispersion angle is essentially nonexistent [66, 67]. Since the semicircle centers of the composites are so close to the actual axis, it is plausible that the composite is electrically homogeneous. An overview of the EIS data that were collected for all samples is shown in Table 4. This shows how the bulk resistance increases in the following order: LTO < Mg-LTO < Mn-LTO < V-LTO. However, after combining the LTO materials with PANI, and due to the highly-branched polymer matrix structure, the Rct order of PANI composites increases in the following order: V-LTO < Mn-LTO < Mg-LTO < LTO.

3.3 Electrochemical Studies

CV is a suitable method for illustrating various capacitive mechanisms kinds. Figure 7 shows the CV of the constructed electrodes at a scanning rate of 10 mV/s. The CV plots show the electrochemical behavior of pure and doped LTO samples as well as their composites. The oxidation and reduction of active sites at the electrodes result in the redox peaks visible in the plots [68, 69].

Fig. 7
figure 7

CV of the investigated samples

Full size image

On the CV of the LTO electrode, redox peaks at − 0.08 V and − 0.2 V demonstrate Ti4+ ↔ Ti3+ process (Fig. 7). [70, 71]. There's also a plateau at − 0.7 V, which might have formed as a result of Li hopping in the LTO crystal structure [72]. Doped LTO has slightly shifted redox peaks that are equivalent to those of LTO. Mg-LTO has a slight redox peak at − 0.33 V, and − 0.37 V, which indicates the Ti+3 ↔ Ti+2 process.

The LES ↔ ES ↔ PRG transformations are responsible for the redox peaks in the CV of LTO@PANI composites [73, 74]. Due to the LES ↔ ES ↔ PRG conversions, PANI@LTO samples displayed two redox peaks at − 0.85 V and − 0.64 V, respectively [73, 74]. Besides, decreased peaks corresponding to PRG ↔ ES ↔ LES occurred at + 0.45 V and − 0.05 V. The doped LTO@PANI composite’s cyclic voltammograms, shown in Fig. 7, show the same LTO of Ti4+ ↔ Ti3+ process peaks as before with a little shift of around 0.01 V, which is explained by a change in the composite’s structure brought on by LTO and PANI interaction. Despite the presence of BaSO4 in our samples, as demonstrated by XRD data, the typical peaks for BaSO4 were not visible in the CV plots. This is because BaSO4 was employed as a seed for PANI crystallization, and its concentration in the samples is too low (< 2 wt%) to be detected in electrochemical experiments, especially when BaSO4 peaks conflict with PANI redox peaks [36]. Using CV data and Eq. (9), the specific capacitance (Csp) values of all the electrodes under investigation were determined [75], and given in Table 5.

$$ C_{sp} \, = \,\frac{1}{{m\,\nu \,{\text{V}}}}\mathop \smallint \limits_{ - V}^{ + V} IV\,\partial V $$
(9)

where I denote current, ΔV denotes applied potential, ν denotes scan rate, and m is the active material’s mass.

Table 5 Electrochemical capacitive data of the investigated materials
Full size table

To more thoroughly analyze the capacitive behavior, the b value was determined using a power law using Eq. (10) [76]

$$ {\text{I}}_{{\text{m}}} \, = \,{\text{a}}\,\nu^{{\text{b}}} $$
(10)

where Im is the highest current density in CV plots, and a as well as b are constant parameters. The power law relationship (Eq. 11), which describes normal battery behavior, states that the b value is generally equal to 1.0 for non-diffusion-controlled surface capacitive and 0.5 for diffusion-controlled redox reaction. According to the studied samples, the b values for pure, Mg–, Mn–, and V-LTO samples at Ti4+ /Ti3+ (− 0.08 V, and − 0.2 V) redox are found to be 0.50, 0.52, 0.54, and 0.55, respectively. That indicates the battery-type property [70]. On the other hand, the b values of composite systems at Ti+4/Ti+3 (~ − 0.05 V, and − 0.19 V) redox are 0.72, 0.76, 0.81, 0.84 for pure, Mg–, Mn–, V-LTO samples respectively. This indicates that the hybrid system performs the battery-supercapacitor hybrid mechanism [77].

Galvanostatic charge–discharge (GCD) is an equivalent technique for determining the Csp of electrochemical capacitors at a constant current. Consquentl, the electrochemical behavior of the electrodes at a current density of 1 A/g was examined using the GCD method. The results are presented in Fig. 8. All discharge plots displayed an internal resistance drop (IR-drop) known as the equivalent series resistance (ESR), which includes all the resistances of the cell (electrode, electrolyte, contact resistance). The specific capacitance values Csp of the electrodes were evaluated from the discharge cycles by using Eq. (11) [62].

$$ C_{sp} \, = \,\frac{I\,\Delta t}{{m\,\Delta V}} $$
(11)

where Δt is the discharge time, and ΔV is the potential range during the charge–discharge measurement. Table 5 exhibits the results and capacity enhancements for LTO samples in either single or binary composite systems in the following sequential manner: Mn-LTO > Mg-LTO > LTO > V-LTO. These are consistent with what was gained from the results of the CV. The V-LTO has a higher capacitance than LTO because of its smaller particle size and a broader electrode/electrolyte contact surface, which shortens the Li-ion route and speeds up Li-ion diffusion [62]. Furthermore, a decline in internal resistance (IR) denotes a decline in electrode resistance [61].

Fig. 8
figure 8

GCD of the investigated samples

Full size image

The supercapacitor device’s energy density (Ed) and average power density (Pd) are two important parameters. They are calculated for the composite systems that exhibit higher capacitances using Eqs. (12,13) [63]

$$ E_{d} \, = \,\frac{1}{2} C_{sp} \,\Delta V^{2} $$
(12)
$$ P_{d} \, = \,\frac{{E_{d} }}{t} $$
(13)

The results are listed in Table 5.

Long cycling stability is an important parameter for supercapacitor operations. Thus, the electrochemical stability of the examined electrodes was investigated, at a current density of 1 A/g. The results are displayed in Fig. 8 and summarized in Table 5, which reveals that the samples have excellent cycling performance, with 79.7–82.6% capacitance preserved after 3000 cycles.

Figure 9 displays the Nyquist plots for the studied electrodes over the frequency range of 10–2-105 Hz. The electrolyte resistance is shown by higher frequency Nyquist plot crossings on the Z/- axis (Rs). The charge transfer resistance (Rct) at the electrode/electrolyte interface produced one depressed semicircle to be seen at the high-frequency section [64], which is linked to the electrode’s surface characteristic. [65]. There was also a spike at the lower frequencies, indicating supercapacitor behavior [78]. The electrode's Warburg impedance (W), also known as the diffusive resistance of Li+ ions into the electrode, is indicated by the spike [24, 66]. To better understand the charge transfer mechanism at the electrolyte–electrode contact, the semicircle that appeared at higher frequencies is enlarged.

Fig. 9
figure 9

Nyquist and bode modulus of the investigated samples

Full size image

The diameter of the extrapolated semicircle on the Z/- axis, which corresponds to the charge transfer resistance Rct, is then used to compute its value at the electrolyte–electrode interface. Table 5 displays the results and shows that Rct increases in either binary composite systems or LTO materials in the following order:

V-LTO < Mn-LTO < Mg-LTO < LTO.

This may be related to the decrease of dopants’ ionic radius that facilitates the ionic diffusion of charge [70]. The main V (as V2O5), and Mn (as MnO2) doped in LTO work as self-oxidizer for PANI formation. That gives V–N bond work as a bridge to ease the charge transfer between different polymer skeletons, beside the different V+5, V+4, V+3, and V+2, beside Mn+4, Mn+3, and Mn+2 (as shown in XPS) enhance the electrical conductivity and capacitive parameters.

The time constants (τ) of the capacitors were derived from the frequency (ω) coordinated at the maximum of the semicircle using the formula in Eq. (14) [67].

$$ \tau \, = \,\frac{1}{\omega } $$
(14)

The results are listed in Table 5, which demonstrates that in τ increases in the order:

V-LTO > Mn-LTO > Mg-LTO > LTO in either LTO or their binary composite systems. The remarkable power responsiveness of the binary system is demonstrated by its small-time constants [68].

The Bode modulus of the phase angle is shown in Fig. 9. The graph implies that the phase angle (Φ) in the lower frequency (LF) region is − 65°, but after PANI composing (Φ) in LF region is − 75° confirming the capacitive properties of the electrode (Φ = 0°) for an ideal resistor and (Φ = 90°) for an ideal supercapacitor in the low-frequency region [79, 80]. Figure 9 shows that the phase angles of the doped LTO samples increase after adding PANI, referring to increasing the capacitance behavior of the composite samples than that of single electrode material.[81].

4 Conclusions

In conclusion, a solid-state reaction was used to synthesize pure Mg–Mn–, and V-LTO nanoparticles. Composite samples of the pure and doped LTO and PANI were produced in situ chemical polymerization. The ac-electrical conductivity, dielectric constant, and electrochemical characteristics of the synthesized materials in a 1 M LiNO3 electrolyte solution were investigated to assess their potential as anode materials for energy storage. The electrochemical process was examined using charge–discharge (CD) and cyclic voltammetry (CV) techniques. The difference in dopants showed a pronounced effect on the electrical (σac, ε/, ε//) and electrochemical properties (Csp) of the single and composite samples. All the tested electrodes showed pseudo-capacitance behavior. Contributions from the pseudo-capacitance of PANI and the capacitance of LTO samples were visible in the composite materials. All the combined effects contributed to the fabricated electrodes’ enhanced capacitance, energy density, and power density. The best performance was achieved for the V-LTO@PANI composite. The highest specific capacitance value of 218 F/g was attained at 1 A/g current density. The V-LTO@PANI electrode showed high cycling stability of 88.6% after 1000 cycles. At 1 A/g, a maximum energy density of 72.8 Wh/kg with a power density of 2430 W/kg was obtained. The tested materials, especially V-LTO@PANI, can be utilized as electrodes for energy storage devices because they are prepared using a simple and inexpensive synthetic method.