Packing spheres with quasi-containment conditions

Abstract

A novel sphere packing problem is introduced. A maximum number of spheres of different radii should be placed such that the spheres do not overlap and their centers fulfill a quasi-containment condition. The latter allows the spheres to lie partially outside the given cuboidal container. Moreover, specified ratios between the placed spheres of different radii must be satisfied. A corresponding mixed-integer nonlinear programming model is formulated. It enables the exact solution of small instances. For larger instances, a heuristic strategy is proposed, which relies on techniques for the generation of feasible points and the decomposition of open dimension problems. Numerical results are presented to demonstrate the viability of the approach.

1 Introduction

A standard sphere packing problem consists in allocating non-overlapping spheres completely inside a container [2]. Typical objectives are minimizing container size for a given number of spheres or maximizing the total number (or the total volume) of spheres packed in a fixed container. In this paper, we are interested in non-standard sphere packing problems, mainly for large-scale instances. Before detailing our contributions, we briefly review related applications and numerical techniques.

In biology and medicine, sphere packing problems arise in fields like spatial distributions in cell neurons and nucleus [28], filling the retinal surface by ganglion cell fields [18], or programming radio-surgical medication of tumors and retinal laser coagulation [38].

Engineering applications range from cable bundling problems and topology optimization in additive manufacturing to arranging fuel units in heat exchangers and nuclear reactors (see [1, 10, 30, 32] and references therein). In physics, sphere packing is used for analyzing structures of crystals, of nano and granular materials [5]. Packing catalysts in columns for gas absorption and distillation in chemical reactors are studied in [7]. For a good overview on circle packing in a square, with particular emphasis on algorithmic and optimization details, see [36]. Note that some further relevant references for research on circle packing are given below.

Numerical techniques for sphere packing problems rely on different approaches. Exact solution methods based on principles like branch-and-bound are of particular importance for small problem instances [15,16,17, 35]. For larger instances, combinations of heuristic and deterministic techniques are applied frequently [2, 29]. Some approaches use nonlinear optimization models and then apply exact or approximation techniques [24, 34, 35] to obtain local solutions. Other methods are based on tessellation or approximation of the container by a grid [21, 27]. Correspondingly, the sphere packing problem is approximated by a binary optimization problem to select grid nodes for the centers of the spheres [21, 22]. Many approaches like [3, 5, 9, 11,12,13, 19] combine several techniques. Eckard Specht’s website [33] provides instances of benchmark problems with known (approximate) solutions and their objective values, see also [23].

In many applications, the condition that all spheres belong completely to a given container is too strong. Our interest in relaxed containment conditions is motivated by modeling structural properties of porous media composed of different spherical particles [4, 26]. To study properties of these media, a volumetric sample (cuboidal or cylindrical container) is extracted for further investigation. However, in many cases, obtaining such a physical sample is too expensive and thus mathematical models should be used instead. Nevertheless, extracting a real sample results in cutting some spheres such that only parts of them remain in the sample. Correspondingly, our mathematical model allows spheres that are not entirely placed in the container or even have their center outside the container.

In what follows, these relaxed containment requirements are referred to as quasi-containment conditions. More specifically, for any sphere of a fixed radius, we assume that the maximum allowable distance between the center of such a sphere and the boundary of the container is given. In addition, modeling structural, physical, or chemical properties of porous media relies on the ratio of spheres with a specified radius to all spheres. Therefore, we assume that upper and lower bounds for these ratios are known.

This paper introduces a non-standard sphere packing problem. A maximum number of spheres (with different radii) should be placed in a fixed cuboidal container subject to non-overlapping, quasi-containment, and ratio conditions.

Our main contributions are:

• 1. A novel sphere packing problem, particularly with quasi-containment and ratio conditions.

• 2. A mixed-integer nonlinear program (MINLP) for the novel sphere packing problem.

• 3. A heuristic strategy for large instances of this problem to obtain good feasible solutions. This includes the development of a procedure for finding feasible points and of an open dimension optimization problem with only continuous variables.

• 4. A decomposition technique for the large-scale open dimension problem to reduce it to a sequence of easier problems.

• 5. Numerical experiments applied to

  • small instances, where exact solutions are obtained by applying the global solver BARON,

  • larger instances, where good feasible solutions are obtained by the heuristic strategy, which involves the local solver IPOPT in the decomposition approach for open dimension problems.

The paper is organized as follows. Section 2 formulates the new sphere packing problem and provides a mixed-integer nonlinear programming formulation. Then, Sect. 3 presents our heuristic strategy for the approximate solution of the sphere packing problem. Numerical results are given in Sect. 4, while Sect. 5 provides conclusions and an outlook.

2 Problem formulation

We first provide necessary preliminaries and notation in Sect. 2.1. Based on this, an abstract nonstandard packing model is given in Sect. 2.2, and a corresponding mixed-integer nonlinear program is developed in Sect. 2.3.

2.1 Preliminaries and notation

For given $L>0$, $W>0$, and $H>0$, the set

$$\begin{aligned} C:=\{(x,y,z)\in \mathbb {R}^3\mid 0\le x\le L,\,0\le y\le W,\,0\le z\le H\} \end{aligned}$$

defines a cuboidal container. Furthermore, a sphere

$$\begin{aligned} \{(x,y,z)\in \mathbb {R}^3\mid (x-\bar{x})^2+(y-\bar{y})^2+(z-\bar{z})^2\le r^2\} \end{aligned}$$

is given by its center $(\bar{x},\bar{y},\bar{z})\in \mathbb {R}^3$ and its radius $r>0$. We are dealing with N spheres indexed by $i\in \mathcal {I}:=\{1,\ldots ,N\}$. Each of these spheres has a positive radius that belongs to the set

$$\begin{aligned} \{r_k\mid k\in \mathcal {T}\}\quad \text{ with }\quad \mathcal {T}:=\{1,\ldots ,K\}, \end{aligned}$$

where $K\in \mathbb {N}$, $r_1,\ldots ,r_K$ are known with $r_1<r_2<\cdots <r_K$. We say that a sphere with radius $r_k$ is of type $k\in \mathcal {T}$. Thus, each given sphere belongs to exactly one of K types. Moreover, the number of spheres in $\mathcal {I}$ that belong to type k is denoted by $N_k\in \mathbb {N}$ so that

$$\begin{aligned} \sum _{k=1}^KN_k=N \end{aligned}$$

holds. Without loss of generality, we assume that $N_k>0$ for all $k\in \mathcal {T}$. In order to place sphere $i\in \mathcal {I}$, its center $u_i=(x_i,y_i,z_i)\in \mathbb {R}^3$ is variable and we use

$$\begin{aligned} S_i(u_i) \end{aligned}$$

for denoting this sphere. Since each sphere $i\in \mathcal {I}$ has a unique type $k\in \mathcal {T}$, there is a function $r:\mathcal {I}\rightarrow \mathcal {T}$ so that r(i) yields the type k of sphere i. A condition on the intersection of a sphere of type k with the container C will later be described by the predefined parameters

$$\begin{aligned} \varepsilon _k\in [-r_k,r_k]\quad \text{ for } k\in \mathcal {T}\end{aligned}$$

(1)

and by means of the set

$$\begin{aligned} C(\varepsilon _k):=\{(x,y,z)\in \mathbb {R}^3\mid -\varepsilon _k\le x\le L+\varepsilon _k,\\ -\varepsilon _k\le y\le W+\varepsilon _k,-\varepsilon _k\le z\le H+\varepsilon _k\}. \end{aligned}$$

Note that $C(\varepsilon _{k_1})$ might be different from $C(\varepsilon _{k_2})$ for $k_1,k_2\in \mathcal {T}$ with $k_1\ne k_2$. Finally, throughout the paper, |A| denotes the cardinality for any finite set A.

2.2 Abstract model

Let I denote a subset of spheres belonging to the set $\mathcal {I}$ of all spheres. Then, any ${\varvec{u}}_I:=(u_i)_{i\in I}\in \mathbb {R}^{3|I|}$ is called placement, and feasible placement, if the placement conditions (2)–(4) below are satisfied. These conditions are formulated for $I\ne \varnothing$. However, by definition, we say that $I=\varnothing$ satisfies the placement conditions as well.

Non-overlapping conditions

$$\begin{aligned} \mathop {\mathrm {\text{ int }}}\limits S_i(u_i)\cap \mathop {\mathrm {\text{ int }}}\limits S_j(u_j)=\varnothing \quad \text{ for } i,j\in I \text{ with } i<j, \end{aligned}$$

(2)

where $\mathop {\mathrm {\text{ int }}}\limits$ is used to denote the interior of a set. Clearly, for each pair (i, j) with $i<j$, this condition provides a restriction on the centers $u_i$ and $u_j$ of the corresponding spheres.

Quasi-containment conditions

$$\begin{aligned} u_i\in C(\varepsilon _{r(i)})\quad \text{ for } i\in I. \end{aligned}$$

(3)

This condition means that the center of sphere $i\in I$ lies in the set $C(\varepsilon _{r(i)})$. If, for all $k\in \mathcal {T}$, $\varepsilon _k$ is replaced by $-r_k$, (3) are just called containment conditions, which then require that all spheres with $i\in I$ completely belong to the container C.

Before giving the final set of placement conditions, let $\tau _k\in \mathbb {Q}\cap (0,1]$ for $k\in \mathcal T$ be given so that

$$\begin{aligned} \sum _{k\in \mathcal T}\tau _k=1. \end{aligned}$$

The value $\tau _k$ describes the desired proportion of spheres of type $k\in \mathcal {T}$ that shall appear in a feasible placement of spheres. The predefined parameters $\underline{\tau }_k$ and $\overline{\tau }_k$ with

$$\begin{aligned} 0<\underline{\tau }_k\le \tau _k\le \overline{\tau }_k\quad \text{ for } k\in \mathcal {T}\end{aligned}$$

serve us to allow a certain deviation from the proportion $\tau _k$. Now, we are able to provide the

Ratio conditions

$$\begin{aligned} \underline{\tau }_k\le \frac{\left| \{i\in I\mid r(i)=k\}\right| }{\left| I\right| }\le \overline{\tau }_k\quad \text{ for } k\in \mathcal {T}. \end{aligned}$$

(4)

For a set I arising from a feasible placement ${\varvec{u}}_I$, the latter means that the ratio between the number of spheres of type k in I and the number of all spheres in I belongs to the interval $[\underline{\tau }_k,\overline{\tau }_k]$. We implicitly assume that there are enough spheres of each type $k\in \mathcal {T}$ so that the ratio conditions (4) can be satisfied for some index set I. In applications, we are often faced with many more spheres of all types so that this assumption is not a problem.

The optimization goal is to find a feasible placement ${\varvec{u}}_I$ with as many as possible spheres, i.e., where $I\subseteq \mathcal {I}$ has maximum cardinality.

2.3 Formulation as mixed-integer nonlinear program

To derive a MINLP from the abstract model in the previous section, we use the decision variables

$$\begin{aligned} {\varvec{u}}:=(u_1,\ldots ,u_N)\in \mathbb {R}^{3N}, \end{aligned}$$

where $u_i=(x_i,y_i,z_i)\in \mathbb {R}^3$ specifies the center of sphere $i\in \mathcal {I}$. To satisfy the quasi-containment conditions (3), we introduce the function $\varphi _i:\mathbb {R}^3\rightarrow \mathbb {R}$ by

$$\begin{aligned} \varphi _i(u_i):=\min \{x_i,y_i,z_i,L-x_i,W-y_i,H-z_i\}+\varepsilon _{r(i)} \end{aligned}$$

(5)

for $i\in \mathcal {I}$. Then, it is easy to see that $\varphi _i(u_i)\ge 0$ if and only if $u_i\in C(\varepsilon _{r(i)})$. The condition $\varphi _i(u_i)\ge 0$ can be replaced by linear box constraints

$$\begin{aligned} \begin{array}{lclcllclcllclcl} -\varepsilon _{\kappa }\le & {} x_i\le & {} L+\varepsilon _{\kappa },\quad -\varepsilon _{\kappa }\le & {} y_i\le & {} W+\varepsilon _{\kappa },\quad -\varepsilon _{\kappa }\le & {} z_i\le & {} H+\varepsilon _{\kappa } \end{array} \end{aligned}$$

(6)

with $\kappa :=r(i)$. The non-overlapping conditions (2) are modeled by means of functions $\psi _{ij}:\mathbb {R}^3\times \mathbb {R}^3\rightarrow \mathbb {R}$ with

$$\begin{aligned} \psi _{ij}(u,v):=\Vert u-v\Vert ^2-(r(i)+r(j))^2 \end{aligned}$$

(7)

for $(i,j)\in \mathcal {I}\times \mathcal {I}$. Then, $\psi _{ij}(u,v)\ge 0$ is an equivalent formulation for non-overlapping of the spheres $S_i(u)$ and $S_j(v)$.

In addition to ${\varvec{u}}$, we introduce auxiliary binary variables $b_i\in \mathbb {B}:=\{0,1\}$ for $i\in \mathcal {I}$. With ${\varvec{b}}:=(b_1,\ldots ,b_N)\in \mathbb {B}^N$, we can now express the packing problem as

$$\begin{aligned} \max _{{\varvec{u}},{\varvec{b}}}{} & {} \sum _{i=1}^N b_i \end{aligned}$$

(8)

$$\begin{aligned} \text{ subject } \text{ to }\nonumber \\ b_i\varphi _i(u_i)&\ge 0&\text{ for } i\in \mathcal {I}, \end{aligned}$$

(9)

$$\begin{aligned} b_i b_j\psi _{ij}(u_i,u_j)&\ge 0&\text{ for } (i,j)\in \mathcal {I}\times \mathcal {I} \text{ with } i<j, \end{aligned}$$

(10)

$$\begin{aligned} \underline{\tau }_k\sum _{i=1}^N b_i\le \sum _{i=1}^{N_k}b_i\le & {} \overline{\tau }_k\sum _{i=1}^Nb_i\quad \text{ for } k\in \mathcal {T}, \end{aligned}$$

(11)

$$\begin{aligned} {\varvec{u}}\in \mathbb {R}^{3N},\,{\varvec{b}}\in \mathbb {B}^N. \end{aligned}$$

(12)

For a feasible point $({\varvec{u}},{\varvec{b}})$ of the model (8)–(12) with ${\varvec{b}}\ne 0$, the resulting placement ${\varvec{u}}_I$ with $I:=\{i\in \mathcal I\mid b_i=1\}$ is feasible, i.e.,

• the non-overlapping conditions (2) hold due to (10),

• the quasi-containment conditions (3) are satisfied because of (9), and

• the ratio conditions (4) are valid thanks to (11).

Vice versa, a feasible placement ${\varvec{u}}_I$ with $I\ne \varnothing$ provides a feasible solution $({\varvec{u}},{\varvec{b}})$ of problem (8)–(12) with ${\varvec{u}}=({\varvec{u}}_I,{\varvec{u}}_{\mathcal I{\setminus } I})$, $b_i=1$ for $i\in I$, and $b_i=0$ for $i\in \mathcal I{\setminus } I$, where ${\varvec{u}}_{\mathcal I{\setminus } I}$ can be chosen freely.

To maximize the objective function in (8), as many as possible binary variables $b_i\,(i\in \mathcal I)$ must be equal to 1. Equivalently, this means that the cardinality of I is maximized. Also note that, due to the constraints (9) and (10), $\varphi _i(u_i)<0$ implies $b_i=0$ for any $i\in \mathcal I$, and $\psi _{ij}(u_i,u_j)<0$ yields $b_i b_j=0$ for any $i,j\in \mathcal I$ with $i<j$.

The model (8)–(12) is a mixed-integer nonlinear program (MINLP). The nonlinearity of the model is caused by the N inequalities in (9) and the $N(N-1)/2$ inequalities in (10). The number of the latter grows quadratically with N. Hence, in general MINLP solvers have no chance for providing an exact solution of the model for large values of N. Therefore, we present a heuristic approach in the next section.

3 The heuristic

Below, we suggest a heuristic strategy to find a feasible solution of problem (8)–(12) with the aim of maximizing the objective in (8). To begin with, let us provide a rough description of the strategy.

A key idea is to replace MINLP (8)–(12) by a sequence of continuous open dimension (OD) problems. In each of these problems, the fixed height H, formerly used to define $C(\varepsilon _k)$, is replaced by the variable h. Moreover, for any OD problem, it is assumed that two feasible placements ${\varvec{u}}_I$ and ${\varvec{u}}_J$ are known in advance with

$$\begin{aligned} I\subset J\subseteq \mathcal {I}\quad \text{ and }\quad {\varvec{u}}_J=({\varvec{u}}_I,{\varvec{u}}_{J\setminus I}). \end{aligned}$$

(13)

The OD problem then aims at minimizing h and at finding a feasible placement ${\varvec{v}}_J^*$ with ${\varvec{v}}_I^*=(v_i^*)_{i\in I}={\varvec{u}}_I$, i.e., the centers associated to the set I of spheres are kept, but the centers of the spheres belonging to $J\setminus I$ are variable and used to minimize h. Accordingly, the OD$({\varvec{u}}_I,{\varvec{u}}_J)$ problem is shown by (14)–(17) below. If the space occupied by the feasible placement ${\varvec{v}}_J^*$ is sufficiently smaller than the space needed for ${\varvec{u}}_J$, Algorithm 2 in Sect. 3.2 is used to place further spheres with indices in $\mathcal {I}\setminus J$, again achieving a feasible placement. The two parts (Algorithm 2 and treating an OD problem) are used successively as often as possible until no further sphere can be placed. Our heuristic strategy (Algorithm 1) is described in more detail in Sect. 3.1.

The OD$({\varvec{u}}_I,{\varvec{u}}_J)$ problem for feasible placements satisfying (13) is the nonlinear optimization problem

$$\begin{aligned} \min _{{\varvec{v}}_J,h}{} & {} h \end{aligned}$$

(14)

$$\begin{aligned} \text{ subject } \text{ to }\nonumber \\ \hat{\varphi }_i(v_i, h)\ge & {} 0\quad \text{ for } i\in J\setminus I, \end{aligned}$$

(15)

$$\begin{aligned} \psi _{ij}(v_i,v_j)\ge & {} 0\quad \text{ for } i,j\in J\times J \text{ with } i<j, \end{aligned}$$

(16)

$$\begin{aligned} {\varvec{v}}_I= & {} {\varvec{u}}_I, \end{aligned}$$

(17)

where $\psi _{ij}$ is given by (7) and $\hat{\varphi }_i:\mathbb {R}^3\times \mathbb {R}\rightarrow \mathbb {R}$ by

$$\begin{aligned} \hat{\varphi }_i(u,h):=\min \{x,y,z,L-x,W-y,h-z\}+\varepsilon _{r(i)}. \end{aligned}$$

The latter is similar to the definition of $\varphi _i$ in (5), except that the fixed height H is now replaced by the variable h. Like the replacement of $\varphi _i(u)\ge 0$ by (6), it is possible to write $\hat{\varphi }_i(u,h)\ge 0$ equivalently as a system of linear inequalities. Note that any feasible point of the OD problem (14)–(17) satisfies the ratio conditions (4) automatically since the spheres in J already satisfy (4).

3.1 The heuristic strategy

Algorithm 1 THE HEURISTIC STRATEGY
Input	Index set $\mathcal I$.
Step A	Set $I:=\varnothing$ and ${\varvec{u}}_I:=[\,]$ (denoting the empty vector).
Step B	Employ Algorithm FEASIBLE PLACEMENT (Algorithm 2) with
	input ${\varvec{u}}_I$ to construct a feasible placement ${\varvec{u}}_J$ so that
	$I\subseteq J\subseteq \mathcal {I}$ and ${\varvec{u}}_J=({\varvec{u}}_I,{\varvec{u}}_{J\setminus I})$.
Step C	If $J=I$, set ${\varvec{u}}_I^*:={\varvec{u}}_I$ and stop.
Step D	Employ Algorithm Decomposition Based Optimization
	(Algorithm 5) with input ${\varvec{u}}_I$ and ${\varvec{u}}_J$ to determine a feasible
	solution $({\varvec{v}}_J^*,h^*)$ of problem OD$({\varvec{u}}_I,{\varvec{u}}_J)$.
	Set $I:=J$, ${\varvec{u}}_I:={\varvec{v}}_J^*$, and go to Step B.
Output	Feasible placement ${\varvec{u}}_I^*$.

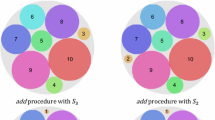
The strategy for finding a good feasible point of problem (8)–(12) involves the main steps shown in Algorithm 1. Before providing the details for Steps B and D in Sects. 3.2 and 3.3, we demonstrate the principle idea of the heuristic strategy by means of Fig. 1. Part (a) of this figure shows a feasible placement of a certain set of spheres obtained by Step B. Then, Step D tries to reduce the height occupied by the spheres from this set within in the container, see part (b) of the figure. The free space gained is now filled by further spheres within Step B so that the resulting placement is again feasible, see part (c). These further spheres are now compressed in Step D with the aim to obtain some free space in the container, see part (d) of Fig. 1. Steps B and D are then repeated as long as possible, i.e., as long as the free space obtained in Step D allows to place at least one additional sphere in a feasible way. Otherwise, the strategy is stopped in Step C with a final feasible placement ${\varvec{u}}_I^*$ (cf. part (e) of Fig. 1).

Fig. 1

Demonstration of the heuristic strategy (Algorithm 1)

3.2 Construction of a feasible placement

Step B of the heuristic strategy (Algorithm 1) aims at constructing a feasible placement ${\varvec{u}}_J$ of spheres with an index set J, where J is assumed to contain the spheres of an already found feasible placement ${\varvec{u}}_I$; at the beginning, I is empty. To construct the feasible placement ${\varvec{u}}_J$, we first introduce the set

$$\begin{aligned} \mathcal F({\varvec{u}}_I,\ell ):=\{u\in \mathbb {R}^3\mid \varphi _\ell (u)\ge 0,\,\psi _{i\ell }(u_i,u)\ge 0 \text{ for } \text{ all } i\in I\} \end{aligned}$$

(18)

for any $\ell \in \mathcal I\setminus I$. Since ${\varvec{u}}_I$ is a feasible placement, it can be seen that $u\in \mathcal F({\varvec{u}}_I,\ell )$ means that the placement ${\varvec{u}}_{I\cup \{\ell \}}$ satisfies the non-overlapping conditions (2), the quasi-containment conditions (3), but not necessarily the ratio conditions (4).

Hence, to determine a feasible placement ${\varvec{u}}_J$ with $I\subset J$, we first choose $\varDelta J$ with $\varDelta J\subseteq \mathcal I{\setminus } I$ so that $I\cup \varDelta J$ satisfies the ratio conditions (4) and then try to place the spheres with indices in $\varDelta J$ so that $I\cup \varDelta J$ also satisfies the non-overlapping and the quasi-containment conditions. As long as possible, the resulting feasible placement is extended to larger feasible placements by an analogous technique. The overall procedure to generate a (large) feasible placement ${\varvec{u}}_J$ is described in Algorithm 2.

Algorithm 2 FEASIBLE PLACEMENT
Input	A feasible placement ${\varvec{u}}_I$.
Step 1	Set $J:=I$, $J_0:=J$, and $signal:=1$.
Step 2	If $signal=3$, stop.
Step 3	Determine an index set $\varDelta J$ by Algorithm SELECT INDEX SET
	(Algorithm 3) with the input parameters J and signal.
Step 4	If $\varDelta J=\varnothing$, set $signal:=signal+1$ and go to Step 2.
Step 5	Choose $\ell \in \varDelta J$ randomly.
	Compute $u_\ell =(x_\ell ,y_\ell ,z_\ell )$ by Algorithm TOP-DOWN BISECTION
	(Algorithm 4) depending on the input parameters ${\varvec{u}}_J$ and $\ell$.
Step 6	If $z_\ell =\infty$, set $J:=J_0$, $signal:=signal+1$, and go to Step 2.
Step 7	Set $J:=J\cup \{\ell \}$ and $\varDelta J:=\varDelta J\setminus \{\ell \}$.
Step 8	If $\varDelta J=\varnothing$, set $J_0:=J$ and go to Step 3.
	Otherwise, go to Step 5.
Output	J so that $I\subseteq J\subseteq \mathcal I$ and ${\varvec{u}}_J$ is feasible.

The Algorithm SELECT INDEX SET (Algorithm 3) used in Step 3 of Algorithm 2 is responsible for fulfilling the ratio conditions (4). More in detail, it generates an index set $\varDelta J$ so that $J\cup \varDelta J$ satisfies (4) with $I:=J\cup \varDelta J$. Since the proportions $\tau _k$ ($k\in \mathcal T=\{1,\ldots ,K\}$) are rational numbers in the interval (0, 1], we can easily find the least possible $q\in \mathbb {N}$ and $p_k\in \mathbb {N}$ ($k\in \mathcal T$) so that

$$\begin{aligned} \tau _k=\frac{p_k}{q}\quad (k\in \mathcal T) \end{aligned}$$

is valid. Algorithm 3 has been developed mainly based on this observation. Another important question for the design of Algorithm 2 is how the spheres in $\varDelta J$ provided by Algorithm 3 can be placed satisfying not only the ratio conditions (4), but also the remaining feasibility conditions (2) and (3). This is the task of Algorithm TOP-DOWN BISECTION (Algorithm 4). Other (more sophisticated) realizations of Algorithms 2–4 are possible, but will not be considered here.

Algorithm 3 SELECT INDEX SET
Input:	Index set J and $signal\in \{1,2\}$.
Step 1.	Set $\varDelta J:=\varnothing$.
Step 2.	If $signal=1$, set
	$\mathcal P_k:=\{\mathcal P\subseteq \mathcal I\setminus J\mid |\mathcal P|=p_k,\,r(i)=k \text{ for } i\in \mathcal P\}$ for $k\in \mathcal T$.
	If $\mathcal P_k\ne \varnothing$ for $k\in \mathcal T$, choose $J_k\in \mathcal P_k$ for $k\in \mathcal T$.
	Otherwise, stop.
	Set $\varDelta J:=\bigcup \limits _{k\in \mathcal T}J_k$ and stop.
Step 3.	If $signal=2$, set $t_k:=|\{i\in J\mid r(i)=k\}|$ for $k\in \mathcal T$.
	If $\mathcal T\ne \{k\in \mathcal T\mid \underline{\tau }_k(|J|+1)\le t_k,\,t_k+1\le \overline{\tau }_k(|J|+1)\}$, stop.
	Set $T:=\{k\in \mathcal T\mid j\in \mathcal I\setminus J \text{ exists } \text{ with } r(j)=k\}$.
	If $T=\varnothing$, stop.
	For the minimal $k_*\in T$ determine $j_*\in \mathcal I\setminus J$ with $r(j_*)=k_*$.
	Set $\varDelta J:=\{j_*\}$ and stop.
Output:	$\varDelta J$ so that the ratio conditions (4) are valid for $I:=J\cup \varDelta J$.

Now, we provide a description of Algorithm 4. Let a sphere $\ell \in \mathcal I\setminus J$ and a placement ${\varvec{u}}_J$ being feasible with respect to the non-overlapping and the quasi-containment conditions (2) and (3) be given. Then, the purpose of Algorithm 4 is to generate a placement ${\varvec{u}}_{J\cup \{\ell \}}$ that is again feasible with respect to (2) and (3). To this end, Algorithm 4 intends to place the sphere $\ell$ with center $u_\ell =(x_\ell ,y_\ell ,z_\ell )\in \mathcal F({\varvec{u}}_J,\ell )$ quite low with respect to the z-coordinate. According to (18), $u_\ell \in \mathcal F({\varvec{u}}_J,\ell )$ means that the sphere $\ell$ satisfies the quasi-containment condition and does not overlap any sphere in J. To generate a small $z_\ell$, we mainly use a bisection technique for the value of the z-coordinate. Moreover, we do this for $M\in \mathbb {N}$ spheres with randomly generated values for the x- and y-coordinates.

Algorithm 4 TOP-DOWN BISECTION
Input	A placement ${\varvec{u}}_J$ satisfying (2), (3) for $I:=J$ and $\ell \in \mathcal I\setminus J$.
Step 1	Choose $M\in \mathbb {N}$ and $0<\delta <1$.
	Set $z_*:=\infty$, $m:=1$, $k:=r(\ell )$, $a:=-\varepsilon _k$, and $b:=H+\varepsilon _k$.
Step 2	Choose $x_m\in [-\varepsilon _k, L+\varepsilon _k]$ and $y_m\in [-\varepsilon _k, W+\varepsilon _k]$ randomly.
	Set $u:=(x_m,y_m,\infty )$.
Step 3	If $(x_m,y_m,a)\in \mathcal F({\varvec{u}}_J,\ell )$, set $u_\ell =(x_\ell ,y_\ell ,z_\ell ):=(x_m,y_m,a)$
	and stop.
	If $(x_m,y_m,b)\in \mathcal F({\varvec{u}}_J,\ell )$, set $z_m:=b$.
	Otherwise, if $(x_m,y_m,b)\notin \mathcal F({\varvec{u}}_J,\ell )$, set $u_\ell :=u$ and
	go to Step 9.
Step 4	Set $z:=\frac{1}{2}(a+b)$ and $u:=(x_m,y_m,z)$.
Step 5	If $u\in \mathcal F({\varvec{u}}_J,\ell )$, set $b:=z$ and $z_m:=b$.
	Otherwise, if $u\notin \mathcal F({\varvec{u}}_J,\ell )$, set $a:=z$.
Step 6	If $b-a\ge \delta$, go to Step 4.
Step 7	Set $u:=(x_m,y_m,z_m)$.
Step 8	If $z_m<z_*$, set $u_\ell :=u$ and $z_*:=z_m$.
Step 9	If $m<M$, set $m:=m+1$ and go to Step 2. Otherwise, stop.
Output	$u_\ell$ so that ${\varvec{u}}_{J\cup \{\ell \}}$ either satisfies (2) and (3) or $z_\ell =\infty$.

3.3 A decomposition algorithm for the OD problem

Algorithm 5 Decomposition Based Optimization
Input	Feasible placements ${\varvec{u}}_I$, ${\varvec{u}}_J$ with $I\subset J\subseteq \mathcal I$.
Step 1	Set ${\varvec{w}}_J:={\varvec{u}}_J$ and $\rho :=\max \{r_k\mid k\in \mathcal T\}$.
Step 2	Determine $({\varvec{v}}_J^*,h^*)$ by applying a local minimization algorithm
	to problem DOD$({\varvec{u}}_I,{\varvec{w}}_J,\rho )$.
Step 3	If ${\varvec{v}}_{J\setminus I}^*$ is an interior point of ${\varvec{B}}({\varvec{u}}_I,{\varvec{w}}_J,\rho )$, stop.
Step 4	Set $\rho :=\Vert {\varvec{w}}_{J\setminus I}-{\varvec{v}}_{J\setminus I}^*\Vert _\infty$, ${\varvec{w}}_J:={\varvec{v}}_J^*$, and go to Step 2.
Output	Feasible solution $({\varvec{v}}_J^*,h^*)$ of problem OD$({\varvec{u}}_I,{\varvec{u}}_J)$.

Let us consider a fixed feasible placement ${\varvec{u}}_I$ and some other feasible placement ${\varvec{u}}_J$ with $I\subset J\subseteq \mathcal I$. Our aim is to optimize the variables $u_i$ with $i\in J\setminus I$ so that the height h of the feasible placement J is reduced. The best for this aim would be to solve the OD problem (14)–(17). Since this problem is of high complexity, a global or even a local solution cannot be determined in a reasonable time if the sets I and J are not particularly small. Therefore, we suggest a decomposition technique to at least find a good feasible solution of the OD problem (14)–(17). This technique replaces the OD problem by a sequence of decomposed OD problems. The latter problems are denoted by DOD$({\varvec{u}}_I,{\varvec{w}}_J,\rho )$ and read as follows.

$$\begin{aligned} \min _{{\varvec{v}}_J,h}{} & {} h \end{aligned}$$

(19)

$$\begin{aligned} \text{ subject } \text{ to }\nonumber \\ \hat{\varphi }_i(v_i, h)\ge & {} 0\quad \text{ for } i\in J\setminus I, \end{aligned}$$

(20)

$$\begin{aligned} \psi _{ij}(v_i,v_j)\ge & {} 0\quad \text{ for } (i,j)\in \varSigma ({\varvec{u}}_I,{\varvec{w}}_J,\rho ), \end{aligned}$$

(21)

$$\begin{aligned} {\varvec{v}}_I= & {} {\varvec{u}}_I \end{aligned}$$

(22)

$$\begin{aligned} {\varvec{v}}_{J\setminus I}\in & {} {\varvec{B}}({\varvec{u}}_I,{\varvec{w}}_J,\rho ), \end{aligned}$$

(23)

where $\rho >0$ and the feasible placements ${\varvec{u}}_I\in \mathbb {R}^{3|I|}$, ${\varvec{w}}_J\in \mathbb {R}^{3|J|}$ with $I\subset J\subseteq \mathcal I$ are given. Moreover, ${\varvec{B}}({\varvec{u}}_I,{\varvec{w}}_J,\rho )$ and $\varSigma ({\varvec{u}}_I,{\varvec{w}}_J,\rho )$ are defined by

$$\begin{aligned} {\varvec{B}}({\varvec{u}}_I,{\varvec{w}}_J,\rho ):=\left\{ {\varvec{v}}_{J\setminus I}\in \mathbb {R}^{3|J\setminus I|}\mid \Vert {\varvec{v}}_{J\setminus I}-{\varvec{w}}_{J\setminus I}\Vert _\infty \le \rho \right\} , \\ \varSigma ({\varvec{u}}_I,{\varvec{w}}_J,\rho ):=\varSigma _1({\varvec{u}}_I,{\varvec{w}}_J,\rho )\cup \varSigma _2({\varvec{u}}_I,{\varvec{w}}_J,\rho ) \end{aligned}$$

with

$$\begin{aligned} \begin{array}{lcl} \varSigma _1({\varvec{u}}_I,{\varvec{w}}_J,\rho )&{}:=&{}\left\{ (i,j)\in I\times (J\setminus I)\mid \Vert u_i-w_j\Vert -(r(i)+r(j))\le \sqrt{3}\rho \right\} ,\\ \varSigma _2({\varvec{u}}_I,{\varvec{w}}_J,\rho )&{}:=&{}\bigg \{(i,j)\in (J\setminus I)\times (J\setminus I)\mid i<j,\\ &{}&{}\,\Vert w_i-w_j\Vert -(r(i)+r(j))\le \sqrt{3}\rho \bigg \}. \end{array} \end{aligned}$$

If compared to the problem OD$({\varvec{u}}_I,{\varvec{w}}_J)$ in (14)–(17), problem DOD$({\varvec{u}}_I,{\varvec{w}}_J,\rho )$ in (19)–(23) reduces the number of non-overlapping conditions, often drastically. In (21), non-overlapping is required only for pairs (i, j) of spheres with $(i,j)\in \varSigma ({\varvec{u}}_I,{\varvec{w}}_J,\rho )$, i.e., for spheres i, j that are quite close to each other. This indeed decomposes the constraints of OD$({\varvec{u}}_I,{\varvec{w}}_J)$. Nevertheless, to guarantee that all existing non-overlapping constraints (16) in the original OD problem are satisfied for any ${\varvec{v}}_J^*$ constructed in Step 2 of Algorithm 5, each variable $v_i$ with $i\in J\setminus I$ has to stay in a box centered at the vector $w_i$ (see the definition of ${\varvec{B}}({\varvec{u}}_I,{\varvec{w}}_J,\rho )$). In this way, overlapping is excluded not only for a local minimizer ${\varvec{v}}_J^*$, but for any feasible point of DOD$({\varvec{u}}_I,{\varvec{w}}_J,\rho )$. This is important for cases, when Step 2 of Algorithm 5 does not provide a local minimizer of problem DOD$({\varvec{u}}_I,{\varvec{w}}_J,\rho )$. The stopping rule in Step 3 can be replaced by other criteria that indicate that the expected improvement of using a further iteration of Algorithm 5 is small; for example one may stop if the difference of two subsequent objective function values $h^*$ generated in Step 2 is less than a predefined parameter. Regardless of this, in our experiments, where IPOPT was applied to the DOD problems, always an interior point of ${\varvec{B}}({\varvec{u}}_I,{\varvec{w}}_J,\rho )$ was generated.

4 Computational results

Two groups of instances are considered. The first contains smaller instances. Almost all of them could be solved exactly based on the MINLP (8)–(12) and the solver BARON. For the second group of larger instances, good feasible solutions were obtained by our heuristic strategy (Algorithm 1), see Sect. 4.2.

4.1 Results for small instances

For several small instances given below, we have applied BARON [20, 31, 37] to determine a global solution of the corresponding model (8)–(12). This has been done by means of the NEOS server [25] together with AMPL [8]. The input data of the instances are described in Tables 1, 2, 3, 4, 5 and 6. Moreover, these tables also provide the following data associated with the solution $({\varvec{u}}^*,{\varvec{b}}^*)$ found:

• $N^*$ denotes the optimal value of the objective (8), i.e., $N^*:=\sum \limits _{i=1}^N b_i^*$,

• $n_k^*$ with $k\in \{1,\ldots ,K\}$ is the number of spheres of type k used in the solution, i.e., $\sum \limits _{k=1}^Kn_k^*=N^*$,

• $\tau _k^*:=\frac{n_k^*}{N^*}$ for $k\in \{1,\ldots ,K\}$ satisfies $\underline{\tau }_k\le \tau _k^*\le \overline{\tau }_k$, i.e., shows in which way the ratio conditions (4) are satisfied.

• $t^*$ is the run time. Note that these times may be affected by unknown influences within the NEOS system (like other jobs running in parallel). Therefore, the run time shown are rounded up to full seconds and should only be used as a rough orientation.

Example 1

Table 1 Data for Examples 1(a)–1(c)

Interestingly, if we use $\varepsilon _1=-1.0$ and $\varepsilon _2=0.0$ instead of the values $\varepsilon _1=\varepsilon _2=0$ in Table 1, BARON found global solutions for cases (a) and (b) of Example 1. However, for case (c), no solution could be found within 8 h, which is the maximal time NEOS allows for running a single instance. The optimal solutions for Examples 1 (a)–(c) provided by BARON are shown in Fig. 2.

Fig. 2

Optimal placement of spheres for Examples 1(a)–1(c)

Example 2

The input data for Example 2(a) provided in Table 2 use a negative value for $\varepsilon _1$ so that the centers of the spheres of type $k=1$ with radius $r_1=2$ lie in the interior of the container. In contrast to this, the centers of all spheres of Example 2(b) are allowed to lie in the container including its boundary. Nevertheless, the optimal values of both examples do not differ. For the corresponding pictures see Fig. 3.

Table 2 Data for Examples 2(a) and 2(b)

Fig. 3

Optimal placements for Examples 2(a) and 2(b)

Example 3

The input data for Examples 3(a) and 3(b) only differ with respect to the given ratios for $\underline{\tau }_i$ and $\overline{\tau }_i$, see Table 3. For Example 3(b), $\underline{\tau }_i=\overline{\tau }_i$ is required for all i. This results in a smaller optimal number of spheres that could be placed in contrast to Example 3(a). For the pictures, see Fig. 4.

Table 3 Data for Examples 3(a) and 3(b)

Fig. 4

Optimal placements for Example 3(a) and Example 3(b)

Example 4

In this example, we have four types of spheres ($K=4$). Moreover, the lower and upper bounds for the ratios of each sphere type are equal, i.e., $\underline{\tau }_i=\overline{\tau }_i$ for $i=1,2,3,4$. For the input data and the results of this example, see Table 4 and Fig. 5a.

Table 4 Data for Example 4

Fig. 5

a An optimal placement for Example 4, b a feasible placement for Example 5, c an optimal placement for Example 6

Example 5

In this example, BARON (via the NEOS server) computed a feasible placement and the time limit of 8 h was exhausted. It remains unclear whether this placement is already optimal. The obtained upper bound for the objective is 119, whereas the feasible placement contains $N'=112$ spheres. Instead of indicating several values of an optimal placement with $^*$ (as we did in the Tables 1, 2, 3, 4), we now use the symbol $'$ for those values of the feasible placement of Example 5, see Table 5. Moreover, a picture of the feasible placement is given in part (b) of Fig. 5.

Table 5 Data for Example 5

Example 6

This example uses $\varepsilon _i=-r_i$ for all sphere types $i\in \mathcal T$ so that all spheres of any feasible placement must be completely contained in the container. We refer to Table 6 for the input data and the optimal solution obtained by BARON. In addition, see part (c) of Fig. 5 for a picture of an optimal placement.

Table 6 Data for Example 6

We observe from part (c) of Example 1 that a modification of the input parameters may cause problems in solving the instance by BARON under the time restriction in the NEOS server, see also Example 5.

4.2 Results obtained by the heuristic

Below, some larger instances are provided to test our heuristic described in Sect. 3. A corresponding implementation is run on an Intel^® Core™ i3-6100T processor.

For obtaining a local minimizer (or a good feasible solution) of the nonlinear programming subproblem in Step 2 of Algorithm Decomposition Based Optimization (Algorithm 5), the solver IPOPT [14] was employed. For the description of the results, we use the notation $N',n'_k,\tau '_k$ for the final feasible point obtained by the heuristic strategy (Algorithm 1) in analogy to $N^*,n_k^*,\tau _k^*$ as introduced in Sect. 4.1 above for the exact solution found by BARON. Moreover, we also report about the number $N_0$ of spheres that were placed by the first run of Algorithm FEASIBILE PLACEMENT (Algorithm 2) in Step B of Algorithm 1, i.e., before IPOPT is called the first time. Finally, the time needed for computing the first feasible solution with $N_0$ spheres, the total run time and the total number of IPOPT runs are reported in the examples below. A picture for the final feasible solution is given in Fig. 6 for all larger examples.

Example 7

Here, we use a container with $L\times W\times H=7\times 7\times 30$. Our aim is to place as many as possible of the given $N=600$ spheres. We have $K=6$ sphere types with $n_1=\cdots =n_6=100$,

$$\begin{aligned} r_1=1,\,r_2=0.95,\,r_3=0.85,\,r_4=0.8,\,r_5=0.7,\,r_6=0.6, \end{aligned}$$

and

$$\begin{aligned} \varepsilon _k=0,\quad \underline{\tau }_k=\overline{\tau }_k=\frac{1}{6}\quad \text{ for } k=1,\ldots ,6. \end{aligned}$$

Within about 11 min including 17 runs of IPOPT, the heuristic found a feasible solution with $N'=564$ spheres and $n'_k=94$ for $k=1,\ldots ,6$. The very first feasible solution consists of $N_0=414$ spheres and was obtained after 6 s.

Example 8

In this example, the container is larger with $L\times W\times H=9\times 9\times 81$. We are given $N=3.000$ spheres with $K=6$ types and $n_1=\cdots =n_6=500$. The remaining data on $r_k, \varepsilon _k,\underline{\tau }_k,\overline{\tau }_k$ are as in Example 7. A feasible point with $N'=2.172$ spheres and $n'_k=372$ for $k=1,\ldots ,6$ was found after about 74 min with 67 IPOPT runs. Moreover, we got $N_0=1.734$ spheres for the first feasible placement within 19 s.

Example 9

For a container with $L\times W\times H=15\times 15\times 110$, $N=12.000$ spheres, $K=6$ sphere types with $n_k=2.000$ for $k=1,\ldots ,6$, and $r_k, \varepsilon _k,\underline{\tau }_k,\overline{\tau }_k$ as in Example 7, the heuristic obtained a feasible point with $N'=7.266$ spheres divided into $n'_k=1.211$ spheres of each type k. The total run time was about 1 h and 47 min with 405 IPOPT runs, the first feasible solution with $N_0=5.754$ spheres was found after about 7 min.

Example 10

In this example, we use different values for $\underline{\tau }_k$ and $\overline{\tau }_k$ for different k, namely

$$\begin{aligned} \begin{array}{l} \underline{\tau }_1=\frac{1}{7}-10^{-2},\; \overline{\tau }_1=\frac{1}{7}+10^{-2},\\ \underline{\tau }_2=\frac{2}{7}-10^{-2},\; \overline{\tau }_2=\frac{2}{7}+10^{-2},\\ \underline{\tau }_3=\frac{4}{7}-10^{-2},\; \overline{\tau }_3=\frac{4}{7}+10^{-2}. \end{array} \end{aligned}$$

The container is given by $L\times W\times H=18\times 12\times 35$. Moreover, $N=700$ spheres of $K=3$ types are available with $n_1=100$, $n_2=200$, $n_3=400$ and radii $r_1=2$, $r_2=1.5$, and $r_3=1$. Further, we set $\varepsilon _k=-\frac{1}{2} r_k$ for $k=1,2,3$. The first feasible placement was found after 25 s with $N_0=428$ spheres. The final feasible placement contains $N'=477$ spheres with $n'_1=65$, $n'_2=135$, $n'_3=277$ and $\tau '_1=0.13626\ldots$, $\tau '_2=0.28301\ldots$, and $\tau '_3=0.58071\ldots$ To get these results, the heuristic needed about 30 min with 23 IPOPT runs.

Fig. 6

Feasible placements obtained by the heuristic for Example 7 in (a), for Example 8 in (b), for Example 9 in (c), for Example 10 in (d), and for Example 11 in (e)

Example 11

This last examples uses a container with $L\times W\times H=15\times 18\times 47$, $N=5.000$ spheres of $K=5$ types such that $n_k=1.000$ for $k=1,\ldots ,5$,

$$\begin{aligned} r_1=1.5,\,r_2=1.25,\,r_3=0.85,\,r_4=0.8,\,r_5=0.7, \\ \varepsilon _1=-1,\,\varepsilon _2=-0.8,\,\varepsilon _3=-0.7,\,\varepsilon _4=-0.6,\,\varepsilon =-0.5, \end{aligned}$$

and

$$\begin{aligned} \underline{\tau }_k=\frac{k}{15}-10^{-2},\;\overline{\tau }_k=\frac{k}{15}+10^{-2}\quad \text{ for } k=1,\ldots ,5. \end{aligned}$$

The first feasible solution with $N_0=2.095$ spheres was found by Algorithm 2 within 28 s. After about 85 min, a better feasible solution with $N'=2.172$ spheres was determined using 93 IPOPT runs. This solution contains $n'_1=133$, $n'_2=266$, $n'_3=400$, $n'_4=577$, and $n'_5=719$ spheres of the different types. The final ratios of this solution are $\tau '_1=0.06348\ldots$, $\tau '_2=0.12696\ldots$, $\tau '_3=0.19093\ldots$, $\tau '_4=0.27541\ldots$, and $\tau '_5=0.34319\ldots$

5 Concluding remarks and outlook

We developed a novel sphere packing model with nonstandard containment and ratio conditions, a corresponding MINLP formulation, and a heuristic strategy for obtaining a good feasible solution. Exact solutions of the MINLP formulation were obtained for smaller instances by applying the global solver BARON at the NEOS server. For larger instances, the proposed heuristic strategy was successfully implemented and tested.

Future research is directed on improvements of the heuristic strategy. In particular, we think of modifying Algorithm Top-Down Bisection (Algorithm 4). By an inexpensive local optimization, certain spheres shall be placed in a lower position. This may reduce the number of IPOPT runs and, due to this, the overall run time. In addition, more sophisticated ways to satisfy and exploit the ratio conditions may increase the number of spheres placed in Algorithm SELECT INDEX SET (Algorithm 3). In this respect, one may think of placing single spheres in a different way or of using a random choice of spheres. Other potential research questions arise if the model is changed. For example, the volume of all placed spheres can be maximized instead of the number of spheres. This also requires adaptations in the heuristic. Moreover, packing spheres into other types of containers (spheres, cylinders) or in containers with prohibited zones [6] is of practical interest. The quasi-containment and non-overlapping constraints (9) and (10) are nonlinear. Therefore, alternative formulations like the use of linearization techniques may have the potential to decrease the run time of global solvers applied to small instances. Along with the global solver BARON used here, other solvers, e.g., COUENNE or SCIP can be employed. The comparison of different problem formulations and of several global solvers requires extensive computational experimentation and is an interesting area for future research.