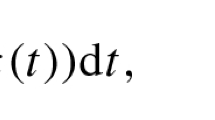Global dynamic optimization with Hammerstein–Wiener models embedded

Abstract

Hammerstein–Wiener models constitute a significant class of block-structured dynamic models, as they approximate process nonlinearities on the basis of input–output data without requiring identification of a full nonlinear process model. Optimization problems with Hammerstein–Wiener models embedded are nonconvex, and thus local optimization methods may obtain suboptimal solutions. In this work, we develop a deterministic global optimization strategy that exploits the specific structure of Hammerstein–Wiener models to extend existing theory on global optimization of systems with linear dynamics. At first, we discuss alternative formulations of the dynamic optimization problem with Hammerstein–Wiener models embedded, demonstrating that careful selection of the optimization variables of the problem can offer significant numerical advantages to the solution approach. Then, we develop convex relaxations for the proposed optimization problem and discuss implementation aspects to obtain the global solution focusing on a control parametrization technique. Finally, we apply our optimization strategy to case studies comprising both offline and online dynamic optimization problems. The results confirm an improved computational performance of the proposed solution approach over alternative options not exploiting the linear dynamics for all considered examples. They also underline the tractability of deterministic global dynamic optimization when using few control intervals in online applications like nonlinear model predictive control.

1 Introduction

Dynamic optimization problems arise in various domains, examples within the field of chemical engineering being process design, operation and control [3]. Among these problems, only a few—relative simple and small ones—allow for an analytical solution. In most cases, the solution requires numerical methods [7].

Deriving local solutions for dynamic optimization problems has been studied extensively in the literature, and mature and efficient technologies are available, which are able to handle even large-scale and complex systems [37]. The two main solution approaches for dynamic optimization problems are variational (indirect) and discretization (direct) methods. A further classification of discretization methods occurs based on whether or not the discretization refers only to the controls or also to the states; resulting in sequential and simultaneous methods, respectively [3].

In practice, most chemical and biochemical engineering problems are nonconvex, and may therefore exhibit multiple local minima [9]. Although the application of local optimization methods to solve these problems is reasonable in terms of computational effort, they do not guarantee global optimality of the final solution. However, in many of these problems global solutions are desired, or even required, e.g., in cases where we are interested in the best fit for model evaluation such as the kinetic mechanism in chemical reactions (cf., e.g., [29, 42]). In general, finding the global solution of a problem can have direct economical, environmental and safety impacts [9].

Deterministic approaches to globally solve problems with ordinary differential equations (ODEs) embedded are an evolving field of study, with significant accomplishments over the past years [12]. Deterministic global optimization guarantees convergence to an $\epsilon$-optimal solution within a finite number of steps. A popular approach to tackle these problems is to combine discretization methods with a spatial branch-and-bound (B &B) algorithm. Such an approach typically provides solutions to finite dimensional optimization problems. Infinite dimensional problems like optimal control problems, where the optimization variables are continuous functions, can be transformed into finite dimensional NLPs by control vector parametrization [17]. Recently, Houska and Chachuat [13] proposed a global optimization algorithm for optimal control problems that includes an adaptive refinement of the control parametrization to guarantee convergence to the solution of the infinite dimensional problem.

The solution of the parametrized problem relies on extensions of sequential and simultaneous methods for local dynamic optimization. The methods based on extensions of the simultaneous approach, similar to their original simultaneous approach as in full discretization for local dynamic optimization, result in large scale NLPs. As the worst-case computational effort of B &B scales exponentially with the number of variables, the applicability of these methods is limited to small problems. Hence, most research efforts on global dynamic optimization have been focused on extensions of sequential approaches. However, for the latter cases, the construction of the lower bounding problem for a convergent B &B algorithm is a challenging topic [37].

Recent attempts on deterministic global dynamic optimization with main focus on extensions of sequential NLP approaches have been reviewed in [9, 13]. One approach is based on extensions of the $\alpha$BB method [1] to NLPs containing ODEs. These methods are computationally expensive, as they typically require the calculation of second-order sensitivities to determine a shift parameter that is not known apriori, cf., e.g., [11, 28]. A different approach based on McCormick relaxations [23] is presented by Singer and Barton [40, 41]. These methods are reported to have better performance than $\alpha$BB-based approaches and can in general handle a wider class of ODEs [9]. Both above mentioned approaches follow a relax-then-discretize fashion, meaning that they first construct relaxations to the infinite dimensional ODE system and then discretize these to get the numerical solution. In contrast, a discretize-then-relax approach that first discretizes the dynamics and then treats the resulting NLP in a reduced space is proposed by Mitsos et al. [25] based on automatic propagation of McCormick relaxations and their subgradients. Sahlodin and Chachuat [31] provide a rigorous discretize-then-relax approach to account for the truncation error arising during the discretization step. Recently, Scott and Barton [33, 34] presented a novel method for constructing relaxations for semi-explicit index-one differential algebraic equations (DAEs) providing the first algorithm for solving problems with DAEs embedded to global optimality [37]. Optimization problems with DAEs embedded are in general very hard to solve globally. This is mainly because the solutions of these systems are typically not factorable, and thus developing relaxation theory for the lower bounding problem is nontrivial [37]. The reader is referred to [33, 36, 37] for more information on the challenges. Overall, progress in this field is still at an early stage, and active research on this topic is necessary to improve computational performance and to make larger problems tractable.

One way of improving computational performance is to exploit special structure of certain important model classes, rather than rely on general-purpose methods. Hammerstein–Wiener (HW) models constitute a significant example of such a class. They are data-driven dynamic models bringing the advantage of capturing nonlinear effects and simultaneously being computationally less complex than fully nonlinear dynamic models. HW models cover a wide range of applications, such as modeling of physical, chemical and biological systems [19]. Extensive research on system identification of those models has been performed in the literature, cf., e.g., [2, 46, 49], and they are often used for model predictive control, cf., e.g., [19, 47]. Upon optimization with HW models embedded, we still get a nonlinear problem. To avoid suboptimal solutions of the resulting optimization problem and high computational effort, tailored deterministic global optimization methods and formulations are required.

In this work, we discuss theoretical aspects and propose a computational approach for global dynamic optimization with HW models. First, we utilize the specific structure of HW models by exploiting the properties of linear dynamics occurring in these models. More precisely, we extend existing theory on deterministic global dynamic optimization with linear systems presented by Singer and Barton [39, 40] to account for the input and output nonlinearities of HW models. Furthermore, we apply the proposed approach to numerically solve several illustrative examples using our open-source optimization software MAiNGO¹ [6] following the method presented by Mitsos et al. [25].

The remainder of this manuscript is structured as follows. In Sect. 2, we present the structure of HW models, we describe the optimization problem and discuss alternative formulations with their impact on the solution approach. In Sect. 3, we derive the required theory for the solution of the presented problem to global optimality and report on the practical implementation aspects. Computational results for three examined case studies are presented in Sect. 4. The model implementations for these case studies are being made available as Supplementary Information. Section 5 concludes this work.

2 Problem description

2.1 General form of Hammerstein–Wiener models

In HW models, two static nonlinear blocks precede and follow, respectively, a linear dynamic system (see Fig. 1). The input nonlinearity $\textbf{f}_\text {H}: \mathbb {R}^{n_u} \rightarrow \mathbb {R}^{n_w}$ is called Hammerstein function and the output nonlinearity $\textbf{f}_\text {W}: \mathbb {R}^{n_z} \rightarrow \mathbb {R}^{n_y}$ is the Wiener function:

$$\begin{aligned} \begin{aligned}&\textbf{w}(t)= \textbf{f}_\text {H}\left( \textbf{u}\left( t\right) \right) ,\ \ \forall t\in [t_0,t_f] \\&\dot{\textbf{x}}(t) = \textbf{A} \textbf{x}(t) + \textbf{B} \textbf{w}(t),\ \ \forall t\in [t_0,t_f] \\&\textbf{z}(t)= \textbf{C} \textbf{x}(t) + \textbf{D} \textbf{w}(t),\ \ \forall t\in [t_0,t_f] \\&\textbf{y}(t)= \textbf{f}_\text {W}\left( \textbf{z}\left( t\right) \right) ,\ \ \forall t\in [t_0,t_f]\\&\textbf{x}(t_0)= \textbf{x}_0, \end{aligned} \end{aligned}$$

(1)

where $\textbf{u}:[t_0,t_f] \rightarrow \mathbb {R}^{n_u}$ are the inputs of the system, $\textbf{w}:[t_0,t_f] \rightarrow \mathbb {R}^{n_w}$ are the inputs to the linear time-invariant (LTI) system, $\textbf{x}:[t_0,t_f] \rightarrow \mathbb {R}^{n_x}$ are the states, $\textbf{z}:[t_0,t_f] \rightarrow \mathbb {R}^{n_z}$ are the outputs of the LTI system, $\textbf{y}:[t_0,t_f] \rightarrow \mathbb {R}^{n_y}$ the outputs of the system, $\textbf{A} \in \mathbb {R}^{n_{x}\times n_{x}}$, $\textbf{B} \in \mathbb {R}^{n_{x} \times n_{w}}$, $\textbf{C} \in \mathbb {R}^{n_{z} \times n_{x}}$, $\textbf{D} \in \mathbb {R}^{n_{z} \times n_{w}}$ are system matrices of the LTI , and $\textbf{x}_0 \in \mathbb {R}^{n_{x}}$ are the initial states. Note that due to the physical meaning of real-world applications, the input variables are bounded, i.e., $\textbf{u}(t) \in U, \ U \subsetneq \mathbb {R}^{n_{u}}$, U compact.

Fig. 1

Structure of a Hammerstein–Wiener model

2.2 Optimization problem formulation

The formulation of an optimization problem with embedded HW models can be written as

$$\begin{aligned} \underset{\textbf{u}(\cdot )}{min } \quad \varPhi \left( \textbf{y}\left( t_f\right) ,t_f\right) +\int _{t_0}^{t_f} l\left( \textbf{y}\left( t\right) ,\textbf{u}\left( t\right) ,t\right) dt, \end{aligned}$$

(2)

where $\textbf{y}(\cdot )$ derives from the solution of the DAE system (1). Problem (2) has a general objective function of Bolza form. Note that all Mayer, Lagrange and Bolza problem formulations are equivalent from a theoretical perspective and can be used interchangeably in practice [3, 7].

In Problem (2), a few simplifications were made for notational convenience. Nevertheless, more general problems can be handled without requiring changes to the developed theory. Since HW models are usually built on an input–output relationship, we consider only a dependence on the final time $t_f$ and the outputs on the final time point $\textbf{y}(t_f)$ for the terminal term, as well as a dependence on model outputs $\textbf{y}(\cdot )$, on the inputs $\textbf{u}(\cdot )$ and explicitly on time t for the integrand l. However, these terms may in general also depend on other variables, e.g., the states $\textbf{x}$ and their derivatives $\dot{\textbf{x}}$. Moreover, the first term of the objective is only dependent on the final time point, yet any additional dependence on the outputs at any finite number of fixed time points can be added. In addition, we could, without any significant changes to the theory, generalize the Wiener block to include any relationship of the form $\textbf{y}(t)=\textbf{f}_\text {W}\left( \textbf{x}\left( t\right) ,\textbf{w}\left( t\right) \right)$ for all $t\in [t_0,t_f]$, or even $\textbf{y}(t)=\textbf{f}_\text {W}(\textbf{x}(t),\textbf{u}(t))$ for all $t\in [t_0,t_f]$. Note that the latter case does no longer satisfy the HW model structure, but can be interesting to consider in general.

Problem (2) contains a DAE system with linear dynamic equations. In the following, we discuss different options for expressing the problem formulation.

2.2.1 Analytical solution of the LTI

Probably the most intuitive solution approach is to incorporate the analytical solution of the linear dynamic system,

$$\begin{aligned} \textbf{x}(t)= e^{\textbf{A}(t-t_0)} \textbf{x}_0+ \int _{t_0}^{t} e^{\textbf{A}(t-\tau )} \textbf{B} \textbf{w}(\tau )\ d\tau , \end{aligned}$$

into Problem (2), and thus eliminate the ODE. By substituting both the input to the LTI system $\textbf{w}(\cdot )$ and the system output $\textbf{y}(\cdot )$, with the functions of the Hammerstein and Wiener blocks, respectively, we derive

(3)

This problem formulation is complicated to solve, since for the inner integral of Equation (3) there may not exist an analytical solution in dependence of t for arbitrary $\textbf{f}_\text {H}$.

2.2.2 Substitution approach

Alternatively, we can only exploit the fact that $\textbf{w}$ and $\textbf{y}$ are explicit functions of $\textbf{u}$ and $\textbf{z}$, respectively, and obtain

$$\begin{aligned} \underset{\textbf{u}(\cdot )}{min } \quad \varPhi \left( \textbf{f}_\text {W}\left( \textbf{z}\left( t_f\right) \right) ,t_f\right) + \int _{t_0}^{t_f} l\left( \textbf{f}_\text {W}\left( \textbf{z}\left( t\right) \right) ,\textbf{u}\left( t\right) ,t\right) \ dt, \end{aligned}$$

(4)

where $\textbf{z}(\cdot )$ is given by the solution of the ODE system

$$\begin{aligned} \begin{aligned}&\dot{\textbf{x}}(t)= \textbf{A}\textbf{x}(t)+\textbf{B}\textbf{f}_\text {H}\left( \textbf{u}\left( t\right) \right) , \ \ \forall t \in [t_0,t_f] \\&\textbf{z}(t)= \textbf{C}\textbf{x}(t)+\textbf{D}\textbf{f}_\text {H}\left( \textbf{u}\left( t\right) \right) , \ \ \forall t \in [t_0,t_f] \\&\textbf{x}(t_0)= \textbf{x}_0. \end{aligned} \end{aligned}$$

(5)

However, unlike the original Problem (2), Problem (4) has nonlinear dynamics given by the ODE system (5). Therefore, the advantage of the linear dynamics will be lost. This is particularly important since relaxations of nonlinear dynamics are typically weak.

2.2.3 Inversion approach

To retain a problem with linear dynamics, one alternative is to treat the Wiener model (LTI system plus Wiener function) separately, using existing theory on linear dynamics by Singer and Barton [39, 40] and optimize for $\textbf{w}(\cdot )$. To treat the dependence on $\textbf{u}(\cdot )$ in the objective, in case of invertibility of the Hammerstein function $\textbf{f}_\text {H}$ or similar condition, we derive

$$\begin{aligned} \underset{\textbf{w}(\cdot )}{min } \quad \varPhi \left( \textbf{f}_\text {W}\left( \textbf{z}\left( t_f\right) \right) ,t_f\right) + \int _{t_0}^{t_f} l\left( \textbf{f}_\text {W}\left( \textbf{z}\left( t\right) \right) ,\textbf{f}^{-1}_\text {H}\left( \textbf{w}\left( t\right) \right) ,t\right) \ dt, \end{aligned}$$

(6)

where $\textbf{z}(\cdot )$ is obtained by the solution of the LTI system

$$\begin{aligned} \begin{aligned}&\dot{\textbf{x}}(t)= \textbf{A} \textbf{x}(t) + \textbf{B} \textbf{w}(t), \ \ \forall t \in [t_0,t_f] \\&\textbf{z}(t)= \textbf{C} \textbf{x}(t) + \textbf{D} \textbf{w}(t), \ \ \forall t \in [t_0,t_f] \\&\textbf{x}(t_0)= \textbf{x}_0. \end{aligned} \end{aligned}$$

(7)

Even in the case where the objective does not depend on $\textbf{u}(\cdot )$, once the optimal solution $\textbf{w}^*(\cdot )$ is given, the above approach would still require specific assumptions on existence and uniqueness of the optimal control $\textbf{u}^*(\cdot )$. With the assumption of an invertible Hammerstein function $\textbf{f}_\text {H}$, once we have the optimal $\textbf{w}^*(t)$ for all $t\in [t_0,t_f]$, we can solve $\textbf{u}^*(t)=\textbf{f}^{-1}_\text {H}\left( \textbf{w}^*\left( t\right) \right)$ to obtain $\textbf{u}^*(t)$ for all $t\in [t_0,t_f]$.

The assumption on invertibility of the nonlinear static functions $\textbf{f}_\text {H}$ and $\textbf{f}_\text {W}$ is often made for identifiability of HW models [49]. However, static nonlinearities are not necessarily invertible, with a typical example being saturations, which frequently describe process characteristics [19]. Thus, this assumption significantly limits the choice of the considered functions, and consequently the applicability of the inversion approach. Furthermore, this approach necessitates exact bounds on $\textbf{w}(t)$ for all $t\in [t_0,t_f]$, to ensure a feasible $\textbf{u}(t)$ for all $t\in [t_0,t_f]$. If that is not the case, an optimal $\textbf{w}^*(\cdot )$ may be found that does not map to a feasible $\textbf{u}^*(\cdot )$ once inverted. This is because potential bounds or constraints on $\textbf{u}(\cdot )$ are not in the optimization problem anymore. The fact that we actually need to find the exact range of $\textbf{f}_\text {H}$ on the domain of $\textbf{u}$, rather than an overestimated box, can be as complex as solving the final optimization problem. It should however be noted that if the function is invertible and exact bounds are known, then the inversion approach is promising. The first numerical example discusses the performance of the inversion approach with and without exact bounds.

2.2.4 Additional optimization variables approach

The idea behind this approach is to introduce additional optimization variables to Problem (4) to re-gain the linearity of the dynamic system. To this end, we optimize with respect to both $\textbf{u}(\cdot )$ and $\textbf{w}(\cdot )$. More precisely, by treating $\textbf{u}(\cdot )$ and $\textbf{w}(\cdot )$ as independent optimization variables and imposing their dependence in an additional constraint, we can retain the linear dynamic behavior of the system with respect to $\textbf{w}(\cdot )$ and use existing theory on global optimization of systems with linear dynamics [39, 40]. The optimization problem is then formulated as

$$\begin{aligned} \begin{aligned}&\underset{\textbf{u}(\cdot ),\textbf{w}(\cdot )}{min } \quad \varPhi \left( \textbf{f}_\text {W}\left( \textbf{z}\left( t_f\right) \right) ,t_f\right) + \int _{t_0}^{t_f} l\left( \textbf{f}_\text {W}\left( \textbf{z}\left( t\right) \right) , \textbf{u}\left( t\right) ,t \right) \ dt \\&\quad \text {s.t.}\,\quad \ \ \textbf{w}(t)=\textbf{f}_\text {H}\left( \textbf{u}\left( t\right) \right) , \ \ \forall t \in [t_0,t_f], \end{aligned} \end{aligned}$$

where $\textbf{z}(\cdot )$ derives from solving the LTI system (7).

The additional optimization variables $\textbf{w}(\cdot )$ are used in a similar way to the additional module and tear variables presented by Bongartz et al. [5] for decoupling the model equations that would require iterative solution in process flowsheet optimization.

By eliminating the intermediate variables $\textbf{z}(\cdot )$ and introducing functions $\tilde{\varPhi }$ defined as $\tilde{\varPhi }\left( \textbf{x}\left( t_f\right) ,\textbf{w}\left( t_f\right) ,t_f\right) := \varPhi \left( \textbf{f}_\text {W}\left( \textbf{C}\textbf{x}\left( t_f\right) +\textbf{D}\textbf{w}\left( t_f\right) \right) ,t_f\right)$ in the terminal term and $\tilde{l}$ defined as $\tilde{l}\left( t,\textbf{x}\left( t\right) ,\textbf{w}\left( t\right) ,\textbf{u}\left( t\right) \right) := l\left( \textbf{f}_\text {W}\left( \textbf{C}\textbf{x}\left( t\right) +\textbf{D}\textbf{w}\left( t\right) \right) ,\textbf{u}\left( t\right) ,t\right)$ in the integral, we obtain

$$\begin{aligned} \begin{aligned}&\underset{\textbf{u}(\cdot ),\textbf{w}(\cdot )}{min } \quad \tilde{\varPhi }\left( \textbf{x}\left( t_f\right) ,\textbf{w}\left( t_f\right) ,t_f\right) + \int _{t_0}^{t_f} \tilde{l}\left( t, \textbf{x}\left( t\right) , \textbf{w}\left( t\right) ,\textbf{u}\left( t\right) \right) \ dt \\&\quad \text {s.t.}\,\ \ \quad \textbf{w}(t)=\textbf{f}_\text {H}\left( \textbf{u}\left( t\right) \right) , \ \ \forall t \in [t_0,t_f], \end{aligned} \end{aligned}$$

(8)

where $\textbf{x}(\cdot )$ is the solution of

In Sect. 3, we show how Problem (8) can be used to derive a solution strategy for deterministic global dynamic optimization with HW models embedded. In more detail, we are concerned with the derivation of an algorithm that is guaranteed to terminate finitely with an $\epsilon$-optimal $\textbf{u}^*(\cdot )$, $\textbf{w}^*(\cdot )$ to Problem (8).

Note that, in contrast to the inversion approach resulting in Problem (6), the additional optimization approach solves the ODE and the equation of the Hammerstein part simultaneously.

3 Solution strategy

In this section, we present theory and implementation of the additional optimization variables approach solving Problem (8).

As the decision variables associated with this problem refer to continuous control inputs $\textbf{u}(\cdot )$, we first apply control parametrization to Problem (8) and then derive an algorithm to solve the parametrized problem to global optimality. Therefore, we need to parametrize the control functions $\textbf{u}$, $\textbf{w}$. An obvious choice is to use piecewise constant discretization for both and impose their nonlinear relationship at the discretization points. Other choices are conceivable as well, e.g., using a piecewise linear approximation. However, these choices may yield additional complications and are out of the scope of this article. Note that the solution of the parametrized problem instead of infinite dimensional Problem (8) introduces an additional parametrization error. A method for overcoming this limitation has been recently proposed by Houska and Chachuat [13]. Nevertheless, the implementation and application of a rigorous method for control parametrization is beyond the scope of the present study.

3.1 Deriving a convex relaxation for the optimization problem

Herein, we present the theory for systems with one input ($n_u=1, \ n_w=1$) and one output y, for notational simplicity. However, the methodology presented here can be extended for systems with multiple input/output signals with no significant changes.

The discretized input vectors are

$$\begin{aligned} \begin{aligned}&u(t)=\hat{u}_i, \ \text {if} \ t \in [t_{i-1},t_{i}),\ i=1,...,n, \\&w(t)=\hat{w}_i , \ \text {if} \ t \in [t_{i-1},t_{i}),\ i=1,...,n, \end{aligned} \end{aligned}$$

with n discretization points, $t_n = t_f$ and parameter vectors

$$\begin{aligned} \hat{{\textbf {u}}} = \begin{pmatrix} \hat{u}_{1} \\ \vdots \\ \hat{u}_{n} \end{pmatrix} \in \mathbb {R}^{n} , \quad \hat{{\textbf {w}}} = \begin{pmatrix} \hat{w}_{1} \\ \vdots \\ \hat{w}_{n} \end{pmatrix} \in \mathbb {R}^{n}. \end{aligned}$$

Hence, we obtain an optimization problem with a finite number of variables and an ODE embedded

$$\begin{aligned} \begin{aligned}&\underset{\hat{{\textbf {u}}},\hat{{\textbf {w}}}}{min } \quad \tilde{\varPhi }\left( \textbf{x}\left( t_f\right) ,\hat{w}_n,t_f\right) + \sum _{i=1}^{n} \int _{t_{i-1}}^{t_i} \tilde{l}\left( t, \textbf{x}\left( t\right) , \hat{w}_i, \hat{u}_i\right) \ dt \\&\ \text {s.t.}\,\ \ \ \hat{{\textbf {w}}}=\textbf{f}_\text {H}(\hat{{\textbf {u}}}), \end{aligned} \end{aligned}$$

(9)

where $\textbf{x}(\cdot )$ is the solution of

(10)

and $\mathbbm {1}_{[t_{i-1},t_{i})}(\cdot )$, $i=1,...,n$, is the indicator or characteristic function defined as

Note that the same discretization is applied to both w(t) and u(t), such that the constraint $\hat{{\textbf {w}}}=\textbf{f}_\text {H}(\hat{{\textbf {u}}})$ can be understood as component-wise equality. In particular, this constraint is only enforced at a finite number of points.

Since Problem (9) contains a finite number of optimization variables, a standard spatial B &B algorithm can be employed. Any feasible point or local solution of Problem (9) constitutes an upper bound. A lower bound can be obtained by solving a convex relaxation of Problem (9). A convex relaxation of Problem (9) is derived in Theorem 1, which is built on the theory presented by Singer and Barton [39, 40]. Note that Theorem 1 follows the notation presented in [39, 40], and thus an explicit dependence of the states ${\textbf {x}}$ also on the control parameters $\hat{{\textbf {w}}}$ is included.

Theorem 1

Let $\hat{{\textbf {u}}}\in U$, where U is a convex subset of $\mathbb {R}^{n_u} ,\ \hat{{\textbf {w}}}\in W$, where W is a convex subset of $\mathbb {R}^{n_w},\ \textbf{x}(t,\hat{{\textbf {w}}})\in X$, where X is a convex subset of $\mathbb {R}^{n_x}$, such that $\textbf{x}(t,\hat{{\textbf {w}}}) \in X~\forall ~(t,\hat{{\textbf {w}}}) \in (t_0,t_f] \times W$; $\textbf{A} \in \mathbb {R}^{n_{x}\times n_{x}}$, $\textbf{B} \in \mathbb {R}^{n_{x} \times n_{w}}$ constant matrices; $\tilde{\varPhi }^{cv}(\cdot , \cdot , t_f)$ a convex relaxation of $\tilde{\varPhi }(\cdot , \cdot , t_f)$, both $\tilde{\varPhi },\tilde{\varPhi }^{cv}: X~\times ~\mathbb {R}\times ~\mathbb {R}\rightarrow \mathbb {R}$ continuous mappings; $\tilde{l}^{cv}(t,\cdot ,\cdot , \cdot )$ a convex relaxation of $\tilde{l}(t,\cdot ,\cdot , \cdot )$ for fixed t; $\tilde{l}^{cv},\tilde{l}:(t_0,t_f]\times X \times U \times W \rightarrow \mathbb {R}$ Lebesgue integrable, where function $\tilde{l}$ is only permitted a finite number of discontinuities; $\textbf{f}_\text {H}^{cv}$ a convex relaxation of $\textbf{f}_\text {H}$; $\textbf{f}_\text {H}^{cc}$ a concave relaxation of $\textbf{f}_\text {H}$; $\textbf{f}_\text {H}^{cv}, \textbf{f}_\text {H}^{cc}, \textbf{f}_\text {H}: U \rightarrow W$ continuous mappings with only finite number of discontinuities; and $\mathbbm {1}_{[t_{i-1},t_{i})}$ the indicator function. Then a convex relaxation of optimization Problem (9) is given by

$$\begin{aligned} \begin{aligned}&\underset{\hat{{\textbf {u}}},\hat{{\textbf {w}}}}{min } \quad \tilde{\varPhi }^{cv}\left( \textbf{x}\left( t_f,\hat{{\textbf {w}}}\right) ,\hat{w}_n,t_f\right) + \sum _{i}\int _{t_{i-1}}^{t_i} {\tilde{l}^{cv}}\left( t, \textbf{x}\left( t,\hat{{\textbf {w}}}\right) , \hat{u}_i,\hat{w}_i\right) \ dt \\&\quad \text {s.t.}\, \quad \textbf{f}_\text {H}^{cv}(\hat{{\textbf {u}}}) \le \hat{{\textbf {w}}} \le \textbf{f}_\text {H}^{cc}(\hat{{\textbf {u}}}), \end{aligned} \end{aligned}$$

(11)

where $\textbf{x}(\cdot ,\hat{{\textbf {w}}})$ is the solution of

Proof

A relaxation of the optimization Problem (9) can be derived by relaxing the objective function and the constraints.

Due to our specific problem formulation, which adds additional optimization variables besides ${u}(\cdot )$, we can apply the relaxation theory described in [39, 40] for systems with embedded linear dynamics, and therefore obtain a valid relaxation for the objective function. For the point term in the objective, the relaxation can be derived via standard techniques. For each of the integral terms in the objective, integral relaxation (Corollary 3.1 in [40]) follows directly from integral monotonicity (Lemma 3.2 in [40]) and integral convexity (Theorem 3.1 in [40]). More precisely, we relax the objective with respect to $\hat{{\textbf {w}}}$, imposing convexity of $\tilde{l}^{cv}$ on both $\hat{{\textbf {w}}}$ and $\hat{{\textbf {u}}}$.

Up to now, we have a methodology for deriving a relaxation for the objective function including the linear system dynamics. In our problem formulation, there is an additional constraint that relates $\hat{{\textbf {w}}}$ and $\hat{{\textbf {u}}}$. Relaxations of this constraint can be also obtained via standard techniques. With this, Problem (11) provides a valid relaxation of Problem (9). $\square$

By following our proposed auxiliary variables approach, we expect that we inherit the tightness and convergence properties of Singer and Barton [39, 40]. However, no detailed analysis and mathematical proofs are included here, as this would require a substantial scope, cf., e.g., [4, 26, 32].

In Theorem 1, standard techniques for relaxations of the point term in the objective as well as the additional constraint refer to any valid relaxation methods for nonconvex functions, e.g., $\alpha$BB [1] or McCormick [23] relaxations.

Note that integral relaxation following from Corollary 3.1 in [40] requires convexity of the relaxation of the integrand function on the controls. Assuming convexity of the relaxation on both $\hat{{\textbf {u}}}$ and $\hat{{\textbf {w}}}$, the relaxation of the objective function accounting for the linear dynamics with respect to $\hat{{\textbf {w}}}$ follows directly from the theory presented in [39, 40].

3.2 Obtaining the numerical solution of the optimization problem

In the following, we discuss implementation aspects for the numerical solution of Problem (8). As discussed, Problem (8) is infinite dimensional, and thus the first step to apply the solution strategy presented above, is to parametrize the controls by piecewise constant functions. To numerically solve the resulting Problem (9), we utilize our open-source optimization software MAiNGO [6], based on (multivariate) McCormick relaxations [23, 44] and their subgradient propagation [25] implemented in MC++ [8]. MAiNGO is a deterministic global optimization software for solving mixed-integer nonlinear programs (MINLPs). Hence, to deal with the dynamic nature of our system, we first apply full discretization to the dynamics and then solve the resulting large scale NLP in a reduced space, using a spatial B &B algorithm, as shown in [25]. The reduced-space formulation treats only the values of the controls at all control discretization points as optimization variables. This solution approach could also be understood as a single shooting method with a simple integration scheme, where the states are thus hidden from the optimizer.

The proposed solution approach offers numerical advantages compared to solving a full-space formulation of the NLP resulting from full discretization, i.e., treating also the values of the states at all discretization points as optimization variables and the integration scheme as constraints. Therefore, using MAiNGO that treats the optimization problem in a reduced space is particularly important in this work. More precisely, this is because the reduced-space formulation dramatically reduces the number of considered optimization variables, while this would not be easily possible in other state-of-the-art global optimization solvers, e.g., [24, 43] that solve the full-space formulation. However, since we only relax the parametrized problem, we actually optimize an approximate problem, and therefore we introduce an additional inherent error to the solution. This is different from the solution approach presented in [39, 40], where the authors discretize the relaxed problem. Therefore, by using tight discretization tolerances they can guarantee convergence to the $\epsilon$-optimal solution of the original problem. A rigorous approach to account for truncation error following a discretize-then-relax fashion has been developed by the authors in [31].

For the numerical solution of the ODE, we implement the explicit Runge Kutta schemes up to 4th order. As commonly done in the literature, e.g., [41], the objective can be treated as an ODE by rewriting it to

$$\begin{aligned} \tilde{\varPhi }\left( \textbf{x}\left( t_f\right) ,\hat{w}_n,t_f\right) + h\left( t_f\right) , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\dot{h}(t) = \tilde{l}\left( t, \textbf{x}\left( t\right) , \hat{w}_i, \hat{u}_i\right) , \ \ \forall t \in [t_{i-1},t_i], \ \ i=1,...,n \\&h(t_0)= 0. \end{aligned} \end{aligned}$$

(12)

Note that in this case the sum over i is not needed, because function h is defined piecewise over the time intervals. Upon numerical integration of the ODE with its initial condition over $t\in [t_0,t_f]$, the original objective function is obtained. Thus, Problem (9) becomes

$$\begin{aligned} \begin{aligned}&\underset{\hat{{\textbf {u}}},\hat{{\textbf {w}}}}{min } \quad \tilde{\varPhi }\left( \textbf{x}\left( t_f\right) ,\hat{w}_n,t_f\right) + h\left( t_f\right) \\&\ \text {s.t.}\,\ \ \ \hat{{\textbf {w}}}=\textbf{f}_\text {H}(\hat{{\textbf {u}}}), \end{aligned} \end{aligned}$$

where $\textbf{x}(\cdot )$ is the solution of the ODE system (10) and $h(\cdot )$ the solution of System (12) for $t\in [t_0,t_f]$. To achieve an accurate evaluation of the objective function and avoid excessive computational effort due to a large number of control parameters, a denser time discretization for the state grid and a coarser for the control grid might be required in practice. For this, we calculate the (piecewise constant) controls for the ODE and intermediate values for the states within the intervals of the control grid. This enables different time discretization for the states and the controls.

MAiNGO solves the above problem without the introduction of auxiliary variables, thus only operating in the variable space $\hat{{\textbf {u}}}, \hat{{\textbf {w}}}$. To solve the optimization problem in MAiNGO, we require bounds for the controls $\hat{{\textbf {u}}}, \hat{{\textbf {w}}}$ and initial conditions at $t=t_0$ for the states. Yet, the optimizer does not directly see the state variables. Hence, bounds for the states are not required, since they are propagated along with the relaxations. Note that depending on the number of steps used in the integration scheme as well as the nonlinearities of the underlying model, the interval bounds of the intermediate variables computed during the propagation of relaxations may become extremely large similar to the work presented in [39, 40]. We come back to this issue in Sect. 4.2.1.

4 Case studies

We demonstrate the feasibility of the presented approach by examining the solution of some numerical case studies. For all case studies presented below, the explicit Runge Kutta scheme of 4th order (ERK4) is applied as integration scheme, and equidistant grids are used. All computations are performed on a desktop computer with an Intel(R) Core(TM) i3-4150 CPU @ 3.50 GHz with 8GB RAM. We use MAiNGO 0.2.0 [6] with default settings unless otherwise stated. CPLEX 12.8.0 is used to solve the lower bounding problems, SLSQP [18] through the NLOPT 2.5.0 toolbox [14] for the upper bounding problems, and IPOPT 3.12.12 [45] is used for preprocessing. Model implementations for these cases studies are provided as Supplementary Information.

The examples presented in this section are similar or somewhat larger than what has been presented in the literature. In general, most studies reporting on global optimization of problems with nonlinear dynamics apply their theory to solve parameter estimation problems, cf., e.g., [10, 11, 20, 25, 29, 42]. The vast majority of these problems are solved for relatively small time horizons ($t_f$ below ten), one to three states and less or equal to five time invariant control parameters. Wilhelm et al. [48] present a global optimization method for initial value problems of stiff parametric ODE systems, and the examples include up to ten states (and consequently ten initial value parameters). Only a few studies on nonlinear global dynamic optimization for optimal control problems are reported in the literature, cf., e.g., [21, 28, 41, 50]. The optimal control examples presented in these studies include only one time variant control with up to eight intervals, one to five states and time horizons almost exclusively bellow 20. As no open implementation of existing approaches exists, we do not compare them on our computer. Also, we do not attempt any comparison of the CPU times reported for these problems in the original works, since computational power has improved drastically over the past 15 years.

4.1 Case study 1: simple numerical example

As a first case study, we consider an extension of Problem 5.4 presented in [39]. The optimization of the original problem is

$$\begin{aligned} \underset{w(t)\in [-4,4]}{min } \quad \int _{0}^{1} -x^2(t) \ dt, \end{aligned}$$

(13)

where $\textbf{x}(\cdot )$ derives from the solution of

$$\begin{aligned} \begin{aligned}&\dot{x}(t) = -2x(t) + w(t), \ \ \forall t \in [0,1] \\&x(0)=1. \end{aligned} \end{aligned}$$

(14)

In Fig. 2, we depict the objective value as a definite integral in dependence of the parameter w for a completely constant discretization, i.e., w is constant. From Fig. 2, we can distinguish the existence of two local minima, a suboptimal local one at $w=-4$ and the global one at $w=4$. The value of the objective for the global solution of Problem (13) is around – 2.516. Depending on the starting point, a local optimizer may converge to the suboptimal local solution.

Fig. 2

Objective function for case study 1 (Figure adjusted from [39])

This problem is a special case of a HW model. More precisely, it can be formulated as a Wiener model with LTI system matrices ${A}=-2$, ${B}=1$, ${C}=1$, ${D}=0$, initial condition $x_0=1$ and static output nonlinearity ${f}_\text {W}(z(t))=-z^2(t)$. Note that in Wiener models the input nonlinearity deriving from the Hammerstein function ${f}_\text {H}$ is omitted, and thus the inputs directly enter the LTI system. In the extension we consider here, we introduce an input nonlinearity by adding a nonlinear static function ${f}_\text {H}$ that maps $u(\cdot )$ to $w(\cdot )$ (i.e. adding a Hammerstein block). In fact, we define function ${f}_\text {H}(u(t))=-u^2(t)+5$, $u(t) \in [1,3]$.

The resulting HW model can be described by the following system of equations

$$\begin{aligned} \begin{aligned}&w(t)=-u^2(t)+5, \ \ \forall t \in [0,1] \\&\dot{x}(t) = -2x(t) + w(t), \ \ \forall t \in [0,1] \\&z(t)= x(t), \ \ \forall t \in [0,1] \\&y(t)=-z^2(t), \ \ \forall t \in [0,1] \\&x(0)= 1. \end{aligned} \end{aligned}$$

Following the additional optimization variables approach presented in Sect. 2.2.4, we can now formulate our HW optimization problem as

$$\begin{aligned} \begin{aligned}&\underset{u(\cdot ),w(\cdot )}{min } \quad \int _{0}^{1} -x^2(t)\ dt \\&\quad \text {s.t.}\,\quad \ \ w(t)=-u^2(t)+5, \ \ \forall t \in [0,1], \end{aligned} \end{aligned}$$

(15)

where $\textbf{x}(\cdot )$ is the solution of (14) and $u(t)\in [1, 3]$, $w(t)\in [-4,4]$ for any $t\in [0,1]$. Problem (15) is equivalent to Problem (13) with respect to w. Therefore, since the global solution to Problem (13) is $w \equiv 4$, the global solution to Problem (15) will be $u\equiv 1, w\equiv 4$.

Fig. 3

Optimization results for case study 1; Computational performance of the substitution, the additional optimization variables and the inversion approach as a function of the number of control discretization points n

To numerically solve Problem (15), we apply the solution strategy presented in Sect. 3. Figure 3 illustrates the solution times when solving Problem (15) with MAiNGO, using different numbers of discretization points n for the controls. For comparison purposes, Fig. 3 also includes the results with the substitution approach (see Sect. 2.2.2, Problem (4)) and the inversion approach (see Sect. 2.2.3, Problem (6)).

Solving Problem (15) following the substitution approach (i.e., as in Problem (4)) translates into solving a nonlinear dynamic system in MAiNGO with only $u(\cdot )$ as a control. Consequently, the mapping from $u(\cdot )$ to $w(\cdot )$ through the Hammerstein function is now directly included in the dynamics, as shown in Equation System (5).

Solving Problem (15) following the inversion approach (i.e., as in Problem (6)) translates into solving a problem with linear dynamics with only $w(\cdot )$ as a control. As previously discussed, an extra assumption on invertibility of the Hammerstein function and exact bounds on $w(\cdot )$ are necessary in this case. In cases where these assumptions are indeed satisfied, the inversion approach takes advantage of the linear dynamics, similarly with the additional optimization variables approach, yet, it does not need to introduce further control variables. However, making these assumptions in a first place is often limiting, and it can be avoided by using the additional optimization variables approach instead. To illustrate this point we consider the following minor modification in the case study. We expand the feasible domain of u, such that $u(t)\in [-3, 3]$, and introduce the constraint $|{u}|\ge 1$ in order to maintain the exact bounds on $w(\cdot )$. Then, $f_\text {H}(\cdot )$ becomes noninvertible, and thus the inversion approach can be no longer applied. Note that both the additional optimization variables and the substitution approaches are not affected by the aforementioned modification.

All results indeed give an objective value of $\approx$ – 2.516 and return as optimal controls $(\hat{\textbf{u}},\hat{\textbf{w}})=(1,4)$, where $\hat{\textbf{u}}$ and $\hat{\textbf{w}}$ are n-dimensional vectors with all entries 1 and 4, respectively. In the substitution approach, the solution time scales unfavorably with refining control parametrization (with n=27, CPU time reached our imposed time limit of 12 h). For this simple case study (with $u(t)\in [1,3]$, thus ${f}_\text {H}(\cdot )$ invertible) the CPU times for the inversion approach are lower than the additional optimization variables approach, as shown in Fig. 3. This is expected, since both approaches consider linear dynamics, yet the additional optimization variables approach has double the amount of control variables than the inversion one. However, by only undertaking a small modification on this problem, namely expanding the domain of u, it becomes clear that the assumption on inveribility is quite limiting and it can lead to a failure of the inversion approach once violated. Therefore, in the following the inversion approach is not further examined. The computational time in the examined case study is observed to scale linearly with the state discretization for all the examined approaches (see “Appendix A”).

At this point we need to point out that the exact bounds on $w(\cdot )$ were used in the additional optimization approach. Yet, as opposed to the inversion approach, this is not required. By loosening these bounds by 10%, 50% and 100%, respectively, and performing the optimizations again we did not observe any systematic effect on the computational performance for this specific example. More precisely, the differences in the CPU time in all cases were less than 1 s, and we did not notice any consistent trend by incrementally relaxing the bounds w. The effect from having tight bounds on $w(\cdot )$ might not be visible due to the relative small solution times of this example, or it can be negligible due to the fact that the input nonlinearities in this example are not so strong.

Note again that for the numerical solution presented in [39], Problem (13) is first relaxed and then discretized. In contrast, for our customized Problem (15), we first discretize and then relax the dynamics, as in [25]. Although theoretically our implemented method introduces an additional optimization error (see relative discussion in Sect. 3.2), by imposing a fine state grid, we obtain the same objective value as in [39].

4.2 Case study 2: tracking problem

As a second case study, we consider a tracking problem presented by Ławryńczuk [19]. In particular, our aim is to find the optimal $u(\cdot )$ to minimize the summed squared error between the output $y(\cdot )$ and an arbitrary chosen set-point trajectory $y_{sp}(\cdot )$. The examined system was first presented by Zhu [51] and then used by Ławryńczuk [19] for nonlinear model predictive control (NMPC). Herein, we aim at solving the problem to global optimality for the first time. We consider the following problem formulation

$$\begin{aligned} \begin{aligned}&\underset{u(\cdot ), w(\cdot )}{min } \quad \sum _{j=1}^{n_t}{(y(t_j)-y_{sp}(t_j))^2} \\&\quad \text {s.t.}\,\quad \ \ w(t)=\frac{u(t)}{\sqrt{(0.1+0.9 u(t))^2 }}, \ \ \forall t \in [t_0,t_f], \end{aligned} \end{aligned}$$

(16)

where $u(t)\in [-2.5, 2.5]$, $w(t)\in [-1.045,1.045]$ for any $t\in [t_0,t_f]$, $t_j = j$ for $j = 1,...,n_t$, $y(t)=z(t)+ 0.2 z^3(t)$ for all $t\in [t_0,t_f]$ and $\textbf{x}(\cdot )$, ${z}(\cdot )$ deriving from the solution of the LTI:

$$\begin{aligned} \begin{aligned}&\dot{x}_1(t) = 0.75 x_1(t) + 0.87 x_2(t) + 0.58 w(t), \ \ \forall t \in [t_0,t_f] \\&\dot{x}_2(t) = 1.24 x_1(t) + 1.11 x_2(t) -0.66 w(t), \ \ \forall t \in [t_0,t_f] \\&z(t)= 0.5 x_1(t) + 0.25 x_2(t), \ \ \forall t \in [t_0,t_f] \\&x_1(t_0)= x_{1,t_0},\qquad x_2(t_0)= x_{2,t_0}. \end{aligned} \end{aligned}$$

The bounds on $w(\cdot )$ follow naturally from plotting w as a function of u. The transformation of the discrete transfer function describing the LTI in [51] to continuous state space formulation in Problem (16) was derived in MATLAB [22]. It is worth noticing that the objective function for this example only contains fixed time points. Although herein we preserve the formulation presented in the literature [19], we could easily generalize it to an integral objective.

For all the results presented below, the relative and absolute optimality tolerances are set to $10^{-2}$. In order to improve tightness of the relaxations and ultimately the convergence of the B &B algorithm, we implemented the convex and concave envelopes of the univariate Hammerstein function ${f}_\text {H}: \mathbb {R}\rightarrow \mathbb {R}, {f}_\text {H}(u)=\frac{u}{\sqrt{(a+b u)^2}}$ for a fixed a, b. For the calculation of the envelopes we use the method presented in Section 4 of [23]. Furthermore, setting higher branching priorities, i.e., branch on specific variables more often than on others during the B &B procedure, can have a significant effect on computational performance. Particularly for this problem, we used higher branching priorities on w ($BP_w=5$), as we observed that this leads to reduced CPU times.

4.2.1 Offline optimization

We first solve Problem (16) offline for $t_0=0$, $t_f=n_t=120$ and $x_{1,t_0}=0$, $x_{2,t_0}=0$. Note that since the objective in Problem (16) requires function evaluations at 120 points, the state grid should be at least that fine. The number of intervals in the state grid is set to 480. The grid resolution is decided in such a way that for all examined cases after doubling the discretization of the state grid the obtained relative difference in the objective is less than the optimization tolerance.

We perform the optimizations for different control parameterizations using the additional optimization variables approach. From Fig. 4, we observe that the CPU time scales exponentially with the number of control discretization points n. Already for a control grid with ten intervals, the problem requires more than 12 h CPU time to converge to the optimal solution. An alternative approach to deal with this limitation is discussed in the next subsection. We observed a linear scaling of computational time with respect to state discretization, see “Appendix A”, Fig. 9.

Here, having tight bounds on $w(\cdot )$ appeared to have a noticeable effect on the numerical performance. More precisely, having exact bounds on w could reduce CPU time up to 50% in this case. The computational benefits from using the exact bounds showed an increasing trend as a higher number of control discretization points was considered. Interestingly, no direct correlation in CPU times with respect to the distance of the considered bounds from the exact ones was observed.

Note that the time of set-point changes in the output trajectory (except the first one occurring shortly after $t=0$), see Fig. 6b, coincides with the control steps for the case of an equidistant control grid with four parameters. Therefore, the choice of four control parameters or its multiples, leads to better objective values compared to other numbers of control parameters, as illustrated in Fig. 5. Nevertheless, spotting physically superior solutions for Problem (16) is not the primary focus of this study, so this effect is not further discussed.

In addition, we again tried to compare the performance of the proposed additional approach with the one from the substitution approach. Already for number of control discretization points equals two, the optimization problem with the substitution approach did not converge to the optimal solution within our imposed CPU time limit of 12 h.

Fig. 4

Case study 2 offline optimization; Comparison of CPU times with the additional optimization variables approach for different numbers of control discretization points n

Fig. 5

Case study 2 offline optimization; Comparison of optimization results in terms of objective value with the additional optimization variables approach for different numbers of control discretization points n

4.2.2 Nonlinear model predictive control

As a next step, we extend our optimization algorithm to solve the tracking problem with an NMPC strategy. Problem (16) is solved repeatedly for each sampling instant $i\in [1,120]$, for a prediction horizon N and a control horizon $N_u$ in time, with $t_{0,i}=i-1$, $t_{f,i}=t_{0,i}+N$, $n_{t,i}=N$ and initial states given by Equation (17). From the $N_u$ elements, indicating the number of control parameters that are determined in each iteration, only the first one is implemented as action to the NMPC scheme. Then, the prediction is shifted one step forward and the process is repeated. At each time instant, from the time between the end of the control horizon until the end of the prediction horizon zero incremental change in the control signal is considered.

$$\begin{aligned} \begin{aligned} \textbf{x}_{t_0,i} = {\left\{ \begin{array}{ll} \textbf{0} , &{}\text { if } i=1 \\ \textbf{x}_{t_f,i-1} , &{}\text { otherwise }. \end{array}\right. } \end{aligned} \end{aligned}$$

(17)

For each iteration i, a state grid with four times the number of intervals used for the prediction horizon N is required, in order to obtain the same final discretization as with the offline approach (i.e., $n=480$). Unlike what is presented in [19], we do not consider an additional term in the objective function to penalize excessive control incremental changes. This is done to maintain the same objective with the offline approach and be able to compare the results. Therefore, a relative aggressive control scheme is obtained, see Fig. 6a.

By solving this case study with the online strategy, we observe that during the propagation of state values through time the constructed relaxations may become extremely loose. We believe that this is due to the shorter time intervals, wherein the controls are considered to be constant. More precisely, allowing a significantly higher number of control intervals for a fixed time horizon enables the control profile to fluctuate more, which leads to a higher flexibility on the potential state values. In other words, the finer control grid gives the opportunity for a much more aggressive realization of the underlying system dynamics. As the derived relaxations need to encompass the whole admissible range of the control profile, relaxations get weaker. There are different methods to provide tight bounds for the states in parametric ODEs, cf., e.g., [30, 31, 35, 38] presented in the literature. However, when the state explosion derives from the enlargement of the admissible set of the state values, rather than the problem dynamics themselves, the improvements obtained from the tighter relaxations might be secondary. In other words, the main problem is not that the relaxations are not tight enough, but rather that the permissible state bounds increase drastically, which unavoidably leads to very loose relaxations. We anticipate this behavior to be in general present in cases where global optimization for control of systems with stiff dynamics is exhibited.

To the authors’ best knowledge, a general solution strategy to account for this limitation is not available in the literature. Herein, we utilize our system knowledge and the fact that we are dealing with a tracking problem to overcome this limitation. More precisely, to avoid the explosion of state values in our specific example we consider additional bounds for the states $\textbf{x}(t)\in [-10,10]\times [-10,10]$, the output of the LTI system $z(t)\in [-5,5]$, as well as for the system output $y(t)\in [-30,30]$ for all $t\in [t_0,t_f]$. The values on the domain of y are obtained by doubling the range of the desired output trajectory, on z by the functional dependence ${f}_\text {W}$ between z and y, and on $\textbf{x}$ by observing the systems behavior for the given control bounds. The considered bounds are imposed through inequality constraints. The ranges of the corresponding functions are restricted to their new bounds using the min and max functions before passing them as arguments to further computations. Although these specific actions are tailored to our problem, the use of system knowledge to constrain the permissible bounds of the problem’s variables can be generalized to any problem. Note that for solution approaches that by default require state bounds to solve the dynamic problem, methods for propagation of these bounds are already in use, and could be beneficial to consider here. It is worth noting, however, that in our case none of these bounds needs to be exact.

Results for different control and prediction horizons, as well as both apriori known and unknown set-point changes are presented in Table 1. From Table 1, we observe that the consideration of the prediction for the set-point change has a drastic effect on the objective function. However, as the prediction horizon increases, the effect of the first control parameter, which is the one we actually implement after each iteration, decreases. Thus, the derived control policy becomes less effective. As the number of control parameters per iteration increases, the prediction generally improves. Yet, in this approach this does not have such a profound influence on the final objective value, as we only apply the first control element each time. Still, by increasing the number of control parameters for each iteration, the computational time increases significantly. In general, obtaining good values for control and prediction horizons is part of tuning in an NMPC problem and is considered out of the scope of the present study.

Note that the worst CPU times presented in Table 1 occur to iterations close to the set-point changes. For the other iterations the CPU times are considerably lower. Note also that in Table 1 the objective values derive from evaluation of the objective function in Problem (16) for the 120 instances that the controls were implemented. This enables the direct comparison of the objective values with the ones obtained from the offline optimization, as discussed in Sect. 4.2.3.

Table 1 Numerical results for case study 2 online optimization with the additional optimization variables approach, with prediction horizon N, control horizon $N_u$ considering either apriori known or unknown set-point changes in the output trajectory

Fig. 6

Optimization results for case study 2 with the additional optimization variables approach; Comparison of online ($N_i=5$, $N_{u,i}=3$, $i=1 \dots 120$) and offline ($n=8$) optimization in terms of (a) control profile and (b) output trajectory

For completeness, we have compared our global solution of the online case with $N=5$ and $N_u=3$ (depicted in Fig. 6) with a local solution, and these coincide. We now analyze the problem for multimodality. Out of the 120 iterations of the global NMPC, the three local searches (by default the number of local searches conducted by MAiNGO as a preprocessing step is set to three) often result in same solutions, within tolerances. However, there do exists iterations where there are differences. The effect on the objective value for a single interval may be quite big (e.g., difference 0.01 to 0.15), whereas the effect on the overall sum is relative small, in the order of up to few percent. Note, however, that we have no way to check if the solutions of the local solvers are indeed locally optimal. Yet, in this particular comparison the first point that the local search converges, which is the one the local optimization finds, happens to be the global one. Hence, we obtain the same objective value for the global and the local solution. This can be due to a good starting point of the local approach, or a large area of attraction for the global solution. Obtaining the global solution was around three times slower compared to the time of the local solution for this example. This can be considered as a very good performance for global optimization. Although local solutions are in general computationally more tractable, our method has the significant advantage that it guarantees that the obtained solution is globally optimal. Unfortunately, in [19, 51] the time step is nondimensional, so that we cannot compare time in the considered system to CPU time for our solution approach, and thus we are not able to draw any conclusion about whether our approach is real-time capable for this example.

4.2.3 Comparison of offline and online optimization

Overall, we observe that the NMPC scheme can obtain much better results in terms of both CPU time and objective value than the offline optimization. More precisely, the objective values for the NMPC with known set-point change are around one order of magnitude lower than the ones attained with offline optimization. Figure 6 illustrates two exemplary control and output trajectories obtained one from the offline and the other from the online approach. With the online approach, we are able to solve the tracking problem with 120 discretization points for each control u and w in a few minutes, and with each subproblem solved globally. In contrast to this, for the offline approach, we were limited to maximum nine points in the control grid, which took almost ten hours for the global optimization. The computational burden of the presented methodology scales in general unfavorably with increasing number of control parameters. However, by following an online approach to solve the dynamic optimization problem globally, we avoid this limitation. More precisely, the repeated solution of small problems, with few control intervals each, in the online approach is much faster than the solution of one large problem in the offline approach. Since this observation is linked to the scaling of B &B algorithms with the number of variables, it likely extends to other global optimization approaches as well. As HW models are used in many applications in control, these results indicate great potential for applications in this field and can contribute substantial benefits in cases where the global solutions are necessitated.

4.3 Case study 3: monoclonal antibody production

As a last case study, we consider an example motivated from antibody production [15, 16]. The HW model has two inputs, one output and six states. The LTI system is given by

$$\begin{aligned} \begin{aligned}&\dot{\textbf{x}}(t) = \textbf{A} \textbf{x}(t) + \textbf{B} \textbf{w}(t), \quad t\in [0,144] \\&z(t)= \textbf{C} \textbf{x}(t) + \textbf{D} \textbf{w}(t), \quad t\in [0,144]\\&\textbf{x}(0)= \textbf{0}, \end{aligned} \end{aligned}$$

(18)

where information about the system’s matrices $\textbf{A}$, $\textbf{B}$, $\textbf{C}$, $\textbf{D}$ is given in “Appendix B”. The input and output nonlinearities are wavelet functions with one or two units and are also provided in “Appendix B”, see Eqs. (20)–(22).

The optimization problem with $\textbf{x}(\cdot )$, $z(\cdot )$ deriving from (18) can be formulated as

$$\begin{aligned} \begin{aligned}&\underset{\textbf{u}(\cdot ),\textbf{w}(\cdot )}{min } \quad \int _{0}^{144} -f_\text {W}(z(t))\ dt \\&\quad \text {s.t.}\,\qquad \textbf{w}(t)=\textbf{f}_\text {H}(\textbf{u}(t)), \ \ \forall t \in [0,144] \\&\qquad \qquad \ \sum _{i} \left( (\hat{u}_{1,i} + \hat{u}_{2,i})\cdot 10^{-4}\cdot \frac{144}{n}\right) -0.02 \le 0 , \ \ i=1,...,n, \end{aligned} \end{aligned}$$

(19)

where $\textbf{u}(t)\in [0.0, 3.3]^2$, $\textbf{w}(t)\in [0.6,2.3]\times [0.35,1.5]$ for any $t\in [0,144]$ and n the number of control discretization points. The bounds on $\textbf{w}$ follow from plotting $\textbf{w}$ as a function of $\textbf{u}$. The inequality constraint in Problem (19) provides an upper bound on the permissible control inputs $\textbf{u}$.

We assume this problem to be multimodal, as different solutions are obtained when a multistart is performed. Thus, global optimization is particularly important. The optimization problem is solved for different numbers of control grid discretization and for a relative and absolute optimality tolerance of $10^{-2}$ and 20 local searches during preprocessing.

Table 2 Numerical results for case study 3 with the additional optimization variables approach with n number of control discretization points

The results for $n=1,2,3,4$ with a state grid with 288 intervals for the additional optimization variables approach are presented in Table 2. Although both $\textbf{u}(\cdot )$ and $\textbf{w}(\cdot )$ are optimization variables, in Table 2, we only present (for compactness) the values of $\textbf{u}(\cdot )$, which are the relevant ones for practical implementations. Interestingly, the objective value does not seem to be significantly affected by the discretization of the controls, taking also into account the imposed optimality tolerance. This can be due to different combinations within the imposed control bounds that can lead to same objective values. Note that due to the high nonlinearity of the static functions and the increased number of states, no convergence to global optimality was attained within 12 h CPU times for a control discretization greater than four. However, we should point out that already a control grid with four elements refers to eight controls for the problem, considering the two control inputs $u_1, u_2$. In our solution approach, we consider both $\textbf{u}$ and $\textbf{w}$ as control variables, which translates to a total number of 16 optimization variables in Problem (19). Also in this case study, the results presented above were obtained by considering bounds on $w(\cdot )$ that are very close to the exact bounds. The effect of relaxing the considered bounds on w is here mostly detected in the preprocessing, where different local solutions for the different bounds were observed, due to the strong multimodality of this case study. These local solutions affected the total solution time, correspondingly. We also tested the substitution approach for this case study. However, optimization with the substitution approach for this case study did not converge to the optimal solution within the time limit of 12 h, even when considering only one control discretization point. Linear scaling with state grid refinement is again observed, see Fig. 10 in the “Appendix A”.

5 Conclusions

Hammerstein–Wiener models are a commonly used class of block-structured models with a wide range of applications in process operations and control. As these models are nonlinear, they can lead to suboptimal local minima when embedding them in process optimization or control problems.

Herein, we propose a novel algorithm for deterministic global optimization with Hammerstein–Wiener models. We extend the theory presented in [39, 40] on global optimization of systems with linear dynamics to HW models. The theory pertains to combining direct methods with a spatial B &B algorithm to tackle dynamic problems based on extensions of sequential methods for local dynamic optimization. We show that different optimization problem formulations can lead to different solution strategies with different levels of difficulty. More precisely, by carefully selecting the optimization variables in the problem formulation, we are able to maintain advantageous properties of linear systems. In a next step, we successfully apply our method to numerical examples from offline and online optimization. For this we follow a discretize-then-relax fashion. The parametrized optimization problems are solved in a reduced space using our open-source global optimization software MAiNGO [6] based on McCormick relaxations [23]. For the case of an invertible Hammerstein function and exact bounds, we argue that an inversion approach can be used.

The results demonstrate the potential benefits of the presented approach and enable future utilization to real-world case studies, with special focus on model predictive control. Our method seems to scale favorably with refining the states grid, but is more sensitive to the control grid. This is a typical problem for similar algorithms proposed in the literature as pointed out in [9]. To address this problem, future emphasis should be placed on methods for obtaining tighter relaxations for the lower bounding problem, cf., e.g., [27]. Furthermore, consideration of sophisticated methods to construct tight state relaxations, cf., e.g., [30, 31, 35, 38] can yield considerable improvements to this work.

In general, due to the exponential worst-case runtime, it makes a profound difference for global optimization whether we solve one problem with a large number of control parameters, or multiple problems with fewer control parameters, although both problems may result in the same total number of control intervals. This work particularly emphasizes the applicability of our approach to NMPC problems, and potentially also of other global dynamic optimization approaches, since they can all benefit from short time intervals and few control parameters at each control iteration.

Appendices

Appendix A: Effect of state grid refinement on the solution approach

Herein we present the computational performance of the presented solution approach by refining the state discretization for the examined case studies. Linear scaling is observed in all cases.

Figure 7 illustrates the results for case study 1 for the substitution, additional optimization variables and inversion approach, for an exemplary control grid with $n=9$ intervals and piecewise constant control functions. Similar results are obtained also for the other values of n. As already indicated in Sect. 4, for all cases the results indicate a linear scaling with refining the state grid.

Fig. 7

Case study 1; Scaling of computational performance with refinement of state grid for a control grid with $n=9$ intervals

Fig. 8

Case study 2 offline optimization with the additional optimization variables approach; Scaling of computational performance with refinement of state grid for different control grids

Similar results are obtained for case study 2, as shown in Fig. 8 for the offline approach for three exemplary control grids. The results for the other values of n are analogous. In Fig. 9, we additionally reproduce the results of Sect. 4.2.1 referring to the scaling of CPU time with number of control intervals for three different state grids (here the linear scaling corresponds to equidistant spacing between the different lines). Fine discretization refers to 480 intervals, and corresponds to the results presented in Fig. 4. Medium discretization corresponds to a state grid with 240 intervals and coarse to 120 intervals, respectively. The results for the objective function are not presented here, since by changing grid refinement the change in the objective value for constant number of control discretization is always less than 10 %.

Fig. 9

Case study 2 offline optimization with the additional optimization variables approach; Scaling of computational performance with refinement of state grid for different numbers of control discretization points n

Fig. 10

Case study 3 with the additional optimization variables approach; Scaling of computational performance with refinement of state grid for different numbers of control discretization points, n

For case study 3, also linear scaling with the number of state discretization points is observed. However, since this problem is strongly multimodal (multiple different objectives values are obtained from different local searches), solution times may also depend on how good is the initial upper-bound-guess that derives from the local solution of the examined optimization problem. The results for different state discretizations and numbers of control discretization points are illustrated in Fig. 10. Fine discretization corresponds to a state grid with 288 intervals (results presented in Table 2), medium discretization to 144 intervals and coarse to 72 intervals. The state grid refinement for each of the different numbers of control intervals led to differences in the objective always within the optimization tolerance, and thus not presented here. As it can be seen in Fig. 10, the CPU time scales unfavorably with increasing the number of control discretization points.

Appendix B: Additional model information for case study 3

The matrices of the LTI system as described in Equation (18) are given by

$$\begin{aligned}{} & {} \textbf{A}= \begin{bmatrix} 0.418 &{} -0.512 &{} 0.094 &{} 0 &{} 0 &{} 0\\ 0.215 &{} -0.091 &{} -0.124 &{} 0 &{} 0 &{} 0\\ -0.284 &{} 0.886 &{} -0.603 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0.365 &{} -0.414 &{} 0.099\\ 0 &{} 0 &{} 0 &{} 0.261 &{} -0.176 &{} -0.171\\ 0 &{} 0 &{} 0 &{} -0.226 &{} 0.598 &{} -0.745 \end{bmatrix}, \quad \textbf{B}= \begin{bmatrix} 0.134 &{} 0\\ -0.082 &{} 0\\ 0.202 &{} 0\\ 0 &{} 0.151\\ 0 &{} -0.110\\ 0 &{} 0.171\\ \end{bmatrix}, \\{} & {} \textbf{C}= \begin{bmatrix} -0.933\quad \ \ {}&1 \quad&\quad \ 0 \ \quad&-0.929 \qquad&1 \qquad&\ \ 0\quad \end{bmatrix}, \quad \textbf{D}= \begin{bmatrix} \quad \ \ 0&\qquad \ \ 0 \quad \end{bmatrix}. \end{aligned}$$

The input nonlinearity $f_\text {H1}$ is given by

$$\begin{aligned} \begin{aligned} f_\text {H1}\left( u_1\left( t\right) \right)&=\left( u_1\left( t\right) -1.521\right) \cdot 0.034\cdot 10^{-4} + 0.852\cdot 10^{-4}\cdot \left( 1 - s_1^2\left( t\right) \right) \cdot \exp \left( -0.5s_1^2\left( t\right) \right) \\&\quad -0.629\cdot 10^{-4}\cdot \left( 1 - s_2^2\left( t\right) \right) \cdot \exp \left( -0.5s_2^2\left( t\right) \right) + 1.339\cdot 10^{-4}, \end{aligned}\nonumber \\ \end{aligned}$$

(20)

with $t\in [0,144]$, $u_1(t)\in [0.0, 3.3]$ and

$$\begin{aligned} \begin{aligned}&s_1(t)=8\cdot \left( \left( u_1\left( t\right) - 1.521\right) \cdot 1072\cdot 10^{-4} - 1.250\right) \ \\&s_2(t)=2\cdot \left( \left( u_1\left( t\right) - 1.521\right) \cdot 1072\cdot 10^{-4} + 1.001\right) . \end{aligned} \end{aligned}$$

The input nonlinearity $f_\text {H2}$ is given by

$$\begin{aligned} \begin{aligned} f_\text {H2}\left( u_2\left( t\right) \right)&=\left( u_2\left( t\right) - 1.624\right) \cdot 0.039\cdot 10^{-4} - 0.871\cdot 10^{-4}\cdot \exp \left( -0.5\cdot s^2\left( t\right) \right) \\&\quad + 1.302\cdot 10^{-4}, \end{aligned}\nonumber \\ \end{aligned}$$

(21)

with $t\in [0, 144]$, $u_2(t)\in [0.0, 3.3]$ and

$$\begin{aligned} s(t)=16\cdot \left( \left( u_2\left( t\right) - 1.624\right) \cdot 9689\cdot 10^{-4}+ 0.750\right) . \end{aligned}$$

The output nonlinearity $f_\text {W}$ is given by

$$\begin{aligned} \begin{aligned} f_\text {W}\left( z\left( t\right) \right)&=\left( z\left( t\right) -0.001\right) \cdot 38898 + 78.733\cdot \left( 1 - s_3^2\left( t\right) \right) \cdot \exp \left( -0.5s_3^2\left( t\right) \right) \\&\quad +15.692\cdot \left( 1 - s_4^2\left( t\right) \right) \cdot \exp \left( -0.5s_4^2\left( t\right) \right) + 89.140, \end{aligned}\nonumber \\ \end{aligned}$$

(22)

with $t\in [0, 144]$ and

$$\begin{aligned} \begin{aligned}&s_3(t)=1\cdot \left( \left( z\left( t\right) - 0.001\right) \cdot 516.573 - 2.000\right) \ \\&s_4(t)=4\cdot \left( \left( z\left( t\right) - 0.001\right) \cdot 516.573 + 1.250\right) . \end{aligned} \end{aligned}$$