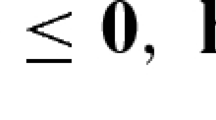Nonconvex constrained optimization by a filtering branch and bound

Abstract

A major difficulty in optimization with nonconvex constraints is to find feasible solutions. As simple examples show, the $\alpha$BB-algorithm for single-objective optimization may fail to compute feasible solutions even though this algorithm is a popular method in global optimization. In this work, we introduce a filtering approach motivated by a multiobjective reformulation of the constrained optimization problem. Moreover, the multiobjective reformulation enables to identify the trade-off between constraint satisfaction and objective value which is also reflected in the quality guarantee. Numerical tests validate that we indeed can find feasible and often optimal solutions where the classical single-objective $\alpha$BB method fails, i.e., it terminates without ever finding a feasible solution.

1 Introduction and motivation

Numerical methods for constrained optimization problems have a multitude of applications in a large range of technical and economical applications. To give a concrete example, we consider an engineering design problem where the overall aim is to minimize the building costs while certain requirements on the quality have to be met. Depending on the structure of the problem at hand, it may already be a challenging task to find feasible solutions, and even more so to find feasible solutions that are provably optimal.

1.1 Constraint handling and multiobjective counterparts

In this paper, we focus on constrained optimization problems where the objective function as well as the constraints are given by twice continuously differentiable functions. Noting that feasibility constraints are a prevalent difficulty in constrained optimization, we take a multiobjective perspective and suggest to relax all complicating constraints and re-interprete them as additional and independent objective functions. From a practical point of view, such multiobjective counterpart models account for the fact that the right-hand-side values of constraints are often based on individual preferences and/or estimations (consider, for example, quality constraints in an engineering design problem). Indeed, slight constraint violations may be acceptable if this allows for a significant improvement of the primary (cost) objective function. Conversely, if a significantly better quality can be obtained at only slightly higher cost, the decision maker may be willing to invest more for a solution that in a sense “oversatisfies” the constraints. A multiobjective counterpart model provides trade-off information between constraint satisfaction on one hand and primary objective function on the other hand, and thus supports the decision making process and the selection of a most preferred solution.

From a numerical point of view, multiobjective counterpart models have another important advantage: By relaxing all complicating constraints, feasible solutions are easily available to initiate the optimization procedure. Depending on the selected constrained programming solver, this may actually be a crucial property, see Example 1 below. Moreover, even when the original constrained optimization problem is infeasible, multiobjective counterpart models have the potential to efficiently compute “best possible” solutions that, naturally, remain infeasible for the original constrained problem, but perform as well as possible w.r.t. both constraint satisfaction and primary objective in a multiobjective sense.

1.2 $\alpha$BB method

The $\alpha$BB-method suggested by [1] is an example of a deterministic constrained programming algorithm that aims at the determination of a globally optimal solution. It can be interpreted as a geometric branch-and-bound algorithm that discards subregions of the feasible set (referred to as boxes) based on efficiently computed lower and upper bounds on the optimal objective value. It terminates with the best found feasible solution as soon as the difference between upper and lower bound falls below a prespecified accuracy requirement. On a specific subbox, a lower bound is obtained by solving an auxiliary convex optimization problem (referred to as convexified problem in the following) restricted to a convex superset of the feasible set in the considered subbox. The objective function of this convexified problem is a convex underestimator of the original objective function, and thus an optimal solution yields a lower bound on the best possible objective value in the subbox in question. Upper bounds, on the other hand, are obtained from images of already known feasible solutions, and thus crucially depend on the ability to efficiently compute such feasible solutions. Usually, feasible solutions are retrieved from the optimal solutions of the convexified problems, i.e., by evaluating the respective solutions with the original constraint functions. However, since the convexified problems operate on relaxed (convex) feasible sets, their solutions do not have to be feasible for the original problem, and in this case the determination of upper bounds becomes complicated. This difficulty was described in [17] and exemplified at the following example problem:

Example 1

[17] Consider the single-objective optimization problem

$$\begin{aligned} \begin{array}{rl} \min &{} f(x)=x_1-x_2 \\ \text{ s.t. } &{} g(x)= -x_1^2-(x_2-5)^2+25+\sqrt{2}\le 0,\\ &{} x\in [1,2]\times [0,1]. \end{array} \end{aligned}$$

(1)

The global optimum of problem (1) is $x^*=(\root 4 \of {2}; 0)\approx (1.1892; 0)$, and the optimal objective value can be obtained as $f(x^*)=\root 4 \of {2}\approx 1.1892$.

As was noted in [17], the $\alpha$BB method does not make any progress when applied to problem (1) since the optimal solutions of the convexified problems are always infeasible for the original problem. As a consequence, lower bounds are constructed, while upper bounds are never obtained. Therefore, the $\alpha$BB method can never satisfy the accuracy requirements and thus does not terminate. In the following, we will use Example 1 as a test case to exemplify the advantages and also the difficulties when considering multiobjective counterpart models and, as a natural consequence, a multiobjective counterpart of the $\alpha$BB method that is specifically tailored for the solution of constrained optimization problems.

1.3 Related literature

The close relationship between constrained optimization problems and multiobjective counterpart models has been discussed and exploited in a variety of different ways. We refer to [18] for a general survey on the interrelation between different relaxation strategies of constrained programming problems (like, for example, Lagrangian relaxation and exact penalty functions) and corresponding scalarizations of the multiobjective counterpart model (in case of Lagrangian relaxation this is the classical weighted-sum scalarization, while exact penalty functions correspond to so-called elastic constraint scalarizations). In [15], a multiobjective counterpart approach is introduced for constrained multiobjective optimization problems and the interrelation of constrained and unconstrained multiobjective optimization is examined. Multiobjective counterpart models have motivated a variety of solution approaches for different classes of constrained optimization problems. As a prominent example, multiobjective counterpart models naturally relate to filter methods where total constraint violation is interpreted as a second objective function, see, for example, [11] and the survey in [12]. Multiobjective counterpart models are also used, among others, to handle constraints in evolutionary algorithms (see, for example, [32] for a survey), and in the context of combinatorial optimization problems to efficiently compute solution alternatives for multiobjective and multidimensional knapsack problems [30]. Finally, we note that besides constraint handling multiobjective optimization is also a powerful tool for other algorithmic aspects; see [34] for a recent example.

Common algorithms to solve multiobjective optimization problems globally can be divided into deterministic and stochastic algorithms. Stochastic algorithms, also named evolutionary methods, construct a population of (feasible) solutions and use evolutionary techniques in order to find new feasible solutions with a better objective value. See [3, 4, 13] for some exemplary procedures. A drawback of such algorithms is that they cannot guarantee to find optimal solutions in a finite amount of time.

Hence, we want to make use of a deterministic algorithm. Good surveys on deterministic methods in multiobjective optimization can be found in the books [22, 25]. Most of the known deterministic methods for biobjective optimization are based on the branch-and-bound approach, see, for example, [10, 21, 35]. The upper and lower bounds for “optimal” points in the image space are often obtained by using interval methods or Lipschitz properties of the objectives. For multiobjective optimization problems (with more than two objectives) only a few branch-and-bound algorithm exist, see [2, 9, 24, 28, 29]. In [24] an improved lower bounding procedure is introduced which uses $\alpha$BB underestimators and Benson’s outer approximation algorithm for convex multiobjective optimization problems, see [7, 19]. Furthermore, the proposed algorithm guarantees a certain accuracy of the computed solutions in the pre-image and in the image space.

1.4 Contribution

It is well known from the literature that using multiobjective counterparts can be highly beneficial as outlined above. In a short conference proceeding, see [8], it was already mentioned by the authors of this paper that solving the nonconvex multiobjective counterpart by a global solution technique can deliver feasible solutions for the original constrained single-objective problem, and first numerical experiments on problem (1) were performed.

In this work, after introducing the basic notations and definitions in Sect. 2, we examine the relations between constrained optimization problems and their multiobjective counterparts in detail, see Sect. 3. We also study $\varepsilon$-optimality as well as weak optimality notions. In Sect. 4, we present for the first time a branch-and-bound based algorithm for the specific nonconvex multiobjective counterpart problem. This algorithm is specifically tailored to find those points which deliver useful information for the original constrained optimization problem—without waisting time by a full determination of the nondominated set of the multiobjective counterpart. We prove the finiteness and the correctness of the proposed new algorithm.

In Sect. 5, we propose some possible post-processing for improving the results further. Finally, we illustrate the new algorithm on various test instances in Sect. 6. We conclude with Sect. 7.

2 Definitions and notations

In this paper, we focus on two variants of constrained optimization problems. Let $X\subseteq {\mathbb {R}}^n$ be a box, i.e., there are vectors ${\underline{x}}, {\overline{x}}\in {\mathbb {R}}^n$ with ${\underline{x}} \le {\overline{x}}$ and $X=\{x\in {\mathbb {R}}^n\mid {\underline{x}} \le x \le {\overline{x}}\}$. The inequality sign $\le$ has to be understood component-wise. Furthermore, let $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ and $g_k:{\mathbb {R}}^n\rightarrow {\mathbb {R}},\ k=1,\ldots ,r$ be twice continuously differentiable functions. For an arbitrary set $A\subseteq {\mathbb {R}}^n$, we denote the image set of A under the map f by $f(A):=\{ f(x)\in {\mathbb {R}}\mid x\in A\}$. The following two constrained optimization problems are equivalent in the sense that they have the same feasible set and objective functions.

We assume in the following that the feasible set S of ($P_1$) and ($P_2$) given by $S:=\{x\in X\mid g_k(x)\le 0, k=1,\ldots ,r\}$ is not empty. We denote the elements of the feasible set of the single-objective optimization problem by feasible solutions.

Definition 1

Let $\varepsilon >0$ be given.

• (i) A feasible solution ${\bar{x}}\in S$ is said to be minimal for ($P_1$) (or ($P_2$), respectively) if $f({\bar{x}})\le f(x)$ for all $x\in S$.

• (ii) A feasible solution ${\bar{x}}\in S$ is said to be $\varepsilon$-minimal for ($P_1$) (or ($P_2$), respectively) if $f({\bar{x}})< f(x)+\varepsilon$ for all $x\in S$.

Next, we formulate two box constrained multiobjective optimization problems that relax the constraints of ($P_1$) and ($P_2$), respectively, and reinterpret them as additional objective functions. We refer to these problems as the multiobjective counterparts to ($P_1$) and ($P_2$), respectively. The relations between the original problems and the counterpart problems are explored later.

Note that the bi-objective problem ($MOP_2$) has an objective function which is in general not differentiable. To simplify the notation, we define the mapping $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} G(x):=\max _{k=1,\ldots , r} g_k(x). \end{aligned}$$

Moreover, we write $(f,g_1,\dots ,g_r)(x)$ and (f, G)(x) to denote the objective vector of a solution $x\in X$ w.r.t. problem ($MOP_1$) and ($MOP_2$), respectively.

2.1 Multiobjective counterpart models

Multiobjective counterpart models fall in the class of multiobjective optimization problems. In this context, optimality concepts are based on comparing outcome vectors subject to order relations. We use the classical concept of Pareto dominance that is based on the following order relation for two vectors $x,y\in {\mathbb {R}}^m$ (see, for example, [6] or [22]):

$$\begin{aligned} x \le y\Leftrightarrow & {} x_j\le y_j \text{ for } \text{ all } j=1,\ldots , m\\ x \lneq y\Leftrightarrow & {} x_j\le y_j \text{ for } \text{ all } j=1,\ldots , m \text{ and } x\ne y\\ x\nleq y\Leftrightarrow & {} x_j> y_j \text{ for } \text{ at } \text{ least } \text{ one } j\in \{1,\ldots , m\} \\ x< y\Leftrightarrow & {} x_j < y_j \text{ for } \text{ all } j=1,\ldots , m \end{aligned}$$

The symbols $\ge , \gneq , \ngeq$ and > are defined analogously.

To simplify notation, we denote the vector-valued objective functions of ($MOP_1$) and ($MOP_2$) by $h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{1+r}$ with $h(x)=(f, g_1,\ldots , g_r)(x)$ and $h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{2}$ with $h(x)=(f, G)(x)$, respectively. Moreover, $e=(1,\ldots ,1)^T\in {\mathbb {R}}^{m}$ is the m-dimensional all-ones vector, where $m=1+r$ or $m=2$, respectively, depending on the dimension of the currently considered problem.

Remark 1

Note that the pair (($P_2$), ($MOP_2$)) is a special case of the pair (($P_1$), ($MOP_1$)) (with $r=1$ and $g_1(x)=G(x)$). The following definitions and relations will be formulated for (($P_1$), ($MOP_1$)). They hold equivalently for (($P_2$), ($MOP_2$)).

Definition 2

Let $\varepsilon >0$ be given.

• (i) A solution ${\bar{x}}\in X$ is said to be efficient for ($MOP_1$) if there does not exist another solution $x\in X$ with $h(x)\lneq h({\bar{x}})$. If $\bar{x}$ is efficient, then the corresponding outcome vector $h(\bar{x})$ is called nondominated.

• (ii) A solution ${\bar{x}}\in X$ is said to be weakly efficient for ($MOP_1$) if there does not exist another solution $x\in X$ with $h(x)< h({\bar{x}})$. If $\bar{x}$ is weakly efficient, then the corresponding outcome vector $h(\bar{x})$ is called weakly nondominated.

• (iii) A solution ${\bar{x}}\in X$ is said to be $\varepsilon$-efficient for ($MOP_1$) if there does not exist another solution $x\in X$ with $h(x)\lneq h({\bar{x}})-\varepsilon e$.

Note that for all considered optimization problems ($P_1$), ($P_2$), and ($MOP_1$), ($MOP_2$), an optimal or efficient solution exists, respectively, because both feasible sets S and X are compact sets and the objective functions are continuous. Moreover, for the efficient sets of ($MOP_1$) and ($MOP_2$) external stability holds since the ordering cone ${\mathbb {R}}^{m}_+$ is a pointed closed convex cone and $h(X):=\{h(x)\mid x\in X\}$ is a compact set, compare with [27, Theorem 3.2.9]. This means that for any $x\in X$ there exists some ${\tilde{x}}\in X$ with ${\tilde{x}}$ is efficient and $h({\tilde{x}})\le h(x)$. As a consequence, the next theorem, which is given for instance in [18], also holds for our setting.

Theorem 1

The set of minimal solutions of the constrained problem ($P_1$) always contains an efficient solution of the associated multiobjective counterpart problem ($MOP_1$), and all minimal solutions of ($P_1$) are weakly efficient for ($MOP_1$). Conversely, the set of efficient solutions of ($MOP_1$) contains at least one minimal solution of ($P_1$).

Since the pair (($P_2$), ($MOP_2$)) is a special case of the pair (($P_1$), ($MOP_1$)), see Remark 1, Theorem 1 also holds for (($P_2$), ($MOP_2$)). As it was explained in [18], the optimal solution of ($P_1$) can be calculated as a specific efficient solution of ($MOP_1$):

Theorem 2

Let $X_E$ be the efficient set for ($MOP_1$) and ${\bar{x}}\in {\text {argmin}}\{f(x)\mid x\in X_E\cap S\}$. Then ${\bar{x}}$ is minimal for ($P_1$).

In general, the determination of the complete efficient set is not practicable if only the solution of a single-objective constrained optimization problem ($P_1$) is sought. However, if an algorithm can compute an approximation of the efficient set in a region of interest, it is possible to find near-optimal solutions of the constrained optimization problem in reasonable time, and additionally provide trade-off information between objective values and constraint satisfaction.

2.2 Lower bounding by convex underestimators

Branch-and-bound algorithms heavily rely on lower bounds for the values of scalar-valued functions on subsets. One possible approach to obtain lower bounds is the formulation of so called convex underestimators. A convex underestimator of a function $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ on a box $X=[{\underline{x}}, {\overline{x}}]\subseteq {\mathbb {R}}^n$ is a convex function ${\underline{f}}:X\rightarrow {\mathbb {R}}$ with ${\underline{f}}(x)\le f(x)$ for all $x\in X$, see, for example, [1]. A convex underestimator for a twice continuously differentiable function f on X can, for example, be calculated as

$$\begin{aligned} {\underline{f}}(x):=f(x)+\frac{\alpha _f}{2}({\underline{x}}-x)^T({\overline{x}}-x), \end{aligned}$$

(2)

where $\alpha _f\ge \max \{0, -\min _{x\in X} \lambda _{\min , f}(x)\}$. Here, $\lambda _{\min ,f}(x)$ denotes the smallest eigenvalue of the Hessian $H_f(x)$ of f in x, see [20]. The minimal value of ${\underline{f}}$ over X, which can be calculated by standard techniques from convex optimization, delivers then a lower bound for the values of f on X. A lower bound for $\lambda _{\min ,f}(x)$ over X can be calculated easily with the help of interval arithmetic, see again [20]. For that, the Matlab toolbox Intlab can efficiently be used [26]. See also [31] for improved lower bounds. The above proposed and some other methods to obtain lower bounds for $\lambda _{\min ,f}(x)$ are described and tested in [1]. There are also other possibilities for the calculation of convex underestimators. For example in [1] special convex underestimators for bilinear, trilinear, fractional, fractional trilinear or univariate concave functions were defined. Here, we restrict ourselves to the above proposed convex underestimator. The theoretical results remain true in case that the above underestimators are replaced by tighter ones.

3 Relations between constrained optimization problems and their multiobjective counterparts

From Sect. 2 we already know that ($P_1$) and ($P_2$) are equivalent and that all optimal solutions of ($P_1$) and ($P_2$) are weakly efficient for ($MOP_1$) and ($MOP_2$), respectively.

Next to some obvious relations, we can state a relationship between the $\varepsilon$-minimal solutions of ($P_1$) and the $\varepsilon$-efficient solutions of ($MOP_1$). Due to Remark 1, an equivalent result holds for (($P_2$),($MOP_2$)).

Lemma 1

Let ${\bar{x}}\in S$ be $\varepsilon$-minimal for ($P_1$). Then ${\bar{x}}$ is $\varepsilon$-efficient for ($MOP_1$).

Proof

Since ${\bar{x}}\in S$ is $\varepsilon$-minimal for ($P_1$) it holds that $f({\bar{x}})< f(x)+\varepsilon$ for all $x\in S$. Now assume that ${\bar{x}}$ is not $\varepsilon$-efficient for ($MOP_1$). Then a solution ${\tilde{x}}\in X$ exists with

$$\begin{aligned} h({\tilde{x}})\lneq h({\bar{x}})-\varepsilon e, \end{aligned}$$

i.e., $f({\tilde{x}})\le f({\bar{x}})-\varepsilon$ and $g_k({\tilde{x}})\le g_k({\bar{x}})-\varepsilon$ for all $k=1,\ldots ,r$ (with at least one strict inequality). Since ${\bar{x}}\in S$ it follows that $g_k({\tilde{x}})\le 0-\varepsilon <0$ for all $k=1,\ldots ,r$ and thus ${\tilde{x}}$ is feasible for ($P_1$). But with $f({\tilde{x}})\le f({\bar{x}})-\varepsilon$ we obtain a contradiction to the $\varepsilon$-minimality of ${\bar{x}}$ for ($P_1$). $\square$

The relationship between the different solution categories for ($P_1$) and ($MOP_1$) according to Theorem 1 and Lemma 1 are visualized in Fig. 1.

Fig. 1

Venn diagram showing the relations between the solutions of ($P_1$) and ($MOP_1$)

In contrast to the equivalence between ($P_1$) and ($P_2$), the optimization problems ($MOP_1$) and ($MOP_2$) are in general not equivalent if $r\ge 2$. However, we can state the following lemma.

Lemma 2

Let ${\bar{x}} \in X$ be weakly efficient (or even efficient) for ($MOP_2$). Then ${\bar{x}}\in X$ is weakly efficient for ($MOP_1$).

Proof

Here we use $h:=(f,g_1,\ldots ,g_r)^T$. Assume that ${\bar{x}}$ is not weakly efficient for ($MOP_1$). Then there is an $x^*\in X$ with $h(x^*)<h({\bar{x}})$, i.e., $f(x^*)<f({\bar{x}})$ and $g_k(x^*)<g_k({\bar{x}})$ for $k=1,\dots ,r$. This implies $\max _{k=1,\ldots ,r} g_k(x^*)<\max _{k=1,\ldots ,r} g_k({\bar{x}})$, which contradicts the assumption that ${\bar{x}}$ is weakly efficient (or efficient) for ($MOP_2$). $\square$

To see that the inverse implication does not hold, set $f,g_1,g_2:{\mathbb {R}}\rightarrow {\mathbb {R}}$ with $f(x)=x^2$, $g_1(x)=x$, and $g_2(x)=-x$, and $X=[-5,5]$. Then all $x\in X$ are weakly efficient for ($MOP_1$), but only $x=0$ is weakly efficient for ($MOP_2$).

Note that for the special case that $r=1$ the two problems ($MOP_1$) and ($MOP_2$) are equivalent by definition.

Lemma 3

Let $X_E^{(MOP_1)}$ be the efficient set of ($MOP_1$) and $X_E^{(MOP_2)}$ be the efficient set of ($MOP_2$).

• (i) Let $r=1$ and ${\bar{x}}\in X_E^{(MOP_1)}$ with ${\bar{x}}\in {\text {argmax}}\{g_1(x)\mid x\in S\}$. Then ${\bar{x}}$ is minimal for ($P_1$).

• (ii) Let $r=1$ and ${\bar{x}}\in X_E^{(MOP_1)}$ with ${\bar{x}}\in {\text {argmax}}\{g_1(x)\mid x\in X_E^{(MOP_1)}\cap S\}$. Then ${\bar{x}}$ is minimal for ($P_1$).

• (iii) Let $r\ge 2$ and ${\bar{x}}\in X_E^{(MOP_2)}$ with ${\bar{x}}\in {\text {argmax}}\{\max _{k=1,\ldots ,r} g_k(x)\mid x\in S\}$. Then ${\bar{x}}$ is minimal for ($P_1$) and ($P_2$).

• (iv) Let $r\ge 2$ and ${\bar{x}}\in X_E^{(MOP_2)}$ with ${\bar{x}}\in {\text {argmax}}\{\max _{k=1,\ldots ,r} g_k(x)\mid x\in X_E^{(MOP_2)}\cap S\}$. Then ${\bar{x}}$ is minimal for ($P_1$) and ($P_2$).

Proof

• (i) Assume that ${\bar{x}}$ is not minimal for ($P_1$). Then there is a point $x^*\in S$ with $f(x^*)<f({\bar{x}})$ and $g_1(x^*)\le 0$. Moreover, it holds $g_1(x^*)\le g_1({\bar{x}})$. But this contradicts the efficiency of ${\bar{x}}$ for ($MOP_1$).

• (ii) Assume that ${\bar{x}}$ is not minimal for ($P_1$). Then there is a point $x^*\in S$ with $f(x^*)<f({\bar{x}})$ and $g_1(x^*)\le 0$. Since ${\bar{x}}\in X_E^{(MOP_1)}$ we obtain $g_1(x^*)>g_1({\bar{x}})$. Therefore, $x^*\notin X_E^{(MOP_1)}$, since otherwise ${\bar{x}}$ would not be an element of ${\text {argmax}}\{g_1(x)\mid x\in X_E^{(MOP_1)}\cap S\}$. For the optimization problem ($MOP_1$) external stability holds. Hence, since $x^*\not \in X_E^{(MOP_1)}$, there exists a point ${\tilde{x}}\in X_E^{(MOP_1)}$ with $f({\tilde{x}})\le f(x^*)<f({\bar{x}})$ and $g_1({\tilde{x}})\le g_1(x^*)\le 0$. The feasible solutions ${\bar{x}}$ and ${\tilde{x}}$ are both efficient of ($MOP_1$) and their images do not dominate each other. Therefore, $0\ge g_1({\tilde{x}})>g_1({\bar{x}})$ holds. This contradicts ${\bar{x}}\in {\text {argmax}}\{g_1(x)\mid x\in X_E^{(MOP_1)}\cap S\}$.

• (iii) The assertion that ${\bar{x}}$ is minimal for ($P_2$) follows analogously to (i). Because of the equivalence of ($P_1$) and ($P_2$), the point ${\bar{x}}$ is also minimal for ($P_1$).

• (iv) The assertion that ${\bar{x}}$ is minimal for ($P_2$) follows analogously to (ii). Because of the equivalence of ($P_1$) and ($P_2$), the point ${\bar{x}}$ is also minimal for ($P_1$).

$\square$

Note that a solution ${\bar{x}}$ according to Lemma 3, cases (i) and (iii), does not have to exist. Consider, for example, the simple linear problem $\min _{x\in S} f(x)$ with $f(x)=x$, $g_1(x)=x-1$, $X=[0,1]$, and $S=\{x\in X\mid x-1\le 0\}$. Then $X_E^{(MOP_1)}=\{0\}$ while ${\text {argmax}}\{g_1(x)\mid x\in S\}=\{1\}$ (note that $x^*=0$ is the unique minimal solution for ($P_1$) in this case). Moreover, Lemma 3, cases (iii) and (iv) with ${\bar{x}}\in X_E^{(MOP_1)}$ instead of ${\bar{x}}\in X_E^{(MOP_2)}$ do not hold in general. This is the reason why we focus on solving problem ($MOP_2$) rather than problem ($MOP_1$) in the following sections.

4 Multiobjective counterpart $\alpha$BB algorithm

We will now focus on the constrained optimization problem ($P_2$) and its multiobjective counterpart ($MOP_2$) as suggested at the end of Sect. 3.

To solve ($MOP_2$) we adapt the branch-and-bound based algorithm for nonconvex multiobjective optimization which was given in [24]. It is based on an iterative subdivision of the feasible set $X=[\underline{x},\overline{x}]$ into successively smaller boxes (see Sect. 4.1 below), combined with a bounding scheme that prunes irrelevant areas of the decision space. While this multiobjective $\alpha$BB algorithm determines an approximation of the complete nondominated set, the multiobjective counterpart $\alpha$BB algorithm (MOCP$\alpha$BB algorithm) directs the search towards the region of interest for the constrained problem ($P_2$) in order to avoid unnecessary computations as much as possible. More precisely, given a required accuracy $\varepsilon >0$, the multiobjective $\alpha$BB algorithm from [24] terminates with an approximation of the complete nondominated set of ($MOP_2$) that consists of $\varepsilon$-nondominated points (i.e., images of $\varepsilon$-efficient solutions) such that for every nondominated point y there exists a representative $\bar{y}$ in the approximation such that $\bar{y}-\frac{\varepsilon }{2} e\le y$. Recognizing the fact that in our case ($MOP_2$) is a multiobjective counterpart of a constrained optimization problem ($P_2$), we suggest appropriately adapted discarding tests (Sect. 4.2) as well as selection and termination rules (Sect. 4.3) to direct the search towards an optimal solution of the constrained problem. The overall MOCP$\alpha$BB algorithm is stated in Sects. 4.4 and 4.5 verifies the existence of appropriate bounds.

4.1 Box generation and branching scheme

The subdivision of the feasible set $X=[\underline{x},\overline{x}]$ of ($MOP_2$) in the decision space is implemented in the standard way of such subdivision algorithms. Thus, it is completely analogous to the subdivision as done in the multiobjective $\alpha$BB algorithm of [24]: Starting from the initial box $X=[\underline{x},\overline{x}]$, a series of subboxes is generated by iteratively splitting a currently selected box $X^{*}$ perpendicularly to a longest edge into two subboxes $X^1$ and $X^2$. For the description of the selection rule for a box $X^*$, which determines in which series the boxes are subdivided, we refer to Sect. 4.3.

We denote the list of current, also called active, boxes by $\mathcal {L}_W$. The list ${{\mathcal {L}}}_W$ is also denoted as working list in the following, and it is initialized with X. The method terminates when the list ${{\mathcal {L}}}_W$ is empty. During the course of the algorithm, boxes that can not contribute to the approximation of the optimal set of problem ($P_2$) are discarded from further consideration. On the other hand, boxes that have achieved a certain accuracy w.r.t. the current bound sets and for which a further refinement is not promising are stored in a tentative solution list ${\mathcal {L}}_S$.

4.2 Bound computation and discarding test

A central element in the MOCP$\alpha$BB algorithm is the discarding test which is used to prune selected boxes from the list ${{\mathcal {L}}}_W$ that do not contain (near) optimal solutions of ($P_2$). For this purpose, upper and lower bounds are computed based on solutions of ($MOP_2$) (upper bounds) and convex underestimators over selected subboxes (lower bounds), respectively.

Upper Bounds During the course of the MOCP$\alpha$BB algorithm and while exploring selected boxes from ${{\mathcal {L}}}_W$, we generate a stable set ${\mathcal {L}}_{PNS}$ of feasible outcome vectors (called provisional nondominated set) representing upper bounds for the global nondominated points of ($MOP_2$). In this context, a set ${\mathcal {N}}\subset {\mathbb {R}}^m$ is called stable if for any $y^1, y^2\in {\mathcal {N}}, y^1\nleq y^2$ holds. Every time a point q is a new candidate for ${\mathcal {L}}_{PNS}$, we check if this point is dominated by any other point of ${\mathcal {L}}_{PNS}$. In this case, q will not be included in ${\mathcal {L}}_{PNS}$. Otherwise, q will be added to ${\mathcal {L}}_{PNS}$ and all points that are dominated by q are removed. Figure 2 shows an example for a provisional nondominated set ${\mathcal {L}}_{PNS}$ for an instance of ($MOP_2$). Note that in the biobjective case considered here, the points $y=(f,G)(x)$ in ${\mathcal {L}}_{PNS}$ can be ordered such that their objective function values f(x) are strictly increasing while their largest constraint values $G(x)=\max _{k=1,\dots ,r}g_k(x)$ are strictly decreasing.

Fig. 2

Example for ${\mathcal {L}}_{PNS}$ for an instance of ($MOP_2$), marked with filled circles, and points $q^1$ and $q^2$ defined in (3) and (4). The point ${\bar{p}}=(q^2_1, q^1_2)^T$ upper bounds the region of interest

Since we want to direct the search towards the region of interest of the constrained problem ($P_2$), we are particularly interested in the two points from ${\mathcal {L}}_{PNS}$ defined by

$$\begin{aligned} q^1:= & {} {\text {argmin}}_{p\in {\mathcal {L}}_{PNS}}\{p_2\mid p_2>0\} \text{ and } \end{aligned}$$

(3)

$$\begin{aligned} q^2:= & {} {\text {argmax}}_{p\in {\mathcal {L}}_{PNS}}\{p_2\mid p_2\le 0\}, \end{aligned}$$

(4)

see Fig. 2 for an illustration. Intuitively, these are the points of ${\mathcal {L}}_{PNS}\subseteq {\mathbb {R}}^2$ which are “around” $G(x)=0$. Note that $q^1={{\text {argmax}}_{p\in {\mathcal {L}}_{PNS}}\{p_1\mid p_2>0\}}$ and $q^2={{\text {argmin}}_{p\in {\mathcal {L}}_{PNS}}\{p_1\mid p_2\le 0\}}$ also hold. It is possible that one of the two points does not exist. This case is considered in Sect. 4.5. For the remainder of this section, we assume that both points $q^1$ and $q^2$ exist. Note that, as the list ${\mathcal {L}}_{PNS}$ changes its cardinality and preciseness during the algorithm, the points $q^1$ and $q^2$ generally change their position during the procedure.

Lower Bounds A main ingredient of the adapted discarding test in our new MOCP$\alpha$BB algorithm is to calculate lower bounds for the image set of a selected box $X^*$ from $\mathcal {L}_W$, i.e., a set LB such that $LB+{\mathbb {R}}^2_+$ is a superset of $\{y\in {\mathbb {R}}^2\mid \exists x\in X^*: y_1=f(x), y_2= G(x)\}$, and compare them with the upper bounds $q^1$ and $q^2$ of the interesting part of the nondominated set.

As a lower bound for the image set of a box $X^*$, we use the so called ideal point of convex underestimators of the objective functions on the considered box $X^*$. In general, the ideal point of a vector-valued function consists of the global minimal values of each function. For ($MOP_2$) this is the point $a=(a_1,a_2)^T$ with

$$\begin{aligned} a_1=\min _{x\in X^*} f(x) \text{ and } a_2=\min _{x\in X^*} G(x) =\min _{x\in X^*}(\max _{k=1,\ldots ,r} g_k(x)). \end{aligned}$$

Determining a in the nonconvex case is not possible without applying techniques from global optimization, which are time consuming. As we have to calculate ideal points repeatedly over many subboxes, we use convex underestimators as defined in Sect. 2.2 for both objective functions. The ideal point of the convex underestimators is denoted by $({\underline{f}}, {\underline{G}})^T$ and is calculated as

$$\begin{aligned} {\underline{f}}=\min _{x\in X^*} f_\alpha (x) \text{ and } {\underline{G}}=\min _{x\in X^*}G_\beta (x), \end{aligned}$$

(5)

where $f_\alpha$ is a convex underestimator of f on $X^*$ and $G_\beta$ is a convex underestimator of G on $X^*$. While we can directly use the convex underestimator (2) to define $f_\alpha$, the particular structure of G as the maximum of r functions suggests several alternative definitions based on (2). In the following lemma, we propose two such definitions for $G_\beta$.

Lemma 4

Let a box $X^*=[{\underline{x}}^*, {\overline{x}}^*]$ be given. Moreover, let $g_k:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, ${k=1,\ldots ,r}$ be twice continuously differentiable functions and let $g_{k,\beta _k}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be the corresponding convex underestimators on $X^*$ according to (2), i. e.,

$$\begin{aligned} g_{k,\beta _k}(x):=g_k(x)+\frac{\beta _k}{2}({\underline{x}}^*-x)^T({\overline{x}}^*-x) \end{aligned}$$

with sufficiently large $\beta _k>0$. Define the map $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ by $G(x):=\max _{k=1,\ldots ,r} g_k(x)$. Then the functions $G_\beta ,G_{{\tilde{\beta }}}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ with

$$\begin{aligned} G_\beta (x)= & {} \max _{k=1,\ldots ,r} g_{k,\beta _k}(x)\\ G_{{\tilde{\beta }}}(x)= & {} \left( \max _{k=1,\ldots ,r} g_k(x)\right) +\frac{{\tilde{\beta }}}{2}({\underline{x}}^*-x)^T({\overline{x}}^*-x) \text{ with } {\tilde{\beta }}:=\max _{k=1,\ldots , r}\beta _k \end{aligned}$$

are convex underestimators of G on $X^*$.

Proof

Follows immediately from [20] and the fact that the maximum of convex functions is again a convex function. $\square$

While $G_{\tilde{\beta }}$ is probably the more intuitive choice for a convex underestimator since it follows directly from (2), the convex underestimator $G_{\beta }$ is generally preferable since it provides stronger lower bounds. To illustrate this, consider an optimization problem with two constraints $g_1$ and $g_2$ where $g_1(x)\ge g_2(x)$ for all $x\in X^*$. Additionally, assume that $g_1$ is a convex function and $g_2$ is nonconvex. Therefore, $\beta _1=0$ and $\beta _2> 0$, and hence $g_{2,\beta _2}(x)\le g_2(x)\le g_1(x)=g_{1,\beta _1}(x)$ hold for all $x\in X^*$. Then, we obtain for the convex underestimators for G on $X^*$:

$$\begin{aligned} G_\beta (x)= g_1(x) \text{ and } G_{{\tilde{\beta }}}(x)=g_1(x)+\frac{\beta _2}{2}({\underline{x}}^*-x)^T({\overline{x}}^*-x), \end{aligned}$$

and hence $G_\beta (x)\ge G_{{\tilde{\beta }}}(x)$ holds for all $x\in X^*$. The following lemma shows that this is true in general, i.e., $G_\beta$ is indeed a stronger convex underestimator than $G_{\tilde{\beta }}$.

Lemma 5

Under the assumptions of Lemma 4, it holds that $G_{\tilde{\beta }}(x) \le G_\beta (x)$ for all $x\in X^*$.

Proof

Let $x\in X^*$ be arbitrary but fixed, and let $k^*\in \{1,\dots ,r\}$ be an index for which $g_{k^*}(x)=\max _{k=1,\dots ,r} g_k(x)$. Then $\tilde{\beta }=\max _{k=1,\dots ,r}\beta _k\ge \beta _{k^*}$ and hence

$$\begin{aligned} G_{\tilde{\beta }}(x)= & {} \left( \max _{k=1,\ldots ,r} g_k(x)\right) +\frac{{\tilde{\beta }}}{2}\underbrace{({\underline{x}}^*-x)^T}_{\le 0}\underbrace{({\overline{x}}^*-x)}_{\ge 0}\\\le & {} g_{k^*,\beta _{k^*}}(x) + \frac{\beta _{k^*}}{2}({\underline{x}}^*-x)^T({\overline{x}}^*-x)\\\le & {} \max _{k=1,\dots ,r} g_{k,\beta _k}(x) = G_\beta (x). \end{aligned}$$

$\square$

Thereby, $G_\beta$ is the preferred convex underestimator and is used in our procedure. As $G_\beta$ is in general not differentiable, we solve the smooth convex optimization problem to obtain the minimum of $G_\beta$ on the box $X^*$:

$$\begin{aligned} \min _{x\in X^*,\ t\in {\mathbb {R}}} t \text{ s.t. } g_{k,\beta _k}(x)\le t,\quad k=1,\ldots ,r. \end{aligned}$$

(6)

Discarding Tests The following lemma is the basis for the first two discarding tests.

Lemma 6

Let $q^1$ and $q^2$ be defined as in (3) and (4). Moreover, let $({\underline{f}}, {\underline{G}})^T$ be a lower bound vector, where ${\underline{f}}$ and ${\underline{G}}$ are lower bounds for f and G on $X^*$, respectively. If ${\underline{f}}>q^2_1$ or ${\underline{G}}> q^1_2$ holds, the box $X^*$ does not contain any minimal solution of ($P_2$).

Proof

If the first condition ${\underline{f}}>q^2_1$ holds, we obtain $q^2_1<{\underline{f}}\le f(x) \text{ for } \text{ all } x\in X^*$. Moreover, the point $q^2$ is the objective vector of a solution ${\tilde{x}} \in X$, and by (4) it holds $G({\tilde{x}})=q^2_2\le 0$. Hence, $q^2$ is an image of a feasible solution ${\tilde{x}}$ of ($P_2$) and the objective function value $q^2_1=f({\tilde{x}})$ is less than any function value attainable in $X^*$. Thus, there is no minimal solution for ($P_2$) in $X^*$ in this case.

If ${\underline{G}}>q^1_2$ holds, by (3) it follows $0<q^1_2< {\underline{G}}\le G(x)=\max _{k=1,\ldots ,r} g_k(x)$ for all $x\in X^*$. Hence, for every $x\in X^*$ there is at least one constraint $g_k$ with $g_k(x)>0$. This means that every $x\in X^*$ is infeasible for ($P_1$) and cannot be a minimal solution of ($P_1$). $\square$

Note that the set $\{({\underline{f}}, {\underline{G}})^T\}+{\mathbb {R}}^2_+$ can be interpreted as an outer approximation of the convex set

$$\begin{aligned} {\mathcal {P}}:=\{y\in {\mathbb {R}}^2\mid y_1=f_\alpha (x), y_2=G_\beta (x), x\in X^*\}+{\mathbb {R}}^2_+ \end{aligned}$$

(7)

and that the discarding test of Lemma 6 actually tests whether ${\bar{p}}:=(q^2_1,q^1_2)^T \not \in \{({\underline{f}}, {\underline{G}})^T\}+{\mathbb {R}}^2_+$ (and hence ${\bar{p}} \not \in {\mathcal {P}}$), see Fig. 2 for an illustration of ${\bar{p}}$. In this context, an outer approximation of a set $A\subseteq {\mathbb {R}}^2$ is given by a set $LB\subseteq {\mathbb {R}}^2$ such that $A\subseteq LB+{\mathbb {R}}^2_+$.

While the discarding test of Lemma 6 is very simple and can be easily evaluated, it is rather weak in practice. In order to obtain a tighter outer approximation of the set $(f_\alpha ,G_\beta )(X^*)$ and, hence, to strengthen the discarding test, we replace the ideal point of the convex underestimators by an improved lower bound set LB that is implicitly obtained from solving a single-objective convex optimization problem to decide whether ${\bar{p}}$ belongs to ${\mathcal {P}}$:

A minimal solution of ($P^*_{X^*,\,{\bar{p}}}$) is named $({\tilde{x}},{\tilde{t}})$. If ${\tilde{t}}\le 0$ holds, we have ${\bar{p}}\in {\mathcal {P}}$. Otherwise, if ${\tilde{t}}>0$ holds, the point ${\bar{p}}$ lies outside ${\mathcal {P}}$ and can thus be separated from ${\mathcal {P}}$ with a supporting hyperplane that can be constructed from a Lagrange multiplier $\lambda ^*\in {\mathbb {R}}^{1+r}$ for the inequality constraints of ($P^*_{X^*,\,{\bar{p}}}$): Given $\lambda ^*$, a normal vector of this hyperplane is obtained as $(\lambda _1^*, 1-\lambda _1^*)=(\lambda _1^*,\sum _{k=2}^{r+1}\lambda _k^*)\in {\mathbb {R}}^2$. Moreover, a support vector of this hyperplane is ${\bar{p}}+{\tilde{t}}e$. This result can be shown by using necessary and sufficient optimality conditions for nonsmooth, convex optimization problems with linear constraints.

Note that the outer approximation of ${\mathcal {P}}$ gets indeed improved by using the constructed supporting hyperplane, since the point $\bar{p}$ is infeasible for this improved approximation.

The next lemma formally proves the above mentioned fact that a box can be discarded for ${\tilde{t}}>0$.

Lemma 7

Let ${\mathcal {L}}_{PNS}$ be a stable subset of h(X), $X^*\subseteq {\mathbb {R}}^n$ be a box, $f_\alpha$ and $G_\beta$ be the convex underestimators of f and G on $X^*$ and $q^1, q^2$ be defined as in (3) and (4). Moreover, consider the optimization problem ($P^*_{X^*,\,{\bar{p}}}$) with ${\bar{p}}=(q^2_1, q^1_2)^T$ with the minimal solution $({\tilde{x}},{\tilde{t}})$. If ${\tilde{t}}>0$ holds, then $X^*$ does not contain any minimal solution for ($P_1$).

Proof

Assume that there is a minimal solution $x^*$ for ($P_1$) with $x^*\in X^*\cap S$. The point $q^2$ is the function value of a feasible solution ${\tilde{x}} \in S$, i.e., there is an ${\tilde{x}}\in S$ with

$$\begin{aligned} q^2_1=f({\tilde{x}}). \end{aligned}$$

(8)

Consider the pair $(x^*,0)\in {\mathbb {R}}^{n+1}$. Using the minimality and feasibility of $x^*$ and properties of convex underestimators, we obtain that this pair is feasible for ($P^*_{X^*,\,{\bar{p}}}$):

$$\begin{aligned} \begin{array}{ll} {\bar{p}}_1+0\ge f_\alpha (x^*), &{} \text{ because } {\bar{p}}_1=q_1^2=f({\tilde{x}})\ge f(x^*)\ge f_\alpha (x^*)\\ {\bar{p}}_2+0\ge {g_{k,\beta _k}(x^*)} , &{} \text{ because } {\bar{p}}_2=q_2^1>0\ge g_k(x^*)\ge g_{k,\beta _k}(x^*)\\ &{}\text{ for } \text{ all } k=1,\ldots ,r. \end{array} \end{aligned}$$

This is a contradiction to the minimality of ${\tilde{t}}>0$. $\square$

Note that the optimization problem ($P^*_{X^*,\,{\bar{p}}}$) is also used for a termination procedure which is discussed in Sect. 4.3 below.

4.3 The selection and termination rule

A selection rule determines within the branch-and-bound procedure which of the remaining subboxes is selected next to be bisected. The aim of every selection rule is to identify boxes whose subboxes deliver good bounds for the globally minimal value. Such rules are usually heuristic. A common rule in multiobjective optimization is to choose the box which has the smallest lower bound w.r.t. one (arbitrary but fixed) objective function, or w.r.t. a weighted sum of all objectives. In our case, we are interested in the minimization of f, but also in finding at least one feasible solution of ($P_1$). Therefore, as long as no point $q^2$ exists, a box with the smallest lower bound for G is selected as the next box which will be bisected, while a box with the smallest calculated lower bound for f is chosen otherwise.

The termination rule decides whether a box is discarded, whether it is stored in the solution list ${\mathcal {L}}_S$ (and thus not further bisected), or whether it is stored in the working list ${\mathcal {L}}_W$ (i.e., the list of active boxes that will be analyzed further). In the work of [24], a termination procedure is introduced which guarantees some accuracies of calculated points in the decision and in the objective space. The minimal solution of the optimization problem ($P^*_{X^*,\,{\bar{p}}}$) plays an essential role for the decision to store a box in the solution list. For our algorithm we use a simpler rule in the first part, which ensures an accuracy of $q^1$ and $q^2$:

1. Termination rule: Solve ($P^*_{X^*,\,{\bar{p}}}$) for the box $X^*$ and ${\bar{p}}=(q^2_1, q^1_2)^T$, where $q^1$ and $q^2$ are defined as in (3) and (4). The minimal solution is denoted by $({\tilde{x}},{\tilde{t}})$. Store $X^*$ in ${\mathcal {L}}_S$ if $0\ge {\tilde{t}}\ge -\frac{\varepsilon }{2}$ holds for a given $\varepsilon >0$.

Note that in case of ${\tilde{t}}>0$, the box is discarded because of Lemma 7.

4.4 The MOCP$\alpha$BB algorithm

As mentioned in Sect. 4.1, the MOCP$\alpha$BB algorithm is based on a box subdivision of $X=[\underline{x},\overline{x}]$. For all not-discarded boxes $X^*$ in the working list ${\mathcal {L}}_W$ and in the solution list ${\mathcal {L}}_S$, an outer approximation of the set ${\mathcal {P}}$ (which is an underestimation of possible outcome vectors on $X^*$, see (7)) is encoded in a set ${\mathcal {H}}$. This outer approximation is initialized using the ideal point $(\underline{f},\underline{G})$ of ${\mathcal {P}}$ and further refined whenever additional supporting hyperplanes of ${\mathcal {P}}$ become available. Every element of ${\mathcal {H}}$ is a pair consisting of the normal vector $\lambda$ of the hyperplane and a scalar value, which is the scalar product of $\lambda$ and one point belonging to the hyperplane. Thus, the initial outer approximation of ${\mathcal {P}}$ obtained by minimizing the convex underestimators on the box $X^*$ is given by

$$\begin{aligned} {\mathcal {H}}=\{((1,0)^T, {\underline{f}}), \mathcal ((0,1)^T, {\underline{G}})\}. \end{aligned}$$

Hence, the lower bounds ${\underline{f}}$ and ${\underline{G}}$ for each objective are stored in ${\mathcal {H}}$ as well.

The complete algorithm consists of two parts. The first part stated above is the main part and includes the discarding test as well as the selection and termination rule which are explained in the previous sections. The second part is a post processing algorithm which includes different (optional) steps in order to further improve the solution quality.

The following theorem states that the algorithm (without the post processing) terminates. We omit the proof as it is a special case of the proof of Lemma 4.1 of [24].

Theorem 3

Algorithm 1 needs finitely many subdivisions in line 7.

Next, we want to derive some properties of the points $q^1$ and $q^2$ computed with Algorithm 1. These properties will be used in a post processing for further improvements.

Theorem 4

Let $q^1, q^2$ be defined by (3) and (4) after Algorithm 1, line 26. In particular, assume that both exist. Denote the pre-images of $q^1$ and $q^2$ by $x^1$ and $x^2$, respectively. Then $x^1$ and $x^2$ are $\varepsilon$-efficient of ($MOP_1$) and ($MOP_2$). Additionally, to each $x^1$ and $x^2$ exist some boxes $X^1, X^2\in {\mathcal {L}}_S$ with $x^1\in X^1$ and $x^2\in X^2$.

Proof

The solution $x^1$ is the pre-image of $q^1$, i.e., it holds $f(x^1)=q^1_1$ and ${\max _{k=1,\ldots ,r}g_k(x^1)}=G(x^1)=q^1_2$. Assume that $x^1$ is not $\varepsilon$-efficient for ($MOP_1$) or for ($MOP_2$). Then there is a solution $x'\in X$ with

$$\begin{aligned} f(x')\le & {} q^1_1-\varepsilon \end{aligned}$$

(9)

$$\begin{aligned} g_k(x')\le & {} G(x') \le q^1_2-\varepsilon \text{ for } \text{ all } k=1,\ldots ,r, \end{aligned}$$

(10)

and at least one inequality is strict. First assume that $x'$ belongs to a box $X'\in {\mathcal {L}}_{S}$. Then the termination rule implies that the minimal solution of ($(P^*_{X',\, {\bar{p}}})$) is $({\tilde{x}},{\tilde{t}})$ with $-\frac{\varepsilon }{2}\le {\tilde{t}}\le 0$. Consider the pair $(x',-\varepsilon )\in {\mathbb {R}}^{n+1}$ for the optimization problem ($(P^*_{X',\, {\bar{p}}})$) with ${\bar{p}}=(q^2_1,q^1_2)$ as before. Then, with (9) and (10) we obtain

$$\begin{aligned}&x'\in X',\\&q^2_1+(-\varepsilon )\ge q^1_1-\varepsilon \ge f(x')\ge f_\alpha (x'),\\&q^1_2+(-\varepsilon ) \ge G(x')\ge g_k(x')\ge g_{k,\beta _k}(x') \text{ for } \text{ all } k=1,\ldots ,r \end{aligned}$$

All constraints of ($(P^*_{X',\, {\bar{p}}})$) are satisfied. Thus, $(x',-\varepsilon )$ is feasible for ($(P^*_{X',\, {\bar{p}}})$), but this contradicts the minimality of ${\tilde{t}}\ge -\frac{\varepsilon }{2}$.

We can conclude that, since the algorithm terminates, $x'$ has to belong to a box $X'$ which was discarded. There are two conditions based on which a box can be discarded. Either because of the test from Lemma 7 or from Lemma 6. As $(x',-\varepsilon )$ is still feasible for ($(P^*_{X',\, {\bar{p}}})$), we can see that $X'$ was not discarded because of Lemma 7.

Let $({\underline{f}}', {\underline{G}}')$ be the ideal point of the convex underestimators of f and G on $X'$. Then the two reasons for discarding $X'$ from Lemma 6 are still possible: (a) ${\underline{f}}'>q^2_1$ and (b) ${\underline{G}}'> q^1_2$. For case (a), we obtain with (9) the following chain of inequalities:

$$\begin{aligned} q^1_1<q^2_1<{\underline{f}}'\le f_\alpha (x')\le f(x') \le q^1_1-\varepsilon . \end{aligned}$$

This is a contradiction to $\varepsilon >0$. Case (b) leads with (10) to

$$\begin{aligned} q^1_2<{\underline{G}}'\le G_\beta (x')\le G(x') \le q^1_2-\varepsilon , \end{aligned}$$

which contradicts $\varepsilon >0$ as well. Hence, $x'$ does not exist and $x^1$ is $\varepsilon$-efficient for ($MOP_1$) and ($MOP_2$).

Now choose any box $X^*$, which is considered during Algorithm 1, with $x^1\in X^*$. Let $({\underline{f}}, {\underline{G}})$ be the ideal point of convex underestimators of f and G on $X^*$. As

$$\begin{aligned} {\underline{f}}= & {} \min _{x\in X^*} f_\alpha (x)\le f_\alpha (x^1)\le f(x^1)=q^1_1<q^2_1 \text{ and }\\ {\underline{G}}= & {} \min _{x\in X^*} G_\beta (x)\le G_\beta (x^1)\le G(x^1)=q^1_2 \end{aligned}$$

hold even for the final points $q^1, q^2$, $X^*$ can not have been discarded by Lemma 6. In addition, with $(x^1,0)\in {\mathbb {R}}^{n+1}$ a feasible solution for ($P^*_{X^*,\,{\bar{p}}}$) is found and thus, for the minimal value ${\tilde{t}}$ of this optimization problem ${\tilde{t}}\le 0$ holds. Hence, $X^*$ does not get discarded. As the algorithm terminates (as shown in Theorem 3) there exists a subbox $X^1$ with $x^1\in X^1\subseteq X^*$ which is stored in ${\mathcal {L}}_S$.

The proof for $x^2$ is analogous. Note that $G(x^2)\le 0< q^1_2$ holds. $\square$

Figure 3 shows that the pre-image of $q^2$ does not have to be $\varepsilon$-minimal for the single-objective problem ($P_1$). Indeed, even in cases where $q^2_2=0$ holds, $f(x^2)=q^2_1$ may be arbitrarily far away from the optimal value $f^*$.

Fig. 3

Example where pre-image of $q^2$ is not $\varepsilon$-minimal of ($P_1$)

Nevertheless, the following lemma states that we can enclose the image point of a minimal solution for ($P_1$) by a tube-shaped set determined by ${\bar{p}}$ and ensure the $\varepsilon$-minimality for ($P_1$) of the pre-image of $q^2$ in a special case.

Lemma 8

Let $x^*$ be a minimal solution of ($P_1$). Then

$$\begin{aligned} (f,G)(x^*)\in (\{{\bar{p}}\}-{\mathbb {R}}^2_+)\setminus (\{{\bar{p}}-\frac{\varepsilon }{2}e\}-int ({\mathbb {R}}^2_+)). \end{aligned}$$

A direct consequence from this is that if $q^1_2>\frac{\varepsilon }{2}$ holds, the pre-image of $q^2$ is $\varepsilon$-minimal for ($P_1$) (actually $(\frac{\varepsilon }{2}+\mu )$-minimal for all $\mu >0$).

Proof

Since $x^*$ is minimal for ($P_1$) and because of the definition of $q^1$ and $q^2$ (see (3) and (4)), we know that $f(x^*)\le q^2_1$ and $G(x^*)\le 0<q^1_2$. Hence, $(f,G)(x^*)\in \{(q^2_1,q^1_2)^T\}-{\mathbb {R}}^2_+=\{{\bar{p}}\}-{\mathbb {R}}^2_+$ holds. Assume now that $(f,G)(x^*)\in \{{\bar{p}}-\frac{\varepsilon }{2}e\}-int ({\mathbb {R}}^2_+)$, i.e., $f(x^*)<q^2_1-\frac{\varepsilon }{2}$ and $g(x^*)<q^1_2-\frac{\varepsilon }{2}$. Then we can choose a parameter $\mu '>0$ such that

$$\begin{aligned} f(x^*)\le q^2_1-(\frac{\varepsilon }{2}+\mu ') \ \text{ and } \ g(x^*)\le q^1_2-(\frac{\varepsilon }{2}+\mu '). \end{aligned}$$

Let $X^*$ be a box from the solution list ${\mathcal {L}}_S$ with $x^*\in X^*$. Because of Lemma 7 and the termination rule, $X^*$ was not discarded, i.e., for the minimal solution $({\tilde{x}}, {\tilde{t}})$ of ($P^*_{X^*,\,{\bar{p}}}$) it holds $0\ge {\tilde{t}}\ge -\frac{\varepsilon }{2}$. But $(x^*,-(\frac{\varepsilon }{2}+\mu ))$ is feasible for ($P^*_{X^*,\,{\bar{p}}}$), which contradicts the minimality of ${\tilde{t}}\ge -\frac{\varepsilon }{2}$. This shows the first part of the result, i.e., that $(f,G)(x^*)\in (\{{\bar{p}}\}-{\mathbb {R}}^2_+)\setminus (\{{\bar{p}}-\frac{\varepsilon }{2}e\}-int ({\mathbb {R}}^2_+))$ holds.

The second part follows immediately: As $(f,G)(x^*)\notin \{{\bar{p}}-\frac{\varepsilon }{2}e\}-int ({\mathbb {R}}^2_+)$, we have two possible cases: $G(x^*)\ge q^1_2-\frac{\varepsilon }{2}$ or $f(x^*)\ge q^2_1-\frac{\varepsilon }{2}$. Because of $q^1_2>\frac{\varepsilon }{2}$, we obtain $q^1_2-\frac{\varepsilon }{2}>0$, and hence $G(x^*)\ge q^1_2-\frac{\varepsilon }{2}$ can not hold because of the feasibility of $x^*$ for ($P_1$). Hence, $f(x^*)\ge q^2_1-\frac{\varepsilon }{2}$ holds. Using the minimality of $x^*$, it follows that

$$\begin{aligned} q^2_1\le f(x^*)+\frac{\varepsilon }{2}<f(x^*)+\frac{\varepsilon }{2}+\mu \le f(x)+\frac{\varepsilon }{2}+\mu \ \text{ for } \text{ all } \ \mu >0,\ x\in S. \end{aligned}$$

Consequently, the pre-image of $q^2$ is $(\frac{\varepsilon }{2}+\mu )$-minimal for ($P_1$), and, in particular, $\varepsilon$-minimal for ($P_1$). $\square$

4.5 Existence of $q^1$ and $q^2$

Recall the definitions of $q^1$ and $q^2$ from (3) and (4). The list ${\mathcal {L}}_{PNS}$ is not empty after a first element is added to this list at the beginning. Therefore, at least one of the two points $q^1,q^2$ exists. However, it is possible that only one of the two points exists during the whole course of the algorithm. This is, for example, the case when $X=S$ or $S=\emptyset$ holds. Nevertheless, we can still define a suitable point ${\bar{p}}$ which can be used for initializing the discarding test from Lemma 7.

$$\begin{aligned} {\bar{p}} :={\left\{ \begin{array}{ll} (q^2_1,q^1_2)^T ,&{} \text{ if } q^1 \text{ and } q^2 \text{ exist }\\ (q^2_1, M)^T ,&{} \text{ if } \text{ only } q^2 \text{ exists } \\ (M, q^1_2)^T ,&{} \text{ if } \text{ only } q^1 \text{ exists }\end{array}\right. } \end{aligned}$$

(11)

Thereby, the constant real number M has to be chosen as an upper bound of $f(\cdot )+\varepsilon$ and $G(\cdot )+\varepsilon$ on the box X, i. e.,

$$\begin{aligned} M\ge \max \{\max _{x\in X}f(x),\max _{x\in X}G(x)\}+\varepsilon . \end{aligned}$$

Such an upper bound can be calculated by interval arithmetic, for instance. If one of the two points $q^1,q^2$ does not exist, it is clearly not possible to apply the corresponding discarding test from Lemma 6 which depends on the missing point. Recall from Sect. 4.3 that the rule to select a box from ${\mathcal {L}}_W$ depends on the existence of $q^2$ as well. As long as $q^2$ does not exist, a box with a smallest lower bound for G is chosen, otherwise the box with a smallest lower bound for f is selected.

By the next lemma, we observe that in case that feasible solutions for problem ($P_2$) exist, the algorithm is able to find at least a so-called $\frac{\varepsilon }{2}$-feasible solution for ($P_2$), i.e., it finds a solution $x\in {\mathbb {R}}^n$ with $G(x)\le \frac{\varepsilon }{2}$.

Lemma 9

If $S\ne \emptyset$ holds, Algorithm 1 finds at least an $\frac{\varepsilon }{2}$-feasible solution for ($P_2$) (within the main while-loop).

Proof

If Algorithm 1 finds a solution x with $(f,G)(x)=q^2$, then x is feasible for ($P_2$) and, thus, also $\frac{\varepsilon }{2}$-feasible. We thus have to consider the case that $q^2$ does not exist. Then $q^1$ exists and $\bar{p}=(M,q^1_2)^T$. If $q^1_2=\bar{p}_2\le \frac{\varepsilon }{2}$, then $q^1$ is $\frac{\varepsilon }{2}$-feasible and the statement is satisfied. Otherwise, we have that $q^1_2=\bar{p}_2>\frac{\varepsilon }{2}$.

Every time a box $X^*$ that contains feasible solutions for ($P_2$) is considered, we obtain for this box a lower bound ${\underline{G}}\le 0$ for G. Define $x^f\in {\text {argmin}}\{f_\alpha (x)\mid x\in X^*\}$ and $x^G\in {\text {argmin}}\{G_\beta (x)\mid x\in X^*\}$. Then the images of $x^f$ and $x^G$ are possible candidates for ${\mathcal {L}}_{PNS}$. If one of $x^f$ and $x^G$ is feasible for ($P_2$), then the algorithm has found a point $q^2$. Similarly, if one of $x^f$ and $x^G$ is $\frac{\varepsilon }{2}$-feasible for ($P_2$), then the image of this point is added to ${\mathcal {L}}_{PNS}$ and an $\frac{\varepsilon }{2}$-feasible solution is found. Otherwise, $G(x^f)>\frac{\varepsilon }{2}$ and $G(x^G)>\frac{\varepsilon }{2}$ hold, i. e., $x^f$ and $x^G$ are both infeasible for ($P_2$). In this case, problem ($P^*_{X^*,\,{\bar{p}}}$) is equivalent to

$$\begin{aligned} \begin{array}{rl} \min \limits _{(x,t)\in {\mathbb {R}}^{n+1}} t \text{ s.t. } &{} x\in X^*, \\ &{} M+t\ge f_\alpha (x), \\ &{} {\bar{p}}_2+t\ge G_{\beta }(x). \end{array} \end{aligned}$$

Note that the first constraint induced by $\bar{p}$, $M+t\ge f_\alpha (x)$, is satisfied for all $x\in X^*$ and for all $t\ge -\varepsilon$ if M is chosen as described above. Moreover, $\bar{p}_2>\frac{\varepsilon }{2}$ and $G_{\beta }(x^G)\le 0$ (recall that $x^G\in X^*$) imply that an optimal solution $({\tilde{x}},{\tilde{t}})$ of problem ($P^*_{X^*,\,{\bar{p}}}$) satisfies ${\tilde{t}}<-\frac{\varepsilon }{2}$. Thus, as long as no $\frac{\varepsilon }{2}$-feasible solution is found, no box with ${\underline{G}}\le 0$ is discarded.

Assume that this is the case every time a box $X^*$ with feasible solutions is considered. Recall that the convex underestimators get better for smaller box widths, see [1]. Thus, if a certain box width is reached, we get $G(x)-G_\beta (x)\le \frac{\varepsilon }{2}$ for all $x\in X^*$ and thus also for $x^G\in X^*$. Moreover, ${\underline{G}}=G_\beta (x^G)\le 0$ and thus

$$\begin{aligned} G(x^G)-\frac{\varepsilon }{2} \le G_\beta (x^G) \le 0. \end{aligned}$$

(12)

Now either $G(x^G)\le \frac{\varepsilon }{2}$, and $x^G$ is $\frac{\varepsilon }{2}$-feasible, or $G(x^G)>\frac{\varepsilon }{2}$, but then with (12) we obtain a contradiction. $\square$

5 Post processing: filtering, box refinement, and local search

The post processing further improves the so far found $\frac{\varepsilon }{2}$-efficient solutions. As before, we assume that the algorithm has found until now two outcome vectors $q^1$ and $q^2$. The pre-image of $q^2$ is a feasible solution for ($P_2$) and thus $q^2_1$ is an upper bound for the minimal value $f^*$ of ($P_2$). In the special case that $q^2$ does not exist, the algorithm continues with $\bar{p}=(M,q^1_2)$ as described in Sect. 4.5. The pre-image of $q^1$ is infeasible for ($P_2$). If it is just slightly infeasible, i. e., if $q^1_2\le \frac{\varepsilon }{2}$, the two procedures Box Refinement and Local Search and Adaptive Discarding aim to find better upper bounds for $f^*$ than $q^2_1$. Otherwise, i. e., in case in which $q^1$ is farer above 0, we can prove that the pre-image of $q^2$ is already $\varepsilon$-minimal for ($P_2$), see Lemma 8. We summarize the proposed steps in Algorithm 2.

5.1 Filtering

The first post processing step eliminates further boxes from the solution list. The reason for that is that boxes can be stored in the solution list during Algorithm 1 at an early iteration where the bounds $q^1$ and $q^2$ may be quite weak, but the termination rule is satisfied. As the bounds $q^1$ and $q^2$ and, thus, ${\bar{p}}$ changes during Algorithm 1 until line 26 and come closer to 0 in their second component, some boxes (which are already in the solution list) would be discarded if they were considered later. The filtering procedure presented in Algorithm 3 aims to find such boxes in order to delete them from the solution list ${\mathcal {L}}_S$.

5.2 Box refinement

The next procedure is a refinement procedure which consists of decreasing the box width of the boxes in the solution list. By using Lipschitz properties (recall that the objective function f is continuous and bounded on a box), we can show that we obtain thereby a collection of $\varepsilon$-efficient solutions for ($MOP_2$). For every box of the solution list we find an $\varepsilon$-efficient solution, see the forthcoming Lemma 11. Moreover, we even get $\varepsilon$-efficient points which are close to a minimal solution for ($P_2$) in the pre-image space.

Let $\omega (X^*)$ be the box width of $X^*=[{\underline{x}},{\overline{x}}]$, i. e., $\omega (X^*)=\Vert {\overline{x}}- {\underline{x}}\Vert$, where $\Vert \cdot \Vert$ is the Euclidean norm. During the refinement a more sophisticated rule to store boxes in the solution list is used to get an additional preciseness in the pre-image space and to ensure the $\varepsilon$-efficiency of the returned solutions:

2. Termination rule: Solve ($P^*_{X^*,\,{\bar{p}}}$) for the box $X^*$ and ${\bar{p}}=(q^2_1, q^1_2)^T$, where $q^1$ and $q^2$ are defined as in (3) and (4). The minimal solution is denoted by $({\tilde{x}},{\tilde{t}})$. Let $\varepsilon >0$ and $\delta >0$ be given. Store $X^*$ in ${\mathcal {L}}_S$ if

• (i) $\omega (X^*)\le \delta$ and

• (ii) $0\ge {\tilde{t}}\ge -\frac{\varepsilon }{2}$ and

• (iii) $(f({\tilde{x}}), G({\tilde{x}}))^T\lneq {\bar{p}}$ or $\omega (X^*)<\sqrt{\frac{\varepsilon }{\max \{\alpha ,\max \limits _{k=1,\ldots ,r}\beta _k\}}}$.

We summarize the proposed steps in Algorithm 4.

Let L be the Lipschitz constant for f on X. A bound for L can be calculated, for example, by using interval arithmetic for the partial derivatives of f. Indeed, as boxes with minimal solutions are not discarded and for each box a representative ${\tilde{x}}$ is stored in ${\mathcal {A}}$, a bound for the minimal value $f^*$ for ($P_1$) can be derived. Using Lipschitz properties for f and condition (i) from the second termination rule, we obtain $\min \left\{ f(x)-L\delta \mid x\in {\mathcal {A}}\right\}$ as a lower bound for $f^*$.

Lemma 10

The Box Refinement, see Algorithm 4, needs finitely many subdivisions in line 9.

Proof

A box $X^*$ with $\omega (X^*)<\min \left\{ \delta ,\sqrt{{\varepsilon }/{\max \{\alpha ,\max _{k=1,\ldots ,r}\beta _k\}}}\right\} :=\delta ^\prime$ is stored in ${\mathcal {L}}_{S_3}$ automatically. Therefore, all boxes from ${\mathcal {L}}_{S_2}$ and their subboxes are either discarded, stored in ${\mathcal {L}}_{S_3}$ or bisected until their box width is smaller than $\delta ^\prime$. $\square$

We omit the proof of the following lemma as it follows the structure of the proofs of Lemma 4.10 and Lemma 4.11 of [24].

Lemma 11

Let ${\mathcal {A}}$ be the output of Algorithm 4. Then every ${\tilde{x}}\in {\mathcal {A}}$ is $\varepsilon$-efficient for ($MOP_2$).

5.3 Local search with adaptive discarding

It is possible to further improve the outcome of Algorithm 1 with a local search algorithm which should be applied after Box Refinement, see Algorithm 4.

As we have proven in Lemmas 4 and 8, the pre-image of $q^2$ is $\varepsilon$-minimal for ($P_2$) if $q^1_2>\frac{\varepsilon }{2}$ holds. In the other case we cannot guarantee any $\varepsilon$-minimality for the pre-image of $q^2$. Figure 3 shows an example, where $q^2$ lies far away from the minimal value $f^*$.

For the local search, we use each solution of ${\mathcal {A}}$, which came from the Box Refinement, see Algorithm 4, as a suitable starting point for a local solver to solve ($P_1$). Here, we solve ($P_1$) instead of ($P_2$) to avoid the handling of the $\max$-term in ($P_2$). At least one of these starting points is in a $\delta$-neighborhood of a minimal solution of ($P_1$). The procedure is described in Algorithm 5. Additionally, we can skip the local search procedure for some boxes in case in which the lower bound of f on a current box, which is given by $f({\tilde{x}})-L\delta$, is larger than a current upper bound for $f^*$. There, ${\tilde{x}}$ is the $\varepsilon$-efficient solution belonging to a box from the previous solution list and L is the Lipschitz constant of f.

The local search strategy can also be applied if the Box Refinement is not done before. In this case the Adaptive Discarding is not possible because the boxes are not small enough. Nevertheless, a local search from an $\varepsilon$-efficient starting point can always be done for every box of the solution list ${\mathcal {L}}_{S_2}$

6 Numerical results

In this section, we examine the performance of the new algorithm MOCP$\alpha$BB on Example 1 and on several additional test instances. First, all steps of the algorithm including the post processing are presented in detail for Example 1. Some of the further test instances are scalable in the number of variables and constraints. The algorithm was implemented in MATLAB R2018a. All experiments have been done on a computer with Intel(R) Core(TM) i5-7400T CPU and 16 GBytes RAM on operating system Windows 10 Enterprise. For the local search step, we obtain the Lipschitz constant by interval arithmetic using Intlab, [26]. For every box $X^*$ a possible Lipschitz constant of f on $X^*$ is $L=\sup (\Vert \nabla F(X^*)\Vert )$, where $\nabla F$ is the natural interval extension of the gradient of f. The local search was performed with fmincon from Matlab using the SQP-algorithm and default parameters. As it is stated in Algorithm 5, for each selected box ${\tilde{X}}$ the starting point for the SQP-algorithm is the $\varepsilon$-efficient solution ${\tilde{x}}\in {\tilde{X}}$.

6.1 Illustrative example

First, we illustrate the new algorithm on the motivating Example 1, as given in (1), cf. [17].

We have chosen $\varepsilon =10^{-5}$ and $\delta =0.0001$. In the following figures, the star marks always the best found minimal solution for the single-objective problem or its image w.r.t. the multiobjective counterpart. The figures representing the pre-image space always show box partitions. The dark gray boxes are the boxes in the current solution list, i. e., those boxes, which could not yet be discarded. The light gray boxes are the discarded boxes. The different color shades represent different criteria based on which the boxes have been discarded.

In the image space, we plot some representatives of the image set by light gray points. They were obtained by discretizing the initial box and taking the function values. These points serve just for illustrative purposes on the structure of the multiobjective counterpart. The black crosses are the points of ${\mathcal {L}}_{PNS}$. In the magnified picture, the first cross with positive second component is $q^1$, and the first with negative second component is $q^2$. The black point above $q^2$ and on the right hand of $q^1$ is ${\bar{p}}$.

Fig. 4

Results after main while-loop

Figure 4 shows the box partition and the image space and their magnifications after the execution of the main while-loop of Algorithm 1 without the post processing step. The lightest gray boxes are the ones which got discarded by the discarding test based on Lemma 7. The middle gray boxes are discarded because of Lemma 6. Here, it holds that $q^1_2>\frac{\varepsilon }{2}$. Hence, with Lemma 8 the pre-image of $q^2$ is already $(\frac{\varepsilon }{2}+\mu )$-efficient for all $\mu >0$. Therefore, the post processing would perform only the filtering step. For illustration, we also present here the other post processing steps.

Fig. 5

Box partition after post processing—filtering and refinement

Figure 5a illustrates the box partition of the feasible set after the first post processing step—the filtering, see Algorithm 3. The two large boxes on the upper left were discarded during this step. Concerning the minimal solution of Example 1 no improvement was obtained, and $q^2$ remains the best found image point so far.

In Figs. 5b and 6a the second step of the post processing is illustrated. In this step, see Algorithm 4, the boxes are usually refined until they are small enough and contain an $\varepsilon$-efficient solution. For this example, the two boxes are already small enough. The star shaped markers are the $\varepsilon$-efficient solutions and their images.

Fig. 6

Image space after post processing (magnified)

The last step of the post processing is a local search. In Fig. 6b, the star marks the image of the solution found by the local search steps. We can see that the minimal value improved slightly, because the star is a bit more on the left of $q^2$.

Table 1 states the number of iterations (# it), the number of boxes in the respective solution list (# sb) and the computational time (t) for each step. After the main loop and the local search step a feasible solution is found with a (nearly) minimal value. Those values are stated in the last column. Here, $q^2_1$ and the minimal value obtained by the local search step are nearly the same. Actually, the difference between both values is $1.87\times 10^{-6}$, and the difference of the computed minimal value at the end to the actual minimal value $\root 4 \of {2}$ is 0 (within the tolerances of MATLAB).

Table 1 Numbers of iterations and computational time for each step of MOPCP$\alpha$BB

6.2 Test instances

In addition to Example 1, we also tested some more instances. The instance KSS2Con is as in Example 1, but with one additional constraint ${x_1+x_2\le 2}$:

Test instance 5

(KSS2Con) The dimension of the pre-image space is $n=2$, and we have $r=2$ constraints.

$$\begin{aligned} \begin{array}{rl} \min &{} f(x)=x_1-x_2 \\ \text{ s.t. } &{} g_1(x)= -x_1^2-(x_2-5)^2+25+\sqrt{2}\le 0,\\ &{}g_2(x)=x_1+x_2-2\le {0},\\ &{} x\in [1,2]\times [0,1]. \end{array} \end{aligned}$$

For HimmCon, which has as objective function the Himmelblau function, see [16], we added one to two constraints which exclude some of the known minima.

Test instance 6

(HimmCon) The dimension of the preimage space is $n=2$, and we have $r\in \{1,2\}$ constraints.

$$\begin{aligned} \begin{array}{rl} \min &{} f(x)= (x_1^2+x_2-11)^2+(x_1+x_2^2-7)^2 \\ \text{ s.t. } &{} g_1(x)= -((x_1+3.5)^2+(x_2+3.5)^2)+4\le 0,\\ &{} g_2(x)=-(x_1+3)^2-x_2+4\le 0\ \text{ only } \text{ if } \ r=2\\ &{} x\in [-5,5]\times [-5,5]. \end{array} \end{aligned}$$

The objective function minimized just with respect to the box constraints is known to have four globally minimal solutions with the minimal value 0:

$$\begin{aligned} \begin{array}{rclrcl} {x^1} &{} = &{} (3,2)^T,\qquad &{} {x^2} &{} = &{} (-2.805118, 3.131312)^T,\\ {x^3} &{} = &{} (-3.779310, -3.283186)^T, &{} {x^4} &{} = &{} (3.584428, -1.848126)^T. \\ \end{array} \end{aligned}$$

The first added nonconvex constraint excludes the minimal solution $x^3$. The second nonconvex constraint excludes $x^2$.

The instance FF is a typical test problem for biobjective optimization, see [13]. Since the second objective has an image within the interval [0, 1] but will serve as a constraint now, we adapted this function slightly.

Test instance 7

(FF) The dimension of the preimage space $n\in {\mathbb {N}}$ can be arbitrarily chosen. We have $r=1$.

$$\begin{aligned} \begin{array}{lll} \min 1-\exp \left( -\sum \limits _{i=1}^n\left( x_i-\frac{1}{\sqrt{n}}\right) ^2\right) \\ \text{ s.t. } \quad {0.5-\exp \left( -\sum \limits _{i=1}^n\left( x_i+\frac{1}{\sqrt{n}}\right) ^2\right) \le 0,\qquad x\in [-2,2]^n} \end{array} \end{aligned}$$

(13)

Since the analytical form of the efficient and nondominated set of the original biobjective optimization problem is known, we can state the minimal solution and the minimal value by

$$\begin{aligned} {x^*=(1/\sqrt{n})}\left( -1+\sqrt{-\ln 0.5}\right) e \text{ and } f(x^*)\approx 0.744089815 \end{aligned}$$

Recall that $e$ is the all-ones vector.

Moreover, we make use of the multiobjective test instance suite DTLZ, in particular of DTLZ2 and DTLZ7, [5]. These instances can be scaled regarding the number of variables and the number of objectives. Thus, the first objective is always the objective function and all other original objectives are the constraints. Again, we had to adapt the functions slightly to ensure that there are some feasible solutions.

Test instance 8

(DTLZ2) The dimension of the preimage space $n\in {\mathbb {N}}$ and the number $r<n$ of constraints can be chosen arbitrarily.

$$\begin{aligned} \begin{array}{rl} \min &{} (1+p(x))\prod \limits _{i=1}^r\cos (0.5\pi x_i)\\ \text{ s.t. } &{} (1+p(x))\sin (0.5\pi x_{r-k+1})\prod \limits _{i=1}^{r-k}\cos (0.5\pi x_i)\le 0.5 \text{ for } \text{ all } k=1,\ldots ,r\\ &{} x\in [0,1]^n \end{array} \end{aligned}$$

(14)

with $p(x)=\sum _{i=r+1}^n(x_i-0.5)^2$.

Test instance 9

(DTLZ7) The dimension of the preimage space $n\in {\mathbb {N}}$ and the number $r<n$ of constraints can be chosen arbitrarily.

$$\begin{aligned} \begin{array}{rl} \min &{} x_1\\ \text{ s.t. } &{} x_{k+1}-0.8\le 0 \text{ for } \text{ all } k=1,\ldots ,r-1\\ &{} (1+p_1(x))p_2(x)\le r+2, \qquad {x\in [0,1]^n} \end{array} \end{aligned}$$

(15)

with

$$\begin{aligned} {p_1(x) = 1+\frac{9}{n-r}\sum _{i=r+1}^n x_i,\qquad p_2(x) = r+1-\sum _{i=1}^r \frac{x_i}{1+p_1(x)}(1+\sin (3\pi x_i)).} \end{aligned}$$

6.3 Numerical results

For all instances we set $\varepsilon =\delta =0.01$ and a time limit of 6 h (21,600 s). Note that for all the instances in Table 2, the main while-loop took a maximum of 3969 s and most instances have been solved much faster.

Table 2 Results of MOCP$\alpha$BB on different test instances

Table 2 shows the overall results for all chosen test instances which were obtained within the time limit. In the first columns, we state the number n of variables and the number r of constraints. Note that for $r\ge 2$, the second objective of the multiobjective counterpart is the maximum function of all constraints. The next block shows the computational time of the main while-loop of Algorithm 1 and the number of needed iterations. Next, the post processing is detailed. PP is the indicator whether the whole post processing is performed. If PP is 0, only the filtering was applied and because of $q^1_2>\frac{\varepsilon }{2}$ and Lemma 8 the refinement and local search are redundant. Then the computational time and the number of needed iterations (# $\hbox {it}_{fi}$) are displayed. If refinement (# $\hbox {it}_{rf}$) and local search (# $\hbox {it}_{ls}$) are applied, we mention all three counts separately. The next columns state the computed nearly minimal values: First, we give $q^2_1$ and then the best found minimal value (best $f^*$). If PP$=0$ holds, this is the value of $q^2_1$, since the pre-image of $q^2$ is always feasible. In case of PP$=1$, the local search was done and thus, we state that minimal value which was found during the local search. To compare with the actual minimal values, we give these in the last column.

We observe that in some cases PP$=0$ holds. The reason for that is $q^1_2>\frac{\varepsilon }{2}=0.005$, and by Lemma 8 the pre-image of $q^2$ is already $\varepsilon$-minimal for the single-objective optimization problem. Thus, the additional post processing, i. e., refinement and local search do not have to be executed. Even if those steps have been performed for most of the cases, we also observed that the value $q^2_1$ is already close to the real minimal value and therefore its pre-image is $\varepsilon$-efficient for ($P_1$). The only instance for which the pre-image of $q^2$ is not $\varepsilon$-efficient is DTLZ2 with $n=4, r=3$, see the italic entry of $q^2_1$.

We give in the following some more details on one of the instances, on HimmCon. Figures 7 and 8 illustrate the results of MOCP$\alpha$BB for the cases $r\in \{1,2\}$, i.e., with one or two constraints. The meaning of the different shades of the boxes and points are the same as in Sect. 6.1. As the run for the optimization problem with one constraint did the refinement and local search step, the minimal solution and minimal value, visualized by the stars in Fig. 7, are found during the local search. In fact, the minimal solution there is $x^*=(-2.8051, 3.1313)^T$ with $f(x^*)\approx 0$. For two constraints, $q^1_2\approx 0.83$ was large enough to skip the refinement and local search steps. Thus, the star in Fig. 8a is the pre-image of $q^2$, i.e, $x^{**}=(3.5844, -1.8481)^T$, and the one in Fig. 8b is $q^2=(0.0000, -37.5066)^T$ itself. Both found solution correspond to one of the minimal solutions of the Himmelblau function without additional constraints, i.e., $x^*\approx {x^2}$ and $x^{**}\approx {x^4}$.

Fig. 7

Results on HimmCon with one constraint after MOCP$\alpha$BB

Fig. 8

Results on HimmCon with two constraints after MOCP$\alpha$BB

6.4 Discussion

The above analysis shows that taking a multiobjective perspective on constrained optimization in general, and on $\alpha$BB-methods in particular, leads to a new and promising class of global optimization algorithms. An additional benefit can be seen in the fact that the solution alternatives that are generated for the multiobjective counterpart problems provide trade-off information on objective value minimization versus constraint satisfaction. This can be nicely seen at the example of the HimmCon instances in Figs. 7b and 8b.

We emphasize that our implementation is prototypical and that no state-of-the-art preprocessing was used. We can thus not expect computational times that are competitive with other (commercial) state-of-the-art solvers. Indeed, the above test instances were solved within (milli-)seconds using GAMS models [14] with BARON [33] (instances KSS2Con, HimmCon, FF) and MINOS [23] (instances DTLZ2 and DTLZ7), and using the built-in advanced pre-processing routines that in most cases already returned near-optimal solutions.

Moreover, our numerical results clearly show one of the main drawbacks of branch and bound type methods in this context: Scaling the number of variables increases the computational time. This is clear, because the branching happens in the pre-image space and for more variables a box has to be bisected more often to become small. Despite this shortcoming, bounding and discarding have proven to be highly effective so that the number of active boxes remains comparably small and storage requirements were never a problem.

7 Conclusions

Within this paper, we proposed to use a multiobjective counterpart to find feasible solutions for nonconvex single-objective constrained optimization problems. It is well-known that finding feasible solutions can be a hard task and we proposed a new approach to find such points. For that approach, we adapted a global solution method for multiobjective optimization problems such that it concentrates on the region of interest. By using such multiobjective counterparts one also gets additional information on the trade-off which one would obtain by relaxing the constraints slightly in favour of an improved objective function value.