Fusion: Expensive and Taking Forever?

Abstract

The road map of fusion power is compared to the development and deployment of other energy technologies. A generic deployment model is presented, which describes the fastest deployment (of any new technology) achievable with the constraint that the industrial capacity that needs to be built up must be continuous and should not overshoot the replacement market in the final, saturated state. It is shown that the development needs an ‘investment’ phase to build up industrial capacity which takes several decades, during which growth is typically exponential, but net energy production is negligible. During the exponential growth the cost is dominated by the capital investment, which allows for a simple comparison of different energy technologies. Fusion is at the start of the exponential growth phase, while still having significant uncertainties concerning its technical feasibility. In comparison to e.g. solar PV and wind, fusion is ‘late’, lagging by some 50 years. To follow the same rate of development that fission, wind and PV have shown, fusion will need to have 3 DEMO reactors operational in the early 2050s, followed by 10 generation one (GEN1) plants in the early 2060s and 100 GEN2 plants in the early 2070s. For the cost development to be comparable, an estimated allowable cost for one DEMO reactor is ~20 G$. While these indicative numbers for the pace and cost of development are very challenging but perhaps not unthinkable for fusion, this analysis does point towards an emphasis on ‘simpler and cheaper’ reactor designs.

Introduction

Nuclear fusion has well known potential as energy technology: it is inherently safe, does not produce CO₂ or other hazardous exhaust products and neither does it produce long-lived radioactive waste, the fuel reserves suffice for millions of years and are not geographically concentrated, a fusion reactor can produce power on demand and there are no practical limits to the fraction of the world energy demand that fusion could supply. In short: ‘Fusion is safe, clean, for all and for ever’. This potential is the reason that many countries collaborate in a world-spanning effort to develop fusion energy, presently culminating in the construction of the ITER test reactor by a consortium of Europe, the USA, Japan, Russia, China, South Korea and India [1]. In an alternative approach to controlled fusion known as inertial confinement, the world-leading experiment is the National Ignition Facility at Lawrence Livermore National Laboratory [2].

There are also critics of the fusion programme, and their criticism can be summarized as: ‘the development of fusion power is extremely expensive and taking forever’. The well known quip being that fusion promises to deliver power in 50 years and has been consistent in promising that over the past five decades. With the political implication that the budget for the development of fusion power could better be redirected towards other sustainable energy options.

It is entirely justified to ask these questions: is the development of fusion actually expensive, is it slow, and won’t fusion energy come too late if it comes at all? In this paper we address these questions by placing fusion in the context of the development of other energy sources, now and in the past. As the starting point we take a paper by Kramer and Haigh [3] in which the authors examine the historical development of the installed power of a number of energy technologies. They observe that the introduction of a new energy technology to the market—be it nuclear fission, solar PV, concentrating solar power, wind or biomass—is characterized by two phases. First, a new technology shows an exponential growth during which the installed power doubles every 2–4 years. Notwithstanding the speed of this growth, this phase lasts decades. During this time the technology is taken from laboratory scale to a level that is visible on the radar of the world energy market, typically at 0.1–1 % of the world energy demand. The source has then reached ‘materiality’ in the words of Kramer and Haigh, but its impact on world energy production is still negligible. Around that time a transition occurs; the growth is no longer exponential but becomes linear, i.e. the growth rate becomes constant. This linear growth phase lasts another few decades before the final saturation level is reached.

In this paper we investigate how fusion fits into this picture. Is it slow? Is it late? And we connect the development rate to the required investment rate, in order to address the question ‘is fusion expensive’? To do so, we have expressed the observations of Kramer and Haigh into a mathematical model, which we have constrained based on economical arguments. We argue why this particular development path is in fact the fastest implementation of a new technology that is economically viable. We deduce generic properties of the development of new energy sources, both regarding the integrated cost and the point at which the transition from exponential to linear growth occurs. With this model, the costs and growth rates can be easily computed and compared. We then apply the analysis to fusion and compare this to other energy technologies, to finally arrive at conclusions regarding the fusion road map. Two comments before we start. First, fusion energy is not a proven technology at this point in time. In fact there are still large uncertainties both scientifically and technically. One of the aims of the ITER and NIF projects is to strongly reduce these uncertainties, but today there is no guarantee that fusion power will ever work. However, in our analysis we will assume that fusion will prove to be technically feasible, and that its deployment will not be hindered by technical, or political or economical, showstoppers. Second, there have been a series of studies into the potential place of fusion power in the energy mix, basically analyzing under which external conditions such as the cost of CO₂ emissions or more generically, policy measures to reduce climate change, fusion could have a significant market share (see e.g. ref [4] and references therein). Our analysis has a different angle: we assume that if fusion becomes available it will get a significant market share and ask the question ‘how fast could fusion be deployed if all external factors are positive, and how much may it cost?’

A Generic Model for the Development of a New Energy Technology

The ‘Fastest Economically Achievable Growth’ Concept: Linear Growth

We consider the introduction of a new energy technology, starting from the point where it leaves the laboratory and ending when a stable market share has been established. To this end, we propose a model for the development of the total worldwide installed effective power (P) as a function of time [5]. The development is best analysed backwards, starting from the saturated state which we assume for the moment to be constant.¹ The fastest way in which this state can be reached is by linear growth: any accelerating growth wastes time at the beginning, any growth that slows down wastes time at the end. The plant building capacity (PBC) is constant during this linear growth phase. The saturated state is reached when the number of old plants that are phased out per year equals this constant PBC. Provided the saturated state is indeed constant, the maximum plant building capacity that is ever needed is therefore equal to the final replacement rate, i.e. the asymptotic value of P, P_sat, divided by the lifetime τ_life of the plants. A faster linear growth would result in excess PBC once the growth saturates, i.e. idle factories and infrastructure, which is to be avoided for economical reasons. Thus, the lifetime of the plants places a limit on the rate of growth during linear growth. In the model introduced below, we will therefore equate the linear growth rate to the asymptotic replacement rate.

The Linear Growth has to be Preceded by a Capacity Building Phase

However, the linear growth can obviously not start at full speed on day one. The technology and industrial capacity need to be built up first: manufacturing processes, factories, dedicated machinery, infrastructure, supply chain of materials, mining of raw materials, and—importantly—a trained workforce. Possibly, legislation will need to be adapted to allow the large-scale deployment of the new technology, too. The energy market is, at an annual turnover of ~10 trillion dollar, by far the largest single market in the world. So we are speaking of a very large infrastructure that needs to be built up, millions of jobs that need to be filled, and generally a significant impact on society.

Therefore, the linear growth phase has to be preceded by a phase in which all of this is developed. As Kramer and Haigh observe, this development is typically exponential. In the model we shall therefore start the development of P with a phase of exponential growth, during which also the PBC grows exponentially. This exponential growth is sustained until the PBC reaches the value that is needed for the linear growth, which in turn is equal to the asymptotic replacement rate. Also at the transition from exponential to linear growth we require the PBC to be continuous: the number of factories and associated infrastructure cannot change overnight. The exponential growth of production capacity will therefore stop once the PBC has been built up that will be needed to sustain the final state. The exponential growth preceding the linear growth shows up as a smooth leading edge on the growth curve, which finds its reflection in a smooth transition to the saturated state.

The Growth Model

With these considerations we can write down the equations that describe the evolution of the total worldwide installed effective power P of an energy source (that is, if a wind turbine with ‘nameplate capacity’ of 5 MW delivers 1.5 MW averaged over the year, then P = 1.5 MW):

$$\begin{aligned} {\text{P}} & = {\text{P}}_{\text{sat}}\frac{\tau_{\exp }}{\tau_{\text{life}}} \left\{\exp \left[\frac{{{\text{t}} - {\text{t}}_{\text{trans}} }}{\tau_{\exp}}\right]\right. \left.-{\exp} \left[{\frac{{\text{t}} -{{\text{t}}}_{\text{trans}}-{\tau_{\text{life}}} }{{\tau_{\exp }}} }\right] \, \right\} \quad {\text{for}}\quad {\text{t}}\,<\,{\text{t}}_{\text{trans}} \\ \end{aligned}$$

(1a)

$$\begin{aligned} {\text{P}} & = {\text{P}}_{\text{sat}}\frac{\tau_{\exp }}{\tau_{\text{life}}} \left\{ 1 + \frac{{{\text{t}}-{\text{t}}_{\text{trans}}}}{\tau_{\exp}}\right. \quad\left.{-}\exp \left[\frac{{\text{t}} - {\text{t}}_{\text{trans}} -\tau_{\text{life}}}{\tau_{\exp }} \right]\right\} \quad {\text{for}}\quad{\text{t}}_{\text{trans}} \, \le \,{\text{t}}\, \le\,{\text{t}}_{\text{sat}} \\ \end{aligned}$$

(1b)

$${\text{P}}\, = \,{\text{P}}_{\text{sat}} \quad {\text{for}}\quad {\text{t}}\, > \,{\text{t}}_{\text{sat}}$$

(1c)

where P_sat denotes the asymptotic value in the saturated state, τ_exp the characteristic time of the exponential growth, τ_life the lifetime of the power-generating installations, t the time and t_trans the time at which the transition from exponential to linear growth occurs.

Figure 1 depicts the model and illustrates the parameters. We distinguish three phases: the final saturated phase at the level P_sat, the linear growth phase with duration τ_life, and the exponential growth phase with time constant τ_exp. Note that when τ_life ≫ τ_exp the second exponential in Eq. (1a) is very small compared to the first.

Fig. 1

The development of installed effective power of a new energy technology is modeled by three consecutive phases: exponential growth, linear growth, and saturation. The entire development is characterized by four parameters as indicated in the figure: the doubling time during exponential growth, the duration of linear growth, the time of transition from exponential to linear growth, and the saturation level. The three phases are connected by the requirement that the derivative is continuous, and the requirement that the total plant building capacity is never greater than what is needed for replacement in the saturated phase equates the linear growth time to the life span of the installations. For the numbers, typical values have been taken, as will be shown in the next sections

The requirement that PBC be continuous, in other words, that the transition from exponential to linear growth is smooth, has a strong economical basis: discontinuity would represent a sudden change in the underlying industry (e.g. the number of factories). A jump up implies that there was plant-building capacity available and sitting idle, a jump down would mean that capacity is suddenly taken out of use. Neither is economical. This condition fixes the level of installed power at which the transition from exponential growth to linear growth occurs (P_trans), placing it at

$${\text{P}}_{\text{trans}} \, = \,{\text{P}}_{\text{sat}} \frac{\tau_{\exp }} {\tau_{\text{life}}}$$

(2)

Application to Typical Energy Systems: Coupling a Short Doubling Time to a Long Lifetime

These two requirements give a quantitative underpinning of the observations of Kramer and Haigh. With a typical value of the doubling time during exponential growth of only a few years, and a typical lifetime of power plants (be they solar panels, wind turbines or fusion reactors) of 30–60 years, relation (2) implies that the transition from exponential to linear growth occurs at around 10 % of the final installed power, and that the linear growth phase lasts almost a full lifetime (We note here, in the passing, that this also demonstrates why the deployment of new power generation is fundamentally different from e.g. the introduction of the smart phone. For the latter, τ_exp and τ_life are of the same order, so that the development can grow exponentially almost to market saturation).

Plugging in some numbers for typical energy systems, we note that a significant energy technology should be expected to be capable of producing (at least) 10–20 % of the world energy demand, i.e. 3–6 TW effective around mid century. This places the exponential-to-linear growth transition, which occurs at 10 % of the final level, at 0.3–0.6 TW. If the exponential growth starts when a technology becomes too large for the laboratory, say at 10 MW, there are more than 4 orders of magnitude, or some 14 doublings, to be bridged by exponential growth. Even at a sustained doubling time of 3 years this requires 40 years, to be followed by a similar period of linear growth. All of this is in full agreement with the observations of Kramer and Haigh.

The Exponential Growth Phase is Irrelevant for Energy Production

It is an obvious mathematical property of exponential growth that in the last doubling period as much new capacity is installed as in the entire preceding development. And since the exponential growth ends at ~10 % of the saturation level, the total energy production during the exponential growth phase is a negligible fraction of the total production of the installation: only a few years’ production of only a fraction of the later installed capacity. This holds a fortiori if we take the energy payback time of the installations into consideration. In that case we see that, perhaps counter-intuitively, if the payback time is longer than the doubling time of the growth, the net energy production is negative during the entire exponential growth phase. All investments made during those decades precede economic return. In general one has to realize that any new energy technology only begins to deliver net energy once it is in its linear growth phase.

A Generic Model: A Template for the Fusion Road Map

The description of the development of energy technologies turns out to allow further generalization, as the historical data show that the doubling time during exponential growth is rather similar for different technologies, typically 2–4 years allowing for some fluctuation over the years. Likewise, the (expected) lifetime of the installations is long, typically 30 or more years.

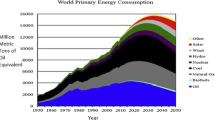
In Fig. 2 we have plotted historical data of total installed effective power versus time for fission, wind and PV, and compared the generic model to this data, while taking the same fixed parameters τ_exp = 4.3 years (i.e. a doubling time of 3 years) and τ_life = 30 years in all cases. For solar and wind the data concern only the exponential growth, therefore we had to take a value for P_sat which we—somewhat arbitrarily—placed at 10 % of the world energy demand around mid-century, i.e. 3 TW. The graph shows that the model, however crude and using the same exponential growth time for all three technologies, gives a reasonable approximation to the data. We stress that the purpose of this exercise is not to find a best fit to each individual data set, but rather to find a template that can be used to make projections for fusion.

Fig. 2

The total globally installed effective power as function of time. The solid lines are data for world energy demand [6], and power from fission [7], wind [8] and solar PV [9]. The dashed lines represent the generic growth model introduced in this paper. The model uses the same 3-year doubling time for the exponential growth in all cases. For fission, the final level has been chosen such that a match is achieved until 1986, after which the data flatten out abruptly as a result of the Chernobyl accident. This template has been adopted to sketch a road map for fusion. Also for the costs of fusion numbers have been taken that are comparable to those for other technologies, so as to get a rough idea of what cost bracket should be targeted. Note that this is effective installed power, i.e. the capacity factor is factored in. Hence the DEMO point at 1 GW_e should be expected to be realized by e.g. 3 DEMOs of 1 GW_e output power each with a capacity factor of 30 % and a cost around 20 G$ each (see “Economics of the Growth” section)

Noting that such diverse technologies as fission, PV and wind develop following so similar patterns, we propose to use that pattern for the development of fusion power, too.

Economics of the Growth

Exponential Growth is an Investment into Future New Energy

The observation that a fast growing technology does not deliver net energy is not a criticism. As long as the economic life of the system is much longer than its energy payback time, each individual unit will have a net energy output over its lifetime. But it is equally true that as long as the total installed power is growing exponentially, there is no significant global net energy production. The exponential growth phase is a necessary investment into a new energy system, not more, not less. Net energy production only starts to build up during the linear growth phase. It is an obvious yet perhaps surprising observation that the introduction of a new energy source calls for a period of investment that extends over about 4 decades and precedes any form of energy or economic payback on the global scale. In practical terms this means that e.g. the solar panels that are being deployed on a large scale in Germany may locally lead to a reduction of CO₂ emission, but this is offset by a larger increase of CO₂ emission in the countries where the panels are produced. Another consequence of the fact that during exponential growth the energy production is negligible is that the substantial investment needed must be pre-financed. And as there is no product to sell yet, the financial burden must necessarily be carried by governments, taxpayers, or society at large. Financial payback only starts when the development is well into the linear growth phase. This is another generic feature of exponential growth of new energy technologies: they must be pre-financed, one way or another. The magnitude of the cumulative investment (see below) and the time to financial breakeven puts the de novo development of a new energy technology beyond the reach of even the largest companies, and points to a necessary role for government.

How Large is the Investment Until Materiality?

It is now a straightforward exercise to compute the investment needed to bring a new energy technology to the end of its exponential growth. In this phase the annual spending will be dominated by the cost of building new plants, i.e. the capital costs. The overnight capital costs (OCC) are well documented for different energy technologies [10], a short summary is given in Table 1. Note that in order to compare the overnight investment capital costs per W of effective installed power, the capacity factors need to be taken into account.

Table 1 Typical values for overnight capital cost (OCC) per Watt installed (name plate) power, as well as per watt effective power (OCC_eff) for a few energy technologies. As a reference coal and gas are given, with and without carbon capture and sequestration (CCS). The values are taken from the United States Energy Information Administration [10, 11], where solar and wind have capacity factors above the global average, whereas coal and gas have capacity factors well below their technical capacity, because they are used as demand followers

Applying the commonly found cost reduction of a factor 2 per factor 10 installed power [12], we can extrapolate this to a common benchmark, for which we will take 300 GW. This is about 1 % of the mid century total world demand and can be assumed to be close to the end of the exponential growth. We use 10 $/W as an average value at this point, taking into account the fact that the capacity factors of the emerging technologies are high in the US case.

Using the numbers given in Table 1, we find the total invested capital to be 2–4 thousand billion dollar up until materiality for wind and solar. The spending profile follows the exponential development, i.e. half of this investment is made in the last few years of the exponential growth, when the annual spending reaches hundreds of billion dollars per year. All of this investment precedes the net energy production. This calculation does not take into account the financing costs, which are obviously high for multi-billion dollar projects. With an interest rate of 7.5 % and a construction time of 10 years, the cost has almost doubled before the installation has been taken into operation, while at the end of the life of the installations the financing costs have run up to ~2.5 times the overnight capital investment. The bottom line is that the development of any new energy source calls for an investment of a few thousand billion dollars before global net energy production reaches a level at which payback starts.

Let us now place fusion energy in this temporal and financial context.

Placing Fusion Energy in this Framework

Could Fusion Follow the Same Universal Growth Curve?

Seeing that such different technologies as wind, PV and fission all have shown exponential growth rates with a doubling time of typically 3 years, we’ll take this as our reference. Hence, rather than trying to predict how fast fusion power could grow, we reverse the question and ask: what should the fusion road map look like if it wants to adhere to the reference?

The first machine that will harvest electricity from fusion is generically called DEMO. The fusion road maps [13] of Europe, South Korea, China, and India all foresee their own DEMO starting operation in 2040–2050. These designs typically aim at 1–2 GW_e. They are meant to deliver to the grid, but most likely—our addition—at a modest capacity factor: 30 % effective, multi-annual averaged availability would already be an achievement. We note, as a reference, that the first generation of fission plants also targeted very modest availability, and increased their capacity factor from ~0.5 to ~0.9 between 1970 and 2000 [14]. This assumption would place the DEMO point—i.e. the combined DEMO reactors—at an estimated 1 GW total effective power in 2050.

After DEMO, the first generation (GEN 1) of fusion plants could be envisaged to be DEMO-like, with somewhat improved plant efficiency and availability, and more economical construction. The European Power Plant conceptual study explores several concepts for this phase in the development [15]. In order to stay on the generic development path, 10 GEN1 plants are needed to start operation within 10 years after the DEMO’s. After that GEN2, about 100 plants with similar characteristics as GEN1 but reduced cost and improved availability, is to follow in a decade. This would bring fusion to materiality, at about 1 % of the world energy demand, around 2070.

In Fig. 2 we have plotted such a projection of the development of fusion power into the graph with other energy technologies.

The graph makes clear that fusion is in any case late compared to other technologies: it lags by some 50 years at least. Yet, even with this late start, if fusion realizes the same 3-year doubling time, it could enter the energy mix in 2070. At this time, the world most likely is still in the transition to sustainable energy production, and depending on how e.g. PV, wind and biomass are doing, fusion could provide a much-needed complement.

However, with today’s knowledge and the experience of ITER, these may seem unrealistically fast steps. Yet, these are the steps that are required to develop and deploy fusion power at the same rate of exponential growth that has been realized for fission, PV and wind in the past. Also for these technologies an incredibly fast growth of the industry was needed to sustain the rapid exponential growth. It would need to be analyzed if fusion has technological aspects that would prevent it from realizing an exponential show with a 3-year doubling time. This could e.g. depend on the availability of materials for superconducting magnets or the efficiency of tritium breeding in operational fusion reactors. For now, we merely want to illustrate what is needed to let fusion develop as fast as other power technologies.

Looking at it in a different way: if fusion is expected to develop its potential and eventually deliver e.g. 30 % of world energy, i.e. ~10 TW, then the fusion industry should sustain a park of some 10,000 plants. With a 50-year lifetime, that is 200 reactors per year. With this perspective, it is not strange at all that GEN2 calls for the construction of 100 plants in 10 years. That is only 10 a year.

And we emphasize that during exponential growth the associated rate of investment must grow exponentially, too. The fusion community is presently struggling to realize ITER within 20 years, so building 10 GEN1 plants in 10 years may seem a daunting task. But it should be realized that the associated budget should be tens of billions dollars per year and that this task should be in the hands of an industry that by then is specializing in the construction of fusion reactors.

We also point here out that all new energy technologies that are presently in the research phase have not even started their exponential growth yet. So fusion may have a late start, it is certainly not the last one to start.

Is Fusion Expensive?

To address the cost of the development of fusion power we will again resort to a reverse analysis. If fusion is to be competitive by the time it reaches materiality, at around 0.3 TW installed power, the overnight capital investment should have dropped to ~10 $/W (today’s money)—allowing for a further cost reduction during the linear deployment phase. Again adopting the commonly used cost decrease of a factor of two per ten times more installed power, that places the price tag at 1GW—the ‘three DEMO point’-, at ~60 $/W, i.e. ~20 G$ per DEMO. Considering the cost of ITER this may seem low, but not totally off the mark, as DEMO should be a simpler machine than ITER, albeit larger and equipped with the electricity generating plant that ITER lacks.

Discussion and Conclusions

In summary, following the lead of ref [1], we have developed a simple model based on economical considerations that describes the development and deployment of a new power technology in a generic form. By comparing this model to historic development data of fission, solar PV and wind we found a rather generic pattern, in which an exponential growth with a doubling time of 3 years is followed by a linear growth that essentially lasts one plant lifetime. As this pattern is seen for such diverse technologies as fission, PV and wind, we propose that fusion could be expected to follow the same pattern.

In that case, fusion—while having a late start, lagging behind solar PV by about 50 years—could reach 100 GW of effective installed power by 2070 and impact the world energy system significantly by the turn of the century. This development is only viable if the overnight investment cost drops to about 10 $/W by the time the linear growth starts. Assuming an experience curve of a factor of 2 per factor of 10 installed power, this leads to a target for the cost of a single DEMO device of ~20 G$, which will be a challenge but may not be totally unrealistic.

So fusion is late, but there is no reason today to say it is slow or expensive. Yet, the numbers presented here do suggest that for DEMO, the emphasis will have to be on simplicity of design and minimization of cost and construction time.

We do note that once the exponential growth has started, there is little time for concept improvement. With the generations following each other within a decade, GEN2 will look similar to GEN1. It is therefore essential that in the DEMO phase the world has settled on the most promising concept, or develops e.g. the tokamak and stellarator lines in parallel.

What sets fusion apart from e.g. wind and solar is the coarse granularity of the development. In particular DEMO and GEN1 represent large steps in technology, with large associated financial risk. As we argued, the exponential growth must necessarily be funded by governments for all new energy technologies, and fusion is no different there. But the financial risks involved in each of the steps of the fusion roadmap are large compared to those in the much more gradual development seen in wind and solar power. This is clearly a drawback for fusion.

On the other hand, it must be realized that the spending profile follows the growth curve, and that the early phase of exponential growth requires funds that are insignificant when compared to the final integrated investment. Hence, the sums involved in launching each generation of new fusion plants will seem staggering at the time they have to be made, but if the programme is successful they will appear as logical and not out of the ordinary in retrospect.

Finally, we may ask how ITER fits in this picture. Although ITER does not produce net electricity, one could assign a virtual net power to it by taking its predicted fusion power, ignore the input and recirculating power, and convert this to electricity with e.g. 30 % efficiency. Next, a capacity factor has to be assigned. Clearly, if ITER is run as an experiment this factor is vanishingly low. But as a thought experiment, one could imagine to run ITER as efficiently as possible, with a high frequency of pulses. A capacity factor of 5–10 % might be feasible. This would put the virtual effective power of ITER at 10 MW, which lies on the line in Fig. 2. So in terms of ‘virtual’ power, ITER fits in the sequence ITER—DEMO—GEN1—GEN2. When it comes to the overnight cost, however, ITER clearly is far too expensive for its power. Which emphasizes the fact that ITER marks the transition from research to development.