The heteronuclear single quantum correlation (HSQC) experiment (Bodenhausen and Ruben 1980) has transfigured the analysis of chemical and three-dimensional molecular structure, including studies of conformational flexibility and interactions. Sensitivity enhanced (SE) versions of the HSQC experiment have been proposed (Palmer et al. 1991) that allow both anti-phase coherence terms (2HZNX and 2HZNY) present during the indirect evolution domain to be detected as different linear combinations in separate scans. Subsequent addition/subtraction of the two data sets yields pure absorption 2D line shapes with an increase in signal-to-noise ratio of √2, neglecting pulse imperfections and relaxation. Without doubt, the most popular implementation of this principle is the one by Kay et al. (Kay et al. 1992), in which the collection of the orthogonal coherences is seamlessly integrated with coherence pathway selection using pulsed field gradients (PFGs). Most importantly, any imbalance during the contiguous reverse INEPT steps resulting from relaxation differences of the two coherence transfer pathways (CTPs) is erased, thereby avoiding quadrature artifacts. However, phase anomalies may still arise as a result of the limited bandwidth of the pulses applied to the heteronuclei (X-nuclei). Additional pairs of PFGs around the refocusing/inversion pulses in the reverse INEPT transfer periods have been suggested to reduce these artifacts (Bax and Pochapsky 1992). Surprisingly, the lengths and strengths of gradient pulses employed during the sensitivity enhancement scheme in various experimental implementations in the literature vary greatly, and appear to be chosen rather arbitrarily. Published versions are available that either use no gradients (Dayie and Wagner 1994; Kay et al. 1992; Mulder et al. 1996; Sattler et al. 1995; Schleucher et al. 1994; Stonehouse et al. 1995), matched gradient pairs (Muhandiram and Kay 1994; Weigelt 1998; Zhang et al. 1994), or unequal gradient pairs (Czisch and Boelens 1998; Muhandiram et al. 1993; Salzmann et al. 1999). To our knowledge, no detailed analysis of these choices has been presented so far, and, as a consequence, published experiments may not adequately suppress the spurious signals. Possibly, the effects have gone largely unnoticed, as the phase errors are relatively modest as long as the RF field strength applied to the X-nuclei significantly exceeds their resonance offset. Nonetheless, upon closer inspection, even under standard operating conditions—in our laboratory, on a 600 MHz spectrometer with a 53 μs nitrogen 90° pulse width—phase differences can be observed between proton traces taken at different nitrogen offsets in a typical 2D HSQC spectrum, unless the PFG strengths are judiciously chosen. As a result, quantitative analysis of peak intensity and position, which relies on spectra with pure-phase line shapes, is compromised. Understanding the origin of the artifacts, and finding effective methods for their removal, is expected to be of interest as (1) HSQC experiments are applied to cover larger chemical shift ranges, and (2) increasing static magnetic field strengths will lead to proportionally larger X-spin resonance frequency offsets, and concomitantly stronger artifacts.

In the present paper we present simulations of the nuclear spin coherence evolution during sensitivity enhanced HSQC experiments that explicitly include off-resonance effects and pulsed field gradients. The simulations identify the excitation and detection of unwanted coherences, allowing us to trace out their coherence transfer paths, and suggest effective strategies for their suppression. The efficacy of the approach is established via experimental PFG-SE 15N-1H HSQC experiments recorded on the small protein calbindin D9k.

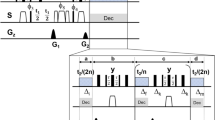
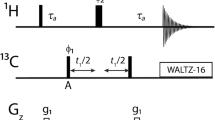
Figure 1 shows the PFG-SE 15N-1H HSQC pulse sequence of Kay et al. (1992), in its water flip-back implementation (Zhang et al. 1994), as used in this study. The ‘encoding’ and ‘decoding’ gradients, G4 and G7, respectively, ensure proper ‘winding’ and successive ‘unwinding’ of the nuclear spin magnetizations to a degree proportional to coherence order and position in the sample. Following the recipe described in the original paper (Kay et al. 1992), two scans of opposite phase-modulated data are recorded, and manipulated prior to Fourier transformation, to generate a 2D spectrum with absorption line shapes in both frequency dimensions.

Fig. 1
figure 1

Pulse sequence of the 2D PFG-SE 1H-15N HSQC experiment used in the simulation and in practice. Narrow (wide) filled bars indicate 90° (180°) RF pulses applied along the x axis, unless otherwise indicated. The 1H carrier is centered at the water resonance (4.76 ppm) and proton pulses are applied with a field strength of ω1/2π = 37.3 kHz. Proton decoupling is achieved using GARP-1 decoupling with ω1/2π = 1.25 kHz. The 90° water flip-back pulse after the first INEPT in the sequence (open dome) has a rectangular shape and a length of 2 ms. The 15N carrier is centered at 119 ppm, and nitrogen pulses were applied with a field strength ω1/2π = 4.7 kHz. Delays are: Δ = 2.3 ms, δ = 1.5 ms, and ε = 0.2 ms. Phase cycling is: ϕ1 = {x,-x}, ϕ2 = x, and ϕrec = {x,−x}. The gradient strengths (G/cm) and durations (ms) are: g0 = 0.9 (t1/2), g1 = 5.3 (1.0), g2 = 14.1 (0.5), g3 = 22.1 (0.5), g4 = 26.6 (1.25), g5 = variable (0.15), g6 = variable (0.15), and g7 = 52.3 (0.125). Two data sets are recorded (in an interleaved manner) with G7 inverted for each data set together with inversion of ϕ2. The two data sets are manipulated in order to generate States type hypercomplex data (see text). Axial peaks are moved to the side of the spectrum by concomitant inversion of ϕ1 with the receiver phase for every other t1 increment

Full size image

The encoding pulsed field gradient is applied as a pair of asymmetric bipolar gradients −1.2 × G4 and 0.8 × G4 to avoid the need for phase cycling on the 180° pulse, which is otherwise necessary to suppress quadrature artifacts due to pulse imperfection or limited band width. PFG pairs G5 and G6 around the 180° pulses in the reverse INEPT transfer periods suppress further artifacts that affect undesired coherence order changes (Bax and Pochapsky 1992).

To understand the origin of the phase errors we now present a product operator analysis of the time evolution of the main terms of the spin density operator for a two-spin HN system that lead to observable proton coherence at the time of detection. The first part of the HSQC experiment shown in Fig. 1 can be summarized as follows:

$$ \begin{gathered} {\text{H}}_{\text{Z}} \mathop{\longrightarrow}\limits^{\text{INEPT}} - 2{\text{H}}_{\text{Z}} {\text{N}}_{\text{Y}} \mathop{\longrightarrow}\limits^{{{\text{t}}_{1} /2 - 180({\text{H}}_{\text{X}} ) - t_{1} /2 - \delta - 180({\text{N}}_{\text{X}} ) - \delta }} - 2{\text{H}}_{\text{Z}} {\text{N}}_{\text{Y}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} ) - 2{\text{H}}_{\text{Z}} {\text{N}}_{\text{X}} \sin \left( {\Upomega_{\text{N}} {\text{t}}_{1} } \right) \hfill \\ \mathop{\longrightarrow}\limits^{{90({\text{N}}_{\text{X}} , {\text{H}}_{\text{X}} )}}2{\text{H}}_{\text{Y}} {\text{N}}_{\text{Z}} \cos \left( {\Upomega_{\text{N}} {\text{t}}_{1} } \right) + 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \sin \left( {\Upomega_{\text{N}} {\text{t}}_{1} } \right) \hfill \\ \end{gathered} $$

In the case of ideal pulses, and momentarily neglecting the gradient pulses and relaxation, the first of the two scans that make up the sensitivity enhancement scheme can be summarized by the following two simultaneous coherence transfer pathways:

$$ \begin{gathered} {\text {\it desired}} \, {\text {SQ}} \,{\text {pathway}}: \hfill \\ 2{\text{H}}_{\text{Y}}{\text{N}}_{\text{Z}} \cos (\Upomega_{\text{N}} {\text{t}}_{1})\mathop{\longrightarrow}\limits^{{\Updelta -180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} ) - \Updelta }} -{\text{H}}_{\text{X}} \cos (\Upomega_{\text{N}} {\text{t}}_{1})\mathop{\longrightarrow}\limits^{{90({\text{N}}_{\text{Y}} ,{\text{H}}_{\text{Y}} )}}{\text{H}}_{\text{Z}} \cos(\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ \mathop{\longrightarrow}\limits^{{\Updelta -180({\text{N}}_{\text{X}} , {\text{H}}_{\text{X}} ) - \Updelta }} - {\text{H}}_{\text{Z}} \cos (\Upomega_{\text{N}} {\text{t}}_{1})\mathop{\longrightarrow}\limits^{{90({\text{H}}_{\text{X}} ) - \varepsilon - 180({\text{H}}_{\text{X}} ) - \varepsilon }} -{\text{H}}_{\text{Y}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ {\text {\it desired}} \, {\text {MQ}} \, {\text{pathway}}: \hfill \\ 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \sin (\Upomega_{\text{N}} {\text{t}}_{1})\mathop{\longrightarrow}\limits^{{\Updelta -180({\text{N}}_{\text{X}} , {\text{H}}_{\text{X}} ) - \Updelta }}- 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \sin(\Upomega_{\text{N}} {\text{t}}_{1})\mathop{\longrightarrow}\limits^{{90({\text{N}}_{\text{Y}},{\text{H}}_{\text{Y}} )}} - 2{\text{H}}_{\text{Y}}{\text{N}}_{\text{Z}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ \mathop{\longrightarrow}\limits^{{\Updelta -180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} ) - \Updelta }} -{\text{H}}_{\text{X}} \sin (\Upomega_{\text{N}} {\text{t}}_{1})\mathop{\longrightarrow}\limits^{{90({\text{H}}_{\text{X}} ) - \varepsilon - 180({\text{H}}_{\text{X}} ) - \varepsilon }} -{\text{H}}_{\text{X}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ \end{gathered} $$

We refer to these two desired pathways as the “single quantum (SQ)” and “multiple quantum (MQ)” pathways, respectively, referring to the coherence state present during the first reverse INEPT transfer period. By simultaneous change of the sign of gradient G7 and phase ϕ2, the signal after repetition of the experiment is described by:

$$ {\text{H}}_{\text{Y}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} ) - {\text{H}}_{\text{X}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} ) $$

By subsequent addition/subtraction of the two signals, and a 90° phase shift to one of the outcomes, the resulting hypercomplex pair can be processed in the usual States (States et al. 1982) or States-TPPI (Marion et al. 1989) manner (Kay et al. 1992; Palmer et al. 1991).

In the case of non-negligible pulse widths additional observable signals will reach the receiver, and unwanted coherence transfer pathways may need to be suppressed by phase cycling or additional pulsed field gradients. Here we will focus in detail on the effect of finite pulse widths on the 15N channel, and will specifically consider the result of off-resonance rotations during the 15N pulses that follow t1-evolution. An analogous situation in 13C-1H correlation spectroscopy can easily be envisaged, where a larger chemical shift range may lead to increased off-resonance effects and concomitant phasing artifacts.

Alternatively, to avoid off-resonance effects band selective, composite or adiabatic pulses may be employed. Because the sensitivity enhancement protocol carries forward orthogonal coherences, pulses are required that can simultaneously invert and refocus magnetization. Here we will consider REBURP pulses for this purpose.

We will now trace out the coherence transfer pathways during sensitivity enhancement that lead to observable magnetization and mixed-phase artifacts. Table 1 presents the eight possible coherence pathways that will lead to proton SQ coherence at the moment of acquisition in case of imperfect 180° nitrogen pulses in the reverse INEPT periods. The influence of 90° pulse imperfections on the CTPs is minor, and can be neglected. For compactness we will express all coherence transfer amplitudes in terms of the dimensionless quantity α, defined as the ratio of the resonance offset and the RF field strength, i.e. α ≡ ΩN/ω1. Following the notation of Table 1, the desired coherences are referred to below as #1 (“SQ”) and #5 (“MQ”).

Table 1 Coherence transfer pathwaysa that lead to observable proton magnetization in the case of imperfect nitrogen pulses in the sensitivity enhancement schemeb
Full size table

To gain insight in the type and magnitude of the relevant spurious signals that can arise during sensitivity enhancement, let us consider the specific case of a J-coupled amide spin pair HN, with a resonance offset ΩN/(2π). The 180° nitrogen pulses in the reverse INEPT periods are applied with RF field strength: |γNB1| = ω1 = 2π/(4 pwN). All other pulses are considered ideal. We shall use notations like 90(Hx) for the effect of an ideal 90° 1H pulse with phase x, and 180(Nx,Hx) for the effect of simultaneous non-ideal 15N and ideal 1H 180° pulses, both with phase x. The main artifact then arises from the “SQ” and “MQ” pathways in the following manner:

$$ \begin{gathered} major\,undesired\,branch\,from\,{\text{SQ}}\,{\text{pathway}}\left( {\# 2} \right): \hfill \\ 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{Z}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} )\mathop{\longrightarrow}\limits^{{\Updelta - 180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} ) - \Updelta }} - 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} )\mathop{\longrightarrow}\limits^{{90({\text{N}}_{\text{Y}} ,{\text{H}}_{\text{Y}} )}}2{\text{H}}_{\text{Y}} {\text{N}}_{\text{Z}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ \mathop{\longrightarrow}\limits^{{\Updelta - 180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} ) - \Updelta }} - {\text{H}}_{\text{X}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} )\mathop{\longrightarrow}\limits^{{90({\text{H}}_{\text{X}} ) - \varepsilon - 180({\text{H}}_{\text{X}} ) - \varepsilon }} - {\text{H}}_{\text{X}} \cos (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ major\,undesired\,branch\,from\,{\text{MQ}}\,{\text{pathway}}\left( {\# 8} \right): \hfill \\ 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} )\mathop{\longrightarrow}\limits^{{\Updelta - 180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} ) - \Updelta }}{\text{H}}_{\text{X}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} )\mathop{\longrightarrow}\limits^{{90({\text{N}}_{\text{Y}} ,{\text{H}}_{\text{Y}} )}} - {\text{H}}_{\text{Z}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ \mathop{\longrightarrow}\limits^{{\Updelta - 180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} ) - \Updelta }}{\text{H}}_{\text{Z}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} )\mathop{\longrightarrow}\limits^{{90({\text{H}}_{\text{X}} ) - \varepsilon - 180({\text{H}}_{\text{X}} ) - \varepsilon }}{\text{H}}_{\text{Y}} \sin (\Upomega_{\text{N}} {\text{t}}_{1} ) \hfill \\ \end{gathered} $$

See Table 1 for the amplitudes of the terms that follow the different pathways.

This situation can be considered a case of “channel confusion”: the resulting 1H magnetizations that carry the orthogonal 15N chemical shift amplitude modulations are both 90° out of phase with respect to the desired signal.

Two important aspects of this dominant artifact need consideration. First, the undesired signals arise from the interconversion of 15N,1H multiple-quantum coherences and 15N single-quantum anti-phase coherences, and therefore the resulting difference in spatial phase encoding due to symmetric gradients around the 180° pulse will only be proportional to γN. Therefore, the effective suppression of this first artifact will require long and/or strong G5 gradients. Second, the evolution pathways stipulate that the artifacts will demonstrate a dependence on 15N offset frequency, as the nitrogen chemical shift evolves only during either the first or second half of the first reverse INEPT period: For the sin(ΩNt1)-modulated MQ 2HYNX coherence, the 15N component is (in part) rotated away to the z axis by the off-resonance action of the π pulse, resulting in SQ coherence of the form 2HYNZ. Therefore, whereas the 1H chemical shift is refocused at the end of the Δ−180(NX,HX)−Δ period, 15N chemical shift evolution will have taken place for a period Δ:

$$ 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \mathop{\longrightarrow}\limits^{\Updelta }2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \cos (\Upomega_{\text{N}} \Updelta )\mathop{\longrightarrow}\limits^{{180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} )}} - 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{Z}} \cos (\Upomega_{\text{N}} \Updelta )\mathop{\longrightarrow}\limits^{\Updelta }{\text{H}}_{\text{X}} \cos (\Upomega_{\text{N}} \Updelta ) $$

Similarly, the cos(ΩNt1)-modulated 2HYNZ SQ coherence is partly converted to 2HYNX. This term will also undergo 15N chemical shift evolution during a period Δ and continue along the same path as the desired MQ coherence, which is sin(ΩNt1)-modulated:

$$ 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{Z}} \mathop{\longrightarrow}\limits^{\Updelta }2{\text{H}}_{\text{Y}} {\text{N}}_{\text{Z}} \mathop{\longrightarrow}\limits^{{180({\text{N}}_{\text{X}} ,{\text{H}}_{\text{X}} )}} - 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \mathop{\longrightarrow}\limits^{\Updelta } - 2{\text{H}}_{\text{Y}} {\text{N}}_{\text{X}} \cos (\Upomega_{\text{N}} \Updelta ) $$

In all CTPs that lead to artifacts the magnetization undergoes an unwanted change in coherence level (of +1 or −1) during at least one of the imperfect nitrogen π pulses. Hence, a symmetrical pair of PFGs around each of these π pulses will be effective in reducing the resulting phasing artifacts. However, in pathways #3 and #7 this change in coherence level happens twice, so a fraction of the magnetization will not show any offset dependence, due to the refocusing effect of the second π pulse. This same fraction will also survive gradient pairs (G5 and G6) when these gradient pairs are of equal strength (G5 = G6). For this reason the use of matched gradient pairs (Muhandiram and Kay 1994; Weigelt 1998; Zhang et al. 1994) must be advised against.

In pathway #4 and #6 the unwanted change in coherence level happens only during the second π pulse. In order to suppress signals from these pathways it is necessary that gradients are applied around the second π pulse. However, since the signals from CTP #4 and #6 are small relative to those from CTPs #2 and #8, the strength of the second gradient pair can be comparatively weaker.

Some of the CTPs that give rise to phase errors (see Table 1) lead to unbalanced contributions to the cos(ΩN t1)- and sin(ΩN t1)-modulated signals. This would cause quadrature artifacts in the final spectrum. However, the action of the encoding and decoding gradients (G4 and G7) ensures that any quadrature artifacts will be suppressed.

In what follows we will evaluate coherence transfer through a PFG-SE 15N-1H HSQC experiment by computer simulation, using in-house routines programmed in Mathematica (Wolfram Research, Inc. 2010). The calculations emulate the situation on a 600 MHz spectrometer with ideal 1H pulses, a 50 μs nitrogen 90° pulse width, and single z axis gradients. The sample is assumed to have a length of 10 mm. The length and strength of the applied gradients is specified with the calculations and figures.

Figure 2 shows the phase errors of the observable proton magnetization that are expected when the 15N resonance offset frequencies are increased from 0 to 3 kHz. The typical beat patterns observed in Fig. 2a are dominated by CTPs #2 and #8, and arise from imperfect π rotations about the effective field, which is slightly tilted out of the transverse plane, and chemical shift evolution during only one of the Δ periods of the first reverse INEPT period. For resonance offsets ΩN < ω1 (i.e., α < 1) this results in modulations approximated by √2 cos(ΩNΔ) × ΩN/ω1 (see Table 1). Panel (a) shows the consequence of incrementing only the first gradient pair, G5, and how this suppresses the major undesired CTPs #2 and #8. Panel (b) demonstrates that application of G6 alone hardly leads to any mitigation of artifacts at all, since only CTPs #4 and #6 are affected. Panel (c) shows that matched gradient pairs G5 = G6 lead to a reduction of the artifacts, but only in part, because CTPs #3 and #7 survive. In panel (d) the effect of mismatched gradient pairs (G5 ≠ G6) is shown. Good suppression is obtained in the latter case, by choosing the second gradient pair to be weaker by about a factor four. Finally, panel (e) shows the expected offset profile when the 180° pulse in the first period is replaced by a 1.5 ms REBURP (Geen and Freeman 1991) shape with peak RF amplitude ω1/2π = 4.2 kHz. Although this pulse is capable of simultaneously refocusing and inverting the magnetizations of the “SQ” and “MQ” pathways to >98% over a 2.5 kHz spectral width, it only marginally reduces the appearance of phasing artifacts, even for small chemical shift offsets.

Fig. 2
figure 2

Numerical simulations of the phase error as a function of resonance offset from 0 to 3 kHz, for different strengths of 0.15 ms gradient pairs G5 and G6. a G6 = 0 G/cm for all curves, and G5 = 0 (red), 6.7 (green), 13.4 (orange), 60 (blue) G/cm. b G5 = 0 G/cm for all curves, and G6 = 0 (red), 6.7 (green), 13.4 (orange), 60 (blue) G/cm. c G5 = G6 = 0 (red), 6.7 (green), 13.4 (orange), 60 (blue) G/cm. d G5 = G6 = 0 G/cm (red); G5 = 60, G6 = 0 (green), G5 = 60, G6 = 6.7 (orange), G5 = 60, G6 = 13.4 (blue), G5 = 60, G6 = 27 G/cm (black). e G5 = G6 = 0 G/cm with a 0.1 ms rectangular pulse (red) and a 1.5 ms REBURP pulse (blue)

Full size image

Since we now understand the emergence of the mixed-phase artifacts from a theoretical point of view we can propose and test several solutions for recording sensitivity enhanced HSQC experiments in practice. A first solution would be to include phase cycling of the two 180° pulses. However, since this would increase the number of scans that need to be recorded per FID, we do not prefer this option. Rather, we use PFGs G5 and G6 for this purpose. As borne out by the simulations, the optimal solution under these circumstances would require strong gradients G5, with G6 applied at about four-fold weaker strength.

Figure 3a shows a PFG-SE 15N-1H HSQC spectrum obtained for the small protein calbindin D9k (Oktaviani et al. 2011), when G5 = G6 = 0. In this case phase differences of up to 25° are observed, as exemplified by the traces taken along the F1 frequency dimension at 114.1 ppm (upper) and 123.0 ppm (lower), respectively (Fig. 3b). The artifacts can be reduced significantly by placing bracketing purging PFGs around the 180° pulses during the reverse INEPT transfers to remove undesired coherence transfer pathways, viz. G5 and G6 in Fig. 1. For example, using strong gradient pairs G5 = G6 = 35.4 G/cm the spectrum of Fig. 3c is obtained. Although much reduced, traces shown next to the 2D spectrum demonstrate that a phase difference of 7 degrees remains. Phase errors were no longer detectable when G5 = 35.4 G/cm and G6 = 7.1 G/cm (Fig. 3e/f).

Fig. 3
figure 3

2D PFG-SE 15N-1H HSQC spectra obtained for calbindin D9k together with traces at 114.1 ppm (upper) and 123.0 ppm (lower). a–b G5 = G6 = 0; c–d G5 = G6 = 35.4 G/cm; e–f G5 = 35.4 G/cm, G6 = 7.1 G/cm. The sample was contained in a Shigemi microcell

Full size image

Figure 4 was obtained using experiments recorded with a 1.5 ms REBURP pulse (peak power 4.2 kHz) in the first reverse INEPT transfers. When G5 = G6 = 0 artifacts are still seen, as predicted by the simulations (Fig. 2e), indicating that wide band refocusing and/or inversion with this pulse does not eliminate artifacts sufficiently. However, with the same gradient setting as used for Fig. 3e/f, phase errors were no longer detectable.

Fig. 4
figure 4

2D PFG-SE 15N-1H HSQC spectra obtained for calbindin D9k using a REBURP refocusing/inversion pulse, together with traces at 114.1 ppm (upper) and 123.0 ppm (lower). a–b G5 = G6 = 0 G/cm; c–d G5 = 35.4 G/cm, G6 = 7.1 G/cm

Full size image

For purpose of illustration of the efficacy of artifact suppression using gradient pulses, Fig. 5 shows PFG-SE 15N-1H HSQC spectra obtained for calbindin D9k when the carrier is deliberately placed off-resonance by 2.0 kHz relative to the value used to obtain Fig. 3 (119 ppm). In panel (a) a phase difference of 72 degrees was observed for G5 = G6 = 0. Traces taken along the F1 frequency dimension at 112.1 ppm (upper) and 121.0 ppm (lower), respectively show the severity of the artifacts in this situation (Fig. 5b). As before, the mixed-phase artifacts can be reduced significantly by setting G5 = G6 = 35.4 G/cm, which eliminates the dominant dispersive artifacts (Fig. 5c/d). In this case a phase difference of 10 degrees remains. Application of the mismatched gradient amplitudes G5 = 35.4 G/cm and G6 = 7.1 G/cm (Fig. 5e/f) removed the remaining dispersive signal, but, as explained in detail above, also eliminated a fraction of absorptive signal. This can be clearly seen by comparison of panels (d) and (f). Unfortunately, REBURP pulses with sufficient band width to avoid these sensitivity losses would require a peak RF amplitude that is unattainable on our probe head (8.4 kHz), but alternative RF pulses could be considered. In many practical cases, however, such as those shown in Fig. 3, ΩN « ω1 (i.e., α « 1) only limited signal loss incurs. Nonetheless, undesired CTP amplitudes are not negligible, and phase errors are still observed. In such a situation mixed-phase artifacts can be satisfactorily reduced over a large offset range by pulsed field gradients alone.

Fig. 5
figure 5

2D PFG-SE 15N-1H HSQC spectra obtained for calbindin D9k with the nitrogen carrier placed 2.0 kHz from the center of the spectrum (119 ppm). Traces are shown at 112.1 ppm (upper) and 121.0 ppm (lower). a–b G5 = G6 = 0 G/cm; c–d G5 = G6 = 35.4 G/cm; e–f G5 = 35.4 G/cm, G6 = 7.1 G/cm

Full size image

To conclude, in any practical case the strategy to remove the mixed-phase artifacts described in this paper will have to be combined with effective control of the residual water magnetization at the point of acquisition. This is particular germane for cryogenically cooled probes with high quality factors, where efficient non-relaxation mechanisms can perturb the water polarization during the course of the pulse sequence and acquisition of the FID. Therefore, the recipe presented for the elimination of the mixed-phase artifacts may require optimization by the operator to achieve good water suppression in addition. It may well be that achieving good solvent suppression has prevailed in selecting alternative values for the gradients presented in the literature. In connection to this, PFGs G5 and G6 may also be expanded to fill the entire delay Δ in which they are placed. This will improve artifact suppression further, and may also help to prevent undesired effects from radiation damping.

In conclusion, we have presented here an explanation for phase errors that can be observed in gradient sensitivity enhanced correlation experiments and suggested a simple and effective procedure for their suppression. We anticipate that our results are of value for optimizing many contemporary triple-resonance NMR experiments that use the sensitivity enhanced HSQC and related building blocks as detection module.