1 Introduction

When an insulator forms between a metal and a semiconductor, the metal–semiconductor (MS) structure or Schottky diode (SD) turns into a metal–insulator–semiconductor (MIS)-type SD or structure [1,2,3,4,5,6]; moreover, this interfacial layer is easily polarized under an external electric or magnetic field. Although conventional SiO2 and SnO2 are very stable and grow easily onto semiconductors’ surfaces, they cause high leakage current and cannot completely pacify unsaturated bonds or Nss. These Nss are usually located between the semiconductor and the interlayer, and their energies correspond to the forbidden bandgap energy (Eg) [5,6,7,8,9,10,11]. Depending on their occupancy, these states may act as recombination centers, releasing or capturing electrons under external influence. In general, C-G/ω-V curves deviate from the ideal situation due to Nss and interfacial-dipole polarization mechanisms. These situations appear particularly noticeable at low and medium frequencies in the depletion region. Because, at low and medium frequencies, as long as the period (T = 1/2πf) values exceed the lifetimes (τ) of the Nss, the chargers in these traps can effectively keep up the external ac signal, allowing dipoles ample time to rotate in response to the electric field direction [10,11,12,13,14]. Therefore, especially at low and medium frequencies, there is a significant increase in both C and G values due to interfacial states and polarization [12,13,14,15]. However, as the frequency increases, the contribution decreases and becomes negligible to both C and G values at high frequencies.

However, instead of classical and low dielectric insulating materials, using some nanocomposite, a pure metal and metal oxide-doped organic interface layer with high dielectric properties can quite increase the performance of these devices by passivating these surface states [13, 16,17,18,19]. Pure polymers usually have low conductivity and dielectric values. However, adding small amounts of metal or metal oxide materials such as Co, Zn, Gr, ZnO, MnO, and CdTe can increase these values. Among polymers, some of the most used as interlayer between metal and semiconductor interface are usually polyvinyl alcohol (PVA) and pyrrolidone (PVP), which can be easily soluble in alcohol or water, and they also have similar functional groups [20,21,22,23,24,25]. In the other words, the basic technical and scientific problems of MS structures with/without an interlayer is to improve their performance and decrease cost production by using especially high-dielectric interfacial layer at M/S interface grown by simple and easily techniques. Especially, CdTe has moderate forbidden bandgap when compared to some insulators such as SnO2 and TiO2. Cadmium telluride (CdTe) is a member of the II–VI group and is commonly used in photonic applications because of its high absorption coefficient in the visible range (VR) and moderate bandgap energy (1.45 eV), huge absorption coefficient (> 104/ cm) near the band edge stability, high mobility (1040 cm2/V s), and low cost [26, 27]. The integration of semiconductor nanoparticles with polymers is a considerably desirable approach. Improving the performance of electronic and optic devices is a crucial issue, and using new materials is key to achieving this goal [28, 29]. PVA is a semicrystalline polymer suitable due to its high thermo-stability, chemical resistance, dynamic strength, solubility in water and alcohol, and controllable electric and dielectric properties when doped [30].

In our previous work [15], the voltage and frequency profiles of Dit, τ, and Rs were obtained with various methods. Some of the main electrical parameters were also calculated from the reverse bias C−2 vs V plot for each frequency. The Nss and their lifetimes were also obtained from the parallel conductance method, which is known as the most accurate and reliable one. Therefore, in this study, the real and imaginary components of the complex dielectric constant (\({\varepsilon }^{*}\)= \(\varepsilon {\prime}\) – \(j\varepsilon {\prime}{\prime}\)), electrical modulus (M* = 1/\({\varepsilon }^{*}\) = \(M{\prime}\)  + \(jM{\prime}{\prime}\)), and impedance (\({Z}^{*} = Z{\prime}-jZ{\prime}{\prime}\)) of the Au/(CdTe:PVA)/n-Si MPS structure, loss tangent (tanδ), and the Nyquist plots (\(M{\prime}{\prime} vs M{\prime}\)) have been investigated in detail over the frequency range of 2 kHz to 0.7 MHz at ± 2.5 V. All of these parameters were found to have strong functions of frequency and applied voltage. The measured value of \(\varepsilon {\prime}\) was found to be 128.38 (at 2.5 V), which is 33.78 times bigger than the value of traditional SiO2, even at 2 kHz. The double logarithmic plot of \({\sigma }_{ac}\) vs ln(f) shows three linear components corresponding to low, intermediate, and high frequencies with different slopes. This observation suggests the existence of two different charge transport mechanisms in the sample. The experimental results indicate that the (CdTe:PVA) interlayer may serve as a viable alternative to traditional insulators for ultra-capacitors, as it exhibits a high value of \(\varepsilon {\prime}\) even at 2 kHz, allowing for the storage of more electronic charges/energy.

2 Experimental procedure

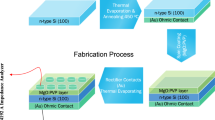
The Au/(CdTe:PVA)/n-Si (MPS) structure was fabricated onto n-Si. First, the n-Si substrate was cleaned in the ultrasonic bath using a mixture of chemical acid and deionized water. It was then rinsed in deionized water and dried with N2 gas. Secondly, the whole back of the n-Si substrate was coated by very pure Al with 150-nm thickness and then annealed at 500 °C for 5 min to form the ohmic contact. The CdTe-PVA was performed by dispersing 10 mg CdTe nanostructure in 5 ml of 0.05% PVA solution. The solution was then applied to the front of an n-Si substrate using the spin coater method. Finally, pure Au rectifier contacts with a thickness of 150 nm were thermally grown onto (CdTe-PVA) interlayer. The C-V and G/ω-V measurements were performed utilizing an HP4192-A impedance meter at room temperature (RT). For more detailed information on the chemical cleaning of the surface of p-Si wafers, fabrication procedures, measurement systems, and structural analysis, refer to our previous work [15].

3 Results and discussion

The frequency-dependent admittance technique, which includes a set of capacitance/conductance (C/G-V) measurements, is generally utilized to calculate the real/imaginary components of complex dielectric constant (\(\varepsilon *=\varepsilon {\prime} - j\varepsilon {\prime}{\prime}\)). With this, the obtained dielectric data can be employed to analyze the complex electrical modulus (\(M*=M{\prime} + jM{\prime}{\prime}\)), loss tangent (tanδ), and electrical conductivity (σ). The measurements were performed in a wide voltage and frequency range to ensure accuracy and reliability. Therefore, in this study, C and G versus V measurements were carried out with a frequency range of 2–700 kHz and a voltage range of ± 2.5 V at RT. After that, the \(\varepsilon {\prime}\), \(\varepsilon {\prime}{\prime}\), and tanδ (= \(\varepsilon {\prime}{\prime}\)/ \(\varepsilon {\prime}\)) values were extracted from the measured C and G using the following relations [12, 16, 24, 26, 31,32,33]. The real part of the dielectric constant is represented with \(\varepsilon {\prime}\), and it is dimensionless and a measure of the capability of a material to store electronic charges. Under an electric field, the dielectric film can be easily polarized, resulting in energy loss due to internal friction. In the literature, this energy loss is called dielectric loss (\(\varepsilon {\prime}{\prime}\)). Tanδ is another method to measure the energy loss as heat under an electric field.

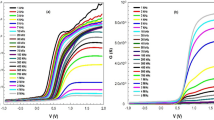
$$\varepsilon^{*} \left( \omega \right) = \varepsilon^{\prime}\left( \omega \right) - j\varepsilon^{\prime\prime}\, = \,\left( {\frac{{C_{{\text{m}}} d_{{\text{i}}} }}{{A\varepsilon_{0} }}} \right)\, - \,j\left( {\frac{{G_{{\text{m}}} d_{{\text{i}}} }}{{A\varepsilon_{0} }}} \right)\, = \,C_{{\text{m}}} /C_{0} - j\left( {G_{{\text{m}}} /\omega C_{0} } \right)$$
(1)

In Eq. (1), \(\left( {\frac{{\varepsilon_{0A} }}{{d_{i} }}} \right)\) is the C value of the empty capacitor (C0), ε0 (8.85 × 10–12 F/cm) is the dielectric constant of free space, di is the interlayer thickness, and ω is the angular frequency (2πf). Cm and Gm/ω are the measured C and G values, respectively. The voltage-dependent profiles of \(\varepsilon {\prime}\) – V, \(\varepsilon {\prime}{\prime}\) – V, and tanδ – V plots for different frequencies, as well as frequency-dependent profiles for various positive biases, are given in Figs. 1, 2, and 3, respectively. Figures 1 and 2 show that the curves for both \(\varepsilon {\prime}\) – V and \(\varepsilon {\prime}{\prime}\) – V have three distinct regions corresponding to voltage ranges of approximately − 2.5/0.0 V (inversion), 0.0/0.7 V (depletion), and 0.7/2.5 V (accumulation). The values of both εʹ and εʺ increase as the frequency decreases for the entire bias voltage range. The charges at traps lead to an excess polarization at low frequencies, depending on their lifetimes (τ). However, this contribution disappears at sufficiently high frequencies because the period (T = 1/ω) becomes lower than τ [33, 34]. In the other words, surface states/traps are effective especially in the depletion regions. At low and intermediate frequencies, these effects can be observed. The external ac signal depends on their relaxation/lifetimes (t), leading to an increase both in the real and imaginary parts of the complex dielectric constant. But at sufficiently high frequencies, the value of period (T = 1/2πf) becomes lower than t and hence both surface states do not have enough time to follow ac signal. As a result, dipoles can only rotate around their own axis, leading to a decrease in the contribution of surface states and dipole polarization with increasing frequency.

Fig. 1
figure 1

a The \(\varepsilon {\prime}\) vs V, b the inset \(\varepsilon {\prime}\) vs ln(f) plots of the MPS structure

Full size image
Fig. 2
figure 2

a The \(\varepsilon {\prime}{\prime}\) vs V and b the inset \(\varepsilon {\prime}{\prime}\) vs ln(f) plots of the MPS structure

Full size image
Fig. 3
figure 3

a The tanδ vs V and b the inset tanδ vs ln(f) plots of the MPS structure

Full size image

The tanδ–V curves exhibit distinct peaks for each frequency (see Fig. 3). The observed peak can be attributed to the reorganization and restructuring of electronic charges localized between the interfacial thin film and semiconductor under an electric field [29]. Figures 1, 2, and 3 show that the \(\varepsilon {\prime}, \varepsilon {\prime}{\prime}\), and tanδ values of the (CdTe:PVA) interfacial thin film are strongly dependent on f and V in both depletion–accumulation regimes. Higher values of \({\varepsilon }{\prime}\) and \(\varepsilon {\prime}{\prime}\) are due to the thin interfacial layer, surface-dipole polarization, and interface traps [33, 34]. When the dipoles have sufficient time to keep up with the change in the direction of the electric field depending on the frequency (T = 1/2\(\pi\)f), increases in \(\varepsilon {\prime}\) and \(\varepsilon {\prime}{\prime}\) values occur at these frequencies [26, 29, 32, 34]. However, charges localized at traps with an adequately long relaxation time (τ ≫ T) to allow migration between the traps cannot contribute to εʹ and εʺ at higher frequencies.

The electric modulus value typically increases because of the relaxation of the electric field in interfacial thin films/layers, as the electric displacement remains almost constant. The complex formalism of the electric modulus can be analyzed employing the following expression:

$${M}^{*}(f)=(\frac{{\varepsilon }{\prime}}{{\varepsilon }^{{\prime}2}+{\varepsilon }^{{\prime}{\prime}2}})+j\left(\frac{{\varepsilon }^{{\prime}{\prime}}}{{\varepsilon }^{{\prime}2}+{\varepsilon }^{{\prime}{\prime}2}}\right)$$
(2)

The obtained experimental \(M{^{\prime}}\) and \(M{^{\prime\prime}}\) values from Eq. 2 are given in Figs. 4 and 5 for various frequencies and applied voltage, respectively. These plots are necessary to see the polarization and interface traps/states’ effects on the dielectric and electric modulus characteristics for various applied dc bias voltages.

Fig.4
figure 4

a The \(M{\prime}\) vs V, b the inset \(M{\prime}\) vs ln(f) plots of the MPS structure

Full size image
Fig.5
figure 5

a The \(M{\prime}{\prime}\) vs V, b the inset \(M{\prime}{\prime}\) vs ln(f) plots of the MPS structure

Full size image

Figures 4 and 5 show that the \(M^{\prime}\) and \(M\) versus voltage graphs peak at around zero bias voltage when ωτ = 1, indicating maximum dielectric loss. These peaks demonstrate the transition in charge carriers' mobility from short to long ranges. Additionally, the peak positions shift to positive voltage values as the frequency increases. The main reason for this peak position shift is due to the reordering and restructures of electronic charges and dipoles under the dc electric field [35,36,37]. The observed essential changes in the real/imaginary parts of \({M}^{*}\) with both frequency and voltage are the result of localized charges and dipoles in the interfacial thin film, and such a special distribution is usually called Maxwell–Wagner polarization (MWP), which occurs at low and moderate frequencies. The decrease in both \(M{\prime}\) and \(M{\prime}{\prime}\) values as frequency increases is demonstrated in Figs. 4 and 5. This is a result of the short-range mobility of electronic charges. It can be readily concluded that the observed change in the real and imaginary parts of \({\varepsilon }^{*}\) and \(M\)* with frequency is due to relaxation phenomena and Nss effects.

The dielectric relaxation behavior can also be explained using complex impedance spectroscopy (\(Z*=Z{\prime}-jZ{\prime}{\prime}\)). This is described by the following relations [12, 15, 32,33,34,35,36].

$${Z}^{*}\left(\omega \right)={Z}{\prime}-j{Z}^{{\prime}{\prime}}=\frac{1}{j\omega {C}_{0}{\varepsilon }^{*}}=\frac{{\varepsilon }^{{\prime}{\prime}}}{\omega {C}_{0}\left[{\varepsilon }^{{\prime}2}+{\varepsilon }^{{\prime}{\prime}2}\right]}-\frac{{\varepsilon }{\prime}}{\omega {C}_{0}\left[{\varepsilon }^{{\prime}2}+{\varepsilon }^{{\prime}{\prime}2}\right]}$$
(3)

In Eq. 3, the quantities of εo, A, and d represent the permittivity of free space, rectifier-contact area, and the distance between rectifier and ohmic contacts, respectively. Thus, the \(Z^{\prime}\) and \(Z^{\prime\prime}\) values versus voltage curves for each frequency were extracted from Eq. 3 and are represented in Figs. 6 and 7.

Fig.6
figure 6

a The Zʹ vs V, b the inset Zʹ vs ln(f) plots of the MPS structure

Full size image
Fig.7
figure 7

a The Zʺ vs V, b the inset Zʺ vs ln(f) plots of the MPS structure

Full size image

The figures demonstrate distinct peaks in both Zʹ and Z″ values as the voltage decreases. However, the values of these peaks decrease with increasing frequency for almost every applied dc bias voltage, as shown in the inset of the figures. The ac electrical conductivity (\({\sigma }_{\text{ac}}\)) values of the Au/ (CdTe:PVA)/n-Si MPS structure can be designated with the tanδ or \(\varepsilon {\prime}{\prime}\) values by utilizing the following expression [37,38,39,40].

$${\sigma }_{\text{ac}}\left(\omega \right)=2\pi f \omega C\left(tan\delta \right)\left(\frac{{d}_{i}}{A}\right)=2\pi f{\varepsilon }_{0}{\varepsilon }^{{\prime}{\prime}}.$$
(4)

It can be clearly seen in Fig. 8 that there are two distinctive peaks in the inversion and depletion regions due to a special density distribution of surface states/traps at interlayer/semiconductor interface. On the other hand, the change in peak magnitudes and their positions with frequency are generally dependent on the lifetimes of traps and their reordering/restructuring under external electric field. The decrease in the series resistance value with increasing frequency causes an increase in the conductivity values (G = 1/R).

Fig. 8
figure 8

a The \({\sigma }_{\text{ac}}\) vs V and b the inset \({\sigma }_{\text{ac}}\) vs ln(f) plots of the MPS structure

Full size image

Some researchers were also investigated both the basis electric and dielectric parameters and conduction mechanisms depend on frequency, temperature, and applied bias voltage in MS-type structures with an interfacial layer in recent years and they reported similar results on the surface states, series resistance, interfacial layer, and barrier inhomogeneities effects on the performance of these structures [41,42,43,44,45]. The inset of Fig. 8a shows that the ac value remains constant at lower frequencies and increases as the frequency increases. This is due to the decrease in the Rs of the MPS structure and the electronic charges at traps. These two different frequency ranges correspond to DC and AC conductivity, as represented in Eq. 3.

$${\sigma }_{\text{ac}}={\sigma }_{\text{dc}}+A{\omega }^{s}$$
(5)

In Eq. 5, A is a constant, and s represents the degree of applied frequency. The slope (s) values were calculated from Fig. 9. This provides information about the conduction mechanism, with expected values between 0 and 1. To achieve this, double logarithmic \({\sigma }_{\text{ac}}\) vs f plots were obtained for three different dc bias voltages, as shown in Fig. 9.

Fig. 9
figure 9

The double logarithmic \({\sigma }_{\text{ac}}\) vs f plots of the sample for various applied bias voltages

Full size image

Figure 9 shows the ln(\({\sigma }_{ac}\)) vs f plots for three different voltages, each with three linear parts having different intercept points within the measured frequency range. This enables direct calculation of the value of s for each bias voltage. The curves also suggest the presence of three distinct charge transports at low/intermediate/high frequencies. The values of s for three applied bias voltages were 0.31, 1.11, and 1.39 for 0.7 V, 0.11, 0.55, and 1.51 for 1.5 V, and 0.12, 0.39, and 1.44 for 1.8 V, respectively. These results indicate that the conduction mechanism known as the relaxation model can occur when electrons migrate from one state/trap to another [39, 40].

Using Cole–Cole curves, (\(M{\prime}{\prime}\) vs \(M{\prime}\)) can provide significant information regarding the nature of the relaxation process of the interfacial layer. Therefore, the Cole–Cole (\(M{\prime}{\prime}\) vs \(M{\prime}\)) curves of the MPS structure at 0.1 and 0.7 MHz are presented in Fig. 10. As demonstrated in this figure, the dielectric relaxation deviates from ideal Debye behavior. The electric modulus curves for interfacial layers or dielectric materials do not always form perfect circles or semicircular arcs; they may become asymmetric. The smaller semicircle observed in the cole-cole curve at 100 kHz disappeared at 700 kHz. The two semicircles observed at 0.1 MHz disappeared in the \(M{\prime}{\prime}\) vs \(M{\prime}\) curve, indicating an enhancement of the material’s conductivity. The high-frequency arc observed in these composites cannot be attributed to interface traps between the interlayer and semiconductor.

Fig. 10
figure 10

The Cole/Cole curves (\(M{\prime}{\prime}\) vs \(M{\prime}\)) of the MPS structure for 0.1 and 0.7 MHz

Full size image

4 Conclusion

In this present study, we were especially focused on the changes in the dielectric parameters, electrical modulus, and ac electrical conductivity with both voltage and frequency for the Au/(CdTe:PVA)/n-Si MPS structure rather than the MIS structures. Therefore, these parameters were calculated from the impedance dielectric spectroscopy, including C/G-V-f measurements. Thus, the \(\varepsilon {\prime}\), \(\varepsilon {\prime}{\prime}\), tanδ, \(M{\prime}{\prime}\), \(M{\prime}\) and \({\sigma }_{\text{ac}}\) values versus voltage and frequency were drawn between wide-range frequency (2 kHz–0.7 MHz) and voltage (± 2.5 V). The experimental results suggest that the parameters are f- and V-dependent, especially at low to moderate frequencies in the depletion zone. This dependence is caused by the existence of Nss, interlayer, and dipole polarizations, which are dependent on relaxation time. The obtained higher values of εʹ (= 128.38 at 2.5 V) even at 2 kHz is almost 34 times higher than the maximum value of traditional SiO2. Additionally, the frequency-dependent AC conductivity data reinforces this conclusion. The ln(\({\sigma }_{\text{ac}}\))–ln(f) plot for three different bias voltages also exhibits three linear regimes, supporting the hypothesis of hopping conduction in the composites. The higher values of \(\varepsilon {\prime}\) observed for the (CdTe:PVA) interlayer suggest that it can be used as a successful alternative to traditional insulators for ultra-capacitors, electronic charge storage, or energy storage. The two semicircles observed at 0.1 MHz are absent in the \(M{\prime}{\prime}\) vs \(M{\prime}\) curve, indicating an enhancement in the material's conductivity.