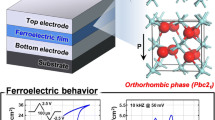
Abstract
The electric breakdown strength (Eb) is an important factor that determines the practical applications of dielectric materials in electrical energy storage and electronics. However, there is a tradeoff between Eb and the dielectric constant in the dielectrics, and Eb is typically lower than 10 MV/cm. In this work, ferroelectric thin film (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 with a dielectric constant of 115 is found to exhibit an ultra-high Eb = 10.99 MV/cm, attributing to the high-entropy effects that could result in dense nanostructures with refined grains, low concentration of oxygen vacancies, low leakage current and small polar nano-regions in the thin film. A recoverable energy storage density of 5.88 J/cm3 with an excellent energy storage efficiency of 93% are obtained for the dielectric capacitor containing the thin-film dielectrics. Remarkably, the dielectric capacitor possesses a theoretical energy storage density of 615 J/cm3 compatible to those of electrochemical supercapacitors. The high-entropy ferroelectric thin films with ultra-high Eb and superior energy storage properties are much promising dielectrics used in next-generation energy storage devices and power electronics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With increasing consumption of electrical energy in human society, energy storage devices with improved energy density, power density and energy efficiency are urgently needed [1, 2]. Compared with batteries and fuel cells, dielectric capacitors possess some outstanding energy storage properties, such as large power density (~ 106 W/kg) with high working voltages, ultrafast charge–discharge rate (~ ns) and good thermal stability [3,4,5,6]. However, their energy storage density is typically low (< 100 J/cm3). In a dielectric capacitor, the electric dipoles are oriented under applied electric fields, accumulating free charges on conductive layers or electrodes at their surfaces, and the storage of electrical energy is thereby achieved. Particularly, for linear dielectric materials [7, 8], the energy storage density U can be described as U = 0.5ε0εrEb2 where \({\varepsilon }_{0}\)=8.854 × 10–12 F/m is the vacuum dielectric constant, \({\varepsilon }_{r}\) is the relative dielectric constant and Eb is the electric breakdown strength. The maximum energy storage is highly dependent on the dielectric constant \({\varepsilon }_{r}\) and Eb. Generally, the large electric breakdown strength is achieved at the cost of reduced dielectric constant. Bulk ferroelectric ceramics have low electric breakdown strengths (< 1 MV/cm) with a high dielectric constant (> 1000), while their thin-film counterparts exhibit high electric breakdown strengths (< 6 MV/cm) accompanied by a low dielectric constant (< 500). Meanwhile, polymer thin films and some metal oxides show ultrahigh electric breakdown strengths while they have extremely low dielectric constants (< 10). Thus, how the electric breakdown strength and dielectric constant are balanced to optimize the energy storage performance of dielectrics becomes a grand challenge in enhancing the energy density of dielectric capacitors.
To address the aforementioned issues, the dielectrics are developed in the framework of high-entropy materials that could enhance the energy storage performance of dielectric capacitors. High-entropy ceramics (HECs) consist of multiple (more than 5) randomly distributed metal ions at their specific lattice sites, and the configuration entropy of HECs could be larger than 1.5 R (R is the gas constant) when those metal ions have equal molar ratio. The dielectric capacitors containing HECs exhibit some distinctive characteristics beneficial to their energy storage properties, such as large lattice distortion, good thermal stability and sluggish kinetic diffusion [9,10,11]. Recently, some attempts have been made to develop high-entropy ferroelectric ceramics for the improvement on energy storage properties of dielectric capacitors,. Sun et al. [12] prepared high-entropy ceramic (Bi0.2Na0.2Ba0.2Ca0.2Sr0.2)TiO3 by a hydrothermal method and found that a recoverable energy density of 1.37 J/cm3 was achieved with a high dielectric constant of 3788. Zhou et al. [13] introduced 0.1 at.% Bi(Zn0.2Mg0.2Al0.2Sn0.2Zr0.2)O3 into ferroelectric ceramic 0.75BaTiO3 − 0.25Na0.5Bi0.5 TiO3 and found the recoverable energy density was improved to 3.74 J/cm3 with an energy efficiency of 82.2%, resulting from the local polar nano-domains in the ferroelectric material. Yang et al. [14] studied high-entropy effects on the Bi2Ti2O7-based thin-film dielectrics, and found that they exhibited a high energy storage density of 182 J/cm3 at an electric field of 6.35 MV/cm. The results suggest that high-entropy ferroelectric thin films could be promising in enhancing the energy storage properties of dielectric capacitors.
In this work, (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 (BNKLST) high-entropy ferroelectric thin films are synthesized, which have ultra-high electric breakdown strength (> 10 MV/cm) and large dielectric constant (> 100). The dielectric capacitors containing the ferroelectric thin films possess an ultra-high energy storage density compatible to that of an electrochemical supercapacitor, and they have excellent energy storage efficiency (> 90%) and good thermal stability. The high-entropy effects on the crystal structure, microstructures, dielectric and electrical property of BNKLST thin films are systematically investigated, revealing the underlying mechanisms that determine their superior energy storage properties.
2 Materials and methods
2.1 Preparation of ferroelectric thin films
High-entropy ferroelectric thin films (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 are synthesized on Pt(111)/Ti/SiO2/Si(100) conductive substrate through a sol–gel synthesis route combined with spin coating approaches. The starting materials are bismuth nitrate (Bi(NO3)3·5H2O), sodium acetate trihydrate (CH3COONa⋅3H2O), potassium acetate (CH3COOK), lanthanum nitrate hexahydrate (La(NO3)3⋅6H2O), strontium acetate ((CH3COO)2Sr), acetic acid, tetrabutyl titanate, acetylacetone and 2-methoxyethanol. Frist, the aforementioned metal nitrates and acetates were added into acetic acid with magnetic stirring at 80 °C. Then, the resulting solution was added dropwise into the other solution prepared by mixing tetrabutyl titanate, acetylacetone and 2-methoxyethanol in a volumetric ratio of 1:2:5. Two solutions were fully mixed and the concentration of metal nitrates and acetates was adjusted to 0.2–0.3 mol/L. Finally, the mixture was stirred for 24 h, followed by aging for 48 h. The precursor was spin-coated on the substrate at a rate of 600 rpm for 9 s and subsequently at 3000 rpm for 30 s. During the spin coating process, five or six drops of the precursor solution were applied to coat one layer on the substrate, whose volume was controlled to be 0.2 ml. The wet thin film was dried at 200 °C, 450 °C and 650 °C for 5 min, respectively. Such drying process was repeated for 4 times. Finally, the BNKLST thin film was crystallized at 650 °C for 15 min in a rapid thermal processor (AccuThermal AW410T).
2.2 Characterizations
The crystal structure was determined by X-ray diffraction (XRD, Rigaku SmartLab) with Cu Kα radiation. The microstructure of sample was observed by field emission scanning electron microscope (FE-SEM, MAIA), where the energy dispersive X-ray spectroscopy (EDX, Oxford Inca EDX system) detector was used for elemental analysis. The piezoelectricity of thin film was measured by a piezoresponse force microscopy (PFM, Bruker Dimension Icon). The substrate coated with the thin film was stuck to a glass slide. Silver glue is drawn from the Pt layer in the substrate to the glass slide, forming a conductive path connecting to the common ground of equipment. Raman spectrum was obtained by using Raman spectrometer (HR800, LAbLAM) with a He–Ne laser at a wavelength of 633 nm. For electric measurements, the disk electrodes with a diameter of 0.5 mm on the surface of thin films were prepared by magnetron sputtering (Denton Explorer 14), where gold was chosen as sputtering target and the substrate was covered by a shadow mask. Dielectric measurement was performed on an impedance analyzer (E4980A, Agilent Technologies). The current–voltage curves were measured by a probe station (450PM, Manual Probe Station) with an electrometer (4200, Keithley), where the temperature range could be adjusted from room temperature to 400 °C. The hysteresis loops were measured by ferroelectric analyzer (Premier II, Radiant).
3 Results and discussion
The crystal structures of thin films were studied by XRD. Figure 1a shows the XRD patterns of BNKLST thin film obtained on the XRD apparatus operated with Cu Kα radiation (λ = 1.5406 Å) under 45 kV and 250 mA and with a grazing angle of 0.5°. It is found that the BNKLST thin film possesses a single-phase perovskite structure, which could be considered as a solid solution of Bi0.5Na0.5TiO3, Bi0.5K0.5TiO3, LaTiO3 and SrTiO3. For the BNKLST thin film, the Goldschmidt tolerance factor \(t=({R}_{A}+{R}_{o})/\sqrt{2}({R}_{B}+{R}_{o})\) is calculated, where \({R}_{A}{, R}_{B}\) and \({R}_{O}\) represent the radius of ions at A- and B-sites and oxygen ion, respectively. Since t = 1.002 is close to 1, it is suggested that the BNKLST thin film is in a pseudo-cubic phase with large lattice distortions [15]. The XRD Rietveld refinement patterns for BNKLST thin film are shown in Fig. 1(b), and the refinement parameters of R-pattern and R-weight pattern are Rp = 6.53% and Rwp = 8.58%, respectively. These low values of refinement parameters indicate that there is a good agreement between the experimental data and calculated data, and the lattice parameters a = b = c = 3.908 Å can be obtained from the refinement. In addition, the Rietveld refinement patterns are well consistent with the Bragg diffraction for SrTiO3 with a cubic phase in the space group of Pm \(\overline{3 }\) m (PDF #35-0743) [16], which further confirm that the BNKLST thin film is in a pseudo-cubic phase. The consistency could be mainly attributed to the average radius (1.442 Å) of ions at A-sites, which is nearly equal to that (1.44 Å) of Sr+2 [17].
a XRD patterns of BNKSLT thin film and standard JCPDS cards [16] of Bi0.5Na0.5TiO3, Bi0.5K0.5TiO3, LaTiO3 and SrTiO3, b Rietveld refinement results of XRD data for BNKLS thin film and peaks of Bragg diffraction for crystal structures in Pm \(\overline{3 }\) m space group
Figure 2a shows the cross sections of BNKLST thin film and the Pt/Ti/SiO2/Si substrate. The thickness of thin film is about 180 nm. The surface morphology of thin film is shown in Fig. 2b. It is worth noting that the BNKLS thin film has dense microstructures with nano-sized grains, which is favorable for enhancing its electric resistivity [18]. The nanostructure of BNKLS thin film may be caused by the sluggish kinetic diffusion in high-entropy materials that could hinder the grain growth in the thin film, resulting in the formation of nano-sized grains [9]. The EDS elemental mappings for BNKLS thin film are shown in Fig. 2e–i, suggesting that Bi, Na, K, La, Sr, Ti and O elements are uniformly distributed and high-entropy BNKLST thin film is successfully prepared.
The Raman spectra of BNKLST thin film at room temperature are shown in Fig. 3a, and the deconvolutions of peaks are implemented by fitting them with Gaussian profiles. There are three regions in the wavenumber ranging from 50 to 1000 cm−1, which are labelled as A-site and Ti–O bond, TiO6 vibrations and A1 + E longitudinal optical vibration of bonds, respectively. Peaks 1–3 are associated with the A–O bond, mainly attributing to the bonding between Bi, Na, K, Sr or La elements at A-site and oxygen. Compared with that for BNKLST bulk ceramics as shown in Fig. 3b, the peak for BNKLST thin film is shifted to a lower wavenumber, i.e., the positions of peaks 1–3 are shifted from 90.25, 110.28, 165.91 cm−1 to 81.11, 100.70 and 144.21 cm−1, respectively. Since the BNKLST thin film is sintered at a temperature (650 °C) lower than that (1050 °C) for BNKLST bulk ceramics, the loss of volatile metal elements such as Bi and Na in the former could be much less than that in the bulk ceramics. Therefore, it is suggested that the average mass of A-site element in the BNKLST thin film is relatively larger than that in BNKLST bulk ceramics, leading to the increase in the strength of A–O bond and the shift of peaks ascribed to the A–O bond towards a lower wavenumber. As indicated in Fig. 3, peak 4 is assigned to Ti–O bond which affects the dielectric property of materials, especially their dielectric polarizations and dielectric losses [19,20,21]. It is found that peak 4 for BNKLST thin film shifts to a lower wavenumber and its full-width at half maximum (FWHM, 149.26 cm−1) becomes larger than that (119.57 cm−1) of BNKLST bulk ceramics, indicating that the structural disorder in the lattice of thin film is more severe than that of bulk ceramics and suggesting a reduced polarity of BNKLST thin film. The FWHM of peak 6 (141.65 cm−1) for BNKLST thin film is larger than that (126.12 cm−1) for bulk ceramics, indicating a large distortion of TiO6 octahedral structure favorable for improving electric breakdown strength in BNKLST thin film [22].
Furthermore, compared with those for Bi0.5Na0.5TiO3 (BNT) ferroelectric thin films previously reported [9, 23, 24], the Raman spectrum for BNKLST thin film is much broader due to the significant chemical disorder at A-site. As shown in Fig. 3a, peak 4 at 210 cm−1 ascribed to Ti–O–Ti bond shifts to a lower wavenumber in comparison with that at 250 cm−1 for BNT thin film [23, 25], indicating a weakened Ti–O–Ti bond in the BNKLST thin film. It is because the multiple metal ions randomly located at A-site may affect the strength of Ti–O bond. Besides, the band in the range of 400–700 cm−1 associated with the distortion of TiO6 is more symmetrical, suggesting the BNKLST thin film has a relatively symmetrical crystal structure. This result is in accordance with the pseudo-cubic phase as determined from XRD analysis. The band in the high wavenumber range of 700–1000 cm−1 is assigned to the collective displacement of oxygen, and its FWHM (136 cm−1) for BNKLST thin film is smaller than that (158 cm−1) for BNT [9], suggesting that the occurrence of displacement of oxygen ions in the BNKLST thin film is less intense than that in BNT thin film. Because the BNKLST thin film has lower contents of volatile elements such as Bi and Na than BNT thin film, and it has less losses of those metal elements during sintering processes at a lower annealing temperature than BNT thin film, therefore the BNKLST thin film could have lower concentration of oxygen vacancies than BNT thin film, which could be favorable for enhancing its electric breakdown strength [26, 27].
Figure 4a shows the surface morphology of BNKLST thin film. It is observed that the grains are small with sizes lower than 100 nm and they overlap with each other with distinct grain boundaries. The average surface roughness is calculated to be 0.55 nm, implying that the BNKLST thin film has a smooth surface. As shown in Fig. 4b–d, the distinct and strong contrast among domains in PFM amplitude and phase images demonstrate that there exist polarized nano-regions with randomly distributed polarization in the BNKLST thin film. Moreover, the piezoelectricity of thin film is investigated by PFM at a contact resonant frequency of 358 kHz (as shown in Fig. 5a). The local piezo-response amplitude and phase are measured under an applied DC bias voltage varied from − 20 V to 20 V at a frequency f. As shown in Fig. 5b, the piezoelectric response is significant and an asymmetrical butterfly loop is evident. The loop is shifted towards a positive voltage, indicating the existence of built-in electric field in the BNKLST thin film [23, 28]. The built-in electric field could result from the accumulated oxygen vacancies at the surface of thin films, which have positive charges [29]. Since the bottom electrode is connected the common ground of equipment, a positive potential VSP resulting from the built-in filed could offset the applied voltages at the PFM tips, shifting the piezoelectric response loop to positive voltages. In addition, the effective piezoelectric modulus d33 could be calculated as \({d}_{33}=dA/dV\), where A and V are the piezo-response amplitude and applied DC voltage, respectively, and the results are shown in Fig. 5c. The maximum value of d33 could reach at 82 pm/V for the BNKLST thin film, which is relatively higher than those for BNT and BaTiO3 thin films (40 pm/V [30] and 50 pm/V [31], respectively). The dense microstructure and refined nano-grains in the BNKLST thin film could be responsible for its large piezoelectric modulus [32, 33]. The phase hysteresis loops for piezo-response shown in Fig. 5d demonstrate that 180° domain switching is achieved in the BNKLST thin film, suggesting that the thin film is ferroelectric. Meanwhile, the phase hysteresis loop for piezo-response expands with increasing frequency f. To be more specific, the coercive field (\({E}_{c}\)) increases from 175 kV/cm to 310 kV/cm with \(f\) increased from 0.2 Hz to 1.0 Hz. The inset in Fig. 5d shows the relationship between \({E}_{c}\) and \(f\), which is well fitted by a power-law relation (\({E}_{c}\sim {f}^{\beta }\)). For conventional ferroelectric materials, the dynamical switching behaviors can be explained by Ginzburg–Landau mean-field theory with the exponent \(\beta\) close to 1 [50]. For the BNKLST thin film, the exponent \(\beta\)=0.38 is much lower than 1, implying that there are strong fluctuations of polarizations in the polar nano-regions.
a The resonant peaks of PFM signals at 358 kHz under different amplitudes of driven voltages; b The amplitude butterfly loop for piezo-responses in the BNKLST thin film; c d33 versus DC bias voltage in the BNKLST thin film; d The phase hysteresis loops for piezo-response in the BNKLST thin film under different frequencies f, and (inset) log–log plots of coercive field \({E}_{c}\) vs. \(f\) fitted with a power-law relation (red line) (Color figure online)
The dielectric spectrum for BNKLST thin film is shown in Fig. 6. The dielectric constant of 110 is obtained at 1000 Hz. The dielectric constant decreases with increasing frequency, which is ascribed to dipole moments in thin films [34]. The dielectric loss also reduces with increasing frequency, while the smallest loss value (0.024) can be reached at about 36 MHz. It is found that the dielectric loss suddenly increases at high frequency (> 50 MHz), which is attributed to the dipole resonance [35]. The dielectric property can be explained by the complex dielectric constant. According to Debye functions described in Eqs. (1, 2), the real part of dielectric constant reflects the ability of dielectrics in storing energy during the polarization process, while its imaginary part describes the energy dissipation during the polarization process.
where \({\varepsilon }_{s}\) and \({\varepsilon }_{\infty }\) are static and optical dielectric constants, respectively. \(\omega\) is the angular frequency, \(\tau\) is the relaxation time. Using the derived formula \({\varepsilon }{\prime}=-\tau \left(\omega {\varepsilon }^{^{\prime\prime} }\right)+{\varepsilon }_{s}\) at low-frequency limit [36], the static dielectric constant is determined to be \({\varepsilon }_{s}=\) 115 with a relaxation time of 1.21 s, as shown in the inset in Fig. 6.
As shown in the inset in Fig. 7a, the I–V curve for BNKLST thin film at room temperatures is measured. Since the leakage current is as small as 2.5 × 10–7 A under an ultra-high electric field of ~ 9.2 MV/cm, it is remarkable that the BNKLST thin film could possess ultra-large electric breakdown strength. At different temperatures (20—200 °C), the electrical conductivity \(\sigma\) can be calculated by Ohm's law under a low voltage of 10 V, and the results are plotted in Fig. 7a. As shown in the orange region in Fig. 7a, the conductivity increases from 5.13 × 10–4 S/m to 3.3 × 10–3 S/m when the temperature increases from room temperature to 60 °C. It then maintains almost the same in the temperature range of 60 – 140 °C, and finally increases dramatically to 0.2 S/m, as shown in the bule region in Fig. 7a. The relationship between conductivity and temperature could be characterized by Arrhenius plots shown in Fig. 7b, c, which is described as follows:
where \({\sigma }_{0}\) is a constant, \({E}_{a}\) is the activation energy of conduction and \({k}_{B}\) is Boltzmann constant. At high temperatures, \({E}_{a}\) is calculated through the slope of fitting curve of ln \(\sigma\) vs. 1000/T with a value of 1.11 eV, suggesting that the conduction of BNKLST thin film may originate from oxygen vacancies [37]. At low temperatures, \({E}_{a}\) is 0.39 eV which may be related to the ion states hopping [38], e.g., Ti4+ + e−1 \(\to\) Ti3+. These two values of activation energy are lower than the band gap of BNT (3.1 eV) [39], suggesting the BNKSLT thin film exhibits intrinsic band-type electronic conduction [40, 41].
a The variation of conductivity of BNKLST thin film at 20–200 °C; the inset shows I–V curve at room temperature. b Linear fitting of lnσ vs. 1000/T in the bule region and c in the orange region highlighted in (a). d Weibull distribution of electric breakdown strength for BNKLST thin film (Color figure online)
The electric breakdown strength is one of the key factors that determine the practical applications of dielectric materials in electrical energy storage. The Weibull distribution function is used to characterize the electric breakdown strength, which could be expressed as:
where \({E}_{i}\) is the electric breakdown field, \(i\) is the serial number of samples, \(n\) is the total number of sample (\(n=10\)) and \({P}_{i}\) is the possibility that the BNKLST thin film breaks down at \({E}_{i}\). As shown in Fig. 7d, the experimental data are well fitted by Weibull distribution with a shape parameter of β = 24.89 (larger than 10), indicating a good reliability [42, 43]. A critical electric breakdown strength \({E}_{b}\)= 10.99 MV/cm with the failure possibility of 63.2% is obtained through the intercept of fitting line with \({Y}_{i}=0\). Such high electric breakdown strength may be attributed to the nano-sized grains in BNKLST thin film with a weakened ferroelectricity. It is suggested that more grain boundaries in the BNKLST thin film could act as depletion space charge layers to hinder the transfer of charge carriers, leading to low leakage currents under applied electric fields [44]. In addition, multiple metal elements at A-site could disturb the long-range ferroelectric order in BNKLST thin film [45], where the resulting polar nano-regions could have reduced polarization currents under applied fields. Consequently, these two effects could work synergistically to enhance the electric breakdown strength of BNKLST thin film. As listed in Table 1, the BNKLST thin film has the largest electric breakdown strength than other ferroelectric thin films reported in previous studies, which is even larger than those of polymer thin films and metal oxides.
As listed in Table 1, the BNKLST thin film has the largest electric breakdown strength among those typical dielectric materials. Thus, the BNKLST thin film could be promising dielectric materials used in dielectric capacitors with high-energy storage density. As shown in Fig. 8a, a slim P–E hysteresis loop for BNKLST thin film is measured at room temperature under an applied electric field of 5.28 MV/cm. The recoverable energy storage density of 5.88 J/cm3 with an excellent energy storage efficiency of 93% can be obtained. In comparison with conventional ferroelectric thin films such as BNT thin film [69, 70], although the BNKLST thin film has relatively smaller maximum polarization, it has much lower remanent polarization due to the existence of polar nano-regions resulting from the intrinsic chemical disorder at A-site. Therefore, the BNKLST thin film could possesses high recoverable energy storage density as well as high energy storage efficiency. As shown in Fig. 8b, the BNKLST thin film has an ultra-high electric breakdown strength of Eb = 10.99 MV/cm with a moderate static dielectric constant of 115. Based on the equation U = 0.5ε0εrEb2, the theoretical energy storage density U of BNKLST thin film is calculated to be 614.9 J/cm3, which is remarkably higher those of dielectrics listed in Table 1 and shown in the inset of Fig. 8b, and is even compatible with that of electrochemical supercapacitor.
a P–E loop of BNKLST thin film under an applied voltage of 95 V. b \({E}_{b}\) versus dielectric constant for dielectric materials [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67], in comparison with an empirical relation \({E}_{b}\sim {k}^{-\gamma }\) [68] (where \(k\) is static dielectric constant and \(\gamma\)=0.5 is field-acceleration parameter); the inset shows the plots for U versus Eb
4 Conclusions
High-entropy ferroelectric thin film (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 with a single- phase perovskite structure is prepared by sol–gel method. Raman spectroscopy illustrates that the chemical disorder at A-site of the BNKLST thin film weakens the Ti–O bond and the low concentration of oxygen vacancies could be caused by low annealing temperatures. The ferroelectric and piezoelectric properties of BNKLST thin film are measured, which exhibit an enhanced piezoelectric modulus of d33 = 82 pm/V larger than that of conventional BNT thin film. More importantly, the electric breakdown strength as estimated by Weibull distribution is found to be as high as 10.99 MV/cm, much higher than those of other ferroelectric thin films reported to date and even higher than those of polymer thin films and metal oxides. The energy storage properties of BNKLST thin film shows a recoverable energy storage density of 5.88 J/cm3 with an excellent energy storage efficiency of 93%. The theoretical energy storage density of BNKLST could reach 614.9 J/cm3, which is compatible to electrochemical supercapacitor. The superior energy storage properties of BNKLST thin film indicate that high-entropy ferroelectric thin films are promising dielectric materials that can be used in next-generation power electronics and semiconductor devices.
Data Availability
Data will be made available on reasonable request.
References
Z. Yang, H. Du, L. Jin, D. Poelman, High-performance lead-free bulk ceramics for electrical energy storage applications: design strategies and challenges. J. Mater. Chem. A 9, 18026–18085 (2021)
K. Zou, Y. Dan, H. Xu, Q. Zhang, Y. Lu, H. Huang et al., Recent advances in lead-free dielectric materials for energy storage. Mater. Res. Bull. 113, 190–201 (2019)
B. Chu, X. Zhou, K. Ren, B. Neese, M. Lin, Q. Wang et al., A dielectric polymer with high electric energy density and fast discharge speed. Science 313, 334–336 (2006)
Z.M. Dang, J.K. Yuan, S.H. Yao, R.J. Liao, Flexible nanodielectric materials with high permittivity for power energy storage. Adv. Mater. 25, 6334–6365 (2013)
X. Hao, A review on the dielectric materials for high energy-storage application. J. Adv. Dielectr. 03, 1330001 (2013)
F.Z. Yao, Q. Yuan, Q. Wang, H. Wang, Multiscale structural engineering of dielectric ceramics for energy storage applications: from bulk to thin films. Nanoscale 12, 17165–17184 (2020)
K. Yao, S. Chen, M. Rahimabady, M.S. Mirshekarloo, S. Yu, F.E.H. Tay et al., Nonlinear dielectric thin films for high-power electric storage with energy density comparable with electrochemical supercapacitors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58, 1968–1974 (2011)
B. Luo, X. Wang, Y. Wang, L. Li, Fabrication, characterization, properties and theoretical analysis of ceramic/PVDF composite flexible films with high dielectric constant and low dielectric loss. J. Mater. Chem. A 2, 510–519 (2014)
W. Yang, G. Zheng, High energy storage density and efficiency in nanostructured (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 high-entropy ceramics. J. Am. Ceram. Soc. 105, 1083–1094 (2022)
C. Oses, C. Toher, S. Curtarolo, High-entropy ceramics. Nat. Rev. Mater. 5, 295–309 (2020)
A. Sarkar, Q. Wang, A. Schiele, M.R. Chellali, S.S. Bhattacharya, D. Wang et al., High-entropy oxides: fundamental aspects and electrochemical properties. Adv. Mater. (2019). https://doi.org/10.1002/adma.201806236
W. Sun, F. Zhang, X. Zhang, T. Shi, J. Li, Y. Bai et al., Enhanced electrical properties of (Bi0.2Na0.2Ba0.2Ca0.2Sr0.2)TiO3 high-entropy ceramics prepared by hydrothermal method. Ceram. Int. 48, 19492–19500 (2022)
S. Zhou, Y. Pu, X. Zhang, Y. Shi, Z. Gao, Y. Feng et al., High energy density, temperature stable lead-free ceramics by introducing high entropy perovskite oxide. Chem. Eng. J. 427, 131684 (2021)
B. Yang, Y. Zhang, H. Pan, W. Si, Q. Zhang, Z. Shen et al., High-entropy enhanced capacitive energy storage. Nat. Mater. (2022). https://doi.org/10.1038/s41563-022-01274-6
S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin et al., A new class of high-entropy perovskite oxides. Scr. Mater. 142, 116–120 (2018)
S. Gates-Rector, T. Blanton, The powder diffraction file: a quality materials characterization database. Powder Diffr. 34, 352–360 (2019)
S. Zhou, Y. Pu, X. Zhao, T. Ouyang, J. Ji, Q. Zhang et al., Dielectric temperature stability and energy storage performance of NBT-based ceramics by introducing high-entropy oxide. J. Am. Ceram. Soc. 105, 4796–4804 (2022)
P. Zhao, B. Tang, Z. Fang, F. Si, C. Yang, S. Zhang, Improved dielectric breakdown strength and energy storage properties in Er2O3 modified Sr0.35Bi0.35K0.25TiO3. Chem. Eng. J. 403, 126290 (2021)
L. Dongxu, S. Zong-Yang, L. Zhipeng, L. Wenqin, W. Xingcai, W. Zhumei et al., P-E hysteresis loop going slim in Ba0.3Sr0.7TiO3-modified Bi0.5Na0.5TiO3 ceramics for energy storage applications. J. Adv. Ceram. 9, 183–192 (2020)
G. Wang, Q. Fu, P. Guo, M. Hu, H. Wang, S. Yu et al., Crystal structure, spectra analysis and dielectric characteristics of Ba4M28/3Ti18O54 (M= La, Pr, Nd, and Sm) microwave ceramics. Ceram. Int. 47, 1750–1757 (2021)
H. Li, R. Xiang, X. Chen, H. Hua, S. Yu, B. Tang et al., Intrinsic dielectric behavior of Mg2TiO4 spinel ceramic. Ceram. Int. 46, 4235–4239 (2020)
X. Jia, J. Zhang, H. Xing, J. Wang, P. Zheng, F. Wen, Large electrostrain response in binary Bi1/2Na1/2TiO3-Ba(Mg1/3Nb2/3)O3 solid solution ceramics. J. Alloys Compd. 741, 7–13 (2018)
S.A. Dargham, F. Ponchel, N. Abboud, M. Soueidan, A. Ferri, R. Desfeux et al., Synthesis and electrical properties of lead-free piezoelectric thin films prepared Bi0.5Na0.5TiO3 by Sol-Gel method. J. Eur. Ceram. Soc. 38, 1450–1455 (2018)
Z. Jiang, H. Yang, L. Cao, Z. Yang, Y. Yuan, E. Li, Enhanced breakdown strength and energy storage density of lead-free Bi0.5Na0.5TiO3-based ceramic by reducing the oxygen vacancy concentration. Chem. Eng. J. 414, 128921 (2021)
C.B. Eom, J.M. Murduck, Synthesis and characterization of superconducting thin films. Thin Film 28, 227–270 (2001)
Y.L. Zhang, W.L. Li, W.P. Cao, T.D. Zhang, T.R.G.L. Bai, Y. Yu et al., Enhanced energy-storage performance of 0.94NBT-0.06BT thin films induced by a Pb0.8La0.1Ca0.1Ti0.975O3 seed layer. Ceram. Int. 42, 14788–14792 (2016)
C. Yan, X. Liu, C. Yue, H. Sun, H. Sui, Y. Wang, Outstanding enhanced breakdown field strength and energy storage properties in Bi0.5Na0.5TiO3-based thin film by the aging process. J. Power. Sources 508, 230331 (2021)
M. Cernea, L. Trupina, C. Dragoi, B.S. Vasile, R. Trusca, Structural and piezoelectric characteristics of BNT-BT 0.05 thin films processed by sol-gel technique. J. Alloys Compd. 515, 166–170 (2012)
J. Anthoniappen, W.S. Chang, A.K. Soh, C.S. Tu, P. Vashan, F.S. Lim, Electric field induced nanoscale polarization switching and piezoresponse in Sm and Mn co-doped BiFeO3 multiferroic ceramics by using piezoresponse force microscopy. Acta Mater. 132, 174–181 (2017)
H. Takashi, K. Tomonori, S. Wataru, Chemical solution processing and properties of (Bi1/2Na1/2)TiO3 thin films. Sixt. IEEE Int. Symp. Appl. Ferroelectr. 2007, 104–105 (2007)
Y. Guo, K. Suzuki, K. Nishizawa, T. Miki, K. Kato, Electrical properties of (1 0 0)-predominant BaTiO films derived from alkoxide solutions of two concentrations. Acta Mater. 54, 3893–3898 (2006)
J.S. Park, M.H. Lee, D.J. Kim, D. Do, M.H. Kim, J.S. Kim et al., Enhanced piezoelectric properties of lead-free 0.935(Bi0.5Na0.5)TiO3-0.065BaTiO3 thin films fabricated by using pulsed laser deposition. J. Korean Phys. Soc. 62, 1031–1034 (2013)
L.F. Zhu, B.P. Zhang, W.G. Yang, Enhancing piezoelectric coefficient d33 in LiF-doped BaTiO3 ceramics by optimizing excess Ba content. Mater. Res. Bull. 52, 158–161 (2014)
L. Xu, S. Wu, K. Zhu, B. Song, X. Zhou, H. Yan et al., Enhanced piezoelectricity and reduced leakage current of a novel (1-: X) Bi0.5Na0.5TiO3-x (Sr0.7Bi0.2□0.1)TiO3 thin film. Inorg. Chem. Front. 8, 700–710 (2021)
H.Y. Lee, J. Luo, Z. Zhou, W. Sun, J.F. Li, Macroscopic and local approaches of phase transition in sol-gel synthesized (Bi0.5Na0.5)TiO3-SrTiO3 thin films. Phys. Chem. Chem. Phys. 20, 15236–15243 (2018)
I. Calisir, X. Yang, E.L. Bennett, J. Xiao, Y. Huang, Enhancing the bandwidth of antennas using polymer composites with high dielectric relaxation. Mater. Today Electron. 3, 100026 (2023)
B.K. Barick, R.N.P. Choudhary, D.K. Pradhan, Dielectric and impedance spectroscopy of zirconium modified (Na0.5Bi0.5)TiO3 ceramics. Ceram. Int. 39, 5695–4704 (2013)
B.K. Barick, K.K. Mishra, A.K. Arora, R.N.P. Choudhary, D.K. Pradhan, Impedance and Raman spectroscopic studies of (Na0.5Bi0.5)TiO3. J. Phys. D Appl. Phys. 44, 355402 (2011)
M. Zhong, Q. Feng, C. Yuan, X. Liu, B. Zhu, L. Meng et al., Photocurrent density and electrical properties of Bi0.5Na0.5TiO3-BaNi0.5Nb0.5O3 ceramics. J. Adv. Ceram. 10, 1119–1128 (2021)
J. Zang, M. Li, D.C. Sinclair, W. Jo, J. Rödel, Impedance spectroscopy of (Bi1/2Na1/2)TiO3-BaTiO3 ceramics modified with (K0.5Na0.5)NbO3. J. Am. Ceram. Soc. 97, 1523–1529 (2014)
Q. Xu, M.T. Lanagan, X. Huang, J. Xie, L. Zhang, H. Hao et al., Dielectric behavior and impedance spectroscopy in lead-free BNT-BT-NBN perovskite ceramics for energy storage. Ceram. Int. 42, 9728–9736 (2016)
S. Wu, L. Xu, K. Zhu, B. Song, H. Yan, B. Shen et al., Improved piezoelectricity and energy storage performance simultaneously achieved in [001]-preferentially oriented Bi0.5Na0.5TiO3–BaTiO3–BiMnO3 thin films grown on Nb-doped SrTiO3 single-crystalline substrates. J. Eur. Ceram. Soc. 41, 2539–2547 (2021)
F. Yan, H. Bai, X. Zhou, G. Ge, G. Li, B. Shen et al., Realizing superior energy storage properties in lead-free ceramics: via a macro-structure design strategy. J. Mater. Chem. A 8, 11656–11664 (2020)
Y. Gao, X. Zhu, B. Yang, P. Shi, R. Kang, Y. Yuan et al., Grain size modulated (Na0.5Bi0.5)0.65Sr0.35TiO3-based ceramics with enhanced energy storage properties. Chem. Eng. J. 433, 133584 (2022)
Z. Jiang, Y. Yuan, H. Yang, E. Li, S. Zhang, Excellent thermal stability and energy storage properties of lead-free Na0.5Bi0.5TiO3-based ceramic. J. Am. Ceram. Soc. 105, 4027–4038 (2022)
S. Song, Y. Jiao, F. Chen, X. Zeng, X. Wang, S. Zhou et al., Ultrahigh electric breakdown strength, excellent dielectric energy storage density, and improved electrocaloric effect in Pb-free (1–x)Ba(Zr0.15Ti0.85)O3-xNaNbO3 ceramics. Ceram. Int. 48, 10789–10802 (2022)
A. Kumar, S.H. Kim, M. Peddigari, D.H. Jeong, G.T. Hwang, J. Ryu, High energy storage properties and electrical field stability of energy efficiency of (Pb0.89La0.11)(Zr0.70Ti0.30)0.9725O3 relaxor ferroelectric ceramics. Electron. Mater. Lett. 15, 323–330 (2019)
F. Gao, X. Dong, C. Mao, W. Liu, H. Zhang, L. Yang et al., Energy-storage properties of 0.89Bi0.5Na0.5TiO3–0.06BaTiO3–0.05K0.5Na0.5NbO3 lead-free anti-ferroelectric ceramics. J. Am. Ceram. Soc. 94, 4382–4386 (2011)
J. Li, F. Li, Z. Xu, S. Zhang, Multilayer lead-free ceramic capacitors with ultrahigh energy density and efficiency. Adv. Mater. 30, 1–7 (2018)
Z. Yang, H. Du, S. Qu, Y. Hou, H. Ma, J. Wang et al., Significantly enhanced recoverable energy storage density in potassium-sodium niobate-based lead free ceramics. J. Mater. Chem. A 4, 13778–13785 (2016)
Y. Xie, H. Hao, J. Xie, S. Zhang, M. Cao, Z. Yao et al., Ultra-high energy storage density and enhanced dielectric properties in BNT-BT based thin film. Ceram. Int. 47, 23259–23266 (2021)
R. Huang, H. Wang, C. Tao, H. Hao, Z. Yao, H. Liu et al., Evolution of polarization crystallites in 0.92BaTiO3–0.08Bi(Ni0.5Zr0.5)O3 microcrystal-amorphous composite thin film with high energy storage capability and thermal stability. Chem. Eng. J. 433, 133579 (2022)
M.D. Nguyen, Ultrahigh energy-storage performance in lead-free BZT thin-films by tuning relaxor behavior. Mater. Res. Bull. 133, 111072 (2021)
P. Wang, X. Wang, G. Li, Y. Li, X. Yao, Z. Pan, Interface engineering to optimize polarization and electric breakdown strength of Ba2Bi3.97Pr0.03Ti5O18/BiFeO3 ferroelectric thin-film for high-performance capacitors. Chem. Eng. J. 433, 133676 (2022)
H. Cheng, J. Ouyang, Y.X. Zhang, D. Ascienzo, Y. Li, Y.Y. Zhao et al., Demonstration of ultra-high recyclable energy densities in domain-engineered ferroelectric films. Nat. Commun. (2017). https://doi.org/10.1038/s41467-017-02040-y
X. Yuan, T.C.M. Chung, Cross-linking effect on dielectric properties of polypropylene thin films and applications in electric energy storage. Appl. Phys. Lett. 98, 1–4 (2011)
G. Picci, M. Rabuffi, Status quo and future prospects for metallized polypropylene energy storage capacitors. PPPS 2001 Pulsed Power Plasma Sci. 2001 1, 417–420 (2015)
X. Zhou, B. Chu, B. Neese, M. Lin, Q.M. Zhang, Electrical energy density and discharge characteristics of a poly(vinylidene fluoride-chlorotrifluoroethylene) copolymer. IEEE Trans. Dielectr. Electr. Insul. 14, 1133–1138 (2007)
E. Fukada, Recent developments of polar piezoelectric polymers. IEEE Trans. Dielectr. Electr. Insul. 13, 1110–1119 (2006)
Y. Huang, Y. Chen, X. Li, G. Wang, L. Xia, Y. Liu et al., Enhanced dielectric breakdown strength in Ni2O3 modified Al2O3-SiO2-TiO2 based dielectric ceramics. J. Eur. Ceram. Soc. 38, 3861–3866 (2018)
S. Chao, F. Dogan, Processing and dielectric properties of TiO2 Thick films for high-energy density capacitor applications. Int. J. Appl. Ceram. Technol. 8, 1363–1373 (2011)
W. Gao, M. Yao, X. Yao, Achieving ultrahigh breakdown strength and energy storage performance through periodic interface modification in SrTiO3 thin film. ACS Appl. Mater. Interfaces 10, 28745–28753 (2018)
J. McPherson, J.Y. Kim, A. Shanware, H. Mogul, Thermochemical description of dielectric breakdown in high dielectric constant materials. Appl. Phys. Lett. 82, 2121–2123 (2003)
Y. Pu, Q. Zhang, R. Li, M. Chen, X. Du, S. Zhou, Dielectric properties and electrocaloric effect of high-entropy (Na0.2Bi0.2Ba0.2Sr0.2Ca0.2)TiO3 ceramic. Appl. Phys. Lett. 115, 1–5 (2019)
Y. Ning, Y. Pu, Q. Zhang, S. Zhou, C. Wu, L. Zhang et al., Achieving high energy storage properties in perovskite oxide via high-entropy design. Ceram. Int. 49, 12214–12223 (2023)
J. Liu, C. Ma, X. Zhao, K. Ren, R. Zhang, F. Shang et al., Structure, dielectric, and relaxor properties of BaTiO3-modified high-entropy (Bi0.2Na0.2K0.2Ba0.2Ca0.2)TiO3 ceramics for energy storage applications. J. Alloys Compd. 947, 169626 (2023)
H. Wang, J. Zhang, S. Jiang, J. Wang, J. Wang, Y. Wang, (Bi1/6Na1/6Ba1/6Sr1/6Ca1/6Pb1/6)TiO3-based high-entropy dielectric ceramics with ultrahigh recoverable energy density and high energy storage efficiency. J. Mater. Chem. A 11, 4937–4945 (2023)
J. McPherson, J. Kim, A. Shanware, H. Mogul, J. Rodriguez, Proposed universal relationship between dielectric breakdown and dielectric constant. Tech. Digèst. Int. Electron. Devices Meet (2002). https://doi.org/10.1109/IEDM.2002.1175919
S. Wu, P. Chen, J. Zhai, B. Shen, P. Li, F. Li, Enhanced piezoelectricity and energy storage performances of Fe-doped BNT–BKT–ST thin films. Ceram. Int. 44, 21289–21294 (2018)
Y. Xie, H. Hao, Z. Huang, S. Zhang, M. Cao, Z. Yao et al., Large energy-storage density with good dielectric property in bismuth sodium titanate-based thin films. J. Alloys Compd. 884, 161031 (2021)
Acknowledgements
This research was supported by Foshan Xianhu Laboratory of the Advanced Energy Science and Technology Guangdong Laboratory, Foshan, Guangdong Province, China.
Funding
Open access funding provided by The Hong Kong Polytechnic University.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study of conception and design. Material preparation, data collection and analysis were performed by Wentao Yang, Guangping Zheng and Sana Ullah. The first draft of the manuscript was written by Wentao Yang and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, W., Ullah, S. & Zheng, G. The ultra-high electric breakdown strength and superior energy storage properties of (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 high-entropy ferroelectric thin films. J Mater Sci: Mater Electron 35, 82 (2024). https://doi.org/10.1007/s10854-023-11774-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10854-023-11774-z