Abstract
Oxygen–carbon defects have been studied for decades in silicon but are less well established in germanium. In the present study we employ density functional theory calculations to study the structure of the CiOi defect in germanium. Additionally, we investigate the interaction the CiOi defect with isovalent dopants such as silicon and tin. It is calculated that the CiOi defects will preferentially form near isovalent dopants in germanium. Interestingly the structure of the dopant-CiOi defects is different with the Sn residing next to the Oi whereas the Si atom bonds with the Ci. The differences in the structure of CiOi defects in the vicinity of isovalent dopants are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Although germanium (Ge) was implemented in the first transistor commencing the solid state electronics era silicon (Si) prevailed for applications in microelectronics, photovoltaics and sensors for many decades due to its high quality crystal growth technology and advantageous native oxide [1,2,3,4,5,6,7,8,9,10,11,12]. In the past few years materials with advantageous physical properties (e.g. higher carrier mobilities, low dopant activation temperatures and smaller band-gap) such as germanium (Ge) are becoming increasingly important [1,2,3,4,5,6,7,8,9,10,11,12]. The consideration of alternative substrates is mainly due to the high-k gate dielectric materials, which have effectively eliminated the requirement of a good quality native oxide in advanced nanoelectronic devices [1]. For decades the characteristic dimensions of devices were reduced and this has constituted the importance of point defects and defect clusters increasingly important as they can impact materials properties. Examples include the need to reduce the concentration of vacancy-oxygen pairs (VO or A-centers) and/or the carbon-related defects (such as CiOi(SiI)n, n = 1, 2,…) in Si [13,14,15,16,17,18,19] and the requirement to contain the fast n-type dopant diffusion in Ge [2, 10, 12].
Although C is not miscible in Ge, however, concentrations of up to 1012 cm−3 have been previously determined [1, 20, 21]. Additionally, high concentrations have been incorporated as C has been used to reduce the n-type copant diffusion in Ge [12]. The oxygen dimer and the A-center are the main oxygen-related defects in Ge [1, 14, 22, 23]. Under irradiation in Si, O and C associate to form the CiOi defect [24, 25]. In Si1−xGex an analogous defect was calculated to exist [26] and we therefore expect the formation of the CiOi defect in Ge.
The introduction of dopants in the lattice can lead to local strains that can in turn impact the defect processes of a material [27,28,29,30,31,32,33]. In previous investigations it was shown that the introduction of large isovalent dopants such as Sn can impact dopant–defect interactions in Ge (and in Si) [12, 19]. In the present study we have employed density functional theory (DFT) modeling to investigate the structure of the CiOi defect in Ge and its interaction with isovalent dopants such as Si or Sn. The results are compared with recent DFT results on related clusters in Si.
2 Methodology
All the calculations were performed using the plane wave DFT code CASTEP [34, 35]. Here the exchange and correlation interactions were introduced by using the corrected density functional of Perdew, Burke and Ernzerhof (PBE) [36]. The calculations involved 250-atomic site supercells, within the generalized gradient approximation (GGA), with ultrasoft pseudopotentials [37], a plane wave basis set cut-off of 350 eV, and a 2 × 2 × 2 Monkhorst–Pack (MP) [38] k-point grid. The efficacy and convergence of this method to describe defects in Ge Si has been discussed in previous studies [39,40,41].
Here we use binding energies to calculate the relative stability of the CiOi defect and its interaction with Si and Sn atoms. The binding energy of a defect cluster is the energy difference of the cluster and its isolated constituent point defect components. For a negative binding energy the defect cluster is stable with respect to its constituent point defect components and it is bound to form. Finally, it should be noted that the dopant concentration considered here is 1/250 (i.e. 0.4%).
3 Results and discussion
Here we have employed DFT to calculate the lowest energy structures of the CiOi defects in Ge and in isovalent (Si or Sn) doped Ge. This defect and its interaction with isovalent dopants is studied mainly in Si and Si1−xGex [42,43,44,45,46,47,48,49,50], however, there is very limited information in Ge [1].
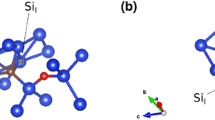
Figure 1 represents the energetically favourable CiOi configurations in Ge (left) and Si (right). In this figure all the related angles and distances around the defect are reported. It was calculated in previous DFT studies [13, 17, 42, 43] that the energetically favourable structure of the CiOi defect is the ring configuration or R-form (refer to Fig. 1, right) with the O-form of the defect (the Oi occupying an interstitial site in between two Si atoms, refer to Fig. 1a of Ref. [13]) although the energy difference between the two configurations is very small (0.003 eV) [13]. In Ge, the lowest energy CiOi defect is different (refer to Fig. 1, left) with the Ci and Oi being only 1.32 Å apart. This configuration is bound with − 2.46 eV (refer to Table 1).
For completeness in Fig. 2 we represent the interaction of the CiOi defect in Si with isovalent dopants (Sn and Ge). It can be observed that the R-form of the defect is preserved with both isovalent dopant atoms residing closer to the Oi atom. Additionally, the distances are similar (d2–d6) with the exception of the isovalent dopant-Oi (i.e. distance d1 in Fig. 2), which is significantly different reflecting the size difference between Sn and Ge.
Figure 3 (left) is a schematic representation of the energetically favourable CiOi configurations in Ge with a nearest neighbor Sn dopant and a nearest neighbour Si dopant (Fig. 3 right). The Sn–CiOi and Si–CiOi defects are bound − 3.53 and − 3.72 eV, respectively (refer to Table 1). These energies are reduced to − 2.52 and − 2.50 eV (i.e. almost the same to CiOi) when the dopant is about 14 Å away from the CiOi defect. The structure of the dopant-CiOi defect is different with the Sn atom residing near the Oi, whereas the Si resides near the Ci atom. The structure of the CiOi defect remains largely unchanged when it is bound near a Sn or a Si atom (refer to distances d1–d3 in Fig. 3) with the only marked difference being distance d4 (Ci–Ge distance in Sn–CiOi and Ci–Si distance in Si–CiOi). In the case of Si-doped Ge d4 is about 5% shorter reflecting the smaller size of the Si atom as compared to the Ge host atoms.
Si is smaller and completely soluble in Ge with the resulting Si1−xGex alloys being random alloys. Additionally, Sn is also soluble in Ge (but not over the complete compositional range) occupying substitutional sites and forming Sn1−xGex alloys. These alloys will have different defect processes as compared to the end members. Even in the low concentration doping limits considered in the present study it is observed that the CiOi defects will preferentially form near the isovalent dopant with the energy gain being considerable (more than 1 eV, refer to Table 1). This is the opposite picture to what was observed in Si where the CiOi defects did not bind with isovalent dopants (Ge, Sn) [45]. Such differences in defect processes between the Si and Ge host materials are common although they share the same crystal structure [1, 12]. For example the CV and BV pairs in Si are bound, whereas in Ge they are not [51]. In the past years interest on Ge is regenerated partially because of the increasing applications of its group IV alloys (for example germanium carbide) [52,53,54], however, many aspects of the defect processes in Ge and its alloys need to be systematically investigated.
4 Conclusions
DFT was employed to calculate the structure and relative stability of CiOi defects in Ge in the presence of Si or Sn. In the present study we calculate that under equilibrium conditions the CiOi defects in Ge will preferentially form near isovalent dopants such as Si or Sn. The energy gain for the CiOi to form near these isovalent dopants exceeds 1 eV. This is different to Si where CiOi defects will preferentially form away from oversized isovalent dopants.
References
C. Claeys, E. Simoen, Germanium-Based Technologies: From Materials to Devices (Elsevier, London, 2007)
A. Chroneos, R.W. Grimes, B.P. Uberuaga, S. Brotzmann, H. Bracht, Appl. Phys. Lett. 91, 192106 (2007)
A. Chroneos, J. Appl. Phys. 105, 056101 (2009)
E. Hüger, U. Tietze, D. Lott, H. Bracht, D. Bougeard, E.E. Haller, H. Schmidt, Appl. Phys. Lett. 93, 162104 (2008)
R. Kube, H. Bracht, A. Chroneos, M. Posselt, B. Schmidt, J. Appl. Phys. 106, 063534 (2009)
S. Decoster, B. De Vries, U. Wahl, J.G. Correia, A. Vantomme, J. Appl. Phys. 105, 083522 (2009)
E. Bruno, S. Mirabella, G. Scapellato, G. Impellizzeri, A. Terrasi, F. Priolo, E. Napolitani, D. De Salvador, M. Mastramatteo, A. Carnera, Phys. Rev. B 80, 033204 (2009)
A. Chroneos, H. Bracht, Semicond. Sci. Technol. 25, 045002 (2010)
A. Chroneos, Semicond. Sci. Technol. 26, 095017 (2011)
G. Impellizzeri, S. Boninelli, F. Priolo, E. Napolitani, C. Spinella, A. Chroneos, H. Bracht, J. Appl. Phys. 109, 113527 (2011)
A. Chroneos, J. Mater. Sci. Mater. Electron. 24, 1741 (2013)
A. Chroneos, H. Bracht, Appl. Phys. Rev. 1, 011301 (2014)
S.-R.G. Christopoulos, E.N. Sgourou, T. Angeletos, R.V. Vovk, A. Chroneos, C.A. Londos, J. Mater. Sci. Mater. Electron. 28, 10295 (2017)
J. Coutinho, R. Jones, P.R. Briddon, S. Oberg, Phys. Rev. B 62, 10824 (2000)
C.A. Londos, A. Andrianakis, V.V. Emtsev, H. Ohyama, Semicond. Sci. Technol. 24, 075002 (2009)
J. Chen, D. Yang, X. Ma, Z. Zeng, D. Tian, L. Li, D. Que, L. Gong, J. Appl. Phys. 103, 123521 (2008)
H. Wang, A. Chroneos, C.A. Londos, E.N. Sgourou, U. Schwingenschlögl, Sci. Rep. 4, 4909 (2014)
T. Angeletos, A. Chroneos, C.A. Londos, J. Appl. Phys. 119, 125704 (2016)
A. Chroneos, E.N. Sgourou, C.A. Londos, U. Schwingenschlögl, Appl. Phys. Rev. 2, 021306 (2015)
E.E. Haller, W.L. Hansen, F.S. Goulding, Adv. Phys. 30, 93 (1980)
E.E. Haller, W.L. Hansen, P. Luke, R. McMurray, B. Jarrett, IEEE Trans. Nucl. Sci. 29, 745 (1982)
J.A. Baldwin Jr., J. Appl. Phys. 36, 793 (1965)
V.P. Markevich, I.D. Hawkins, A.R. Peaker, V.V. Litvinov, L.I. Murin, L. Dobaczewski, J.L. Lindström, Appl. Phys. Lett. 81, 1821 (2002)
M.R. Brozel, R.C. Newman, D.H.J. Totterdell, J. Phys. C 8, 243 (1975)
G. Davies, R.C. Newman, in Handbook in Semiconductors, vol. 3b, ed. by T. S. Moss, S. Mahajan (Elsevier, Amsterdam, 1994), pp. 1557–1635
A. Balsas, J. Coutinho, V.J.B. Torres, P.R. Briddon, M. Barroso, Phys. Rev. B 70, 085201 (2004)
H. Höhler, N. Atodiresei, K. Schroeder, R. Zeller, P. Dederichs, Phys. Rev. B 71, 35212 (2005)
A. Chroneos, C.A. Londos, E.N. Sgourou, J. Appl. Phys. 110, 093507 (2011)
A. Chroneos, C.A. Londos, E.N. Sgourou, P. Pochet, Appl. Phys. Lett. 99, 241901 (2011)
E.N. Sgourou, D. Timerkaeva, C.A. Londos, D. Aliprantis, A. Chroneos, D. Caliste, P. Pochet, J. Appl. Phys. 113, 113506 (2013)
H.A. Tahini, A. Chroneos, R.W. Grimes, U. Schwingenschlögl, H. Bracht, Phys. Chem. Chem. Phys. 15, 367 (2013)
H. Wang, A. Chroneos, C.A. Londos, E.N. Sgourou, U. Schwingenschlögl, Phys. Chem. Chem. Phys. 16, 8487 (2014)
M.J.D. Rushton, A. Chroneos, Sci. Rep. 4, 6068 (2014)
M.C. Payne, M.P. Teter, D.C. Allan, T.A. Arias, J.D. Joannopoulos, Rev. Mod. Phys. 64, 1045 (1992)
M.D. Segall, P.J.D. Lindan, M.J. Probert, C.J. Pickard, P.J. Hasnip, S.J. Clark, M.C. Payne, J. Phys. Condens. Matter 14, 2717 (2002)
J. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996)
D. Vanderbilt, Phys. Rev. B 41, 7892 (1990)
H.J. Monkhorst, J.D. Pack, Phys. Rev. B 13, 5188 (1976)
A. Chroneos, C.A. Londos, J. Appl. Phys. 107, 093518 (2010)
A. Chroneos, C.A. Londos, H. Bracht, Mater. Sci. Eng. B 176, 453 (2011)
A. Chroneos, R.W. Grimes, B.P. Uberuaga, H. Bracht, Phys. Rev. B 77, 235208 (2008)
R. Jones, S. Öberg, Phys. Rev. Lett. 68, 86 (1991)
J. Coutinho, R. Jones, P.R. Briddon, S. Öberg, L.L. Murin, V.P. Markevich, J.L. Lindström, Phys. Rev. B 65, 014109 (2001)
D.J. Backlund, S.K. Estreicher, Phys. Rev. B 77, 205205 (2008)
S.-R.G. Christopoulos, E.N. Sgourou, R.V. Vovk, A. Chroneos, C.A. Londos, Solid State Commun. 263, 19 (2017)
J.M. Trombetta, G.D. Watkins, Appl. Phys. Lett. 51, 1103 (1987)
J. Coutinho, R. Jones, P.R. Briddon, S. Öberg, L.I. Murin, V.P. Markevich, J. L. Lindström, Physica B 308–310, 305 (2001)
P. Venezuela, R.H. Miwa, A. Fazzio, Phys. Rev. B 69, 115209 (2004)
D.J. Backlund, S.K. Estreicher, Physica B 401–402, 163 (2007)
L.I. Khirunenko, M.G. Sosnin, Yu..V. Pomozov, L.I. Murin, V.P. Markevich, A.R. Peaker, L.M. Almeida, J. Coutinho, V.J.B. Torres, Phys. Rev. B 78, 155203 (2008)
A. Chroneos, B.P. Uberuaga, R.W. Grimes, J. Appl. Phys. 102, 083707 (2007)
A. Tessema, M. Bekele, R. Vianden, J. Mater. Sci. Mater. Electron. 21, 1144 (2010)
C. Demaria, P. Benzi, A. Arrais, E. Bottizzo, P. Antoniotti, R. Rabezzana, L. Operti, J. Mater. Sci. Mater. Electron. 48, 6357 (2013)
N. Gupta, B.P. Veettil, H.Z. Xia, S.K. Karuturi, G. Conibeer, S. Shrestha, Thin Solid Films 592, 162 (2015)
Acknowledgements
Dr Eddy Simoen (IMEC) is gratefully thanked for his comments and information on carbon defects in germanium.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Christopoulos, SR.G., Sgourou, E.N., Vovk, R.V. et al. Isovalent doping and the CiOi defect in germanium. J Mater Sci: Mater Electron 29, 4261–4265 (2018). https://doi.org/10.1007/s10854-017-8372-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10854-017-8372-6