Abstract
This work is a comparative study of four different techniques to determine the crystallinity of high-density polyethylene (HDPE) nanocomposites filled with different diameter sizes (5, 15 and 25 μm) of graphene nanoplatelets (GNPs) at various amounts (0.5–5 wt%). The structure of HDPE/GNPs nanocomposites was extensively studied by using different experimental methods, such as X-ray diffraction, X-ray photoelectron spectroscopy, Fourier transform infrared spectroscopy, and Raman spectroscopy. To further provide a complete comparison, differential scanning calorimetry measurements were utilized to calculate the crystallinity values, while temperature-modulated DSC was employed to investigate the possible mechanism of the different crystalline structures. It was found that these methods can be used to estimate the crystallinity, but the sample parameters and experimental conditions must be taken into consideration. All the techniques showed that the crystallinity depends on GNPs size and content. The distance between dispersed platelets was substantial at low concentrations of GNPs, making it comparatively easy for additional nucleation sites to incorporate the polymer matrix, and the crystal nucleus was simply formed. However, at high concentrations of GNPs, the diffusion of polymer chains to the growing crystallites was hindered by large GNPs particles, despite the formation of additional nucleation sites.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Nanocomposites used in thermally conductive polymeric materials have recently attracted science's curiosity. Polyethylene (PE) is a low-cost semicrystalline polymer with good thermal and mechanical properties. It works well in a variety of applications such as automotive, films, pressure pipes and fittings, bottles, tubes, and cable jacketing [1]. PE crystals have an orthorhombic structure, with two polymeric chains per unit cell, and belong to the Pnma space group. The lattice parameters of PE are a = 7.43 Å, b = 4.94 Å, and c = 2.55 Å [2]. The average molecular weight and distribution, degree of branching and/or cross-linking, presence of copolymers, the concentration of fillers, and the thermal history of the polymer formulation are some of the factors that affect the polymer’s crystalline content.
To address low mechanical, thermal, electrical, and gas barrier properties, several fillers have been used [3]. Graphene nanoplatelets (GNPs), with a two-dimensional lattice of sp2- bonded carbon, are platelet-like graphite nanocrystals containing several graphene layers and a platelet thickness of 0.35–100 nm [4]. The addition of graphene to the PE matrix has been proved to improve the polymer's properties [5, 6]. However, the end-use properties of products comprised of semicrystalline thermoplastics are very much dependent on the overall degree of crystallinity achieved by the material production. It has been proposed that matrix crystallinity and crystal size have a considerable impact on stiffness and yield strength, respectively [7]. Only a few studies have been done presenting the size effect of GNPs on the crystallinity of a polymer matrix.
X-ray diffraction (XRD) and differential scanning calorimetry (DSC) are the two most popular techniques for determining the crystallinity of a polymer matrix. XRD determination is based on the comparison of the integrated intensity of the features related to the amorphous and crystalline phases, while DSC, on the measurement of the melting or crystallization enthalpy. According to the DSC results of Batista et al. [5] and Bourque et al. [8], the crystallinity values for HDPE/graphene nanocomposites were found to be in the range of 60–63%. Shafiei et al. [9] showed that the crystallinity of HDPE/GNPs/carbon black nanocomposites decreases with the addition of the fillers as indicated by DSC and XRD measurements. Jiang et al. [10] reported the maximum crystallinity at 3 vol% GNP loading because a compromise occurs between the nucleating and the retarding effects of GNP on the matrix during non-isothermal crystallization. A difference in HDPE/carbon nanofiller nanocomposites between DSC and WAXD crystallinity values was found by Xiang et al. [11] because of the recrystallization of imperfect crystallites during the DSC heating process. Olesik et al. [12] reported that the changes in the crystalline structure of HDPE composites filled with glassy carbon depend on the carbon filler type.
Fourier transform infrared spectroscopy (FTIR) and Raman spectroscopy can also provide reliable values for the crystalline phase content of a polymer [13]. IR spectroscopy has been applied many times to determine the crystalline phase content of HDPE because it is a sensitive and fast technique, requiring only a small amount of sample. For this estimation, a probing band (which varies with crystallinity) and a reference band (which acts as an internal standard to eliminate inaccuracies) were chosen. According to Zerbi et al. [14], the bending band vibrations at 1474 and 730 cm−1 (crystalline phase) and 1464 and 720 cm−1 (amorphous phase) can be used. Additionally, Raman spectroscopy can offer significant information on the structural characterization of PE. Several studies have improved and modified Strobl and Hagedorn method, and it is now generally accepted and used in the morphological structure investigation of various PEs samples [15, 16]. Paradkar et al. [17] used the normalized intensity of the 1418 cm−1 Raman band to estimate the crystalline fraction in HDPE fibers. According to Failla et al. [18], the crystallinity calculated by DSC and Raman spectroscopy was found to be in good agreement. Lin et al. [15] confirmed the correlation of the Raman deduced crystallinity with those obtained from other analytical methods applied to PE.
In our previous works, crystallization kinetics of HDPE/GNPs nanocomposites in non-isothermal conditions was studied at several constant cooling rates by means of conventional DSC and fast scanning calorimetry (FSC). However, the structure formation was far from thermodynamic equilibrium due to the high cooling rates used. Additionally, it was found that GNPs M25 reduced the chain mobility in the matrix, while HDPE/M25 nanocomposites exhibited delayed crystallization and improved rheological properties [19,20,21,22]. Concerning the mechanical properties, GNPs M25 improved the tensile modulus and tensile strength and decreased the elongation at break and tensile stress at break of the HDPE/GNP nanocomposites at low filler content. However, the size effect of GNPs on crystallinity and crystalline morphology, and specifically the calculation of crystallinity by using four different techniques, has not been discussed.
The aim of this work is to determine the crystallinity values of HDPE nanocomposites using four different techniques: XRD, DSC, FTIR, and Raman spectroscopy. The advantages and disadvantages of the above-mentioned techniques, as well as the accuracy of the crystallinity measurement of HDPE/GNPs nanocomposites with various GNPs content and sizes, are highlighted. The melt mixing method was used to produce HDPE/GNPs nanocomposites in the loading range of 0.5–5 wt%. with three different diameter sizes: 5, 15, and 25 μm. The effect of GNPs on thermal properties of HDPE matrix, such as melting and crystallization temperature, was investigated with conventional DSC and temperature-modulated differential scanning calorimetry (TM-DSC). A detailed structural study of GNPs in the HDPE matrix was performed by combining XRD, Raman spectroscopy, X-ray photoelectron spectroscopy (XPS), and FTIR.
Experimental section
Materials
HDPE under the brand name Luminece mPE M5510 EP was supplied by Total Petrochemicals (Feluy, Belgium). It has a density of 0.955 g cm−3 and a melt flow index of 0.028 g min−1. XG Sciences Inc., USA, provided GNPs with an average thickness of 8 nm and three different average diameters: GNPs with an average platelet diameter of 5 μm (GNPs M5), 15 μm (GNPs M15), and 25 μm (GNPs M25). The average surface area ranges from 120 to 150 m2 g−1. The bulk density of all GNPs is reported to be 2.2 g cm−3.
Nanocomposites preparation
HDPE/GNPs nanocomposites, having various loading levels ranging from 0.1 to 5 wt% (0.5, 1, 2.5, 3, and 5 wt% of GNPs), were produced by melt mixing in a Haake–Buchler Reomixer (model 600) at 200 °C for 300 s using a torque speed of 35 rpm. The prepared materials were then hot pressed at 180 ± 5 °C using an Otto Weber, Type PW 30 hydraulic press coupled to an Omron E5AX Temperature Controller to prepare films of various thicknesses. The nanocomposite samples are referred to here as HDPE/xM5, HDPE/xM15, and HDPE/xM25 where x is GNP content in wt%.
Characterization methods
X-ray diffraction (XRD)
The X-ray diffraction (XRD) patterns of the prepared materials (10–30 mm thick) were recorded by a 2-cycles Rigaku Ultima + X-ray diffractometer with CuKa radiation (1.5418 Å), using a step size of 0.05° and a step time of 2 s in Bragg–Brentano geometry, operating at 40 kV and 30 mA. The systematic error in the 2θ degrees was found to be ± 0.015º. The Bragg diffraction formula was used to calculate the inter-planar spacings (d):
where n is an integer indicative of the reflection order, λ is the wavelength of CuKaα radiation (λ = 1.5418 Å), and θ is the diffraction peak.
The average out of plane crystallite size of the HDPE/GNPs nanocomposites (L) was estimated from the (110) and (200) reflections using the Scherrer equation:
where β is the line width (FWHM) in radians, λ is the X-ray wavelength, K is the coefficient taken to be 0.89, and θ is the diffraction peak [23].
The deconvolution of the X-ray diffractograms was performed using a Gaussian–Lorentzian function [24] to separate the amorphous and the crystalline content and calculate the crystallinity percentage, crystalline size, and the space between the structural layers of the HDPE/GNPs nanocomposites. According to the profile fitting process, the weight crystalline fractions of the prepared materials were calculated:
X-ray photoelectron spectroscopy (XPS)
X-ray photoelectron spectroscopy spectra were recorded using an Axis UltraDLD system by Kratos Analytical (Shimadzu Group Company). XPS spectra were acquired using an Al-Ka1 X-ray source (energy 1486.6 eV) with a pass energy of 160 eV for survey scans and 20 eV for high-resolution spectra. The binding energy (BE) of the C 1 s peak (284.6 eV ± 0.2 eV) was used to calibrate all binding energies. The spectra were decomposed using the software’s least-squares fitting with a Gauss/Lorentz function and a Shirley background. Atomic ratios were calculated from background-subtracted peak areas using sensitivity factors provided by the data analysis system.
Fourier transform infrared spectroscopy (FTIR)
The GNPs–HDPE matrix interaction was studied using Fourier transform infrared spectroscopy (FTIR) in transmittance mode. The spectra of neat HDPE and HDPE/GNPs nanocomposites were obtained with a Spectrum 1000 PerkinElmer spectrometer in the spectral area 4000–400 cm−1, with a resolution of 2 cm−1 and 32 scans. The systematic error in the wavenumber values was found to be ± 0.13 cm−1. The crystalline phase content was determined by the empirical relations proposed by Zerbi et al. [14], where X is the percentage of amorphous and Iα and Ib are the infrared intensities in the spectral bands of doublets 1472 and 1462 cm−1 or the bands 730 and 720 cm−1. The intensity ratio of the bands in a spectrum of a 100% crystalline PE is 1.233:
Raman measurements
Raman measurements were taken in the back-scattering geometry using a LabRAM HR (HORIBA) spectrometer with a 515 nm solid state laser (COBOLT) as an excitation source, at a power of less than 0.1 mW on the sample. The laser beam was focused on the sample by means of a 100 × objective to a spot of ~ 1 μm in diameter, which was rapidly scanned over an area of 10 × 10 μm2, taking advantage of the DuoScan system (HORIBA), for reducing the effective laser power density as well as providing spatial averaging of the signal. Three different sample areas were measured and averaged. The systematic error in the wavenumber values was found to be ± 0.15 cm−1. The crystalline fraction was obtained using the equation:
where I1416 is the integrated intensity of the band at 1416 cm−1 normalized to that of the CH2 twisting band around 1300 cm−1. The constant 0.46 was determined in the literature from the corresponding intensity of the 1416 cm−1 peak of 100% crystalline polyethylene [25].
Differential scanning calorimetry (DSC) and temperature-modulated differential scanning calorimetry (TM-DSC)
Differential scanning calorimetry (DSC) measurements have been taken in a DSC141 (Setaram). The instrument's temperature and energy calibrations were carried out for various heating rates, using well-known melting temperatures, and melting enthalpies of high-purity zinc, tin, and indium. HDPE/GNPs nanocomposites of 8 mg were placed in an aluminum-sealed crucible, while an identical empty crucible was used as a reference in each measurement. The samples were heated from room temperature to 170 °C at a rate of 2.5 °C min−1 in a 50 ml· min−1 flow of nitrogen.
Temperature-modulated differential scanning calorimetry (TM-DSC) was also used to separate the reversing and non-reversing melting processes (DSC 214 Polyma). HDPE/GNPs nanocomposites of 8 mg were heated from 40 to 160 °C at a heating rate of 2.5 °C min−1 with a modulation period of 60 s and a temperature amplitude of 0.5 K. A nitrogen flow rate of 20 mL min−1 was used throughout. The degree of crystallinity (Xc) of HDPE/GNPs nanocomposites was calculated by:
where ΔHm is the measured heat of fusion, \(\Delta H_{{\text{m}}}^{0}\) is the heat of fusion of 100% crystalline HDPE (293 J g−1 [26]), and w is the weight fraction of GNPs in the polymer matrix. The systematic error in the temperature values was found to be lower than 0.4 °C.
Results and discussion
Structural properties of HDPE/GNPs nanocomposites
XRD was used to determine the crystallinity and investigate the effect of filler size and content on the crystalline structure of HDPE/GNPs nanocomposites. Figure 1 shows selected XRD patterns for HDPE/M15 nanocomposites. The orthorhombic phase (Pnma space group) of HDPE/GNPs nanocomposites shows three peaks at 21.6°, 24°, and 36.4°, corresponding to (110), (200), and (020) reflections [27]. All HDPE/GNPs nanocomposites show similar XRD patterns to that of the neat HDPE; the only difference is a sharp diffraction peak of the (002) crystal plane of GNPs located at 2θ ~ 26.5°. Figure S1 shows the crystalline structure of the GNPs, which reveals a highly crystalline material. The intense and sharp peak observed at 2θ ~ 26.5° is due to the crystallographic plane (002) of the graphitic structure. It is assumed that the higher GNPs intensity of HDPE/M25 nanocomposites results from the greater quantity of stacks of graphene layers [28]. This also shows that during the melt mixing process, some GNPs may aggregate and form a more ordered stacking structure, which is consistent with our previous TEM studies [22].
To further examine the effect of GNPs on the crystalline structure, the space between the structural layers (d) of the HDPE nanocomposites was also calculated using Bragg’s law (Eq. 1). Scherrer’s equation (Eq. 2) was used to estimate the crystallite size (L) perpendicular to the planes (110) and (200) of HDPE/GNPs nanocomposites, as well as perpendicular to the planes (002) of GNPs (Table 1). The L110, L200, and d for neat HDPE were found to be 289 (Å), 224 (Å), and 4.1138 (Å), respectively, in agreement with the literature [29]. The d-spacing values for the HDPE samples filled with GNPs do not change significantly, as shown in Table 1. The crystallite size along with the two main crystallographic directions, L110 and L200, of HDPE/M5 nanocomposite decreases with increasing filler loading up to 3 wt% and then it increases. The L110 and L200 of HDPE/M15 and HDPE/M25 nanocomposites follow the same trend; they slightly decrease with GNPs loading up to 2.5 wt% because of the suppressed crystal growth caused by the presence of GNPs (the crystal packing becomes a little tighter and the crystals get smaller) and then increase for higher filler concentration. The incorporation of GNPs with higher diameter size in HDPE at higher filler concentration results in a larger crystallite size that can withstand the applied load [22]. Crystallite sizes in HDPE/GNPs nanocomposites are a two-factor process: the nucleating effect of GNPs and the slow diffusion of polymer molecular chains, which limits crystal growth [30]. Additionally, L002 of GNP increases with increasing filler diameter, indicating that GNPs M25 have a more agglomerated structure than GNPs M5 and GNPs M15. These explanations support the varying crystallite sizes, indicating that a decrease in crystallite improves mechanical properties [22].
X-ray photoelectron spectroscopy (XPS) measurements were taken on selected HDPE/GNPs nanocomposites to examine the incorporation and the interaction of GNPs into the HDPE matrix. Figure S2 and S3 show the wide scan C 1s and O 1s XPS spectra of GNPs as well as HDPE/5 M5 and HDPE/5 M25 nanocomposites, which demonstrate the presence of carbon and oxygen in these materials with only slight differences in intensity. The decomposition of the C1s peak of neat HDPE reveals the presence of four components: C–C (or C–H), C–OH, O–C–O (or C=O), and O–C=O with binding energies of 285.0 eV, 286.5 eV, 288.0 eV and 289.5 eV [31] (Fig. 2). Table 2 presents the deconvolution of the C1s peak of HDPE/GNPs nanocomposites into five subpeaks. Through the four typical peaks of neat HDPE, the C1s core level analysis of HDPE/GNPs nanocomposites confirms the presence of C–C/C–H, C–OH, O–C–O, and O–C=O bonds. However, a new C1s peak appears at ~ 284.5 eV, corresponding to the GNPs’ C=C bond (sp2 hybridized graphitic structure). The spectrum of HDPE is symmetric and appears at a BE of 285.6 eV. However, the peak becomes asymmetric for nanocomposites because of the presence of graphite materials. So, the spectra of HDPE/GNPs nanocomposites are a combination of two components: GNPs sp2 and PE sp3 contributions. The increased C–C sp2 content with increasing both filler content and size confirms the presence of GNPs. As shown in Fig. 2a for HDPE/GNPs Μ5 nanocomposites, the peak intensity corresponding to C–C (sp3- hybridized orbital similar to that of diamond-like carbon) decreases, while an increase in C=C and C–OH bonds are seen as a shoulder peak. These findings demonstrate that the overall levels of carbon linked to oxygen at the surface of neat HDPE are increased by the addition of GNPs. The contribution of GNPs M25 looks to be even more noteworthy as the sp2 area for the HDPE/5 M25 composite was found to be 6.8%.
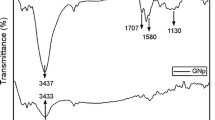
FTIR was used to estimate the crystalline phase content and study filler–polymer matrix interaction in HDPE/GNPs nanocomposites at various filler content in the range from 4000 to 500 cm−1 (Fig. 3a). There are four characteristic bands in the spectrum of neat HDPE. The strongest IR peaks of neat HDPE are assigned as follows: 2915 and 2845 cm−1 to asymmetric and symmetric stretching vibrations of methylene (–CH2–) groups; 1460–1470 cm−1 to bending deformation of methylene groups; 1367 cm−1 to CH2 wagging vibrational modes of crystalline PE, and the 700–800 cm−1 to CH2 rocking deformation of methylene groups of PE [32]. All the characteristic PE vibrations are visible in the HDPE/GNPs nanocomposites, including the symmetric and antisymmetric stretching of − CH2 groups, at ~ 2900 and 2844 cm −1, respectively, and the doublets at 1472/1462 cm−1 (− CH2 bending) and 730/719 cm−1 (− CH2 rocking). However, the presence of GNPs in HDPE composites leads to appearance of the C=C band at around 1570 cm−1 (Fig. 3b) in absorbance mode. A small amount of oxygen found in GNPs also gives rise to the carbonyl peak around 1720 cm−1. The normalized intensity for the carbonyl peak for HDPE/5 M5, HDPE/5 M15, and HDPE/5 M25 was found to be 0.011, 0.013, and 0.014, respectively. As can be seen from the collected spectra and the intensified 1720 cm−1 peak, the presence of GNPs causes a slight increase in the –OH and C=O content of nanocomposites with increasing GNPs diameter. Similar observations have been reported on composites of multi-walled carbon nanotubes and ultra-high-density polyethylene treatment [33].
Raman spectroscopy has been widely used to study the interaction between polymeric matrices and carbon fillers and estimate the crystalline fraction [34]. Figure 4a shows the Raman spectra of selected nanocomposites. In detail, the Raman spectrum of neat HDPE exhibits characteristic spectral features in the regions of 1000–1500 cm−1 and 2700–3000 cm−1. In the first region, Raman spectra of neat HDPE can be divided into three spectral areas. In area I, the main Raman peaks can be attributed to the antisymmetric (1063 cm−1) and symmetric (1130 cm−1) C–C stretching modes, vibrations of the skeletal chains parallel and perpendicular to chain axis, respectively, while the 1168 cm−1 band is assigned to the C–C stretching mode of the amorphous chains; area I is sensitive to molecular orientation, stress, and conformation. In area II, the main Raman peaks can be attributed to the CH2 twisting vibrations can be observed resulting in one sharp peak at 1295 cm−1 due to the vibrations of the crystalline components of PE, and a broad amorphous band with a maximum at around 1303 cm−1. In the literature, the 1295 cm−1 peak has been proposed as a reliable internal intensity standard because it has been proved to be independent of conformational changes [25]. In area III, the 1415 and 1440 cm−1 peaks are assigned to a split doublet of the CH2 bending mode vibrations. This crystal field splitting is characteristic of the orthorhombic unit cell in which two molecular chains occupy the unit cell and their interaction results in two components for the bending Raman and IR active peaks. The 1415 cm−1 peak, assigned to CH2 bending in the orthorhombic crystal, is of Ag symmetry and it is also useful for the estimation of the PE crystalline fraction. The 1460–1470 cm−1 broad band can be associated with the amorphous or an intermediate disordered phase of the system [35]. The second region includes two sharp peaks at ~ 2848 and 2882 cm−1, corresponding to the symmetric and asymmetric stretching vibration of the CH2 group, respectively, as well as a weaker peak at 2724 cm−1.
The characteristic D, G, and 2D bands of GNPs can be observed in all HDPE nanocomposites even at the lowest filler concentration. Raman spectra of the M5, M15, and M25 GNPs are illustrated in Fig. S4. Evidently, they are very similar and spectral features can be observed at 1362, 1581, 1620, 2451, 2694 and 2720 (doublet), and 3246 cm−1, attributed to the D, G, D′, D + D″, 2D, and 2D′ modes, respectively. So, the D band peak of HDPE/GNPs nanocomposites in Fig. 4 at around 1362 cm−1 originates from the K-point phonons of A1g symmetry in graphite, which is defect activated, while the G band peak at around 1581 cm−1 is assigned to the zone center phonons of E2g symmetry. The 2D band at around 2720 cm−1 is the second order Raman scattering associated with the D band, being Raman active even for perfect crystalline graphitic materials [36].
The peak intensity ratio, I(D)/I(G), for all the starting GNPs and their nanocomposites ranges non-systematically from 0.2 to 0.5, compatible with the presence of localized sp3 defects within the sp2 carbon network. This is consistent with marginal alteration of the GNPs upon their incorporation in the polymer matrix, which is not unexpected since the particles are in the microscale. Furthermore, the frequency and the line shape of the 2D band in the samples suggest their multilayer graphitic structure.
Thermal properties of HDPE/GNPs nanocomposites
DSC is also used to calculate the crystallinity of nanocomposites. The melting and crystallization behaviors of neat HDPE and HDPE/GNPs nanocomposites were studied by standard DSC and TM-DSC as a function of GNPs size and content. Table 3 summarizes the peak melting temperatures (Tm), enthalpy of melting (ΔHm), and degree of crystallinity for HDPE/GNPs nanocomposites during the first and second heating cycles at heating rates of 20 °C min−1 and 2.5 °C min−1, respectively. The thermal history of HDPE/GNPs nanocomposites is reflected in the first heating curve, which is influenced by the synthesis process. The second heating curve shows the crystallization of the melts. The ΔHm of HDPE/GNPs nanocomposites is not the same during the first and second heating cycles due to the thermal and flow histories from the melt mixing process. To accurately compare the different methods used to measure crystallinity, it is important to present the values of crystallinity for the samples without any additional heat treatment, as was done when using XRD, RAMAN, and FTIR methods. The incorporation of GNPs at low filler content into the HDPE matrix slightly increases Tm values compared to neat HDPE during the second cycle because of the presence of an enhanced number of heterogeneous nuclei (Fig. 5a). However, the melting temperature was shown to diminish with increasing GNPs content and size (HDPE/5 M25), indicating that the excess additive or its agglomeration affect chain compaction and crystal perfection. This result agrees with data from similar systems [37].
Figure 5b shows the results of crystallization behavior of HDPE/GNPs nanocomposites from the melt at a cooling rate of 2.5 °C min−1. Table 3 presents the crystallization parameters: peak temperature (Tc), crystallization enthalpy (ΔHc), and the degree of crystallinity (Xc). The addition of GNPs does not significantly alter the Tc of HDPE nanocomposites obtained from the exothermic peak on the DSC cooling curves following the melting results.
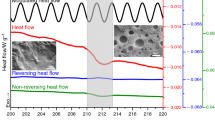
TM-DSC was employed to comprehend the melting behavior and separate the simultaneously occurring events during the melting of the samples. In a previous study [21], we reported the multiple melting behavior of HDPE/GNPs nanocomposites that appeared only in specific combinations of cooling and heating rates during fast scanning calorimetry (FSC). It was found that the structure formation was far from thermodynamic equilibrium due to the high cooling rates used. In this work, the modulated raw heat flow data are deconvoluted by Fourier transformation into the total heat flow (the average, corresponding to conventional DSC data) and the reversing heat flow. Figure 6 shows the TM-DSC curves of total heat flow, non-reversing heat flow, and reversing heat flow as a function of temperature for neat HDPE, HDPE/M5, HDPE/M15, and HDPE/M25 nanocomposites filled with 5 wt% of GNPs. The total curve of neat HDPE shows a relatively narrow, single melting endothermic peak and it splits into a reversing and a non-reversing signal. Nevertheless, the standard DSC curves (Fig. 5) or total TM-DSC curves did not indicate any recrystallization during the scanning. However, a recrystallization process during heating was found in the non-reversible heat flow, while the reversing contribution (broader and smaller in magnitude than the total and non-reversing curves) exhibits multiple overlapped melting peaks because of overlapping of melting and crystal reorganization and different populations of crystal sizes. According to Wei et al. [38], the double melting peaks in the non-reversing heat flow curve of PEEK were attributed to the melting–recrystallization mechanism and different morphologies.
For HDPE/GNPs nanocomposites, the total heat flow curves exhibit one sharp melting peak. A non-reversing characteristic and a reversing contribution that can be attributed to recrystallization, crystal annealing, perfection of the non-equilibrium crystals, and melting–recrystallization mechanism (melting of primary crystals and remelting of secondary crystals), different populations of crystal sizes, nucleation activity of GNPs [39, 40]. The enthalpy of the reversing endotherms of HDPE/GNPs nanocomposites was found to be larger than that of neat HDPE, forming more unstable crystals [41]. The non-reversing melting enthalpies of HDPE/5 M5, HDPE/5 M15, and HDPE/5 M25 nanocomposites were found to be small enough due to the presence of GNPs agglomeration that prevents the reorganization of imperfect crystals into more stable or perfect crystals and to the formation of secondary crystals. On the contrary, the bigger non-reversing contribution of HDPE/GNPs filled with 2.5% wt. of filler signifies the ongoing crystal perfection, accompanied by the reversing melting of the imperfect crystals in the same temperature region, decreasing the degree of crystallinity (Table 4).
Table 4 and Fig. 6b also show the crystallization characteristics of the nanocomposites. It is observed that the crystallization temperature (Tc) of HDPE/GNPs nanocomposites shifts to slightly higher values with increasing GNPs content. This is evidence of the enhancement of heterogeneous nucleation because the time to form the critical nucleus has been diminished. Moreover, small peaks (shoulders) can be seen in addition to the main peak (inset in Fig. 6b). Crystals growing at the surface of GNPs might have different lamellar thicknesses or crystal sizes, resulting in a heterogeneous distribution of crystalline structures (heterogeneous nucleation) and various peaks. This is supported by the observed relatively broad multiple endotherms and exothermic peak in the reversing and non-reversing heat flow curves (Fig. 6a-c).
The crystallization enthalpy and the crystallinity of the HDPE/GNPs nanocomposites have decreased compared to neat HDPE, starting from 218.2 J g−1 for neat HDPE, down to 199.8 J g−1 and 200.8 J g−1 for samples containing 5 wt% GNPs M5 and 5 wt% GNPs M25, respectively. The same trend has been presented in the conventional DSC measurements (Table 3). On the one hand, there are more nucleating sites in GNPs due to the increase in surface area to volume ratio. On the other hand, the mobility of the molecular chains may decrease because of the filler’s presence, slowing the formation of the crystals and decreasing the efficiency of the filler. A similar phenomenon has been reported by Magniez et al. [42] in the poly(m-xylene diamide)/dodecaphenyl polyhedral oligomeric silsesquioxane/montmorillonite systems. The authors hypothesized that in the primary stages of crystallization, the polymer spherulites nucleate quicker in the presence of the nanoparticles [42]. However, in the secondary stage of crystallization, the presence of nanoparticles might cause steric hindrance resulting in reduced crystallinity. Biswas et al. [43] also thought that the crystallization of polymer chains from the melt might cause GNPs aggregation outside of the crystalline areas. This is true in our case especially when the existence of GNPs M25 with the large diameter and high aspect ratio reduces the mobility of the HDPE molecules and causes steric hindrance in the semicrystalline HDPE matrix.
Degree of crystallinity of HDPE/GNPs nanocomposites
Calculating the crystallinity of HDPE/GNPs nanocomposites is crucial since the degree of crystallinity (Xc) greatly influences the properties of the polymer. Semicrystalline polymers such as HDPE contain two primary components: a crystalline phase and an amorphous phase. The crystallinity of neat HDPE can be calculated by:
where d is the density of HDPE, dc is the density of 100% HDPE crystal (0.985 g cm−3), and dα is the density of completely amorphous HDPE (0.824 g cm−3). The density d and the crystallinity of neat HDPE were found to be 0.955 g cm−3 and 84%, respectively.
The crystallinity of the HDPE/GNPs nanocomposites was estimated by using a Gaussian–Lorentzian function to fit the XRD profiles in Fig. 7a and then calculating the ratio between the crystalline diffraction area and the total area of the diffraction profile [24]. The Gaussian–Lorentzian function is a mathematical function that is able to accurately model the shape of the diffraction peaks in the X-ray diffractograms. It consists of a combination of a Gaussian function, which describes the shape of the diffraction peak due to the ordered arrangement of atoms in the material, and a Lorentzian function, which describes the shape of the diffraction peak due to the presence of disorder or defects in the material. Figure 7b shows the trend of crystallinity as a function of the filler content for HDPE/M5, HDPE/M15, and HDPE/M25 nanocomposites, which increases with increasing the diameter size and content. This agrees with the XPS results, which show that the C–C sp2 content increases with increasing both filler content and size. There is a significantly higher crystallinity of HDPE matrix at low concentrations of GNPs M25 compared to that of neat HDPE, HDPE/M5, and HDPE/M15 nanocomposites. Once again, some GNPs may aggregate and form a more ordered stacking structure. So, GNPs M25 have a significant nucleating effect and operate as heterogeneous nucleating sites, increasing the crystallinity of HDPE. However, the crystallinity of the matrix does not rise linearly as the concentration of GNPs increases. With a higher content of GNPs M25 in the matrix, GNPs hinder the mobility and diffusion of the HDPE chains, limiting the growth of the HDPE crystallites. It is hypothesized that these two mechanisms counteract each other at 5 wt% in agreement with the calculated crystallite size values LHDPE of the (110) and (200) planes in Table 1. The incorporation of GNPs with higher diameter size in HDPE at higher filler concentration results in a larger crystallite size that can withstand the applied load.
FTIR may provide additional information about the polymers crystalline content since some of the absorption peaks in the infrared spectrum of PE are sensitive to crystallinity. HDPE’s crystalline forms and amorphous phase absorptions can also be determined using the infrared-active scissoring vibrations in the 1472 to 1462 cm−1 and/or rocking vibrations in the 735 to 715 cm−1 spectral region [23]. The crystallinity was calculated by the empirical relations proposed by Zerbi et al. [14], where X is the percentage of amorphous and Iα and Ib are the infrared intensities in the spectral bands of doublets 1472 and 1462 cm−1 or the bands 730 and 720 cm−1 (Eq. 4). The 1472/730 cm−1 are the crystalline bands while the 1462/720 cm−1 bands are associated with the amorphous component. The band component was assumed to be a weighted mixture of Lorentzian and Gaussian functions, and the variables (the relative weight of these two functions, the height, the width, and the peak position) were adjusted by a nonlinear least-squares method so that the summed spectral profile was fitted to the measured pattern as well as possible [44]. Figure 8 shows the deconvolution results for HDPE/1 M25 and HDPE/5 M25 nanocomposites. The lower-frequency components (1462/719 cm−1) were found to have greater normalized intensity than the higher-frequency ones (1472/730 cm−1). A general observation was that the more crystalline the sample, the closer the two peaks were to being equal in intensity [45]. The intensity of the lower-frequency component decreases with increasing the GNPs M25 content until the two peaks are equal in intensity.
The results indicate significant differences depending on the spectral bands used to evaluate the crystalline content. The crystalline phase content was determined by the empirical relations proposed by Zerbi et al. [14] using the intensity ratio of the methylene bending bands at 1472/1462 cm−1. The degree of crystalline phase content of neat HDPE and HDPE/GNPs nanocomposites is plotted as a function of GNPs concentration in Fig. 9a. As expected from the estimation of crystalline phase content by FTIR spectroscopy, a relatively higher value of crystalline phase content (75.9%) was measured for neat HDPE compared to that by XRD. However, this value is very close to that calculated by density. Additionally, the crystallinity of HDPE/M25 nanocomposites was found to be higher than neat HDPE, HDPE/M5, and HDPE/M15 nanocomposites. Once again, the GNPs M25 act as a nucleating site at low concentrations (< 3%) improving crystallinity, but it decreases as the GNPs M25 begin to obstruct the molecular mobility of the HDPE polymer matrix at higher concentrations.
Raman spectroscopy has been used to estimate the load transfer between polymeric matrixes and carbon-related fillers. For the nanocomposites, both HDPE and GNPs structures are expected to coexist, and hence, the vibrational modes of both structures contribute to the overall spectra. The Strobl and Hagedorn method was used to estimate the crystalline fraction from the Raman spectra [25] (Eq. 5). The 1415 cm−1 bending band is commonly attributed to the orthorhombic phase, and its content can be estimated by dividing the intensity by the integral intensity of the PE twisting vibrations bands. The crystalline fraction can then be obtained by Eq. 5 (Fig. 9b). It can be clearly observed that the Raman crystalline fraction is in the same order as the values obtained by the FTIR method and follows the same trend as the other testing techniques. Once again, GNPs M25 lead to the formation of a material with a higher degree of crystallinity, as revealed by XRD, and FTIR analysis. At lower filler content, the overall finer dispersion of GNPs M25 in the matrix leads to reinforced polymer composites with superior mechanical properties, indicating that the shear mixing forces overcome the intrinsic van der Waals interactions of GNPs.
As shown by FTIR and Raman spectroscopy measurements, the absence of chemical interactions by bonds between the matrix and the fillers reveals that the weak van der Waals attractions between GNPs cause the observed agglomeration, while the shear force from melt mixing contributes to randomly array them. The overall fine dispersion of GNPs M25 in the HDPE matrix at low filler contents, which is essential for making reinforced polymer composites with superior properties [22], proves that the shear mixing forces overcome the intrinsic van der Waals attractions of GNPs.
In DSC, the degree of crystallinity was determined from the heat of fusion under the area of melting and crystallization peaks of HDPE/GNPs nanocomposites (Table 3). All the crystallinity calculations were normalized by the HDPE weight (Eq. 6). The degree of crystallinity of neat HDPE and HDPE/GNPs nanocomposites was around 60%, while the crystallinity slightly decreases with the GNPs content and size in case of HDPE/M25 nanocomposites. This result agrees with the Tm values (Table 3). It was found that the incorporation of GNPs at low filler content slightly increases Tm values compared to neat HDPE, while the melting temperature was shown to diminish with increasing GNPs content and size. This decrease can be attributed to chain mobility, the existence of GNPs, and the formed agglomerations that obstruct crystal growth. In this way, the folding of polymeric chains is difficult and, consequently, a decrease in crystallinity is more likely. Cheng et al. also have reported insignificant changes in crystallinity for reduced graphene oxide and polyethylene nanocomposites during DSC measurements [46].
Figure 10 also shows the crystallinity values calculated by TM-DSC, which were used to study the multiple melting events that occur. The reorganization process often comprises a change in the crystal form and the crystallinity, and thus, the melting and recrystallization that simultaneously occur during heating must be taken into account for the calculation of crystallinity. Table 4 reveals that the non-reversing melting enthalpies were sufficiently low due to the existence of GNPs agglomeration. So, the crystallinity of the HDPE/GNPs nanocomposites have decreased compared to neat HDPE. However, the degree of crystallinity for HDPE/GNPs nanocomposites was found to be slightly higher compared to those of conventional DSC.
Summing up, Fig. 10 shows a comparative plot of crystallinity versus filler content (wt%) for HDPE/M5 and HDPE/M25 nanocomposites as calculated by XRD, DSC, FTIR, Raman, and TM-DSC measurements. The degree of crystallinity varies because of the restrictions that each technique places on its use. HDPE has a degree of crystallinity that ranges from 70 to 80%. According to Batista et al. [5], the degree of crystallinity of neat HDPE was determined to be around 60% using DSC analysis, based on the melting peaks observed. Pelto et al. [47] found that the degree of crystallinity for neat HDPE, as determined using XRD data, was proportional to the values obtained from the first DSC heating cycle. The sample had a slightly higher degree of crystallinity (2–4%) during the first heating cycle compared to the second heating cycle. Bourque et al. [8] demonstrated that the crystallinity values of the neat high and low molecular weight HDPE were 61.6% and 88.0%, respectively. Shafiei et al. [9] found a high degree of crystallinity (74.23%) for neat HDPE calculated by XRD.
FTIR and Raman values of crystallinity were found to be in the same order of magnitude. FTIR is based on the absorption of infrared radiation by the material, while Raman spectroscopy is based on the scattering of light by the material; both techniques can provide information about the vibrational modes and chemical bonds within the material. Strong Raman scattering and strong IR absorption are caused by nonpolar molecular and polar groups, respectively. So, the vibrations of the substituents on the carbon chain may be investigated using IR spectroscopy in chainlike polymer molecules, and the vibrations of the backbone carbon chain can be analyzed using Raman spectroscopy. One of the drawbacks of using IR spectra to determine polymer crystallinity is that few polymers (such as PE) exhibit the crystal field splitting seen in certain situations because the splitting is highly susceptible to polymer chain separation. PE has the highest crystal field splitting of any polymer because of its tighter chains than any other. XRD and vibrational spectroscopy measure long-range/intermolecular order and short-range/intramolecular order, respectively. XRD uses either individual peaks from the pattern or the complete pattern to establish a correlation between peak intensity and/or cumulative area and phase composition. Therefore, both methods do not always measure the same crystallinity, because short-range intramolecular order is required for long-range order to exist, but not vice versa [48].
Thermal analysis, although widely used for determining crystallinity, may have limited precision with oriented polymers due to the differential nature and overlap of multiple thermal events (cold crystallization, chain relaxation, etc.). DSC crystallinity is determined by comparing the enthalpy of fusion of the measured polymer matrix to the enthalpy of fusion of 100% crystalline material at the equilibrium melting point. The disadvantages of this method include the lack of consideration for temperature dependencies of thermodynamic parameters and the comparison to the heat of fusion of 100% crystalline material at equilibrium melting point [49]. Since the crystallinity of the polymer is temperature dependent, the estimated crystallinity determined by DSC at the melting temperature will differ from the value at ambient temperature [50]. Additionally, it was shown that all melting peaks must be taken into consideration. The differential nature and overlap of multiple thermal events (cold crystallization, crystal perfection, recrystallization, chain relaxation, and melting of different crystal forms) would make the DSC crystallinity much more difficult.
The results obtained by the above-mentioned techniques are complementary to achieve a better comprehensiveness about the structure and crystallinity of the HDPE/GNPs nanocomposites. While each technique has its own strengths and limitations, they all provide valuable information about the crystallinity of these materials. Many studies have employed a combination of techniques including density measurements, DSC, XRD, FTIR, and Raman spectroscopy to determine the degree of crystallinity [51,52,53]. On the one hand, XRD, FTIR, and Raman measurements show greater values for crystallinity of HDPE/GNPs nanocomposites. This is likely because GNPs is a highly crystalline material. A higher crystallinity and smaller amorphous layer thickness were reported for the nanocomposites, meaning tighter nanoconfinement for the amorphous phase, possibly accounting for the lower mobility [54]. There is a trend as the crystallinity of HDPE/M15 and HDPE/M25 nanocomposites increases until 2.5–3 wt% and then decreases, whereas the crystallinity of HDPE/M5 nanocomposites increases monotonically with increasing filler content. On the other hand, the crystallinity determined by conventional DSC was found to be with lower values compared to those of TM-DSC values. According to TM-DSC, the melting and recrystallization that simultaneously occur during heating, must be taken into account for the calculation of crystallinity. Summing up, the incorporation of GNPs within the HDPE matrix affects the crystallization process in two different competing ways. Initially, the nanofillers act as nuclei for heterogeneous crystallization, but thereafter they place constraints on the polymer chains, restricting their mobility and crystal growth. However, as the filler content increases, limits to polymer chain mobility are imposed and a restricted network is formed via geometrical contacts, reducing crystal growth [55].
Conclusions
This study provides a comparative study of four different techniques to determine the crystallinity of HDPE nanocomposites filled with GNPs of different diameter sizes at various fillers contents. XRD results revealed a substantially higher intensity of the GNPs in the HDPE/M25 nanocomposites because of the higher number of graphene layers structured in stacks. FTIR and Raman findings showed that the addition of GNPs led to slight differences in the spectra of the nanocomposites compared to that of neat HDPE. GNPs M25 exhibited a strong nucleating effect at low concentrations, increasing the degree of crystallinity of HDPE. However, the crystallinity of the matrix did not increase monotonically with the concentration of GNPs. With a higher density of GNPs M25 in the matrix, GNPs hindered the mobility and diffusion of the HDPE chains, limiting the growth of the HDPE crystallites. FTIR, Raman spectroscopy, and XRD method yielded higher crystallinity for HDPE/GNPs nanocomposites, whereas the DSC method was the lowest. However, all the results obtained by the above-mentioned techniques are complementary to achieve a better comprehensiveness about the structure and crystallinity of the HDPE/GNPs nanocomposites.
Data and code availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Ren PG, Di YY, Zhang Q, Li L, Pang H, Li ZM (2012) Composites of ultrahigh-molecular-weight polyethylene with graphene sheets and/or MWCNTs with segregated network structure: Preparation and properties. Macromol Mater Eng 297:437–443. https://doi.org/10.1002/mame.201100229
Peeters M, Goderis B, Vonk C, Reynaers H, Mathot V. Morphology of homogeneous copolymers of ethene and 1-octene. I. Influence of thermal history on morphology. J Polym Sci B Polym Phys 1997;35:2689–713. https://doi.org/10.1002/(SICI)1099-0488(19971130)35:16<2689::AID-POLB12>3.0.CO;2-5.
Yang Z, Peng H, Wang W, Liu T (2010) Crystallization behavior of poly(ε-caprolactone)/layered double hydroxide nanocomposites. J Appl Polym Sci 116:2658–2667. https://doi.org/10.1002/app
Biswas S, Drzal LT (2009) A novel approach to create a highly ordered monolayer film of graphene nanosheets at the liquid-liquid interface. Nano Lett 9:167–172. https://doi.org/10.1021/nl802724f
Batista NL, Helal E, Kurusu RS, Moghimian N, David E, Demarquette NR et al (2019) Mass-produced graphene—HDPE nanocomposites: thermal, rheological, electrical, and mechanical properties. Polym Eng Sci 59:675–682. https://doi.org/10.1002/pen.24981
Wei P, Bai S (2015) Fabrication of a high-density polyethylene/graphene composite with high exfoliation and high mechanical performance via solid-state shear milling. RSC Adv 5:93697–93705. https://doi.org/10.1039/c5ra21271e
Navarro-Pardo F, Martínez-Barrera G, Martínez-Hernández AL, Castaño VM, Rivera-Armenta JL, Medellín-Rodríguez F et al (2013) Effects on the thermo-mechanical and crystallinity properties of nylon 6,6 electrospun fibres reinforced with one dimensional (1D) and two dimensional (2D) carbon. Materials 6:3494–3513. https://doi.org/10.3390/ma6083494
Bourque AJ, Locker CR, Tsou AH, Vadlamudi M (2016) Nucleation and mechanical enhancements in polyethylene-graphene nanoplate composites. Polymer (Guildf) 99:263–272. https://doi.org/10.1016/j.polymer.2016.07.025
Shafiei M, Ghasemi I, Gomari S, Abedini A, Jamjah R (2021) Positive temperature coefficient and electrical conductivity investigation of hybrid nanocomposites based on high-density polyethylene/graphene nanoplatelets/carbon black. Physica Status Solidi (A) Appl Mater Sci 2100361. https://doi.org/10.1002/pssa.202100361
Jiang X, Drzal LT (2012) Multifunctional high-density polyethylene nanocomposites produced by incorporation of exfoliated graphene nanoplatelets 2: crystallization, thermal and electrical properties. Polym Compos 33:636–642. https://doi.org/10.1002/pc.22187
Xiang D, Wang L, Zhang Q, Chen B, Li Y, Harkin-Jones E (2018) Comparative study on the deformation behavior, structural evolution, and properties of biaxially stretched high-density polyethylene/carbon nanofiller (carbon nanotubes, graphene nanoplatelets, and carbon black) composites. Polym Compos 39:E909–E923. https://doi.org/10.1002/pc.24328
Olesik P, Godzierz M, Kozioł M, Jała J, Szeluga U, Myalski J (2021) Structure and mechanical properties of high-density polyethylene composites reinforced with glassy carbon. Materials 14:4024. https://doi.org/10.3390/ma14144024
Mallapragada SK, Narasimhan B. Infrared spectroscopy in analysis of polymer crystallinity. Encyclopedia of Analytical Chemistry, Wiley. 2006. https://doi.org/10.1002/9780470027318.a2012.
Zerbi G, Gallino G, Del Fanti N, Baini L (1989) Structural depth profiling in polyethylene films by multiple internal reflection infra-red spectroscopy. Polymer (Guildf) 30:2324–2327. https://doi.org/10.1016/0032-3861(89)90269-3
Lin W, Cossar M, Dang V, Teh J (2007) The application of Raman spectroscopy to three-phase characterization of polyethylene crystallinity. Polym Test 26:814–821. https://doi.org/10.1016/j.polymertesting.2007.05.004
Shrestha R, Li P, Chatterjee B, Zheng T, Wu X, Liu Z et al (2018) Crystalline polymer nanofibers with ultra-high strength and thermal conductivity. Nat Commun 9:1664. https://doi.org/10.1038/s41467-018-03978-3.
Paradkar RP, Sakhalkar SS, He X, Ellison MS. Estimating crystallinity in high density polyethylene fibers using online raman spectroscopy, vol. 88;2003.
Failla M, Alamo RG, Mandelkern L. On the analysis of the Raman internal modes of crystalline polyethylene, vol 11;1992.
Tarani E, Terzopoulou Z, Bikiaris DN, Kyratsi Th, Chrissafis K, Vourlias G (2017) Thermal conductivity and degradation behavior of HDPE/graphene nanocomposites. J Therm Anal Calorim 129:1715–1726. https://doi.org/10.1007/s10973-017-6342-0
Tarani E, Wurm A, Schick C, Bikiaris DN, Chrissafis K, Vourlias G (2016) Effect of graphene nanoplatelets diameter on non-isothermal crystallization kinetics and melting behavior of high density polyethylene nanocomposites. Thermochim Acta 643:94–103. https://doi.org/10.1016/j.tca.2016.09.018
Tarani E, Papageorgiou DG, Valles C, Wurm A, Terzopoulou Z, Bikiaris DN et al (2018) Insights into crystallization and melting of high density polyethylene/graphene nanocomposites studied by fast scanning calorimetry. Polym Test 67:349–358. https://doi.org/10.1016/j.polymertesting.2018.03.029
Tarani E, Chrysafi I, Kállay-Menyhárd A, Pavlidou E, Kehagias T, Bikiaris DN et al (2020) Influence of graphene platelet aspect ratio on the mechanical properties of HDPE nanocomposites: microscopic observation and micromechanical modeling. Polymers (Basel) 12:1719. https://doi.org/10.3390/POLYM12081719
Scherrer P, Debye P (1918) Werk Übergeordnetes Werk. Nachr Ges Wiss Göttingen, Math-Physik Klasse 2:101–120
Hindeleh AM, Johnson DJ (1971) The resolution of multipeak data in fibre science. J Phys D Appl Phys 4:259–263. https://doi.org/10.1088/0022-3727/4/2/311
Strobl GR, Hagedorn W (1978) Raman Spectroscopic method for determining the crystallinity of polyethylene. AIP Conf Proc 16:1181–1193. https://doi.org/10.1002/pol.1978.180160704
Wunderlich B, Czornyj G (1977) A study of equilibrium melting of polyethylene. Macromolecules 10:906–913. https://doi.org/10.1021/ma60059a006
PC Powder Diffraction Files 2003:JCPDS-ICDD.
Bai Q, Wei X, Yang J, Zhang N, Huang T, Wang Y et al (2017) Dispersion and network formation of graphene platelets in polystyrene composites and the resultant conductive properties. Compos Part A Appl Sci Manuf 96:89–98. https://doi.org/10.1016/j.compositesa.2017.02.020
Pereira RA, Mano EB, Dias ML, Acordi EB (1997) Comparative study on the lamellar crystal structure of high and low density polyethylenes. Polym Bull 38:707–714. https://doi.org/10.1007/s002890050109
Zhang F, Peng X, Yan W, Peng Z, Shen Y (2011) Nonisothermal crystallization kinetics of in situ nylon 6/graphene composites by differential scanning calorimetry. J Polym Sci B Polym Phys 49:1381–1388. https://doi.org/10.1002/polb.22321
Stark NM, Matuana LM (2004) Surface chemistry changes of weathered HDPE/wood-flour composites studied by XPS and FTIR spectroscopy. Polym Degrad Stab 86:1–9. https://doi.org/10.1016/j.polymdegradstab.2003.11.002
Gulmine JV, Janissek PR, Heise HM, Akcelrud L (2002) Polyethylene characterization by FTIR. Polym Test 21:557–563. https://doi.org/10.1016/S0142-9418(01)00124-6
Ansón-Casaos A, Aylón E, Ríos R, Puértolas JA (2019) Effects of argon ion sputtering on the surface of graphene/polyethylene composites. Surf Coat Technol 374:1059–1070. https://doi.org/10.1016/j.surfcoat.2019.06.091
Gall MJ, Hendra PJ, Peacock CJ, Cudby MEA, Willis HA (1972) Laser-Raman spectrum of polyethylene: Part 1. Structure and analysis of the polymer. Polymer (Guildf) 13:104–108. https://doi.org/10.1016/S0032-3861(72)80003-X
Taddei P, Affatato S, Fagnano C, Bordini B, Tinti A, Toni A (2002) Vibrational spectroscopy of ultra-high molecular weight polyethylene hip prostheses: Influence of the sterilisation method on crystallinity and surface oxidation. J Mol Struct 613:121–129. https://doi.org/10.1016/S0022-2860(02)00141-2
Malard LM, Pimenta MA, Dresselhaus G, Dresselhaus MS (2009) Raman spectroscopy in graphene. Phys Rep 473:51–87. https://doi.org/10.1016/j.physrep.2009.02.003
Menezes B, Campos T, Montanheiro T, Ribas R, Cividanes L, Thim G (2019) Non-isothermal crystallization kinetic of polyethylene/carbon nanotubes nanocomposites using an isoconversional method. J Compos Sci 3:21. https://doi.org/10.3390/jcs3010021
Wei CL, Chen M, Yu FE (2003) Temperature modulated DSC and DSC studies on the origin of double melting peaks in poly(ether ether ketone). Polymer (Guildf) 44:8185–8193. https://doi.org/10.1016/j.polymer.2003.10.009
Androsch R, Wunderlich B (1999) A study of annealing of poly(ethylene-co-octene) by temperature-modulated and standard differential scanning calorimetry. Macromolecules 32:7238–7247. https://doi.org/10.1021/ma9905223
Amarasinghe G, Shanks RA (2004) TMDSC analysis of single-site copolymer blends after thermal fractionation. J Therm Anal Calorim 78:349–361. https://doi.org/10.1023/B:JTAN.0000042181.39589.e8
Gill PS, Sauerbrunn SR, Reading M (1993) Modulated differential scanning calorimetry. J Therm Anal 40:931–939. https://doi.org/10.1007/BF02546852
Magniez K, Fox BL, Looney MG (2012) Nanocomposites of poly(m-xylene diamide) with polyhedral oligomeric silsesquioxane, montmorillonite, and their combination: structure and properties. Polym Eng Sci 52:1402–1412
Biswas S, Fukushima H, Drzal LT (2011) Mechanical and electrical property enhancement in exfoliated graphene nanoplatelet/liquid crystalline polymer nanocomposites. Compos Part A Appl Sci Manuf 42:371–375. https://doi.org/10.1016/j.compositesa.2010.12.006
Tashiro K, Sasaki S, Kobayashi M (1996) Structural investigation of orthorhombic-to-hexagonal phase transition in polyethylene crystal: The experimental confirmation of the conformationally disordered structure by X-ray diffraction and infrared/Raman spectroscopic measurements. Macromolecules 29:7460–7469. https://doi.org/10.1021/ma960333+
Stein RS, Sutherland GBBM (1954) Effect of intermolecular interactions between CH frequencies on the infrared spectra of N-paraffins and polythene. J Chem Phys 22:1993–1999. https://doi.org/10.1063/1.1739980
Cheng S, Chen X, Hsuan YG, Li CY (2012) Reduced graphene oxide-induced polyethylene crystallization in solution and nanocomposites. Macromolecules 45:993–1000. https://doi.org/10.1021/ma2021453
Pelto J, Verho T, Ronkainen H, Kaunisto K, Metsäjoki J, Seitsonen J et al (2019) Matrix morphology and the particle dispersion in HDPE nanocomposites with enhanced wear resistance. Polym Test 77:105897. https://doi.org/10.1016/j.polymertesting.2019.105897.
Koenig JL (1992) Spectroscopy of polymers. American Chemical Society, Washington
Kong Y, Hay JN (2002) The measurement of the crystallinity of polymers by DSC. Polymer (Guildf) 43:3873–3878. https://doi.org/10.1016/S0032-3861(02)00235-5
Pascaud RS, Evans WT, McCullagh PJJ, FitzPatrick D (1996) Effects of batch to batch variations and test methodology on degree of crystallinity and melting temperature of UHMW-PE as measured by differential scanning calorimetry. J Biomed Mater Res 32:619–626. https://doi.org/10.1002/(SICI)1097-4636(199612)32:4%3c619::AID-JBM15%3e3.0.CO;2-8
Saidi S, Portale G, Bras W, Longo A, Amigo JM, Chapron D et al (2021) Data mining of polymer phase transitions upon temperature changes by small and wide-angle x-ray scattering combined with raman spectroscopy. Polymers (Basel) 13:4203. https://doi.org/10.3390/polym13234203
Doumeng M, Makhlouf L, Berthet F, Marsan O, Delbé K, Denape J, et al. A comparative study of the crystallinity of Polyetheretherketone by using density, DSC, XRD, and Raman spectroscopy techniques 2021. https://doi.org/10.1016/j.polymertesting.2020.106878ï.
Hong T, Yin JY, Nie SP, Xie MY (2021) Applications of infrared spectroscopy in polysaccharide structural analysis: Progress, challenge and perspective. Food Chem X 12:100168. https://doi.org/10.1016/j.fochx.2021.100168
Yuan Q, Yang Y, Chen J, Ramuni V, Misra RDK, Bertrand KJ (2010) The effect of crystallization pressure on macromolecular structure, phase evolution, and fracture resistance of nano-calcium carbonate-reinforced high density polyethylene. Mater Sci Eng, A 527:6699–6713. https://doi.org/10.1016/j.msea.2010.07.007
Pielichowska K, Bieda J, Szatkowski P (2016) Polyurethane/graphite nano-platelet composites for thermal energy storage. Renew Energy 91:456–465. https://doi.org/10.1016/j.renene.2016.01.076
Funding
Open access funding provided by HEAL-Link Greece. This research received no external funding.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by ET, IA, and DC. The first draft of the manuscript was written by ET and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This research does not include experiments involving human tissue and does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Handling Editor: Catalin Croitoru.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tarani, E., Arvanitidis, I., Christofilos, D. et al. Calculation of the degree of crystallinity of HDPE/GNPs nanocomposites by using various experimental techniques: a comparative study. J Mater Sci 58, 1621–1639 (2023). https://doi.org/10.1007/s10853-022-08125-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-022-08125-4