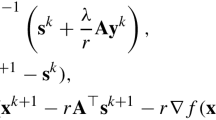Abstract
We consider image denoising problems formulated as variational problems. It is known that Hamilton–Jacobi PDEs govern the solution of such optimization problems when the noise model is additive. In this work, we address certain nonadditive noise models and show that they are also related to Hamilton–Jacobi PDEs. These findings allow us to establish new connections between additive and nonadditive noise imaging models. Specifically, we study how the solutions to these optimization problems depend on the parameters and the observed images. We show that the optimal values are ruled by some Hamilton–Jacobi PDEs, while the optimizers are characterized by the spatial gradient of the solution to the Hamilton–Jacobi PDEs. Moreover, we use these relations to investigate the asymptotic behavior of the variational model as the parameter goes to infinity, that is, when the influence of the noise vanishes. With these connections, some non-convex models for nonadditive noise can be solved by applying convex optimization algorithms to the equivalent convex models for additive noise. Several numerical results are provided for denoising problems with Poisson noise or multiplicative noise.

















Similar content being viewed by others
References
Achim, A., Kuruoglu, E.E., Zerubia, J.: Sar image filtering based on the heavy-tailed Rayleigh model. IEEE Trans. Image Process. 15(9), 2686–2693 (2006). https://doi.org/10.1109/TIP.2006.877362
Afonso, M.V., Sanches, J.M.R.: Blind inpainting using \(\ell _{0}\) and total variation regularization. IEEE Trans. Image Process. 24(7), 2239–2253 (2015). https://doi.org/10.1109/TIP.2015.2417505
Anscombe, F.J.: The transformation of Poisson, binomial and negative-binomial data. Biometrika 35(3/4), 246–254 (1948)
Aubert, G., Aujol, J.F.: A variational approach to removing multiplicative noise. SIAM J. Appl. Math. 68(4), 925–946 (2008). https://doi.org/10.1137/060671814
Bauschke, H.H., Borwein, J.M.: Legendre functions and the method of random Bregman projections. J. Convex Anal. 4(1), 27–67 (1997)
Benning, M.: Singular regularization of inverse problems. Ph.D. thesis, University of Münster (2011)
Bertero, M., Boccacci, P., Desiderà, G., Vicidomini, G.: Image deblurring with Poisson data: from cells to galaxies. Inverse Probl. 25(12),(2009). https://doi.org/10.1088/0266-5611/25/12/123006
Bouman, C., Sauer, K.: A generalized Gaussian image model for edge-preserving map estimation. IEEE Trans. Image Process. 2(3), 296–310 (1993). https://doi.org/10.1109/83.236536
Bregman, L.: The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7(3), 200–217 (1967). https://doi.org/10.1016/0041-5553(67)90040-7
Buades, A., Coll, B., Morel, J.M.: Image denoising methods. A new nonlocal principle. SIAM Rev. 52(1), 113–147 (2010). https://doi.org/10.1137/090773908
Chambolle, A., Darbon, J.: On total variation minimization and surface evolution using parametric maximum flows. Int. J. Comput. Vis. 84(3), 288–307 (2009)
Combettes, P.L., Reyes, N.N.: Moreau’s decomposition in Banach spaces. Math. Program. 139(1–2, Ser. B), 103–114 (2013). https://doi.org/10.1007/s10107-013-0663-y
Darbon, J.: On convex finite-dimensional variational methods in imaging sciences and Hamilton–Jacobi equations. SIAM J. Imaging Sci. 8(4), 2268–2293 (2015). https://doi.org/10.1137/130944163
Darbon, J., Meng, T.: On decomposition models in imaging sciences and multi-time Hamilton–Jacobi partial differential equations. SIAM J. Imaging Sci. 13(2), 971–1014 (2020). https://doi.org/10.1137/19M1266332
Darbon, J., Osher, S.: Algorithms for overcoming the curse of dimensionality for certain Hamilton–Jacobi equations arising in control theory and elsewhere. Res. Math. Sci. 3, 26 (2016). https://doi.org/10.1186/s40687-016-0068-7. ((Paper No. 19))
Darbon, J., Sigelle, M.: Image restoration with discrete constrained total variation part I: fast and exact optimization. J. Math. Imaging Vis. 26(3), 261–276 (2006). https://doi.org/10.1007/s10851-006-8803-0
Dong, Y., Zeng, T.: A convex variational model for restoring blurred images with multiplicative noise. SIAM J. Imaging Sci. 6(3), 1598–1625 (2013). https://doi.org/10.1137/120870621
Durand, S., Fadili, J., Nikolova, M.: Multiplicative noise removal using L1 fidelity on frame coefficients. J. Math. Imaging Vis. 36(3), 201–226 (2010). https://doi.org/10.1007/s10851-009-0180-z
Ekeland, I., Temam, R.: Convex Analysis and Variational Problems. North-Holland Publishing Company, Amsterdam (1976)
Figueiredo, M.A.T., Bioucas-Dias, J.M.: Restoration of Poissonian images using alternating direction optimization. IEEE Trans. Image Process. 19(12), 3133–3145 (2010). https://doi.org/10.1109/TIP.2010.2053941
Giryes, R., Elad, M.: Sparsity-based Poisson denoising with dictionary learning. IEEE Trans. Image Process. 23(12), 5057–5069 (2014). https://doi.org/10.1109/TIP.2014.2362057
Hiriart-Urruty, J., Plazanet, P.: Moreau’s decomposition theorem revisited. Annales de l’Institut Henri Poincare (C) Non Linear Analysis 6, 325–338 (1989). https://doi.org/10.1016/S0294-1449(17)30028-8
Hiriart-Urruty, J.B., Lemarechal, C.: Convex Analysis and Minimization Algorithms I: Fundamentals, vol. 305. Springer, Berlin (1993). https://doi.org/10.1007/978-3-662-02796-7
Hiriart-Urruty, J.B., Lemarechal, C.: Convex Analysis and Minimization Algorithms II: Advanced Theory and Bundle Methods, vol. 306. Springer, Berlin (1993). https://doi.org/10.1007/978-3-662-06409-2
Hiriart-Urruty, J.B., Lemarechal, C.: Fundamentals of Convex Analysis. Springer, Berlin (2004)
Hochbaum, D.S.: An efficient algorithm for image segmentation, Markov random fields and related problems. J. ACM 48(2), 686–701 (2001)
Huang, Y., Ng, M., Wen, Y.W.: A new total variation method for multiplicative noise removal. SIAM J. Imaging Sci. 2, 20–40 (2009)
Jin, Z., Yang, X.: Analysis of a new variational model for multiplicative noise removal. J. Math. Anal. Appl. 362(2), 415–426 (2010). https://doi.org/10.1016/j.jmaa.2009.08.036
Jung, M., Resmerita, E., Vese, L.: Dual norm based iterative methods for image restoration. J. Math. Imaging Vis. 44, 128–249 (2012). https://doi.org/10.1007/s10851-011-0318-7
Kassam, S.A.: Signal Detection in Non-Gaussian Noise. Springer Texts in Electrical Engineering. Springer, New York (1988). https://doi.org/10.1007/978-1-4612-3834-8 . ((A Dowden & Culver Book))
Le, T., Chartrand, R., Asaki, T.J.: A variational approach to reconstructing images corrupted by Poisson noise. J. Math. Imaging Vis. 27(3), 257–263 (2007). https://doi.org/10.1007/s10851-007-0652-y
Meyer, Y.: Oscillating Patterns in Image Processing and Nonlinear Evolution Equations: The Fifteenth Dean Jacqueline B. Lewis Memorial Lectures. American Mathematical Society, Boston (2001)
Moreau, J.J.: Proximité et dualité dans un espace hilbertien. Bulletin de la Société Mathématique de France 93, 273–299 (1965). https://doi.org/10.24033/bsmf.1625
Oh, A.K., Harmany, Z.T., Willett, R.M.: Logarithmic total variation regularization for cross-validation in photon-limited imaging. In: 2013 IEEE International Conference on Image Processing, pp. 484–488 (2013). https://doi.org/10.1109/ICIP.2013.6738100
Oh, A.K., Harmany, Z.T., Willett, R.M.: To e or not to e in Poisson image reconstruction. In: 2014 IEEE International Conference on Image Processing (ICIP), pp. 2829–2833 (2014). https://doi.org/10.1109/ICIP.2014.7025572
Peyré, G., Bougleux, S., Cohen, L.D.: Non-local regularization of inverse problems. In: Computer Vision—ECCV 2008, 10th European Conference on Computer Vision, Marseille, France, October 12–18, 2008, Proceedings, Part III, Lecture Notes in Computer Science, vol. 5304, pp. 57–68. Springer (2008). https://doi.org/10.1007/978-3-540-88690-7_5
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)
Rudin, L., Lions, P., Osher, S.: Multiplicative denoising and deblurring: theory and algorithms. In: Geometric Level Set Methods in Imaging, Vision, and Graphics (2003). https://doi.org/10.1007/0-387-21810-6_6
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60(1–4), 259–268 (1992). https://doi.org/10.1016/0167-2789(92)90242-F
Shaobing Chen, Donoho, D.: Basis pursuit. In: Proceedings of 1994 28th Asilomar Conference on Signals, Systems and Computers, vol. 1, pp. 41–44 (1994). https://doi.org/10.1109/ACSSC.1994.471413
Shi, J., Osher, S.: A nonlinear inverse scale space method for a convex multiplicative noise model. SIAM J. Imaging Sci. 1(3), 294–321 (2008). https://doi.org/10.1137/070689954
Steidl, G., Teuber, T.: Removing multiplicative noise by Douglas–Rachford splitting methods. J. Math. Imaging Vis. 36(2), 168–184 (2010). https://doi.org/10.1007/s10851-009-0179-5
Tendero, Y., Osher, S.: On a mathematical theory of coded exposure. Res. Math. Sci. 3, 39 (2016). https://doi.org/10.1186/s40687-015-0051-8. ((Paper No. 4))
Vese, L., Le Guyader, C.: Variational Methods in Image Processing, 1st edn. Chapman and Hall, Boca Raton (2015)
Wen, Y., Chan, R., Zeng, T.: Primal-dual algorithms for total variation based image restoration under Poisson noise. Sci. China Math. 59, 141–160 (2016). https://doi.org/10.1007/s11425-015-5079-0
Acknowledgements
The authors gratefully acknowledge the support of IPAM (UCLA), where this collaboration started during the “High Dimensional Hamilton–Jacobi PDEs” program (2020). This work was funded by NSF DMS 1820821. The authors thank the reviewers for providing fruitful comments that improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research supported by NSF DMS 1820821.
A Mathematical Background
A Mathematical Background
In this section, several basic definitions and theorems in convex analysis are reviewed. All the results and notations can be found in [19, 23,24,25]. We use the angle bracket \(\langle \cdot , \cdot \rangle \) to denote the inner product operator in any Euclidean space \({\mathbb {R}}^n\).
We denote \(\Gamma _0({\mathbb {R}}^n)\) to be the set of proper, convex and lower semi-continuous functions from \({\mathbb {R}}^n\) to \({\mathbb {R}}\cup \{+\infty \}\). Recall that a function \(f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{\pm \infty \}\) is called proper if there exists a point x such that \(f(x)\in {\mathbb {R}}\). In this paper, we assume every function is proper if not mentioned specifically. The functions in \(\Gamma _0({\mathbb {R}}^n)\) have good continuity properties, which are stated below.
Proposition 7
[23, Lem.IV.3.1.1 and Chap.I.3.1–3.2] Let \(f\in \Gamma _0({\mathbb {R}}^n)\). If \(x\in \mathrm {ri\ }\mathrm {dom}~f\), then f is continuous at x in \(\mathrm {dom}~f\). If \(x\in \mathrm {dom}~f {\setminus } \mathrm {ri\ }\mathrm {dom}~f\), then for all \(y\in \mathrm {ri\ }\mathrm {dom}~f\),
A vector p is called a subgradient of f at x if it satisfies
The collection of all such subgradients is called the subdifferential of f at x, denoted as \(\partial f(x)\). It is straightforward to check that \(0\in \partial f(x)\) if and only if x is a minimizer of f. As a result, one can check whether x is a minimizer by computing the subdifferential.
Moreover, in most cases, the subdifferential operator commutes with summation. One set of assumption is given in the following proposition.
Proposition 8
[19, Proposition 5.6, Ch. I] Let \(f,g\in \Gamma _0({\mathbb {R}}^n)\). Assume there exists a point \(u\in \mathrm {dom}~f\cap \mathrm {dom}~g\) where f is continuous. Then, we have \(\partial (f+g)(x) = \partial f(x) + \partial g(x)\) for all \(x\in \mathrm {dom}~f \cap \mathrm {dom}~g\).
One important class of functions in \(\Gamma _0({\mathbb {R}}^n)\) is called indicator functions. For any convex set C, the indicator function \(I_C\) is defined by
One can compute the subdifferential of the indicator function and obtain
where \(N_C(x)\) denotes the normal cone of C at x. Note that \(N_C(x) = \{0\}\) when x is in the interior of the set C (see [23, p. 137] for details).
Next, we recall one important transform in convex analysis called Legendre–Fenchel transform. For all \(f\in \Gamma _0({\mathbb {R}}^n)\), the Legendre–Fenchel transform of f, denoted as \(f^*\), is defined by
The Legendre–Fenchel transform gives a duality relationship between f and \(f^*\). In other words, if \(f\in \Gamma _0({\mathbb {R}}^n)\) holds, then there hold \(f^*\in \Gamma _0({\mathbb {R}}^n)\) and \(f^{**} = f\). Similarly, along with this duality, some properties are dual to others, as stated in the following proposition. Recall that a function g is called 1-coercive if \(\lim _{\Vert x\Vert \rightarrow +\infty } \frac{g(x)}{\Vert x\Vert } = +\infty \).
Proposition 9
[25, Propositions E.1.3.8 and E.1.3.9] Let \(f\in \Gamma _0({\mathbb {R}}^n)\). Then, f is finite-valued if and only if \(f^*\) is 1-coercive.
In particular, the subdifferential set of \(f^*\) is characterized by the maximizers in (99), as stated in the following proposition.
Proposition 10
[25, Corollary E.1.4.4] Let \(f\in \Gamma _0({\mathbb {R}}^n)\) and \(p,x \in {\mathbb {R}}^n\). Then, \(p\in \partial f(x)\) holds if and only if \(x\in \partial f^*(p)\) holds, which is equivalent to \(f(x) + f^*(p) = \langle p, x\rangle \).
Except from the Legendre–Fenchel transform, there is another operator defined on convex functions, called inf-convolution. Given two functions \(f,g\in \Gamma _0({\mathbb {R}}^n)\), assume there exists an affine function l such that \(f(x)\ge l(x)\) and \(g(x)\ge l(x)\) for all \(x\in {\mathbb {R}}^n\). Then, the inf-convolution between f and g, denoted by \(f\square g\), is a convex function taking values in \({\mathbb {R}}\cup \{+\infty \}\) defined by
In the following proposition, the relation between Legendre–Fenchel transform and inf-convolution is stated.
Proposition 11
[25, Theorem E.2.3.2] Let \(f,g \in \Gamma _0({\mathbb {R}}^n)\). Assume the intersection of \(\mathrm {ri\ }\mathrm {dom}~f\) and \(\mathrm {ri\ }\mathrm {dom}~g\) is non-empty. Then, there hold \(f^*\square g^*\in \Gamma _0({\mathbb {R}}^n)\) and \(f^*\square g^* = (f+g)^*\). Moreover, the minimization problem
has at least one minimizer whenever x is in \(\mathrm {dom}~f^*\square g^*=\mathrm {dom}~f^* + \mathrm {dom}~g^*\).
Let f be a function in \(\Gamma _0({\mathbb {R}}^n)\) and \(x_0\) be an arbitrary point in \(\mathrm {dom}~f\). The asymptotic function of f, denoted by \(f'_\infty \), is defined by
for all \(d\in {\mathbb {R}}^n\). In fact, this definition does not depend on the point \(x_0\).
Proposition 12
[25, Example B.3.2.3] Let \(f\in \Gamma _0({\mathbb {R}}^n)\). Take \(x_0\in \mathrm {dom}~f\). Then, the function defined by
is in \(\Gamma _0({\mathbb {R}}^n\times {\mathbb {R}})\). As a result, we have
Proposition 13
[25, Proposition E.1.2.2] Let \(f\in \Gamma _0({\mathbb {R}}^n)\). Then, the support function of \(\mathrm {dom}~f\) is given by the asymptotic function of \(f^*\) as follows:
There is another important class of functions called Legendre functions, whose definition is given as follows. Note that here we use an equivalent definition to simplify our proofs.
Definition 1
[37, Section 26] Suppose f is a function in \(\Gamma _0({\mathbb {R}}^n)\). Then, f is Legendre (or a Legendre function or a convex function of Legendre type), if f satisfies
-
1.
\(\mathrm {int\ }\mathrm {dom}~f\) is non-empty.
-
2.
f is differentiable on \(\mathrm {int\ }\mathrm {dom}~f\).
-
3.
The subdifferential of f satisfies
$$\begin{aligned} \partial f(x) = {\left\{ \begin{array}{ll} \emptyset , &{} \text {if }x\in (\mathrm {dom}~f){\setminus } (\mathrm {int\ }\mathrm {dom}~f),\\ \{\nabla f(x)\}, &{} \text {if }x\in \mathrm {int\ }\mathrm {dom}~f. \end{array}\right. }\nonumber \\ \end{aligned}$$(106) -
4.
f is strictly convex on \(\mathrm {int\ }\mathrm {dom}~f\).
For a Legendre function f, we have the following property which is used in proofs of this paper. For more properties of Legendre functions, we refer readers to [37, Section 26] and [5].
Proposition 14
[37, Theorem 26.5] Let f be a function in \(\Gamma _0({\mathbb {R}}^n)\). Then, f is a Legendre function if and only if \(f^*\) is a Legendre function.
Now, we are going to define the primal–dual Bregman distance denoted by d and the (primal–primal) Bregman distance denoted by D. For properties of Bregman distances, we refer readers to [5] and [9], for instance. For \(f\in \Gamma _0({\mathbb {R}}^n)\), the primal–dual Bregman distance with respect to \(f\) between a vector x in the primal space \({\mathbb {R}}^n\) and a vector p in the dual space \({\mathbb {R}}^n\), denoted by \(d_f(x,p)\), is defined as follows:
When we have \(f\in \Gamma _0({\mathbb {R}}^n)\), since the equality \((f^*)^* = f\) holds, we have
Additionally, for two points \(x,u\in \mathrm {dom}~f\), let \(f\) be differentiable at u. The Bregman distance \(D_f\) between x and u with respect to the function \(f\) is defined as
These two definitions are related to each other by the following result.
Proposition 15
Let \(f\in \Gamma _0({\mathbb {R}}^n)\). Then, for all \(x,u\in \mathrm {dom}~f\) such that \(f\) is differentiable at u, we have
Proof
For all \(x,u\in \mathrm {dom}~f\), we have
where the second equality holds by Proposition 10. \(\square \)
We also have the following equality for \(D_f\).
Proposition 16
Let \(f\in \Gamma _0({\mathbb {R}}^n)\). Let \(t>0\) and \(\frac{x}{t}, \frac{u}{t}\in \mathrm {dom}~f^*\). Assume \(f^*\) is differentiable at \(\frac{u}{t}\). Then, we have
Proof
By definition of \(D_{f^*}\) in (109), it follows that
Define \(g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}\) by \(g(w):= tf^*(\frac{w}{t})\) for all \(w\in {\mathbb {R}}^n\), then there hold \(\nabla g(u) = \nabla f^*(\frac{u}{t})\) and \(g= (tf)^*\). And hence by (113) we obtain
which proves the statement. \(\square \)
Rights and permissions
About this article
Cite this article
Darbon, J., Meng, T. & Resmerita, E. On Hamilton–Jacobi PDEs and Image Denoising Models with Certain Nonadditive Noise. J Math Imaging Vis 64, 408–441 (2022). https://doi.org/10.1007/s10851-022-01073-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-022-01073-3