Abstract
We present an approach for variational regularization of inverse and imaging problems for recovering functions with values in a set of vectors. We introduce regularization functionals, which are derivative-free double integrals of such functions. These regularization functionals are motivated from double integrals, which approximate Sobolev semi-norms of intensity functions. These were introduced in Bourgain et al. (Another look at Sobolev spaces. In: Menaldi, Rofman, Sulem (eds) Optimal control and partial differential equations-innovations and applications: in honor of professor Alain Bensoussan’s 60th anniversary, IOS Press, Amsterdam, pp 439–455, 2001). For the proposed regularization functionals, we prove existence of minimizers as well as a stability and convergence result for functions with values in a set of vectors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Functions with values in a (nonlinear) subset of a vector space appear in several applications of imaging and in inverse problems, e.g.,
-
Interferometric Synthetic Aperture Radar (InSAR) is a technique used in remote sensing and geodesy to generate, for example, digital elevation maps of the earth’s surface. InSAR images represent phase differences of waves between two or more SAR images, cf. [44, 53]. Therefore, InSAR data are functions \(f:\Omega \rightarrow {\mathbb {S}}^1\subseteq {\mathbb {R}}^2\). The pointwise function values are on the \({\mathbb {S}}^1\), which is considered embedded into \({\mathbb {R}}^2\).
-
A color image can be represented as a function in HSV space (hue, saturation, value) (see, e.g., [48]). Color images are then described as functions \(f:\Omega \rightarrow K \subseteq {\mathbb {R}}^3\). Here \(\Omega \) is a plane in \({\mathbb {R}}^2\), the image domain, and K (representing the HSV space) is a cone in three-dimensional space \({\mathbb {R}}^3\).
-
Estimation of the foliage angle distribution has been considered, for instance, in [39, 51]. Therefore, the imaging function is from \(\Omega \subset {\mathbb {R}}^2\), a part of the Earth’s surface, into \(\mathbb {S}^2 \subseteq {\mathbb {R}}^3\), representing foliage angle orientation.
-
Estimation of functions with values in \(SO(3) \subseteq {\mathbb {R}}^{3 \times 3}\). Such problems appear in Cryo-Electron Microscopy (see, for instance, [38, 58, 61]).
We emphasize that we are analyzing vector-, matrix-, tensor- valued functions, where pointwise function evaluations belong to some given (sub)set, but are always elements of the underlying vector space. This should not be confused with set-valued functions, where every function evaluation can be a set.
Inverse problems and imaging tasks, such as the ones mentioned above, might be unstable, or even worse, the solution could be ambiguous. Therefore, numerical algorithms for imaging need to be regularizing to obtain approximations of the desired solution in a stable manner. Consider the operator equation

where we assume that only (noisy) measurement data \(v^\delta \) of \(v^0\) become available. In this paper the method of choice is variational regularization which consists in calculating a minimizer of the variational regularization functional

Here
-
w is an element of the set of admissible functions.
-
 is an operator modeling the image formation process (except the noise).
is an operator modeling the image formation process (except the noise). -
\(\mathcal {D}\) is called the data or fidelity term, which is used to compare a pair of data in the image domain, that is to quantify the difference of the two data sets.
-
\(\mathcal {R}\) is called regularization functional, which is used to impose certain properties onto a minimizer of the regularization functional \(\mathcal {F}\).
-
\(\alpha > 0\) is called regularization parameter and provides a trade off between stability and approximation properties of the minimizer of the regularization functional \(\mathcal {F}\).
-
\(v^\delta \) denotes measurement data, which we consider noisy.
-
\(v^0\) denotes the exact data, which we assume to be not necessarily available.
The main objective of this paper is to introduce a general class of regularization functionals for functions with values in a set of vectors. In order to motivate our proposed class of regularization functionals, we review a class of regularization functionals appropriate for analyzing intensity data.
1.1 Variational Regularization for Reconstruction of Intensity Data
Opposite to what we consider in the present paper, most commonly, imaging data v and admissible functions w, respectively, are considered to be representable as intensity functions. That is, they are functions from some subset \(\Omega \) of an Euclidean space with real values.
In such a situation, the most widely used regularization functionals use regularization terms consisting of powers of Sobolev (see [12, 15, 16]) or total variation semi-norms [54]. It is common to speak about Tikhonov regularization (see, for instance, [59]) when the data term and the regularization functional are squared Hilbert space norms, respectively. For the Rudin, Osher, Fatemi (ROF) regularization [54], also known as total variation regularization, the data term is the squared \(L^2\)-norm and \(\mathcal {R}(w) = |w|_{TV}\) is the total variation semi-norm. Nonlocal regularization operators based on the generalized nonlocal gradient are used in [35].
Other widely used regularization functionals are sparsity promoting [22, 41], Besov space norms [42, 46] and anisotropic regularization norms [47, 56]. Aside from various regularization terms, there also have been proposed different fidelity terms other than quadratic norm fidelities, like the p-th powers of \(\ell ^p\) and \(L^p\)-norms of the differences of F(w) and v , [55, 57], maximum entropy [26, 28] and Kullback–Leibler divergence [52] (see [50] for some reference work).
Our work utilizes results from the seminal paper of Bourgain, Brézis and Mironescu [14], which provides an equivalent derivative-free characterization of Sobolev spaces and the space  , the space of functions of bounded total variation, which consequently, in this context, was analyzed in Dávila and Ponce [23, 49], respectively. It is shown in [14, Theorems 2 and 3’] and [23, Theorem 1] that when \((\rho _\varepsilon )_{\varepsilon > 0}\) is a suitable sequence of nonnegative, radially symmetric, radially decreasing mollifiers, then
, the space of functions of bounded total variation, which consequently, in this context, was analyzed in Dávila and Ponce [23, 49], respectively. It is shown in [14, Theorems 2 and 3’] and [23, Theorem 1] that when \((\rho _\varepsilon )_{\varepsilon > 0}\) is a suitable sequence of nonnegative, radially symmetric, radially decreasing mollifiers, then

Hence, \(\tilde{{\mathcal {R}}}_\varepsilon \) approximates powers of Sobolev semi-norms and the total variation semi-norm, respectively. Variational imaging, consisting in minimization of \(\mathcal {F}\) from Eq. 1.2 with \({\mathcal {R}}\) replaced by \(\tilde{{\mathcal {R}}}_\varepsilon \), has been considered in [3, 11].
1.2 Regularization of Functions with Values in a Set of Vectors
In this paper we generalize the derivative-free characterization of Sobolev spaces and functions of bounded variation to functions \(u:\Omega \rightarrow K\), where K is some set of vectors, and use these functionals for variational regularization. The applications we have in mind contain that K is a closed subset of \({\mathbb {R}}^M\) (for instance, HSV data) with nonzero measure, or that K is a submanifold (for instance, InSAR data).
The reconstruction of manifold-valued data with variational regularization methods has already been subject to intensive research (see, for instance, [4, 17,18,19, 40, 62]). The variational approaches mentioned above use regularization and fidelity functionals based on Sobolev and TV semi-norms: a total variation regularizer for cyclic data on \({\mathbb {S}}^1\) was introduced in [18, 19], see also [7, 9, 10]. In [4, 6] combined first- and second-order differences and derivatives were used for regularization to restore manifold-valued data. The later mentioned papers, however, are formulated in a finite-dimensional setting, opposed to ours, which is considered in an infinite-dimensional setting. Algorithms for total variation minimization problems, including half-quadratic minimization and nonlocal patch-based methods, are given, for example, in [4, 5, 8] as well as in [37, 43]. On the theoretical side the total variation of functions with values in a manifold was investigated by Giaquinta and Mucci using the theory of Cartesian currents in [33, 34], and earlier [32] if the manifold is \({\mathbb {S}}^1\).
1.3 Content and Particular Achievements of the Paper
The contribution of this paper is to introduce and analytically analyze double integral regularization functionals for reconstructing functions with values in a set of vectors, generalizing functionals of the form Eq. 1.3. Moreover, we develop and analyze fidelity terms for comparing manifold-valued data. Summing these two terms provides a new class of regularization functionals of the form Eq. 1.2 for reconstructing manifold-valued data.
When analyzing our functionals, we encounter several differences to existing regularization theory (compare Sect. 2):
-
(i)
The admissible functions, where we minimize the regularization functional on, do form only a set but not a linear space. As a consequence, well-posedness of the variational method (that is, existence of a minimizer of the energy functional) cannot directly be proven by applying standard direct methods in the Calculus of Variations [20, 21].
-
(ii)
The regularization functionals are defined via metrics and not norms, see Sect. 3.
-
(iii)
In general, the fidelity terms are non-convex. Stability and convergence results are proven in Sect. 4.
The model is validated in Sect. 6 where we present numerical results for denoising and inpainting of data of InSAR type.
2 Setting
In the following we introduce the basic notation and the set of admissible functions which we are regularizing on.
Assumption 2.1
All along this paper, we assume that
-
\(p_1, p_2 \in [1, +\infty )\), \(s \in (0,1]\),
-
\(\Omega _1, \Omega _2 \subseteq {\mathbb {R}}^N\) are nonempty, bounded and connected open sets with Lipschitz boundary, respectively,
-
\(k \in [0,N]\),
-
\(K_1 \subseteq {\mathbb {R}}^{M_1}, K_2 \subseteq {\mathbb {R}}^{M_2}\) are nonempty and closed subsets of \({\mathbb {R}}^{M_1}\) and \({\mathbb {R}}^{M_2}\), respectively.
Moreover,
-
 and \(\Vert \cdot \Vert _{{\mathbb {R}}^{M_i}}, \ i=1,2,\) are the Euclidean norms on \({\mathbb {R}}^N\) and \({\mathbb {R}}^{M_i}\), respectively.
and \(\Vert \cdot \Vert _{{\mathbb {R}}^{M_i}}, \ i=1,2,\) are the Euclidean norms on \({\mathbb {R}}^N\) and \({\mathbb {R}}^{M_i}\), respectively. -
 denotes the Euclidean distance on \({\mathbb {R}}^{M_i}\) for \(i=1,2\) and
denotes the Euclidean distance on \({\mathbb {R}}^{M_i}\) for \(i=1,2\) and -
 denote arbitrary metrics on \(K_i\), which fulfill for \(i=1\) and \(i=2\)
denote arbitrary metrics on \(K_i\), which fulfill for \(i=1\) and \(i=2\)-
 ,
, -
\(\,{\mathrm {d}}_i\) is continuous with respect to
 , meaning that for a sequence
, meaning that for a sequence  in \(K_i \subseteq {\mathbb {R}}^{M_i}\) converging to some \(a \in K_i\) we also have
in \(K_i \subseteq {\mathbb {R}}^{M_i}\) converging to some \(a \in K_i\) we also have  .
.
In particular, this assumption is valid if the metric \(d_i\) is equivalent to
 . When the set \(K_i, \ i=1,2\), is a suitable complete submanifold of \({\mathbb {R}}^{M_i}\), it seems natural to choose \(d_i\) as the geodesic distance on the respective submanifolds.
. When the set \(K_i, \ i=1,2\), is a suitable complete submanifold of \({\mathbb {R}}^{M_i}\), it seems natural to choose \(d_i\) as the geodesic distance on the respective submanifolds. -
-
\((\rho _{\varepsilon })_{\varepsilon > 0}\) is a Dirac family of nonnegative, radially symmetric mollifiers, i.e., for every \(\varepsilon > 0\) we have
-
(i)
\(\rho _\varepsilon \in \mathcal {C}^{\infty }_{c}({\mathbb {R}}^N, {\mathbb {R}})\) is radially symmetric,
-
(ii)
\(\rho _\varepsilon \ge 0\),
-
(iii)
\(\int \limits _{{\mathbb {R}}^N} \rho _\varepsilon (x) \,{\mathrm {d}}x= 1\), and
-
(iv)
for all \(\delta > 0\),
 .
.
We demand further that, for every \(\varepsilon > 0\),
-
(v)
there exists a \(\tau > 0\) and \(\eta _{\tau }> 0\) such that
 .
.
This condition holds, e.g., if \(\rho _{\varepsilon }\) is a radially decreasing continuous function with \(\rho _{\varepsilon }(0) > 0\).
-
(i)
-
When we write p, \(\Omega \), K, M, then we mean \(p_i\), \(\Omega _i\), \(K_i\), \(M_i\), for either \(i=1,2\). In the following we will often omit the subscript indices whenever possible.
Example 2.2
Let \(\hat{\rho } \in C_c^\infty ({\mathbb {R}},{\mathbb {R}}_+)\) be symmetric at 0, monotonically decreasing on \([0, \infty )\) and satisfy
Defining mappings \(\rho _\varepsilon : {\mathbb {R}}^N \rightarrow {\mathbb {R}}\) by

constitutes then a family \((\rho _\varepsilon )_{\varepsilon > 0}\) which fulfills the above properties (i)–(v). Note here that
-
by substitution \(x = t \theta \) with \(t > 0, \theta \in \mathbb {S}^{N-1}\) and \(\hat{t}=\frac{t}{\varepsilon }\),
 (2.1)
(2.1)Here, \(d\theta \) refers to the canonical spherical measure.
-
Again by the same substitutions, taking into account that \(\hat{\rho }\) has compact support, it follows for \(\varepsilon > 0\) sufficiently small that
 (2.2)
(2.2)
In the following we write down the basic spaces and sets, which will be used in the course of the paper.
Definition 2.3
-
The Lebesgue–Bochner space of \({\mathbb {R}}^M\)-valued functions on \(\Omega \) consists of the set

which is associated with the norm
 , given by
, given by 
-
Let \(0< s < 1\). Then the fractional Sobolev space of order s can be defined (cf. [1]) as the set

equipped with the norm
 (2.3)
(2.3)where
 is the semi-norm for
is the semi-norm for  , given by
, given by  (2.4)
(2.4) -
For \(s = 1\) the Sobolev space \(W^{1,p}(\Omega , {\mathbb {R}}^M)\) consists of all weakly differentiable functions in \(L^1(\Omega ,{\mathbb {R}}^M)\) for which

where \(\nabla w\) is the weak Jacobian of w.
-
Moreover, we recall one possible definition of the space
 from [2], which consists of all Lebesgue–Borel measurable functions \(w:\Omega \rightarrow {\mathbb {R}}^M\) for which
from [2], which consists of all Lebesgue–Borel measurable functions \(w:\Omega \rightarrow {\mathbb {R}}^M\) for which 
where

where \(\left\| \varphi (x)\right\| _F\) is the Frobenius-norm of the matrix \(\varphi (x)\) and \(\text {Div}\varphi = (\text {div} \varphi _1, \dots , \text {div} \varphi _M)^\text {T}\) denotes the row–wise formed divergence of \(\varphi \).
Lemma 2.4
Let \(0 < s \le 1\) and \(p \in [1,\infty )\), then  and the embedding is compact. Moreover, the embedding
and the embedding is compact. Moreover, the embedding  is compact for all
is compact for all
Proof
The first result can be found in [24] for \(0< s < 1\) and in [29] for \(s = 1\). The second assertion is stated in [2]. \(\square \)
Remark 2.5
Let Assumption 2.1 hold. We recall some basic properties of weak convergence in  , \(W^{1,p}(\Omega , {\mathbb {R}}^M)\) and weak* convergence in
, \(W^{1,p}(\Omega , {\mathbb {R}}^M)\) and weak* convergence in  (see, for instance, [1, 2]):
(see, for instance, [1, 2]):
-
Let \(p > 1\), \(s\in (0,1]\) and assume that \((w_n)_{n \in {\mathbb {N}}}\) is bounded in
 . Then there exists a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) which converges weakly in
. Then there exists a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) which converges weakly in  .
. -
Assume that \((w_n)_{n \in {\mathbb {N}}}\) is bounded in
 . Then there exists a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) which converges weakly* in
. Then there exists a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) which converges weakly* in  .
.
Before introducing the regularization functional, which we investigate theoretically and numerically, we give the definition of some sets of (equivalence classes of) admissible functions.
Definition 2.6
For \(0 < s \le 1\), \(p \ge 1\) and a nonempty closed subset \(K \subseteq {\mathbb {R}}^M\), we define

and equip each of these (in general nonlinear) sets with some subspace topology:
-
 is associated with the strong
is associated with the strong  -topology,
-topology, -
 is associated with the weak
is associated with the weak  -topology, and
-topology, and -
 is associated with the weak*
is associated with the weak*  -topology.
-topology.
Moreover, we define

Consistently, \(W(\Omega ,K)\)
-
is associated with the weak
 -topology in the case \(p \in (1, \infty )\) and \(s \in (0,1]\) and
-topology in the case \(p \in (1, \infty )\) and \(s \in (0,1]\) and -
with the weak*
 -topology when \(p=1\) and \(s=1\).
-topology when \(p=1\) and \(s=1\).
When we speak about

and mean weak convergence on \(W^{s,p}(\Omega ,K)\) and weak* convergence on  , respectively.
, respectively.
Remark 2.7
-
In general
 and
and  are sets which do not form a linear space.
are sets which do not form a linear space. -
If \(K = {\mathbb {S}}^1\), then
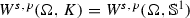 as occurred in [13].
as occurred in [13]. -
For an embedded manifold K, the dimension of the manifold is not necessarily identical with the space dimension of \({\mathbb {R}}^M\). For instance, if \(K = {\mathbb {S}}^1\subseteq {\mathbb {R}}^2\), then the dimension of \({\mathbb {S}}^1\) is 1 and \(M=2\).
The following lemma shows that \(W(\Omega ,K)\) is a sequentially closed subset of  .
.
Lemma 2.8
(Sequential closedness of \({{W}}({{\Omega }},{{K}})\) and \({{L}}^{{{p}}}({{\Omega }}, {{K}})\))
-
(i)
Let
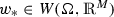 and \((w_n)_{n\in {\mathbb {N}}}\) be a sequence in
and \((w_n)_{n\in {\mathbb {N}}}\) be a sequence in  with \(w_n \overset{W(\Omega , {\mathbb {R}}^M)}{\longrightarrow } w_*\) as \(n \rightarrow \infty \). Then
with \(w_n \overset{W(\Omega , {\mathbb {R}}^M)}{\longrightarrow } w_*\) as \(n \rightarrow \infty \). Then  and
and  in
in  .
. -
(ii)
Let
 and \((v_n)_{n \in {\mathbb {N}}}\) be a sequence in
and \((v_n)_{n \in {\mathbb {N}}}\) be a sequence in  with \(v_n \rightarrow v_*\) in
with \(v_n \rightarrow v_*\) in  as \(n \rightarrow \infty \). Then
as \(n \rightarrow \infty \). Then  and there is some subsequence \((v_{n_k})_{k \in {\mathbb {N}}}\) which converges to \(v_*\) pointwise almost everywhere, i.e., \(v_{n_k}(x) \rightarrow v_*(x)\) as \(k \rightarrow \infty \) for almost every \(x \in \Omega \).
and there is some subsequence \((v_{n_k})_{k \in {\mathbb {N}}}\) which converges to \(v_*\) pointwise almost everywhere, i.e., \(v_{n_k}(x) \rightarrow v_*(x)\) as \(k \rightarrow \infty \) for almost every \(x \in \Omega \).
Proof
For the proof of the second part, cf. [27], Chapter VI, Corollary 2.7, take into account the closedness of \(K \subseteq {\mathbb {R}}^M\). The proof of the first part follows from standard convergence arguments in  ,
,  and
and  , respectively, using the embeddings from Lemma 2.4, an argument on subsequences and part two. \(\square \)
, respectively, using the embeddings from Lemma 2.4, an argument on subsequences and part two. \(\square \)
Remark 2.9
Lemma 2.4 along with Lemma 2.8 imply that  is compactly embedded in
is compactly embedded in  , where these sets are equipped with the bornology inherited from
, where these sets are equipped with the bornology inherited from  and the topology inherited from
and the topology inherited from  , respectively.
, respectively.
In the following we postulate the assumptions on the operator  which will be used throughout the paper:
which will be used throughout the paper:
Assumption 2.10
Let  be as in Eq. 2.5 and assume that
be as in Eq. 2.5 and assume that  is an operator from
is an operator from  to
to  .
.
We continue with the definition of our regularization functionals:
Definition 2.11
Let Assumptions 2.1 and 2.10 hold. Moreover, let \(\varepsilon > 0\) be fixed and let \(\rho :=\rho _\varepsilon \) be a mollifier.
The regularization functional  is defined as follows
is defined as follows

where
-
(i)
 ,
, -
(ii)
\(s \in (0,1]\),
-
(iii)
\(\alpha \in (0, +\infty )\) is the regularization parameter,
-
(iv)
\(l \in \left\{ 0, 1\right\} \) is an indicator and
-
(v)
\({\left\{ \begin{array}{ll} k \le N &{}\text{ if } W (\Omega _1, K_1) = W^{s,p_1}(\Omega _1, K_1), \ 0{<}s{<}1, \\ k=0 &{} \text{ if } W (\Omega _1, K_1) = W^{1,p_1}(\Omega _1, K_1)\text { or if }\\ &{}\quad W (\Omega _1, K_1) = BV(\Omega _1, K_1), \text { respectively.} \end{array}\right. }\)
Setting

and

Equation 2.6 can be expressed in compact form

For convenience we will often skip some of the super- or subscript and use compact notations like, e.g.,

Remark 2.12
-
(i)
\(l = \left\{ 0,1\right\} \) is an indicator which allows to consider approximations of Sobolev semi-norms and double integral representations of the type of Bourgain et al. [14] in a uniform manner.
-
when \(k=0\), \(s=1\), \(l=1\) and when \(d_1\) is the Euclidean distance, we get the double integrals of the Bourgain et al.-form [14]. Compare with Eq. 1.3.
-
When \(d_1\) is the Euclidean distance, \(k=N\) and \(l=0\), we get Sobolev semi-norms.
We expect a relation between the two classes of functionals for \(l=0\) and \(l=1\) as stated in Sect. 5.2.
-
-
(ii)
When \(d_1\) is the Euclidean distance then the second term in Eq. 2.6 is similar to the ones used in [3, 11, 14, 23, 49].
In the following we state basic properties of  and the functional
and the functional  .
.
Proposition 2.13
Let Assumption 2.1 hold.
-
(i)
Then the mapping

 satisfies the metric axioms.
satisfies the metric axioms. -
(ii)
Let, in addition, Assumption 2.10 hold, assume that
 and that both metrics \(d_i\), \(i=1,2\), are equivalent to
and that both metrics \(d_i\), \(i=1,2\), are equivalent to  , respectively. Then the functional
, respectively. Then the functional  does not attain the value \(+\infty \) on its domain
does not attain the value \(+\infty \) on its domain 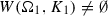 .
.
Proof
-
(i)
The axioms of non-negativity, identity of indiscernibles and symmetry are fulfilled by
 since
since  is a metric. To prove the triangle inequality, let \(\phi ,\xi ,\nu \in L^{p_2}(\Omega _2, K_2)\). In the main case
is a metric. To prove the triangle inequality, let \(\phi ,\xi ,\nu \in L^{p_2}(\Omega _2, K_2)\). In the main case  Hölder’s inequality yields
Hölder’s inequality yields 
meaning

If
 , the triangle inequality is trivially fulfilled.
, the triangle inequality is trivially fulfilled.In the remaining case
 applying the estimate \((a+b)^p \le 2^{p-1} (a^p + b^p)\), see, e.g., [55, Lemma 3.20], to
applying the estimate \((a+b)^p \le 2^{p-1} (a^p + b^p)\), see, e.g., [55, Lemma 3.20], to 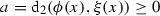 and
and  yields
yields 
implying the desired result.
-
(ii)
We emphasize that
 because every constant function \(w(\cdot ) = a \in K_1\) belongs to
because every constant function \(w(\cdot ) = a \in K_1\) belongs to  for \(p_1 \in (1, \infty )\) and \(s \in (0,1]\) as well as to
for \(p_1 \in (1, \infty )\) and \(s \in (0,1]\) as well as to  for \(p_1 = 1\) and \(s = 1\). Assume now that the metrics \(d_i\) are equivalent to
for \(p_1 = 1\) and \(s = 1\). Assume now that the metrics \(d_i\) are equivalent to 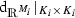 for \(i=1\) and \(i=2\), respectively, so that we have an upper bound
for \(i=1\) and \(i=2\), respectively, so that we have an upper bound  . We need to prove that
. We need to prove that 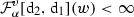 for every
for every  . Due to
. Due to  for all
for all  it is sufficient to show
it is sufficient to show  for all
for all  .
.
3 Existence
In order to prove existence of a minimizer of the functional  , we apply the direct method in the Calculus of Variations (see, e.g., [20, 21]). To this end we verify continuity properties of
, we apply the direct method in the Calculus of Variations (see, e.g., [20, 21]). To this end we verify continuity properties of  and
and  , resp.
, resp.  and apply them along with the sequential closedness of
and apply them along with the sequential closedness of  , already proven in Lemma 2.8.
, already proven in Lemma 2.8.
In this context we point out some setting assumptions and their consequences on  , resp.
, resp.  and \({\mathcal {R}}\) in the following remark. For simplicity we assume \(p :=p_1 = p_2 \in (1, \infty )\), \(\Omega :=\Omega _1 = \Omega _2\) and
and \({\mathcal {R}}\) in the following remark. For simplicity we assume \(p :=p_1 = p_2 \in (1, \infty )\), \(\Omega :=\Omega _1 = \Omega _2\) and  .
.
Remark 3.1
-
The continuity of
 with respect to
with respect to  guarantees lower semicontinuity of
guarantees lower semicontinuity of  and
and  .
. -
The inequality
 carries over to the inequalities
carries over to the inequalities  for all
for all  , and
, and  for all
for all  , allowing to transfer properties like coercivity from
, allowing to transfer properties like coercivity from  to
to  . Moreover, the extended real-valued metric space
. Moreover, the extended real-valued metric space  stays related to the linear space
stays related to the linear space  in terms of the topology and bornology induced by
in terms of the topology and bornology induced by  , resp. those inherited by
, resp. those inherited by  .
. -
The closedness of \(K \subseteq {\mathbb {R}}^M\) is crucial in showing that
 is a sequentially closed subset of the linear space
is a sequentially closed subset of the linear space  . This closedness property acts as a kind of replacement for the, a priori not available, notion of completeness with respect to the “space”
. This closedness property acts as a kind of replacement for the, a priori not available, notion of completeness with respect to the “space”  .
.
For \(l=0\), \(k=N\) note in the latter item that equipping  with
with  and
and  does not even lead to an (extended real-valued) metric space, in contrast to the classical case
does not even lead to an (extended real-valued) metric space, in contrast to the classical case  .
.
We will use the following assumption:
Assumption 3.2
Let Assumption 2.1 hold,  and let
and let  and the associated topology be as defined in Eq. 2.5.
and the associated topology be as defined in Eq. 2.5.
In addition we assume:
-
 is well defined and sequentially continuous with respect to the specified topology on
is well defined and sequentially continuous with respect to the specified topology on  and
and -
For every \(t > 0\) and \(\alpha > 0\), the level sets
 (3.1)
(3.1)are sequentially pre-compact subsets of \(W(\Omega _1, {\mathbb {R}}^{M_1})\).
-
There exists a \(\bar{t} > 0\) such that
 is nonempty.
is nonempty. -
Only those
 are considered which additionally fulfill
are considered which additionally fulfill  .
.
Remark 3.3
The third condition is sufficient to guarantee  . In contrast, the condition
. In contrast, the condition  , cf. Definition 2.11, might not be sufficient if \(d_2\) is not equivalent to
, cf. Definition 2.11, might not be sufficient if \(d_2\) is not equivalent to  .
.
Lemma 3.4
Let Assumption 3.2 hold. Then the mappings  ,
,  and
and  have the following continuity properties:
have the following continuity properties:
-
(i)
The mapping
 is sequentially lower semi-continuous, i.e., whenever sequences
is sequentially lower semi-continuous, i.e., whenever sequences  ,
,  in
in 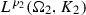 converge to
converge to  and
and  , respectively, we have
, respectively, we have  .
. -
(ii)
The functional
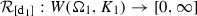 is sequentially lower semi-continuous, i.e., whenever a sequence \((w_n)_{n \in {\mathbb {N}}}\) in
is sequentially lower semi-continuous, i.e., whenever a sequence \((w_n)_{n \in {\mathbb {N}}}\) in  converges to some
converges to some  we have
we have 
-
(iii)
The functional
 is sequentially lower semi-continuous.
is sequentially lower semi-continuous.
Proof
-
(i)
It is sufficient to show that for every pair of sequences
 ,
,  in
in  which converge to previously fixed elements
which converge to previously fixed elements  and
and  , respectively, we can extract subsequences \((\phi _{n_j})_{j \in {\mathbb {N}}}\) and \((\nu _{n_j})_{j \in {\mathbb {N}}}\), respectively, with
, respectively, we can extract subsequences \((\phi _{n_j})_{j \in {\mathbb {N}}}\) and \((\nu _{n_j})_{j \in {\mathbb {N}}}\), respectively, with 
To this end let \((\phi _n)_{n \in {\mathbb {N}}},(\nu _n)_{n \in {\mathbb {N}}}\) be some sequences in
 with
with  and
and  in
in  . Lemma 2.8 ensures that there exist subsequences \((\phi _{n_j})_{j \in {\mathbb {N}}}, (\nu _{n_j})_{j \in {\mathbb {N}}}\) converging to \(\phi _*\) and \(\nu _*\) pointwise almost everywhere, which in turn implies \(\big (\phi _{n_j}(\cdot ), \nu _{n_j}(\cdot ) \big ) \rightarrow \big ( \phi _*(\cdot ), \nu _*(\cdot ) \big )\) pointwise almost everywhere. Therefrom, together with the continuity of
. Lemma 2.8 ensures that there exist subsequences \((\phi _{n_j})_{j \in {\mathbb {N}}}, (\nu _{n_j})_{j \in {\mathbb {N}}}\) converging to \(\phi _*\) and \(\nu _*\) pointwise almost everywhere, which in turn implies \(\big (\phi _{n_j}(\cdot ), \nu _{n_j}(\cdot ) \big ) \rightarrow \big ( \phi _*(\cdot ), \nu _*(\cdot ) \big )\) pointwise almost everywhere. Therefrom, together with the continuity of  with respect to
with respect to  , cf. Sect. 2, we obtain by using the quadrangle inequality that
, cf. Sect. 2, we obtain by using the quadrangle inequality that 
and hence

for almost every \(x \in \Omega _2\). Applying Fatou’s lemma, we obtain

-
(ii)
Let \((w_n)_{n \in {\mathbb {N}}}\) be a sequence in
 with
with 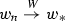 as
as  . By Lemma 2.8 there is a subsequence \((w_{n_j})_{j \in {\mathbb {N}}}\) which converges to \(w_*\) both in
. By Lemma 2.8 there is a subsequence \((w_{n_j})_{j \in {\mathbb {N}}}\) which converges to \(w_*\) both in  and pointwise almost everywhere. This further implies that
and pointwise almost everywhere. This further implies that 
for almost every
$$\begin{aligned} (x,y) \in \Omega _1 \times \Omega _1 \supseteq \{(x,y) \in \Omega _1 \times \Omega _1 : x \ne y \} =:A.\nonumber \\ \end{aligned}$$(3.2)Defining

for all \(j \in {\mathbb {N}}\) and

we thus have
 for almost every \((x,y) \in \Omega _1 \times \Omega _1\). Applying Fatou’s lemma to the functions \(f_j\) yields the assertion, due to the same reduction as in the proof of the first part.
for almost every \((x,y) \in \Omega _1 \times \Omega _1\). Applying Fatou’s lemma to the functions \(f_j\) yields the assertion, due to the same reduction as in the proof of the first part. -
(iii)
It is sufficient to prove that the components
 and
and  of
of 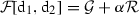 are sequentially lower semi-continuous. To prove that \(\mathcal {G}\) is sequentially lower semi-continuous in every \(w_* \in W(\Omega _1, K_1)\), let \((w_n)_{n \in {\mathbb {N}}}\) be a sequence in \(W(\Omega _1, K_1)\) with
are sequentially lower semi-continuous. To prove that \(\mathcal {G}\) is sequentially lower semi-continuous in every \(w_* \in W(\Omega _1, K_1)\), let \((w_n)_{n \in {\mathbb {N}}}\) be a sequence in \(W(\Omega _1, K_1)\) with  as
as  . Assumption 3.2, ensuring the sequential continuity of
. Assumption 3.2, ensuring the sequential continuity of  , implies hence
, implies hence  in
in  as
as  . By item (i) we thus obtain
. By item (i) we thus obtain  .
.\({\mathcal {R}}\) is sequentially lower semi-continuous by item (ii).
\(\square \)
3.1 Existence of Minimizers
The proof of the existence of a minimizer of  is along the lines of the proof in [55], taking into account Remark 3.1. We will need the following useful lemma, cf. [55], which links
is along the lines of the proof in [55], taking into account Remark 3.1. We will need the following useful lemma, cf. [55], which links  and
and  for
for  .
.
Lemma 3.5
It holds

for every \(w \in W(\Omega _1, K_1)\) and \(v_\star , v_\diamond \in L^{p_2}(\Omega _2, K_2)\).
Proof
Using the fact that for \(p \ge 1\) we have that \(|a+b|^p \le 2^{p-1}(|a|^p + |b|^p), \ a,b \in {\mathbb {R}}\cup \{\infty \}\) and that  fulfills the triangle inequality, we obtain
fulfills the triangle inequality, we obtain

\(\square \)
Theorem 3.6
Let Assumption 3.2 hold. Then the functional  attains a minimizer.
attains a minimizer.
Proof
We prove the existence of a minimizer via the direct method. We shortly write  for
for  . Let \((w_n)_{n \in {\mathbb {N}}}\) be a sequence in \(W(\Omega _1, K_1)\) with
. Let \((w_n)_{n \in {\mathbb {N}}}\) be a sequence in \(W(\Omega _1, K_1)\) with

The latter infimum is not \(+\infty \), because  would imply also
would imply also  due to Lemma 3.5, violating Assumption 3.2. In particular, there is some \(c \in {\mathbb {R}}\) such that
due to Lemma 3.5, violating Assumption 3.2. In particular, there is some \(c \in {\mathbb {R}}\) such that  for every \(n \in {\mathbb {N}}\). Applying Lemma 3.5 yields
for every \(n \in {\mathbb {N}}\). Applying Lemma 3.5 yields  due to Assumption 3.2. Since the level set
due to Assumption 3.2. Since the level set  is sequentially pre-compact with respect to the topology given to \(W(\Omega _1, {\mathbb {R}}^{M_1})\) we get the existence of a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) which converges to some \(w_* \in W(\Omega _1, {\mathbb {R}}^{M_1})\), where actually \(w_* \in W(\Omega _1, K_1)\) due to Lemma 2.8. Because
is sequentially pre-compact with respect to the topology given to \(W(\Omega _1, {\mathbb {R}}^{M_1})\) we get the existence of a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) which converges to some \(w_* \in W(\Omega _1, {\mathbb {R}}^{M_1})\), where actually \(w_* \in W(\Omega _1, K_1)\) due to Lemma 2.8. Because  is sequentially lower semi-continuous, see Lemma 3.4, we have
is sequentially lower semi-continuous, see Lemma 3.4, we have  . Combining this with Eq. 3.3 we obtain
. Combining this with Eq. 3.3 we obtain

In particular,  , meaning that \(w_*\) is a minimizer of
, meaning that \(w_*\) is a minimizer of  . \(\square \)
. \(\square \)
In the following we investigate two examples, which are relevant for the numerical examples in Sect. 6.
Example 3.7
We consider that \(W(\Omega _1,K_1) = W^{s, p_1}(\Omega _1, K_1)\) with \(p_1>1, \ 0< s < 1\) and fix \(k = N\).
If the operator  is norm coercive in the sense that the implication
is norm coercive in the sense that the implication

holds true for every sequence \((w_n)_{n \in {\mathbb {N}}}\) in \(W^{s,p_1}(\Omega _1, K_1)\subseteq W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\), then the functional  :
:

is coercive. This can be seen as follows:
The inequality between  and
and  resp.
resp.  and
and  , see Assumption 2.1, carries over to
, see Assumption 2.1, carries over to  and
and  , i.e.,
, i.e.,

for all \(w \in W^{s,p_1}(\Omega _1, K_1)\).
Thus, it is sufficient to show that  is coercive: To prove this, we write shortly
is coercive: To prove this, we write shortly  instead of
instead of  and consider sequences \((w_n)_{n \in {\mathbb {N}}}\) in \(W^{s,p_1}(\Omega _1, K_1)\) with
and consider sequences \((w_n)_{n \in {\mathbb {N}}}\) in \(W^{s,p_1}(\Omega _1, K_1)\) with  as
as  . We show that
. We show that  , as
, as  . Since
. Since
the two main cases to be considered are  and
and  .
.
Case 1 .
.
The inverse triangle inequality and the norm coercivity of  , Eq. 3.4, give
, Eq. 3.4, give 
 . Therefore, also
. Therefore, also

Case 2 .
.
If \(l=0\), then  is exactly the \(W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\)-semi-norm \(|w|_{W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})}\) and we trivially get the desired result.
is exactly the \(W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\)-semi-norm \(|w|_{W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})}\) and we trivially get the desired result.
Hence, we assume from now on that \(l = 1\). The assumptions on \(\rho \) ensure that there exists a \(\tau > 0\) and \(\eta _{\tau }> 0\) such that

cf. Fig. 1.
Splitting \(\Omega _1 \times \Omega _1\) into \({\mathcal {S}}_{\tau }=:{\mathcal {S}}\) and its complement \((\Omega _1 \times \Omega _1) \setminus {\mathcal {S}}_{\tau }=:{\mathcal {S}}^{c}\), we accordingly split the integrals  and consider again two cases
and consider again two cases  and
and  , respectively.
, respectively.
Case 2.1 .
.
By definition of \({\mathcal {S}}\) we have \(\rho (x-y) \ge \tau > 0\) for all \((x,y) \in {\mathcal {S}}\). Therefore,

Since \(\alpha > 0\), it follows

Case 2.2 .
.
For \((x, y) \in {\mathcal {S}}^{c}\) it might happen that \(\rho (x-y) = 0\), and thus instead of proving  , as in Case 2.1, we rather show that
, as in Case 2.1, we rather show that  . For this it is sufficient to show that for every \(c > 0\) there is some \(C \in {\mathbb {R}}\) such that the implication
. For this it is sufficient to show that for every \(c > 0\) there is some \(C \in {\mathbb {R}}\) such that the implication

holds true for all \(w \in W^{s,p_1}(\Omega _1, K_1) \subseteq W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\). To this end let \(c > 0\) be given and consider an arbitrarily chosen \(w \in W^{s,p_1}(\Omega _1, K_1)\) fulfilling  .
.
Then  . Using the triangle inequality and the monotonicity of the function \(h: t \mapsto t^{p_2}\) on \([0, +\infty )\), we get further
. Using the triangle inequality and the monotonicity of the function \(h: t \mapsto t^{p_2}\) on \([0, +\infty )\), we get further

Due to the norm coercivity, it thus follows that \(\left\| w\right\| _{L^{p_1}(\Omega _1, {\mathbb {R}}^{M_1})} \le \bar{c}\), \(\bar{c}\) some constant. Using [55, Lemma 3.20], it then follows that

for all \((x,y) \in \Omega _1 \times \Omega _1\). Using Eq. 3.6, Fubini’s Theorem and Eq. 3.5 we obtain

Combining  for all \((x,y) \in {\mathcal {S}}^{c}\) with the previous inequality, we obtain the needed estimate
for all \((x,y) \in {\mathcal {S}}^{c}\) with the previous inequality, we obtain the needed estimate

The second example concerns the coercivity of  , defined in Eq. 2.9, when
, defined in Eq. 2.9, when  denotes the masking operator occurring in image inpainting. To prove this result, we require the following auxiliary lemma:
denotes the masking operator occurring in image inpainting. To prove this result, we require the following auxiliary lemma:
Lemma 3.8
There exists a constant \(C \in {\mathbb {R}}\) such that for all \(w \in W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1}), \ 0<s< 1, \ l \in \{0,1\}, \ 1< p_1 < \infty \) and \(D \subsetneq \Omega _1\) nonempty such that

Proof
The proof is inspired by the proof of Poincaré’s inequality in [29]. It is included here for the sake of completeness.
Assume first that \(l=1\). Let \({\mathcal {S}}\) be as above,

If the stated inequality Eq. 3.7 would be false, then for every \(n \in {\mathbb {N}}\) there would exists a function \(w_n \in W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\) satisfying

By normalizing we can assume without loss of generality
-
(i)
\(\left\| w_n\right\| _{L^{p_1}\left( D, {\mathbb {R}}^{M_1}\right) }^{p_1} = 1\).
Moreover, by Eq. 3.8
-
(ii)
\(\left\| w_n\right\| _{L^{p_1}(\Omega _1 \setminus D, {\mathbb {R}}^{M_1})}^{p_1} < \frac{1}{n}\),
-
(iii)
 .
.
By item (i) and item (ii), we get that \(\left\| w_n\right\| _{L^{p_1}(\Omega _1, {\mathbb {R}}^{M_1})}^{p_1} = \left\| w_n\right\| _{L^{p_1}\left( D, {\mathbb {R}}^{M_1}\right) }^{p_1} + \left\| w_n\right\| _{L^{p_1}(\Omega _1 \setminus D, {\mathbb {R}}^{M_1})}^{p_1}< 1 + \frac{1}{n} < 2 \) is bounded. Moreover

where c is independent of n. This yields that the sequence \((w_n)_{n \in {\mathbb {N}}}\) is bounded in \(W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\) by \((2 + c)^{\frac{1}{p_1}}\). By the reflexivity of  for \(p_1 \in (1, \infty )\) and Lemma 2.8, there exists a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) of \((w_n)_{n \in {\mathbb {N}}}\) and \(w_* \in W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\) such that
for \(p_1 \in (1, \infty )\) and Lemma 2.8, there exists a subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) of \((w_n)_{n \in {\mathbb {N}}}\) and \(w_* \in W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1})\) such that  strongly in \(L^{p_1}(\Omega _1, {\mathbb {R}}^{M_1})\) and pointwise almost everywhere.
strongly in \(L^{p_1}(\Omega _1, {\mathbb {R}}^{M_1})\) and pointwise almost everywhere.
Using the continuity of the norm and dominated convergence, we obtain
-
(i)
\(\left\| w^*\right\| _{L^{p_1}\left( D, {\mathbb {R}}^{M_1}\right) }^{p_1} = 1\), in particular, \(w^*\) is not the null function on D,
-
(ii)
\(\left\| w^*\right\| _{L^{p_1}(\Omega _1 \setminus D, {\mathbb {R}}^{M_1})}^{p_1} = 0\) since \(n \in {\mathbb {N}}\) is arbitrary and hence \(w^* \equiv 0\) on \(\Omega _1 \setminus D\).
-
(iii)

i.e., \(w^*(x) = w^*(y) \) for \((x,y) \in {\mathcal {S}}\) yielding that \(w^*\) locally constant and hence even constant since \(\Omega _1\) is connected,
which gives the contradiction.
In the case \(l=0\) we use similar arguments, where the distance  in the last inequality can be estimated by \(\text {diam}|\Omega _1|\) (instead of \(\eta \)) since \(\Omega _1\) is bounded. \(\square \)
in the last inequality can be estimated by \(\text {diam}|\Omega _1|\) (instead of \(\eta \)) since \(\Omega _1\) is bounded. \(\square \)
Remark 3.9
In case \(l=1\) it follows that the sharper inequality holds true: There exists a constant \(C \in {\mathbb {R}}\) such that for all \(w \in W^{s,p_1}(\Omega _1, {\mathbb {R}}^{M_1}), \ 0<s< 1, \ 1< p_1 < \infty \) and \(D \subsetneq \Omega _1\) nonempty such that

Example 3.10
As in Example 3.7, we consider that \(W(\Omega _1,K_1) = W^{s, p_1}(\Omega _1, K_1)\) with \(p_1>1, \ 0< s < 1\) and fix \(k = N\).
Assume that  is the inpainting operator, i.e.,
is the inpainting operator, i.e.,

where \(D \subseteq \Omega _1, \ w \in W^{s,p_1}(\Omega _1, K_1)\). Since the dimension of the data w and the image data  has the same dimension at every point \(x \in \Omega _1\), we write \(M :=M_1 = M_2\).
has the same dimension at every point \(x \in \Omega _1\), we write \(M :=M_1 = M_2\).
Then the functional  :
:

is coercive for \(p_2 \ge p_1\):
The fact that \(p_2 \ge p_1\) and that \(\Omega _1\) is bounded ensures that
The proof is done using the same arguments as in the proof of Example 3.7, where we additionally split Case 1 into the two subcases
- Case 1.1 :
-

- Case 1.2 :
-

4 Stability and Convergence
In this section we will first show a stability and afterwards a convergence result. We use the notation introduced in Sect. 2. In particular, \(W(\Omega _1, K_1)\) is as defined in Eq. 2.5. We also stress that we use notationally simplified versions  of
of  and \({\mathcal {R}}\) of
and \({\mathcal {R}}\) of  whenever possible. See Eqs. 2.6, 2.7 and 2.8.
whenever possible. See Eqs. 2.6, 2.7 and 2.8.
Theorem 4.1
Let Assumption 3.2 be satisfied. Let \(v^\delta \in L^{p_2}(\Omega _2, K_2)\) and let \((v_n)_{n \in {\mathbb {N}}}\) be a sequence in \(L^{p_2}(\Omega _2, K_2)\) such that  . Then every sequence
. Then every sequence  with
with

has a converging subsequence w.r.t. the topology of \(W(\Omega _1, K_1)\). The limit \(\tilde{w}\) of any such converging subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) is a minimizer of  . Moreover, \(({\mathcal {R}}(w_{n_k}))_{k \in {\mathbb {N}}}\) converges to \({\mathcal {R}}(\tilde{w})\).
. Moreover, \(({\mathcal {R}}(w_{n_k}))_{k \in {\mathbb {N}}}\) converges to \({\mathcal {R}}(\tilde{w})\).
The subsequent proof of Theorem 4.1 is similar to the proof of [55, Theorem 3.23].
Proof
For the ease of notation, we simply write  instead of
instead of  and
and  .
.
By assumption the sequence  converges to 0 and thus is bounded, i.e., there exists \(B \in (0, +\infty )\) such that
converges to 0 and thus is bounded, i.e., there exists \(B \in (0, +\infty )\) such that

Because  it follows that
it follows that

By Assumption 3.2 there is a \(\overline{w} \in W(\Omega _1, K_1)\) such that  . Set \(c :=2^{p_2-1}\). Using Assumption 3.2 and applying Lemma 3.5, Eqs. 4.2 and 4.1 implies that for all \(n \in {\mathbb {N}}\)
. Set \(c :=2^{p_2-1}\). Using Assumption 3.2 and applying Lemma 3.5, Eqs. 4.2 and 4.1 implies that for all \(n \in {\mathbb {N}}\)

Applying again Lemma 3.5, we obtain  . Hence, from item (3.1) it follows that the sequence
. Hence, from item (3.1) it follows that the sequence  contains a converging subsequence.
contains a converging subsequence.
Let now \((w_{n_k})_{k \in {\mathbb {N}}}\) be an arbitrary subsequence of  which converges in \(W(\Omega _1, K_1)\) to some \({\tilde{w}} \in W(\Omega _1, {\mathbb {R}}^{M_1})\). Then, from Lemma 2.8 and the continuity properties of
which converges in \(W(\Omega _1, K_1)\) to some \({\tilde{w}} \in W(\Omega _1, {\mathbb {R}}^{M_1})\). Then, from Lemma 2.8 and the continuity properties of  it follows that \({\tilde{w}} \in W(\Omega _1, K_1)\) and
it follows that \({\tilde{w}} \in W(\Omega _1, K_1)\) and  in \(L^{p_2}(\Omega _2, K_2) \times L^{p_2}(\Omega _2, K_2)\). Moreover, using Lemma 3.4, Eq. 4.2 and the triangle inequality it follows that for every \(w \in W(\Omega _1, K_1)\) the following estimate holds true
in \(L^{p_2}(\Omega _2, K_2) \times L^{p_2}(\Omega _2, K_2)\). Moreover, using Lemma 3.4, Eq. 4.2 and the triangle inequality it follows that for every \(w \in W(\Omega _1, K_1)\) the following estimate holds true

This shows that \({\tilde{w}}\) is a minimizer of  . Choosing \(w = {\tilde{w}}\) in the previous estimate, we obtain the equality
. Choosing \(w = {\tilde{w}}\) in the previous estimate, we obtain the equality

Due to  this gives
this gives

\(\square \)
Before proving the next theorem, we need the following definition, cf. [55].
Definition 4.2
Let  . Every element \(w^* \in W(\Omega _1, K_1)\) fulfilling
. Every element \(w^* \in W(\Omega _1, K_1)\) fulfilling

is called an \({\mathcal {R}}\)-minimizing solution of the equation  or shorter just \({\mathcal {R}}\)-minimizing solution.
or shorter just \({\mathcal {R}}\)-minimizing solution.
The following theorem and its proof are inspired by [55, Theorem 3.26].
Theorem 4.3
Let Assumption 3.2 be satisfied. Let there exist an \({\mathcal {R}}\)-minimizing solution \(w^\dagger \in W(\Omega _1, K_1)\) and let  be a function satisfying
be a function satisfying

Let \((\delta _n)_{n \in {\mathbb {N}}}\) be a sequence of positive real numbers converging to 0. Moreover, let \((v_n)_{n \in {\mathbb {N}}}\) be a sequence in \(L^{p_2}(\Omega _2, K_2)\) with  and set \(\alpha _n :=\alpha (\delta _n)\).
and set \(\alpha _n :=\alpha (\delta _n)\).
Then every sequence  of minimizers
of minimizers

has a converging subsequence  as \(k \rightarrow \infty \), and the limit \(\tilde{w}\) is always an \({\mathcal {R}}\)-minimizing solution. In addition,
as \(k \rightarrow \infty \), and the limit \(\tilde{w}\) is always an \({\mathcal {R}}\)-minimizing solution. In addition,  .
.
Moreover, if \(w^\dagger \) is unique, it follows that  and
and  .
.
Proof
We write shortly  for
for  . Taking into account that
. Taking into account that  it follows that
it follows that

yielding  as
as  . The triangle inequality gives
. The triangle inequality gives  as
as  and Remark 3.1 ensures
and Remark 3.1 ensures  as
as  , so that
, so that

Since

we also get

Set \(\alpha _{\text {max}} :=\max \{\alpha _n : n \in {\mathbb {N}}\}\). Since

the sequence  is bounded. From Assumption 3.2, item (3.1) it follows that there exists a converging subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) of
is bounded. From Assumption 3.2, item (3.1) it follows that there exists a converging subsequence \((w_{n_k})_{k \in {\mathbb {N}}}\) of  . The limit of \((w_{n_k})_{k \in {\mathbb {N}}}\) is denoted by \(\tilde{w}\). Then, from Lemma 2.8 it follows that \(\tilde{w} \in W(\Omega _1, K_1)\). Since the operator
. The limit of \((w_{n_k})_{k \in {\mathbb {N}}}\) is denoted by \(\tilde{w}\). Then, from Lemma 2.8 it follows that \(\tilde{w} \in W(\Omega _1, K_1)\). Since the operator  is sequentially continuous, it follows that
is sequentially continuous, it follows that  in \(L^{p_2}(\Omega _2, K_2)\). This shows that actually
in \(L^{p_2}(\Omega _2, K_2)\). This shows that actually  since Eq. 4.5 is valid. Then, from Lemma 3.4 it follows that the functional
since Eq. 4.5 is valid. Then, from Lemma 3.4 it follows that the functional  is sequentially lower semi-continuous, so that
is sequentially lower semi-continuous, so that  . Combining this with Eq. 4.6, we also obtain
. Combining this with Eq. 4.6, we also obtain

using the definition of \(w^\dagger \). This, together with the fact that  we see that \(\tilde{w}\) is an \({\mathcal {R}}\)-minimizing solution and that
we see that \(\tilde{w}\) is an \({\mathcal {R}}\)-minimizing solution and that  .
.
Now assume that the solution fulfilling Eq. 4.3 is unique; we call it \(w^\dagger \). In order to prove that  , it is sufficient to show that any subsequence has a further subsequence converging to \(w^\dagger \), cf. [55, Lemma 8.2]. Hence, denote by \((w_{n_k})_{k \in {\mathbb {N}}}\) an arbitrary subsequence of \((w_n)\), the sequence of minimizers. Like before we can show that
, it is sufficient to show that any subsequence has a further subsequence converging to \(w^\dagger \), cf. [55, Lemma 8.2]. Hence, denote by \((w_{n_k})_{k \in {\mathbb {N}}}\) an arbitrary subsequence of \((w_n)\), the sequence of minimizers. Like before we can show that  is bounded and we can extract a converging subsequence \((w_{n_{k_l}})_{l \in {\mathbb {N}}}\). The limit of this subsequence is \(w^\dagger \) since it is the unique solution fulfilling Eq. 4.3, showing that
is bounded and we can extract a converging subsequence \((w_{n_{k_l}})_{l \in {\mathbb {N}}}\). The limit of this subsequence is \(w^\dagger \) since it is the unique solution fulfilling Eq. 4.3, showing that  . Moreover, \(w^\dagger \in W(\Omega _1, K_1)\). Following the arguments above, we obtain as well
. Moreover, \(w^\dagger \in W(\Omega _1, K_1)\). Following the arguments above, we obtain as well  \(\square \)
\(\square \)
Remark 4.4
Theorem 4.1 guarantees that the minimizers of  depend continuously on \(v^\delta \), while Theorem 4.3 ensures that they converge to a solution of
depend continuously on \(v^\delta \), while Theorem 4.3 ensures that they converge to a solution of  , \(v^0\) the exact data, while \(\alpha \) tends to zero.
, \(v^0\) the exact data, while \(\alpha \) tends to zero.
5 Discussion of the Results and Conjectures
In this section we summarize some open problems related to double integral expressions of functions with values on manifolds.
5.1 Relation to Single Integral Representations
In the following we show for one particular case of functions that have values in a manifold, that the double integral formulation  , defined in Eq. 2.8, approximates a single energy integral. The basic ingredient for this derivation is the exponential map related to the metric \(d_1\) on the manifold. In the following we investigate manifold-valued functions \(w \in W^{1,2}(\Omega , \mathcal {M})\), where we consider \(\mathcal {M} \subseteq {\mathbb {R}}^{M \times 1}\) to be a connected, complete Riemannian manifold. In this case some of the regularization functionals
, defined in Eq. 2.8, approximates a single energy integral. The basic ingredient for this derivation is the exponential map related to the metric \(d_1\) on the manifold. In the following we investigate manifold-valued functions \(w \in W^{1,2}(\Omega , \mathcal {M})\), where we consider \(\mathcal {M} \subseteq {\mathbb {R}}^{M \times 1}\) to be a connected, complete Riemannian manifold. In this case some of the regularization functionals  , defined in Eq. 2.8, can be considered as approximations of single integrals. In particular, we aim to generalize Eq. 1.3 in the case \(p=2\).
, defined in Eq. 2.8, can be considered as approximations of single integrals. In particular, we aim to generalize Eq. 1.3 in the case \(p=2\).
We have that
In the following we will write  instead of
instead of  to stress the dependence on \(\varepsilon \) in contrast to above; the factor \(\frac{1}{2}\) was added due to reasons of calculation. Moreover, let \(\hat{\rho } : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+\) be in \(C_c^\infty ({\mathbb {R}}_+, {\mathbb {R}}_+)\) and satisfy
to stress the dependence on \(\varepsilon \) in contrast to above; the factor \(\frac{1}{2}\) was added due to reasons of calculation. Moreover, let \(\hat{\rho } : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+\) be in \(C_c^\infty ({\mathbb {R}}_+, {\mathbb {R}}_+)\) and satisfy
Then for every \(\varepsilon > 0\)

is a mollifier, cf. Example 2.2.
 (with \(p_1=2\)) then reads as follows:
(with \(p_1=2\)) then reads as follows:

Substitution with spherical coordinates \(y = x - t \theta \in {\mathbb {R}}^{N \times 1}\) with \(\theta \in \mathbb {S}^{N-1} \subseteq {\mathbb {R}}^{N \times 1}\), \(t \ge 0\) gives

Now, using that for \(m_1 \in \mathcal {M}\) fixed and \(m_2 \in \mathcal {M}\) such that \(m_1\) and \(m_2\) are joined by a unique minimizing geodesic (see, for instance, [30] where the concept of exponential mappings is explained)
where \(\partial _2\) denotes the derivative of \(d_1^2\) with respect to the second component. By application of the chain rule we get
where w(x) and w(y) are joined by a unique minimizing geodesic. This assumption seems reasonable due to the fact that we consider the case \(\varepsilon \searrow 0\). Let \(\cdot \) denote the scalar multiplication of two vectors in \({\mathbb {R}}^{N \times 1}\), then the last equality shows that
Thus, from Eq. 5.2 it follows that

Now we will use a Taylor series of power 0 for \( t\mapsto \nabla w(x-t \theta )\) and of power 1 for \(t \mapsto (\exp _{w(x-t \theta )})^{-1}(w(x))\) to rewrite Eq. 5.4. We write
and define
Note that because \((\exp _{w(x)})^{-1}(w(x))\) vanishes, \(\dot{F}(w(x);\theta )\) is the leading order term of the expansion of \((\exp _{w(x-t \theta )})^{-1}(w(x))\) with respect to t. Moreover, in the case that \(\nabla w(x) \ne 0\) this is the leading order approximation of \(\nabla w(x-t \theta )\). In summary we are calculating the leading order term of the expansion with respect to t.
Then from Eq. 5.4 it follows that

The previous calculations show that the double integral simplifies to a double integral where the inner integration domain has one dimension less than the original integral. Under certain assumption the integration domain can be further simplified:
Example 5.1
If  , \(p_1=2\), then
, \(p_1=2\), then
Thus, from (5.7) it follows that

This is exactly the identity derived in Bourgain et al. [14].
From these considerations we can view  as functionals, which generalize Sobolev and \(\text {BV}\) semi-norms to functions with values on manifolds.
as functionals, which generalize Sobolev and \(\text {BV}\) semi-norms to functions with values on manifolds.
5.2 A Conjecture on Sobolev Semi-norms
Starting point for this conjecture is Eq. 2.8. We will write \(\Omega ,M\) and p instead of \(\Omega _1, M_1\) and \(p_1\).
-
In the case \(l=0\), \(k=N\), \(0<s<1\) and
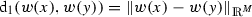 the functional
the functional  from Eq. 2.8 simplifies to the p-th power of the Sobolev semi-norm and reads
from Eq. 2.8 simplifies to the p-th power of the Sobolev semi-norm and reads  (5.9)
(5.9)For a recent survey on fractional Sobolev spaces, see [25].
-
On the other hand, when we choose \(k=0\), \(l=1\) and
 , then
, then  from Eq. 2.8 reads (note \(\rho =\rho _\varepsilon \) by simplification of notation):
from Eq. 2.8 reads (note \(\rho =\rho _\varepsilon \) by simplification of notation):  (5.10)
(5.10) -
Therefore, in analogy to what we know for \(s=1\) from [14], we conjecture that
 (5.11)
(5.11)The form Eq. 5.11 is numerically preferable to the standard Sobolev semi-norm Eq. 5.9, because \(\rho =\rho _\varepsilon \) and thus the integral kernel has compact support.
6 Numerical Examples
In this section we present some numerical examples for denoising and inpainting of functions with values on the circle \({\mathbb {S}}^1\). Functions with values on a sphere have already been investigated very diligently (see, for instance, [13] out of series of publications of these authors). Therefore, we review some of their results first.
6.1 \({\mathbb {S}}^1\)-Valued Data
Let \(\emptyset \ne \Omega \subset {\mathbb {R}}\) or \({\mathbb {R}}^2\) be a bounded and simply connected open set with Lipschitz boundary. In [13] the question was considered when  can be represented by some function
can be represented by some function  satisfying
satisfying
That is, the function u is a lifting of w.
Lemma 6.1
([13])
-
Let \(\Omega \subset {\mathbb {R}}\), \(0< s < \infty \), \(1< p < \infty \). Then for all
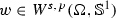 there exists
there exists  satisfying Eq. 6.1.
satisfying Eq. 6.1. -
Let \(\Omega \subset {\mathbb {R}}^N\), \(N \ge 2\), \(0< s < 1\), \(1< p < \infty \). Moreover, let \(sp < 1\) or \(sp \ge N\), then for all
 there exists
there exists  satisfying Eq. 6.1.
satisfying Eq. 6.1.If \(sp \in [1,N)\), then there exist functions
 such that Eq. 6.1 does not hold with any function
such that Eq. 6.1 does not hold with any function  .
.
For

we consider the functional (note that by simplification of notation below \(\rho =\rho _\varepsilon \) denotes a mollifier)

on  , in accordance to Eq. 2.8.
, in accordance to Eq. 2.8.
Writing \(w = \Phi (u)\) as in Eq. 6.1, we get the lifted functional

over the space  .
.
Remark 6.2
-
We note that in the case \(k=0\), \(s=1\) and \(l=1\) these integrals correspond with the ones considered in Bourgain et al. [14] for functions with values on \({\mathbb {S}}^1\).
-
If we choose \(k=N\), \(s=1\) and \(l=0\), then this corresponds with Sobolev semi-norms on manifolds.
-
Let \(\varepsilon > 0\) fixed (that is, we consider neither a standard Sobolev regularization nor the limiting case \(\varepsilon \rightarrow 0\) as in [14]). In this case we have proven coercivity of the functional
 only with the following regularization functional, cf. Example 3.7 and Example 3.10:
only with the following regularization functional, cf. Example 3.7 and Example 3.10: 
We summarize a few results: The first lemma follows from elementary calculations:
Lemma 6.3
 and \(\,{\mathrm {d}}_{{\mathbb {R}}^2}\big |_{{\mathbb {S}}^1\times {\mathbb {S}}^1}\) are equivalent.
and \(\,{\mathrm {d}}_{{\mathbb {R}}^2}\big |_{{\mathbb {S}}^1\times {\mathbb {S}}^1}\) are equivalent.
Lemma 6.4
Let  . Then
. Then  .
.
Proof
This follows directly from the inequality \(\Vert {\mathrm {e}}^{ia}-{\mathrm {e}}^{ib}\Vert \le \Vert a-b\Vert \) for all \(a,b \in {\mathbb {R}}\). \(\square \)
Below we show that  is finite on
is finite on  .
.
Lemma 6.5
 maps
maps  into \([0,\infty )\) (i.e., does not attain the value \(+\infty \)).
into \([0,\infty )\) (i.e., does not attain the value \(+\infty \)).
Proof
Let  . Then by Lemma 6.4 we have that
. Then by Lemma 6.4 we have that  . Therefore, from Lemma 6.3 and Proposition 2.13 item (ii) it follows that
. Therefore, from Lemma 6.3 and Proposition 2.13 item (ii) it follows that  . Hence, by definition,
. Hence, by definition,  . \(\square \)
. \(\square \)
6.2 Setting of Numerical Examples
In all numerical examples presented, we use a simplified setting with
\(\Omega _1 = \Omega _2 =:\Omega \) when considering image denoising, \(\Omega _1 = \Omega \), \(\Omega _2 = \Omega \setminus D\) when considering image inpainting, and

As a particular mollifier, we use \(\rho _\varepsilon \) (see Example 2.2), which is defined via the one-dimensional normal distribution \( \hat{\rho }(x) = \frac{1}{\sqrt{\pi }} {\mathrm {e}}^{-x^2}.\)
6.3 Regularization Functionals
Let  and
and  be as defined in Eqs. 6.3 and 6.4, respectively. In what follows, we consider the following regularization functional
be as defined in Eqs. 6.3 and 6.4, respectively. In what follows, we consider the following regularization functional

on  and the lifted variant
and the lifted variant

over the space  (as in Sect. 6.1), where \(\Phi \) is defined as in (6.1). Note that
(as in Sect. 6.1), where \(\Phi \) is defined as in (6.1). Note that  .
.
Lemma 6.6
Let \(\emptyset \ne \Omega \subset {\mathbb {R}}\) or \({\mathbb {R}}^2\) be a bounded and simply connected open set with Lipschitz boundary. Let \(1< p < \infty \) and \(s \in (0,1)\). If \(N=2\) assume that \(sp < 1\) or \(sp \ge 2\). Moreover, let Assumption 3.2 and Assumption 2.10 be satisfied. Then the mapping  attains a minimizer.
attains a minimizer.
Proof
Let  . Then by Lemma 6.4 we have that
. Then by Lemma 6.4 we have that  . As arguing as in the proof of Lemma 6.5, we see that
. As arguing as in the proof of Lemma 6.5, we see that  .
.
Since we assume that Assumption 3.2 is satisfied, we get that  attains a minimizer
attains a minimizer  . It follows from Lemma 6.1 that there exists a function \(u^* \in W^{s,p}(\Omega , {\mathbb {R}})\) that can be lifted to \(w^*\), i.e., \(w^* = \Phi (u^*)\). Then \(u^*\) is a minimizer of (6.6) by definition of
. It follows from Lemma 6.1 that there exists a function \(u^* \in W^{s,p}(\Omega , {\mathbb {R}})\) that can be lifted to \(w^*\), i.e., \(w^* = \Phi (u^*)\). Then \(u^*\) is a minimizer of (6.6) by definition of  and \(\Phi \). \(\square \)
and \(\Phi \). \(\square \)
6.4 Numerical Minimization
In our concrete examples, we will consider two different operators  . For numerical minimization we consider the functional from Eq. 6.6 in a discretized setting. For this purpose, we approximate the functions \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\), \(0<s<1,1<p<\infty \) by quadratic B-spline functions and optimize with respect to the coefficients. We remark that this approximation is continuous and thus that sharp edges correspond to very steep slopes.
. For numerical minimization we consider the functional from Eq. 6.6 in a discretized setting. For this purpose, we approximate the functions \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\), \(0<s<1,1<p<\infty \) by quadratic B-spline functions and optimize with respect to the coefficients. We remark that this approximation is continuous and thus that sharp edges correspond to very steep slopes.
The noisy data \(u^\delta \) are obtained by adding Gaussian white noise with variance \(\sigma ^2\) to the approximation or the discretized approximation of u.
We apply a simple Gradient Descent scheme with fixed step length implemented in \(\text {MATLAB}\).
6.5 Denoising of \({\mathbb {S}}^1\)-Valued Functions: The InSAR Problem
In this case the operator  is the inclusion operator. It is norm-coercive in the sense of Eq. 3.4 and hence Assumption 3.2 is fulfilled. For \(\emptyset \ne \Omega \subset {\mathbb {R}}\) or \({\mathbb {R}}^2\) a bounded and simply connected open set, \(1< p < \infty \) and \(s \in (0,1)\) such that additionally \(sp < 1\) or \(sp \ge 2\) if \(N=2\) we can apply Lemma 6.6 which ensures that the lifted functional
is the inclusion operator. It is norm-coercive in the sense of Eq. 3.4 and hence Assumption 3.2 is fulfilled. For \(\emptyset \ne \Omega \subset {\mathbb {R}}\) or \({\mathbb {R}}^2\) a bounded and simply connected open set, \(1< p < \infty \) and \(s \in (0,1)\) such that additionally \(sp < 1\) or \(sp \ge 2\) if \(N=2\) we can apply Lemma 6.6 which ensures that the lifted functional  attains a minimizer \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\).
attains a minimizer \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\).
Function on \({\mathbb {S}}^1\) represented in \([0,2\pi )\): Left to right, top to bottom: original data (black) and noisy data (blue) with 100 data points. Denoised data (red) where we chose \(s=0.1, p=1.1, \alpha = 0.19\). Denoised data with \(s=0.6, p=1.1, \alpha = 0.19\) resp. \(s=0.1, p=2, \alpha =0.19\) (Color figure online)
In the examples we will just consider the continuous approximation again denoted by u.
6.6 One-Dimensional Test Case
Let \(\Omega = (0,1)\) and consider the signal  representing the angle of a cyclic signal.
representing the angle of a cyclic signal.
For the discrete approximation shown in Fig. 2a, the domain \(\Omega \) is sampled equally at 100 points. u is affected by an additive white Gaussian noise with \(\sigma = 0.1\) to obtain the noisy signal which is colored in blue in Fig. 2a.
In this experiment we show the influence of the parameters s and p. In all cases the choice of the regularization parameter \(\alpha \) is 0.19 and \(\varepsilon = 0.01\).
The red signal in Fig. 2b is obtained by choosing \(s = 0.1\) and \(p = 1.1\). We see that the periodicity of the signal is handled correctly and that there is nearly no staircasing. In Fig. 2c the parameter s is changed from 0.1 to 0.6. The value of the parameter p stays fixed. Increasing of s leads the signal to be more smooth. We can observe an even stronger similar effect when increasing p (here from 1.1 to 2) and letting s fixed, see Fig. 2d. This fits the expectation since s only appears once in the denominator of the regularizer. At a jump, increasing of s leads thus to an increasing of the regularization term. The parameter p appears twice in the regularizer. Huge jumps are hence weighted even more.
In Fig. 3a we considered a simple signal with a single huge jump. Again it is described by the angular value. We proceeded as above to obtain the approximated discrete original data (black) and noisy signal with \(\sigma = 0.1\) (blue). We chose again \(\varepsilon = 0.01\).
As we have seen above, increasing of s leads to a more smooth signal. This effect can be compensated by choosing a rather small value of p, i.e., \(p \approx 1\). In Fig. 3b the value of s is 0.9. We see that it is still possible to reconstruct jumps by choosing, e.g., \(p=1.01\).
Moreover, we have seen that increasing of p leads to an even more smooth signal. In Fig. 3c we choose a quite large value of p, \(p=2\) and a rather small value of s, \(s = 0.001\). Even for this very simple signal, it was not possible to get sharp edges. This is due to the fact that the parameter p (but not s) additionally weights the height of jumps in the regularizing term.
6.7 Denoising of a \({\mathbb {S}}^1\)-Valued Image
Our next example concerned a two-dimensional \({\mathbb {S}}^1\)-valued image represented by the corresponding angular values. We remark that in this case where \(N=2\) the existence of such a representation is always guaranteed in the cases where \(sp < 1\) or \(sp \ge 2\), see Lemma 6.1.
The domain \(\Omega \) is sampled into \(60 \times 60\) data points and can be considered as discrete grid, \(\{1, \dots ,60\} \times \{1, \dots ,60\} \). The B-spline approximation evaluated at that grid is given by
The function u is shown in Fig. 4. We used the \(\text {hsv}\) colormap provided in \(\text {MATLAB}\) transferred to the interval \([0, 2\pi ]\).
Left to right. Top to bottom: original image and the noisy data with \(\sigma ^2 = 0.001\). Noisy image with masking filter and denoised data with \(s=0.3, p=1.01, \alpha = 0.3\), 6000 steps. TV-denoised data. Original image and the noisy data with \(\sigma ^2 = 0.001\). Noisy image with masking filter and denoised data with \(s=0.4, p=1.01, \alpha = 0.4\), 10000 steps. TV-denoised image
This experiment shows the difference of our regularizer respecting the periodicity of the data in contrast to the classical total variation regularizer. The classical TV minimization is solved using a fixed point iteration ([45]); for the method see also [60].
In Fig. 5a the function u can be seen from the top, i.e., the axes correspond to the i resp. j axis in Fig. 4. The noisy data are obtained by adding white Gaussian noise with \(\sigma = \sqrt{0.001}\) using the built-in function \(\texttt {imnoise}\) in \(\text {MATLAB}\). It is shown in Fig. 5b. We choose as parameters \(s=0.9, \ p=1.1, \ \alpha = 1,\) and \(\varepsilon = 0.01\). We observe significant noise reduction in both cases. However, only in Fig. 5d the color transitions are handled correctly. This is due to the fact that our regularizer respects the periodicity, i.e., for the functional there is no jump in Fig. 4 since 0 and \(2\pi \) are identified. Using the classical TV regularizer, the values 0 and \(2\pi \) are not identified and have a distance of \(2\pi \). Hence, in the TV-denoised image there is a sharp edge in the middle of the image, see Fig. 5c.
6.8 Hue Denoising
The \(\text {HSV}\) color space is shorthand for Hue, Saturation, Value (of brightness). The hue value of a color image is \({\mathbb {S}}^1\)-valued, while saturation and value of brightness are real-valued. Representing colors in this space better match the human perception than representing colors in the RGB space.
In Fig. 6a we see a part of size \(70 \times 70\) of the RGB image “fruits” (https://homepages.cae.wisc.edu/~ece533/images/).
The corresponding hue data are shown in Fig. 6b, where we used again the colormap HSV, cf. Fig. 4. Each pixel value lies, after transformation, in the interval \([0, 2\pi )\) and represents the angular value. Gaussian white noise with \(\sigma = \sqrt{0.001}\) is added to obtain a noisy image, see Fig. 6c.
To obtain the denoised image, in Fig. 6d we again used the same fixed point iteration, cf. [45], as before.
We see that the denoised image suffers from artifacts due to the non-consideration of periodicity. The pixel values in the middle of the apple (the red object in the original image) are close to \(2\pi \) while those close to the border are nearly 0, meaning they have a distance of around \(2\pi \).
We use this TV-denoised image as starting image to perform the minimization of our energy functional. As parameters we choose \(s = 0.49, \ p = 2, \ \alpha = 2, \ \varepsilon = 0.006\).
Since the cyclic structure is respected, the disturbing artifacts in image in Fig. 6d are removed correctly. The edges are smoothed due to the high value of p, see Fig. 6e.
6.9 \({\mathbb {S}}^1\)-Valued Image Inpainting
In this case the operator  is the inpainting operator, i.e.,
is the inpainting operator, i.e.,

where \(D \subseteq \Omega \) is the area to be inpainted.
We consider the functional

on  .
.
According to Example 3.10, the functional  is coercive and Assumption 3.2 is satisfied. For \(\emptyset \ne \Omega \subset {\mathbb {R}}\) or \({\mathbb {R}}^2\) a bounded and simply connected open set, \(1< p < \infty \) and \(s \in (0,1)\) such that additionally \(sp < 1\) or \(sp \ge 2\) if \(N=2\) Lemma 6.6 applies which ensures that there exists a minimizer \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\) of the lifted functional
is coercive and Assumption 3.2 is satisfied. For \(\emptyset \ne \Omega \subset {\mathbb {R}}\) or \({\mathbb {R}}^2\) a bounded and simply connected open set, \(1< p < \infty \) and \(s \in (0,1)\) such that additionally \(sp < 1\) or \(sp \ge 2\) if \(N=2\) Lemma 6.6 applies which ensures that there exists a minimizer \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\) of the lifted functional  \(u \in W^{s, p}(\Omega ,{\mathbb {R}})\)
\(u \in W^{s, p}(\Omega ,{\mathbb {R}})\)
6.10 Inpainting of a \({\mathbb {S}}^1\)-Valued Image
As a first inpainting test example, we consider two \({\mathbb {S}}^1\)-valued images of size \(28 \times 28\), see Fig. 7, represented by its angular values. In both cases the ground truth can be seen in Fig. 7a, f. We added Gaussian white noise with \(\sigma = \sqrt{0.001}\) using the \(\text {MATLAB}\) build-in function \(\texttt {imnoise}\). The noisy images can be seen in Fig. 7b, g. The region D consists of the nine red squares in Fig. 7c, h.
The reconstructed data are shown in Fig. 7d, i.
For the two-colored image, we used as parameters \(\alpha = s = 0.3\), \(p = 1.01\) and \(\varepsilon = 0.05\). We see that the reconstructed edge appears sharp. The unknown squares, which are completely surrounded by one color, are inpainted perfectly. The blue and green color changed slightly.
As parameters for the three-colored image, we used \(\alpha = s = 0.4\), \(p=1.01\) and \(\varepsilon = 0.05\). Here again the unknown regions lying entirely in one color are inpainted perfectly. The edges are preserved. Just the corner in the middle of the image is slightly smoothed.
In Fig. 7e, j the TV-reconstructed data are shown. The underlying algorithm ([31]) uses the split Bregman method (see [36]).
In Fig. 7e the edge is not completely sharp. There are some lighter parts on the blue side. This can be caused by the fact that the unknown domain in this area is not exactly symmetric with respect to the edge. This is also the case in Fig. 7j where we observe the same effect. Unknown squares lying entirely in one color are perfectly inpainted.
6.11 Hue Inpainting
As a last example, we consider again the hue component of the image “fruits”, see Fig. 8a. The unknown region D is the string \(\textit{01.01}\) which is shown in Fig. 8b. As parameters we choose \(p=1.1\), \(s=0.1\), \(\alpha = 2\) and \(\varepsilon = 0.006\). We get the reconstructed image shown in Fig. 8c. The edges are preserved and the unknown area is restored quite well. This can be also observed in the TV-reconstructed image in Fig. 8d, using again the split Bregman method as before, cf. [31].
6.12 Conclusion
In this paper we developed a functional for regularization of functions with values in a set of vectors. The regularization functional is a derivative-free, nonlocal term, which is based on a characterization of Sobolev spaces of intensity data derived by Bourgain, Brézis, Mironescu and Dávila. Our objective has been to extend their double integral functionals in a natural way to functions with values in a set of vectors, in particular functions with values on an embedded manifold. These new integral representations are used for regularization on a subset of the (fractional) Sobolev space \(W^{s,p}(\Omega , {\mathbb {R}}^M)\) and the space \(BV(\Omega , {\mathbb {R}}^M)\), respectively. We presented numerical results for denoising of artificial InSAR data as well as an example of inpainting. Moreover, several conjectures are at hand on relations between double metric integral regularization functionals and single integral representations.
References
Adams, R.A.: Sobolev Spaces. Pure and Applied Mathematics, vol. 65. Academic Press, New York (1975)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs, p. xviii+434. Oxford University Press, New York (2000)
Aubert, G., Kornprobst, P.: Can the nonlocal characterization of Sobolev spaces by Bourgain et al. be useful for solving variational problems? SIAM J. Numer. Anal. 47(2), 844–860 (2009). https://doi.org/10.1137/070696751
Bacák, M., Bergmann, R., Steidl, G., Weinmann, A.: A second order non-smooth variational model for restoring manifold-valued images. SIAM J. Sci. Comput. 38(1), A567–A597 (2016). https://doi.org/10.1137/15M101988X
Bergmann, R., Chan, R.H., Hielscher, R., Persch, J., Steidl, G.: Restoration of manifold-valued images by half-quadratic minimization. Inverse Probl. Imaging 10(2), 281–304 (2016). https://doi.org/10.3934/ipi.2016001
Bergmann, R., Fitschen, J.H., Persch, J., Steidl, G.: Priors with coupled first and second order differences for manifold-valued image processing. J. Math. Imaging Vis. 60, 1459–1481 (2018)
Bergmann, R., Laus, F., Steidl, G., Weinmann, A.: Second order differences of cyclic data and applications in variational denoising. SIAM J. Imaging Sci. 7(4), 2916–2953 (2014). https://doi.org/10.1137/140969993
Bergmann, R., Persch, J., Steidl, G.: A parallel Douglas–Rachford algorithm for restoring images with values in symmetric Hadamard manifolds. SIAM J. Imaging Sci. 9(3), 901–937 (2016). https://doi.org/10.1137/15M1052858
Bergmann, R., Weinmann, A.: A second order TV-type approach for inpainting and denoising higher dimensional combined cyclic and vector space data. J. Math. Imaging Vis. 55(3), 401–427 (2016). https://doi.org/10.1007/s10851-015-0627-3
Bergmann, R., Weinmann, A.: Inpainting of cyclic data using first and second order differences. In: Tai, X.-C., Bae, E., Chan, T.F., Leung, S.Y., Lysaker, M. (eds.). EMMCVPR 2015, pp. 155–168. Springer, Berlin (2015). https://doi.org/10.1007/978-3-319-14612-6_12
Boulanger, J., Elbau, P., Pontow, C., Scherzer, O.: Non-local functionals for imaging. In: Bauschke, H.H., Burachik, R.S., Combettes, P.L., Elser, V., Luke, D.R., Wolkowicz, H. (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer Optimization and Its Applications, vol. 49, pp. 131–154. Springer, New York (2011). ISBN: 978-1-4419-9568-1. https://doi.org/10.1007/978-1-4419-9569-8
Bouman, C., Sauer, K.: A generalized Gaussian image model for edge-preserving MAP estimation. IEEE Trans. Image Process. 2(3), 296–310 (1993)
Bourgain, J., Brezis, H., Mironescu, P.: Lifting in Sobolev spaces. J. Anal. Math. 80, 37–86 (2000)
Bourgain, J., Brézis, H., Mironescu, P.: Another look at Sobolev spaces. In: Menaldi, J.L., Rofman, E., Sulem, A. (eds.) Optimal Control and Partial Differential Equations-Innovations and Applications: In honor of Professor Alain Bensoussan’s 60th Anniversary, pp. 439–455. IOS Press, Amsterdam (2001)
Chambolle, A., Lions, P.-L.: Image recovery via total variation minimization and related problems. Numer. Math. 76(2), 167–188 (1997)
Cimrák, I., Melicher, V.: Mixed Tikhonov regularization in Banach spaces based on domain decomposition. Appl. Math. Computat. 218(23), 11583–11596 (2012). https://doi.org/10.1016/j.amc.2012.05.042
Cremers, D., Koetter, S., Lellmann, J., Strekalovskiy, E.: Total variation regularization for functions with values in a manifold. In: IEEE international conference on computer vision, ICCV 2013, Sydney, Australia, 1–8 December 2013, pp. 2944–2951 (2013). https://doi.org/10.1109/ICCV.2013.366
Cremers, D., Strekalovskiy, E.: Total cyclic variation and generalizations. J. Math. Imaging Vis. 47(3), 258–277 (2013)
Cremers, D., Strekalovskiy, E.: Total variation for cyclic structures: convex relaxation and efficient minimization. In: CVPR, pp. 1905–1911. IEEE Computer Society (2011). ISBN: 978-1-4577-0394-2
Dacorogna, B.: Direct Methods in the Calculus of Variations. Applied Mathematical Sciences, vol. 78. Springer, Berlin (1989)
Dacorogna, B.: Weak Continuity and Weak Lower Semicontinuity of Non-Linear Functionals. Lecture Notes in Mathematics, vol. 922. Springer, Berlin (1982)
Daubechies, I., Defrise, M., De Mol, C.: An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 57(11), 1413–1457 (2004)
Dávila, J.: On an open question about functions of bounded variation. Calc. Var. Partial Differ. Equ. 15(4), 519–527 (2002)
Demengel, F., Demengel, G.: Functional Spaces for the Theory of Elliptic Partial Differential Equations. Springer, New York (2007)
Di Nezza, E., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136(5), 521–573 (2012). https://doi.org/10.1016/j.bulsci.2011.12.004
Eggermont, P.P.B.: Maximum entropy regularization for Fredholm integral equations of the first kind. SIAM J. Math. Anal. 24(6), 1557–1576 (1993)
Elstrodt, J.: Maß- und Integrationstheorie. Springer, Berlin (2002)
Engl, H.W., Landl, G.: Convergence rates for maximum entropy regularization. SIAM J. Numer. Anal. 30(5), 1509–1536 (1993)
Evans, L.C.: Partial Differential Equations. Graduate Studies in Mathematics, vol. 19. American Mathematical Society, Providence (2010)
Figalli, A., Villani, C.: Optimal transport and curvature. In: Ambrosio, L., Savaré, G. (eds.) Nonlinear PDE’s and Applications. Lecture Notes in Mathematics, vol. 2028, pp. 171–217. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21861-3_4
Getruer, P.: tvreg. From MathWorks—File Exchange
Giaquinta, M., Modica, G., Souček, J.: Variational problems for maps of bounded variation with values in S1. Calcul. Var. Partial Differ. Equ. 1(1), 87–121 (1993). https://doi.org/10.1007/BF02163266
Giaquinta, M., Mucci, D.: Maps of bounded variation with values into a manifold: total variation and relaxed energy. Annali della Scuala Normale Superiore di Pisa. Classe di Scienze (5) 5(4), 483–548 (2006)
Giaquinta, M., Mucci, D.: The BV-energy of maps into a manifold: relaxation and density results. Int. J. Pure Appl. Math. 3(2), 513–538 (2007)
Gilboa, G., Osher, S.: Nonlocal operators with applications to image processing. Multiscale Model. Simul. SIAM Interdiscip. J. 7(3), 1005–1028 (2008). https://doi.org/10.1137/070698592
Goldstein, T., Osher, S.: The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2, 323–343 (2009)
Grohs, P., Sprecher, M.: Total Variation Regularization by Iteratively Reweighted Least Squares on Hadamard Spaces and the Sphere. Technical Report, 2014-39. Seminar for Applied Mathematics, ETH Zürich, Switzerland (2014)
Hadani, R., Singer, A.: Representation theoretic patterns in three dimensional cryo-electron microscopy I: the intrinsic reconstitution algorithm. Ann. Math. 174(2), 1219–1241 (2011)
Helliwell, C.A., Anderssen, R.S., Robertson, M., Finnegan, E.J.: How is FLC repression initiated by cold? Trends Plant Sci. 20, 76–82 (2015)
Kimmel, R., Sochen, N.A.: Orientation diffusion or how to comb a Porcupine. J. Vis. Commun. Image Represent. 13(1–2), 238–248 (2002). https://doi.org/10.1006/jvci.2001.0501
Kolehmainen, V., Lassas, M., Niinimäki, K., Siltanen, S.: Sparsity-promoting Bayesian inversion. Inverse Probl. 28(2), 025005, 28 (2012). https://doi.org/10.1088/0266-5611/28/2/025005
Lassas, M., Saksman, E., Siltanen, S.: Discretization-invariant Bayesian inversion and Besov space priors. J. Inverse Ill Posed Probl. 3(1), 87–122 (2009)
Laus, F., Nikolova, M., Persch, J., Steidl, G.: A nonlocal denoising algorithm for manifold-valued images using second order statistics. SIAM J. Imaging Sci. 10(1), 416–448 (2017)
Liu, J.G., Mason, J.: Image Processing and GIS for Remote Sensing, 2nd edn. Wiley, London (2016)
Loendahl, C., Magiera, P.: ROF Denoising Algorithm. From MathWorks—File Exchange
Lorenz, D., Trede, D.: Optimal convergence rates for Tikhonov regularization in Besov scales. Inverse Probl. 24(5), 055010 (2008). (14 pp)
Osher, S., Esedoglu, S.: Decomposition of Images by the anisotropic Rudin–Osher–Fatemi model. Commun. Pure Appl. Math. 57(12), 1609–1626 (2004)
Plataniotis, K., Venetsanopoulos, A.N.: Color Image Processing and Applications. Springer, Berlin (2000)
Ponce, A.: A new approach to Sobolev spaces and connections to \(\Gamma \)-convergence. Calcul. Var. Partial Differ. Equ. 19, 229–255 (2004)
Pöschl, C.: Tikhonov Regularization with General Residual Term. English. Ph.D. Thesis. University of Innsbruck, Innsbruck, Austria (2008)
Puttonen, E., Briese, C., Mandlburger, G., Wieser, M., Pfennigbauer, M., Zlinszky, A., Pfeifer, N.: Quantification of overnight movement of Birch (Betula pendula) branches and foliage with short interval terrestrial laser scanning. Front. Plant Sci. 7, 222 (2016)
Resmerita, E., Anderssen, R.S.: Joint additive Kullback–Leibler residual minimization and regularization for linear inverse problems. Math. Methods Appl. Sci. 30(13), 1527–1544 (2007)
Rocca, F., Prati, C., Ferretti, A.: An overview of SAR interferometry. In: 3rd ERS Symposiumm, Florence 97—Abstracts and Papers (1997)
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 60(1–4), 259–268 (1992)
Scherzer, O., Grasmair, M., Grossauer, H., Haltmeier, M., Lenzen, F.: Variational Methods in Imaging. Applied Mathematical Sciences, vol. 167. Springer, New York (2009). https://doi.org/10.1007/978-0-387-69277-7
Scherzer, O., Weickert, J.: Relations between regularization and diffusion filtering. J. Math. Imaging Vis. 12(1), 43–63 (2000). https://doi.org/10.1023/A:1008344608808
Schuster, T., Kaltenbacher, B., Hofmann, B., Kazimierski, K.S.: Regularization Methods in Banach Spaces. Radon Series on Computational and Applied Mathematics, vol. 10, p. xii+283. De Gruyter, Berlin (2012). https://doi.org/10.1515/9783110255720
Singer, A., Shkolnisky, Y.: Viewing direction estimation in cryo-EM using synchronization. SIAM J. Imaging Sci. 5(3), 1088–1110 (2012). https://doi.org/10.1137/120863642
Tikhonov, A.N., Arsenin, V.Y.: Solutions of Ill-Posed Problems. Wiley, Washington, DC (1977)
Vogel, C.R., Oman, M.E.: Iterative methods for total variation denoising. SIAM J. Sci. Comput. 17, 227–238 (1996)
Wang, L., Singer, A., Wen, Z.: Orientation determination of cryo-EM images using least unsquared deviations. SIAM J. Imaging Sci. 6(4), 2450–2483 (2013). https://doi.org/10.1137/130916436
Weinmann, A., Demaret, L., Storath, M.: Total variation regularization for manifold-valued data. SIAM J. Imaging Sci. 7(4), 2226–2257 (2014)
Acknowledgements
Open access funding provided by Austrian Science Fund. We thank Peter Elbau for very helpful discussions and comments. MH and OS acknowledge support from the Austrian Science Fund (FWF) within the national research network Geometry and Simulation, Project S11704 (Variational Methods for Imaging on Manifolds). Moreover, OS is supported by the Austrian Science Fund (FWF), with SFB F68, Project F6807-N36 (Tomography with Uncertainties) and I3661-N27 (Novel Error Measures and Source Conditions of Regularization Methods for Inverse Problems).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ciak, R., Melching, M. & Scherzer, O. Regularization with Metric Double Integrals of Functions with Values in a Set of Vectors. J Math Imaging Vis 61, 824–848 (2019). https://doi.org/10.1007/s10851-018-00869-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-018-00869-6




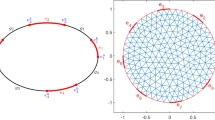
 is an operator modeling the image formation process (except the noise).
is an operator modeling the image formation process (except the noise). and
and  denotes the Euclidean distance on
denotes the Euclidean distance on  denote arbitrary metrics on
denote arbitrary metrics on  ,
, , meaning that for a sequence
, meaning that for a sequence  in
in  .
. . When the set
. When the set  .
. .
.


 , given by
, given by 


 is the semi-norm for
is the semi-norm for  , given by
, given by 

 from [
from [

 . Then there exists a subsequence
. Then there exists a subsequence  .
. . Then there exists a subsequence
. Then there exists a subsequence  .
. is associated with the strong
is associated with the strong  -topology,
-topology, is associated with the weak
is associated with the weak  -topology, and
-topology, and is associated with the weak*
is associated with the weak*  -topology.
-topology. -topology in the case
-topology in the case  -topology when
-topology when  and
and  are sets which do not form a linear space.
are sets which do not form a linear space.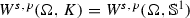 as occurred in [
as occurred in [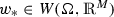 and
and  with
with  and
and  in
in  .
. and
and  with
with  as
as  and there is some subsequence
and there is some subsequence  ,
,
 satisfies the metric axioms.
satisfies the metric axioms. and that both metrics
and that both metrics  , respectively. Then the functional
, respectively. Then the functional  does not attain the value
does not attain the value 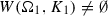 .
. since
since  is a metric. To prove the triangle inequality, let
is a metric. To prove the triangle inequality, let  Hölder’s inequality yields
Hölder’s inequality yields 

 , the triangle inequality is trivially fulfilled.
, the triangle inequality is trivially fulfilled. applying the estimate
applying the estimate 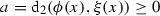 and
and  yields
yields 
 because every constant function
because every constant function  for
for  for
for 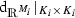 for
for  . We need to prove that
. We need to prove that 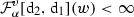 for every
for every  . Due to
. Due to  for all
for all  it is sufficient to show
it is sufficient to show  for all
for all  .
. this is guaranteed by [
this is guaranteed by [ by [
by [ ,
,  , we have that
, we have that  for
for 
 , we can estimate
, we can estimate 
 .
.  with respect to
with respect to  guarantees lower semicontinuity of
guarantees lower semicontinuity of  and
and  .
. carries over to the inequalities
carries over to the inequalities  for all
for all  , and
, and  for all
for all  , allowing to transfer properties like coercivity from
, allowing to transfer properties like coercivity from  to
to  . Moreover, the extended real-valued metric space
. Moreover, the extended real-valued metric space  stays related to the linear space
stays related to the linear space  in terms of the topology and bornology induced by
in terms of the topology and bornology induced by  , resp. those inherited by
, resp. those inherited by  .
. is a sequentially closed subset of the linear space
is a sequentially closed subset of the linear space  . This closedness property acts as a kind of replacement for the, a priori not available, notion of completeness with respect to the “space”
. This closedness property acts as a kind of replacement for the, a priori not available, notion of completeness with respect to the “space”  .
. is well defined and sequentially continuous with respect to the specified topology on
is well defined and sequentially continuous with respect to the specified topology on  and
and
 is nonempty.
is nonempty. are considered which additionally fulfill
are considered which additionally fulfill  .
. is sequentially lower semi-continuous, i.e., whenever sequences
is sequentially lower semi-continuous, i.e., whenever sequences  ,
,  in
in 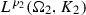 converge to
converge to  and
and  , respectively, we have
, respectively, we have  .
.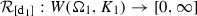 is sequentially lower semi-continuous, i.e., whenever a sequence
is sequentially lower semi-continuous, i.e., whenever a sequence  converges to some
converges to some  we have
we have 
 is sequentially lower semi-continuous.
is sequentially lower semi-continuous. ,
,  in
in  which converge to previously fixed elements
which converge to previously fixed elements  and
and  , respectively, we can extract subsequences
, respectively, we can extract subsequences 
 with
with  and
and  in
in  . Lemma
. Lemma  with respect to
with respect to  , cf. Sect.
, cf. Sect. 


 with
with 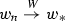 as
as  . By Lemma
. By Lemma  and pointwise almost everywhere. This further implies that
and pointwise almost everywhere. This further implies that 


 for almost every
for almost every  and
and  of
of 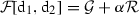 are sequentially lower semi-continuous. To prove that
are sequentially lower semi-continuous. To prove that  as
as  . Assumption
. Assumption  , implies hence
, implies hence  in
in  as
as  . By item (i) we thus obtain
. By item (i) we thus obtain  .
.
 .
.


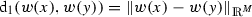 the functional
the functional  from Eq.
from Eq. 
 , then
, then  from Eq.
from Eq. 

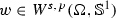 there exists
there exists  satisfying Eq.
satisfying Eq.  there exists
there exists  satisfying Eq.
satisfying Eq.  such that Eq.
such that Eq.  .
. only with the following regularization functional, cf. Example
only with the following regularization functional, cf. Example 






