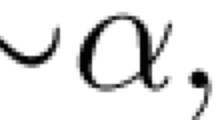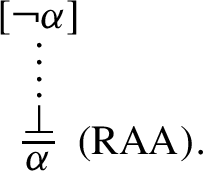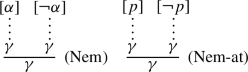Skip to main content
SpringerLink
Log in

Rules of Explosion and Excluded Middle: Constructing a Unified Single-Succedent Gentzen-Style Framework for Classical, Paradefinite, Paraconsistent, and Paracomplete Logics

  • Published:
Journal of Logic, Language and Information Aims and scope Submit manuscript

Abstract

A unified and modular falsification-aware single-succedent Gentzen-style framework is introduced for classical, paradefinite, paraconsistent, and paracomplete logics. This framework is composed of two special inference rules, referred to as the rules of explosion and excluded middle, which correspond to the principle of explosion and the law of excluded middle, respectively. Similar to the cut rule in Gentzen’s LK for classical logic, these rules are admissible in cut-free LK. A falsification-aware single-succedent Gentzen-style sequent calculus fsCL for classical logic is formalized based on the proposed framework. The calculus fsCL is obtained from the existing falsification-aware single-succedent Gentzen-style sequent calculus GN4 for Nelson’s paradefinite (or paraconsistent) four-valued logic N4 by adding the rules of explosion and excluded middle. A falsification-aware single-succedent Gentzen-style sequent calculus GN3 for Nelson’s paracomplete three-valued logic N3 is also obtained from GN4 by adding the rule of explosion. The cut-elimination theorems for fsCL, GN3, and some of their neighbors as well as the Glivenko theorem for fsCL are proved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. (ex-middle) and its restricted version were originally introduced by von Plato (1999) and were also presented in Negri and von Plato (2001).

  2. (cut) is well-known to be a structural rule. However, the proposal for saying that (explosion) and (ex-middle) are structural rules has an issue. These two rules involve the negation and the validity of the rules depends on the definition of the negation. Thus, in this aspect, they seem to rather logical inference rules. Besides, the corresponding properties of paraconsistency and paracompleteness are the properties that deal not only with consequence relation, but also with the negation. Thus, the issue with classification of these rules is not clear or simple.

  3. The logic N4 was originally introduced as a first-order predicate logic refereed to as N\(^-\) (Almukdad & Nelson, 1984; Nelson, 1949) which has the following axiom schemes: \(\lnot \forall x \alpha (x) \leftrightarrow \exists x \lnot \alpha (x)\) and \(\lnot \exists x \alpha (x) \leftrightarrow \forall x \lnot \alpha (x)\).

  4. The logic N3 was originally introduced as a first-order predicate logic refereed to as N Almukdad and Nelson (1984); Nelson (1949). Odintsov (2002) showed that propositional N3 can be faithfully embedded into propositional N4.

  5. Avron also used the name Pac for the implication-less fragment of this logic.

  6. Since the cut-elimination theorem for GN4 holds, it is sufficient to check the additional cases for (we-right) and (explosion) in GN3.

  7. (Peirce), (r-Peirce), (Raa), as well as (ex-middle) can be seen as the sequent calculus rule versions of the corresponding natural deduction rules. For example, (Raa) is the sequent calculus rule version of the well-known natural deduction rule of the form:

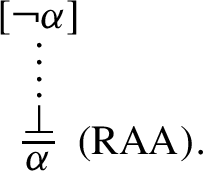
  8. In von Plato (1999); Negri and von Plato (2001), he also introduced the following natural deduction rules (Nem) and (Nem-at) that correspond to (ex-middle) and (ex-middle-at), respectively.

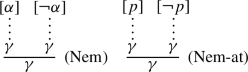
    where p is a propositional variable. He construct natural deduction systems (for classical logic) with these rules and proved a normalization theorem for the natural deduction system with (Nem-at).

References

  • Africk, H. (1992). Classical logic, intuitionistic logic, and the Peirce rule. Notre Dame Journal of Formal Logic, 33(2), 229–235.

    Article  Google Scholar 

  • Almukdad, A., & Nelson, D. (1984). Constructible falsity and inexact predicates. Journal of Symbolic Logic, 49(1), 231–233.

    Article  Google Scholar 

  • Arieli, O., & Avron, A. (2016) Minimal paradefinite logics for reasoning with incompleteness and inconsistency. In Proceedings of the 1st international conference on formal structures for computation and deduction (FSCD), Leibniz International Proceedings in Informatics (LIPIcs) 52, pp. 7:1-7:15.

  • Arieli, O., & Avron, A. (2017). Four-valued paradefinite logics. Studia Logica, 105(6), 1087–1122.

    Article  Google Scholar 

  • Asenjo, F. G. (1966). A calculus of antinomies. Notre Dame Journal of Formal Logic, 7, 103–106.

    Article  Google Scholar 

  • Asenjo, F. G., & Tamburino, J. (1975). Logic of antinomies. Notre Dame Journal of Formal Logic, 16(1), 17–44.

    Article  Google Scholar 

  • Avron, A. (1986). On an implicational connective of RM. Notre Dame Journal of Formal Logic, 27(2), 201–209.

    Article  Google Scholar 

  • Avron, A. (1991). Natural 3-valued logics: Characterization and proof theory. Journal of Symbolic Logic, 61(1), 276–294.

    Article  Google Scholar 

  • Avron, A. (2003) Classical Gentzen-type methods in propositional many-valued logics. Studies in Fuzziness and Soft Computing, pp. 117–155

  • Avron, A., Arieli, O., & Zamansky, A. (2018). Theory of effective propositional paraconsistent logics. Studies in Logic - Mathematical Logic and Foundations, Volume 75, 550 pages, College Publications.

  • Batens, D. (1980). Paraconsistent extensional propositional logics. Logique et Anal., 23(90–91), 195–234.

    Google Scholar 

  • Belnap, N. D. (1977). A useful four-valued logic, In Modern uses of multiple-valued logic, G. Epstein and J. M. Dunn (eds.), Dordrecht: Reidel, pp. 5–37.

  • Belnap, N. D. (1977). How a computer should think. In G. Ryle (ed.) Contemporary aspects of philosophy, Oriel Press, Stocksfield, pp. 30–56

  • Béziau, J.-Y. (2009) Bivalent semantics for De Morgan logic (The uselessness of four-valuedness), In W.A. Carnieli, M.E. Coniglio and I.M. D’Ottaviano (Eds.), The many sides of logic, pp. 391–402, College Publications.

  • Bolotov, A., & Shangin, V. (2012). Natural deduction system in paraconsistent setting: Proof search for PCont. Journal of Intelligent Systems, 21(1), 1–24.

    Article  Google Scholar 

  • Czermak, J. (1977). A remark on Gentzen’s calculus of sequents. Notre Dame Journal of Formal Logic, 18, 471–474.

    Article  Google Scholar 

  • Curry, H. B. (1963). Foundations of mathematical logic. McGraw-Hill.

  • da Costa, N. C. A. (1974). On the theory of inconsistent formal systems. Notre Dame Journal of Formal Logic, 15(4), 497–510.

    Article  Google Scholar 

  • D’Ottaviano, I. M. L., & da Costa, N. C. A. (1970). Sur un probléme de Jaśkowski. Comptes Rendus Acad. Sci. Paris., 270A, 1349–1353.

    Google Scholar 

  • Dunn, J. M. (1976). Intuitive semantics for first-degree entailment and ‘coupled trees’. Philosophical Studies, 29(3), 149–168.

  • Dunn, T. J. M. (2019) The Algebra of intensional logics, a republication of a Ph.D. thesis, which was originally defended at the University of Pittsburgh in 1966, College Publications, London, UK.

  • Felscher, W. (1975). Kombinatorische Konstruktionen mit beweisen und schnittelimination. Lecture Notes in Mathematics, 500, 119–151.

    Article  Google Scholar 

  • Gentzen, G. (1969) Collected papers of Gerhard Gentzen. In M. E. Szabo (Ed.), Studies in logic and the foundations of mathematics, North-Holland (English translation).

  • Goodman, N. D. (1981). The logic of contradiction. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 27, 119–126.

    Article  Google Scholar 

  • Goranko, V. (1994). Refutation systems in modal logic. Studia Logica, 53, 299–324.

    Article  Google Scholar 

  • Goranko, V. (2019). Hybrid deduction-refutation systems. Axioms, 8(4) 118–119.

  • Goranko, V., Pulcini, G., Skura, T. (2020) Refutation systems: An overview and some applications to philosophical logics, In Knowledge, proof and dynamics, pp. 173–197.

  • Gordeev, L. (1987). On cut elimination in the presence of Peirce rule. Archiv für Mathematische Logik und Grundlagenforsch, 26, 147–164.

    Article  Google Scholar 

  • Horn, L. R., Wansing, H. (2017). Negation, The Stanford Encyclopedia of Philosophy (Spring 2017 Edition), Edward N. Zalta (editor), Last modified on January, https://plato.stanford.edu/archives/spr2017/entries/negation/.

  • Kamide, N. (2005). Cut-free single-succedent systems revisited. Bulletin of the Section of Logic, 34(3), 165–175.

    Google Scholar 

  • Kamide, N. (2005). Natural deduction systems for Nelson’s paraconsistent logic and its neighbors. Journal of Applied Non-Classical Logics, 15(4), 405–435.

    Article  Google Scholar 

  • Kamide, N. (2018). Proof theory of paraconsistent quantum logic. Journal of Philosophical Logic, 47(2), 301–324.

    Article  Google Scholar 

  • Kamide, N. (2022). Falsification-aware semantics and sequent calculi for classical logic. Journal of Philosophical Logic, 51(1), 99–126.

    Article  Google Scholar 

  • Kamide, N. (2023). Falsification-aware calculi and semantics for normal modal logics including S4 and S5. Journal of Logic, Language and Information, 32(3), 395–440.

    Article  Google Scholar 

  • Kamide, N. (2023). Refutation-aware Gentzen-style calculi for propositional until-free linear-time temporal logic. Studia Logica, 111(6), 979–1014.

    Article  Google Scholar 

  • Kamide, N., & Wansing, H. (2012). Proof theory of Nelson’s paraconsistent logic: A uniform perspective. Theoretical Computer Science, 415, 1–38.

    Article  Google Scholar 

  • Kamide, N., Wansing, H. (2015). Proof theory of N4-related paraconsistent logics. Studies in Logic, 54, College Publications, pp. 1–401.

  • Kapsner, A. (2014). Logics and falsifications: A new perspective on constructivist semantics. Trends in Logic Book 40, Springer.

  • Kürbis, N., & Petrukhin, Y. (2021). Normalisation for some quite interesting many-valued logics. Logic and Logical Philosophy, 30(3), 493–534.

    Google Scholar 

  • Kleene, S. C. (2009). Introduction to Metamathematics (with a new foreworded by M. Beeson). ISHI Press International.

  • Łukasiewicz, J. (1987). Aristotle’s syllogistic from the standpoint of modern formal logic, Oxford, 1951 (Aristotle’s syllogistic from the standpoint of modern formal logic - Greek & Roman philosophy, Taylor & Francis).

  • Łukowski, P. (2002). A deductive-reductive form of logic: General theory and intuitionistic case. Logic and Logical Philosophy, 10, 59–78.

    Article  Google Scholar 

  • Moore, E. (2021). Hybrid deduction-refutation systems for FDE-based logics. The Australasian Journal of Logic, 18(6), 597–615.

    Article  Google Scholar 

  • Negri, S., & von Plato, J. (2001). Structural proof theory. Cambridge University Press.

  • Nelson, D. (1949). Constructible falsity. Journal of Symbolic Logic, 14, 16–26.

    Article  Google Scholar 

  • Odintsov, S. P. (2002). On the embedding of Nelson’s logics. Bulletin of the Section of Logic, 31(4), 241–248.

    Google Scholar 

  • Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8(1), 219–241.

    Article  Google Scholar 

  • Priest, G. (2002) Paraconsistent logic. In D. Gabbay and F. Guenthner (Eds.) Handbook of Philosophical Logic (Second Edition), vol. 6, Kluwer, Dordrecht, pp. 287–393.

  • Rauszer, C. (1974). A formalization of the propositional calculus of H-B logic. Studia Logica, 33, 23–34.

    Article  Google Scholar 

  • Rauszer, C. (1977). Applications of Kripke models to Heyting–Brouwer logic. Studia Logica, 36, 61–71.

    Article  Google Scholar 

  • Rauszer, C. (1980). An algebraic and Kripke-style approach to a certain extension of intuitionistic logic. Dissertations Mathematicae, Polish Scientific Publishers, pp. 1–67.

  • Rozonoer, L. I. (1989). On interpretation of inconsistent theories. Information Sciences, 47(3), 243–266.

    Article  Google Scholar 

  • Shramko, Y. (2005). Dual intuitionistic logic and a variety of negations: The logic of scientific research. Studia Logica, 80(2–3), 347–367.

    Article  Google Scholar 

  • Shramko, Y. (2016). A modal translation for dual-intuitionistic logic. Review of Symbolic Logic, 9(2), 251–265.

    Article  Google Scholar 

  • Skura, T. F. (1995). A Łukasiewicz-style refutation system for the modal logic S4. Journal of Philosophical Logic, 24, 573–582.

    Article  Google Scholar 

  • Skura, T. F. (2002). Refutations, proofs, and models in the modal logic K4. Studia Logica, 70(2), 193–204.

    Article  Google Scholar 

  • Skura, T. F. (2011). Refutation systems in propositional logic. Handbook of Philosophical Logic, 16, 115–157.

    Article  Google Scholar 

  • Skura, T. F. (2017). Refutations in Wansing’s logic. Reports on Mathematical Logic, 52, 83–99.

    Article  Google Scholar 

  • Urbas, I. (1996). Dual-intuitionistic logic. Notre Dame Journal of Formal Logic, 37(3), 440–451.

    Article  Google Scholar 

  • von Plato, J. (1999). Proof theory of full classical propositional logic. Manuscript, 16 pages.

  • Wansing, H. (1993). The logic of information structures. Lecture Notes in Artificial Intelligence 681, 163 pages.

  • Wansing, H. (1995). Semantics-based nonmonotonic inference. Notre Dame Journal of Formal Logic, 36, 44–54.

    Article  Google Scholar 

  • Wansing, H. (2010). Proofs, disproofs, and their duals. Advances in Modal Logic, 8, 483–505.

    Google Scholar 

  • Wansing, H. (2016). Falsification, natural deduction and bi-intuitionistic logic. Journal of Logic and Computation, 26(1), 425–450.

    Article  Google Scholar 

Download references

Acknowledgements

We would like to thank the anonymous referees for their valuable comments. Specifically, the relationship among ELP, PI\(^s\), RM\(^{\supset }_3\), Pac, and PCont was pointed out by a referee. This research was supported by JSPS KAKENHI Grant Number 23K10990.

Author information

Authors and Affiliations

  1. School of Data Science, Nagoya City University, Yamanohata 1, Mizuho-cho, Mizuho-ku, Nagoya, Aichi, 467-8501, Japan

    Norihiro Kamide

Authors
  1. Norihiro Kamide
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Norihiro Kamide.

Ethics declarations

Conflict of interest

The authors have no Conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kamide, N. Rules of Explosion and Excluded Middle: Constructing a Unified Single-Succedent Gentzen-Style Framework for Classical, Paradefinite, Paraconsistent, and Paracomplete Logics. J of Log Lang and Inf (2024). https://doi.org/10.1007/s10849-024-09416-6

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10849-024-09416-6

Keywords

Search

Navigation