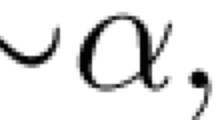Skip to main content
SpringerLink
Log in

Kripke-Completeness and Cut-elimination Theorems for Intuitionistic Paradefinite Logics With and Without Quasi-Explosion

  • Published:
Journal of Philosophical Logic Aims and scope Submit manuscript

A Correction to this article was published on 04 August 2020

This article has been updated

Abstract

Two intuitionistic paradefinite logics N4C and N4C+ are introduced as Gentzen-type sequent calculi. These logics are regarded as a combination of Nelson’s paraconsistent four-valued logic N4 and Wansing’s basic constructive connexive logic C. The proposed logics are also regarded as intuitionistic variants of Arieli, Avron, and Zamansky’s ideal paraconistent four-valued logic 4CC. The logic N4C has no quasi-explosion axiom that represents a relationship between conflation and paraconsistent negation, but the logic N4C+ has this axiom. The Kripke-completeness and cut-elimination theorems for N4C and N4C+ are proved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Change history

  • 04 August 2020

    The original version of this article unfortunately contains several errors introduced by the typesetter during the publishing process. It has been corrected.

References

  1. Almukdad, A., & Nelson, D. (1984). Constructible falsity and inexact predicates. Journal of Symbolic Logic, 49(1), 231–233.

    Article  Google Scholar 

  2. Angell, R. (1962). A propositional logics with subjunctive conditionals. Journal of Symbolic Logic, 27, 327–343.

    Article  Google Scholar 

  3. Arieli, O., & Avron, A. (1996). Reasoning with logical bilattices. Journal of Logic Language and Information, 5, 25–63.

    Article  Google Scholar 

  4. Arieli, O., & Avron, A. (1998). The value of the four values. Artificial Intelligence, 102(1), 97–141.

    Article  Google Scholar 

  5. Arieli, O., & Avron, A. (2016). Minimal paradefinite logics for reasoning with incompleteness and inconsistency. In Proceedings of the 1st international conference on formal structures for computation and deduction (FSCD), Leibniz International Proceedings in Informatics (LIPIcs), (Vol. 52 pp. 7:1-7:15).

  6. Arieli, O., & Avron, A. (2017). Four-valued paradefinite logics. Studia Logica, 105(6), 1087–1122.

    Article  Google Scholar 

  7. Arieli, O., Avron, A., & Zamansky, A. (2011). Ideal paraconsistent logics. Studia Logica, 99(1-3), 31–60.

    Article  Google Scholar 

  8. Avron, A., Arieli, O., & Zamanskey, A. (2018). Theory of effective propositional paraconsistent logics, Studies in Logic (Mathematical Logic and Foundations) (Vol. 75, p. 550). Oxford: College Publications.

    Google Scholar 

  9. Belnap, N.D. (1977). A useful four-valued logic. In Epstein, G., & Dunn, J.M. (Eds.) Modern uses of multiple-valued logic (pp. 5–37). Dordrecht: Reidel.

  10. Belnap, N.D. (1977). How a computer should think. In Ryle, G. (Ed.) Contemporary aspects of philosophy (pp. 30–56). Stocksfield: Oriel Press.

  11. Béziau, J.Y. (2009). Bivalent semantics for De Morgan logic (The uselessness of four-valuedness). In Carnieli, W.A., Coniglio, M.E., & D’Ottaviano, I.M. (Eds.) The many sides of logic (pp. 391–402). Oxford: College Publications.

  12. De, M., & Omori, H. (2015). Classical negation and expansions of Belnap-Dunn logic. Studia Logica, 103(4), 825–851.

    Article  Google Scholar 

  13. Dunn, J.M. (1976). Intuitive semantics for first-degree entailment and coupled trees. Philosophical Studies, 29(3), 149–168.

    Article  Google Scholar 

  14. Gabbay, D.M., & Wansing, H. (Eds.). (1999). What is negation? Applied Logic Series 13. Norwell: Kluwer Academic Publishers.

    Google Scholar 

  15. Gentzen, G. (1969). Collected papers of Gerhard Gentzen. In Szabo, M.E. (Ed.) Studies in logic and the foundations of mathematics, North-Holland (English translation).

  16. Gurevich, Y. (1977). Intuitionistic logic with strong negation. Studia Logica, 36, 49–59.

    Article  Google Scholar 

  17. Horn, L.R., & Wansin, H. (2017). Negation. In Zalta, E.N. (Ed.) The Stanford Encyclopedia of Philosophy (Spring 2017 Edition). https://plato.stanford.edu/archives/spr2017/entries/negation/.

  18. Kamide, N. (2015). Trilattice logic: an embedding-based approach. Journal of Logic and Computation, 25(3), 581–611.

    Article  Google Scholar 

  19. Kamide, N. (2017). Extending ideal paraconsistent four-valued logic. In Proceedings of the 47th IEEE international symposium on multiple-valued logic (ISMVL 2017) (pp. 49–54).

  20. Kamide, N., & Shramko, Y. (2017). Embedding from multilattice logic into classical logic and vice versa. Journal of Logic and Computation, 27(5), 1549–1575.

    Google Scholar 

  21. Kamide, N., & Wansing, H. (2012). Proof theory of Nelson’s paraconsistent logic: a uniform perspective. Theoretical Computer Science, 415, 1–38.

    Article  Google Scholar 

  22. Kamide, N., & Wansing, H. (2015). Proof theory of N4-related paraconsistent logics. In Studies in logic, (Vol. 54 pp. 1–401). London: College Publications.

  23. Kamide, N., & Zohar, Y. (2019). Yet another paradefinite logic: the role of conflation. Logic Journal of the IGPL, 27(1), 93–117.

    Google Scholar 

  24. McCall, S. (1966). Connexive implication. Journal of Symbolic Logic, 31, 415–433.

    Article  Google Scholar 

  25. Nelson, D. (1949). Constructible falsity. Journal of Symbolic Logic, 14, 16–26.

    Article  Google Scholar 

  26. Omori, H., & Wansing, H. (2015). A web site on connexive logic. https://sites.google.com/site/connexivelogic/home.

  27. Priest, G. (2002). Paraconsistent logic. In Gabbay, D., & Guenthner, F. (Eds.) Handbook of philosophical logic. 2nd edn., (Vol. 6 pp. 287–393). Dordrecht: Kluwer Academic Publishers.

  28. Rautenberg, W. (1979). Klassische und nicht-klassische Aussagenlogik. Braunschweig: Vieweg.

    Book  Google Scholar 

  29. Shramko, Y. (2016). Truth, falsehood, information and beyond: the American plan generalized. In Bimbo, K. (Ed.) J. Michael Dunn on information based logics, outstanding contributions to logic, (Vol. 8 pp. 191–212). Berlin: Springer.

  30. Shramko, Y., & Wansing, H. (2005). Some useful sixteen-valued logics: how a computer network should think. Journal of Philosophical Logic, 34, 121–153.

    Article  Google Scholar 

  31. Takeuti, G. (2013). Proof theory, 2nd edn. New York: Dover Publications, Inc. Mineola.

    Google Scholar 

  32. Vorob’ev, N.N. (1952). A constructive propositional calculus with strong negation (in Russian). Doklady Akademii Nauk SSSR, 85, 465–468.

    Google Scholar 

  33. Wansing, H. (1993). The logic of information structures. Lecture Notes in Artificial Intelligence, 681, 163.

    Google Scholar 

  34. Wansing, H. (2005). Connexive modal logic. Advances in Modal Logic, 5, 367–385.

    Google Scholar 

  35. Wansing, H. (2014). Connexive logic, Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/logic-connexive/.

  36. Wansing, H., & Odintsov, S.P. (2016). On the methodology of paraconsistent logic. In Logical studies of paraconsistent reasoning in science and mathematics. Trends in Logic Book Series (pp. 175–204). Berlin: Springer.

  37. Wansing, H., Omori, H., & Ferguson, T.M. (2016). Special issue: connexive logics. IfCoLog Journal of Logics and their Applications, 3(3).

Download references

Acknowledgments

We would like to thank the anonymous referees for their valuable comments. This research was supported by JSPS KAKENHI Grant Numbers JP18K11171, JP16KK0007, and JSPS Core-to-Core Program (A. Advanced Research Networks).

Author information

Authors and Affiliations

  1. Department of Information and Electronic Engineering, Faculty of Science and Engineering, Teikyo University, Toyosatodai 1-1, Utsunomiya, Tochigi, 320-8551, Japan

    Norihiro Kamide

Authors
  1. Norihiro Kamide
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Norihiro Kamide.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kamide, N. Kripke-Completeness and Cut-elimination Theorems for Intuitionistic Paradefinite Logics With and Without Quasi-Explosion. J Philos Logic 49, 1185–1212 (2020). https://doi.org/10.1007/s10992-020-09553-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10992-020-09553-w

Keywords

Search

Navigation