Introduction

Milling is a flexible and highly productive manufacturing process. A rotating cutting movement of a tool is overlaid by a linear feed movement resulting in a cyclically intermittent cut with a defined edge. The productivity, workpiece quality, and safety of the milling process strongly depend on the force acting on the tool. A high mechanical tool load usually signifies productivity but may deflect the tool causing a violation of the desired dimensional accuracy of the workpiece, which is a measure of quality. Further, large peaks in the force may boost tool wear and ultimately provoke tool failure (process safety). As a result, running the process at its productivity optimum while ensuring process safety and workpiece quality requires to maintain a specific process force at any time.

The great advances in construction and design of machine tools and their controllers cannot overshadow the defect that machine tool setpoints (e.g. tool position) are controlled rather than process variables (e.g. force) (Thombansen et al. 2018). Past research on controlling process variables used classic controllers, which were unable to prevent force peaks at abrupt changes in the tool engagement, e.g. when the tool enters the workpiece, because they react to a deviation of the force. “The basic problem arises from the fact that the effective process gains and time constants depend upon process variables such as feed, speed, and depth of cut. Furthermore, process related parameters such as tool geometry, work, and tool material properties are difficult to characterize and can have a significant effect on the process dynamics. This unpredictability of the process can lead to poor performance, tool breakage, or even instability when fixed gain process controllers are used” (Ulsoy and Koren 1993).

Advanced control methods address the limitations of classic controllers. As one representative, model predictive control (MPC) predicts the future behavior explicitly considering a process model and technological constraints (e.g. actuator saturation).

Due to higher forces, the proposed method is focusing on roughing processes. To avoid chatter and thus limit complexity a rigid process setup with a minimal protruding length is used. Further only the feed was manipulated and the cutting speed was constant (\(v_{c}= 80\hbox { mm s}^{-1}\)).

The previous works of the authors at the RWTH Aachen University demonstrated the applicability of MPC to the milling process focusing on distinct parts of the control system (Stemmler et al. 2016; Adams et al. 2016; Stemmler et al. 2017; Schwenzer et al. 2017; Ay et al. 2018; Stemmler et al. 2019; Ay et al. 2019). The presented contribution outlines the entire system extending the work at the feedback of the force. Therefore, the state of the art is presented in “State of the art” section. The proposed force control system is described in “Approach” section, while “Results and discussion” section experimentally validates it.

State of the art

This sections presents first, the state of the art regarding force control approaches in milling (“Force control in milling” section) and second, regarding the identification of a process model (“Force model identification” section).

Force control in milling

In milling, predominantly the maximum active forceFootnote 1\(F_{a,max}\) is used as the control variable. The feed rate is almost exclusively the manipulated variable, which is the output of the controller. Taking these definitions into account, the control approaches of the state of the art can be clustered into:

  • fixed-gain controllers,

  • adaptive controllers, and

  • simulation-enhanced and advanced controllers.

The fixed-gain controllers are characterized by a predefined control law with a constant controller parameterization, such as PID controllers. Tu and Corless (2014) examined different controller designs and control variables at The Boeing Company in the 1980s. They reduced spindle failure by 90% at the beginnings of high-speed milling focusing on the spindle power as the control variable. Commercial control systems for milling today still work with similar strategies to avoid an individual design for each machine tool. They control the effective power of the spindle, e.g. Ceratizit S.A., Marposs Monitoring Solutions GmbH, or MCU GmbH. All commercial vendors apply time-invariant controllers—although misleadingly promoted as “adaptive controllers” arguing that they adapt the feedrate. The reactive nature of fixed-gain controllers make them unable to prevent overshoots at abrupt changes of engagement conditions.

Adaptive controllers, on the other hand, often combine online parameter estimation with an a priori determined control law (structure) (Ulsoy and Koren 1993). Altintas and Ma (1990) used a simple nonlinear model of the maximum force (per revolution) to the feedrate based on a static deformation model. Simulation and experiments showed good results for a slowly changing ramp in the depth of cut but overshot the desired force level by 80% at sudden changes. Nonetheless, adaptive controllers eliminated the constant offset of a P controller by adapting the controller gain e.g. Nolzen and Isermann (1995). Fussell and Srinivasan (1991) could not confirm a better transient behavior of adaptive control in milling (as simulation) than fixed-gain control but concluded that adaptive control was more stable over a wide range of cutting conditions. As a consequence, more advanced techniques, such as model reference adaptive control (MRAC), have been examined. MRAC improved the transient behavior in the occurrence of a change of the depth of cut but it suffered from poor convergence in case of a constant reference compared to a PI controller (Lauderbaugh and Ulsoy 1989).

Fig. 1
figure 1

Block diagram of the model predictive force control system

Full size image

Nolzen (1997) noted that adaptive control systems have not been reliable enough for a broad success in industry. The primary reason was the limited reaction time (Cus et al. 2011), which is inherent in terms of inertia (Park and Altintas 2004). Adaptive control can stabilize process setpoints at slowly varying process conditions. “Any effective control scheme must be able to anticipate geometry changes” (Richards et al. 2002). Thus, simulation-enhanced approaches were developed. A process simulation was used as a separate source of information without a feedback in conjunction with a closed-loop fixed-gain controller, e.g. in (Spence and Altintas 1991; Yamazaki et al. 1991; Richards et al. 2002). Spence and Altintas (1991) superposed the measured force with predicted force from simulation letting the controller react to the future process behavior. Instead of manipulating the feedback, Yamazaki et al. (1991) performed an offline simulation of the milling process to generate the optimal reference in terms of material removal rate (MRR). This reference feedrate was then implemented by a fixed-gain controller. Richards et al. (2002) picked up this concept comparing a P controller and an adaptive controller for compensating inaccuracies of the model, which generated the reference. Tukora and Szalay (2011) proposed an online process simulation including an adapted force model, but the demonstration was conducted offline. An approach using a neural network was suggested by Zuperl et al. (2012) and Zuperl and Cus (2012) combined it with an offline feed-rate optimization. Only recently, Altintas and Aslan (2017) applied the idea of identifying the force model online in combination with an adaptive controller. A 1-s prediction was used in the model to anticipate changes in the engagement conditions. Kluge (1999) even suggested MPC for metal cutting processes but dismissed it because of its high metrological effort.

Adams and Stemmler (Adams 2016; Stemmler et al. 2016; Schwenzer et al. 2017; Stemmler 2020) picked up the idea of advanced control implementing MPC for the first time in order to control the active force in milling. They predicted the future active force based on an a priori simulation of the engagement conditions, the current feedrate and an online calibrated force model. An overview on how it works and the current trends in MPC is provided by Schwenzer et al. (2021).

Force model identification

Modeling the force in cutting technology is predominantly conducted with so-called “mechanistic” force models relating data-driven material coefficients to the geometry of the undeformed chip. For calibration or identification of these models, recently the method of instantaneous undeformed chip thickness has evolved. It is essentially a curve fit between measured and simulated force. While often global optimization algorithms were used, e.g. Ghorbani and Moetakef-Imani (2015), Grossi (2017), Chen et al. (2018) and Zhang et al. (2017), local optimization algorithms required less computational effort with no loss in accuracy (Schwenzer et al. 2019). Freiburg et al. (2015) even reported a lack of convergence if unconstrained optimization was used. If constrained, local optimization algorithms can ensure a technologically plausible result and may be suitable for online identification.

Adams (2016) identified the model coefficients online every three cutter revolutions, which translated to 80 ms allowed execution time or 1 mm tool path. A later study showed only little reduction potential of the computation through other optimization algorithms (Schwenzer et al. 2019). The discrete, independent nature of the identified models demanded for an additional smoothing when used in closed-loop control (Adams 2016; Stemmler 2020). Altintas and Aslan (2017) picked this idea up using a fit based on recursive least squares (RLS). Recent prior works of the author introduced ensemble Kalman filtering for this problem in simulations, demonstrating that this disturbance-observer-based method outperforms RLS (Schwenzer et al. 2020).

Approach

First, the overall system is introduced in “System overview” section. Then, the major modules are explained in detail. Finally, “Experimental setup” section outlines the experimental setup.

System overview

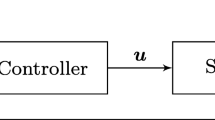
The model predictive force controller (MPFC) consists of MPC-based controller, a reference generator, and an ensemble Kalman filter (EnKF)-based identification. Figure 1 illustrates the system. The feed velocity \(v_{f,act}\) is controlled by manipulating the commanded feed velocity \(v_{f,cmd}\) through MPC. MPC considers a model that describes the behavior of the controlled actuators of the machine tool. The reference generator translates the desired active force \(F_{a,des}\) to a reference of the feed velocity by inverting the process model (“Process model” section). The feedback loop of the force is closed by identifying the parameters of the process model online. The identification is performed on force measurements in the coordinate system of the machine tool \({\varvec{F}} = [F_{X} F_{Y}]^\intercal \).

From the control point of view, the controlled system is divided into two parts: one with time delay (the machine tool) and another part with an immediate reaction (the process). Although the machine tool is controlled over time, the MPC works in the one-dimensional space along the tool path (position domain).

In order to model the milling process, the current undeformed chip parameters are required, which depend on the current feed per tooth and the macroscopic engagement conditions, s. “Process model” section. The engagement is predefined along the tool path (in peripheral milling: depth of cut \(a_{p}\) and the difference in the engagement angle from start of the engagement to the exit of the cutting edge \(\varphi _{ex}-\varphi _{in}\), which relates to the width of cut \(a_{e}\)). The engagement conditions are determined once beforehand by a geometric simulation considering the diameter of the (cylindrical) tool and are stored as a look-up table. The table is synchronized online via the position of the tool and used within the identification and the reference generator.

Model-based predictive controller

The popularity of MPC “comes in great part from the fact that a suitable model being given, the controller can be easily implemented with a direct physical understanding of the parameters to be tuned and easy constraints handling (Richalet 1993). According to this, the MPC algorithm of this contribution makes explicit use of a time-discrete state-space model:

$$\begin{aligned}&{\varvec{x}}(k+1) = {\varvec{f}}_m({\varvec{x}}(k),u(k)), \end{aligned}$$
(1)
$$\begin{aligned}&{\varvec{y}}(k) = {\varvec{h}}({\varvec{x}}(k)) , \end{aligned}$$
(2)

with state vector \({\varvec{x}}\), output vector \({\varvec{y}}\), and input u. The model function \({\varvec{f}}_m(\cdot )\) (the m in the index shall indicate that it is the machine tool model in the case of MPFC) and the measurement function \({\varvec{h}}(\cdot )\) predict the future behavior of the controlled system. The output vector \({\varvec{y}}\) consists of the measured position \(y_p\) and the feed velocity \(y_v\). Their corresponding predictions are defined by the trajectories \({\varvec{y}}_p\), \({\varvec{y}}_v\), respectively. The optimization problemFootnote 2 considers the tracking accuracy of these trajectories:

$$\begin{aligned}&\min _{{\varvec{\varDelta u}}, {\varvec{\xi }}} \sum _{i=0}^{H_p} \Vert w(k+i\arrowvert k) - {\varvec{y}}_p(k+i\arrowvert k) \Vert ^2_{{\varvec{W}}_w} + \cdots \end{aligned}$$
(3)
$$\begin{aligned}&\quad \sum _{j=1}^{{{\varvec{H}}_u}-1} \Vert {\varvec{\varDelta u}}(k+j\arrowvert k) \Vert ^2_{{\varvec{W}}_u} + \sum _{i=0}^{H_p} \Vert {\varvec{\xi }}(k+j\arrowvert k) \Vert ^2_{{\varvec{W}}_{{\varvec{\xi }}}} \\&\hbox {s.t.} u_{lb}~{\varvec{I}} \leqslant u(k) + {\varvec{\varDelta u}}(k+j\arrowvert k) \leqslant u_{ub}~{\varvec{I}}, \nonumber \\&{\varvec{y}}_v(k+i\arrowvert k) \leqslant {\varvec{y}}_{ub}(k+i\arrowvert k) + {\varvec{\xi }}(k+i\arrowvert k), \nonumber \\&0 \leqslant {\varvec{\xi }}(k+i\arrowvert k), \nonumber \\&\quad \forall \,i \in \{0, \ldots , H_p\} \quad \text {and}\quad j \in \{0, \ldots , {H_u}\}.\nonumber \end{aligned}$$
(4)

The problem is solved at each time instance k in such a way that the tracking error between the predicted positions \({\varvec{y}}_p\) and the desired reference w is minimized within the finite prediction horizon \(H_p\) (Stemmler 2020; Stemmler et al. 2017; Schwenzer et al. 2021). providing an optimal sequence \({\varvec{u}}\) of the manipulated variable, of which only the first entry u is implemented (principle of “receding horizon”). Thus, the feed velocity \(u = v_{f,cmd}\) is maximized along the 1D, flattened tool path under consideration of the constraints on the feed velocity to \({\varvec{y}}_{ub}\). This limitation is calculated by the process model and the predicted positions \({\varvec{y}}_p\).

Furthermore, the change \({\varvec{\varDelta u}}\) of the manipulated variable is considered within the finite horizon \(H_u\) in order to avoid high-frequent control changes. The last term of the cost function includes so-called slack variables \({\varvec{\xi }}\), which quantify the violation of output constraints in the cost function. Softening the output constraints in this way guarantees feasibility of the constrained optimization problem. Each term posses an individual weighting matrix \({\varvec{W}}_{w}\), \({\varvec{W}}_{u}\) and \({\varvec{W}}_{{\varvec{\xi }}}\), respectively.

The implicit formulation of the controller maintains physical interpretability of the system shifting the design effort towards modeling of the to-be-controlled process (Schwenzer et al. 2021). The double-lined arrows in Fig. 1 shall indicate that the problem is solved for \(H_p\) time steps, so that the variables become vectors.

With regard to setup and tuning of the MPFC in this work, the sample time was set to \(T_s = 20\,\hbox {ms}\), which is three times smaller than the time delay of the machine tool and eight times smaller than its reaction time, “Machine model” section. The sampling time allows the MPFC to manipulate the feed twice per revolution. The hard box constraints on the controller output u, which are bounded by the upper limit \(u_{ub}\), the lower limit \(u_{lb}\) and the identity matrix \({\varvec{I}}\), are applied to protect machine and tool from overload: feed per tooth \(f_{z} \in [0\hbox { mm}; 0.25\hbox { mm}].\)

The control horizons were indirectly determined by the model of the machine tool. The time delay of the machine tool was considered in the model of its behavior. The upper prediction horizon \(H_p\) was defined by the settling time \(T_95\%\) and a maximum feed velocity of \(v_{f,max} = 21.225\hbox { mm s}^{-1} = 1273.5\hbox { mm min}^{-1}\), which resulted in a maximum prediction horizon of ten time steps \(H_p = \frac{T_{95\%}}{T_{s}} = 10\). The control horizon was set to \(H_{u} = H_{p}\) in order to determine the control behavior for the prediction horizon.

In the MPC, the open-source optimization algorithm qpOASES was used as it is dedicated for linear MPC problems (Ferreau et al. 2017). The weight matrices of the cost function, Eq. 3, were tuned by experience to \({\varvec{W}}_{w}=0.1\,{\varvec{I}}\), \({\varvec{W}}_{u}=0.01\,{\varvec{I}}\) and \({\varvec{W}}_{{\varvec{\xi }}} = 10^4 {\varvec{I}}\), with identity matrix \({\varvec{I}}\).

Machine model

This work used a five-axis, vertical machining center Mazak VARIAXIS i600 with a numerical controller (NC) of type Siemens SINUMERIK 840D SL. The spindle is mounted on the Z-axis, which rests on the X-axis, which again rests on the Y-axis. The identical construction of the X- and Y-axes allowed to describe their behavior by a single joint model.

The position controller was a proportional controller (P gain), while the velocity control loop was a PI controller (Siemens 2016). Since the feed was manipulated, the MPC algorithm required a model of the velocity behavior along the tool path, which was a mixed movement of the involved axes. The linear axes of machine tools were often modeled as a second order system, e.g. Fussell and Srinivasan (1991), Altintas (1994), Rober et al. (1997) and Zuperl and Cus (2012), with time delay \(T_{d}\):

$$\begin{aligned} G_{s} = \frac{K~\omega _{0}^{2}}{s^2 + 2~\zeta ~\omega _{0}~s + \omega _{0}^2}~e^{-s~T_{d}}, \end{aligned}$$
(5)

in frequency domain s with a gain K, a damping constant \(\zeta \), and the cut-off frequency \(\omega _{0}\).

Step tests in the XY-plane suggested an overdamped behavior of the feed velocity: \(\zeta =1.5552\), \(K=0.9978\), \(\omega _{0}=80.5162\), with a time delay of \(T_{d}=60\hbox { ms}\). This translated to a rise time of \(T_{95\%} = 167\hbox { ms}\), in which 95% of the commanded value were reached. Figure 2 illustrates the reaction of the machine and of the suggested model to a command profile of pseudorandom steps.

Fig. 2
figure 2

Reaction of the X- and Y-axis of the Mazak VARIAXIS i600 to pseudorandom step changes in the commanded velocity modeled as a second order system

Full size image

Modern motion controllers strive to reduce the attack time by additional feedforward control yielding a step-variant behavior, i.e. depending on the value of the manipulated variable. Ay et al. (2018) and Ay et al. (2019) modeled this nonlinear behavior with support vector regression (SVR), a data-driven machine learning method. Nonetheless, this work refrains from activating feedforward control and uses a second order system as machine tool model.

Process model

A model of the process was build from a mechanistic force model together with a model of the radial deviation and the current macroscopic engagement conditions. Without lack of generality, the nonlinear model according to Kienzle (1952) was used as force model:

$$\begin{aligned} F_{i} = k_i \, bh^{1-m_{i}}, \quad \text {where}\quad i\in \{t, r, p\}, \end{aligned}$$
(6)

presents a nonlinear relationship of the force to the undeformed thickness h while the undeformed width b of the chip exhibits a constant influence. The parameters \(k_{i}\) and \(m_i\) represent coefficients specific to the combination of workpiece material and tool. The same function is assumed for the tangential (index t), radial (index r), and passive force (index p).

Other well-established models, e.g. by Altintas and Lee (1996), assume a linear relation but are often extended by modeling the coefficients again as an exponential function of the undeformed chip thickness (Wan et al. 2007, 2009; Guo et al. 2017; Zhang et al. 2018). Studies suggested that nonlinear models may be generally more accurate than linear versions (Adem et al. 2015; Wei et al. 2018; Wimmer et al. 2018).

Radial deviation of a tool—often also called “runout”—provokes a dissimilar feed per tooth yielding a periodically varying chip load. The most common modeling approach was introduced by Kline and DeVor (1983) and Kline (1982). They model it as a parallel offset of the axis of rotation (and an additional tilt whose influence is often neglected). The error manifests itself in a different local radius for each tooth t of all \(N_{z}\) teeth. Even considering just the radial offset improves the accuracy of the simulated force significantly (Rivière-Lorphèvre and Filippi 2009).

In combination of both models, the force of the milling process can be modeled as a function of the current rotating position of the cutting edge \(\varphi _{z}\):

$$\begin{aligned} F_{i}&(\varphi _z) = ~{k_i} ~ \frac{{b}}{N_s} \sum ^{N_s}_{n = 1}{ \phi _n \sum ^{N_z}_{j = 1}} \left\{ \right. \nonumber \\&\cdots \left. \underbrace{ {f}_z~\sin \overbrace{ \left[ \varphi _z-(n-0.5)~\varDelta \varphi _{{\beta }}\right] }^{\varphi _{z,s}} }_{{h}_{\text {nominal}}(n)}- \varDelta {h}_{\text {offset}}(n,j) \right\} ^{1-{m_i}}, \end{aligned}$$
(7)

where the nominal undeformed chip thickness \({h}_{\text {nominal}}(n)\) is the as circle-movement approximated trochoidal path of a point on the cutting edge. The tool is sliced into \(N_s\) disk elements, in which the helical cutting edge is approximated as an upright cutting edge (to obtain orthogonal cutting). This staircase-like approximation is standard to model the helix angle \({\beta }\). The force \(F_{i}(\varphi _z)\) is the sum over all \(N_z\) teeth. The effect of the radial offset (polar coordinates, amount \(\rho \) and direction \({\lambda }\)) is calculated by:

$$\begin{aligned} \varDelta {h}_{\text {offset}}(n,j) =&\, 2\rho ~ \sin \left[ \frac{\tan (2{\beta })}{D} \frac{{b}}{N_s}(n-0.5) - {\lambda } + \right. \nonumber \\&\left. \cdots \frac{\pi }{N_z}(2\,j-3) \right] ~ \sin \left( \frac{\pi }{N_z}\right) . \end{aligned}$$
(8)

The equation assumes that the tool is sliced into \(N_s\) disk elements—as it is common practice to approximate the helix angle \({\beta }\) of the cutting edge. Modeling the cutting edge as a spiral staircase accounts for that mechanistic force models originate from turning, thus, assume orthogonal cutting conditions. The helical cutting edge let it tilt backwards from the tip. The amount of this projection \(\varDelta \varphi _{{\beta }}\) per slice is:

$$\begin{aligned} \varDelta \varphi _{{\beta }} = \frac{{b}}{N_s~{R}~\tan (\pi /2-{\beta })}. \end{aligned}$$
(9)

The model describes the height of the tool by the center of each disk element \((n-0.5)\).

The boolean function \(\phi _n\) models whether a slice \(\varphi _{z,s}\) is engaged or not at a certain time step:

$$\begin{aligned} \phi _n = \left\{ \begin{array}{l@{\quad }l} 1&{} \quad \varphi _{z,s} \ge \varphi _{in}\, \text {and}\, \varphi _{z,s} \le \varphi _{ex}=180^{\circ },\\ 0&{} \quad \text {otherwise}. \end{array} \right. \end{aligned}$$

The undeformed chip width b can be easily determined for peripheral end milling since the tool is always perpendicular to the feed direction resulting in the depth of cut being \({b} = {a_p}\).

Process model identification by EnKF

As a further development of works in simulation, e.g. Schwenzer et al. (2020), the online identification of the process model is conducted by an EnKF. The idea coincides with an disturbance observer but since the model was nonlinear and nonobservable (i.e. it was not biunique), this particle-based method was used. The particles in the EnKF approximate the underlying probability distribution of the model parameters instead of the expectation value (Evensen 1994), which is why the demand of an “observable” system could be dropped. The mean of the particles was taken as the current best guess of the EnKF. The computation time scales linearly with the ensemble size J while the error of the estimation follows an inverse square root of the number of particles \(1/\sqrt{J}\) (Evensen 2003). The approach presents an instantaneous identification and can be considered unique compared to other works.

Introduced by Evensen (1994), the idea was to propagate a group of particles (states \({\varvec{x}}\)):

$$\begin{aligned} {\varvec{X}}_{k\vert k-1} = \left\{ {\varvec{x}}_{k\vert k-1}^1, \ldots , {\varvec{x}}_{k\vert k-1}^{J}\right\} , \end{aligned}$$
(10)

forward in time k rather than just a single state vector \({\varvec{x}}\) as the classic Kalman filter (KF) does. The EnKF simultaneously propagates independent solutions that share the same measurement-based update. The index \(k\vert k-1\) indicates that the value in the current time step k is based on the information from the previous time step \(k-1\).

First, the empirical covariance matrix \({\overline{{\varvec{P}}}}\) is calculated based on the output of the model \({\varvec{f}}_p({\varvec{u}},{\varvec{x}})\)—in the case here, this is the process model equation 7 (therefore the index p)—for each ensemble member \({\varvec{x}}^j\) of the previous time step \(k-1\):

$$\begin{aligned}&\hat{{\varvec{X}}}_{k\vert k-1} ={\varvec{f}}_p\left( {\varvec{u}}_{k}, {\varvec{x}}^j_{k-1}\right) \quad j\in \lbrace 1,\ldots ,J\rbrace ,\end{aligned}$$
(11)
$$\begin{aligned}&{\overline{{\varvec{P}}}}_{k} =\frac{1}{J} (\hat{{\varvec{X}}}_{k\vert k-1} - \overline{{\varvec{X}}}_{k\vert k-1}) \nonumber \\&\cdots (\hat{{\varvec{X}}}_{k\vert k-1} -\overline{{\varvec{X}}}_{k\vert k-1})^\intercal . \end{aligned}$$
(12)

Lines (\(\overline{\,\cdot \,}\)) denote mean values and hats (\(\hat{\,\cdot \,}\)) predicted values while undecorated symbols indicate the actual or corrected values. The covariance matrix represents how much to trust the model in comparison to the measurements \({\varvec{z}}^j\). The predicted state vectors \(\hat{{\varvec{x}}}^j\) are then updated through measurements weighted by the Kalman-gain \({\varvec{G}}_{k}\):

$$\begin{aligned} {\varvec{G}}_{k}&= {\overline{{\varvec{P}}}}_{k} ~ {\varvec{H}}_{k}^\intercal ~ \left[ {\varvec{H}}_{k} ~ {\overline{{\varvec{P}}}}_{k} ~ {\varvec{H}}_{k}^\intercal + \overline{{\varvec{R}}}_{k} \right] ^{-1}, \end{aligned}$$
(13)
$$\begin{aligned} {\varvec{x}}_{k\vert k}^j&= \hat{{\varvec{x}}}_{k\vert k-1}^j + {\varvec{G}}_{k} \left[ {\varvec{z}}_{k}^j - {\varvec{H}}_{k} ~\hat{{\varvec{x}}}_{k\vert k-1}^j \right] , \end{aligned}$$
(14)

where the output matrix \({\varvec{H}}\) extracts those states that can be measured \({\varvec{y}}^j = {\varvec{H}}~\hat{{\varvec{x}}}^j\). All members share the same measurements \({\varvec{z}}\), which are artificially augmented with zero mean gaussian noise \({\varvec{\eta }}\sim \mathcal {N}({\varvec{0}},~{\varvec{\varGamma }})\) creating individual measurements for every member:

$$\begin{aligned} {\varvec{z}}_{k}^j&= {\varvec{y}}_{k} + {\varvec{\eta }}_{k}^j,\quad \text {with}\, j \in \{1,\dots ,J\}, \end{aligned}$$
(15)
$$\begin{aligned} \overline{{\varvec{R}}}_{k}&= \frac{1}{J}~ {\varvec{\eta }}_{k} ~ {\varvec{\eta }}_{k}^\intercal \approx {\varvec{\varGamma }}. \end{aligned}$$
(16)

In the limit of infinite ensemble members \(J \rightarrow \infty \), the empirical measurement noise covariance \(\overline{{\varvec{R}}}\) coincides with the measurement noise covariance \({\varvec{\varGamma }}\).

Table 1 Coefficients of the Kienzle-model: selected examples and a technological reasonable range for X5CrNi18-10
Full size table

In essence, the EnKF is a particle-based sequential optimization that offers a cheaper derivative-free approximation than traditional methods (Iglesias et al. 2013; Chada et al. 2019).

Without presenting the theory further, this work uses an EnKF with \(J = 50\) particles to identify the process model equation 7. The interested reader is referred to the original references (Evensen 1994, 2003), the mathematical analysis of its well-posedness (Iglesias et al. 2013; Kelly et al. 2014; Schillings and Stuart 2017, 2018), or a recent work describing the application to the problem of identifying a mechanistic force model (Schwenzer et al. 2020).

The filter converges within the search space spanned by the initial distribution of the particles (this is the so-called “subspace property”). An advantage of mechanistic force models—especially the Kienzle-model—is the extensive literature on them, which allows to determine a technologically reasonable range of their parameters (Table 1). The polar coordinates of the radial offset automatically limit the parameters (by wrapping at \(360^{\circ }\)) but impose the challenge of defining a continuous mean in them. The EnKF requires a proper mean of its particles in order to converge. As a trick, we suggest to transform the polar coordinates \(\rho \), \({\lambda }\) of the radial offset to cartesian coordinates \({\rho _x}\), \(\rho _y\) for the EnKF and transforming them back to polar coordinates when evaluating the process model equations 7–8.

The technological bounds, Table 1, were additionally imposed as box constraints in the EnKF to keep the filter from running into model-induced singularities.

For an undeformed chip thickness h smaller than a critical thickness, cutting turns into ploughing and mechanistic models loose their validity. In the mechanistic models, this is called “size effect”, which manifests itself in drastically increasing model coefficients. These rather unreasonable coefficients pull the filter towards higher coefficients in every cutter revolution. Thus, the identification benefits from excluding the size effect in identification by putting the EnKF on throughout if the undeformed chip thickness is below the critical undeformed chip thickness \({h}_{TH}\). Although, the recursive nature of the EnKF provides a certain robustness against the size effect, the identification was set to ignore samples where the sum of the undeformed chip thicknesses along the helical cutting edge was less than:

$$\begin{aligned} \sum _{n=1}^{N_s} {h}(n) < {h}_{TH} = 0.05\hbox { mm}. \end{aligned}$$
(17)

It is a reasonable choice, comparing it to other works where the size effect was observed e.g. below \({h} = 0.01\hbox { mm}\) for Al 2618 (Wan et al. 2008) or below \({h} = 0.2\hbox { mm}\) for TiAl6V4 (Wang et al. 2012).

Experimental setup

The experiments were conducted on the five-axis, vertical machining center of type Mazak VARIAXIS i600 with an NC of type Siemens SINUMERIK 840D SL. Figure 3 is showing the experimental setup.

Fig. 3
figure 3

Experimental setup on the Mazak VARIAXIS i600 including a Kistler type 9255B dynamometer, a X5CrNi18-10 (AISI 304) workpiece and a Seco JS512100D2C.0Z2-NXT solid carbide cutting tool

Full size image

Furthermore, stainless steel X5CrNi18-10 (AISI 304) was manufactured by a solid carbide end mill (number of teeth \(N_z=2\), diameter \( D=10\hbox { mm}\), helix angle \({\beta }=46^{\circ }\), Seco JS512100D2C.0Z2-NXT) at a cutting speed of \(v_{c} = 8\hbox { mm s}^{-1}\), which was recommended by the manufacturer Seco Tools GmbH. The workpiece geometry (Fig. 4) combines all features that are especially challenging for force control in milling: abrupt changes in the engagement conditions, slow changes, as well as different depths of cuts.

Fig. 4
figure 4

Tool path of the workpiece

Full size image

The tool center point (TCP) was read from the internal bus system at \(200\hbox { Hz}\), which was four times faster than the sample time \(T_{s} = 20\hbox { ms}\) of the MPFC. The feed velocity f was calculated based on the velocity of the X- and Y-axes. Due to the high noise level, the internally commanded and measured values were fused in a Kalman filter for an improved measurement.

The force was measured by a piezoelectric dynamometer (Kistler 9255B) at \(10\hbox { kHz}\) with a low-pass filter of \(f_{edge} = 300\hbox { Hz}\) for proper signal conditioning.

The rotary position of the cutting edges \(\varphi _z\) was determined via a spindle encoder, the knowledge of the spacing of the cutting edges, and measuring the fixed rotary offset between spindle encoder and cutting edges.

The velocity command was fed to the numerical control unit (NCU) via an analog I/O module that manipulated the overwrite as it is a common approach, e.g. reported by (Tu and Corless 2014).

The MPFC ran on an AMD Ryzen7-2700 eight-core (3.06 GHz) CPU, with Microsoft Windows 10 and 16 GB DDR3 RAM.

Results and discussion

We present here the performance of the force control system in different configurations:

  • MPFC with EnKF-based identification,

  • MPFC with EnKF-based identification, whose ensemble is repeatedly inflated, and

  • a process with constant feed as the current state-of-the-industry benchmark.

The first presents the MPFC with the novel identification method based on the EnKF. The second extends the identification by a repeated inflation of the ensemble in order to maintain its initial agility as Schwenzer et al. (2020) suggested in a simulation study. The last entry in this list presents a process designed based on the suggestions of the tool manufacturer (Seco Tools GmbH).

The results are presented in Figs. 5, 6 and 7 providing the signals of the active force (top row), the feed velocity (second row), the identified model parameters (if apply, third and fourth row), and the engagement conditions of the tool for orientation (bottom row). All figures share the same axes limits for an easy comparison. All signals are presented over the position on the tool path p. The three columns show the three phases of engaged tool according to the tool path (Fig. 4) when the tool is engaged, ignoring the phases of air cutting in between.

The first rows present the active force \(F_a\), as the controlled variable, in three ways: the measured force (gray line), the simulated maximum active force per revolution \({F_{a,sim}|_{max}}\) (blue line), and the desired force reference \({F_{a,max,des}}\) (red, dashed line). The simulated force uses the instantaneous model parameters from the identification and represents what the MPC-based controller thinks that the force was.

The figures further (second row) illustrate the feed velocity \({v_f}\), which was the manipulated variable. The signal of the measured velocity \(v_{f,act}\) is drawn in red. The output of the MPFC, which is the commanded velocity \({v_{f,cmd}}\), is denoted in blue, and the desired velocity reference \({v_{f,des}}\) as black line. The last presents the translation from the desired force \({F_{a,des}}\) by an inversion of the current process model in the reference generator.

The identification output of the Kienzle-model (third row) and of the Kline & DeVor-model (fourth row) are provided as continuous signals of the EnKF.

The bottom row illustrates the engagement conditions depth of cut \({a_p}\) (black line) and the difference of the exit and the entry of the rotation angle \(\varphi _{ex} - \varphi _{in}\) (light blue area), as well as the feed direction angle \({\alpha _f}\) (dark blue line). The feed direction angle \({\alpha _f}\) is required to transform the modeled force in the coordinate system of the cutting edge to the coordinate system of the machine tool, in which the force is measured.

The proposed work showed a method for tracking a desired force, which is dependent on the tool in use. The determination of the desired force is not within the scope of this work.

MPFC with an EnKF-based identification

This work used a novel identification method based on an EnKF. Figure 5 presents the results of an MPFC with a non-inflated EnKF-based identification.

Fig. 5
figure 5

Results of the MPFC with EnKF-based identification (no ensemble inflation). The three columns are showing the three phases along the toolpath (Fig. 4) when the tool is engaged

Full size image

The first contact of tool and workpiece is particularly interesting since the identification started with a randomly chosen initial guess (or rather randomly distributed initial ensemble). Therefore, when the identification became active, this guess was drastically corrected. It becomes visible in peak of the simulated maximum force \({F_{a,sim}|_{max}}\) in the first column where the MPC overestimated the force, right after it entered the material. The large changes of the model parameters caused a somehow erratic control behavior at the beginning until the parameters settled.

There are three other exceptional points in the force (top row). First, when the tool exited the workpiece under an angle (first column), the MPFC presumed a higher force than it was measured. Second, at the beginning of the second column (the tool entered under an angle), the circumference of the measured active force \({F_a}\) formed a dent, of which the controller was unaware. Both observations suggested that the parameters of the process model were not accurate in this section. Apparently, the identification was not accurate at changes of the engagement conditions (the engagement angle in this case). Third, the last column shows constantly overestimated force, which did not meet the reference—however, the MPC-based velocity controller perfectly met its reference. Again, the error was caused by an inaccurate process model. Although the model parameters adapted (as a result one can see a steady increase in the measured force), the identification was incapable of identifying the parameters at one time step.

MPFC with an EnKF-based identification and repeated ensemble inflation

In particular, the constantly inaccurate identification suggested a limited agility of the EnKF. The particles were dragged towards the same value at every step. However, the subspace property states that they converge only in the subspace spanned by the initial ensemble. With induction one can deduce that at every time step, the particles converge in the subspace spanned by them. Therefore, the ensemble looses the ability to explore the entire search space at every step in time. If one assumes that the model parameters can change (i.e. leading to a time-variant inverse problem), they may pop out of the ensemble subspace. As long as the ensemble exhibits a minimum spread, it may move towards the new ideal set of parameters. In fact, literature suggests to maintain a minimum inflation by constantly inflating the variance \({\overline{{\varvec{P}}}}\) of the filter (Kelly et al. 2014). Based on these observations, the authors introduced a repeated drastic inflation of the ensemble itself (of the particles, not just of its variance) (Schwenzer et al. 2020). This ensured larger agility of the particles while allowing it to converge to the best guess between these inflations.

Ensemble inflation can be tuned by the step size \(k^{*}\), in which the ensemble should be inflated, and to what size the covariance matrix of the inflated should be \({\overline{{\varvec{P}}}} = 1/{\lambda ^*}~{{\varvec{P}}_{{\varvec{X}}0}}\) based on the covariance \({{\varvec{P}}_{{\varvec{X}}0}}\) of the initial ensemble.

Fig. 6
figure 6

Results of the MPFC with EnKF-based identification (ensemble inflation \({k^*}=50\), \({\lambda ^*}=10\)). The three columns are showing the three phases along the toolpath (Fig. 4) when the tool is engaged

Full size image

Figure 6 provides the results of MPFC with inflated EnKF-based identification. The measured force \({F_a}\) agrees much more with the simulated force \({F_{a,sim}|_{max}}\) of the controller. In particular at the last column, the signals present a much better course. The model parameters show the same trend over the entire tool path indicating a constantly good identification.

Milling with constant feed

Tool manufacturers today provide extensive tables on what process parameters to pick for a given engagement. In the case presented here, the tool manufacturer recommended a feed velocity of \({v_f} = 266\hbox { mm min}^{-1} = 4.43\hbox { mm s}^{-1}\) (and a cutting velocity of \({v_c} = 80\hbox { mm s}^{-1}\), as was also used before).

Figure 7 presents the signals from such a conventionally designed process. One may note the higher force in the last column due to the increased depth of cut \({a_p} = 2.5\hbox { mm}\) as well as the descending course at the exit of the tool in the first column. If compared to the figures before, this downward slope emphasizes the productivity gain of MPFC. At the next entry (beginning of column two), there is again a dent in the force, which may not be caused by the velocity. This might be a resonance artifact of the dynamometer, which is more pronounced when X- and Y-axes are excited simultaneously (it is less pronounced at the entries in the first and third column, where the movement is only in X- or Y-direction, respectively).

Fig. 7
figure 7

Results of a process with constant feed \({v_f} = 4.43\hbox { mm s}^{-1}\). The three columns are showing the three phases along the toolpath (Fig. 4) when the tool is engaged

Full size image

Table 2 compares the times of the different approaches: the total process time \({T_{total}}\) for the entire tool path and the cutting time \({T_{cut}}\), in which the tool was engaged. The difference to the process with constant feed was striking. Both measures of time show a reduction by 55% with MPFC. The small improvement of the MPFC with ensemble inflation over the experiment without the repeated inflation is small but clear. The shorter time is a result of the closer match of measured force and desired force reference.

Due to the higher relevance of forces in rough milling, this work focuses on this case. Nonetheless, the method is equally applicable to finishing or micro milling but may require a more sophisticated force model (e.g. incorporating ploughing or extending to ball-shaped tools as are common for finishing) and specialized measurement equipment for an even higher signal-to-noise ratio. The current setup is only applicable for 2.5 dimensional milling as moving the dynamometer would introduce an acceleration-induced error. There are efforts to correct force signals from such effects as well as substituting the dynamometer by indirect force measurement methods.

Table 2 Comparison of the total time \({T_{total}}\) and of the engaged cutting time \({T_{cut}}\)
Full size table

Conclusion

This work described a model predictive approach to control the active force in rough milling. It was build upon an model-based predictive feed velocity controller, which was turned into a cascaded force controller by a reference generator and an online identification of the process model. The reference generator inverts the process model translating the desired force reference into a feed velocity reference for the model-based predictive feed velocity controller. The resulting system was called a model predictive force controller (MPFC).

The process model was based on the well-established mechanistic force model according to Kienzle (1952) and the popular radial deviation of Kline and DeVor (1983). For the recursive identification based on an EnKF, the parameters of the radial deviation model were expressed in cartesian coordinates to obtain a proper definition of a mean.

The experiments demonstrated the effectiveness of the proposed system. It reduced and increased the velocity just in time so that the force almost perfectly met the desired force reference. This held in spite of abrupt changes in the engagement between tool and workpiece—or of slowly varying changes. With regard to state-of-the-industry solutions, the improvement was a reduction of the manufacturing time by 55% compared to a conventionally designed process with constant feed. The obtained improvement does not claim to be representative whatsoever. Apart from the improvement over the conservative feed suggested by the tool manufacturers, the system works particularly well at tool path with changing engagement conditions.