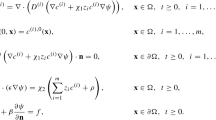Integral equation method for the 1D steady-state Poisson-Nernst-Planck equations

Abstract

An integral equation method is presented for the 1D steady-state Poisson-Nernst-Planck equations modeling ion transport through membrane channels. The differential equations are recast as integral equations using Green’s 3rd identity yielding a fixed-point problem for the electric potential gradient and ion concentrations. The integrals are discretized by a combination of midpoint and trapezoid rules, and the resulting algebraic equations are solved by Gummel iteration. Numerical tests for electroneutral and non-electroneutral systems demonstrate the method’s 2nd order accuracy and ability to resolve sharp boundary layers. The method is applied to a 1D model of the K$^+$ ion channel with a fixed charge density that ensures cation selectivity. In these tests, the proposed integral equation method yields potential and concentration profiles in good agreement with published results.

1 Introduction

Ion transport through membrane channels is a fundamental process in cell biology [1]. However, atomistic simulations of this process are expensive, and an alternative continuum approach is based on the Poisson-Nernst-Planck (PNP) equations, where the Poisson equation for the electric potential is coupled to the Nernst-Planck equation for the ion concentrations [2]. The continuum PNP model accounts for two effects, (1) molecular diffusion due to ion concentration gradients and (2) ion drift in the applied and self-consistent electric fields. The PNP equations have been employed to study many aspects of ion channel selectivity [3], including the effect of fixed charge [4], ion size [5], and membrane surface charge [6].

Despite the relative efficiency in comparison with atomistic simulations, numerical solution of the PNP equations is still challenging due to several factors, (1) nonlinear coupling of the electric potential and ion concentrations, (2) the need to resolve the channel geometry, as well as boundary layers and internal layers at material interfaces, and (3) maintaining stability in convection-dominated cases [7]. Many PNP solvers have been developed using finite-difference methods [8,9,10], finite-element methods [6, 11,12,13], and finite-volume methods [14,15,16]. It is also important for numerical PNP solvers to preserve positivity of the ion concentrations and conserve mass in time-dependent simulations, and several schemes have been developed for this purpose [10, 17,18,19,20].

The boundary element method (BEM) is another approach to solving linear elliptic boundary value problems, where the differential equation is recast as an integral equation on the domain boundary by convolution with an appropriate Green’s function [21]. While the BEM requires discretization of singular integrals, it has the advantage of reduced spatial dimension. Closely related to the PNP equations is the Poisson-Boltzmann (PB) equation for the electrostatic potential of a solvated protein. The BEM has been applied to solve the 3D linear PB equation on the molecular surface of a protein (see [22, 23] and references therein), but aside from some early work using a Green’s function to solve the PB equation for an ion channel in 1D [24], as far as we know this approach has not been further developed for 2D and 3D ion channel problems.

In fact there are two challenges to applying an integral equation approach to the PNP system, (1) nonlinear coupling of the electric potential and ion concentrations, and (2) the ions are distributed throughout the channel and solvent domain requiring costly volume integrals in 2D and 3D. Nonetheless, we believe that these obstacles can be overcome using iteration to handle the nonlinearity and a fast summation method with adaptive quadrature for the volume integrals. As a step in that direction, the present work develops a novel integral equation method for the 1D steady-state PNP equations.

The paper is organized as follows. Section 2 introduces the 1D steady-state PNP equations. Section 3 uses Green’s 3rd identity to recast the PNP equations as a fixed-point problem involving integral operators for the potential gradient and ion concentrations. Section 4 presents the numerical implementation. Section 5 presents tests for electroneutral and non-electroneutral systems with Robin boundary conditions on the potential and no-flux boundary conditions on the ion concentrations. Section 6 presents a K$^+$ ion channel simulation following [25], and the work is summarized in Section 7.

2 PNP equations

This work focuses on the 1D steady-state PNP equations with two ion species. The electrostatic potential $\phi (x)$ satisfies the Poisson equation,

$$\begin{aligned} -\left( \epsilon \phi ^\prime (x)\right) ^\prime = z_1 e c_1(x) + z_2 e c_2(x), \end{aligned}$$

(1)

where $\epsilon$ is the permittivity, the valence is $z_1 = -1$ for anions and $z_2 = 1$ for cations, e is the proton charge, $c_1(x), c_2(x)$ are the ion concentrations, and the domain is $[-L,L]$. This is supplemented with the Nernst-Planck equation,

$$\begin{aligned} \left[ D_{i}\left( c_{i}^\prime (x)+\frac{z_{i} e}{k_{B} T} c_{i}(x)\phi ^\prime (x)\right) \right] ^\prime =0, \end{aligned}$$

(2)

for $i = 1,2$, where $D_i, k_B, T$ are the diffusion coefficient of ion species i, Boltzmann constant, and absolute temperature.

Following [10], the PNP equations are non-dimensionalized with respect to the bulk concentration $c_0$ [ions/Å$^3$], channel half-length L [Å], characteristic diffusion coefficient $D_0$ [Å$^2$/s], characteristic potential $\phi _0$ [V], and water permittivity $\epsilon _t$ [F/Å]. The resulting non-dimensional equations are

$$\begin{aligned}&-\epsilon \phi ^{\prime \prime }(x) = \chi _2 \left( z_1c_1(x) + z_2c_2(x) \right) , \end{aligned}$$

(3a)

$$\begin{aligned}&\left( D_i\left( c_i^\prime (x) + \chi _1 z_i c_i(x) \phi ^\prime (x)\right) \right) ^\prime = 0, \end{aligned}$$

(3b)

for $i = 1,2$ with domain $[-1,1]$. The coefficients are

$$\begin{aligned} \chi _1 = \frac{e \phi _{0}}{k_{B} T}, \quad \chi _ 2 = \frac{e c_{0} L^{2}}{\phi _{0} \epsilon _{t}}, \end{aligned}$$

(4)

where $\chi _{1}$ is the ratio of electric potential energy to thermal energy, and $\chi _{2}/\epsilon$ is the inverse square Debye length. Except as otherwise noted, the non-dimensional diffusion coefficient is $D_i=1$.

2.1 Problem specification

The first set of examples are electroneutral and non-electroneutral systems, where the non-dimensional PNP equations (3) are solved on the interval $[-1,1]$. We consider Robin boundary conditions for the potential,

$$\begin{aligned} \phi (x)\pm \eta \phi ^\prime (x) =\phi _{\pm }, \quad x =-1,1, \end{aligned}$$

(5)

where $\eta , \phi _{\pm }$ are constants that depend on biological modeling considerations. Note that if $\eta =0$, then (5) reduces to Dirichlet boundary conditions for the potential. The channel is assumed to be closed at both ends; hence, the no-flux boundary condition is applied for the ion concentrations,

$$\begin{aligned} D_i\left( c_i^\prime (x) + \chi _1 z_i c_i(x)\phi ^\prime (x) \right) = 0, \quad x = -1,1. \end{aligned}$$

(6)

Finally, the total concentration for each ion species is a specified positive constant,

$$\begin{aligned} \int _{-1}^{1}c_i(x)\text {d}x = a_i, \quad i = 1,2. \end{aligned}$$

(7)

In addition to the electroneutral and non-eletroneutral systems, we also consider a K$^+$ ion channel model, and the problem specification in that case is given further below.

3 Integral form

This section recasts the 1D steady-state PNP differential equations as a set of integral equations in the form

$$\begin{aligned} \phi ^\prime&= \textbf{P}[c_1, c_2], \end{aligned}$$

(8a)

$$\begin{aligned} c_i&= \textbf{NP}[c_i, \phi ^\prime ], \quad i = 1,2, \end{aligned}$$

(8b)

where $\textbf{P}, \textbf{NP}$ are operators obtained by integrating the Poisson and Nernst-Planck equations while incorporating the Robin and no-flux boundary conditions and the total concentration condition. Note that (8) defines a fixed-point problem, where $\textbf{P}$ maps the concentrations $c_1, c_2$ into the potential gradient $\phi ^\prime$, while $\textbf{NP}$ maps the concentration $c_i$ and potential gradient $\phi ^\prime$ into the concentration $c_i$ for $i=1,2$. The integral form of the PNP equations in (8) is solved by Gummel iteration [26] for $\phi ^\prime , c_1, c_2$, and once it converges, further processing yields the potential $\phi$, and the concentration gradients $c_1^\prime , c_2^\prime$ needed to compute the current. Note that a fixed-point formulation and Gummel iteration were also used in the analysis of semiconductor drift-diffusion equations, although without recasting the differential equations as integral equations [27].

The derivation of the $\textbf{P}$ and $\textbf{NP}$ operators relies on Green’s 3rd identity,

$$\begin{aligned} \begin{aligned} f(x) =&\Big [g(x,y)f^\prime (y) - g_y(x,y)f(y)\Big ]_{y=-1}^{y=1} \\&- \int _{-1}^1 g(x,y)f^{\prime \prime }(y) \text {d}y, \end{aligned} \end{aligned}$$

(9)

where f(x) is twice continuously differentiable on $[-1,1]$ and g(x, y) is the 1D free-space Laplace Green’s function,

$$\begin{aligned} g(x,y) = -\frac{1}{2}|x-y|. \end{aligned}$$

(10)

Note that among the two terms on the right side of (9), the first term (or bracket term) involves the boundary values $f(\pm 1), f^\prime (\pm 1)$, and the second term (or volume integral term) involves $f^{\prime \prime }(x)$ over the entire interval. One can think of (9) as defining an operator, where $f(\pm 1),f^\prime (\pm 1),f^{\prime \prime }(x)$ are the input, and f(x) is the output. This point of view is taken in reformulating the PNP equations.

3.1 Derivation of P operator

Here, we assume that the ion concentrations $c_1(x), c_2(x)$ are given, and we shall derive an integral expression for the potential gradient $\phi ^\prime (x)$. The Poisson equation (3a) is written as

$$\begin{aligned} \phi ^{\prime \prime }(x) = -\frac{\chi _2}{\varepsilon } \sum \limits _{i=1}^2 z_i c_i(x), \end{aligned}$$

(11)

and then applying (9) with $f(y) = \phi (y)$ yields an integral expression for the potential,

$$\begin{aligned} \begin{aligned} \phi (x) =&\Big [g(x,y) \phi ^\prime (y) -g_y(x,y)\phi (y)\Big ]_{y=-1}^{y=1} \\&+ \frac{\chi _2}{\epsilon } \sum _{i=1}^2 z_i\int _{-1}^1 g(x,y)c_i(y)\text {d}y. \end{aligned} \end{aligned}$$

(12)

Differentiating (12) yields an analogous expression for the potential gradient,

$$\begin{aligned} \begin{aligned} \phi ^\prime (x) =&\Big [g_x(x,y) \phi ^\prime (y) - g_{xy}(x,y)\phi (y)\Big ]_{y=-1}^{y=1} \\&+\frac{\chi _2}{\epsilon } \sum _{i=1}^2 z_i\int _{-1}^1 g_x(x,y)c_i(y)\text {d}y. \end{aligned} \end{aligned}$$

(13)

The bracket terms in (12) and (13) involve the boundary values of the potential $\phi (\pm 1)$ and potential gradient $\phi ^\prime (\pm 1)$. The Robin boundary conditions (5) provide two equations for these four unknowns, and two more equations are obtained as follows.

Integrating the Poisson equation (11) over $[-1,x]$ yields

$$\begin{aligned} \phi ^\prime (x) - \phi ^\prime (-1) = -\frac{\chi _2}{\epsilon } \int _{-1}^x \sum _{i=1}^2 z_i c_i(s) \text {d}s, \end{aligned}$$

(14)

and setting $x=1$ yields

$$\begin{aligned} \phi ^\prime (1) - \phi ^\prime (-1) = -\frac{\chi _2}{\epsilon } \sum _{i=1}^2 z_i a_i. \end{aligned}$$

(15)

Then, integrating (14) over $[-1,1]$ yields

$$\begin{aligned} \phi (1) - \phi (-1) - 2\phi ^\prime (-1) = -\frac{\chi _2}{\epsilon } \sum _{i=1}^2 z_i (a_i - b_i), \end{aligned}$$

(16)

where $a_i$ is the total concentration of ion species i defined in (7) and

$$\begin{aligned} b_i = \int _{-1}^1 xc_i(x) dx, \quad i = 1,2, \end{aligned}$$

(17)

is the first moment of the ion concentration. By similar steps, integrating the Poisson equation (11) over [x, 1] yields

$$\begin{aligned} \phi (1) - \phi (-1) -2\phi ^\prime (1) = \frac{\chi _2}{\epsilon }\sum _{i=1}^2 z_i (a_i + b_i). \end{aligned}$$

(18)

Then, adding (16) and (18) yields

$$\begin{aligned} \phi (1) - \phi (-1) -\phi ^\prime (1) - \phi ^\prime (-1) = \frac{\chi _2}{\epsilon }\sum _{i=1}^2 z_i b_i. \end{aligned}$$

(19)

Combining the Robin boundary conditions (5) with (15) and (19) yields the linear system

$$\begin{aligned} \begin{pmatrix} 1 &{} \eta &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} -\eta \\ 0 &{} 1 &{} 0 &{} -1 \\ 1 &{} -1 &{} -1 &{} -1 \\ \end{pmatrix} \begin{pmatrix} \phi (1) \\ \phi ^\prime (1) \\ \phi (-1) \\ \phi ^\prime (-1) \end{pmatrix} = \begin{pmatrix} \phi _+ \\ \phi _- \\ \displaystyle -\frac{\chi _2}{\epsilon } \sum \limits _{i=1}^2 z_i a_i \\ \displaystyle \frac{\chi _2}{\epsilon } \sum \limits _{i=1}^2 z_i b_i \\ \end{pmatrix}. \end{aligned}$$

(20)

Hence, given ion concentrations $c_1(x), c_2(x)$ for $x \in [-1,1]$, the $\textbf{P}$ operator in (8a) is defined by the following steps.

• Compute the side right of the linear system (20) and solve for the potential boundary values $\phi (\pm 1), \phi ^\prime (\pm 1)$

• Compute the interior values of the potential gradient $\phi ^\prime (x)$ for $x \in (-1,1)$ from (13)

These steps require computing certain integrals, and the discretization schemes will be explained further below.

3.2 Derivation of NP operator

Here, we assume that the ion concentration $c_i(x)$ and potential gradient $\phi ^\prime (x)$ are given, and we shall derive an integral expression for $c_i(x)$. The Nernst-Planck equation (3b) is written as

$$\begin{aligned} c_i^{\prime \prime }(x) = -\chi _1 z_i (c_i(x)\phi ^\prime (x))^\prime , \end{aligned}$$

(21)

after cancelling the constant diffusion coefficient $D_i$, and then, applying (9) with $f(x) = c_i(x)$ yields an integral expression for the ion concentration,

$$\begin{aligned} \begin{aligned} c_i(x) =&\Big [g(x,y) c_i^\prime (y) - g_y(x,y)c_i(y)\Big ]_{y=-1}^{y=1} \\&+ \chi _1z_i\int _{-1}^{1} g(x,y) \left( c_i(y)\phi ^\prime (y)\right) ^\prime \text {d}y. \end{aligned} \end{aligned}$$

(22)

Differentiating (22) yields an analogous expression for the concentration gradient,

$$\begin{aligned} \begin{aligned} c_i^\prime (x) =&\Big [g_x(x,y) c_i^\prime (y) - g_{xy}(x,y)c_i(x)\Big ]_{y=-1}^{y=1} \\&+ \chi _1z_i\int _{-1}^{1} g_x(x,y) \left( c_i(y)\phi ^\prime (y)\right) ^\prime \text {d}y. \end{aligned} \end{aligned}$$

(23)

The bracket terms in (22) and (23) involve the boundary values of the concentration $c_i(\pm 1)$ and concentration gradient $c_i^\prime (\pm 1)$. The solution procedure in this case is somewhat different than what was described above for the $\textbf{P}$ operator.

From the Nernst-Planck equation (3b) and no-flux boundary conditions (6), it follows that

$$\begin{aligned} c_i^\prime (x) + \chi _1 z_i c_i(x)\phi ^\prime (x) = 0, \quad x \in (-1,1). \end{aligned}$$

(24)

Integrating (24) over $[-1,x]$ yields

$$\begin{aligned} c_i(x) - c_i(-1) = -\chi _1 z_i \int _{-1}^x c_i(s)\phi ^\prime (s)\text {d}s, \end{aligned}$$

(25)

and setting $x = 1$ yields

$$\begin{aligned} c_i(1) - c_i(-1) = -\chi _1 z_i \int _{-1}^1 c_i(s)\phi ^\prime (s)\text {d}s. \end{aligned}$$

(26)

Then, integrating (25) over $[-1,1]$ yields

$$\begin{aligned} c_i(1) + c_i(-1) = a_i - \chi _1z_i\!\int _{-1}^1 \!\! xc_i(x)\phi ^\prime (x)\text {d}x. \end{aligned}$$

(27)

Hence, given the ion concentration $c_i(x)$ and potential gradient $\phi ^\prime (x)$ for $x \in [-1,1]$, the $\textbf{NP}$ operator in (8b) is defined by the following steps.

• Compute the integrals on the right of (26, 27) and solve for the concentration boundary values $c_i(\pm 1)$ on the left

• Compute the concentration gradient boundary values $c_i^\prime (\pm 1)$ using $c_i(\pm 1)$ and the no-flux boundary conditions (6)

• Compute the interior concentration $c_i(x)$ for $x \in (-1,1)$ from (22)

This concludes the derivation of the $\textbf{P}, \textbf{NP}$ operators in the integral form of the PNP equations (8).

4 Numerical method

This section presents the numerical method used to solve the integral form of the PNP equations with the Robin and no-flux boundary conditions and total concentration constraint. The domain $[-1,1]$ is divided into N subintervals with endpoints $x_k, k=0:N$, where $x_0 = -1, x_N = 1$, and the grid spacing is $h_k = x_{k+1}-x_k$. We consider two point sets, uniform and Chebyshev,

$$\begin{aligned} x_k&= -1 + 2k/N, \quad k = 0:N, \end{aligned}$$

(28a)

$$\begin{aligned} x_k&= -\cos \theta _k, \quad \theta _k = k\pi /N, \quad k = 0:N. \end{aligned}$$

(28b)

The potential and concentration values and their gradients are denoted as

$$\begin{aligned} \phi _k&= \phi (x_k), \quad \phi ^\prime _k = \phi ^\prime (x_k) \end{aligned}$$

(29a)

$$\begin{aligned} c_{i,k}&= c_i(x_k), \quad c_{i,k}^\prime = c_i^\prime (x_k). \end{aligned}$$

(29b)

Two types of integrals appear in the $\textbf{P}, \textbf{NP}$ operators depending on whether or not the Green’s function is involved. When the Green’s function is not involved, the integral is discretized by the trapezoid rule,

$$\begin{aligned} b_i = \int _{-1}^1 xc_i(x) \text {d}x \approx \sum _{k=0}^N x_k c_{i,k}w_k, \end{aligned}$$

(30a)

$$\begin{aligned} \int _{-1}^1 c_i(x)\phi ^\prime (x)\text {d}x\approx \sum _{k=0}^N c_{i,k}\phi ^\prime _k w_k, \end{aligned}$$

(30b)

$$\begin{aligned} \int _{-1}^1 xc_i(x)\phi ^\prime (x)\text {d}x\approx \sum _{k=0}^N x_k c_{i,k}\phi ^\prime _kw_k, \end{aligned}$$

(30c)

where $w_k$ are the trapezoid weights. Next, we explain how the integrals involving the Green’s function are computed.

4.1 Integrals for P operator

First consider the integral in the potential expression (12),

$$\begin{aligned} \int _{-1}^1&g(x,y)c_i(y)\text {d}y \end{aligned}$$

(31a)

$$\begin{aligned}&= \sum _{j=0}^{N-1}\int _{x_j}^{x_{j+1}}g(x,y)c_i(y)\text {d}y \end{aligned}$$

(31b)

$$\begin{aligned}&\approx \sum _{j=0}^{N-1}g(x,x_{j+1/2})\int _{x_j}^{x_{j+1}}c_i(y)\text {d}y \end{aligned}$$

(31c)

$$\begin{aligned}&\approx \sum _{j=0}^{N-1}g(x,x_{j+1/2}) \frac{c_{i,j}+c_{i,j+1}}{2}h_j, \end{aligned}$$

(31d)

where $x_{j+1/2} = (x_j+x_{j+1})/2$. Note that a midpoint approximation is used in (31c), and the trapezoid rule is used in (31d). Then, setting $x = x_k$ in (12) yields

$$\begin{aligned} \begin{aligned} \phi _k =&\Big [g(x_k, y) \phi ^\prime (y) - g_y(x_k,y)\phi (y)\Big ]_{y=-1}^{y=1} \\&+\frac{\chi _2}{\epsilon } \sum \limits _{i=1}^2 z_i \sum _{j=0}^{N-1} g(x_k,x_{j+1/2})\frac{c_{i,j}+c_{i,j+1}}{2}h_j. \end{aligned} \end{aligned}$$

(32)

Applying the same steps to the integral in the potential gradient exression (13) yields

$$\begin{aligned} \begin{aligned} \phi _k^\prime =&\Big [g_x(x_k, y) \phi ^\prime (y) - g_{xy}(x_k, y)\phi (y)\Big ]_{y=-1}^{y=1} \\&+\frac{\chi _2}{\epsilon } \sum \limits _{i=1}^2 z_i \sum _{j=0}^{N-1} g_x(x_k, x_{j+1/2})\frac{c_{i,j}+c_{i,j+1}}{2}h_j. \end{aligned} \end{aligned}$$

(33)

Equations (32) and (33) are used to compute the interior values of the potential and its gradient, $\phi _k, \phi _k^\prime , k=1:N-1$, where the boundary values $\phi (\pm 1), \phi ^\prime (\pm 1)$ in the bracket terms are computed as described in Section 3.1. Note that the terms $g(x_k,x_{j+1/2})$ in (32) and $g_x(x_k,x_{j+1/2})$ in (33) avoid the singularity in the Green’s function.

4.2 Integrals for NP operator

Now consider the integral in the concentration expression (22),

$$\begin{aligned}&\int _{-1}^{1} g(x,y) \left( c_i(y)\phi ^\prime (y)\right) ^\prime \text {d}y \end{aligned}$$

(34a)

$$\begin{aligned}&= \sum _{j=0}^{N-1}\int _{x_j}^{x_{j+1}} g(x, y)\left( c_i(y)\phi ^\prime (y)\right) ^\prime \text {d}y \end{aligned}$$

(34b)

$$\begin{aligned}&\approx \sum _{j=0}^{N-1}g(x,x_{j+1/2})\int _{x_j}^{x_{j+1}} \left( c_i(y)\phi ^\prime (y)\right) ^\prime \text {d}y \end{aligned}$$

(34c)

$$\begin{aligned}&= \sum _{j=0}^{N-1} g(x, x_{j+1/2}) (c_{i,j+1}\phi ^\prime _{j+1} - c_{i,j}\phi ^\prime _j), \end{aligned}$$

(34d)

where a midpoint approximation is used in (34c) and the fundamental theorem of calculus is used in (34d). Then, setting $x = x_k$ in (22) yields

$$\begin{aligned} \begin{aligned} c_{i,k} =&\Big [g(x_k,y) c_i^\prime (y) - g_y(x_k, y)c_i(y)\Big ]_{y=-1}^{y=1} \\&+ \chi _1z_i\sum _{j=0}^{N-1} g(x_k,x_{j+1/2}) (c_{i,j+1}\phi ^\prime _{j+1} - c_{i,j}\phi ^\prime _j). \end{aligned} \end{aligned}$$

(35)

Applying the same steps to the integral in the concentration gradient expression (23) yields

$$\begin{aligned} \begin{aligned} c_{i,k}^\prime =&\Big [g_x(x_k, y) c_i^\prime (y)- g_{xy}(x_k, y)c_i(y)\Big ]_{y=-1}^{y=1} \\&+ \chi _1z_i\sum _{j=0}^{N-1} g_x(x_k,x_{j+1/2}) (c_{i,j+1}\phi ^\prime _{j+1} - c_{i,j}\phi ^\prime _j). \end{aligned} \end{aligned}$$

(36)

Equations (35) and (36) are used to compute the interior values of the concentration and its gradient, $c_{i,k}, c_{i,k}^\prime , k=1:N-1$, where the boundary values $c_i(\pm 1), c_i^\prime (\pm 1)$ in the bracket terms are computed as described in Section 3.2.

4.3 Gummel iteration

Define vectors containing the grid values of the potential, ion concentration, and their gradients,

$$\begin{aligned} {\varvec{\Phi }}&= [\phi _0, \ldots , \phi _N]^T, \end{aligned}$$

(37a)

$$\begin{aligned} \mathbf{D\Phi }&= [\phi _0^\prime , \ldots , \phi _N^\prime ]^T, \end{aligned}$$

(37b)

$$\begin{aligned} \textbf{c}_i&= [c_{i,0}, \ldots , c_{i,N}]^T, \quad i=1,2, \end{aligned}$$

(37c)

$$\begin{aligned} \textbf{Dc}_i&= [c_{i,0}^\prime , \ldots , c_{i,N}^\prime ]^T, \quad i=1,2. \end{aligned}$$

(37d)

Then after discretizing, the integral form of the PNP equations (8) becomes a system of nonlinear equations for the grid values,

$$\begin{aligned} \mathbf{D\Phi }&= \textbf{P}[\textbf{c}_1, \textbf{c}_2], \end{aligned}$$

(38a)

$$\begin{aligned} \textbf{c}_i&= \textbf{NP}[\textbf{c}_i, \mathbf{D\Phi }], \quad i=1,2. \end{aligned}$$

(38b)

To solve (38), we employ Gummel iteration with relaxation [26]. Letting superscript n denote the iteration step, we have

$$\begin{aligned} \mathbf{D\Phi }^*&= \textbf{P}[\textbf{c}_1^{(n)}, \textbf{c}_2^{(n)}], \end{aligned}$$

(39a)

$$\begin{aligned} \mathbf{D\Phi }^{(n+1)}&= \omega \mathbf{D\Phi }^* + (1-\omega ) \mathbf{D\Phi }^{(n)}, \end{aligned}$$

(39b)

$$\begin{aligned} \textbf{c}_i^*&= \textbf{NP}[\textbf{c}_i^{(n)}, \mathbf{D\Phi }^{(n+1)}], \quad i = 1,2, \end{aligned}$$

(39c)

$$\begin{aligned} \textbf{c}_i^{(n+1)}&= \omega \textbf{c}_i^* + (1-\omega ) \textbf{c}_i^{(n)}, \quad i=1,2, \end{aligned}$$

(39d)

where the relaxation parameter is chosen with $0< \omega < 1$. The intermediate potential gradient $\mathbf{D\Phi }^*$ is computed by the procedure in Section 4.1, and the intermediate concentration $\textbf{c}_i^*, i=1,2$ is computed by the procedure in Section 4.2. Hence, each iteration has two stages; the first stage comprising (39a)-(39b) computes the potential gradient using the ion concentrations from the previous iteration, and the second stage comprising (39c)-(39d) computes the ion concentrations using the potential gradient from the first stage.

The scheme starts with constant initial guesses for the potential gradient and ion concentrations,

$$\begin{aligned}&(\mathbf{D\Phi }^{(0)})_j = \frac{\phi _+ - \phi _-}{2}, \end{aligned}$$

(40a)

$$\begin{aligned}&(\textbf{c}_i^{(0)})_j = \frac{1}{2}a_i, \quad i=1,2, \end{aligned}$$

(40b)

where $j = 0:N$ is the grid-point index, the right side of (40a) is the gradient determined by the formal potential boundary values $\phi _{\pm }$, and (40b) satisfies the total concentration constraint (7). The stopping criterion is

$$\begin{aligned} ||\mathbf{D\Phi }^{(n+1)}-\mathbf{D\Phi }^{(n)}||_2 < 10^{-6}, \end{aligned}$$

(41a)

$$\begin{aligned} \max \limits _{i=1,2}\, ||\textbf{c}_i^{(n+1)}-\textbf{c}_i^{(n)}||_2 < 10^{-6}. \end{aligned}$$

(41b)

After the scheme converges, the grid values of the potential $\phi _k$ are computed from (32), and the grid values of the concentration gradient $c_{i,k}^\prime$ are computed from (36). Note that the potential is presented for diagnostic purposes, and the concentration gradient is used to compute the current in the K$^+$ channel simulation further below.

This completes the description of the proposed integral equation method for the 1D steady-state PNP equations. Several antecedents have used integral equation formulations to solve two-point boundary value problems although, to the best of our knowledge, they used Green’s functions that satisfy homogeneous boundary conditions [24, 28, 29], whereas the present PNP solver uses the free-space Green’s function which we expect will better facilitate a future extension to 2D and 3D problems.

5 Numerical results

In this section, the integral method is applied to compute several examples from prior work in which the PNP equations were solved by finite-difference or finite-element methods [10, 30]. In these examples, there are two ion species with valence $z_1=-1$ (anions), $z_2=1$ (cations), and two types of systems depending on the total ion concentration, electroneutral ($a_1 = a_2$) and non-electroneutral ($a_1 \ne a_2$). Table 1 gives the parameter values. The calculations used either Chebyshev or uniform grid points as noted, and the relaxation parameter $\omega$ was chosen by trial and error. The method was programmed in Python, and the calculations were done on an iMac computer with the Apple M1 chip.

Table 1 Parameters for electroneutral and non-electroneutral systems, case number, reference, total concentration of anions and cations $a_1, a_2$, Robin boundary condition potential parameters $\phi _\pm$, permittivity $\epsilon$, capacitance parameter $\eta$, energy ratio $\chi _1$, inverse square Debye length $\chi _2$, and relaxation parameter $\omega$

5.1 Electroneutral systems

Here, we consider three electroneutral systems in which the total anion and cation concentrations are equal, $a_1 = a_2$, the formal potential boundary values are either $\phi _- = -1, \phi _+ = 1$ (cases 1 and 2) or $\phi _- = 1, \phi _+ = -1$ (case 3).

5.1.1 Electroneutral case 1

In this case, the capacitance parameter is equal to the permittivity, $\eta = \epsilon$, and two values are considered, $\epsilon = 1/4, 1/64$ [10, 30]. Figure 1 shows the computed potential $\phi$ and anion concentration $c_1$; the cation concentration $c_2$ is not shown, since it is simply the reflection of $c_1$ about the channel midpoint, $c_2(x) = c_1(-x)$. With $\phi _\pm = \pm 1$, the potential is an odd function, $\phi (-x) = -\phi (x)$, and it increases monotonically from left to right across the channel. The anions are repelled from the low potential at $x=-1$ and are attracted to the high potential at $x=1$ where they accumulate due to the no-flux boundary condition. For large permittivity $\epsilon = 1/4$, the potential and concentration profiles have mild gradients, but for small permittivity $\epsilon = 1/64$, the profiles have sharp boundary layers. These results agree well with Fig. 1 in [10, 30].

Fig. 1

Electroneutral systems, cases 1.1 and 1.2 in Table 1, large permittivity $\epsilon = 1/4$, small permittivity $\epsilon = 1/64$, a potential $\phi$, b anion concentration $c_1$, integral method with Chebyshev points, $N=100$ subintervals

Next, we consider convergence of the method. Following [10], the convergence rate for the potential is defined by

$$\begin{aligned} p = -\log _2 \frac{\Vert {\varvec{\Phi }}_{4N}-{\varvec{\Phi }}_{2N}\Vert _2}{\Vert \mathbf{\Phi }_{2N}-{\varvec{\Phi }}_{N}\Vert _2}, \end{aligned}$$

(42)

where ${\varvec{\Phi }}_N$ denotes the vector of computed potential grid values using N subintervals. Table 2 shows results for both uniform and Chebyshev points indicating that $p \approx 2$, so the integral method is 2nd order accurate. For large permittivity $\epsilon = 1/4$, where the solution is smooth, both point sets require the same number of iterations, while the Chebyshev points yield slightly smaller error. For small permittivity $\epsilon = 1/64$, where the solution has a sharp boundary layer, the number of iterations is higher for both point sets, but the Chebyshev points require fewer iterations and yield smaller error than the uniform points.

Table 2 Electroneutral system (cases 1.1 and 1.2), parameters in Table 1, large permittivity $\epsilon = 1/4$, small permittivity $\epsilon = 1/64$, N subintervals, uniform and Chebyshev points, number of iterations iter, potential error $\Vert \mathbf{\Phi }_{2N}-{\varvec{\Phi }}_{N}\Vert _2$, convergence rate p, nc = did not converge

5.1.2 Electroneutral case 2

This case extends case 1 by considering five values of the capacitance parameter, $\eta = 0, \epsilon ^2, \epsilon , \epsilon ^{1/2}, 1$. Figure 2 shows the potential $\phi$ and anion concentration $c_1$, where the computed boundary values of $\phi (1), c_1(1)$ are printed alongside the curves for comparison with [30]. As in case 1, the anions are repelled from the potential minimum at $x=-1$ and are attracted to the potential maximum at $x=1$; moreover, for large permittivity $\epsilon = 1/4$, the profiles have mild gradients, but for small permittivity $\epsilon = 1/64$, they have sharp boundary layers. The dependence on $\eta$ is interesting. As $\eta \rightarrow 0$, the potential boundary values converge to the formal values, $\phi (\pm 1) \rightarrow \phi _\pm$, as required by the Robin boundary conditions (5). On the other hand, as $\eta$ increases, the potential vanishes, $\phi (x) \rightarrow 0$, and the anion concentration tends to the bulk value, $c_1(x) \rightarrow 1/2$; these features are consistent with the Robin and no-flux boundary conditions (5), (6) and the total concentration condition (7). The present results agree well with Fig. 1 in [30].

Fig. 2

Electroneutral systems, cases 2.1 and 2.2 in Table 1, potential $\phi$, anion concentration $c_1$, large permittivity $\epsilon = 1/4$ (a,b), small permitivity $\epsilon = 1/64$ (c,d), integral method with Chebyshev points, $N=100$ subintervals

5.1.3 Electroneutral case 3

This case uses the more realistic values of $\chi _1, \chi _2, \eta$ in Table 1 [10]. Figure 3 shows the potential $\phi$ and anion concentration $c_1$. In this case with small capacitance parameter $\eta$ = 4.63e-5, the Robin boundary conditions are almost Dirichlet boundary conditions, so $\phi (\pm 1) \approx -\phi _\pm$ as shown in Fig. 3a. The anions are attracted to the potential maximum at $x = -1$, leading to a boundary layer in the concentration. Note that the concentration boundary value $c_1(-1) \approx 21.6$ is higher than in case 1 and case 2; this is attributed to the higher total concentration $a_1 = 2$ in this case. These results agree well with the late time results for the time-dependent PNP equations in Fig. 2 of [10].

Fig. 3

Electroneutral system, case 3 in Table 1, a potential $\phi$, b anion concentration $c_1$, integral method with Chebyshev points, $N=100$ subintervals

5.2 Non-electroneutral systems

This is case 4 in Table 1. In contrast with the previous cases, here, the total cation concentration $a_2=2$ is greater than the total anion concentration $a_1=1$, and the formal potential boundary values are equal, $\phi _\pm = 1$ [30].

Figure 4 shows the results, where the top frames use large permittivity $\epsilon = 1/4$ (case 4.1), and the bottom frames use small permittivity $\epsilon = 1/16$ (case 4.2). Five values of the capacitance parameter are considered, $\eta = 0, \epsilon ^2, \epsilon , \epsilon ^{1/2}, 1$. Results are shown for the potential $\phi$, potential gradient $\phi ^\prime$, and ion concentrations $c_1, c_2$ (in this case, the concentrations have different profiles). The potential is maximum at $x=0$, and the potential boundary values $\phi (1)$ are printed on the right side of the plots; these results are in good agreement with [30]. The high potential at $x=0$ attracts anions and repels cations, leading to boundary layers in the ion concentrations.

As the capacitance parameter $\eta$ increases, the potential also increases, but the profiles have almost the same shape, and the potential gradient is almost independent of $\eta$ (the curves overlap); the ion concentrations are also almost independent of $\eta$ because the Nernst-Planck equation (3b) depends on $\phi ^\prime$, but not $\phi$. As the permittivity $\epsilon$ decreases, the potential gradient and ion concentrations develop sharp boundary layers. In [30], it was proven that as $\epsilon \rightarrow 0$, the potential $\phi (x) \rightarrow \infty$ for all $x \in [-1,1]$ and Fig. 4 is consistent with this. Figure 4 also suggests that the ion concentration boundary values converge like $c_1(\pm 1) \rightarrow 0, c_2(\pm 1) \rightarrow \infty$ as $\epsilon \rightarrow 0$.

Fig. 4

Non-electroneutral systems, cases 4.1 and 4.2 in Table 1, total concentration $a_1=1$ (anion), $a_2=2$ (cation), large permittivity $\epsilon = 1/4$ (top), small permittivity $\epsilon = 1/16$ (bottom), equal formal potential boundary values $\phi _\pm = 1$, capacitance parameter $\eta = 0, \epsilon ^2, \epsilon , \epsilon ^{1/2}, 1$, (a,d) potential $\phi$, (b,e) potential gradient $\phi ^\prime$, (c,f) ion concentration ($c_1$ anion, $c_2$ cation), integral method with Chebyshev points, $N=100$ subintervals

Table 3 shows the potential error and convergence rate confirming 2nd order accuracy $p \approx 2$ for this non-electroneutral system with capacitance ƞ=0. As before, for large permittivity $\epsilon = 1/4$, the uniform and Chebyshev points yield similar results. For small permittivity $\epsilon = 1/16$, the number of iterations is higher for both points sets, but Chebyshev points require fewer iterations and yield smaller error.

Table 3 Non-electroneutral system (cases 4.1 and 4.2) [30], parameters in Table 1, capacitance ƞ=0, large permittivity $\epsilon = 1/4$, small permittivity $\epsilon = 1/16$, N subintervals, uniform and Chebyshev points, number of iterations iter, potential error $\Vert {\varvec{\Phi }}_{2N}-{\varvec{\Phi }}_{N}\Vert _2$, convergence rate p, nc = did not converge

6 K$^+$ ion channel

Finally, we consider a potassium (K$^+$) ion channel model following [25]. Figure 5 shows a cross-section of the model comprising two conical baths with KCl solvent and a cylindrical channel with four subregions (buffer, nonpolar, central cavity, and selectivity filter). In this example, the PNP equations are solved in dimensional form with the 1D approximation from [25],

$$\begin{aligned} -&A^{-1}\left( \epsilon A\phi ^\prime \right) ^\prime = e(z_1c_1 + z_2c_2 - \rho _n), \end{aligned}$$

(43a)

$$\begin{aligned}&A^{-1}\left( A\left( D_ic_i^\prime + z_i\mu _ic_i\phi ^\prime \right) \right) ^\prime = 0, \end{aligned}$$

(43b)

where $A(x)= \pi r(x)^2$ is the cross-sectional area in terms of the radius r(x). Note that the Poisson equation (43a) now includes a fixed negative charge density $\rho _n(x)$. The model extends over the interval $[-5,8.5]$ (the spatial unit is nm), and Dirichlet boundary conditions are imposed,

$$\begin{aligned} \phi (-5)&= 0, \quad \phi (8.5) = -100 \;{\text {mV}}, \end{aligned}$$

(44a)

$$\begin{aligned} c_i(-5)&= c_i(8.5) = 0.15 \; {\text {molar}}, \quad i = 1,2. \end{aligned}$$

(44b)

Table 4 gives the parameter values with units in the caption. The material parameters are constant in each bath and each channel subregion, where the ion mobility is $\mu _i = eD_i/k_BT$ in terms of the diffusion coefficient $D_i$. The four channel subregions have constant radius $r(x) = 0.5$, and while [25] took r(x) to be linear in the baths with $r(-5) = r(8.5) = 5.5$; here, we consider a piecewise constant approximation indicated schematically by the red dotted lines in Fig. 5. In practice, we used 20 steps in each bath, so altogether there are 43 interfaces (19 in each bath, three in the channel interior, and two at the bath/channel interfaces). At each interface, the potential and ion concentrations satisfy continuity conditions,

$$\begin{aligned}&[\phi ] = 0, \quad \left[ \epsilon A\phi ^\prime \right] = 0, \end{aligned}$$

(45a)

$$\begin{aligned}&[c_i] = 0, \quad \left[ A\left( D_ic_i^\prime + z_i\mu _ic_i\phi ^\prime \right) \right] = 0, \end{aligned}$$

(45b)

where the bracket indicates the jump across the interface.

Fig. 5

Schematic diagram of K$^+$ ion channel model [25] comprising interior/exterior conical baths with KCl solvent and a cylindrical channel with four subregions (buffer, nonpolar, central cavity, and selectivity filter), channel subregions have constant radius $r = 0.5$ [nm], bath radius is linear (black, solid line) in [25] and piecewise constant (red, dotted line) in the present work

Table 4 K$^+$ channel parameters [25], interval [nm], length $\ell$ [nm], radius r(x) [nm], cross-sectional area A(x) [nm]$^2$, total fixed charge Q [e], fixed charge density $\rho _n$ [1/nm³], dielectric constant $\epsilon$, mobility $\mu _i = eD_i/k_BT$ [1e-5 cm$^2$/(V $\cdot$ s)], diffusion coefficient $D_i$ [1e-5 cm$^2$/s]

The integral method previously described for systems with one domain was extended to this example with multiple subdomains, and the scheme has the same Gummel iteration form as (39). The unknown boundary and interface variables $\phi , \phi ^\prime , c_i, c_i^\prime$ at the domain boundary and 43 interfaces satisfy a coupled linear system which is solved in each iteration after which the interior variables are computed using Green’s 3rd identity.

To illustrate the idea in a simple case, consider the Poisson equation (43a) on the interval $[x_L,x_R]$ with Dirichlet BC $\phi _L,\phi _R$ and one interface at $x_I$. Here, there are two subdomains, $[x_L,x_I], [x_I,x_R]$, and six unknown boundary/interface values of the potential and potential gradient, $\phi ^\prime (x_L), \phi ^\prime (x_R), \phi (x_I^{\pm }), \phi ^\prime (x_I^{\pm })$, which satisfy six linear equations comprising two interface conditions (46a),(46b), two equations from integrating once over each subdomain (46c),(46d), and two equations from integrating twice (46e),(46f),

$$\begin{aligned}&\phi (x_I^{-}) =\phi (x_I^{+}), \end{aligned}$$

(46a)

$$\begin{aligned}&\epsilon _L A_L \phi ^{\prime }(x_I^{-}) = \epsilon _R A_R \phi ^{\prime }(x_I^{+}), \end{aligned}$$

(46b)

$$\begin{aligned}&\phi ^{\prime }(x_L) - \phi ^{\prime }(x_I^{-}) = \frac{e}{\epsilon _L}\Big [\sum _{i=1}^2 z_i a_i^L-a_f^L\Big ], \end{aligned}$$

(46c)

$$\begin{aligned}&\phi ^{\prime }(x_I^{+}) - \phi ^{\prime }(x_R) = \frac{e}{\epsilon _R}\Big [\sum _{i=1}^2 z_i a_i^R-a_f^R\Big ], \end{aligned}$$

(46d)

$$\begin{aligned}&\phi _L - \phi (x_I^{-}) - \frac{x_L-x_I}{2} [\,\phi ^{\prime }(x_L)+\phi ^{\prime }(x_I^{-})\,] \nonumber \\&= \frac{e}{\epsilon _L} \Big [\frac{x_I+x_L}{2}\Big [\sum _{i=1}^2 z_i a_i^L-a_f^L\Big ] - \sum _{i=1}^2 z_i b_i^L + b_f^L\Big ], \end{aligned}$$

(46e)

$$\begin{aligned}&\phi (x_I^{+}) -\phi _R-\frac{x_I-x_R}{2}[\;\phi ^{\prime }(x_I^+)+\phi ^{\prime }(x_R)\;] \nonumber \\&=\frac{e}{\epsilon _R}\Big [\frac{x_I+x_R}{2}\Big [\sum _{i=1}^2 z_i a_i^R-a_f^R\Big ] -\sum _{i=1}^2 z_i b_i^R+b_f^R\Big ], \end{aligned}$$

(46f)

where the integrations follow the process described in Section 3.1 leading to (20). In the equations (46), the subscripts and superscripts L and R correspond to the two subdomains, and on the right side of the equal sign, we have the following definitions for the left subdomain,

$$\begin{aligned} a_i^L = \int _{x_L}^{x_I}c_i(x)\text {d}x, \quad b_i^L = \int _{x_L}^{x_I}xc_i(x)\text {d}x, \end{aligned}$$

(47a)

$$\begin{aligned} a_f^L = \int _{x_L}^{x_I}\rho _n(x)\text {d}x, \quad b_f^L = \int _{x_L}^{x_I}x\rho _n(x)\text {d}x, \end{aligned}$$

(47b)

with corresponding definitions for the right subdomain. The Nernst-Planck equation (43b) is treated similarly.

Returning to the model of the K$^+$ channel with 43 interfaces, the linear system has dimension 174 (four unknowns at each interface and two unknowns at the boundary). The computations used uniform grid spacing $h = 0.01$ and the same stopping criterion as before (41). In this problem, the mobility/diffusion coefficient ratio is $\mu _i/D_i = 40$/V, and the resulting potential gradient $\phi ^\prime (x)$ is large in some places; hence, the model is drift-dominated, and we used the following continuation scheme; the problem is solved for an increasing sequence of ratios $\mu _i/D_i$ = 1/V, 10/V, 20/V, and 40/V, with relaxation parameters $\omega = 0.9, 0.4, 0.26, 0.18$, requiring 12, 69, 148, and 218 iterations, respectively, and the converged solution for one ratio $\mu _i/D_i$ is the initial guess for the next ratio; the total run time for all four ratios was 44 seconds. The continuation scheme was not needed for the electroneutral and non-electroneutral systems considered earlier since they were not drift-dominated.

Figure 6 shows the computed potential and ion concentration profiles which agree well with the previous results [25]. The negative fixed charge density $\rho _n$, indicated by green dashed lines, has substantial impact on the potential and ion concentrations. In particular, the polar subregions with negative fixed charge have local potential minima below the boundary potential (−133.7 mV in the buffer and −155.8 mV in the filter), while the potential rises to a local maximum in the nonpolar subregion (−34.3 mV). As a result, the K$^+$ cations are attracted to the buffer and filter and are expelled from the nonpolar region, while the opposite is true for the Cl$^-$ anions; this demonstrates the cation selectivity property of the K$^+$ channel.

Fig. 6

K$^+$ ion channel model depicted in Fig. 5 [25], parameters in Table 4, Dirichlet boundary conditions (44), fixed negative charge density $\rho _n$ (green dashed lines), potential $\phi$ [mV], ion concentration $c_i$ [molar], K$^+$ (red solid line), Cl$^-$ (blue solid line), integral equation method with uniform points, grid spacing $h = 0.01$

We also computed the current–voltage curve for the K$^+$ channel model, where the current is

$$\begin{aligned} I(V_{\textrm{app}})&= -\sum _{i=1}^2 z_ieA(D_ic_i^\prime + z_i\mu _ic_i\phi ^\prime ), \end{aligned}$$

(48a)

$$\begin{aligned} V_{\textrm{app}}&= \phi (-5) - \phi (8.5), \end{aligned}$$

(48b)

in terms of the applied voltage $V_{\textrm{app}}$ across the channel. All other parameters are the same as in Table 4. It follows from the NP equation (43b) that the current (48a) is constant throughout the domain, and in the present calculations, this was satisfied to machine precision.

Figure 7 shows the computed I–V curve which closely matches the expected linear relation. For $V_{\textrm{app}}$ = 100 mV, the current is 19.4 pA comprising 19.1 pA for K$^+$ cations and 0.3 pA for Cl$^-$ anions, which again shows the cation selectivity of the K$^+$ channel. We checked that the computed current is not sensitive to the number of steps in the bath, and Table 5 shows that the computed current converges to 20.9 pA as the grid spacing h is reduced with convergence rate $p \approx 2$. For comparison, [25] reported current 22.5 pA comprising 22.2 pA for cations and 0.3 pA for anions. Hence, the two calculations agree for the anion current, but there is a small discrepancy in the cation current.

Fig. 7

K$^+$ ion channel, parameters in Table 4 [25], current I [pA] versus applied voltage $V_{\textrm{app}}$ [mV], grid spacing $h = 0.01$ nm

Table 5 K$^+$ channel [25], applied voltage $V_{\textrm{app}}$ = 100 mV, grid spacing h [nm], current I [pA], error $|I_{2h} - I_{h}|$, convergence rate $p = -\log _2(|I_{4h} - I_{2h}|/|I_{2h} - I_{h}|)$

7 Summary

An integral equation method was presented for the 1D steady-state PNP equations modeling ion transport through membrane channels. Green’s 3rd identity was applied to recast the PNP differential equations as a fixed-point problem involving integral operators for the potential gradient and ion concentrations. The integrals were computed by midpoint and trapezoid rules at either uniform or Chebyshev grid points, and the resulting nonlinear equations were solved by Gummel iteration with relaxation. Each iteration requires solving a small linear system for the boundary and interface variables.

The integral equation method was applied to electroneutral and non-electroneutral systems with Robin boundary conditions on the potential and no-flux boundary conditions on the ion concentrations. The method is 2nd order accurate even in cases with sharp boundary layers. The method was also applied to a drift-dominated K$^+$ ion channel model following [25]. In this case, the fixed charge density in the channel ensures the selectivity of K$^+$ ions and exclusion of Cl$^-$ ions. In these tests, the integral method results agree well with published finite-difference and finite-element results [10, 25, 30].

Various techniques have been used in numerical PNP solvers to improve stability such as positivity-preserving schemes, Slotboom variables, and streamwise upstream differencing. The integral equation method presented here did not employ these techniques, although it did use relaxation to accelerate the iteration and continuation to compute a good initial guess for drift-dominated systems. It is noteworthy that in these calculations, the integral equation method preserved the positivity of the ion concentrations.

In the future work, we aim to extend the integral equation PNP solver to time-dependent problems as well as 2D and 3D ion channel models, where the volume integral can be efficiently computed using adaptive quadrature and a fast summation method [31,32,33].