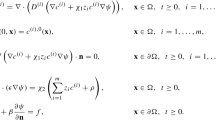Abstract
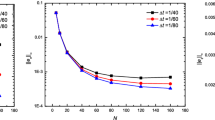
The Poisson–Nernst–Planck (PNP) equations have recently been used to describe the dynamics of ion transport through biological ion channels besides being widely employed in semiconductor industry. This paper is about the design of a numerical scheme to solve the PNP equations that preserves exactly (up to roundoff error) a discretized form of the energy dynamics of the system. The proposed finite difference scheme is of second-order accurate in both space and time. Comparisons are made between this energy dynamics-preserving scheme and a standard finite difference scheme, showing a difference in satisfying the energy law. Numerical results are presented for validating the orders of convergence in both time and space of the new scheme for the PNP system.

Similar content being viewed by others
References
Britz, D., Strutwolf, J.: Several ways to simulate time dependent liquid junction potentials by finite differences. Electrochim. Acta. 137, 328–335 (2014)
Chaudhry, J., Comer, J., Aksimentiev, A., Olson, L.: A stabilized finite element method for modified Poisson–Nernst–Planck equations to determine ion flow through a nanopore. Commun. Comput. Phys. 15(1), 93–125 (2014)
Doyle, D., Cabral, J.M., Pfuetzner, R.A., Kuo, J.G., Cohen, S., Chait, B., MacKinnon, R.: The structure of the potassium channel: molecular basis of \(\text{K}^+\) conduction and selectivity. Science 280, 69–77 (1998)
Eisenberg, R.: Ion channels in biological membranes: electrostatic analysis of a natural nanotube. Contemp. Phys. 39, 447 (1998)
Flavell, A., Machen, M., Eisenberg, B., Kabre, J., Liu, C., Li, X.: A conservative finite difference scheme for Poisson–Nernst–Planck equations. J. Comput. Electron. 13, 235–249 (2014)
Fogolari, F., Briggs, J.: On the variational approach to Poisson–Boltzmann free energies. Chem. Phys. Lett. 281, 135–139 (1997)
Gagneux, G., Millet, O.: A survey on properties of Nernst–Planck–Poisson system. application to ionic transport in porous media. Appl. Math. Model. 40, 846–858 (2016)
Gardner, C., Nonner, W., Eisenberg, R.: Electrodiffusion model simulation of ionic channels: 1D simulations. J. Comput. Electron. 3, 25–31 (2004)
Gillespie, D.: A Singular Perturbation Analysis of the Poisson–Nernst–Planck System. Ph.D. thesis, Rush University (1999)
Gillespie, D.: Energetics of divalent selectivity in a calcium channel: the ryanodine receptor case study. Biophys. J. 94, 1169–1984 (2008)
He, D., Pan, K.: An Energy Preserving Finite Difference Scheme for the Poisson–Nernst–Planck System. arXiv:1506.0025v1 (2015)
Hyon, Y., Eisenberg, R., Liu, C.: A mathematical model for the hard sphere repulsion in ionic solutions. Commun. Math. Sci. 9, 459–475 (2011)
Ji, S., Liu, W., Zhang, M.: Effects of (small) permanent charge and channel geometry on ionic flows via classical Poisson–Nernst–Planck models. SIAM J. Appl. Math. 75(1), 114–135 (2015)
Lee, C., Lee, H., Hyon, Y., Lin, T., Liu, C.: New Poisson–Boltzmann type equations: one-dimensional solutions. Nonlinearity 24, 431 (2011)
Liu, C., Kelly, R.: The use of finite element methods (fem) in the modeling of localized corrosion. Electrochem. Soc. Interface 23(4), 47–51 (2014)
Liu, C., Metti, M., Xu, J.: Energetically stable discretizations for charge carrier transport and electrokinetic models. arXiv:1503.04471v1 (2015)
Liu, H., Wang, Z.: A free energy satisfying finite difference method for Poisson–Nernst–Planck equations. J. Comput. Phys. 268, 363–376 (2014)
Markowich, P., Ringhofer, C., Schmeiser, C.: Semiconductor Equations. Springer, Wien (1990)
Mirzadeh, M., Gibou, F.: A conservative discretization of the Poisson–Nernst–Planck equations on adaptive cartesian grids. J. Comput. Phys. 274, 633–653 (2014)
Pittino, F., Selmi, L.: Use and comparative assessment of the CVFEM method for Poisson–Boltzmann and Poisson–Nernst–Planck three dimensional simulations of impedimetric nano-biosensors operated in the DC and AC small signal regimes. Comput. Methods Appl. Mech. Eng. 278, 902–923 (2014)
Tu, B., Xie, Y., Zhang, L., Lu, B.: Stabilized finite element methods to simulate the conductances of ion channels. Comput. Phys. Commun. 188, 131–139 (2015)
Xu, Z., Ma, M., Liu, P.: Self-energy-modified Poisson–Nernst–Planck equations: WKB approximation and finite-difference approaches. Phys. Rev. E 90(1), 013,307 (2014)
Acknowledgements
The work is partially supported by NSF under the grant DMS-1620449. The authors would like to thank Bob Eisenberg and Chun Liu for helpful discussion on the research.
Author information
Authors and Affiliations
Corresponding author
Appendix: The local truncation error of the energy-preserving scheme (23)
Appendix: The local truncation error of the energy-preserving scheme (23)
In this “Appendix: The local truncation error of the energy-preserving scheme (23),” we show that the local truncation error of our scheme (23) is of second order in both space and time to the Nernst–Planck Eq. (5a) with the chemical potential defined in (2).
First, we define the functions \(\mu _{i,-}\) and \(\mu _{i,+}\) corresponding to the discrete counterparts in (21) and (22), respectively,
where \(g_1\) is defined by
Then, we build upon these functions by defining
Using Taylor expansion, one can easily show that
where \(g_2\) and \(g_3\) are smooth functions depending on the derivatives of \(c_i\) with respect to time t.
Substituting (57) and (58) into (53) and (54), we obtain
By replacing \(\mu _{i,+}\) and \(\mu _{i,-}\) in (56) by (59) and (60), we obtain
where the smooth functions \(g_4\) and \(g_5\) are defined as
Noting the central differencing operator \(\nabla _{\Delta x}\) has the truncation error \(\displaystyle {\nabla _{\Delta x} f(x) = f^{\prime }(x) + O(\Delta x)^2}\) and from the Taylor’s expansions centered at \((x,t+\frac{\Delta t}{2})\), we have
where \(g_{6}\) and \(g_{7}\) are smooth functions of the derivatives of the unknowns \(c_i\)’s and \(\phi \) and the grid size \((\Delta x, \Delta t)\).
Therefore,
where \(g_8(x,t)= o((\Delta x)^2)\) and \(g_8(x,t)= o((\Delta t)^2)\). Thus, the truncation error of the scheme (23) is
Rights and permissions
About this article
Cite this article
Flavell, A., Kabre, J. & Li, X. An energy-preserving discretization for the Poisson–Nernst–Planck equations. J Comput Electron 16, 431–441 (2017). https://doi.org/10.1007/s10825-017-0969-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10825-017-0969-8