Dimensionality Effects on the Mixed Spin-1/2 and Spin-2 Blume-Capel Model: Renormalization Group Theory

Abstract

We have used the real-space Migdal-Kadanoff renormalization group technique on d-dimensional hypercubic lattice to study the mixed spin-1/2 and spin-2 Blume-Capel model. First, we indicate a critical dimension d_C ≈ 2.05, above and below which different topologies of phase diagrams occur. The phase diagrams have been plotted in the (crystal field, temperature) plane around d_C, in which there is a second-order phase transition. Moreover, using the variation of the free energy at low temperatures, we have established the ground-state phase diagrams in the (∆/J, C/J) plane for d < d_C and d ≥ d_C. In particular, we have seen the appearance of two first-order transitions at very low temperatures by the use of the free energy and its isotherm derivative. A detailed analysis of fixed points and flow diagrams indicates that there is no tricritical point.

Appendices

The Migdal-Kadanoff recursion equations (Eqs. 7)

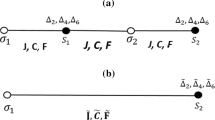
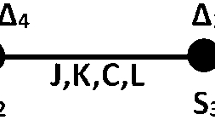
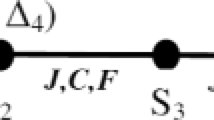
We first replace the expression of Eq. (3) in the first side of Eq. (5) with σ₁ = {±1/2} and S₂ = {0, ±1 and ± 2}, which gives us ten forms. But considering that the cases (σ₁, S₂) and (−σ₁, -S₂) are equivalent, we only obtain five different forms ${F}_{\sigma_1,{S}_2}$:

$$ \mathrm{For}\left({\sigma}_1,{S}_2\right)=\left\{\left(1/2,2\right);\left(-1/2,-2\right)\right\} $$

$$ {\displaystyle \begin{array}{l}{F}_{\frac{1}{2},2}={F}_{-\frac{1}{2},-2}=2{e}^{12\frac{\Delta}{z}+48\frac{\Delta_4}{z}}\left[{e}^{J+4C} ch\left(2J+8C\right)+{e}^{-J-4C}\right]\\ {}\kern4.75em +2{e}^{6\frac{\Delta}{z}+18\frac{\Delta_4}{z}}\left[{e}^{\frac{J}{2}+\frac{C}{2}} ch\left(\frac{3J+9C}{2}\right)+{e}^{-\frac{J}{2}-\frac{C}{2}} ch\left(\frac{J+7C}{2}\right)\right]+2{e}^{4\frac{\Delta}{z}+16\frac{\Delta_4}{z}} ch\left(J+4C\right)\end{array}} $$

(9)

$$ \mathrm{For}\left({\sigma}_1,{S}_2\right)=\left\{\left(-1/2,2\right);\left(1/2,-2\right)\right\} $$

$$ {\displaystyle \begin{array}{l}{F}_{-\frac{1}{2},2}={F}_{\frac{1}{2},-2}=2{e}^{12\frac{\Delta}{z}+48\frac{\Delta_4}{z}}\left[{e}^{-J-4C} ch\left(2J+8C\right)+{e}^{J+4C}\right]\\ {}\kern5em +2{e}^{6\frac{\Delta}{z}+18\frac{\Delta_4}{z}}\left[{e}^{-\frac{J}{2}-\frac{C}{2}} ch\left(\frac{3J+9C}{2}\right)+{e}^{\frac{J}{2}+\frac{C}{2}} ch\left(\frac{J+7C}{2}\right)\right]+2{e}^{4\frac{\Delta}{z}+16\frac{\Delta_4}{z}} ch\left(J+4C\right)\end{array}} $$

(10)

$$ \mathrm{For}\left({\sigma}_1,{S}_2\right)=\left\{\left(1/2,1\right);\left(-1/2,-1\right)\right\} $$

$$ {\displaystyle \begin{array}{l}{F}_{\frac{1}{2},1}={F}_{-\frac{1}{2},-1}=2{e}^{9\frac{\Delta}{z}+33\frac{\Delta_4}{z}}\left[{e}^{J+4C} ch\left(\frac{3J+9C}{2}\right)+{e}^{-J-4C} ch\left(\frac{J+7C}{2}\right)\right]\\ {}\kern4.75em +2{e}^{3\frac{\Delta}{z}+3\frac{\Delta_4}{z}}\left[{e}^{\frac{J}{2}+\frac{C}{2}} ch\left(J+C\right)+{e}^{-\frac{J}{2}-\frac{C}{2}}\right]+2{e}^{\frac{\Delta}{z}+\frac{\Delta_4}{z}} ch\left(\frac{J+C}{2}\right)\end{array}} $$

(11)

$$ \mathrm{For}\left({\sigma}_1,{S}_2\right)=\left\{\left(-1/2,1\right);\left(1/2,-1\right)\right\} $$

$$ {\displaystyle \begin{array}{l}{F}_{-\frac{1}{2},1}={F}_{\frac{1}{2},-1}=2{e}^{9\frac{\Delta}{z}+33\frac{\Delta_4}{z}}\left[{e}^{-J-4C} ch\left(\frac{3J+9C}{2}\right)+{e}^{J+4C} ch\left(\frac{J+7C}{2}\right)\right]\\ {}\kern4.75em +2{e}^{3\frac{\Delta}{z}+3\frac{\Delta_4}{z}}\left[{e}^{-\frac{J}{2}-\frac{C}{2}} ch\left(J+C\right)+{e}^{\frac{J}{2}+\frac{C}{2}}\right]+2{e}^{\frac{\Delta}{z}+\frac{\Delta_4}{z}} ch\left(\frac{J+C}{2}\right)\end{array}} $$

(12)

$$ \mathrm{For}\left({\sigma}_1,{S}_2\right)=\left\{\left(1/2,0\right);\left(-1/2,0\right)\right\} $$

$$ {F}_{\frac{1}{2},0}={F}_{-\frac{1}{2},0}={A}_0=4{e}^{8\frac{\Delta}{z}+32\frac{\Delta_4}{z}}{ch}^2\left(J+4C\right)+4{e}^{2\frac{\Delta}{z}+2\frac{\Delta_4}{z}}{ch}^2\left(\frac{J+C}{2}\right)+2 $$

(13)

So according to Eq. (6), we get a system of six equations that gives us the interactions after decimation (Eq.6). By moving the potentials, we obtained the renormalized interactions (Eq. 7).

The invariant subspace J = C = 0

For J = C = 0, the following relations are obtained between the forms (9–12):

$$ {F}_{\frac{1}{2},2}/{F}_{-\frac{1}{2},2}={F}_{\frac{1}{2},1}/{F}_{-\frac{1}{2},1}=1\ \mathrm{i}.\mathrm{e}.\ln \left({F}_{\frac{1}{2},2}/{F}_{-\frac{1}{2},2}\right)=\ln \left({F}_{\frac{1}{2},1}/{F}_{-\frac{1}{2},1}\right)=0 $$

(14)

Therefore, we obtained: J '  = C '  = 0 (15).

Finally, we see that the subspace J = C = 0 is invariant by the transformation of the group (Eq. 7). The recursion equations in this subspace are written as follows:

$$ {\Delta}^{\prime }={b}^{d-1}.\Delta \kern0.5em \mathrm{and}\kern0.5em {\Delta_4}^{\prime }={b}^{d-1}.{\Delta}_4 $$

(16)

The recursion eqs. (16) indicate that any positive value of Δ brings the system to Δ’ = +∞, but a negative value of Δ brings the system to Δ’ = -∞. We can also follow the same reasoning for Δ₄. This gives us the following four fixed points: (0, 0, +∞, −∞), (0, 0, −∞, −∞), (0, 0, +∞, +∞) and (0, 0, −∞, +∞). Moreover, Δ = 0 lead to Δ’ = 0, and also Δ₄ = 0 lead to Δ’₄ = 0; thus we have the five fixed points: (0, 0, 0, +∞), (0, 0, 0, −∞), (0, 0, +∞, 0), (0, 0, −∞, 0) and (0, 0, 0, 0). Finally, we conclude that Eqs. (16) give us nine trivial fixed points.

• The fixed point C^*

At the fixed point C^*, we have the following relations: J = -7C, Δ = +∞ and Δ₄ = -∞, with |∆|˃˃|∆₄|. From where:

$$ {F}_{\frac{1}{2},2}={A}_0.\exp \left(\tilde{x}+4\frac{\tilde{\Delta}}{z}\right)=\exp (x).\cosh (2x)+\exp \left(-x\right) $$

(17)

$$ {F}_{-\frac{1}{2},2}={A}_0.\exp \left(-\tilde{x}+4\frac{\tilde{\Delta}}{z}\right)=\exp \left(-x\right).\cosh (2x)+\exp (x) $$

(18)

where $\tilde{x}=\frac{3\tilde{J}}{7}$ and $x=\frac{3J}{7}$,

The division of (17) by (18) gives us:

$$ \exp \left(2\tilde{x}\right)=\frac{\exp (x).\cosh (2x)+\exp (x)}{\exp \left(-x\right).\cosh (2x)+\exp (x)} $$

(19)

• For d = 2:

The renormalized interaction (x’ = b^d-1.x̃) becomes (x’ = 3.x̃), and Eq. (19) is written as follows:

$$ \exp \left(\frac{2}{3}{x}^{\prime}\right)=\exp (2x).\frac{3+\exp (4x)}{1+3.\exp (4x)} $$

(20)

Since at the fixed point: x’ = x, we have:

$$ \exp \left(\frac{4}{3}x\right)=\frac{1+3\exp (4x)}{3+\exp (4x)} $$

(21)

We put $y=\exp \left(\frac{4}{3}x\right)$, thus Eq. (21) becomes:

$$ {y}^4-3{y}^3+3y-1=0 $$

(22)

Eq. (22) has four solutions: $y=\pm 1\ \mathrm{and}\ \frac{3\pm \sqrt{5}}{2}$, but since y > 0, the accepted solutions are: $y=1\ \mathrm{and}\ \frac{3+\sqrt{5}}{2}$, and using the relations between y, x and J, we found $J=0\ \mathrm{and}\ \frac{7}{4}\ln \left(\frac{3+\sqrt{5}}{2}\right)$. Finally, it is clear that the coordinates of point C^* are: $\left(\frac{7}{4}\ln \left[\frac{3+\sqrt{5}}{2}\right],-\frac{1}{4}\ln \left[\frac{3+\sqrt{5}}{2}\right],+\infty, -\infty \right)$ or (1.6842, −0.2406, +∞, −∞) representing the second-order ferromagnetic-paramagnetic transition. On the other hand, the point that has the coordinates: $\left(\frac{7}{4}\ln \left[\frac{3-\sqrt{5}}{2}\right],-\frac{1}{4}\ln \left[\frac{3-\sqrt{5}}{2}\right],+\infty, -\infty \right)$ or (−1.6842, 0.2406, +∞, −∞) describes the second-order antiferromagnetic-paramagnetic transition.

• For d = 3:

The renormalized interaction (x’ = b^d-1.x̃) becomes (x’ = 9.x̃), and following the same steps as for d = 2, Eq. (19) is written in the form:

$$ \exp \left(\frac{32}{9}x\right)=\frac{1+3\exp (8x)}{3+\exp (8x)} $$

(23)

Eq. (23) gives us three solutions: x = ±0.17709560 and 0, and since we know that x = 3 J/7, the value of x that corresponds to C^* is 0.17709560 and therefore the coordinates of point C^* are: (0.4132, −0.0590, +∞, −∞) representing the second-order ferromagnetic-paramagnetic transition. Concerning the negative solution of x, it corresponds to second-order antiferromagnetic-paramagnetic transition; the coordinates of C^* in this case are: (−0.4132, 0.0590, +∞, −∞).