Mixed Spin-1/2 and Spin-5/2 Model by Renormalization Group Theory: Recursion Equations and Thermodynamic Study

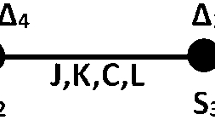
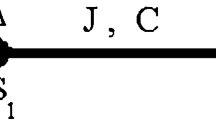Abstract

Using the renormalization group approximation, specifically the Migdal-Kadanoff technique, we investigate the Blume-Capel model with mixed spins S = 1/2 and S = 5/2 on d-dimensional hypercubic lattice. The flow in the parameter space of the Hamiltonian and the thermodynamic functions are determined. The phase diagram of this model is plotted in the (anisotropy, temperature) plane for both cases d = 2 and d = 3 in which the system exhibits the first and second order phase transitions and critical end-points. The associated fixed points are drawn up in a table, and by linearizing the transformation at the vicinity of these points, we determine the critical exponents for d = 2 and d = 3. We have also presented a variation of the free energy derivative at the vicinity of the first and second order transitions. Finally, this work is completed by a discussion and comparison with other approximation.

Appendices

Appendix A

The six forms F_i,j obtained from (3), (4) and (5):

• For (S₁, S₄) = {(1/2, 5/2); (− 1/2,− 5/2)}

$$\begin{array}{@{}rcl@{}} F_{\frac{1}{2},\frac{5}{2}}&\,=\,&2\text{e}^{\frac{75}{4}\frac{{\Delta}_{2}}{z}+\frac{1875}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{5}{4}j+\frac{125}{16}C+\frac{3125}{64}F}ch\left( \frac{5}{2}+\frac{125}{8}C+\frac{3125}{32}F\right)+\text{e}^{\frac{5}{4}J-\frac{125}{16}C-\frac{3125}{64}}\right)\\ &&\text{e}^{\frac{43}{4}\frac{{\Delta}_{2}}{z}+\frac{787}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{3}{4}J+\frac{27}{16}C+\frac{243}{64}F}ch\left( 2J\,+\,\frac{19}{2}C \,+\, \frac{421}{8}F \right)\text{e}^{\frac{3}{4}J-\frac{27}{16}C-\frac{243}{64}F}ch\right.\\&&\left.\times\left( \frac{1}{2}J\,+\,\frac{49}{8}C\,+\,\frac{1441}{32}F\right)\right)\\ &&\text{e}^{\frac{24}{7}\frac{{\Delta}_{2}}{z}+\frac{627}{16}\frac{{\Delta}_{4}}{z}}\!\left( \text{e}^{\frac{1}{4}J+\frac{1}{16}C+\frac{1}{64}F}ch\!\left( \frac{3}{2}J\,+\,\frac{63}{8}C \,+\, \frac{1563}{32}F \right)\text{e}^{\frac{1}{4}J-\frac{1}{16}C-\frac{1}{64}F}ch\right.\\&&\left.\times\left( J\,+\,\frac{31}{4}C\,+\,\frac{781}{16}F\right)\right) \end{array} $$

(12)

• For (S₁, S₄ = {(1/2,− 5/2); (− 1/2, 5/2)})

$$ F_{\frac{1}{2},\frac{-5}{2}}=F_{\frac{-1}{2},\frac{5}{2}}=F_{\frac{1}{2},\frac{5}{2}}(J=-J,C=-C,F=-F) $$

(13)

• For (S₁, S₄ = {(1/2, 3/2); (− 1/2,− 3/2)})

$$\begin{array}{@{}rcl@{}} F_{\frac{1}{2},\frac{3}{2}}&\,=\,&2\text{e}^{\frac{59}{4}\frac{{\Delta}_{2}}{z}+\frac{1331}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{5}{4}j+\frac{125}{16}C+\frac{3125}{64}F}ch\left( 2J\,+\,\frac{19}{2}C+\frac{421}{8}F\right)\,+\,\text{e}^{\frac{-5}{4}J-\frac{125}{16}C-\frac{3125}{64}F}ch\right.\\&&\left.\times\left( \frac{1}{2}J+\frac{49}{8}C+\frac{1441}{32}F\right)\right)\\ &&2\text{e}^{\frac{27}{4}\frac{{\Delta}_{2}}{z}+\frac{243}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{3}{4}J+\frac{27}{16}C+\frac{243}{64}F}ch\left( \frac{3}{2}J+\frac{27}{8}C + \frac{243}{32}F \right)\text{e}^{\frac{-3}{4}J-\frac{27}{16}C-\frac{243}{64}F}\right)\\ &&2\text{e}^{\frac{11}{4}\frac{{\Delta}_{2}}{z}+\frac{83}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{1}{4}J+\frac{1}{16}C+\frac{1}{64}F}ch\left( J+\frac{7}{4}C + \frac{61}{16}F \right)\text{e}^{\frac{-1}{4}J-\frac{1}{16}C-\frac{1}{64}F}ch\right.\\&&\left.\times\left( \frac{1}{2}J+\frac{13}{8}C+\frac{121}{32}F\right)\right) \end{array} $$

(14)

• For (S₁, S₄ = {(1/2,− 3/2); (− 1/2, 3/2)})

$$ F_{\frac{1}{2},\frac{-3}{2}}=F_{\frac{-1}{2},\frac{3}{2}}=F_{\frac{1}{2},\frac{3}{2}}(J=-J,C=-C,F=-F) $$

(15)

• For (S₁, S₄ = {(1/2, 1/2); (− 1/2,− 1/2)})

$$\begin{array}{@{}rcl@{}} F_{\frac{1}{2},\frac{1}{2}}&\,=\,&2\text{e}^{\frac{51}{4}\frac{{\Delta}_{2}}{z}+\frac{1251}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{5}{4}j+\frac{125}{16}C+\frac{3125}{64}F}ch\left( \frac{3}{2}J\,+\,\frac{63}{8}C\,+\,\frac{1563}{32}F\right)+\text{e}^{\frac{5}{4}J-\frac{125}{16}C-\frac{3125}{64}F}ch\right.\\&&\left.\times\left( J+\frac{31}{4}C+\frac{781}{16}F\right)\right)\\ &&2\text{e}^{\frac{19}{4}\frac{{\Delta}_{2}}{z}+\frac{163}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{3}{4}J+\frac{27}{16}C+\frac{243}{64}F}ch\left( J+\frac{7}{4}C + \frac{61}{16}F \right)\text{e}^{\frac{3}{4}J-\frac{27}{16}C-\frac{243}{64}F}ch\right.\\&&\left.\times\left( \frac{1}{2}J+\frac{13}{8}C+\frac{121}{32}F\right)\right)\\ &&2\text{e}^{\frac{3}{4}\frac{{\Delta}_{2}}{z}+\frac{13}{16}\frac{{\Delta}_{4}}{z}}\left( \text{e}^{\frac{1}{4}J+\frac{1}{16}C+\frac{1}{64}F}ch\left( \frac{1}{2}J+\frac{1}{8}C + \frac{1}{32}F \right)\text{e}^{\frac{1}{4}J-\frac{1}{16}C-\frac{1}{64}F}\right) \end{array} $$

(16)

• For (S₁, S₄ = {(1/2,− 1/2); (− 1/2, 1/2)})

$$ F_{\frac{1}{2},\frac{-1}{2}}=F_{\frac{-1}{2},\frac{1}{2}}=F_{\frac{1}{2},\frac{1}{2}}(J=-J,C=-C,F=-F) $$

(17)

Appendix B

The Hamiltonian of this system is written as: $H=-\bar {j}\sum \limits _{i\in (A)\atop J\in (B)} S_{i}S_{j}-\delta \sum \limits _{j\in (B)}S_{j}$

It can also be written in the reduced form: $-\beta H=J\sum \limits _{i\in (A)\atop J\in (B)} S_{i}S_{j}+{\Delta }_{2} \sum \limits _{j\in (B)} S^{2}_{j}$

With: $J=\beta .\bar {j}$ and Δ₂ = β.δ

The total quadrupole moment Q is given by:

$$\begin{array}{@{}rcl@{}} Q&=&\left\langle\sum\limits_{j}S^{2}_{j}\right\rangle=\frac{N}{2}\left\langle S^{2}_{j}\right\rangle=\frac{N}{2} q\\ &=&Tr \ \rho \sum\limits_{j}S^{2}_{j}=\frac{Tr \sum\limits_{j}S^{2}_{j}.e^{-\beta H}}{Z}=\frac{Tr \sum\limits_{j}S^{2}_{j}.e^{\beta \delta\sum\limits_{j}S^{2}_{j}+\ldots}}{Z}\\ &=&\frac{\displaystyle\frac{\partial Z}{\partial(\beta\delta)}}{Z}=\left( \frac{\partial\log Z}{\partial(\beta\delta)}\right)_{T=cte}=\frac{1}{\beta}\left( \frac{\partial\log Z}{\partial\delta}\right)_{T=cte} \end{array} $$

(18)

Where q is quadrupole moment per spin, the Z is the partition function.

The free energy is defined by: $f=-\frac {\log Z}{\beta }$, then: $\left . Q=\frac {1}{\beta }\frac {\partial (-\beta f)}{\partial \delta }\right )_{T=cte}=\left .-\frac {\partial f}{\partial \delta }\right )_{T=cte}$

Therefore, the negative first derivative of free energy with respect to crystal field gives the quadrupole moment.

Taking into account that: $x=\frac {{\Delta }_{2}}{J}=\frac {\delta }{\bar {j}} and T=\frac {1}{J}=\frac {1}{\beta \bar {j}}=\frac {K_{B}T}{\bar {j}}$ (In our case: $\bar {j}=K_{B}= 1)$.

We will have: $Q=-\frac {\partial f}{\partial \delta }=-\frac {\partial x}{\partial \delta }.\frac {\partial f}{\partial x}=-\frac {1}{\bar {j}} . \frac {\partial f}{\partial x}$

Finally: $Q=-\frac {\partial f}{\partial x}$

Hence the negative first derivative of free energy with respect to x (with x = Δ₂/|J|) gives also the quadrupole moment.