Numerical Modeling of Photothermal Experiments on Layered Samples with Mirage-Effect Signal Detection

Abstract

Modeling of the probe beam deflection caused by temperature gradients for layered sample was realized in COMSOL Multiphysics, which utilizes finite element method to analyze heat transport. The sample consisted of a 100-nm-thick layer on a 500-$\upmu$m-thick substrate. It was also assumed that the sample was illuminated with either a Gaussian or a flat top beam of harmonically modulated intensity. To obtain the probe beam deflection signal, the normal and tangential components of the temperature gradient in the air above the sample were integrated over the probe beam path. The numerical model of the experiment gave insight into the various parameter dependencies, e.g., the thermal and optical properties of the substrate and the layer, and the geometry of the experiment. These insights are used in the analysis of experimental data and in the planning of future measurements.

1 Introduction

The detection of temperature disturbances by the use of the mirage effect is the basis of various optical techniques known as photothermal deflection measurements. Illuminating a sample with an intensity-modulated light beam generates a non-stationary temperature disturbance connected with temperature gradients. These temperature gradients induce changes in the refractive index through the thermo-optic effect, which is essential to the optical detection of temperature gradients. A probe light beam passing through the disturbed region can be deflected, changing the intensity distribution in its cross section. This effect is called the mirage effect. Application of the mirage effect for signal detection in photothermal measurements was proposed by Boccara and Fournier [1], and Murphy and Aamodt [2].

Qualitative descriptions of the mirage effect are simple. However, its quantitative model—especially when the real probe beam and 3D temperature field are taken into account—is quite complicated. The ray model is the simplest theoretical model. It is based on the principles of geometrical optics and the assumption that the probe beam can be treated as a single ray [3]. This ray is deflected on temperature gradients, and the sum of the deflections along a ray path is proportional to the measured signal. This model was recently improved to take into account the finite cross section of the probe beam [4]. The probe beam was considered as a bundle of rays. The signal was the weighted sum of the rays’ deflections over the beam cross section. However, this model does not take into account the differences in the phase shifts for rays using different pathways and having varying interference effects. The wave nature of the probe beam was taken into account in the model proposed by Glazov and Muratikov [5]. The propagation of probe beam through the region with a perturbed refractive index distribution—called the thermal lens—was analyzed. The thermal lens was treated as a single phase, so the influence on the distribution of the probe beam amplitude was not considered. A model considering both the amplitude and the phase change of light in the probe beam caused by the thermal lens was proposed in Ref. [6,7,8,9]. It is based on the complex geometrical optics equations, but is restricted to probe beams with Gaussian profiles.

This short review of existing models of photothermal deflection measurements contains only the main proposals for theoretically modeling. However, even in the simplest geometrical optics models, an analytical solution for probe beam deflection can only be obtained in simple cases, e.g., 1D temperature fields.

The aim of this work is to show that analysis of photothermal deflection measurements can be done by numerical analysis of temperature disturbance caused by an absorption of light from the power beam, and numerical calculation of the probe beam deflection. The main advantages of this approach are first the possibility for modeling experiments with any power beam distribution (Gaussian, flat top, etc.), and second the ability to use samples of any optical and thermal properties. The proposed approach was used to analyze the signal in measurements utilizing infrared radiometry for signal detection [10,11,12].

Fig. 1

Geometry of the model. Detailed description in the text

2 Numerical Model

2.1 Temperature Field

The first step in the modeling of the photothermal deflection measurement is the determination of the temperature field in the sample and its surrounding. Consider a sample with a 100-nm-thin layer on 500-$\upmu$m-thick substrate. The sample was surrounded by air modeled by two 3-mm-thick layers above and below the sample. To maintain axial symmetry, all layers were enclosed in a cylinder 5 mm in radius. The geometry of the system is shown in Fig. 1. In such geometry, the symmetry axis coincides with the z-axis, the temperature field is a function of two variables r and z, and the solution must be found at the half-plane $r > 0$.

Absorption of light from the power beam causes a rise in the number of heat sources in the considered system. It was assumed that the light intensity distribution in the beam cross section kept the system symmetry. Two types of power beams were considered:

• the Gaussian beam with the light intensity at $z = 0$

  $$\begin{aligned} I\left( {r,t} \right) =I_0 \hbox {exp}\left( {-\frac{r^{2}}{2R^{2}}} \right) \hbox {sin}\left( {2\pi ft} \right) , \end{aligned}$$

  (1)

• and the flat top beam with the light intensity at z = 0

  $$\begin{aligned} I\left( {r,t} \right) =\frac{I_0 }{\hbox {exp}\left( {\frac{r-R}{u}} \right) +1}\hbox {sin}\left( {2\pi ft} \right) , \end{aligned}$$

  (2)

  where $I_{0}$ is the maximum light intensity in the power beam, R is a parameter characterizing its radius, u is a parameter describing the width of the flap top beam edge, and f is the light modulation frequency.

Assuming that the light absorption in the film and the substrate obeys the Beer–Lambert law—and there is no light reflection at the film–substrate interface—volume densities of heat sources in the system can be described as

$$\begin{aligned} w_1 \left( {r,z,t} \right)= & {} \beta _1 I\left( {r,t} \right) \hbox {exp}\left( {\beta _1 z} \right) ,\quad \hbox {for}\quad -d<z<0, \end{aligned}$$

(3)

$$\begin{aligned} w_2 \left( {r,z,t} \right)= & {} \beta _2 I\left( {r,t} \right) \hbox {exp}\left( {-\beta _1 d} \right) \hbox {exp}\left( {\beta _2 \left( {z+d} \right) } \right) ,\quad \hbox {for}\quad z<-d, \end{aligned}$$

(4)

where $\beta _{1}$, $\beta _{2}$ are light absorption coefficients of the film and the substrate, respectively, and d is the layer thickness. The heat transport model of the system must have defined boundary conditions. In photothermal experiments using modulated light, the harmonic component of the temperature field with frequency f is the only factor influencing the measured signal. This component propagates as a heavily damped thermal wave, for which penetration depth is defined by the thermal diffusion length

$$\begin{aligned} \mu =\sqrt{\frac{\alpha }{\pi f}}, \end{aligned}$$

(5)

where $\alpha$ is the thermal diffusivity of the sample. For modulation frequencies greater than $100\,\hbox {Hz}$, and $R < 1.0\,\hbox {mm}$, it can be assumed that the harmonic temperature disturbance does not reach the outer borders of the system, and the temperature at these borders is equal to ambient. Due to symmetry, the heat flux through the border at $r = 0$ is equal to zero. An interfacial layer between the thin film and the substrate creates a barrier for the heat flux. This barrier is described by interfacial thermal resistance $R\mathrm{th}$, which connects the heat flux through the barrier j with the temperature jump on it $\Delta T$

$$\begin{aligned} j=\frac{\Delta T}{R_{\mathrm{th}} }. \end{aligned}$$

(6)

The thermal model of the system was built in COMSOL Multiphysics$^{\textregistered }$ using the heat transfer module. The temperature distribution as a function of time was calculated for 30 periods after switching on the heat sources with time resolution of 20 points per period. The radial and z-direction temperature gradients in air above the sample were then calculated on a regular spatial grid with $10\,\upmu \hbox {m}$ steps for $0 \le r \le 2000\,\upmu \hbox {m}$, and $0 \le z \le 200\,\upmu \hbox {m}$. Results were exported to a file for further analysis.

Fig. 2

Temperature (a), the radial (b), and z-axis (c) gradients calculated for homogeneous PET sample illuminated by intensity-modulated Gaussian beam at $t = 0.059$ s (maximum of the light intensity). Parameters of the model used in calculations are listed in the text

Fig. 3

Geometry of the signal detection scheme. Detailed description in the text

Exemplary temperature and temperature gradient distributions obtained for the Gaussian beam with $R = 88\, \upmu \hbox {m}$, and homogeneous polyethylene (PET) sample (thermal conductivity $\kappa = 0.052\,\hbox {W}{\cdot }\hbox {m}^{-1}\hbox {K}^{-1}$, density $\rho = 950\,\hbox {kg}{\cdot }\hbox {m}^{-3}$, specific heat $c = 2300\,\hbox {J}{\cdot }\hbox {kg}^{-1}\hbox {K}^{-1}$, and the optical absorption coefficient $\beta _{1} = \beta _{2} = 80\, \hbox {m}^{-1})$) are shown in Fig. 2. These calculations were carried out for the modulation frequency $f = 500\hbox { Hz}$, with maximum light intensity $I_{0} = 3{\times }10^{7}\hbox { W}{\cdot }\hbox { m}^{-2}$, and the distributions shown correspond to $t = 0.059\,\hbox {s}$.

2.2 Photodeflection Signal

According to the ray model, proposed by Aamodt and Murphy [3], the deflection of the probe beam passing through the thermal lens is given by the formula

$$\begin{aligned} \vec {\psi } = - \frac{1}{n}\frac{{dn}}{{dT}} \int \nolimits _{\varGamma } \vec {\nabla }T \times d\vec {\varGamma } \end{aligned}$$

(7)

where the integration is carried out along a beam path $\varGamma$. In practice, two components of this deflection are measured, the deflection perpendicular to the sample surface, the so-called normal deflection

$$\begin{aligned} \psi _{\mathrm{n}} =-\frac{1}{n}\frac{dn}{dT} \int \nolimits _{-\infty }^\infty \frac{\partial T}{\partial z}dx, \end{aligned}$$

(8)

and the deflection parallel to the sample surface, tangential deflection

$$\begin{aligned} \psi _{\mathrm{t}} =-\frac{1}{n}\frac{dn}{dT}\int \nolimits _{-\infty }^\infty \frac{\partial T}{\partial y}dx. \end{aligned}$$

(9)

The last two equations were obtained under the assumption that the probe beam defection is small and the probe beam is parallel to the x-axis. Integrals in Eqs. (8, 9) can be calculated numerically if partial derivatives $\partial T/\partial z$ and $\partial T/\partial y$ are known. The first one is obtained directly from the finite element model built in COMSOL Multiphysics$^{\textregistered }$. The other can be calculated from the radial temperature gradient $\partial T/\partial r$. The geometry corresponding to the signal detection scheme is depicted in Fig. 3. The probe beam goes in parallel to the x-axis at a distance s from the symmetry axis of the temperature field, at a height h over the sample surface. The beam intersects consecutive circles for which the radial temperature gradient $\partial T/\partial r = \hbox {f}(z = h, r, t)$ was calculated. The $\partial T/\partial y$ temperature gradient is

$$\begin{aligned} \frac{\partial T}{\partial y}=\frac{s}{r}\frac{\partial T}{\partial r}. \end{aligned}$$

(10)

The normal and the tangential deflections as functions of time were calculated using trapezoidal rule. Then, amplitudes and phases of both deflections were obtained by digital signal processing analogous to this used in lock-in amplifiers. Exemplary dependences obtained for the same model parameters as listed at the end of Sect. 2.1 and the sample–probe beam distance $h = 100\, \upmu \hbox {m}$ are shown in Fig. 4.

Fig. 4

Amplitudes and phases of normal and tangential probe beam deflections as functions of the distance between the power beam axis and the probe beam obtained for the same parameters as Fig. 2 (PET sample illuminated by intensity-modulated Gaussian beam)

3 Analysis

The numerical model of photothermal deflection measurements allows for the analysis of the influence of various parameters of the model on measured signals. Two main goals of this analysis are follows: (1) Does the variation of selected sample parameters influence measured dependencies and can it be determined? And (2) does the simplified method for analysis of experimental data give correct values of sample parameters? It is important to carry out the analysis for realistic distributions of the light intensity in the power beam cross section. The general assumption is that the power beam is Gaussian. Nowadays, the laser diodes are used in many photothermal experiments to generate the disturbance of the temperature field. The light from the source is guided to the sample through an optical fiber. The light intensity distribution along the diameter of a light spot is depicted in Fig. 5. The spot is obtained by focusing light from optical fiber on the sample surface. The experimental distribution is fitted by two theoretical distributions: the Gaussian one described by Eq. 1, and the flat top beam described by Eq. 2.

The central part of the experimental distribution is noisy. Nevertheless, it is clear that the flat top beam fits experimental points much better than the Gaussian distribution. Parameters of fitted curves are as follows:

• Gaussian beam: $R = 88.4\,\upmu \hbox {m}$, $I_{0} = 4.9\,\hbox {a.u.}$

• flat top beam: $R = 114\,\upmu \hbox {m}$, $u = 10\,\upmu \hbox {m}$, $I_{0} = 4.4\,\hbox {a.u.}$

In further analysis, two samples (or sample substrates) are considered—PET and silicon (Si). Basic properties of PET are given in Sect. 2.1. It is a transparent material with low thermal conductivity. Basic parameters of Si used in modeling are as follows: $\kappa = 131 \hbox { W}{\cdot }\hbox { m}^{-1}\hbox {K}^{-1}$, $\rho = 2330 \hbox { kg}{\cdot }\hbox { m}^{-3}$, $c = 703\hbox { J}{\cdot }\hbox { kg}^{-1}\hbox {K}^{-1}$, and $\beta = 8.5\,\times \,10^{4} \hbox { m}^{-1}$. The thermal diffusivities of these materials are as follows: $\alpha _{\mathrm{PET}} = 0.24\,\times \,10^{-9}\hbox { m}^{2}\hbox {s}^{-1}$, $\alpha _{\mathrm{Si}} = 0.80\,\times \,10^{-4}\hbox { m}^{2}\hbox {s}^{-1}$. The influence of the light intensity distribution in the power beam cross section on amplitudes and phases of normal and tangential deflections for Si and PET samples is shown in Figs. 6 and 7, respectively. Amplitudes are normalized to the amplitude of the normal deflection for $s = 0$. Signals were calculated for $h = 100 \upmu \hbox {m}$.

Fig. 5

Light intensity distribution in the power beam cross section fitted with Gaussian (solid line) and flat top (dash line) distribution

Fig. 6

Normalized amplitudes and phases of normal tangential deflections as functions of the power–probe beams distance calculated for Gaussian and flat top power beams at $100\,\upmu \hbox {m}$ over the Si sample

Fig. 7

Normalized amplitudes and phases of normal tangential deflections as functions of the power–probe beams distance calculated for Gaussian and flat top power beams at $100\, \upmu \hbox {m}$ over the PET sample

The main conclusion built on a comparison of Figs. 6 and 7 is that the influence of the power beam shape on analyzed dependencies is more pronounced in the transparent sample with low thermal diffusivity. In the sample with high thermal diffusivity and relatively long thermal diffusion length, the temperature disturbance propagates along the sample surface. This leads to broadening of calculated dependencies, but also homogenizes the temperature distribution. Therefore, differences between dependencies for Gaussian and flat top beams are small. In the PET sample, these dependencies are narrower and the influence of power beam shape is more pronounced.

As the power beam used in experiments can be better described as the flat top beam, further analysis was carried out for this type of beam.

3.1 Influence of Transparent Thin Layer on Thick Substrate

As is mentioned in the previous section, an demonstrative analysis presented in the paper was carried out for two sample substrates—PET and Si. The purpose of this analysis described in this section is to determine how a thin layer can be deposited onto a $500\,\upmu \hbox {m}$ substrate to still be “visible” in photothermal deflection measurements. Calculations were carried out for semitransparent layers $(\beta _{1}= 80\,\hbox {m}^{-1})$ of various thicknesses ($10\,\upmu \hbox {m}, 1\,\upmu \hbox {m}, and\;0.1\,\upmu \hbox {m}$). In the case of a Si substrate, layers with high ($\kappa _{1} = 500\,\hbox {W}{\cdot }\hbox { m}^{-1}\hbox {K}^{-1})$ and low ($\kappa _{1} = 10 \hbox { W}{\cdot }\hbox { m}^{-1}\hbox {K}^{-1})$ thermal conductivities were considered. In both cases, the layer density was $\rho = 2250\,\hbox {kg}{\cdot }\hbox { m}^{-3}$, and the heat capacity $c = 707\hbox { J}{\cdot }\hbox { kg}^{-1}\hbox {K}^{-1}$. These parameters correspond to the thermal diffusivities $3.14\times 10^{-4}\,\hbox { m}^{2}{\cdot }\hbox { s}^{-1}$ and $6.29 \times 10^{-6}\,\hbox { m}^{2}{\cdot }\hbox { s}^{-1}$, respectively. In the case of a PET substrate only, the layer with high thermal diffusivity was considered.

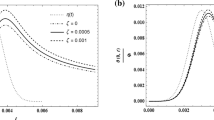
The normal and the tangential phases of the probe beam deflection calculated for a pure Si substrate sample and a layered sample with various layer thicknesses are shown in Fig. 8. Calculations were carried out for the layer with relatively high thermal conductivity ($\kappa _{1} = 500\,\hbox {W}{\cdot }\hbox {m}^{-1}\hbox {K}^{-1})$, and $h = 100\, \upmu \hbox {m}$. The influence of the layer on the photodeflection signal is visible only for the 10-$\upmu \hbox {m}$-thick layer. The influence of thinner layers is practically insignificant. Moreover, similar graphs obtained for the layer with lower thermal conductivity ($\kappa _{1} = 10\,\hbox {W}{\cdot }\hbox { m}^{-1}\hbox {K}^{-1})$ revealed that even a 10-$\upmu \hbox {m}$-thick layer on Si does not cause noticeable changes in analyzed dependencies.

Thus, the photothermal deflection measurements are not suitable for the investigation of thin layers deposited on thick substrates with relatively high thermal conductivity.

Fig. 8

Phases of normal and tangential deflections of the probe beam as functions of power–probe beams distance s. Calculations were carried out for Si substrate and layered structures with various layer thicknesses. The thermal conductivity of the layer $\kappa _{1} = 500\,\hbox {W}{\cdot }\hbox {m}^{-1}\hbox {K}^{-1}$

Fig. 9

Phases of normal and tangential deflections of the probe beam ac functions of power–probe beams distance s. Calculations were carried out for PET substrate and layered structures with various layer thicknesses. The thermal conductivity of the layer $\kappa _{1} = 500\,\hbox {W}{\cdot }\hbox {m}^{-1}\hbox {K}^{-1}$

In the case of a conductive film deposited on semitransparent substrate with very low thermal conductivity, different behavior is observed. The influence of the layer on both the normal and the tangential phases is well pronounced (Fig. 9). The same conclusion can be made for respective amplitudes. The analysis performed for the layer with lower thermal conductivity ($\kappa _{1} = 10\,\hbox {W}{\cdot }\hbox {m}^{-1}\hbox {K}^{-1})$ showed that even 1-$\upmu \hbox {m}$-thick layer should be detectable in a photothermal deflection experiment.

3.2 Simplified Analysis Based on Linear Relations

The possibility of a simplified analysis of data from photothermal deflection measurements was analyzed by Salazar and Sánchez-Lavega [13]. They concluded that in the case of a probe beam passing over a parallel sample surface, linear relations can be used in two aspects: the phase of normal deflection depends linearly on h for $s = 0$, and the phase of tangential deflection depends linearly on s for $h = 0$. In both cases, a point-like heat source was assumed. In the case of $\psi _{n}(h)$ dependence, it remains linear also for 1D temperature field (homogeneously illuminated sample surface).

Figure 10 shows the $\psi _{n}(h)$ dependencies obtained for Si sample and two radii of the flat top power beam: $11.4\,\upmu \hbox {m}$ and $1140\,\upmu \hbox {m}$. In a tightly focused beam, the dependence is not linear. A broad power beam exhibits good linearity. The slope of fitted straight line a allows for the calculation of thermal diffusivity of air $\alpha _{\mathrm{air}} = \pi f/a^{2}$. The value calculated from data shown in Fig. 10 was $1.94\,\times \,10^{-5}\hbox { m}^{2}\hbox {s}^{-1}$. This value is exactly the same as the one used for air in COMSOL Multiphysics$^{\textregistered }$.

Fig. 10

Phase of normal deflection versus probe beam—sample surface distance for two diameters of the power beam. Straight line fitted to points obtained for $R = 1140\,\upmu \hbox {m}$ is shown

Fig. 11

Phase of tangential deflection versus power–probe beams distance for two diameters of the power beam

Fig. 12

Values of the thermal diffusivity obtained from simplified analysis of $\psi _{\mathrm{t}}(s)$ dependence based on linear regression. Calculation were carried out for two diameters of the power beam 11.4 and $114\,\upmu \hbox {m}$. In each case, straight line was fitted to calculated points in two ranges of s: $600\,\upmu \hbox {m}$–$900\,\upmu \hbox {m}$ and 1200$\,\upmu \hbox {m}$–$1500\,\upmu \hbox {m}$. Actual value of the thermal diffusivity of Si is also shown (dashed line)

The other expected linear dependence is the phase of tangential deflection as a function of the power–probe beam distance s. Two such dependencies obtained for a Si sample with power beam radii $11.4\, \upmu \hbox {m}$ and $114\,\upmu \hbox {m}$ are shown in Fig. 11. Both dependencies are practically linear for $s > 200\, \upmu \hbox {m}$ and have almost the same slopes.

More detailed analysis revealed that the dependence calculated for a tightly focused beam is less steep. The slopes calculated for $h = 100\,\upmu \hbox {m}$ and the s in range 1000 $\upmu \hbox {m}$–1500 $\upmu \hbox {m}$ were $4.59\times 10^{3}\hbox { m}^{-1}$ and $4.61\,\times \,10^{3}\hbox { m}^{-1}$ for R equaled to $11.4\, \upmu \hbox {m}$ and $114\, \upmu \hbox {m}$, respectively. Calculated slopes depend also on h and the range of s taken. As a consequence, the thermal diffusivity value obtained from simplified analysis based on linear regression varies when h or s ranges are changed. Figure 12 shows dependencies of thermal diffusivities on the sample—probe beam distance h calculated for two s ranges: 600–900$\upmu \hbox {m}$ and 1200–1500$\upmu \hbox {m}$, and two diameters of the power beam: $11.4 \upmu \hbox {m}$ and $114 \upmu \hbox {m}$.

As it follows from the figure, the thermal diffusivity obtained from regression analysis carried out for s from 600 $\upmu \hbox {m}$ to 900 $\upmu \hbox {m}$ is underestimated of about 20 %. But analysis for 1200 $\upmu \hbox {m}$–1500 $\upmu \hbox {m}$ gives an overestimated value of the thermal diffusivity. However, in this case, the error is smaller, and values obtained for small h give good estimation of the actual thermal diffusivity of the sample. It is worth mentioning that the influence of the power beam radius on obtained values is relatively small.

As it follows from Figs. 6 and 7, determination of the thermal diffusivity from the slope of the linear part of $\psi _{\mathrm{t}}(s)$ dependence is possible only for opaque samples. For a transparent sample (Fig. 7), it is not possible to identify a linear portion in this behavior.

4 Conclusions

Numerical modeling of physical experiments has become more and more popular due to its flexibility and ability to consider complex models, which better convey real experiments. In photothermal experiments, this concerns the geometry of measurements (the distribution of the light intensity in power beam) and the thermal and optical properties of the sample. Pure analytical models are based on many simplifications because obtaining an analytical solution for more realistic models is not possible. As we have shown in this paper, the numerical modeling of photothermal deflection measurements allows for the analysis of the influence of various parameters of a model on measured signals, including the influences of power beam shape and the thin film deposited on the thick substrate. However, it is also possible to add further complexity, such as the influence of anisotropy in thermal properties of the layer and the influence of the thermal resistance at layer–substrate interface. It is also shown that numerical modeling allows for the analysis of the correctness of oft-used simplified methods for experimental data analysis based on linear relations.

Another merit of numerical modeling is the possibility of preliminary analysis regarding the usefulness of selected measuring methods for the determination of defined sample properties. Results presented in this work illustrated the sensitivity of measurement to various parameters of a model and hint at possible modifications of experimental procedure to achieve defined goals.

Numerically modeling an experiment can be also used for the determination of physical properties of a sample based on best fitting procedures. In this case, calculations are more time-consuming in comparison with curve fitting based on an analytical model, but it is still possible.