Research on the feasibility of introducing algebra in primary education has been ongoing since the 1990s. Early algebra, the curricular proposal stemming from that research, seeks to further modes of algebraic thinking and enhance primary school students’ ability to understand and express generalisation (Brizuela & Blanton, 2014). The impact of these ideas on curricular guidelines in countries such as Australia, China, Japan, Portugal, Spain and the USA has determined a need for surveys of primary school students’ first conceptions and reactions when interacting with algebraic elements (Merino, Cañadas, & Molina, 2013; Molina, Ambrose, & del Río, 2018).

The country’s curricular guidelines recommend that primary school students should be able to ‘describe and analyse change in situations, identify patterns, regularities and mathematical laws in numeric, geometric and functional contexts’ (Ministerio de Educación, Cultura y Deporte, 2014, p. 19387). Research is consequently needed to inform the application of such guidelines in an education system accustomed to a traditional approach to algebra instruction.

Functional thinking is a major gateway to algebraic thinking (Carraher & Schliemann, 2007). Precedents have shown that affording students the opportunity to discuss functional tasks leads to an understanding of variability (Brizuela, Blanton, Gardiner, Newman-Owens, & Sawrey, 2015; Cañadas, Brizuela, & Blanton, 2016). Building on that premise, this article aims to contribute to the understanding of the meanings and use attributed by primary school students to letters to represent variable quantities when solving problems involving functional relationships.

Letters in a Functional Approach to Algebra

Functional thinking, a component of algebraic thinking, involves working with functions and families of functions in real life situations (Cañadas & Molina, 2016). It includes generalising relationships between quantities that vary jointly; the expression of such relationships in natural language, symbols, tables or graphs; and the use of such expressions to analyse functional behaviour (Blanton, Levi, Crites, & Dougherty, 2011). Smith (2008) identified three types of functional relationships: (a) recursive patterning, (b) covariation and (c) correspondence. Blanton et al. (2011), noting that recursive patterning is a limited application that implies no inter-variable relationships as it refers to only one of the variables, deemed it to be a first step to making sense of the data.

Kaput, Blanton, and Moreno (2008) described symbolisation as a social process closely related to generalisation. It is also a dynamic process, for by symbolising general ideas students build a new platform for expressing and thinking about unfamiliar situations. As a result, symbols and what they represent may be experienced separately. Radford (2011, 2018) contended that algebraic thinking consists in reasoning with indeterminate quantities analytically and that people can think in terms of indeterminate quantities before having symbols to express them. Pursuant to that author’s (Radford, 1999) premises, the perspective adopted in this study is that learning algebra entails the formulation of signs in specific mathematical activities, in which the application and formulation of meanings are individual and social processes associated with other systems of signs used in the classroom. From that perspective, signs are not cognitively neutral. In this study, letters acquired meanings for students, albeit not necessarily the ones expected, and induced them to certain types of action.

When representing indeterminate quantities, letters may be associated with different meanings depending on the context: generalised numbers, variable quantities, unknowns or parameters. Students must be afforded the opportunity to participate in a diversity of learning experiences to help them generate substance-rich, wide-ranging meanings (Schoenfeld & Arcavi, 1988; Ursini, 1994).

Previous Research

The earliest studies on the meanings attributed by students to indeterminate quantities and their representation with literal symbols (Booth, 1988; Küchemann, 1981; MacGregor & Stacey, 1997) are focused on secondary education and general arithmetic. They observed that students found it difficult to interpret letters as variable quantities, tending to adopt a static perspective, associating letters with specific objects or ignoring them when performing algebraic tasks (Küchemann, 1981). MacGregor and Stacey (1997) found that students interpreted letters in a variety of ways, suggesting that the origin of such interpretations might be: (a) intuitive assumptions and pragmatic reasoning around the new notation; (b) analogies with familiar systems; (c) interference from new learning; and (d) deceptive teaching materials.

In a study on sixth- to eighth-year students’ understanding of equivalence and letters to denote indeterminate quantities, Knuth, Alibali, McNeil, Weinberg, and Stephens (2011) stressed that helping students acquire that understanding and grasp the idea that letters may adopt multiple values might contribute to the development of algebraic thinking. They also recommended teaching students to use letters at earlier ages.

Building on the conclusions of such studies, later authors explored the use of letters by primary school students in the context of early algebra and described their capacities in that regard. Blanton, Stephens, Knuth, Gardiner, Isler, and Kim (2015) compared the traditional approach with early algebra and its impact. Based on an analysis of students’ answers to a pre- and post-test questionnaire, they concluded that the third-year students participating in the experience were able to correctly represent unknown quantities, generalise, relate natural language to algebraic notation and use the latter to represent functional relationships. Other reports concurred that students in different years of primary school accepted the use of letters and that their ideas around their use changed over time as they participated in further learning experiences. Students were observed to spontaneously assign values to literal symbols in keeping with their position in the alphabet or, whilst acknowledging that they may represent different values, attribute specific, randomly chosen values to them when performing explicit tasks (Brizuela & Blanton, 2014; Brizuela et al., 2015; Cañadas et al., 2016). Blanton, Brizuela, Gardiner, Sawrey, and Newman-Owens (2017) described a possible progression in first-year primary school students’ thinking about variables and their notation. They designed a two-cycle instructional sequence consisting in 16 lessons and three semi-clinical individual interviews (before cycle 1, between cycles 1 and 2 and after cycle 2). After analysing the interviews, they concluded that the difficulties experienced by students in assimilating symbolism were associated less with age than with the way notation clashed with their prior experience and understanding. They identified six levels of progression in the understanding of variables and their notation, the first two of which involved internalising the meaning of letters as variables. Students failed to think of the variable amount as an unknown or indeterminate quantity and therefore sought ways to find a numerical value that would enable them to complete the task, including counting, measuring or other more familiar methods of quantification. From the third to the fifth level, meaning was condensed; students began to understand variability and the notion that letters may represent an unknown, variable quantity. Reification occurred on the sixth level, in which children mathematised unknown quantities and realised that they could be regarded as objects in and of themselves or even combined with others.

Research Goal

This study forms part of a research project that explores the algebraic capacities of Spanish primary school pupils in tasks involving functional relationships. Within this project, previous studies have described fifth graders’ (10 to 11 years old) ability to generalise, identifying the functional relationships they applied and the types of representation they used to express them (Pinto & Cañadas, 2018a; b). In this study, they describe the type of questions in which students respond in a generalised manner and the patterns/structures that students recognise. The ability to generalise and represent generalisations of fourth-grade students (9–10 years old) and the interviewer’s mediator role in interacting with these students (Ureña, Ramírez, & Molina, 2019) have also been described.

The studies cited in the earlier section clearly showed that primary school students can understand letters as representations of variables when afforded the opportunity to participate in tasks and discussions about functions and their representation. They are also a source of examples of tasks that can be used to those ends and describe students’ progression in their understanding of letters in algebraic contexts. In this article our aim is to compare some of the data contained in two Blanton et al. (2015, 2017) papers to findings in Spain for students who had no previous experience with either generalisation or functional tasks.

In particular, our study was designed not only to ascertain the meaning given to letters and whether students used them but also to determine how they used them to represent the dependent variable when they were given the independent variable represented with a letter. This is part of the process of generalisation of the functional relationship involved in the problem situations presented. The aim was to supplement previous studies interpretations of the use of letters by relating such use to the meanings given to literal symbols by students through joint analysis of their written answers and their participation in group dLnts generalise functional relationships and use letters to represent the dependent variable, how is this use related to the meanings they give the letters that represent the independent variable?

Third-year primary school students were chosen for the study for two reasons. Firstly, the aim was to compare the findings with those of previous studies on the issue. Secondly, the curricular guidelines in place in a number of countries (e.g. Chile, USA) recommend the introduction of (particularly the literal) representation of indeterminate quantities from the age of 8 or 9 (Ministerio de Educación de Chile, 2012, p. 33; National Governors Association Center for Best Practices & Council of Chief State School Officers [NGA & CCSSO], 2010).

The answers to both research questions may inform the design of teaching methods geared to introducing the notation of variables from a functional approach in the primary years.

Methodology

A qualitative, exploratory and descriptive study, this classroom teaching experiment (Cobb & Gravemeijer, 2008), was conducted with 25Footnote 1 third-year primary school students (8–9 years old) enrolled in a private school in southern Spain. This experiment had a wider objective than that of this paper: to globally explore students’ functional thinking including various dimensions such as the patterns/structures that they recognise, their capacity to generalise and express generalisations, as well as their understanding and use of letters, in this context, as representations of indeterminate quantities.

Like most Spanish third graders, the students had never performed tasks involving functions or used letters to represent indeterminate quantities, for although the legislation in place defines functional relationships as a curricular requirement, those provisions have yet to have any significant effect on classroom practice.

Design and Implementation of the Teaching Experiment

The teaching experiment consisted in four classroom sessions lasting around 90 min each. In each session, a task was proposed to the students. It consisted in a word problem that involved a linear function with a single unknown, natural numbers and a several related questions. This paper discusses the data collected in the first three sessions as the use of letters was absent in the questions posed in the fourth. Some characteristics of the word problems are summarised in Table 1. Although the background information used in the second and third sessions was the same, the questions differed.

Table 1 Background information for word problems
Full size table

A team of researchers with different roles collected the data, one as researcher-teacher, the second as support teacher and observer and the third as video-camera operator. The students’ classroom teacher was present during the sessions as an observer only because she did not have time to become more involved in the research process. In a teaching experiment, the person acting as a teacher has to be fully involved in the study. Research objectives take precedence over what from the teacher’s point of view might be most appropriate for students (Kelly & Lesh, 2000). This is why it is usually one of the researchers who does the interventions in the classroom rather than the usual teacher.

The data were collected from students’ written worksheets and video recordings taken both with a fixed camera located at the back of the classroom and a mobile camera that recorded some of the groups as they worked.

Moments of the Sessions.

Each of the session was composed of three moments: (a) Presentation of the background information of the task to the whole group, (b) work in small groups or individually in one or several worksheets and (c) whole group discussions of the answers. These moments were not done in a linear way, after a group discussion the class could end, return to work in small groups or present a new question.

When initially presenting the background information, the objective was to corroborate that everyone understood the proposed task. In discussions, the students could present their ideas, ask another student to explain something or suggest ways to improve an answer. The role of the researcher-teacher was to encourage students to participate actively in the activities, clarify their doubts about the tasks and encourage interaction between students. In the discussions, the researcher-teacher got involved with the students’ contributions, posed questions that allowed the students to reflect on the tasks and their answers, evaluate if they were correct or not, and thus, as a whole, be able to solve the activities.

Students were seated in their usual classroom arrangement, in groups of three or four, and allowed to work individually or in groups, at their discretion, to ensure they felt at ease throughout. They had opportunities to talk to one another whilst problem solving as well as discussing their ideas in the whole class discussion.

The possibility to discuss either in small or large groups is very important in the design of the teaching experiment. Students’ participation in discussions of mathematics is the central activity of learning (Boaler & Greeno, 2000). Social interaction with others helps students modifies their ways of symbolising and their mathematical meanings (Cobb, Yackel, & McClain, 2012).

Design of Worksheets.

The design of the tasks (e.g. the functional relationship involved, the representation used) was inspired by previous studies on functional thinking previously cited, but contexts and vocabulary were chosen to be familiar to the participating students. The tasks were organised around the inductive reasoning model proposed by Cañadas and Castro (2007). The first questions referred to specific cases presented non-consecutively so as not to foster recursive reasoning. Students were then asked to verbalise the relationships observed and check their validity. Letters were subsequently introduced to represent indeterminate quantities and the students encouraged to use them to verbally generalise the relationship observed. Letters were introduced at the same time as students were asked to deal with and express variability. According to research on secondary students’ understanding of letters and of variables and their notation (Fernández-Millán & Molina, 2016; Furinghetti & Paola, 1994; Küchemann, 1981; Molina, Rodríguez-Domingo, Cañadas, & Castro, 2017) in algebraic contexts, traditional approaches to algebra instruction have proved unsuccessful in helping them satisfactorily develop such an understanding. Those findings are an indication that students need more opportunities and more time if they are to reach that goal. So, we introduced the use of letters to provide students with opportunities to grapple with algebraic notation and build on their incipient ideas. Learning to use symbols allows students to participate in communication; symbols are an integral part of individual and collective activity (Cobb et al., 2012). In this case, symbols allow students to work with the idea of indeterminate quantities.

Questions addressed the correspondence relationship (primarily) and covariation (Smith, 2008) and revolved around both direct (how the dependent was related to the independent variable) and inverse (how the independent was related to the dependent variable) functional relationships.

The ‘siblings’ problem was introduced in the first session. It was deemed to be accessible for students because age differences and the change in age over time were believed to be ideas familiar enough to engage them in the task and make them think about variations in quantities that differ by a constant amount. In Table 2, we describe the tasks presented in the first session and relate them to the phases of Cañadas and Castro’s (2007) inductive model. In this and the following sessions, the intention of each task is a suggestion to guide the process; however, the students could generalise in phases prior to the suggested one.

Table 2 Tasks presented in a worksheet, session 1
Full size table

The T-shirt problem was introduced in the second session. The students were also deemed to be familiar with situations involving product sales. In this task, true/false sentences were proposed. In our experience, they are useful to help primary school students focus on relations and leave aside the computational mindset that they tend to show in arithmetic settings (Molina, Castro, & Mason, 2008). The independent variable was only represented by the letter Z, and the dependent variable was represented in different ways: by the letters Z, N or Y (see Table 3). Sentences 7 and 14 could be true or false depending on the conditions to be met by letters N and Y .

Table 3 Tasks presented in a worksheet, session 2
Full size table
Table 4 Tasks presented in a worksheet, session 3
Full size table

Students also worked on the T-shirt problem in the third session. In this case, various letters were proposed to represent the dependent or independent variable (see Table 4).

Data Analysis

The review of the information from each session included a detailed analysis of students’ written work as well as the classroom interventions. The transcripts of the sessions recorded with the stationary and mobile cameras and the students’ written work were coded qualitatively. First, the episodes involving indeterminate quantities and letters were identified in each medium used to collect the data. The transcripts were reviewed line by line. In the students’ written work, the units of analysis were students’ written answers, which were contrasted with the video recordings. Students’ anonymity was ensured by assigning each a code: Ei where i = 1 ... 25. The researchers were identified as Ri (i = 1 or 2).

The categories discussed below were formulated on the grounds of an inductive analysis of the data collected. Two groups of categories were established, one for the meanings attributed to letters and the other for the ways indeterminate quantities were represented.

The categories referring to meanings were defined in keeping with earlier research (Blanton et al., 2017; Küchemann, 1981; Molina et al., 2018) and organised by complexity, ranging from the dismissal of letters to their acceptance as indeterminate, variable quantities. The general and specific sub-categories are listed in Table 5. Imprecise replies were coded using general categories (e.g. ‘use of letter accepted’), whereas more complete replies were classified under the respective specific sub-categories (e.g. ‘letter as variable/generic example’).

Table 5 Meanings attributed to letters: categories
Full size table

The definitions of the categories for representing indeterminate quantities listed in Table 6 were based both on earlier research (Blanton et al., 2015; Molina et al., 2018) and the characteristics of students’ answers. The focus was on how students represented the dependent variable, given a symbolic representation for the independent variable. Broad categories were defined and sub-divided into more specific categories because it was not always possible to determine why students proposed a specific number or letter.

Table 6 Categories of representations used to denote variables
Full size table

Results

The following discussion addresses first the meanings attributed to letters and then the representations used to designate the dependent variable.

Meanings Attributed to Letters

This section begins with an overview of the meanings put forward by students in classrooms discussions and their written answers. The specific categories are discussed in greater depth below, with examples drawn from the students’ explanations.

Meanings Observed by Session.

In classroom discussions, 15 students (out of 25) spoke a total of 31 times: 8 times in session 1, 16 times in session 2 and 7 times in session 3. Their classification is shown in Fig. 1. Interventions (I1 to I31, numbered chronologically) were associated with the meanings described in Table 5, which were indicated by the symbol “X” in Fig. 1. In cases where student interventions relate to two meanings, the first observed meaning was indicated by “Xa” whilst the next was indicated by “Xb”. On the whole, students tended to consider letters either as values or as variables (category A.2). All but one accepted the use of letters and only four used them as labels or objects (category A.1) across the three sessions.

Fig. 1
figure 1

Meanings put forward in classroom discussions

Full size image

The frequency of the meanings gleaned from the written answers and shown in Fig. 2 is consistent with the data on the classroom discussions described above. Meanings were observed to be diverse and change across the three sessions.

Fig. 2
figure 2

Meanings observed by session in written answers (Q6, question 6; T/F, true/false statement; N, sold N T-shirts; 3 × Y, sold 3 × Y T-shirts; Z:3, earned Z:3 euros; D, earned D euros)

Full size image

The data in Fig. 2 show that students accepted the use of letters in the first session, attributing them meanings based on familiar references such as the alphabet or assigning them a numerical value in pursuit of an arithmetic solution.

Some of the students’ written answers in session 2 denoted dismissal of the use of letters. As in the classroom discussions, when letters were accepted, they were most frequently interpreted as indeterminate quantities (category A.2.3). Students most commonly contended that letters can represent ‘whatever number you want’. That interpretation generated misconceptions in connection with the last T/F question (‘Carlos wants to earn Z euros so he has to sell Z T-shirts’). As the same letter cannot represent different quantities in the same situation, here the correct answer was ‘false’. Only three students (of the ten who answer this question) answered correctly to this sentence: two who interpreted the letter as an indeterminate quantity and one who assigned it the value of its position in the alphabet.

No specific pattern was discerned in students’ answers to the third session tasks and, as written explanations were lacking on the worksheets for that session, the meanings attributed to the letters could not be identified. In the classroom discussion (see Fig. 1) two students resorted to the alphabet to attribute a value to the letter representing the independent variable, which they then multiplied by 3 to find the value of the dependent variable. One student dismissed the use of letters and two interpreted them to be any number.

A comparison of the results for sessions 2 and 3 suggest that the latter task was more difficult for students although more students answered. There they again resorted to familiar elements to express their ideas, such as alphabetical order and arithmetic notions, whilst persistently interpreting letters to be whatever number you want. True/false questions seem to help students broaden their understanding of the use of letters, with a substantial proportion of answers inferring that they interpreted letters as indeterminate values (A.2.3).

Description of Meanings.

Like the subjects of earlier studies (Brizuela & Blanton, 2014; Cañadas et al., 2016; MacGregor & Stacey, 1997), some students interpreted letters to be labels or objects. In session 2, students sought words related to the letters: N to mean ‘nothing’, for instance. In session 1, the letters chosen were the initials for characters’ names, with students contending that they represented the names and showing no signs of references to quantities. By way of example, E5 explained:

E5: Here I wrote ‘R’ for Raúl (pointing to the first column) and here a ‘C’ for 5Footnote 2 (pointing to the second),

R: ‘C’ for five, why did you write a ‘C’ for 5?

E5: Because you had to add 5 to everything.

R: Okay, and if ‘R’ is Raúl’s age, how would you write María’s age?

E5: ‘M’.

R: Why?

E5: Because it’s her initial.

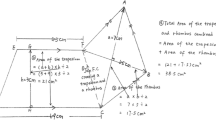
Interestingly, here the initials of key words were on occasion used to refer to determinate quantities. One example can be found in E15’s session 1 (Fig. 3) choice of R for Raúl. In the video, she explained that R was 19, its position in the alphabet. Her answer was classified as ‘letter attributed a value for a reason’.

Fig. 3
figure 3

E15’s answer in session 1

Full size image

The recording of the conversations between E15 and the other members of her working group showed that they initially represented Raúl’s age as R and María’s as ‘M’ and sought numbers beginning with those letters to attribute the respective values. As that strategy was unsuccessful, they decided that the value of R was its position in the alphabet. No value was attributed to M, initially chosen to represent María’s age. They calculated her age by adding five to the value of R, i.e. by applying the functional relationship.

The researcher’s discussion with this group of students also showed that they accepted the idea that the problem could have different answers. They noted that María’s age could be any number, which would depend on the letter chosen. That denoted an understanding of variability, mirrored in their use of different letters to describe the situation, as in the following excerpt from a conversation with E15.

R: If we don’t know how old Raúl is, ‘R’ could be another number, no?

E15 [nods assent].

R: How could you find María’s age, if Raúl is ‘R’ (years old)?

E15: I’d say she’s twenty-four.

R: Why?

E15: María, and Raúl is nineteen.

R: But we don’t know. He might be older.

E15: If you choose A, for instance, the number would be smaller.

As in previous studies, letters were observed here to be assigned numbers based on their position in the alphabet. Not all these cases implied a lack of awareness of the variable character of the dependent and independent variables. In the following excerpt from the session 1 discussion, E4 made no reference to a specific age, whilst nonetheless using alphabetical order to choose the letters to represent the two quantities.

R: A plus five equals E. Explain how you got that answer.

E4: From A to E goes five.

This use of alphabetical order entailed construing letters to have an indeterminate value and their position in the alphabet a mere reference to express the functional relationship (as in E4’s explanation above). Alphabetical order was also used to assign a unique, fixed value to letters, although possibly associated with variability. These findings corroborated other authors’ reports (Brizuela & Blanton, 2014; Cañadas et al., 2016; MacGregor & Stacey, 1997) in which the use of alphabetical order was viewed as a natural and spontaneous tendency among primary school students, although they associated it with the assignment of (fixed) numerical values.

Students also showed that they recognised the variability represented by letters in other ways. In those cases, their answers were classified under category A.2.2 (letter as variable/generic example) or A.2.3 (‘letter as variable/indeterminate value’). The subcategory letter as variable/generic example grouped answers in which students’ use of examples denoted an understanding that letters can represent different values. In the session 1 classroom discussion, E6 referred to letters as representing different quantities, attributing a numerical value to the letter by way of example only: ‘A plus five. And I say for instance 45’. In other words, she did not rule out the possibility of some other amount.

A second example arose in the session 3 discussion. E4 referred to the letter as an indeterminate number, noting that it could be whatever number you want. His explanation that the independent variable had to be multiplied by three constituted recognition of the existence of a relationship between the two variables. He ultimately attributed the letter a numerical value to clarify his argument.

E14: I wrote N and then I wrote S, I think.

R1: Another letter, S.

E14: Yes, I used N which is, say, the number that we want. I used S because I think N would be the number and then the result would be a different number. That’s why I wrote S.

R: You wrote S because it’s a different number. Fine.

R2: And that number, E14, could it be any number?

E14: Yes, for instance, N could be three and S could be nine, for instance.

R2: And how would you always find that S, E14?

E14: Multiplying N times three.

Students first verbalised the idea of letters being whatever number you want in session 2 (Table 7 lists further examples in the students’ written work), such as in the discussion of the statement ‘Carlos sells Z T-shirts and earns N euros’. E7 and E14 verbalised that argument, as shown in the following excerpt.

E7: I say it’s true because if Carlos sells Z T-shirts, Z is a number and he earns N euros, N is another number. If he sells Z T-shirts, he earns N euros. Then I think that if Carlos sells whatever number, he earns a different number of euros.

R: If the two are different, then, you say it’s true.

E7: Yes.

E14: True because Z can be whatever number you want and N can also be any number you want. If Carlos has however many T-shirts you want, then he can earn however much you want.

Table 7 Meanings attributed to letters in true/false questions: letter as variable/indeterminate value
Full size table

The idea that letters can be any number led some students to conclude that the statements in questions 7, 14 and 15 were (always) true (e.g. see E14’s answers in Table 7). Some students nevertheless realised that the two quantities had to be related as per the functional relationship specified (e.g. E4 and E17 in session 1).

Representation of Indeterminate Quantities: The Dependent Variable

This section analyses how students represented the dependent variable when the independent variable was represented symbolically. As noted above, whereas students were asked to represent the dependent variable in sessions 1 and 3, in session 2, the researchers themselves proposed the representations. In this later case, we analyse students’ explanations to determine how they interpreted and used letters. As the categories discussed above showed, students used letters, numbers or both to represent the dependent variable. Whilst the use of letters prevailed in the first session, in session 3 numbers acquired a certain predominance (see Table 8).

Table 8 General categories for representation used to denote the dependent variable
Full size table

Use of a Letter to Represent the Dependent Variable.

Students represented the functional relationship in one of two ways. In some answers, classified as ‘related letter’, the independent variable formed part of the (not necessarily syntactically correct) expression used. The examples in Fig. 4 were taken from E19’s answers in session 1 and E4’s in session 3.

Fig. 4
figure 4

Excerpts from E19’s and E4’s written answers in session 3

Full size image

E4’s explanation, reproduced below, of why he repeated the independent variable three times to represent the dependent variable, attested to his interpretation of the former as a variable with an indeterminate value.

E4: If it were multiplied times three, you add N three times.

R: Then N three times [writing on the blackboard].

E4: N plus N plus N, three Ns.

R: What does that mean? Can you explain, E4?

E4: It’s as if you were multiplying. Three Ns because it’s multiplied times three.

In other answers classified as ‘new related letter’, students took the alphabet as a reference to choose a letter for the dependent variable and express the functional relationship. For example, in session 1 three students chose a letter located five positions after the letter denoting the independent variable to represent the function x + 5 (see Fig. 5).

Fig. 5
figure 5

Excerpts from E8’s and E10’s written answers in session 1

Full size image

This is complemented by what E5 points out in the discussion of session 1. There, E5 made no reference to a specific age, whilst nonetheless using alphabetical order to choose the letters to represent the two quantities. The argument was that if Raúl was Z years old, as ‘Z’ is the last letter of the alphabet, María’s age would have to be found by going back to ‘A’; María would be D years old. These students did not replace letters with numerical values.

Some of the session 2 answers were also classified under new related letter. When representing the functional relationship, some students used a different letter for the dependent variable, contending that different letters represented different quantities and that letters can represent whatever number you want, an argument that, as noted in the preceding section, implies viewing letters as variable and indeterminate quantities (category A.2.3). Some students (e.g. E7) applied that argument broadly whilst others (e.g. E1) did so more restrictively, noting that although a given letter can be any number the functional relationship between the two variables had to hold. They were nonetheless unable to express that relationship with letters. The following excerpts exemplify these arguments.

E7: I say it’s true because if Carlos sells Z T-shirts, Z is a number and he earns N euros, N is another number. If he sells Z T-shirts, he earns N euros. Then I think if Carlos sells whatever number, he earns a different number of euros.

E1: It’s true. Because if Z is a lot, N has to be a large number. And if Z is small, then the other number also has to be small. For instance, if Z is 20, twenty times 3 would be 60. And you write 60 for N. And it would be 60 and that’s why I say it’s true.

Another example of the new related letter category, taken from the session 3 discussion, was E11’s reason for choosing the letter S, claiming that since he deemed N to be 15 the answer after multiplying was a different number, so he chose another letter, different from N.

In contrast, some students used different, unrelated letters. Such replies were classified under the category ‘new unrelated letter’. In the first session, for instance, two students (E21 and E25) used letters as labels, choosing R and M, the initials of the names of the two siblings (Fig. 6).

Fig. 6
figure 6

Excerpts from E21’s and E25’s answers in session 1

Full size image

Some students were also observed to believe that a given letter could represent both the dependent and the independent variables in the function and different amounts in one and the same situation. Four students claimed that true/false question 15 was true. E14 asserted that it was true ‘because Z can be 13 or whatever number you want’. They contended that letters could be whatever number you want, interpreting them as indeterminate quantities.

Use of a Number to Represent the Dependent Variable.

The criteria for choosing numbers to represent the dependent variable were not always verbalised. Where they were, two categories could be distinguished: random and alphabet related. Sometimes, students assigned a value to the independent variable and after applying the functional relationship used the result to represent the dependent variable. That is illustrated in Fig. 7, where E5 wrote in the values for the letters N and D in the margin and used them to fill in the table by applying the direct and inverse functional relationships to the assigned values.

Fig. 7
figure 7

Excerpt from E5’s answers in session 3

Full size image

Some students’ explanations suggested that the number chosen was used as a generic example (category N.2). The mobile recording of session 1 included a conversation in which student E10 explained why she used the number 100 to represent the variable. She construed the letter to be a variable and explained that 100 was just an example, because letters can represent ‘any number’.

In other students’ explanations the number was alphabet-related (category N.1). In the session 3 discussion, E3 contended that she thought N was 14 because of its position in the alphabet and therefore represented the dependent variable as 42 (= 3 × 14).

Discussion and Conclusions

The first question posed in this study sought to determine the meanings attributed by students to letters when exploring the functional relationships between two quantities. The meanings detected were as a label, value and variable. They varied across the sessions.

The Blanton et al. (2017) contention that progression in thinking about variables and their notation is non-linear, with meanings varying with the task involved, was both confirmed by the present findings and shown to apply to third-year students. Most of the students used familiar elements in the first session, in keeping with observations by Radford (2000), who noted that when students attribute meanings to symbols they seek recognisable references. In the first session, meanings alluding to areas previously worked on by the students, such as alphabetical order or arithmetic, prevailed. Previous studies interpret this as a tendency to assign fixed values to unknown quantities and to not perceive variability (Blanton et al., 2017); however, our data show that this is not always the case. We discuss it below when we talk about students’ representations of the dependent variable.

In the second session, the meaning of letters as variables with indeterminate values, associated with the idea that letters can be whatever number you want, prevailed. Students tended to support their letter as variable/indeterminate value reasoning with reference to specific quantities. That category would therefore be closely related to letter as variable/generic example, in which students realised that letters could represent different amounts, but proposed a set quantity as an example. Whilst able to express the algebraic relationship correctly, it seems that they fail to deem the answer as suitable because arithmetic logic induces them to seek numerical solutions. They might also resort to examples due to limitations in their competence to express their thinking in abstract terms.

In the third session, where a more open task was considered, the meanings observed varied, with five of the eight contributions to the discussion attributing a value to the letter to explain the answer.

Students tended to represent more the direct than the indirect relationship no matter which of these relations was ask for. When in session 2 the dependent variable was shown in connection with the operation relating it to the independent variable (such as in T/F question 6), the students viewed the latter as an indeterminate quantity, validated with previously generalised procedures based on tasks involving specific numbers. In contrast, when the dependent variable was expressed as a letter (T/F question 7), they tended to represent the other variable with a letter as well. They construed letters as indeterminate quantities, although in general they deemed that the two amounts had to be different and since the letters were different, the respective statements would be true.

The second research question posed the possible relationship between the meanings given to letters and their use to represent indeterminate quantities. That issue was explored with an in-depth analysis of how students represented the dependent variable when the independent variable was a letter. This study furnishes new information on students’ tendency to relate letters to their alphabetic order and use them as indeterminate quantities. Earlier studies revealed that students innately attributed numbers to letters according to their position in the alphabet. Here, further exploration of that idea showed that whilst students sometimes used alphabetical order to replace letters with numbers (letter attributed a value for a reason), in others they applied that criterion only to choose the letter representing the dependent variable. They then assigned variables indeterminate values to express the functional relationship (letter as variable/indeterminate value). In other cases, whilst attributing a unique value to each letter in keeping with its alphabetical order, they acknowledged that values could vary depending on the letter chosen to represent the independent variable. Such answers are an indication that, even when resorting to alphabetical order, students realised that the answer could involve more than one indeterminate quantity. They nonetheless lacked a system of symbols with which to express that variability with a single notation.

The study also revealed that representation of the dependent variable was affected by the meaning category letter as variable/indeterminate value. Students used the same or different letters to represent the two variables, reasoning that letters can be whatever number you want or contending that they can represent any number. Whilst some felt no need to include the functional relationship in their representation, others tried to explain that letters cannot adopt just any number but were governed by that relationship.

When students represented the dependent variable as a number they might be thought to be assigning the letter a fixed value, confirms the static view of letters described by Küchemann (1981). However, the analysis of students’ explanations for choosing a given number to represent a letter, showed that they deemed the choice to be a mere example, for in their belief that letters can be any number they assumed that replies involving a specific case would not be wrong.

Although in all three sessions at least one student dismissed the use of letters, on the whole they acknowledged the idea of variability which they associated with indeterminate quantities. Nonetheless, they deployed a personal system of symbols consisting in letters, numbers or both. These findings support Blanton et al.’s (2017) and Kaput et al.’s (2008) argument to the effect that variability as a notion and its symbolic representation can be experienced separately. An aware and effective reference to letters by students of this age is not so quickly approachable. Few children appropriate variable notation readily. Let us remember that our results come from just three 90-min sessions. Nevertheless, our description provides interesting examples of how students might make sense of this notation.

Students, who had no prior introduction to algebra, were able to reason abstractly and associate letters with indeterminate quantities. That was favoured by tasks involving true/false sentences but not so much in those in which they had to represent functional relationships by themselves. This study showed that participants could use letters in ways reported by earlier authors.

The categories defined here were useful for analysing students’ replies and may be applicable in future research. Whilst based on earlier studies, they were supplemented and adapted here to the data collected. The originality of this study rests in part on the categories proposed to analyse representation of the dependent variable when the independent variable is given as another letter, for this particular has not been previously addressed.

Further research along the present lines would include the exploration of other meanings related to indeterminate quantities, such as unknowns. Here, students indicated that letters can represent indeterminate quantities and argued that they can be whatever number you want, but that is not true in other contexts.