Dynamic heuristic acceleration of linearly approximated SARSA($\lambda$): using ant colony optimization to learn heuristics dynamically

Abstract

Heuristically accelerated reinforcement learning (HARL) is a new family of algorithms that combines the advantages of reinforcement learning (RL) with the advantages of heuristic algorithms. To achieve this, the action selection strategy of the standard RL algorithm is modified to take into account a heuristic running in parallel with the RL process. This paper presents two approximated HARL algorithms that make use of pheromone trails to improve the behaviour of linearly approximated SARSA($\lambda$) by dynamically learning a heuristic function through the pheromone trails. The proposed dynamic algorithms are evaluated in comparison to linearly approximated SARSA($\lambda$), and heuristically accelerated SARSA($\lambda$) using a static heuristic in three benchmark scenarios: the mountain car, the mountain car 3D and the maze scenarios.

1 Introduction

Reinforcement learning (RL) involves the use of agents that learn how to maximize the expected reward obtained by acting in their environment. RL has been successfully applied many domains: Salkham et al. (2008) apply it to optimization of traffic control, Bitzer et al. (2010) apply it to robotics, Rezzoug and Gorce (2009) define an algorithm for obstacle avoidance, Partalas et al. (2009) use it in a machine learning scenario to prune classifier ensembles, finally Daskalaki et al. (2013) use it in a medicine scenario to control glycaemic curves. As Sutton and Barto (1998) state, the learner is not told what to do, it rather has to learn what are the best actions to perform according to the rewards provided by the environment in which it is situated. More formally, in RL the goal of the agents involved in the computation is to find the policy that maximizes the expected discounted reward in time.

Exact and approximated approaches exist towards solving the RL problem. Q-learning as proposed by Watkins and Dayan (1992), and SARSA as as proposed by Sutton (1988), are probably the most popular exact algorithms respectively for off policy and on policy reinforcement learning [see the works of Menache et al. (2002), van Hasselt (2010), Bonarini et al. (2009) for a discussion on off policy algorithms and of Aleo et al. (2010) for a discussion on on policy algorithms]. As reported by Busoniu et al. (2010), amongst the most popular approaches towards approximated RL there are linear approximations. Sutton (1995) defined one of the most used approximator for this task, that is tile coding/coarse coding.

Similar to reinforcement learning, ant-colony optimization (ACO) algorithms, as studied by Dorigo and Blum (2005), make use of a swarm of simple agents to annotate the environment with pheromone traces so to find the best trajectory to a goal. The most famous application of ACO is in the Travelling Salesman Problem (TSP), where ACO is shown to find good solutions in a short time, revealing a good heuristic for NP-hard problems. Amongst the applications of ACO, Ding et al. (2012) apply it to vehicle routing, Vatankhah et al. (2012) apply it to obstacle avoidance, Huang (2009) apply it to feature selection, and Han and Shi (2007) apply it to clustering and image segmentation.

This paper is motivated by the problem of extending RL algorithms with heuristics that are dynamically learned by means of the trajectories performed by a RL agent in its environment.

Therefore, the main contribution of the paper is in providing an approach, called approximated pheromone heuristically accelerated reinforcement learning (AP-HARL) to avoid the manual definition of heuristic algorithms, an activity that usually requires specific expert knowledge concerning the domain where the RL algorithm is being applied. Furthermore, the paper also shows that the learned heuristic functions are of good quality and can be re-used to accelerate other RL algorithms.

The problem of idenfying good heuristic function for RL algorithms has been studied under various perspectives in the research literature, as it can be seen in the work of Ng et al. (1999), Devlin and Kudenko (2012), and Bianchi et al. (2014).

Ng et al. (1999) study the problem of reward shaping in the context of RL, demonstrating that with a potential based approach, the RL algorithm converges to the optimum, and that with a proper heuristic function the convergence to the optimum is faster. Ng et al. (1999) report that the main problem to solve when defining reward shaping is to model the heuristic function for the shaping process. This is not an easy problem to solve: defining an heuristic function for a maze environment with a goal state is a very well studied problem and many heuristics have been defined concerning this scenario, but for other RL scenarios, the definition of a heuristic function is quite a challenging task as scenarios are very often governed by differential equations, making the relationship between a state of the problem and the goal state, very difficult to derive.

To avoid this issue, Devlin and Kudenko (2012) study the definition of dynamic heuristics for reward shaping, illustrating the conditions for which a dynamic approach to reward shaping is convergent and showing empirically that the decision of the reward function can improve or worsen the convergence rate. The main issue with the reward shaping approach is that by modifying the reward function then the convergence properties of the algorithm can change.

Towards the use of heuristics, a particularly promising approach is the one presented by Bianchi et al. (2012, 2014), concerning the heuristically accelerated reinforcement learning (HARL) family of algorithms. HARLs change the action selection strategy and not the underling model associated with the reward and value functions, allowing thus to retain most of the convergence properties demonstrated for the original RL algorithms.

In addition to the definition of heuristics, an often overlooked problem of RL is that of experience replay. In experience replay, an agent retains trajectories of interaction related to previous experience in order to replay them at a later moment. Adam et al. (2012) show that the use of experience replay improves the speed of convergence in RL.

Another issue that often arose in the reinforcement learning research is how to combine the results of reinforcement learning and ant colony optimization (ACO) approaches. Notably, this problem has been discussed by Dorigo and Blum (2005), Socha and Dorigo (2008) and Liao et al. (2014). Zhu and Mastorakis (2014) have highlighted that one of the main advantages of ACO is the ability of keeping a memory concerning the trajectories performed, thus providing an opportunity for RL to improve the results with respect to an approach solely based on Markov decision processes (MDPs).

Monekosso and Remagnino (2001) define Phe-Q, an algorithm that enhance Q-learning with a belief factor, represented as pheromone, associated to a state. Such a pheromone would increase depending on the amount of agents finishing the RL task correctly, and it would decrease due to an evaporation rate. Gambardella and Dorigo (1995) define an extension of Q-learning, called Ant-Q, to work on the asymmetric travelling salesman problem (ATSP) using a set of ant agents updating a Q-learning function by means of the quality of the solution found. Another interesting approach is defined by Juang and Lu (2009), where ACO and a fuzzy Q-learning are blended together, with the Q-learning part of the algorithm working as the heuristic for the ACO algorithm, but changing the properties of both the ACO and fuzzy Q-learning process, with the problem of demonstrating the convergence of the algorithm. In addition, Bianchi et al. (2009) show that the ant colony system (ACS) algorithm is strongly related with the heuristically accelerated distributed Q-learning algorithm (HADQL).

HARL, reward shaping, experience replay and ACO have an important influence on the current contribution. First of all, this contribution builds on the HARL framework defined by Bianchi et al. (2009) and on the ACO concept of pheromone deposition. This solution is useful in practical terms as it allows to automatize the inclusion of heuristics in RL.

Secondly, if we consider existing algorithms that combine RL and ACO, with respect to Phe-Q, the proposed algorithms make use of the quality of the found trajectories to build a dynamic heuristic with the purpose of modifying the action selection strategy. Concerning the relationship with Ant-Q, the algorithms proposed are general purpose and for discrete and continuous domains, as they combine the knowledge about the trajectories in a approximated SARSA($\lambda$) algorithm, whereas Ant-Q explicitly focuses on the ATSP problem, which has a set of discrete states and does not make use of approximation. Thirdly, the algorithms proposed in this paper are influenced the experience replay approach proposed by Adam et al. (2012): this contribution develops heuristic models based on the previous trajectories of the learning agent to change the behaviour of exploration strategy, whereas for Adam et al. (2012) parts of the trajectory are replayed during the learning to change the learned policy, making the two approaches complementary. The contribution presented in this paper is inspired by the work of Bianchi et al. (2012, 2014) and Juang and Lu (2009). With respect to Bianchi et al. (2012) this contribution proposes to use a dynamic heuristic modelled with pheromone deposition to modify dynamically the exploitation part of the temporal difference learning of SARSA($\lambda$).

Concerning the contribution of Juang and Lu (2009), this paper exploits the properties of SARSA($\lambda$) to learn locally using the MDP process update, and the properties of ACO to learn a global heuristic, this allows us to keep ACO and TD learning as separated processes, thus maintaining the same convergence properties of SARSA($\lambda$), with the possibility to provide a bound to the heuristic loss caused by the ACO process.

The contribution provides error bounds with respect to a standard approximated SARSA($\lambda$) and complexity considerations, giving an idea on the trade off with respect to applying RL without dynamic heuristics. The proposed algorithms are evaluated in the mountain car, mountain car 3D, and maze scenarios.

The rest of this paper is organized as follows: Sect. 2, presents a background on RL and RL with linear approximation; Sect. 3 presents the approximated algorithms with the addition of the pheromone trails update; Sect. 4 presents an evaluation of the proposed algorithms; Sect. 5 discusses possible opportunities to extend the presented work and additional tests; Sect. 6 discusses the intersection of this contribution with relevant related work; Sect. 7 gives a reference to the code developed for this work; finally Sect. 8 presents the conclusion of the paper and the planned future work.

2 Background

This Section presents the concepts used throughout the paper, focusing on exact and approximated solutions to the RL problem.

2.1 Exact solutions to the RL problem

A concept that is central to the RL problem is that of Markov Decision Process (MDP).

Definition 1

(Markov Decision Process) A MDP is a tuple $\langle X,A,P,R \rangle$, for which X is a set of environment states, A is a set of possible actions the agent can perform, P is the probability of moving from one state to another given an action that can be expressed as $P: X \times A \times X \rightarrow \mathbb {R}$ , and R is the reward function associated to the transition that can be expressed as $R: X \times A \times X \rightarrow \mathbb {R}$.

The goal of the agent in a MDP is to learn an optimal policy $\pi ^* : X \rightarrow A$ that maps the current state x into the most desirable action a to be performed in x. A policy is stationary if it does not evolve in time. One way to achieve this is to explicitly store the value of the state and actions in a function $Q: X \times A \rightarrow R$ which returns the cost associate to taking an action $a \in A$ when the current state is $x \in X$. One algorithm achieving this is Q-learning, shown in Algorithm 1. In Algorithm 1, $\alpha \in (0,1]$ denotes a learning rate and $\gamma \in [0,1]$ the discount factor of the Q-learning algorithm. In particular, a high learning rate implies that the algorithm will give more importance to recently observed events. On the contrary a high $\gamma$ implies that the RL algorithm will give more importance to the consolidated experience of the agent.

As reported by Buşoniu et al. (2010) and Watkins and Dayan (1992), Q-learning converges to a global optimum, if the following conditions are satisfied:

• explicit, distinct values of the Q-function are stored and updated for each state-action pair;

• the sum $\sum \limits _{t=0}^{\infty } \alpha$ is infinite and the sum $\sum \limits _{t=0}^{\infty } \alpha ^2$ converges;

• all the state-action pairs are visited infinitely often.

The first condition is usually satisfied by implementing a lookup table (Q-Table). The second condition is satisfied if the learning rate $\alpha \in (0,1]$. The third condition is generally satisfied by applying a policy where the probability of a random action selection is $\epsilon >0$ and the probability of selecting the best action is 1-$\epsilon$. An interesting variation of Q-learning is provided by the SARSA algorithm of Sutton (1995). SARSA is very similar to Q-learning except that to update the Q-Table, the following equation is used:

$$\begin{aligned} Q(x,a)\leftarrow Q(x,a) + \alpha \left[ r + \gamma Q(x',a')-Q(x,a)\right] \end{aligned}$$

(1)

The main difference between Q-learning and SARSA is that Q-learning is an off-policy algorithm whereas SARSA is an on-policy one: off-policy algorithms would not base the learning solely on the values of the policy, but would rather use an optimistic estimation of the policy (in this case the $max_{a'}$ selection condition), whereas an on-policy algorithm bases its learning solely on the values of the policy at a given time.

Another important concept in RL is the one of eligibility trace. Sutton and Barto (1998) specify that an eligibility trace is an additional memory variable associated to each state taking into consideration the frequency with which each state is visited. There exist three different approaches to express eligibility traces: accumulating traces, replacing traces and recently Seijen and Sutton (2014) defined true online traces. Accumulating eligibility traces for state-action pairs can be expressed as shown in equation 2,

$$\begin{aligned} e_{t+1}(x,a) = \left\{ \begin{array}{l l} \gamma \lambda e_{t}(x,a) &{} \quad \text {if }x \ne x_t, a \ne a_t \\ \gamma \lambda e_{t}(x,a) +1 &{} \quad \text {if }x = x_t, a = a_t \\ \end{array} \right. \end{aligned}$$

(2)

where $\gamma$ represents the discount factor and $\lambda \in [0,1]$ a decaying factor for the trace defining how much the strength of a choice in the past should be discounted. Replacing traces can be defined as:

$$\begin{aligned} e_{t+1}(x,a) = \left\{ \begin{array}{l l} \gamma \lambda e_{t}(x,a) &{} \quad \text {if }x \ne x_t, a \ne a_t \\ 1 &{} \quad \text {if }x = x_t, a = a_t \\ \end{array} \right. \end{aligned}$$

(3)

With respect to accumulating traces, replacing traces have been found to speed up convergence in many scenarios. Eligibility traces can then be used to define the SARSA($\lambda$) algorithm (accumulating traces) as shown in Algorithm 2.

In Algorithm 2, $\delta$ denotes the temporal difference learning error (TD-error). In such an algorithm, at each moment the current $\delta$ is assigned to each state according to its eligibility trace. The use of eligibility traces allows for a faster convergence to a global optimum than SARSA alone, but this comes at the cost of keeping the information about past visited states.

In addition, true online traces have been recently found to speed up further the convergence of the algorithms with respect to accumulating and replacing traces, and are based on the three equations below.

$$\begin{aligned}&\delta _t = r_{t+1} + \gamma Q_t(x',a') - Q_{t-1}(x,a) \end{aligned}$$

(4)

$$\begin{aligned}&e_t = \gamma \lambda e_{t-1} + \alpha [1 - \gamma \lambda e^{T}(x,a)] \end{aligned}$$

(5)

$$\begin{aligned}&Q_{t+1}(x,a) = Q_t(x,a) + \delta _t e_t + \alpha [ Q_{t-1}(x,a) - Q_t(x,a)] \end{aligned}$$

(6)

The contributions of Seijen and Sutton (2014) and Van Seijen et al. (2016) fully discuss true online traces, this contribution focuses therefore on using them for the experimentation. Furthermore, this paper focuses on using true online traces as these in any case perform better than replacing traces and accumulating traces in the experimentation scenarios selected.

Finally, two concepts that is important to define are those of transition and trajectory.

Definition 2

(Transition) A tuple $d_k = \langle x,a,x',a' \rangle$ denotes a transition between a state-action pair x, a and state-action pair $x',a'$ at time k.

Definition 3

(Trajectory) A trajectory of length n is defined as a set D of transitions $D = \{d_1,d_2,\ldots ,d_n \}$

2.2 Heuristically accelerated reinforcement learning

Bianchi et al. (2012, 2014) define the family of Heuristically Accelerated Reinforcement Learning (HARL) algorithms. In such an algorithm, the MDP problem is solved using a heuristic function $H :X \times A \rightarrow \mathbb {R}$ to influence the action selection of an agent. As reported by Bianchi et al. (2012, 2014) the main advantage of such an approach is that the heuristic function does not interfere with the standard update mechanism of RL algorithms. In HARL, the action selection method uses a combination of the action-value estimation and of a heuristic estimation function as follows:

$$\begin{aligned} {[}Q(x,a) \bowtie \psi H(x,a)^\beta ] \end{aligned}$$

(7)

where $\bowtie$ could for example be a sum or a subtraction operator. In this paper, $\bowtie$ will always be a sum, because it has convenient properties when dealing with convergence. For instance, the $\epsilon$-greedy selection strategy can be expressed as:

$$\begin{aligned} \pi (x) = {\left\{ \begin{array}{ll} \pi '(x) \text{ if } \xi \le \epsilon , \\ a_{random} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(8)

where $\xi$ is a random parameter between 0 and 1, $\epsilon$ specifies the exploration/exploitation trade-off and $a_{random}$ is a random action chosen amongst those available at state x.

$\pi '(x)$ is defined as:

$$\begin{aligned} \pi '(x) = arg max_a [Q(x,a) \bowtie \psi H(x,a)^\beta ] \end{aligned}$$

(9)

where $\beta$ and $\psi$ are parameters used to specify the importance of the heuristic function. This paper will always assume $\beta =1$ and $\bowtie$ to be a sum, so to be able to specify H(x, a) in terms of the following difference:

$$\begin{aligned} H(x,a) = {\left\{ \begin{array}{ll} max_{a'\in A}[Q(x,a')] - Q(x,\pi ^H(x))+ \eta \\ \text{ if } a=\pi ^H(x), a \ne a',\\ 0, \text{ otherwise } \end{array}\right. } \end{aligned}$$

(10)

since this difference is always a positive number, to influence the action choice, the value of H(x, a) must be larger than the variation amongst the values of Q(x, a). To achieve this, the design parameters $\psi$ and $\eta$ have to be selected opportunely. The $\pi ^H$ action selection strategy in the case of HARL depends on the heuristic selected. For what it concerns this paper, $\pi ^H$ is defined later in Sect. 3.

2.3 Approximated solutions to the RL problem

When the MDP presents a large number of states then it becomes infeasible to express the Q-function explicitly and an approximation method must be used. Approximation methods require to store estimates for every state-action pair of the Q-function. A quite successful approach to approximation is represented by linearly parametrized approximators. The Q-function then becomes:

$$\begin{aligned} \hat{Q}(x,a) = \sum _{i=1}^n \theta _i(x,a)\phi _i(x,a) = \theta ^T\phi (x,a) \end{aligned}$$

(11)

in this case the parameter vector is $\theta \in \mathbb {R}^n$ and $\phi : X \times A \rightarrow \mathbb {R}^n$ is a vector of basis functions (BFs), $[\phi _1(x,a),\ldots ,\phi _n(x,a)]^T$.

Algorithm 3 shows an approximated version of SARSA($\lambda$) using a linear approximator and true online elegibility traces [adapted from Van Seijen et al. (2016)].

Approximated SARSA($\lambda$) does not have the same convergence properties as exact SARSA, but, as reported by Melo et al. (2008), it converges if the policy is fixed and the action selection strategy $\pi _{\theta }$ assumes a behaviour that is greedy in the $\theta$ space, which sufficiently visit each state, with $\pi (x,a)>0$, meaning that actions are tried infinitely often in such states. This contribution uses tile coding as a function approximator. In tile coding the variable space is subdivided into several overlapping tiles with a weight associated. The approximate value of each point is then obtained as the sum of the weights of the tiles.

2.4 Ant colony optimization

ACO algorithms are a family of heuristic algorithms where the quality of newly found solutions is used to annotate an internal memory in the form of a transition matrix, usually called pheromone matrix, representing the transitions between states of the problem at hand (for example: finding the shortest paths to traverse all the nodes in a graph).

In particular, ACO annotates the transition between states x and y with a transition score $\tau (x,y)$, known as pheromone trail. Such a score is updated each time a solution passes through states x and y with a numerical reward $\varDelta \tau (x,y)$, known as pheromone deposition process, that is usually associated to the quality of the solution found. If multiple solutions pass through these states, the state transition accumulates a higher score, making it more desirable with respect to other transitions. In addition to the pheromone trail $\tau (x,y)$, ACO also takes into consideration a heuristic function $\eta (x,y)$ specifying the a priori desirability of the transition. If one considers the case of the shortest routing path between the nodes of a graph, then $\eta (x,y)$ could be the euclidean distance between x and y. The $\tau (x,y)$ level can also be seen as an a posteriori evaluation of how desirable is a transition from one state to another given the currently discovered solutions to a given problem. To allow for exploration in the search, in ACO the selection of the next transition is performed probabilistically, thus $p^k(x,y)$, whose formula is shown in equation equation 12, represents the probability that the kth solution will include the transition between state x and state y.

$$\begin{aligned} p^k(x,y)= \frac{\tau (x,y)^\alpha \cdot \eta (x,y)^\beta }{\sum _{y \in Y_{allowed}} \tau (x,y)^\alpha \cdot \eta (x,y)^\beta } \end{aligned}$$

(12)

with $\alpha ,\beta \ge 1$ defining respectively the importance of the pheromone trail transition score identified by $\tau (x,y)$ and the a priori heuristic function identified by $\eta (x,y)$.

After each cycle, the pheromone trail transition score is updated according to the quality of the solution found as shown in Eq. 13.

$$\begin{aligned} \tau (x,y) \leftarrow \rho \cdot \tau (x,y) + \sum _1^k \varDelta ^k\tau (x,y) \end{aligned}$$

(13)

where $\tau (x,y)$ represent the current value of the pheromone trail transition score between x and y, $\rho$ is a decaying rate and $\varDelta \tau ^{k}(x,y)$ is a numerical reward associated with the kth solution, that can typically be expressed as:

$$\begin{aligned} \varDelta \tau ^{k}(xy) = {\left\{ \begin{array}{ll} z/c_k &{} \text{ if } \text{ solution } k \text{ uses } \text{ curve } xy \text{ in } \text{ its } \text{ tour } \\ 0 &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(14)

where $c_k$ is the cost of the kth newly found solution and z is a constant. The rationale of the $\varDelta ^k\tau (x,y)$ term is that solutions with a lower cost would have a higher reward, reflecting in a higher probability to select a transition that if often selected in good solutions. The decaying rate is necessary to mitigate the issue of local minima or maxima in the search. ACO mimics the way an ant colony works. Each of the solutions is understood to be an ant that deposits a certain amount of pheromone ($\varDelta ^k\tau (x,y)$) on a known path towards food. Then, pheromone evaporates in time (by means of $\rho$), thus shorter paths towards the food would have a stronger pheromone intensity ($\tau (x,y)$), making them preferred to longer ones with lower pheromone intensities.

3 Approximated pheromone heuristically accelerated reinforcement learning

This section presents the approximated pheromone heuristically accelerated reinforcement learning (AP-HARL) algorithms that make use of pheromone deposition as in the ACO algorithms.

Such algorithms use a linear approximator based on tile coding to keep trace of the pheromone associated to a transition from one state to another. The motivation to do this by using an approximator rather than keeping an explicit table of transitions is because, differently from a traditional ACO, RL problems may involve a large number of different transitions. Approximated RL algorithms can work with large state spaces, consequently also the process of depositing pheromone should be represented through an approximation mechanism such as a tile coding. To achieve this, one can specify that

$$\begin{aligned} \hat{\tau }(x_{old},a_{old},x,a) = \sum _{i=1}^n \theta _i^p\phi ^p_i(x_{old},a_{old},x,a) = \theta ^{pT}\phi ^{p}(x_{old},a_{old},x,a)\quad \end{aligned}$$

(15)

where the function $\hat{\tau }: (X,A) \times (X,A) \rightarrow \mathbb {R}$ is a function associating a weight, in terms of a pheromone trail transition score, to a particular state-action transition. The algorithm updates the transition matrix with the solution found in each reinforcement episode.

The update rule for the pheromone trail transition score is then specified as:

$$\begin{aligned} \hat{\tau }(x_{old},a_{old},x,a) = \rho \cdot \hat{\tau }(x_{old},a_{old},x,a) + \varDelta \tau (x_{old},a_{old},x,a) \end{aligned}$$

(16)

The rationale of such an approach is to create a long term learning model to be used in addition to the MDP. In MPDs each state is thought to depend only on the previous state. Considering a pheromone trail transition score, allows us to evaluate a state in terms of the quality of the solutions passing through it, thus creating dependencies between states that are not necessarily adjacent. Furthermore, to allow for a non deterministic selection of states amongst episodes, the pheromone trail transition score decays like in the ACO algorithm, using the same $\rho$ coefficient as in ACO. Algorithm 4 presents the approximated pheromone based heuristically accelerated SARSA($\lambda$) algorithm (AP-HARL), with respect to the case with replacing traces.

where:

• $\mathcal {Q}:X \times A \rightarrow \mathbb {R}$ is the Q-function as in Eq. 11.

• $\mathcal {H}:X \times A \rightarrow \mathbb {R}$ is a heuristic function depending on pheromone.

• $\psi$ is the parameter defining the importance of the heuristic function.

• $\rho$ is the pheromone evaporation rate.

• c represent the cumulative reward.

In particular, the heuristic function $\mathcal {H}:X \times A \rightarrow \mathbb {R}$ is expressed as in Eq. 10.

Two heuristic selection strategies $\pi ^H(x)$ can be proposed, according to perspective selected in the heuristic function. Figure 1 shows the forward and the backward perspectives.

Fig. 1

Forward and Backward selection strategies

The backward selection strategy looks in the past state and selects the action that maximises the current link in which the agent resides:

$$\begin{aligned} \pi ^H(x) = argmax_{a}[\hat{\tau }(x_{old},a_{old},x,a)] \end{aligned}$$

(17)

This strategy uses only the $\epsilon$-greedy algorithm for the exploration and the state with the highest pheromone trail transition score is selected by the heuristic function according to the $\psi$ value. The forward selection strategy can be expressed by the following equation:

$$\begin{aligned} \pi ^H(x) = argmax_{a}[\hat{\tau }(x,a,x',a')] \end{aligned}$$

(18)

This selection strategy selects the action according to the maximum future pheromone score on the transition, independently of whether or not the state $x',a'$ is visited. This approach is more complex as it requires to evaluate the actions that can be performed in the future state, therefore requiring the agent to store a transition model of the environment. It is also important to notice that AP-HARL presents two occasions in which the pheromone score trail is updated: during the learning, with a local update and after an episode of learning, with a global update. Convergence considerations of this choice will be discussed in the next Section.

These forward and backward approaches follow the same philosophy of the HARL algorithms presented by Bianchi et al. (2014), but here the heuristic is defined by the pheromone trail transition score in the trajectories attempted by the agent. Furthermore, maximizing over the action does not cause infinite loops as exploration is still enforced by the $\epsilon$-greedy algorithm that produces a random action with probability $\epsilon$. It is important to state that the underlying temporal difference behaviour of the algorithm has not been modified, meaning that most of the results obtained for approximated SARSA($\lambda$) by Melo et al. (2008), are also valid in our heuristic accelerated algorithms. The forward and backward strategies are evaluated in Sect. 4.

3.1 Convergence considerations and error bounds

As already mentioned in Sect. 2, the convergence properties of approximated RL algorithms are more complex to demonstrate and are less understood. Nevertheless, Melo et al. (2008) provided an analysis of the conditions for which an approximated SARSA converges. According to this analysis, convergence is possible in environments where the policy is fixed, the states are all sufficiently explored and the algorithms are greedy in $\theta$. Given that the proposed algorithms utilise $\psi$ to govern the importance of the heuristic function, but they do not change the exploration rate expressed with $\xi$, what is to be expected is that an ill-choice of $\psi$ may slow down the convergence, but that the underlying approximated algorithm properties of convergence are maintained. More formally, following the theoretical results presented by Bianchi et al. (2012), the loss between the $\epsilon$-greedy algorithm and the heuristic in the approximated case can be defined as:

Definition 4

(Heuristic Loss) $L_H = \hat{Q}(x,\pi ) - \hat{Q}(x,\pi ^H)$

Then it is possible to state that:

Theorem 1

Provided that a HARL agent is learning a policy in a deterministic MDP with a finite state-action space with bounded finite rewards, discount factor $0 \le \gamma < 1$, a heuristic function H(x, a) bounded so that $h_{min} \le H(x,a) \le h_{max}$, and that each state is visited infinitely often, then the agent converges with probability one uniformly over all states $x \in X$ to the optimal $Q^*$.

Proof

The proof, proposed by Bianchi et al. (2012), is built on the fact that despite the action selection performed by the heuristic, until the algorithm uses an $\epsilon$-greedy strategy with a random action selection probability, then state-action pairs are still visited infinitely often and the state-action values updated until convergence. $\square$

Furthermore, building on this proof, Bianchi et al also state that:

Theorem 2

The maximum loss caused by a heuristic function, for which it holds that $h_{min}\le H(x,a) \le h_{max}$ is $L_h= \psi [h_{max}^\beta -h_{min}^\beta ]$, if we consider a discount factor $0\le \gamma <1$ and $\bowtie$ is the sum.

Proof

The proof starts by considering $x_{max}$ as a state causing maximal loss, that can be written as $\forall x \in X, L_h(x_{max}) > L_h(x)$. In this state, an optimal action can be expressed as $a= \pi ^*(x_{max})$, and an action selected by the heuristic function can be expressed as $b = \pi ^H(x_{max)}$ . Therefore it is possible to obtain the following equation:

$$\begin{aligned} Q(x_{max},a) + \psi H(x_{max},a)^\beta \le Q(x_{max},b) + \psi H(x_{max},b)^\beta \end{aligned}$$

(19)

from this equation one can get the difference in quality between the selected actions by rearranging the equation as follows:

$$\begin{aligned} Q(x_{max},a) - Q(x_{max},b) \le \psi ( H(x_{max},b)^\beta - H(x_{max},a)^\beta ) \end{aligned}$$

(20)

Finally, considering the definition of heuristic loss, one can substitute it in the equation above (remembering that the heuristic loss is bounded by $h_{max}$ and $h_{min}$), and obtain the following equation:

$$\begin{aligned} L_h(x_{max}) \le \psi ( h_{max}^\beta - h_{min}^\beta ), \forall x \in X \end{aligned}$$

(21)

$\square$

In the case of the algorithms presented in this contribution, the theorems above hold only with a dynamic heuristic whose values are bounded by $h_{min}$ and $h_{max}$. Adapting the work of Stützle and Dorigo (2002), the maximum pheromone score on a transition in the AP-HARL algorithms is bounded by:

$$\begin{aligned} \lim _{t \rightarrow \infty } \tau (x_{old},a_{old}, x,a) \le \frac{1}{\rho } \cdot \frac{1}{c^*} \end{aligned}$$

(22)

where $c^*$ is the cost of the best trajectory found. If the inferior limit of the pheromone score is $h_{min} = 0$ and the superior limit is $h_{max} =\frac{1}{\rho } \cdot \frac{1}{c^*}$ then the bound for the loss becomes:

$$\begin{aligned} L_h= \psi \cdot h_{max}^\beta = \psi \cdot \left( \frac{1}{\rho } \cdot \frac{1}{c^*}\right) ^\beta \end{aligned}$$

(23)

An interesting consideration concerning this loss is that the dynamic heuristic algorithms defined will tend to have a larger loss when $\psi$ has higher values, and larger loss when $\rho$ has lower values. This also defines a basic possible strategy when trying to find parameters: the grid search for good parameters should start with high values of $\psi$ and high values of $\rho$, an then gradually lower the values of $\psi$ and $\rho$.

A possibility different from the implicit bounds of the pheromone trail transition score obtained in ACO, would be to define the parameters $h_{min}$ and $h_{max}$ explicitly, similarly to what happens in Min-Max ACO algorithm of Stützle and Hoos (2000). This contribution uses the implicit bounds of the pheromone trail transition score, leaving to future work the possibility of using explicit bounds. Finally, one may consider local pheromone trail transition score updates in addition to the global ones considered in this contribution. If a local update is introduced, the bounds defined above may change as the limits defined by Stützle and Dorigo (2002) are calculated only with respect to a global ACO update. Therefore a conservative approach in which the pheromone is kept between $h_{min}$ and $h_{max}$ is necessary to maintain good convergence properties. In this contribution, the following equations are used for local pheromone updates (see Algorithm 4):

$$\begin{aligned} \theta ^{p}(x,a,x',a') \leftarrow \rho \cdot \theta ^{p}(x,a,x',a') + (1-\rho )\cdot \delta ^p \end{aligned}$$

(24)

if the pheromone concentration score is bigger in the transition $\langle x_{old},a_{old},x,a \rangle$, where $\delta ^{p}$ in this case is calculated as:

$$\begin{aligned} \delta ^{p} = \theta ^{pT}\phi ^{p}(x_{old},a_{old},x,a) - \theta ^{pT}\phi ^{p}(x,a,x',a') \end{aligned}$$

(25)

Vice versa, the following equation is used if the pheromone concentration score is higher in the future transition:

$$\begin{aligned} \theta ^{p}(x_{old},a_{old},x,a) \leftarrow \rho \cdot \theta ^{p}(x_{old},a_{old},x,a) + (1-\rho )\cdot \delta _p \end{aligned}$$

(26)

where $\delta ^{p}$ now is expressed as:

$$\begin{aligned} \delta ^{p} = \theta ^{pT}\phi ^{p}(x,a,x',a') - \theta ^{pT}\phi ^{p}(x_{old},a_{old},x,a) \end{aligned}$$

(27)

On one hand, Equations 24, 26 move pheromone score from one transition to another in the pheromone traces of the AP-HARL agent. This creates variability between the trajectories. A similar update was introduced in the Ant Colony System (ACS) by Dorigo and Gambardella (1997), but in ACS the discount would happen in the present transition with respect to the future transition. In AP-HARL, the future transition is discounted and updated depending on which state has the higher pheromone score. This choice may seem counter-intuitive, but it is justified by the fact that the pheromone score calculated with a global update tends to concentrate in the transitions containing the start and goal states (see the Maze scenario for an example), where all the trajectories intersect, therefore such an update is necessary to spread the pheromone score towards the intermediate states, where most of the learning takes place. In addition, in order to avoid the repeated selection of actions within a trajectory, Equation 28 is also introduced.

$$\begin{aligned} \theta ^{p}(x_{old},a_{old},x,a)\leftarrow \rho \cdot \theta ^{p}(x_{old},a_{old},x,a) \end{aligned}$$

(28)

This equation is important as it introduces the effect of discounting pheromone score when an agent leaves a particular transition, discouraging loops in which a transition is selected more than once in the same trajectory. It is easy to observe that these equations make the total pheromone score tend to zero for a trajectory with infinite steps, which causes the heuristic loss $L_h$ also to tend to zero. This means that, in the worst case, AP-HARL would converge to the behaviour of a normal SARSA($\lambda$) algorithm.

3.2 Time complexity considerations

Concerning the complexity of the algorithms at hand, for each learning episode of the algorithm in Fig. 4 it is possible to consider a discretization of the actions in the environment in n different actions:

$$\begin{aligned} A = \{a_1,a_2, \ldots , a_n\} \end{aligned}$$

(29)

where n is small. Considering this discretization, then the maximization over the actions performed in the SARSA($\lambda$) algorithm can be solved by enumeration and so it is O(n). Furthermore, approximated SARSA($\lambda$) requires to update the eligibility traces, which are represented by a vector of length $L_t$. As a consequence linearly approximated SARSA($\lambda$) has the following complexity:

$$\begin{aligned} O((n+ n_t + L_t)T) \end{aligned}$$

(30)

Similar considerations hold for the backward view of the pheromone heuristic which also has a complexity of O(n) for selecting an action, plus another O(n) to select an action using the heuristic function. In additions, in every episode of algorithm 4, the algorithms modifies the pheromone trail transition score on the trajectory of length T, where T is the number of time steps per episode, and update $n_t$ tiles of the vector $\theta ^p$, plus $2n_t$ tiles for the local pheromone score updates. Algorithm 4 also applies the decaying rate to $\theta ^p$ at each episode, which has a complexity equal to the length of $\theta ^p$, $L^p$. The complexity of the AP-HARL-BACKWARD algorithm is then:

$$\begin{aligned} O((2n+ 3n_t +L_t)T + L^p) \end{aligned}$$

(31)

Concerning the forward view, AP-HARL has to consider also the future actions given a selected action in the present, this implies a quadratic complexity $O(n^2)$ with respect to the number of actions. The complexity of the forward view is therefore

$$\begin{aligned} O((n+ n^2 + 3n_t +L_t)T + L^p) \end{aligned}$$

(32)

On one hand, this analysis shows that AP-HARL is sensitive to the length of the learned trajectory in the case of the backward view, and also to the number of actions in the case of the forward view. One limitation of AP-HARL is that, with respect to a standard linearly approximated SARSA($\lambda$), it would take a longer time to train. On the other hand, the different exploration approach of the views may allow to find a better solution than the standard approximated SARSA($\lambda$) and take less iterations to converge. The purpose of the following experiments is to evaluate empirically the convergence properties of the two views to understand if there is a gain in using AP-HARL algorithms with respect to algorithms that are not heuristically accelerated or accelerated with simple static heuristics.

4 Experiments

This section presents a set of experiments to compare the linearly approximated SARSA($\lambda$) algorithm using tile coding and the AP-HARL algorithms presented in the previous Section. Furthermore, the AP-HARL algorithms are also compared with the HA-SARSA($\lambda$) algorithm presented by Bianchi et al. (2012). It is important to state that given the dynamic nature of the heuristics, the goal is not to improve the results with respect to the contribution of Bianchi et al. (2012), but rather to understand whether by learning dynamically an heuristic function, one can obtain comparable results with respect to a static heuristic and thus avoid the issue of modelling an ad-hoc heuristic for a particular domain. This is important as in many cases modelling the heuristic explicitly may not be an easy task. Finally, HA-SARSA($\lambda$) is also combined with a static pheromone trace (the algorithm is named HA-SARSA($\lambda$) + Pheromone in the experiments) trained by running AP-HARL until it reaches convergence and then saving the obtained pheromone trace, to understand if AP-HARL can learn re-usable heuristic functions.

One of the main disadvantages of using a HARL approach is that it implies a large number of parameters as it requires to find the best parameters for the RL and heuristic part. Concerning the RL part, the Mountain Car and Mountain Car 3D scenarios use the same parameters used in recent literature. As a consequence, the parameters of the Mountain Car scenario are set as specified by Van Seijen et al. (2016) concerning learning rate $\alpha$, discount factor $\gamma$, the decaying rate for elegibility traces $\lambda$. The same parameters are also used for the Mountain Car 3D scenario as they work equally well. The Maze scenario is illustrative and ad hoc, so no parameters can be found in literature, therefore $\alpha =0.1$ and $\gamma =0.99$ have been used because the work well with approximated SARSA($\lambda$) and true online traces. Table 1 shows the values of the parameters utilized by the studied algorithms, where the tiling parameter is a vector of dimension n, whose $n-1$ first elements represent how the dimensions of the environment are discretized and the $n_{th}$ element represent the number of tiling layers used.

Table 1 RL parameters for the three scenarios

Concerning the heuristic part of the two variants of the AP-HARL algorithm and the HA-SARSA($\lambda$) algorithm, a grid search is necessary to select $\psi$, $\eta$ and $\rho$. Table 2 shows the intervals in which the grid search was performed for each of the parameters of the heuristic part of the algorithms. The best average cumulative reward over 25 episodes and 50 learning steps was used to select the values of the parameters.

Table 2 Grid search for the heuristic algorithms

Finally, Table 3 shows the values of $\psi$, $\eta$ and $\rho$ for the heuristically accelerated algorithms. HA-SARSA($\lambda$) does not have a value for $\rho$ as it does not use pheromone traces. HA-SARSA($\lambda$) + Pheromone also does not have a value for $\rho$ because it uses a previously calculated pheromone trace as a static heuristic, so the pheromone trace does not evolve and does not need a discount factor.

Table 3 Selected value for the parameters

The experiments show the learning curves, the average time to finish the simulation for each of the considered algorithms and the average time to find the best solution within a simulation: it is necessary to show this to know if, given the higher computational complexity of the proposed algorithms, these would also require a much longer time to train with respect to the standard approximated SARSA($\lambda$) or HA-SARSA($\lambda$), and if the AP-HARL algorithms can find better solutions than SARSA($\lambda$). As previously mentioned, the tests are conducted using true online traces, as they hold better results in the selected scenarios.

The tests were conducted on an Intel(R) Core(TM) i7-6700HQ, 2.60 GHz with 4 cores and 16 gigabytes of RAM.

4.1 The mountain car scenario

In the mountain car domain, an agent has to drive an under-powered car up to a hill towards the goal. The state space has two variables, the position x of the car in the hill and the velocity of the car $\dot{x}$, where $x \in \{-1.2,0.6\}$ and $\dot{x} \in \{-0.07,0.07\}$. Furthermore the agent has a control action $a \in \{-1,0,1\}$. At each time the state variables are regulated by the following equations:

$$\begin{aligned}&x(t+1) = x(t) + \dot{x}(t) \end{aligned}$$

(33)

$$\begin{aligned}&\dot{x}(t+1) = \dot{x}(t) + a(t)\cdot 0.001 + cos(3\cdot x(t))\cdot (-0.0025) \end{aligned}$$

(34)

The agent’s goal is to reach the state with $x_1(t_n) = 0.6$. At each time step the agents received a reward of $-1$ until it reaches the goal state wherein it receives a reward of 1. Figure 2 gives a representation of the Mountain Car problem.

Fig. 2

A representation of the mountain car scenario

For what it concerns the heuristic used for HA-SARSA($\lambda$), the same heuristic proposed by Bianchi et al. (2012) was used. This implies preferring actions and states that always increase the module of the velocity. The experiments where repeated 100 times for each algorithm.

Fig. 3

Approximated SARSA($\lambda$) HA-SARSA($\lambda$) and HA-SARSA($\lambda$) + Pheromone versus AP-HARL algorithms learning curves in the mountain car scenario with true online traces

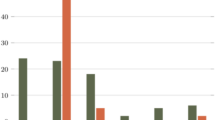
Figure 3 shows the learning curves with a 95% confidence interval of the five learning agents selected. Table 4 shows the best result found on average by the algorithms with a 95% confidence interval.

As the results suggests, both AP-HARL versions speed up the convergence of SARSA($\lambda$) without impairing the quality of the results. They discover better policies on average, but they are also more computationally expensive than approximated SARSA($\lambda$) and HA-SARSA($\lambda$). AP-HARL-BACKWARD seems to have a similar behaviour to HA-SARSA($\lambda$). Both AP-HARL-BACKWARD and AP-HARL-FORWARD converge at earlier iterations than SARSA($\lambda$) and HA-SARSA($\lambda$).

Table 4 Comparison between the results found by linearly approximated SARSA($\lambda$) and the AP-HARL algorithms in the mountain car scenario with replacing traces and true online traces

The slowest algorithm is AP-HARL-FORWARD. This is consistent with the complexity analysis previously performed. AP-HARL-FORWARD is also the algorithm that finds the best solution on average. There exists therefore a trade-off between computational complexity and quality of the solution found, therefore a choice on whether to use or not a AP-HARL algorithm depends on how time critical is an application versus how precise it should be. In any case, if the application requires it, it is always possible to learn a heuristic function with AP-HARL, save it, and then re-use it as a static pheromone function, as shown in the case of HA-SARSA($\lambda$) + Pheromone, whose computational complexity is almost as contained as that one of HA-SARSA($\lambda$) with a hand defined heuristic producing comparable results in terms of quality. The first experiment seems to confirm the hypothesis that dynamic heuristics can accelerate the convergence of SARSA($\lambda$) and that the heuristic function found is also of good quality.

4.2 The mountain car 3D scenario

The mountain car 3D scenario is a generalization of the mountain car scenario and its environment is depicted in Fig. 4. The problem develops along the two positions x, y and the velocities $\dot{x},\dot{y}$.

Fig. 4

The 3D mountain car scenario

The equations used to regulate the Mountain Car 3D scenario are the same as the mountain car one, but one for each of the axis. The agent’s goal is to reach the state $x(t_n) = 0.6$ and $y(t_n) = 0.6$, with $x \in \{-1.2,0.6\}$, $y \in \{-1.2,0.6\}$, $\dot{y} \in \{-0.07,0.07\}$ and $\dot{y} \in \{-0.07,0.07\}$. The agent can select from five actions that are {North, West, East, South, Neutral}, West and East modify $\dot{x}$ by $-0.001$ and $+0.001$ respectively, while South and North modify $\dot{y}$ by $-0.001$ and $+0.001$ respectively.

Similarly to Taylor et al. (2008), an exploration rate $\epsilon =0.5$ was kept, multiplied by 0.9 at each iteration to let the algorithms stabilize on the learned policy. All the algorithms have the following parameters values $\lambda =0.9$, $\gamma = 1$. The state variables are discretized by splitting each of them in 4 parts, as the environment is bigger than in the normal mountain car scenario, and keeping 5 layers of tiles. A similar tile coding structure was used for the pheromone process.

Fig. 5

SARSA($\lambda$) versus AP-HARL algorithms learning curves in the Mountain Car 3D scenario for true online traces

Figure 5 shows the convergence behaviour of SARSA($\lambda$), HA-SARSA($\lambda$), AP-HARL-BACKWARD and AP-HARL-FORWARD and HA-SARSA($\lambda$) + Pheromone for true online traces. Table 5 shows the best results found by each of the algorithms. For HA-SARSA($\lambda$) the heuristic used prefers states that would increase the logic AND of the values of the module of the velocities $\dot{x},\dot{y}$. The static heuristic selected for HA-SARSA($\lambda$) seems to replicate precisely the behaviour observed in the Mountain Car scenario, although now the bigger number of actions renders HA-SARSA($\lambda$) a bit slower than SARSA($\lambda$).

Table 5 Comparison between the results found by linearly approximated SARSA($\lambda$) and the AP-HARL algorithms in the Mountain Car 3D scenario for True Online Traces

Similarly to HA-SARSA($\lambda$), AP-HARL-BACKWARD seems to be very effective in this scenario as it converges in less iterations than SARSA($\lambda$) and it also achieves better results on average and absolute terms. The behaviour of HA-SARSA($\lambda$) and AP-HARL-BACKWARD seems to be very similar, confirming the fact that AP-HARL algorithms can learn an heuristic from the trajectories performed by the agents. This is also further confirmed by the behaviour of HA-SARSA($\lambda$) + Pheromone, which manages to improve the results with respect to HA-SARSA($\lambda$), and is the fastest at computing amongst the heuristic algorithms.

AP-HARL-FORWARD performs similarly to both AP-HARL-BACKWARD and HA-SARSA($\lambda$) in terms of solution found and convergence, but it is 3 to 3.5 times more expensive, computationally speaking, than a standard SARSA($\lambda$). In term of control problems like Mountain Car and Mountain Car 3D, the AP-HARL-BACKWARD strategy seems to be more effective than the AP-HARL-FORWARD strategy as it is less expensive and the difference in solution found is minimal and also a good compromise between trying to engineer by hand a static heuristic and simply using SARSA($\lambda$) without any heuristic function.

4.3 The maze world scenario

This scenario uses randomly generated maze worlds, with 30$\times$30 cells, where the start is in cell [0,0] and the goal is set to be in cell [25,25]. This scenario was selected for illustrative purposes as it allows to visualize the pheromone traces and it gives an intuition concerning AP-HARL algorithms.

Fig. 6

A trajectory learned by an agent after 100 episodes of training

In the maze world an agent has to find the exit in a maze. The agent does not know the maze in advance and the goal is to find the optimal path between the starting point and the exit. In particular an agent can move up, down, left or right, while the environment can have tiles that represent obstacles. The reward is set to be -1 for every tile that is not the goal. A depiction of the environment utilized for the tests is given in Fig. 6.

For this scenario, two tile coding approximations for SARSA($\lambda$) and the pheromone model with 20 tiles per dimension and 10 layers of tiles were used, for all the algorithms considered. All the algorithms considered learn in the environment without knowing the position of the goal, except for the HA-SARSA($\lambda$), that uses the euclidean distance from the goal as the heuristic function, which can be considered as a good heuristic for this scenario. This choice was made for illustrative purposes to understand how AP-HARL algorithms behave with respect to a heuristic providing a lot of information about the environment. HA-SARSA($\lambda$) + Pheromone does not have knowledge of the location of the goal, it only uses the pheromone trace as a static heuristic function. The parameters selected for this environment are reported in Tables 1 and 3.

Fig. 7

Comparison between learning curves for approximated SARSA($\lambda$), HA-SARSA($\lambda$) and AP-HARL algorithms with true online traces in the maze world scenario

Figure 7 shows the convergence behaviour of the examined algorithms with a 95% confidence interval with respect to true online traces. Table 6 shows a comparison of the best results that are found on average by the four algorithms, providing also the 95% confidence interval for each of the results.

Table 6 Comparison between the results found by linearly approximated SARSA($\lambda$) and the AP-HARL algorithms in the maze world scenario

The interesting insight about these results is that, despite having the knowledge about the position of the goal, HA-SARSA($\lambda$) requires more iterations than the AP-HARL counterparts to identify an optimal policy. This happens because, despite the knowledge of the euclidean distance from the goal, the walls in the maze environment work as an obstacle, and therefore the heuristic does not work in complete synergy with the RL algorithm as it makes the agent collide with the obstacles. The AP-HARL algorithms favour short trajectories in states that can be visited by the agent and therefore the agent learns to avoid obstacles faster than HA-SARSA($\lambda$). An illustration of how the pheromone is deposited with the AP-HARL algorithms is shown in Fig. 8.

Fig. 8

Comparison between global only pheromone updates, local pheromone updates and backward strategy, local pheromone updates and forward strategy

AP-HARL-FORWARD tends to be better than AP-HARL-BACKWARD at pure exploration tasks. From the stand point of learning a re-usable heuristic, HA-SARSA($\lambda$) + Pheromone presents again good convergence properties and fast computation times confirming that the heuristic function learned by AP-HARL is of good quality and it can be re-used in HARL algorithms when a heuristic function is not know.

Finally, Fig. 8 shows the importance of introducing local updates of the pheromone score. With local updates the pheromone score quickly distributes on a close to optimal path towards the goal. This allows for a fast convergence to a good solution. The backward and forward strategies seem to achieve the same distribution of pheromone score.

Given the three scenarios considered, it is possible to say that AP-HARL algorithms can handle both control and exploration tasks, but the complexity of AP-HARL-FORWARD makes it more suitable for exploration tasks, whereas AP-HARL-BACKWARD performs better in control tasks. It is also possible to say that AP-HARL algorithms can learn re-usable heuristics of good quality in both control and exploration tasks.

5 Opportunities, further considerations, further tests

This section presents some opportunities stemming from this contribution, but also some additional attempted tests to extend the framework.

5.1 Opportunities

The presented framework has some interesting extension opportunities, amongst which:

• Apply further algorithms from the ACO family: after the definition of the first ACO algorithms, there has been a proliferation of ACO algorithms such as Elitist ACO, defined by Dorigo et al. (1996), and Max-Min ACO. This contribution focused on working with simple pheromone trail transition scores following the basic philosophy of ACO, but there are many other possibilities in this sense.

• Change the concept of trajectory: this contribution considered trajectories as a sequence of states and actions and used the length of the trajectory as the main quality measure. A change of the interpretation of the concept of trajectory may bring further advantages in terms of convergence and quality of the solutions found.

• Change the properties of the pheromone trail transition scores: rather than simply indicating the quality of the solution if a state is accessed, the pheromone trail transition score could give also information concerning the surrounding area.

• Introduce a dynamic $\psi$ threshold based on the pheromone trail transition score: one way to reduce the parameters space is to modify the $\psi$ threshold according to the particular pheromone trail transition score distribution in the local surrounding of a state.

• Summarize trajectories: an unsupervised approach that tries to find common patterns or prototypes amongst the states visited by the trajectories and modify such prototypes periodically may be effective in improving the complexity of the algorithms considered.

• Regress on trajectories: similar to the previous proposition, finding the prototype trajectory that best represent a set of trajectories may improve the complexity of the considered algorithm.

• Consider trajectories from multiple agents: in a collaborative task, utilizing heterogeneous agents trajectories may improve the convergence of the multi-agent reinforcement learning task, similarly to what proposed by Bianchi et al. (2014), but without the burden of modelling a static heuristic.

Some of the above opportunities have been already attempted by the author and the associated results will be reported in future contributions.

5.2 Further considerations and tests

Further considerations can be made concerning the action selection strategy. In Sect. 3 a hard selection strategy has been defined for both the forward and backward views of AP-HARL. A probabilistic selection strategy can also be defined as follows:

$$\begin{aligned} p(x_{old},a_{old}, x, a) =\frac{\hat{\tau }(x_{old},a_{old},x,a)}{\sum _{x \in X_{allowed}, a \in A_{allowed}} \hat{\tau }(x_{old},a_{old},x,a) } \end{aligned}$$

(35)

or as follows using a softmax approach:

$$\begin{aligned} p(x_{old},a_{old}, x, a) =\frac{\exp {\hat{\tau }(x_{old},a_{old},x,a)}}{{\sum _{x \in X_{allowed}, a \in A_{allowed}} \exp {\hat{\tau }(x_{old},a_{old},x,a)}}} \end{aligned}$$

(36)

and then defining the $\pi ^H(x)$ as:

$$\begin{aligned} \pi ^H(x) = a, \text{ with } \text{ probability } p(x_{old},a_{old}, x, a) \end{aligned}$$

(37)

With respect to the probabilistic selection strategy, it can be expect that a softer approach to the selection of the next action to perform may present advantages from the perspective of the quality of the solution found, as they also imply additional informed exploration on the side of the agent. The additional exploration may though imply a longer convergence time. After a set of tests conducted on the soft strategies, they have though been found less performing than their simpler counterpart presented in this contribution. Certainly, finding a way to apply a softer action selection strategy is also an opportunity of development for AP-HARL algorithms and possibly a connection with research happening in deep learning (Silver et al. 2016).

The author has also attempted to link pheromone traces with potential based reward-shaping as presented by Ng et al. (1999) and by Devlin and Kudenko (2012). The main advantage of potential based reward-shaping is that the framework has nice convergence properties and the formulation is easier than the HARL approach, as the $\psi$ and $\eta$ values disappear, in virtue of the fact that it is the reward that becomes dynamic and not the action selection strategy. For this purpose, There is the problem of specifying a potential function that is adequate for reward shaping, for which the following formulation was selected:

$$\begin{aligned} F(x,a) = \rho \theta ^{pT}\phi (x,a,x',a') - \theta ^{pT}\phi (x_{old},a_{old},x,a) \end{aligned}$$

(38)

otherwise stated, the potential has been set to the difference in pheromone concentrations between two transitions. As in the reward-shaping framework, the total reward then becomes:

$$\begin{aligned} R(x,a) = r(x,a) + F(x,a) \end{aligned}$$

(39)

the equations for the local and global pheromone updates were kept the same as in AP-HARL.

Fig. 9

Reward Shaping (RS) applied to Approximated Sarsa($\lambda$), with a backward strategy. Comparison with AP-HARL-BACKWARD and a normal Approximated SARSA($\lambda$) in the Mountain Car Scenario

The same set of tests are in Sect. 4 were attempted using the reward shaping approach, Figure 9 and Table 7 show the comparison between the convergence curves with reward shaping and SARSA($\lambda$) for the Mountain Car scenario. Parameters used for this test were the same as those in Sect. 4, with $\rho =0.99$ for the reward shaping algorithms.

Table 7 SARSA($\lambda$) with static and dynamic pheromone traces and reward shaping

The results highlight that reward shaping does not benefit from the extra information coming from the dynamic pheromone score updates. This happens because in reward shaping the action selection is solely done on the state-action values, which are updated with a MDP process. Following the HARL philosophy, AP-HARL select the actions also through the heuristic function, that encodes the dependency between multiple states through trajectories. When pheromone traces produced by AP-HARL are used as a static heuristic for reward shaping (RS-SARSA($\lambda$) + Pheromone algorithm), an interesting result can be found. This test shows that potential based reward shaping can also accelerate approximated SARSA($\lambda$), with the advantage, with respect to HA-SARSA($\lambda$), of not having $\psi$ and $\eta$ as additional parameters. Given these results, a possible future direction of research includes finding a way to combine potential based reward shaping and AP-HARL solutions and identify the relationship between the two approaches.

6 Related work

In addition to the seminal work of Bianchi et al. (2008) in defining a link between heuristics and RL, it is possible to find an interest in the research literature towards combining RL with optimization algorithms of various sorts: Poli et al. (2007) discuss particle swarm optimization (PSO), Snoek et al. (2012) focus on Bayesian optimization (BO), while Lagoudakis and Parr (2003) work on trajectory optimization (TO) and batch RL. In addition, as discussed by LeCun et al. (2015), research in Deep Learning (DL), has shown how long-short term memory networks (LSTM networks) can efficiently learn sequences of various type, allowing Foerster et al. (2016) to design agents that can learn how to communicate.

Hein et al. (2016) transform the problem of action selection in a PSO problem, providing accurate state-action estimates. As reported by the authors, the main issue of using PSO to identify the best action sequence is its computational complexity. Following the HARL phylosophy, this contribution does not change the underlying RL problem, using a step-wise local/global update of the dynamic heuristic, which allows to keep the computational complexity contained. It could be possible to reformulate the PSO problem of Hein et al. (2016) with a step-wise approach similar to AP-HARL and therefore mitigate the computational complexity issue.

Fonteneau et al. (2013) approach the issue of batch RL by considering the generation of artificial trajectories given a pool of initial trajectories. In their contribution Fonteneau et al. (2013) solve two important problems, that is to define when an artificial trajectory for batch learning guarantees a good performance and how to define sampling strategies to generate new system transitions. For the moment, the author has not attempted to combine AP-HARL with batch RL or least square policy iteration (LSQI), but one possible way to exploit the pheromone trace is to sample system transitions that may have never happened in the learning history of the agent, but that still present a high pheromone score.

A similar approach to AP-HARL is taken by Luo et al. (2017), who combine policy and value iteration to obtain a fast converging value iteration algorithm. To obtain such a result, multiple steps of policy iterations are evaluated and used to speed up value iteration. This approach is quite similar to the one of AP-HARL in which two different types of updates (step wise temporal differences and pheromone updates) are simultaneously used to learn a policy, although AP-HARL approaches never mix the state-action values with the pheromone intensity, whereas Luo et al explicitly use a combination of value iteration and policy iteration. Certainly, finding a relationship between the pheromone distribution and the state-action values could be interesting future research.

Wilson et al. (2014) design a new Gaussian process (GP) kernel on sequential trajectories to estimate the similarity between two policies and therefore apply a policy search approach based on BO. One of the main issues of BO is that often the lack of data limits the quality of the estimations performed, leading to poor results. In this sense, the learned pheromone distribution could help into defining a function to generate new trajectories and therefore improve the results of BO. The learning of heuristic functions is also important towards transfer learning [see the contribution of Weiss et al. (2016) for a survey of transfer learning applied on several domains] in the reinforcement learning domain, as also shown by Bianchi et al. (2015). With little modification, the heuristic function learned with AP-HARL could be simply used as a model for a particular task or problem and then re-used in a related problem.

Finally, concerning DL and communication as discussed by Foerster et al. (2016), an important aspect of this contribution is that, although pheromone was used to build an heuristic representation, the main function of pheromone is to communicate. It may be possible to use mechanisms as stigmergy to specify a language that evolves together with the multi-agent trajectories performed in an environment. DL methods could also be used for sequence learning, remembering that a trajectory is also a sequence, rather than training a tile coding structure, one could train an LSTM network, this would open also the possibility of extracting features from trajectories by using intermediate layers of the neural network, or to define an encoder decoder model to generate new trajectories.

7 Reproducibility

The code of the experimentation has been published in the GITHUB permanent repository at URL https://github.com/SB-BISS/RLACOSarsaLambda. The code is implemented in Python and based on GYM library for reinforcement learning as presented by Brockman et al. (2016).

8 Conclusion and future work

In this paper two approximated SARSA($\lambda$) algorithms belonging to the heuristically accelerated reinforcement learning family were presented. In these algorithms the heuristic function is learned dynamically by means of a process of annotating state-action transitions with a transition score, known as pheromone trail transition score, associated to the quality of the solution. The computational complexity of the approach is linear with respect to the trajectories considered and it does not change the underlying temporal difference learning approach of approximate SARSA($\lambda$). A bound for the heuristic loss of the considered algorithms is also provided, specifying a strategy to set the parameters of the algorithms. The main contribution of the paper resides in the fact that AP-HARL learns dynamically a heuristic function that allows for convergence to a solution in less iterations than a normal SARSA($\lambda$) algorithm. A secondary contribution of the paper, is to show that the learned heuristic functions are of good quality and can be saved and re-used to accelerate other HARL algorithms.

For future work, different schema than the one proposed in this paper will be investigated in addition to the opportunities identified in Sect. 5. In particular, the use of options, similarly to the work of Menache et al. (2002), would be an interesting addition to the AP-HARL algorithms. Another possibility could be to consider different meta-heuristics and then combine RL algorithms with the Artificial Bee Colony algorithm of Karaboga and Ozturk (2011) rather than the ACO algorithm considered in this paper.