Abstract
For polyhedral mass bodies having arbitrary shape and density distribution of polynomial type we present a tensorial approach to derive analytical expressions of the gravitational potential and gravity vector. They are evaluated at an arbitrary point by means of formulas, referred to a Cartesian reference frame having an arbitrary origin, that are shown to be singularity-free whatever is the position of the observation point with respect to the body. The solution is expressed as a sum of algebraic quantities depending solely upon the 3D coordinates of the polyhedron vertices and the coefficients of the polynomial density function. Hence, no recursive expression needs to be invoked as in the recent contribution by Ren et al. (Surv Geophys 41:695–722, 2020). Moreover, the tensorial formalism developed in the paper allows one to obtain more concise, coordinate-free expressions that can also be extended to address polynomial functions of greater order. The analytical expressions of the gravitational potential and gravity vector are numerically validated and compared with alternative methods retrieved from the literature.
Similar content being viewed by others
1 Article Highlights
-
A tensor-based formalism is shown to yield analytical formulas for the gravitational field of polyhedrons having a polynomial density contrast
-
Analytical formulas are provided as function of the 3D coordinates of the vertices of the polyhedron and the parameters of a fourth-order polynomial density contrast
-
Singularity-free formulas for the gravitational potential and gravity vector, referred to an arbitrary position of the observation point, have been implemented in a MATLAB code
2 Introduction
Gravity modeling plays a fundamental role in interpreting gravity data sets that are measured using gravimeters based on land, in boreholes or on board satellite, marine or aircraft vessels and used to estimate locations and shapes of bodies embedded in the earth, see, e.g., Nabighian et al. (2005) for a recent historical account.
In practice gravity data may be inverted, in conjunction with geophysical data sets such as seismic data and electromagnetic induction data (Moorkamp et al. 2011; Aydemir et al. 2014; Roberts et al. 2016), in order to provide more accurate models of the earth.
Recent improvements in gravimeter efficiency and inversion algorithms allow for a wide application of the gravity methods in several geophysical and geodetic problems such as studies addressing Moho and Crustal structure (Van der Meijde et al. 2013; De Castro et al. 2014), mineral exploration (Beiki and Pedersen 2010; Martinez et al. 2013; Abtahi et al. 2016) and geoid determination (Bajracharya and Sideris 2004).
Accordingly, it is of paramount importance to efficiently and accurately approximate the true mass density variations of the earth, e.g., sedimentary basins and bedrock topography, by suitable volume discretization techniques.
To this end several approaches have been exploited over time, both numerical and analytical, and increasing levels of refinement have been adopted for the basic geometric block used to discretize the earth volume (prism, polyhedron, etc.) and for selecting the related density variation (constant, linear, exponential, etc.).
Common to all gravity forward modeling techniques is the evaluation of the so-called Newton’s integrals that can be performed either numerically or analytically, adopting in both strategies either a spatial or a spectral, of Fourier, domain (Kuhn and Seitz 2005).
Numerical strategies approximate the integrals by exploiting, e.g., the finite element method (Cai and Wang 2005; Kaftan et al. 2005), or finite difference methods (Farquharson and Mosher 2009; Jahandari and Farquharson 2013).
Alternatively, the integrand is expanded in terms of harmonic series and the potential harmonic coefficients are evaluated by different techniques (Colombo 1981; Cunningham 1970; Gottlieb 1993; Chao and Rubincam 1989; Balmino 1994; Werner 1997; Jamet and Thomas 2004; Chen et al. 2019; Jamet and Tsoulis 2020).
In the context of numerical methods Newton’s integrals are evaluated in the spectral domain by using Fast Fourier Transform (FFT) or spherical transform algorithms. A brief review of FFT-based algorithms has been provided in Wu (2016; 2018). Subsequently, both 2D and 3D Fourier-domain expressions of gravity effects due to an arbitrary polyhedron with constant or exponential density distributions have been provided in Wu (2019).
Concerning the analytical approach in the spatial domain, closed-form expressions of the integrals have been evaluated, in the case of constant density, in Nagy (1966), Banerjee and Das Gupta (1977), Cady (1980), Nagy et al. (2000), Tsoulis (2000), Jiancheng and Wenbin (2010) and D’Urso (2012), see also Plouff (1975, 1976), Won and Bevis (1987) and Montana et al. (1992) for computer codes.
Analytical expressions of the gravity anomaly for prisms have been derived by D’Urso (2016), for a linearly varying density, by Rao (1985, 1986, 1990), Rao et al. (1994), Gallardo-Delgado et al. (2003) for a quadratic density contrast, by García-Abdeslem (1992, 2005), for a cubic density variation with depth by Fukushima (2018) as well as Zhang and Jiang (2017) for density varying as an arbitrary-order polynomial function. A good collection of earlier references for 3D prisms can be found in Li and Chouteau (1998).
Non-polynomial density contrast models for 3D bodies have been considered by Cordell (1973), Chai and Hinze (1988), Litinsky (1989), Rao et al. (1990), Chakravarthi et al. (2002), Silva et al. (2006), Chakravarthi and Sundararajan (2007), Chappell and Kusznir (2008) and Zhou (2009b) while, for 2D bodies, by Gendzwill (1970), Murthy and Rao (1979), Pan (1989), Guspí (1990), Ruotoistenmäki (1992), Martín-Atienza and García-Abdeslem (1999), Zhang et al. (2001) and Zhou (2008, 2009a, 2010). For more complicated forms of the density contrast, see, e.g., Cai and Wang (2005) and Mostafa (2008).
Besides the case of prisms endowed with complicated functions describing density contrast, research has addressed the case of polyhedrons having complicated density contrast. In this respect analytical formulas for the gravimetric analysis have been contributed by Paul (1974), Barnett (1976), Strakhov (1978), Okabe (1979), Waldvogel (1979), Golizdra (1981), Strakhov et al. (1986), Götze and Lahmeyer (1988), Pohanka (1988), Murthy et al. (1989), Kwok (1991b), Werner (1994), Holstein and Ketteridge (1996), Petrović (1996), Werner and Scheeres (1997), Li and Chouteau (1998), Tsoulis (2012), D’Urso (2013a, 2014a), Conway (2015) and Werner (2017). Subsequent advancements have been only concerned with a linear density variation (Pohanka 1998; Hansen 1999; Holstein 2003; Hamayun et al. 2009; D’Urso 2014b).
Significant advancements in the evaluation of closed-form solutions for the gravitational field and gravitational contrast of polyhedral bodies having a polynomial density function of arbitrary order have been recently contributed by D’Urso and Trotta (2017), extending a similar treatment addressing the gravity anomaly of polygonal bodies D’Urso (2015), and later addressed in Chen et al. (2018) and a series of papers by Ren and coworkers (2017; 2018a; b; 2020).
Remarkably, in the last paper, the authors provide closed-form solutions of the gravitational potential and the gravitational field that are singularity-free, an issue previously discussed in Kwok (1991a), for prism-based modeling, and Tsoulis and Petrović (2001) for polyhedra.
The methodology outlined in D’Urso and Trotta (2017) is further generalized in order to derive an analytical expression of the gravitational potential and gravitational vector for polyhedral bodies having density contrast expressed as a polynomial function of arbitrary degree. The result is obtained by a version of the generalized Gauss theorem that extends to tensors of arbitrary order the result first presented in D’Urso (2012, 2013a), and subsequently applied to several problems ranging from geodesy (D’Urso 2014a, b; D’Urso and Trotta 2015; D’Urso 2016), to geomechanics (D’Urso and Marmo 2009; Sessa and D’Urso 2013; D’Urso and Marmo 2015), to geophysics (D’Urso and Marmo 2013), elasticity (Marmo and Rosati 2016; Marmo et al. 2016a, b, 2017, 2018; Trotta et al. 2016a, b, 2018) and to heat transfer (Rosati and Marmo 2014).
Specifically, the volume integral of quantities expressed as tensor products of suitable vectors is first reduced to a 2D boundary integral and subsequently written as a finite sum of 2D integrals extended to the faces of the polyhedral body \(\varOmega \). By a further application of the generalized Gauss theorem, each face integral is reduced to the sum of 1D integrals, extended to the edges of the face, that are analytically evaluated.
Due to space limitations the tensorial formalism developed in this paper is explicitly illustrated only for polynomial functions up to the fourth-order but it can be easily adapted to functions of greater order by suitably exploiting the general approach outlined in the paper. This leads to algebraic expressions of the gravitational potential and the gravity vector that are shown to be well-defined and singularity-free whatever is the position of the observation point with respect to \( \varOmega \).
The paper is organized as follows. Section 2 sets the stage for the formalism adopted in the paper by making reference to concepts and methods of tensor analysis briefly presented in Appendix A.
The gravitational potential of a polyhedral body, endowed with a polynomial density function of fourth-order as a maximum, is elaborated upon in Sect. 2.1 where Gauss’ theorem is used to provide the expression of the potential in terms of integrals extended to the boundary of the target. Being the body polyhedral such integrals are expressed in Sect. 2.2 as 2D integrals extended to each face of the target. Based on results of tensor analysis, detailed in Appendix B, and a further application of Gauss’ theorem the 2D integrals extended to each face are expressed in Sect. 2.3 in terms of 1D integrals over each edge of the generic face.
Subsequently, in Sect. 2.4, the 1D integrals are transformed into algebraic expressions, invoking the results presented in Appendix C, that depend upon the 2D coordinates of the vertices of the face expressed in a reference frame local to the face. The singularity-free nature of the final expression is proved in Sect. 2.5.
Basically the same path of reasoning is adopted for the gravity vector in Sects. 3.1–3.5. Section 4 shows how to express the algebraic expressions of the gravitational potential and gravity vector in terms of the 3D coordinates of the vertices of the polyhedron, while Sect. 5 is devoted to the numerical validation of the proposed approach.
Specifically, Sect. 5.1 includes a comparison with similar results presented in the literature. Sect. 5.2 shows the results of some numerical tests carried out to assess the rounding error sensitivity of the analytical formulas derived in the paper with respect to the dimensionless target distance (Holstein and Ketteridge 1996). Furthermore Sect. 5.3 validates the proposed tensorial approach by proving that the results of the formulas presented in the paper hold true irrespective of arbitrary rotations of the observation point and the target body that leave unaltered their mutual position.
Finally, the Conclusions in Sect. 6 summarize the main findings of the paper and highlight the future developments of the research.
3 Gravitational Potential of a Polyhedral Body Having a Polynomial Density
Let us consider a Cartesian reference frame having origin at an arbitrary point O and a polyhedral body \(\varOmega \) whose continuum mass distribution is assumed to have a density \( \delta (\textbf{s})\) varying as a polynomial function of the position vector \( \textbf{s}= (x,y,z)\) of an arbitrary point belonging to it:
In the above formula, the constants \( c_{ijk} \) with non-negative suffixes i, j, k are taken as known coefficients of the assumed polynomial density law while N represents the maximum power of the polynomial density function. We shall confine the treatment to the case \( N {\le } 4 \) since this will suffice to address the majority of the practical applications and, at the same time, to present our formulation with a sufficient degree of generality to deduce the cases \(N > 4\).
More explicitly, for \(N = 4\), Eq. (1) becomes
Denoting by \(\textbf{p}\) the position vector of an arbitrary point P, the gravitational potential U induced at P by the mass of \(\varOmega \) is expressed as
where G is the gravitational constant and the function \(\delta \) is given by (1).
In order to simplify the previous expression it is convenient to introduce the relative position \( \textbf{r}=\textbf{s}-\textbf{p}\) of an arbitrary point of \(\varOmega \) with respect to \( \textbf{p}\), see, e.g., Fig. 1. Accordingly, we express the function \(\delta \) as follows
where \( \delta _o = c_{000} \) is the density at \( \textbf{s}=\textbf{o}\), i.e., at the origin of the reference frame, \( \mathcal {D}_{\textbf{s}}^{(1)}=\textbf{s}\) while \( \mathcal {D}_{\textbf{s}}^{(2)} \), \( \mathcal {D}_{\textbf{s}}^{(3)} \) and \( \mathcal {D}_{\textbf{s}}^{(4)} \) are defined in the formulas (204), (207) and (210), respectively, of Appendix A. Matrix representation of \( \mathcal {C}^{(1)} \), \( \mathcal {C}^{(2)} \), \( \mathcal {C}^{(3)} \) and \( \mathcal {C}^{(4)} \) is provided in the formulas (229) and (232) while the dot product between tensors is defined in formula (227).
In conclusion, setting \( \textbf{r}=\textbf{s}-\textbf{p}\) in (3) and exploiting (4) the gravitational potential of a polyhedral body \(\varOmega \) whose density varies as in (1) is given by
where \( U^{(k)}(\textbf{p}) \) denotes the contribution to the gravitational potential associated with the k-th power of the polynomial law representing the density variation.
In order to actually compute the gravitational potential in (5) we notice that the statement of \( U^{(0)}(\textbf{p}) \) is elementary
since it amounts to consider a polyhedron of constant density; on the contrary, the evaluation of the additional terms \( U^{(i)}(\textbf{p}) \) in (5), \( i\in [1,4] \), requires further manipulations. Actually, recalling the definition of \( \mathcal {D}^{(i)}_{\textbf{s}} \), provided in (204), (207) and (210), for i = 2, 3 and 4, respectively, one has to consider tensors in which some of the building blocks require some integration.
To set the stage, let us first consider the trivial case \( i =1 \)
Hence, setting
where
one has
Accordingly, recalling (204), we can set:
Similarly, on account of (207), (208) and (209) one has
where the meaning of the symbol \(\otimes _{132}\) is detailed in Appendix A.
Finally, based on (210), (211), (212) and (213), it turns out to be
where
the symbol \(\otimes _{1243}\) and the analogous ones being specified in Appendix A.
3.1 Analytical Expression of the Gravitational Potential (GP) in Terms of 2D Integrals
It is apparent from the previous formulas that the only real burden required to compute the generic addend \( U^{(i)}(\textbf{p}) \) is that associated with the evaluation of the integrals \( \mathcal {R}_{\varOmega }^{(m, 1/2)} \) in (8). This has already been done in D’Urso (2013a), for \( m=0 \) and \( m=1 \).
However, to illustrate a more general approach, we prove the following preliminary result
where \(\textbf{n}\) is the 3D outward unit normal to the boundary \( \partial \varOmega \) of the polyhedral body.
To fix the ideas, we shall prove the identity (18) for \(m=2\)
since it allows us to illustrate our approach to a degree of generality sufficient to extend the final result to all integrals in (18).
Recalling the differential identity (255) reported in Appendix B it turns out to be
Applying the further identity (250) one has \( \text {grad}\,(\textbf{r}\cdot \textbf{r})=2\, \textbf{r}\) since \(\text {grad}\,\textbf{r}=\mathcal {I}^{(2)}\), being \(\mathcal {I}^{(2)}\) the rank-two identity tensor. Hence, formula (20) becomes
Finally, integrating the previous identity over \(\varOmega \) yields
The second integral on the right-hand side can be computed by means of the general result Tang (2006)
where \(\varphi \) is a continuous scalar field and the quantity \(\alpha \) represents the angular measure, expressed in steradians, of the intersection between \(\varOmega \) and a spherical neighborhood of the singularity point \(\textbf{r}=\textbf{o}\), see, e.g., D’Urso (2012, 2013a, 2014a) for additional details. The previous expression can be extended to arbitrary tensors by applying it to each scalar component of the tensor.
On account of (23) one infers that the second integral on the right-hand side of (22) is the null rank-two tensor \(\textbf{O}\) since
However, the expression \([(\textbf{r}\cdot \textbf{r})(\textbf{r}\otimes \textbf{r})]_{\textbf{r}=\textbf{o}}\) amounts to evaluating the quantity \((\textbf{r}\cdot \textbf{r})(\textbf{r}\otimes \textbf{r})\) at the singularity point \(\textbf{r}=\textbf{o}\), that yields trivially the null tensor \(\textbf{O}\). Hence, according to (24), the last integral in (22) is always the null tensor, independently of the position of singularity point \(\textbf{r}=\textbf{o}\) with respect to the domain \(\varOmega \) of integration.
Upon application of Gauss’ theorem to the second integral in (22), we finally infer the identity (19), according to which the singularity at \(\textbf{r}=\textbf{o}\) of the integrand function appearing on the left-hand side, can be actually ignored. Furthermore, it is not difficult to rephrase the path of reasoning detailed in formulas (20–24) so as to prove the more general formula (18).
In conclusion, we have proved that the expression (5) of the gravitational potential is well-defined whatever is the order of the polynomial law expressing the density variation of \(\varOmega \) in the sense that it exhibits no singularity whatever is the position of the point \( \textbf{p}\) with respect to \(\varOmega \). It should be mentioned, however, that the algebraic counterparts of the integrals (18) do contain further singularities; nevertheless, it will be proved in Sect. 2.5 that such singularities are removable. They can be made ineffective from a computational point of view provided that the above-mentioned algebraic expressions are suitably programmed.
To actually compute the generic addend \( U^{(i)}(\textbf{p}) \) in (5) we exploit formula (18) to express the generic integral \( \mathcal {R}_{\varOmega }^{(m,1/2)} \) in (5) by means of boundary integrals
However, the previous expressions, and hence those expressing \( U^{(i)}(\textbf{p}) \), can be further elaborated upon to transform 2D integrals to 1D integrals.
3.2 Analytical Expression of the GP in Terms of Face Integrals
In order to derive an expression suitable for programming, we specialize formula (25) to polyhedral domains since this is by far the most general case for practical applications.
For a polyhedral body characterized by \(N_F\) faces, the generic integral in (25) can be written as
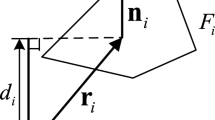
where \( \textbf{r}_i \) represents the generic vector spanning the i-th face \( F_i \) of \(\varOmega \) and \( \textbf{n}_i \) the unit vector, orthogonal to \( F_i \), pointing outwards \( \varOmega \). However the previous integrals can be further simplified as follows
where \( d_i=\textbf{r}_i\cdot \textbf{n}_i=\textbf{r}^{\perp }_i\cdot \textbf{n}_i \).
The 2D integrals above can be transformed to a line integral by a further application of Gauss’ theorem. To this end we denote by \(O_i\) the orthogonal projection on \(F_i\) of the observation point P and assume \(O_i\) as origin of a 2D reference frame local to the face.
Furthermore, we express \( \textbf{r}_i \) as
where the vector \({\varvec{\rho }}_i=(\xi _i,\eta _i)\) represents the position vector of a generic point of the i-th face with respect to \(O_i\) and
is the linear operator mapping the 2D vector \({\varvec{\rho }}_i\) to the 3D one \(\textbf{r}_i^\parallel \). In turn \(\textbf{u}_i\) and \(\textbf{v}_i\) represent two distinct, yet arbitrary, 3D unit vectors coplanar with \(F_i\).
Accordingly, being \( \textbf{r}_i \cdot \textbf{r}_i ={\varvec{\rho }}_i \cdot {\varvec{\rho }}_i +d^{2}_i \), we are thus led to computing the following integrals
where we have introduced the symbol
To simplify the following expressions we further introduce the formal operator \(\mathbb {T}_{F_i}^{(m)}\) that transforms a rank-m tensor of order 2 to the corresponding rank-m tensor of order 3. Notice that, being the definite integral a kind of sum, the operator \(\mathbb {T}_{F_i}^{(m)}\) and the integral sign can be interchanged. For instance, observing that \(\mathbb {T}_{F_i}^{(1)}=\textbf{T}_{F_i}\), one has
so that (32) can also be written as
Hence
and
where
In conclusion, recalling (5), the expression of \( U^{(i)}(\textbf{p}) \) reported in (6), (10), (11), (12) and (13), as well as that of \( \mathcal {R}_{\partial \varOmega }^{(m, 1/2)} \) in (26), we are finally led to compute the 2D integrals in (33). This will be addressed in the following subsections.
3.3 Analytical Expression of Face Integrals Related to the GP in Terms of 1D Integrals
It has been shown in the previous subsections that the actual evaluation of the gravitational potential in (5) ultimately amounts to evaluating the 2D integrals (33). However, they can be computed by simpler 1D integrals invoking once more the generalized Gauss theorem Tang (2006). As a matter of fact this has already been done for \( m=0 \) and \( m=1 \) in previous papers D’Urso (2013a, 2014a, 2014b); for \( m>1 \) it has been carried out in Appendix B.
For the sake of clarity the expressions of the integral (33) are reported in the sequel for increasing values of m while the relevant proofs, as well as the related notation, is detailed in Appendix B.
To help the reader fully grasp the notation used with forthcoming formulas we also introduce the following notation
and
where \(\nu _i \) represents the 2D vector belonging to the face and normal to the edge.
Some of the previous quantities will be also combined to produce expressions that will be tensorially multiplied by the rank-two tensor \( \mathcal {I}^{(2)} \). For this reason we also introduce the following symbols
where
By means of the previous notation we can set
-
Integral (33) for \( m=0 \), see, e.g., formula (20) in D’Urso (2013a)
$$\begin{aligned} \displaystyle \textrm{P}_{F_i}^{(0,1/2)}=\displaystyle \int \limits _{F_i} \frac{\textrm{d}A_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{1/2}}=\displaystyle \textrm{P}_{\partial F_i}^{[(1/2)1\cdot ,1]}-\alpha _i |d_i|{.} \end{aligned}$$(47) -
Integral (33) for \( m=1 \), see, e.g., formula (19) in D’Urso (2014b)
$$\begin{aligned} \textrm{P}_{F_i}^{(1,1/2)}= & {} \displaystyle \int \limits _{F_i} \frac{{\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{1/2}}\textrm{d}A_i =\displaystyle \int \limits _{\partial F_i} \Bigl [{\varvec{\rho }}_i(s_i)\cdot {\varvec{\rho }}_i(s_i)+d_i^2\Bigr ]^{1/2}\,{\varvec{\nu }}_i(s_i)\,\textrm{d}s_i \nonumber \\= & {} \displaystyle \textrm{P}_{\partial F_i}^{[(1/2) \, 0]}{.} \end{aligned}$$(48) -
Integral (33) for \( m=2 \), on account of formula (266) in Appendix B
$$\begin{aligned} \textrm{P}_{F_i}^{(2,1/2)}=\int \limits _{F_i} \frac{{\varvec{\rho }}_i \otimes {\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{1/2}}\textrm{d}A_i =\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}-\frac{\mathcal {I}^{(2)}}{3}\,\textrm{P}_{\partial F_i}^{0 \, \mathcal {I}}{.} \end{aligned}$$(49) -
Integral (33) for \( m=3 \), on account of formula (272) in Appendix B.
$$\begin{aligned} \textrm{P}_{F_i}^{(3,1/2)}=\int \limits _{F_i} \frac{{\varvec{\rho }}_i \otimes {\varvec{\rho }}_i\otimes {\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{1/2}}\textrm{d}A_i=\textrm{P}_{\partial F_i}^{[(1/2)2\otimes ]}- \frac{1}{4}\Biggl [\mathcal {I}^{(2)}\otimes _{132} \textrm{P}_{\partial F_i}^{1\,\mathcal {I}}+\textrm{P}_{\partial F_i}^{1\,\mathcal {I}}\otimes \mathcal {I}^{(2)}\Biggr ]{.} \nonumber \\ \end{aligned}$$(50) -
Integral (33) for \( m=4 \), on account of formula (278) in Appendix B.
Recalling the definition (45) for \(\textrm{P}_{\partial F_i}^{2\,\mathcal {I}}\),we get
Accordingly, all integrals in (33) have been evaluated by means of boundary integrals.
3.4 Algebraic Expression of Face Integrals Related to the GP in Terms of 2D Vectors
At this stage of the formulation we have expressed the domain integrals \( \mathcal {R}_{F_i}^{(m,1/2)} \), \( m= 1,..., 4 \), appearing in the expression (5) of the potential as function of integrals \( \mathcal {R}_{\partial \varOmega }^{(m,1/2)} \) extended to the boundary \(\partial \varOmega \) by means of formula (25).
In turn each of the integral \( \mathcal {R}_{\partial \varOmega }^{(m,1/2)} \), extended to the face \( F_i \) of \(\partial \varOmega \) for a polyhedral body, has been expressed as function of the 2D integrals \( \mathcal {R}_{ F_i}^{(m,1/2)}\), see, e. g., formula (27), and each of them further specialized to the expressions (32), (36) and (37) depending upon the integrals \( \textrm{P}_{ F_i}^{(m,1/2)}\) introduced in formula (33).
Finally, the 2D integrals \( \textrm{P}_{ F_i}^{(m,1/2)}\) have been converted to 1D integrals by exploiting formulas (47), (48), (49), (50) and (51) detailed above.
Hence our next step is to express the boundary integrals in formulas (42–46) as sums extended to the \( N_{E_i} \) edges defining the boundary \(\partial F_i\). Actually, a suitable parameterization of the j-th edge of \(\partial F_i\) allows us to transform each 1D integral to an integral of a real variable scaled by a suitable combination of the vectors \({\varvec{\rho }}_j\) and \({\varvec{\rho }}_{j+1}\) that define the position vectors of the end vertices of the edge in the 2D reference frame local to \(F_i\).
In particular we set
where the function \(\hat{{\varvec{\rho }}_i}\) associates the position vector spanning the j-th edge with each value of the adimensional abscissa
The quantity \(s_j\), \(s_j\in [0,\;l_j]\), is the curvilinear abscissa along the j-th edge and \(l_j = |{\varvec{\rho }}_{j+1}-{\varvec{\rho }}_j|\) is the edge length. The position vector spanning the j-th edge of \(F_i\) can also be expressed as function of \(s_j\) and a new function \({\varvec{\rho }}_i\), fulfilling the condition \({\varvec{\rho }}_i(s_i)=\hat{{\varvec{\rho }}}_i(\lambda _j)\). Hence
where, according to (52)
Furthermore
where \(v_j=u_j+d_i^2\). We shall also set \(P_v(\lambda _j)=P_u(\lambda _j)+d_i^2\).
We shall also express the outward unit normal \({\varvec{\nu }}_j\) to the j\(-th \) edge, normal contained within the face \( F_i \), according to the formula
where the symbol \((\cdot )^\perp \) denotes a clockwise rotation of the 2D vector \((\cdot )\) with respect to the normal to \( F_i \).
In turn such a clockwise rotation depends on the convention adopted to circulate along the boundary \(\partial F_i\). In particular, we have assumed that the vertices of each face have been numbered consecutively by circulating along \(\partial F_i\) in a counter-clockwise sense with respect to the unit outward normal \(\textbf{n}_i\) to the face. Thus
In conclusion one can write for the integral in (46)
where the expression of the definite integral \( I_j ^{(1/2\cdot 0,1)} \) is detailed in the formula (282) of Appendix C.
Analogously, with reference to the integral in (43)\(_1\), one has
see, e.g., formula (283) of Appendix C, while the integral (44)\(_1\) by
hence that one has
the quantities \( I_j ^{(1/2\cdot 0)} \) and \( I_j ^{(1/2\cdot 1)} \) being detailed in formulas (283) and (284) of Appendix C, respectively. Notice that the additional boundary integral appearing in formula (43)\( _2 \) is simply the trace (tr) of the previous expression; hence one has
since tr\((\varDelta {\varvec{\rho }}_j\otimes \varDelta {\varvec{\rho }}_j^{\perp })=\varDelta {\varvec{\rho }}_j\cdot \varDelta {\varvec{\rho }}_j^{\perp }\).
To simplify the ensuing developments we introduce the following notation
where
and
being
Accordingly, we can set for the integral (44)\( _2 \)
where \( I_j ^{(1/2\cdot 0)}\), \( I_j ^{(1/2\cdot 1)}\) and \( I_j ^{(1/2\cdot 2)}\) are given by the formulas (283), (284) and (285) of Appendix C, respectively.
The integral \(\textrm{P}_{\partial F_i}^{[(1/2)\,2\cdot ]}\) in (43)\( _3 \) can be computed as follows:
while \(\textrm{P}_{\partial F_i}^{[(1/2)\,3\cdot ]}\) is given by
Finally, we need to compute the integral in(44)\( _3 \)
where \( I_j ^{(1/2\cdot 3)}\) is given by the formulas (286).
In conclusion, all the integrals in (43), (44) and (46), and hence in (45) and (47–51), can be explicitly computed as combination of scalar quantities multiplied by suitable tensor products of \( {\varvec{\rho }}_j \), \( \varDelta {\varvec{\rho }}_j \) and \( \varDelta {\varvec{\rho }}_j^{\perp } \).
3.5 Removable Singularities of the Algebraic Expressions of the Gravity Potential
It is already been shown that the analytical expression (5) of the gravity potential is obtained as sum of the integrals \( \mathcal {R}_{F_i}^{(m,1/2)} \), defined in (26), that are singularity-free whatever is the position of the observation point P with respect to \( \varOmega \).
However, the algebraic counterparts of the integrals \( \mathcal {R}_{F_i}^{(m,1/2)} \), expressed as function of the line integrals \( \textrm{P}_{\partial F_i} \) defined in the formulas (43–51) and of the relevant algebraic expressions reported in the previous section, do include further singularities.
They are associated with the expression of the line integrals \( I_j\) reported in Appendix C since they can become singular when the generic \( F_i \) of the boundary \(\partial \varOmega \) contains the observation point or the projection of the observation point \( F_i \) belongs to the line containing the j-th edge of the boundary \( \partial F_i \).
However, it will be proved that the contribution of the singular line integral vanishes in the computation of the associated domain integral. Hence, the singularity of the j-th line integral pertaining to a generic face \( F_i \) does not have any harmful effect.
To prove the results of interest we shall set
where \( p_j \), \( q_j \) and \( u_j \) have been defined in formula (55), and
whose positive value is consequence of the Cauchy-Schwartz inequality (Tang 2006).
To show which are the line integrals that can become singular we indicate in the sequel the set of formulas required to compute each integral \( \mathcal {R}_{F_i}^{(m,1/2)} \), \( m= 0,..., 4 \), by concisely reporting the sequence to be used. For instance
meaning that the computation of \( \mathcal {R}_{F_i}^{(0,1/2)} \) requires the evaluation of the integrals \( I_j^{(1/2\cdot 0,1)} \), expressed in the formula (282), over the edges of \( \partial F_i \).
Analogously
meaning that the integral \( I_j^{(1/2\cdot 0)} \) in the formula (283) needs to be computed in addition to \( I_j^{(1/2\cdot 0,1)} \). This is a general rule in the sense the computation of the integral \( \mathcal {R}_{F_i}^{(m+1,1/2)} \) requires to evaluate an additional integral with respect to those associated with \( \mathcal {R}_{F_i}^{(m,1/2)} \). Actually
requires to compute \( I_j^{(1/2\cdot 1)} \) in addition to \( I_j^{(1/2\cdot 0,1)} \) and \( I_j^{(1/2\cdot 0)} \).
Furthermore
requires the extra calculation of \( I_j^{(1/2\cdot 2)} \) while for
the evaluation of \( I_j^{(1/2\cdot 3)} \) is also needed.
In conclusion the computation of the integrals \( \mathcal {R}_{F_i}^{(m,1/2)} \), \( m= 0,..., 4 \), requires the evaluation of the five integrals \( I_j^{(1/2\cdot 0,1)} \), \( I_j^{(1/2\cdot 0)} \), \( I_j^{(1/2\cdot 1)} \), \( I_j^{(1/2\cdot 2)} \) and \( I_j^{(1/2\cdot 3)} \). They can become singular when the projection of P over the face is a such that \({\varvec{\rho }}_j=0\) or \({\varvec{\rho }}_{j+1}=0\) or belongs to the segment [\(\,{\varvec{\rho }}_j, {\varvec{\rho }}_{j+1}\)]. For what concerns \( I_j^{(1/2\cdot 0,1)} \) this may happen independently from the value of \( d_i \), i.e., whether or not the i-th face \( F_i \) does contain the observation point. Conversely, the additional four integrals are always well defined if \( d_i\ne 0 \).
The singularity-free nature of \( I_j^{(1/2\cdot 0,1)} \) and \( I_j^{(1/2\cdot 0)} \) has been proved in Sections 4.1 and 4.2 of D’Urso and Trotta (2017) which the interested reader is referred to.
To prove the well-posedness of the additional three integrals we exploit the expression
reported in formula (73) of D’Urso (2014b), where \( \textbf{r}_j \) and \( \textbf{r}_{j+1} \) are defined in (72). Actually, according to (72), \( LN_j \) is always well defined when \( d_i\ne 0 \) independently of the values of \({\varvec{\rho }}_i\) and \({\varvec{\rho }}_{i+1}\) since both the numerator and denominator are the algebraic counterparts of positive integrands.
Conversely, should it be \( d_i=0 \) and \({\varvec{\rho }}_j=\textbf{o}\) or \({\varvec{\rho }}_{j+1}=\textbf{o}\) or \({\varvec{\rho }}_{j+1}=\beta _j {\varvec{\rho }}_j \,\,(\beta _j<0)\), \( LN_j \) becomes indefinite. However, its evaluation can be skipped since \( LN_j \) is scaled by coefficients that tend to zero with a greater order. Actually, the last addend of formula (284) for \( I_j^{(1/2\cdot 1)} \) reads
Hence, if \({\varvec{\rho }}_j=\textbf{o}\) or \({\varvec{\rho }}_{j+1}=\textbf{o}\) or \({\varvec{\rho }}_{j+1}=\beta _j {\varvec{\rho }}_j \,\,(\beta _j<0)\), \(\varDelta _j\) tends to zero quadratically while \( LN_j \) tends to infinity with an arbitrary low degree. Stated equivalently, the contribution of the addend including \( LN_j \) can be ignored.
Exactly the same does occur for the last addend of formula (285) for \( I_j^{(1/2\cdot 2)} \)
in which the coefficient of \( LN_j \) can tend to zero with a degree equal at least to two.
For what concerns the last addend of the formula (286) for \( I_j^{(1/2\cdot 3)} \) it turns out to be
so that, also in this case, the coefficient scaling \( LN_j \) can tend to zero with a degree not less than two.
In conclusion, edges characterized by singularity of \( LN_j \) can be actually skipped in the computation of the relevant integral.
4 Gravity Vector of Polyhedral Body Having a Polynomial Density
The gravity vector, i.e., the derivative of the gravitational potential, is obtained by differentiating the expression (5) with respect to \( \textbf{p}\).
It has been proved by Kellogg (1929) that the potential U and its gradient exist and are continuous whatever is the position of the point P with respect to \(\varOmega \) provided that the density \(\delta \) is continuous and \(\varOmega \) is bounded; these properties are certainly fulfilled since \(\delta \) is polynomial and \(\varOmega \) is polyhedral. Hence the derivative can be moved inside the integral so that, being \( \textrm{d}_{\textbf{p}}=-\textrm{d}_{\textbf{r}} \), we can write
where \( \mathcal {D}_{\textbf{s}}^{(1)}=\textbf{s}\) and the symbols \( \mathcal {D}_{\textbf{s}}^{(k)}\), \( k=2, 3, 4\), have been defined in (204), (207) and (210).
At this stage two different approaches can be exploited for the computation of \( \textrm{d}_{\textbf{p}}U(\textbf{p}) \), each one having pros and cons. The first one amounts to performing the derivatives on the right-hand side of the previous formula and allows one to prove, by following a path of reasoning detailed in Sect. 5.1, that the gravity vector of a polyhedral body endowed with a polynomial density is non-singular whatever is the position of the observation point.
Such an approach leads to particularly compact expressions although it requires a significant amount of mathematical manipulations and the necessity of computing further 2D integrals with respect to those required for the computation of the potential.
The second approach for evaluating the gravity vector is to apply a further variant of the Gauss theorem to the first integral in formula (84) so as to directly obtain boundary integrals. This approach leads to formulas containing a greater number of addends with respect to the ones associated with the first approach but include most of the integrals that are required for the computation of the potential.
Space limitations do not allow us to show the formulas associated with the second approach; hence, an answer on which is the most convenient approach to be adopted will be given in a forthcoming paper on the basis of numerical experiments and of theoretical considerations since the second approach considerably simplifies the computation of second and higher-order derivatives of the potential.
In conclusion, in this paper we shall limit ourselves to adopt the first approach and we proceed to evaluate the derivatives in (84) on the basis of the expressions of \(U^{(k)}\), k=0,...,4, detailed in (6), (7), (11), (12) and (13), respectively. In turn, this requires the preliminary evaluation of \(\textrm{d}_{\textbf{p}}\mathcal {R}_{\varOmega }^{(m,1/2)}\) where this last symbol has been defined in (8).
Introducing the additional symbol
and exploiting the differential identities (252) - (257) one has
Finally, to evaluate the contributions \(\textrm{d}_{\textbf{p}}U^{(k)}(\textbf{p})\), k=0,...,4, we need the following identity, holding for \( m\ge 1 \)
according to which the vector field resulting from the differentiation of the scalar field \(\mathcal {A}^{(m)}\cdot \mathcal {B}^{(m)}\) is obtained by contracting in the product \(\cdot _{1,\ldots ,m} \) the first m indices of the rank \( m+1 \) tensor on the left (right) with the m indices of the rank m tensor on the right (left). The previous formula is extended to the case \( m=0 \) by using the identity (250). In conclusion we have from formula (6)
from formula (10),
from formula (11),
from formula (12)
and, finally, from formula (13)
where
It is worth emphasizing that the derivation of the formulas (95) and (96) is far from trivial and the reader should not be cheated by the fact that \(\textrm{d}_{\textbf{p}}U^{(3)}\) \((\textrm{d}_{\textbf{p}}U^{(4)})\) contains the same number of terms as \(U^{(3)}\) \((U^{(4)})\). Actually the eight (sixteen) terms in \(\textrm{d}_{\textbf{p}}U^{(3)}\) \((\textrm{d}_{\textbf{p}}U^{(4)})\) obtained during the differentiation result from the cancellation of 24 (64) addends of formulas (12) and (13), whose expressions originally contained 32 and 80 addends, respectively.
For this reason, in order to the help the interested reader to trace back the manipulations required to get the final expressions (95) and (96), we also report their counterparts expressed in terms of components
where
In particular the component expressions are useful for programming.
4.1 Analytical Expression of the Gravity Vector (GV) in Terms of 2D Integrals
In order to evaluate the generic \(\textrm{d}_{\textbf{p}}U^{(k)})\) we need to analytically compute the integrals in \(\mathcal {R}_{\varOmega }^{(m,\, 3/2)}\) (85). This has already been done in D’Urso (2014b) for \( m=0 \) and \( m=1 \) by means of an approach based on the use of the following formula
where \( \textbf{n}\) is the 3D outward unit normal to the boundary \( \partial \varOmega \) of the polyhedral body.
Proof of the above formula is based on the identity
a result that can be obtained by adopting an approach similar to that leading to (20).
Integrating the previous identity over \( \varOmega \) one has
leading to formula (107), since the second integral on the right-hand side vanishes on account of (24) applied componentwise to each entry of the tensors \( [\otimes \textbf{r},m] \). In particular, formula (109) allows us to prove that the integrals \(\mathcal {R}_{\varOmega }^{(m,\, 3/2)}\) are well defined, for each m, independently from the position of the point \( \textbf{r}=\textbf{o}\) with respect to \( \varOmega \).
Hence we can write, for \(m\ge 1 \),
by obtaining expressions that are well defined whatever is the position of the observation point with respect to \( \varOmega \).
4.2 Analytical Expression of the GV in Terms of Face Integrals
Let us now specialize formula (110) to the significant case of a polyhedral domain by writing
where, as in (26), \( \textbf{r}_i \) represents the generic vector spanning the i-th face \( F_i \) of \( \varOmega \), \( \textbf{n}_i \) the unit vector orthogonal to \( F_i \), pointing outwards \( \varOmega \) and \( d_i=\textbf{r}_i\cdot \textbf{n}_i\).
To compute \( \mathcal {R}_{F_{i}}^{(m,3/2)} \) we follow a procedure analogous to that adopted for \(\mathcal {R}_{F_{i}}^{(m,1/2)}\). Thus, recalling also the decomposition (28) we have
where we have introduced the symbol
analogous to that introduced in formula (33).
Furthermore, using the terminology introduced in Sect. 2.2, we have
and
where
To derive the formula relevant to \(\mathcal {R}_{F_i}^{(5,3/2)}\) we need to extend the terminology introduced in Appendix A to the fifth-order tensors obtained by combining two vectors. Namely we shall set
Please notice that the order of the elements in the six groups of fifth-order tensors above is not casual. Actually, grouping the six tensors in three groups of complementary tensors, e.g., \(\mathcal {D}^{(5)}_{\textbf{n}_i\textbf{n}_i\textbf{n}_i{\varvec{\rho }}_i{\varvec{\rho }}_i} \) and \(\mathcal {D}^{(5)}_{{\varvec{\rho }}_i{\varvec{\rho }}_i{\varvec{\rho }}_i\textbf{n}_i\textbf{n}_i} \), the k-th element of the first tensor in each group is obtained from the \((N-k)\)-th element of the complementary tensor, N being the total number of elements in each tensor, by exchanging \(\textbf{n}_i\) and \({\varvec{\rho }}_i\).
According to the general rule illustrated above, we finally have
where
In conclusion, replacing formulas (112), (114), (115), (116) and (127) in (92), (93), (94), (95) and (96), we realize that the computation of \(\textrm{d}_{\textbf{p}} U^{(k)}\) amounts to evaluating the 2D integrals (113), an issue addressed in the following subsection.
4.3 Analytical Expression of Face Integrals Related to the GV in Terms of 1D Integrals
The 2D integrals (113) required to evaluated the gravity vector in formulas (92), (93), (94), (95) and (96) can be further simplified by using the generalized Gauss theorem (Tang 2006) and transforming them to simpler 1D integrals. This has already been done for \( m=0, 1, 2 \) in D’Urso (2014b) and D’Urso and Trotta (2017); the additional formulas required in the cases \( m=3, 4, 5 \) are reported in Appendix D. They make use of the following additional notation
For the reader’s convenience the formulas expressing the integrals (113) as function of boundary integrals are reported in the sequel
-
Integral (113), for \( m=0 \), see, e.g., formula (37) of D’Urso (2014b)
$$\begin{aligned} \displaystyle \textrm{P}_{F_i}^{(0,3/2)}=\int \limits _{F_i} \frac{\textrm{d}A_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{3/2}}=\frac{\alpha _i}{|d_i|}-\textrm{P}_{\partial F_i}^{[1\cdot , 1(1/2)]}{.} \end{aligned}$$(139) -
Integral (113), for \( m=1 \), see, e.g., formula (38) of D’Urso (2014b)
$$\begin{aligned} \displaystyle \textrm{P}_{F_i}^{(1,3/2)}= & {} \int \limits _{F_i} \frac{{\varvec{\rho }}_i\,\textrm{d}A_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{3/2}}\nonumber \\= & {} -\textrm{P}_{\partial F_i}^{[0,1/2]}{.} \end{aligned}$$(140) -
Integral (113), for \( m=2 \), see, e.g., formula (40) of D’Urso (2014b)
$$\begin{aligned} \displaystyle \textrm{P}_{F_i}^{(2,3/2)}= & {} \displaystyle \int \limits _{F_i} \frac{{\varvec{\rho }}_i\otimes {\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{3/2}}\textrm{d}A_i\nonumber \\= & {} -\textrm{P}_{\partial F_i}^{(1\otimes , 1/2)}+\mathcal {I}^{(2)}\Bigl [\textrm{P}_{\partial F_i}^{[(1/2)1\cdot ,1]}-\alpha _i |d_i|\Bigr ]{.} \end{aligned}$$(141) -
Integral (113), for \( m=3 \), on account of formula (299)
$$\begin{aligned} \displaystyle \textrm{P}_{F_i}^{(3,3/2)}= & {} \displaystyle \int \limits _{F_i} \frac{{\varvec{\rho }}_i \otimes {\varvec{\rho }}_i\otimes {\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{3/2}}\textrm{d}A_i\nonumber \\= & {} -\textrm{P}_{\partial F_i}^{(2\otimes ,\,1/2)}+ \mathcal {I}^{(2)}\otimes _{132}\textrm{P}_{\partial F_i}^{[(1/2)\,0]} +\textrm{P}_{\partial F_i}^{[(1/2)\,0]}\otimes \mathcal {I}^{(2)}{.} \end{aligned}$$(142) -
Integral (113), for \( m=4 \), on account of formula (301)
$$\begin{aligned} \begin{array}{rl} \displaystyle \textrm{P}_{F_i}^{(4,3/2)}=&{}\displaystyle \int \limits _{F_i} \frac{{\varvec{\rho }}_i \otimes {\varvec{\rho }}_i \otimes {\varvec{\rho }}_i\otimes {\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{3/2}}\textrm{d}A_i\\ =&{}\displaystyle -\textrm{P}_{\partial F_i}^{[3\otimes ,\,1/2]}+\mathcal {I}^{(2)} \otimes _{1423}\Biggl [\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}-\frac{\mathcal {I}^{(2)}}{3}\,\textrm{P}_{\partial F_i}^{0 \, \mathcal {I}}\Biggr ]\\ &{}\displaystyle +\mathcal {I}^{(2)} \otimes _{1243}\Biggl [\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}-\frac{\mathcal {I}^{(2)}}{3}\,\textrm{P}_{\partial F_i}^{0 \, \mathcal {I}}\Biggr ]+\Biggl [\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}-\frac{\mathcal {I}^{(2)}}{3}\,\textrm{P}_{\partial F_i}^{0 \, \mathcal {I}}\Biggr ]\otimes \mathcal {I}^{(2)}{.} \end{array} \end{aligned}$$(143) -
Integral (113), for \( m=5 \), on account of formula (304)
$$\begin{aligned} \begin{array}{rl} \displaystyle \textrm{P}_{F_i}^{(5,3/2)}=&{}\displaystyle \int \limits _{F_i} \frac{{\varvec{\rho }}_i \otimes {\varvec{\rho }}_i \otimes {\varvec{\rho }}_i \otimes {\varvec{\rho }}_i\otimes {\varvec{\rho }}_i}{({\varvec{\rho }}_i\cdot {\varvec{\rho }}_i + d_i^2)^{3/2}}\textrm{d}A_i\\ =&{}\displaystyle -\textrm{P}_{\partial F_i}^{[4\otimes ,\,1/2]}+\textrm{P}_{\partial F_i}^{(5,\,3/2,A)}+\textrm{P}_{\partial F_i}^{(5,\,3/2,B)}+\textrm{P}_{\partial F_i}^{(5,\,3/2,C)}+\textrm{P}_{\partial F_i}^{(5,\,3/2,D)}{,} \end{array} \end{aligned}$$(144)
where
4.4 Algebraic Expression of the Face Integrals Related to the GV in Terms of 2D Vectors
There are now available formulas that express the integrals (113) as function of 1D integrals. There have been derived to facilitate the computation of the integrals \(\textrm{P}_{F_i}^{(m,3/2)}\), \( m=0,\ldots ,5 \), appearing in the formulas (112), (32), (36), (37) and (127) for \(\mathcal {R}_{F_i}^{(m,3/2)}\), \( m=1,\ldots ,5 \).
In turn such integrals are required to compute \(\textrm{d}_{\textbf{p}} U^{(k)}, k=0,\ldots ,4,\) by means of formulas (92), (93), (94), (95) and (96).
Our next step is to further simplify the evaluation of the boundary integrals entering the formulas for \(\textrm{P}_{F_i}^{(m,3/2)}\) by expressing them as sums over the \(N_{E_i}\) edges defining the boundary \(\partial F_i\). Specifically, adopting the parameterization (52) for the j-th edge of the face \(F_i\) and the notation introduced in Sect. (2.4). Specifically, with reference to the integral (133) appearing in formula (139), it turns out to be
where the symbols \( p_j \), \( q_j \), \( u_j \) and \( v_j \) are defined in (55) and (56) while \( ATN1_j \), \( ATN2_j \) in the expression (287) of \( I_j^{[0,1(1/2)]} \) are defined in (280) and (281), respectively.
Concerning the integral (134) we have
where the integral \( I_j^{(0,1/2)}\) is evaluated in (288).
The integral (135) is obtained by the formula
where the integral \( I_j^{(0,1/2)}\) and \( I_j^{(1,1/2)}\) are defined in (288) and (289), respectively.
The integral (136) is given by
where the symbols \(\mathcal {E}^{(2)}_{{\varvec{\rho }}_j{\varvec{\rho }}_j}\), \(\mathcal {E}^{(2)}_{{\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\), and \(\mathcal {E}^{(2)}_{\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\) are defined in (65) and the integrals \(I_j^{(0,1/2)}\), \(I_j^{(1,1/2)}\) and \(I_j^{(2,1/2)}\) are reported in the formulas (288), (289) and (290), respectively.
The integral (137) reads
where the symbols \(\mathcal {E}^{(3)}_{{\varvec{\rho }}_j{\varvec{\rho }}_j{\varvec{\rho }}_j}\), \(\mathcal {E}^{(3)}_{{\varvec{\rho }}_j{\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\), \(\mathcal {E}^{(3)}_{{\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\) and \(\mathcal {E}^{(3)}_{\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\) are defined in (67) and \(I_j^{(0,1/2)}\), \(I_j^{(1,1/2)}\), \(I_j^{(2,1/2)}\) and \(I_j^{(3,1/2)}\) are reported in the formulas (288), (289), (290) and (291), respectively.
Finally the integral (138) has the following expression
or equivalently
where
and the expressions of the symbols \(\mathcal {E}^{(4)}_{{\varvec{\rho }}_j{\varvec{\rho }}_j{\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\), \(\mathcal {E}^{(4)}_{{\varvec{\rho }}_j{\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j} \) and \(\mathcal {E}^{(4)}_{{\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j\varDelta {\varvec{\rho }}_j}\) can be inferred from the symbols \(\mathcal {D}^{(4)}_{\textbf{p}\textbf{p}\textbf{p}\textbf{r}}\), \(\mathcal {D}^{(4)}_{\textbf{p}\textbf{p}\textbf{r}\textbf{r}}\) and \(\mathcal {D}^{(4)}_{\textbf{p}\textbf{r}\textbf{r}\textbf{r}}\) in (211), (212) and (213), respectively, by replacing \( \textbf{p}\) with \({\varvec{\rho }}_j\) and \( \textbf{r}\) with \(\varDelta {\varvec{\rho }}_j\). Furthermore, the expressions of \(I_j^{(0,1/2)}\), \(I_j^{(1,1/2)}\), \(I_j^{(2,1/2)}\), \(I_j^{(3,1/2)}\) and \(I_J^{(4,1/2)}\) are reported in the formulas (288), (289), (290), (291) and (292), respectively.
4.5 Removable Singularities of the Algebraic Expressions of the Gravity Vector
It has been proved in formula (107) that expression of the integrals \( \mathcal {R}_{\varOmega }^{(m,3/2)} \), \( m=1,\ldots ,5 \), entering formula (92–96) for the addends \( \textrm{d}_{\textbf{p}}U^{(k)}\), \( k=0,\ldots ,4 \), of the gravity vector are singularity-free independently from the position of the observation point P with respect to \(\varOmega \).
Nevertheless, the algebraic counterparts \( \mathcal {R}_{F_i}^{(m,3/2)} \) can include integrals extended to the generic edge of the face \( F_i \) that can exhibit singularities whenever the observation point belongs to \( F_i \) or when its projection over \( F_i \) belongs to an edge defining its boundary.
However, this possible singularity of the generic integral \( I_j \) extended to the j-th edge of \( \partial F_i \) is actually ineffective from the computational point of view since it will be proved by analytical arguments that its contribution to the integral \( \mathcal {R}_{F_i}^{(m,3/2)} \) is null.
To prove the results of interest we shall make use of the notation introduced it in the formulas (55) and (72) and observe that the combination of the formulas (110) and (111) yields
when the expression of \( \mathcal {R}_{F_i}^{(m,3/2)} \), \( m=1,\ldots ,5 \), are provided in the formulas (112), (114–116) and (127). In turn, they depend upon the integrals \( \textrm{P}_{F_i}^{(m,3/2)} \) defined in (113) whose value is computed as a sum of the integrals (133–138) extended to the boundary \( \partial F_i \).
Due to the intricate combination of integrals to be evaluated it is convenient to indicate the set of formulas required to compute \( \mathcal {R}_{F_i}^{(m,3/2)} \) by concisely reporting the sequence of formulas to be invoked. For instance
meaning that the computation of \( \mathcal {R}_{\varOmega }^{(1,3/2)} \) requires the evaluation of the integrals \( I_j^{[0,1(1/2)]} \) and \( I_j^{(0,1/2)} \) over the edges of \( \partial F_i \).
Analogously,
so that one needs to compute the integrals \( I_j^{(1,1/2)} \) in addition to those required for computing \( \mathcal {R}_{\varOmega }^{(2,3/2)} \). As a matter of fact this represents are general rule in the sense that the computation of the integral \( \mathcal {R}_{F_i}^{(m+1,3/2)} \) requires to evaluate an additional integral with respect to those associated with \( \mathcal {R}_{F_i}^{(m,3/2)} \). Actually
what requires computation of \( I_j^{(2,1/2)} \) in addition to the previously indicated integrals.
Furthermore
requires the extra calculation of \( I_j^{(3,1/2)} \) while
needs to evaluate the additional integral \( I_j^{(4,1/2)} \).
To sum up, the computation of the integrals \( \mathcal {R}_{F_i}^{(m,3/2)} \), \( m=1,\ldots ,5 \), requires the computation of the six integral \( I_j^{[0,1(1/2)]} \), \( I_j^{(m,1/2)} \), \( m=0,\ldots ,4 \). It has been anticipated that they can become singular when \( d_i=0 \), i.e., the observation point P belongs to the face \( F_i \), or the projection of P over the face, i.e., when \( d_i\ne 0 \), is such that \( {\varvec{\rho }}_j=\textbf{o}\), \( {\varvec{\rho }}_{j+1}=\textbf{o}\) or belongs to the segment [\({\varvec{\rho }}_j\), \({\varvec{\rho }}_{j+1}\)].
Let us first show that, independently from the value of \( d_i \), the integral \(\mathcal {R}_{\varOmega }^{(1,3/2)}\) is always well-defined. Actually, on account of (157), (111) and (112) it turns out to be
Hence, one has to prove both \(\textrm{P}_{F_i}^{(0,3/2)}\) and \(\textrm{P}_{F_i}^{(1,3/2)}\) are well-defined. Equivalently, according to (139) and(140), it has to be proved that \(\textrm{P}_{\partial F_i}^{[1\cdot , 1(1/2)]}\) and \(\textrm{P}_{\partial F_i}^{[0,1/2]} \) are non-singular. To this end it is convenient to invoke formulas (139) and(140) to express (163) as follows
where sgn denotes the signum function and the last equality follows from (149) and(150).
To ascertain the well-posedness of the integral \( I_j^{[0,1(1/2)]} \) if \( d_i\ne 0 \) we proceed as follows. Such an integral can be computed, on the basis of the formula (287) and invoking formula (55), by defining
and setting \( t=\lambda _j+\frac{q_j}{p_j} \). Hence, one obtains
Notice that the denominator in (166) is positive if \(-\varDelta _j=A_j>0\). Accordingly, the previous integral becomes
Being \( B_j>0 \) the previous expression can become indefinite whenever \( \varDelta _j=0 \) or, equivalently, when \( A_j=0 \) in (167) since the integrand becomes singular at one point belonging to the interval \(\left[ \frac{q_j}{p_j},1+\frac{q_j}{p_j} \right] \). In turn, this happens at the left (right) extreme of the integration interval if \( {\varvec{\rho }}_j=\textbf{o}\) ( \( {\varvec{\rho }}_{j+1}=\textbf{o}\)) or at an internal point if \( \textbf{o}\in ]{\varvec{\rho }}_j,{\varvec{\rho }}_{j+1}[ \), i.e., \( {\varvec{\rho }}_j \) and \( \varDelta {\varvec{\rho }}_j \) have negative scalar product.
Actually if \({\varvec{\rho }}_j=\textbf{o}\) \(\Big ({\varvec{\rho }}_{j+1}=\textbf{o}\Big )\), it turns out to be \(\frac{q_j}{p_j}=0\) \(\Big (1+\frac{q_j}{p_j} =0\Big )\); hence the denominator in (166) becomes singular at the left (right) extreme of the integration interval. Furthermore, should the projection of the observation point belong to the segment \([{\varvec{\rho }}_j,\;{\varvec{\rho }}_{j+1}]\), one has \({\varvec{\rho }}_{j+1}=\beta _j{\varvec{\rho }}_j\) \((\beta _j< 0)\) where \(\frac{q_j}{p_j}=(\beta _j-1)\frac{{\varvec{\rho }}_j\cdot {\varvec{\rho }}_j}{p_j}<0\) and \(1+\frac{q_j}{p_j}=\beta _j(\beta _j-1)\frac{{\varvec{\rho }}_j\cdot {\varvec{\rho }}_j}{p_j}>0\). Accordingly, the integration interval in (166) splits in two intervals having 0 as right (left) extreme. At that point, however, \(t=0\) and \(A_j =\frac{ -\varDelta _j}{p_j^2}=0\) by assumption so that the integrand in (166) becomes singular.
However, we are going to prove that, in the previous three cases, the singularity is eliminable and that the integral attains a finite value. Let us discuss separately the three cases, namely \({\varvec{\rho }}_j=\textbf{o}\), \({\varvec{\rho }}_{j+1}=\textbf{o}\) and \({\varvec{\rho }}_{j+1}=\beta _j\,{\varvec{\rho }}_j\;\;(\beta _j<0)\).
In the first case, \({\varvec{\rho }}_j=\textbf{o}\), the integration interval is \([0,\;1]\) and we have singularity of the integrand in (166) at the left extreme. However, we recall that the computation of \( I_j^{[0,1(1/2)]} \) is required in the expression (149) of \( \textrm{P}_{\partial F_i}^{[1\cdot , 1(1/2)]} \) so that they real quantity to compute is \(({\varvec{\rho }}_j\cdot {\varvec{\rho }}_{j+1}^{\bot })\, I_j^{[0,1(1/2)]} \).
Setting \({\varvec{\rho }}_j=|{\varvec{\rho }}_j|\textbf{e}=\varepsilon \,\textbf{e}\) and observing that, on account of (73),
we infer that \(\sqrt{-\varDelta _j}\) is infinitesimal of the same order as \(\varepsilon =|{\varvec{\rho }}_j|\) when \(\varepsilon \rightarrow 0\), a property we state by writing \(\sqrt{-\varDelta _j}=\mathcal {O}(\varepsilon )\).
Being \({\varvec{\rho }}_j\cdot {\varvec{\rho }}_{j+1}^\perp =\mathcal {O}(\varepsilon )\) if \(\varepsilon \rightarrow 0\). one has
where \( l_j \) = \(\sqrt{\varDelta \rho _j\cdot \varDelta \rho _j }\).
If \( {\varvec{\rho }}_{j+1}=\textbf{o}\) the quantity \(({\varvec{\rho }}_j\cdot {\varvec{\rho }}_{j+1}^{\bot })\, I_j^{[0,1(1/2)]} \) is still given by the previous expression but the integration limits are \( -1 \) and \( \varepsilon \). Hence, the final result coincides with the previous one but with the reversed sign.
Should the projection of the observation point be internal to the edge, \({\varvec{\rho }}_j\) and \({\varvec{\rho }}_{j+1}\) are parallel so that the product \({\varvec{\rho }}_j\cdot {\varvec{\rho }}_{j+1}^\perp \) is zero. Accordingly, both \({\varvec{\rho }}_j\cdot {\varvec{\rho }}_{j+1}^\perp \) and \(\sqrt{-\varDelta _j}\) are \(\mathcal {O}(\varepsilon )\), that is both of them are infinitesimal of order \(\varepsilon \) as \(\varepsilon \rightarrow 0\). Hence
Actually, the arctan function attains finite and opposite values both at \(t=\varepsilon \) and \(t=\pm 1 \).
On account of the previous results we can conclude that the first two terms in (164) are zero if \( d_i =0 \) so that their computation can be skipped in this case.
For what concerns, the integral \(I_j^{(0,1/2)}\) in (164) we notice that, according to (288), its evaluation requires that of the quantity \( LN_j \) in (279) since \( p_j\) is always positive on the basis of its definition in (55). However, the equivalent expression of \( LN_j \) provided in (79) shows that it is always well-defined if \( d_i\ne 0\).
Conversely, if the projection of the point P over the face is such that if \( {\varvec{\rho }}_j=\textbf{o}\) or \( {\varvec{\rho }}_{j+1}=\textbf{o}\) or it belong to \(] {\varvec{\rho }}_j,{\varvec{\rho }}_{j+1} [\), \(LN_j\) tends to infinity with an arbitrary low degree. Since \(I_j^{(0,1/2)}\) is multiplied by \( d_i \) in (164), a quantity that has been assumed to be zero, we ultimately infer that \(\mathcal {R}_{\varOmega }^{(1,3/2)}\) is zero if \( d_i =0 \) so that its computation can be actually avoided.
In conclusion, the integral \(\mathcal {R}_{\varOmega }^{(1,3/2)}\) is well-defined if \( d_i \ne 0 \) and its computation can be avoided if \( d_i =0 \) since the relevant value is null.
Let us now prove that the integral \(\mathcal {R}_{\varOmega }^{(2,3/2)}\) is well-defined independently from the value of \(d_i\). Recalling (157), (111) and (114) one has
We have already proved, with reference to \(\mathcal {R}_{\varOmega }^{(1,3/2)}\), that \(\textrm{P}_{F_i}^{(0,3/2)}\) and \(\textrm{P}_{F_i}^{(1,3/2)}\) are well-defined whatever is the value of \(d_i\). Hence, \(\mathcal {R}_{\varOmega }^{(2,3/2)}\) is singularity-free provided that \(\textrm{P}_{F_i}^{(2,3/2)}\) does share this property whatever is the value of \(d_i\).
To this end we invoke formula (141), (151) and (59) to write
According to (289) the integral \(I_j^{(1,1/2)}\) is the sum of the algebraic quantity \((\sqrt{p_j+2q_j +v_j}-\sqrt{v_j})/p_j\), that is always well-defined independently from \(d_i\), and the projection of the observation point P over the face, and of the quantity \(q_j\,I_j^{(0,1/2)}/p_j\) where \(I_j^{0,1/2)}\) depends on \(LN_j\) on account of (288).
However both \(I_j^{(0,1/2)}\) and \(I_j^{(1,1/2)}\), being addends of \(\textrm{P}_{F_i}^{(2,3/2)}\), are multiplied by \(d_i\) in (171) so that their expressions are well-defined, whatever is the value of \(d_i\), as already shown for the product \(d_i\,LN_j\) with reference to the integral \(\mathcal {R}_{\varOmega }^{(1,3/2)}\).
For what concerns the integral \(I_j^{(1/2\cdot 0,1)}\) in (172) we infer from formula (282) that it can be expressed as
Being this integral multiplied by \(\bigl ({\varvec{\rho }}_j\cdot {\varvec{\rho }}_{j+1}^{\perp }\bigr )\) in (172) the first addends is well-defined, whatever is the value of \(d_i\), as already proved in (169) and (170).
Hence, in the special case \(d_i=0\), the integral \( I_j^{[0,1(1/2)]} \) does not even need to be computed since \(\textrm{P}_{F_i}^{(2,3/2)}\) in which \( I_j^{[0,1(1/2)]} \) does appear, is scaled by \(d_i\) in (171). The same does occur for the additional terms \(LN_j\) in (173) since it has to be multiplied by \(d_i\) in (171) producing a quantity that is well-defined if \(d_i\ne 0\) and equal to zero if \(d_i=0\). Actually, in this last case, \(d_i\) tends to zero while \(LN_j\) can tend to infinity but with are infinitesimally low rate.
It is worth noting at this stage that proving the well-posedness of \(\mathcal {R}_{\varOmega }^{(2,3/2)}\) has only required to prove the well-posedness of the integral of \(\textrm{P}_{F_i}^{(2,3/2)}\) since the additional terms entering the expression of \(\mathcal {R}_{\varOmega }^{(2,3/2)}\) are also included in the expression of \(\mathcal {R}_{\varOmega }^{(1,3/2)}\), i.e., the first integral that has been proved to be singularity-free. On the other hand this is apparent if one compares formulas (164) and (171) that are based, according (157), on formulas (112) and (114).
Hence, comparing formulas (114) and (115), this means \(\mathcal {R}_{\varOmega }^{(3,3/2)}\) is well defined if and only if \(\textrm{P}_{F_i}^{(3,3/2)}\) is singularity-free. This is certainly true since this integral, according to (142), depends upon the integrals \(\textrm{P}_{\partial F_i}^{[2\otimes ,1/2]}\) and \(\textrm{P}_{\partial F_i}^{[(1/2)0]}\). Formulas (152), refereed to the former integral, shows that one needs to compute the integrals \(I_j^{(0,1/2)}\), \(I_j^{(1,1/2)}\) and \(I_j^{(2,1/2)}\); furthermore, one infers from (60) that the integral \(I_j^{(1/2\cdot 0)}\) is required for \(\textrm{P}_{\partial F_i}^{[(1/2)0]}\). In turn formulas (288), (289) and (290) for the first three integrals, and formula (283) for the fourth one show that, apart from algebraic quantities that are always well-defined, they all depend upon the quantity \(LN_j\). However, this quantity is multiplied by \(d_i\), according to (157); hence, the product \(d_i\,LN_j\), as a previously shown, is well-defined and null if \(d_i=0\).
Basically, the same path of reasoning can be followed for \(\mathcal {R}_{\varOmega }^{(4,3/2)}\) and \(\mathcal {R}_{\varOmega }^{(5,3/2)}\) whose well-posedness depends upon the fact that \(\textrm{P}_{F_i}^{(4,3/2)}\) and \(\textrm{P}_{F_i}^{(5,3/2)}\) are singularity-free, see, e.g., formulas (110), (116) and (127).
Actually, according to formula (143), \( \textrm{P}_{F_i}^{(4,3/2)}\) depends upon \( \textrm{P}_{\partial F_i}^{[3\otimes ,\,1/2]} \), \(\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}\) and \(\textrm{P}_{\partial F_i}^{0 \, \mathcal {I}}\). In turn the first integral depends, according to (153), upon \(I_j^{(0,1/2)}\), \(I_j^{(1,1/2)}\), \(I_j^{(2,1/2)}\) and \(I_j^{(3,1/2)}\) defined, respectively, in formulas (288), (289), (290) and (291). All of them depend upon algebraic quantities, these are non-singular whatever is the position of the observation point P with respect to the target body, and the quantity \(LN_j\). Since this quantity is multiplied by \(d_i\), see, e.g., formula (110), we conclude from the well-posedness of the quantity \(d_i\,LN_j\), an issue repeatedly addressed above, that the addend of \( \mathcal {R}_{\varOmega }^{(4,3/2)} \) related to the integral \( \textrm{P}_{\partial F_i}^{[3\otimes ,\,1/2]} \) is singularity-free and null if \(d_i=0\).
On account of (62) the integral \( \textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]} \) depends upon the integrals \(I_j^{(1/2\cdot 0)}\) and \(I_j^{(1/2\cdot 1)}\) whose expressions are provided, respectively, in formula (283) and (284). As before they are sum of algebraic quantities and an additional term depending upon \(LN_j\). Hence the considerations just discussed for \( \textrm{P}_{\partial F_i}^{[3\otimes , 1/2]} \) do apply to \(\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}\).
Finally, formula (45)\(_1\) shows that \(\textrm{P}_{\partial F_i}^{0 \, \mathcal {I}}\) depends upon the integrals \(\textrm{P}_{\partial F_i}^{[(1/2)\,1\cdot ]}\) and \(\textrm{P}_{\partial F_i}^{[(1/2)\,1\cdot , 1]}\). The well-posedness of the latter has been already discussed in (172) while that of the former depends, according to formula (63), upon \(I_j^{(1/2\cdot 0)}\) that is one of the integrals considered with reference to \(\textrm{P}_{\partial F_i}^{[(1/2)\,1\otimes ]}\).
This proves that the integral \(\mathcal {R}_{\varOmega }^{(4,3/2)}\) is non-singular whatever is the position of the observation point with respect to the target body and null if \(d_i=0\).
Basically, the same path of reasoning can be followed for \(\mathcal {R}_{\varOmega }^{(5,3/2)}\) so that we limit ourselves to report just the sequence of formulas and/or integrals that the interested reader has to consult in order to check the well-posedness of \( \textrm{P}_{F_i}^{(5,3/2)} \), that is the only additional term to be considered with respect to terms \(\textrm{P}_{F_i}^{(m,3/2)}\), m=1, 2, 3, 4.
where
while the integrals \(\textrm{P}_{\partial F_i}^{(5,\,3/2,A)}\), \(\textrm{P}_{\partial F_i}^{(5,\,3/2,B)}\), \(\textrm{P}_{\partial F_i}^{(5,\,3/2,C)}\) and \(\textrm{P}_{\partial F_i}^{(5,\,3/2,D)}\) depend upon \( \textrm{P}_{\partial F_i}^{[(1/2)\,2\otimes ]} \) and \(\textrm{P}_{\partial F_i}^{1 \, \mathcal {I}}\), see, e.g., formulas (145–148).
In turn
Hence, looking at Appendix C, it is easy to check that all the previous integrals are composed of an algebraic quantity and an additional one depending upon \(LN_j\). The former is always well-defined while the latter, being multiplied by \(d_i\), is non-singular and equal to zero if \(d_i=0\) as previously proved in this section.
In conclusion we can state that all integrals appearing in the expression of the gravity vector are well-defined whatever is the position of the observation point with respect to the polyhedral body.
5 Algebraic Expression of the Integrals Related to the GP and GV in Terms of 3D Vectors
It is useful at this stage to sum up the different steps carried out evaluate the gravitational potential \( U(\textbf{p}) \) by means of the expressions (5) and the gravity vector by means of (84).
Basically, we have shown that this amounts to computing the tensors \(\mathcal {R}_{\varOmega }^{(m,1/2)}\) in formula (8) and the tensors \(\mathcal {R}_{\varOmega }^{(m,3/2)}\) in formula (85). In turn, exploiting formula (25), tensors \(\mathcal {R}_{\varOmega }^{(m,1/2)}\) have been expressed as a sum of tensors \(\mathcal {R}_{\partial \varOmega }^{(m,1/2)}\) associated with the \( N_F \) faces \( F_i \) composing the polyhedral body \(\varOmega \). The same procedure has been exploited in formula (107) by replacing the volume integral \(\mathcal {R}_{\varOmega }^{(m,3/2)}\) with the boundary integral \(\mathcal {R}_{\partial \varOmega }^{(m,3/2)}\).
The target \(\varOmega \) being polyhedral, both \(\mathcal {R}_{\partial \varOmega }^{(m,1/2)}\) and \(\mathcal {R}_{\partial \varOmega }^{(m,3/2)}\) have been expressed as a sum of 2D integrals defined on the faces \( F_i \) of \( \partial \varOmega \), in formula (27) and (85), respectively, introducing the 3D tensors \(\mathcal {R}_{F_i}^{(m,1/2)}\) and \(\mathcal {R}_{F_i}^{(m,3/2)}\). In turn, the computation of these tensors is based on that of the two-dimensional tensors \(\textrm{P}_{F_i}^{(m,1/2)}\) defined in (33), and that of the tensors \(\textrm{P}_{F_i}^{(m,3/2)}\) defined in (113). Accordingly, both of them have to be mapped back to the 3D space in order to provide the correct expression of \(\mathcal {R}_{\varOmega }^{(m,1/2)}\) and \(\mathcal {R}_{\varOmega }^{(m,3/2)}\). This is trivial for \( m=0, 1, 2 \), see, e.g., formulas (32) and (114), while it is more cumbersome for \( m=3, 4 \) since the tensors \(\textrm{P}_{F_i}^{(m,1/2)}\) and \(\textrm{P}_{F_i}^{(m,3/2)}\) of rank three and four have to be combined with the formal operator \( \mathbb {T}\) to evaluate, e.g.,
in formulas (36) and (37), respectively.
On account of (50) and (51), and related algebraic counterparts (272) and (277), we need to apply \( \mathbb {T}_{F_i}^{(3)} \) and \( \mathbb {T}_{F_i}^{(4)} \) to tensors such as \(\varvec{\alpha }\otimes \varvec{\beta }\otimes \varvec{\gamma }\), \(\varvec{\alpha }\otimes \varvec{\beta }\otimes \varvec{\gamma }\otimes \varvec{\delta }\) or tensor product of \( \mathcal {I}^{(2)} \) by \(\varvec{\alpha }\) or \(\varvec{\alpha }\otimes \varvec{\beta }\), where the two-dimensional vectors \(\varvec{\alpha }\), \(\varvec{\beta }\), \(\varvec{\gamma }\) and \(\varvec{\delta }\) stand for \( {\varvec{\rho }}_j \), \( \varDelta {\varvec{\rho }}_j \) or \( \varDelta {\varvec{\rho }}_j^{\perp } \).
To fix the ideas, let us set \(\varvec{\alpha }={\varvec{\rho }}_j\), \(\varvec{\beta }=\varDelta {\varvec{\rho }}_j\), \(\varvec{\gamma }=\varDelta {\varvec{\rho }}_j^{\perp }\). Hence
an expression that can be further simplified. Actually, inverting (28), we can express the 2D coordinates of each vertex as function of the relevant 3D ones. In particular, premultiplying relation (28) by \(\textbf{T}_{F_i}^T\), where \((\cdot )^T\) stands for transpose, one obtains
since it is easy to check that \(\textbf{T}_{F_i}^T\textbf{T}_{F_i}=\mathcal {I}^{(2)}\). Analogously
Accordingly, setting \( \textbf{T}_{F_i}\textbf{T}_{F_i}^T=\textbf{Z}_{F_i} \), where \( [\textbf{Z}_{F_i}] \) is a 3x3 matrix, we have
In other words, during the evaluation of the different quantities contributing to (50) and (51), we can directly make reference to three-dimensional expressions.
For what concerns the tensor product of \( \mathcal {I}^{(2)} \) by \(\varvec{\alpha }\) or \(\varvec{\alpha }\otimes \varvec{\beta }\) we observe that \(\mathcal {I}^{(2)}={\textbf {e}}_{1}\otimes {\textbf {e}}_{2}+{\textbf {e}}_{2}\otimes {\textbf {e}}_{1}\) where \( {\textbf {e}}_{1}=(1,0)\) and \({\textbf {e}}_{2}=(0,1)\). Hence
where \( \textbf{u}_i \) and \( \textbf{v}_i \) are the vectors used to define the 2D reference frame on the generic face \( F_i \), see, e.g., (29).
In conclusion, setting again \(\varvec{\alpha }={\varvec{\rho }}_j\), \(\varvec{\beta }=\varDelta {\varvec{\rho }}_j\), \(\varvec{\gamma }=\varDelta {\varvec{\rho }}_j^{\perp }\) to fix the ideas, one has
and
The transformation of additional tensor product such as \(\otimes _{132}\), \(\otimes _{1423}\) etc. can be addressed in a similar way.
6 Numerical Examples
This section illustrates the results of several numerical tests that have been carried out in order to fully validate the proposed formulation. This has been done by considering three different issues that are dealt with in separate subsections.
The first one is concerned with a comparison of the results of the current approach with those previously contributed by different authors, with a special emphasis on the results regarding the case of an observation points leading to removable singularity.
The second issue addressed in this section draws the reader’s attention on the usage limitations of the proposed formulas imposed by numerical instability. In this respect three different aspects are specifically dealt with, namely i) the separation between the origin of the reference frame and the observation point; ii) the separation between this last one and the target body; iii) the numerical effects associated with a finer subdivision of a polyhedral body.
Finally, a stress test is carried out by comparing the results presented in the first subsection with those obtained by considering arbitrary reference frame whose axes are not necessarily aligned with the edges of the polyhedral bodies considered in the examples retrieved from the literature.
In all examples, the test platform is a personal computer with 2.7GHz Intel core i7 CPU and 16GB RAM; version R2022b has been used for the MATLAB software.
6.1 Comparison of Results Between the Current Approach and Those Available in the Literature
The singularity-free analytical formulas developed in the previous sections have been validated by comparing the results obtained by a home-made MATLAB code with those refereed to a classical example reported in the literature, i.e., the García-Abdeslem (2005) prism model, and to a triangular prism model, obtained by halving the latter, considered in Ren et al. (2017) they are shown in Fig. 2a, b, respectively.
Two different cases of polynomial density functions have been considered for the model in Fig. 2a, namely a third-order vertically varying density contrast and a purely quartic density function. To address more severe test cases, a density contrast varying in both vertical and horizontal directions has been assumed for the more complicated geometry represented by the triangular prism in Fig. 2b.
We emphasize that the Cartesian reference frame can be arbitrary in the sense that it does not necessarily coincide with the observation point since its actual position is explicitly taken into account in the formulas presented in the paper. Hence, there is no need to make the origin of the reference frame coincide with the observation point and thus no need to assume different reference frames as the observation point changes.
6.1.1 A Prismatic Body with Vertically Varying Density Contrast
Let us consider the prism in Fig. 2a whose dimensions range as follows: x \(\in \) [10 km, 20 km], y \(\in \) [10 km, 20 km], z \(\in \) [0 km, 8 km]. The density contrast is taken from García-Abdeslem (2005) and reads
where density is expressed in kg m\( ^{-3} \) and z in km; the value of the gravitational constant G is \(6,673 \,\cdot 10^{-11} \) m\(^3\) kg\(^{-1}s^{-2}\). Hence, one can set c\( _{000} \) = \(-\)747.7, c\( _{001} \) = 203.435, c\( _{002} \) = - 26.764 and c\( _{003} \) = 1.4247 in (2).
Three different combinations of the observation point are considered. The first one assumes y = 15 km, z = \(-\)0.15 m, so as to avoid the singularity of the formulas reported in García-Abdeslem (2005), while x assumes three different values in the interval [9.99995, 10.00005].
Table 1 shows the comparison of the vertical gravity field provided by our solution with those by García-Abdeslem (2005) and Ren et al. (2017) in four different cases corresponding to the cases of constant, linear, quadratic and cubic density contrast represented by the four addends in the formula (187).
Table 2 is similar to Table 1 with the only difference that z = 0, meaning that the observation point belongs to the plane containing the upper face of the prism. It is worth noting that both for z = \(-\)0.15 m, Table 1, and z = 0, Table 2, our results do coincide with those reported in the literature when x = 9.99995 km and x = 10 km. Conversely, for x = 10.00005 km, our solution coincides with those due to García-Abdeslem (2005) and Ren et al. (2017) only up to the second/third significant digit, a condition that has been considered worth of further investigation on account of the fact that the coordinates x = 10.00005, y = 15, z = 0 are indicative of an observation point that belongs to the body, thus excluding any sort of singularity.
For this reason we have computed the vertical gravity field at points characterized by slightly increasing values of x, viz. x = 10.0001 and x = 10.00015, in order to check a smooth variation of the field for values of x ranging in the interval [9.99995,10.00015]. This property is apparent for our solution in the last column of Table 2 while there is a sudden change, for x = 10.00005, in the values of the gravity field published in García-Abdeslem (2005) and Ren et al. (2017); in these last papers the results pertaining to the values x = 10.0001 and x = 10.00015 are not available.
Furthermore, we have checked our solution numerically, by evaluating the integrals by the Gauss rule, and compared it with the analytical results in Table 3. Numerical solutions have been obtained by adopting \(5 \times 5 \times 5\) rule in four, eight and twelve subdomains in which the faces parallel to the planes of the reference frame have been divided. This resulted in a total of \(100 \times 100 \times 100\), \(200 \times 200 \times 200\) and \(300 \times 300 \times 300\) Gauss points, respectively; in particular, Fig. 3 displays the faces \(10 \times 10\) and \(8 \times 10\) and the actual distribution of Gauss point corresponding to a partition of each face in four subdomains.
By examining the results in Table 3 it is apparent that, apart from the constant density distribution, the correctness of the numerical results does not necessary improve as the number of Gauss points increases when the observation point does belong to the target body. Actually, as witnessed by a series of further experiments not reported for brevity, the accuracy of the Gauss integration depends on how much integration points lie close to, or distance from, points of the domain of integration in which the field to be computed tends to become singular, see, e.g., the expression (83) of the gravity field.
In the last numerical test for the prism model in Fig. 2a, similar to that presented in Ren et al. (2017), the observation point coincides with the corner of the prism having coordinates x = 20 km, y = 10 km, z = 0 km, or is slightly above it (z = \(-\)0.15 m). The relevant results are compared in Tables 4 and 5, respectively, with those by García-Abdeslem (2005) and Ren et al. (2017). It is apparent that the agreement of our results with the existing ones is quite good in all cases.
6.1.2 A Prismatic Body with Quartic Density Contrast
We consider again the prism in Fig. 2a but now endowed with the quartic density contrast
already considered in Ren et al. (2017).
Fifteen observation points are considered, all characterized by y = 15 km, z = 0 m as coordinates, and values of x progressively increasing from 0 to 15 km.
The relevant results in terms of vertical gravity are reported in Table 6 and compared with those reported in Table 8 of Ren et al. (2017). The quite good agreement of our results with those contributed by Ren et al. (2017) confirms the correctness of the proposed approach, particularly when the removable singularity comes into play (x= 10).
In accordance with what has been shown in Table 3, there is some evidence that the Gaussian approximation yields higher error than the analytical methods when the observation point is near the target, x \(\in \) [8,15], while the opposite may be true when the observation points are further away, due to increasingly destructive numerical cancellation errors when using analytical formulas. This issue will be specifically addressed in Sect. 5.2.2.
6.1.3 A Prismatic Body with an Arbitrary Density Contrast
Let us now address the polyhedron in Fig. 2b and the density contrast
so as to consider a function varying in both the vertical and horizontal direction.
This case is simulated by assuming \( c_{211}=10^4 \) in formula (2) and setting to zero \( \delta _o\) as well as the entries of \( \mathcal {C}^{(1)} \), \( \mathcal {C}^{(2)} \), \( \mathcal {C}^{(3)} \) in formula (4). Three different observation points are considered, namely one at the barycenter of the upper face (P\( _3 \)), one at median point of the edge (P\( _2 \)) and one coincident with the vertex (P\( _1 \)).
The relevant results are reported in Table 7 and compared with those obtained by Gauss integration with a total number of \(72 \times 72 \times 72\) quadrature points and 200x200x200 quadrature points, respectively, referred to the domains obtained by dividing the base of the prism in three irregular quadrilaterals by halving each edge, see, e.g., Fig. 4.
6.2 Usage Limitations Imposed by Numerical Instability
Aim of this subsection is to present the results of some numerical tests aimed at testing the sensitivity of the analytical formulas presented thus for with respect to several effects associated with geometric quantities involved. in the computation of the gravitational potential and gravity vector.
Specifically, with reference to error control under finite length arithmetic, we shall investigate in three separate subsections the consequences of adopting large offsets of the origin from the observation point, of considering large distances of the observation point from the target body and of subdividing a given polyhedron in smaller polyhedra.
Prism model analogous to that of Fig. 2a with: a increasing distances between the origin of the reference frame and the observation point (\(y = 10\) km, \(y = 100\) km, \(y = 1000\) km); b increasing separation between the observation point and the target body (\(x = 10\) km, \(x = 100\) km, \(x = 1000\) km)
6.2.1 Origin-Observation Point Separation
In order to evaluate the effects of large offsets between the origin of the reference frame and the observation point on the accuracy of the formulas derived in the paper we consider the prism in fig. 5a and evaluate the potential and the vertical component of the gravity vector at observation points \(P = [0, y, 0]\) having progressively increasing values of y. Specifically, Table 8 shows the values of the gravitational potential for \(y = \)15 km, \(y =\) 105 km and \(y =\) 1005 km separately for the four contributions of the density contrast. Similar computations have been carried out for the vertical component of the gravity vector and the relevant results are reported in Table 9
Inspection of Tables 8 and 9 shows that the results are unaffected by the separation between the origin and the observation point. This is quite reasonable since the computational of the gravity effects depends upon the relative position between the observation point and the target body, an issue that will be further addressed in the following two subsections.
6.2.2 Observation Point—Target Body Separation
In a seminal paper Holstein and Ketteridge (1996) showed that analytical formulas for the gravity anomaly of a uniform polyhedral body are subjected to numerical error that increases with distance from the target. This leads to a limited range of target distances in which the formulas are effective, beyond which the calculations are dominated by rounding error. Clearly, this range is precision dependent in the sense that, if the floating point precision were higher, then the range would increase.
In particular, Holstein and Ketteridge (1996) expressed their estimates on the relative error of the analytical computation by introducing the so-called aspect ratio \( \gamma =\alpha /\delta \) between the typical linear dimension \(\alpha \) of the target body and the typical distance \(\delta \) of the target from the observation point. In particular, defining the dimensionless target distance \(\varGamma =1/\gamma \), they proved that, for the constant density case, analytical formulas for the potential expressed in terms of line integrals leads to terms that are \(\mathcal {O}(\delta ^3/\alpha ^3)=\mathcal {O}(\varGamma ^3)\) larger than the result. Hence, differently from a Gaussian integration in which no numerical cancellation does occur, if \(\delta>>\alpha \) destructive cancellation will take place and the relative error of the analytical computation will grow with \(\varGamma \).
For polyhedral bodies having a spatially linear density (Pohanka 1998) and (Hansen 1999) noted that the analytical formulas for the gravitational field at increasing target distances produced results characterized by larger numerical errors than those associated with the corresponding uniform polyhedral formulas. This property was confirmed by (Holstein 2003) who proved that analytical formulas for the linear density case leads to terms that are \(\mathcal {O}(\varGamma ^{3+1})\) larger than the result.
Hence, for the maximum density variation considered in this paper, i.e., of fourth-order, a magnification by \(\mathcal {O}(\varGamma ^4)\) of the largest term in the analytical formulas with respect to the smallest is expected, making an overall growth factor of \(\mathcal {O}(\varGamma ^{3+4})\) of the summed term compared to the result.
Furthermore, the calculation of the vertical component of gravity of a finite target at increasing horizontal distances induces a further level of destructive cancellation, since we are seeking the vertical component and the field is primarily horizontal. For the constant case, this induces relative error growth proportional to \(\varGamma ^4\) in the constant density case, or \(\varGamma ^{4+4}\) in the quartic density case. One would therefore expect g\( {_z} \) to be more rapidly corrupted than the potential, at increasing target distances.
Motivated by the previous considerations this subsection presents the results of some numerical tests aimed at testing the sensitivity of the analytical formulas presented thus far with respect to the dimensionless target distance.
To this end we consider the prism model in Fig. 5b and a progressively increasing distance between the observation point P = [0, 15 km, 0] and the target body by assuming for the vertices of the left face the values \(x = 10\) km, \(x = 100\) km, \(x = 1000\) km and for those of the right face \(x = 20\) km, \(x = 110\) km, \(x = 1010\) km. In this way the dimensionless target distance \(\varGamma \) assumes value approximatively equal to 1, 10 and 100. The values of the gravitational potential and of vertical component of the gravity vector are reported in Tables 10 and 11, respectively.
Assuming the result obtained by Gauss integration as correct, a comparison of the values presented in Table 10 and 11 is reported in Fig. 6 by plotting on log–log axes the quantity
where V stands for value of the gravitational potential or the vertical component of the gravity vector.
The results reported in Tables 10 and 11 show that the values of the gravitational potential and of the gravity vector computed analytically become more and more unreliable as the offset between the observation point and the target body increases due to numerical cancellation errors. Moreover the error associated with the use of the analytical formulas has a rate of increase that is by far more pronounced for the gravity vector.
6.2.3 Effects of a Subdivision of the Target Body
It is of some interest to understand to what extent the computation of gravity fields associated with a polyhedral body is influenced by a finer subdivision of the polyhedron in smaller polyhedra. Actually, this produces an inhomogeneous distribution of the dimensionless target distance \(\varGamma \) that can significantly increase for smaller polyhedra more distant from the observation point, even if the value of \(\varGamma \) can be sufficiently low when the target body is modeled as a unique polyhedron.
Prism model of Fig. 2a and related subdivision in smaller subprisms
In the first test the target body is left at a very low dimensionless distance, \(\varGamma \simeq 1\) considering the prism as a whole, but this value is increased and made inhomogeneous by dividing the prism model of Fig. 7a in smaller subprisms by increasing the number of subdivisions of each edge of the original prism.
In this way the subprisms more distant from the observation point, namely those near the bottom right vertex of the prism, are characterized by greater dimensionless target distance. For instance, for N=100, the linear dimensions \(\alpha \) of the subprism is 10/100=0.1 km and the distance \(\delta \) from the observation point is \(\simeq \)20, yielding a value of \(\varGamma =200\).
This is sufficient to provide values of the gravitational potential whose precision, for an assigned type of density variation, degradates with N, see, e.g., Table 12, in which the first four columns refer to the four addends in (187) while the results of the last column have been obtained by considering the density contrast in (188). It is also worth being emphasized in Table 12 that the number of significant digits decreases as the order of the density variation increases.
Conversely, as shown in Table 13, such a phenomenon is not experienced by adopting a Gauss integration in which the number of Gauss point for each subprism has been chosen so as to keep approximately constant, and equal to \(200 \times 200 \times 200\), the number of Gauss points pertaining to the prism as a whole.
The above-mentioned properties of the solution are experienced as well in the computation of the vertical component of the gravity vector, see, e. g., Tables 14 and 15.
The error in the analytical solutions increases dramatically when the prism model is placed at a very long distance from the observation point as show in Fig. 8 in which the prism of Fig. 2a is shifted by 1000 km along the x axis. In this case \(\varGamma >100\) and its value increases even further with N (Tables 16, 17).
Table 16, referred to the gravitational potential, and Table 18, referred to the vertical component of the gravity vector, show that the number of significant digits decreases with increasing order of the density variation. For the cubic and quartic cases, the order of magnitude of the solution is obtained only for \(N=1\), 10, 20 and, in a rather unpredictable way, for other values of N.
Hence, the only reliable solution is obtained by Gauss integration, as shown in Table 17 for the gravitational potential and Table 19 for the vertical component of the gravity vector.
Prism model obtained by shifting the prism model in Fig. 2a of 1000 km along the x axis and related subdivision in smaller subprisms
It is worth noting that the increase in the \(\varGamma \) values associated with grid refinement produces instability of the numerical results characterized by different properties with respect to those described in the previous subsection. Actually, the most distant polyhedra undoubtedly have the highest relative error but their absolute anomaly is much smaller since they are more distant with respect to the polyhedra nearest to the observation point. Consequently, the most distant polyhedra, even if characterized by low or no correct significant figures, just contribute noise when combined with the nearest ones.
This means that the overall anomaly may not be substantially affected so that the most distant polyhedra can be ignored if the observation point is shifted for from the discretized body; in this case also the nearest polyhedra would be affected by numerical instability as shown in Table 16.
6.3 Invariance of the Results Under Arbitrary Rotations of the Reference Frame
In order to fully exploit the tensorial approach developed in the paper, that makes the applications coordinate invariant, it has been decided to express the models in Fig. 2 endowed with the density function (187), (188) and (189). In this way the faces are no longer aligned with the reference axis and density functions expressed in the rotated frame are no longer a function of one variable alone.
In particular, computing the potential in rotated reference frame would (theoretically) give results identical to the unrotated case but, in this case, the full algorithmic steps for a general cubic in x, y, z would be used if one adopts the density function (187). Analogously, a much more general 4-th degree function is addressed by considering the density functions in formulas (188) and (189).
To this end we remind that the rotation of a vector of an arbitrary angle \(\theta \) around an axis defined by the unit vector \( \textbf{u}\) is governed by the orthogonal tensor
where \( \textbf{W}_{\textbf{u}} \) is the skew-symmetric tensor associated with \( \textbf{u}\), i.e., \( \textbf{W}_{\textbf{u}}\,\textbf{a}=\textbf{u}\times \textbf{a}, \,\forall \textbf{a}\).
Denoting by
the unit vectors directed along the axes x, y and z, respectively, the relevant rotated axes will be
and the matrix representation of \( \textbf{R}_{\textbf{u}\theta } \) in the original reference frame
As an example Fig. 9 shows the new reference frame that is obtained by rotating the old one around the axis defined by the unit vector
by a rotation of \(\theta =-60^\circ \). This is equivalent to rotate the old reference frame around -\( \textbf{u}\) by \(\theta =60^\circ \).
The coordinates \([\textbf{s}]^*=(x^*,y^*,z^*)\) of a generic point \( \textbf{s}\) in the new reference frame can been expressed as function of the original coordinates \([\textbf{s}] =(x,y,z)\) by means of the well-known relation
i.e.,
In passing we also notice that expressing above is equivalent to rotate the prism model around \( \textbf{u}\) by an angle \(\theta =60^\circ \). This is due to the fact that \( \textbf{R}_{\textbf{u}(-\theta )}=\textbf{R}_{\textbf{u}\theta }^{-1}=\textbf{R}_{\textbf{u}\theta }^{T} \), the last equality stemming from the property of \( \textbf{R}_{\textbf{u}\theta } \) of being an orthogonal tensor.
To leave unaltered the density distribution with respect to the rotated frame, we need to express the density function by adopting the same functional dependence referred to the original reference frame but using as independent variables the coordinates of the generic point with respect to the reference frame rotated by \( \textbf{R}_{\textbf{u}\theta } \).
Let us now check if and to what extent formulas derived in the paper are really frame- indifferent by considering, separately, the examples presented in Sects. 5.1, 5.2.1 and 5.2.2.
6.3.1 Effects of the Rotation of the Reference Frame for the Examples in Subsection 5.1
The first task to accomplish in order to evaluate the gravity field in a rotated reference frame of the examples in Sect. 5.1 is to properly modify the expressions of the density contrast according to the formula (197).
Accordingly, the density function (187) can be reformulated as follows
where \(\delta _{o}= -747.7\), \(\delta _{1}=203.435\), \(\delta _{2}=-26.764\) and \(\delta _{3}= 1.4247\)
Observing that, given arbitrary vectors \( \textbf{a}\), \( \textbf{b}\), \( \textbf{c}\), \( \textbf{d}\), \( \textbf{e}\), \( \textbf{f}\), one has
and
formula (198) can also be written as
where \(\mathcal {C}^{(1)}=\delta _{1}\,\textbf{e}_3^*\), \(\mathcal {C}^{(2)}=\delta _{2}\,(\textbf{e}_3^*\otimes \textbf{e}_3^*)\), \(\mathcal {C}^{(3)}=\delta _{3}\,(\textbf{e}_3^*\otimes \textbf{e}_3^*\otimes \textbf{e}_3^*)\) and the symbols \(\mathcal {D}_{\textbf{s}}^{(1)}\), \(\mathcal {D}_{\textbf{s}}^{(2)}\), \(\mathcal {D}_{\textbf{s}}^{(3)}\) have been introduced in (4) and defined in the formulas (204) and (207), respectively.
Analogously, formula (188) becomes, in the rotated reference frame \( x^*\), \( y^*\), \( z^*\),
Finally, formula (189) becomes
The gravitational potential and the gravity vector have been computed by assuming the unit vector (195) as axis of rotation and considering rotations of \(\theta =-30^\circ \) and \(\theta =-60^\circ \).
For simplicity, only the most distant observation has been considered, viz \( \textbf{p}\)=(0, 15, z), z being either \(-\)0.15 m or 0 m. Tables 20 and 21 contain, for z = -0,15 m and z = 0 m, respectively, the values of the potential for the prism model in Fig. 2a assuming the density contrast (187) for the original reference frame and the density contrast (198) for the rotated ones.
Assuming the density contrasts considered in the previous two examples, Tables 22 and 23 contain the vertical component of the gravity field evaluated separately in the original reference frame \((\theta =0^\circ \)) and in the rotated ones obtained by assuming \(\theta =-30^\circ \) and \(\theta =-60^\circ \).
Similarly to (197) the component \( g_{z^*} \) of the gravity field with respect to the rotated axis \( z^*\) has been computed by setting \( g_{z^*} = \textbf{E}_3^*\cdot \textbf{g}\) where \( \textbf{g}\) is the gradient vector evaluated with respect to the unrotated vertical frame.
Table 24 contains the vertical component of the gravity field, for the prism in Fig. 2a, and the component of the gravity field along the axis \( z^*\) obtained by rotating the axes of the reference frame around the vector in (195). The density contrast (188) has been assumed for the original reference frame and the density contrast (202) for the rotated one. Specifically, the values \(\theta =-30^\circ \), \(\theta =-45^\circ \) and \(\theta =-60^\circ \) have been assumed.
Finally, for the prism in Fig. 2b, Table 25 contains the vertical component of the gravity field and the component of the gravity field along the axis \( z^*\) obtained by rotating the axes of the reference frame around the vector in (195). The density contrast (189) has been assumed for the original reference frame and the density contrast (203) for the rotated one. Also in this case the values of \(\theta =-30^\circ \), \(\theta =-45^\circ \) and \(\theta =-60^\circ \) have been assumed as angles of rotation.
The examination of the results reported in Tables 20-25 clearly shows that the computation of the gravitational potential and of the gravity vector is substantially unaffected by the rotation of the reference frame although, in this last case, more term are needed to express the density contrast. For this reason we have reported in Table 26 the run-times associated with the results of Table 24; it can be noted that, as a mean, one obtains increments in the run-time up to the 19%.
6.3.2 Effects of the Rotation of the Reference Frame on the Origin-Observation Point Separation
In order to check how the effects of the origin-observation point separation are influenced by an arbitrary rotation of the reference frame, we make reference to the results reported in Tables 21 and 23 by comparing them with those obtained by considering the same example referred to a rotated frame.
Tables 21 and 23 shows that the values of the gravitational potential and of the gravity vector are insensitive to the rotation of the reference frame. For the reason, in order to avoid duplicating the same values, we report the results of our numerical experiment in the format of Tables 27 and 28 for the gravitational potential and the gravity vector, respectively.
Inspection of Tables 27 and 28 shows that the effects associated with the rotation of the reference frame increase with the order of the density variation, the amount of the rotation and with the distance of the reference point from the origin. Specifically, this last effect is more pronounced for greater values of the rotation since this produces a larger inhomogeneity in the coordinates of the vertices and, hence, of the dimensionless target distance \(\varGamma \).
6.3.3 Effects of the Rotation of the Reference Frame on the Observation Point- Target Body Separation
Let us now investigate the influence of arbitrary rotations of the reference frame on the observation point-target body separation by taking into account the results reported in Tables 10 and 11. These last ones are included in the first column of Tables 29 nd 30 that refer, respectively, to gravitational potential and to the gravity vector
The results of Table 30, similarly to those included in Table 29 and in the previous subsection, show that the values of the gravitational potential and of the gravity vector are substantially insensitive to the rotation of the reference frame for low values of the dimensionless target ratio \(\varGamma \).
As a matter of fact this can be considered as a more general feature that characterizes the computation of the gravity fields since discrepancies between the values associated with increasing values of \(\theta \) are mainly due to greater values of \(\varGamma \).
A further interesting result that prompts by examining the results in Table 29 when x = 1000 km, i.e., when \(\varGamma \) is large, is that the values corresponding to \(\theta =-30^\circ \) and to \(\theta =-60^\circ \) are almost opposite each other and have significantly different orders of magnitude with respect to the case \(\theta =0^\circ \) for constant and quadratic density contrasts. Conversely, when the vertical component of the gravity vector is computed, this happens for linear and cubic density contrasts.
7 Conclusions
The gravitational potential (GP) and gravity vector (GV) induced at an arbitrary point by a polyhedral body having arbitrary shape and polynomial density contrast have been obtained in tensor form and expressed as the sum of quantities that depend only upon the 3D coordinates of the vertices of the polyhedron and upon the parameters defining the density contrast. Remarkably, the formulation holds true whatever is the origin of the Cartesian reference frame assumed in the calculations in the sense that is does not have to necessarily coincide with the observation point.
Differently from the recent contribution by (Ren et al. 2020), the algebraic expressions of the GP and the GV reported in the paper allow for their computation without any use of recursive formulas. Furthermore, by means of rigorous mathematical arguments, singularities are ruled out from the analytical expression of both the GP and GV as well as from their algebraic counterparts.
Though limited to a polynomial density contrast varying with a quartic law as a maximum, the formulation developed in the paper can be easily extended to polynomials of higher degree. In additional, being expressed in tensor form, the resulting formulas can be specialized to arbitrary reference frames.
The effectiveness of the proposed approach has been intensively tested by numerical comparisons, carried out by means of a MATLAB code, with several examples derived from the specialized literature. The numerical stability issue associated with the analytical approach to gravity field modeling has been investigated by assuming the growth of the relative error in the computation as a function of the dimensionless target distance, i.e., the distance between the observation point and the center of a building block in a meshed model over, the size of the polyhedral element.
Future contributions will address the derivation of analytical formulas for the second- and third-order gradient of polyhedral bodies endowed with a polynomial density contrast of arbitrary order.
References
Abtahi SM, Pedersen LB, Kamm J, Kalscheuer T (2016) Consistency investigation, vertical gravity estimation and inversion of airborne gravity gradient tensor data: a case study from northern Sweden. Geophysics 81(3):B65–B76
Aydemir A, Ates A, Bilim F, Buyuksarac A, Bektas O (2014) Evaluation of gravity and aeromagnetic anomalies for the deep structure and possibility of hydrocarbon potential of the region surrounding Lake Van, Eastern Anatolia, Turkey. Surv Geophys 35:431–448
Balmino G (1994) Gravitational potential harmonics from the shape of an homogeneous body. Celest Mech Dyn Astron 60(3):331–364
Bajracharya S, Sideris M (2004) The Rudzki inversion gravimetric reduction scheme in geoid determination. J Geodesy 78(4–5):272–282
Banerjee B, Das Gupta SP (1977) Gravitational attraction of a rectangular parallelepiped. Geophysics 42:1053–1055
Barnett CT (1976) Theoretical modeling of the magnetic and gravitational fields of an arbitrarily shaped three-dimensional body. Geophysics 41:1353–1364
Beiki M, Pedersen LB (2010) Eigenvector analysis of gravity gradient tensor to locate geologic bodies. Geophysics 75(6):I37–I49
Cady JW (1980) Calculation of gravity and magnetic anomalies of finite length right polygonal prisms. Geophysics 45:1507–1512
Cai Y, Wang C (2005) Fast finite-element calculation of gravity anomaly in complex geological regions. Geophys J Int 162(3):696–708
Chai Y, Hinze WJ (1988) Gravity inversion of an interface above which the density contrast varies exponentially with depth. Geophysics 53:837–845
Chakravarthi V, Raghuram HM, Singh SB (2002) 3-D forward gravity modeling of basement interfaces above which the density contrast varies continuously with depth. Comp Geosc 28:53–57
Chakravarthi V, Sundararajan N (2007) 3D gravity inversion of basement relief: a depth-dependent density approach. Geophysics 72:I23–I32
Chao BF, Rubincam DP (1989) The gravitational field of Phobos. Geophys Res Lett 16(8):859–862
Chapin DA (1998) Gravity instruments: past, present, future. Lead Edge 17:100–112
Chappell A, Kusznir N (2008) An algorithm to calculate the gravity anomaly of sedimentary basins with exponential density-depth relationships. Geophys Prosp 56:249–258
Chen C, Ren Z, Pan K, Tang J, Kalscheuer T, Maurer H, Su Y, Li Y (2018) Exact solutions of the vertical gravitational anomaly for a polyhedral prism with vertical polynomial density contrast of arbitrary orders. Geophys J Int 214:2115–2132
Chen C, Chen Y, Bian S (2019) Evaluation of the spherical harmonic coefficients for the external potential of a polyhedral body with linearly varying density. Celest Mech Dyn Astron 131(2):8
Colombo OL (1981) Numerical methods for harmonic analysis on the sphere. Airforce Geophysics Laboratory, Scientific Report n, p 7
Conway JT (2015) Analytical solutions from vector potentials for the gravitational field of a general polyhedron. Cel Mech Dyn Astr 121:17–38
Cordell L (1973) Gravity analysis using an exponential density depth function-San Jacinto graben, California. Geophysics 38:684–690
Cunningham LE (1970) On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite. Celest Mech 2(2):207–216
De Castro DL, Fuck RA, Phillips JD, Vidotti RM, Bezerra FH, Dantas EL (2014) Crustal structure beneath the Paleozoic Parnaíba Basin revealed by airborne gravity and magnetic data, Brazil. Tectonophysics 614:128–145
D’Urso MG, Russo P (2002) A new algorithm for point-in polygon test. Surv Rev 284:410–422
D’Urso MG, Marmo F (2009) Vertical stresses due to linearly distributed pressures over polygonal domains. ComGeo I. First International Symposium on Computational Geomechanics. Juan les Pins, France, pp 283–289
D’Urso MG (2012) New expressions of the gravitational potential and its derivates for the prism. In Hotine-Marussi international symposium on mathematical geodesy, 7rd. Sneeuw N, Novák P, Crespi M, Sansò F. Springer-Verlag, Berlin Heidelberg pp. 251–256
D’Urso MG (2013) On the evaluation of the gravity effects of polyhedral bodies and a consistent treatment of related singularities. J Geod 87:239–252
D’Urso MG, Marmo F (2013) On a generalized Love’s problem. Comp Geosc 61:144–151
D’Urso MG (2014) Analytical computation of gravity effects for polyhedral bodies. J Geod 88:13–29
D’Urso MG (2014) Gravity effects of polyhedral bodies with linearly varying density. Cel Mech Dyn Astr 120:349–372
D’Urso MG, Marmo F (2015) Vertical stress distribution in isotropic half-spaces due to surface vertical loadings acting over polygonal domains. Zeit Ang Math Mech 95:91–110
D’Urso MG, Trotta S (2015) Comparative assessment of linear and bilinear prism-based strategies for terrain correction computations. J Geod 89:199–215
D’Urso MG (2015) The gravity anomaly of a 2d polygonal body having density contrast given by polynomial functions. Surv Geophys 36:391–425
D’Urso MG (2016) Some remark on the computation of the gravitational potential of masses with linearly varying density. In: VIII Hotine-Marussi International Symposium on Mathematical Geodesy, 8rd. Sneeuw N, Novák P, Crespi M, Sansò F. Rome
D’Urso MG, Trotta S (2017) Gravity anomaly of polyhedral bodies having a polynomial density contrast. Surv Geophys 38:781–832
Farquharson C, Mosher C (2009) Three-dimensional modelling of gravity data using finite differences. J Appl Geophys 68(3):417–422
Fukushima T (2018) Recursive computation of gravitational field of a right rectangular parallelepiped with density varying vertically by following an arbitrary degree polynomial. Geophys J Int 215:864–879
Gallardo-Delgado LA, Pérez-Flores MA, Gómez-Treviño E (2003) A versatile algorithm for joint 3D inversion of gravity and magnetic data. Geophysics 68:949–959
García-Abdeslem J (1992) Gravitational attraction of a rectangular prism with depth dependent density. Geophysics 57:470–473
García-Abdeslem J (2005) Gravitational attraction of a rectangular prism with density varying with depth following a cubic polynomial. Geophysics 70:J39–J42
Gendzwill J (1970) The gradational density contrast as a gravity interpretation model. Geophysics 35:270–278
Golizdra GY (1981) Calculation of the gravitational field of a polyhedra. Izv Earth Phys (English Translation) 17:625–628
Gottlieb RG (1993) Fast gravity, gravity partials, normalized gravity, gravity gradient torque and magnetic field: Derivation, code and data. In NASA Contractor Report 188243. National Aeronautics and Space Administration Lyndon B. Johnson Space Center Houston, Texas
Götze HJ, Lahmeyer B (1988) Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 53:1096–1108
Gurtin ME, Fried E, Anand L (2010) The mechanics and thermodynamics of continua. Cambridge University Press
Guspí F (1990) General 2D gravity inversion with density contrast varying with depth. Geoexpl 26:253–265
Hamayun P, Prutkin I, Tenzer R (2009) The optimum expression for the gravitational potential of polyhedral bodies having a linearly varying density distribution. J Geod 83:1163–1170
Hansen RO (1999) An analytical expression for the gravity field of a polyhedral body with linearly varying density. Geophysics 64:75–77
Hansen RO (2001) Gravity and magnetic methods at the turn of the millennium. Geophysics 66:36–37
Holstein H, Ketteridge B (1996) Gravimetric analysis of uniform polyhedra. Geophysics 61:357–364
Holstein H (2003) Gravimagnetic anomaly formulas for polyhedra of spatially linear media. Geophysics 68:157–167
Jacoby W, Smilde PL (2009) Gravity interpretation: fundamentals and application of gravity inversion and geological interpretation. Springer, Berlin
Jahandari H, Farquharson CG (2013) Forward modeling of gravity data using finite-volume and finite element methods on unstructured grids. Geophysics 78(3):G69–G80
Jamet O, Thomas E (2004) A linear algorithm for computing the spherical harmonic coefficients of the gravitational potential from a constant density polyhedron. In: Proceedings of the 2nd international GOCE user workshop, GOCE, the geoid and oceanography Lasserre JB (1999)
Jamet O, Tsoulis D (2020) A line integral approach for the computation of the potential harmonic coefficients of a constant density polyhedron. J Geodesy 94(3):30
Jekeli C (2006) Airborne gradiometry error analysis. Surv Geophys 27:257–275
Jiancheng H, Wenbin S (2010) Comparative study on two methods for calculating the gravitational potential of a prism. Geo-spat Inf Sci 13:60–64
Kaftan I, Salk M, Sari C (2005) Application of the finite element method to gravity data case study: western Turkey. J Geodyn 39(5):431–443
Kellogg OD (1929) Foundations of potential theory. Springer, Berlin
Kwok YK (1991) Singularities in gravity computation for vertical cylinders and prisms. Geophys J Int 104:1–10
Kwok YK (1991) Gravity gradient tensors due to a polyhedron with polygonal facets. Geophys Prosp 39:435–443
Kuhn M, Seitz K (2005) Comparison of Newton’s integral in the space and frequency domains, In: Sanso F (Ed) A Window on the Future of Geodesy. IAG Symposia, vol. 128, pp. 386–391
Li X, Chouteau M (1998) Three-dimensional gravity modelling in all spaces. Surv Geophys 19:339–368
Litinsky VA (1989) Concept of effective density: key to gravity depth determinations for sedimentary basins. Geophysics 54:1474–1482
Marmo F, Rosati L (2016) A general approach to the solution of Boussinesq’s problem for polynomial pressures acting over polygonal domains. J Elast 122:75–112
Marmo F, Sessa S, Rosati L (2016) Analytical solution of the Cerruti problem under linearly distributed horizontal pressures over polygonal domains. J Elast 124:27–56
Marmo F, Toraldo F, Rosati L (2016) Analytical formulas and design charts for transversely isotropic half-spaces subject to linearly distributed pressures. Meccanica 51:2909–2928
Marmo F, Toraldo F, Rosati L (2017) Transversely isotropic half-spaces subject to surface pressures. Int J Solids Struct 104–105:35–49
Marmo F, Toraldo F, Rosati A, Rosati L (2018) Numerical solution of smooth and rough contact problems. Meccanica 53:1415–1440
Martín-Atienza B, García-Abdeslem J (1999) 2-D gravity modeling with analytically defined geometry and quadratic polynomial density functions. Geophysics 64:1730–1734
Martinez C, Li Y, Krahenbuhl R, Braga MA (2013) 3D inversion of airborne gravity gradiometry data in mineral exploration: a case study in the Quadrilatero Ferrfero. Brazil. Geophys. 78(1):B1–B11
Moorkamp M, Heincke B, Jegen M, Roberts AW, Hobbs RW (2011) A framework for 3-D joint inversion of MT, gravity and seismic refraction data. Geophy J Int 184(1):477–493
Montana CJ, Mickus KL, Peeples WJ (1992) Program to calculate the gravitational field and gravity gradient tensor resulting from a system of right rectangular prisms. Comp Geosc 18:587–602
Mostafa ME (2008) Finite cube elements method for calculating gravity anomaly and structural index of solid and fractal bodies with defined boundaries. Geophys J Int 172:887–902
Murthy IVR, Rao DB (1979) Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth. Geophysics 44:1525–1530
Murthy IVR, Rao DB, Ramakrishna P (1989) Gravity anomalies of three dimensional bodies with a variable density contrast. Pure Appl Geophys 30:711–719
Nabighian MN, Ander ME, Grauch VJS, Hansen RO, LaFehr TR, Li Y, Pearson WC, Peirce JW, Phillips JD, Ruder ME (2005) Historical development of the gravity method in exploration. Geophysics 70:63–89
Nagy D (1966) The gravitational attraction of a right rectangular prism. Geophysics 31:362–371
Nagy D, Papp G, Benedek J (2000) The gravitational potential and its derivatives for the prism. J Geod 74:553–560
Okabe M (1979) Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translation into magnetic anomalies. Geophysics 44:730–741
Pan JJ (1989) Gravity anomalies of irregularly shaped two-dimensional bodies with constant horizontal density gradient. Geophysics 54:528–530
Paul MK (1974) The gravity effect of a homogeneous polyhedron for three-dimensional interpretation. Pure Appl Geophys 112:553–561
Petrović S (1996) Determination of the potential of homogeneous polyhedral bodies using line integrals. J Geod 71:44–52
Plouff D (1975) Derivation of formulas and FORTRAN programs to compute gravity anomalies of prisms. Nat Tech Inf Serv No PB-243-526. US Dept of Commerce, Springfield, VA
Plouff D (1976) Gravity and magnetic fields of polygonal prisms and application to magnetic terrain corrections. Geophysics 41:727–741
Pohanka V (1988) Optimum expression for computation of the gravity field of a homogeneous polyhedral body. Geophys Prospect 36:733–751
Pohanka V (1998) Optimum expression for computation of the gravity field of a polyhedral body with linearly increasing density. Geophys Prospect 46:391–404
Rao DB (1985) Analysis of gravity anomalies over an inclined fault with quadratic density function. Pageoph 123:250–260
Rao DB (1986) Modeling of sedimentary basins from gravity anomalies with variable density contrast. Geophys J R Astr Soc 84:207–212
Rao DB (1990) Analysis of gravity anomalies of sedimentary basins by an asymmetrical trapezoidal model with quadratic function. Geophysics 55:226–231
Rao DB, Prakash MJ, Babu RN (1990) 3D and 2 \(1/2\) modeling of gravity anomalies with variable density contrast. Geophys Prosp 38:411–422
Rao CV, Chakravarthi V, Raju ML (1994) Forward modelling: gravity anomalies of two-dimensional bodies of arbitrary shape with hyperbolic and parabolic density functions. Comp Geosci 20:873–880
Ren Z, Chen C, Pan K, Kalscheuer T, Maurer H, Tang J (2017) Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surv Geophys 38(2):479–502
Ren Z, Zhong Y, Chen C, Tang J, Kalscheuer T, Maurer H, Li Y (2018) Gravity gradient tensor of arbitrary 3D polyhedral bodies with up to third-order polynomial horizontal and vertical mass contrasts. Surv Geophys 39(5):901–935
Ren Z, Zhong Y, Chen C, Tang J, Pan K (2018) Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics 83(1):G1–G13
Ren Z, Chen C, Zhong Y, Chen H, Kalscheuer T, Maurer H, Tang J, Hu X (2020) Recursive Analytical Formulae of Gravitational Fields and Gradient Tensors for Polyhedral Bodies with Polynomial Density Contrasts of Arbitrary Non-negative Integer Orders. Surv Geophys 41:695–722
Roberts AW, Hobbs RW, Goldstein M, Moorkamp M, Jegen M, Heincke B (2016) Joint stochastic constraint of a large data set from a salt dome. Geophysics 81(2):ID1–ID24
Rosati L, Marmo F (2014) Closed-form expressions of the thermo-mechanical fields induced by a uniform heat source acting over an isotropic half-space. Int J Heat Mass Transf 75:272–283
Ruotoistenmäki T (1992) The gravity anomaly of two-dimensional sources with continuous density distribution and bounded by continuous surfaces. Geophysics 57:623–628
Sessa S, D’Urso MG (2013) Employment of Bayesian networks for risk assessment of excavation processes in dense urban areas. Proc 11th Int Conf ICOSSAR 2013, 30163-30169
Silva JB, Costa DCL, Barbosa VCF (2006) Gravity inversion of basement relief and estimation of density contrast variation with depth. Geophysics 71:J51–J58
Strakhov VN (1978) Use of the methods of the theory of functions of a complex variable in the solution of three-dimensional direct problems of gravimetry and magnetometry. Dokl Akad Nauk 243:70–73
Strakhov VN, Lapina MI, Yefimov AB (1986) A solution to forward problems in gravity and magnetism with new analytical expression for the field elements of standard approximating body. Izv Earth Phys (English Translation) 22:471–482
Tang KT (2006) Mathematical methods for engineers and scientists. Springer, Berlin
Trotta S, Marmo F, Rosati L (2016) Analytical expression of the Eshelby tensor for arbitrary polygonal inclusions in two-dimensional elasticity. Compos B 106:48–58
Trotta S, Marmo F, Rosati L (2016) Evaluation of the Eshelby tensor for polygonal inclusions. Compos B. https://doi.org/10.1016/j.compositesb.2016.10.018
Trotta S, Zuccaro G, Sessa S, Marmo F, Rosati L (2018) On the evaluation of the Eshelby tensor for polyhedral inclusions of arbitrary shape. Composites B 144:267–281
Tsoulis D (2000) A note on the gravitational field of the right rectangular prism. Boll Geod Sc Aff LIX-1:21-35
Tsoulis D, Petrović S (2001) On the singularities of the gravity field of a homogeneous polyhedral body. Geophysics 66:535–539
Tsoulis D (2012) Analytical computation of the full gravity tensor of a homogeneous arbitrarily shaped polyhedral source using line integrals. Geophysics 77:F1–F11
Van der Meijde M, Juli J, Assumpo M (2013) Gravity derived Moho for South America. Tectonophysics 609:456–467
Waldvogel J (1979) The Newtonian potential of homogeneous polyhedra. J Appl Math Phys 30:388–398
Werner RA (1994) The gravitational potential of a homogeneous polyhedron. Celest Mech Dynam Astr 59:253–278
Werner RA (1997) Spherical harmonic coefficients for the potential of a constant density polyhedron. Comput Geosci 23(10):1071–1077
Werner RA, Scheeres DJ (1997) Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia. Celest Mech Dynam Astr 65:313–344
Werner RA (2017) The solid angle hidden in polyhedron gravitation formulations. J Geod 91:307–328
Won IJ, Bevis M (1987) Computing the gravitational and magnetic anomalies due to a polygon: algorithms and Fortran subroutines. Geophysics 52:232–238
Wu L (2016) Efficient modelling of gravity effects due to topographic masses using the Gauss-FFT method. Geophys J Int 205(1):160–178
Wu L (2018) Efficient modeling of gravity fields caused by sources with arbitrary geometry and arbitrary density distribution. Surv Geophys 39(3):401–434
Wu L (2019) Fourier-domain modeling of gravity effects caused by polyhedral bodies. J Geodesy 93:635–653
Zhang J, Zhong B, Zhou X, Dai Y (2001) Gravity anomalies of 2D bodies with variable density contrast. Geophysics 66:809–813
Zhang J, Jiang L (2017) Analytical expressions for the gravitational vector field of a 3-D rectangular prism with density varying as an arbitrary-order polynomial function. Geophys J Int 210:1176–1190
Zhou X (2008) 2D vector gravity potential and line integrals for the gravity anomaly caused by a 2D mass of depth-dependent density contrast. Geophysics 73:I43–I50
Zhou X (2009) General line integrals for gravity anomalies of irregular 2D masses with horizontally and vertically dependent density contrast. Geophysics 74:I1–I7
Zhou X (2009) 3D vector gravity potential and line integrals for the gravity anomaly of a regular prism with 3D variable density contrast. Geophysics 74:I43–I53
Zhou X (2010) Analytical solution of gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function. Geophysics 75:I11–I19
Acknowledgements
The second author gratefully acknowledges the grant EARLY STAGE—Cod. 21AR018—"Computational Methods for the Study of the Gravitational Field and related Anomalies" received by the Department of Engineering and Applied Sciences of the University of Bergamo. Both authors are particularly indebted to prof. Horst Holstein, who acted as one of the reviewers, for his continuous support, very useful suggestions in the organization of the paper, especially for the section dedicated to the numerical examples, and constructive criticism of the earlier versions of the manuscript. Two further anonymous reviewers are also gratefully acknowledged.
Funding
Open access funding provided by Università degli studi di Bergamo within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Contributions
The methodology was conceived and formulated by MGDU who also wrote the manuscript. DDL was responsible for LaTeX typesetting and MATLAB coding. Both authors revised and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest for the present contribution.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Notation
To help the reader suitably manage and interpret the higher-order tensors introduced in the paper it is convenient to introduce the following notation.
Apart from scalar quantities, a generic tensor of order k will be denoted by a calligraphic symbol \( \mathcal {A}^{(k)} \). It may also be equipped with a suffix denoting composition of tensors of the same order. In particular, we introduce the following quantities
where the rank-two tensor product \( \textbf{a}\otimes \textbf{b}\) between vectors \( \textbf{a}\) and \( \textbf{b}\) is defined as
and \( \mathcal {V}\) is a vector space of suitable dimension.
The previous definition can be generalized to tensors of order greater than two
and so on.
Extending further the definition (204) we have
where \( \mathcal {D}^{(3)}_{\textbf{p}\textbf{p}\textbf{p}}=\textbf{p}\otimes \textbf{p}\otimes \textbf{p}\), \( \mathcal {D}^{(3)}_{\textbf{r}\textbf{r}\textbf{r}}=\textbf{r}\otimes \textbf{r}\otimes \textbf{r}\),
and
Analogously, we shall set
where \( \mathcal {D}^{(4)}_{\textbf{p}\textbf{p}\textbf{p}\textbf{p}}=\textbf{p}\otimes \textbf{p}\otimes \textbf{p}\otimes \textbf{p}\), \( \mathcal {D}^{(4)}_{\textbf{r}\textbf{r}\textbf{r}\textbf{r}}=\textbf{r}\otimes \textbf{r}\otimes \textbf{r}\otimes \textbf{r}\) and
In the body of the paper we shall also use the symbol \( \mathcal {D}^{(2)}_{\textbf{s}_i} \) to emphasize that the vector \( \textbf{r}\) appearing in the definition of \( \mathcal {D}^{(2)}_{\textbf{s}} \) does belong to the \( i^{th} \) face \( F_i \) of the polyhedral boundary \( \partial \varOmega \) of \(\varOmega \). Hence
Finally, setting \( \textbf{r}=\textbf{r}_i \), \( \mathcal {D}^{(3)}_{\textbf{s}_i} \) is provided by formulas (207–209) and \( \mathcal {D}^{(4)}_{\textbf{s}_i} \) by formulas (211–213).
To effectively handle tensor operation, each tensor has to be associated with the relevant matrix representation. While this is trivial for first-order (vector) and second-order (rank-two) tensors
the task is less trivial for tensors whose rank is greater than two. Actually, there is not a unique way to construct a matrix associated with such tensors. Accordingly, as a hint for programming, we shall adopt the procedure exploited in MATLAB. In particular, for a rank-three tensor, MATLAB stores the components associated with the third index in pages; in turn these are ordered along the third dimension of an ideal cube whose slices are the usual two-dimensional matrices.
Hence, to be specific
where
and the three blocks of the previous vector represent the three pages of the matrix representation adopted by MATLAB to represent the tensor \( \textbf{a}\otimes \textbf{b}\otimes \textbf{c}\). In particular
where
We generalize the previous approach to tensors having rank greater than three by defining a matrix of matrices, i.e., a hypermatrix, for rank-four tensors and a vector of hypermatrices for rank-five tensors. For instance

Its specialization to \( \mathcal {D}^{(4)}_{\textbf{s}} \) yields

where
The previous tensors can be combined to provide scalar quantities or, more generally, lower-rank tensors according to the following rules expressed in terms of their Cartesian components.
and
Actually, formula (227) allows one to express the density function (1) in the more concise form (4) by setting

where

Analogously, it turns out to be

Its particular, setting
where
one has
In conclusion, it prompts from the previous formulas that the elements of \( \mathcal {D}_{\textbf{s}}^{(k)} \), \( k=1,\dots ,4 \), have the same structure as \( \mathcal {C}^{(k)} \) with the subscripts 1, 2, 3 in \( \mathcal {C}^{(k)} \) indicating which factors x, y, z are present in the corresponding elements of \( \mathcal {D}_{\textbf{s}}^{(k)} \).
Finally, in the body of the paper we shall carefully distinguish between
and
Analogously
while
and
Furthermore
but
and so on.
Appendix B: Evaluation of 2D Integrals Related to the GP by Means of 1D Integrals
We are going to show how to evaluate analytically the 2D integrals
introduced in (33) and extended to polygonal faces \( F_i \).
As a matter of fact we only need to evaluate the integrals (249) for \( m > 1 \) since the additional ones have been computed in D’Urso (2012, 2013a, 2014a); the relevant expressions being reported in Sect. 2.3. To evaluate the integral (249) we shall exploit the following differential identities [ Gurtin et al. (2010)]
where \( \varphi \), \( \textbf{a}\),\( \textbf{b}\) and \( \textbf{c}\) are smooth scalar and vector fields while \((\cdot )^T\) stands for transpose. They are needed to apply generalized versions of Gauss’ theorem (Tang 2006) so as to express 2D integrals as integrals extended to the boundary.
To make the paper reasonably self-contained we report a short proof of some of the identities (250–257). Adopting the convention of repeated indices and denoting by \( (\cdot ),_{j} \) the derivation of the quantity \( (\cdot ) \) with respect to the j-th variable, one has
Analogously
and so on.
We shall also set
and make use of the symbol introduced in (43).
-
Integral (249) for \( m=2 \)
Let us first apply the differential identity (252) to the following expression
where \( \mathcal {I}^{(2)} \) is the rank-two identity tensor. Hence
To express the last integral on the right-hand side as a function of boundary integrals we exploit the differential identity (251) to get
Hence
or equivalently, invoking (47),
Replacing the previous formula in (262) we finally get the desired result
an expression depending only upon boundary integrals.
Analogously
and so on.
-
Integral (249) for \(m=3\)
Exploiting the differential identity (254) we get
whose integral extended to \( F_i \) provides, on account of (260)
To express \( \textrm{P}_{F_i}^{(1/2\cdot 1)} \) as a function of a boundary integrals we apply formula (253) to
Accordingly, it turns out to be
on account of (45).
In conclusion, substituting the previous expression in (269), one has
-
Integral (249) for \(m=4\)
The differential identity (256) provides
Hence, integrating over \( F_i \) one gets
To express \( \textrm{P}_{F_i}^{(1/2\cdot 2)} \) in terms of boundary integrals, we invoke formula (255) to get
so that
Thus, we infer, upon integrating over \( F_i \)
where we have invoked formula (266). Hence replacing the previous expression in (274) we get
Appendix C: Explicit Expressions of Integrals
We report the algebraic expressions of some definite integrals repeatedly referred to in the body of the paper although some of them have been already computed elsewhere, D’Urso (2013a, 2014a, 2014b), and denominated in a different way.
Recalling the definition of the quantities \( p_j \), \( q_j \), \( u_j \), \( v_j \), introduced in formulas (55) and (56), we set
where the suffix \((\cdot )_j\) has been added to remind that they all refer to the j-th edge of the generic face \(F_i\).
It turns out to be
Appendix D: Evaluation of 2D Integrals Related to the GV by Means of 1D Integrals
We are going to show how to evaluate analytically the 2D integrals
introduced in (113), required to compute the gravity potential.
As a matter of fact the integrals (293) for \( m=0, 1, 2 \) have been already computed in D’Urso (2014b) and D’Urso and Trotta (2017) and are reported here after for the sake of completeness. Specifically
For brevity the derivation of the additional formulas required for computing \(\textrm{P}_{F_i}^{(m,3/2)}\) in the cases \( m=3, 4, 5 \) is detailed only for \( m=3 \) while final formulas are directly reported for \( m=4, 5 \).
Exploiting the differential identity (256) one has
so that
that can also be written as
By following a similar path of reasoning one has
or, equivalently
Finally, it turns out to be
so that one has
an expression that can also be written as
where
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
D’Urso, M.G., Di Lieto, D. Gravitational Fields of Polyhedral Bodies with 3D Polynomial Density Contrast. Surv Geophys (2024). https://doi.org/10.1007/s10712-023-09822-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10712-023-09822-8