1 Introduction

Slopes, and their stability, constitute one of the primary concerns in any civil and mining engineering project (Kirschbaum et al. 2010; Petley 2012; Sasaoka et al. 2015; Heidarzadeh et al. 2019; Jing et al. 2023, Hou et al. 2023). This endeavor becomes considerably complex in rock engineering due to the presence of discontinuities. An immediate consequence of the presence of discontinuities in a rock mass is the formation of discrete rock blocks that vary in size from a few cubic millimeters to several cubic meters. Due to the low-stress state near these free surfaces, the primary factors that influence the dynamic stability of the blocks are their own weight, possible fluid pressures acting on the massif, static loads or overloads, and external dynamic loads, such as those produced by earthquakes. The gross stability of blocks is typically assessed through a factor of safety, denoted as FS, and finding the critical slip surface with the minimum factor of safety is a common goal in geotechnical engineering.

One of the first decisions the rock engineer has to take is how to consider the rock mass (Alzo’ubi 2016). On the one hand, by a discreet analysis of kinematics and dynamics taking into account the frictional behavior of present joint sets (weathering, roughness JRC values, …) and one of the limit equilibrium methods, LEM (De Freitas and Watters 1973; Goodman and Shi 1985; Abramson et al. 2001; Wyllie and Mah 2004; Bar and Barton 2017; Azarafza et al. 2021); on the other, the consideration of the mass as a continuum whole and use finite elements modeling (FEM) and similar robust numerical approaches with constitutive resistance equations, as the Hoek–Brown (H–B) criterion (Jing et al. 2023). Classically, these are two very different approaches to studying rock mass failure and, following Jing and Hudson (2002), we may call them continuum and discrete -discontinuum- analyses. Continuum (FEM, for instance) may make sense, for instance, for Q values (Q-System, Barton et al. 1974) under 0.1 (pseudo continuum for Barton 2021, 2022) or over 100. In intermediate cases, for middling Q values, discontinuum analyses mostly either consider frictional resistance on joint planes, apply distinct element methods (Cundall 1971; Cundall and Hart 1985; Shen and Abbas 2013; Grindheim et al. 2022; Sun et al. 2022; Zhao et al. 2022), or use block theory models (Shi and Goodman 1989).

In heavily jointed rock masses, say with Q < 0.1 or RMR < 30, the abundance of discontinuities creates uncertainty in the orientation and nature of the critical surface. This, coupled with the presence of a tension crack release surface, leads to a complex stability configuration (Lin and Sheng 2021; Park 2023) that may be better dealt with by considering the resistance of the rock mass rather than deterministically characterizing a discrete joint set.

According to Barton (1971), tension cracks result from small movements within the rock mass, which, although individually small, can accumulate and significantly displace the slope surface. His model determined that the tensile crack generated by tangential movements is a relevant indicator of shear failure initiation within the rock mass. However, Wyllie and Mah (2004) and Wyllie (2017) note that many rock slopes with tensile cracks have not yet failed and have maintained their stability for decades. Nevertheless, the presence of a tensile crack should be considered a potential indicator of instability in any case. Ideally, we would know the position of the tensile crack, but in field surveys, it can be challenging to determine the exact depth of the crack, as it is often obstructed by rock fragments or sediments. Therefore, it is more conservative to analyze the most critical potential failure block as a function of the distance from the crack to the edge of the slope face. On the other hand, FEM methods, while appropriate for pseudo continuum rock masses, experience difficulties when modeling cases with tension cracks, as the crack must be included as a boundary condition (Park 2023). Moreover, scarce attention has been paid to rock masses with tension cracks, especially when compared to soil slopes, and then applying linear approaches (Zhao et al. 2017), or the H–B criterion (Zhu and Yang 2018; Lee and Pietruszczak 2021).

In such scenarios, it is important to have a failure criterion for the rock mass (Hoek and Brown 1980, 2019; Kulatilake et al. 2006; Úcar 2021), preferably a non-linear one that fits the significant curvature (Barton 2016) of the failure envelope at low normal stresses (as expected in slope stability cases). While Belandria et al. (2021) studied a case where the position of the tension crack was known and applied the Mohr–Coulomb criterion to estimate its shear strength, which was suitable for analyzing well-characterized joint sets, this paper uses a non-linear failure criterion where the position of the critical tension crack is an unknown variable. Additionally, the rock mass is considered to behave as a pseudo continuum rather than a structurally controlled mass where displacement occurs along well-defined joint sets. In these cases, the approach as a continuum model typically involves time-consuming procedures such as finite element, finite difference, and boundary element methods, which require special computational requirements and training to use effectively (Raghuvanshi 2019). Empirical methods based on rock mass classifications are often in use in preliminary stages of stability assessment (Duran and Douglas 2000; Basahel and Mitri 2017).

This paper focuses on the slope stability of a heavily jointed rock mass with tension cracks, where the presence of discontinuities at different attitudes can result in planar failure and the opening of tension cracks upslope. We consider dynamic loads, such as earthquakes, and static overload upslope, as well as pore pressure acting on the tension crack and sliding plane.

The H–B criterion (Hoek and Brown 1980, 2019) is the best-known non-linear criterion for rock masses. However, in this paper, we explore the application of a novel criterion: Úcar's Focus procedure, extended to the rock mass case (Úcar 2021).

The procedure presented in this paper provides a useful addition to preliminary surveys. An easy-to-use spreadsheet gives an approximate value of the Factor of Safety, which can then be refined further through more robust and complex modeling approaches.

2 Úcar's Focus Procedure: Non-linear Strength Criterium

As mentioned earlier, the application of non-linear criteria has long been recognized as a necessity in rock engineering. In this paper, we compare the use of the well-known H–B criterion (Hoek and Brown 1980, 2019) with a novel approach called Úcar's Focus procedure, which is less well known. To introduce this new criterion (Úcar 2011, 2021), we provide a brief overview of its main points.

In this criterion, the relationship between the major principal stress (\({\sigma }_{1}\)) and the minor principal stress (\({\sigma }_{3}\)) is given by Eq. (1):

$$\overline{\sigma }_{1} = k_{1} \left( {\overline{\sigma }_{3} - \xi } \right) + k_{2} \left( {\overline{\sigma }_{3} - \xi } \right)^{1/2}$$
(1)

where \(\overline{{\sigma }_{1}}=\left({\sigma }_{1}/{\sigma }_{c}\right)\) and \(\overline{{\sigma }_{3}}=\left({\sigma }_{3}/{\sigma }_{c}\right)\), the constants \({k}_{1}\) and \({k}_{2}\) are material dependent, \(\xi =({\sigma }_{t}/{\sigma }_{c})\); \({\sigma }_{c}\) is the uniaxial strength of the rock, and \({\sigma }_{t}\) is the uniaxial tensile strength. This equation is derived from the analysis of the Mohr envelope, which represents the failure envelopes of a set of curves (i.e., Mohr circles) in the \(\sigma -\tau\) space obtained by pairs of \({\sigma }_{1}-{\sigma }_{3}\) in failure tests, such as uniaxial compression and triaxial tests. The equation obtained by Úcar (2021) describes the envelope in canonical form as a parabola. The criterion can also be expressed in terms of normal and shear stresses. The normal stress \({\sigma }_{n}\) acting in the failure plane can be parametrically expressed as a function of the dip of the tangent to the envelope (\(\beta\)) or the instantaneous friction angle (\({\varphi }_{i}\)), which depends on the stress level, \(d\tau_{\alpha } /d\sigma_{n} = \tan \beta\). We refer interested readers to Úcar (2011, 2021) for full mathematical development.

On the other hand, considering Eq. (1) and the fact that the family of curves \(f({\sigma }_{n},{\tau }_{\alpha },{\sigma }_{3})=0\) has an envelope, Úcar (2021) derived the equation of the envelope, which can be expressed parametrically as:

$$\begin{aligned} \frac{\sigma_n}{\sigma_c}=\xi + (1-\sin \beta) \cdot \left\{k_4+\left(\frac{k_2}{2\left(1+k_1\right)}\right)^2 \right\}\cdot \\ \cdot \left(\frac{4 k_1+\left(3-k_1\right)\left[\left(1-k_1\right)+\left(1+k_1\right) \sin \beta\right]}{\left[\left(1-k_1\right)+\left(1+k_1\right) \sin \beta\right]^2}\right) \end{aligned}$$
(2)

And the shear stress, \({\tau }_{\alpha }\):

$$\begin{aligned}\left(\frac{\tau_{\alpha}}{\sigma_{\mathrm{c}}}\right)=\left(\frac{\sigma_{n}}{\sigma_{\mathrm{c}}}-\xi\right) \cdot \\\cdot \tan \left(45^{\circ}+\frac{\beta}{2}\right)-\frac{\left(\frac{\mathrm{k}_{2}}{2}\right)^{2} \cdot \tan \left(45^{\circ}+\frac{\beta}{2}\right)}{\left[\tan ^{2}\left(45^{\circ}+\frac{\beta}{2}\right)-\mathrm{k}_{1}\right]^{2}}\end{aligned}$$
(3)

The material constants, \({k}_{1}\) and \({k}_{2}\), are obtained from the parabola properties as

$$k_{1} = k_{1} \left( \xi \right) = \frac{{ - \left( {1 + {\mid }\xi {\mid }} \right) + \sqrt {\left( {1 + 7{\mid }\xi {\mid }} \right)\left( {1 - {\mid }\xi {\mid }} \right)} }}{{2{\mid }\xi {\mid }}}$$
(4)

and

$$k_{2} = k_{2} \left( \xi \right) = \frac{{\left[ {1 - k_{1} \left( { - \xi } \right)} \right]}}{{\sqrt { - \xi } }}$$
(5)

Their obtention involves the latus rectum concept -the chord through a focus parallel to the conic section directrix (Coxeter 1961)—by applying a coordinates switch (Úcar 2021). Because of this, the author often refers to this criterion as Úcar's Focus procedure. The constant \({k}_{4}\), that appears as an integration constant, is obtained from the boundary conditions, for example, by imposing that \({\sigma }_{3}\) is equal to 0 (uniaxial compression test, so that \({\sigma }_{1}\) is \({\sigma }_{c}\)).

The criterion is extended to rock masses as

$$\overline{\sigma }_{1} = k_{1} \left( {\overline{\sigma }_{3} - \xi_{m} } \right) + k_{2} \left( {\overline{\sigma }_{3} - \xi_{m} } \right)^{1/2}$$
(6)

where, as before, \(\overline{{\sigma }_{1}}=\left({\sigma }_{1}/{\sigma }_{c}\right)\), \(\overline{{\sigma }_{3}}=\left({\sigma }_{3}/{\sigma }_{c}\right)\), \({k}_{1}\) and \({k}_{2}\) are rock mass dependent constants, and now \({\xi }_{m}=({\sigma }_{tm}/{\sigma }_{c})\), where \({\sigma }_{c}\) is the uniaxial strength of the intact rock, and \({\sigma }_{tm}\) is the tensile strength of the rock mass.

$$k_{2} = k_{2} \left( {\xi_{m} } \right) = \frac{{\left[ {\eta_{m} - k_{1} \left( { - \xi_{m} } \right)} \right]}}{{\sqrt { - \xi_{m} } }}$$
(7)
$$k_{1} = k_{1} \left( {\xi_{m} } \right) = \frac{{ - \left( {\eta_{m} + \left| {\xi_{m} } \right|} \right) + \sqrt {\eta_{m}^{2} + 6 \cdot \eta_{m} \cdot \left| {\xi_{m} } \right| - 7\xi_{m}^{2} } }}{{2\left| {\xi_{m} } \right|}}$$
(8)

The new constant, \({\eta }_{m}\), is obtained from the rock mass classification, in this case from the Rock Mass Rating (RMR, Bieniawski 1989), although it could be expressed, as well, as a function of the Geological Strength Index (GSI, Hoek and Brown 2019), Q-system (Barton et al. 1974) or Rock Mass index (RMi, Palmström, 1995):

$$\eta_{m} = \left( {\frac{{\sigma_{cm} }}{{\sigma_{c} }}} \right) \approx \exp \left( {\frac{RMR - 100}{{a_{c} }}} \right)$$
(9)

The factor \({a}_{c}\) varies, according the literature, between \(18.75\le {a}_{c}\le 24\), as for Ramamurthy (1986), \({a}_{c}=18.75\); for Kalamaras and Bieniawski (1995), \({a}_{c}=24\); and for Sheorey (1997), \({a}_{c}=20\). Finally, the tensile strength of the rock mass is derived from:

$$\xi_{m} = \left( {\frac{{\sigma_{tm} }}{{\sigma_{c} }}} \right) \approx \xi \cdot \exp \left( {\frac{RMR - 100}{{14}}} \right)$$
(10)

Therefore, when RMR is 100 (akin to intact rock), it follows that \({\xi }_{m}=\xi\). Consequently, when considering the rock mass resistance with Eqs. 1 and 2, parameter \(\xi\) is replaced by \({\xi }_{m}\), and similarly, \({k}_{1}(\xi )\) and \({k}_{2}(\xi )\) become \({k}_{1}({\xi }_{m})\) and \({k}_{2}({\xi }_{m})\), respectively.

In summary, this criterion requires the determination of both the uniaxial compressive and tensile strength of the intact rock, as well as the characterization of the rock mass. It is worth noting that direct tensile strength (DTS) testing is rarely performed due to difficulties in preparing the specimens; many poorly prepared specimens fail invalidly, and adequately lathing specimens to achieve the desired testing shape remains a strong limiting factor (Klanphumeesri 2010; Perras and Diederichs 2014). However, indirect tensile tests, specifically the results of the Brazilian Test (BTS), have been found to provide a reasonably good correlation with DTS, albeit lithology dependent, with \(DTS=f\cdot BTS\), where \(f\) can be considered approximately 0.9 for metamorphic, 0.8 for igneous, and 0.7 for sedimentary rocks (Perras and Diederichs 2014). The uncertainties associated with the proposed correlation will likely limit this approach to preliminary design purposes unless triaxial tests are available, and a regression fitting to the data allows for a better determination of \(\xi\).

The relative simplicity (if the direct tensile test is obtained by correlation with the Brazilian test) and ease of obtaining input data make this criterion a very interesting and cost-effective alternative in the preliminary stages of geotechnical surveys.

3 Notation, Geometry, and Dynamics of the Problem

The entire procedure for estimating the factor of safety, as presented here, can be carried out using a spreadsheet (available as supplementary material with this paper). To input the required data into the spreadsheet, we must first define the parameters of the problem.

A common approach to analyzing the rupture surface, both in soils and rock masses, is to divide it into two rupture planes (Gadeus 1970; Kranz 1972; Hoek and Bray 1977; Wyllie and Mah 2004; Priest 2005; Pariseau 2006). An important precursor to rigid block analysis is the determination of kinematic feasibility. A given block is kinematically feasible if it is '… physically capable of being removed from the rock mass without disturbing the adjacent rock' (Priest 1985). Let us, then, consider (Fig. 1) the 2D case of a slope of finite height, where a block is kinematically feasible (Markland 1972; Priest 1993). The geometrical prerequisites for the analysis, following similar models (Hoek and Bray 1977; Priest 1993; Wyllie and Mah 2004), are as follows:

Fig. 1
figure 1

Slope geometry showing the potential failure plane, and the depth of the tensile crack

Full size image

We shall consider the case where a rock face, AB, the potential sliding plane, AD, the top of the slope, BC, and the tension crack, CD, all strike within some 20–25° of each other and intersect to form a kinematically feasible block along the planar discontinuity AD (Fig. 1). The height of the rock face (vertical distance between A and B) is H; it dips \({\beta }_{t}\), and its upper slope dips \({\beta }_{c}\). The plane dips \({\alpha }_{d}<{\beta }_{t}\), so it may daylight at the slope face (Markland 1972), and will intersect at the slope's toe (maximum volume for the sliding block). Let us assume that a tension crack has developed upslope in the rock mass, possibly along a favorably oriented joint set or by coalescing several pre-existing fractures. The crack reaches an unknown depth z, and its dip angle is denoted by \({\psi }_{g}\). For ease of calculation, we set the slope toe as the coordinate datum (X = 0, Y = 0). In our case, we seek to determine the most critical block and, consequently, the safety factor.

Regarding forces and stresses (Fig. 2), we will consider a unit width slice perpendicular to the slope face. In tension cracks, opening is the only kinematical consideration in the absence of tangential stress. The tension crack, of vertical depth z, may contain water to a vertical depth \({z}_{w}\). Initially, we will assume \({z}_{w}=0\). Once we determine the critical plane (z and \({\alpha }_{d}\)), we can incorporate pore pressure (both in the tension crack and the main plane) and additional loads (static overload upslope and dynamic seismic loads) into the model to obtain the modified safety factor, F. The maximum water pressure at the base of the tension crack is \({u}_{\mathrm{max}}={\gamma }_{w}\cdot {z}_{w}\), where \({\gamma }_{w}\) is the unit weight of water. This water pressure also acts within the sliding plane AD, and possible groundwater pressures configurations are (Wyllie and Mah 2004): uniform pressure on the slide plane for drainage blocked at the toe; triangular pressure on the slide plane for water table below the base of tension crack, or a linear decay to zero at the rock face, also as a triangular distribution, in our case this last configuration, which is probably one of the most commonly in use (see, for instance, Raghuvanshi 2019) has been adopted, as expressed in Fig. 2. The distribution of normal stress acting on the main plane is triangular as well.

Fig. 2
figure 2

Force distribution in the slope

Full size image

In a sense, by adopting this pore pressure distribution it is assumed that only the water in the tension crack and along the slip surface influences slope stability. For Wyllie and Mah (2004) this is tantamount to assuming that the rest of the rock mass is impermeable, an assumption that is certainly not always justified.

The spreadsheet has an input area where the following data are to be specified:

  • Geometric parameters: H, \({\beta }_{t}\), \({\beta }_{c}\), distance d (horizontal distance from the slope rim to the tension crack daylight in the upslope), \({\psi }_{g}\).

  • Force and stress parameters: \(\gamma\) (average bulk weight of the rock mass, in \(\mathrm{kN}/{\mathrm{m}}^{3}\)), q (overload, in \(\mathrm{kN}/{\mathrm{m}}^{2}\)), \({k}_{h}\) and \({k}_{v}\) (seismic accelerations, as fractions of g),

  • Resistance parameters: RMR, \({\sigma }_{c}\) (uniaxial strength, in \(\mathrm{MPa}\)), \({\sigma }_{t}\) (tensile strength, in \(\mathrm{MPa}\)), \({a}_{c}\) and \({a}_{t}\) (necessary for the Focus procedure, see Eqs. 7 and 8).

To evaluate the safety factor, F, we need to know the weight of the sliding block, hence its volume. The coordinates of the corresponding vertices, B, C, D, of the block must be determined (vertex A is known: it is the reference point or datum).

Considering the sliding plane AD and the tension crack CD, the coordinates of point D are:

$$Y_{D} = X_{D} \cdot \tan \alpha_{d}$$
(11)

where \(X_{A} \le X \le X_{D}\), and

$$Y_{D} = X_{D} \cdot \tan \psi_{g} + b$$
(12)

where \({X}_{D}\le X\le {X}_{C}\), and b is the intercept. Developing Eqs. (11) and (12), we obtain:

$$X_{D} = \frac{{ - \left( {\frac{b}{{\tan \psi_{g} }}} \right)}}{{1 - \tan \alpha_{d} \cdot \cot \psi_{g} }}$$
(13)

Considering now the point C, of coordinates \(X_{C} = d + H\cot \beta_{t}\), and \(Y_{C} = d\tan \beta_{t} + H\), and that additionally, by considering the plane CD, the ordinate at point C is:

$$Y_{C} = X_{C} \cdot \tan \psi_{g} + b\therefore - \frac{b}{{\tan \psi_{g} }} = \left( {X_{C} - Y_{C} \cdot \cot \psi_{g} } \right)$$
(14)

Replacing \({X}_{C}\) and \({Y}_{C}\) results in:

$$- \frac{b}{{\tan \psi_{g} }} = \left[ {d \cdot \left( {1 - \tan \beta_{c} \cdot \cot \psi_{g} } \right) + H\left( {\cot \beta_{t} - \cot \psi_{g} } \right)} \right] = M$$
(15)

Following Priest (1993, 2005), we define M in Eq. (15), as an intermediate geometrical parameter, as M allows us to relate other parameters belonging to the geometry of the slope. On the other hand, the abscissa \({X}_{D}\) value depends on \({X}_{C}\) through Eqs. 13 and 14) and taking into account that \(d = X_{C} - H \cdot \cot \beta_{t}\) is also determined in the following expression:

$$X_{D} = \left( {\frac{{X_{C} \cdot \left( {\tan \psi_{g} - \tan \beta_{c} } \right) + H\left( {\frac{{\tan \beta_{c} }}{{\tan \beta_{t} }} - 1} \right)}}{{\left( {\tan \psi_{g} - \tan \alpha_{d} } \right)}}} \right)$$
(16)

It is easy to check that \(\tan \psi_{g} \to \infty \Rightarrow X_{D} = X_{C}\), and that M tends towards \(X_{C}\). Likewise, from Eq. (16), can be obtained:

$$M = X_{D} \left( {1 - \tan \alpha_{d} \cdot \cot \psi_{g} } \right)$$
(17)

And from Eqs. (17) and (11) we obtain:

$$Y_{D} = X_{D} \cdot \tan \alpha_{d} = \frac{M}{{\left( {\cot \alpha_{d} - \cot \psi_{g} } \right)}}$$
(18)

In Fig. 1 we can observe the meaning of angles \(\beta_{c}\) and \(\beta_{t}\), and also that \(\overline{CD} = \frac{{\left( {Y_{C} - Y_{D} } \right)}}{{sen\psi_{g} }}\), and \(Z = \left( {Y_{C} - Y_{D} } \right) = \overline{CD} \cdot sen\psi_{g}\), so

$$Z = \left( {H + d \cdot \tan \beta_{c} } \right) - \frac{M}{{\left( {\cot \alpha_{d} - \cot \psi_{g} } \right)}}$$
(19)

Finally, for clarity in the analytical process, Table 1 summarizes the values of the vertex coordinates of the sliding block. Knowing these values, the area of the polygon ABCDA can be obtained by cross multiplication and knowing that \({X}_{A}=0\) and \({X}_{B}=0\).

$${\text{Area}} = \frac{1}{2}\left[ {X_{C} \cdot \left( {Y_{B} - Y_{D} } \right) + Y_{C} \cdot \left( {X_{D} - X_{B} } \right)} \right]$$
(20)
Table 1 Coordinates of relevant points and parameters M and d
Full size table

As we are considering a slice of unit width, the weight of the sliding block derives from:

$$W_{T} = \frac{\gamma }{2}\left[ {X_{C} \left( {Y_{B} - Y_{D} } \right) + Y_{C} \left( {X_{D} - X_{B} } \right)} \right] + q \cdot \left( {\overbrace {{X_{C} - X_{B} }}^{d}} \right)$$
(21)

The distance d quite often varies between a fifth and a half the height of the slope (Coates 1967). We can easily incorporate other forces into the analysis. For instance, to add seismic dynamic loading we can use the horizontal and vertical acceleration coefficients to evaluate the seismic forces acting in the slope:

$$R = W_{T} \sqrt {k_{h}^{2} + \left( {1 + k_{v}^{2} } \right)} \Rightarrow R = W_{T} .k$$
(22)

where \(k=\sqrt{{k}_{h}^{2}+\left(1+{k}_{v}^{2}\right)}\)

Next, \({X}_{C}\) is expressed as a function of the depth z of the tensile crack, because later the safety factor will be minimized depending on \({\alpha }_{d}\) and z. In Fig. 1 we can observe that \({Y}_{D}={Y}_{C}-z\) and \(Y_{D} = X_{D} \cdot \tan \alpha_{d}\) (Eq. 11). The equation of the straight line BC comes as

$$Y_{C} = X_{C} \tan \beta_{t} + H\left( {1 - \frac{{\tan \beta_{C} }}{{\tan \beta_{t} }}} \right)$$
(23)

Equating both ordinates belonging to point D and replacing the value of \(Y_{C}\) given in Eq. (23), and given the value of \(X_{D} = X_{C} - z \cdot \cot \psi_{g}\), then the abcissa \(X_{C}\) can be expressed in this way:

$$X_{C} = \frac{{H\left( {1 - \cot \beta_{t} \cdot \tan \beta_{c} } \right) - z\left( {1 - \cot \psi_{g} \cdot \tan \alpha_{d} } \right)}}{{\left( {\tan \alpha_{d} - \tan \beta_{c} } \right)}}$$
(24)

In Fig. 2 it can be observed the maximum pressure due to water occurs at point D, and its value is \(u_{\max } = \gamma_{w} \cdot z_{w}\). Thus, the resulting hydraulic force U generated by the water pressures that act over the plane of area \(AD\cdot 1\) (unit width) equals to

$$U = \frac{1}{2}\gamma_{w} \cdot z_{w} \cdot \overline{AD} = \frac{1}{2}\gamma_{w} \cdot z_{w} \cdot \frac{{Y_{D} }}{{\sin \alpha_{d} }}$$
(25)

From Eq. (18) we obtain:

$$U = \frac{1}{2}\gamma_{w} \cdot z_{w} \cdot \left( {\frac{M}{{\cos \alpha_{d} - \sin \alpha_{d} \cdot \cot \psi_{g} }}} \right)$$
(26)

At the same time, it has been considered that this interstitial pressure u is acting on the slip plane and decreases to zero at the slope toe. Additionally, the resulting of the interstitial pressure that act over the tensile crack, V, is,

$$V = \frac{1}{2}\gamma_{w} \cdot z_{w}^{2} \cdot \cos ec\psi_{g}$$
(27)

On the other hand, from Figs. 2 and 3 the normal and tangential components of V are:

$$V_{n} = V \cdot \cos \left( {\psi_{g} - \alpha_{d} } \right)$$
(28)
$$V_{t} = V \cdot \sin \left( {\psi_{g} - \alpha_{d} } \right)$$
(29)

and

$$R_{t} = R \cdot \sin \left( {\alpha_{d} + \varepsilon } \right) = W_{T} \cdot k \cdot \sin \left( {\alpha_{d} + \varepsilon } \right)$$
(30)
Fig. 3
figure 3

Workflow chart

Full size image

Applying the equilibrium equations results to the normal forces (\(F_{n}\))

$$\sum F_{n} = 0 \Rightarrow N + V_{n} + U - R_{n} = 0$$
(31)
$$R_{n} = R \cdot \cos \left( {\alpha_{d} + \varepsilon } \right) = W_{T} \cdot k \cdot \cos \left( {\alpha_{d} + \varepsilon } \right)$$
(32)

where

$$N = W_{T} \cdot k \cdot \cos \left( {\alpha_{d} + \varepsilon } \right) - U - V \cdot \cos \left( {\psi_{g} - \alpha_{d} } \right)$$
(33)

On the other hand, with the tangential forces, (\(F_{t})\)

$$\sum F_{t} = 0 \Rightarrow T - R_{t} - V_{t} = 0$$
(34)
$$T = W_{T} \cdot k \cdot \sin \left( {\alpha_{d} + \varepsilon } \right) + V \cdot \sin \left( {\psi_{g} - \alpha_{d} } \right)$$
(35)

4 Determining the Safety Factor, F

Usually, slope stability is analyzed with limit equilibrium methods and it is expressed as a safety factor. As is well known, it is common practice to determine the safety factor by applying the linear Mohr–Coulomb failure criterion through the equations

$$F = \frac{{C \cdot \overline{AD} + \left( {R_{n} - U - V_{n} } \right)\tan \phi }}{{R_{t} + V_{t} }}$$
(36)
$$F = \frac{{C \cdot \overline{AD} + \left( {W_{T} \cdot k\cos \left( {\alpha_{d} + \varepsilon } \right) - V\cos \left( {\psi_{g} - \alpha_{d} } \right) - U} \right)\tan \phi }}{{\left( {W_{T} \cdot k \cdot \sin \left( {\alpha_{d} + \varepsilon } \right) + V \cdot \sin \left( {\psi_{g} - \alpha_{d} } \right)} \right)}}$$
(37)

This section describes, in contrast, the procedure for determining the factor of safety by applying two different non-linear failure criteria, those of Úcar and Hoek and Brown (Hoek and Brown 1980, 2019; Úcar 2011, 2021).

4.1 Slope stability assessment with Úcar criterion

We shall consider that the safety factor is constant all over every sliding plane. First, \({\sigma }_{np}{\prime}\) the normal effective stress (average value) due to the wedge weight, is determined with Eq. (29). Then, observing Fig. 2 and considering the length of the sliding segment AD, it results in the following equation

$$\sigma_{np}^{\prime } = \frac{{W_{T} \cdot k \cdot \cos \left( {\alpha_{d} + \varepsilon } \right) - U - V \cdot \cos \left( {\psi_{g} - \alpha_{d} } \right)}}{{\overline{AD} }} = \frac{N}{{\overline{AD} }}$$
(38)

If we modify Eq. (33) to be dimensionless by dividing by \({\sigma }_{c}\), we can equate Eqs. (2) and (33), obtaining:

$$\begin{aligned} \left(\frac{1}{\sigma_{\mathrm{c}}}\right)\left[\frac{\mathrm{W}_{\mathrm{T}} \cdot \mathrm{k} \cdot \cos \left(\alpha_{\mathrm{d}}+\varepsilon\right)-\mathrm{U}-\mathrm{V} \cdot \cos \left(\psi_{g}-\alpha_{\mathrm{d}}\right)}{\overline{\mathrm{AD}}}\right]=\\=\xi_{m}+(1-\sin \beta)\left\{k_{4}+\left(\frac{k_{2}}{2\left(1+k_{1}\right)}\right)^{2} \right\} \\ \left[\frac{4 k_{1}+\left(3-k_{1}\right)\left[\left(1-k_{1}\right)+\left(1+k_{1}\right) \sin \beta\right]}{\left[\left(1-k_{1}\right)+\left(1+k_{1}\right) \sin \beta\right]^{2}}\right] \end{aligned}$$
(39)

And likewise, from Eq. (3):

$$\begin{aligned}\left(\frac{\tau_{\alpha}}{\sigma_{\mathrm{c}}}\right)=\left(\frac{\sigma_{\mathrm{n}}}{\sigma_{\mathrm{c}}}-\xi_m\right) \cdot \tan \left(45+\frac{\beta}{2}\right)- \\ -\frac{\left(\frac{\mathrm{k}_{2}}{2}\right)^{2} \cdot \tan \left(45+\frac{\beta}{2}\right)^{2}}{\left[\tan ^{2}\left(45+\frac{\beta}{2}\right)-\mathrm{k}_{1}\right]^{2}}\end{aligned}$$
(40)

At this point, if we know \(\beta\) we can immediately obtain the normal and shear stresses with Eqs. (34) and (35). As the normal stress, \(\sigma_{np}^{\prime }\), is actually an average value of the normal stress distribution acting on AD, and must equal to the normal stress expressed by Eq. (34), the obtained values of \(\beta\) will represent in this case average values of the friction angle,\({\phi }_{i}\), along the sliding surface (Fig. 4).

Fig. 4
figure 4

Force polygon

Full size image

Finally, the safety factor can be obtained as:

$$F = \frac{{\left( {\frac{{\sigma_{n} }}{{\sigma_{c} }} - \xi_{m} } \right) \cdot \tan \left( {45^{ \circ } + \frac{\beta }{2}} \right) - \frac{{\left( {\frac{{k_{2} }}{2}} \right)^{2} \cdot \tan \left( {45^{ \circ } + \frac{\beta }{2}} \right)}}{{\left[ {\tan^{2} \left( {45^{ \circ } + \frac{\beta }{2}} \right) - k_{l} } \right]^{2} }}}}{{\left( {\frac{1}{{\sigma_{c} }}} \right) \cdot \left( {\frac{1}{{\overline{AD} }}} \right)\left( {W_{T} \cdot k \cdot \sin \left( {\alpha_{d} + \varepsilon } \right) + V \cdot \sin \left( {\psi_{g} - \alpha_{s} } \right)} \right)}}$$
(41)

Now, this expression of the safety factor is a function of \(\overline{AD}\), that in turn depends on the position of the tension crack (Fig. 1).

$$\overline{AD} = \left( {\frac{{Y_{C} - z}}{{\sin \alpha_{d} }}} \right) = \frac{{\left[ {X_{C} \cdot \tan \beta_{c} + b - \lambda \cdot H} \right]}}{{\sin \alpha_{d} }}$$
(42)

It is worth noting the importance of the dimensionless parameter \(\lambda =z/H\), which is intended to better understand and analyze the geometry of the wedge as a whole because it indicates which fraction of the slope height corresponds to the depth of the tensile crack. For example, if z = 0, then \(\lambda =0\) and, of course, there is no fracture due to traction; and on the contrary, if z = H then \(\lambda =1\), that is to say, the tensile crack corresponds to the slope height. Experience has shown that values of \(\lambda\) are in the interval of 0.20–0.50 (Coates 1967).

Additionally, one can determine the weight of the two potential failure blocks depending on the abscissa \({X}_{C}\), which is \({X}_{C}=f\left({\alpha }_{d},\lambda \right)\) considering \({\psi }_{g},{\beta }_{t},{\beta }_{c}\), and H constants. This allows a more global and integral vision of the problem by determining the F with respect to the variables \(\lambda\), \({\alpha }_{d}\), and \(\beta\). As previously mentioned, \(\beta\) is the inclination of the tangent to the rupture envelope for each value of normal stress. This angle is known as the instantaneous friction angle (\(\beta ={\phi }_{i}\)).

The main advantage is that \({X}_{C}\) represents the location of the tensile crack at the crown of the slope, being also the abscissa that serves as a link to determine \({Y}_{C}\) of the tensile crack.

The weight in Eq. (22) can be put into function of \({X}_{C}\) in this way:

$$ \begin{gathered} W_{T} = \frac{\gamma }{2}( {H \cdot X_{C} - X_{C}^{2} \tan \beta_{c} - b_{1} \cdot XC + z \cdot X_{C} + [ \overbrace {{X_{C} \tan {\beta_{c} +} b_{1} }}^{{YC^{2} }} ]^{2} \cdot \cot \alpha_{d} } ) \hfill \\ \quad \quad + \frac{\gamma }{2}\cdot( { - z \cdot X_{C} \cdot \tan \beta_{c} \cdot \cot \alpha_{d} - z \cdot \cot \alpha_{d} \cdot b_{1} - XC\tan \beta_{c} \cdot H \cdot \cot \beta_{t} }) \hfill \\ \quad \quad - H \cdot \cot \beta_{t} \cdot b_{1} + q \cdot XC - q \cdot H \cdot \cot \beta_{t} \hfill \\ \end{gathered} $$
(43)

The value of \({b}_{1}\) is indicated in Table 1. Substituting \(z=\lambda \cdot H\), we obtain:

$$ \begin{gathered} W_{T} = \frac{\gamma }{2}\left( {H \cdot X_{C} - X_{C}^{2} \tan \beta_{c} - b_{1} \cdot XC + \lambda \cdot H \cdot X_{C} + [ \overbrace{ {X_{C} \tan {{\beta_{c} }}} + b_{1} }^{YC^{2}}] ^{2} \cdot \cot \alpha_{d} } \right) \hfill \\ \quad \quad + \frac{\gamma }{2}( - \lambda \cdot H \cdot X_{C} \cdot \tan \beta_{c} \cdot \cot \alpha_{d} - \lambda \cdot H \cdot \cot \alpha_{d} \cdot b_{1} - XC\tan \beta_{c} \cdot H \cdot \cot \beta_{t} \hfill \\ \quad \quad - H \cdot \cot \beta_{t} \cdot b_{1} ) + q \cdot XC - q \cdot H \cdot \cot \beta_{t} \hfill \\ \end{gathered} $$
(44)

On the other hand, we already know that \({W}_{T}=\eta \left({\alpha }_{d},\lambda \right)\), \(\overline{AD}=\xi \left({\alpha }_{d},\lambda \right)\), \({X}_{C}=\zeta \left({\alpha }_{d},\lambda \right)\) and \({\sigma }_{n}=\vartheta (\beta )\). It is important to note that, by applying the numerical methods of the Solver add-in program within the spreadsheet, it is possible to determine the minimum safety factor together with the parameters \(\lambda\), \({\alpha }_{d}\) and \(\beta\) quickly. All this without the need to carry out the laborious analytical process of deriving to minimize the safety factor as we will see next.

Another way to calculate the minimum safety factor is by applying the classical mathematical analytical tools, where a new function \(f\), is considered attached to the condition of Eq. (34):

$$\begin{aligned} f=\frac{\left(\frac{\tau_\alpha}{\sigma_c}\right)}{\left(\frac{1}{\sigma_c}\right) \cdot\left(\frac{1}{A D}\right)\left(W_T \cdot k \cdot \operatorname{sen}\left(\alpha_d+\varepsilon\right)+V \cdot \operatorname{sen}\left(\psi_g-\alpha_d\right)\right)}+ \\+\mu\left(\frac{1}{\sigma_{c}}\right)\left[\frac{W_{T} \cdot k \cdot \cos \left(\alpha_{d}+\varepsilon\right)-U-V \cdot \cos \left(\psi_{g}-\alpha_{d}\right)}{\overline{A D}}\right]- \\ -\mu \cdot \left(\frac{\sigma_{n}}{\sigma_{c}}\right)\end{aligned}$$
(45)

In Eq. (39), the terms \(\left({\tau }_{\alpha }/{\sigma }_{c}\right)\) and \(\left({\sigma }_{n}/{\sigma }_{c}\right)\) correspond to Eqs. (34) and (35) and were obtained by Úcar (2021) and \(\mu\) is the Lagrange’s multiplier. Thus, to calculate the minimum safety factor, the following derivatives are required:

$$\frac{\partial f}{{\partial \alpha_{d} }} = f_{{\alpha_{d} }} = 0$$
$$\frac{\partial f}{{\partial \varphi_{i} }} = f_{{\varphi_{i} }} = 0$$
$$\frac{\partial f}{{\partial \mu }} = f_{\mu } = 0$$

Undoubtedly, calculating these derivatives involves a painstaking and laborious process, in addition to having to subsequently solve the system of non-linear equations to determine the parameters \(\lambda\), \({\alpha }_{d}\) and \(\beta\). Fortunately, all this is solvable in a few seconds by applying the useful numerical tools and their algorithms through the Solver add-in by constraining the problem with the appropriate conditions.

4.2 Slope stability Assessment with Hoek and Brown’s Failure Criterion

Taking into account the H–B criterion, Kumar (1998) determined the rupture envelope and the normal tension for the general case of \(a\ge 1/2\) by means of a simple analytical procedure, without the need to solve any differential equation; as previously found by Úcar (1986), using the original equation that relates the main stresses \({\sigma }_{1}\) and \({\sigma }_{3}\) of such a criterion, by means of the well-known quadratic equation represented by the following equation, that is to say \(a=1/2\).

$$\frac{{\sigma_{1} }}{{\sigma_{c} }} = \frac{{\sigma_{3} }}{{\sigma_{c} }} + \left[ {m \cdot \frac{{\sigma_{3} }}{{\sigma_{c} }} + s} \right]^{1/2}$$
(46)

Considering the values of \({\tau }_{\alpha }\) and \({\sigma }_{n}\) obtained by Kumar (1998) and whose expressions are given below, the calculation procedure is otherwise exactly the same as described in Sect. 4.1:

Kumar’s Eqs. (17) and (20):

$$\frac{\tau }{{\sigma_{c} }} = \left( {\frac{m \cdot a}{2}} \right)^{{\left( {\frac{a}{1 - a}} \right)}} \left( {\frac{{1 - \sin \phi_{i} }}{{\sin \phi_{i} }}} \right)^{{\left( {\frac{a}{1 - a}} \right)}} \left( {\frac{{\cos \phi_{i} }}{2}} \right)$$
(47)
$$\begin{aligned}\frac{\sigma}{\sigma_c}&=\frac{1}{m} \cdot\left(\frac{m \cdot a}{2}\right)^{\left(\frac{1}{1-a}\right)} \cdot\left(\frac{1-\sin \phi_i}{\sin \phi_i}\right)^{\left(\frac{1}{1-a}\right)} \cdot &\\& \,\,\cdot\left(1+\frac{\sin \phi_i}{a}\right)- \frac{s}{m}\end{aligned}$$
(48)

Therefore, the expression of the safety factor is:

$$F = \frac{{\left\{ {\left( \frac{ma}{2} \right)^{{\left( {\frac{a}{1 - a}} \right)}} \left( {\frac{{1 - \sin \phi_{i} }}{{\sin \phi_{i} }}} \right)^{{\left( {\frac{a}{1 - a}} \right)}} \left( {\frac{{\cos \phi_{i} }}{2}} \right)} \right\}}}{{\left( {\frac{1}{{\sigma_{c} }}} \right) \cdot \left( \frac{1}{AD} \right)\left( {W_{T} \cdot k \cdot \sin \left( {\alpha_{d} + \varepsilon } \right) + V \cdot \sin \left( {\psi_{g} - \alpha_{d} } \right)} \right)}}$$
(49)

5 Influence of Water Pressure on Stability

The presence of groundwater in a rock slope has several detrimental effects on stability (Wyllie 2017): Water pressure reduces the shear resistance of potential failure surfaces. When present in tension cracks, it increases the forces that favor sliding. Water accelerates weathering and decreases the shear strength of intact rock. Freezing of groundwater can cause wedging in water-filled fissures. Also, ice can block drainage paths. Excavation costs can be increased when working below the water table. In any case, the most important effect of groundwater in a rock mass is the reduction in stability resulting from water pressures within the discontinuities.

There are two possible approaches to introducing water pressure distributions into stability calculations: either applying a flow pattern deduced from the distribution of discontinuities, and their hydraulic conductivities, or obtaining data from direct measurements of water levels in wells, or of water pressure by means of piezometers installed in boreholes.

Obviously, given the multiplicity of possible geometric scenarios of fluid pressure distribution, in the absence of other data, we will apply the model most frequently used in these cases, albeit some caution is warranted; in this regard, (Wyllie 2017) recommends analyzing the sensitivity of our slope-problem to a variety of realistic fluid pressure distributions, paying particular attention to rapid recharge phenomena and the transient pressures that may generate. The considered case, with water present in the tension crack hydraulically connected to the water generating pressure on the sliding surface, probably is a worst-case scenario or close enough to it.

In this procedure, we proceed at first as if there is no water in the rock mass and, once z, \({\alpha }_{d}\) and F are determined in dry conditions, it is possible to incorporate different values of \({z}_{w}\) (water height within the tension crack) to explore the detrimental effect of water in the F.

6 Step by Step Procedure with the Spreadsheet and SOLVER

As previously mentioned, the full procedure can be implemented via a dedicated spreadsheet available as supplementary material with this paper, it includes a detailed step-by-step procedure. The spreadsheet has an input area where relevant data on the studied slope can be included in the model. The presented equations are employed to determine the value of the factor of safety, and its value is then minimized by varying the geometric parameters to obtain the worst-case scenario. Solver is an add-in program for spreadsheets that can find an optimal (maximum or minimum) value for a formula in one cell—called the Objective cell, which in our case contains the Factor of Safety—subject to constraints, or limits, on the values of other formula cells on a worksheet. Simply put, it serves to determine the maximum or minimum value of one cell by changing other cells.

6.1 Instructions for Using the Spreadsheet

This spreadsheet comprises two sheets that should be used sequentially. The parameters entered in the first sheet are automatically transferred to the second sheet. The reason for structuring it into two sheets is so that SOLVER does not need to be configured each time.

We start on the [parameters] sheet.

  1. 1.

    Enter the starting parameters. Under the header "1 PARAMETERS" there are cells for entering the uniaxial compressive strength of intact rock (\({\sigma }_{c}\)), tensile strength (\({\sigma }_{t}\)), and the RMR value of the rock mass. Additionally, we can vary the values assigned to the constants \({a}_{t}\) and \({a}_{c}\). By default, they appear as \({a}_{t}=14\) and \({a}_{t}=20\), as seen in previous paragraphs.

    When these parameters are entered, the spreadsheet automatically computes the values of \(\xi\), \({\xi }_{m}\), \({\mu }_{m}\), and the constants \({k}_{1}\), \({k}_{2}\), and \({k}_{3}\).

  2. 2.

    Obtain \({k}_{4}\). We must obtain \({k}_{4}\) in an iterative process using SOLVER, with the target being cell "Eq. k4" making it equal to zero by modifying the cell "solver adj" (under the cell labeled K4).

    Now we move to the [FS] sheet.

    We check that the sheet has successfully captured the values entered in step 1, as well as the calculations performed: s \({k}_{1}\), \({k}_{2}\), \({k}_{3}\), and \({k}_{4}\).

  3. 3.

    Input of basic slope geometry (see Fig. 1 for guidelines, and notice the location of the spatial datum at the toe of the slope for coordinates determination). Enter the height of the slope (in cell \({Y}_{B}\), under cell \(H={Y}_{B}\)), coordinates of point B, slope inclination in degrees (under the cell labeled "BETAtalud"), and inclination of the crest of the slope in degrees (under the cell labeled "BETAcorona").

  4. 4.

    Enter the average bulk weight of the rock present in the slope (in \(\mathrm{kN}/{\mathrm{m}}^{3}\)).

  5. 5.

    Enter, if necessary, the overload on the crest of the slope, and the horizontal and vertical seismic acceleration coefficients, \({k}_{h}\) and \({k}_{v}\).

  6. 6.

    Apply SOLVER to obtain the value of the safety factor, F. The target cell is F, minimizing its value by changing the cells \(\lambda\) (relative depth of the tensile crack), \({\alpha }_{d}\) (dip of the failure plane), and \(\phi\) (instantaneous friction angle), subject to the conditions that \({X}_{C}\) is greater than or equal to \({X}_{B}\), d is less than or equal to \({d}_{s}\) and greater than or equal to \({d}_{l}\), \(\delta\) is equal to zero, and \(\lambda\) is between zero and one. In this step, once we obtain the minimized value of F, the values in cells \(\lambda\) and \({\alpha }_{d}\) reflect now the relative depth of the tensile crack, and the dip of the failure plane, determining the geometry of the sliding block in the critical condition.

  7. 7.

    Once the basic value of F has been obtained, we can add the effect of the presence of water on the slope by introducing the factor \({K}_{w}\), the ratio between \({z}_{w}\) and z. The safety factor will be updated accordingly.

A flow chart illustrating this procedure is in Fig. 5.

Fig. 5
figure 5

Flowchart for safety factor calculation in the spreadsheet

Full size image

7 Worked Example: Comparing Results Between Using H–B Criterion, Úcar Criterion, Limit Equilibrium Method (Slide), and Finite Element Method (Plaxis 2D) with an Idealized Slope

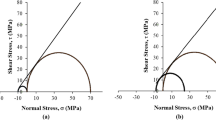
The geometric characteristics and mechanical and elastic properties of the slope under study are presented in Table 2. From the simulations using the finite element and limit equilibrium method and analytically with the H–B criterion for the analyzed slope, and comparing their results with the proposed analytical method of the Úcar criterion, it is observed (see Table 3 and Fig. 6):

Table 2 Geometry and mechanical and elastic properties
Full size table
Table 3 Summary of results
Full size table
Fig. 6
figure 6

Comparison of results of the different methods for the proposed example. a Geometry of the case. Red dashed line, results of the method proposed in this work. b Crack surface generated by Finite Element Method (Plaxis 2D). c Results obtained through the Limit Equilibrium Method (SLIDE). The FS, the distance of the tensile crack at the slope crest and the depth of the tensile crack are shown

Full size image

For the case with seismic loading and linear overload, the FS with the Úcar criterion yielded a value of 2.392. The correlation percentages with respect to the other 3 methods are between 86.42 and 95.82%.

The distance of the formation of the tensile crack at the head of the slope by the Úcar criterion is 17.28 m and the correlation percentages are between 94.22 and 84.26%. For the tensile crack depth 18.18 m of the Úcar criterion, the percentage correlations would be 53.64 and 94.28%. It should be noted that the value of 53.64% corresponds to that obtained by the limit equilibrium method and its correspondence is low, however for the other two methods the correspondence is very good, being above 88.01%. Finally, when comparing the dip of the rupture surface, which in the case of the Úcar rupture criterion is obtained \(\beta ={50.64}^{\circ }\), the percentage value of correspondence with the other methods are between 96.13 and 97.32%.

The results show that there is a good correlation and a high correspondence of the proposed method with the Úcar breakage criterion with the other methods because most of the results are above 90% correlation.

8 Conclusions

We present a method for calculating or estimating the factor of safety in a highly jointed rock mass, considering plane failure with an unknown depth of a tensile crack. The Úcar's Focus Procedure and Hoek and Brown's failure criteria are applied by implementing the necessary formulas in a spreadsheet. The required parameters include the slope geometry, strength parameters, and either the RMR of the massif or its \({m}_{i}\), depending on the chosen criterion. An iterative process with conventional tools is used to obtain an estimate of the safety factor. The resulting value is reasonably close, with a similarity degree of around 86–96% in the solved example, to that obtained with more sophisticated numerical calculation tools. Thus, the proposed procedure is a useful and cost-effective contribution in the early stages of a project or as a starting point for more detailed investigations.