Abstract
In this work, the essential work of fracture (EWF) method is introduced for a peridynamic (PD) material model to characterize fracture toughness of ductile materials. First, an analytical derivation for the path-independence of the PD J-integral is provided. Thereafter, the classical J-integral and PD J-integral are computed on a number of analytical crack problems, for subsequent investigation on how it performs under large scale yielding of thin sheets. To represent a highly nonlinear elastic behavior, a new adaptive bond stiffness calibration and a modified bond-damage model with gradual softening are proposed. The model is employed for two different materials: a lower-ductility bainitic-martensitic steel and a higher-ductility bainitic steel. Up to the start of the softening phase, the PD model recovers the experimentally obtained stress–strain response of both materials. Due to the high failure sensitivity on the presence of defects for the lower-ductility material, the PD model could not recover the experimentally obtained EWF values. For the higher-ductility bainitic material, the PD model was able to match very well the experimentally obtained EWF values. Moreover, the J-integral value obtained from the PD model, at the absolute maximum specimen load, matched the corresponding EWF value.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The peridynamic (PD) theory is a nonlocal formulation of solid mechanics, originally introduced for handling crack initiation, extension and final failure of a body, without the need of supplementary methods (Silling 2000; Silling and Askari 2005). PD is based upon integro-differential equations, thereby avoiding spatial derivatives, which are not defined at discontinuities, such as crack surfaces. For brittle and small scale yielding fracture, in which methods from linear and nonlinear elastic fracture mechanics apply, fracture characterization can be achieved with a single parameter, the J-integral value, for example. In certain cases of large scale yielding, ductile failure may be similarly characterized by the essential work of fracture (EWF) method. We next briefly review these concepts from the classical theory and, when available, their perdynamic-based versions.
1.1 The classical and the PD J-integral
The J-integral is an expression for calculating the strain energy release rate of a cracked body, or the amount of energy available at the tip of a crack to form new crack surfaces as the crack extends (Rice 1968). It is a firmly established parameter that applies both to linear and nonlinear elastic materials. The J-integral is used as a toughness measure and failure criterion, for ranking of materials and for dimensioning, but it can also be used for testing the accuracy of material models, such as PD models. Furthermore, since the J-integral can be expressed and discretized in various ways, there is also a need for comparison of different approaches. In the PD literature, both Rice’s classical J-integral (\(J_\mathrm {{\scriptscriptstyle R}}\)) and the nonlocal PD formulation of Rice’s J-integral (\(J_\mathrm {{\scriptscriptstyle PD}}\)) have been studied for testing the expressions and for testing PD numerical implementations, in comparison with analytical values, experimental data and the finite element method (FEM) of the classical model.
The \(J_\mathrm {{\scriptscriptstyle PD}}\) has been derived by Silling and Lehoucq (2010) for state-based PD, based on an energy balance approach. Later, Hu et al. (2012) presented a bond-based \(J_\mathrm {{\scriptscriptstyle PD}}\), using an infinitesimal virtual crack extension method. The bond-based \(J_\mathrm {{\scriptscriptstyle PD}}\) expression is a special case of the more general state-based \(J_\mathrm {{\scriptscriptstyle PD}}\) expression.
The displacements are the principal unknowns in PD, from which other quantities subsequently can be obtained. A general expression of the contour \(J_\mathrm {{\scriptscriptstyle R}}\) as a function of displacement derivatives was derived by Bruck (1989) and Hart and Bruck (2021). A rectangular integration treatment of the \(J_\mathrm {{\scriptscriptstyle R}}\) has been given by Stenström and Eriksson (2019) for use in PD.
Both the \(J_\mathrm {{\scriptscriptstyle R}}\) and \(J_\mathrm {{\scriptscriptstyle PD}}\) expressions have for separate studies shown results in line with analytical expressions, experimental results and FEM calculations of the classical model.
Hu et al. (2012) evaluated the \(J_\mathrm {{\scriptscriptstyle PD}}\) on single and double edge notched PD models, and with refined discretization, achieved results approaching \(J_\mathrm {{\scriptscriptstyle R}}\) of FEM solutions of the classical model. In the formulation of Hu et al. (2012), the stress tensor is considered through computation of a set of force interactions over inner and outer regions associated with the contour integral. The width of these regions depends on the degree of nonlocality of the \(J_{\textrm{PD}}\). Panchadhara and Gordon (2016) used the method of Hu et al. (2012), but approximated the stress tensor of \(J_\mathrm {{\scriptscriptstyle PD}}\) from force interactions at the contour. Details were left out, but the number of interactions to account for is stated by the authors to be fewer. Nevertheless, it need to be noticed that in Hu et al.’s expression, the force interactions is counted only from one region to the other and not from both.
Breitenfeld et al. (2014) computed the \(J_\mathrm {{\scriptscriptstyle R}}\) by using a material point method (particle-based) and the displacement gradient of state-based PD. The displacement boundary condition along a circular boundary of a mode I PD specimen corresponded to the classical analytical K-field solution. Using a rectangular \(J_\mathrm {{\scriptscriptstyle R}}\), the K-field solution and the corresponding PD model were compared, while varying the lattice orientation.
Stenström and Eriksson (2019) also used the \(J_\mathrm {{\scriptscriptstyle R}}\) expression by writing it as a function of displacement derivatives and approximating the displacement derivatives by using the central difference scheme on the material model’s displacement field, as used by Hu et al. (2012) for the \(J_\mathrm {{\scriptscriptstyle PD}}\). The specimen was a central crack with mode I stress boundary condition along a rectangular boundary, extracted from an exact analytical stress–strain-displacement solution. The \(J_\mathrm {{\scriptscriptstyle R}}\) was then applied on the classical exact analytical displacement field and on the corresponding PD model and compared, while studying the convergence.
The above studies were for mode I loading. Panchadhara and Gordon (2016) studied the \(J_\mathrm {{\scriptscriptstyle PD}}\) for mode I edge notch and mode II Kalthoff-Winkler PD models, with results in agreement to published experimental results. Jung and Seok (2017) studied fatigue crack modeling for mixed-mode loading and decomposed the \(J_\mathrm {{\scriptscriptstyle PD}}\) into mode I and II, with comparison to experimental results. Furthermore on mixed mode, Imachi et al. (2018) applied the \(J_\mathrm {{\scriptscriptstyle R}}\) to inclined cracks of rectangular and L-shaped PD specimens, with close resemblance to experimental results. Imachi et al. derived the displacement derivatives based on the moving least-squares approximation.
Considering the area/domain formulation of J, the area \(J_\mathrm {{\scriptscriptstyle R}}\) has been studied within PD by Imachi et al. (2018), Fallah et al. (2020) and Stenström and Eriksson (2021). Imachi et al. used the area formulation in the above previously mentioned mixed mode study. Fallah et al. derived the bond-based PD stress tensor and used it for calculating the area \(J_\mathrm {{\scriptscriptstyle R}}\) and compared it to the \(J_\mathrm {{\scriptscriptstyle PD}}\) of Hu et al. (2012). Lastly, Stenström and Eriksson carried out a comparison of the contour \(J_\mathrm {{\scriptscriptstyle R}}\) and the area \(J_\mathrm {{\scriptscriptstyle R}}\). Nevertheless, the studies does not compare the \(J_\mathrm {{\scriptscriptstyle PD}}\) and \(J_\mathrm {{\scriptscriptstyle R}}\) integrals.
The various J expressions of the above mentioned studies show in general errors less than one percent when applied on PD displacement fields and compared with the analytical expressions of a classical model or FEM approximations of the \(J_\mathrm {{\scriptscriptstyle R}}\). With finer PD discretization, the error can be much less than one percent, and vice versa for coarser discretization. When the J expressions are applied to classical exact analytical displacement solutions, the error is less than a per mille from \(J_0 = K_\textrm{I}^2/E\) (Breitenfeld et al. 2014; Stenström and Eriksson 2019).
In the present study, we will use the following notation of J:
-
Classical J computed on displacements of a classical continuum mechanics material model is termed \(J_\mathrm {{\scriptscriptstyle R}}\).
-
PD J computed on displacements of a PD material model is termed \(J_\mathrm {{\scriptscriptstyle PD}}\).
-
\(J_\mathrm {{\scriptscriptstyle R}}\) and \(J_\mathrm {{\scriptscriptstyle PD}}\) values computed on a different model than their natural one is termed \(J_\mathrm {{\scriptscriptstyle R}}^*\) and \(J_\mathrm {{\scriptscriptstyle PD}}^*\), respectively.
-
Critical J are denoted by adding a ‘c’, e.g. \(J_\mathrm {{\scriptscriptstyle Rc}}^*\).
-
Lastly, the classical expression \(K_\textrm{I}^2/E = J_0\).
The reason why we would like to compute J on a different model than their natural one is that the contour \(J_\mathrm {{\scriptscriptstyle R}}\) is less affected by PD boundary effects of narrow ligaments of double edge notched tension (DENT) specimens typically used in the EWF method. As \(J_\mathrm {{\scriptscriptstyle PD}}\) is computed along a strip, it comes closer to the boundaries of a coarsely discretized ligament. However, an advantages of \(J_\mathrm {{\scriptscriptstyle PD}}\) is that it can average out local disturbances of the displacement field, similar to the classical area \(J_\mathrm {{\scriptscriptstyle R}}\).
1.2 The EWF method to evaluate fracture toughness
The EWF method considers the fracture energy with two parameters; the energy required to form new crack surfaces and the energy dissipated during plastic deformation. The former one can be approximated to the critical \(J_\mathrm {{\scriptscriptstyle c}}\) as long as a set of requirements are met. Since J only considers crack initiation resistance, the EWF method may be preferable over J for studying overall fracture resistance, if there is a significant energy contribution from plastic yielding (Frómeta et al. 2020).
Broberg (1968) laid the foundation for the determination of fracture toughness of thin sheet material. The region in front of a crack tip can be separated into an inner and outer zone. The inner zone is the fracture process zone (FPZ). For thin ductile materials, it is possible to identify the FPZ by necking. In plane stress, the necking region is dependent on material thickness. The energy dissipated from the FPZ can be seen as a thickness dependent pseudo material constant, while the outer much larger region is characterized by plastic deformation. Cotterell and Reddel (1977) defined the conditions for the determination of EWF for thin sheets with regard to ligament length and thickness. An experimental method for EWF to be applied to thin sheet metal was proposed by Marchal and Delannay (1996). The EWF method have been used successfully on a wide range of materials including polymers (Bárány et al. 2010), aluminium (Vendra et al. 2017), and steel (Efthymiadis et al. 2017). Casellas et al. (2017) and Frómeta et al. (2020) showed the possibility of fracture toughness determination using the EWF method for several advanced high-strength steel (AHSS) grades like, dual and complex phase, press hardened, TRIP (transformation induced plasticity) and high manganese steels.
1.3 Peridynamic material models and their calibration
In ductile failure problems in which the EWF can be useful, the material response is nonlinear. To represent that behavior, a PD model requires calibration of the parameters that determine the force-strain relationship of a PD bond. Calibration for linear-elastic material response is simple and it is based on enforcing a match between the strain energy density of a classical and of a PD material. For a nonlinear material response, this calibration can be accomplished in several ways.
PD constitutive models can be categorized into bond-based, ordinary state-based, and non-ordinary state-based, with the bond-based type being a special case of the ordinary state-based type. In bond-based PD, the pairwise force between two material points depends only on the two material points and no other points (Silling 2000). In state-based PD, deformation at each bond depends on the collective deformation in its vicinity (Silling et al. 2007). In ordinary state-based PD, the pairwise force acts in the direction of the corresponding bond, a restriction that is relaxed for non-ordinary state-based PD. Classical constitutive models can be “directly embedded” in PD formulations via the so-called correspondence models (initiated in Silling et al. 2007), which tend to be of the non-ordinary kind but suffer from zero energy modes instabilities in regions of high strain gradients, such as around crack tips. Various stabilization methods have been proposed to resolve this issue, among them being the bond-associated PD models, which provide accurate and stable correspondence-based PD solutions (Breitzman and Dayal 2018; Chen 2018; Gu et al. 2019; Behzadinasab and Foster 2020; Behzadinasab et al. 2021).
The original constitutive law is the prototype microelastic brittle material (Silling 2000), accompanying a linear elastic bond law up to a sudden failure, to mimic brittle-type failure. Subsequently, in order to better capture quasi-brittle damage and failure, models in which bond force-strain features a softening phase before full bond failure was developed (Macek and Silling 2007). These models utilize, for example, a piecewise linear representation for bond force in terms of bond relative elongation, with ”bilinear” (linear up to max load, then linear for the softening phase to zero force) and ”trilinear” being the most popular. Multi-parameter models, like the piecewise linear ones, are needed in order to be able to match both the critical fracture energy and strength of a material when using an arbitrary PD horizon size. With a single-parameter bond-damage model, like the prototype microelastic brittle model, one can match, for example, the material’s fracture toughness when using an arbitrary horizon size, but it can also match the material’s strength only for a specific value of the horizon size. That value, in many instances, ends up being too small to be of practical use, since it leads to very large-scale computational models.
Bilinear bond force-strain models have been studied previously for quasi-brittle materials, considering crack nucleation (Silling et al. 2010) and crack propagation (Zaccariotto et al. 2015; Niazi et al. 2021). In these studies, curve fitting was used to match the bilinear model to an experimental stress–strain response, at the point where the stress–strain departs from linearity and crack nucleation/propagation takes place. Bilinear fitting for quasi-brittle materials have also been accomplished by use of material properties (Yang et al. 2018) and by analytical formulas (Niazi et al. 2021). Bilinear models have also been employed to model elasto-plastic behavior of metals, considering high speed loading (Macek and Silling 2007; Lee et al. 2016) and crack mouth opening displacement (Yolum et al. 2016). Material softening of quasi-brittle materials has as well been studied, by using a trilinear law (Yang et al. 2018; Niazi et al. 2021).
In state-based PD, the original constitutive model is the linear peridynamic solid (Silling et al. 2007), later accompanied by perfect plasticity (Mitchell 2011b), visco-elasticity (Mitchell 2011a) and correspondence models, reviewed in Mitchell et al. (2015).
Work on bond force-strain curves to match global elasto-plastic behavior with hardening is sparse. One study can be found, on state-based PD, where an automated calibration method, together with manually adjusted piecewise linear hardening, is employed to model experimental tensile test of 304 L stainless steel (Littlewood et al. 2012; Littlewood 2015a). However, since the purpose of these studies was to introduce the reader to the PD theory, the bond calibration method was not provided.
1.4 The objective and paper organization
The goal of this paper is to establish the use of the EWF method with a PD model that employs nonlinear elasticity for bond deformation, up to maximum bond-load, followed by bond-softening, to represent the deformation theory of plasticity and ductile failure. In this way, the \(J_\mathrm {{\scriptscriptstyle PD}}\) can be used to characterize fracture for brittle or elasto-plastic fracture problems in which small scale yielding assumptions holds, and the EWF for elasto-plastic fracture under large scale yielding that can be reasonably approximated by the deformation theory of plasticity.
Uniformly discretized peridynamic body \(\varOmega \), showing point \({\textbf{x}}\)’s interaction with one of its neighbors \({\textbf{x}}^\prime \), within the region \({\mathcal {H}}_{\textbf{x}}\) of radius \(\delta \). \(\varvec{\xi } = {\textbf{x}}^\prime - {\textbf{x}}\) is the relative position of the points, \(\varvec{\eta } = {\textbf{u}}^\prime - {\textbf{u}}\) is the relative displacement and \(\varvec{f}\) is the pairwise force
The paper is organized as follows: we first introduce the bond-based PD, \(J_\mathrm {{\scriptscriptstyle PD}}\), \(J_\mathrm {{\scriptscriptstyle R}}\) and give a proof for the PD J-integral path independence. In the section thereafter, we describe the EWF and then give the algorithm (procedure) for the PD linear material model, the numerical computation of the J-integrals, and their verification for a number of linear example problems with available analytical solutions for the classical model: an infinite center cracked tension (CCT) specimen, a finite CCT specimen, and a DENT specimen. We then extend the model to include adaptive bond calibration for nonlinear elastic behavior of AHSS grade specimens (therefore implementing the deformation theory of plasticity). An AHSS grade is chosen because of its Poisson’s ratio close to  fits well to a bond-based constitutive equation. Using the so-calibrated nonlinear model with brittle failure, the EWF is computed for several ligament lengths of DENT specimens. In order to better represent plastic dissipation, gradual softening is added. The last two sections present an in-depth discussion and conclusions.
fits well to a bond-based constitutive equation. Using the so-calibrated nonlinear model with brittle failure, the EWF is computed for several ligament lengths of DENT specimens. In order to better represent plastic dissipation, gradual softening is added. The last two sections present an in-depth discussion and conclusions.
The major contributions are, therefore, the introduction of a new adaptive bond micromodulus calibration method, and the extension of PD modelling to include the evaluation of the EWF and its validation against experiments.
2 Bond-based peridynamic theory
The peridynamic equation of motion of the material point at position \({\textbf{x}}\) at time t is given as (Silling 2000; Silling and Askari 2005)
where \(\varOmega \) is the domain of the body, \({\textbf{u}}\) is the displacement vector field, \(\rho \) is the mass density and \({\textbf{b}}\) is a prescribed body force density. \({\textbf{f}}\) is the pairwise force function (a vector) per unit volume squared, denoting the force the material point at \({\textbf{x}}^\prime \) exerts on the material point at \({\textbf{x}}\). This interaction between pairs of material points is called bond. The integral is defined over a region \({\mathcal {H}}_{\textbf{x}}\) of radius \(\delta \), called the horizon, Fig. 1, which can be seen as a sphere, disk or range, for 3D-, 2D- and 1D-models, respectively. A suitable horizon size is chosen and the material body discretized in accordance with problem geometry, loading and desired accuracy of the results (Silling 2016; Xu et al. 2018). Convergence studies may be performed to justify the selection of horizon and discretization. The horizon factor (Bobaru et al. 2009), \(m = \delta /\varDelta x\), where \(\varDelta x\) is the uniform grid spacing, should in a plane square lattice arrangement have a ratio of at least 3 (Silling and Askari 2005; Madenci and Oterkus 2014) and in many cases 4 or higher (Ha and Bobaru 2010; Henke and Shanbhag 2014; Dipasquale et al. 2016), to provide grid independent crack growth patterns. Studying the effect of increasing m is a so-called m-convergence study (Bobaru et al. 2009).
A material is called microelastic if the pairwise force between material points is derivable from a micropotential \(\omega \) (Silling 2000):
where \(\varvec{\xi } = {\textbf{x}}^\prime - {\textbf{x}}\) is the relative position of two material points of the reference configuration, and \(\varvec{\eta } = {\textbf{u}}\left( {\textbf{x}}^\prime , t \right) - {\textbf{u}}\left( {\textbf{x}}, t \right) = {\textbf{u}}^\prime - {\textbf{u}}\) is the corresponding relative displacement of the deformed configuration. A linear microelastic material results in the micropotential
where \(s= \frac{|| \varvec{\xi } + \varvec{\eta } || - || \varvec{\xi } ||}{|| \varvec{\xi } ||}\) is the relative elongation of a bond. Differentiation of Eq. (3) according to Eq. (2) gives
where \((\varvec{\xi } + \varvec{\eta })/|| \varvec{\xi } + \varvec{\eta } || = {\textbf{e}}\),
is a unit vector along a line through the two points of a bond in the deformed configuration. As we assume that a material point \({\textbf{x}}\) does not interact with material points outside its horizon, \({\textbf{f}} = {\textbf{0}}\) for \(||\varvec{\xi }|| > \delta \). The particular kernel of the integrand in Eq. (1), here the ratio \(c(||\varvec{\xi }||) / ||\varvec{\xi }||\), is common for peridynamic mechanical problems. Other kernels are possible and the selection influences the nonlocality, convergence, and thus the discretization applied (Chen et al. 2016).
2.1 Micromodulus
The elastic stiffness of a bond is determined by the micromodulus function \(c(||\varvec{\xi }||)\), which is found by calibrating the peridynamic strain energy density against the classical strain energy density, for a homogeneous body under a) isotropic (dilatational) deformation and b) pure shear (distortional) deformation. The micropotential \(\omega \) is the energy of a single bond with dimension ‘energy per unit volume squared’. The strain energy density of a single point is therefore
The factor  appears as the points for a bond shares the bond energy between them equally. For a 2D body
appears as the points for a bond shares the bond energy between them equally. For a 2D body
where t is the thickness of the body, and \(c_1\) comes from assuming a constant micromodulus \(c(||\varvec{\xi }||) = c_1\). Isotropic deformation and plane stress give the classical strain energy density  . Setting \(W = W_0\) yields the corresponding micromodulus:
. Setting \(W = W_0\) yields the corresponding micromodulus:
The isotropic and pure shear deformations must result in the same \(c_1\), which for 2D plane stress restricts Poisson’s ratio to  , and to
, and to  for 2D plane strain and 3D models (Silling 2000; Gerstle et al. 2005). This is because the forces within a bond depends only on the two material points of a bond (and no other points). This restriction has been overcome for state-based PD (Silling et al. 2007). However, an advantage of bond-based PD is that it is computationally less expensive.
for 2D plane strain and 3D models (Silling 2000; Gerstle et al. 2005). This is because the forces within a bond depends only on the two material points of a bond (and no other points). This restriction has been overcome for state-based PD (Silling et al. 2007). However, an advantage of bond-based PD is that it is computationally less expensive.
Other types of micromoduli (triangular, conical, higher degree polynominal) are derived in a similar fashion as the constant one and are available for 1D (Bobaru et al. 2009), 2D (Ha and Bobaru 2010) and 3D (Silling and Askari 2005). Notice that these micromoduli are calculated assuming a continuous body, i.e. an infinite number of points inside the horizon. For a finite number of points in this region, the micromodulus is, depending upon the type, more or less dependent upon the number of points there; see Eriksson and Stenström (2020a, 2020b) for 1D and (Stenström and Eriksson (2021), App. A) for 2D. This dependence must usually be taken into account.
Since we are using relatively low grid density in the present study, approximate values of \(c(m=3)\) and \(c(m=5)\) have been derived (see appendix) and are \(c_{m=3}=1.1507c_{\infty }\) and \(c_{m=5}=1.0697c_{\infty }\). An alternative approach for correcting c, with a similar effect is to apply PD surface effect correction procedures to the bonds of the entire material body.
2.2 Peridynamic surface effect
Each material point \({\textbf{x}}\) interacts with its neighboring points, the family of \({\textbf{x}}\), within a radius \(\delta \). Therefore, material points at a distance smaller than \(\delta \) from a free surface will experience a truncated horizon, resulting in a smaller domain of integration. This PD surface effect (Ha and Bobaru 2011) leads to a softer material and larger strains near boundaries. Various correction methods exist, and have conveniently been reviewed and compared by Le and Bobaru (2018).
In this study, ‘the energy method’ method by Madenci and Oterkus (2014) will be used for PD surface effect correction (Le and Bobaru 2018, p. 507).
2.3 Constraint conditions and stresses
The PD equation of motion is a nonlinear integro-differential equation in time and space, without spatial derivatives, and therefore does not involve any classical boundary constraints. Instead volume constraints can be applied through a nonzero volume rather than on a surface (Silling and Askari 2005; Du et al. 2012), commonly introduced within a layer of thickness \(\varDelta x\) or \(\delta \) (Hu et al. 2012).
The treatment of stresses at boundaries also differ from that of classical continuum mechanics, for that boundary stresses are introduced to PD as body forces \({\textbf{b}}\) within a layer \(\varDelta x\) (Madenci and Oterkus 2014) or \(\delta \) (Silling and Askari 2005). In practice, to prescribe a stress \(\sigma \) to a material point \({\textbf{x}}\), one divides \(\sigma \) with the grid spacing \(\varDelta x\), to obtain an equivalent force per unit volume.
2.4 Partial volume scheme
Numerical integration of a material point \({\textbf{x}}\) over its region \({\mathcal {H}}_{\textbf{x}}\) including the entire volume of each material point \({\textbf{x}}^\prime \) within the horizon \(\delta \) (Fig. 20), results in an integration area somewhat larger than the area of the disc-shaped (2D) integration region. A correction factor was introduced, commonly varying linearly between 1 and  (Parks et al. 2010), for elements intersected by the horizon:
(Parks et al. 2010), for elements intersected by the horizon:
where \(r = \varDelta x / 2\), and a uniform cubic lattice is assumed. Equation (8), which is called the LAMMPS method, will be used in this study. Other correction methods exist and can be found in Seleson (2014) and Seleson and Littlewood (2018).
2.5 Evaluation of the peridynamic equation of motion
For meshfree numerical implementation (Silling and Askari 2005), the integral for the PD equation of motion, Eq. (1), is replaced by a summation (Niazi et al. 2021):
where \(\textrm{Fam}(i)\) is the family of nodes j of the horizon region of node i. For dynamic or quasi-static simulation, the common implementation in practice is by time integration through a finite number of small time or load steps and looping over the equilibrium equations of the material points. Detailed algorithms are found in Littlewood (2015b) and Madenci and Oterkus (2014), and a supportive flowchart can be found in Javili et al. (2019). For static modeling, matrix solutions are found in Bobaru et al. (2009), Sarego et al. (2016) and Eriksson and Stenström (2020a, 2020b).
For further reading, reviews are offered by Javili et al. (2019) and Diehl et al. (2019). For peridynamic modeling of Mode I loading, which is used in the present study, see Diehl et al. (2016) for investigation on convergence and crack initiation. For the state-based peridynamic theory, the reader is referred to Silling et al. (2007).
3 The bond-based nonlocal peridynamic J-integral (\(J_\mathrm {{\scriptscriptstyle PD}}\))
J is a contour integral evaluated counterclockwise along an arbitrary path \(\partial {\mathcal {R}}\), enclosing the tip of a straight through crack along the x-axis. The bond-based peridynamic J, derived by Hu et al. (2012), is given as:
where W is the strain energy density, Eq. (6), \(n_1\) is the x-component of the outward unit normal vector of \(\partial {\mathcal {R}}\), \(\textrm{d}s\) is an element of arc length along \(\partial {\mathcal {R}}\), \({\mathcal {R}}_1\) is the region inside the contour, and \({\mathcal {R}}_2\) is the region outside the contour (see Fig. 2).
Illustration of the \(J_\mathrm {{\scriptscriptstyle PD}}\) contour, here made rectangular, enclosing a crack of length a. \(\varOmega \) is the domain of the body and includes the regions \({\mathcal {R}}_{0, \, 1, \, 2}\) and the contour \(\partial {\mathcal {R}}\). \({\mathcal {R}}_0 + {\mathcal {R}}_1 = {\mathcal {R}}\)
\(J_\mathrm {{\scriptscriptstyle PD}}\) was derived using the infinitesimal virtual crack extension method. The identity of Eqs. (12) and (18) of Hu et al. (2012) can likewise be derived from the left and right sides of the energy balance Eq. (31) of Silling and Lehoucq (2010).
3.1 Path independence
So far the \(J_\mathrm {{\scriptscriptstyle PD}}\) has been shown through numerical calculations to be path independent within an error of a few percents (Hu et al. 2012; Panchadhara and Gordon 2016). However, like the original, path independence can be derived analytically.
Let \({\mathcal {R}}\) be a subregion enclosing a crack tip of a plane body \(\varOmega \), in static equilibrium. Path independence is proved by showing that \(J_\mathrm {{\scriptscriptstyle PD}}\) vanishes for any regular region, i.e. a region not containing a crack.
We start from the first integral in Eq. (10), apply the divergence theorem and substitute for the energy density W, Eq. (6):
Here, the integral \(\int _{\varOmega } {\textbf{f}} \cdot \frac{\partial {\textbf{u}}}{\partial x_1} \, \textrm{d} V_{{\textbf{x}}^\prime }\) vanishes because of static equilibrium. Thus,
where the integration boundary of the inner integral is different from that of the corresponding part of the \(J_\mathrm {{\scriptscriptstyle PD}}\) expression. To adjust the integration boundary and the integrand accordingly, Eq. (12) is expanded to
where \(\varOmega \setminus {\mathcal {R}}\) is \(\varOmega \) but not \({\mathcal {R}}\). The identity Eq. (31), (see appendix), is invoked in the first integral, Eq. (13) then becomes
Thus, the left side of Eq. (11) equals Eq. (14), which implies that \(J_\mathrm {{\scriptscriptstyle PD}}\) vanishes for any region \({\mathcal {R}}\) not containing a crack tip. This statement proves path independence of \(J_\mathrm {{\scriptscriptstyle PD}}\).
\(J_\mathrm {{\scriptscriptstyle R}}\) and discretization For \(J_\mathrm {{\scriptscriptstyle R}}\) formulated as a function of displacement derivatives, and the discretization of both the two J formulations, see appendix.
4 The EWF method
The EWF method follows the approach developed by Cotterell and Reddel (1977) and Marchal and Delannay (1996). Performing a test series on geometrically similar specimens but of different ligament lengths, allows the energy spent in the fracture process to be split into two terms. The energy dissipated from the FPZ is called essential work of fracture (\({{{\mathcal {W}}}}_\textrm{e}\)), and the energy spent at the region outside the FPZ is called non-essential plastic work (\({{{\mathcal {W}}}}_\textrm{p}\)). A DENT specimen is commonly used for thin sheets as its symmetry prevents buckling and ensures mode I crack propagation during the whole test. The total work of fracture
where L is the DENT ligament length, i.e. the distance between the two edge notches, and t is the specimen thickness. \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) is the specific essential work of fracture per unit area. Following this definition \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) is the fracture toughness, equivalent to the J-integral value. \({\scriptstyle {{\mathcal {W}}}}_\textrm{p}\) is the specific non-essential plastic work per unit volume. \(\beta \) is a dimensionless shape factor, depending on the shape of the plastic zone.
Normalizing Eq. (15) by the cross-sectional area, allows determination of the specific total work of fracture \({\scriptstyle {{\mathcal {W}}}}_\textrm{f}\):
By tensile testing, with load F as a function of the displacement s, \({\scriptstyle {{\mathcal {W}}}}_\textrm{f}\) is obtained. The ligament length L is determined using, e.g., light optical microscopy. The value \({\scriptstyle {{\mathcal {W}}}}_\textrm{f}\) is calculated by integration of the load–displacement curve:
where \(s_\textrm{f}\) is displacement at fracture.
By plotting \({\scriptstyle {{\mathcal {W}}}}_\textrm{f}\) against the ligament length L, a straight line is obtained and its intercept at the limit \(L\rightarrow 0\) is taken as the \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\). A schematic representation of the evaluation of the EWF method is shown in Fig. 3. However, some restrictions must be met for the validity of the EWF method. The entire ligament must be in a state of plane stress and completely yielded before crack initiation. Cotterell and Reddel (1977) found that if the shortest ligament length is three to five times the sheet thickness and the longest ligament length not greater than one third of the width, W, of the specimen, or two times the radius of the plastic zone, \(r_\textrm{p}\), in plane stress:
valid results are obtained, and \({\scriptstyle {{\mathcal {W}}}}_\textrm{e} \approx J_\mathrm {{\scriptscriptstyle c}}\). This relationship has been studied for example by Rink et al. (2014).
5 Algorithm for the linear PD material model and verification of \(J_\mathrm {{\scriptscriptstyle PD}}\)
The algorithm for the linear PD model and evaluation of \(J_\mathrm {{\scriptscriptstyle PD}}\) and \(J_\mathrm {{\scriptscriptstyle R}}^*\) is as follows:
-
1.
Specify input parameters:
-
Material body width and height
-
Material properties \(\nu \) and E
-
Grid spacing \(\varDelta x\) and horizon factor m
-
Remote loading \(\sigma _0\)
-
Integration contour number, e.g. contour 1 is the contour through the four points next to the crack tip
-
-
2.
Discretize the material body into spatial coordinates x and y.
-
3.
Set-up and run the peridynamic model:
-
4.
Calculate \(J_\mathrm {{\scriptscriptstyle PD}}\) and \(J_\mathrm {{\scriptscriptstyle R}}^*\):
The J expressions are going around the crack tip, from one crack face to the other. Therefore, to avoid peridynamic boundary effects where J crosses the x-axis, i.e. a symmetry line, the peridynamic models include the material body of both sides of the crack.
In the set-up of the overall PD model, we apply a constant micromodulus c as per Eq. (7) (see appendix), PD surface effect correction by using the energy method (Le and Bobaru 2018, p. 507), constraints and stresses within a layer of thickness \(\varDelta x\) (Sect. 2.3), volume correction as per Parks et al. (2010), and adaptive dynamic relaxation of Madenci and Oterkus (2014) for obtaining quasi-static solutions.
A constant c gives a linearly increasing bond force with increasing strain, and thus a linear elastic material model. Therefore, for modeling non-linear materials and EWF, c will be calibrated accordingly.
The numerical implementation, including EWF, is done using Matlab software.
5.1 Verification of \(J_\mathrm {{\scriptscriptstyle PD}}\)
The \(J_\mathrm {{\scriptscriptstyle PD}}\) and \(J_\mathrm {{\scriptscriptstyle R}}\) integrals are given in Eqs. (36) and (37). We start out the modeling with the infinite CCT specimen.
5.1.1 Infinite CCT specimen
For the classical exact analytical stress–strain-displacement solution of the infinite geometry problem, see appendix. From the remote loading \(\sigma _0\) of the exact solution, we can calculate the boundary stresses using Eq. (38a), of the specimen shown in Fig. 4a. The boundary stresses are then introduced as input to the PD model. The J methods can now be evaluated for the exact solution using Eq. (38c) and on the modeled PD solution’ displacement field.
Problem set-up
To facilitate comparison with previous results of others, e.g. Hu et al. (2012), Stenström and Eriksson (2019, 2021), we will use a Young’s modulus of 72 GPa and a Poisson’s ratio of  (plane stress) for modeling. The dimensions of the specimen is set to 10 cm by 10 cm (\(W \times 2h\)), the half crack length \(a = 5\) cm and \(\sigma _0=1\) MPa.
(plane stress) for modeling. The dimensions of the specimen is set to 10 cm by 10 cm (\(W \times 2h\)), the half crack length \(a = 5\) cm and \(\sigma _0=1\) MPa.
Our reference value for the problem is the classical analytical \(J_0 = K_\textrm{I}^2/E = (\sigma \sqrt{\pi a})^2/E=2.1817\) N/m.
Peridynamic model discretization
We will keep the horizon factor m constant at three, i.e. \(\delta = 3\varDelta x\), and decrease the horizon \(\delta \) for \(\delta \)-convergence. The error of the PD model is expected to decrease as the number of material points of the model is increased and the PD surface effect diminishes.
Note that for the examples shown in Sects. 6–8 below, we use a grid factor m of 4 and 5 for the DENT and EWF examples to achieve a better accuracy for the energy flow. In certain problems, especially for cracks with curving or branching paths, using a larger m-value may be warranted (see Dipasquale et al. 2016). In the examples shown in this work, the crack paths are simple: straight. For such problems, as long as the grid is aligned with the propagation direction, using a large m-value is generally not needed.
Evaluation of J
The resulting J values are shown in Fig. 5. The relative difference is calculated as \((J-J_0)/J_0\). Using the finer \(\delta =\) 0.6 mm, the difference is less than one percent for both J methods, on both the analytical solution and the PD solution. The difference of the coarser \(\delta \) is due to PD surface effect and treatment of corner points, and a reason for the difference at the finer discretization is numerical error.
Infinite CCT model results. The nonlocal and classical Js calculated on the PD model (\(J_\mathrm {{\scriptscriptstyle PD}}\) and \(J_\mathrm {{\scriptscriptstyle R}}^*\)) and on the classical analytical displacement solution (\(J_\mathrm {{\scriptscriptstyle PD}}^*\) and \(J_\mathrm {{\scriptscriptstyle R}}\))
5.1.2 Finite CCT specimen
The finite CCT specimen is loaded at the upper and lower edges by a constant \(\sigma _y\) as shown in Fig. 4b. For estimating the stress intensity factor, Isida’s (1971) classical solution is commonly regarded as the most accurate one (ASM 1996):
where the dimensionless geometry function \(f_1\) can be found in standard books, e.g. (Anderson 2005), i.e. different from the components of PD \({\textbf{f}}\).
The problem set-up and discretization is the same as for the previous infinite CCT specimen. Thus, \(\frac{a}{W}\) and \(\frac{h}{W}\) both becomes 0.5, giving \(f_1\) = 1.967 (Isida 1971), given \(\sigma _y = \sigma _0 = 1\) MPa. The relative difference is then calculated based on the reference value \(J_0=K_\textrm{I}^2/E=8.44\) N/m.
The results are presented in Fig. 6 and show differences of about one percent or less at the finer \(\delta \). We notice that the difference at the coarser \(\delta \) is less than of the infinite model results (Fig. 5).
5.1.3 Half DENT specimen
In a similar fashion as for the finite CCT specimen, we test the J methods on a half DENT specimen, Fig. 4c. Our classical reference solution is that of Wu and Carlsson (1991):
The problem set-up differs from the previous case only in height; \(h = 0.2\) m, leading to \(h/W = 2\) and \(f_2(2)= 1.169\) (Wu and Carlsson 1991). With \(\sigma _y = \sigma _0 = 1\) MPa, the relative difference is based on the reference value \(J_0=K_\textrm{I}^2/E=2.981\) N/m.
Since the verification on the CCT models shown good agreement with their classical analytical J values, we use only one discretization here; \(\delta =\) 3 mm, leading to 100\(\times \)400 materials points (\(W\times h\)). This \(\delta \) gives the differences \(e_{J_\mathrm {{\scriptscriptstyle R}}}=2.2\)% and \(e_{J_\textrm{PD}}=2.7\)%. The \(\delta \) is the same as for the previous 1002 models, but we have less PD surface effect in the y-direction due to 400 material points. Thus, the differences are similar to the differences at the 1002 and 2502 models in Figs. 5 and 6.
6 Adaptive calibration of PD model to a given nonlinear stress–strain hardening curve
For evaluating EWF, the PD model needs to be calibrated for non-linear materials. The EWF method is going to be applied to a PD model calibrated to an experimentally obtained stress–strain response. Therefore, an adaptive calibration is carried out with data of a standard (defect free) tensile test specimen. The calibration is carried out on the bond force level so as to obtain a global stress–strain behavior similar to the experimentally measured stress–strain response. Once calibrated, a DENT specimen and EWF is modeled.
The calibration procedure includes five constants; \(c_{\textrm{cal}}\),  , \(c_\textrm{t}\), \({\hat{e}}_c\) and \(c_E\). \(c_{\textrm{cal}}\) is a vector of calibration constants of unit interval. Each constant of \(c_{\textrm{cal}}\) corresponds to a local bond strain segment (subinterval) of vector
, \(c_\textrm{t}\), \({\hat{e}}_c\) and \(c_E\). \(c_{\textrm{cal}}\) is a vector of calibration constants of unit interval. Each constant of \(c_{\textrm{cal}}\) corresponds to a local bond strain segment (subinterval) of vector  . Since multiplying each bond with a calibration factor is computationally intensive, calibration of local bonds and checking of the resulting global error \(e_c = \sigma _\mathrm {{\scriptscriptstyle PD}}/\sigma _0\), are carried out at load steps evenly divisible with \(c_\textrm{t}\). \(\sigma _\mathrm {{\scriptscriptstyle PD}}\) is the PD global stress and \(\sigma _0\) is the experimental stress. \({\hat{e}}_c\) is the error limit when a new calibration constant is calculated and added to \(c_{\textrm{cal}}\). The fifth and optional constant, \(c_E\), is a global strain value between the true elastic limit and the proportionality limit; this is the strain where the calibration starts.
. Since multiplying each bond with a calibration factor is computationally intensive, calibration of local bonds and checking of the resulting global error \(e_c = \sigma _\mathrm {{\scriptscriptstyle PD}}/\sigma _0\), are carried out at load steps evenly divisible with \(c_\textrm{t}\). \(\sigma _\mathrm {{\scriptscriptstyle PD}}\) is the PD global stress and \(\sigma _0\) is the experimental stress. \({\hat{e}}_c\) is the error limit when a new calibration constant is calculated and added to \(c_{\textrm{cal}}\). The fifth and optional constant, \(c_E\), is a global strain value between the true elastic limit and the proportionality limit; this is the strain where the calibration starts.
6.1 Algorithm
The calibration of the PD model is as follows:
-
1.
Specify input parameters:
-
Material body width\(\times \)height, in accordance with ISO and ASTM standards (ISO 2019; ASTM 2016)
-
Virtual strain gauge’s x and y coordinates within the gauge length
-
Properties \(\nu \), E, m and \(\varDelta x\)
-
Experimental stress–strain response data
-
Velocity boundary condition \(v_0\) at the short edges of the body
-
Calibration constants \(c_E\),
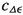 , \(c_\textrm{t}\), \({\hat{e}}_c\) and \(c_{\textrm{cal}}\)
, \(c_\textrm{t}\), \({\hat{e}}_c\) and \(c_{\textrm{cal}}\)
-
-
2.
Discretize the material body into spatial coordinates x and y.
-
3.
Set-up and run the peridynamic model:
-
Integrate the peridynamic equation of motion at all nodes x and y, by rewriting Eq. (1) as a summation
-
At each load step, add \(v_0\) to the outermost material points of the specimen’s short edges (strips with thickness of \(\varDelta x\) or \(m\varDelta x\))
-
At load steps that are evenly divisible with \(c_\textrm{t}\): Calculate the bond force strain of all bonds and multiply each bond force with its corresponding \(c_{\textrm{cal}}\) factor. Also, calculate \(\sigma _\mathrm {{\scriptscriptstyle PD}}\) through the gauge coordinates (Fig. 7).
-
At load steps that are evenly divisible with \(c_\textrm{t}\): If the global strain is larger than \(c_E\) and the model error \(e_c > {\hat{e}}_c\), calculate the next calibration constant \(c_{\textrm{cal}}^{i+1} = c_{\textrm{cal}}^{i}/e_c\) that corresponds to the strain subinterval \(c_E+(i+1)c_{{\scriptscriptstyle \varDelta } \epsilon }\) (\(c_{\textrm{cal}}^0=1, \; i=0,1,2,...\)).
-
The obtained \(c_{\textrm{cal}}\) vector can now be used in the general four steps algorithm (Sect. 5) by calibrating all bonds at given bond strains.
\(\sigma _\mathrm {{\scriptscriptstyle PD}}\) is the stress through a point interface by summing the x-components along m points (Fig. 7):
where the first summation are the m points along a line along the stress direction, and \(\mathrm {Fam^+}(i)\) are the family members of point i that are located in front of the m points dividing line. Multiplication with the area of the point interface, \((\varDelta x)^2\), gives the force, and summation along a strip gives then the cross-sectional global force.
In the above algorithm, a calibration constant is added when \(e_c > {\hat{e}}_c\). Alternatively, the calibration constant can be added at certain (evenly distributed) load steps, bond strains or global strains. However, we have found that using a \({\hat{e}}_c\) limit gives a PD stress–strain curve with less oscillations and better necking compared to the other criteria.
a Calibrated PD global stress–strain and experimental engineering stress–strain (Golling et al. 2019). b Corresponding local PD bond force. c \(c_{\textrm{cal}}\) versus  . d Displacement at a point for steady check
. d Displacement at a point for steady check
6.2 Problem set-up and discretization
For model calibration and evaluation, we will use experimental data of a bainite–martensite sheet metal (AHSS) provided by Golling et al. (2019). The engineering stress–strain from Fig. 4 of Golling et al. is reproduced in Fig. 8a. The stress–strain data is obtained using a standard specimen of 12.5 mm in width and 2.0 mm in thickness (ISO 2019; ASTM 2016), and gives an \(E_0\) of 200 GPa. Thus, the PD model constants E and \(\nu \) are set to 200 GPa and  , respectively, and the problem geometry used for the calibration is set to 12.5 mm \(\times \) 62.5 mm.
, respectively, and the problem geometry used for the calibration is set to 12.5 mm \(\times \) 62.5 mm.
The geometry is discretized into 40\(\times \)200 material points, with \(m = 5\), thus \(\delta = 5\cdot 0.3125\) mm. The opposite ends of the specimen is loaded with a constant velocity \(v_0 = 1.6\cdot 10^{-7}\) m/s, and a virtual strain gauge is set 6.4 mm (20.5\(\varDelta x\)) from the lengthwise mid. The loading rate is chosen small enough to avoid specimen oscillations.
The PD recovered E modulus before calibration is 0.8 % below \(E_0\), measured at the strain gauge, and 0.1 % below when measured as a mean across the specimen width. The approach used to find the stress, and thus E, is presented in Fig. 7 and Eq. (21).
6.2.1 Adaptive calibration
The adaptive calibration is performed during a single specimen loading. The calibration procedure begins at \(c_E = 0.003\) global strain and the first calibration constant is of unity. The global stress is checked against the experimentally obtained stress–strain response for each \(c_\textrm{t} = 5\) steps. As the specimen is loaded, a new calibration constant is supplied each time that the global stress error reaches the limit \({\hat{e}}_c = 2\%\). Calibration of all bonds are carried out for each \(c_\textrm{t} = 5\) steps.
The calibrated bond force-strain model and global PD stress–strain response are shown in Fig. 8. The measurement is carried out at the virtual strain gauge point and the bond force-strain is of one bond in the global load direction, Fig. 8a, b. \(c_{\textrm{cal}}\) and  amounts to 107 calibration constants/parameters. The total number of load steps, at the strain where the standard sheet metal specimen fractured, is 10 540.
amounts to 107 calibration constants/parameters. The total number of load steps, at the strain where the standard sheet metal specimen fractured, is 10 540.
Since material bonds reach their respective yield strain at different times/loads, the global stress–strain response is “smoothed”. Not least for a bi-linear law, this leads to an apparent hardening and/or necking effect (Silling 2016, p. 44). The noise in Fig. 8b comes from oscillations due the quasi-static model and numerical approximation.
6.2.2 Recovered stress–strain curve
Since the calibration factors are adaptively supplied one at a time during the calibration, based on monitoring at one gauge point, the recovered stress–strain curve will differ when all factors (\(c_{\textrm{cal}}\) and  ) are supplied initially. The recovered stress–strain with a loading rate of \(v_0 = 0.2\cdot 10^{-7}\) m/s is shown in Fig. 9. ‘No dmg’ is without bond break and ‘With dmg’ is with bond break at the last calibration constant of 0.0465 bond strain. The green cross in Fig. 9a is were it fractured. \(s_1\) in Fig. 9b indicates the failure bond law used here and in the next section.
) are supplied initially. The recovered stress–strain with a loading rate of \(v_0 = 0.2\cdot 10^{-7}\) m/s is shown in Fig. 9. ‘No dmg’ is without bond break and ‘With dmg’ is with bond break at the last calibration constant of 0.0465 bond strain. The green cross in Fig. 9a is were it fractured. \(s_1\) in Fig. 9b indicates the failure bond law used here and in the next section.
To notice is that the calibration values are more or less independent of the number of material points and grid density m, as seen in Fig. 10.
7 EWF on full DENT specimen
We found from the literature review that bond force calibration studies are presently going on and that EWF modeling for PD is new. Therefore, this preliminary EWF study is limited regarding influencing parameters and applications. Moreover, the EWF modeling includes estimation of the J-integral and to avoid generation of duplicate results, we will apply the classical \(J_\mathrm {{\scriptscriptstyle R}}\) formulation, Eq. (37), only, in particular because of the small number of points of narrow ligaments.
7.1 Problem set-up and discretization
The full DENT specimen of Golling et al. (2019) is 45 mm wide and 2.0 mm thick. The corresponding tensile test was monitored with an extensometer with a gauge length of 50 mm. In the PD model, we use a geometry of 45 mm \(\times \) 225 mm (2\(W\times 2h\); see Fig. 4d). A virtual gauge for logging the displacement is set 25 mm from the two notches, i.e. 50 mm gauge length. For logging the force, another gauge is set 10 mm from the two notches. This is to avoid a delay/bump of the force-elongation response that appears if the force is logged at 25 mm. The grid density m is set to 5. Discretization and ligament lengths (L) are given in Table 1. The loading rate \(v_0\) is \(0.4\cdot 10^{-7}\) m/s for \(\delta =\) 2.8, 1.9 and 1.4, and \(0.6\cdot 10^{-7}\) m/s for \(\delta =\) 1.1.
We will use two different crack tip definitions that we call sharp and fuzzy tips; see explanation in Fig. 12.
DENT results of \(\delta =\) 1.1 mm (\(200\times 1000\)) and sudden failure at \(S_1\). a Global cross section force. Colored curves are PD results. Black curves are experimental results with L = 6.7, 8.7, 11.2, 12.9 (Golling et al. 2019), dotted vertical lines are integration limits and dashed curves are ligament damage. b Specific total work of fracture (\({\scriptstyle {{\mathcal {W}}}}_\textrm{f}\)). The circles are of PD and the crosses are of 15 experimental specimens in Golling et al. (2019). c Magnified global force and \(J_\mathrm {{\scriptscriptstyle R}}^*\) plotted with dashed lines
7.2 Evaluation of EWF and J
The adaptive calibration of Fig. 8c is used for the full DENT specimen without further adjustments. PD bonds break at the bond strain \(s_1=\) 0.0465 and drops suddenly to zero, Fig. 9b, and the PD model is of a nonlinear-elastic type.
The simulation result for \(\delta =1.1\) mm is shown in Fig. 11a. Force is the global cross sectional force. The dashed lines indicate the amount of damage, or fractured ligament, between the two notches. 100% damage means fully fractured ligament. For calculation of \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\), the upper integration limit is set to 90% damage; see the dotted vertical lines.
Integration of the force-elongation curves using Eq. (17) gives \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\). See Fig. 11b. Experimental data (crosses) of Golling et al. (2019) gives \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) = 78±6 kN/m while PD gives \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) = 182 kN/m and lack plastic work.
Monitoring J, Eq. (37), critical \(J_\mathrm {{\scriptscriptstyle R}}^*=\frac{1}{4}(95+89+93+92) \cdot 10^3 = 92\) kN/m. Individual values are given by the small circles in Fig. 11c. Here, the vertical lines of the maximum global force have been set manually and is therefore somewhat subjective.
For studying \(\delta \)-convergence, we complement with three more discretizations. \(\delta \)-convergence is performed keeping the grid density m constant while decreasing the horizon radius \(\delta \), i.e. increasing the total number of material points of the model (Bobaru et al. 2009). See Fig. 15. By increasing the number of material points in the model, the PD surface effect is reduced. Only \(J_c\) is traced as \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) lack plastic work.
8 Softening
PD materials with a linear bond force-strain relationship contains a single parameter (critical bond strain) to simulate both the strength and toughness. For a certain horizon size, one is then able to match both, but the likelihood is that the particular horizon is too small to make it practical for computations. In order to allow matching of both strength and toughness for any horizon size, one needs to introduce a two-parameter bond force-strain model. For crack nucleation, propagation and strongly nonlinear materials, bi- and trilinear constitutive laws have been developed (see Sect. 1.3). PD trilinear laws for brittle and quasi-brittle materials have been studied by Yang et al. (2018) and Niazi et al. (2021). The adaptively calibrated constitutive law of the present study, resulted in a piecewise linear approximation of the experimental stress–strain response. In the preset model, for a more pronounced softening part, we also assume a linear behavior for the bond-response, for simplicity. See Fig. 16. Softening starts at \(s_1\) and continues linearly to \(s_2\).
We keep \(s_1 = 0.0465\) and manually calibrate \(s_2 = 2\) for capturing the plastic work. We decrease the horizon \(\delta \) to 0.28 mm, and for computational efficiency set \(m = 4\). With the added softening, the PD model is still able to recover the experiment tensile specimen (Fig. 17). For the PD DENT, \(v_0 = 0.2\cdot 10^{-7}\) m/s, bond calibration every \(c_\textrm{t} = 5\), sample size is 45 mm \(\times \) 63 mm for computational efficiency, and the global force gauge is shifted from 10 mm to 5 mm from the mid for better force response. Lastly, we set the ligament lengths closer to the experimental, to 6.61, 8.72, 11.25 and 12.80 mm (this was not possible before with \(\delta =\) 2.8 mm). The resulting DENT model is shown in Fig. 18. Ligament damage, Fig. 18a, is the fraction of bonds that have passed \(s_1\). The PD DENT model shows improved plastic work but appears too strong, i.e. the bainitic-martensitic material appears too brittle. We therefore try a more ductile material of Golling et al. (2019) called ‘Bainite’; see calibrated and recovered standard tensile test in Fig. 17.
The values \(s_1\) and \(s_2\) are calibrated manually to 0.03 and 1.2, respectively. The loading speed is lowered to \(v_0 = 0.1\cdot 10^{-7}\) m/s, and for computational efficiency, the horizon \(\delta \) is increased to 1.4 mm, with \(m = 5\). The ligament lengths are set as close as possible to the experimental ones.
\(J_\mathrm {{\scriptscriptstyle R}}^*\) under \(\delta \)-convergence. The x-axis is linear, going from 0 to 200 000. \(78\pm 6\) kN/m is the critical J obtained by Golling et al. (2019) by assuming \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) equals critical J
The resulting PD DENT model now better match the maximum global force and the EWF-line (Fig. 19). PD obtained \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) = 369 kN/m, experimental \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) = 349 kN/m \(\approx J_\mathrm {{\scriptscriptstyle c}}\), and PD obtained \(J_\mathrm {{\scriptscriptstyle R}}^*\) = 365 kN/m.
If the force-elongation curves are integrated to the crack initiation, an alternative toughness measure is obtained, called fracture toughness at crack initiation (\({\scriptstyle {{\mathcal {W}}}}_\textrm{e}^*\)), and is the average of the resulting EWF data points, with the slope assumed zero (Frómeta et al. 2021). In Fig. 19b,  = 166 kN/m.
= 166 kN/m.
The bainite standard tensile test response has a narrow bend from the elastic region to the hardening phase (Fig. 17). This caused slightly more noise to the calibration constants compared to the constants of the bainite-martensite material (Fig. 10). It did not affect the recovered tensile test, but caused more oscillations in the adaptive dynamic relaxation solver. To remove the noise, a curve was fitted to the calibration constants. Curves tested includes polynomial, two terms exponential, Weibull, three terms Gaussian and two terms power function. Several fittings gave an accurate recovered tensile test, but a tenth order polynomial gave the least amount of noise for the DENT, and where therefore chosen. By curve fitting, the number of calibration constants can be chosen. 30, 100 and 180 constants were tested. More constants produced smoother DENT test and therefore the polynomial function was supplied directly to the PD code instead of calibration constants. However, 30 constants did work as well.
Recovered PD stress–strain with the added softening for ‘Bainite-martensite’ and for another added material called ‘Bainite’. The blue lines are from experimental data by Golling et al. (2019). For the \(s_1\) values used, softening occurred at the cross symbols
9 Discussion
The martensitic-bainitic material turned out to have too low ductility for the PD material model. Experimental data showed high ultimate strength (1730 MPa) and sudden fracture of DENT specimens, at the point where the DENT experimental curves ends in Fig. 18a. This is due to microscale effects discussed later.
The bainitic PD material model was able to match both the standard tensile test specimen strength and the DENT specimens strength. By studying the softening part, Fig. 19a, the PD DENT curves meet at a single point (beyond 1 mm elongation) while the experimental curves ends at different elongations, e.g. 0.7, 0.8 and 0.9 mm. To obtain similar EWF, we integrated the PD DENT curves to a remaining strength of 6.1 kN. The reason to stop at this value is the difference between the actual last stages of the ductile failure and the deformation theory (nonlinear elasticity) approximation of it in our model. Note that if one chooses a lower force level (on the softening side) to integrate to, the resulting EWF line (in Fig. 18b) only slightly shifts downward. Changing the \(S_1\) or \(S_2\) values affects both the maximum force and ductility of the DENT.
Since we are using the deformation theory (nonlinear elasticity) plasticity instead of an incremental plasticity model, the part where unloading happens (monotonic loading is no longer satisfied) will not be very accurate. DENT softening is a challenge experienced for FEM as well (Sandin et al. 2021), but due to reasons inherent to FEM.
The disturbance of the PD DENT force elongation responses seen in Fig. 19a) comes from bonds entering the linear softening (discontinuous function). The linear softening can be replaced by a curved softening (bell-shaped), to better match the curvature of the experimental softening part. Here we use linear for computational simplicity.
The PD DENT responses makes slightly sharper bend from the elastic-to-hardening region compared to the experimental results (Fig. 19a). This can be due to microscale effects.
DENT results of \(\delta =\) 0.28 mm (\(640\times 896\)). a Global cross section force and ligament damage. Colored curves are PD results. Black curves are experimental results with L = 6.7, 8.7, 11.2, 12.9, dashed curves are damage and dotted vertical lines are integration limits. b PD and experimental specific total work of fracture \({\scriptstyle {{\mathcal {W}}}}_\textrm{f} = {\scriptstyle {{\mathcal {W}}}}_\textrm{e} + L{\scriptstyle {{\mathcal {W}}}}_\textrm{p}\), circles and crosses, respectively. c Magnified global force and \(J_\mathrm {{\scriptscriptstyle R}}^*\)
DENT results of \(\delta =\) 1.4 mm (\(160\times 224\)). a Global cross section force. Colored curves are PD results. Black curves are experimental results with L = 5.1, 7.0, 9.0, 10.7, 12.6. Dotted vertical lines are integration limits. b PD and experimental specific total work of fracture \({\scriptstyle {{\mathcal {W}}}}_\textrm{f} = {\scriptstyle {{\mathcal {W}}}}_\textrm{e} + L{\scriptstyle {{\mathcal {W}}}}_\textrm{p}\), circles and crosses, respectively. c Magnified global force and  = 365 kN/m
= 365 kN/m
9.1 Microscale effects
Microscale properties that can have an influence on the result are:
Different materials The experimental DENT specimens have fatigue cracks and is therefore in a different damage phase compared to the PD DENT that does not have any fatigued bonds. Also, there are different failure mechanisms taking place; the standard tensile specimen used for calibration is polished (Golling et al. 2019) and has a fracture zone with a radius approaching infinity while the DENT specimen has a crack tip approaching zero in radius.
Microstructure The PD model lacks a microstructure. In the experimental DENT specimens, following dislocation motions, fracture takes place along a minimum energy path. Thus, the PD model may appear too strong.
Crack tip shielding The crack tip of the experimental DENT specimens is under compression when the loading starts due to asperities mismatch, thus, leading to higher strain at fracture compared to the PD model.
Discretization The horizon radius \(\delta \) is much larger than an actual crack tip radius; thus, the not enough refined horizon leads to a blunt PD crack tip.
Surface correction The PD model includes a surface correction factor, which increase the surface stiffness but leave some stiffness fluctuation.
Strain hardening The experimental DENT specimen may experience strain hardening, and therefore a strengthening effect.
9.2 J-integral
Before adding softening, the J-integral of the PD DENT model converges to the experimental J, when J is taken at maximum global force (Fig. 15).
With added softening to the bainite-martensite material, J takes of about where the softening starts, before the maximum force. J shows an increase, or elbow, around 100–150 kN/m, Fig. 18c. This elbow becomes more pronounced and closer to the experimental J when \(\delta \) is shrunken. At \(\delta = 0.14\) mm, the elbow is around 100 kN/m, but was not studied further due to computational time. An elbow may also be distinguished in Fig. 11 at 120–140 kN/m, which explains the slower convergence of the model with softening. The elbow can also be seen by plotting J versus bond damage.
With the bainite material and softening, at the absolute maximum force, the mean \(J_\mathrm {{\scriptscriptstyle Rc}}^*\) of 365 kN is close to the value obtained by Golling et al. (2019) \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) = 349 kN/m \(\approx J_\mathrm {{\scriptscriptstyle c}}\). An elbow cannot be seen.
9.3 Experimental data
The experimental DENT results are somewhat uncertain. The narrow temperature-time process window of bainite formation under quenching makes it difficult to obtain specimens with small variation in phase volume fractions (Golling et al. 2016). Another source of uncertainty is that the crack length of the experimental DENT was measured using a stereomicroscope. Recommendation is, e.g. by ASTM, to heat tint the specimen surface and measure the crack length after a fracture test, as the actual crack tip is often not visible in a stereomicroscope and the crack tip front is convex.
10 Conclusions
A peridynamic (PD) material model calibrated for highly nonlinear elastic behavior has been adopted to investigate, computationally, the use of the EWF method in characterizing fracture toughness of ductile materials.
The \(J_\mathrm {{\scriptscriptstyle PD}}\)-integral was shown analytically to be path independent, in analogy with its classical counterpart.
First, we compared the classical and peridynamic forms of the J integral value on a number of example problems. On the classical analytical displacement solution of the infinite center cracked tension specimen, the relative differences between the J values were less than one percent compared to the classical analytical \(J_0\) value (Fig. 5).
Thereafter, to match nonlinear constitutive behavior, the PD model was calibrated using a novel automated procedure. Under small scale yielding assumptions, the classical J-integral, applied on the PD double edge notched tension (DENT) model, converged to the experimentally obtained J value (Fig. 15).
For capturing the energy dissipated during plastic deformation, a linear bond softening model was adopted (Fig. 16). The model was employed for two very different materials; a lower-ductility bainitic-martensitic steel and a higher-ductility bainitic steel. Up to the start of the softening phase, the model recovers excellently the material response, of both materials (Fig. 17).
The lower-ductility material has an ultimate strength of 1730 MPa, while the higher-ductility material has a strength of 970 MPa. A similar large difference in strength is not seen in the experimental DENT response due to high sensitivity to defects of the lower-ductility material. This sensitivity to defects is seen in the results, as we could not recover the specific essential work of fracture (\({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\)) value of the lower-ductility martensitic-bainitic steel with the nonlinear elastic model (Fig. 18).
While we only used a nonlinear elastic model (equivalent to the deformation theory of plasticity), we were able to match very well the experimentally obtained \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) value for the higher-ductility bainitic steel (Fig. 19). Also, the J-integral value obtained from the PD model, at the absolute maximum specimen load, matched the corresponding \({\scriptstyle {{\mathcal {W}}}}_\textrm{e}\) value.
While being aware of the model limitations, future work will investigate the use of incremental plasticity models on this topic.
References
Anderson T (2005) Fracture mechanics: fundamentals and applications, 3rd edn. CRC Press, Boca Raton
ASM (1996) ASM handbook, fatigue and fracture, vol 19. ASM International, Materials Park
ASTM (2016) E8/E8M–16a, Standard test methods for tension testing of metallic materials. ASTM International, Materials Park
Bárány T, Czigány T, Karger-Kocsis J (2010) Application of the essential work of fracture (EWF) concept for polymers, related blends and composites: a review. Prog Polym Sci 35(10):1257–1287. https://doi.org/10.1016/j.progpolymsci.2010.07.001
Behzadinasab M, Foster JT (2020) A semi-Lagrangian constitutive correspondence framework for peridynamics. J Mech Phys Solids 137:103862. https://doi.org/10.1016/j.jmps.2019.103862
Behzadinasab M, Trask N, Bazilevs Y (2021) A unified, stable and accurate meshfree framework for peridynamic correspondence modeling—Part I: core methods. J Peridyn Nonlocal Model 3(1):24–45. https://doi.org/10.1007/s42102-020-00040-z
Bobaru F, Yang M, Alves LF, Silling SA, Askari E, Xu J (2009) Convergence, adaptive refinement, and scaling in 1D peridynamics. Int J Numer Methods Eng 77(6):852–877. https://doi.org/10.1002/nme.2439
Breitenfeld M, Geubelle P, Weckner O, Silling S (2014) Non-ordinary state-based peridynamic analysis of stationary crack problems. Comput Methods Appl Mech Eng 272:233–250
Breitzman T, Dayal K (2018) Bond-level deformation gradients and energy averaging in peridynamics. J Mech Phys Solids 110:192–204. https://doi.org/10.1016/j.jmps.2017.09.015
Broberg KB (1968) Critical review of some theories in fracture mechanics. Int J Fract Mech 4(1):11–19. https://doi.org/10.1007/BF00189139
Bruck HA (1989) Analysis of 3-D effects near the crack tip on Rice’s 2-D integral using digital image correlation and smoothing techniques. Master’s thesis, University of South Carolina
Casellas D, Lara A, Frómeta D, Gutiérrez D, Molas S, Pérez L, Rehrl J, Suppan C (2017) Fracture toughness to understand stretch-flangeability and edge cracking resistance in AHSS. Metall Mater Trans 48(1):86–94. https://doi.org/10.1007/s11661-016-3815-x
Chen H (2018) Bond-associated deformation gradients for peridynamic correspondence model. Mech Res Commun 90:34–41. https://doi.org/10.1016/j.mechrescom.2018.04.004
Chen Z, Bakenhus D, Bobaru F (2016) A constructive peridynamic kernel for elasticity. Comput Methods Appl Mech Eng 311:356–373. https://doi.org/10.1016/j.cma.2016.08.012
Cotterell B, Reddel JK (1977) The essential work of plane stress ductile fracture. Int J Fract 13(3):267–277. https://doi.org/10.1007/BF00040143
Diehl P, Franzelin F, Pflüger D, Ganzenmüller GC (2016) Bond-based peridynamics: a quantitative study of Mode I crack opening. Int J Fract 201(2):157–170
Diehl P, Prudhomme S, Lévesque M (2019) A review of benchmark experiments for the validation of peridynamics models. J Peridyn Nonlocal Model 1(1):14–35
Dipasquale D, Sarego G, Zaccariotto M, Galvanetto U (2016) Dependence of crack paths on the orientation of regular 2D peridynamic grids. Eng Fract Mech 160:248–263. https://doi.org/10.1016/j.engfracmech.2016.03.022
Du Q, Gunzburger M, Lehoucq R, Zhou K (2012) Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev 54(4):667–696. https://doi.org/10.1137/110833294
Efthymiadis P, Hazra S, Clough A, Lakshmi R, Alamoudi A, Dashwood R, Shollock B (2017) Revealing the mechanical and microstructural performance of multiphase steels during tensile, forming and flanging operations. Mater Sci Eng A 701:174–186. https://doi.org/10.1016/j.msea.2017.06.056
Eriksson K, Stenström C (2020a) Homogenization of the 1D peri-static/dynamic bar with constant micromodulus. J Peridyn Nonlocal Model 2(2):205–228. https://doi.org/10.1007/s42102-019-00028-4
Eriksson K, Stenström C (2020b) Homogenization of the 1D peri-static/dynamic bar with triangular micromodulus. J Peridyn Nonlocal Model
Fallah AS, Giannakeas IN, Mella R, Wenman MR, Safa Y, Bahai H (2020) On the computational derivation of bond-based peridynamic stress tensor. J Peridyn Nonlocal Model 2(4):352–378
Frómeta D, Parareda S, Lara A, Molas S, Casellas D, Jonsén P, Calvo J (2020) Identification of fracture toughness parameters to understand the fracture resistance of advanced high strength sheet steels. Eng Fract Mech 229:1–17
Frómeta D, Cuadrado N, Rehrl J, Suppan C, Dieudonné T, Dietsch P, Calvo J, Casellas D (2021) Microstructural effects on fracture toughness of ultra-high strength dual phase sheet steels. Mater Sci Eng A 802:140631. https://doi.org/10.1016/j.msea.2020.140631
Gerstle WH, Sau N, Silling SA (2005) Peridynamic modeling of plain and reinforced concrete structures. In: 18th International Conference on Structural Mechanics in Reactor Technology, Beijing, China
Golling S, Östlund R, Oldenburg M (2016) A study on homogenization methods for steels with varying content of ferrite, bainite and martensite. J Mater Process Technol 228:88–97
Golling S, Frómeta D, Casellas D, Jonsén P (2019) Influence of microstructure on the fracture toughness of hot stamped boron steel. Mater Sci Eng A 743:529–539
Gu X, Zhang Q, Madenci E, Xia X (2019) Possible causes of numerical oscillations in non-ordinary state-based peridynamics and a bond-associated higher-order stabilized model. Comput Methods Appl Mech Eng 357:112592. https://doi.org/10.1016/j.cma.2019.112592
Ha Y, Bobaru F (2010) Studies of dynamic crack propagation and crack branching with peridynamics. Int J Fract 162(1–2):229–244. https://doi.org/10.1007/s10704-010-9442-4
Ha YD, Bobaru F (2011) Characteristics of dynamic brittle fracture captured with peridynamics. Eng Fract Mech 78(6):1156–1168
Hart DC, Bruck HA (2021) Predicting failure of cracked aluminum plates with one-sided composite patch. To be published
Henke S, Shanbhag S (2014) Mesh sensitivity in peridynamic simulations. Comput Phys Commun 185(1):181–193. https://doi.org/10.1016/j.cpc.2013.09.010
Hu W, Ha YD, Bobaru F, Silling SA (2012) The formulation and computation of the nonlocal J-integral in bond-based peridynamics. Int J Fract 176(2):195–206. https://doi.org/10.1007/s10704-012-9745-8
Imachi M, Tanaka S, Bui TQ (2018) Mixed-mode dynamic stress intensity factors evaluation using ordinary state-based peridynamics. Theoret Appl Fract Mech 93:97–104
Isida M (1971) Effect of width and length on stress intensity factors of internally cracked plates under various boundary conditions. Int J Fract Mech 7(3):301–316
ISO (2019) ISO 6892-1, Metallic materials—tensile testing—Part 1: method of test at room temperature. International Organization for Standardization
Javili A, Morasata R, Oterkus E, Oterkus S (2019) Peridynamics review. Math Mech Solids 24(11):3714–3739. https://doi.org/10.1177/1081286518803411
Jung J, Seok J (2017) Mixed-mode fatigue crack growth analysis using peridynamic approach. Int J Fatigue 103:591–603
Le QV, Bobaru F (2018) Surface corrections for peridynamic models in elasticity and fracture. Comput Mech 61(4):499–518. https://doi.org/10.1007/s00466-017-1469-1
Lee J, Liu W, Hong JW (2016) Impact fracture analysis enhanced by contact of peridynamic and finite element formulations. Int J Impact Eng 87:108–119
Littlewood D (2015a) Peridynamics. In: State-of-the-art report on multi-scale modelling of nuclear fuels, OECD
Littlewood DJ (2015b) Roadmap for peridynamic software implementation. Tech. rep., SAND2015-9013, Sandia National Laboratories, Albuquerque, NM and Livermore, CA
Littlewood D, Foster J, Boyce B (2012) Peridynamic modeling of localization in ductile metals. Rep. no, SAND2012-8102C, presented on IWCMM XXII, Sandia National Laboratories, Albuquerque, NM and Livermore, CA
Macek RW, Silling SA (2007) Peridynamics via finite element analysis. Finite Elem Anal Des 43(15):1169–1178
Madenci E, Oterkus E (2014) Peridynamic theory and its applications. Springer, New York
Marchal Y, Delannay F (1996) Influence of test parameters on the measurement of the essential work of fracture of zinc sheets. Int J Fract 80(4):295–310. https://doi.org/10.1007/BF00018509
Mitchell JA (2011a) A non-local, ordinary-state-based viscoelasticity model for peridynamics. Tech. rep., SAND2011-8064, Sandia National Laboratories, Albuquerque, NM and Livermore, CA
Mitchell JA (2011b) A nonlocal, ordinary, state-based plasticity model for peridynamics. Tech. rep., SAND2011-3166, Sandia National Laboratories, Albuquerque, NM and Livermore, CA
Mitchell J, Silling S, Littlewood D (2015) A position-aware linear solid constitutive model for peridynamics. J Mech Mater Struct 10(5):539–557
Niazi S, Chen Z, Bobaru F (2021) Crack nucleation in brittle and quasi-brittle materials: a peridynamic analysis. Theoret Appl Fract Mech 112:102855. https://doi.org/10.1016/j.tafmec.2020.102855
Panchadhara R, Gordon PA (2016) Application of peridynamic stress intensity factors to dynamic fracture initiation and propagation. Int J Fract 201(1):81–96
Parks ML, Plimpton SJ, Lehoucq RB, Silling SA (2010) Peridynamics with LAMMPS: a user guide. Tech. rep., 2010-5549, Sandia National Laboratories, Albuquerque, NM and Livermore, CA
Rice JR (1968) A path independent integral and the approximate analysis of strain concentration by notches and cracks. J Appl Mech 35(2):379–386. https://doi.org/10.1115/1.3601206
Rink M, Andena L, Marano C (2014) The essential work of fracture in relation to \(J\)-integral. Eng Fract Mech 127:46–55
Sandin O, Jonsén P, Frómeta D, Casellas D (2021) Stating failure modelling limitations of high strength sheets: implications to sheet metal forming. Materials 14(24):7821. https://doi.org/10.3390/ma14247821
Sarego G, Le QV, Bobaru F, Zaccariotto M, Galvanetto U (2016) Linearized state-based peridynamics for 2-D problems. Int J Numer Methods Eng 108(10):1174–1197
Seleson P (2014) Improved one-point quadrature algorithms for two-dimensional peridynamic models based on analytical calculations. Comput Methods Appl Mech Eng 282:184–217
Seleson P, Littlewood DJ (2018) Numerical tools for improved convergence of meshfree peridynamic discretizations. In: Voyiadjis GZ (ed) Handbook of nonlocal continuum mechanics for materials and structures. Springer, New York, pp 1–27
Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209. https://doi.org/10.1016/S0022-5096(99)00029-0
Silling SA (2016) Introduction to peridynamics. In: Bobaru F, Foster JT, Geubelle PH, Silling SA (eds) Handbook of peridynamic modeling. CRC Press, Boca Raton, pp 25–60
Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17–18):1526–1535. https://doi.org/10.1016/j.compstruc.2004.11.026
Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics, Adv. Appl. Mech., vol 44. Elsevier, Amsterdam, pp 73–168. https://doi.org/10.1016/S0065-2156(10)44002-8
Silling SA, Epton M, Weckner O, Xu J, Askari E (2007) Peridynamic states and constitutive modeling. J Elast 88(2):151–184. https://doi.org/10.1007/s10659-007-9125-1
Silling SA, Weckner O, Askari E, Bobaru F (2010) Crack nucleation in a peridynamic solid. Int J Fract 162(1–2):219–227
Stenström C, Eriksson K (2019) The \(J\)-contour integral in peridynamics via displacements. Int J Fract 216:173–183
Stenström C, Eriksson K (2021) The J-area integral applied in peridynamics. Int J Fract
Unger DJ, Gerberich WW, Aifantis EC (1983) Further remarks on an exact solution for crack problems. Eng Fract Mech 18(3):735–742. https://doi.org/10.1016/0013-7944(83)90065-6
Vendra SL, Goel S, Kumar N, Jayaganthan R (2017) A study on fracture toughness and strain rate sensitivity of severely deformed al 6063 alloys processed by multiaxial forging and rolling at cryogenic temperature. Mater Sci Eng A 686(Supplement C):82–92. https://doi.org/10.1016/j.msea.2017.01.035
Wu XR, Carlsson J (1991) Weight functions and stress intensity factor solutions. Pergamon, Oxford
Xu Z, Zhang G, Chen Z, Bobaru F (2018) Elastic vortices and thermally-driven cracks in brittle materials with peridynamics. Int J Fract 209(1):203–222
Yang D, Dong W, Liu X, Yi S, He X (2018) Investigation on mode-i crack propagation in concrete using bond-based peridynamics with a new damage model. Eng Fract Mech 199:567–581
Yolum U, Taştan A, Güler MA (2016) A peridynamic model for ductile fracture of moderately thick plates. Procedia Struct Integrity 2:3713–3720
Zaccariotto M, Luongo F, Galvanetto U et al (2015) Examples of applications of the peridynamic theory to the solution of static equilibrium problems. Aeronaut J 119(1216):677–700
Acknowledgements
We would like to thank Dr. Lars-Olof Nordin, LKAB, for contributing with insights into microstructural properties and fracture toughness testing, and Dr. Daniel Casellas, Eurecat/LTU, for contributing with insights into the EWF method. The work of Florin Bobaru was supported, in part, by the NSF (USA) Award # 1953346.
Funding
Open access funding provided by Luleå University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
1.1 Approximation of c ( m )
For a finite number of family members (\(N_h\)) within the horizon region, Eq. (6) for a 2D body becomes:
where \(v_i\) is a volume correction factor. \(m=3\) gives \(N_h=28\) family members (see Fig. 20), thus
By using the volume correction method by Parks et al. (2010), i.e. Eq. (8), the volume correction factor of Eq. (22) yields
Setting \(W_3 = W_0 = E\epsilon ^2/(1-\nu )\) yields the corresponding micromodulus:

The ratio
follows from Eq. (7) with \(\nu =1/3\). Therefore, \(c_3 \approx 1.1507c_{\infty }\)
Following the same procedure for \(m=5\) and counting the weight of elements intersected by the horizon as half,
and thus, \(c_5 \approx 1.0697c_{\infty }\).
1.2 Identity \(\mathbf{f'} = - \textbf{f}\)
By switching variables \({\textbf{x}}\rightarrow {\textbf{x}}^\prime \),
From the identity \({\textbf{f}}^\prime =-{\textbf{f}}\),
and since \(\int _{\varOmega } {\textbf{f}} \cdot \frac{\partial {\textbf{u}}}{\partial x_1} \, \textrm{d} V_{{\textbf{x}}} = 0\), and \(\varOmega = {\mathcal {R}} + \varOmega {\setminus }{\mathcal {R}}\),
Thus
The classical J-integral as a function of displacement derivatives
For a rectangular integration path, Rice’s J-contour integral on strain components formulation can be written as (Stenström and Eriksson 2019):
On the left side is the general path independent formulation, where W for a linear elastic material is \(\frac{1}{2}\, \sigma _{ij} \epsilon _{ij}\), and \(\sigma _{ij}n_j\) is (the components of) the traction vector. On the right side, the factor 2 accounts for the rectangular contour to be symmetric across the straight crack. \(\textrm{I}\), \(\textrm{II}\) and \(\textrm{III}\) are the right, top and left sides, respectively, of the contour above the symmetry line (Fig. 2). By substitution of stress–displacements derivatives relationships of W for a linear elastic material, we obtain:
\(w_i\) corresponds to the second term of the general J expression. With similar substitution of stress-displacements derivatives, and by taking the contour as a rectangle around the crack tip, the second term of the general J expression develops into three parts; right, top and left hand side contours:
Thus, \(w_\textrm{I}\), \(w_\textrm{II}\) and \(w_\textrm{III}\) are calculated on the right, top and left sides of the contour, respectively.
Discretization of the J-integral expressions
The material domain is discretized uniformly to allow for a mid-point integration scheme (one-point Gaussian quadrature) (Silling and Askari 2005).
The strain components of W Eqs. (10) and (32) can be approximated by applying the central difference scheme on the displacement field. For a material point i, the strains are given as follows (Hu et al. 2012):
The J-integrals are approximated by using the trapezoidal rule. The \(J_\mathrm {{\scriptscriptstyle PD}}\) of Eq. (10) is then discretized as follows:
\(n_{\partial {\mathcal {R}}}\), \(n_{{\mathcal {R}}1}\) and \(n_{{\mathcal {R}}2}\) are the number of material points within the contour path, inner region and outer region, respectively. The subscripts 1 and 2 refer to the x- and y-components, t is the material thickness and \(A_{j/i}\) refers to the area.
The classical J of Eq. (32) is discretized as:
where \(n_i\) is the number of material points along the three regions \(\textrm{I}\)–\(\textrm{III}\).
Exact analytical solution of the CCT specimen
Classical exact analytical solutions of stresses and displacements for the infinite center cracked tension (CCT) specimen have been derived by Unger et al. (1983) under plane strain conditions. We have in an analogue manner derived the stresses and displacements under plane stress conditions (Stenström and Eriksson 2019):
where X, Y and A–C are dimensionless variables, \(\alpha \) and \(\beta \) are constants for plane stress and plane strain, respectively. The dimensionless variables are given as
\(\alpha \) and \(\beta \) are given by:
x and y in Eqs. (39a) and (39b) are the spatial coordinates. With Eq. (38) the stresses and displacements can be calculated at any point of the infinite plate.
The benefit of this exact solution is that the stresses or displacements can be used as input to peridynamic modeling, or more precisely, as boundary conditions for finite models of the infinite geometry problem.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stenström, C., Eriksson, K., Bobaru, F. et al. The essential work of fracture in peridynamics. Int J Fract 242, 129–152 (2023). https://doi.org/10.1007/s10704-023-00705-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-023-00705-y




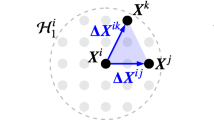






 ,
, 



 with varying number of material points and grid density m
with varying number of material points and grid density m








