1 Introduction

Modeling brittle fracture in an FE framework has proven to be a challenging task. In particular, the problem of how to represent the sharp crack discontinuity in an FE continuum has caught the attention of many researchers. Techniques such as element erosion and node-splitting to drive cracking based on a local criterion are commonly used. These techniques are typically prone to pathological mesh dependence, as the FE discretization determines the crack path resulting in the minimum potential energy. To mitigate the pathological mesh dependence, several non-local fracture formulations such as eigenfracture and fracture phase-field have been suggested.

Eigenfracture was proposed by Schmidt et al. (2009) and is based on the concept of eigendeformation. In mechanics, eigendeformations are typically used to describe deformation modes of zero local energy cost. The eigenfracture formulation depends on two fields, a displacement field and an eigendeformation field. Combined, the two fields describe the fractures that occur in a body. The method has been the subject of multiple studies (Pandolfi and Ortiz 2012; Pandolfi et al. 2021; Stochino et al. 2017; Qinami et al. 2019). Qinami et al. (2019) discussed how the FE discretization, including the number of elements and element orientation, affected the admissible fracture geometry and fracture patterns using eigenfracture, and proposed remedies using r- and h-adaptivity schemes.

The phase-field approach to fracture stems from the variational formulation of brittle fracture by Francfort and Marigo (1998). Their variational formulation relates the quasi-static process of crack initiation, propagation and branching to the minimization of the energy functional

$$\begin{aligned} E \left( {\textbf{u}}, \Gamma \right) = \int _{\Omega } \psi _{e} \left( \varvec{\varepsilon } \left( {\textbf{u}}\right) \right) \textrm{d}\varvec{x} + G_{c} \int _{\Gamma } \textrm{d}\Gamma \end{aligned}$$
(1)

where \(\psi _{e}\) is the elastic energy density function, \({\textbf{u}}\) is the displacement field, \(\varvec{\varepsilon }\) is the strain field, \(G_{c}\) is the critical energy release rate, \(\Omega \) is the domain representing the elastic body and \(\Gamma \) is the crack set. Bourdin et al. (2000) regularized the formulation of the crack set \(\Gamma \) to enable numerical treatment with the energy functional

$$\begin{aligned} E_{l} \left( {\textbf{u}}, \phi \right)= & {} \int _{\Omega } \left( {\left( 1 - \phi \right) }^{2} + k\right) \psi _{e} \left( \varvec{\varepsilon } \left( {\textbf{u}}\right) \right) \textrm{d}\varvec{x} \nonumber \\{} & {} + G_{c} \int _{\Omega } \left( \frac{1}{4l} \phi ^{2} + l {|\nabla \phi |}^{2} \right) \textrm{d}\varvec{x} \end{aligned}$$
(2)

where \(\phi \) is the phase-field variable indicating fracture, \(l>0\) is the length scale controlling the width of the fracture phase-field and k is a small dimensionless parameter modeling an artificial residual stiffness when the material is completely fractured to prevent numerical difficulties.

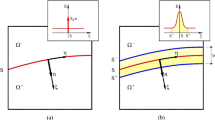
Figure 1 illustrates the introduction of the diffuse fracture phase-field to represent the sharp crack topology, \(\Gamma \). The value of \(\phi \) varies smoothly from 0 (undamaged material) to 1 (completely fractured) and degrades the elastic strain energy. The resulting phase-field differential equation is Miehe et al. (2010a)

$$\begin{aligned} \frac{G_{c}}{l} \left[ \phi - l^{2} \Delta \phi \right] = 2 \left( 1-\phi \right) \psi _{e} \end{aligned}$$
(3)

with the Neumann-type boundary conditions given by

$$\begin{aligned} \nabla \phi \cdot {\textbf{n}} = 0. \end{aligned}$$
(4)

Here, \(\nabla \phi \) is the spatial gradient of the phase-field and \({\textbf{n}}\) is the outward normal on \(\partial \Omega \).

Fig. 1
figure 1

Representation of the phase-field approach to fracture. The displacement field \({\textbf{u}}\) and the fracture phase-field \(\phi \) are both defined on the body \(\Omega \), where \(\phi \) is the regularized version of the sharp crack topology \(\Gamma \) with half-width controlled by the length scale l. The displacement field is constrained by the Dirichlet-type and Neumann-type boundary conditions \({\textbf{u}} = \bar{{\textbf{u}}}\) on \(\partial \Omega _{{\textbf{u}}}\) and \(\varvec{\sigma } \cdot {\textbf{n}} = \bar{{\textbf{t}}}\) on \(\partial \Omega _{{\textbf{t}}}\) with \( \partial \Omega = \partial \Omega _{{\textbf{u}}} \cup \partial \Omega _{{\textbf{t}}} \). The fracture phase-field is constrained by the Neumann-type condition \(\nabla \phi \cdot {\textbf{n}} = 0\) on the full surface \(\partial \Omega \)

Full size image

The phase-field approach introduces an extra degree of freedom, \(\phi \), to the system of equations. There are two common solution methods for the coupled phase-field problem, referred to as monolithic and staggered. In the monolithic solution approach, the entire system of equations is solved directly, resulting in a complete coupling. However, the monolithic approach is computationally expensive and prone to convergence issues (Miehe et al. 2010b). For this reason, the staggered solution approach where the displacement field and phase-field are solved separately is often preferred. The staggered approach has proven to be robust and increase computational efficiency (Miehe et al. 2010a), and will therefore be used in this work.

Crack propagation is typically dependent on the dynamic nature of the loading (Kalthoff and Winkler 1988; Kalthoff 2000). Crack paths display an increasing tendency to branch with increasingly dynamic loading. Early studies (Bourdin et al. 2008; Kuhn and Müller 2010, 2008; Amor et al. 2009) on the phase-field approach investigated static fracture, while some more recent studies (Borden et al. 2012; Hofacker and Miehe 2012, 2013; Bourdin et al. 2011; Ren et al. 2019) consider dynamic fracture. Dynamic crack propagation is more violent than the static case, which may lead to numerical instabilities. Miehe et al. (2010a) introduced a viscous regularization through a viscous extended dissipation functional to stabilize the numerical phase-field solution. The viscous regularization extends the phase-field evolution equation to

$$\begin{aligned} \frac{G_{c}}{l} \left[ \phi - l^{2} \Delta \phi \right] + \eta {\dot{\phi }} = 2 \left( 1-\phi \right) \psi _{e} \end{aligned}$$
(5)

where \(\eta \) is the viscosity parameter.

With focus on brittle cracking, we assume small deformations where \(\Vert \nabla {\textbf{u}} \Vert \) is small, resulting in the linearized strain tensor

$$\begin{aligned} \varvec{\varepsilon } = \frac{1}{2} \left[ \nabla {\textbf{u}} + \nabla ^{T} {\textbf{u}} \right] . \end{aligned}$$
(6)

A physically meaningful fracture model should distinguish between tension and compression loads in such a way that cracking only arises from tension load states. Basic formulations (Bourdin et al. 2000, 2008; Kuhn and Müller 2010, 2008) without this type of tension-compression split, often referred to as isotropic models, are only valid in a limited number of load cases. Amor et al. (2009) proposed a split based on separation of the strain tensor into a volumetric and deviatoric part, where the volumetric part of the strain tensor only contributes to damage evolution if it is positive and the deviatoric part always contributes. The split will later be referred to as the Amor split, and is defined as

$$\begin{aligned} \psi _{e}= & {} \psi _{e}^{+} + \psi _{e}^{-}, \nonumber \\ \psi _{e}^{+}= & {} K \frac{ {\langle \textrm{tr}\left( \varvec{\varepsilon }\right) \rangle }_{+}^{2} }{2} + G \varvec{\varepsilon }^{dev}: \varvec{\varepsilon }^{dev}, \nonumber \\ \psi _{e}^{-}= & {} K \frac{ {\langle \textrm{tr}\left( \varvec{\varepsilon }\right) \rangle }_{-}^{2} }{2} \end{aligned}$$
(7)

where \(K > 0\) is the bulk modulus, \(G > 0\) is the shear modulus, \( \varvec{\varepsilon }^{dev} = \varvec{\varepsilon } - \frac{1}{3} \textrm{tr}\left( \varvec{\varepsilon }\right) {\textbf{I}} \) is the deviatoric strain tensor, \(\textrm{tr} \left( \varvec{\cdot } \right) \) is the trace of a tensor, the Macaulay brackets \({\langle \varvec{\cdot } \rangle }_{\pm }\) represent the ramp function \({\langle x \rangle }_{\pm } = \left( x \pm |x |\right) /2\). Miehe et al. (2010a, 2010b) proposed an anisotropic formulation using the spectral decomposition of the strain tensor to separate the positive and negative components, given by

$$\begin{aligned} \varvec{\varepsilon }= & {} \varvec{\varepsilon }_{+} + \varvec{\varepsilon }_{-}, \quad \varvec{\varepsilon }_{+} = \sum _{i=1}^{3} {\langle \varepsilon _{i} \rangle }_{+} {\textbf{n}}_{i} \otimes {\textbf{n}}_{i}, \nonumber \\ \varvec{\varepsilon }_{-}= & {} \sum _{i=1}^{3} {\langle \varepsilon _{i} \rangle }_{-} {\textbf{n}}_{i} \otimes {\textbf{n}}_{i}, \end{aligned}$$
(8)

where \(\varepsilon _{i}\) is the ith eigenvalue, and \({\textbf{n}}_{i}\) is the corresponding unit eigenvector of the strain tensor. The positive and negative strain tensors are used to construct the two parts of the elastic strain energies

$$\begin{aligned} \psi _{e}= & {} \psi _{e}^{+} + \psi _{e}^{-}, \quad \psi _{e}^{+} = \lambda \frac{ {\langle \textrm{tr}\left( \varvec{\varepsilon }\right) \rangle }_{+}^{2} }{2} + \mu \textrm{tr}\left[ \varvec{\varepsilon }_{+}^{2}\right] , \nonumber \\ \psi _{e}^{-}= & {} \lambda \frac{ {\langle \textrm{tr}\left( \varvec{\varepsilon }\right) \rangle }_{-}^{2} }{2} + \mu \textrm{tr}\left[ \varvec{\varepsilon }_{-}^{2}\right] \end{aligned}$$
(9)

where \(\lambda > 0\) and \(\mu > 0\) are Lamè constants. The split will later be referred to as the Miehe split. For both the Amor and Miehe split, the stress tensor is defined by

$$\begin{aligned} \varvec{\sigma } \left( \varvec{\varepsilon }, \phi \right) = \left[ {\left( 1-\phi \right) }^{2} + k\right] \varvec{\sigma }^{+} \left( \varvec{\varepsilon } \right) + \varvec{\sigma }^{-} \left( \varvec{\varepsilon } \right) \end{aligned}$$
(10)

where \(\varvec{\sigma }^{+} = \frac{\partial \psi _{e}^{+} \left( \varvec{\varepsilon } \right) }{\partial \varvec{\varepsilon }} \) and \( \varvec{\sigma }^{-} = \frac{\partial \psi _{e}^{-} \left( \varvec{\varepsilon } \right) }{\partial \varvec{\varepsilon }} \) are the positive and negative parts of the stress tensor. Ambati et al. (2014) proposed a hybrid formulation containing features from both isotropic and anisotropic models where the elastic strain energy is split similarly to the splits presented above, but the stress tensor is kept isotropic to increase the computational efficiency. The split will later be referred to as the hybrid split. In this work, the elastic strain energy of the hybrid split follows Eq. (9). For the hybrid split, the stress tensor is defined by

$$\begin{aligned} \varvec{\sigma } \left( \varvec{\varepsilon }, \phi \right) = \left[ {\left( 1-\phi \right) }^{2} + k\right] \frac{\partial \psi _{e} \left( \varvec{\varepsilon } \right) }{\partial \varvec{\varepsilon }}. \end{aligned}$$
(11)

Cracking is considered to be a fully dissipative process, meaning that the crack surface, \(\Gamma \), must either stay constant or increase with time to be thermodynamically consistent. To ensure this consistency, Miehe et al. (2010b) proposed the following constraints on the fracture phase-field

$$\begin{aligned} \frac{1}{l} \left[ \phi - l^{2}\Delta \phi \right] \ge 0 \quad \textrm{and} \quad {\dot{\phi }} \ge 0, \end{aligned}$$
(12)

where the first constraint relates the functional derivative to a positive field driving force, while the latter ensures irreversible crack evolution. By introducing a history variable for the field driving force, \(\mathcal {H}\), referred to as the maximum positive reference energy, given by

$$\begin{aligned} \mathcal {H}\left( {\textbf{x}}, t\right) := \underset{\tau \in \left[ 0,t\right] }{\max }\ \,\, \psi ^{+}_{e} \left( \varvec{\varepsilon } \left( {\textbf{x}}, \tau \right) \right) , \end{aligned}$$
(13)

Miehe et al. (2010a) presented an elegant way of incorporating the irreversibility of the crack evolution numerically, with the evolution equation

$$\begin{aligned} \frac{G_{c}}{l} \left[ \phi - l^{2} \Delta \phi \right] + \eta {\dot{\phi }} = 2 \left( 1-\phi \right) \mathcal {H}. \end{aligned}$$
(14)

In the current formulation, the fracture phase-field evolution is based on an energy dependent crack driving force. With this type of crack driving force, it is difficult to control crack initiation. Miehe et al. (2015) proposed a purely stress-based crack driving force for the fracture phase-field evolution, given by

$$\begin{aligned} \mathcal {H} \left( {\textbf{x}}, t\right) := \underset{\tau \in \left[ 0, t\right] }{\max }\ \,\, \zeta {\Bigg \langle \sum _{a=1}^{3} {\left( \frac{\langle {\tilde{\sigma }}_{i} \left( {\textbf{x}}, \tau \right) \rangle }{\sigma _{c}} \right) }^{2} - 1 \Bigg \rangle }_{+} \end{aligned}$$
(15)

where \({\tilde{\sigma }}_{i} = \sigma _{i} / {\left( 1-\phi \right) }^{2}\) is the effective principal stress i, \(\sigma _{c}\) is a critical stress and the dimensionless parameter \(\zeta >0\) controls the slope of the failure surface in stress space. Bilgen and Weinberg (2019) compared multiple crack driving forces and demonstrated that the choice of crack driving force has a strong influence on the predicted crack path. Further, we introduce a conditional energy-based crack driving force, given by

$$\begin{aligned} \mathcal {H} \left( {\textbf{x}}, t\right) := \underset{\tau \in \left[ 0, t\right] }{\max }\ \,\, H \left( \sigma _{\mathcal {B}} - \sigma _{c} \right) \psi ^{+}_{e} \end{aligned}$$
(16)

where \(\sigma _{\mathcal {B}} = \max \{ \sigma _{1}: \, {\textbf{x}} \in \Omega , \, \tau \in \left[ 0, t\right] \} \) is the maximum major principal stress (\(\sigma _{1}\ge \sigma _{2}\ge \sigma _{3}\)) experienced in the body during the loading history and \(H\left( x\right) \) is the Heaviside step function taking the value 1 if \(x>0\) and 0 otherwise. This formulation of the crack driving force allows for a surplus of elastic strain energy at fracture initiation.

Using the proposed crack driving force in Eq. (16), we aim to investigate the prediction capabilities of a dynamic fracture phase-field formulation implemented in the commercial FE solver LS-DYNA [24] on quasi-statically loaded L-shaped soda-lime glass specimens (Rudshaug et al. 2023) with varying critical load levels using the three implemented tension-compression splits. In particular, we focus on the crack propagation path and speed for the lowest and highest critical load levels using the new crack driving force. First, we present the implementation details and perform validation studies of the fracture formulation using standard numerical examples. Then, we perform numerical simulations on the quasi-statically loaded L-shaped soda-lime glass specimens. The three tension-compression splits, namely the Amor, Miehe and hybrid splits, are used and compared for the numerical simulations. To evaluate the numerical predictions in relation to the experiments, we compare the crack propagation path and speed for two specimen strengths.

2 Implementation

The dynamic fracture phase-field model is implemented in the user interface of version R12 of the general-purpose FE solver LS-DYNA. To enable scalability and reduce computational time, we parallelized the implementation using MPI. The implementation includes the Amor et al. (2009), Miehe et al. (2010a, 2010b) and hybrid (Ambati et al. 2014) tension-compression splits. To ensure control over the fracture initiation, we implemented the proposed crack driving force in Eq. (16) that allows the user to initiate the phase-field solver based on a critical major principal stress.

To model the dynamic fracture phase-field we follow the dynamic formulation and robust staggered solution scheme proposed by Hofacker and Miehe (2013). The additional degree of freedom obtained by introducing the fracture phase-field is included in a modular fashion in the user element framework of LS-DYNA for both shells (usrshl) and solids (usrsld). The shell user element is based on the Belytschko-Tsay shell element (Belytschko and Tsay 1983; Belytschko et al. 1984), while the solid element is fully integrated and employs the B-bar method to prevent locking (Simo and Hughes 1986). We solve the displacement field and phase-field separately in a staggered fashion, where the system of equations related to the displacement field is assembled and solved internally in LS-DYNA in an explicit fashion. The phase-field system of equations is assembled and solved implicitly using the external Portable, Extensible Toolkit for Scientific Computation (PETSc) (Balay et al. 2023).

To implement the phase-field evolution in Eq. (14) into an FE framework, we use the weak form given by

$$\begin{aligned}{} & {} \int _{\Omega } \left[ -2\left( 1-\phi \right) \mathcal {H} \cdot \delta \phi + \frac{G_{c}}{l} \phi \cdot \delta \phi \right. \nonumber \\{} & {} \quad \left. + G_{c} l \nabla \phi \cdot \nabla \delta \phi + \eta {\dot{\phi }} \cdot \delta \phi \right] \textrm{d}\varvec{x} = 0 \end{aligned}$$
(17)

where \(\delta \phi \) is the virtual infinitesimal variation of the fracture phase-field. The displacement field and fracture phase-field, along with their respective differential quantities, are discretized as

$$\begin{aligned} {\textbf{u}}&= \sum _{i=1}^{m} {\textbf{N}}_{i}^{{\textbf{u}}} {\textbf{u}}_{i} = {\textbf{N}}^{{\textbf{u}}} {\textbf{r}}^{{\textbf{u}}} \quad \textrm{and} \quad \phi = \sum _{i=1}^{m} N_{i}^{\phi } \phi _{i} = {\textbf{N}}^{\phi } {\textbf{r}}^{\phi } \end{aligned}$$
(18)
$$\begin{aligned} \varvec{\varepsilon }&= \sum _{i=1}^{m} {\textbf{B}}_{i}^{{\textbf{u}}} {\textbf{u}}_{i} = {\textbf{B}}^{{\textbf{u}}} {\textbf{r}}^{{\textbf{u}}} \quad \textrm{and} \quad \nabla \phi = \sum _{i=1}^{m} {\textbf{B}}_{i}^{\phi } \phi _{i} = {\textbf{B}}^{\phi } {\textbf{r}}^{\phi } \end{aligned}$$
(19)

where m is the number of nodes per element, \({\textbf{u}}_{i}\) and \(\mathbf {\phi }_{i}\) are the displacement and phase-field values at node i, \({\textbf{N}}_{i}^{{\textbf{u}}}\) and \(N_{i}^{\phi }\) are the shape function matrix and shape function associated with node i for the displacements and phase-field, respectively, and \({\textbf{B}}_{i}^{{\textbf{u}}}\) and \({\textbf{B}}_{i}^{\phi }\) are the matrices of their respective spatial derivatives. \({\textbf{N}}^{{\textbf{u}}}\), \({\textbf{N}}^{\phi }\), \({\textbf{B}}^{{\textbf{u}}}\) and \({\textbf{B}}^{\phi }\) are the corresponding matrices for all the nodes, and \({\textbf{r}}^{{\textbf{u}}}\) and \({\textbf{r}}^{\phi }\) are the vectors containing the displacement and phase-field degrees of freedom. The virtual quantities (\(\delta {\textbf{u}}\), \(\delta \phi \), \(\delta \varvec{\varepsilon }\) and \(\delta \nabla \phi \)) are discretized in the same fashion. We define the rate of the fracture phase-field \({\dot{\phi }} = \left( \phi _{n+1}-\phi _{n} \right) / \Delta t\) where \(\Delta t = t_{n+1} - t_{n}\) is the time increment. Inserting the interpolations into Eq. (17) and eliminating the arbitrary virtual quantities yields the nonlinear fracture phase-field system of equations

$$\begin{aligned} {\textbf{R}}^{\phi } \left( {\textbf{r}}^{\phi }\right)&= \int _{\Omega } \left( -2\left( 1 - {\textbf{N}}^{\phi } {\textbf{r}}^{\phi } \right) \mathcal {H} {\left( {\textbf{N}}^{\phi }\right) }^{T} \right. \nonumber \\&\quad + \frac{G_{c}}{l} {\left( {\textbf{N}}^{\phi }\right) }^{T} {\textbf{N}}^{\phi } {\textbf{r}}^{\phi } \nonumber \\&\quad \left. + \frac{\eta }{\Delta t} {\left( {\textbf{N}}^{\phi }\right) }^{T} {\textbf{N}}^{\phi } \Delta {\textbf{r}}^{\phi } + G_{c} l {\left( {\textbf{B}}^{\phi }\right) }^{T} {\textbf{B}}^{\phi } {\textbf{r}}^{\phi } \right) \,\nonumber \\&\quad \textrm{d}\varvec{x} = {\textbf{0}} \end{aligned}$$
(20)

where \({\textbf{R}}^{\phi }\left( {\textbf{r}}^{\phi } \right) \) is the global fracture phase-field residual vector and \(\Delta {\textbf{r}}^{\phi } = {\textbf{r}}^{\phi }_{n+1}-{\textbf{r}}^{\phi }_{n}\) is the increment of the phase-field degrees of freedom at time \(t_{n+1}\). By linearizing the nonlinear system of equations through a first order Taylor expansion, we find a linear system of equations for the fracture phase-field increment

$$\begin{aligned} {\textbf{R}}^{\phi } \left( {\textbf{r}}^{\phi } \right)&= {\textbf{R}}^{\phi } \left( {\textbf{r}}^{\phi }_{n}\right) + \frac{\partial {\textbf{R}}^{\phi }}{\partial {\textbf{r}}^{\phi }} \left( {\textbf{r}}^{\phi }_{n}\right) \Delta {\textbf{r}}^{\phi } + H.O.T. \nonumber \\&= {\textbf{R}}^{\phi } \left( {\textbf{r}}^{\phi }_{n}\right) + {\textbf{K}}^{\phi } \left( {\textbf{r}}^{\phi }_{n}\right) \Delta {\textbf{r}}^{\phi } + H.O.T. \nonumber \\&\approx {\textbf{R}}^{\phi } \left( {\textbf{r}}^{\phi }_{n}\right) + {\textbf{K}}^{\phi } \left( {\textbf{r}}^{\phi }_{n}\right) \Delta {\textbf{r}}^{\phi } = {\textbf{0}} \end{aligned}$$
(21)

where \({\textbf{K}}^{\phi }\left( {\textbf{r}}^{\phi }_{n}\right) \) is the phase-field stiffness at time \(t_{n}\) given by

$$\begin{aligned} {\textbf{K}}^{\phi }\left( {\textbf{r}}^{\phi }_{n}\right)&= \frac{\partial {\textbf{R}}^{\phi }}{\partial {\textbf{r}}^{\phi }}\left( {\textbf{r}}^{\phi }_{n}\right) \nonumber \\&= \int _{\Omega } \left( \left[ 2 \mathcal {H} + \frac{G_{c}}{l} + \frac{\eta }{\Delta t} \right] {\left( {\textbf{N}}^{\phi }\right) }^{T} {\textbf{N}}^{\phi } \right. \nonumber \\&\quad \left. + G_{c} l {\left( {\textbf{B}}^{\phi }\right) }^{T} {\textbf{B}}^{\phi } \right) \, \textrm{d}\varvec{x}. \end{aligned}$$
(22)

Box 1 presents the applied staggered scheme for solving the fracture phase-field evolution, which differs slightly from the scheme presented by Hofacker and Miehe (2013). In our implementation, we solve the displacement field explicitly and use the fracture phase-field from the previous increment, \(\phi _{n}\), to degrade the stress used to construct the stress divergence vector, \({\textbf{F}}_{n}\left( \phi _{n}\right) \). The choice of degrading the stress using the fracture phase-field from the previous increment is mainly due to the user interface of LS-DYNA, where the phase-field for the new increment is solved for in a user control routine (uctrl) which is called after the calls to the element and material routines.

The scheme is as follows. For every increment, we know the displacement and crack driving force field from the previous time step and fracture phase-field from the previous two time steps. In addition, the velocity field at time \(t_{n-1/2}\) is known. To drive the solution forward, we first use the known quantities to compute the stress field, \(\varvec{\sigma } \left( \varvec{\varepsilon }, \phi _{n} \right) \) at the integration points. For the Amor and Miehe tension-compression splits, the stress field is first split into a positive and negative part, and then the positive part is degraded using the fracture phase-field at the integration point from the previous increment. The stress field is not split for the hybrid split. Next, we compute the integration point crack driving force obtained in the solution history, \(\mathcal {H}\), from the expression in Eq. (16). Together with the global fracture phase-field degrees of freedom from the two previous time step, \({\textbf{r}}^{\phi }_{n}\) and \({\textbf{r}}^{\phi }_{n-1}\), the crack driving force is used to solve the linear incremental system of equations for the fracture phase-field in Eq. (21)

$$\begin{aligned} \Delta {\textbf{r}}^{\phi } = - {\left( {\textbf{K}}^{\phi }\left( {\textbf{r}}^{\phi }_{n}\right) \right) }^{-1} \cdot {\textbf{R}}^{\phi }\left( {\textbf{r}}^{\phi }_{n}\right) \end{aligned}$$
(23)

Next, the displacement field of the new increment, represented by its degrees of freedom, is computed based on the current body force and external loads, \({\textbf{P}}_{n}\), hourglass resistance, \({\textbf{H}}_{n}\), and stress divergence vector, \({\textbf{F}}_{n}\left( \phi _{n}\right) \). The stress divergence vector is integrated based on the stresses degraded by the fracture phase-field from the previous increment. Finally, the history fields are stored for the new increment.

figure a

3 Validation

We adopted two of the representative numerical examples used by Miehe et al. (2010a), namely the single edge notch tension (SENT) test and the single edge notch shear (SENS) test, to validate the behavior of the fracture phase-field models for quasi-static mode I and mixed mode loading using the Amor, Miehe and hybrid splits. For validation of the performance in the case of dynamic fracture we model the experiments performed by Kalthoff and Winkler (1988) and Kalthoff (2000) in 2D and in a 3D extension case using the Miehe split. In this section the critical principal stress \(\sigma _{c}\) in Eq. (16) is equal to 0 in order to compare the implementation to previous work.

3.1 Single edge notch tests

The single edge notch tests consist of a square plate with a horizontal notch at mid-height spanning from the left edge to the center point of the specimen. The geometry and boundary conditions are presented in Fig. 2. The specimen is loaded either vertically or horizontally for tension or shear loading, respectively. The model parameters are: Lamé’s first parameter \(\lambda = {121.15}\,\hbox {GPa}\), shear modulus \(\mu = {80.77}\,\hbox {GPa}\), critical energy release rate \(G_{c} = {2.7\times 10^{-3}}\,\hbox {J}/{\textrm{m}}^{2}\), length scale \(l = {7.5\times 10^{-3}}\,{\textrm{mm}}\), artificial residual stiffness \(k=0\), phase-field viscosity \(\eta = {10^{-9}} \hbox { N}\,{\textrm{s}}/{\textrm{mm}}^{2}\), and we assume plane strain conditions. An element size of \({2.5\times 10^{-3}}\,{\textrm{mm}}\) is used in both load cases with the proposed model, resulting in 160 000 elements.

Figure 3 presents the resulting crack patterns for the two load cases using the three splits. We see no notable difference in the predicted crack patterns from the SENT tests, which are straight for all three tension-compression splits. When comparing the crack path predictions from the SENS tests, we note slight differences between the respective tension-compression splits. However, they all resemble the crack patterns predicted by Miehe et al. (2010a) and Ambati et al. (2014).

Fig. 2
figure 2

The single edge notch specimen with dimensions and boundary conditions for tension (SENT) and shear (SENS) loading

Full size image
Fig. 3
figure 3

Crack patterns from numerical simulations of the SENT (a–c) and SENS (d–f) tests using the Amor (a, d), Miehe (b, e) and hybrid (c, f) splits

Full size image

3.2 Kalthoff–Winkler test

Kalthoff and Winkler (1988) performed impact tests on a double pre-notched steel plate at different velocities, documenting the resulting crack path. Similar to Hofacker and Miehe (2013), we will use the experimental results as a reference to verify the performance of our phase-field implementation with the Miehe split. The specimen geometry and boundary conditions are presented in Fig. 4a. We use constant loading velocities, \(v_{0}\), of \({5}\,\hbox {m}/\hbox {s}\), \({16.5}\,\hbox {m}/\hbox {s}\) and \({50}\,\hbox {m}/\hbox {s}\). To avoid numerical instabilities, we ramp up the velocity from 0 to \(v_{0}\) for a duration \(t_{0} = {0.5}\,{\upmu {\textrm{s}}}\). The velocity profile is presented in Fig. 4b. The model parameters are: density \(\rho = {8000}\,\hbox {kg}/{\textrm{m}}^{3}\), Young’s modulus \(E = {190}\,\hbox {GPa}\), Poisson ratio \(\nu =0.3\), critical energy release rate \(G_{c} = {2.213\times 10^{4}}\,\hbox {J}/{\textrm{m}}^{2}\), length scale \(l = {0.3}\,{\hbox {mm}}\), artificial residual stiffness \(k = {0}\), phase-field viscosity \(\eta = {10^{-9}}\hbox { N}\,{\textrm{s}}/{\textrm{mm}}^{2}\), and we approximate the experimental setup by assuming plane strain conditions. The plate is discretized into \({\sim 155\,000}\) elements, with a refined mesh in areas where the crack is expected to propagate. The element size is half the value of l in the refined area. To reduce computational cost, we exploit the symmetry line A in Fig. 4a and model only the upper part of the specimen.

Figure 5 presents the crack patterns from the numerical simulations for the three impact velocities. The average angle between the initial crack tip plane and the propagated crack is \(\sim {70}^{\circ }\), which is in good agreement with the experimental results and the predictions by Hofacker and Miehe (2013). We observe increasing crack branching with increasing impact velocity, from no branching for an impact velocity of \({5}\,{\textrm{m}}/{\textrm{s}}\) to extensive branching when the impact velocity is \({50}\,{\textrm{m}}/{\textrm{s}}\). A notable trend is that the crack branching occurs earlier for the highest impact velocity, and that a second crack propagates from the lower right corner. The results are similar to those reported by Hofacker and Miehe (2013).

Fig. 4
figure 4

The Kalthoff–Winkler specimen with a dimensions and boundary conditions and b applied loading history

Full size image
Fig. 5
figure 5

Crack patterns from numerical simulations of the Kalthoff–Winkler test with impact velocities of a 5 m/s, b 16.5 m/s and c 50 m/s

Full size image

3.3 Kalthoff–Winkler test, 3D extension

We make the same 3D extension of the Kalthoff–Winkler test as Hofacker and Miehe (2013), where we assume a circular cross section of the projectile. Again, we perform numerical simulations for loading velocities of 5 m/s, 16.5 m/s and 50 m/s, and we use the Miehe split. The model parameters are identical to the parameters used for the 2D case, except for the length scale which is set to \(l = {1.0}\,{\textrm{mm}}\) due to a coarser discretization. The specimen geometry and boundary conditions are presented in Fig. 6a. All the outer boundaries are fixed except for the circular impact area and the boundary opposite to the loading plane. The geometry is discretized into \({\sim 9.8}\) million elements with a size of \({\sim 0.5\,{\textrm{mm}} \times 0.5\,{\textrm{mm}} \times 0.5}\,{\textrm{mm}}\). To reduce computational time, we exploit the symmetry planes A and B in Fig. 6a, and only model the upper left part of the specimen.

The resulting crack pattern evolution in symmetry plane B is presented in Fig. 7 for the three impact velocities. Similar to the 2D case, we get more crack branching for increasing impact velocity. However, for the 3D case, the crack branching occurs for the cracks initiating on the side opposite to the loading side. Here, we do not see crack branching in the curved cracks propagating directly from the circular notch. Figure 8 presents the crack patterns at the sections illustrated in Fig. 6b, where the distance is measured from the loading plane. The crack patterns stem from the same time instances as the lowest row in Fig. 7 for each respective impact velocity. Again, we find a similar trend, with more crack branching for increasing impact velocity. In their work, Hofacker and Miehe (2013) performed the same numerical experiment with en element size of \(\sim 1.0\,{\textrm{mm}} \times 1.0\,{\textrm{mm}} \times 1.0\,{\textrm{mm}}\) with \(l = {2.0}\,{\textrm{mm}}\) using a loading velocity of 5 m/s. With those conditions, they did not predict crack initiation from the back side of the specimen. However, the curved crack path propagating from the notch is similar to what is observed in our work for the same loading velocity. This deviation is most likely related to the difference in element size and length scale.

Fig. 6
figure 6

a The 3D extension of the Kalthoff–Winkler specimen seen from the front with dimensions and boundary conditions. b The side-view of symmetry plane B with the section planes used in visualization of the crack pattern

Full size image
Fig. 7
figure 7

Crack pattern evolution seen from the side-view of symmetry plane B, see Fig. 6a, for numerical simulations of the Kalthoff–Winkler test with impact velocities of 5 m/s (a, d, g), 16.5 m/s (b, e, h) and 50 m/s (c, f, i)

Full size image
Fig. 8
figure 8

The section views presented in Fig. 6b of the nearly fully evolved crack pattern for numerical simulation of the 3D extension of the Kalthoff–Winkler test with an impact velocity of 5 m/s (a, d, g, j), 16.5 m/s (b, e, h, k) and 50 m/s (c, f, i, l) at \(x = 50\) mm (a–c), \(x = 60\) mm (d–f), \(x= 70\) mm (g–i) and \(x = 80\) mm (j–l)

Full size image

4 L-shape tests

Rudshaug et al. (2023) performed 20 experiments on L-shaped soda-lime glass specimens subjected to quasi-static loading. For each experiment, the crack propagation was captured using high-speed cameras. Figure 9a presents the experimental setup, where the top of the specimen is clamped and pulled upwards, while the right-hand-side is restrained using a tie-strap. Figure 12f presents the resulting crack paths colored by crack propagation speed and Fig. 12c presents the evolution of the crack propagation speed. The crack propagation paths were consistent and the force level at fracture initiation varied from \(\sim \) 75 N to \(\sim \) 115 N. The experimental study revealed a positive correlation between the force level at fracture initiation and the initial crack propagation speed. We aim to investigate if we are able to capture the trends seen in the experimental study performed by Rudshaug et al. (2023) using our dynamic fracture phase-field implementation in LS-DYNA. To consider the different force levels at fracture initiation, we select two critical principal stress values at which we trigger the fracture phase-field evolution and investigate how this influences the predicted crack propagation both in terms of crack propagation speed and path.

Fig. 9
figure 9

The experimental setup (a) and the boundary conditions used in the numerical experiment (b) on the L-shaped glass specimen. Two rigid parts (A and B) are used to model the boundary conditions of the experiment. A translational spring with stiffness \(k_{t}\) and a rotational spring with stiffness \(k_{r}\) are used to reduce the translational and rotational movement of rigid part B

Full size image

The applied boundary conditions are presented in Fig. 9b. Two rigid parts (A and B) are used to model the boundary conditions of the experiment. Both the rigid parts are attached to the glass elements through coincident nodes. Rigid part A is restrained in the x- and z-directions, not allowed to rotate about any axis, and prescribed a displacement in the positive y-direction. Rigid part B is restrained in the z-direction and not allowed to rotate about the x and y axis. Rigid part B is connected to a translational spring with stiffness \(k_{t}\) reducing displacement in the x- and y-directions and a rotational spring with stiffness \(k_{r}\) reducing rotation about the z axis. Both springs are connected to the mass center of rigid part B and are used to replicate the behavior of the tie-strap. The spring stiffness values are \(k_{t} = 38.0\) N/mm and \(k_{r} = 4750.0\) N mm, based on the reported spring stiffness from Rudshaug et al. (2023).

The model parameters are: density \(\rho = {2500}\hbox { kg}/{\textrm{m}}^{3}\), Young’s modulus \(E = {70}\hbox { GPa}\), Poisson ratio \(\nu = {0.23}\), critical energy release rate \(G_{c} = {8}\hbox { J}/{\textrm{m}}^{2}\), length scale \(l = {0.4}\,{\textrm{mm}}\), artificial residual stiffness \(k=0\) and phase-field viscosity \(\eta = {10^{-9}}\hbox { N}\,{\textrm{s}}/{\textrm{mm}}^{2}\). We discretized the L-shaped specimen in two ways, presented in Table 1.

Table 1 Discretizations of the L-shaped glass specimen
Full size table

To determine the critical principal stress values, \(\sigma _{c}\), at the minimum and maximum load level at fracture initiation, we performed a failure-free linear elastic version of the numerical experiment for each discretization and noted the maximum values of the major principal stress at the respective critical force levels seen in the experiments. We note that these values differ depending on the discretization.

Figures 10 and 11 present the predicted crack paths using shell and solid elements, respectively. We note that the predicted crack paths are nearly identical. The initial crack propagation angle resembles what was found in the experiments. However, for both the weak and strong specimens we note that the inclination of the crack propagation path towards the left-hand-side of specimen deviates from the experimental paths, see Fig. 12f. We also note that the crack paths from the numerical simulations using the Miehe split are less curved than those based on the Amor and hybrid splits.

Fig. 10
figure 10

Crack patterns for numerical simulations with shell elements of the weakest (a–c) and strongest (d–f) L-shaped glass specimen using the Amor (a, d), Miehe (b, e) and hybrid (c, f) splits

Full size image
Fig. 11
figure 11

Crack patterns for numerical simulations with solid elements of the weakest (a–c) and strongest (d–f) L-shaped glass specimen using the Amor (a, d), Miehe (b, e) and hybrid (c, f) splits

Full size image

The evolution of the crack propagation speed and path for the shell element simulations are presented in Fig. 12a, b and d, e, comparing the three tension-compression splits for the weak (a, d) and strong (b,e) specimen. The propagation speeds are similar for all splits, except from \({\sim 60}\,{\upmu {\textrm{s}}}\) and later for the strong specimen with the Miehe split. We note that the initial crack propagation speeds for both the weak \(({\sim 800}-{1000}\,{{\textrm{m}}/{\textrm{s}}})\) and strong \(({\sim 1500}\,{{\textrm{m}}/{\textrm{s}}})\) specimen are close to the experimental values. However, in both cases the crack propagation speed drops too quickly compared to what was seen in the experiments. Similar to what we noted from Figs. 10 and 11, Fig. 12d, e confirms that the Miehe split results in less curved crack paths. The evolutions were identical for the solid element simulations, however, the computational time increased drastically.

Fig. 12
figure 12

Crack propagation speed (a–c) and path (d–f) for numerical simulations with shell elements of the weakest (a, d) and strongest (b, e) L-shaped glass specimen and the experiments (c, f)

Full size image

5 Discussion

Our implementation of the fracture phase-field approach was validated for static and dynamic problems. All the specimens used in the validations were discretized using regular hexahedral solid elements. The numerical simulations of the SENS and Kalthoff–Winkler tests all resulted in smooth curved crack propagation paths, indicating that there is no pathological mesh dependence. The SENT and SENS tests resulted in crack paths resembling what was found by Miehe et al. (2010a) and Ambati et al. (2014), indicating a successful implementation. Furthermore, the dynamic version of the implementation was validated against different versions of the Kalthoff–Winkler tests. When comparing the resulting crack patterns to what was found by Hofacker and Miehe (2013), it is clear that the implementations is able to handle dynamic cracking phenomena like crack branching.

The dynamic fracture phase-field was implemented in the commercial FE solver LS-DYNA, solving the displacement field and fracture phase-field separately in a staggered fashion. The displacement field is updated explicitly, while the fracture phase-field increment is solved implicitly. The lack of a temporal dependency (except for the stabilizing viscosity parameter \(\eta \)) in the fracture phase-field evolution equation, see Eq. (14), implies that the field is fully evolved at every increment. Instead of applying an iteration scheme, we approximate the incremental change in the phase-field by a linear system of equations. As discussed in Ambati et al. (2014), the staggered solution scheme requires sufficiently small increments to achieve convergence. In this explicit FE framework, this requirement is normally met, but care must be taken if time scaling is used, as this effectively increases the increment size and affects the viscous term \(\eta {\dot{\phi }}\) in Eq. (14).

The length scale parameter, l, controls the half-width of the regularized crack. To properly represent the diffuse approximation of the sharp crack topology, we need a sufficiently fine discretization that is able to adequately resolve the length scale parameter. In the case of brittle fracture, the length scale tends to zero. This implies that a very fine discretization is necessary to properly predict brittle crack propagation. However, a length scale close to zero is not practically feasible. For this reason, the length scale is typically way bigger than the physical crack width. A consequence of a large length scale is that the degradation of the potential energy is overestimated, decreasing the crack propagation speed.

With the new proposed crack driving force in Eq. (16), we introduced a global fracture initiation criterion based on the maximum major principal stress \(\sigma _{\mathcal {B}}\). To ensure fracture initiation at the correct load levels in the numerical simulations on the L-shaped specimens, we had to determine the appropriate critical principal stress values \(\sigma _{c}\) through initial damage-free simulations. Depending on the specimen discretization, the stress representation near the inner corner will vary. Because of the location of the integration points, we do not sample directly at the inner corner, but at a distance. For this reason, the critical principal stress values change for both different discretizations and distributions of integration points. However, when we ensure fracture initiation at the same critical load level, we find that this does not affect the crack propagation path and speed. This is confirmed when comparing the shell to the solid element simulations.

For the quasi-static SENT and SENS tests and the L-shaped glass tests we conducted the simulations using the three implemented tension-compression splits, namely the Amor, Miehe and hybrid splits. The splits all produced the same crack pattern for the SENT test, which was expected. However, for the SENS test and the L-shaped glass specimen test we see some differences. The crack path of the SENS test with the Amor split exhibits a gradual ramp down from the initial crack, while the two other splits result in a crack path that propagates directly downwards. In addition, a small crack starts growing from the lower right corner in the SENS test with the Amor split. If we consider the L-shaped glass tests, we note that the predicted crack paths of the Amor and hybrid splits are similar, while the crack path of the Miehe split is less curved. These examples illustrate that the tension-compression splits impact the crack propagation paths, and that the predictions might coincide for some problems and deviate for others.

When we consider the crack propagation speed in the simulations of both the weak and strong L-shaped specimens (Fig. 12a, b), we note that the initial crack propagation speed is similar to what was reported in the experiments (Fig. 12c). This indicates that the initial crack propagation speed is correlated to the critical load level, and thus the amount of potential energy at fracture. In addition, it implies that the crack driving force proposed in Eq. (16) is suited for handling crack propagation at various critical load levels. Unlike what was observed in the experiments, the crack paths for the weak specimen propagate downwards close to the left edge. This downward propagation might be linked to the applied boundary conditions. However, it might also deviate due to the early drop in crack propagation speed. When the crack propagation speed is too low, it affects the resulting concurrent stress fields, which may result in different optimal crack paths. In future studies, it would be interesting to investigate how different formulations of the crack driving force affect the crack propagation speed and path.

By implementing the fracture phase-field into a commercial FE code we get access to a well established and full featured FE framework. This makes it easy to use the dynamic phase-field formulation in complex simulations involving advanced contact formulations, fluid structure interaction and ballistics, which are not common features in in-house codes. With these additional options, including the new proposed crack driving force, we facilitate further validation and investigation of the potential of the phase-field approach to fracture.

6 Conclusions

In this work we implemented a dynamic fracture phase-field formulation into the commercial FE code LS-DYNA through both solid and shell user elements. The fracture phase-field evolution was solved with a staggered explicit update of the displacement field and an implicit update of the fracture phase-field. The implementation proved capable of predicting complex, dynamic crack topologies through static and dynamic numerical simulations of numerical examples from the literature. We introduced a new crack driving force including a fracture initiation criterion based on the critical major principal stress, that allows for crack predictions for specimens of varying strength. The prediction capacity of the model was tested on quasi-statically loaded L-shaped soda-lime glass specimens of two different specimen strengths. We compared the predicted crack propagations of the numerical simulations to the experiments in terms of crack path and speed, and found that the predicted initial crack propagation speed is close to the experimental values, but that the speed drops too quickly. The predicted crack paths initially resemble the experimental crack paths, but start to deviate with time as the crack propagates across the specimen. Similar to what was observed in the experiments, the strongest specimen experienced a greater initial crack propagation speed than the weakest.