1 Introduction

Fracture is one of the crucial failure mechanisms for engineering structural applications and the reliable prediction of fracture is of great importance and necessity. Experimentally motivated, the theory of classical brittle fracture is outlined by Griffith (1921) that crack formation irreversibly dissipates a specific amount of elastic strain energy. The amount of energy consumed per unit crack surface to evolve fracture is defined by the fracture toughness \({\mathcal {G}}_{c}\), or known as the critical energy release rate. The condition to evolve fracture based on the classical Griffith definition has to satisfy that the instantaneous energy release rate \({\mathcal {G}}\) reaches or exceeds the critical value \({\mathcal {G}}\ge {\mathcal {G}}_{c}\). Nevertheless, the classical Griffith fracture theory is not capable to predict crack propagation pathology. The recent promising phase-field approach, which is originated from a variational framework by minimizing the total energy, approximates a discrete crack as a numerically smeared representation. This variational theory for discontinuities, see Mumford and Shah (1989) for image segmentation, is subsequently regularized by De Giorgi and Carriero (1989) and Ambrosio and Tortorelli (1990) to yield smeared approximations of the discontinuities. Based on a similar methodology, Francfort and Marigo (1998) incorporate the classical Griffith theory to formulate a brittle fracture theory by minimizing the internal strain energy potential and the fracture energy. For detailed introduction, it is referred to the work of Bourdin et al. (2008). In the sequel, similar works for brittle fracture simulation can be found in Bourdin et al. (2000), Hakim and Karma (2009), Miehe et al. (2010), Pham et al. (2011) to name a few. Meanwhile, the reliability of crack approximation by phase-field modeling is discussed by studying classical \(\Gamma \)-convergence theory, see Borden et al. (2014), Linse et al. (2017), Chambolle et al. (2018) for representative contributions. The advantages of this method are that crack initiation, propagation as well as branching with complex patterns can be properly captured to show good agreement with experimental results.

Another key aspect, the physically realistic material degradation, plays significantly important role to obtain the trustworthy crack kinematics. The simple definitions proposed by Amor et al. (2009) and Freddi and Royer Carfagni (2009) are to split the energy into volumetric and deviatoric parts. The volumetric energy only contributes to evolve the crack when the material is expanding. Another alternative outlined by Miehe et al. (2010) defines the material degradation according to a spectral decomposition of the strain tensor, that only tensile components drive crack evolution, also see Hofacker (2013). Nevertheless, as pointed out in May et al. (2015), Strobl and Seelig (2015), Schlüter (2018), Steinke and Kaliske (2019), both the volumetric–deviatoric (V–D) split and spectral split phase-field modeling fail to predict the force transferring through the crack correctly for arbitrary crack deformations. To overcome this issue, several efforts are subsequently carried out. Restricted within isotropic, linear elasticity at small deformations, the conceptual directional decomposition (Steinke and Kaliske 2019; Strobl and Seelig 2016) overcomes the observed discrepancies of the V–D and spectral split by deriving the constitutive law according to the local crack coordinate system, which is determined by a local crack orientation. As a result, a reasonable material degradation equivalent to a discrete crack is obtained. In particular, taking advantages of the variational homogenization concept (Blanco et al. 2016), a Representative Crack Element (RCE) concept is formulated in Storm et al. (2020) by considering a kinematic coupling of the phase-field model (continuous crack approximation) to a discrete crack model (discontinuous crack representation), which allows to evaluate complex crack behaviors, e.g. crack surface contact and friction, in a smeared and continuous domain. This novel framework is formulated by a consistent variational derivation. The simulation results regarding the self-consistent test indicate the kinematic consistency for arbitrary crack deformations. These approaches aforementioned strongly depend on the determination of a local crack orientation, especially at the crack tip. Nevertheless, finding the local crack orientation is not convincingly solved yet. Several contributions define this characteristic direction by the gradient of the phase-field (Strobl and Seelig 2016), the maximum principal stress direction (Steinke and Kaliske 2019) and the direction of maximum dissipated fracture energy (Bryant and Sun 2018).

In addition to brittle phase-field modeling (Bourdin et al. 2000; Hakim and Karma 2009; Miehe et al. 2010; Pham et al. 2011), several subsequent extensions are postulated as well, e.g. for dynamic fracture studies (Kuhn and Müller 2010; Schlüter et al. 2014; Steinke et al. 2016; Yin et al. 2020), for ductile fracture simulation (Duda et al. 2015; Kuhn et al. 2016; Borden et al. 2016; Miehe et al. 2016; Ambati et al. 2016; Alessi et al. 2018; Aldakheel et al. 2018; Kienle et al. 2019; Yin and Kaliske 2020a), for anisotropic fracture (Storm et al. 2020; Hakim and Karma 2005; Nasseri and Mohanty 2008; Raina and Miehe 2015; Gültekin et al. 2016; Clayton and Knap 2014, 2015; Gültekin et al. 2018; Teichtmeister et al. 2017; Li et al. 2014; Yin and Kaliske 2020b) as well as for fatigue failure prediction (Alessi et al. 2018; Carrara et al. 2020; Seiler et al. 2020). Nevertheless, very limited applications of phase-field modeling for viscoelastic materials are available. Based on classical V–D split, Shen et al. (2019) presents a viscoelastic phase-field formulation by defining the driving force consisting of the elastic energy and a portion of the dissipated energy simultaneously at small strains. Besides, Schänzel (2015), Loew et al. (2019), Yin and Kaliske (2020c) extend the viscoelastic phase-field application to finite deformation to sufficiently capture the behavior of polymeric materials fracture. None of the viscoelastic phase-field applications is based on the spectral split, since this algorithm is mainly motivated by pure elasticity. So far, nearly no contribution has applied the spectral decomposition to inelasticity yet. Regarding viscoelastic characteristics, it significantly increases complexity to express the elastic strain energy density functional as a spectral split form.

The purpose of this contribution is, on the one hand, formulating a viscoelastic phase-field model by taking advantage of the RCE framework for phase-field fracture to achieve physically accurate crack kinematics. The rheological constitutive model of linear viscoelasticity depends on the classical convolution integral algorithm. Following Schänzel (2015), Yin and Kaliske (2020c), the phase-field driving force depends on the total elastic strain energy, excluding the viscous dissipation. This strictly follows the criteria of classical Griffith-type fracture. On the other hand, extending the developments (Storm et al. 2020) from elasticity to inelasticity, this contribution is meant to examine the application of the RCE approach to more comprehensive and complex analyses. Thus, inelastic deformation behavior of the crack is modeled by introducing internal variables. Furthermore, another progress out of Storm et al. (2020) is that this work takes the inertia effects into consideration, consequently yielding a consistent transient analysis.

The framework of this paper is outlined as follows. In Sect. 2, the fundamental constitutive formulation of the classical viscoelastic material is introduced along with a derivation of the stress tensor and the consistent tangent. In Sect. 3, the concept of the RCE formulation for viscoelastic materials is developed, and the governing equations for the multi-field problem is derived. To validate and demonstrate the capability of the present approach, several representative numerical simulations are outlined in Sect. 4. Consequently, Sect. 5 summarizes the findings and closes the paper with potential perspectives.

2 Constitutive law for viscoelastic material

2.1 General Helmholtz free energy functional with internal variables

The derivation of a generalized viscoelastic Maxwell model is based on a one-dimensional setup at small strains, which is subsequently straightforward extended to a three-dimensional framework. In order to achieve a general description of the Helmholtz free energy density, the concept of internal variable \(\varvec{\varepsilon }_{v}^{I}\) is employed to represent the strain quantities of the dash-pot for each non-equilibrium viscoelastic branch \(I=1,2,\ldots ,m\), see Fig. 1. Accordingly, the elastic strain of the spring in each non-equilibrium branch \(\varvec{\varepsilon }_{e}^{I}\) and the effective strain energy stored in the spring read

$$\begin{aligned} \varvec{\varepsilon }_{e}^{I}=\varvec{\varepsilon }-\varvec{\varepsilon }_{v}^{I} \qquad \text {and} \qquad \varphi ^{ne,I} = \varphi \left( \varvec{\varepsilon }_{e}^{I} \right) , \end{aligned}$$
(1)

respectively. The total elastic strain is defined by \(\varvec{\varepsilon }\), which is illustrated in Fig. 1. The general form of the Helmholtz free energy is isothermally defined by

$$\begin{aligned} \varphi ^{tot}\left( \varvec{\varepsilon }, \varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m} \right) =\varphi ^{eq}\left( \varvec{\varepsilon } \right) + \sum _{I=1}^{m}\varphi ^{ne,I}\left( \varvec{\varepsilon }, \varvec{\varepsilon }_{v}^{I} \right) .\nonumber \\ \end{aligned}$$
(2)

It is noteworthy that, this paper considers a linear viscoelastic model, which characterizes the spring devices and the dash-pot devices at the non-equilibrium branches as linear responses simultaneously. In the sequel, the total stress is obtained as

$$\begin{aligned} \varvec{\sigma }^{tot}= & {} \partial _{\varvec{\varepsilon }}\, \varphi ^{eq}\left( \varvec{\varepsilon } \right) + \sum _{I=1}^{m} \partial _{\varvec{\varepsilon }}\, \varphi ^{ne,I}\left( \varvec{\varepsilon }, \varvec{\varepsilon }_{v}^{I} \right) \nonumber \\= & {} \varvec{\sigma }^{eq} + \sum _{I=1}^{m}\varvec{\sigma }^{ne,I}, \end{aligned}$$
(3)

which is sum of the equilibrium stress \(\varvec{\sigma }^{eq}\) and all non-equilibrium stresses \(\varvec{\sigma }^{ne,I}\). According to Holzapfel (1996), Simo and Hughes (1998), the conjugate description of \(\varvec{\sigma }^{ne,I}\) also reads

$$\begin{aligned} \varvec{\sigma }^{ne,I}= & {} \partial _{\varvec{\varepsilon }_{e}^{I}}\, \varphi ^{ne,I}\left( \varvec{\varepsilon }, \varvec{\varepsilon }_{v}^{I} \right) =\partial _{\varvec{\varepsilon }}\, \varphi ^{ne,I}\left( \varvec{\varepsilon } \varvec{\varepsilon }_{v}^{I} \right) \nonumber \\= & {} -\partial _{\varvec{\varepsilon }_{v}^{I}}\, \varphi ^{ne,I}\left( \varvec{\varepsilon }, \varvec{\varepsilon }_{v}^{I} \right) . \end{aligned}$$
(4)
Fig. 1
figure 1

Rheology of the generalized Maxwell element for linear viscoelastic material by illustratively showing only one non-equilibrium branch

Full size image

2.2 Stress and material tangent tensors

The rheological generalized Maxwell model has been validated to exhibit the time-dependent or frequency-dependent properties. According to Holzapfel (1996), Kaliske and Rothert (1997), Simo and Hughes (1998), the evolution of the non-equilibrium stress \(\varvec{\sigma }^{ne,I}\) is obtained by a convolution integral algorithm

$$\begin{aligned} \dot{\varvec{\sigma }}^{ne,I} + \frac{1}{\tau ^{I}} \varvec{\sigma }^{ne,I} = \chi ^{I} \dot{\varvec{\sigma }}^{eq}, \end{aligned}$$
(5)

where the material parameter \(\tau ^{I}\) represents the relaxation time for the \(I^{th}\) non-equilibrium response. The factor \(\chi ^{I}\) describes the ratio of the material parameters of the non-equilibrium branches with respect to the equilibrium branch, i.e. \(\chi ^{I}=\lambda ^{ne,I} / \lambda =\mu ^{ne,I} / \mu \). The Lamé constants for the viscoelastic material are denoted by \(\lambda , \mu \) for the equilibrium branch and \(\lambda ^{ne,I}, \mu ^{ne,I}\) for the \(I^{th}\) non-equilibrium branch. According to the derivation in Kaliske and Rothert (1997), the time integral is numerically discretized and the internal stress at the non-equilibrium branch eventually yields

$$\begin{aligned} \begin{aligned} \varvec{\sigma }^{ne,I}_{t^{n+1}}&= \underbrace{\text {exp}\left( -\frac{\Delta t}{\tau ^{I}} \right) }_{\beta ^{I}\cdot \beta ^{I}}\cdot \varvec{\sigma }^{ne,I}_{t^{n}} \\&\quad + \chi ^{I}\cdot \underbrace{\text {exp}\left( - \frac{\Delta t}{2\,\tau ^{I}} \right) }_{\beta ^{I}}\cdot \,\Big ( \varvec{\sigma }^{eq}_{t^{n+1}} - \varvec{\sigma }^{eq}_{t^{n}} \Big ) \\&= \beta ^{I}\cdot \beta ^{I}\cdot \varvec{\sigma }^{ne,I}_{t^{n}}+ \chi ^{I}\cdot \beta ^{I}\cdot \Big ( \varvec{\sigma }^{eq}_{t^{n+1}} - \varvec{\sigma }^{eq}_{t^{n}} \Big ) \end{aligned} \end{aligned}$$
(6)

where the terms \(\varvec{\sigma }^{eq}_{t^{n}}\) and \(\varvec{\sigma }^{ne,I}_{t^{n}}\) are two history variables at the previous time step \(t^{n}\) regarding the stress responses of the equilibrium and the non-equilibrium branches, respectively. It is noteworthy that, the non-equilibrium stress \(\varvec{\sigma }^{ne,I}_{t^{n+1}}\) is not straightforwardly obtained by the derivation in Eq. (3), nevertheless, the strain quantity \(\varvec{\varepsilon }_{e}^{I}\) can be reversibly computed due to the linear elastic spring at the non-equilibrium branch, which also leads to the analytical solution of the strain energy \(\varphi ^{ne}\) for the non-equilibrium branches. In order to consider a consistent algorithm, the general relation in Eq. (3) is assumed to exist, which yields the total stress response for the rheological generalized Maxwell model

$$\begin{aligned}&\varvec{\sigma }^{tot}_{t^{n+1}}\nonumber =\,\partial _{\varvec{\varepsilon }_{t^{n+1}}}\, \varphi ^{tot}_{t^{n+1}} = \partial _{\varvec{\varepsilon }}\, \varphi ^{eq}_{t^{n+1}}\left( \varvec{\varepsilon } \right) \nonumber \\&\qquad +\,\sum _{I=1}^{m} \partial _{\varvec{\varepsilon }}\, \varphi ^{ne,I}_{t^{n+1}}\left( \varvec{\varepsilon }, \varvec{\varepsilon }_{v}^{I} \right) \\&\quad =\,\varvec{\sigma }^{eq}_{t^{n+1}} + \sum _{I=1}^{m}\varvec{\sigma }^{ne,I}_{t^{n+1}} \nonumber \\&\qquad =\underbrace{ \left( 1+ \sum _{I=1}^{m}\chi ^{I}\,\beta ^{I} \right) }_{\alpha } \varvec{\sigma }^{eq}_{t^{n+1}} \nonumber \\&\qquad + \, \underbrace{\sum _{I=1}^{m} \beta ^{I} \left( \beta ^{I} \varvec{\sigma }^{ne,I}_{t^{n}} - \chi ^{I} \varvec{\sigma }^{eq}_{t^{n}} \right) }_{{\varvec{h}}_{t^{n}}} \nonumber \\&\quad =\,\alpha \,\varvec{\sigma }^{eq}_{t^{n+1}} \Big (\varvec{\varepsilon }_{t^{n+1}} \Big ) +{\varvec{h}}_{t^{n}}\Big (\varvec{\sigma }^{eq}_{t^{n}},\varvec{\sigma }^{ne}_{t^{n}} \Big ),\nonumber \end{aligned}$$
(7)

and the linearized material tangent

$$\begin{aligned} \begin{aligned} {\mathbb {C}}_{t^{n+1}}^{tot}&= \partial _{\varvec{\varepsilon }_{t^{n+1}}}\,\varvec{\sigma }^{tot}_{t^{n+1}} \\&= \partial _{\varvec{\varepsilon }_{t^{n+1}}} \left( \alpha \,\varvec{\sigma }^{eq}_{t^{n+1}} \Big (\varvec{\varepsilon }_{t^{n+1}} \Big ) + {\varvec{h}}_{t^{n}}\Big (\varvec{\sigma }^{eq}_{t^{n}},\varvec{\sigma }^{ne}_{t^{n}} \Big ) \right) \\&= \alpha \,{\mathbb {C}}^{eq}_{t^{n+1}} \end{aligned}\nonumber \\ \end{aligned}$$
(8)

with the definition of the coefficient \(\alpha \) in Eq. (7). Furthermore, the linear elastic isotropic tangent is expressed as \({\mathbb {C}}^{eq} = \lambda \, {\varvec{1}}\otimes {\varvec{1}} + 2\mu \,{\mathbb {I}}\) by using the fourth order identity tensor \({\mathbb {I}}\).

Remark: Motivated by Holzapfel (1996), the internal strain-type quantity \(\varvec{\varepsilon }^{I}_{v}\) is introduced in this work to yield a straightforward variational framework with respect to the present internal stress governed viscoelastic constitutive law, since the total Helmholtz energy density potential can be simply defined as a strain based functional. Due to the linearity of the presented viscoelastic constitutive model, the strain of the elastic spring device at the non-equilibrium branch is characterized as \(\varvec{\varepsilon }^{I}_{e}=\left( \varvec{\varepsilon }-\varvec{\varepsilon }^{I}_{v}\right) \), which can actually be obtained by \(\varvec{\varepsilon }^{I}_{e}={\mathbb {D}}^{ne,I}:\varvec{\sigma }^{ne,I}_{t^{n+1}}\). The conjugate elasticity tensor \({\mathbb {D}}^{ne,I}\) is constant due to assumption of linearity and is determined by the model parameters \(\lambda ^{ne,I}\) and \(\mu ^{ne,I}\). Thus, the elastic strain energy density of the linear spring at the non-equilibrium branch is alternatively obtained by \(\varphi ^{ne,I}\left( \varvec{\varepsilon },\varvec{\varepsilon }^{I}_{v}\right) =({1}/{2})\varvec{\sigma }^{ne,I}_{t^{n+1}}:\left( \varvec{\varepsilon }-\varvec{\varepsilon }^{I}_{v}\right) =({1}/{2})\varvec{\sigma }^{ne,I}_{t^{n+1}}:{\mathbb {D}}^{ne,I}:\varvec{\sigma }^{ne,I}_{t^{n+1}}\). The superposition of the elastic strain energy density of the equilibrium and the non-equilibrium branches, \(\varphi ^{tot}=\varphi ^{eq}+ \sum _{I=1}^{m}\varphi ^{ne,I}\), is subsequently considered for the phase-field evolution within the RCE framework.

3 Rate-dependent RCE phase-field approach

3.1 Phase-field topology

Fig. 2
figure 2

Discrete and diffusive crack topology

Full size image

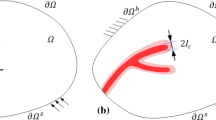
Within a continuous solid domain, a sharp crack can be numerically approximated by a diffusive phase-field distribution, which is illustrated in Fig. 2. A scalar order parameter, namely the phase-field variable \(d({\varvec{x}},t)\), is introduced to identify the material state, i.e. the sound material is denoted by \(d=0\) and the fully cracked state is represented by \(d=1\). Mathematically motivated by a one-dimensional bar with an infinite length \(L\in \left[ -\infty , +\infty \right] \), which is assumed to be cracked at position \(x=0\), the closed form solution for a continuous phase-field according to Miehe et al. (2010) is approximated by an exponential function

$$\begin{aligned} d(x)=\text {exp}\left( -\frac{|x|}{l}\right) . \end{aligned}$$
(9)

Nevertheless, this function is not the unique approximation of phase-field profile for one-dimensional representation. This solution in Eq. (9) is appropriately and naturally bounded by \((0 < d \le 1)\). Another important parameter, the length scale l, is employed to govern the width of the transition zone between fractured and sound state of the material. Extending to a two- or three-dimensional framework, the second order functional of the crack surface density is defined as

$$\begin{aligned} \gamma _{l}= \frac{1}{2l}\left( d^{2}+l^{2}|\nabla _{{\varvec{x}}} d|^{2}\right) , \end{aligned}$$
(10)

where \(\nabla _{{\varvec{x}}} \left( * \right) \) denotes the spatial gradient operator. Highlighted in Borden et al. (2014), the crack domain \({\bar{\Gamma }}\) is approximately obtained by the phase-field crack domain \(\Gamma _{l}\) as long as \(l \rightarrow 0\), i.e.

$$\begin{aligned} {\bar{\Gamma }}\approx \underset{l \rightarrow 0}{\text {lim}}\;{\bar{\Gamma }}_{l}=\underset{l \rightarrow 0}{\text {lim}}\;\int _{\varOmega } \gamma _{l}\,dV, \end{aligned}$$
(11)

which is known as \(\Gamma \)-convergence condition for fracture.

The defined crack surface density function in Eq. (10) is also known as the AT2 model, which yields an exponentially shaped crack profile as described by Eq. (9). By applying this function, the numerical derivation and implementation is straightforward and efficient without additional numerical treatment due to the differentiable (except for \(d=0\)) and continuous properties of the phase-field solution in Eq. (9). Nevertheless, this model does not present an elastic limit and the simulation result largely depends on the length scale parameter l. As Hofacker (2013) investigated with regard to the FEM application, a minimum element size \(h_{e} \le l/2 \) in the potential crack region is necessary in order to achieve realistic results. Meanwhile, in addition to the AT2 model, another common alternative to approximate the crack surface density function is the classical AT1 model. One of the main differences between these models is that the AT1 model only consists of the linear term d rather than the quadratic term \(d^2\) in Eq. (10), see Pham et al. (2011). The AT1 model can guarantee an ideally linear elastic response up to the elastic stress limit. Nevertheless, due to the lack of differential continuity, additional numerical treatments are of importance to avoid negative phase-field evolution, which may lead to a non-linear phase-field evolution. In this contribution, a standard AT2 model based on Eq. (10) is taken into account.

Fig. 3
figure 3

Crack kinematics of the RCE approach

Full size image

3.2 Concept of the representative crack elements (RCE)

The concept of the representative crack elements (RCE) developed in Storm et al. (2020) is a novel framework to derive phase-field fracture models with realistic crack kinematics. The fundamental formulation is motivated by classical homogenization theory. For the assumptions and the derivations in detail, it is particularly referred to Storm et al. (2020). The aim of the RCE concept is to explain the crack kinematics of a discrete crack explicitly and transfer it to the diffusive phase-field formulation. One of the main advantages is that the numerical degradation of a fully cracked model leads to physically expected results in case of different loading modes, i.e. no resistance for tension and shear (parallel to the crack) whereas fully contact for compression.

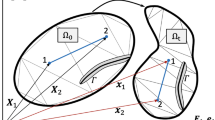
According to Storm et al. (2020), the RCE model describes the deformation of an arbitrary material point, where it is fully cracked, by the relative deformation of the two crack surfaces, see Fig. 3. The core formulation of the RCE approach for small strain problems reads

$$\begin{aligned} \varvec{\varepsilon }= \bar{\varvec{\varepsilon }} - \varvec{\Gamma }, \end{aligned}$$
(12)

where \(\bar{\varvec{\varepsilon }}\) represents the total strain at the material point. The quantity \(\varvec{\varepsilon }\) defines the uniform strain for the two blocks (see Fig. 3), which may contain internal variables in case of inelastic material, e.g. \(\varvec{\varepsilon }_{v}^{I}\) aforementioned for viscoelastic strain. Another important strain quantity \(\varvec{\Gamma }\), namely the so-called crack deformation, is derived to describe the relative deformation of the crack surfaces of the blocks. Particularly, the form of the crack deformation \(\varvec{\Gamma }\) reads

$$\begin{aligned}&\varvec{\Gamma }=\sum _{a=1}^{3}\Gamma _{a}\varvec{P}^{a} \qquad \qquad \text {with}\nonumber \\&\varvec{P}^{a} = \frac{1}{2}\Big ( \varvec{n}_{a}\otimes \varvec{n}_{1} + \varvec{n}_{1}\otimes \varvec{n}_{a} \Big ), \end{aligned}$$
(13)

where \(\Gamma _{a}\) with \(a=1,2,3\) are three non-unit scalar quantities to measure the crack deformation along the crack normal direction \({\varvec{n}}_{1}\) and two tangential directions \({\varvec{n}}_{2}\) and \({\varvec{n}}_{3}\). The detailed mathematical derivation is based on variational homogenization theories and it is referred to Storm et al. (2020). The orientation of the orthogonal local RCE system \({\mathcal {E}}^{c}\sim \left\{ {\varvec{n}}_{1},{\varvec{n}}_{2},{\varvec{n}}_{3} \right\} \) with respect to the global coordinate system \({\mathcal {E}}^{e}\sim \left\{ {\varvec{e}}_{1},{\varvec{e}}_{2},{\varvec{e}}_{3} \right\} \) is determined by a subsequent crack orientation criterion. Nevertheless, it is still a challenge to determine a robust crack orientation around the crack tip for the standard phase-field method. In this work, the orthogonal eigen-space of the total stress tensor at the previous time step \(\varvec{\sigma }_{t^{n}}\) is employed to characterize the local crack orientation in the RCE. With this algorithmic setup, the derivation work is largely simplified due to \(\partial _{\bar{\varvec{\varepsilon }}_{t^{n+1}}}{\varvec{n}}_{i}={\varvec{0}}\).

The effective mechanical energy density for the phase-field model is defined by

$$\begin{aligned} \varphi ^{mech} = \varphi ^{tot}_{c} +g\left( d\right) \cdot \left( \varphi ^{tot}_{0} - \varphi ^{tot}_{c} \right) , \end{aligned}$$
(14)

where the Helmholtz free strain energy for the intact material and the fully broken state are denoted by \(\varphi ^{tot}_{0}\) and \(\varphi ^{tot}_{c}\), respectively. The energy density functional of intact material is also applied to the bulk material of the RCE. Considering homogeneous deformation and stress distribution, the homogenized energy density \(\varphi ^{tot}_{c}\) of the cracked material is characterized to have the same form of the bulk material energy density \(\varphi ^{tot}_{0}\), which are interpreted as

$$\begin{aligned}&\varphi ^{tot}_{0} = \varphi ^{tot}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{0,v}^{1},\ldots ,\varvec{\varepsilon }_{0,v}^{m} \right) \,\,\,\,\,\,\text {and}\nonumber \\&\,\varphi ^{tot}_{c}= \varphi ^{tot}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m},\varvec{\Gamma } \right) , \end{aligned}$$
(15)

respectively. The internal variables \(\varvec{\varepsilon }_{0,v}^{I}\) and \(\varvec{\varepsilon }_{c,v}^{I}\) (\(I=1,2,\ldots ,m\)) are involved to describe the inelastic behavior for the intact and the fully broken material. Thus, the effective stress tensor and the consistent tangent are straightforward obtained as

$$\begin{aligned} \begin{aligned} \varvec{\sigma }^{mech}_{t^{n+1}}&=\partial _{\bar{\varvec{\varepsilon }}_{t^{n+1}}}\, \varphi ^{mech}_{t^{n+1}} \\&= \varvec{\sigma }^{tot}_{c,t^{n+1}}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m},\varvec{\Gamma } \right) \\&\quad +g\left( d\right) \cdot \Big ( \varvec{\sigma }^{tot}_{0,t^{n+1}}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{0,v}^{1},\ldots ,\varvec{\varepsilon }_{0,v}^{m} \right) \\&\quad -\varvec{\sigma }^{tot}_{c,t^{n+1}}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m},\varvec{\Gamma } \right) \Big ) \\ \end{aligned} \end{aligned}$$
(16)

and

$$\begin{aligned} {\mathbb {C}}^{mech}_{t^{n+1}}&=\partial _{\bar{\varvec{\varepsilon }}_{t^{n+1}}}\, \varvec{\sigma }^{mech}_{t^{n+1}} = {\mathbb {C}}^{tot}_{c,t^{n+1}}\nonumber \\&\quad +g\left( d\right) \cdot \Big ( {\mathbb {C}}^{tot}_{0,t^{n+1}}-{\mathbb {C}}^{tot}_{c,t^{n+1}} \Big ), \end{aligned}$$
(17)

respectively. The quantities \(\varvec{\sigma }^{tot}_{0,t^{n+1}}\), \({\mathbb {C}}^{tot}_{0,t^{n+1}}\) and \(\varvec{\sigma }^{tot}_{c,t^{n+1}}\), \({\mathbb {C}}^{tot}_{c,t^{n+1}}\) represent the intact and the broken state of stress and tangent, which consist of the response of both the equilibrium and non-equilibrium branches of viscoelastic model. It is noteworthy to point out that, due to the argumentation of homogeneous deformation and stress distribution aforementioned, the resultant forms of the stress terms \(\varvec{\sigma }^{tot}_{0,t^{n+1}}\) and \(\varvec{\sigma }^{tot}_{c,t^{n+1}}\) are the same, which are based on Eq. (7) expressed as

$$\begin{aligned}&\varvec{\sigma }^{tot}_{0,t^{n+1}} = \alpha \,\varvec{\sigma }^{eq}_{0,t^{n+1}} + {\varvec{h}}_{0,t^{n}}\Big (\varvec{\sigma }^{eq}_{0,t^{n}},\varvec{\sigma }^{ne}_{0,t^{n}} \Big ) \quad \text {and} \nonumber \\&\varvec{\sigma }^{tot}_{c,t^{n+1}} = \alpha \,\varvec{\sigma }^{eq}_{c,t^{n+1}} + {\varvec{h}}_{0,t^{n}}\Big (\varvec{\sigma }^{eq}_{c,t^{n}},\varvec{\sigma }^{ne}_{c,t^{n}} \Big ). \end{aligned}$$
(18)

Therefore, solving the unknown crack deformation \(\Gamma _{i}\) yields the consequent constitutive law of the RCE approach. According to Storm et al. (2020), the unknown \(\Gamma _{i}\) can be solved by applying a minimization principle of the total Helmholtz free energy of the RCE, which reads

$$\begin{aligned}&\partial _{\Gamma _{i}}\varphi ^{mech}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{0,v}^{1},\ldots ,\varvec{\varepsilon }_{0,v}^{m},\right. \left. \varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m}, \varvec{\Gamma }\right) = 0.\nonumber \\ \end{aligned}$$
(19)

In the sequel, the extremal problem with respect to the unknown crack deformations reads

$$\begin{aligned}&\Gamma _{i} = \arg \Bigg \{ \underset{\Gamma _{1,2,3} \in {\mathcal {R}}}{\text {min}} \, \varphi ^{mech} \left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{0,v}^{1},\ldots ,\varvec{\varepsilon }_{0,v}^{m}\right. ,\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \,\quad \left. \varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m}, \varvec{\Gamma }\right) \Bigg \} \end{aligned}$$
(20)

in case there are no constraints on the crack deformations (for an open crack). Subsequently, crack surface penetration has to be tested via \(\Gamma _{1}<0\) and, possibly, a closed crack solution can be determined from the constrained minimization problem that

$$\begin{aligned} \begin{aligned}&\Gamma _{2,3} = \arg \Bigg \{ \underset{\Gamma _{2,3} \in {\mathcal {R}}}{\text {min}} \, \varphi ^{mech} \left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{0,v}^{1},\ldots ,\varvec{\varepsilon }_{0,v}^{m},\right. \\&\left. \varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m}, \varvec{\Gamma }\right) \Bigg | _{\Gamma _{1} = 0} \Bigg \} \,\,\,\,\,\,\\&\text {for} \,\,\,\,\,\, \Gamma _{1} < 0, \\&\Gamma _{1} = 0, \end{aligned} \end{aligned}$$
(21)

in order to take crack surface contact into account. Hence, the unconstrained and the constrained minimization problem provide the solutions for an open crack and a closed crack, respectively. With the crack deformations \(\Gamma _{i}\) at hand, the strain relation of the RCE model is fully defined and the corresponding stress and the material tangent of the smeared crack model are obtained straightforward. The algorithmic examination of the open or closed crack is illustrated in Fig. 4.

Fig. 4
figure 4

Solution procedure for the RCE with homogeneous block deformations

Full size image

In particular, the solution of \(\Gamma _{i}\) according to Eq. (19) for an arbitrary phase-field value is subsequently expanded as

$$\begin{aligned}&\quad \quad \frac{\partial \,\varphi ^{mech}}{\partial \,\Gamma _{a}}=0 \quad \nonumber \\&\Rightarrow \quad \frac{\partial \,\varphi ^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m},\varvec{\Gamma } \right) }{\partial \,\Gamma _{a}} \nonumber \\&\quad = \frac{\partial \,\varphi ^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m},\varvec{\Gamma } \right) }{\partial \,\varvec{\Gamma }}: \frac{\partial \,\varvec{\Gamma }}{\partial \,\Gamma _{a}} =0. \end{aligned}$$
(22)

Due to the fundamental definition of the RCE approach in Eq. (12), the relationship \(\partial _{\varvec{\Gamma }}\,\varphi ^{tot}_{c} = -\partial _{\bar{\varvec{\varepsilon }}}\,\varphi ^{tot}_{c}=-\varvec{\sigma }^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m},\varvec{\Gamma } \right) \) naturally exits, which further simplifies Eq. (22) as

$$\begin{aligned} \begin{aligned}&\quad \quad \frac{\partial \,\varphi ^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m},\varvec{\Gamma } \right) }{\partial \,\varvec{\Gamma }}: \frac{\partial \,\varvec{\Gamma }}{\partial \,\Gamma _{a}} =0 \\&\Rightarrow \quad -\frac{\partial \,\varphi ^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m},\varvec{\Gamma } \right) }{\partial \,\bar{\varvec{\varepsilon }}}: \frac{\partial \,\varvec{\Gamma }}{\partial \,\Gamma _{a}} =0 \\&\Rightarrow \quad -\varvec{\sigma }^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{v}^{1},\ldots ,\varvec{\varepsilon }_{v}^{m},\varvec{\Gamma } \right) :{\varvec{P}}^{a} = 0. \end{aligned} \end{aligned}$$
(23)

As a result, the minimization problem turns to the free surface condition \(\varvec{\sigma }^{tot}_{c}:{\varvec{P}}^{a}=0\). Hence, the stress does not contribute to any work regarding the strain resulted in by opening a crack. According to the form in Eq. (18), Eq. (23) is rewritten as

$$\begin{aligned} \Big ( \alpha \,\varvec{\sigma }^{eq}_{c,t^{n+1}}\left( \bar{\varvec{\varepsilon }},\varvec{\Gamma } \right) + {\varvec{h}}_{c,t^{n}} \left( \varvec{\sigma }^{eq}_{c,t^{n}},\varvec{\sigma }^{ne}_{c,t^{n}} \right) \Big ):{\varvec{P}}^{a} = 0,\nonumber \\ \end{aligned}$$
(24)

which leads to the closed form solution for the unknown crack deformations \(\Gamma _{i}\) as

$$\begin{aligned} \begin{aligned} \Gamma _{1}&= \frac{\lambda }{ \lambda + 2\mu }\,\text {tr} \left( \bar{\varvec{\varepsilon }}_{t^{n+1}} \right) + \frac{2\,\mu }{ \lambda + 2\mu }\,\bar{\varvec{\varepsilon }}_{t^{n+1}}:{\varvec{P}}^{1}\\&\quad + \frac{{\varvec{h}}_{c,t^{n}}:{\varvec{P}}^{1}}{\alpha \, \left( \lambda + 2\mu \right) } , \\ \Gamma _{2}&= 2\,\bar{\varvec{\varepsilon }}_{t^{n+1}}:{\varvec{P}}^{2} + \frac{ {\varvec{h}}_{c,t^{n}}:{\varvec{P}}^{2}}{\alpha \, \mu }, \\ \Gamma _{3}&= 2\,\bar{\varvec{\varepsilon }}_{t^{n+1}}:{\varvec{P}}^{3} + \frac{ {\varvec{h}}_{c,t^{n}}:{\varvec{P}}^{3}}{\alpha \, \mu }. \\ \end{aligned} \end{aligned}$$
(25)

A similar solution structure can be found in Storm et al. (2020) for isotropic linear elasticity, nevertheless, the history terms are not involved compared to Eq. (25) due to the viscoelastic constitutive law. Furthermore, as the result of the bilinear algorithmic definition of RCE in Eqs. (19) and (21), the cracked stress and tangent for a crack closure (\(\Gamma _i\le 0\)) read

$$\begin{aligned} \varvec{\sigma }^{tot}_{c,t^{n+1}}= & {} \alpha \, \Bigg ( \lambda \,\text {tr}\Big (\bar{\varvec{\varepsilon }}_{t^{n+1}}-\Gamma ^{2}\,{\varvec{P}}^{2} - \Gamma ^{3}\,{\varvec{P}}^{3} \Big ){\varvec{1}} \nonumber \\&\quad + \,2\,\mu \Big (\bar{\varvec{\varepsilon }}_{t^{n+1}}-\Gamma ^{2}\,{\varvec{P}}^{2} - \Gamma ^{3}\,{\varvec{P}}^{3} \Big ) \Bigg )\nonumber \\&\quad + \,{\varvec{h}}_{c,t^{n}}\left( \varvec{\sigma }^{eq}_{c,t^{n}},\varvec{\sigma }^{ne}_{c,t^{n}} \right) \end{aligned}$$
(26)

and

$$\begin{aligned} {\mathbb {C}}^{tot}_{c,t^{n+1}}= & {} \alpha \, \Bigg ( \lambda \, {\varvec{1}} \otimes {\varvec{1}}\nonumber \\&+ 2\,\mu \,\left( {\mathbb {I}} - 2\,{\varvec{P}}^{2} \otimes {\varvec{P}}^{2} \right. \left. \quad - 2\,{\varvec{P}}^{3} \otimes {\varvec{P}}^{3} \right) \Bigg ),\nonumber \\ \end{aligned}$$
(27)

respectively. Alternatively, in the case of crack separation (\(\Gamma _i>0\)), the cracked stress and tangent yield

$$\begin{aligned} \begin{aligned}&\varvec{\sigma }^{tot}_{c,t^{n+1}}\\&\quad =\, \alpha \, \Bigg ( \lambda \,\text {tr}\Big (\bar{\varvec{\varepsilon }}_{t^{n+1}}-\Gamma ^{1}\,{\varvec{P}}^{1}-\Gamma ^{2}\,{\varvec{P}}^{2} - \Gamma ^{3}\,{\varvec{P}}^{3} \Big ){\varvec{1}}\\&\qquad +\,2\,\mu \Big ( \bar{\varvec{\varepsilon }}_{t^{n+1}}-\Gamma ^{1}\,{\varvec{P}}^{1}-\Gamma ^{2}\,{\varvec{P}}^{2} - \Gamma ^{3}\,{\varvec{P}}^{3} \Big ) \Bigg )\\&\qquad +\,{\varvec{h}}_{c,t^{n}}\left( \varvec{\sigma }^{eq}_{c,t^{n}},\varvec{\sigma }^{ne}_{c,t^{n}} \right) \end{aligned} \end{aligned}$$
(28)

and

$$\begin{aligned} \begin{aligned}&{\mathbb {C}}^{tot}_{c,t^{n+1}}\\&\quad =\, \alpha \, \Bigg (\frac{2\,\lambda \,\mu }{\lambda +2\mu } \bigg ( {\varvec{1}} \otimes {\varvec{1}} - {\varvec{1}} \otimes {\varvec{P}}^{1} - {\varvec{P}}^{1} \otimes {\varvec{1}} \bigg )\\&\qquad +\,2\,\mu \,\left( {\mathbb {I}} - \frac{2\mu }{\lambda +2\mu }{\varvec{P}}^{1} \otimes {\varvec{P}}^{1}\right. \\&\qquad \left. - 2\,{\varvec{P}}^{2} \otimes {\varvec{P}}^{2} - \,2\,{\varvec{P}}^{3} \otimes {\varvec{P}}^{3} \right) \Bigg ), \end{aligned} \end{aligned}$$
(29)

respectively. Meanwhile, the total intact stress \(\varvec{\sigma }^{tot}_{0,t^{n+1}}\) and tangent \({\mathbb {C}}^{tot}_{0,t^{n+1}} \) are simply following the formulation of Eqs. (7) and (8). Thus, the total effective stress \(\varvec{\sigma }^{mech}_{t^{n+1}}\) and tangent \({\mathbb {C}}^{mech}_{t^{n+1}}\) in the RCE framework are consequently obtained according to Eqs. (16) and (17), respectively. Meanwhile, observing the consequent tangent modulus, a constant quantity is obtained regardless the crack projection tensor \({\varvec{P}}^i\) and yields a linear problem, which appropriately capture the linearity of the proposed viscoelastic model.

3.3 Dissipation

The second law of thermodynamics, namely the Clausius-Plank inequality, describes the entropy of a closed system either constant or growing, see Holzapfel (1996). Restricted by an isothermal process, the dissipation rate of the viscoelastic material is defined by

$$\begin{aligned}&{\mathscr {D}}^{vis}\nonumber \\&\quad =\,\varvec{\sigma }^{mech}:\dot{\bar{\varvec{\varepsilon }}}-{\dot{\varphi }}^{mech}\ge 0,\,\,\,\,\,\forall \,\,\, t\in \left[ 0,t^{n+1} \right] ,\quad \end{aligned}$$
(30)

where \({\dot{\varphi }}^{mech}\) denotes the internal energy rate and can be written as

$$\begin{aligned} \begin{aligned}&{\dot{\varphi }}^{mech}\\&\quad = \partial _{\bar{\varvec{\varepsilon }}}\,\varphi ^{mech}:\dot{\bar{\varvec{\varepsilon }}} + \sum _{I=1}^{m} \partial _{\varvec{\varepsilon }_{0,v}^{I}}\,\varphi ^{mech}:\dot{\varvec{\varepsilon }}_{0,v}^{I}\\&\qquad +\,\sum _{I=1}^{m} \partial _{\varvec{\varepsilon }_{c,v}^{I}}\,\varphi ^{mech}:\dot{\varvec{\varepsilon }}_{c,v}^{I}+\partial _{\varvec{\Gamma }}\,\varphi ^{mech}:\dot{\varvec{\Gamma }}\\&\quad = \varvec{\sigma }^{mech}:\dot{\bar{\varvec{\varepsilon }}}\\&\qquad + \,\sum _{I=1}^{m} \partial _{\varvec{\varepsilon }_{0,v}^{I}}\,\varphi ^{mech}:\dot{\varvec{\varepsilon }}_{0,v}^{I}+\sum _{I=1}^{m} \partial _{\varvec{\varepsilon }_{c,v}^{I}}\,\varphi ^{mech}:\dot{\varvec{\varepsilon }}_{c,v}^{I}\\&\qquad +\, \underbrace{\frac{\partial \,\varphi ^{mech}}{\partial \, \Gamma _{i}}\cdot \frac{\partial \,\Gamma _{i}}{\partial \,\varvec{\Gamma }} :\dot{\varvec{\Gamma }}}_{={\varvec{0}}, \text {see Eq.} (19)}, \end{aligned} \end{aligned}$$
(31)

Applying Eqs. (3) and (4) and (31) to Eq. (30), the dissipation rate \({\mathscr {D}}^{vis}\) due to the viscous effect is obtained as

$$\begin{aligned} \begin{aligned} {\mathscr {D}}^{vis}&= - \sum _{I=1}^{m} \frac{\partial \,\varphi ^{mech}}{\partial \,\varvec{\varepsilon }_{0,v}^{I}}:\dot{\varvec{\varepsilon }}_{0,v}^{I} - \sum _{I=1}^{m} \frac{\partial \,\varphi ^{mech}}{\partial \,\varvec{\varepsilon }_{c,v}^{I}}:\dot{\varvec{\varepsilon }}_{c,v}^{I} \\&= - \sum _{I=1}^{m} g\left( d \right) \frac{\partial \,\varphi ^{tot}_0}{\partial \,\varvec{\varepsilon }_{0,v}^{I}}:\dot{\varvec{\varepsilon }}_{0,v}^{I}\\&\quad - \sum _{I=1}^{m} \big (1- g\left( d \right) \big ) \frac{\partial \,\varphi ^{tot}_c}{\partial \,\varvec{\varepsilon }_{c,v}^{I}}:\dot{\varvec{\varepsilon }}_{c,v}^{I} \\&= \quad \sum _{I=1}^{m} g\left( d\right) \varvec{\sigma }^{ne,I}_{0}:\dot{\varvec{\varepsilon }}_{0,v}^{I}\\&\quad + \sum _{I=1}^{m} \left( 1-g\left( d\right) \right) \varvec{\sigma }^{ne,I}_{c}:\dot{\varvec{\varepsilon }}_{c,v}^{I}. \end{aligned} \end{aligned}$$
(32)

Thus, the computation of the accumulated total dissipation is approximated by

$$\begin{aligned} \begin{aligned} {\mathscr {W}}^{vis}_{t^{n+1}}&=\int _{0}^{t^{n+1}}{\mathscr {D}}^{vis}\,dt\, \\&= \underbrace{ \int _{0}^{t^{n}}{\mathscr {D}}^{vis}\,dt}\, + \underbrace{ \int _{t^{n}}^{t^{n+1}}{\mathscr {D}}^{vis}\,dt}\\&\approx \,{\mathscr {W}}^{vis}_{t^{n}} \quad + \quad {\mathscr {D}}^{vis}_{t^{n+1}}\cdot \Delta t \\&\approx \,{\mathscr {W}}^{vis}_{t^{n}} \quad \\&\quad +\,\sum _{I=1}^{m} \left( g\left( d\right) \varvec{\sigma }^{ne,I}_{0,t^{n+1}}: \Delta \, \varvec{\varepsilon }_{0,v}^{I}\right. \\&\left. \quad +\, \left( 1-g\left( d\right) \right) \varvec{\sigma }^{ne,I}_{c,t^{n+1}}: \Delta \,\varvec{\varepsilon }_{c,v}^{I} \right) , \end{aligned} \end{aligned}$$
(33)

where \({\mathscr {W}}^{vis}_{t^{n+1}}\) and \({\mathscr {W}}^{vis}_{t^{n}}\) are the amount of total internal dissipation at the current step \(t^{n+1}\) and at the previous step \(t^{n}\), respectively.

3.4 Governing equations of multi-field problem

In this section, a variational phase-field model for rate-dependent fracture in a viscoelastic continuum is developed. The governing equations of the multi-field problem are derived straightforward according to the balance of energy equilibrium, which reads

$$\begin{aligned} \frac{D{\mathcal {K}}}{Dt}+{\mathscr {P}}_{int}={\mathscr {P}}_{ext}. \end{aligned}$$
(34)

The kinetic energy and the external power quantities are defined as

$$\begin{aligned}&{\mathcal {K}} = \int _{\varOmega }\frac{1}{2}\,\rho \,\dot{{\varvec{u}}}\cdot \dot{{\varvec{u}}}\,dV \quad \text {and} \quad \nonumber \\&{\mathscr {P}}_{ext}= \int _{\varOmega } {\mathfrak {b}}\cdot \dot{{\varvec{u}}}\,d V + \int _{\partial \varOmega } {\mathfrak {t}}\cdot \dot{{\varvec{u}}}\,d A, \end{aligned}$$
(35)

respectively. The material density, velocity, body force and surface traction quantities are expressed by \(\rho \), \(\dot{{\varvec{u}}}\), \({\mathfrak {b}}\) and \({\mathfrak {t}}\), respectively. The internal power \({\mathscr {P}}_{int}\) in Eq. (34) is

$$\begin{aligned} \begin{aligned}&{\mathscr {P}}_{int}\\&\quad = \,\int _{\varOmega } \bigg \{\partial _{\varvec{{\bar{\varepsilon }}}}\,\varphi ^{mech} : \dot{\bar{\varvec{\varepsilon }}} + \Big ( \partial _{d}\,\varphi ^{mech} + {\mathcal {G}}_{c}\,\partial _{d}\,\gamma _{l} \Big ) {\dot{d}} \\&\qquad \qquad \quad +\, {\mathcal {G}}_{c}\,\partial _{\nabla _{{\varvec{x}}} d}\,\gamma _{l}\cdot \nabla _{{\varvec{x}}}{\dot{d}} \bigg \}dV \\&\quad = \,\int _{\varOmega } \bigg \{\varvec{\sigma }^{mech} : \dot{\bar{\varvec{\varepsilon }}} + \Big ( \partial _{d}\,\varphi ^{mech} + {\mathcal {G}}_{c}\,\partial _{d}\,\gamma _{l} \Big ) {\dot{d}} \\&\qquad +\,{\mathcal {G}}_{c}\,\partial _{\nabla _{{\varvec{x}}} d}\,\gamma _{l} \cdot \nabla _{{\varvec{x}}}{\dot{d}} \bigg \} dV \\&\quad =\,\int _{\varOmega } \bigg \{-\nabla _ {{\varvec{x}}}\cdot \varvec{\sigma }^{mech} \cdot \dot{{\varvec{u}}} \\&\qquad + \,\left( \partial _{d}\,\varphi ^{mech} + \frac{{\mathcal {G}}_{c}}{l} d - {\mathcal {G}}_{c}\,l\,\nabla _{{\varvec{x}}}\cdot d \right) {\dot{d}} \bigg \} dV + \\&\qquad \int _{\partial \varOmega } \bigg \{ \varvec{\sigma }^{mech}\cdot {\mathfrak {n}} \cdot \dot{{\varvec{u}}} + {\mathcal {G}}_{c}\,l\Big ( \nabla _{{\varvec{x}}}\,d \cdot {\mathfrak {n}} \Big ){\dot{d}}\bigg \}dA. \end{aligned} \end{aligned}$$
(36)

The divergence operator is denoted by \(\nabla _{{\varvec{x}}}\cdot \left( * \right) \). The governing equations for this multi-field problem are obtained by inserting Eqs. (35) and (36) into Eq. (34), yielding

$$\begin{aligned}&\rho \,\ddot{{\varvec{u}}}-\nabla _{{\varvec{x}}}\cdot \varvec{\sigma }^{mech}-{\mathfrak {b}}={\mathbf {0}} \quad \text {in} \quad \varOmega \qquad \text {and}\nonumber \\&\varvec{\sigma }^{mech} \cdot {\mathfrak {n}} = {\mathfrak {t}} \quad \text {at} \quad \partial \,\varOmega \end{aligned}$$
(37)

and

$$\begin{aligned}&\partial _{d}\,g\left( d\right) \,\left( \varphi ^{tot}_{0} - \varphi ^{tot}_{c} \right) + \frac{{\mathcal {G}}_{c}}{l} \Big ( d - l^2\, \nabla _{{\varvec{x}}}\cdot d \Big )=0\quad \nonumber \\&\quad \text {in} \qquad \varOmega \qquad \text {and} \qquad \nabla _{{\varvec{x}}}d \cdot {\mathfrak {n}}=0 \quad \text {at} \quad \partial \,\varOmega , \end{aligned}$$
(38)

for the mechanical response and the phase-field evolution, respectively. In order to avoid healing during phase-field evolution, several options to define the driving force are available. Following the proposal of \(\textsc {Miehe}\) et al. (Miehe et al. 2010), \( \left( \varphi ^{tot}_{0} - \varphi ^{tot}_{c} \right) \) in Eq. (38) is replaced by an internal variable

$$\begin{aligned} {\mathcal {H}}= & {} \underset{0 \le t\le t_{n+1}}{\text {Max}}\,\,\left( \varphi ^{tot}_{0}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{0,v}^{1},\ldots ,\varvec{\varepsilon }_{0,v}^{m} \right) \right. \nonumber \\&\left. \qquad \qquad \qquad -\,\varphi ^{tot}_{c}\left( \bar{\varvec{\varepsilon }},\varvec{\varepsilon }_{c,v}^{1},\ldots ,\varvec{\varepsilon }_{c,v}^{m},\varvec{\Gamma } \right) \right) , \end{aligned}$$
(39)

where a monotonically increasing phase-field is numerically achieved. Furthermore, outlined by Kuhn et al. in Kuhn and Müller (2010), Dirichlet conditions are imposed to the phase-field variables as soon as the material is assumed to be cracked, i.e. \(d\ge 0.9999\). The driving force does not depend on the history variable and is calculated promptly at current step. In this contribution, \(\textsc {Miehe}\)’s approach is employed for the viscoelastic RCE modeling at small strain and Eq. (38) is rewritten as

$$\begin{aligned} \partial _{d}\,g\left( d\right) \,{\mathcal {H}} + \frac{{\mathcal {G}}_{c}}{l} \Big ( d - l^2\, \nabla _{{\varvec{x}}} \cdot d \Big )=0. \end{aligned}$$
(40)

Subsequently, the algorithmic derivation is numerically implemented into a standard finite element method, which is not presented in this context.

Remark: It is noteworthy that the resultant phase-field modeling yields a rate-dependent fracture evolution. The governing mechanism is the phase-field driving energy consisting of the elastic strain energy for both the equilibrium and non-equilibrium responses. The fracture toughness \({\mathcal {G}}_c\) in the work at hand is not characterized as rate-independent. As a result, the overall fracture response is rate-dependent since the elastic strain energy for the non-equilibrium branch is depending upon the loading rate. Nevertheless, a recent publication (Yin et al. 2020) has addressed the strain rate-dependent fracture toughness for linear elastic solids. Coupling of these two different rate-dependent mechanisms in the RCE framework will be a subsequent priority for the future perspective.

Fig. 5
figure 5

Geometric setup for contact surface and phase-field crack

Full size image
Fig. 6
figure 6

Displacement loading function a tension, compression and shear deformation for linear elasticity and b only compression and relaxation for linear viscoelasticity

Full size image
Fig. 7
figure 7

Crack deformation at \(t=1\,\text {s}\), \(t=3\,\text {s}\) and \(t=5\,\text {s}\) regarding the loading function in Fig. 6a for spectral split, V–D split and RCE approach

Full size image
Fig. 8
figure 8

Reaction forces of \(f_x\) and \(f_y\) with respect to the loading time

Full size image
Fig. 9
figure 9

Deformed shape at \(t=1\,\text {s}\) regarding compressive load by a the RCE and b V–D split approaches

Full size image
Fig. 10
figure 10

Comparison of the distribution of the vertical stress \(\sigma _{y}\) for contact modeling, RCE simulation and V–D split simulation at \(t=1\) s (a–c) and \(t=6\) s (d–f), respectively

Full size image
Fig. 11
figure 11

Investigation of energy components: elastic strain energy \(\varphi ^{mech}\), viscous dissipation energy \({\mathcal {W}}^{vis}\) and their summation \({\hat{\varphi }}=\varphi ^{mech}+{\mathcal {W}}^{vis}\) for a contact modeling, b RCE simulation and c V–D split simulation. Reaction force f for the three approaches compared as well in d

Full size image

4 Representative examples

4.1 Self-consistent compression test

Phenomenologically, an open-crack leads to a stress-free boundary and the surface tractions between two crack surfaces naturally vanish. Nevertheless, a closed and friction-free crack at a compressive state is supposed to fully transfer the normal compressive stress, which is characterized as an equivalent contact mechanism. Furthermore, a pure shearing deformation along the friction-free crack surface should not transfer any force neither. The aforementioned characteristics have been studied in Steinke and Kaliske (2019), Strobl and Seelig (2016), Storm et al. (2020) to evaluate the correct crack kinematics for realistic applications, nonetheless, their material constitutive laws are restricted within a linear elastic property. The first numerical example follows the examinations of crack kinematics in Steinke and Kaliske (2019), Strobl and Seelig (2016), Storm et al. (2020) to demonstrate the advantages of the presented RCE phase-field modeling compared to classical spectral split and V–D split approaches with respect to tension, compression and shearing deformation.

Both, linear elasticity and viscoelasticity, are taken into consideration for the comparisons. Nevertheless, it is necessary to point out that the spectral split according to Miehe et al. (2010) is not included for linear viscoelasticity due to difficulties in application . The coupled constitutive equations of the spectral split in Miehe et al. (2010) are straightforwardly and consistently derived out of a predefined strain energy density functional involving the spectral decomposition of the strain tensor. However, the present linear viscoelastic model is governed by internal stress-type quantities, which cannot be obtained by a straightforward variational algorithm of strain based energy density function. Furthermore, the elastic energy for the non-equilibrium branches is obtained based on the non-equilibrium stress and the conjugate elastic tensor due to the constitutive linearity characteristics, see Sect. 2.1. Therefore, the spectral split of the internal stress governed viscoelastic model has shown significant complexities. As a result, several existing phase-field models regarding fracture of viscoelastic material, see Shen et al. (2019), Schänzel (2015), Loew et al. (2019), Yin and Kaliske (2020c), are developed depending on the framework of the V–D split. Instead of the spectral split, a classical contact model is additionally considered for a representative reference for the crack kinematics demonstration in viscoelastic materials.

The two-dimensional boundary value problem is depicted in Fig. 5, which consists of a contact model and a phase-field model with same dimensions. The contact model consists of two blocks and a contact pair and the phase-field model describes the straight crack by prescribing the phase-field value \(d=1\) at the nodes attached to the middle row of element. Both models are discretized by 2500 four-node elements uniformly with the element size \(h_e=2\,\text {mm}\). The upper and lower edges are fully bounded and a displacement load is subjected to the upper edge with a loading function given in Fig. 6a for tension, compression and shear deformation in a linear elastic body. The simulations consist of the spectral split, V–D split as well as the RCE phase-field modeling. Furthermore, another loading function in Fig. 6b describes a pure compression and a subsequent relaxation for the viscoelastic solid. The spectral split simulation is replaced by a classical contact modeling. In a detailed description, the viscoelastic response of the material is supposed to relax from \(t=1\,\text {s}\) to \(t=6\,\text {s}\) at a compressive state and from \(t=7\,\text {s}\) to \(t=10\,\text {s}\) at a non-external load state. The material parameters are given as \(\lambda =19.6\,\text {MPa}\), \(\mu =2.06\,\text {MPa}\) for linear elasticity. Regarding viscoelasticity, only one Prony series is considered and the parameters are given as \(\tau =0.98\,\text {s}\) and \(\chi =0.6\). Since this numerical study concentrates on the correct and robust crack kinematics, the crack evolution is out of consideration. Hence, the fracture toughness is assumed to be sufficiently large to prevent the phase-field evolution, i.e. \({\mathcal {G}}_{c}=5\,e^{20}\,\text {J}/\text {mm}^2\). The length-scale parameter is given as \(l=4\,\text {mm}\). All simulations are performed using a quasi-static analysis.

First of all, the linear elastic simulations subjected to the loading in Fig. 6a are shown in Fig. 7. Apparently, all three simulations, the spectral split, the V–D split and the RCE approach, have obtained realistic crack opening deformations, i.e. non residual material deformations exist in the upper and lower blocks at the maximum separation \(t=1\) s. In the sequel, the material is compressed and both the spectral and the V–D split simulations are not capable to capture the realistic crack closing deformations at \(t=3\) s. A slight unphysical lateral expansion by the spectral split is investigated. Unfortunately, this lateral expansion is significantly increased by the V–D split result. Nevertheless, this unphysical behavior is not shown at all for the proposed RCE modeling. As a further evaluation, the reaction forces \(f_y\) are measured as well in Fig. 8a, where the difference of the minimum loads for three methods is the result of the unphysical lateral expansion at the crack region. When the vertical loading returns to the initial 0 state, the subsequent horizontal load leads to a pure shear deformation. This procedural principally should not yield any reaction forces along both x- and y-directions considering a friction-free crack surface. Meanwhile, non residual deformations of the upper and lower blocks should be observed. From this point of view, the spectral split result fails to capture a realistic shear deformation at the crack, see Figs. 7a and 8c.

Then, the material compressive relaxation in viscoelastic solids is evaluated by using a classical contact model, the V–D split and the RCE approach. In this case, a compressive vertical displacement is applied to the structure and horizontal displacement is not considered any more, see Fig. 6b. As aforementioned, the V–D split model is not capable to capture an appropriate compressive deformation in a viscoelastic body neither due to an unrealistic lateral stretch. Nevertheless, the RCE simulation properly addresses this issue and shows similar behaviors compared to the contact model, see Figs. 9 and 10. Meanwhile, the contour distributions of the vertical stress \(\sigma _y\) for three approaches are compared at \(t=1\,\text {s}\) and \(t=6\,\text {s}\) in Fig. 10, where the RCE modeling successfully predicts the results that the contact model shows.

Furthermore, the effective strain energy \(\varphi ^{mech}\), the viscous dissipation \({\mathcal {W}}^{vis}\) as well as their summation \({\hat{\varphi }}=\varphi ^{mech}+{\mathcal {W}}^{vis}\) for three models are observed. The V–D split model uses the standard form of \(\varphi ^{mech} = \varphi ^{-} +g\left( d\right) \, \varphi ^{+} \), where the detailed algorithmic setup is referred to the Schänzel (2015), Yin and Kaliske (2020c). In the sequel, by a post-processing technique of volume integration of these two quantities, the total elastic strain energy and dissipation energy are obtained. Then, the quantity \({\hat{\varphi }}=\varphi ^{mech}+{\mathcal {W}}^{vis}\) is also evaluated, since it straightforward indicates the external work induced into the closed system. Observing the energy components evolution in Figs. 11a–c, \(\varphi ^{mech}\) and \({\mathcal {W}}^{vis}\) increase initially along with the external load application. Subsequently, the constant load leads to a slight decrease of \(\varphi ^{mech}\) and a gradual increase of \({\mathcal {W}}^{vis}\) up to the situation that the specimen is fully relaxed. The summation \({\hat{\varphi }}\) stays almost constant during the relaxation. It is explained that the external work does not change as long as the external load is kept constant. After the displacement returns to \(u=0\) mm and the material is fully relaxed, e.g. \(t=10\) s, \(\varphi ^{mech}\) returns to 0 kJ and the total external work is fully dissipated due to viscous effects. Comparing these three approaches, the RCE approach sufficiently agrees to the results of the contact modeling. However, the V–D split always underestimates the results, also see the reaction forces shown in Fig. 11 (d). Based on the aforementioned comments, the RCE approach is demonstrated to capture realistic crack kinematics for a closing crack within linear elastic and viscoelastic materials.

Fig. 12
figure 12

a Geometry and compressive stress wave setup for the longitudinal bar test and b proportional loading function

Full size image
Fig. 13
figure 13

Visualization of the stress wave propagation of a non-fracture simulation by a three-dimensional setup. Magnitude of \(\sigma _x\) represented by the wave-shaped profiles towards out-plane direction

Full size image
Fig. 14
figure 14

Evolution of energy components during the wave propagation

Full size image
Fig. 15
figure 15

Phase-field evolution d and axial stress \(\sigma _x\) distribution for different relaxation times \(\tau \)

Full size image

4.2 Spallation of a viscoelastic bar

Motivated by Yin et al. (2020), Steinke et al. (2017), the second example studies the transient analysis of the spallation of a viscoelastic bar. The main purpose of this simulation is to demonstrate the capabilities of the RCE approach for transient analysis by incorparating the stress wave propagation phenomena in a viscoelastic solid. Simplified from classical Split-Hopkinson pressure bar test, an academic model is postulated in Steinke et al. (2017) to investigate the bar spallation at a tensile stress wave in an elastic solid. In the sequel, Yin et al. (2020) studies the example by strain rate-dependent fracture toughness. In particular, a portion of energy dissipation is introduced during the fracture evolution, nevertheless, the material is still characterized as linear elastic. These two works are developed based on a spectral split phase-field model, since the V–D split yields unphysical results in the pressure bar test. As aforementioned, the complexity of viscoelastic material for the spectral decomposition, this example is postulated to examine the RCE framework for viscoelastic phase-field fracture analyzed dynamically.

The geometric setup of the two-dimensional boundary value problem, which is assumed to be a plane strain problem, is depicted in Fig. 12a. All the boundaries are constraint-free, and a half-sinusoidal compressive stress wave is subjected to the specimen from the left end. The surface load is defined by \(\sigma (t)={\hat{\sigma }} \cdot f(t)\), where the magnitude is given as \({\hat{\sigma }}=1\,\text {MPa}\). f(t) is a half-sinusoidal function defined as

$$\begin{aligned} f(t)={\left\{ \begin{array}{ll} \text {sin}\left( \dfrac{\pi \cdot t}{32\,\,\mu \text {s}} \right) , &{} \text {if}\,\,\,0 \le t\le 32~\mu \text {s} \\ 0, &{} \text {if} \,\,\, 32~\mu \text {s}< t \end{array}\right. } \end{aligned}$$
(41)

and is visualized in Fig. 12b. Therefore, the external work is introduced only during the initial period \(0 \le t \le 32\, \mu \text {s}\) and the sum of internal energy (including kinetic energy, elastic strain energy and viscous dissipation) of the whole system is expected to be constant for \(t>32\,\mu \text {s}\). The FE model is discretized by 6400 four-node quadratic elements with the size \( h_e=0.25\,\text {mm}\) along the longitudinal direction. Only one branch of \(\textsc {Prony}\) series is considered and the model parameters are \(\lambda =4.5\,\text {GPa}\), \(\mu =6.7\,\text {GPa}\), \(\chi =0.96\) and \(\rho = 2300\,\text {kg}/\text {m}^3\). A set of trial relaxation times \(\tau =[1e^{4}, 1e^{3}, 1e^{2}]\,\mu \text {s}\) is chosen to examine viscoelastic responses by impact loading. Moreover, the length scale is \(l=0.5\,\text {mm}\) and the fracture toughness is \({\mathcal {G}}_{c}=7.2e^2\,\text {J}/\text {m}^2\). The transient analysis is carried out by classical \(\textsc {Newmark}\) time integration scheme with constants \(\beta =0.25\) and \(\gamma =0.5\), which leads to solutions without numerical dissipation and unconditionally stable. According to Steinke et al. (2016), the time step \(\Delta t=0.005\,\mu \text {s}\) is sufficiently small to obtain an effective wave propagation. One of the major scopes of this example is the investigation of the global energy balance, which consists of effective elastic strain energy \(\varphi ^{mech}\), kinetic energy \({\mathcal {K}}\), fracture energy \({\mathcal {W}}^{frac}={\mathcal {G}}_{c}\int _\varOmega \gamma _{l}\,dV\) and viscous dissipation energy \({\mathcal {W}}^{vis}\). The summation is defined as \({\mathcal {E}}=\varphi ^{mech}+{\mathcal {K}}+{\mathcal {W}}^{frac}+{\mathcal {W}}^{vis}\), which reflects to the external work.

The first simulation does not involve phase-field evolution, and only examines the stress wave propagation in a viscoelastic solid with \(\tau =1e^{3}\,\mu \text {s}\). The phase-field fracture evolution can be numerically avoided by setting a sufficiently large value of the fracture toughness, e.g. \({\mathcal {G}}_{c}=10^{20}\,\text {J}/\text {m}^2\). Therefore, \({\mathcal {W}}^{frac}\) remains nearly zero due to the lack of fracture evolution. The compressive stress wave propagates to from the left edge of the specimen and reaches the rear end, where a tensile stress wave is reflected. The quantities \({\mathcal {K}}\) and \(\varphi ^{mech}\) are converting to compensate each other, meanwhile, a portion of energy is dissipated due to viscous effects. However, the total energy \({\mathcal {E}}\) keeps constant after the external stress wave completely induced, see Fig. 14 (a). The visualization of this stress wave propagation is shown in Fig. 13 at different time steps. The magnitude of axial stress components \(\sigma _x\) is represented by the wave-shape profile outwards of the plane direction, which provides a clear and apprehensible visualization of the stress wave propagation and reflection.

The next simulations include the fracture evolution by reducing the fracture toughness to \({\mathcal {G}}_{c}=7.2e^2\,\text {J}/\text {m}^2\), where the first reflected tensile stress wave has potential to generate crack surfaces as long as the phase-field driving force is sufficiently large. A set of relaxation times is evaluated, where the viscous effect increases along with the decrease of relaxation time. Applying a comparatively large relaxation time (\(\tau =1e^{4}\,\mu \text {s}\)), less viscous dissipation leads to the first reflected tensile stress wave strong enough to generate a fully evolved phase-field crack, which naturally results in an increase of the fracture energy \({\mathcal {W}}^{frac}\), see Fig. 14b. After the fully evolved phase-field crack, the bar is broken into two separated components by the crack surface. Within each of these segments, stress waves propagate and are reflected as well. The simulation with \(\tau =1e^{3}\,\mu \text {s}\) dissipates more energy due to viscose effect, nevertheless, it still obtains a similar crack profile compared to the result for \(\tau =1e^{4}\,\mu \text {s}\), see Figs. 14c and 15b. Further reducing the relaxation time to \(\tau =1e^{2}\,\mu \text {s}\) yields a high viscous dissipation rate, which largely decreases the tensile stress wave magnitude after the first reflection. Therefore, the remaining elastic energy \(\varphi ^{mech}\) is not sufficient enough to yield a complete fracture with \(d=1\). As a result, the crack only starts to evolve until the phase-field value \(d\approx 0.21\), see Fig. 15, which does not have the physical explanation. Thus, no crack has finally initiated and the phase-field should return to zero when the tensile wave has faded away. However, the aforementioned irreversibility algorithm from Miehe et al. (2010) does not allow the phase-field healing.

It is noteworthy that, due to lack of crack singularity in this example, the fracture initiation is governed by material strength instead of fracture toughness. According to the work of Tanné et al. (2018), the material strength is also represented by the phase-field model, but here, the length scale parameter needs to be considered as a material parameter and cannot chosen freely.

Fig. 16
figure 16

Geometry setup for classical Mode I test

Full size image
Fig. 17
figure 17

Visualisation of the stress wave propagation of a non-fracture simulation by a three-dimensional setup. The magnitude of \(\sigma _x\) represented by the wave-shaped profiles towards out-plane direction

Full size image
Fig. 18
figure 18

Reaction force for a different loading rates for \(\tau =0.1\) h and b different relaxation times for \({\dot{u}}=5\) mm/h

Full size image
Fig. 19
figure 19

Convergence study for \(\tau =0.1\) h and \({\dot{u}}=5\) mm/h, a before crack initiation (\(d\approx 0.2\)) and b during the crack propagation (\(d = 1\)), the first 20 steps and the consequently converged status

Full size image

4.3 Rate-dependent failure of Mode I test

This example studies rate-dependent fracture evolution by examining a classical Mode I benchmark, where the geometric setup of the two-dimensional boundary value problem is depicted in Fig. 16. The left and right boundaries are constraint and a monotonically increasing displacement is subjected horizontally at the right edge. The FE model is uniformly discretized by 62625 four-node quadratic elements and the element size is \(h=2\,\text {mm}\). The model parameters are \(\lambda =1.12\,\text {GPa}\), \(\mu =0.48\,\text {GPa}\), \(\chi =1.2\), \({\mathcal {G}}_{c}=500\,\text {J}/\text {m}^2\) and \(l=4\,\text {mm}\). A set of relaxation times \(\tau =[0.05, 0.1, 0.2]\,\text {h}\) and a set of loading rates \({\dot{u}}=[2.5, 5, 50]\) mm/h are applied to evaluate the rate-dependency of phase-field fracture. This example considers a quasi-static analysis, which is numerically solved based on a staggered solution scheme.

The general phase-field evolution at different loading steps is shown in Fig. 17a, that crack initiates at the notch tip and propagates straight towards the bottom. Particularly, the crack orientation \({\varvec{n}}_1\) along the evolved crack path and around the phase-field crack tip is shown in Fig. 17b. To obtain an effective crack orientation, a simple definition of \({\varvec{n}}_i\) is based on the principal direction of the stress at the previous step, since this assumption can avoid the derivative term \(\partial _{\bar{\varvec{\varepsilon }}}\,{\varvec{n}}_i\) to largely reduce the complexity of the RCE constitutive law. Apparently, the normal direction of the crack \({\varvec{n}}_1\) in Fig. 17b always shows approximately perpendicular to the evolved as well as potentially evolving phase-field crack. The reaction forces are measured at different loading rates for the same relaxation time and for different relaxation times at the same loading rate in Figs. 18a and b, respectively. An important observation is that the peak load increases and the ultimate displacement decreases along with increasing the loading rates, see Fig. 18a. Meanwhile, Fig. 18b indicates that a smaller relaxation time \(\tau \) leads to a decreasing peak force but an increasing ultimate displacement. This finding completely agrees to the observation of viscoelastic polymer rupture in Loew et al. (2019), Yin and Kaliske (2020c).

Furthermore, the numerical convergence for the staggered solution scheme is evaluated as well. The convergence criteria of the multi-field problem for the staggered solution are generally based on the converged solution of the decoupled equilibriums. In particular, two evolution equations at current step are solved by classical Newton-Raphson algorithm in an iterative manner up to their residual norms are lower than the tolerance. For simplification, the same tolerance is used for both solutions of the RCE and the phase-field evolution. The numerical tolerance \(10^{-8}\) with respect to a reference residual norm is considered for both the RCE and the phase-field solution simultaneously. In this example, taking advantages of High Performance Computation, the simulation is solved by an iterative staggered scheme. Based on the result of \(\tau =0.1\) h and \({\dot{u}}=5\) mm/h, the numerical convergence is investigated by evaluating the logarithmic value of the residual norm (lg(R)) before the phase-field initiation (\(d\approx 0.2\)) and the crack propagation (\(d=1\)) in Figs. 19a and b, respectively. Due to the linearity of the viscoelastic material formulation and the phase-field evolution, only two Newton-Raphson iterations are required to solve the mechanical and the phase-field solution once. Observing Fig. 19a, before the phase-field crack initiation, the phase-field already converges from the third solution onward, nevertheless, the interactive feedback to the mechanical evolution does not converge yet up to the 15\(^{th}\) solution. As a result, the consequent solution for the decoupled evolutions are simultaneously converged, ending up with a total of 45 iterations. During the crack propagation, the total iterations significantly increase up to 557 steps, where the first 20 steps and the last simultaneously converged steps are shown in Fig. 19b. Based on this investigation, more solution iterations are required during the crack propagation than that before crack initiation.

Fig. 20
figure 20

Geometry and boundary setup of three-point bending test

Full size image
Fig. 21
figure 21

Visualization of the phase-field crack by plot the iso-surface at \(d=0.95\) in a transparent gray solid

Full size image
Fig. 22
figure 22

Comparison of the crack profiles for a numerical and experimental results in Song et al. (2006), b simulation by the present RCE approach and c by the V–D split modeling. According to Song et al. (2006), red line representing the numerical crack by cohesive element approach and the cracks obtained experimentally denoted by green and blue lines in a

Full size image

4.4 Three-point bending of viscoelastic asphalt concrete

The last example studies a three-dimensional boundary value problem based on a three-point bending test of asphalt concrete, which is characterized by a viscoelastic bulk material and is studied in Song et al. (2006). According to Song et al. (2006), a bilinear cohesive zone model is developed to investigate the fracture evolution. The cohesive elements are imposed in the potential region to allow cracks to propagate in any possible direction. As a result, the simulation result appropriately captures the experimental observation. In the sequel, Shen et al. (2019) ncorporates phase-field modeling of viscoelastic material to simulate this benchmark, nevertheless, using a classical volumetric-deviatoric split. Meanwhile, unlike the phase-field driving force definition in Shen et al. (2019), the present model does not include the viscous dissipation to evolve the phase-field evolution. Furthermore, using a V–D split, a concentrated displacement load on the top surface cannot yield the phase-field crack initiation from the tip of pre-notch. The fracture evolution straightforward evolves at the concentrated loading edge, due to the limitation of the V–D split for compression status. Therefore, Shen et al. (2019) applies uniform surface loading instead of concentrated line loads. Nevertheless, the RCE phase-field approach can effectively overcome this issue by applying concentrated line loading in accordance to the setup of Song et al. (2006).

The fundamental geometry and boundary setup are depicted in Fig. 20 and the FE discretization consists of 57960 eight-node brick elements. A local refinement is applied at the potential region where cracks may propagate. The uniform element length in x–y plane is \(h_e\approx 1.6\,\text {mm} \). The prescribed notch is located at left the bottom vertically towards the top surface with a length of 19 mm and the external loading is applied to the mid-span of the beam downwards at the top surface. The viscoelastic material model involves five Maxwell branches and the model parameters are \(\lambda =34765\,\text {MPa}\), \(\mu =9481\,\text {MPa}\), \(\chi ^{1}=0.133\), \(\tau ^{1}=0.17\,\text {s}\), \(\chi ^{2}=0.133\), \(\tau ^{2}=2.29\,\text {s}\), \(\chi ^{3}=0.235\), \(\tau ^{3}=26.16\,\text {s}\), \(\chi ^{4}=0.266\), \(\tau ^{4}=246.86\,\text {s}\), \(\chi ^{5}=0.228\), \(\tau ^{5}=6574.81\,\text {s}\). Furthermore, the parameters for the phase-field approach are given as \({\mathcal {G}}_{c}=345\,\text {J}/\text {m}^2\) and \(l=4\,\text {mm}\). A quasi-static analysis is applied and the loading rate is \({\dot{u}}=1\) mm/min. The evolution of the phase-field crack is shown in Fig. 21 by plotting the iso-surface of \(d=0.95\), which indicates a mixed-mode of fracture. Furthermore, the crack trajectories obtained by the cohesive approach as well as the experimental investigation (Song et al. 2006) are compared to the simulation result by present model, which show complete agreement with each other, see Figs. 22a and b. As aforementioned regarding the V–D split simulation, the concentrated line load does not evolve the crack at the pre-notched tip. Instead of that, the initial damage is exactly located at the loading region, see Fig. 22c. It is noteworthy that, so far in literature, a viscoelastic phase-field model with spectral split is not available.

5 Conclusion

The promising phase-field method has been intensively studied to simulate fracture evolution and a variety of approaches are developed to appropriately capture realistic crack kinematics in complex crack patterns. Nonetheless, the standard V–D split and the spectral decomposition only yield realistic predictions in limited conditions. The recent approaches presented in Steinke and Kaliske (2019), Strobl and Seelig (2016) consider a consistent degradation, leading to physical crack kinematics. Nevertheless, their formulations are restricted to isotropic and linear elasticity. The comprehensive RCE approach proposed in Storm et al. (2020) develops a general variational phase-field evolution, which allows to derive realistic and kinematically consistent material degradation without any restrictions of material properties. The contribution (Storm et al. 2020) has analyzed isotropic, anisotropic linear elasticity and thermo-elasticity in the framework of RCE modeling. As a meaningful application, this work incorporates the conceptual RCE approach to investigate fracture within viscoelastic materials, which considers other internal variables in addition to the crack deformation in a comprehensive derivation.

Several viscoelastic rheological models coupled to phase-field modeling are studied as well. This work takes the classical linear viscoelastic approach based on the convolution theorem into consideration to simulate viscoelastic solids at small strains. Due to the linearity of the elastic response at the non-equilibrium branch, the strain energy of the entire system can be obtained analytically based on the introduced stress-type internal quantity. As a result, the phase-field driving force can be explicitly defined by summing the elastic strain energy from both the equilibrium and the non-equilibrium branches, which strictly follows the definition of Griffith-type fracture. Nevertheless, Shen et al. (2019) postulates the fracture driving force including a portion of viscous dissipation as well in addition to the elastic strain energy.

To further demonstrate the capability of viscoelastic phase-field modeling using the novel RCE framework, several representative benchmark studies are examined. For material relaxation during compressive loading, a contact approach is compared to the RCE modeling, where full agreement is identified. Then, a transient analysis is performed for a bar spallation test, which evaluates the evolution of energy components in detail. The classical Mode I test shows the rate-dependent fracture and the numerical convergence for staggered solution is studied. The last three-point bending test of a pre-notched asphalt concrete specimen shows complex mixed-mode fracture.

In addition to current content in this publication, other inelastic characteristics, e.g. plasticity or viscoplasticity can be formulated by incorporating it into the RCE approach. Furthermore, the extension of the RCE to finite deformation is the next priority, for fracture of polymeric materials. One of the main challenges of the RCE framework extending towards finite deformation is that an appropriate solution scheme for the crack deformation \(\Gamma _i\) is required, which cannot be obtained as a closed solution anymore due to geometric and material nonlinearity. To address this issue, an internal Newton iteration is necessarily adopted to yield the numerical solution of \(\Gamma _i\), which is an interesting topic in an upcoming paper.