Phase-field fracture modelling of crack nucleation and propagation in porous rock

Abstract

In this work, we suggest a modified phase-field model for simulating the evolution of mixed mode fractures and compressive driven fractures in porous artificial rocks and Neapolitan Fine Grained Tuff. The numerical model has been calibrated using experimental observations of rock samples with a single saw cut under uniaxial plane strain compression. For the purpose of validation, results from the numerical model are compared to Meuwissen samples with different angles of rock bridge inclination subjected to uni-axial compression. The simulated results are compared to experimental data, both qualitatively and quantitatively. It is shown that the proposed model is able to capture the emergence of shear cracks between the notches observed in the Neapolitan Fine Grained Tuff samples as well as the propagation pattern of cracks driven by compressive stresses observed in the artificial rock samples. Additionally, the typical types of complex crack patterns observed in experimental tests are successfully reproduced, as well as the critical loads.

1 Introduction

The ability to predict rock behaviour using numerical models is pivotal to solve many rock-engineering problems. Numerical modelling can also be used to improve our understanding of the complicated failure process in rock. With models that better capture the fundamental failure mechanisms observed in laboratory, our ability to generate reliable large-scale models improves. Prediction of brittle fractures in rock and soil is a complex problem, which is relevant for a number of active research areas, ranging from landslides and fault mechanics to hydraulic fracturing. During the past decades a number of different methods have been developed for simulation of crack nucleation and propagation in various types of rock and soil. Most methods of analysing fractures stem from the pioneering work by Griffith (1921) and Irwin (1957) on brittle fractures, which relates crack propagation to a critical value of the energy release rate. However, one issue with these models is that the classical Griffith theory fails to predict crack formation even in notched specimens. One way to overcome these issues is to introduce cohesive zones, Hillerborg et al. (1976), in which the fractures are modelled. The cohesive zone model does however require the crack to follow the element boundaries of the finite element mesh. Other methods use enrichment techniques such as the extended finite element method introduced by Melenk and Babuška (1996) and Moës et al. (1999), see e.g. Liu and Borja (2008) for a work on fractures in rock. During recent years, the phase-field approach has emerged as an attractive alternative to simulate brittle fractures. The phase-field approach is based on the variational formulation for quasi-static brittle fracture mechanics first introduced by Francfort and Marigo (1998) and further developed by Bourdin (2007), who first introduced a numerical implementation of the regularised approximation of the variational formulation. Following the work of Miehe et al. (2010b), which gave an interpretation of the phase-field parameter in the context of a gradient damage model, the phase-field fracture approach has extended in a number of directions, e.g. dynamic fracture (Carlsson and Isaksson 2018; Schlüter et al. 2014; Borden et al. 2012), thermo-mechanical-driven fracture (Hesch and Weinberg 2014), experimental verification (Wu et al. 2017), and high-order phase-field approaches (Weinberg and Hesch 2017) to name a few.

One advantage of using the phase-field approach for simulation of fractures is the ability to predict crack nucleation in notched specimens. A number of articles have been published on the topic of crack nucleation using the phase-field approach. The work of Mesgarnejad et al. (2015), among others, point out that for crack nucleation, the critical load upon which a crack nucleate depend significantly on the regularisation parameter. Furthermore, Tanné et al. (2018) demonstrate the capability of the phase-field model to predict crack nucleation for Mode I cracks for geometries without any singularities in the stress field.

However, these contributions assume that the critical energy release rate for different fracture modes are equal, which is not the case for rock and rock-like materials, see, e.g. Shen and Stephansson (1994). In recent times, a number of contributions have been published dealing with crack propagation in granular materials using the phase-field approach. In Ambati et al. (2015) an overview of different phase-field fracture formulations is given, including the approaches proposed by Miehe et al. (2010a); Amor et al. (2009); Kuhn and Müller (2010) among others. Furthermore, Choo and Sun (2018) propose an alternative, where the regularisation length $\ell _0$ and the fracture energy density ${\mathcal {G}}_c$ are chosen such that the peak stress under uniaxial loading matches to the Mohr-Coulomb yield criterion. The work presented in Wu et al. (2017) demonstrates the capability of the deviatoric and volumetric split approach, first proposed by Amor et al. (2009), to simulate crack propagation in cement mortar. Zhang et al. (2017) introduce a split of the critical energy release rate to handle mixed mode cracks. However, fractures in compression remains an issue in phase-field models. Although several approaches have been proposed that consist in splitting the strain energy into damage inducing and non-damage inducing terms, none of the proposed splits are fully satisfying. In particular, it is not clear if these models are capable of simultaneously accounting for nucleation under compression and self-contact.

The goal of this work is to present a modified phase-field fracture model that can predict crack nucleation in porous rock and rock-like material. In porous rock, the critical release rate for tensile cracks can be orders of magnitude smaller than the critical energy release rate for shear cracks and compressive stresses can lead to the formation of compaction driven cracks. To capture these characteristic behaviours, we follow the work of Zhang et al. (2017) and introduce a split of the fracture energy release rate, where ${\mathcal {G}}^{+}_{cI}$ represents the critical energy release rate for Mode I, ${\mathcal {G}}^{+}_{cII}$ the critical energy release rate for Mode II and where ${\mathcal {G}}^{-}_{cI}$ and ${\mathcal {G}}^{-}_{cII}$ are introduced to represent the critical energy release rate for fractures driven by compressive stresses. Furthermore, to demonstrate the capability of the proposed model to predict nucleation of fractures for notched specimens, we compare the numerical results to digital image correlation (DIC) of experiments performed on rock specimens subjected to uniaxial plane strain compression (Nguyen 2011).

The outline of this article starts with a brief description of the phase-field fracture model first suggested by Miehe et al. (2010b). We continue Sect. 2 by proposing a modified phase-field fracture model that distinguishes between fractures in Mode I and Mode II as well as fractures driven by compressive stress. In Sect. 3 we discuss the calibration of the proposed model and in Sect. 4 we compare experimental and numerical results for different rock specimens subjected to uniaxial compression load. Finally, conclusions are drawn in Sect. 5.

Fig. 1

a Representation of a solid body $\varOmega$ with internal discontinuity boundary $\varGamma$. b Approximation of internal discontinuity boundaries by the phase-field d(x, t)

2 Phase-field formulation

In this section we describe the fundamental theory of phase-field fracture approach, where a fracture is indicated by a scalar order parameter coupled to the material properties in order to model the change in stiffness between broken and undamaged material. Undamaged material is indicated by that the order parameter has the value one and the material properties remain unaltered, whereas broken material is characterised by the value zero of the order parameter and the stiffness of the material is reduced accordingly. The section continues with a presentation of a modified phase-field fracture model that distinguishes between fractures in Mode I and Mode II as well as fractures driven by compressive stress.

2.1 Griffith’s theory of brittle fracture

In this section we give a brief recapitulation of the Griffith energy-based failure criterion. Consider an arbitrary body $\varOmega \ \subset \ {\mathbb {R}}^n$, $n \ \in \ \{2,3\}$, with the external boundary $\partial \varOmega$ and internal discontinuity boundary $\varGamma$, see Fig. 1a. Griffith’s theory of brittle failure states that the total energy of the body is given by

$$\begin{aligned} \varPsi = \varPsi _e + \varPsi _d - \varPsi _{ext} \end{aligned}$$

(1)

where $\varPsi _{ext}$ is the potential energy of the external forces, $\varPsi _d$ the energy needed for evolution of the internal discontinuity $\varGamma (t)$, and $\varPsi _e$ the elastic energy of the undamaged body $\varOmega$. If we let $\varvec{u}_i$ denote the displacement vector and $\varvec{\varepsilon }$ the infinitesimal strain tensor, then for the case of isotropic linear elasticity, the elastic energy of a body $\varOmega$ is given by

$$\begin{aligned} \varPsi _e = \int _{\varOmega }\psi ^0_e(\varvec{\varepsilon }) \ dV \end{aligned}$$

(2)

where $\psi ^0_e$ is the undamaged elastic energy density, i.e.

$$\begin{aligned} \psi ^0_e(\varvec{u}) = \frac{1}{2} \lambda [\text {tr} \varvec{\varepsilon }]^2 + \mu \text {tr}[\varvec{\varepsilon }^2] \end{aligned}$$

(3)

where $\lambda$ and $\mu$ are the Lamé constants. Furthermore, the energy needed for a crack to propagate can be given from

$$\begin{aligned} \varPsi _d = \int _{\varGamma } {\mathcal {G}}_c \ dA \end{aligned}$$

(4)

where ${\mathcal {G}}_c$ is the critical strain energy release rate.

2.2 Phase-field fracture approximation

To avoid the problems associated with numerically tracking the evolution of an internal discontinuity boundary $\varGamma$, the phase-field method approximates the fracture surface with an additional field parameter, $d(\varvec{x},t) \ \in \ [0,1]$. Where the material is undamaged the phase-field parameter $d=1$, and a fracture is represented by $d=0$, see Fig. 1b. The foundation of the phase-field fracture model is the approximation of the total energy of a fractured body Eq. (1). A number of different methods have been suggested to approximate the fracture energy. A widely used formulation was suggested by Miehe et al. (2010a), where the fracture energy is approximated as

$$\begin{aligned} \varPsi _d = \int _{\varGamma } {\mathcal {G}}_c \ dA \ \approx \int _{\varOmega } {\mathcal {G}}_c \Big [\frac{(d-1)^2}{4 \ell _0} + \ell _0 \vert \nabla d \vert ^2 \Big ] \ dV\nonumber \\ \end{aligned}$$

(5)

in which $\ell _0$ is a model parameter that controls the width of the approximation of the fracture zone, see Fig. 1. Borden et al. (2012) and Kuhn and Müller (2010) suggest that the regularised length, $\ell _0$, can be regarded as a material parameter, determined as $\ell _0 = \frac{27 E {\mathcal {G}}_c}{512 \sigma _t^2}$, where E is the Young’s modulus, $\sigma _t$ the tensile strength. Bourdin et al. (2000) noticed that the early phase-field approximations gave unrealistic crack patterns during compression. To remedy this problem, Miehe et al. (2010a) suggested a decomposition of the elastic energy density $\psi ^0_e(\varvec{u}, d) = \psi (\varvec{\varepsilon })^{+}_{e} + \psi (\varvec{\varepsilon })^{-}_{e}$. To model the decrease of material stiffness as the fracture propagates, the elastic energy density is defined as

$$\begin{aligned} \psi ^0_e(\varvec{u}, d) = [(1 - \eta )d^2 + \eta ]\psi _e^{+} +\psi _e^{-} \end{aligned}$$

(6)

where $0 < \eta \ll 1$ is a numerical parameter that limits the residual stiffness of fully damaged material to a very small but finite value. Additionally, the elastic energy is given by:

$$\begin{aligned}&\psi ^+_{e}(\varvec{\varepsilon })= \frac{1}{2} \lambda \langle \text {tr} \varvec{\varepsilon } \rangle ^{2} + \mu \text {tr}[(\varvec{\varepsilon }^{+})^{2}] \end{aligned}$$

(7)

$$\begin{aligned}&\psi ^-_{e}(\varepsilon )= \frac{1}{2} \lambda [\text {tr} \varvec{\varepsilon } - \langle \ \text {tr} \varvec{\varepsilon } \rangle ]^{2} +\mu \text {tr}[(\varvec{\varepsilon }^{-})^{2}] \end{aligned}$$

(8)

where $\psi ^+_{e}$ and $\psi ^-_{e}$ are the strain energies computed from the positive and negative principal parts of the strain tensor defined as

$$\begin{aligned} \begin{aligned}&\varvec{\varepsilon }^+ = \sum _{i=1}^\delta \langle \varepsilon ^i\rangle _{+} \varvec{n^i}\otimes \varvec{n^i} \quad \\&\varvec{\varepsilon }^{-} = \sum _{i=1}^\delta \langle \varepsilon ^i\rangle _{-} \varvec{n^i}\otimes \varvec{n^i} \end{aligned} \end{aligned}$$

(9)

Whereby $\langle x\rangle = \langle x\rangle _{+} = [x+ | x |]/2$ are the Macaulay brackets and $\langle x\rangle _{-} = [x - | x |]/2$ a similar bracket operator for the negative range. Additionally, $\{\varepsilon ^i\}_{i=1\ldots \delta }$ are the principal strains and $\{\varvec{n}^i\}_{i=1\ldots \delta }$ are the orthonormal eigenvectors of the strain tensor $\varvec{\varepsilon }$.

Following Miehe et al. (2010a), we get two coupled local equations

$$\begin{aligned}&\text {div} \varvec{\sigma } + \varvec{f} = \varvec{0} \end{aligned}$$

(10)

$$\begin{aligned}&{\dot{d}} + M\left[ 2d[1 - \eta ] \psi _e^{+} +\frac{{\mathcal {G}}_c}{2 \ell _0 }[d-1] + 2{\mathcal {G}}_c \ell _0 \varDelta d \right] = 0 \, . \end{aligned}$$

(11)

The kinetic coefficient or mobility parameter M is a non-negative scalar function $M=M(\varvec{\varepsilon },d,\nabla d, {\dot{d}})$ introduced to control the crack velocity. The most simple assumption, $M=$ constant, leads to the standard Ginzburg-Landau evolution equation, see Kuhn and Müller (2010).

The split in the elastic strain energy suggested by Miehe et al. (2010a) prevents propagation of fractures in compression. Moreover, Eq. 11 implies that the critical energy release rates in Mode I and Mode II cracks are equal, which is not the case for most rocks.

2.2.1 Modified phase-field approximation

A number of different approaches have been presented to overcome the phase-field fracture models limitation to simulate materials with different values of critical energy release rates for fractures for Mode I and Mode II, e.g. (Choo and Sun 2018; Wu et al. 2017). In this work we approach this limitation of the phase-field fracture with a an approach inspired by Zhang et al. (2017). We use a modified version of the phase-field model to accommodate for the characteristic behaviours of porous rock. To allow for fractures to propagate in both compression and tension, we make a modification to the elastic strain energy, by redefining Eq. (6) into

$$\begin{aligned} \psi _e(\varvec{u}, d) = [(1 - \eta )d^2 + \eta ]{\mathcal {H}}(\varvec{\varepsilon }) \end{aligned}$$

(12)

where ${\mathcal {H}}$ is a reformulation of the elastic strain energy introduced to control the evolution of cracks in both tension and compression, which will be discussed further shortly. First, we need to discuss how to separate between Mode I and Mode II fractures, as the critical energy release rates in general are not the same for shear and tensile cracks for rocks. One alternative is the deviatoric-volumetric split of the elastic strain energy suggested by Amor et al. (2009). Using the formulation of Amor et al. (2009) has the benefit of presenting a straightforward way for a pure split between the volumetric and deviatoric strains in contrast to the approach proposed by Miehe et al. (2010a). On the other hand, this formulation leads to cracking in regions where all principal strains are negative.

To overcome this problem, whilst still having a pure split of the volumetric and deviatoric strain tensor, we use the volumetric-deviatoric split of the strain energy defined as

$$\begin{aligned} {\mathcal {H}}(\varvec{\varepsilon })= & {} {\mathcal {H}}^{vol}(\text {tr} \varvec{\varepsilon }) + {\mathcal {H}}^{dev}(\varvec{\varepsilon }_{d}) \nonumber \\= & {} \frac{1}{2} K [\text {tr} \varvec{\varepsilon }] + \mu \text {tr} [\varvec{\varepsilon }^2_{d}] \end{aligned}$$

(13)

where $\varvec{\varepsilon }_{d} = \varvec{\varepsilon } - 1/3\,\text {tr} \varvec{\varepsilon }$ is the deviatoric part of the strain tensor and K the bulk modulus. From this expression the stress for the local equilibrium condition Eq. 10 is determined as

$$\begin{aligned} \varvec{\sigma }= & {} \partial _{\varepsilon } \psi _e(\varvec{\varepsilon },d) \nonumber \\= & {} [(1 - \eta )d^2 + \eta ] {\partial _\varepsilon } {\mathcal {H}}(\varvec{\varepsilon }) \end{aligned}$$

(14)

thus allowing stress degradation due to evolution of the phase-field d in tension and compression.

Next, we suggest a modified mobility parameter, ${\tilde{M}} = M {\mathcal {G}}_c$, which, by rearranging Eq. 11, allows us the isolation of the ratio $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ that controls the evolution of the crack, i.e.

$$\begin{aligned} 2d[1 - \eta ] \frac{{\mathcal {H}}}{{\mathcal {G}}_c} +\frac{1}{2 \ell _0}[d-1] + 2 \ell _0 \varDelta d +\frac{{\dot{d}}}{{\tilde{M}}} = 0,\nonumber \\ \end{aligned}$$

(15)

The isolation and, therefore, the generalisation of the ratio $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ allows the final proposed formulation for the Mode I/Mode II split. We propose a change to Eq. 15 by modifying the ratio $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ as

$$\begin{aligned} \frac{{\mathcal {H}}}{{\mathcal {G}}_c} = \frac{{\mathcal {H}}^{+}_{I}}{{\mathcal {G}}^{+}_{cI}} + \frac{{\mathcal {H}}^+_{II}}{{\mathcal {G}}^{+}_{cII}} + \frac{{\mathcal {H}}_{II}^{-}}{{\mathcal {G}}^{-}_{cII}} + \frac{{\mathcal {H}}_{I}^{-}}{{\mathcal {G}}^{-}_{cII}} \end{aligned}$$

(16)

where ${\mathcal {H}}^{\pm }_{I}$ and ${\mathcal {H}}^{\pm }_{II}$ represent parts of the volumetric-deviatoric split of the elastic strain energy:

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}^+_{I} = \frac{1}{2} K \langle \text {tr}\varvec{\varepsilon } \rangle ^2 H(\text {tr}\varvec{\varepsilon })\\&{\mathcal {H}}^+_{II} = \mu \ \text {tr}[\varvec{\varepsilon }^2_{d+}]H(\text {tr}\varvec{\varepsilon }) \\&{\mathcal {H}}^{-}_{I} = \frac{1}{2} K [\text {tr}\varvec{\varepsilon } - \langle \text {tr}\varvec{\varepsilon } \rangle ]^2 [1-H(\text {tr}\varvec{\varepsilon })]\\&{\mathcal {H}}^{-}_{II} = \mu \ \text {tr}[\varvec{\varepsilon }^2_{d-}] [1-H(\text {tr}\varvec{\varepsilon })]. \end{aligned} \end{aligned}$$

(17)

The parameters ${\mathcal {G}}^{+}_{cI}$ and ${\mathcal {G}}^{+}_{cII}$ represent the critical energy release rates for Mode I and Mode II during tensile stresses, and ${\mathcal {G}}^{-}_{cI}$ and ${\mathcal {G}}^{-}_{cII}$ represent the critical energy release rate during compression. In Eq. 17 the Heaviside function $H(\text {tr}\varvec{\varepsilon })$ is used and we introduced, analogue to Eq. 9, a split of the deviatoric strain tensor in a positive and negative part by

$$\begin{aligned} \begin{aligned}&\varvec{\varepsilon }_{d+} = \sum _{i=1}^\delta \langle \varepsilon ^i_d\rangle _{+} \varvec{n^i}\otimes \varvec{n^i} \quad \\&\varvec{\varepsilon }_{d-} = \sum _{i=1}^\delta \langle \varepsilon ^i_d\rangle _{-} \varvec{n^i}\otimes \varvec{n^i} \end{aligned} \end{aligned}$$

(18)

with $\{\varepsilon ^i_d\}_{i=1\ldots \delta }$ are the principal values of the deviatoric strain tensor. Observe, that the strain tensor and its deviatoric part have the same orthonormal eigenvectors $\{\varvec{n}^i\}_{i=1\ldots \delta }$ and the eigenvalues are related by $\varepsilon ^i_d = \varepsilon ^i - 1/3 \text {tr} \varvec{\varepsilon }$. Furthermore, $\text {tr}[\varvec{\varepsilon }^2_{d}] = [\varepsilon ^1_d]^2 + [\varepsilon ^2_d]^2 + [\varepsilon ^3_d]^2$ as the eigenvectors are pairwise orthogonal. To summarise, in our proposed model the expressions in Eq. 17 enter the evolution equation Eq. 15 but not the stress computation for local equilibrium condition.

In this work the spatial discretisation is formulated by means of the Galerkin method, using $C^1$-continuous NURBS basis functions, see e.g. Cottrell et al. (2009), as the finite dimensional approximations to the function spaces of the weak form of the coupled local equations. Moreover, we use the staggered approach, which allows for robust solution of the incremental update of both the displacement and phase fields, as suggested by Miehe et al. (2010a). We solve for the field variables for each discrete time step $0,t_{1},...,t_{n},t_{n+1},...,T$, where $t_{n}$ denotes the last time step for which all field variables, $\varvec{u}_{n}, d_{n}$, are assumed to be known. In this work we use the Newton-Raphson method with a line search algorithm to determine the field variables in the current time step $t_{n+1}$ for the time increment $\varDelta t = t_{n+1} - t_{n}$. The rate of the phase-field is considered to be constant over each time increment, and is defined as ${\dot{d}} = (d_{n+1}-d_{n}) / \varDelta t$.

Fig. 2

a The geometry and boundary conditions of the FGT specimen used to calibrate the material parameters used in the models. b A schematic of the crack patterns at failure. c A comparison between the stress–strain curves of experiment and simulation

To prevent the phase-field from healing, we make the assumption that the current modified strain energy expression $\tilde{{\mathcal {H}}} = {\mathcal {H}}^{+}_{I} + {\mathcal {H}}^{+}_{II} + {\mathcal {H}}^{-}_{I} +{\mathcal {H}}^{+}_{II}$ assumes the largest absolute value of the history field. If the value of the strain energy $\tilde{{\mathcal {H}}}_{n+1}$ of the current time step is lower than the history field $\tilde{{\mathcal {H}}}_n$, then $\tilde{{\mathcal {H}}}_{n+1} = \tilde{{\mathcal {H}}}_{n}$.

3 Calibration

To model the nucleation and evolution of fractures using the proposed phase-field fracture model, we need to establish the material parameters used by the model. In this work we have chosen to calibrate the material parameters against the experimental results presented in Hall et al. (2006) for the Neapolitan fine-grained tuff. According to Hall et al. (2006) the failure of Neapolitan tuff specimens with an artificial inclined cut is almost completely controlled by the flaw, which makes them very repeatable despite the significant heterogeneity of the material. For simplicity we have chosen to make use of the same geometry to calibrate the material parameters for the artificial rock CPIR09 presented in Nguyen (2011). Furthermore, we set the modified mobility parameter ${\tilde{M}} = 1$ based on a numerical parameter study. I.e. in our proposed model the mobility parameter is not just a viscous regularisation of a rate independent model as introduced in Miehe et al. (2010a). The numerical parameter defining the residual stiffness of fully damaged material is set as $\eta = 1\times 10^{-12}$.

3.1 Neapolitan fine grained tuff (FGT)

The Neapolitan tuff is a very porous natural pyroclastic rock, with a uniaxial compression strength ranging from 1.2 to 25 MPa. A number of papers have been published on the experimental work of capturing the failure process on Neapolitan tuff using both acoustic emissions and digital image correlation, e.g. (Nguyen 2011; Hall et al. 2006; Nguyen et al. 2011). The main physical and mechanical properties used in this work have been gathered from Nguyen (2011). The material parameters needed for the phase-field model has then been calibrated to results of a Neapolitan tuff sample subjected to uniaxial plane strain compression load, presented in Hall et al. (2006). The samples were subjected to a displacement rate of 0.01 mm/min until failure. The geometry and boundary conditions for the rock specimen is given in Fig. 2a). According to Nguyen (2011) the Young’s modulus $E = 2.1$ GPa and we chose to set the Poisson’s ratio to $\nu = 0.27$.

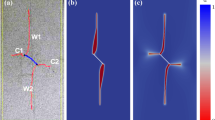
Figure 2b illustrates the typical crack pattern from the experimental work presented in Hall et al. (2006), where the failure mode is through the formation of wing cracks from the tip of the pre-defined inclined cuts, or sometimes through secondary tensile cracks as illustrated in the lower crack of Fig. 2b.

The experimental results from Nguyen (2011) do not provide any data on the critical energy release rates. To determine them, we make use of the suggestion by Borden et al. (2012), and Kuhn and Müller (2010), stating that the regularisation length $\ell _0$ should be regarded as a material parameter which governs the thickness of the damage zone, determined as $\ell _0 = \frac{27 E {\mathcal {G}}_c}{512 \sigma _t^2}$. The relation between the critical energy release rate ${\mathcal {G}}_c$ and the regularisation length $\ell _0$ needs to be further studied experimentally. In this work, the unknown material parameters have be calibrated by matching the evolution of the crack path from the numerical simulation to the experimental observations and using two assumptions. First, we make use of the work of Kuhn and Müller (2010), stating that the effective element size, $h_e$, should be approximately one half of the regularisation length $\ell _0$ for the phase-field model to capture the accurate crack paths. Secondly, by setting the strength of the Napolitan Fine Grained Tuff to $\sigma _c = 10$ MPa and the critical energy release rate to ${\mathcal {G}}^{+}_{cI}=10$ N/m, the value of the regularisation length is calculated to $\ell _0 = 0.10$ mm. This led to a mesh of approximately 300,000 elements, with an almost constant size of $h_e = \frac{1}{2}\ell _0$ throughout the entire specimen. Through a parameter study we could then determine the material parameters for the phase-field model for the Neapolitan Fine Grained Tuff according to Table 1.

Table 1 Material parameters used for simulation of the Neapolitan Fine Grained Tuff

Fig. 3

a The geometry of the specimen used to calibrate the material parameters used in the models. b The state of the crack evolution at the marked point in the graph. c A comparison between the stress–strain curves of experiment and simulation

3.2 Artificial rock CPIR09

For the calibration of the artificial rock we followed the same procedure as for the Neapolitan Fine Grained Tuff, using the results presented in Nguyen (2011). According to Nguyen (2011) the artificial rock exhibits a crack pattern with initial anti-symmetric wing cracks, starting at the tips of the initial cut, see Fig. 3b. The wing cracks are followed by secondary cracks which according to Nguyen (2011) are compressive cracks, that emerge on the opposite side from the wing cracks at tips of the initial notches.

Using the observation recorded in Nguyen (2011) for specimens of the artificial rock CPIR09 during uniaxial compression in plane strain, we calibrated the model by matching the numerical simulation to the experimental observations. As for the Neapolitan FGT, the parameters for the critical energy release rates, mobility parameters and the tensile strength of the artificial rock are not reported in Nguyen (2011). For the artificial rock we chose to set the mode I critical energy release rate to ${\mathcal {G}}^{+}_{cI} = 1.0$ N/m and the tensile strength selected to $\sigma _t = 1.6$ MPa to calibrate the phase-field model. According to the results presented in Nguyen (2011) the stiffness of the tested rock samples varied within a range of approximately 30%, while both the fracture patterns and the strength of the material are consistent throughout the experiments. We have chosen to set the Young’s modulus $E = 5$ GPa and Poisson’s ratio $\nu = 0.18$, which is in the upper region of the stiffness measured during the experiments. Through a parameter study we could then set the material parameters for the phase-field model for the artificial rock CPIR09 according to Table 2. From the results of the calibration depicted in Fig. 3, we notice that the general stress–strain behaviour from the simulation is in good agreement with the experimental observation until closure of the compressive cracks takes place.

Table 2 Material parameters used for simulation of the artificial rock CPIR09

Fig. 4

Level set plots of the crack-driving ratio $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ with respect to strain. a Neapolitan Fine Grained Tuff (FGT). b Artificial rock CPIR09

Fig. 5

Geometries of the rock specimens used

3.3 Effect on the crack driving ratio ${\mathcal {H}}/{\mathcal {G}}_c$

In order to illustrate how the split of $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$, see Eq. 16, affects the evolution of a crack with regards to the principal strains $\varepsilon ^1$ and $\varepsilon ^2$. Figure 4 plots the level set of the crack driving ratio $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ for the calibrated material parameters shown in Tables 1 and 2. Figure 4a displays the level set of $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ for the Neapolitan Fine Grained Tuff. From the figure we can see that by increasing the critical energy release rate ${\mathcal {G}}^{-}_{cI}$, the fracture toughness is increased in the direction of pure compression. Figure 4b displays the level set of the crack driving ratio for the artificial rock CPIR09. By studying the level set of $\frac{{\mathcal {H}}}{{\mathcal {G}}_c}$ we can see that by increasing the critical energy release rate ${\mathcal {G}}^{-}_{cI}$ and ${\mathcal {G}}^{-}_{cII}$ we decrease the tendency for compressive or shearing cracks to appear.

4 Comparison between experimental and numerical results

In this section we present the results from simulations of CPIR09 Meuwissen and Neapolitan FGT samples with the dimensions of $100 \times 50 \times 35$ mm$^3$ in uniaxial compression. The numerical results are compared to experimental observations presented in Nguyen (2011). For the two materials, three different angles of rock bridge inclination were examined: $35^{\circ }$, $45^{\circ }$ and $55^{\circ }$, see Fig. 5. The experimental results were documented using digital image correlation, DIC, measurements of the maximum shear strains, $\varepsilon _{s-max}$, and volumetric strain, $\varepsilon _{vol}$. Defined as, $\varepsilon _{s-max} = \frac{1}{2}(\varepsilon _{max}-\varepsilon _{min})$ and $\varepsilon _{vol} = \varepsilon _{max}+\varepsilon _{min}$ with $\varepsilon _{max}$ being the maximum value of the principal strains and $\varepsilon _{min}$ the minimum value. Furthermore, the experiments were conducted under uniaxial compression, and the sample was subjected to a displacement rate of 0.1 mm/min until failure. For all the simulations the regularisation length is chosen to $\ell _0 = 0.10$ mm and to capture the evolving crack paths we use an almost constant element size of $h_e = \frac{1}{2}\ell _0$ throughout the entire specimen, which leads to a mesh with approximately 320,000 elements. The material parameters used are presented in Tables 1 and 2 respectively. Moreover, we would like to note that by comparing the photos of the fractures to the DIC measurements, we estimate that the DIC measurements blur the cut thickness by approximately a factor 5.

Fig. 6

a Geometry. b The volumetric strain, $\varepsilon _{vol}$ DIC measurements from the uniaxial compression test of the CPIR09 sample with $35^{\circ }$ bridge angle before crack initiation (Nguyen 2011). c The volumetric strains, $\varepsilon _{vol}$, from the numerical simulations before any cracks have been formed

Fig. 7

Comparison between measurements of nominal stress–strain curves presented in Nguyen (2011), to the numerical results from simulations for the CPIR09 Meuwissen samples

Fig. 8

The maximum shear strain, $\varepsilon _{s-max}$ during the evolution of the cracks for the CPIR09 sample with $55^{\circ }$ bridge angle. a–d Display the DIC measurements from the experiments. e–h Display the numerical results

4.1 Uniaxial compression of artificial rock CPIR09

According to Nguyen, before the appearance of any crack, the localisation of shear deformation was less pronounced in the CPIR09 Meuwissen samples than what was observed in the Neapolitan FGT samples. However, the presence of the compaction zones at the notches are clearly detectable in the DIC measurements of the volumetric strains, see Fig. 6b.

With an increased load, compressive cracks are formed in these compaction zones for all three geometries. An initial drop in the measured nominal stress follows the initiation of the compressive cracks shown in Fig. 7. By studying the nominal stress–strain curves in Fig. 7 we observe that the nominal stresses increase after the initial drop in the experimental results. The increased nominal stress is likely taking place as the internal crack surfaces come into contact. As the compressive cracks close and full contact is achieved, the rock sample carries additional load before total failure. This increase in stress after the initial onset of the compressive cracks is not observed in the numerical results, as the implemented model does not include a method for treating self-contact of the internal surfaces.

Even though an appropriate additional contact formulation is not included in our proposed model, and this is outside the scope of this work, the observed stable evolution of the compressive cracks towards the opposite edge of the rock samples is observed also in the numerical simulations. Nguyen reports that, in the experiments presented in Nguyen (2011), the compressive cracks stop when they reach the level of the opposite notch, approximately 10 mm from the opposite edge, after which new cracks appear in the shape of more compressive cracks as well as tensile cracks in the vertical direction. Figure 8 displays the evolution of the maximum shear strain $\varepsilon _{s-max}$ as the cracks propagate for the CPIR09 sample with a $55^{\circ }$ bridge angle. In Fig. 8d, h the propagation of the horizontal cracks have stopped and new cracks are appearing. In the experimental results, the DIC analysis indicates a stress concentration due to material imperfections which leads to an onset of new cracks above the edge of the bottom notch. In the simulation, the original crack is met by a new horizontal crack from the opposite side of the sample.

Studying the volumetric strains, $\varepsilon _{vol}$, after the onset of new cracks in Fig. 9, it is possible to state that the horizontal cracks displayed in the DIC analysis are compressive cracks, as $\varepsilon _{vol}<0$ and that the vertical cracks are tensile fractures as $\varepsilon _{vol}>0$. We also note that the confronting cracks that appear in the simulations are tensile cracks as $\varepsilon _{vol}>0$.

Fig. 9

a Geometry. b The volumetric strain, $\varepsilon _{vol}$ DIC measurements from the uniaxial compression test of CPIR09 sample with $55^{\circ }$ bridge angle after the Nguyen (2011). c The volumetric strains, $\varepsilon _{vol}$, from the numerical simulations before any cracks have been formed

Fig. 10

a Photo of the rock sample with a $35^{\circ }$ bridge angle with the crack highlighted in red. b The DIC measurements of the maximum shear strains $\varepsilon _{s-max}$. c The measured volumetric strain $\varepsilon _{vol}$ DIC analysis. d The phase-field distribution from the numerical simulation. e, f Displays the maximum shear strains $\varepsilon _{s-max}$ and volumetric strain from the numerical simulations, (Nguyen 2011)

Figure 10a shows a picture of the CPIR09 sample with a $35^{\circ }$ bridge angle right before the crack reaches the level of the opposite notch. Figure 10d displays the phase-field, with cracks represented by zero value. Furthermore, comparing the maximum shear strain $\varepsilon _{s-max}$ and volumetric strain $\varepsilon _{vol}$ from the DIC analysis in Fig. 10b to the numerical results in Fig. 10e–f, it is clear that the numerical simulation produces slightly larger strains than measured in the DIC analysis. This is likely an effect of the self-contact of the fracture surfaces restricting the deformations. Moreover, by studying Fig. 10c, f it is clear that the horizontal cracks are compressive in nature, as $\varepsilon _{vol}<0$.

4.2 Uniaxial compression of Neapolitan FGT

As for the CPIR09 samples, we compare the numerical results for the Neapolitan FGT with the observations and measurement documented in Nguyen (2011). According to Nguyen (2011), before the appearance of cracks, the localisation of shear deformation and compaction zones were systematically observed at the notches and in the rock bridge for all the Neapolitan FGT samples. Figure 11 shows the maximum shear strains $\varepsilon _{s-max}$, before the formation of any cracks in the FGT sample with $45^{\circ }$ bridge angle. The numerical results are in good agreement to the obtained measurements from the DIC analysis, where the observed localisations of the shear strains at the notches are clearly noticeable in Fig. 11.

Fig. 11

a Geometry. b The maximum shear strain, $\varepsilon _{s-max}$ measured using DIC during the uniaxial compression test of Neapolitan FGT samples with $45^{\circ }$ bridge angle (Nguyen 2011) before crack initiation. c Displays the maximum shear strains, $\varepsilon _{s-max}$, from the numerical simulations before any cracks have been formed

Fig. 12

a Geometry. b The volumetric strain, $\varepsilon _{vol}$ DIC measurements from the uniaxial compression test of Neapolitan FGT sample with $55^{\circ }$ bridge angle before crack initiation (Nguyen 2011). c The volumetric strains, $\varepsilon _{vol}$, from the numerical simulations before any cracks have been formed

The deformations in the compaction and shear zones intensify with the increase of the applied load and the first cracks always appeared at the localisation of $\varepsilon _{s-max}$. In the experiments two main types of cracks are reported: wing cracks, W, that propagate in Mode I in the vertical direction between the ends of the notches and the load bearing surfaces of the samples, and mixed Mode I and Mode II crack, referred to as P cracks, that appeared in the rock bridge joining the notches. In addition to the two main types of cracks, a third crack type was observed in the zone where concentrations of compaction were localised at the notches, see Fig. 12. According to Nguyen (2011), these third crack types were always a mixed compaction and shear crack. By studying the volumetric strains we get more information of the crack type, where a positive volumetric strain indicates that the crack is opening (tensile mode I) and where a negative value indicates a closing or compressive crack, shearing or any combination of mode I and mode II.

Fig. 13

The left column displays the geometries of the rock samples, the middle column the $\varepsilon _{s-max}$ measured using DIC during the uniaxial compression test of Neapolitan FGT samples at failure. The right column displays the maximum shear strains, $\varepsilon _{s-max}$, from the numerical simulations at the end of the simulations

Fig. 14

Comparison of measurements nominal stress–strain curves presented in Nguyen (2011), to the numerical results simulations of Neapolitan FGT Meuwissen samples

In the simulations we observed all three types of cracks, and the localisation of initiation for the cracks are in good agreement with the experimental results. However, for the sample with a $35^{\circ }$ bridge angle, the wing cracks propagates further into the centre of the rock sample until a mixed mode crack, P appeared in the rock bridge joining the notches, see Fig. 13c. This behaviour was not observed in the experiment, where the wing cracks propagated in a vertical direction without connecting the notches, see Fig. 13b, Nguyen (2011). For the samples with a $45^{\circ }$ bridge angle, both wing cracks and mixed mode cracks where frequently observed, which was also the case for the numerical results. However, we would like to point out that due to symmetry and the lack of both material and geometrical imperfections, the numerical simulation results in two symmetric cracks, which is not observed in the experiments. By comparing Fig. 13e, f it is clear that for the $45^{\circ }$ sample, the proposed modified phase-field fracture model is in good agreement with experimental observations. In the specimen with a $55^{\circ }$ bridge angle, the observed failure mode in the experiments was through the formation of P cracks located on the rock bridge. According to Nguyen (2011), the formation of these cracks is often the result of the coalescence of smaller cracks that appear before the peak stress, Fig. 13h. From Fig. 13i it clear that the proposed phase-field model has a difficulty to capture the P cracks. Instead, tensile cracks are formed on the opposite side of the notches leading to a Mode I crack propagating in horizontal direction through the rock specimen. The occurrence of these tensile cracks are likely due to the interpenetration between the internal surfaces of the cracks propagating from the notches, leading to tensile stress concentrations opposite to the notches. An appropriate additional contact formulation is not included in our proposed model, and this is outside the scope of this work. Another interesting observation is that the observed behaviour during the experiments is more brittle than the numerical results. This becomes clear by observing the nominal stress–strain behaviour after the peak stress is reached in Fig. 14.

Figure 14 depicts the nominal stress–strain curves from the simulation of the compression test of the Neapolitan FGT together with the measurements performed by Nguyen (2011) for the Meuwissen samples. Even though the general stress–strain behaviour from the simulations are in good agreement with the experimental observations one should note that, as expected, the dispersion between the peak nominal stresses are greater for the experimental measurements than for the numerical result. We would also like to point out that for the sample with a $35^{\circ }$ bridge angle the measured peak nominal stress is a fair bit larger then the numerical results. The reason for the difference between experimental observation and numerical results can be manifold, i.e. the rock samples include both material and geometrical imperfections, which are not included in the numerical simulations. Another aspect that might affect the results are the boundary conditions. In the experimental set up, friction between the loading plate and the rock sample might affect the results, an aspect which is not accounted for in the simulations.

5 Conclusion

In this work we have presented a modified phase-field fracture model for simulation of crack propagation in porous rocks. The presented model introduces a split of the fracture energy release rate to capture the characteristic behaviour of fractures in porous rock. In porous rock, the critical release rate for tensile cracks can be orders of magnitude smaller than the energy release rate for shear cracks and compressive stresses can lead to the formation of compressive cracks. To capture these characteristic behaviours we have introduced a split of the fracture energy release rate, where ${\mathcal {G}}^{+}_{cI}$, ${\mathcal {G}}^{+}_{cII}$ represent the critical energy release rates for Mode I and Mode II during tensile stresses and where ${\mathcal {G}}^{-}_{cI}$ and ${\mathcal {G}}^{-}_{cII}$ represent the critical energy release rate during compression. To calibrate the numerical model we have compared the numerical results to experimental observations performed on rock samples with a sawed inclined cut subjected to uni-axial plane strain compression. Further, to demonstrate the capability of the modified phase-field fracture model first introduced in this work, we compared the calibrated model to Meuwissen samples with different angles of rock bridge inclination subjected to uni-axial compression. The presented comparison shows that the modified phase-field fracture model gives results in good agreement with the experimental observations both with respect to crack patterns and critical stress loads. We have also shown that the proposed phase-field model is able to reproduce the formation of compressive cracks as well as complex crack patterns without any additional algorithmic treatment.