A Modified Phase-Field Fracture Model for Simulation of Mixed Mode Brittle Fractures and Compressive Cracks in Porous Rock

Abstract

In this work, we propose a modified phase-field model for simulating the evolution of mixed mode fractures and compressive driven fractures in porous artificial rocks. For the purpose of validation, the behaviour of artificial rock samples, with either a single or double saw cuts, under uniaxial plane strain compression has been numerically simulated. The simulated results are compared to experimental data, both qualitatively and quantitatively. It is shown that the proposed model is able to capture the commonly observed propagation pattern of wing cracks emergence followed by secondary cracks driven by compressive stresses. Additionally, the typical types of complex crack patterns observed in experimental tests are successfully reproduced, as well as the critical loads.

1 Introduction

The prevention of fracture-induced failure is an important aspect to consider in most designs. The consequences of brittle fractures are often critical for any design, and numerical simulations have become common practice to analyse the fracture process. Most methods of analysing fractures stem from the pioneering work by Griffith (1921) and Irwin (1957) on brittle fractures. In these works, crack propagation is related to a critical value of the energy release rate. During the last decades, a number of methods have been developed for numerical analysis using the finite element method (FEM). These methods have two significant drawbacks, the first being that crack propagation leads to a change of the geometrical discretisation and the second that the crack path needs to follow the mesh lines. There are methods to overcome the second issue. One method is to use enrichment techniques such as the extended finite element method introduced by Melenk and Babuška (1996) and Moës et al. (1999), see e.g., Liu and Borja (2008) or Shen et al. (2014) for a work on fractures in rock. Another method is the discontinuous finite element method as described by Mergheim and Steinmann (2006). Here strong discontinuities in the form of a cohesive zone model are introduced independent of the mesh structure. Whereas in classical cohesive zone modelling cracks have to follow mesh lines, see Hillerborg et al. (1976) and e.g., Ottosen and Ristinmaa (2016) for a recent work. The issue of tracking the evolution of complex fractures has, however, proven to be difficult.

In recent times, an alternative method has been introduced for numerical simulations of brittle fractures, using a phase-field to simulate the fracture zone. In these phase-field models, a fracture is indicated by a scalar order parameter, which is coupled to the material properties to model the change in stiffness between broken and undamaged material. Where the material is undamaged, the order parameter takes the value one and the material properties remain unaltered. Broken material is characterised by the value zero and the stiffness of the material is reduced accordingly. Thus, in the phase-field model, cracks are represented as lines or areas in the material, where the order parameter has the value zero and the stiffness is significantly reduced. The variational formulation of quasi-static brittle fracture mechanics was introduced by Francfort and Marigo (1998). A numerical implementation of the regularised approximation of the variational formulation was first introduced by Bourdin (2007) and further explored in Bourdin et al. (2012). Miehe et al. (2010b) presented the interpretation in the context of a gradient damage model and introduced alternative models based on a history field that ensures growth of the phase-field parameter. The phase-field fracture model has since been extended in a number of directions, including dynamic fracture (Borden et al. 2012; Tanné et al. 2018; Schlüter et al. 2014; Carlsson and Isaksson 2018; Schlüter et al. 2014), coupled thermo-mechanical-driven fracture (Hesch and Weinberg 2014), high-order phase-field approaches (Weinberg and Hesch 2017), and various solution techniques (Wick 2017) to name a few.

However, these contributions are not specific for rocks and rock-like materials and, therefore, are not capable of capturing their behaviour. The fracturing process in rocks is complex and often accompanied by other failure mechanisms, like conjugated microcracks and shear bands, as shown by Lewis et al. (2019). A number of authors have made an effort to numerically analyse this complex phenomenon. Li et al. (2018) investigated the influence of microcracks distribution in a rock specimen based on a stochastic model. The model provides reasonable results but requires pre-knowledge about the material that is difficult to obtain for full scale simulations. Backers and Stephansson (2012) studied the development of fractures for varying boundary conditions suggesting that these influence significantly the behaviour of the material and consequently the model parameters. Phase-field methods have also been used to simulate fracture propagation in rocks in different conditions. Santillán et al. (2018) explored the effect of hydraulic pressure in fractured rock. Nguyen et al. (2016) compared phase-field simulations with micro-CT images of tension cracks in lightweight plaster and concrete and identified material parameters by inverse analysis. These works, however, are based on models not specific to rock-like materials.

In fact, in these materials the Mode I and Mode II fracture toughness for energy (${\mathcal {G}}_{\text {Ic}}$ and ${\mathcal {G}}_{\text {IIc}}$) can differ significantly. Shen and Stephansson (1994) state that ${\mathcal {G}}_{\text {IIc}}$ in rocks is much greater than ${\mathcal {G}}_{\text {Ic}}$, typically ${\mathcal {G}}_{\text {IIc}} \ge 100{\mathcal {G}}_{\text {Ic}}$, due to differences in failure mechanisms. They further demonstrated that failure under compression is not correctly predicted when this difference is ignored as, e.g., in the original maximum strain energy release rate criterion (G-criterion). They proposed, therefore, a modified criterion based on the normalised strain energy release for Mode I and Mode II. Based on this idea, Zhang et al. (2017) proposed a phase-field fracture model that distinguishes between Mode I and Mode II toughness for energy. However, their suggested split does not allow the uncoupling between deviatoric and volumetric strain, which is a common split in rock mechanics. Moreover, porous rocks, e.g., sandstone and volcanic rock, often display fractures in compression, referred to as compaction bands, see e.g. Labuz and Drescher (2003). A further modification to the model is required to allow the correct simulation of this kind of fracture.

In this work we propose a modified phase-field fracture model that distinguishes between fractures in Mode I and Mode II and assures the uncoupling of volumetric and deviatoric strain. The model also enables for simulation of compression driven fractures (compaction bands) in porous rock-like materials. The model is a quasi-static phase-field model, where the evolution of the crack field with respect to time is described by a thermodynamically motivated Ginzburg-Landau type evolution equation (Miehe et al. 2010b). To obtain a robust implementation of the phase-field model a staggered integration scheme has been utilised. Information about the energy release during the advancement of compressive driven fractures was found in Vajdova and Wong (2003) while Rudnicki and Sternlof (2005) presented a model to determine the energy release rate for the compression driven fractures ${\mathcal {G}}_{\text {band}}$. Furthermore, most of the work proposed on phase-field models of fractures have thus far been applied to academic benchmarks. It is, therefore, of interest to evaluate the method against experimental observations. In this work, we compare the proposed phase-field fracture model with experimental data on the evolution of wing cracks and compression cracks in a porous artificial rock, see the extensive experimental work in Nguyen (2011). Our model is restricted to wing cracks and the onset of compaction band formation and is able to capture the experimental results both qualitatively and quantitatively. Further experimental data would be needed to extend our model to other types of cracks observed in porous rocks.

The outline of this work is as follows. In Sect. 1.1 we compare the experimentally observed crack paths in a porous artificial rock (Nguyen (2011)) with the numerically predicted crack path by the unified phase-field theory presented in Wu (2017). In Sect. 2, we give an outline of the proposed modified phase-field model for brittle fracture including a brief description of the numerical formulation in Sect. 2.3. In Sect. 3 we present numerical examples that demonstrate the capability of the proposed modified phase-field model. The paper is summarised with concluding remarks.

1.1 Crack Path Prediction with the Unified Phase-Field Theory

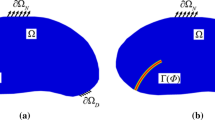
We consider here the experimentally observed crack paths in a sample of an artificial porous rock CPIR09 with one initial inclined cut under uniaxial compression load, see Fig. 1a, as described in detail in Nguyen (2011). Plane strain conditions are experimentally enforced by two very stiff sapphire glass platens to confine the specimen in thickness direction. The sample is manufactured from an artificial mixture based on clay mixed with water, organic glues and fly ash. This mixture is pressed (solidified) and afterwards sintered at 1300$^\circ$C. The resulting artificial rock has very high porosity $\phi =0.45 \ldots 0.5$ and shows hollow spheric pores with a diameter in the range $0.1\ldots 0.4$ mm, see Nguyen (2011) for further details. The artificial rock sample has dimensions of $100 \times 50 \times 35$ mm$^3$ and a 0.4 mm wide and 12 mm long initial sawed cut inclined at 45$^\circ$ as indicated by the blue line in Fig. 1a. Under displacement controlled compression load in vertical direction, so called wing cracks, W1 and W2, are evolving from both ends of the initial sawed cut. At a certain load level additional compaction bands C1 and C2 start growing from the sawed cut ends. See Fig. 7 for a more detailed evolution of the experimentally observed cracks.

In the following, we want to compare these experimentally observed crack paths with simulation based on the unified phase-field theory presented in Wu (2017). An implementation of this model is available in the open source FEM code MOOSE (Permann et al. 2020), see also Naumov et al. (2021) for a similar model provided by the open source FEM code OpenGeoSys. To be specific, we choose the unified model parameters of Wu (2017) such that the model coincides with the widely used phase-field fracture model described in Miehe et al. (2010a). Without going into details, we set Young’s modulus $E=5$ GPa, Poisson’s ratio $\nu = 0.18$, and the critical energy release rate ${\mathcal {G}}_c = 1.0$ N/m. From the artificial rocks tensile strength $\sigma _t = 1.6$ MPa we determine a regularisation length parameter $\ell _0 = 0.104$ mm. We discretised the specimen with approximately 350,000 second order Lagrange finite elements. The predicted crack path is depicted in Fig. 1b and one observes quite large deviations between the experimentally observed and numerically predicted paths of the two wing cracks. Furthermore, the model formulation explicitly assumes that no cracks under compressive strains evolve thus the experimentally observed compaction bands can not be modelled. For comparison we depict beforehand in Fig. 1c the predicted crack paths using our modified phase-field fracture model. One observes a considerably better agreement with the experimental result. In the following, we describe this modified model in detail.

Fig. 1

a Experimentally observed crack path (red lines) initiated by the initial sawed cut (blue line), Nguyen (2011), b crack path prediction based on the unified phase-field theory by Wu (2017) and c predicted crack path by our modified phase-field fracture model. For details, see Sect. 3.2

2 Formulation of the Modified Model

In this section, we give a brief recapitulation of the Griffith energy-based failure criterion. The criterion is based on elastic fracture mechanics and states that the elastic energy released during fracture propagation is balanced by newly created surface energy.

2.1 Griffith’s Theory of Brittle Failure

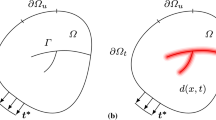
Consider an arbitrary body $\varOmega$ with boundary $\partial \varOmega$ and internal discontinuity boundary $\varGamma$, see Fig. 2a. Let $\varvec{u}$ denote the displacement vector, then the infinitesimal strain tensor $\varvec{\varepsilon }$ is defined as the symmetric part of the displacement gradient tensor $\nabla \varvec{u}$, i.e. $\varvec{\varepsilon }(\varvec{u}) = \frac{1}{2}[\nabla \varvec{u} + [\nabla \varvec{u}]^{T}]$.

Fig. 2

a Representation of a solid body $\varOmega$ with internal discontinuity boundary $\varGamma$. b Approximation of internal discontinuity boundaries by the phase-field d(x, t)

By assuming isotropic linear elasticity, the elastic energy stored in the undamaged bulk of a body $\varOmega$ is given by

$$\begin{aligned} \varPsi _e= & {} \int _{\varOmega }\psi _e^0(\varvec{\varepsilon }) \ dV \nonumber \\= & {} \int _{\varOmega } \frac{1}{2} \lambda [\text {tr} \varvec{\varepsilon }]^2 + \mu \text {tr}[\varvec{\varepsilon }^2] \ dV \end{aligned}$$

(1)

where $\lambda$ and $\mu$ are the Lamé constants. Griffith’s theory of brittle failure states that the total energy $\varPsi$ of the body is given by

$$\begin{aligned} \varPsi = \varPsi _e + \varPsi _d - \varPsi _{\text {ext}} \end{aligned}$$

(2)

where $\varPsi _{\text {ext}}$ is the potential of the external forces and $\varPsi _d$ is the energy needed for evolution of the internal discontinuity boundary $\varGamma (t)$, defined as

$$\begin{aligned} \varPsi _d = \int _{\varGamma } {\mathcal {G}}_c \ dA \end{aligned}$$

(3)

with ${\mathcal {G}}_c$ the critical fracture energy density.

2.2 Modified Phase-Field Approximation

The basic idea behind the phase-field fracture models is to let a scalar order field parameter $d(\varvec{x},t)\in [0,1]$ indicate a fracture in the body $\varOmega$, see Fig. 2b. In this work the material is undamaged as long as the phase-field $d=1$, and a fracture is represented by $d=0$. The phase-field model is based on an approximation of the total energy needed for a fracture to grow, $\varPsi _d$, in a body $\varOmega$. A number of different methods have been suggested to approximate the fracture energy, one widely used formulation was suggested by Bourdin et al. (2000). Where the fracture energy is approximated as

$$\begin{aligned} \varPsi _d= & {} \int _{\varGamma } {\mathcal {G}}_c \ dA \nonumber \\\approx & {} \int _{\varOmega } {\mathcal {G}}_c \Big [\frac{(d-1)^2}{4 \ell _0} + \ell _0 \vert \nabla d \vert ^2 \Big ] \ dV \end{aligned}$$

(4)

with $\nabla d$ representing the spatial gradient of the phase-field, imperative for driving the crack propagation, and where $\ell _0$ is a model parameter that controls the width of the approximation of the fracture zone. Earlier work (Pham and Marigo 2010a, b; Kuhn and Müller 2010; Pham et al. 2011) have suggested that the length, $\ell _0$, can be regarded as a material parameter. The suggested expression links the length parameter to the Young’s modulus E, the tensile strength $\sigma _t$, and the critical energy release rate ${\mathcal {G}}_c$ by the relation $\ell _0 = \frac{27 E {\mathcal {G}}_c}{512 \sigma _t^2}$. Bourdin et al. (2000) pointed out that the early phase-field approximations gave unrealistic crack patterns during compression. Miehe et al. (2010a) suggested a decomposition of the elastic energy $\psi _e(\varvec{\varepsilon }) = \psi ^{+}_{\text {e}}(\varvec{\varepsilon }) + \psi ^{-}_{\text {e}}(\varvec{\varepsilon })$ based on positive and negative eigenvalues of the strain tensor to remedy the problem with unrealistic cracks during compression. An alternative split of the strain energy was proposed earlier by Amor et al. (2009). Using the decomposition of the elastic energy, Miehe et al. (2010a) proposed a reformulation of the elastic energy density Eq. (1), to

$$\begin{aligned} \psi _e^0(\varvec{\varepsilon }, d) = [(1 - \eta )d^2 + \eta ]\psi _e^{+} +\psi _e^{-} \end{aligned}$$

(5)

where $\eta \ll 1$ is a small residual stiffness, introduced to prevent numerical problems and where $\psi _e^{+}$ and $\psi _e^{-}$ are the strain energies based on positive and negative eigenvalues of the strain tensor.

Following Miehe et al. (2010a and 2015) we get a coupled set of equations,

$$\begin{aligned} \varvec{0} =&\text {div}{\varvec{\sigma }} + \varvec{f} \quad \text {with} \quad \varvec{\sigma n}\vert _{\partial \varOmega _t} = \varvec{t}^*&\end{aligned}$$

(6)

$$\begin{aligned} \frac{\dot{d}}{\tilde{M}} =&-2d[1 - \eta ] \tilde{{\mathcal {H}}} - \left[ \frac{1}{2 \ell _0}[d-1] \right. \nonumber \\&\quad \left. + 2\ell _0 \varDelta d \right] \quad \text {with} \quad \nabla d \cdot \varvec{n}\vert _{\partial \varOmega } = 0&\end{aligned}$$

(7)

where the crack driving ratio

$$\begin{aligned} \tilde{{\mathcal {H}}}= &\, {} \frac{{\mathcal {H}}}{{\mathcal {G}}_c} \nonumber \\= &\, {} \frac{1}{{\mathcal {G}}_c}\max \limits _{s\in [0,t]}(\psi _e^{+}(\varvec{x},s)) \end{aligned}$$

(8)

is introduced as a local history field which drives the phase-field and prevents the crack from healing in the case of unloading. In Eq. (7) the term $\left[ \frac{1}{2 \ell _0}[d-1] + 2\ell _0 \varDelta d \right]$ is called the geometric resistance of the regularised crack and the term $-2d[1 - \eta ] \tilde{{\mathcal {H}}}$ is a crack driving force. The kinetic coefficient or mobility parameter $\tilde{M}$ in the evolution term $\frac{\dot{d}}{\tilde{M}}$ is a non-negative scalar function $\tilde{M}(\varvec{\varepsilon },d,\nabla d, \dot{d})$ introduced to control the crack velocity. The most simple assumption, $\tilde{M}=$ constant, leads to the standard Ginzburg-Landau evolution equation, see Kuhn and Müller (2010).

Remark 1

This evolution equation of the phase-field d is interpreted in Miehe et al. (2015) as a generalised formulation of a constitutive balance equation for the regularised crack surface in the sense of a Ginzburg–Laudau equation. It is open for different constitutive models of energetic and non-energetic crack driving forces. It is not an approximation of Francfort and Marigo (1998) variational approach as shown by May et al. (2015). Miehe et al. (2016) show the thermodynamic consistency of this evolution equation in the sense of the (reduced) Clausius-Duhem dissipation inequality. E.g., positive dissipation is achieved for material parameters ${\mathcal {G}}_c, \ell _0, \tilde{M} > 0$, a positive and monotone increasing history field $\tilde{{\mathcal {H}}}$ etc.

The main idea is to propose a constitutive model of the crack driving force term, by modifying the crack driving ratio $\tilde{{\mathcal {H}}}={\mathcal {H}}/{\mathcal {G}}_c$. We start with the common volumetric-deviatoric split of the isotropic linear elastic strain energy density

$$\begin{aligned} \psi _e(\varvec{\varepsilon })= &\, {} \psi _e^{vol} + \psi _e^{dev}\nonumber \\= &\, {} \frac{1}{2} K [\text {tr} \varvec{\varepsilon }] + \mu \text {tr} [\varvec{\varepsilon }^2_{\text {d}}] \end{aligned}$$

(9)

where $\varvec{\varepsilon }_{\text {d}} = \varvec{\varepsilon } - 1/3\,\text {tr} \varvec{\varepsilon }$ is the deviatoric part of the strain tensor and K the bulk modulus. Furthermore, we introduce a split of the deviatoric part of the strain tensor in a positive and negative part by

$$\begin{aligned} \varvec{\varepsilon }_{d+}= & {} \sum _{i=1}^\delta \langle \varepsilon ^i_d\rangle _{+} \varvec{n^i}\otimes \varvec{n^i} \quad \text {and}\nonumber \\ \varvec{\varepsilon }_{d-}= & {} \sum _{i=1}^\delta \langle \varepsilon ^i_d\rangle _{-} \varvec{n^i}\otimes \varvec{n^i} \end{aligned}$$

(10)

where $\{\varepsilon ^i_d\}_{i=1\ldots \delta }$ are the principal values and $\{\varvec{n}^i\}_{i=1\ldots \delta }$ are the orthonormal eigenvectors of the deviatoric strain tensor. $\langle x\rangle = \langle x\rangle _{+} = [x+ | x |]/2$ are the Macaulay brackets and $\langle x\rangle _{-} = [x - | x |]/2$ a similar bracket operator for the negative range. With this at hand we define

$$\begin{aligned} \begin{aligned} \psi _e^{vol+}&= \frac{1}{2} K \langle \text {tr}[\varvec{\varepsilon }] \rangle ^2 H(\text {tr}[\varvec{\varepsilon }])&\\ \psi _e^{dev+}&= \mu \text {tr}[(\varvec{\varepsilon }_{\text {d}}^+)^2] H(\text {tr}[\varvec{\varepsilon }])&\\ \psi _e^{-}&= \frac{1}{2} K [\text {tr}[\varvec{\varepsilon }] - \langle \text {tr}[\varvec{\varepsilon }] \rangle ]^2 \\&\quad + \mu \text {tr}[(\varvec{\varepsilon }_{\text {d}}^-)^2] [1-H(\text {tr}[\varvec{\varepsilon }])] \end{aligned} \end{aligned}$$

(11)

where the Heaviside function $H(\text {tr}[\varvec{\varepsilon }])$ is used. With these parts of the strain energy density we propose the following crack driving ratio

$$\begin{aligned} \tilde{{\mathcal {H}}}= &\, {} \max \limits _{s\in [0,t]}(\psi ^{\pm }) \quad \text {with}\nonumber \\ \psi ^{\pm } = &\, {} \frac{\psi _e^{vol+}}{{\mathcal {G}}_{\text {vol}}^+} + \frac{\psi _e^{dev+}}{{\mathcal {G}}_{\text {dev}}^+} + \frac{\psi _e^{-}}{{\mathcal {G}}_{\text {band}}} \end{aligned}$$

(12)

In comparison to Eq. (8), we use two different model parameters ${\mathcal {G}}_{\text {vol}}^+$ and ${\mathcal {G}}_{\text {dev}}^+$ to scale the crack driving forces stemming from positive volumetric strain (leading to $\psi _e^{vol+}$) and positive deviatoric strains $\varvec{\varepsilon}_{d}^{+}$ (leading to $\psi _e^{dev+}$).

Moreover, porous rocks, e.g., sandstone or volcanic rock, in general exhibit cracks during compression, see e.g., Rudnicki (2002). To allow for so-called compaction bands caused by compressive strains, i.e., negative volumetric and negative deviatoric strains $\varvec{\varepsilon}_{d}^{-}$, we use a third model parameter ${\mathcal {G}}_{\text {band}}$ to scale the corresponding strain energy part $\psi _e^{-}$. This is motivated by the energy release model of compaction bands by Rudnicki and Sternlof (2005). They introduced an energy release per unit area created of compaction band with thickness h

$$\begin{aligned} {\mathcal {G}}_{\text {band}} = \frac{1}{2} \Big [ E \left( \frac{\delta }{h} \right) \Big ]\delta \end{aligned}$$

(13)

with $\delta$ the applied displacement which is necessary to create the compaction band.

As compressive strains now lead to crack-like failures, i.e., compaction bands, we modify the stress computation in the balance of linear momentum, Eq. (6) as

$$\begin{aligned} \psi _e^0(\varvec{\varepsilon }, d)= &\, {} [(1 - \eta )d^2 + \eta ]\psi _e(\varvec{\varepsilon }) \quad \hbox {and}\nonumber \\ \varvec{\sigma }= &\, {} \frac{\partial \psi _e^0}{\partial \varvec{\varepsilon }}. \end{aligned}$$

(14)

Besides the modification of the crack driving ratio $\tilde{{\mathcal {H}}}$, we further propose a non-constant mobility parameter $\tilde{M}(\varvec{\varepsilon }) = \tilde{m}_1 + \tilde{m}_2 H(\text {tr}[\varvec{\varepsilon }])$. Making use of the equations of above the proposed phase-field fracture model may be written as

$$\begin{aligned} \begin{aligned} \varvec{0} =&\,\ \text {div}{\varvec{\sigma }} + \varvec{f}\\ 0 =&\ 2d[1 - \eta ] \tilde{{\mathcal {H}}} + \frac{1}{2 \ell _0}[d-1] + 2 \ell _0 \varDelta d +\frac{\dot{d}}{\tilde{M}} \quad \hbox {with} \\ \tilde{{\mathcal {H}}} =&\,\max \limits _{s\in [0,t]}(\psi ^{\pm }) \quad \hbox {and}\\ \psi ^{\pm } =&\frac{\psi _e^{vol+}}{{\mathcal {G}}_{\text {vol}}^+} + \frac{\psi _e^{dev+}}{{\mathcal {G}}_{\text {dev}}^+} + \frac{\psi _e^{-}}{{\mathcal {G}}_{\text {band}}} \end{aligned} \end{aligned}$$

(15)

Remark 2

The failure mechanism observed in compaction bands of porous rocks is the collapse of hollow pores under compressive load. This results in a strong reduction of the local stiffness. Further loading leads the compaction band to close and full contact is achieved. Thus, the local stiffness of the compaction band increases again. Our model can predict with the help of Eq. (14) in combination with the evolution Eq. (15) only the onset of the compaction band formation. I.e., the initial strong reduction of the stiffness in a localized band. In our model further compressive loading leads to interpenetration of the compaction band faces as Eq. (14) does not contain an unilateral contact. Nevertheless, we can model the onset of compaction bands and also the evolution of relative small compaction bands quite good as shown later by comparing numerical examples with experimental results.

Remark 3

Following Miehe et al. (2016) positive dissipation is achieved for ${\mathcal {G}}_{\text {vol}}^+, {\mathcal {G}}_{\text {dev}}^+, {\mathcal {G}}_{\text {band}} > 0$ as this results in a positive and monotone increasing history field $\tilde{{\mathcal {H}}}$. Furthermore, observe that in the case we set ${{\mathcal {G}}_{\text {vol}}^+} = {{\mathcal {G}}_{\text {dev}}^+} = {\mathcal {G}}_c$ and formally set the factor $1/{\mathcal {G}}_{\text {band}} = 0$ in Eq. (12) then we obtain the same crack driving ratio as in Eq. (8) because $\psi _e^+ = \psi _e^{vol+} + \psi _e^{dev+}$.

2.3 Numerical Formulation

We briefly present the spatial discretisation of the phase-field model presented in the previous section. The spatial discretisation is formulated by means of the Galerkin method, using $C^1$-continuous NURBS basis functions as the finite dimensional approximations to the function spaces of the weak form. Moreover, earlier work by Wick (2017) have shown that the non-linearities and non-convexity of the phase-field fracture model has proved difficult to solve using a fully monolithic scheme. In this work we utilise a staggered scheme, first presented by Bourdin et al. (2000), to solve the displacements and phase-field separately. The staggered approach allows for robust solution of the incremental update of both the displacement and phase-fields. We solve for the field variables for each discrete time step $0,t_{1},\ldots ,t_{n},t_{n+1},\ldots ,T$, where $t_{n}$ denotes the last time step for which all field variables, $\varvec{u}_{n}, d_{n}$, are assumed to be known. With the staggered scheme we determine the field variables in the current time step $t_{n+1}$ for the time increment $\varDelta t = t_{n+1} - t_{n}$. The rate of the phase-field is considered to be constant over each time increment, and is defined as $\dot{d} = (d_{n+1}-d_{n}) / \varDelta t$ and we use a Euler backward method for the time integration of the phase-field evolution equation.

Furthermore, we define the displacement field using a vector-matrix notation, i.e., ${\mathbf {u}}^e = {\mathbf {N}}_u^{e} \hat{{\mathbf {u}}}^{e}$ and the phase-field as $d^e = {\mathbf {N}}_d^e \hat{{\mathbf {d}}}^e$ for each control point in the support of an element, see Cottrell et al. (2009). Moreover, ${\mathbf {N}}_u^{e}$ and ${\mathbf {N}}_d^e$ are the NURBS basis functions. Using these definitions we can write the discretised version of the weak form of the mechanical part of the phase-field model as

$$\begin{aligned} \sum ^{n}_{e=1} (\delta \varvec{u}^e) \Bigg [ \int _{\varOmega } \Big [ -[{\mathbf {B}}_{\delta u}^e]^{T} \varvec{\sigma }_h + {\mathbf {N}}_{\delta u}^e \ f_h \Big ] dV + \int _{\partial \varOmega _t} {\mathbf {N}}_{\delta u}^e \ \varvec{t}^* dA \Bigg ]= 0 \end{aligned}$$

(16)

where ${\mathbf {B}}_u^e$ is an operator mapping the element discrete displacements to the local strains. Likewise, the discretised version of the weak form of the phase-field part is defined as

$$\begin{aligned} \begin{aligned}&\sum ^{n}_{e=1} \delta {d}^{e} \Bigg [ - \int _{\varOmega } {\mathbf {N}}_{\delta d}^e \Big ( \frac{\dot{d}^e}{\tilde{M}} + \frac{1}{2\ell _0}(d^e-1) \Big ) -[{\mathbf {B}}_{\delta d}^e]^T 2 \ell _0 \nabla d^e \\&\quad + ..\quad {\mathbf {N}}_{\delta d}^e \Big ( 2d^e(1 - \eta ) \tilde{{\mathcal {H}}}\Big ) \ \text {dV} \Bigg ] = 0. \end{aligned} \end{aligned}$$

(17)

where the discrete gradient of the phase-field is determined as $\nabla d^e = {\mathbf {B}}_d^e \hat{{\mathbf {d}}}^e$, where ${\mathbf {B}}_d^e$ is an operator containing the derivative of the basis functions.

3 Numerical Examples

In this section we demonstrate the performance of the proposed modified phase-field fracture model. First, we present results for a standard benchmark test, presented by Miehe et al. (2010a). Furthermore, we showcase the capacity of the proposed model for simulation of brittle fracture and compaction band propagation in a porous artificial rock, CPIR09, during compression under plane strain conditions. The simulations of the rock samples follow the experimental work presented in Nguyen (2011). For all the simulations the residual stiffness has been selected to $\eta = 1 \times 10^{-12}$.

Remark 4

For phase-field fracture simulations based on a Finite Element framework typically $\eta = 1 \times 10^{-6}$ is set. For much lower values one may get a bad conditioned stiffness matrix which leads to numerical problems during the solution procedure. A value of $\eta = 1 \times 10^{-6}$ may still have non-negligible influence on the predicted crack path as shown in Geelen et al. (2018). They introduced additional cutting elements in the phase-field fracture approach to model the fully broken material with zero residual stiffness. Whereas in our isogeometric analysis (IGA) based approach we can set $\eta$ to a six order of magnitude lower value without observing a bad conditioned stiffness matrix. We assume that this is due to larger support of the IGA knots in comparison to the support of a FEM node. Variation of $\eta = 10^{-11}\ldots 10^{-13}$ did not show any visible influence on the predicted crack paths.

3.1 Single Edge Notched Shear Test

In this section we consider a shear benchmark test, comprised of a square plate with a single initial crack from the left edge to the middle of the plate along the horizontal centre-line, see Fig. 3a. The aim of this shear benchmark test is to check whether our modified model has a significant influence on the predicted crack path and force-deflection behaviour. For the simulation we set the Young’s modulus $E = 210$ GPa, Poisson’s ratio $\nu =0.3$ and our crack driving parameters ${\mathcal {G}}_{\text {vol}}^+ = {\mathcal {G}}_{\text {dev}}^+ = 2.7 \times 10^{-3}$ MN/m. Furthermore, we set ${\mathcal {G}}_{\text {band}} = 1 \times 10^{10}$ MN/m, an artificially high value, such that no fractures will evolve from compressive stresses during the simulation. According to Kuhn and Müller (2010) the effective element size, $h_e$, should be approximately one half of the regularisation length $\ell _0$ for the phase-field model to capture the accurate crack paths. We choose a uniform mesh with element size $h_e = \frac{1}{2} \ell _0$ which coincides with a mesh of approximately 74,000 elements. Furthermore, the simulation is conducted in a displacement driven context with constant displacement increment of $\varDelta u = 1 \times 10^{-5}$ mm, and the mobility parameter $\tilde{m}_1 = 1.0 \times 10^{-12}$ and $\tilde{m}_1 + \tilde{m}_2 = 1.0$.

Fig. 3

a Geometry and boundary conditions for the $1 \times 1$ mm$^2$ plate in the single edge notched shear test. b Force-displacement curve for the single edge notched shear test

Figure 4 presents the crack pattern at different stages of the simulation while Fig. 3b shows the load-deflection curve for the single edge notched test. The results produced with the suggested modified phase-field model are in good agreement with the results presented by Miehe et al. (2010a).

Fig. 4

Crack patterns for the single edge notched shear test. a $u=9.8 \times 10^{-3}$ mm, b $u=11.8 \times 10^{-3}$ mm and c $u=14.0 \times 10^{-3}$ mm

The results shown in Figs. 3b and  4 demonstrate that the proposed modified phase-field fracture model produces negligible changes in the predicted crack path as well as only small differences in the load-deflection curves compared to earlier work using the standard phase-field fracture model.

3.2 Uniaxial Compression of CPIR09 Sample with One Initial Inclined Cut

In this section we consider a plane strain compression test of an artificial rock, CPIR09, with an inclined cut. The results from the simulation are compared to the results from experiments conducted by Nguyen (2011), see also Nguyen et al. (2011). The rock sample has dimensions of $100 \times 50 \times 35$ mm$^3$ with a 0.4 mm wide and 12 mm long initial sawed cut inclined at $45^{\circ }$, see Fig. 5. The experiment was conducted under plane strain uni-axial compression, and the sample was subjected to a displacement rate of 0.01 mm/min until failure. The left and the right faces of the sample are load free. The artificial rock exhibits a crack pattern with initial anti-symmetric cracks, called wing cracks W, starting at the tips of the initial cut, see Fig. 7a–c. The wing cracks are followed by secondary compression cracks C, which emerge on the opposite side from the wing cracks at tips of the initial notches. For the numerical simulations of the experiment we use the set-up and geometry of the experiment. According to the results presented in Nguyen (2011) the stiffness of the tested rock samples varied within a range of approximately $30\,\%$, while both the fracture patterns and the strength of the material are consistent throughout the experiments. We have chosen to set the Young’s modulus $E = 5$ GPa and Poisson’s ratio, $\nu = 0.18$, which is in the upper region of the stiffnesses measured during the experiments. The values for the crack driving force parameters, the mobility parameters and the tensile strength of the artificial rock are not reported in Nguyen (2011). Thus we have chosen to set ${\mathcal {G}}_{\text {vol}}^+ = 1.0$ N/m, ${\mathcal {G}}_{\text {dev}}^+ = 10$ N/m, and ${\mathcal {G}}_{\text {band}} = 100$ N/m, see also Spetz et al. (2020). The mobility parameters $\tilde{m}_1 = 1.0$ and $\tilde{m}_2 = 0.0$. With the tensile strength selected to $\sigma _t = 1.6$ MPa the regularisation length is calculated to $\ell _0 = 0.104$ mm. To capture the evolving crack paths we use an almost constant element size of $h_e \approx \frac{1}{2}\ell _0$ throughout the entire specimen, which leads to a mesh with approximately 350,000 elements.

Fig. 5

Geometry of the CPIR09 sample with an inclined notches

To illustrate how the choice made for the strain energies affects the evolution of a crack, Fig. 6 plots the level set of the crack driving ratio $\tilde{{\mathcal {H}}}$, see Eq. (12), with regards to the principal strains $\varepsilon ^1$ and $\varepsilon ^2$ for the artificial rock CPIR09. From the figure we can see that by, e.g., increasing ${\mathcal {G}}_{\text {band}}$ we decrease the tendency for compressive or shearing cracks to appear.

Fig. 6

Level set plots of the crack-driving ratio $\tilde{{\mathcal {H}}}$ with respect to principal strains $\varepsilon ^1$ and $\varepsilon ^2$ for artificial rock CPIR09

Figure 7 illustrates the crack evolution at different stages, where Fig. 7a–c are displaying photos taken during the experiments conducted by Nguyen (2011), where the initial cut is highlighted in blue colour and the propagating cracks in red. For comparison, Fig. 7d–f shows the evolution of the phase-field parameter d from the simulation at equivalent nominal compression strains. From Fig. 7 it is clear that the model is able to reproduce the crack patterns from the experiment conducted by Nguyen (2011) with high accuracy.

Figure 8 depicts the nominal stress–strain curve from the simulation of the compression test of the artificial rock together with the measurements performed by Nguyen (2011). The general stress–strain behaviour from the simulation is in good agreement with the experimental observations until closure of the compressive cracks take place, at point 5, where the experimental measurements show that when the compressive fractures close and full contact is achieved the rock sample carries additional load before total failure. An appropriate additional contact formulation is not included in our proposed model, and this is outside the scope of this work. To illustrate that the horizontal fractures indeed arise from compressive stress state, Fig. 9 compares the maximum shear strains, $\varepsilon _{\text {s-max}}$, and volumetric strain, $\varepsilon _{\text {vol}}$, from the simulations to results from a digital image correlation, DIC, measurements presented in Nguyen (2011). Hereby, $\varepsilon _{\text {s-max}} = \frac{1}{2}(\varepsilon _{\text {max}}-\varepsilon _{\text {min}})$ and $\varepsilon _{\text {vol}} = \varepsilon _{\text {max}}+\varepsilon _{\text {min}}$ with $\varepsilon _{\text {max}}$ being the maximum value of the principal strains and $\varepsilon _{\text {min}}$ the minimum value.

Fig. 7

a–c Displays pictures from the experimental results, Nguyen (2011), of the crack pattern at point 3–5 in Fig. 8 and d–f the phase-field parameter from the numerical simulation for the corresponding points

Fig. 8

Comparison of measured Nguyen (2011), and simulated nominal stress–strain curves for CPIR09 sample with one inclined cut

From Fig. 9c and d it is obvious that the volumetric strain takes a negative value where the compressive cracks are formed. Moreover, it can be noted that the fracture zones appear much wider in the DIC images Fig. 9a and c compared to the numerical results. This is a result of the blurring effect caused by the DIC measurements. A measure of the blurring effect can be estimated by comparing the thickness of the initial inclined cut in Fig. 9a with the inclined cut of correct thickness depicted in Fig. 9b. Comparing the images, we estimate that the DIC measurements blur the cut thickness by approximately a factor 5. Additionally, we want to indicate that we use the same colour bar ranges for the DIC images as for the results from the numerical simulation.

Fig. 9

Comparison of experimental results from Nguyen (2011) a and c and numerical results b and d at point 5 in Fig. 8, a and b displays the maximum shear strain $\varepsilon _{s-max}$, and c and d the volumetric strain $\varepsilon _{\text {vol}}$

Another interesting observation in Fig. 9c,d is that in the large wing cracks W1 and W2 one find a positive volumetric strain. That means the wing cracks show a positive jump in the displacement field and the crack surface are not in contact. Thus, potential friction forces between the crack surfaces are zero or at least very small. We investigated this further by computing the normal strain component $\varepsilon _{nn}$ from our simulation in three positions of the wing cracks. The three selected positions are given by the three yellow lines in Fig. 7d, f. The lines are aligned to the normal direction n of the wing crack. The resulting normal strain component $\varepsilon _{nn}$ along the normal direction n is depicted in Fig. 10. As they show across the crack positive values we can conclude that the wing cracks are opened during the compressive loading of the specimen.

Fig. 10

Normal strain component $\varepsilon _{nn}$ across the diffuse wing crack. The positions of Lines 1–3 are indicated by yellow lines in Fig. 7d, f

3.3 Uniaxial Compression of CPIR09 Sample with Two Initial Inclined Cuts

In this section we consider a plane strain compression test of an artificial rock, CPIR09, with two inclined cuts conducted by Nguyen (2011). The rock sample presented has the dimensions of $100 \times 50 \times 35$ mm$^3$ with two 0.4 mm wide and 12 mm long initial cuts, inclined at $45^{\circ }$, see Fig. 11. The experiments were conducted under plane strain uni-axial compression, and the sample was subjected to a displacement rate of 0.05 mm/min until failure. We kept the material parameters to the same values as for the previous example.

Fig. 11

Geometry of the CPIR09 sample with two inclined cuts

Fig. 12 illustrates the crack evolution at different stages, where Fig. 12a–c shows photos from the experiments conducted by Nguyen (2011), and Fig. 12d–f the evolution of the phase-field parameter d for the corresponding points during the simulation. We have chosen the first point Fig. 12d to be at 0.9 of the peak stress, the second point Fig. 12e at the peak stress and the third point Fig. 12f where contact between the internal crack surfaces has been reached in the compressive cracks during the experiments, see Fig. 13. From Fig. 12 we note that the evolution of the phase-field is in good agreement with the experimental observation of the crack patterns. We also note some deviation between the numerical results and the observed velocity of the crack evolution of the compression cracks, C1 and W4. The small difference between the results may stem from a variety of factors, for one, the differences in boundary condition might affect the crack paths in the rock sample as the cracks get closer to the boundary. In the experimental set-up, friction will naturally exist between the compression plates of the testing machine and the rock sample, whereas we assume no horizontal constraints neither at the top or bottom boundaries in our simulations.

Fig. 12

a–c Displays pictures from the experimental results, Nguyen (2011), of the crack pattern at point 3–5 in Fig. 15 and d–f the phase-field from the numerical simulation for the corresponding points

Fig. 13

Comparison of measured Nguyen (2011), and simulated nominal stress–strain curves for CPIR09 sample with two inclined cuts

Figure 13 compares the simulated nominal stress–strain behaviour to the measurements performed by Nguyen (2011). The measured nominal stress–strain behaviour starts with an unexpected nonlinear part. According to Nguyen (2011), this non-linear behaviour can be related to three factors; (i) closure of pre-existing cracks, (ii) non-linear behaviour of the material, (iii) imperfections in the contact surfaces between the rock sample and testing machine. The results presented in Fig. 13 have therefore been adjusted to accommodate these factors by adding an initial axial strain $\varepsilon _{\text {initial}} = 0.0015$. Furthermore, we can see a difference in stiffness between the numerical and experimental results, which is within the difference in stiffness observed from the experiments. Except for the difference in stiffness, the general stress–strain behaviour from the simulation is in good agreement with the experimental observations until closure of the compressive cracks take place, see point 5 in Fig. 13. To give a better picture of where compressive cracks are formed and where the cracks are driven from tensile stresses, Fig. 14 compares the maximum shear strains and volumetric strain from the simulation to DIC images presented in Nguyen (2011).

Fig. 14

Comparison of experimental results from Nguyen (2011) a, c and numerical results b, d at point 5. Figure 13, a and b displays the maximum shear strain $\varepsilon _{\text {s-max}}$, and c and d the volumetric strain $\varepsilon _{\text {vol}}$

Figure 14 illustrates the strain states at point 5. Figs. 13 and  15 give a close-up of the zone between the two initial cuts, where we observe that the model captures the complex crack patterns with only small deviations. Additionally, we observe the same blurring effect in the DIC measurements as in Fig. 9.

Fig. 15

A close-up of the zone between the two initial cuts, comparing the experimental measurement from Nguyen (2011) a, c and numerical results b, d at point 5 in Fig. 13, where a and b displays the maximum shear strain $\varepsilon _{\text {s-max}}$, and c and d the volumetric strain $\varepsilon _{\text {vol}}$

4 Conclusion

In this work we have presented a modified phase-field fracture model for simulation of wing crack and compaction band propagation in porous rocks. The presented model introduces a split in the crack driving force to capture the characteristic behaviour of fractures in porous rock. In porous rock, the fracture toughness for energy for Mode I cracks can be orders of magnitude smaller than the fracture toughness for energy for Mode II cracks and compressive stresses can lead to the formation of compressive cracks. To capture these characteristic behaviours we have introduced three model parameters ${\mathcal {G}}_{\text {vol}}^+, {\mathcal {G}}_{\text {dev}}^+, {\mathcal {G}}_{\text {band}}$ to scale the different parts of the elastic strain energy density which enters the crack driving force. We have illustrated how the scaling of the crack driving forces can be used to control the tendency for wing cracks and compressive cracks to appear. Furthermore, to demonstrate the capability of the modified phase-field fracture model first introduced in this work, we have compared the numerical results to experimental observations performed on rock samples subjected to uni-axial plane strain compression. The presented comparison shows that the modified phase-field fracture model gives results in good agreement to the experimental observations both with respect to crack patterns and critical stress loads. We have also shown that the proposed phase-field model is able to reproduce the formation of compressive cracks as well as complex crack patterns without any additional algorithmic treatment.