Phase structural ordering kinetics of second-phase formation in the vicinity of a crack

Abstract

The formation of a second phase in presence of a crack in a crystalline material is modelled and studied for different prevailing conditions in order to predict and a posteriori prevent failure, e.g. by delayed hydride cracking. To this end, the phase field formulation of Ginzburg–Landau is selected to describe the phase transformation, and simulations using the finite volume method are performed for a wide range of material properties. A sixth order Landau potential for a single structural order parameter is adopted because it allows the modeling of both first and second order transitions and its corresponding phase diagram can be outlined analytically. The elastic stress field induced by the crack is found to cause a space-dependent shift in the transition temperature, which promotes a second-phase precipitation in vicinity of the crack tip. The spatio-temporal evolution during nucleation and growth is successfully monitored for different combinations of material properties and applied loads. Results for the second-phase shape and size evolution are presented and discussed for a number of selected characteristic cases. The numerical results at steady state are compared to mean-field equilibrium solutions and a good agreement is achieved. For materials applicable to the model, the results can be used to predict the evolution of an eventual second-phase formation through a dimensionless phase transformation in the crack-tip vicinity for given conditions.

1 Introduction

Most metallic materials experience some type of interaction with their surrounding environment, which often results in changes in the material morphology that may induce deterioration of their mechanical and physical properties. For many practical applications such changes may derogate a material function and its usefulness, which may eventually lead to failure. If stresses are applied to a structure subjected to a corrosive environment, cracks that would not occur in the absence of one of these two controlling conditions will appear, even for virtually inert material. Thus, the combination of these factors may lead to failure, which is commonly referred to as stress corrosion cracking (Jones 1992).

Hydrogen embrittlement (HE) can be considered to be a type of stress corrosion, since it commonly concerns a ductile metal undergoing a brittle fracture as a result of the combination of applied stresses and a corrosive environment. HE can also occur in mechanically loaded materials that already contain hydrogen emanating from either the manufacturing process or from earlier exposure to hydrogen. For some cases of HE, hydride formation plays a central role in the detoriation process. A hydride is a brittle non-metallic phase that may cause the embrittlement of metallic materials such as titanium- and zirconium-based alloys and reduce their load bearing capabilities (Coleman and Hardie 1966; Coleman et al. 2009; Chen et al. 2004; Luo et al. 2006). For metal based components exposed to hydrogen-rich environments, such as fuel cladding materials in nuclear power reactors or components in rocket engines, there is an impending risk of hydrides forming, which could lead to the so called delayed hydride cracking (DHC). This is a subcritical crack growth mechanism (Coleman et al. 2009; Singh et al. 2004; Coleman 2007; Northwood and Kosasih 1983) that can severely reduce the component life-time and jeopardize its integrity.

Hydride formation occurs as a result of a combination of complex mechanisms, including for instance simultaneous hydrogen diffusion, hydride precipitation and material deformation (Varias and Massih 2002). For some metals, including zirconium and titanium, such formation has been specifically observed in the vicinity of stress concentrators, following the increased hydrogen transport toward regions of high hydrostatic stresses (Birnbaum 1976; Takano and Suzuki 1974; Grossbeck and Birnbaum 1977; Shih et al. 1988; Cann and Sexton 1980). It is also known that the transformation is not only driven by changes of concentration of species, such impurities and alloying elements, but mechanical stresses can per se promote the precipitation of a second phase (Birnbaum 1984; Allen 1978; Varias and Massih 2002). This type of transformation can be beneficial for instance for certain ceramic materials, which may experience an increase in fracture toughness following the transformation. For such cases, the crack propagation may be impeded following the transformation of metastable phase particles into stable particles with increased volume at the crack tip (Hutchinson 1989; Evans and Cannon 1986). Thus, the resulting transformation-induced compressive stresses in front of the crack-tip may obstruct its opening and, consequently, limit the crack growth. However, for the case of transition metals and hydrogen, such beneficial transformation is rarely observed. In fact, for the hydride forming materials the effect is rather the opposite, leading to embrittlement and reduction of the fracture toughness.

Over the years, numerous models have been developed to describe the formation of a second phase at a flaw tip in a variety of crystalline materials (Varias and Massih 2002; Deschamps and Bréchet 1998; Gómez-Ramírez and Pound 1973; Boulbitch and Korzhenevskii 2016; Léonard and Desai 1998; Hin et al. 2008; Massih 2011a; Bjerkén and Massih 2014; Jernkvist and Massih 2014; Jernkvist 2014). Among those are the models resting on the phase-field approach based on Ginzburg–Landau theory, see e.g. Provatas and Elder (2010). Such modeling has found many applications, especially in the areas of magnetic field theory where it has been found useful for providing predictive models (Cyrot 1973; Berger 2005; Barba-Ortega et al. 2009; Cao et al. 2013; Gonçalves et al. 2014). But more importantly for the present application it has also proven to be an efficient methodology to model and predict microstructure evolution in materials. The review paper by Chen (2002) and the references therein give a thorough account of applications for which phase-field modeling has been successfully used to predict the microstructural evolution. For phase field theory applied to solid material microstructure modeling order parameters are used to describe the evolution of a material state (Desai and Kapral 2009). Typically, two different order parameters may be identified to describe different type of phase transformations: the non-conserved structural order parameter corresponding to a diffusionless-type transformation and the conserved composition order parameter which represents a diffusional transformation. With this in mind, Hohenberg and Halperin (1977) defined three types of models based on the use of these order parameters individually (model A and B, respectively) and their coupling (model C).

In the material, the solid solution may be defined as a disordered material state and crystal structures with a lower degree of symmetry are considered ordered. Under stress field conditions, such as stresses induced by the presence of flaws, the evolution of the order parameters are used to model a second-phase formation. One such study was reported by Massih (2011a), who presented a general set-up with coupled conserved and non-conserved field variables in the presence of cracks and dislocations in an elastic solid. Further, in a paper by Boulbitch and Korzhenevskii (2016), a non-conserved order parameter is used to study quasi-static phase transformation in the process zone of a propagating crack. These works constitute a suitable base reference to study the second-phase formation in presence of a crack. In the present paper, the effect of stress concentration in the presence of a crack on the second-phase formation kinetics in crystalline materials is modeled. This work is an extension of the Massih’s and Bjerkén’s works (Bjerkén and Massih 2014; Massih 2011b), where precipitation kinetics at dislocations is studied by using a scalar non-conserved order parameter (Model A), accounting for microstructural reordering. The time-dependent Ginzburg–Landau (TDGL) equation is solved numerically to capture the different spatio-temporal state changes of the material in the vicinity of the crack tip. This is achieved by assessing the spatio-temporal fluctuations of the structural order parameter for different sets of material parameters, loads and phenomenological coefficients, making of this paper a full parametrical study, usually undone in the literature. The driving force of this equation, which gives the rate of change the structural order parameter, is the functional derivative of the total free energy with respect to the non-conserved order parameter (Provatas and Elder 2010). To include the effect of the crack to the modeling, a mechanical equilibrium condition is added to the free energy formulation for the system at hand. The mechanical equilibrium is solved analytically reducing the number of equations to be solved to one, the TDGL equation, as in Boulbitch and Korzhenevskii (2016). To this end, a small perturbation from a stressed reference configuration under known stress conditions due to the presence of the crack is assumed. A sixth-order Landau potential energy is incorporated in the structural free energy of the system in order to model first and second order transitions. Moreover, the total free energy of the system takes into account a coupling between the dilatation of the second phase and the order parameter (Boulbitch and Tolédano 1998). The effect of hydrogen concentration is not considered in the model.

The paper is organized as follows: first, the model employed to study the formation of the second phase in presence of the crack is described in Sect. 2. This description is followed by a theoretical steady-state analysis, accompanied by a phase diagram, in Sect. 3. Thereafter, the methodology for the numerical simulations is presented in Sect. 4. The following section, Sect. 5, demonstrates the results obtained for different cases and parameters which contains comparisons between theoretical steady-state and long-time numerical data and the influence of the interface energy on the solutions. Finally, in Sect. 6, the findings are summarized and the conclusions are stated.

2 Model description

In the Ginzburg–Landau formalism, a parameter field $\eta$ is defined as a scalar function that represents the order of the crystal structure and characterizes the presence of two concurrently prevailing phases. The order parameter depends on time and space and defines the morphology such that the high-temperature solid solution that constitutes the initial phase corresponds to $\eta =0$, whereas the transformed second-phase precipitates are represented by $\eta \ne 0$. For such systems the total free energy, ${\mathscr {F}}$, can be expressed as

$$\begin{aligned} {\mathscr {F}}={\mathscr {F}}_{st}+{\mathscr {F}}_{el}+{\mathscr {F}}_{int} , \end{aligned}$$

(1)

where ${\mathscr {F}}_{st}$ stands for the structural free energy, ${\mathscr {F}}_{el}$ the elastic-strain energy and ${\mathscr {F}}_{int}$ is the striction energy, which represents the interaction between the structure order parameter and the strain field (Ohta 1990; Massih 2011b). Each individual contribution to the free energy in (1) can be represented by an integral over the system volume, V. The structural free energy is expressed by:

$$\begin{aligned} {\mathscr {F}}_{st}=\int \Big [\frac{g}{2}(\nabla \eta )^{2}+\varPsi (\eta )\Big ]\text {d}\varvec{V}. \end{aligned}$$

(2)

in which the term $\frac{1}{2}g(\nabla \eta )^{2}$ accounts for a spatial dependence of the order parameter and the existence of interfaces within an equilibrium inhomogeneous system (Desai and Kapral 2009). The positive coefficient g takes part in the surface energy by multiplying the gradient in order parameter which only varies significantly at interfaces where a change of order occurs (Provatas and Elder 2010). The second term $\varPsi (\eta )$ is a phenomenological contribution to the free energy that was introduced by Landau and Lifshitz (1980) as the Landau potential and coincides with the bulk free density. In the present work we assume a sixth order description, expressed in the format

$$\begin{aligned} \varPsi (\eta )=\frac{1}{2}\,\alpha _{0}\,\eta ^{2}+\frac{1}{4\,}\beta _{0}\,\eta ^{4}+\frac{1}{6}\,\gamma \,\eta ^{6}. \end{aligned}$$

(3)

where $\alpha _{0}, \beta _{0}$ and $\gamma$ are named Landau coefficients in the present paper. The coefficient $\alpha _0$ displays a linear variation with the material temperature as $\alpha _0=[T-T_{c_0}]$, where the parameter a is assumed to be a positive constant and T is the material temperature and the parameter $T_{c_0}$ is the transition temperature for a defect free crystal (Provatas and Elder 2010). The definition of $\alpha _0$ is the result of an assumption of the Landau’s theory which states that $\alpha _0$ changes sign at $T_{c_0}$ (Cowley 1980). The coefficient $\beta$ and $\gamma$ are supposed to be temperature independent when the material temperature is sufficiently close to $T_{c_0}$ (Cowley 1980; Massih 2011a). Additionally, to ensure stability of the system the condition $\gamma >0$ is required whenever $\beta _{0}<0$. The elastic strain energy is expressed as

$$\begin{aligned} {\mathscr {F}}_{el} = \int M\left[ \epsilon _{ij}^{2}+\left( \frac{K}{2\,M}-\frac{1}{d}\right) \,\epsilon _{ll}^2\right] \text {d}\varvec{V}, \end{aligned}$$

(4)

where K and M are the bulk and the shear moduli respectively. The parameter d represents the space dimensionality of the considered system, while the strain tensor is defined within the small perturbations hypothesis, i.e. $\epsilon _{ij}=\frac{1}{2}(\partial u_{j}/\partial x_{i}\,+\,\partial u_{i}/\partial x_{j})$. The striction energy is written on the format

$$\begin{aligned} {\mathscr {F}}_{int} = \int -\xi \,\eta ^2\,\nabla \cdot {\mathbf {u}} \, \text {d}\varvec{V}. \end{aligned}$$

(5)

that represents the interaction between the order parameter and the displacement vector field ${\mathbf {u}}=u_i$. This contribution is characterized by the assumed positive constant $\xi$, also known as the striction factor. The striction factor is related to e.g. lattice mismatch and volume changes between phases, and represents the stress derived from the stress-free strain, i.e. the stress-free expansion. The quantity $\nabla \cdot {\mathbf {u}}$ represents the strain resulting from the stress induced by the crack (Eshelby 1957). The dilatational effects are assumed to be isotropic and are taken into account in the interface between second phase and solid solution, and in the second phase.

Based on Eqs. (2), (4) and (5), the total free energy of the system can be rewritten in a more compact notation

$$\begin{aligned} {\mathscr {F}}=\int \varphi (\eta (\varvec{r},t),{\mathbf {u}}(\varvec{r},t))\text {d}\varvec{V} \end{aligned}$$

(6)

with

$$\begin{aligned} \varphi (\eta (\varvec{r},t),{\mathbf {u}}(\varvec{r},t))= & {} \frac{g}{2}(\nabla \eta )^{2}+\varPsi (\eta )\nonumber \\&+\,M\left[ \epsilon _{ij}^{2}+\left( \frac{K}{2\,M}-\frac{1}{d}\right) \,\epsilon _{ll}^2\right] \nonumber \\&-\, \xi \,\eta ^2\,\nabla \cdot {\mathbf {u}}. \end{aligned}$$

(7)

such that $\varphi$ is the volume specific energy density of the system. Thus, mechanical equilibrium for the system, which is assumed to exist at all time, requires that

$$\begin{aligned} \frac{\partial \sigma _{ij}}{\partial x_{j}}=-\frac{\delta {\mathscr {F}}}{\delta u_{i}} = \frac{\partial }{\partial x_{j}}\left( \frac{\partial \varphi }{\partial \epsilon _{ij}}\right) = Q_i \end{aligned}$$

(8)

where $\sigma _{ij}$ is the stress tensor and $Q_i$ denotes a body force field, which is induced by the presence of an elastic defect in the solid (Massih 2011b). In the present work the considered flaw is a crack. Equation (8) can be further reduced to

$$\begin{aligned} M\,\nabla ^{2}{\mathbf {u}}+(\varLambda -M)\nabla \nabla \cdot {\mathbf {u}}-\xi \nabla \eta ^{2}=M\, {\mathbf {f}}({\mathbf {r}}) \end{aligned}$$

(9)

where $\varLambda =K+2M(1-d^{-1})$ and ${\mathbf {f}}({\mathbf {r}})$ is a function of space that describes the strain field due to the crack (Massih 2011a). By solving Eq. (9) with respect to the elastic strain field, as proposed in Massih (2011b) it can be substituted into Eq. (7), which leads to the total free energy of the system being transformed to a functional described solely by the order parameter $\eta (t,\varvec{r})$:

$$\begin{aligned} {\mathscr {F}}[\eta ]= & {} \int \Big [\frac{g}{2}\,(\nabla \eta )^{2}+\frac{1}{2}\alpha \,\eta ^{2}\nonumber \\&+\,\frac{1}{4}\,\beta \,\eta ^{4}+\frac{1}{6}\,\gamma \,\eta ^{6}\,\Big ]d\varvec{r} \end{aligned}$$

(10)

Following this rewrite, based on the assumptions of linear elastic fracture mechanics under plane strain conditions and mechanical equilibrium, the modified Landau coefficients for the quadratic and quartic terms (i.e. $\alpha$ and $\beta$ in Eq. (3), respectively) are given by

$$\begin{aligned} \alpha \equiv \left| \alpha _{0}\right| \left( \text {sgn}(\alpha _{0})-\sqrt{\frac{r_{0}}{r}}\cos \frac{\theta }{2}\right) \end{aligned}$$

(11)

and

$$\begin{aligned} \beta = \beta _{0}-\frac{2\xi ^{2}}{\varLambda }, \end{aligned}$$

(12)

where

$$\begin{aligned} r_{0}\equiv \frac{1}{2\,\pi }\left( \frac{2\,\xi \,K_{I}}{\left| \alpha _{0}\right| \,(\varLambda -M)}\right) ^{2}. \end{aligned}$$

(13)

is considered as a local characteristic length related to the presence of the crack and $K_{I}$ is the mode I stress intensity factor. It should be noted that for a defect-free crystal, $\alpha =\alpha _{0}$ and $\beta =\beta _{0}$.

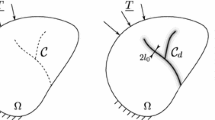
The considered geometry of the crack is described by polar coordinates with the origin placed at the crack tip, as shown in Fig. 1. Under plane strain, the crack may be seen as semi-infinite, i.e. its thickness is infinite in the out-of-plane direction.

Fig. 1

Geometry of the crack. The coordinates are represented by the polar coordinates r and $\theta$

Depending on the stress field induced by the crack, the solubility limit may vary at different positions relative to the crack tip. In order to capture such a behaviour, $\alpha$ [in Eq. (11)] is expressed as

$$\begin{aligned} \alpha = a\,\left[ T-T_{c}(r,\theta )\right] , \end{aligned}$$

(14)

where

$$\begin{aligned} T_{c}(r,\theta ) \equiv T_{c_0}+\frac{2 \, \xi \, K_{I}}{a \, (\varLambda -M)}\frac{\cos (\theta /2)}{\sqrt{2\,\pi \,r}}. \end{aligned}$$

(15)

The parameter $T_{c}(r,\theta )$ defined above is the transition temperature for a crystal containing a crack. Thus, the initial phase of a defect-free material is stable for $T>T_{c_0}$, while that of a cracked material requires $T>\max (T_c, T_{c_0})$, which implies $\alpha >0$. Consequently, a secondary phase will form in the region of the material where these conditions are not met. Likewise, owing to their influence on $\beta$, an increase of $\xi$ and a decrease in $\varLambda$ contribute to the formation and growth of a second phase.

The evolution of the non-conserved structural order parameter is determined by the employment of the TDGL, which corresponds to a diffusionless phase transformation model (Hohenberg and Halperin 1977), i.e.,

$$\begin{aligned} \frac{\partial \eta }{\partial t}=-\varGamma \frac{\delta {\mathscr {F}}}{\delta \eta }. \end{aligned}$$

(16)

where $\varGamma$ is the kinetic coefficient that represents the interface boundary mobility. By substituting the total free energy term of Eq. (10) into (16), the governing equation for the spatio-temporal order evolution becomes

$$\begin{aligned} \frac{1}{\varGamma }\frac{\partial \eta }{\partial t} = g\nabla ^{2}\eta -\big (\alpha \,\eta +\beta \,\eta ^{3}+\gamma \,\eta ^{5}\big ). \end{aligned}$$

(17)

For practicality in the modeling and the subsequent analyses, a parameter change to obtain a dimensionless equation is made:

$$\begin{aligned} \eta= & {} \sqrt{|{\alpha _{0}}|/|{\beta }|}\,\varPhi ,\, x_i=\sqrt{g/|\alpha _0|}\,\tilde{x_i}, \, r=\sqrt{g/|\alpha _0|}\,\rho ,\\ r_0= & {} \sqrt{g/|\alpha _0|}\,\rho _0\, \text { and } t=\tau /\left( |{\alpha _{0}|\,\varGamma }\right) . \end{aligned}$$

Following this manipulation, via the dimensionless analogues of Eqs. (16) and (17), the relation describing the transformed order parameter, $\varPhi$, is given by

$$\begin{aligned} \frac{\partial \varPhi }{\partial \tau } = \tilde{\nabla }^{2}\varPhi -\left( A\,\varPhi +\text {sgn}(\beta )\,\varPhi ^{3}+\kappa \,\varPhi ^{5}\right) \end{aligned}$$

(18)

where $A=\left( \text {sgn}(\alpha _{0})-\sqrt{\frac{\rho _{0}}{\rho }}\cos \frac{\theta }{2}\right)$, $\tilde{\nabla }$ is the dimensionless gradient operator for the rescaled coordinates $\tilde{x_i}=(\tilde{x},\tilde{y})$ and $\kappa =\gamma \,|\alpha _0|/\beta ^{2}$.

To gain insight behind the second phase nucleation around a crack tip, in the present study we solve Eq. (18) for different sign combinations of $\alpha _{0}$ and $\beta$. This aims to investigate the importance of temperature induced solubility variation for different materials, while the interaction between displacement field and order parameter are varied.

3 Steady-state analysis

As an initial study, we analyze the steady-state solution of Eq. (18). This corresponds to the long-time limit, at which the system does not evolve further and no additional transformations occur. This implies that $\partial \eta /\partial t=0$. Here, the Laplacian term is neglected. The physical interpretation of this simplification is that the value of the order parameter in a material point is not affected by the surrounding points. The neglect of the Laplacian term is also expected to induce the appearance of discontinuities of the function $\varPhi (x,y)$ at the crack tip and at the transition between zero and non-zero values of the order parameter. Thus, Eq. (18) is simplified as

$$\begin{aligned} \bar{\varPhi }\left( A+\text {sgn}(\beta )\,\bar{\varPhi }^{2}+\kappa \,\bar{\varPhi }^{4}\right) =0, \end{aligned}$$

(19)

where $\bar{\varPhi }$ is the order parameter of such a steady-state system containing a crack. Depending on the parameter set, the solutions to (19), which either minimize or maximize the total free energy of the system in steady state, can be found analytically. The real analytical solutions of Eq. (19) may be expressed as:

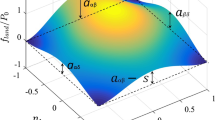
The stability condition $\gamma >0$ ensures positive values of $\kappa$ for any couple $\{\alpha _0,\,\beta \}$, and if $\bar{\varPhi }$ exists, the solutions always correspond to local extrema of the modified Landau potential. Thus, the existence of non-zero solutions to Eq. (19) depend on the signs of $\alpha _0$ and $\beta$ and the value of $\kappa$. The deduction of stability limits and phase transition characteristics for different values of $\{\alpha _0,\,\beta \}$ are given in “Appendix”, and is summarized for $\alpha _0>0$ in Fig. 2 as a phase diagram.

Fig. 2

Phase diagram presenting the length ratio $\rho \,/\left[ \rho _0\cos ^2(\theta /2)\right]$ versus $\kappa \,\text {sgn}(\beta )$ for $\alpha _0>0$. The star (*) indicates that the phase is metastable, and the disorded phase is denoted I, while the ordered is denoted II. The vertical asymptotes of the curves given by $A=\frac{1}{4\kappa }$ and $A=\frac{3}{16\,\kappa }$ are indicated with dashed lines

When $\alpha _0<0$, the parameter A is always negative. This means that the transition temperature $T_c$ becomes higher than the material temperature T, regardless of the distance from the crack. Thus, the whole material is expected to transform into the second phase. If instead $\alpha _0 > 0$, a second-phase region may form in the proximity of the crack tip with the size of the zone depending on the value of $\kappa \,\text {sgn}(\beta )$. For this case the transition temperature is higher than the material temperature only locally, which explains the limited local transformation. For $\beta >0$, only second order transitions between the phases may take place as the stability lines of the phases coincides (at $A=0$), regardless of the value of $\kappa$. For negative $\beta$, the regions of stability of the individual phases overlap, where a phase either may be stable or metastable. The stability limits for phase I ($A=0$) and II ($A=1/4\kappa$) are indicated in the figure. Between these limits the transition line $A=\frac{3}{16\,\kappa }$ can be identified, which represents a situation at which both phases are equally stable and only first order transitions are expected.

It can be seen that in immediate proximity to the crack tip (i.e. $\rho /[\rho _0\,\cos ^2(\theta /2)]<1$), the stress concentration induces a transformation from solid solution into the second phase. Further away from the crack, the situation may vary depending on the sign of $\beta$ and the value of $\kappa$. As $\kappa \, \text {sgn}(\beta ) < -3/16$, the material can be in four different states, and sorting them with increasing distance from the crack tip, they correspond to:

• a pure second-phase area, II,

• an area with second phase and metastable solid solution, I* + II,

• an area with solid solution with metastable second phase, I + II*, and

• a pure solid solution, I.

For $-\frac{3}{16}<\kappa \,\text {sgn}(\beta )<0$, it is found that the whole material is supposed to be transformed into second phase (II) with the possible presence of metastable solid solution away from the crack tip ($\rho /[\rho _0\,\cos ^2(\theta /2)]>1$). Finally, when $\kappa \,\text {sgn}(\beta )>0$ no metastable state can exist but a confined pure second-phase region should develop in the region close to the crack tip (i.e. $\rho /[\rho _0\,\cos ^2(\theta /2)]<1$).

4 Numerical method

To numerically solve the TDGL equation, presented in Sect. 2, we use the open-source partial differential equation solver package FiPy (Guyer et al. 2009), which is based on a standard finite volume approach. For the modeling, the 2d-domain illustrated in Fig. 1 is discretized using a square mesh consisting of $1000\times 1000$ equally-sized square elements with the dimensionless side length corresponding to $\varDelta \tilde{l}=0.2$. This setup, combined with a LU-factorization solution scheme, was found to yield well converged results and the system is large enough such that the boundary conditions do not affect the results. The size of the time step is deduced from a convergence study, which revealed that a time step $\varDelta \tau =0.1$ is sufficient to ensure a stable solution.

At the boundary, the gradient of $\varPhi$ is prescribed to be perpendicular to the boundary such that $\nabla \varPhi \cdot \mathbf n =0$, where $\mathbf n$ is a unit vector perpendicular to the boundary.

As initial condition the order parameter, $\varPhi _{init}$ was randomly set throughout the entire domain, with values in the range $[5 \times 10^{-5}, 1 \times 10^{-4}]$.

5 Results and discussion

In this section, the spatio-temporal evolution of the dimensionless order parameter $\varPhi$ is presented. Particular emphasis is on modeling and elucidating the material transformation for varying signs of $\alpha _0$ and $\beta$ and the varying value of $\kappa$. These combinations represent different characteristic locations in the phase diagram illustrated in Fig. 2. Thereafter, the numerically obtained steady-state results are discussed with reference to the analytical mean-field solutions given in Sect. 3. Moreover, the width of inherent smooth interface is discussed, and finally, the influence of material stiffness and strength of interaction between strain field and order parameter are investigated.

Fig. 3

a–c Evolution of the dimensionless order parameter $\varPhi =\varPhi (x,y)$ for the case with $\alpha _0>0$ and $\kappa \,\text {sgn}(\beta )=-1$ at different instants; d Profiles of $\varPhi (\tilde{x},\tilde{y}=0)$ between $\tau =0$ and $\tau =50$. The arrow illustrates the evolution direction with time for $\tilde{x}>0$

5.1 Temperature higher than bulk transition temperature: $T >T_{c_0}$

If the temperature $T >T_{c_0}$, no phase transition is expected in an un-cracked material, and implies that $\alpha =\alpha _0>0$. The introduction of a loaded crack results in a shift of $\alpha$, see Eqs. (11), (14), whose magnitude depends on the position relative to the crack tip. In general, the closer to the crack tip, the higher the stress, and the larger the shift, which inevitably implies that the driving force for the phase transformation is larger.

With a sixth order potential, both second and first order transitions can be modeled. According to the phase diagram in Fig. 2, both first order transitions can occur in a homogeneous material when $\kappa \text {sgn}(\beta )<-3/16$. Thus, it could be of interest to investigate of the evolution of a second phase in the presence of a loaded crack for a corresponding case; here $\kappa \text {sgn}(\beta )=-1$ is chosen. The results from the numerical simulation of the evolution of the order parameter are presented in Fig. 3a–c. From this figure sequence, it is seen that a ”kidney”-shaped zone with $\varPhi \ne 0$ is developing in the vicinity of the crack tip, which is an indication of precipitation of a second phase. To further illustrate the space dependence of $\varPhi$ during the evolution, the profile of the cross-section of the $\varPhi$-surface along the $\tilde{x}$-axis $(\tilde{y} =0)$ is given at different instants in Fig. 3d. Two main stages in the order parameter evolution may be identified: initially a relatively sharp peak emerges close to the crack tip where the material locally transforms, thereafter the transformed region expands in space until a steady state (ss) is reached. The successive increase of the order peak value $\varPhi _{peak}$ is evaluated and its temporal evolution is presented in Fig. 4a (cyan line). During the expansion stage, it is found that the phase interface moves in the positive $\tilde{x}$-direction with a seemingly constant slope, see Fig. 3d. Because the model inherently relies on the assumption that the interface between the two phases is smooth, no exact boundary can be distinguished. Thus, to quantify the expansion of the second phase, we monitor the width $\tilde{w}$ of the $\varPhi$-profile illustrated in Fig. 3d and defined $\tilde{w}$ as the distance from the origin to the point along positive $\tilde{x}$ at which $\varPhi = 0.01$. The results in Fig. 4b (cyan line) reveal that $\tilde{w}$ converges following an asymptote, implying that there is a steady-state size.

Fig. 4

Evolution of a the peak value of the order parameter $\varPhi _{peak}$, and b the shape width w of the $\varPhi$-profile where $\varPhi =0.01$ for $\theta = 0$. ($\alpha _0>0$ in all cases.)

Other cases where $\kappa \,\text {sgn}(\beta )< -3/16$ are also studied. Similar evolution patterns are obtained as for $\kappa \,\text {sgn}(\beta )=-1$, i.e. an initial order parameter peak rises followed by a limited space expansion. Yet, the evolution have other characteristic values, e.g. the maximum values of $\varPhi _{peak}$ and $\tilde{w}$, respectively, vary, see Fig. 4.

To investigate the span $-3/16<\kappa \,\text {sgn}(\beta )<0$, the evolution of $\varPhi$ is calculated for the specific case of $\kappa \,\text {sgn}(\beta )=-1/9$, which is deemed representative for the interval. The evolution of the $\varPhi$-profile is presented in Fig. 5. Initially, the evolution pattern is similar to that observed for the previously considered parameter sets. However, as the precipitate continues to grow, it expands with seemingly constant speed with no tendency to slow down in order to eventually reach a steady state. According to the phase diagram in Fig. 2, no matrix phase (I) should exist at steady-state in a homogeneous material when $\alpha >0$, thus making the proposed scenario plausible.

Fig. 5

Evolution of $\varPhi (x,y = 0)$ for $\alpha _0>0$, $\kappa \text {sgn}(\beta )= -1/9$. Profiles are shown for $\tau =0$ to $\tau = 50$

Additionally, the situation for positive values of $\beta$ is considered, which is motivated by the phase diagram that only predicts second order transition regardless of value of $\kappa$, cf. the limit A $=$ 0 in Fig. 2. Figure 6 shows the evolution of the $\varPhi$-profile for $\kappa =1$, whose behavior somewhat resembles that of the case for $\kappa \,\text {sgn}(\beta )=-1$ (Fig. 3d) with a fast initial increase of $\varPhi$ close to the crack tip. However, the broadening is accompanied with a gradually decreasing slope of the order parameter in the interface proximity, as opposed to the relatively constant slope observed for $\kappa \,\text {sgn}(\beta )=-1$. Simulations with three different values of $\kappa$ are performed, and the evolution of $\varPhi _{peak}$ and $\tilde{w}$ for theses cases are included in Fig. 4. Neglecting small numerical variations, the evolution of $\tilde{w}$ is found independent of $\kappa$, i.e. the precipitation shape and growth rate are expected to be similar for all cases such that $\beta >0$.

Fig. 6

Evolution of $\varPhi (\tilde{},\tilde{y}=0)$ for $\alpha _0>0$, $\beta >0$ and $\kappa = 1$. Profiles are shown for $\tau =0$ to $\tau = 50$

5.2 Temperature lower than bulk transition temperature: $T <T_{c_0}$

To further extend the investigation, modeling of the situation for which the material temperature is lower than the bulk transition temperature is performed, i.e. $T <T_{c_0}$ corresponding to $\alpha _0<0$. Based on Eqs. (11) and (14), it can be shown that for the situation at hand $\alpha \le 0$ and $T < T_c$ must prevail everywhere in the domain. An example of the evolution of the order parameter is monitored in Fig. 7 at different times and Fig. 8 illustrates the evolution of the $\varPhi$-profile along the $\tilde{x}$-axis. For the stated conditions, the order parameter $\varPhi$ increases in the whole computational cell, i.e. the whole material, but its value is higher in the crack-tip neighborhood where a stress concentration resides. Similar to the considered situations in the previous section, the order parameter displays a peak in the vicinity of the crack tip, which early on reaches a maximum value, while a slower transformation is taking place away from the crack tip.

Fig. 7

Evolution of the dimensionless order parameter $\varPhi =\varPhi (x,y)$ for the case with $\alpha _0<0, \kappa \text {sgn}(\beta )<0$ at different instants

Fig. 8

Evolution of $\varPhi (\tilde{x},\tilde{y}=0)$ for $\alpha _0<0$, $\kappa \,\text {sgn}(\beta ) = 1$ from $\tau = 0$ to $\tau = 50$

5.3 Comparisons of evolution characteristics

In order to quantitatively describe the evolution behavior, some characteristics measurements are defined: $\varPhi _{max}$ denotes the maximum value of $\varPhi _{peak}, \tau _{mp}$ the time to reach this value, $\tilde{w}_{ss}$ steady-state width, and $\tau _{95\%ss}$ required for the system to reach 95% of $\tilde{w}_{ss}$. Results for the presented cases are summarized in Table 1.

For the situation where $\alpha _0>0$, three different types of evolution patterns are obtained relating to different intervals of $\kappa \,\text {sgn}(\beta )$: $\beta>0, \beta <0 \wedge \kappa >3/16$ and $\beta<0 \wedge \kappa <3/16$, respectively. Results from the simulations of the corresponding cases are presented in the following paragraphs, and in the last paragraph results for $\alpha _0<0$ are discussed.

For all investigated cases where $\alpha _0>0$ and $\beta <0$, it is found that $\varPhi _{max}, \tilde{w}_{ss}$ and $\tau _{95\%ss}$ decrease with increasing $\kappa$, see Table 1. In contrast, the time $\tau _{mp}$ that characterizes the initial stage of the precipitation is approximately the same ($\approx$5) and not exceeding 20% of $\tau _{95\%ss}$ for any of the considered cases. The latter observations are also true for $\beta >0$. Further, larger $\varPhi _{max}$ are reached for negative $\beta$ than for positive $\beta$ with same value of $\kappa$.

It is also found that in cases where $\kappa \,\text {sgn}(\beta )<-3/16$, $w_{ss}$ increases with increasing $\kappa \,\text {sgn}(\beta )$. It can be deduced that there is an approximate linear relation between the two with $\text {d}w_{ss}/\text {d}\tau _{95\%ss}\approx \rho _0/50$. However if $\beta >0$, all choices of $\kappa$ result in similar values of the final width $w_{ss}$ and the time to reach 95% of $w_{ss}$, respectively. Thus, as been mentioned earlier, the precipitation process is not influenced by the value of $\kappa$, and it can be concluded that a Landau potential of lower order than what is used in this study may be sufficient to simulate the evolution if $\beta >0$.

The characteristic values for two studied cases for which $\alpha _0<0$ are also given in Table 1. The maximum peak value $\varPhi _{max}$ is found to be larger for negative $\beta$ than for positive $\beta$ for the same value of $\kappa$, in line what is found for positive $\alpha _0$. The time to reach this maximum, $\tau _{mp}$, is approximately equal in both cases, but about half the time for cases with $\alpha _0>0$. That the evolution process is faster is expected, since the whole material is quenched and the contribution from stress concentration to the driving force for phase transformation is added on top.

Table 1 Summary of the characteristic values {$\varPhi _{max}$, $\tau _{mp}$, $\tilde{w}_{ss}$ and $\tau _{95\%ss}$} for different combinations of $\kappa \,\text {sgn}(\beta )$ and $\alpha _0$

Fig. 9

Comparison between analytical and numerical computations for spatial variation $(\tilde{x},\tilde{y}=0)$ of order parameter in a steady state for a $\alpha _0<0$ and $\kappa \,\text {sgn}(\beta )=1$ and for b $\alpha _0>0$ and $\kappa \,\text {sgn}(\beta )=-1$

5.4 Comparison with analytic local steady-state solutions

Here, the numerical results are compared with the analytically deduced local steady-state solutions that are presented in Sect. 3, which from now on is referred to as the analytical solutions. This aims at investigating the possibilities and limitations of using these analytical results to predict the evolution pattern for different configurations.

In the analytical study, the Laplacian term in Eq. (18) is neglected, roughly implying that the solution in each point in space is unaware of its neighbors. The Laplacian term not only governs the smoothening of the interface between disordered matrix and second phase, but it also affects the peak shape of the $\varPhi$-profile. In addition, it influences the non-zero values of $\varPhi$ along the crack surfaces.

Figure 9a presents the numerically steady-state and analytical solutions for the case with $\alpha _0<0$ and $\kappa \,\text {sgn}(\beta )=1$, where it is found that the curves match very well. However, an exception is found very close to the crack tip where the analytical solution goes to infinity and the effect of the interface energy on the numerical results is pronounced. The same observations can be done for all studied cases for which $\alpha _0<0$ and, $\alpha _0>0$ with $-3/16<\kappa \,\text {sgn}(\beta )<0$.

In Fig. 9b, steady-state profiles for the case with $\alpha _0>0$ and $\kappa \,\text {sgn}(\beta )=-1$ are displayed. A match is found between the numerical and analytical results although differences subsist in the direct vicinity of the crack tip and at the interface between second phase and solid solution. The location corresponding to the stability limits of phase I and II are included, as well as the transition line between region I*+ II and I + II* given by the phase diagram in Fig. 2. It can be seen that the smooth interface is located about the line that indicates the first order transition between globally stable phases. Similar observations can be done for all studied cases for which $\alpha _0>0$ with $\kappa \,\text {sgn}(\beta )<-3/16$ and $\alpha _0>0$ with $\beta >0$. In the latter case however, the smooth interface is approximately centered at $\tilde{x}=\rho _0$, which corresponds to the second order transition location for the analytical solution.

The strong resemblances of the curve appearance indicate the numerical steady-state shape and approximate size of the second phase can be predicted by using the analytic local steady-state solutions for all cases. However, the assumption that transformation takes place wherever $\varPhi \ne 0$ is disputable since that numerical solution renders a larger precipitate than the analytical solution is considered, see e.g. Fig. 9b. Indeed, the numerical result display an interface with a certain thickness whereas it is sharp in the analytical solution. The intersection between the curves ahead the crack tip in Fig. 9b corresponds to an apparent inflexion point of the interface profile obtained numerically, and the same observation is made for all cases where $\alpha _0>0$ and $\kappa \,\text {sgn}(\beta ) < -3/16$. The smoothness of the interface depends on the interface energy and thus cannot directly be predicted from the analytical solution. Additionally, the steady-state solutions display possible metastable phases. The stability analysis was performed only in a point wise way. However, the metastable phases might not appear if the total energy of the system and the temporal evolution of the space-dependent field are considered.

5.5 Influence of stresses on interface width

To explore the influence of the crack induced stress field on the characteristics of the diffuse interface, its width $\lambda$ is measured for different values of the gradient energy coefficient g in Eq. (2). For a phase boundary with an interface profile that is symmetric in the radial direction, $\lambda$ is proportional to $\left( g/\varDelta \varPsi \right) ^{1/2}$, see e.g. Moelans et al. (2008), Provatas and Elder (2010), where $\varDelta \varPsi$ is the bulk energy barrier for phase transition, as illustrated in Fig. 12 in “Appendix”. Further, the width $\lambda$ is often defined as the distance between two positions for which $\varPhi =L_1\,\varPhi _0$ and $\varPhi =L_2\,\varPhi _0$, see Fig. 10, where $\varPhi _0$ is the maximum value of $\varPhi$. For example, the limits 0.1 and 0.9 could be chosen to characterize the interface width. In present study, all results are presented using a dimensionless length obtained by scaling with $\sqrt{|\alpha _0|/g}$. In case of a symmetric interface, then a dimensionless interface width $\tilde{\lambda }$ would be independent of g.

Fig. 10

Interface width definition

In this study, the investigation of how $\lambda$ depends on g in the presence of the loaded crack is limited to a single case: $\alpha _0>0, \beta <0$ and $\kappa =1$ at steady state. In Fig. 9 numerical result $\left( g\ne 0\right)$ and the analytical solution $(g=0)$ are compared for the considered case. This comparison reveals that the analytical solution is discontinuous at the transition point, and $\varDelta \varPhi$ is taken as the difference in $\bar{\varPhi }$ at this location. Different limits couples $(L_1,L_2)$ are considered for $g=\{1,5,7,10,50,70\}\times 10^{-3}$ and the results are shown into Fig. 11. From this figure, it is found that $\lambda$ is not proportional to $g^{1/2}$, but rather that the relationship $\lambda =C_1(g^{1/2} +C_2)$ can be deduced, where $C_1$ is a linear function of the limit, and the constant $C_2\approx 0.08$, which is not of negligible for the studied cases. Thus, it may be noted that the space dependence of the order parameter, induced by a local stress concentration, results in an interface width which cannot be deduced by simply scaling the numerically obtained results from the parametric study.

Fig. 11

Interface width $\lambda$ versus $g^{1/2}$ for different limits defining the width. A linear fit of the results is included

5.6 Effect of material properties and load

In the presented model, the coefficients $\alpha _0, \beta _0$ and $\gamma$ in the Landau potential Eq. (3) are material dependent, but they are not related to the elastic parameters, neither is the interface energy coefficient g. Instead changes in the elastic properties are introduced in the model via the shift in the transition temperature as seen in Eq. (15) and the value of $\beta$, cf. Eq. (12). The strength of the interaction between the displacement field and the field parameter represented by $\xi$ also affects the evolution of a precipitate. For a stiffer material (larger $\varLambda$), $\beta$ has a lower value than for a more compliant material, which corresponds to an increased $\kappa$. In the case of $\beta >0$, this means that the phase transition mode is still of second order (see Fig. 2) but a higher transition rate is achieved, cf. Table 1. However, if $\varLambda$ is reduced such that there is change in sign of $\beta$ to a negative value, first order transitions may be possible. The same argument can be made for a material with a less pronounced interaction between the displacement field and the order parameter, i.e. a lower $\xi$. Additionally, if $K_I$ increases, $r_0$ [see Eq. (13)] and $\rho _0$ also increase, which leads to a stronger influence of the crack on its surrounding area.

In the case of diffusionless phase transformation, the approach in the present work may be useful. If all necessary material properties and the stress intensity factor are known, the steady state of the second-phase precipitation can be deduced by using the phase diagram outlined in Fig. 2. Size, shape, growth rate, time to complete transformation, and to some extent the smoothness of the interface, can be thereafter be calculated using the dimensionless results presented in this work.

5.7 Further remarks

The presented work, which includes a full parametric study, allows capturing all different scenarii corresponding to different combinations of load, phenomenological coefficients and material properties in time and space for a phase transformation induced by the presence of a crack in a elastic structure. This type of study is usually omitted in the literature. In addition, the microstructure evolution of a material is traditionally modeled by considering two coupled aspects: the phase kinetics and the mechanical equilibrium, and, usually, they are numerically solved separately e.g. Bair et al. (2017), Ma et al. (2006), Thuinet et al. (2013). Here, an analytical solution for the mechanical equilibrium in plane strain for an elastic structure containing a crack is found through the use of the Irwin’s analytical solutions and is directly incorporated into the TDGL equation as in Boulbitch and Korzhenevskii (2016) in order to account for the presence of a fixed crack-induced stress. Thus, only one equation has to be solved rendering the model time-efficient.

A large number of models in the literature, which are based on phase field theory, and the present one employ a phenomenological Landau potential, which derives from a power series in the order parameter. However, these models are not fully quantitative. This limits the study vis-a-vis the effects of temperature transient and temperature gradient (Shi and Xiao 2015), and our understanding of the meaning of the Landau coefficients. An attempt was made by Shi and Xiao (2015) to relate the Landau potential coefficients to physical quantities but the study still lies on several arbitrary simplifying assumptions.

For most engineering materials, the structural changes are accompanied by a concentration re-distribution of species, and coupled evolution laws for structural and concentration order parameters may be the tool to successfully capture such behaviour.

In the case of hydride forming metals, there is a lack of some of the necessary material data and the phase transition kinetics are not fully mapped. Nevertheless, ab-initio calculations such as reported in Olsson et al. (2014, 2015) may contribute to fill in the gaps, as well as recently performed experiments, cf. Maimaitiyili et al. (2015), Maimaitiyili et al. (2016). Further experiments that are especially designed for capturing phase transformation induced by a crack, are recommended.

6 Summary and conclusions

A phase field approach is used to investigate the formation of a second phase at the vicinity of a crack tip in an isotropic and linear elastic material. The tempo-spatial evolution of the microstructure is computed by numerically solving the TDGL equation. To capture the phase transitions, we use a sixth order Landau potential for a single structural order parameter, which represents the degree of ordering of the crystal structure.

For the considered systems the phase diagram for mean-field thermodynamic equilibrium is derived, clearly showing the existence of possible meta-stable phases and first order transitions, which might not emerge by considering the total energy of the system and the temporal evolution of the space-dependent field. The driving force for the phase transformation at the crack tip can be attributed to the phase transition temperature being locally shifted as a result of the crack induced stress field, which effectively acts as quenching in the crack tip vicinity. Different phase transformation scenarios are simulated by using a wide range of combinations of parameters, which represent varying material properties and stress levels. It is found that close to the crack tip, the driving force is always large enough to induce precipitation within a confined area through a second order transformation. The subsequent evolution pattern depends on the parameter set at hand, and a shift to first order transition during growth of the precipitate is observed occasionally. However, the presence of any metastable phases cannot be revealed from the calculations.

The complete steady-state solutions, with the exception of the shape of the smooth interface, is found to be accurately predicted by using the mean-field solution for each location. The interface width is found not to scale with the interface gradient energy coefficient because of the inhomogeneous stress field around the crack. Finally, the evolution of the order parameter is studied following quenching of the whole material. It is shown that the formation of the second phase is enhanced by the presence of the crack, despite that the entire system undergoes transformation simultaneously.

Once the diffusionless phase-transformation model parameters of an applicable material system are known, the presented results will allow to predict the kinetics of precipitations, e.g hydride formation, in the crack-tip vicinity. Thus, this will contribute to the failure risk quantification of structures avoiding the use of expensive experiments.

Appendix: Theoretical analysis of the steady state solutions

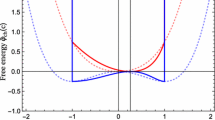
In this paragraph the solutions of Eq. (19) presented in Eqs. (20) and (21) are discussed depending on the signs of $\alpha _0$, $\beta$ and the positive value of $\kappa$. All cases described below are illustrated by the graphs showing the potential $\varPsi$ versus the dimensionless order parameter $\varPhi$ in Fig. 12.

Fig. 12

The Landau potential $\varPsi$ versus the dimensionless order parameter $\varPhi$. a $\beta > 0$, b $\beta < 0$

The condition for $\bar{\varPhi }_{\pm }^{^{2}}$ to exist allowing the formation a second phase is $A\le 1/(4\,\kappa )$ which corresponds to $(\rho _0/\rho )^{1/2}\ge [\mathrm {sgn}(\alpha _0)-1/(4\kappa )]/\cos (\theta /2)$. When this condition is fulfilled several situations for which a second phase may nucleate are possible:

• if $\alpha _0<0$, which induces $A<0$, the value $\bar{\varPhi }_{-}$ cannot exist for any values of $\beta$. Consequently, the three solutions are $\{-|\bar{\varPhi }_{+}|, 0, |\bar{\varPhi }_{+}|\}$ where the non-zero solutions minimize the system energy. Thus, a stable second phase is suppose to form in every point of the system;

• if $\alpha _0>0$, $\beta <0$ and $A>0$, i.e.$\frac{\rho }{\rho _0}\ge \cos ^{2}\frac{\theta }{2}$, there are five solutions: $\{-|\bar{\varPhi }_{+}|, -|\bar{\varPhi }_{-}|, 0, |\bar{\varPhi }_{-}|, |\bar{\varPhi }_{+}|\}$. Since the equation solving gives 3 minima, two non-zero and 0, both phases can exist in 2 states: stable or metastable. The stable phase is designed by a global minimum and the metastable one corresponds to a local minimum. When $\varPsi (\bar{\varPhi })=0$ together with $\delta \,\varPsi (\bar{\varPhi })/\delta \bar{\varPhi }=0$ which yields $A=\frac{3}{16\,\kappa }$ all minima are equal, i.e. both phases are equally stable. For $\frac{3}{16\,\kappa }\le A\le \frac{1}{4\,\kappa }$ then the solid solution is expected to be stable and the second phase to be metastable. If $0\le A\le \frac{3}{16\,\kappa }$ then the solid solution is expected to be metastable and the second phase to be stable.

• if $\alpha _0>0$, $\beta <0$ and $A\le 0$, i.e. $\frac{\rho }{\rho _0}< \cos ^{2}\frac{\theta }{2}$, the solutions of the equation are $\{-|\bar{\varPhi }_{+}|, 0, |\bar{\varPhi }_{+}|\}$. In this situation, both minima induces the formation of a stable second phase.

• if $\alpha _0>0$, $\beta >0$ and $A\le 0$, i.e. $\frac{\rho }{\rho _0}\le \cos ^{2}\frac{\theta }{2}$, the system has 2 minima, $\{-|\bar{\varPhi }_{+}|, |\bar{\varPhi }_{+}|\}$, and one maximum, 0. In these condition, the stable second phase is expected to form;

If the system has the configurations $\{\alpha _0>0$, $\beta <0$, $A>\frac{1}{4\,\kappa }\}$ and $\{\alpha _0>0$, $\beta >0$, $A>0\}$, the solid solution is stable and no second phase is expected to nucleate.