The second Sandia Fracture Challenge: predictions of ductile failure under quasi-static and moderate-rate dynamic loading

Abstract

Ductile failure of structural metals is relevant to a wide range of engineering scenarios. Computational methods are employed to anticipate the critical conditions of failure, yet they sometimes provide inaccurate and misleading predictions. Challenge scenarios, such as the one presented in the current work, provide an opportunity to assess the blind, quantitative predictive ability of simulation methods against a previously unseen failure problem. Rather than evaluate the predictions of a single simulation approach, the Sandia Fracture Challenge relies on numerous volunteer teams with expertise in computational mechanics to apply a broad range of computational methods, numerical algorithms, and constitutive models to the challenge. This exercise is intended to evaluate the state of health of technologies available for failure prediction. In the first Sandia Fracture Challenge, a wide range of issues were raised in ductile failure modeling, including a lack of consistency in failure models, the importance of shear calibration data, and difficulties in quantifying the uncertainty of prediction [see Boyce et al. (Int J Fract 186:5–68, 2014) for details of these observations]. This second Sandia Fracture Challenge investigated the ductile rupture of a Ti–6Al–4V sheet under both quasi-static and modest-rate dynamic loading (failure in $\sim$0.1 s). Like the previous challenge, the sheet had an unusual arrangement of notches and holes that added geometric complexity and fostered a competition between tensile- and shear-dominated failure modes. The teams were asked to predict the fracture path and quantitative far-field failure metrics such as the peak force and displacement to cause crack initiation. Fourteen teams contributed blind predictions, and the experimental outcomes were quantified in three independent test labs. Additional shortcomings were revealed in this second challenge such as inconsistency in the application of appropriate boundary conditions, need for a thermomechanical treatment of the heat generation in the dynamic loading condition, and further difficulties in model calibration based on limited real-world engineering data. As with the prior challenge, this work not only documents the ‘state-of-the-art’ in computational failure prediction of ductile tearing scenarios, but also provides a detailed dataset for non-blind assessment of alternative methods.

1 Introduction

Computational simulations are often called upon to render predictions for a wide range of failure scenarios in mechanical, structural, aerospace, and civil engineering, where full-scale field tests are usually difficult, expensive, and time-consuming. Fracture simulation is deeply rooted in computational solid mechanics that can date back to the 1970s, e.g. Norris et al. (1977). Since that time, there have been ongoing efforts to develop realistic physical models and efficient computational implementation that improve reliability, speed, robustness and above all, accuracy. However, generating predictions that have adequate confidence levels still pose significant difficulties to the simulation community. To elucidate the accuracy of these predictions, it is necessary to evaluate existing models in validation scenarios that approximate the conditions seen in practical applications. For this purpose, Sandia National Laboratories has organized a series of fracture challenges where participants are asked to predict quantities of interest (QoIs) in a given fracture scenario. The participants have never seen the challenge scenario previously, so the predictions are “blind” as is often the case in real engineering predictions. Moreover, while the scenarios are geometrically simple, they present mechanical complexities that are impossible to predict with intuition or simple calculations alone. After the blind predictions are reported, they are subsequently compared against experimental results to determine how closely they replicated the fracture behavior observed in the laboratory. The current paper describes the second Sandia Fracture Challenge (SFC2) issued in 2014 to exercise capabilities in predicting fracture at both quasi-static and modest dynamic loading rates in a Ti–6Al–4V sheet.

The Sandia Fracture Challenge series has three main purposes. Firstly, the Challenge is an assessment of state-of-the-art techniques to predict problems involving ductile fracture accurately. These methods cover many models and approaches pursued by academia and industry to deal with ductile fracture analysis. Secondly, the blind prediction environment offers individual participating teams an environment of “true blindness” to evaluate the strengths and weaknesses of their methodology. This unique setup is a precious opportunity to refine their methods and tools. Thirdly, the Sandia Fracture Challenge has brought together a group of teams that have been actively working in the ductile fracture area for many years. Each team worked independently on the same fracture problem. The collective wisdom obtained by attacking a single specific task with a variety of strategies strengthens our understanding of ductile fracture. This Challenge process facilitates identifying current difficulties, acquiring experience to avoid certain pitfalls in future efforts, and fosters collaboration between universities, national laboratories, and industries around the world. It also contributes to a cumulative learning process.

In 2012, the first Sandia Fracture Challenge (SFC1) was designed to assess the mechanics community’s capability to predict the failure of a ductile structural metal in an unfamiliar test geometry. The results were documented in a special issue of the International Journal of Fracture (Boyce et al. 2014). With no direct funding provided to the participants, thirteen teams with over 50 participants from over 20 different institutions responded to the challenge. The task was to predict the initiation and propagation of a crack in a ductile structural stainless steel (15-5PH) under quasi-static room temperature test conditions. The test geometry was a flat panel that contained a round root pre-cut slot and multiple nearby holes that could influence the notch-tip stress state. The placement of the holes created a competition between a tensile-dominated and shear-dominated failure mode. To calibrate their models, the participants were provided with tensile test data, sharp crack mode-I fracture data, and some limited microstructural information.

The first Sandia Fracture Challenge was designed based on lessons learned in earlier double-blind assessments, where it became obvious that the double-blind evaluation methodology should be governed by some common constraints (Boyce et al. 2011). These common constraints also apply to the second Sandia Fracture Challenge presented here. They include: (1) The sample geometry should be readily manufactured with easily measured geometric features. (2) The manufacturing process should avoid unintentional complications such as significant residual stresses or non-negligible surface damage. (3) The QoIs, such as forces and displacements, should be readily measurable with common instrumentation so that the tests can be repeated in multiple labs in a cost effective manner. (4) The experiment should involve simple, uniaxial loading conditions that are readily tested with common lab-scale load frames and common grips. (5) The sample and loading conditions should avoid unwanted modes of deformation such as buckling. Since the challenge scenario involves a novel test geometry, the repeatability of the behavior may not be apparent until after significant experimental effort. In the present work and similar, prior efforts at Sandia, the experiments were not performed until after the computational challenge had been issued. This approach ensured that all participants, including the experimentalists, were not biased by any prior knowledge of the outcome.

The outcome of the first Challenge motivated this second Challenge, which explores several new facets: (1) in addition to quasi-static loading, the scenario also involves modest dynamic loading spanning three orders of magnitude in strain-rate, (2) the sharp-crack fracture toughness data is replaced with V-notch shear failure data, (3) rather than providing only machining tolerances based on engineering drawings, the participants were provided with actual specimen dimension measurements, (4) the alloy was changed to a titanium alloy with low work hardening behavior. Ti–6Al–4V is a common lightweight, heat treatable, alloy that provides an excellent combination of mechanical properties with high specific strength, corrosion resistance, and weldability, widely used in aircraft, spacecraft, and medical devices.

As with the first challenge, the second challenge provided all participants with experimental data, for model calibration, on the same lot of material used to produce the blind challenge geometries. Two types of material testing were performed and provided to all participants. One is the commonly used simple tension test of a dog-bone coupon. Because of possible anisotropy, the simple tension tests were performed in the rolling (longitudinal) direction and the transverse direction. A shear-dominated test was also performed on a double V-notch plate for the rolling and transverse material directions. These tests may not be sufficient to calibrate all parameters for the material constitutive models used by the participants since some of these models are complicated and can have several dozen parameters. These materials tests were chosen to mimic a real engineering scenario where limited material testing data is available, but should be sufficient to characterize the essential parts of the mechanical response for use in a numerical simulation. These tests are all performed at the two different nominal loading rates that are three orders of magnitude apart and that are the same as the loading rates used for loading the Challenge sample.

Similar to the first Sandia Fracture Challenge, the Second Challenge specimen was also a flat plate with multiple geometrical features that facilitates fracture initiation and growth. Two anti-symmetric slots perpendicular to the loading direction were cut. The roots of these initial slots were rounded to obscure the fracture initiation site. Three holes of different sizes were drilled in the vicinity of the two slots. The spatial arrangement of the holes was chosen to create a competition between tensile and shear-dominated failure, so that the failure path was not simply intuitive. In the Second Sandia Fracture Challenge, the loading rate creates additional complexity. This includes hardening, strain rate dependence and the influence of thermal dissipation of plastic work on deformation. These rate effects were not accounted for in the computational approaches in the first Sandia Fracture Challenge, so these phenomena represented an uncharted area for blind predictions.

As with the first challenge, this second challenge was performed under conditions that are generally commensurate with typical engineering tasks: (a) the outcome is unknown during the simulation process (the prediction is blind), (b) the time for the project is limited, and (c) the available calibration data is limited. After prediction results are submitted, the adopted methodologies are evaluated in their ability to predict macroscopic scalar QoIs such as the peak allowable force before failure and the amount of component deflection at various force levels. The experimental results were only shared with the simulation teams after their blind predictions had been reported. After the blind predictions and experimental outcomes had been disseminated to all participants, a meeting was held at the University of Texas at Austin on March 2–3, 2015 to synthesize commonalities that contributed to accurate predictions or systematic errors. The workshop laid the groundwork for this paper that presents the Challenge and the comparison of the predictions.

This paper is organized as follows: Sect. 2 poses the challenge scenario and describes the experimental testing and results for the material characterization. Section 3 provides details of the geometry, test setups, and the experimental results of the Challenge problem specimen. Section 4 is a synopsis of the models and methods used by the participating teams, while the comparison of the prediction results from each team is given in Sect. 5. This is followed by Sect. 6, with discussions on the results and the strength and weakness of adopted methods. Section 7 provides a brief summary. The detailed contributions of each team’s procedure and their engineering judgment are given in “Appendix 1” and detailed measurements of test sample dimensions are provided in “Appendix 2” for potential future assessment.

2 The Challenge

A meaningful, efficient, and ‘fair’ Challenge should be governed by a set of common constraints (Boyce et al. 2011, 2014). First, this ‘toy problem’ or ‘puzzle’ should have no obvious or closed-form solution. It should be sufficiently distinct from other standard or known test geometries so that the outcome of the exercise is unknown to the participants. The scenario should be readily confirmed through experiments. It may be desirable for the challenge scenario to result in a single unambiguous repeatable experimental outcome, or as was the case for the first Sandia Fracture Challenge, the scenario could be near a juncture of two competing outcomes. Since the challenge scenario involves a novel test geometry, the repeatability of the behavior may not be apparent until after significant experimental effort. In the present work and similar, prior efforts at Sandia, the experiments were not performed until after the computational challenge had been issued. This approach ensured that all participants (including the experimentalists) were not biased by any prior knowledge of the outcome.

2.1 The 2014 Sandia Fracture Challenge Scenario

The fracture challenge was advertised and issued to potentially interested parties through a mechanics weblog site, imechanica.org, and through an e-mail solicitation to many known researchers in the fracture community. The fracture challenge was issued on May 30, 2014 and final predictions from participants were due on November 1, 2014, approximately five months after the issuance of the challenge. The initial packet of information contained material processing and tensile test data on mechanical properties, the test specimen geometry, the loading conditions, and instructions on how to report the predictions. Supplemental shear test data was released on August 13, 2014. The degree of detail provided was intended to be commensurate with the information that is typically available in real engineering scenarios in industry. These details regarding the material, test geometry/loading conditions, and QoIs are described in the following three subsections.

Fig. 1

Tensile bar geometry used to provide stress–strain data for model calibration. Dimensions are in millimeters. Mean thickness of tensile specimens was 3.150 mm

Fig. 2

Engineering stress–strain curves for eighteen tensile coupons. “RD” and “TD” refer respectively to those oriented along the rolling direction and the transverse-to-rolling direction

2.1.1 Material

The alloy of interest was a commercial sheet stock of mill-annealed Ti–6Al–4V. This alloy was chosen because it is a commonly used alloy in aerospace applications—it is moderately rate sensitive and its very shallow work hardening rate can be challenging for computational models. All test specimens were extracted from a single plate purchased from RTI International Metals, Inc. with a specified thickness of $3.124\pm 0.050$ mm. The original material certification was provided to the participants, and included the following chemical analysis (in wt%): C 0.010, N 0.004, Fe 0.19, Al 6.02, V 3.94, O 0.16, and Ti 89.676 (Y was also present with less than 50 ppm). The sheet was annealed by the mill first at $381.3\,^{\circ }\hbox {C}$ ($718.3\,^{\circ }\hbox {F}$) for 20 min and then at $419.9\,^{\circ }\hbox {C}$ ($787.8\,^{\circ }\hbox {F}$) for 15 min.

Rockwell C hardness measurements were performed on the Ti–6Al–4V plate. The average of 6 measurements was 36.1 HRC (Rockwell C) which is consistent with mill-annealed Ti–6Al–4V.

2.1.2 Tensile calibration tests

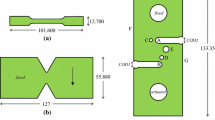
Eighteen tensile coupons were tested, in two orientations and at two loading rates, fast (25.4 mm/s) and slow (0.0254 mm/s), in the Structural Mechanics Laboratory at Sandia National Laboratories. Eight tensile tests were oriented along the rolling direction, with three at the fast rate and five at the slow rate, and ten were oriented along the transverse direction, with five at the fast rate and five at the slow rate. All tests were conducted according to ASTM E8/E8M-13 using the nominal geometry shown in Fig. 1. The as-measured thickness and width dimensions of all eighteen tensile coupons were provided to the participants. The tensile specimen tests were conducted using a uniaxial MTS servo-hydraulic load frame with a 100-kN load cell ($\pm 1\,\%$ uncertainty of the measured value) at ambient temperature, controlled by an MTS FlexTest Controller. The actuator has an internal calibrated linear variable displacement transformer (LVDT) (${\pm }0.5\,\%$ uncertainty of the measured value) that measured the actuator stroke displacement, which was the control variable. The specimens were gripped using standard manual wedge grips. The velocity of the fast-rate test as measured by the actuator LVDT in the tension tests was also confirmed using digital image correlation to track fiducial markings on the grips imaged by a high-speed Phantom 611 camera. Strain was measured using an extensometer with a 25.4 mm gage length. Engineering stress–strain curves were provided, as well as the raw force-displacement data for each tensile test. Figure 2 shows the resulting engineering stress–strain curves for all eighteen tests. The yield strength, ultimate strength, and elongation values are presented in Table 1.

Table 1 Average tensile yield strength, ultimate strength, and strain at failure at two loading rates and in two orthogonal loading directions

Fig. 3

Images of fracture morphology for the tensile specimens with different loading rates and material orientations: a–d are optical images from a Keyence microscope and e–f are SEM images. a RD4—25.4 mm/s loading rate. b TD11–25.4 mm/s loading rate. c RD7—0.0254 mm/s loading rate. d TD4—0.0254 mm/s loading rate. e RD8—0.0254 mm/s loading rate. f RD9—25.4 mm/s loading rate

Fig. 4

Images of the geometry of the necking for the tensile specimens with different loading rates and material orientations. Note: The grid lines in each image have a spacing of 5.08 mm, and each sample had a grip vertical height of 12.6 mm. a RD7—0.0254 mm/s loading rate. b TD4—0.0254 mm/s loading rate. c RD4—25.4 mm/s loading rate. d TD12—25.4 mm/s loading rate

Fig. 5

Specimen geometry for shear tests. Dimensions are in millimeters. The average plate thickness for these specimens was 3.100 mm. VA specimens have the sheet rolling direction parallel to the 55.88 mm length, and the rolling direction in VP specimens is perpendicular to the rolling direction in VA specimens

The test data indicates that there is a dependence of the tensile behavior on the loading rate and to a lesser extent on loading direction. Optical and electron microscope images of the fracture surface morphology (Fig. 3) as well as side-view macro images of the necking profile and fracture plane (Fig. 4) were also provided to the participants.

2.1.3 Shear calibration tests

Eight shear specimens were tested in the Structural Mechanics Laboratory in the same load frame as the tensile samples. Four were loaded in shear in the rolling direction (denoted as VA for the remainder of this section), with two at the fast loading rate and two at the slow loading rate. Four were loaded in shear transverse to the rolling direction (denoted as VP for the remainder of this section), with two at the fast loading rate and two at the slow loading rate. The geometry of the shear specimens were based on ASTM D7078/D7078M-05 with the V-notched rail shear geometry modified (deeper notch than the standard) to reduce the stress area by more than half and allow induced failure at lower forces to minimize grip rotation and minimize grip slippage. The test specimen geometry for the shear test is shown in Fig. 5. The as-measured dimension of the shear specimens were provided to the participants.

As shown in Fig. 6, stacked rosette strain gages, with a gauge length of 3.18 mm, were affixed to the center of the V-notch shear test specimens and to the left (relative to the front face) of the center. The rosette strain gages to the left of the front face were stacked for four of the test specimens and unstacked for the remaining three test specimens. The rosette gages on the front were paired with gages on the back. The elastic shear modulus was calculated using the central stacked strain gage rosette measurements for the shear strain and an assumption that the shear stress was the measured load divided by the V-notch gage area. The elastic shear modulus from these calculations was 44 GPa, which is consistent with literature values for Ti–6Al–4V.

The shear test fixture was a commercial off the shelf “Adjustable Combined Loading Shear (CLS) Fixture” from Wyoming Test Fixtures. In this fixture, each test specimen was held in place by a grip on each side. Each grip had two face grip inserts pressed against the front and back face of the test specimen and one horizontal insert. The specimen was held in place by tightening 5/8-18 UNF stainless bolts on the face grip inserts to 67.8 N m torque and hand tightening 1/2-20 UNF stainless bolts to secure the horizontal insert for each grip. The grip fixtures were made of 17-4PH stainless steel and were rigidly attached to the load frame. Figure 7 shows a close up view of the shear test setup, including the grip inserts on the fixed side. An axial LVDT mounted in the back of the fixture between the two grip halves provided the overall displacement measurement and the load cell provided the load measurement.

Two issues arose when performing the shear tests. The first was that the shear specimen slipped within the grips. The second was that the fixture itself had a non-negligible compliance. Additional tests (including tests on non-notched rectangular specimens to quantify the fixture compliance and cyclic load tests to quantify the slip) were performed, and those detailed measurements were provided to the participants. As discussed later, most participants made use of the axial LVDT displacement vs. load data provided either in the direct form as shown in Fig. 8, or with a slip correction that was provided. The non-ideal behavior of this shear test method highlights the need to develop better shear testing standards for metal failure characterization.

Figure 9 shows the post-test failure surfaces of selected shear specimens. As seen from the figure, the failure surfaces are at a slight angle with respect to the loading direction. The VA specimens showed a larger angle of the failure surface than the VP specimens. Additionally, the VA slow specimens visually showed a rougher failure surface than the other specimens.

2.1.4 Fracture challenge geometry and loading condition

The Challenge geometry consisted of an S-shaped sheet specimen with two notches and three holes, as shown in Fig. 10 with detailed dimensions. The notch locations were labeled “A” and “B”, in Fig. 11, and consist of a 6.35 mm wide notch of overall length 28.575 mm. The size of the three holes for “C”, “D”, and “E” were nominally 3.175, 3.988, and 6.35 mm, respectively. In addition, ‘knife-edge’ features were added to each notch edge for the purpose of mounting Crack Opening Displacement (COD) gages. Three holes were introduced into the S-shaped geometry to provide multiple competing crack initiation sites and propagation paths at each notch location.

Fig. 6

Strain gage configurations for the shear specimens. a Sample VA1 with stacked rosettes in the center and to the left of the center. b Sample VP4 with stacked rosettes in the center and adjacent gages to the left of the center

Fig. 7

Close view of the shear test facility showing the axial displacement measurement cell LVDT 1

Fig. 8

Load versus displacement response of shear failure calibration tests

Fig. 9

Post-test images of shear specimens at slow and fast loading rates in both directions (ruler scale: $\hbox {smallest\, division} = 0.254$ mm)

Fig. 10

Dimensions of the second Sandia Fracture Challenge S-shape specimen geometry in millimeters

Fig. 11

Plate orientation, actuation direction, Crack Opening Displacement (COD) gauges and legend of features labeled A–G

Pin holes were machined away from each notch tip for the insertion of an 18-mm diameter loading pin. These pin holes provided for standard clevis grip loading in a hydraulic uniaxial load frame. Clevis grips conforming to ASTM E 399 were used; these grips have D-shaped holes with flats to provide a rolling contact that minimizes friction effects. It is important to note that each computational team and experimental testing lab was provided no additional constraints regarding the decision of how to apply boundary conditions. This limited definition of the boundary conditions bears similarity to real world engineering problems, where the detailed boundary conditions are rarely well defined. This limited definition of the boundary conditions for the Challenge geometry would prove to be a source of discrepancy among the participants.

The participants were instructed that the Fracture Challenge would evaluate two different displacement rates of 25.4 and 0.0254 mm/s, spanning 3 orders of magnitude in strain-rate. Any undeclared aspects of loading that were salient to the outcome were considered as sources of potential uncertainty.

2.1.5 Quantities of interest

A set of quantitative questions were posed to the participants to facilitate comparing the analyses to the experimental results. These questions were meant to evaluate the robustness of the analysis technique in predicting deformation, necking conditions, crack initiation, and crack propagation. All challenge participants were requested to provide the QoIs embedded in the following six questions to facilitate quantitative evaluation and analysis of the blind predictions:

For each of the two loading rates, please predict the following outcomes:

• Question 1: Report the force at the following Crack-Opening-Displacements (COD):

  • COD1 $=$ 1-, 2-, and 3-mm.

• Question 2: Report the peak force of the test.

• Question 3: Report the COD1 and COD2 values after peak force when the force has dropped by 10 % (to 90 % of the peak value).

• Question 4: Report the COD1 and COD2 values after peak force when the force has dropped by 70 % (to 30 % of the peak value).

• Question 5: Report the crack path (use the feature labels in Fig. 11 to report crack path).

• Question 6: Report the expected force-COD1 and force-COD2 curves as two separate ASCII data files.

A COD gage was used to monitor load-line displacement at the point of the ‘knife-edge’ features, akin to fracture toughness testing. Figure 11 shows the locations of COD1 and COD2. The COD measurement was defined for the participants in the following way: “COD1 and COD2 $= 0$ at the start of the test; the COD values refer to the change in length from the beginning of the test”. All participants were also asked to report their entire predicted force-COD displacement curve. These force-COD curves provided further insight into the efficacy of the methods.

3 Experimental method and results

The behavior of the challenge specimens were evaluated by three different experimental teams. The primary results are those from the Sandia Structural Mechanics Laboratory, with additional experiments performed at the Sandia Material Mechanics Laboratory and the laboratory of Prof. Ravi-Chandar at the University of Texas at Austin. All three laboratories tested specimens that had been fabricated at the same time from the same plate of material. All three sets of experimental data were generally consistent with one another with regard to the force-displacement behavior and observed failure path. The primary differences in the tests from each laboratory can be summarized as follows: the Sandia Structural Mechanics Lab performed in situ imaging for both loading rates, the Sandia Material Mechanics Lab provided independent confirmation tests with additional local thermal measurements in the high-deformation zones, and the University of Texas Lab performed optical measurements to capture local and global kinematic fields for the slow loading rate. The following subsections cover the pretest characterization of the challenge specimens, the details of the experimental methods used in each laboratory to test them, and post-test characterization of the specimens.

3.1 Observations from the Sandia Structural Mechanics Laboratory

3.1.1 Test setup and methodology

Pre-test geometry measurements

All of the challenge specimens were fabricated by the same machine shop, where the specimens were inspected and measured to ensure compliance with the fabrication drawing. Detailed specimen dimensions were provided to the participants and are tabulated in “Appendix 2”.

Test setup in structural mechanics laboratory

In the Structural Mechanics Lab, eight specimens were tested at a loading rate of 0.0254 mm/s, and seven specimens were tested at a loading rate of 25.4 mm/s. The test setup is shown in Fig. 12. These tests were conducted in displacement control using the same uniaxial MTS servo-hydraulic load frame and 100-kN load cell as was used for the tensile and shear tests. The actuator LVDT was the control variable. Clevis grips from Materials Testing Technology (model number ASTM.E0399.08) were made of 17-4PH stainless steel with a pin diameter of 17.93 mm. These clevis grips conformed to the ASTM E 399 testing standard, as prescribed by the Challenge. Each grip was securely mounted in the load frame using spiral washers to allow for individual rotational alignment of each clevis grip relative to the uniaxial load-train. Precision-cut spacers were used on either side of the sample at each clevis to center the sample in each clevis. Prior to testing, the clevises were aligned using a strain gaged dummy sample, loaded in its elastic regime. The relative displacement between the two clevis grips was measured during each test using an LVDT mounted on each side of the grips. The clevis grip LVDTs were calibrated at the time of use with a Boeckeler Digital Micrometer, with $\pm 0.508\,\upmu \hbox {m}$ resolution and repeatability within $\pm 0.508\,\upmu \hbox {m}$. Two COD gages from Epsilon Tech Corp. (SNs E93896, S93897) were used to measure the opening of the two notches in the challenge specimens. The Epsilon COD gages were calibrated at the time of use with a Starret Micrometer, with $\pm 0.508\,\upmu \hbox {m}$ resolution and repeatability within $\pm 2.54\,\upmu \hbox {m}$.

Fig. 12

Experimental test setup in the Structural Mechanics Laboratory

Fig. 13

Load versus COD1 measurement for all samples tested in the Structural Mechanics Laboratory: a samples tested at 0.0254 mm/s; b samples tested at 25.4 mm/s

In the fast loading rate tests, a vibrational response was induced in the COD gages, thus causing oscillations in the recorded output. The frequency of the oscillation was approximately 440 Hz. The frequency of the output signal matched what was recorded in the tests. To remove the oscillations, the COD data from all fast-rate tests were filtered using a low-pass, second-order Butterworth filter with cutoff frequency of 220 Hz.

A sequence of images of the deforming samples was collected for both the slow and fast tests. The slow-rate test imaging was controlled by Correlated Solutions VicSnap software with NI-DAQ synced data collection from the MTS FlexTest Controller. The imaging setup included two Point Grey Research 5MP Grasshopper monochromatic CCDs ($2448 \times 2048$ pixels) with 50-mm Schneider lenses, viewing the front and back surfaces of the samples, with a frame rate of 2 fps. The fast-rate test imaging included a Phantom V7 high-speed camera $(800 \times 600$ pixels) with a 24–85 mm lens, viewing the front of the samples, and controlled by Phantom camera software based on a trigger sent by the MTS FlexTest controller at the start of the test, with a frame rate of 3200 fps and a 0.3-ms exposure. Black and white fiducial markings applied to the sample close to the COD gage knife edges enabled a secondary COD measurement via a digital image correlation (DIC) algorithm (Chu et al. 1985) based on a custom image tracking script in a software package called ImageJ (Schneider et al. 2012). Since the markings were not precisely at the COD knife edges, these were not used to determine the COD measurements that served as the basis for the Challenge questions. In hindsight, these markings were useful for capturing the COD measurement after the Epsilon COD gages had fallen off the samples at the onset of unstable crack growth. The displacements from the COD gages and the DIC tracking of the markings will be compared in the next section.

Fig. 14

Load versus displacement for the Samples 11 and 30 with two different crack paths: a displacement is measured by COD gages; b displacement is measure by the clevis LVDT

3.1.2 Test results and observations

Load versus COD profiles

Seven of the eight samples tested at 0.0254 mm/s and all seven of the samples tested at 25.4 mm/s in the Structural Mechanics Laboratory failed along the B–D–E–A path defined in Fig. 11, while Sample 30 tested at 0.0254 mm/s failed along the A–C–F path. Figure 13 contains the load-COD1 profiles for all of the samples. For the samples that failed via the B–D–E–A path, the COD1 gage fell off the sample at the onset of unstable crack growth, so the load-COD1 profiles are all truncated to the crack initiation point. The load-COD1 profile of Sample 30 has been truncated to when the crack first initiated (in the A–C ligament). At each loading rate, the load-COD profiles for the B–D–E–A samples show that these samples have repeatable behavior through peak load, with variation in the COD1 value at crack initiation. In comparing the responses from the two loading rates, the faster loading rate led to higher peak loads, smaller COD1 values at unstable crack initiation, and less spread in COD1 values at unstable crack initiation.

The failures of the B–D and D–E ligaments occurred nearly simultaneously and were indistinguishable in the load-displacement data. The sequential still images collected during testing did not provide sufficient temporal resolution to clearly identify which ligament failed first. The high speed camera used during the high rate testing lacked the needed spatial resolution to definitively identify the first ligament failure. Later post-challenge observations at the University of Texas indicated that ligament D–E likely failed first for the slower rate load case (Gross and Ravi-Chandar 2016), as described in detail in “Post-Challenge experimental observations from the Ravi-Chandar Lab at University of Texas at Austin” section of “Appendix 2”. The load-COD1 profile of Sample 30 falls in line with all the other samples up to failure, with the A–C ligament failing at least 0.5 mm earlier than any B–D–E failure in the other samples. Figure 14 compares the load-displacement profiles for Samples 11 and 30. The load-COD1 profiles are remarkably similar up to the A–C failure of Sample 30, but the load-COD2 profiles deviate earlier at around 1.4 mm, well before peak load. The load-clevis LVDT behavior is nearly identical up to the crack initiation in notch A of Sample 30. The early failure of Sample 30 is thought to be an outlier based on fractography, as will be discussed later in Sects. 3.1 and 3.3.

Figures 15 and 16 show the load-COD measurements for both COD gages with six associated in situ images for Samples 11 and 27, representing typical sample behavior for each displacement rate. The force-COD1 data was used extensively for evaluation of predictions in Sect. 5, and the COD2 curves and corresponding images are included here for completeness. For Sample 11 at the 0.0254 mm/s displacement rate, the COD1 gage, tracking the opening of notch B where a crack formed, lags behind COD2 for images 1 and 2, catching up by image 3, and then increasing more rapidly until failure. Alternatively, for Sample 27 at the 25.4 mm/s displacement rate, the COD1 gage lagged for most of the high-loading regime, except immediately before failure. For both loading rates, considerable strain localization is evident in the B–D, D–E and A–C ligaments as the tests progressed. Videos of the tests for Samples 11 and 27 are available in the Supplementary Information.

Fig. 15

Load versus COD measurements for Sample 11 with associated in situ images

Fig. 16

Load versus COD measurements for Sample 27 with associated in situ images

Fig. 17

Load versus displacement for COD1 and DIC Fiducial Markings for Samples 11 and 27

After the conclusion of the challenge, Team E performed follow-up DIC analysis of the fiducial marking motion for Samples 11 and 27 using their custom feature tracking algorithm in ImageJ. The core purpose of this analysis was to evaluate the change in COD with force after unstable fracture when the clip gage extensometers detached. The fiducial marking displacements were slightly less than the COD gages since the fiducial markings were inboard of the knife edges in each notch. Figure 17 includes the load versus COD1/COD1-DIC (the fiducial marking displacements across the notch with the COD1 gage) curves for Samples 11 and 27. COD1-DIC measurements are similar in profile to the COD1 measurements. For Sample 27, the frame rate was fast enough to capture a few measurements during the load drop; the load versus COD1-DIC curve at the first failure shows that the load immediately drops with very little change in COD1. This near-vertical unloading associated with unstable cracking is used later to compare to model predictions.

3.2 Confirmation observations from the Sandia Material Mechanics Laboratory

The Sandia Material Mechanics Laboratory provided four tests to confirm the results independently from the Sandia Structural Mechanics Laboratory: three at the slow displacement rate (Samples 13, 23, and 29) and one at the fast displacement rate (Sample 20). The tests were performed on a MTS 311.21 four-post load frame under LVDT displacement control using a FlexTest 40 digital controller. The LVDT had a range of $\pm 100$ mm (SN 645LS) with a maximum calibrated error of $\pm 0.35\,\%$ across the entire range. The Interface model 1020AF load cell (SN 3069) had a capacity of 55,600 N with a maximum calibrated error of $\pm 0.45\,\%$ in tension. The same COD gages were used by both labs, although the gages were independently calibrated at the time of testing in the Material Mechanics Laboratory with a MTS Calibrator model 650.03 with a maximum calibration error of $\pm 1\,\%$. The clevis grips were the same model used by the Sandia Structural Mechanics Laboratory. Angular and concentric misalignments between the two grips were compensated using a MTS model 609 alignment fixture. Three-dimensional (3-D) printed plastic spacers ensured that the test coupon was located in the center of the wide clevis grips. Type K thermocouples with 0.25 mm wide junction tips were spot welded in the center of the B–D ligament (Position 1) and in the A–C ligament (Position 2) to monitor the thermal history during the tests for Sample 20 and 29.

All four samples tested in the Material Mechanics Laboratory failed along the B–D–E–A path. The load-COD1 profiles for these samples are plotted with the data from the Structural Mechanics Laboratory in Fig. 18. Good agreement between the data demonstrates repeatability of the experimental results at two independent labs.

Fig. 18

Comparison of force-displacement curves measured by the two Sandia mechanical testing labs

Fig. 19

Thermal histories of ligaments B–D and A–C: a Samples 29 at the slow displacement rate; and b Sample 29 at the fast displacement rate. Note that scales for the axes are not the same. The thermal rise in the fast test is delayed after the mechanical event presumably due to the rate of thermal conduction to transfer to the thermocouple

Figure 19 contains the thermal histories of ligaments B–D (Position 1) and A–C (Position 2) of Samples 20 and 29 during the tests measured via the thermocouples installed on the test samples. Generally, the temperature rise on the surface in the B–D ligament during the slow rate test was less than $10\;^{\circ }\hbox {C}$, whereas the temperature rise during the fast rate test was greater than $45\,^{\circ }\hbox {C}$. For both samples, the temperature rise in the B–D ligament was greater than that in the A–C ligament. These thermal measurements are only approximate values; there was no diagnosing the thermal resolution of the thermocouple readout. The thermocouple size was 1-mm; the position may not have been precisely at the midpoint in the ligament between the notch and hole. The instantaneous spikes at the end of the slow rate data and during the deformation process in the fast rate test are artifacts likely caused by the motion of the thermocouple wire and not representative of the actual temperature. Beyond these details, it is important to see the major trends of greater temperature rise in the fast rate test and for the B–D ligament where the samples failed.

3.3 Collation of experimental values for the challenge assessment based on both Sandia Laboratories’ testing

Prior to collating the experimental values for the QoIs of the Challenge, two aspects of the experimental results require additional discussion. The first aspect is that one of the specimens followed the path A–C–F, while all the rest of the specimens followed the path B–D–E. While it may be tempting to consider the one experiment indicating path A–C–F to be an outlier, and not representative of the response of the specimen, any such decision must be based on proper evaluation of the underlying reasons for the observed response. We recall that in the 2012 Challenge, one specimen exhibited a different path from all the rest, but a careful analysis indicated that this response was the nominal response to the challenge problem, while the other dominant response observed in the experiments was due to systematic deviations in the specimen geometry. In the present Challenge, Sample 30 exhibited path A–C–F, while all others followed the path B–D–E–A; geometrical measurements identified this specimen to have a greater out-of-plane warpage than all other specimens. However, no causal link has been established to connect the lack of flatness to the observed failure. Fractographic evaluation of the failed surface A–C of Sample 30 indicated that the failure was not consistent with typical tensile failures observed previously (see section “Fractographic observations” of Appendix 2). Based on these factors, it is considered that the failure along A–C is not the expected or nominal response of the specimen and the correct failure path identified from the experiments is along path B–D–E–A. The second issue is that since the COD gages fell off the samples at the initiation of unstable crack growth at a force greater than 90 % of the peak load, two of the QoIs posed in the original challenge—the COD1 and COD2 values when the load had dropped by 10 and 70 % of the peak load—were not directly measured; only the questions related to the force at COD1 of 1, 2, and 3 mm, the peak load and the crack path could be used for comparison to the computational predictions. Additional QoIs, not listed in the original Challenge that help characterize the failure, become necessary in order to compare the experiments and simulations. Such additional QoIs must be identified carefully so as to maintain the original intent of the challenge. While there are many options for this selection, it is clear that the experimental results themselves point to key features of the response that should be predictable: all experiments indicated unstable crack initiation and growth through the ligaments B-E and D-E. Therefore, three additional QoIs are chosen from the experiments: the binary quantity on the nature of crack initiation (stable/unstable), and the force and COD1 values at the initiation of unstable crack growth. The specific values of the QoIs obtained from the challenge experiments are summarized in Tables 2 and 3, including the force and COD1 values when unstable crack propagation began. As can be seen from the results, the forces obtained at the different COD levels, at the peak and at onset of unstable fracture, do not exhibit a large scatter: about $\pm 3.2\,\%$ of the average for the slow-rate tests and $\pm 1.8\,\%$ of the average for the fast-rate tests. In contrast, the COD value at onset of unstable crack propagation had significantly greater variation, with the range being $\pm 19\,\%$ of the average for the slow-rate tests and $\pm 5.4\,\%$ of the average for the fast-rate tests. This scatter in the load and COD values is intrinsic and points to an important issue in understanding the nature of the problem and generating models: fracture is a much more stochastic process than deformation.

Table 2 Summary of the load and COD measurements for slow rate testing from the two Sandia Labs

Table 3 Summary of the load and COD measurements for fast rate testing from the two Sandia Labs

4 Brief synopsis of modeling approach

In this section, a brief synopsis that compares and contrasts the varied approaches employed for prediction is provided. Each approach illustrated in subsequent appendices has been partitioned into methods and models in this section. The methods component highlights the character and solution of the partial differential equations while the modeling component focuses on the constitutive models requisite for localization, crack initiation, and unstable propagation. The selected partition and array of preferred terminology only seeks to be helpful. One must be careful to note that disparate solutions can stem from the application of the same methods and model.

Table 4 Methods employed by teams participating in the Sandia Fracture Challenge

The finite element method was employed by all teams except Team K who instead employed the Reproducing Kernel Particle Method (RKPM). Although most teams employed dynamics to characterize the unstable process, some did adopt a quasi-static approach that neglected inertial effects. Both implicit and explicit schemes for time integration were used. These characteristics are grouped into Solver in Table 4. Higher rates of loading can lead to temperature effects which can be modeled through the inclusion of energy balance. The Coupling label differentiates between the inclusion of thermo-mechanical coupling (segregated) and approaches that employ variations of the adiabatic assumption. Teams that did not utilize a coupled thermo-mechanical model attempted to capture the effects of temperature through the material fitting process. The application of the loading is categorized as Boundary conditions. An important boundary condition in the model is the method used to define the pin loading. Methods included specimen-pin contact, a contiguously meshed pin, and the direct application of essential boundary conditions to the surface of the specimen. For approaches that employ contact, the pin is specified as deformable or rigid and the specimen-pin interface is classified as having friction or being frictionless. In Table 4, a label describing the frictionless contact of a rigid pin would be contact, frictionless, rigid. Less rigorous approaches avoid the complexity of contact through a contiguously meshed pin. This assumption can also employ a deformable or rigid pin. In an attempt to approximate specimen rotation relative to the pin, the contiguously meshed pin can both translate and rotate (about its centerline). The label rotating communicates that the contiguously meshed pin is both rotating and translating while the label fixed implies a contiguously meshed pin that can translate but not rotate. Thus, the label contiguous, rotating, deformable would highlight a contiguously meshed, deformable pin that can rotate about its centerline. The last simplification involves the direct application of displacements to surface nodes. Although this approach can accommodate translation, the direct application of displacements on a patch of nodes will constrain specimen rotation and is thus labeled surface nodes, fixed.

In addition to specifying the balance laws and boundary conditions, the element type, discretization, and numerical approach for crack initiation and propagation is highlighted. Regarding element technology, approaches that employ full integration and reduced integration via Element type are distinguished. In this brief summary, fully integrated refers to the deviatoric response. The pressure is almost always on a lower-order basis to avoid volumetric locking. Reduced integration implies element formulations that seek to reduce computational time through a single integration point and require hourglass stiffness and/or viscosity to suppress zero-energy modes (Reese 2005). The level of refinement is noted in Discretization. The in-plane element size, through-thickness element size, and degrees of freedom are labeled IP, TT, and DOF, respectively. If a single element was employed in the through-thickness direction, 2D is appended. The method employed for free surface creation is labeled Fracture methodology. The most common methodology employed was element deletion. Elements may be loaded and unloaded (via damage evolution) prior to deletion. Teams employing criteria (of loaded elements) may have also employed a crack-band model for unloading. Crack band models attempt to maintain a common measure of surface energy (Bazant and Pijaudier-Cabot 1988). Teams also employed surface element approaches which regularize the effective surface energy through a characteristic length scale. Those paths were seeded or adaptively simulated through X-FEM (Dolbow and Belytschko 1999). The fracture process originates from smooth notch having a bounded stress concentration. After crack initiation, the process is over-driven. This particular problem may exhibit less sensitivity to non-regularized methods (de Borst 2004) because solutions will be less sensitive to the modeled fracture resistance. The final category, Uncertainty, summarizes each team’s effort to characterize uncertainty in the methods and/or models. For this effort, all teams employed bounds to characterize uncertainty. Those bounds are partitioned into geometry, boundary conditions, and material parameters.

Table 5 Models employed by teams participating in the Sandia Fracture Challenge

The solution of the balance laws requires the specification of a constitutive model. Both the literature and the provided data characterize Ti–6Al–4V sheet as anisotropic and having rate and temperature dependence for the applicable loading rates. The flow characteristics of the models used by the different teams are noted under Plasticity in Table 5. The yield function and the hardening, labeled Yield function and Hardening, respectively, may have rate and temperature dependence. Table 5 contrasts yield functions which employ a single invariant (von Mises, $J_{2})$, or multiple invariants $(J_{2}/J_{3})$ with anisotropic yield surfaces [Hill (Hill 1948), Cazacu–Plunkett–Barlat (Cazacu et al. 2006)]. The labels Hill and CPB06 represent the Hill and Cazacu–Plunkett–Barlat yield surfaces respectively. The hardening is characterized through a functional form. There is no distinguishing between approaches that employ only the equivalent plastic strain or additional internal state variables for hardening. Models for fracture/failure are partitioned into Criteria and Damage evolution. Criteria refers to the failure metric for a material point. The post-failure response may be abrupt or be governed by an additional law for unloading (such as the crack-band model). Damage evolution attempts to communicate if models include the micromechanics of the failure process through a softening response termed Damage accumulation. That response may depend on the evolution of an additional internal state variable (such as void volume fraction) or a post-processed quantity. Continuum damage mechanics approaches are contrasted with methods that lump damage evolution into an effective traction-displacement law. The Calibration label in Table 5 communicates if the team employed the provided tension and shear data for model calibration.

Table 6 Comparison of blind predictions to experimental values for both the slow and fast loading rates

Fig. 20

Evaluation of plasticity predictions up to the onset of necking: comparison of blind predictions to the range of experimental data

Fig. 21

Evaluation of predictions of the first unstable fracture event: comparison of blind predictions to the range of experimental data. Note that there were no upper or lower prediction bounds, since these quantities were assessed after the results had been reported

Fig. 22

Combined comparisons of force-COD predictions (colored lines) to experimental observations (gray circles). a Slow (0.0254 mm/s) loading rate. b Fast (25.4 mm/s) loading rate

Fig. 23

Individual team comparisons of force-COD1 predictions (black lines) to experimental observations (colored lines) for the slow (0.0254 mm/s) loading rate

Fig. 24

Individual team comparisons of force-COD1 predictions (colored lines) to experimental observations (gray circles) for the fast (25.4 mm/s) loading rate

5 Comparison of predictions and experiments

5.1 Comparison of scalar quantities of interest and crack path

In real-world engineering scenarios, modeling is often used to predict scalar performance metrics such as the maximum allowable service load that a component can support or how far the component can be deformed before it will fail. Motivated by this, the challenge scenario specified certain scalar QoIs to be reported, as previously described in Sect. 2. Table 6 compares the scalar QoI predictions of all 14 teams to the experimentally measured range. In this table, several key QoIs are tabulated: the applied load when COD1 was equal to 1 and 2 mm, the peak applied load, and the crack path for both the slow and fast loading rates. In the original challenge, the teams were asked to predict the COD1 value when the load had dropped by 10 and 70 % below peak load. However, as discussed earlier, these QoI’s were not experimentally measurable quantities due to the dynamic nature of the unstable crack initiation and growth. This was the reason for the formulation of alternate QoIs described in Sect. 3.2. Therefore, Table 6 includes two additional columns for these additional QoIs: COD1 and force values at the point of unstable crack initiation. These QoIs were readily extracted from the force-COD curves reported by each team. A sudden drop in the load at fixed COD1 level was taken as indication of prediction of unstable fracture; the force and COD1 corresponding to this transition was taken to be the prediction of failure load and COD1. Some teams predicted a gradual drop in the load, with either an increasing or decreasing COD1 level, indicative of stable fracture. In these cases, it was not possible to evaluate the alternative QoI.

The expected value column for the scalar QoI metrics reported in Table 6 are color coded to indicate if the predicted values were consistent with experimental observation. Black values were within the range of experimental scatter, with an additional buffer of $\pm 10\,\%$ added to the experimental range. This somewhat arbitrary buffer is intended to allow for the possibility of ‘valid’ scenarios outside of the limited number of experimental observations. Numbers reported in the expected value column that are color coded red or blue indicate predictions that are high or low, respectively, compared to the buffered experimental range.

Figures 20 and 21 provide a graphical representation of the tabulated data from Table 6, comparing each team’s predictions (points) to the upper and lower bounds for the experimental range (horizontal dashed lines). Figure 20 assesses the QoI metrics for early deformation up to the point of necking whereas Fig. 21 assesses the QoI metrics for the first unstable crack event. In addition to the numerical data, an indication is made if the team did not predict the B–D–E–A crack path, or if the team predicted a stable crack growth process (e.g. slowly evolving damage) rather than an unstable crack event. Four teams predicted crack paths that deviated from the B–D–E–A. One team (Team N) predicted a failure path for the slow rate test of A–C–F, and for the high rate test of B–D–E–A. Two other teams predicted an A–C–F failure path for both the slow and fast rate tests (Team C and G). One team (Team F) predicted a mixed failure path (for the slow rate test, A–C failure, followed by partial failure along the B–D–E path, and then finally through the remaining ligament, C–F; and for the high rate test B-D-E failure, followed by failure along the A–C ligament, and then finally failure through the remaining E–A ligament).

5.2 Comparison of force-COD curves

Force-COD1 curves can provide additional insights into the efficacy of the various modeling approaches. Figure 22 provides a comparison between the experimentally measured force-COD1 curves and those predicted by the teams. While this figure provides an overview of the extent of prediction scatter, it is difficult to assess any specific team’s direct comparison to experimental observations. For that purpose, Figs. 23 and 24 provide a team-by-team comparison of the same force-COD1 curves for the slow and fast loading rates, respectively. A more detailed discussion comparing the predictions to the experimentally measured values is contained in Sect. 6.

6 Discussion

The goal of the present study was to assess the predictive capability of modeling and simulation methodology when applied to a model engineering problem of ductile deformation and fracture. The success of the predictive tools relies on five successful elements: (1) realistic physical constitutive models for deformation and failure, (2) accurate calibration of model parameters based on available data, (3) proper numerical implementation in a simulation code, (4) representative boundary conditions, and (5) correct post-processing to extract desired quantities. The chosen problem explored several phenomenological aspects of material behavior such as elasticity, anisotropic plasticity with coupled heat generation, localization, damage initiation, coalescence, crack propagation, and final failure. Furthermore, the damage and failure process considered a competition between a tensile mode failure process and a shear mode failure process. The challenge was open to the public and agnostic with regard to the computational methods employed. The challenge merely postulated a specific set of QoI’s to be predicted based on the provided geometry, material properties, and loading conditions. This report combined with the outcome of the previous challenge provide an assessment of the state-of-the art in failure modelling and areas for improvement.

6.1 Assessing agreement and discrepancy between predictions and experiments

6.1.1 Generic categorization of potential sources of discrepancy

In the context of the present challenge, multiple repetitions of data were provided on the material calibration tests to enable treatment of material property uncertainty. The as-machined specimen dimensions of the challenge geometry were also provided to enable bounding based on dimensional variability. No guidance was provided on how to use this uncertainty information and different teams chose differing approaches depending on engineering judgement and available time/resources. Most teams only utilized what was considered as the most representative features of both the material response and the geometry in calibration and simulation. Only one team, Team M, reported that they had intentionally explored geometric variations across the range of reported specimen dimensions to help bound their blind predictions. The representation of the compliant boundary condition for the shear calibration test and the pin-loaded contact boundary condition for the challenge geometry were addressed differently by each team, resulting in different responses, even in the elastic regime. Some teams accounted for anisotropy of the plastic response of the material through the use of the Hill48 or equivalent models, whereas other teams considered only the isotropic yielding model. The decision was based on engineering judgment and/or model availability. Similarly, some teams ignored the heat generation during high-rate deformation while others chose adiabatic or coupled-thermomechanical conditions. Some teams incorporated strain-based damage induced softening of the plastic response, while others used a strain-to-failure criterion based on a damage indicator function, in the spirit of the Johnson-Cook model. This lack of consensus on the modeling assumptions and techniques, as compared in Tables 4 and 5, results in significant heterogeneities in the predictions. Nevertheless, overall predictions were more consistent and in line with the experimental results than in previous challenges. The general improvement in predictions is likely due, at least in part, from learning and model improvement as a result of prior challenges.

Elastic stiffness Perhaps one of the most surprising outcomes of the challenge was that several teams predicted a stiffness in the elastic regime that deviated $>$10 % beyond the experimental slope. When predictions were in error, they were all consistently too stiff relative to the experimental stiffness. For most if not all of the teams in error, the stiffness was overestimated due to an unrealistic representation of the pin loading boundary condition (e.g. no free rotation at the pin). A comparison of the results for all of the teams suggests that if similar, realistic pin-loading boundary conditions had been adopted by the teams all of the results would be more consistent with the experimental elastic slope. It is also interesting to speculate that the elastic slopes were better modelled in the previous challenge because data from a compact tension specimen with pin loading was provided to calibrate models for the blind prediction.

Yield surface The yield behavior and all post-yield deformation/failure processes can depend on extrinsic factors of the environment and loading conditions, including strain-rate, temperature, triaxiality, Lode angle, and load-path history. In addition, yield behavior can depend on intrinsic aspects of the material itself such as grain size, grain shape, crystal structure, phase distribution, etc. Rarely are all of these extrinsic and intrinsic factors described in a single plasticity model, due in part to the limited calibration data that is available, and also to uncertainty on the proper mathematical descriptions. In the absence of a comprehensive, universally-accepted plasticity law, and all the necessary data to calibrate its parameters, each team chooses to represent some subset of the dependencies. Two characteristics of the challenge material response that were included by some teams in their constitutive model description of the material are the dependence of the yield locus on Lode angle and material anisotropy. Wrought titanium alloys are known to display plastic anisotropy. The test data provided, be it the uniaxial tension test data or the shear test data, indicated some anisotropy in the material’s response. Comparison of the tension test data against the shear test data also indicated dependence of the yield surface on Lode angle. Several teams made note of this behavior, pointing out that use of a von Mises yield locus (which has no dependence on Lode angle) resulted in a poor fit between the model response and the shear test data when the tensile test data was utilized to determine the model parameters. This is because the challenge material exhibited yielding under shear loading at a stress that was approximately 0.88 times lower than that predicted by a von Mises model (indicating that the yield surface for this alloy is closer to a Tresca like yield surface). To account for these response characteristics (anisotropy and Lode angle dependence) several teams (B, E, F, I, J, and M) made use of material models that are capable of capturing these dependencies. (Teams C and H accounted for some of these dependencies in an approximate way, using different sets of material properties/models in different regions to account for the expected material response characteristics.) Most of these teams (all, except B and C) made use of the Hill plasticity model, with its ability to capture anisotropy and/or Lode angle dependence of the yield locus. While teams that accounted for Lode Angle (J3) dependence, and/or sheet anisotropy generally produced better elastoplastic predictions, the Challenge may not have been able to sufficiently discriminate between relative importance of these two different contributions. Team I noted that the Hill yield function could be utilized to account for the Lode angle dependence of the yield locus without incorporation of material anisotropy, with acceptable results. Analyses by Team H and Team J concluded that an isotropic model would be more likely to predict failure along the incorrect path A–C–F, whereas the models with lode angle dependent yield loci were necessary to drive failure to the correct B–D–E–A path. The results suggest that models incorporating Lode angle dependence of the yield locus were able to predict the elasto-plastic response more accurately (perhaps prior to the onset of localization). Predictions of loads and CODs by teams using the von Mises yield criterion (which has no lode angle dependence) differed by about 10 %. Several teams also incorporated anisotropy in addition to Lode angle dependence of the yield locus. Based on the QoIs requested, it is difficult to ascertain if the inclusion of anisotropy for the challenge problem was truly necessary; however, post-challenge assessments carried out by one team suggest that alternate, more intrusive QoIs (such as inter-ligament strains) are more sensitive to the incorporation of anisotropy and if used may have resulted in a more conclusive determination of the importance of anisotropy (Gross and Ravi-Chandar 2016).

Work-hardening Calibration and extrapolation of the hardening behavior was typically handled either by fitting specific functional forms or by a spline/multi-linear approach. Models that represent the stress–strain curve through splines or other piecewise functions provide greater flexibility. On the other hand, functional forms of work hardening such as the Swift and Voce forms are perhaps cheaper computationally because they reduce the number of simulations required for calibration and uncertainty quantification. While the additional flexibility associated with the added parameters in a spline or piecewise-linear approach may at first seem more accommodating, the alternative functional forms were generally more successful in the elastoplastic regime. In fact, among the teams that had the most accurate quantitative predictions for the elastoplastic regime (Teams E, H, I, J), none of them used a spline or piecewise-linear approach. In discussion, one team noted that the flexibility of the extra degrees of freedom in a spline or piecewise linear approach can be challenging to calibrate given limited data, can be more difficult to assess in terms of uncertainty quantification, and can also be difficult to incorporate into coupled physics models such as a thermomechanical coupling.

Thermal effects This was crucial for this class of materials, especially under the moderate rate loading conditions, where the conversion of plastic work to heat, as well as heat conduction play a role in the local response. Load versus COD curves in the fast-rate case indicated a rounded response at the peak in the force-displacement curve rather than being flat-topped as in the slow-rate case. Some teams that incorporated the thermo-mechanical coupling (e.g. Teams G, H, and M) or adiabatic conditions (Team J) were able to better capture this feature at the faster rate. Several teams reported ambiguity in determining the appropriate thermal work coupling parameter, i.e. Taylor–Quinney coefficient.

Localization The experiments indicated a clear peak-load and geometric softening associated with localization of the structural response. The localization was subtle in the slow-rate force-COD curves and more pronounced at the fast-rate. Most teams predicted some degree of localization at least in a qualitative sense. This is not too surprising, because the onset of localization is essentially a geometric effect due to inter-ligament necking and a sufficiently fine mesh should capture this feature. The fidelity of models for work hardening and thermal softening will impact the accurate prediction of the onset of necking, and this is a potential source of discrepancy. It bears emphasis that the Sandia tests provide information about the onset and process of localization in both the tensile and shear testing that was carried out, but the lack of full-field measurements of strain in the challenge sample prevent further validation of the model with regard to onset and progress of localization. Follow-up experiments at the University of Texas at Austin provided this detailed full-field ligament deformation data (Gross and Ravi-Chandar 2016).

Crack initiation and propagation The prediction QoI metrics for this challenge focused on elastoplasticity and the conditions for initial unstable fracture from a smooth notch. When the crack did initiate, it was overdriven and propagated catastrophically to the next arrest feature. The elements of this challenge could be successfully navigated without wrestling with resistance curve behavior or incorporating a crack length scale and the related mesh dependence of sharp crack behavior. For this reason, the current challenge does not delve into the relative merits of different crack propagation modeling approaches. Most teams had marked success in predicting the correct propagation path and in predicting the unstable rupture. Incorrect predictions may be attributed to inadequate yield surface, work hardening response or boundary conditions. The adopted crack initiation models fall into three categories: a threshold strain value, voids, or damage. In the two instances of the cohesive zone and the XFEM-based XSHELL model, cracks and their location are assumed at the onset of the computation so initiation is not a consideration. Crack propagation was modeled using element deletion, XFEM, and the cohesive zone approaches. Based on the load-COD predictions, there are discrepancies in the onset and propagation of cracks. A key source of the discrepancy is the translation of model parameters from the tension and shear tests. For most mesh-based methods there is difficulty scaling the mesh size commensurately for the calibration and challenge geometries so that the calibration parameters translate appropriately. Cohesive zone and the XFEM approaches seek to bypass these difficulties. At the post-challenge workshop, there was considerable discussion on the tradeoffs between relatively simple models for failure that may lack fidelity or universality versus more sophisticated models that may be more challenging to calibrate or are less mature.

Numerical methods The finite element method was the method used by all of the teams, except Team K who used the Reproducing Kernel Particle Method. Meshes with fine zones in regions of potential crack propagation in the challenge sample and meshes with similar densities to model the calibration tests were employed with the expectation that mesh-dependence would be mitigated. Only two teams that adopted the XFEM and a non-local approach tried to mitigate the dependence of results on the mesh characteristics that is expected in failure modelling. This remains a source of discrepancy and is suggested as an item for improvement for blind predictions in future challenges. A second aspect is the time integration scheme. With the exception of four teams, all other teams used explicit time integration; mass-scaling was used to reduce computational time. The degree of discretization varied widely, with the in-plane element sizes spanning an order of magnitude from 0.05–0.5 mm, and the number of degrees of freedom varying by more than two orders of magnitude from 30 K to $>$3 M. While a detailed sensitivity study would be needed to fully address the discretization tradeoff for a given method, there was not an immediately clear general trend that more elements and higher spatial discretization consistently improved accuracy. The tradeoff between computational cost and prediction accuracy is specific to the individual method employed. It is not trivial to achieve Einstein’s complexity balance that “everything should be made as simple as possible, but not simpler”.

Post processing An often undiscussed source of discrepancy is the process of extracting the correct quantities, translating them into desired units, and communicating them correctly. This can be particularly problematic with a looming deadline, as the post-processing occurs in haste and rudimentary mistakes are made. In a previous challenge for example, one team reported QoIs in incorrect units. In the current challenge, Team L accidentally accounted for reaction forces at only one boundary node rather than summing the forces on all boundary nodes. This mistake was not discovered until after the comparison to the experimental predictions. While the team requested to report the corrected summed values, we have also included their original mistake for the purpose of illustrating this point. Even the most accurate model can be rendered useless if these mistakes are not painstakingly avoided. In critical applications where the model has implications such as loss of life, it is recommended to utilize at least two independent prediction teams to provide a peer review or cross-check for glaring discrepancies.

6.1.2 Overview of agreement between predictions and experiments

It is possible to assess the efficacy of each team’s prediction methodology comparison to the experimental outcome. The prescribed QoI’s that were readily measured are the metrics associated with elasticity, plasticity, work hardening, and the onset of necking (peak force). With respect to the metrics associated with plastic deformation up to peak force, half of the teams (E, G, H, I, J, M, N) were able to successfully predict all prescribed quantitative metrics within the 10 % buffered experimental range. This result reinforces the notion that the elastoplastic behavior is not trivial to correctly capture. In fact, all seven teams that did not capture the peak force, were also outside the buffered experimental range in their early deformation prediction at COD1 $= 1$ mm. Six of those seven teams overpredicted the early deformation and subsequently overpredicted the peak force of the test. As discussed previously, one of the most common culprits for this overprediction was inadequate pin-loading boundary conditions.

Of the seven teams that predicted the elastoplastic response, five (E, H, I, J, M) were able to also predict the B–D–E–A crack path for both loading rates. Based on these prescribed QoI’s that were experimentally measured, all five teams could claim success in the fracture challenge. However, there were additional post-Challenge QoI’s that shed additional light on the ability to predict the onset of cracking. Of the five teams that successfully predicted all the deformation and crack path metrics, four of the teams (E, H, I, J) also predicted the forces associated with crack advance. All four of these teams overpredicted the COD1 value for cracking for at least one of the two loading rates. This highlights a general tendency for overpredicting the COD1 value for cracking: of the eight teams that predicted unstable B–D–E–A cracking, seven overpredicted the COD1 value of cracking for at least one of the loading rates. This outcome suggests the need for a more comprehensive, accurate suite of failure calibration tests.

6.1.3 Uncertainty bounds

To this point, the assessment has focused largely on a comparison of the predicted ‘expected’ values for the quantities of interest. However, each team was also allowed to report uncertainty bounds for their prediction. The use of uncertainty bounds is an important engineering tool to represent the potential sources of error in the prediction so that they do not result in misleading engineering interpretation.

The uncertainty bound also plays a psychological role in conveying the degree of confidence in a prediction. For example, reporting an uncertainty bound that varies by a factor of 10 from the lower to upper bound helps the user of the data understand that the result is only an order of magnitude estimate, whereas reporting a uncertainty bound that only differs by 1 % from the lower to upper bound suggests a much higher degree of confidence in the prediction. When teams reported uncertainty bounds, they typically ranged from $\sim$5–20 % variation on the expected value, however there were cases where the uncertainty bounds were $\sim$1 % and other cases where the uncertainty bounds were quite large. Team B, for example, predicted an expected value for force at COD1 $=2$ mm (fast rate) of 20,202 N, remarkably consistent with the experimental range of 20,230–20,650 N. However, for that same quantity, Team B bounded their prediction from 10,058 to 24,983 N, more than a factor of 2 different from the lower bound to the upper bound. From a practical perspective, such a broad uncertainty window may lead engineers to overcompensate for the low (underpredicted) allowable minimum force.

It is possible to assess the efficacy of the predicted uncertainty bounds in their ability to bracket the experimental outcomes. It is only possible to make this assessment on the pre-fracture QoIs associated with plasticity and the onset of necking (COD1 $=1$ mm, COD1 $=2$ mm, and Peak Force), since the prescribed post-fracture QoIs were not measured experimentally. There were 14 teams that reported prediction on these 3 QoIs at each of the 2 different loading rates, resulting in a product of 84 predicted outcomes. Of these 84 predictions, the predicted ‘expected value’ fell within the experimentally observed range in only 17 (20 %) of the 84. Of these 84 predictions, 69 were reported with uncertainty bounds and the remaining 15 predictions were reported as expected values with no declaration of an uncertainty bound, presumably because the team ran out of time to assess the bounds. Of these 69 reported values with uncertainty bounds, there were 16 cases where the expected value was outside the range of experimental values, but the bounds successfully overlapped, at least partially, with the experimental range. To put this in perspective, while 20 % of the 84 predictions had expected values that fell within the experimental range; another 19 % (16/84) of the predictions had employed bounds that included some portion of the experimental range. The positive conclusion is that the use of uncertainty bounds roughly doubles the chances of capturing the outcome. Conversely, the negative conclusion is that $77\,\% ((69{-}16)/69)$ of the time that uncertainty bounds were employed, they still did not bracket the experimental outcome.

This rather weak performance for uncertainty bounds is likely attributed to the time consuming nature of a formal detailed Uncertainty Quantification (UQ) analysis. Most teams instead bound their predictions by identifying one or two key parameter(s) that were difficult to calibrate, and varying them over some range. Based on the outcome of the previous challenge, a few teams intentionally varied the dimensions of the geometry across the range of values in the manufacturing tolerances. Even this degree of rudimentary parametric analysis can be much more time consuming than the baseline prediction, since it requires running several instantiations. There is also a tradeoff between the fidelity of the baseline prediction, and the feasibility of detailed UQ analysis. For example, the fine-zoned meshes used in some cases to model the challenge sample preclude implementation of UQ in a timely manner. As with the previous challenge, integration between solid mechanics modeling and UQ has not matured to the point where it is readily accessed for time-sensitive, resource-limited predictions. Beyond the time-consuming nature of UQ, there is a lack of standardized processes for the assessment.

6.1.4 Computational efficiency

There is generally a trade-off between fidelity and speed to solution, known in cognitive psychology as the speed-accuracy tradeoff (Wickelgren 1977). In engineering practice, it is often viewed that a reasonable approximation within a short timeframe is more valuable than a highly accurate estimate obtained in a much longer timeframe. The two Sandia Fracture Challenges both provided only the most basic of constraints in this regard: all teams had the same number of months to arrive at their prediction. Yet the number of man-hours each team spent in arriving at their predictions likely varied widely, although that number may be difficult to estimate.

While it may be difficult to evaluate the overall efficiency of the team’s entire prediction stream, one clear first-order metric is the number of computational degrees of freedom (DOF) in the team’s analysis method. Even this parameter varied over a surprisingly wide range: nearly 2 orders of magnitude from 30 K to 2.5 M DOF. The two teams with the lowest DOF ($<$100 K, Teams D and E) both noted the relative speed of their approach as a pragmatic path to solution. To achieve the lowest DOF of 30 K, Team D employed an intriguing shell element approach. Team E was notable in that they were able to predict the scalar QoI’s with only 90 K DOF. Team I was also notably efficient in this regard, with only 135 K DOF. In an engineering environment these pragmatic approaches may be more attractive. Of the other teams that fared well in the QoI predictions, Teams H, J, and M utilized 600 K, 2.5 M, and 2.1 M DOF respectively. The overall team efficiency is a metric that will be valuable to track in future Challenges.

6.2 Future needs for improving predictive ability of computational models in the area of ductile fracture

The style of this challenge does not isolate a single modeling phenomenology (e.g. crack initiation) to render a detailed comparison between differing methods while holding all other factors constant. Indeed, such a pure assessment is difficult to make because often each phenomenological model is constrained to certain numerical implementations, calibration requirements, etc. For this reason, while the effort is dubbed the “Sandia Fracture Challenge”, it is not simply an assessment of fracture modeling paradigms but rather a holistic assessment of approaches that can render predictions of fracture scenarios.

6.2.1 Constitutive modeling

While the quantities of interest (QoIs) were selected to reflect the quantities that would be called upon in a typical engineering design scenario in industry, these global QoIs such a far-field force and displacement are not the most sensitive discriminating parameters for assessing the relative efficacy of different modeling paradigms. As shown in Figs. 20 and 21, even when teams predicted an incorrect crack path or a stable fracture event, they still could obtain reasonable values for the far-field QoIs. In pursuit of a more rigorous assessment of constitutive modeling of both the deformation and fracture events, it will be necessary to employ more invasive QoIs that probe the local state in the vicinity of extensive deformation and failure. For example, the QoIs probed in the current challenge did not fully probe the impact of anisotropy of strength on predictions—an isotropic model would have given all of the load and COD predictions to within 10 %. As demonstrated by the DIC measurements of Gross and Ravi-Chandar, if more invasive QoIs such as the inter-ligament strains are measured, existing plasticity models may need improvement to capture these details. Of course, improvements to constitutive descriptions will entail varied experiments for model calibration or alternatively, full-field measurements in standard tension tests to calibrate anisotropy of strength description, e.g. Gross and Ravi-Chandar (2016).

6.2.2 Failure modeling

There appears to be consensus on the importance of incorporating triaxiality and Lode-angle dependence on the failure strain. Because the test data provided in the challenge spans limited triaxialities and shear paths, only a limited calibration of damage models was possible. Some of the teams used published empirical data for the Ti–6Al–4V failure locus of failure strain as a function of stress triaxiality, also known as the “garland curve”, e.g. Giglio et al. (2013, 2012), to calibrate the dependence of the failure strain on triaxiality and Lode angle. Furthermore, the effect of orientation and rate dependence on this type of failure curve is not known and techniques to obtain such data are still to be developed. There appears to be an emerging consensus on the importance of incorporating triaxiality and Lode-angle dependence on the failure strain. However, the fact that teams that used simple triaxiality-dependent strain-to-failure criterion without damage were also able to predict equally well the failure path, instability and most of the scalar QoIs makes it difficult to indicate that any one model is better than another; for example four teams were able to predict all QoIs except the critical COD. A different kind of challenge, where the stress state is systematically altered to introduce failure under different triaxiality and Lode angle could be triggered, may have to be developed in order to sort out the suitability of different types of models. The precise nature of such a model and methods of obtaining a calibration of these models remain topics of active research and further development is necessary.

While the previous challenge provided crystallographic texture and microstructural information for the stainless steel that was tested, the current challenge did not. Instead, the current challenge assumed that the effects of microstructure would be effectively captured in the provided macroscale mechanical tests. Tensile and V-notch shear properties were only measured in the two orthogonal in-plane directions. However, given the recent community-wide emphasis on multiscale modeling, a future challenge may focus instead on providing detailed microstructural information and predicting the ensuing mechanical response.

A pervasive disconnect between the models and experimental observations lies in the details of the fracture morphology. As shown in Fig. 3e, the slow loading rate tensile test resulted in a well-defined cup-and-cone morphology with a flat fibrous zone in the central region of high triaxial stress and a clear transition to shear lips around the perimeter of the fracture surface. There are clearly two distinct failure modes with an abrupt transition, yet failure models generally lack this detail (e.g. compare to Figs. 54b, 63b, or 68b). Moreover, in the experimental tensile tests there was a transition from this cup-and-cone morphology which dominated at the slow loading rate to a slant fracture more reminiscent of sheet failure that occurred at the higher loading rate, as seen in the comparison between Fig. 3e, f (also see Fig. 4a, b compared to Fig. 4c, d). It should be possible to predict these feature transitions with a sufficiently fine 3D mesh and a failure model that can accurately discriminate between tensile and shear failure modes. As the community strives to add fidelity to failure prediction and more physically-realistic micromechanical models for failure, this apparent disconnect may be a valuable area for future detailed assessment.

6.2.3 Computational methods

In the present challenge, only Team K used a meshless method, in this case the Reproducing Kernel Particle Method. The absence of these other methods such as Peridynamics may be happenstance as the voluntary nature of this effort may not have captured the interest of a team with other methods. The relative lack of meshless methods may also be due to their rarity or the maturity of these techniques for engineering fracture scenarios compared to conventional approaches. Enhancements to conventional finite elements using cohesive zones and XFEM were used by some teams to model crack propagation in the former case, and initiation and propagation in the latter. Team E, who employed a cohesive zone approach to describe the damage evolution, was not able to capture the abrupt unstable crack advance and instead predicted a steady softening behavior. The majority of teams instead used element deletion to advance the crack and with a sufficiently dense mesh. This approach appeared to yield reasonable results, although admittedly, the metrics or QoIs of the current study focused largely on the deformation and first crack initiation rather than crack advance.

Most teams bound uncertainty in their predictions based on variations in material parameters and/or boundary conditions. Only two of the fourteen teams considered geometric variation, even though geometric variation was revealed to be a critical source of outcome discrepancy in the previous challenge. This is likely because of the time consuming nature of a geometric variation study. While many simulation codes now offer the possibility to vary geometry, the automatic meshing that is needed may not be sufficiently robust.

6.3 Recommendations for future challenge scenarios

6.3.1 Specific topical areas in deformation and fracture where blind assessment is needed

The present challenge provided insight into the modeling of ductile failure at quasi-static and moderately high rates. In contrast to the SFC1 predictions, the SFC2 predictions were more in line with the experimental results; and as suggested this may likely be the targeted nature of the calibration data provided. However, the current challenge and the post challenge summit held at the University of Texas at Austin highlighted the need for measurements of local behavior using optical techniques. In the current study, clip-on gauges used to measure the COD were easy to implement but unreliable. Optical methods like DIC provide more detailed measurements, which highlighted the short comings of the constitutive description. Full-field calibration data would allow for more fidelity in model calibration, while at the same time more invasive QoIs could be interrogated in the challenge scenario. Aside from local DIC in the vicinity of failure, DIC may also prove useful in other locations such as near the loading pins to characterize the degree of sliding and validate boundary conditions. Beyond DIC, other local QoIs such as could be provided by an infrared temperature map could also prove useful for dynamic loading scenarios. An important caveat is that the DIC and infrared measurements described here will only provide surface information. This surface information is unfortunately removed from the high triaxial stresses subsurface where cracks nucleate. In fact, these surface metrics may better reflect the formation of shear lips in failure, a feature that most models fail to capture. For subsurface information, x-ray computed tomography may prove useful to indicate the state of subsurface damage evolution.

In addition to full-field data for calibration and validation, there was continued interest in adding more material calibration data. Some examples include: (1) temperature-dependent mechanical properties would aid the thermomechanical coupling analysis, (2) thermocouple temperature measurements in the gauge section during tensile tests to estimate the thermal work coupling parameter, (3) in-plane 45-degree orientation tensile tests to more completely evaluate the anisotropy, (4) additional tests to estimate the out-of-plane anisotropy, (5) additional strain-to-failure tests under a broader range of stress states. While access to this breadth of data should enhance the predictive ability of some models, there is a countervailing motivation to mimic the breadth of data that is typically available for engineering assessment. Clearly, this and the previous Sandia Fracture Challenge exercise have demonstrated the need for extensive material calibration data to render accurate predictions.

A round-table discussion at the summit and subsequent post-summit discussions yielded several potential focus areas for follow-up challenges in ductile failure:

• 1. Elevated temperature Subject the candidate material to loading under high temperature. High-temperature constitutive behavior will be crucial.

• 2. Complex load history and load path This could include either multi-axial loads or alternatively, interrupted loading with change in direction. Note that this will bring kinematic hardening effects into play.

• 3. Assembled systems, welds, connected systems with bolts, welds or fasteners It is interesting to note that the stiffness predictions of the current challenge are a consequence of the interaction of the machine and the sample which functions as an assembly. Modelling welds will pose problems with a lack of information regarding the weld constitutive behavior and the need for residual stress fields.

• 4. Puncture and out-of-plane deformation Using laboratory-scale tests to calibrate models and make blind predictions of tests which involve perforation and out-of-plane deformation. This exercise could also explore even higher rate deformation, as is often found in puncture scenarios.

• 5. Effect of microstructure/multiscale modeling Some of the teams are engaged in developing multiscale models for deformation and fracture. While these models may lack the maturity of continuum macroscale failure modeling, it could be instructive to evaluate the efficacy of various modeling approaches to predict the effects of a modified microstructure on the outcome of a failure scenario.

6.3.2 Guidance for execution of a future challenge

The ‘lessons learned’ in the previous challenge had been assimilated in this second challenge; most importantly, sample manufacturing tolerances were maintained within sufficient bounds so as to eliminate (save the one test) crack path ambiguities. With regard to the key lessons learned in the current challenge, it is the deployment of full-field optical-based instrumentation, in addition to the conventional clip gauges. With the full-field measurements in place a more invasive set of QoIs could be demanded (principal strains in the ligament region prior to localization for instance). As discussed in the last section of the article on the previous challenge, specification of a conditional set of QoIs is recommended. These conditional QoIs mimic the distinct phases of elastic, elastic-plastic response followed by localization and failure. Conditional QoIs which serve as ‘go/no-go’ decision points could be postulated. If elastic response is correctly predicted, proceed to evaluate the elastic–plastic response and so on. See section 6.3.2 of Boyce et al. (2014) for further elaboration.

The discussion from the post-prediction summit suggested that the next challenge might employ the same material on a more challenging problem (see list in previous section): on the one hand, this is an economical option as fewer tests need to performed, less time will be spent for returning teams on model calibration, and predictions should improve accordingly; on the other hand if the challenge seeks to replicate real-world demands on engineering predictions, this ‘comfort’ of working with the same material may be less realistic. An additional recommendation was raised to employ more localized quantities of interest such as displacements in the ligament region between the holes and notches. While these more local measures would likely be more discriminating, it will continue to be important to also assess the far-field metrics that mimic the needs of “real world” scenarios.

In the conclusion of the previous article on the challenge, there was a call to apply modern uncertainty quantification techniques to the challenge problem. Likewise, we conclude by suggesting that future challenges could call for confidence intervals, or probabilities on the predictions. While it may be difficult for ‘volunteer’ teams to allocate sufficient resources for an intensive uncertainty assessment, one of the benefits of conducting a follow-up challenge on the same material is that more effort could be spent exploring the uncertainty landscape. A focus on uncertainty assessment will likely require adoption of efficient iterative methods. Calibrated material uncertainties must be deconvoluted from the applied boundary conditions and specimen geometry. Stochastic distributions must then be efficiently propagated through blind predictions and response surfaces for the QoIs to be adequately sampled. Unless the community can become more efficient in this iterative process, intuition-based uncertainty bounds will continue to be the norm.

Finally, in addition it will be useful in future scenarios to track the efficiency of the team solution. While the computational degrees of freedom provide one clear metric, it may also be beneficial for teams to track man-hours spent on the solution.

7 Summary and conclusions

The current study documented the capability of 14 independent computational mechanics teams to predict blindly the quasi-static and moderate-rate dynamic rupture of a geometrically complex specimen manufactured from a common titanium alloy, Ti–6Al–4V. This ‘challenge’ scenario is the second such challenge, following on a similar challenge two years prior evaluating predictions of quasi-static rupture of a precipitation hardened stainless steel. On average, the predictions were generally more consistent with the experimental outcome compared to the first challenge. The improvements are thought to be due to two factors (1) the material test data provided was more extensive than the first challenge (or typical engineering scenarios), including the provision of a shear failure test to complement the more common tensile tests, (2) while this second challenge scenario was markedly different from the first scenario in material, geometry, and loading conditions, the outcome of the first challenge still helped guide teams away from immature or difficult modeling paradigms towards robust approaches.

It was evident that the modeling of ductile rupture relies first and foremost on an accurately calibrated model of orientation-dependent, stress-state dependent, rate-dependent elastoplastic deformation and localization. Under modest dynamic loading rates, the heat generated by plastic work can also lead to a non-negligible coupled thermal contribution. When teams erred in their prediction of the elastoplastic behavior there was a consistent trend towards over-prediction of the stiffness and the peak force during deformation. This over-prediction of the stiffness and effective strength appears to be correlated to inaccurate boundary conditions associated with the pin loading condition. Without getting these ‘basic’ boundary conditions right, efforts to implement more advanced mechanics models for deformation and failure are in vain. There were significant differences from team to team in the approach to model the failure process, ranging from cohesive zone damage evolution to element deletion based on a critical strain criterion; and there was significant quantitative disagreement across the models regarding the conditions associated with the onset of failure. It is clear that the mechanics community will benefit from the development, standardization, and adoption of test methods to explore ductile rupture loading modes beyond simple tension.

Detailed uncertainty analyses continue to be challenging under real-world time constraints. While information was provided on variation of material properties and variation of geometry, only a few teams had an opportunity to explore these variations, and even then by the simple-but-often-effective method of sampling the extremes. Under real-world engineering scenarios with firm deadlines, detailed sensitivity analyses and uncertainty studies are typically underutilized. Finally, there is a clear benefit from comparing predictions from multiple teams. In critical engineering scenarios, peer review and/or multiple independent predictions can provide a broader perspective on true uncertainty, mitigate ‘tunnel vision’, and catch common pitfalls.

Appendices

Appendix 1: Additional details on modeling approaches and results

1.1 Team A

Team members:

J.A. Moore, johnallanmoore@gmail.com, Northwestern University, Evanston IL, USA

K. Elkhodary, khalile@aucegypt.edu, The American University in Cairo, New Cairo, Egypt

1.1.1 Approach

Simulations were performed using the finite element (FE) software ABAQUS 6.12. A dynamic analysis, with explicit time stepping was used. Failure surfaces were generated by the element removal method. An element is removed when a proposed damage variable $\delta ^{*}\ge \delta ^{*Crit}$. Domain decomposition parallelization was also applied for computational expediency.

Fig. 25

Comparison of tensile testing stress–strain curves (for transverse and rolling direction) to finite element prediction. The equivalent plastic strain in the dog-bone mesh is shown for reference. The analysis showed failure at the point marked “x”

Material Law Isotropic elasticity was assumed. For inelastic behavior, the von Mises stress $r({\varvec{\sigma }})$ is tested against an isotropically hardening yield surface, whose radius $r(\sigma _{y})$ is defined via a proposed simple modification to the Johnson-Cook flow rule. The modification herein proposed aims to account for the evolving damage with a single variable and a corresponding parameter. As such,

$$\begin{aligned} r({\varvec{\sigma }})= & {} \sqrt{\frac{1}{2}\left[ (\sigma _{1}-\sigma _{2})^{2} +(\sigma _{1}-\sigma _{3})^{2}+(\sigma _{2}-\sigma _{3})^{2}\right] }\nonumber \\\le & {} r(\sigma _{y}), \end{aligned}$$

(1)

with a modified Johnson-Cook (JC) rule defined as,

$$\begin{aligned} r(\sigma _{y})= & {} \left( A+B\varepsilon _{p}^{n}\right) \left( 1+C\hbox {In }\dot{\varepsilon }^{*}\right) \nonumber \\&\left( 1+T^{*m}\right) \left( 1-D\delta ^{*2}\right) . \end{aligned}$$

(2)

Here, A, B, C, n and m are the ordinary JC material parameters, $\varepsilon _{p}$ is the effective plastic strain, $\dot{\varepsilon }^{*}$ is a normalized strain rate, and $T^{*}$ is the homologous temperature. The first term on the right hand side of (2) accounts for hardening, the second accounts for rate effects, and the third for thermal softening. Temperature rise is computed herein from adiabatic heating due to plastic dissipation, which ignores heat transfer. To avoid over-heating at slow (quasi-static) rates, a small fraction for the rate of conversion from plastic dissipation to heat is taken (i.e. 0.3 instead of 0.9).

In addition, a fourth term in (2) is proposed, and accounts for damage nucleation and evolution at a material point. D is a single parameter introduced to pre-multiply the newly defined damage variable $\delta ^{*}$ outlined below. Of importance, $\delta ^{*}$ does not require any additional parameters in its definition. This model was implemented as a user material subroutine (VUMAT), using a radial return algorithm.

Damage Law In nonlinear solids, the necessary and sufficient condition for compatible deformation may be expressed by the first-order differential law (Kroner 1981), $Curl(\mathbf{F}^{e}{} \mathbf{F}^{p})\mathbf{=0}$, having assumed a multiplicative decomposition of the deformation gradient F into a plastic distortion $\mathbf{F}^{p}$ followed by an elastic distortion $\mathbf{F}^{e}$. Application of Stokes’ theorem to the differential law yields an incompatibility vector $\delta$ (Kroner 1981),

$$\begin{aligned} \delta \equiv \oint _{c}{} \mathbf{F}d\mathbf{X}=\oint _{c}{} \mathbf{F}^{e}{} \mathbf{F}^{p}d\mathbf{X} \end{aligned}$$

(3)

Any non-zero value of $\delta$ indicates the initiation of a topological defect at a material point, which we herein interpret as crack nucleation in the continuum.

In finite elements, the deformation gradient F is computed from unique nodal displacements and the assumption of differentiable displacement fields, irrespective of the constitutive behavior that evolves at the integration points. We will designate such a deformation gradient by $\mathbf{F}^{FE}$ (i.e. $\nabla _{\mathrm{X}}{{\mathbf {x}}}\equiv \mathbf{F}^{FE}$). $\mathbf{F}^{FE}$ is compatible throughout an FE simulation by definition (i.e. contour integral (3) vanishes identically with $\mathbf{F} = \mathbf{F}^{FE})$. It follows that (3) can be re-hashed as,

$$\begin{aligned} -\delta =\mathbf{0}-\delta =\oint _{c}(\mathbf{F}^{FE}-\mathbf{F}^{e}{} \mathbf{F}^{p})d\mathbf{X}. \end{aligned}$$

(4)

As such, the integrand in (4) becomes non-zero only when the product $\mathbf{F}^{e}{} \mathbf{F}^{p}$ is not equal to $\mathbf{F}^{FE}$, which means that the evolving physical mechanisms in the solid cannot accommodate the deformation imposed in the FE simulation at that given time. Thus Eq. (4) serves as a condition for crack nucleation. We herein further simplify (4), and define a scalar measure of incompatibility $\delta _{s}$ by Elkhodary and Zikry (2011),

$$\begin{aligned} \delta _{s}\left| \left| \mathbf{F}^{FE}-\mathbf{R}^{e}\mathbf{U}^{P}\right| \right| \mathbf{L}_{0}^{e} \end{aligned}$$

(5)

where $L_{0}^{\mathrm{e}}$ is the initial element characteristic length. In (5) we have ignored elastic stretching; hence we took $\mathbf{F}^{e}\cong \mathbf{R}^{\mathrm{e}}$, where $\mathbf{R}^{e}$ is the rotation from the polar decomposition of $\mathbf{F}^{e}$. We also assumed plasticity is irrotational, so that $\mathbf{F}^{p}=\mathbf{U}^{p}$, where $\mathbf{U}^{p}$ is the right plastic stretch tensor. Finally, in (2), $\delta ^{*}=\delta _{s}/L^{e}$, where $L^{e}$ is the current element characteristic length.

1.1.2 Selection of parameters for material model and failure

This modified Johnson-Cook rate, temperature and damage dependent flow rule was calibrated against tensile data using a finite element model of a dog-bone sample. The linear-elastic, density, and heat transfer properties were taken from MMPDS (Rice 2003); whereas, failure and Johnson-Cook parameters were fit to the provided tensile stress strain data. The dog-bone mesh and resulting stress strain curves are compared to experimental tensile test data in Fig. 25. Note, shear test-data was not used for calibration.

1.1.3 Modeling details for the challenge specimen

The nominal dimensions provided were used for modeling the test specimen. The region where FE boundary conditions where applied to the pin holes is shown in Fig. 26. This region was fixed for the upper hole and loaded with a prescribed velocity for the lower hole. For the slow load rate (0.0254 mm/s), a constant velocity was applied to the bottom hole and a fixed mass-scaling factor of 1000 was used, having removed the rate dependence from the flow rule. For the fast load rate (25 mm/s), two velocity profiles were tested. A smooth “actuator” type profile was applied to the bottom hole for the first 0.05 s; a constant velocity of 25 mm/s was applied after this time. For the fast simulation, no mass scaling was used. Lateral velocity was set to zero over this region for both holes. Out of plane velocity was also set to zero over the entire surface of both holes.

Fig. 26

The loaded surface for the upper hole

Element removal, based on the above defined fracture criterion, was used to model failure surface generation. No initial crack or preferential crack direction was applied. To allow for unbiased crack growth a uniform finite element mesh density was used throughout the model. The element type was an 8-node reduced integration linear hexahedral element with coupled thermal analysis capabilities (C3D8RT in ABAQUS$\backslash$Explicit). No formal mesh convergence study was performed on the sample; however, the mesh density was based on values from the previous fracture challenge. A mesh density of 12 elements through the thickness was thus used. This resulted in 36 elements around the radii of the large notch tips, and a total of 1,280,112 elements. A total of 48 processors were used in the parallelized analysis.

Fig. 27

The failed specimen shapes from both the 0.0254 and 25.4 mm/s analyses. On the left, the deformed and undeformed 0.0254 mm/s results are superimposed and the crack path is shown in both configurations

Table 7 Force displacement results

Fig. 28

Force and COD from the 0.0254 and 25.4 mm/s analyses

1.1.4 Blind predictions

The failed specimen shape for both the 0.0254 and 25.4 mm/s analyses are shown in Fig. 27. From these results the predicted crack path was B–D–E–A for both loading rates. The 25.4 mm/s analysis was not run to complete failure; however, based on the plastic strain and failure criteria profile, we were confident that the crack would terminate in the upper notch.

The maximum load and CODs at first crack initiation for both load rates are given in Table 7. The reaction force and COD are shown in Fig. 28.

1.1.5 Sources of discrepancy

We have identified three main sources of discrepancy with experimental results caused by the boundary conditions, post-processing method and failure criterion calibration method. We found that boundary conditions were very influential, particularly in the dynamic case. We tried two other sets of boundary conditions. Prior to blind predictions we did not constrain lateral motion at grips, and after the blind predictions we used rigid cylinders (Fig. 29) to load the specimen. For both these boundary conditions we observed fracture initiation in the top hole; when we constrained the lateral direction (which is what we reported) we predicted the experimentally observed failure sequence.

The post processing method we used for the reported blind predictions extracted forces only at boundary nodes and lead to an erroneous over-estimate of the force curve, in the dynamic model in particular, due to highly localized deformation at the grips. Therefore, this node averaging does not represent the experimentally observed values. For our corrected curves (Fig. 30), the forces at the reference nodes that drive the motion of the rigid cylinders was extracted. These forces give a better representation of the experimental results (less sensitive to grip localized behavior).

Fig. 29

Modified rigid cylinder boundary conditions

Fig. 30

Corrected 25 mm/s force displacement curves with original blind prediction

Finally, we believe the COD at failure predictions would be more accurate if we used a more systematic approach for determining the $\delta _{\mathrm{critical}}^{*}$ (for element removal) as a function of mesh and sample size. For the analysis presented here, the same $\delta _{\mathrm{critical}}^{*}$ was used for calibration and specimen failure predictions.

1.2 Team B

Team members:

C.H.M. Simha, Hari.Simha@NRCan-RNCan.gc.ca, CanmetMATERIALS, Natural Resources Canada, Hamilton, Ontario, Canada

B.W. Williams, Bruce.Williams@NRCan-RNCan.gc.ca CanmetMATERIALS, Natural Resources Canada, Hamilton, Ontario, Canada

Table 8 Hardening law coefficients for determined for Ti–6Al–4V from tensile tests in the rolling and transverse orientations

Fig. 31

Left results of tensile test simulations for slow loading. Right results of tensile test simulations for fast loading

Finite element models, meshed with 8-noded brick elements, were used to simulate loading of the tensile, shear, and fracture specimens. The approximate element size near localization and failure in each of the specimens ranged from about 0.2 to 0.4 mm transitioning to larger elements away from the failure zone. Simulations were performed using the explicit dynamic solvers in ABAQUS and DYNA3D. For both solvers, a user-defined subroutine was implemented to describe the material behavior. The subroutine implemented in ABAQUS was based on von Mises yielding, with a hardening rule of the form,

$$\begin{aligned} \bar{\sigma }-\sigma _{y}(1+K\bar{\varepsilon }^{p})^{n} \end{aligned}$$

(6)

with the Xue–Weirzbicki damage model used to describe the failure of the material (Simha et al. 2014; Xue 2007). The DYNA3D subroutine also utilized the hardening rule given by Eq. 6 and the Xue-Wierzbicki damage model, but the deformation was based on the Cazacu–Plunkett–Barlat 2006 (CPB06) asymmetric/anisotropic yield function (Cazacu et al. 2006). Both subroutines used the Bazant-Pijaudier-Cabot non-local approach to mitigate the mesh dependence of finite element simulations (Simha et al. 2014). Though the two subroutines were very similar, there were small differences in the implementations of the two models, such as the tolerances utilized for convergence, which led to two slightly different predictions. The Cowpers-Symonds form, $(\dot{\bar{\varepsilon }}/\dot{\bar{\varepsilon }}_{ref})^{m}$ , was used to capture the effect of strain-rate in the DYNA3D simulations, whereas two different sets of hardening law coefficients were used for the slow and fast cases in the ABAQUS simulations. The hardening law coefficients at the slow and fast rates are provided in Table 8 and the hardening law is compared to the experimental stress versus strain curves in Fig. 31. Three simulation results are presented; ‘Mean’, ‘LB’, and ‘UB’ which correspond to the curves used in the mean, lower, and upper bound predictions of the fracture specimen.

Fig. 32

Comparison of yield surfaces at zero plastic strain

Fig. 33

Left results of shear test simulations for slow loading. Right results of shear test simulations for fast loading

In the determination of the yield function coefficients required for the CPB06 model, it was deemed reasonable to assume that the material behavior in the RD and TD directions of the sheet was equal. Odenberger et al. (2013) showed that the balanced biaxial flow stress state at room temperature for Ti–6Al–4V sheet was about 1.1 times the flow stress in the rolling direction. Hammer (Hammer 2012) showed that the compressive stress is about 1.1 times the tensile stress for Ti–6Al–4V sheet. These data were used to calibrate the in-plane coefficients for the CPB06 model with $L_{11}=1.0, L_{12}=0.0, L_{13}=0.0, L_{22}=1.0$, $L_{23}=0.0, L_{33}=0.82$, and $k=-0.12$. The in-plane yield surface obtained from the CPB06 yield function is compared to the isotropic von Mises yield function (Fig. 32). The data from the shear tests conducted in the current work were used to determine the shear coefficient, $L_{44}(=L_{55}=L_{66})=1.15$. The predicted shear behavior is compared with the experimental data in Fig. 33. Differences in predictions between ABAQUS and DYNA3D simulations were attributed to different boundary conditions employed to model the shear tests.

In addition to the tensile and shears tests, additional fracture data for Ti–6Al–4V provided by Hammer (2012) and Giglio et al. (2012) were used to determine the coefficients for the damage model. To account for the influence of mesh sensitivity on failure, a non-local implementation of the damage model was used in the simulations (Simha et al. 2014), in which the effective plastic strain used in the failure model was based on an averaged value between elements within a specified radius. In the current work, the non-local radius was about 1.5 mm in the ABAQUS simulations and 0.25 mm in the DYNA3D simulations. As discussed by Xue (2007), the damage model parameters can be estimated based on calculating an upper and lower bound to experimental fracture data. The upper and lower bound estimated for Ti–6Al–4V for the slow rate case is compared to experimental data in Fig. 34 for the DYNA3D sets of parameters. Though the upper and lower bounds do not bound the experimental data, they provide a reasonable estimate to capture the response of the Ti–6Al–4V alloy. The coefficients determined for Ti–6Al–4V based on the tensile and shear tests are provided in Table 9.

The predicted force versus COD at Location 1 (COD1) are shown in Figs. 35 and 36 for the ABAQUS and DYNA3D simulations of the fracture specimen and compared with the experimental data. A contour plot of the effective stress predicted from the slow DYNA3D simulation, after initial crack propagation, is shown in Fig. 37.

Table 9 Damage model coefficients utilized in ABAQUS and DYNA3D simulations for Ti–6Al–4V

Fig. 34

Comparison of experimental fracture data of Ti–6Al–4V with upper and lower bounds predicted from damage model

Fig. 35

Results for slow loading of challenge sample

Fig. 36

Results for fast loading of challenge sample

1.2.1 Sources of discrepancy

The results show that the ABAQUS simulations over predicted the force response and under predicted COD1 at failure in both the slow and fast cases. The DYNA3D simulations better captured the force response, but marginally under predicted COD1 at crack propagation in both the slow and fast cases. After crack propagation, there were oscillations predicted in the DYNA3D simulations, which were not predicted in the ABAQUS simulations. The cause of these oscillations was unknown, but could be due differences applied boundary conditions of the two finite element models. Both the ABAQUS and DYNA3D simulations were able to predict the crack propagation path correctly (B–D–E). Results from the DYNA3D were used as the lower bound, and results from ABAQUS served to provide mean and upper bounds. For a discussion of the sources of the discrepancies between predictions and experiments and a description of Team B’s attempt to reduce the discrepancies, this team’s separate paper in this special issue can be consulted.

Fig. 37

Left contour plot of predicted damage after fracture of the Ti–6Al–4V specimen for the slow simulation performed with DYNA3D. Right typical mesh density used in model

The difference in the size of the local radius is attributed to different implementations in the two codes and the mesh density; higher mesh density in DYNA3D and lower in the ABAQUS model. In the ABAQUS implementation during the stress-return procedure the stress, strain, and damage are calculated during each increment of the stress return. In the DYNA3D implementation, only the stresses and strain are computed during the stress-return procedure. The damage is computed after the stress return algorithm has completed. The different implementation might account for some of the discrepancy. Also, the radius of 1.5 mm is similar to what has been reported in the literature (see, for instance, Belnoue et al. 2010) and it is smaller than the diameter of the hole so that non-interacting boundaries do not impact the non-local calculation. Furthermore, it is our experience with the current non-local model in abaqus, that the non-local radius is usually a fraction of the smallest feature in the sample.

1.3 Team C

Team members:

A.R. Cerrone, albert.cerrone@ge.com, GE Global Research Center, Niskayuna, NY, USA

A. Nonn, aida.nonn@oth-regensburg.de, Ostbayerische Technische Hochschule (OTH) Regensburg, Germany

J.D. Hochhalter, jacob.d.hochhalter@nasa.gov, NASA Langley Research Center, Hampton, VA, USA

G.F. Bomarito, geoffrey.f.bomarito@nasa.gov, NASA Langley Research Center, Hampton, VA, USA

J.E. Warner, james.e.warner@nasa.gov, NASA Langley Research Center, Hampton, VA, USA

B.J. Carter, bjc21@cornell.edu, Cornell University, Ithaca, NY, USA

D.H. Warner, dhw52@cornell.edu, Cornell University, Ithaca, NY, USA

A.R. Ingraffea, ari1@cornell.edu, Cornell University, Ithaca, NY, USA

1.3.1 Approach

An over-the-counter methodology was used to predict fracture initiation and propagation in the challenge specimen. Specifically, the finite element software Abaqus/Explicit was used to simulate deformation and damage in the challenge specimen geometry with nominal dimensions. The continuum (Ti–6Al–4V) was modeled as linear elastic isotropic with the von Mises yield criterion. Hardening was defined by a tabular function of plastic strain. Damage initiation, in turn, was modeled with a ductile damage initiation criterion wherein the equivalent plastic strain at failure was a function of stress triaxiality. Damage propagation, finally, was modeled with an energy-based law with exponential softening. To discriminate between the fast (dynamic) and slow (static) actuation rates, a different set of plasticity and damage parameters was calibrated for each individually.

1.3.2 Material models

Linear elastic isotropic material parameters

The linear elastic isotropic (LEI) properties of room temperature Ti–6Al–4V used in this study are given in Table 10.

Table 10 LEI properties of room temperature Ti–6Al–4V

Calibration of hardening laws

For both loading rates, yielding in shear started at approximately a 12 % lower von-Mises stress than in tension. Clearly, the material exhibited anisotropic hardening. Hardening curves from both the tensile and shear tests were fit for both the static and dynamic cases. These curves are plotted in Fig. 38.

Fig. 38

Calibrated flow curves

The anisotropic Drucker–Prager yield criterion in Abaqus/Explicit could have been employed to address the issue of anisotropic hardening; however, due to lack of time for calibration, it was passed over in favor of a simpler approach. Sensitivity studies showed that when assigned to the entire discretization, both the tensile and shear flow curves consistently yielded the A–C–F failure path; however, based on engineering good judgment, the B–D–E–A path was expected. To establish upper bound and best (“expected”) predictions, the tensile flow curve was assigned to the entire discretization. To establish lower bound predictions, the model was split into two regions. The shear and tensile flow curves were assigned to the shear-stress controlled region (beyond the lower notch including the B–D–E–A path) and axial-stress controlled region (beyond the upper notch including the A–C–F path), respectively, Fig. 39a.

Fig. 39

a Flow curve assignment to establish lower bound predictions: red demarcates shear–stress controlled region and gray demarcates axial-stress controlled region. b Stress triaxiality at predicted time of initiation (A–C–F) for slow actuation rate

Fig. 40

Fracture loci. Note that each faint dashed-dotted line represents the evolution of strain as a function of stress triaxiality at the presumed location of failure

Fig. 41

Force versus COD profiles from experimental data and original and improved predictions for slow (a) and fast (b) actuation rates

Calibration of damage initiation and propagation laws

Two damage initiation laws were considered, Fig. 40. The first is a failure locus calibrated against the slow tensile (stress triaxiality $= 0.8$) and shear (stress triaxiality $= 0$) test data. However, as evident from Fig. 39b, the relevant triaxiality levels for the challenge specimen are in the range between 0.2 and 0.6. Consequently, the remainder of the locus had to be estimated with good engineering judgment. Based on results from the shear test wherein failure strain for the fast actuation rate was approximately 20 % lower than for the slower one, this locus was decreased by 20 % to give its dynamic counterpart. Denoted “estimated” in forthcoming sections, it was employed to establish all blind predictions. The second is another failure locus given by Giglio et al. (2013) for room-temperature Ti–6Al–4V under quasi-static loading. This locus was also reduced by 20 % to give a locus appropriate for dynamic loading. Due to lack of available calibration data, damage was assumed to evolve based on a critical fracture energy (10 N/mm) criterion with exponential softening.

1.3.3 Modeling details

Geometry and boundary conditions

The nominal dimensions of the tensile, shear, and challenge specimens were considered in the calibration and prediction phases. With regards to boundary conditions, rigid bodies were used for both the shear and challenge specimens. For the shear specimen specifically, all contact nodes were tied to a rigid body. The challenge specimen, in turn, showed considerable sensitivity to how its pins were modeled—in general, frictionless rigid body pins favored the B–D–E–A failure path whereas rigid body pins with friction favored the A–C–F path. It is noteworthy that Pack et al. (2014) explored this issue during the First Sandia Fracture Challenge (Boyce et al. 2014) and noted that boundary condition selection had no influence on the crack path and minimal influence on the specimen’s response. Clearly, this was not the case for the challenge geometry. To resolve this ambiguity, kinematic coupling constraints were considered which yielded the A–C–F path. Additionally, based on good engineering judgment, pins with friction were deemed to be more representative of the actual loading conditions. Consequently, rigid body pins with friction (with coefficient 0.10) were adopted for this study.

Crack propagation

Elements began to accumulate damage once a critical failure strain was reached. Damage evolved according to an energy-based criterion. If a given element’s stiffness degraded beyond acceptable limits, it was removed from the discretization (no remeshing or element-state mapping was required). This removal introduced new free surface into the discretization, and with subsequent removals, a faceted “crack” began to form in the discretization.

Mesh refinement

A mesh refinement study on the challenge specimen was conducted. It was observed that doubling the number of elements from four to eight in the thickness direction beyond the notches resulted in steeper load drops. A mesh size of 0.2 mm beyond the notches was adopted based on the authors’ past experiences with high-strength materials and plasticity-based damage models (Cerrone et al. 2014). 98,460 eight-noded brick elements with reduced integration discretized the geometry.

1.3.4 Blind predictions

The predictions and experimental results are given in Fig. 41. The A–C–F path was predicted for both actuation rates when no anisotropy was considered (the “expected” predictions). In the case of the lower bound predictions, the B–D–E–A failure path was predicted. In experiments, all eight samples failed B–D–E–A in the fast test while ten of eleven failed B–D–E–A in the slow test. It is noteworthy that the lower bound predictions captured maximum load accurately; however, the predicted COD1 at failure was off by well over 50 %. Moreover, the predicted maximum load and COD1 at failure in the expected predictions were off by approximately 15 %. Additionally, the predictions were too stiff during loading. In hindsight, the simplifications made to address the issue of anisotropic hardening were inadequate. Furthermore, it seems that the estimated failure locus over-predicted damage initiation for low stress triaxialities.

These two issues were addressed shortly after submission of the blind predictions to Sandia. First, earlier onset of yielding due to shear stress was enforced by leveraging the tensile flow curve in conjunction with the “*POTENTIAL” option in Abaqus/Explicit. As noted earlier, yielding in shear starts at approximately a 12 % lower von-Mises stress than in tension in this titanium alloy. Consequently, the R12 parameter was set to 0.88 to obtain the reduction of the yield stress by 12 % under shear. Additionally, the failure locus given by Giglio et al. (2013) was used as it gave more realistic failure strains for low stress triaxialities. As was done for the blind prediction, the static failure locus was decreased by 20 % to give the dynamic locus. These two minor adjustments resulted in a marked improvement in the predictions, Fig. 41—not only was the B–D–E–A crack path now predicted for both actuation rates, but the maximum loads and COD1 values at failure were well within the scatter of the experimental data.

1.3.5 Sources of discrepancy

Failure to account for anisotropic hardening/yielding favored the A–C–F failure path while discriminating between tensile and shear-dominance favored the experimentally-consistent B–D–E–A path. Under the current scheme, this implies that accounting for anisotropy in the nonlinear regime is necessary to predict the correct failure path. The reader is directed to Cerrone et al. (2016) for a detailed discussion on this topic. Additionally, applying a failure locus curve that gave lower failure strains for lower stress triaxialities resulted in a more accurate prediction of damage initiation. While these modifications improved the quality of the predictions considerably, the discrepancy of stiffness during early loading was left unaddressed. The predictions did not account for some compliance in the challenge specimen. This is an indication that perhaps the proposed boundary conditions were incorrect; for example, the 0.10 friction coefficient assigned between the loading pin and specimen might have been too high. Additionally, differences between the as-tested geometries and specimen with nominal dimensions and variation in the elastic properties could have also contributed to the discrepancy.

1.4 Team D

Team members:

T. Zhang, tzhang@gem-innovation.com, Global Engineering and Materials Inc., Princeton, NJ, USA

X. Fang, xfang@gem-innovation.com, Global Engineering and Materials Inc., Princeton, NJ, USA

J. Lua, jlua@gem-innovation.com, Global Engineering and Materials Inc., Princeton, NJ, USA

1.4.1 Summary of XSHELL methodology

The XSHELL toolkit developed in house is employed to predict the fracture patterns and its associated load-deflection curves at two different loading rates for the 2014 Sandia Challenge problems. Plane strain core model in XSHELL is used to capture the stress triaxiality effect in the vicinity of the crack tip. Crack initiation and propagation is accomplished through an element-wise crack insertion with cohesive injection once its accumulative plastic strain reaches a critical value. Maximum plastic strain direction is employed as the crack growth direction law.

XSHELL is an extended finite element based toolkit for Abaqus, which is developed for dynamic failure prediction of thin walled shell structures (Zhang et al. 2014). The use of the extended finite element methodology (XFEM) allows a mesh topology independent of any arbitrary crack surface and is proven to have great potential in automating the process as the crack grows with time with fixed mesh. The XSHELL toolkit features the kinematic representation of a cracked shell via its phantom paired elements, crack initiation prediction using an accumulative plastic strain criterion, mesh independent crack insertion through a cracked shell along the direction determined by the crack growth law, cohesive injection for characterization of the energy dissipation during crack growth, and display of the fractured pattern and the load displacement curve using a customized Abaqus CAE interface.

Table 11 Summary of material properties for Sandia challenge problem

1.4.2 Calibration of material properties and failure parameters

Based on the uniaxial tensile experimental testing data from Sandia National Lab, the true stress strain curves at two different loading rates have been iteratively calibrated (Fig. 42). Abaqus 3D FEA model with data look rate dependent plasticity is employed to determine the material constitutive properties by matching the numerically predicted load displacement curve with the experimentally measured load displacement curves. An additional stress strain curve at strain rate 400/s is selected by referring to the paper by Lee and Lin (1998) with a small modification to ensure that it is always higher than the other two stress stain curves at lower strain rates (Fig. 42). This curve serves as the upper bound for the numerical analysis. The failure strains at two testing rates can be also calibrated using uniaxial tensile tests, which are the same as around 0.6.

Fig. 42

Stress strain curves at different strain rate

With Sandia Challenge 3D Abaqus model and rate dependent data look model, two analyses have been performed: one with the displacement loading rate 0.0254 mm/s; and another with the displacement loading rate 25.4 mm/s. Average strain rates at critical area can be estimated for these two loading cases: 0.015/s for slow loading and 40/s for fast loading. Based on these two average strain rates, the stress strain curves for Sandia Challenge problem at low loading rate and high loading rate can be interpreted from the material stress strain curves at different strain rates as in Fig. 42. The resulting stress strain curves for these two loading cases and the elastic material properties are listed in Table 11.

Mesh sensitivity study has also been performed using Abaqus shell FEA model with S4R element to identify a rational mesh size. The load displacement curves obtained from a dense mesh and a coarse mesh agree with each other, which indicates that the coarse mesh is good enough for the numerical simulation of the Sandia Challenge problem.

1.4.3 Blind prediction for Sandia challenge problem with XSHELL

Sandia Challenge FEA model for XSHELL plane strain core application is shown in Fig. 43. Given the location of the notch and holes in the Sandia challenge problem, a user defined XSHELL zone denoted by the red box in Fig. 43 is used with plane strain core option. Due to the nature of this Sandia Challenge problem, the plane strain core model will be invoked only at the crack tip. The edges of the loading holes are linked with two Reference Points by using kinematic coupling. A constant velocity loading condition is applied at the upper Reference Point while the lower Reference Point is fixed. Abaqus explicit solver is used to perform the numerical analysis.

The Sandia Challenge Problem has been analyzed with the calibrated failure strain as 0.6 and the approximate plane strain core coefficient $\alpha$ as 0.001 based on experience. As shown in Fig. 44c, the predicted crack path for 0.0254 mm/s loading rate is B–D–E, which agrees with experimental tested crack path shown in Fig. 44d. The predicted Load-CODs curve for 0.0254 mm/s loading rate is compared with the experimental testing curve in Fig. 44a. The solid red line in this figure represents GEM’s prediction, while the dotted blue line represents the experimental testing curve. The predicted COD1 value at the instant of the first crack initiation is 2.21 mm, and the peak load from the numerical simulation is 23,830.9 N which is higher than the experimental tested average peak force value 19,643.36 N.

Fig. 43

XSHELL model for the Sandia challenge problem

Fig. 44

a Load versus COD1 curves between XSHELL and experiment for 0.0254 mm/s loading case; b numerical predicted deformation shape before crack initiation; c numerical predicted crack path and d experimental tested crack path

The predicted crack path for 25.4 mm/s loading rate is shown in Fig. 45c with crack initiation at Hole D followed by its growth to Hole B and the second crack initiation at Hole D followed by its growth to Hole E. The predicted Load-CODs curves are compared with experimental result in Fig. 45a. The predicted COD1 value at first crack initiation is 2.4 mm, and the peak load from the XSHELL prediction is 23,815.8 N, which is higher than the experimental tested average peak value 20,435.88 N.

Fig. 45

a Load versus COD1 curves between XSHELL and experiment for 25.4 mm/s loading case; b numerical predicted deformation shape before crack initiation; c numerical predicted crack path and d experimental tested crack path

1.4.4 Sources of discrepancy

The initial stiffness of Load-COD1 curves predicted by the XSHELL toolkit has a discrepancy in comparison with the test data. This is mainly due to the use of kinematic coupling boundary condition with all degrees of freedom fixed for the loading hole. The high peak load prediction may be related to the use of a plasticity model without $J_{3}$ dependence.

1.5 Team E

Team members:

V. Chiaruttini*, vincent.chiaruttini@onera.fr, Onera, Université Paris-Saclay, Châtillon, France.

M. Mazière, matthieu.maziere@mines-paristech.fr, MINES ParisTech, PSL Research University, Centre des Matériaux, CNRS UMR 7633, Evry, France.

S. Feld-Payet, sylvia.feld-payet@onera.fr, Onera, Université Paris-Saclay, Châtillon, France.

V.A. Yastrebov, vladislav.yastrebov@mines-paristech.fr, MINES ParisTech, PSL Research University, Centre des Matériaux, CNRS UMR 7633, Evry, France.

J. Besson, jacques.besson@mines-paristech.fr, MINES ParisTech, PSL Research University, Centre des Matériaux, CNRS UMR 7633, Evry, France.

J.-L. Chaboche, jean-louis.chaboche@onera.fr, Onera, Université Paris-Saclay, Châtillon, France.

*corresponding author: vincent.chiaruttini@onera.fr

For the blind round robin prediction of ductile fracture, we used finite element simulation with a visco-elasto-plastic material model in finite strain. This model has been calibrated for both tensile and shear tests. Afterwards some numerical analyses were performed to identify a suitable approach to obtain a satisfactory crack path and force-displacement curve for different loading rates.

1.5.1 Visco-elasto-plastic constitutive model

To identify the model, a finite element analysis has been carried out on uni-axial tests on samples oriented mainly in the rolling direction, which is the most representative loading condition for the Sandia Fracture Challenge. The strain rate has been estimated close to the gauge for both loading rates (0.66 10$^{-3}$ s$^{-1}$ and 0.66 s$^{-1})$. At the higher rate, the hardening effects should be lower than expected due to a considerable thermal heat produced. The provided test curves were transformed to represent the effective strain and stress but they do not take into account the necking effects.

Fig. 46

Comparison between finite element simulations and uni-axial tests in rolling direction

The chosen constitutive model is initially based solely on a modified Norton flow with an anisotropic Hill criterion. To insure an accurate description of hardening at both low and high rates, a softening evolution is added using a negative value for K:

$$\begin{aligned} \dot{p}=\frac{{\left( {\frac{3}{2}\hat{\sigma }:M_{{Hill}}:\hat{\sigma }} \right) -R}}{{K_{0}+K\left( 1-e^{{-bp}}\right) }}^{n} \end{aligned}$$

To allow a finer tuning of the hardening in the studied plastic strain domain up to four terms were tested in combination with nonlinear isotropic terms in the final model:

$$\begin{aligned} R=R_{0}+\sum \nolimits _{i=1}^{N} Q_{i}\left( {1-e^{-\beta _i p}}\right) \end{aligned}$$

This model was calibrated using implicit 3D finite element computation within the Z-set finite element software (Besson and Foerch 1997). Such an approach allows us to accurately fit uni-axial tests using a finite strain implicit quasi-static finite element solution process, the mesh size was chosen to ensure the correct deformation level for the appearance of the necking effect (Fig. 46).

To deal with material anisotropy, the provided shear test result was studied. The first stage was to correctly fit the initial stiffness of the numerical model with the testing data, dealing with modification on the prescribed boundary conditions. To satisfactory reproduce those experiments, an anisotropic Hill criterion was finally used, whose calibration was done using results from Gilles et al. (2012, 2011).

1.5.2 Failure modeling

Our driving idea was to identify the simplest model that could produce sufficiently accurate results on the Sandia challenge’s specimen. Due to the specific specimen geometry, only two different kind of failure can be observed: dominant shear failure under low triaxiality for crack path B–D–E–A, or high triaxiality failure along crack path A–C–F. Thus, it is not strictly necessary to apply a Gurson-type model, which can predict a failure path whose geometry would highly depend on triaxiality. A pragmatic approach could be adopted, involving a cohesive zone model to insure the softening process due to the material damaging. The chosen model (Alfano and Crisfield 2001) (allowing to decouple the material toughness for traction and shear failure modes), was calibrated using both tests (uni-axial and shear, see Fig. 47), with a special attention paid to the region of the negative slope observed in the shear experiments, the mesh size was chosen according to the necking effect.

Fig. 47

Calibrated cohesive model compared with traction (a) and shear (b) test experiment

Fig. 48

Comparison between experimental results and our blind prediction: deformed mesh (showing accumulated plastic strain isolines) and fast testing at the synchronized time step, after the unstable crack propagation stage

1.5.3 Numerical simulation and discussion

To predict the crack path, complete 3D finite element computations were performed with only visco-elastic-plastic constitutive model up to the maximal force before the necking appears. Only after the peak force cohesive elements were introduced in the zones with high accumulated plastic strain, which were observed in certain ligaments when reaching the peak load.

Both fast and slow loading cases were simulated using a 3D mesh in finite strain, with a quasi-static implicit solution and quadratic elements producing about 90,000 degrees of freedom. Approximately 250 incremental loading steps were used to reach the E–A ligament failure (with a computational time limited to less than 2 h).

The obtained result confirmed that, as expected, the shear dominant failure occurs through the B–D–E–A crack path with the first B–D–E failure stage followed a second crack initiation process on the E–A final ligament. As the test COD gauges were not able to deliver global Force-COD plots after the first failure, a simple image analysis from the organizers movie (on the fast case) has been carried out to extend the curve after the unstable crack propagation (Fig. 48). This analysis shows quite a good agreement with our blind prediction and the experimental data during the stable failure phases (see Fig. 49).

Fig. 49

Comparison between blind prediction (solid curve) and rebuilt experimental data (from image analysis and force sensor, dashed curve), for the Force-COD1 (N vs. mm) plot

1.5.4 Sources of discrepancy

The pragmatic approach that was applied for our predictions has some evident drawbacks and limitations: the quasi-static simulation, combined with excessively dissipative cohesive zone, failed to start the damage process sufficiently early (especially at high speed) and hence produced the softening slope which is not sufficiently steep. Furthermore, for a much more complex case (where triaxiality has a significant impact on the crack path), such a method cannot be successful. However, this rather simple approach (from computational point of view) offers the possibility to properly capture the peak force and to correctly fit the testing curve during the ultimate crack initiation process on this specific Sandia Fracture Challenge conditions.

1.6 Team F

Team members:

J. Lian, junhe.lian@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

Y. Di, yidu.di@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

B. Wu, bo.wu@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

D. Novokshanov, denis.novokshanov@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

N. Vajragupta, napat.vajragupta@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

P. Kucharczyk, pawel.kucharczyk@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

V. Brinnel, victoria.brinnel@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

B. Döbereiner, benedikt.doebereiner@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

S. Münstermann, sebastian.muenstermann@iehk.rwth-aachen.de, RWTH Aachen University, Aachen, Germany

1.6.1 Approach

The material model used in the team is based on a hybrid damage mechanics model (Lian et al. 2013) which was further extended to incorporate the effect of strain rate and temperature for Charpy test and machining under adiabatic condition (Buchkremer et al. 2014; Münstermann et al. 2012). The distinction of the model is that it differentiates the damage initiation and fracture and it is developed in a hybrid way by combining the uncoupled model to act as the damage threshold and coupled model to represent the microstructure degradation till final fracture. The model is implemented into the FE code Abaqus/Explicit by means of a user material subroutine (VUMAT) and all the simulations presented here are conducted in this environment.

The yield function of the model is given in Eq. 7. It is noted that the coupling effect of the damage into the yield function is only valid once the damage initiation criterion is fulfilled.

$$\begin{aligned} \varPhi =\bar{\sigma }-\left( 1-D\right) \sigma _{y}\left( \bar{\varepsilon }^{p},\eta ,\theta ,\dot{\bar{\varepsilon }}^{p},T\right) \le 0 \end{aligned}$$

(7)

Generally, the isotropic yielding and hardening are employed based on the negligible difference between the flow responses from tensile tests along rolling and transverse direction for the investigated material. However, a more general plasticity model (Bai and Wierzbicki 2008) to account for the stress state effect on yielding is employed, as defined in Eq. 8. In addition, the influence of strain rate and temperature on the yielding is also defined (Eq. 8).

$$\begin{aligned}&\sigma _{y}\left( {\bar{\varepsilon }^{p}, \dot{\varepsilon }^{p},T,\eta , \uptheta }\right) \nonumber \\&\quad = \left[ {\sigma _{y} \left( {\bar{\varepsilon }^{p}}\right) \cdot \left( c_{{\dot{\bar{{\varepsilon }}}^{{\mathrm{p}}}}}^{1} ln\dot{\bar{\varepsilon }}^{{\mathrm{p}}} + c_{{\dot{\bar{{\varepsilon }}^{{\mathrm{p}}}}} ^{2}} \right) + c_{{\dot{\bar{{\varepsilon }}}^{{\mathrm{p}}}}} ^{3}\cdot \dot{\bar{\varepsilon }}^{p}} \right] \nonumber \\&\quad \quad \times \left[ {c_{{\mathrm{T}}}^{1} exp\left( {c_{{\mathrm{T}}}^{2} T} \right) + c_{{\mathrm{T}}}^{3}} \right] \left[ {1 - c_{{{\upeta }}}\cdot \left( {\eta - \eta _{0}} \right) } \right] \nonumber \\&\qquad \times \left[ {c_{{{\uptheta }}}^{{\mathrm{s}}} + \left( {c_{{{\uptheta }}}^{{{\mathrm{ax}}}} - c_{{{\uptheta }}} ^{{\mathrm{s}}}} \right) \cdot \left( {\lambda - \frac{{\lambda ^{{m + 1}}}}{{m + 1}}} \right) } \right] \end{aligned}$$

(8)

In the equation, $\sigma _y ({\bar{\varepsilon }}^{\mathrm{p}})$ stands for the flow curve under the reference condition, in the context, i.e. quasistatic tensile test at room temperature; $c_{\dot{\bar{\varepsilon }}^{\mathrm{p}}}^1 -c_{\dot{\bar{\varepsilon }}^{\mathrm{p}}}^3$ are the material parameters for the strain rate effect; $c_\mathrm{T}^1 - c_\mathrm{T}^3$ are the material parameters for temperature effect; $c_{\upeta }$ and $\eta _0$ are the material parameters for the effect of stress triaxiality; $c_{\uptheta }^\mathrm{s}$, $c_{\uptheta }^{\mathrm{ax}}$ and m are the material parameters for the effect of the Lode angle. For details, readers are referred to Bai and Wierzbicki (2008) and Münstermann et al. (2013).

It is also noted that under the adiabatic condition, the temperature evolution is defined according to Eq. 9.

$$\begin{aligned} \dot{T}= \frac{\delta \cdot \bar{\sigma }\cdot {\dot{\bar{{\varepsilon }}}}^{{\mathrm{p}}}}{\rho \cdot c_{\mathrm{p}}} \end{aligned}$$

(9)

where $\delta , \rho$ and $c_{\mathrm{p}}$ are the specific heat fraction, material density and heat capacity, respectively.

Fig. 50

Experimental and numerical force–displacement responses for tensile tests under both slow (a) and fast (b) loading rates

For damage modelling, a discontinuous damage evolution law is assumed, i.e. the initiation of damage is not associated with the plastic deformation but a characteristic strain-based criterion which depends on stress triaxiality and Lode angle. Afterwards, a simple linear increase is assumed with respect to the equivalent plastic strain, and the rate of damage evolution is governed by the energy dissipation between damage initiation and the complete fracture of the material point. The critical damage to fracture is assumed to be a function of Lode angle. Element deletion technique is used for the crack propagation.

$$\begin{aligned} D=\left\{ {{\begin{array}{ll} 0;&{}\quad \bar{\varepsilon }^{\mathrm{p}}\le \bar{\varepsilon }_{\mathrm{i}}^\mathrm{p} \\ \int _{\bar{\varepsilon }_\mathrm{i}^\mathrm{p}}^{\bar{\varepsilon }^{\mathrm{p}}} \frac{\sigma _{\mathrm{y}0}}{2G_\mathrm{f}} d\bar{\varepsilon }^{\mathrm{p}}; &{}\quad {\bar{\varepsilon }_\mathrm{i}^\mathrm{p} < \bar{\varepsilon }^{\mathrm{p}}<\bar{\varepsilon }_\mathrm{f}^\mathrm{p}} \\ {D_{\mathrm{cr}} ;}&{}\quad {\bar{\varepsilon }_\mathrm{f}^\mathrm{p} \le \bar{\varepsilon }^{\mathrm{p}}} \\ \end{array}}}\right. \end{aligned}$$

(10)

where $G_\mathrm{f}$ is the material parameter and $\sigma _{\mathrm{y}0}$ is the stress at damage initiation. The damage initiation strain, $\bar{\varepsilon }_\mathrm{i}^\mathrm{p}$, and the critical damage accumulation for fracture are defined in Eqs. 11 and 12, respectively.

$$\begin{aligned} \bar{\varepsilon }_i^p= & {} \left[ {C_1 e^{-C_2 \eta } -C_3 e^{-C_4 \eta }} \right] \bar{\theta }^{2}+C_3 e^{-C_4 \eta } \end{aligned}$$

(11)

$$\begin{aligned} D_{\mathrm{cr}}= & {} c_{\mathrm{cr}}^1 \cdot \bar{\theta }^{2}+c_{\mathrm{cr}}^2 \end{aligned}$$

(12)

where $C_1 -C_4$ are material parameters for damage initiation locus and $c_{\mathrm{cr}}^1$ and $c_{\mathrm{cr}}^2$ are the material parameters for the fracture locus.

Fig. 51

Experimental and numerical force–displacement responses for shear tests under both slow (a) and fast (b) loading rates

Table 12 Calibrated material parameters for the model

1.6.2 Material parameter calibration

The model involves a large number of material parameters for accurate characterization of material behavior. For a complete material parameter calibration procedure, several types of tests and specimens are required as described by Lian et al. (2013, 2015) and Buchkremer et al. (2014). In the SFC2, as only limited tests were provided, the calibration of the plasticity parameters, including the effect of stress state, strain rate and temperature, and damage initiation locus was assisted by material database of the Steel Institute. The reference flow curve was derived from the tensile tests along the rolling direction (specimen RD5) provided by Sandia National Laboratory. The Ludwik equation was used to extrapolate the flow curve to large strains. The most important parameters for fracture prediction, the damage evolution and critical damage accumulation parameters, were calibrated by an iterative fitting procedure such that force–displacement responses of tensile and shear tests from simulations can meet the experiments. The 8-node linear brick element with reduced integration (C3D8R) was used for both models and a mesh size of 0.1 mm was applied to the critical region to represent the high order of strain gradient. The comparison of the force–displacement response between the experiment and simulation with the final calibrated material parameters are shown in Figs. 50 and 51 for both tensile and shear tests, respectively. It is noted that only the tests under slow loading rate were used for the calibration and it is assumed that the damage parameters keep the same for fast loading rate for simplicity as the simulations of tensile and shear tests with the same damage parameters under fast loading rate also give reasonably good results compared to the experiments. All the calibrated material parameters are listed in Table 12.

Fig. 52

The numerical model for the blind prediction simulation along with the schematic sketch of the implemented boundary condition and the crack path sequence comparison

1.6.3 Blind prediction

For the simulation of the blind prediction challenge, the numerical model was constructed based on the received ideal geometry and the dimension scattering as a result from the manufacturing process was neglected. The same element type (C3D8R) was applied to the model. To account for the high strain gradient in the critical deformation region, a finer mesh was implemented in this area whereas the coarser mesh was applied on the rest of the model and the model finally consisted of about 800,000 elements. As the calibration models, the mesh size of 0.1 mm was chosen for the fine mesh. The loading roll and the fixing roll were modeled as the rigid body while the contact interaction between the specimen and the rolls were assumed to be frictionless. Regarding the boundary condition assignment, the fixing roll was constrained in all degrees of freedom and only displacement along the vertical axis was applied to the loading roll. The overview of the model before deformation and the critical region after loading for both slow and fast loading rates are shown in Fig. 52. To balance the predictive quality and computational efficiency, time and mass scaling were applied to the simulations for slow and fast loading rates, respectively. A convergence of the force–displacement response was reached for the time scaling and a minor effect of the kinetic energy over the internal energy was also met for the mass scaling.

As illustrated in Fig. 52, the crack path prediction of the slow loading rate is A–C–(B–D–E)–F. In general, the crack path A–C–F is in a competition with the crack path B–D–E, and these two are roughly corresponding to the fracture patterns under tensile and shear loadings, respectively. Based on the calibrated parameters, the model gives very sensitive and similar responses of these two modes as these two crack paths are concurrent. This observation is also confirmed by the experiments. Although most of the fracture path for slow loading rate is B–D–E, A–C–F was also observed for one specimen. For the fast loading rate, the prediction agrees with the experiments. Despite the small crack from A to C during the deformation owning to the sensitivity of the model, the dominant crack path is B–D–E–A. The force versus COD1 for both loading rates are plotted in Fig. 53. For both rates, the maximum force is overestimated 10–15 %, but the predicted fracture displacements are in a reasonable agreement with the experiments consistently for both slow and fast loading rates.

Fig. 53

Experimental and numerical force–displacement responses for tensile tests under both slow (a) and fast (b) loading rates

1.6.4 Sources of discrepancy

Although overall accepted prediction was achieved with several assumptions and literature data, there is still certain degree of space to improve the blind prediction, such as an optimized strain hardening extrapolation, mesh regularization or non-local formulation to decrease the scaling factors. The overestimation of the force level for both slow and fast condition is clearly related to a higher description of the stress–strain response of the material. Both the strain hardening extrapolation and the damage evolution parameters are responsible for this, as the material owns a quite early damage initiation from microstructural point of view. Another critical point for the challenge simulation is the expensive computational cost. As the mesh size is pre-defined in the calibration test, to maintain consistent softening response of the material, a large number of elements resulted in the challenge simulation. To balance the computational time and predictive accuracy, high time and/or mass scaling factor is employed, which also results in the oscillation of the force response under fast loading condition. In this regard, the implementation of mesh regularization or non-local formulation is of interest. The further improvement together with the details for the modeling is reported in a full length paper in the same Special Issue as this article.

1.7 Team G

Team members:

M.K. Neilsen, mkneils@sandia.gov, Sandia National Laboratories, Albuquerque, NM, USA

K. Dion, kdion@sandia.gov, Sandia National Laboratories, Livermore, CA, USA

Fig. 54

Comparison of uniaxial tension simulations with experimental measurements and observations. a Engineering stress–strain. b Deformed shape after failure with life contours (white elements have failed)

1.7.1 Approach

Predictions for the SFC2 challenge were generated using a quasi-static finite element code in SIERRA solid mechanics (2011). A unified creep plasticity model was used to capture temperature and strain rate effects. For this model, the inelastic (creep + plastic) strain rate is given by

$$\begin{aligned} {{\varvec{\dot{\varepsilon }}}}^{in}=\frac{1}{3}\dot{\gamma }\mathbf{n}=\frac{3}{2}e^{f} \hbox { sinh}^{p}\left[ \frac{\tau }{\alpha D(1-cw^{d})}\right] \mathbf{n} \end{aligned}$$

(13)

where $\dot{\gamma }$ is the equivalent plastic strain rate, $\mathbf{n}$ is the associated flow direction, $\tau$ is the vonMises effective stress, D is a user-prescribed function of equivalent plastic strain to define isotropic strain hardening, f, p, and $\alpha$, are temperature-dependent material parameters, and w is a scalar measure of damage. Material parameters c and d define the reduction in isotropic strength due to damage. Damage evolution is given by Wilkins et al. (1980).

$$\begin{aligned} w=\int \left( \frac{1}{1+\frac{p}{\hat{p}}} \right) ^{\hat{a}}\left( 2-A\right) ^{\hat{\beta }}\hbox {d}\gamma \end{aligned}$$

(14)

where

$$\begin{aligned} s_1 \ge s_2 \ge s_3\qquad A=Max\left( \frac{s_2 }{s_1 },\frac{s_2 }{s_3}\right) \quad p=\frac{-1}{3}{\varvec{\sigma }}:{\varvec{i}}\nonumber \\ \end{aligned}$$

(15)

$s_{i}$ are the eigenvalues of the stress deviator, p is pressure. Damage evolution depends on both pressure (first invariant of total stress) and third invariant of deviatoric stress. The pressure-dependent, first term in Wilkins et al. damage evolution equation is similar to the damage evolution equation proposed by Wellman (2012) and used by us in the initial Sandia Fracture Challenge (Boyce et al. 2014; Neilsen et al. 2014). Note that the stress dependence can be removed by setting the material parameters ${\hat{\alpha }}$ and ${\hat{\beta }}$ equal to zero in Eq. 14, then damage is simply accumulated equivalent plastic strain. When damage has reached a critical level, the element is not instantaneously removed nor is the stress instantaneously reduced to zero; instead the constitutive response is changed in five solutions steps to be that of a very flexible elastic material with moduli equal to 0.0001 times the original elastic moduli. This approach is used to make the acquisition of post failure equilibrium solutions possible for most problems.

The effects of heating due to plastic work were captured with fully coupled thermal stress simulations in which the volumetric heating rate, $\dot{Q}$, was given by

$$\begin{aligned} \dot{Q}=\eta \dot{W}^{p}=\eta {\varvec{\sigma }}:{\varvec{\varepsilon }}^{in} \end{aligned}$$

(16)

where $\eta$, the Taylor-Quinney coefficient prescribes the fraction of plastic work that is converted to heat, $\dot{W}^{p}$ is the plastic work rate, ${\varvec{\sigma }}$ is the Cauchy stress, and ${\dot{\varvec{\varepsilon }}}^{in}$ the inelastic strain rate. A survey of literature yielded a wide range of values, 0.1 to 0.9, for the fraction of plastic work converted to heat. A value of 0.5 was used for $\eta$ in these simulations.

Fig. 55

Comparison of experimental measurements with model predictions for shear test. (a) Model with displacement prescribed. b Experimental and predicted crack on front and back surfaces of sample. c Model with loading blocks, friction coeff. $= 0.36$. d Load-displacement curves

Fig. 56

Comparison of experimental measurements with blind model predictions—challenge geometry. a Path A–C–F predicted w/free pin rotation. b Path B–D–E–A predicted w/no pin rotation. c Force-COD1 for 0.0254 mm/s loading. d Force-COD1 for 25.4 mm/sec loading

Material parameters for the model were obtained from simulations of the uniaxial tension tests at different rates. Values for $\alpha$ in Eq. 13 which define the effects of temperature on the isotropic strength were based on data from (Rice 2003). Strain hardening was based on a fit to the slow rate experiment (black curve in Fig. 54a). The high rate test was then simulated (blue curve in Fig. 54a). Finally, a fully coupled thermal stress simulation predicted that the apparent ductility of the material would be dramatically reduced when heating due to plastic work was included (red curve in Fig. 54a). This occurs because heating causes the apparent hardening of the material to decrease which leads to the initiation of necking and subsequent cracking earlier in the simulation. The predicted deformed shape at failure is in reasonably good agreement with experiments (Fig. 54b). In this figure, LIFE is simply the current damage divided by the critical damage, so when LIFE obtains a value greater than one the element is cracked and turns white. The model predictions were insensitive to changes in the damage parameters; however, these parameters were highly correlated with the failure strain.

Next, the shear test was simulated with y-displacements applied directly to all surface nodes on the specimen where the loading blocks contacted the specimen (Fig. 55a). These simulations predicted a crack similar to the experiment (Fig. 55b) but load-displacement curves that had a much higher initial slope and peak value than experiments (Fig. 55d). To try and understand this discrepancy, loading blocks were added to the shear test simulation (Fig. 55c). The loading blocks were preloaded by preventing normal displacement of the back surface of the back blocks and clamping the sample by displacing nodes on the front surface of the front blocks to generate a total clamping force of 170.8 kN which is equal to the expected clamping force of the eight bolts torqued to 5.65 N-m. This simulation matched the experimental load-displacement curve better (green curve in Fig. 55d) but did not fail because the sample was just rotating between the loading blocks. In the tests, the horizontal grip inserts (Fig. 7) which were hand-tightened would eventually prevent rotation of the sample and cause the observed shear failure. Due to this shear test discrepancy, we decided to go ahead and generate SFC2 challenge geometry predictions with parameters we had obtained from the uniaxial tension tests.

The SFC2 challenge geometry was then simulated using a model with 451,536 elements and a typical element edge length of 0.254 mm. Contact between the loading pins and sample was not included and instead half of each loading pin was modeled. The nodes at the centerline of the bottom pin were given zero displacement in all three directions while the nodes at the centerline of the top pin were given vertical displacement at the prescribed rate. Sliding was not allowed between the pin and the sample but the center of the pin could freely rotate about the pin axis for ‘free rotation’ simulations. Pin rotation was not allowed in ‘no rotation’ simulations. The free rotation and no rotation simulations were performed to bound expected behavior. Free rotation simulations were expected to be closer to the experiments. Free rotation simulations predicted a crack path of A–C–F (Fig. 56a) and no pin rotation simulations a crack path of B–D–E–A (Fig. 56b). The models bound the experimental displacements to failure but predict too high of a failure load.

1.7.2 Sources of discrepancy

The experimentally measured peak load for the challenge geometry was 86 to 91 percent of the predicted peak load. This discrepancy indicates that the material is likely weaker in shear than this model predicted with a von Mises yield. Simulations of the shear test with loading blocks indicated that the sample may be rotating more than expected which would contribute to the displacement discrepancy in the experiment. However, even with this discrepancy the model should have still predicted close to the correct loads. The discrepancy in load at yield and peak load in the shear test is similar in magnitude to load discrepancy with the challenge geometry again indicating that this material is likely weaker in shear than our model predicted. The most significant weakness in these simulations was that they did not account for this reduced strength in shear.

1.8 Team H

Team members:

K.N. Karlson, knkarls@sandia.gov, Sandia National Laboratories, Livermore, CA, USA

J.W. Foulk III, jwfoulk@sandia.gov, Sandia National Laboratories, Livermore, CA, USA

A.A. Brown, aabrown@sandia.gov, Sandia National Laboratories, Livermore, CA, USA

M.G. Veilleux, mgveill@sandia.gov, Sandia National Laboratories, Livermore, CA, USA

1.8.1 Approach

The material, time scale, and mode of loading dictated our path forward. Provided experimental data and literature advocate models that incorporate rate dependence, temperature dependence, and anisotropy in both the yield stress and the hardening. Void evolution must include multi-axial nucleation, growth, and coalescence. The low thermal conductivity of titanium and the time scales for characterization and testing requires thermomechanical coupling and implicit time integration. Local material softening requires regularized methods for solution.

Team Sandia California (Team H) used SIERRA Solid Mechanics (SIERRA SM) to capture the required physics and numerics for solution. SIERRA SM is a Lagrangian, three-dimensional, implicit code for the analysis of solids and structures. It contains a versatile library of continuum and structural elements, and an extensive library of material models. For all SFC2 related simulations, our team used Q1P0, 8 node hexahedral elements with element side lengths on the order 0.175 mm in failure regions. To model crack initiation and failure, element death removed elements from the simulation according to a continuum damage model. Exploratory studies were also conducted with regularized methodologies (nonlocality, surface elements). Unstable modes of fracture were resolved with implicit dynamics [HHT time integration with numerical damping (Hilber et al. 1977)].

Thermo-visco-poro-plasticity. We chose SIERRA SM’s isotropic Elasto Viscoplastic (EV) material model for our simulations because it contains the most relevant physics to accurately predict the SFC2 challenge problem such as the flexibility to include temperature and rate dependence for a material. However, since the EV model does not support anisotropic plastic behavior, the anisotropy evident in the provided data was included through other means described in detail in the following section.

The EV plasticity model is an internal state variable model for describing the finite deformation behavior of metals. The model incorporates strain rate and temperature sensitivity, as well as damage, and tracks history dependence through the use of internal state variables. In its full form, the model has considerable complexity, but most of the material parameters and resulting behavior are optional. The form of the material model specific to our use for SFC2 will now be outlined for the simplified case of uniaxial tension. For this simplified case, the stress evolves according to

$$\begin{aligned} \dot{\sigma }=E(\dot{\epsilon }-\dot{\epsilon }_{p}) \end{aligned}$$

(17)

where $\epsilon$ is the total strain and $\epsilon _{p}$ is the plastic strain. The flow rule is defined by

$$\begin{aligned} \dot{\epsilon }_{p}=f \hbox {sinh}^{n} \left( \frac{\sigma _{y}-k}{Y}-1\right) \end{aligned}$$

(18)

where $\sigma _{y}$ is the equivalent stress; Y is a material parameter representing the rate independent, initial yield stress; f and n are material parameters that govern the material rate dependence; and $\kappa$ is the isotropic hardening variable for the material, which evolves according to a hardening minus dynamic recovery model originally proposed by Kocks and Mecking (1980):

$$\begin{aligned} \dot{\kappa }=\kappa \frac{\dot{\mu }}{\mu }+(H-R_{d}\kappa ) \dot{\epsilon }_{p}. \end{aligned}$$

(19)

The temperature dependence for all material parameters ($Y, f, n, H, R_d$) can be specified explicitly with user specified scaling functions or using functional forms built into the model. Heat generation due to plastic work is calculated with

$$\begin{aligned} \dot{q}=\beta \sigma \dot{\epsilon }_p \end{aligned}$$

(20)

where the material parameter $\beta$ is the fraction of plastic work dissipated as heat.

Fig. 57

The parameter set calibrated to the tension test data accurately captures the plasticity and failure behavior of the data

The EV model contains a void growth model and a void nucleation model to account for isotropic material damage. For void growth, damage evolves according to the model proposed by Cocks and Ashby (1980):

$$\begin{aligned} \dot{\phi }=\sqrt{\frac{2}{3}}\dot{\epsilon }_p\frac{1-(1-\phi )^{m+1}}{(1-\phi )^{m}}\hbox {sinh}\left[ \frac{1(2m-1)}{2m+1}\frac{p}{\sigma _{vm}}\right] \nonumber \\ \end{aligned}$$

(21)

where $\sigma _{vm}$ is the von Mises stress, p is the hydrostatic stress, $\phi$ is the void volume fraction of the material and the damage exponent m is a material parameter. With this void growth model, damage will only increase when $p/\sigma _{vm} >0$. To account for damage resulting from other stress states, a void nucleation model based on $J_{3}$ (Horstemeyer and Gokhale 1999; Nahshon and Hutchinson 2008) was also included in the material model:

$$\begin{aligned} \dot{\eta }=\eta \dot{\epsilon }_{p} N_1\left[ \frac{4}{27}-\frac{J_3^2}{J_3^2}\right] \end{aligned}$$

(22)

where $N_1$ is a material parameter, $\eta$ is the number of nucleated voids, and $J_i$ are the deviatoric stress invariants. These two damage models can be used independently or concurrently to model void nucleation and growth. Including damage evolution through these models reduces the material’s elastic modulus and shear modulus by a factor of $1-\phi$, and the flow rule becomes

$$\begin{aligned} \dot{\epsilon }_{p}=f\hbox {sinh}^n\left[ \frac{\sigma _y-\kappa (1-\phi )}{Y(1-\phi )}-1\right] . \end{aligned}$$

(23)

The damage models require the definition of the initial void volume fraction $\phi _0$, the initial size of nucleated voids $\phi _0^\eta$, and the initial void count per volume $\eta _0$. Void coalescence is modeled through $\phi _{coal}$. The material point is unloaded for $\phi >\phi _{coal}$. In contrast to surface elements, we remove elements (element death) when any integration points satisfy the coalescence criteria. Stabilization of fully integrated formulations is problematic with loaded and unloaded integration points.

1.8.2 Material parameter calibration

We populated the EV material parameters for Ti–6Al–4V sheet using a combination of the data provided in the challenge announcements and data from literature. Initially, the yield (Y, f, and n) and hardening (H and $R_d$) parameters were calibrated to the provided tensile data using a non-linear, least squares algorithm where the objective function consisted of the error between the provided data and model data. Since the rate dependence for the initial yield stress is not uniquely constrained by two data points, we used rate dependence data from Follansbee and Gray (1989) to supplement the data at two rates provided for the challenge. Temperature dependence was added to the initial yield stress Y and the elastic material properties according to data available in MMPDS-08 (Rice 2003). Various literature sources were employed to inform our choice of $\beta$. Accurately modeling the temperature rise in the calibration specimens and the resulting softening required a coupled thermo-mechanical simulation with thermal expansion, specific heat, thermal conductivity and emissivity determined from MMPDS-08. Void growth damage parameters were chosen based on prior experience with the material model and a sensitivity study of the model to the damage exponent m. Figure 57 contains initial tension simulation results and parameter values.

After calibrating the model to the tension data, the shear data was incorporated into the model. Using material parameters calibrated to the tension data, a model of the shear test did not accurately predict the yield behavior of the specimen thus indicating that the material exhibits an anisotropic yield surface. By reducing the initial yield parameter Y by $\sim 83\,\%$, the shear simulation results improved and compared well to the test data.

Since the triaxiality driven void growth model cannot evolve damage in pure shear, sensitivity studies for void nucleation lead to the selection of the appropriate $N_1, \phi _0^\eta$ and $\eta _0$ parameters to capture shear failure. Figure 58 contains the calibrated shear simulation results and the corresponding parameters.

Fig. 58

A separate parameter set with lower yield and void nucleation parameters accurately models the yield behavior of the shear test for both rates and failure for the slow rate

1.8.3 Challenge specimen modeling details

Model development for the challenge specimen included specifying the appropriate boundary conditions and incorporating anisotropy. The solid mechanics boundary conditions consisted of a symmetry boundary condition along the half-thickness plane of the specimen and approximations of the pin boundary conditions in the test. A half-pin contiguously meshed into the specimen with the center node line having prescribed displacements approximated frictionless pins. The top pin’s centerline was fixed and the bottom pin’s centerline was displaced downward with a rate corresponding to the test rates. As stated previously, accurately modeling the calibration specimens required a coupled thermo-mechanical simulation. The thermal boundary conditions included radiation from the specimen surface to the room temperature surroundings and a symmetry boundary condition along the half-thickness plane of the specimen. Since the EV model cannot accommodate an anisotropic yield surface, the model of the specimen was split into two element blocks: Block 1 with a yield corresponding to the tension initial yield $Y_{RT}^t$ and Block 2 with a lower yield $Y_{RT}^{s*} =441$ MPa since that region is initially predominantly in shear. Figure 59 depicts Block 2 outlined in red with the remaining elements belonging to Block 1. Since the stress state in Block 2 does not directly correspond to that of the failure region in the shear model, a simulation of the challenge specimen at the slow rate using a rate and temperature independent Hill plasticity model influenced the selection of $Y_{RT}^{s*} =441$ MPa. All simulations consisted of models constructed at the nominal dimensions according to the specimen drawings.

1.8.4 Blind predictions

Using the material model parameters and boundary conditions specified in the previous sections, the challenge specimen model predicted failure through crack path B–D–E–A for both rates. For both rates, the crack propagated unstably through B–D–E, as shown in Fig. 59, while the remaining ligament carried load until tensile failure occurred much further into the simulation (${\sim }375$ s for the slow rate and $\sim .36$ seconds for the fast rate). Table 13 lists the maximum loads and CODs at crack initiation for each rate and Fig. 60 displays the predicted load versus COD1 plot for both rates.

Table 13 Results predicted using the challenge specimen model

Fig. 59

On the left, Block 2 is outlined in red on the undeformed model geometry. On the right, the deformed geometry is shown after the crack has propagated into the upper hole in an unstable manner

Fig. 60

The load versus COD1 predictions for fast rate (left) and the slow rate (right) correspond to the experimental data; however, both models over predicted COD1 at crack initiation

1.8.5 Sources of discrepancy

Several sources of error were present in the challenge specimen model. For example, an isotropic material model was used to simulate the anisotropic material through the use of separate element blocks and material parameters. Ideally, an anisotropic material model with rate and temperature dependence similar to EV would have been used. Additionally, material parameter uncertainties were large (e.g. $\upbeta$) and sensitivity studies show these uncertain parameters had significant effects on the simulation results. Numerical modeling issues also introduced error. SIERRA SM’s implicit contact algorithm would not converge. Consequently, we employed a contiguously meshed and rotating half-pin. Our inability to quickly resolve the evolution of local damage did not permit resources for regularized solutions. We were able to nicely resolve both crack initiation and propagation with surface elements (without thermomechanical coupling). Nonlocal studies will be the subject of future work.

1.9 Team I

Team members:

J.L. Bignell, jbignel@sandia.gov, Sandia National Laboratories, Albuquerque, NM, USA

S.E. Sanborn, sesanbo@sandia.gov, Sandia National Laboratories, Albuquerque, NM, USA

C.A. Jones, cajone@sandia.gov, Sandia National Laboratories, Albuquerque, NM, USA

P.D. Mattie, pdmatti@sandia.gov, Sandia National Laboratories, Albuquerque, NM, USA

Team I approached the problem using the commercially available general purpose finite element software Abaqus (Abaqus Standard Versions 6.13 and 6.14). Team I chose to use a “typical” finite element approach to this problem because in many real world applications (given time and budget constraints) this is the only viable approach. An implicit solver was used with numerical stabilization to overcome global instabilities during the fracture event. To reduce the run time, reduced integration 8-node hexahedral elements were used rather than fully integrated elements. Abaqus allows tabular input of yield, potential functions, and strain-to-failure curves. This feature was used to assign multiple yield functions and multiple strain-to-failure curves corresponding to different strain rates.

Fig. 61

Tension test mesh and model details (left); close-up view of shear test mesh and model details (right). a Tension test model. b Shear test model

The Hill plasticity material model was used with rate dependent yield curves and isotropic hardening. In the Hill model, the strain rate is decomposed into the sum of an elastic strain rate and an inelastic strain rate. In the Abaqus implementation of the model, the user inputs six stress ratios $R_{ij}$ to define the Hill yield surface. If they are all unity, the von Mises yield surface is recovered. The parameters of the Hill yield surface were determined for different strain rates during the calibration procedure.

To capture material degradation and failure, strain-to-failure curves, that are dependent on both the stress state (in terms of stress triaxiality $\eta$) and the strain rate, were employed:

$$\begin{aligned} \bar{\varepsilon }_D^{pl}\left( {\eta , \dot{\bar{\varepsilon }}_D^{pl}} \right) , \end{aligned}$$

where $\eta =-\frac{p}{q}, p$ is the pressure stress, q is the von Mises equivalent stress, and $\dot{\bar{\varepsilon }}_D^{pl}$ is the equivalent plastic strain rate. Because the stress and strain rate are changing throughout the simulation, degradation initiates when the state variable $\omega _D$, given by the following integral:

$$\begin{aligned} \omega _{D}=\int \frac{\hbox {d}{\bar{\varepsilon }}_{D}^{pl}}{{\bar{\varepsilon }}_{D} ^{pl}\left( {\eta , {\bar{\varepsilon }}_{D}^{pl}}\right) } =1, \int \frac{\hbox {d}{\bar{\varepsilon }}_{D}^{pl}}{{\bar{\varepsilon }}_{D}^{pl} \left( {\eta , {\bar{\varepsilon }}_{D}^{pl}}\right) }=1 \end{aligned}$$

reaches unity. For the time discretized problem, the integral above is calculated by incrementing $\omega _D$ at each time step, for each integration point, in the following way (note $\omega _D$ can never decrease):

$$\begin{aligned} \varDelta \omega _{D}=\frac{\mathbf{\Delta }{\bar{\varepsilon }}_{D}^{pl}}{{\bar{\varepsilon }}_{D}^{pl}\left( \eta ,{{\bar{\varepsilon }}_{D}^{pl}} \right) }\ge 0 \end{aligned}$$

Once $\omega _{D}$ reaches unity, the material stress is degraded in the following way,:

$$\begin{aligned} {\varvec{\sigma }} =\left( {1-D} \right) {\bar{{\varvec{\sigma }}}}, \end{aligned}$$

using a continuum damage variable D whose value ranges from zero to unity.

As the plastic strain increases the damage variable evolves as follows:

$$\begin{aligned} \dot{D}=\frac{L{\dot{\bar{\varepsilon }}}^{{pl}}}{\dot{\bar{u}}_{f}^{{pl}}}= \frac{{\dot{\bar{u}}}^{pl}}{{\dot{\bar{u}}}_{f}^{{pl}}},\quad \hbox {where }\quad {{\bar{u}}}_{f}^{pl}=\frac{2G_f}{\sigma _{y0}} \end{aligned}$$

Here $G_f$ is the material fracture energy, L is the characteristic element length, and $\sigma _{y0}$ is the value of the yield stress at the time of failure initiation. This method attempts to ensure that the energy dissipated during the damage evolution process equals the fracture energy for the material. While this method attempts to remove the dependence of failure on the size of the elements used, the same element size used in the calibration process was also used for the prediction. Degraded elements are removed from the model when D attains a value near unity (full degradation).

Fig. 62

a Yield stress versus plastic strain curves at different strain rates input into the model. Curves at strain rates of 0.001 and 1.0 were determined by fitting the A, B, and n parameters to the test data. b Plastic failure strain versus stress triaxiality curves at different strain rates input into the model

Finite element models representing the uniaxial tension and shear tests were constructed (see the mesh representations in Fig. 61). Two mesh sizes were initially investigated for this calibration, 0.5 and 0.25 mm, with 0.25 mm being adopted for the challenge predictions. Symmetry was utilized when possible. Using the two models, along with the given uniaxial tension and shear test data, the following steps were employed in the calibration process:

• Use the uniaxial tension test data and model to determine the material hardening curves.

• Use the shear test data and model to define the Hill plasticity potential ratios

• Use the uniaxial tension test data and model to determine the failure initiation parameters in the tension regime ($\eta \ge 0.33$)

• Use the shear test data and model to determine the failure initiation parameters in the pure shear regime ($\eta =0.0$)

• Rerun the uniaxial tension and shear test models to verify all the inputs

• Using the calibrated model inputs, make predictions for the two double-notch tension tests

Fig. 63

Calibrated tension test model response. a Model response versus test data. b Example response

Fig. 64

Calibrated shear test model response. a Slow loading rate. b Fast loading rate. c Example response

Fig. 65

Double notch coupon (challenge problem) mesh and boundary conditions

For the calibration of the material hardening parameters the following strain rate relationship was assumed for the yield stress loaded at an arbitrary strain rate:

$$\begin{aligned} \sigma _{y}\left( {\dot{\bar{\varepsilon }}}^{pl}\right)= & {} \left( 1+C\left( {{\bar{\varepsilon }}}^{pl}\right) ln \left( \frac{{\dot{\bar{\varepsilon }}}^{pl}}{{\dot{\bar{\varepsilon }}}^{pl}_{ref}}\right) \right) \sigma _{y0.001}, \hbox {where},\\ C\left( {{\bar{\varepsilon }}}^{pl}\right)= & {} \frac{\left( \left( {\sigma _{y1.0}\left( {\bar{\varepsilon }}^{pl} \right) /\sigma _{y0.001} \left( {\bar{\varepsilon }}^{pl}\right) } \right) -1\right) }{ln\left( 1.0/0.001\right) }, \end{aligned}$$

along with the following assumed hardening relationships:

$$\begin{aligned} \sigma _{y0.001}\left( {\bar{\varepsilon }}^{pl} \right)= & {} A_{0.001}+B_{0.001}{\bar{\varepsilon }}^{{pl}^{n_{0.001}}}\; \hbox {and }\\&\sigma _{y1.0}\left( {\bar{\varepsilon }^{pl}}\right) =A_{1.0} +B_{1.0}{\bar{\varepsilon }}^{{pl}^{n_{1.0}}}. \end{aligned}$$

The parameters $A_{0.001}$, $B_{0.001}$, $n_{0.001}$, $A_{1.0}$, $B_{1.0}$, $n_{1.0}$ were determined by fitting the model response to the available tension test data. Figure 62a shows the yield stress vs. plastic strain curves at the 0.001 and 1.0 strain rates determined from the calibration process, along with the curves at other rates determined using the assumed relationships above. Since Abaqus linearly interpolates between the hardening curves that are defined in the input, it is necessary to enter a sufficient number of curves to maintain the assumed log-linear relationship above.

Using the rate dependent yield stress curves determined, the shear model was run with Hill stress ratios equal to unity. Results showed that the model over predicted the onset of yielding when compared with the available shear test data. Hill stress ratios were adjusted to $R_{12} =R_{23} =R_{13} =0.88$ to bring the model’s shear response in line with the test data.

The strain to failure curves were determined starting with data found in the literature for Ti–6Al–4V (Giglio et al. 2012). This is referred to as the reference curve $\bar{\varepsilon }_{D-ref}{}^{pl}\left( \eta \right)$ in the following discussion. The following rate dependent relationship was assumed:

$$\begin{aligned} \bar{\varepsilon }_{D}^{pl}\left( \eta ,{\bar{\varepsilon }}_{D}{}^{pl} \right)= & {} \left( 1+E\left( \eta \right) ln\left( \frac{\dot{\bar{\varepsilon }}^{pl}}{\dot{\bar{\varepsilon }}^{pl}{}_{ref}}\right) \right) \\&\bar{\varepsilon }_{D-ref}{}^{pl}\left( \eta \right) Q\left( \eta \right) . \end{aligned}$$

The scaling factors $Q\left( \eta \right)$ and rate multiplier constants $E\left( \eta \right)$ were determined through a fitting process using the shear and tensile test models and test data. Figure 62b shows the final fitted plastic strain to failure vs. stress triaxiality curves for the strain rates input into the model.

Figure 63 illustrates the response of the calibrated tension test model and Fig. 64 illustrates the response of the calibrated shear model. As mentioned above, only two mesh sizes were studied during the calibration and prediction efforts. Ultimately, the mesh size of 0.25 mm was used for the final calibration and prediction. Due to time constraints and Abaqus license restrictions, other mesh refinements were not considered. As discussed above, the material degradation and failure model used removes the dependence on the element size, no mesh sensitivity studies were performed to assess the degree to which this holds true.

Having fitted the parameters for the material model, the double notch coupon (challenge problem) model was run (Fig. 65 illustrates the mesh representation utilized). A half symmetry model was created with an element size of 0.25 mm in the potential failure regions. The loading pins were not explicitly modeled. Instead, velocities were prescribed to the top and bottom halves of the pin holes. It was recognized that this choice of boundary conditions artificially restricts rotation of the two ends of the coupon while the pins utilized in the testing likely allow for rotation. It was demonstrated later by additional analyses, that this choice of boundary conditions introduces only a small error in the predictions up to the first fracture in the specimens, whereas the behavior following the first fracture event (along ligament B–D–E) is significantly affected. Figure 67 illustrates the differences. The nominal dimensions provided were used to construct the model. Implicit dynamic simulations were performed with numerical dissipation added to stabilize the solution during the fracture event. Blind predictions were made for both the slow and fast loading rates. Table 14 summarizes the results of these analyses. Figure 66 shows the predicted location 1 load vs. COD1 curves, along with illustrations of the predicted fractures in the specimens for the two loading rates. The results show that the model over predicts both the peak force and COD1 at failure for both loading rates, with the discrepancy being more pronounced for the fast loading case. In addition, the model fails to capture the softening in the response corresponding to localization of the strain immediately preceding the first fracture event for both loading rates, again with the discrepancy being more pronounced for the fast loading case. It is thought that these discrepancies are directly attributable to the model’s neglect of the plastic strain induced heating and thermal softening of the material.

Fig. 66

a Predicted load versus COD1 curves for the challenge specimen. b Close-up view of deformation and fracture paths for the slow and fast loading rates

Fig. 67

Comparison of the response for the original prediction model (with pin boundary conditions that restricted coupon rotation) and a model with modified (more representative) boundary conditions. a Slow loading rate. b Fast loading rate. c Model response comparison with test

1.9.1 Sources of discrepancy

There are a number of potential sources of discrepancy between the blind prediction and the actual challenge problem results. The most significant source being the lack of inclusion of thermal effects in the material response and the accounting of temperature changes induced by plastic straining of the material (coupled thermal-mechanical response modeling). Results of the challenge problem tests indicated a significant temperature rise in the material in the failure regions, particularly for the fast loading cases. Another potential significant source of discrepancy is the boundary conditions used. After the results of the challenge were released, Team I reran the challenge predictions with “pin-like” boundary conditions achieved using multi-point constraints. It was found that there was not much difference in the response up to and including the peak load; however, beyond the peak load the response of the specimen was significantly different with a much larger COD achieved before fracture of the final ligament (Fig. 67). This is expected as with the updated boundary conditions, rotation of the specimen ends is allowed as fracture progresses.

1.10 Team J

Team members:

K. Pack, kpack@mit.edu, Massachusetts Institute of Technology, Cambridge, MA, USA

T. Wierzbicki, wierz@mit.edu, Massachusetts Institute of Technology, Cambridge, MA, USA

1.10.1 Plasticity modeling

The MIT team modeled the plasticity of the Ti–6Al–4V sheet using conventional description of continuum mechanics for metallic materials, namely a yield function, a hardening law, and a flow rule. The observation of negligible difference in the engineering stress–strain curve before necking between the rolling direction (RD) and the transverse direction (TD) at each loading speed led to the assumption of the identical flow stress under uniaxial tension along three perpendicular axes of RD, TD, and the thickness direction. However, additional information from a shear test required to make use of the Hill’48 yield function (Hill 1948) given in Eq. (24), which has the parameter N controlling the plastic flow under in-plane pure shear stress.

$$\begin{aligned}&\bar{\sigma }_{Hill}\left[ F(\sigma _{22}-\sigma {33})^{2} +G(\sigma _{33}-\sigma {11})^{2}\right. \nonumber \\&\quad \left. +H(\sigma _{11}-\sigma {22})^{2}+2L\sigma _{23}^{2}+2M_{13}^{2}+2N\sigma _{12}^{2}\right] ^{\frac{1}{2}}\nonumber \\ \end{aligned}$$

(24)

Parameters other than N are reduced to those of the von-Mises yield function, and N was calibrated so as for numerical simulation to predict a correct level of force in the V-notched rail shear test as demonstrated in Fig. 68a. The value of N larger than 1.5 implies the relative weakness in deformation resistance under pure shear loading.

Fig. 68

Comparison between experiments and simulations for: a V-notched rail shear test for quasi-static loading; b uniaxial tension test for quasi-static and dynamic loadings

Table 14 Plasticity parameters of the Ti–6Al–4V sheet for the lower bound case

Accurate prediction of crack initiation in ductile metals depends highly on the hardening curve in the post-necking regime. Moreover, dynamic loading considered in the 2nd Sandia Fracture Challenge is inextricably linked with the thermal softening as well as the strain-rate effect. The MIT team employed a modified Johnson–Cook law, proposed by Roth and Mohr (2014), which uses a weight-average of the Swift and the Voce law for the strain hardening in the form of Eq. (25).

$$\begin{aligned}&K[\bar{\varepsilon }_{p}, \dot{\bar{\varepsilon }}_{p}, T] \nonumber \\&\qquad =\left[ \alpha \cdot A(\varepsilon _{0}+\bar{\varepsilon }_{p})^{n}+(1{-}\alpha ) \cdot (k_{0}+Q(1-e^{{\beta \bar{\varepsilon }}_{p}}))\right] \nonumber \\&\qquad \left[ 1+C\hbox {In}\left( \frac{\dot{\bar{\varepsilon }}_{p}}{\dot{\varepsilon }_{0}}\right) \right] \left[ 1-\left( \frac{T-T_{r}}{T_{m}-T_{r}}\right) ^{m}\right] \end{aligned}$$

(25)

In order to avoid high computational costs and ambiguity of boundary conditions, fully coupled thermo-mechanical analysis was simplified by purely mechanical analysis in which a fraction of incremental plastic work was converted into heat causing temperature rise based on Eq. (26).

$$\begin{aligned} dT=w\left[ \dot{\bar{\varepsilon }}_{p}\right] \frac{\eta _{k}}{\rho C_{p}}\bar{\sigma } d\bar{\varepsilon }_{p} \end{aligned}$$

(26)

$\eta _{k}$ is the Taylor–Quinney coefficient assumed to be constant. The weighting factor changes smoothly from zero to unity by Eq. (27), which implies transition from isothermal to adiabatic condition.

$$\begin{aligned} w\left[ \dot{\bar{\varepsilon }}_{p}\right] = \left\{ {\begin{array}{ll} 0&{}\; \hbox {for }\,\dot{\bar{\varepsilon }}_{p}<\dot{\varepsilon }_{it}\\ \frac{(\dot{\bar{\varepsilon }}_{p}-\dot{\varepsilon }_{it})^{2}(3\dot{\varepsilon }_{a}-2\dot{\bar{\varepsilon }}_{p}\dot{\varepsilon }_{it})}{\dot{\varepsilon }_{a}-\dot{\varepsilon }_{it}^{3}} &{}\; \hbox {for }\, \dot{\varepsilon }_{it}\le \dot{\bar{\varepsilon }}_{p}\le \dot{\varepsilon }_{a}\\ 1&{}\;\hbox {for }\,\dot{\bar{\varepsilon }}_{a}<\dot{\bar{\varepsilon }}_{p}\\ \end{array}}\right. \nonumber \\ \end{aligned}$$

(27)

The optimized parameters for the lower bound case are provided in Table 14 together with six parameters of the yield function. The recommended calibration procedure through inverse analysis is explained in Roth and Mohr (2014). The only distinction was made in that a dog-bone specimen was used to find hardening parameters instead of a notched tensile specimen with circular cutouts, which was found to be more appropriate for the hardening curve optimization (see Pack et al. 2014). Careful attention was paid to the velocity profile applied to the boundary of the specimen for fast loading because it is not constant due to the compliance of the cross-head of a testing machine. It was confirmed that the engineering stress–strain curve predicted by finite element simulation showed a good agreement all the way to fracture with test results that showed the lowest stress after necking (regarded as lower bound cases) as depicted in Fig. 68b. Very fine mesh of 0.1 mm was used in the necked region, following the recommendation by Dunand and Mohr (2010).

Fig. 69

Sequence of damage accumulation and crack development for fast loading

1.10.2 Fracture modeling

Crack is assumed to initiate when the indicator D, calculated by a linear damage accumulation rule in Eq. (28) reaches unity. The corresponding finite element is then eliminated from a whole model.

$$\begin{aligned} D=\int _{0}^{\bar{\varepsilon }_{f}}\frac{d\bar{\varepsilon }_{p}}{\bar{\varepsilon }_{f}^{pr}(\eta , \theta )} \end{aligned}$$

(28)

The function $\bar{\varepsilon }_{f}^{pr}$ defines the strain to fracture under proportional loading as a function of two stress-state dependent variables: the stress triaxiality $\eta$ and the Lode angle $\bar{\theta }$, whose combination specifies a loading path. Following Roth and Mohr (2014), the rate-dependent Hosford–Coulomb fracture model was taken for $\bar{\varepsilon }_{f}^{pr}$ .

$$\begin{aligned}&\bar{\varepsilon }_{f}^{pr}(\eta , \bar{\theta }) =b_{0}\left( 1+\gamma \hbox {In} \left( \frac{\dot{\bar{\varepsilon }}_{p}}{\dot{\varepsilon }_{0}}\right) \right) \nonumber \\&\quad (1+c)^{\frac{1}{n}}\left[ \left\{ \frac{1}{2}((f_{1}-f_{2})^{a}((f_{2}-f_{3})^{a}\right. \right. \nonumber \\&\quad \left. \left. +\,(f_{3}-f_{1})^{a})^{\frac{1}{a}}\right\} +c(s\eta +f_{1}+f_{3})\right] ^{\frac{1}{n}} \end{aligned}$$

(29)

$$\begin{aligned}&f_{1}(\bar{\theta })=\frac{2}{3}\hbox {cos}\left[ \frac{\pi }{6}(1-\bar{\theta })\right] \end{aligned}$$

(30)

$$\begin{aligned}&f_{2}(\bar{\theta })=\frac{2}{3}\hbox {cos}\left[ \frac{\pi }{6}(1-\bar{\theta })\right] \end{aligned}$$

(31)

$$\begin{aligned}&f_{3}(\bar{\theta })=\frac{2}{3}\hbox {cos}\left[ \frac{\pi }{6}(1-\bar{\theta })\right] \end{aligned}$$

(32)

Mohr and Marcadet (2015) formulated the original rate-independent Hosford–Coulomb fracture model, inspired by the onset of microscopic shear localization. Even though shear tests were carried out by Sandia, and the test data were provided, the fact that slip occurred during the tests and the axial displacement was measured with an LVDT attached to fixtures whose compliance was not negligible is attributed to not including shear tests for the present fracture calibration. As a consequence, the identification of five fracture parameters had to rely solely on two uniaxial tensile tests. The MIT team was in possession of the fracture parameters for a similar alloy, so a, c, and n were taken from our database. This basically assumes that the current alloy of interest has the same dependence on $\eta$ and $\bar{\theta }$ as the similar alloy in our database. The remaining parameters of $b_{0}$ and $\gamma$ control the height of a fracture envelope and its strain-rate sensitivity, respectively. These two values were found such that the engineering strain (equivalently displacement) to fracture of a dog-bone specimen in both slow and fast loading condition is accurately captured as noted in Fig. 68b.

1.10.3 Blind prediction

In light of the symmetry through thickness, only a half of the specimen geometry with print dimensions was discretized by approximately 750,000 reduced-integration eight-node three-dimensional tri-linear solid elements (C3D8R of the Abaqus element library) with the smallest ones of $0.1\times 0.1\times 0.1\,\hbox {mm}^{3}$ around two notches and three holes. This size of elements was chosen to be the same as the one used for the dog-bone and the shear specimen to minimize a possible mesh size effect. Abaqus/Explicit was used in simulation with the material models implemented through the user material subroutine (VUMAT). The upper and the lower pin were modeled as analytical rigid bodies, and the penalty contact with no friction was defined between the pins and the specimen. The lower pin was pulled down at 0.0254 mm/s for slow and 25.4 mm/s for fast loading with the first one tenth of the total simulation time reserved for acceleration. Uniform mass scaling was applied to reduce computational time in so far as it guarantees the negligible ratio of kinetic energy to internal energy before the first crack initiation. Crack propagation was considered to be nothing more than the problem of consecutive crack re-initiation, thus being modeled by continuing element deletion.

Figure 69 visualizes the sequence of damage accumulation and crack path for fast loading. Slow loading exhibited a similar non-uniform distribution of the damage indicator and ended up with the same crack path of B–D–E–A. In the early stage, plasticity comes into play in the ligament between A and C by tension and in two ligaments between B and D and D and E by combined shear and tension. Because of the relative weakness in shear resistance characterized by $N=1.95$, the specimen prefers shear localization to necking, which results in rapid crack propagation. The two ligaments between B and D and D and E fracture almost at the same time, by which a huge amount of elastic energy is released all of a sudden. This causes the vibration of the whole system. Finally, the ligament between A and E deforms mostly due to bending and reaches complete failure.

Fig. 70

Comparison of the force-COD1 curve between experiments and simulations in slow and fast tensile tests of the second Sandia Fracture Challenge specimen

1.10.4 Sources of discrepancy

The comparison of the force-COD1 curve between experiments and simulations is made in Fig. 70. Elastic region as well as the maximum force was very accurately predicted for both slow and fast loading with 3.6 % overestimation of the maximum force for slow loading. This error might have been caused partially by dimensional discrepancy between actual specimens and the finite element model. The COD1 at the first crack (abrupt load drop) for fast loading was predicted with great accuracy while it was 37 % overshot for slow loading. This is mainly due to the over-adjusted hardening curve after necking as can be deduced from the delayed COD1 at the maximum load. As noted by Pack et al. (2014), the flow stress after necking optimized by a dog-bone specimen deteriorates numerical prediction in other specimen geometries, and a notched tensile specimen with circular cutouts serves an improvement in the prediction.

1.10.5 Concluding remarks

Plasticity and fracture modeling on the basis of uniaxial tension and shear tests subjected to two different loading speeds made a satisfying prediction both in the slow and the fast challenge problem. The present plasticity model accounts for relatively low shear resistance of the Ti–6Al–4V sheet, which was crucial to capture the type of instability that led to a correct prediction of the crack path. More detailed explanation about the calibration procedure and the improvement in numerical prediction based on an exhaustive testing program performed on the leftover material can be found in Pack and Roth (2016).

1.11 Team K

Team members:

S.-W. Chi, swchi@uic.edu, University of Illinois at Chicago, USA

S.-P. Lin, slin46@ford.com, University of Illinois at Chicago, USA

A. Mahdavi, amahda2@uic.edu, University of Illinois at Chicago, USA

1.11.1 Approach

The simulation methodology in this work is based on an enriched Reproducing Kernel Particle Method (RKPM) (Chen et al. 1996; Dolbow and Belytschko 1999; Krysl and Belytschko 1997; Liu et al. 1995). The crack surface/tip discontinuity is embedded in the displacement approximation as follows.

$$\begin{aligned} \mathbf{u}^{h}= & {} \sum _{{I \in N - N_{{cut}} - N_{{tip}} }} {\Psi _{I} } \left( {\mathbf{x}} \right) {{\mathbf{d}}}_{I}\nonumber \\&+\sum _{{J \in N_{{cut}} }} {\sum _{{i = 1,2}} {S_{i}}} \left( {\mathbf{x}} \right) \Psi _{J} \left( {\text {x}} \right) a_{j}\nonumber \\&+ \sum _{{K \in N_{{tip}} }} {\sum _{{j = 1,2}} {f_{i}}} \left( {\mathbf{x}} \right) {\mathbf{b}}_{K} \equiv \sum _{I} \bar{\Psi }_{I}(\mathbf{x})\bar{d}_{I} \end{aligned}$$

(33)

Here $\Psi _{I}$ is the reproducing kernel (RK) shape function with the Cubic B-spline ($C^{2}$ continuous) as the kernel function centered at node $\mathbf{x}_{I}$; $N_{cut}$ and $N_{tip}$ are node sets, in which the support of node contains the crack surface and crack tip, respectively; N is the total node set; $\mathbf{d}_{I}$, $\mathbf{a}_{J}$, and $\mathbf{b}_{K}$ are nodal coefficients. $S_{i}$ is introduced to represent the continuity across the crack surface and expressed as:

$$\begin{aligned} S_{I}(\mathbf{x})=\left\{ \begin{array}{ll} 1&{} \zeta ^{+}>0\\ 0&{} \zeta ^{-}<0\\ \end{array}\right. \hbox {and } S_{2}=1-S_{1}. \end{aligned}$$

(34)

where $\zeta ^{+}$ and $\zeta ^{+}$ denote the above and below crack regions, respectively. The crack tip enrichment function, $f_{j}$, is formulated based on the visibility criterion (Krysl and Belytschko 1997; Lin 2013) and has the following form:

$$\begin{aligned} \begin{array}{ll} \begin{array}{l} \hbox {For } \theta _{0}>0, f_{1}(\mathbf{x})=\left\{ \begin{array}{ll} 1&{}\theta _{0}-\pi /2 \le \theta \le \pi \\ \sin (\theta -\theta _{0}+\pi )&{} -(\pi -\theta _{0}) \le \theta <\theta _{0}-\pi /2\\ 0&{} -\pi \le \theta <-(\pi -\theta _{0})\\ \end{array}\right. \\ \hbox {For } \theta _{0}\le 0, f_{1}(\mathbf{x})=\left\{ \begin{array}{ll} 0 &{}\pi +\theta _{0}\le \theta <\pi \\ \sin (\theta _{0}-\theta +\pi )&{} -\theta _{0}+\pi /2<\theta \le \pi +\theta _{0}\\ 1&{} -\pi \le \theta \le \theta _{0}+\pi /2\\ \end{array} \right. \end{array} &{}\hbox { and } f_2=1-f_1\\ \end{array} \end{aligned}$$

(35)

where $\theta _{0}$ is the angle from the crack direction to the enriched node and $\theta$ is the angle from the crack direction to the evaluation point. Note that the enrichment shape functions in (33), $\bar{\Psi }_{I}$, satisfy the partition of unity condition, $\sum \bar{\Psi }_{I}=1$. Therefore, the mass lumping in the explicit time integration in the Galerkin formulation is straightforward (Lin 2013).

1.11.2 Material model and calibration of material parameters

The material in simulations is modeled by the Johnson–Cook rate-dependent model with a bi-linear hardening $J_{2}$ elastoplasticity:

$$\begin{aligned}&{H}(\bar{e}^p)=1 \end{aligned}$$

(36)

$$\begin{aligned}&K(\bar{e}^p, \dot{\bar{e}}^p) \left\{ \begin{array}{ll} K_s(\bar{e}^p)[1+C \ln (\dot{\bar{e}}^p)/\dot{\bar{e}}_0) ], &{}\quad \hbox { if } \dot{\bar{e}}^p<\dot{\bar{e}}^p_{\mathrm{crit}}\\ K_s(\bar{e}^p)[1+C \ln (\dot{\bar{e}}^p_{\mathrm{crit}})/\dot{\bar{e}}_0) ], &{}\quad \mathrm{esle} \end{array} \right. \nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned}&K_s(\bar{e}^p)\nonumber \\&\quad =\left\{ \begin{array}{ll} [Y_0+\alpha _0 \bar{e}^p], &{}\quad \hbox {if } \bar{e}^p<\bar{e}^p_{\mathrm{crit}}\\ Y_1+\alpha _1(\bar{e}^p-\bar{e}^p_\mathrm{crit}), &{}\quad \hbox {if } \bar{e}^p<\bar{e}^p_{\mathrm{crit}}, Y_1=Y_0+\alpha _0 \bar{e}^p_\mathrm{crit}\end{array}\right. \nonumber \\ \end{aligned}$$

(38)

where H and K are the kinematic and isotropic hardening parameters, respectively; $\bar{e}^{p}$ is the effective plastic strain. The initial yield stress, $y_{0}=1.0474$ GPa, the hardening parameters $\alpha _{0}=1.157$ GPa, and $\alpha _{1}=0.45$ GPa, and the critical equivalent plastic strain $\bar{e}_{\mathrm{crit}}^{p}=0.12$ were calibrated from slow-loading-rate tensile test data (Fig. 71). For rate effect, the reference plastic strain rate $\dot{\bar{e}}_{0}$ was chosen to be the unity; the constant $C= 0.015$ and the critical plastic strain rate $\bar{e}_{\mathrm{crit}}^{p}=28$ were obtained from the numerical tensile tests as shown in Fig. 71. Considering the maximum principle tensile strain as the crack initiation criterion and assuming that the tensile failure is the predominant failure mode, the crack opening strain in the initiation criterion can be obtained according to the rupture point in the tensile test. The principal strain at the rupture point, 0.946, was assumed as the crack initiation strain for both slow- and fast- loading-rate cases.

Fig. 71

Nominal stress–strain of the tensile failure test. The numerical tensile failure test was conducted to obtain the hardening and rate parameters in the plasticity model. The crack opening strain in the initiation criterion was also calibrated from the rupture point in the simulation

Fig. 72

Deformation, von Mises stress, and failure pattern

Fig. 73

Comparison of force-COD curves

1.11.3 Numerical simulations

An explicit updated Lagrangian reproducing kernel formulation with the enriched displacement approximation in (33) was employed to model the challenge problem. The crack propagation speed in the dynamic simulations was assumed to be 0.02 % of Rayleigh wave speed, based on analytical and empirical studies for non-branching crack propagation (Freund 1972, 1979). A RKPM discretization containing a total of 55,520 nodes, with 2 nodes in the thickness direction, was used for simulations. The mean in-plane nodal distance near the notched area in the discretization is 0.44 mm, which is consistent with the nodal density used for material parameter calibration.

Figure 72 shows the predicted deformations and von Mises stress contours for both slow- and fast-loading-rate cases. The predicted crack paths for both cases follow a similar pattern, “B–D–E–A”, which agrees with experimental results. Figure 73 compares numerical load-COD curves to experimental ones for both loading cases. The numerical simulations over-predict the slopes of load-COD before yielding and peak loading values. This is likely mainly due to inappropriate boundary conditions. Unlike loaded at both bolt-holes through low-friction pins in the experiments, the specimen in the simulations was loaded through prescribed leftward displacement with fixed vertical direction on the left hole (Fig. 72). The extra constraint limits the COD development and therefore leads to an increase in force response. Furthermore, for the case with fast loading rate, the numerical model predicts much larger rupture COD than the experimental data. The main cause of the discrepancy may be attributed to an inaccurate crack initiation threshold and an inaccurate constant crack propagation speed for fast loading rate.

1.11.4 Sources of discrepancy

The crack paths obtained from simulations for both slow- and fast-loading-rate cases are in good agreement with experimental data; however, the force responses and the crack initiation COD are over-predicted. The over-prediction is mainly attributed to inappropriate boundary conditions, and inappropriate material parameters, including, but not limited to, rate-dependent hardening parameters and crack initiation thresholds. In the dynamic simulation, the crack tip speed also plays an important role and needs to be properly estimated based on a fracture energy release rate algorithm.

1.12 Team L

Team members:

J. Predan, jozef.predan@um.si, University of Maribor, Slovenia

J. Zadravec, zadravec.jozef@gmail.com, University of Maribor, Slovenia

1.12.1 Approach

The 2D plane strain simulation was performed with Abaqus CAE 6.14 software using an elasto-plastic model (continuum) and a damage model (damage initiation and damage evolution). The Abaqus Standard/Static solver and isotropic elastic plastic material behaviour including isotropic deformation hardening was employed. The elastic, plastic, damage initiation and evolution parameters were fit to experimental data. The parameter fitting utilized both tensile and shear data at both loading rates. The Extended Finite Element Method (XFEM) was used to simulate damage in the specimens. The finite elements mesh was refined in the regions where predicted crack propagation, as shown in Fig. 74. The damage initiation criterion was based on the quadratic traction-interaction law and the damage evolution criterion was energy dissipation with linear softening. Damage stabilization was used to reach convergence in the static solver.

Fig. 74

FE model configuration

Procedure for selection of parameters for material model and failure

For parameter calibration, CAE models of the tensile and shear specimens were constructed. The initial calibration utilized the elastoplastic tensile data. The cross section of a broken test specimen was used to calculate true stress and calibrate the plastic parameters. Further refinement of the parameters was achieved by first explicitly simulating the tensile test and subsequently simulating the shear test to achieve results that matched the experimentally reported outcomes.

Cohesive zone elements were used and the failure criteria chosen was a nominal stress based on a quadratic combination of all three ratios for crack initiation and maximal deformation energy for crack propagation. Results of both loading rates simulations were fit to the reported experimental calibration data.

Modeling details

A 2D assembly model was used for crack growth path prediction. This model consisted of the challenge specimen with exact nominal dimensions that were defined in challenge documentation and two pins. Between the pins and specimen the following contact properties were defined: for normal behaviour hard contact and for tangential behaviour the friction coefficient of 0.05. The center of the bottom pin was a fixed constraint in directions X and Y with free rotations about the Z axis. At the centre of upper pin, the following motions were prescribed: displacement of 4 mm in direction Y, and fixed in direction X, free rotation around axis Z. The model was quasi-static. A surface region was defined to allow possible cracking. The crack was formed from notch geometry according based on the cohesive zone damage criteria. For crack growth, XFEM technology was employed. The XFEM region was prescribed around all holes and notches to allow for possible crack initiation and propagation.

The Quads criterion was used for cohesive zone element placement, which is based on a quadratic combination of nominal stress ratios between a given stress value and the peak nominal stress value in each of three directions.

Mesh refinement

In the model, 61,315 linear quadrilateral plane strain elements were used of type CPE4. The maximum global size of any element was 1 mm or 0.25 mm in the XFEM crack prediction region. Refinement edges are shown in purple in Fig. 75. Because of the small, unstructured elements there was no influence of element orientation.

Fig. 75

Mesh with refinement edges

1.12.2 Blind predictions

Based on results of simulation shown on Figs. 76 and 77, Team L predicted, that the crack will follow path B–D–E–A. The predicted Force-COD1 curve for both the slow and fast loading rates are shown in Fig. 78.

Fig. 76

Results of von Mises stress (left loading rate 0.0254 mm/s, right 25.4 mm/s)

Fig. 77

Results of plastification stress (left loading rate 0.0254 mm/s, right 25.4 mm/s)

1.12.3 Sources of discrepancies

The primary source of discrepancy likely was related to inadequate shear calibration due to convergence problems. Further, Team L also had made a post-processing mistake by exporting the reaction force for only 1 fixing point, whereas the pin had been constrained at 8 points and for this reason, our initial blind predictions reported forces that were too low.

1.13 Team M

Team members:

A.J. Gross, andrew.gross@mail.utexas.edu, University of Texas at Austin, Austin, TX, USA

K. Ravi-Chandar, ravi@utexas.edu, University of Texas at Austin, Austin, TX, USA

In some recent work we have identified that, for a class of ductile materials, plastic deformation proceeds without intervening damage until very large strain levels; this is confirmed through observations and measurements of deformation at multiple scales, from the macroscopic to the level of the grains (Ghahremaninezhad and Ravi-Chandar 2012, 2013; Haltom et al. 2013). The upshot of these investigations is twofold: first, it is essential that the plastic response of the material be calibrated to much larger strain levels than is usually achieved in a standard tensile test. Second, the mechanisms of final failure—void nucleation, growth and coalescence—occur within a highly localized zone in the plastically deformed material, and only at the very end of the material’s ability to withstand deformation. Thus, a model for the final failure of the material may be implemented numerically by a simple damage criterion such as element deletion. However, it is necessary to perform a careful evaluation of the plastic strain levels at which damage may initiate under multiaxial loading. We have adopted this approach in formulating the simulation of the challenge problem.

The plastic constitutive properties of Ti–6Al–4V are modeled by the flow theory of plasticity with isotropic hardening. Due to both the limited time to implement an appropriate yield criterion for HCP metals in ABAQUS (the FEM package that was used for this work) and the sparsity of stress paths used the calibration experiments, Hill’s 1948 anisotropic yield criterion (Hill 1948) was selected as the governing model for plasticity. The two parameters affecting the yield stress for out of plane shear conditions are assumed to be equal to their isotropic values since no data are available to calibrate them; this is considered to be appropriate because the corresponding stresses will be negligible in both the calibration experiments and challenge geometry. The remaining four parameters are subject to calibration. It is evident that uniaxial tensile test results cannot be used to determine the stress–strain behavior beyond a logarithmic strain of ${\sim }4\,\%$ because of the inhomogeneous deformation that occurs beyond the Considère strain. After this point, some model for the stress–strain relation must be considered. In this work, the behavior is represented by a monotonically increasing spline with seven segments beyond the Considère strain (Gross and Ravi-Chandar 2015). This form is chosen because it provides much more flexibility in the shape of the stress–strain curve than typical power law behavior, yet does not have an undue number of parameters. Temperature and rate effects were included by a multiplicative modification to the stress–strain curve defined by three parameters, following the form first used by Johnson and Cook (1983).

The parameters for the spline and the yield criterion are then found by an inverse procedure, where iterative finite element simulations of the slow rate calibration tests are performed with different trial parameters for the constitutive model. A nonlinear optimization scheme is used to minimize the sum of the errors for the rolling direction (RD) tensile, transverse direction (TD) tensile, and shear (VA; shear against grain) simulations. Error for each simulation is measured as the sum of the relative error between the net load in the experiment and simulation at 100 levels of global deformation. The resulting stress–strain curve and simulated load-elongation behavior for the calibration experiments are shown in Fig. 79. The VP shear data (shear parallel to grains) was not used, as the chosen constitutive model is not influenced by the orientation difference between VP and VA shear. Thus, only one shear test, or an average of the two could be used for calibration. VA shear was used exclusively for model calibration as it corresponds to the dominant orientation of shear loading in the challenge geometry. After calibration of the anisotropy and stress–strain curve from the slow rate tests was completed, the parameters for temperature and rate sensitivity were found using the high rate RD tensile and VA shear tests with the same inverse procedure. TD tension was not used because temperature and rate sensitivity are expected to be isotropic. The two tests used for calibration were chosen because they are dominated by different strain rates and temperature ranges.

Fig. 78

Force versus COD plot

Fig. 79

a Calibrated true-stress–strain behavior found for Ti–6Al–4V by simultaneously minimizing the load-displacement error in b RD tension, c TD tension, and d VA shear

Fig. 80

The equivalent plastic strain field at COD1 values of a 1 mm, b 1.75 mm, c 3 mm, and d after failure

Fig. 81

Load-COD1 curves with the predicted outcome and experimental results for a slow rate and b high rate loading

Material failure is modeled by a strain to failure model where the failure strain, $\upvarepsilon ^{\mathrm{f}}$, is dependent exclusively on stress triaxiality. When an element in the FEM simulations accumulates a damage parameter equal to unity according to the rule, $\int \frac{d\varepsilon ^{p}}{\varepsilon ^{f}}$, its stiffness is set to zero, where $d\varepsilon ^{p}$ is the plastic strain increment. The failure strain was calibrated by using the optimized RD tensile and VA shear simulations. For tension, the central element in the neck has both the highest triaxiality and strain. Since rupture of the specimen occurs rapidly, it corresponds to failure of this central element. By matching the experimental elongation at rupture in the simulation, the central element in the neck provides a strain to failure estimate under moderate levels of triaxiality. Strain to failure estimation in the shear specimen is based on past experimental experience indicating that the peak load in the test corresponds to the formation of a crack at one of the notch tips. Then the grip displacement at peak load in the experiment corresponds to global deformation state where the element at the current notch tip in the simulation must fail. This provides an estimate on the strain to failure under negative triaxiality conditions. After crack initiation, stable growth occurs in the experiment and could be used to perform a more detailed failure calibration. Due to time constraints this data was not used. It was found that the strains to failure over the large range of triaxiality spanned by these two tests were nearly identical (0.79 from tension and 0.82 from shear), so the strain to failure between them was simply interpolated linearly. For triaxialities in excess of those in the tensile test, a conservative strain to failure curve that is motivated by the exponential behavior first suggested by McClintock (1968) was adopted.

The challenge geometry is simulated with an ABAQUS/Explicit FEM model for both the slow and fast rate scenarios. Mass scaling is used to increase the stable time step to for both the slow and fast rate simulations. A highly refined mesh is used in the ligaments between the holes and notches, where strain localization is most likely to occur. Typical elements in this region were about 40 x 45 micron with 22 elements through the thickness. A total of about 700,000 eight-noded linear elements with reduced integration and hourglass control were used. 1.26 million and 0.93 million time steps were used in the slow and fast rate tests respectively, each simulation requiring several hundred hours of CPU time. Loading is applied on rigid, frictionless pins. The bottom pin was held fixed and a quadratic displacement rate was applied at the top pin for the slow loading scenario. For the fast loading a linear displacement rate at the top pin was imposed, consistent with the loading rate in the experiment. The results are summarized in Figs. 80 and 81 where the strain field at selected levels of deformation from the slow rate prediction and the load-COD1 variations for the slow and high rate predictions are shown.

For the slow rate test, early strain accumulation is the largest in ligament A–C, and remains so until a COD1 value of about 1.75 mm. After this point, both ligaments B–D and D–E have comparable levels of strain that exceed those in ligament A–C. The prediction indicates an increase in load carrying capability of the specimen until a COD1 of about 4.5 mm, where, on the cusp of localization, failure initiates, triggering fast fracture in ligament D–E, almost immediately followed by the fast fracture of ligament B–D. At initiation of failure, the load is predicted to drop abruptly to nearly zero, thus ending the simulation. It is projected that ligament EA will fail under continued loading, but this was not examined. The main details of the high rate test are similar to the slow rate.

1.13.1 Sources of discrepancy

The largest difference between predictions and experiments is that failure was predicted to occur at a COD1 ${\sim }4.1$ mm while it was observed at a COD1 ${\sim }3.03$ mm in the slow-rate tests, with a similar difference in the high-rate tests. All other aspects of the response were predicted within the desired tolerance. After a careful examination of the predictions in comparison to additional experiments that were instrumented to measure local deformation fields (see Gross and Ravi-Chandar 2015, 2016), it was determined that the elastic–plastic constitutive model did not satisfactorily represent the yield surface along the stress paths followed in the critical ligaments of the challenge geometry beyond a strain of ${\sim }0.2$; this deficiency in identifying and calibrating a proper constitutive model was the main source of the discrepancy between the predictions and the experiments. However, this deficiency did not manifest itself in the calibration exercise; this points to the need for a better approach to designing, performing and implementing experiments that are used in the calibration procedure.

1.14 Team N

Team Members:

L. Xue, xue@alum.mit.edu, Thinkviewer LLC, Sugar Land, TX, USA

1.14.1 Approach

The second Sandia Fracture Challenge gives an excellent opportunity to evaluate how different loading rate conditions can influence fracture behavior of a given configuration of ductile metals. In general, the effects of loading rate on mechanical behavior of metals can come in from several aspects, for instance (1) many metals display higher resistances under high strain rates; (2) the post-yield plastic hardening exhibits lower hardening capability at high strain rates; (3) the plastic work in the deformation zone converts to thermal energy at high strain rates, which heat up the material locally and hence reduces the material resistance; (4) high strain rates can activate different plastic flow mechanism and thus results in higher or lower fracture strain depending on the micro structures of the material. In the present study, the effects (1) and (2) are modeled by calibrating the material yielding and strain hardening behaviors separately for each loading rates, while the effect (3) and (4) are not considered explicitly, but rather they are inherently embedded in the calibration procedure because they are not singled out in the modeling.

Two pulling rates at the grips are used for the coupon tests of the material properties and the S-shaped specimen for fracture prediction. Several fracture initiation sites can be foreseen for the S-shaped flat plate with three holes in the vicinity of the roots of rounded slots. At first glance, this S-shaped structure is in several ways like the first Sandia Fracture Challenge, except that a second slot was added to the configuration. Previous studies have shown that, in this type of ductile fracture simulations, the constitutive relationship of the material plays a central role in the accuracy of the prediction results (Boyce et al. 2014). There are many choices of constitutive models that are capable of discerning between a mode I dominant and a mode II dominant ductile fracture (Xue 2007, 2008, 2009). The Xue (2009) damage plasticity model requires only one parameter to be calibrated for the simplest case. Yet, this model is enabled by a full 3D non-linear damage coupled yield function and has been shown to be able to capture different fracture modes through a series of numerical simulations. In the first Sandia Fracture Challenge, the Xue (2009) model was used and showed extraordinary capability in predicting fracture behavior of the given structure using limited simple material testing data. In this second Sandia Fracture Challenge, the same procedure was used to calibrate necessary material parameters and to obtain finite element predictions.

From the material testing results at the two loading rates, it is clear that the selected material Ti–6Al–4V exhibits some rate sensitivity. The nominal loading rates at the pins of the slow and fast condition are 0.0254 and 25.4 mm/s respectively. The strain rate in the deformation region of the S-shaped structure is further higher than that of the high rate in the tensile material testing, because the deformation zone in the material testing is greater than the deformation zone in the S-shaped structure while the end separation velocity are the same. This difference in strain rate should be about an order or so given the size of the holed zone in the S-shaped structure, which converts to about 3 % increase in the magnitude of yield stresses for the S-shaped structure considering a logarithmic relationship of the rate hardening coefficient. Note, this difference should be about the same in the slow rate scenario. However, it is considered relatively a small error and is not factored in the present study, i.e. the calibrated matrix stress–strain relationship from curve fitting of the tensile coupon in the rolling direction was used directly for the S-shaped specimen at the same nominal loading rate.

Table 15 Material parameters for Ti–6Al–4V for damage plasticity model

A parallel finite element simulation was used to calibrate the material parameters. In both calibration and prediction simulations, a one-point reduced explicit time integration scheme was adopted. In this type of ductile fracture analyses, it is well-known that the simulation results are subjected to mesh size of the finite element model. In order to minimize mesh size dependence, the element sizes were carefully chosen such that the elements in the material tests and the central region of the S-shaped structure used for prediction were about the same. A total of 16 elements through the thickness were used in order to capture the through thickness fracture pattern and this through thickness element length was used in meshing the in-plane elements. Thus, the element size was about 0.2 mm in all directions. Same mesh was used for both slow and fast loading rate.

1.14.2 Material parameters calibration

The material tension test data in the rolling directions for the two rates were used to calibrate the material stress–strain curve using Swift relationship, see Eq. (39) $\upsigma _{\mathrm{M}}=\upsigma _{\mathrm{y0}}(1+\frac{\upvarepsilon _{\mathrm{p}}}{\upvarepsilon _{0}})^{\mathrm{n}}$ where $\upsigma _{\mathrm{M}}$ is the material matrix resistance at given plastic strain $\upvarepsilon _{\mathrm{p}}$, $\upsigma _{{\mathrm{y}}0}$ is the initial yield stress, $\varepsilon _{0}$ is a reference strain and n is the hardening exponent. A set of initial fitting parameters for low loading rate were used to run a detailed finite element analysis of the tensile tests and are then adjusted by matching the simulation load-displacement curve with the experimental one [Xue EFM 2009]. Due to the coupled nature of the stress–strain relationship with damage associated weakening in the damage plasticity model, an iterative process is needed to calibrate all the material parameters in Eqs. (39–42), where $\upsigma _{\mathrm{f}0}$ is a reference fracture stress, $\hbox {k}_{\mathrm{p}}$ is a pressure sensitivity parameter, and m and $\beta$ are damage and weakening exponents. In the present study, both m and $\beta$ were set to 2.0 according to previous studies on various metals. A reference fracture strain $\upvarepsilon _{\mathrm{f}0}$ is substituted for the reference fracture stress $\upsigma _{\mathrm{f}0}$, which is related to $\upvarepsilon _{\mathrm{f}0}$ by $\upvarepsilon _{\mathrm{f}0}=\upvarepsilon _{0}\left( {\frac{\upsigma _{\mathrm{f}0}}{\upsigma _{\mathrm{y}0}}-1} \right) ^{1/\mathrm{n}}$. After several iterations, the final fitted material parameters that give good match of the load-displacement curves for simple tension coupon tests are listed in Table 15 for the two loading rates. Then, the above process was repeated for the high loading rate.

$$\begin{aligned}&{\upsigma }_{\mathrm{M}}={\upsigma }_{\mathrm{y}0}\left( {1+\frac{\upvarepsilon _{\mathrm{p}}}{\upvarepsilon _{0}}} \right) ^{{\mathrm{n}}} \end{aligned}$$

(39)

$$\begin{aligned}&{\upvarepsilon }_{\mathrm{f}}={\upvarepsilon }_{0} \left\{ {\left( {\frac{{\upsigma }_{\mathrm{f}0}}{{\upsigma }_{\mathrm{y}0}}}\right) ^{1/{\mathrm{n}}}\left[ {\left( {1+\hbox {k}_{\mathrm{p}} \hbox {p}}\right) \frac{\sqrt{3}}{2\cos {\uptheta }_{\mathrm{L}}}}\right] ^{1/{\mathrm{n}}}-1}\right\} \nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned}&\dot{\hbox {D}}=\hbox {m}\left( \frac{\upvarepsilon _{\mathrm{p}}}{\upvarepsilon }_{\mathrm{f}}\right) ^{\mathrm{m-1}}\frac{\dot{\upvarepsilon }_{\mathrm{p}}}{\upvarepsilon _{\mathrm{f}}} \end{aligned}$$

(41)

$$\begin{aligned}&{\upsigma }_{\mathrm{eq}}=\left( {1-\hbox {D}^{{\upbeta }}}\right) {\upsigma }_{\mathrm{M}} \end{aligned}$$

(42)

From the given tensile coupon tests, the material stress–strain curves show that the fracture strains under simple tension at the two loading rates are not too different from each other; however, the hardening exponent appears to be lowered significantly when the loading rate is high. It is also noticed that the material yield stress displays some strain rate hardening. At the high loading rate, the yield stress is about 10% higher when the strain rate is 1000 times higher.

Experiments in literature show that at higher loading rates, the fracture pattern often favors shear mode, e.g. it can change from a mode I to a mixed model I/III for a flat panel when a compact tension specimen loaded dynamically (Rivalin et al. 2001; Xue and Wierzbicki 2009). In the present study, path A–C–F represents a mode I fracture and path B–D–E–A represents an in-plane shear mode. These two modes should be the dominant fracture modes of the present structure for most metallic materials.

Fig. 82

Predicted fracture paths using the damage plasticity model: A–C–F for slow (left) loading rate and B–D–E–A for fast (right) loading rate. Plotted contours are the accumulated plastic strains

In addition to the tensile tests, a double V-notched specimen was also used for material shear testing. The fracture plane of the double V-notched specimen under simple shear is a little skewed and is not exactly along the straight line connecting the roots of the V-notches. The shear test shows the material yield stress under nominal simple shear is lower than that under simple tension. It was estimated that the initial yield stress was about 13 % lower under nominal simple shear condition. There are two possibilities to model this difference: (1) adopt a Tresca yield condition or similar J3-dependent yield condition or (2) assuming the material is anisotropic (likely due to rolling process, but we were not sure because of limited experimental data) and choose an anisotropic yield function such as Hill1948. In either way, it should be more accurate in describing the yield condition, at least in the initial yielding phase of the material. However, this J3-dependence yielding is ignored in the present prediction using the simple damage plasticity model (Xue 2009).

1.14.3 Results and discussions

Damage plasticity model for the material was used throughout the numerical simulation. Using the above described method and the calibrated material parameters, the pulling of the S-shaped structures at the two loading rates were simulated. The nominal geometry of the specimen was used. No variation in the actual size was considered for the geometrical tolerance. Two sets of hole-pin contacts used to pull the specimen apart were modeled explicitly, such that the rotation at the pin-hole contact was allowed. Fracture is simulated by element removal, i.e. when damage index D is accumulated to unity for an element, that element loses all its load carrying capacity. This can be seen from Eq. (42).

In the low loading rate case, a tensile fracture path (A–C–F) was predicted; in the high loading rate case, an in-plane shear fracture path (B–D–E–A) was predicted. The after fracture paths are shown in Fig. 82.

The predicted COD1-loading curves are shown in Fig. 83. There are some minor oscillations in the COD1-loading curve due to the exaggerated pulling rate used in the explicit numerical simulation. The load oscillation in the fast loading rate scenario after fracture occurred in the B–D–E segments is due to the sudden break of the structure.

Fig. 83

Predicted load-COD1 curves for the slow (left) and fast (right) loading rates using the damage plasticity model

The post-mortem experiment examination reveals that all S-shaped specimens fractured in the in-plane shear mode (B–D–E–A) under remote extension, except one that was believed to be not entirely flat that failed in A–C–F path. This differs from the numerical predictions in that the slow rate experiments result in a B–D–E–A fracture path as well as under the fast loading rate. The simulation of the fast loading rate case matches the experimental results well. In both cases, the predicted peak loads is about 10 % higher than that obtained experimentally.

Fig. 84

Thickness and surface height measurements of the Challenge geometry samples: a measurement locations; b relative surface height measurement setup with a dial indicator, surface plate, and jackscrews

1.14.4 Sources of discrepancy

In retrospect, neglecting the J3-dependence of the yield condition of the material appears to be the single most significant source of discrepancy in these predictions. For instance, it was shown by the MIT team that the Hill 1948 yield condition are capable of prediction the in-plane shear mode (path B–D–E–A) for both slow and fast loading rate. When the Hill 1948 yield condition degenerates to von Mises yield condition, the fracture path changes to A–C–F. Furthermore, the higher predicted peak loads were also resulted from the tensile stress–strain curve used in simulations. In both slow and fast loading the regions along the shear path were subjected to the most severe deformation, where the resistance was over-predicted. Meanwhile, the predicted COD1 values at fracture of both slow and fast loadings have a good match with the experimental data. This suggests the calibration procedure are fairly accurate under the assumption of the material obeys a von Mises yield criterion. It also suggests the adoption of a J3-dependent yield condition or an anisotropic yield function such as Hill 1948 will fix these observed errors in the current prediction. In either case, a re-calibration of the material parameters for damage accumulation and fracture initiation may be necessary.

Appendix 2: Further experimental details

1.1 Dimensional measurements

A calibrated coordinate measurement machine was utilized for in-plane dimensional measurements, and a calibrated micrometer was utilized for thickness measurements. All tested specimens had dimensions within the drawing tolerances. In addition to the in-plane dimensional measurements, thickness measurements were performed at Sandia with a calibrated Mitutoyo IP65 micrometer with 0.001-mm resolution in eight locations (TL, TC, TR, Pt. O, 5, BL, BC, and BR) shown in Fig. 84a; Tables 16 and 17 in “Appendix 2” provide the details of these measurements. Despite being within the thickness tolerance of the drawing, the challenge specimens had out-of-plane distortions that were caused by unbalanced milling of the plate thickness. The relative surface height measurements were taken using a Brown & Sharpe BestTest dial indicator with a 0.0127-mm precision attached to a height gage resting on a flat precision ground granite surface plate. The height was measured in 12 locations relative to the reference height “PT. O” as shown in Fig. 84a. Tables 18 and 19 provide the relative surface height measurements for each test sample. Sample 30 had the largest relative curvature out of all the samples, which may have contributed to this one sample failing by a different crack path than all other samples.

Table 16 Thickness measurements for all samples tested at the 0.0254 mm/s displacement rate

Table 17 Thickness measurements for all samples tested at the 25.4 mm/s displacement rate

Table 18 Surface height measurements for all samples tested at the 0.0254 mm/s displacement rate

Table 19 Surface height measurements for all samples tested at the 25.4 mm/s displacement rate

1.2 Fractographic observations

Images of the fracture surfaces and crack paths for Samples 11 (‘slow’ loading rate) and 27 (‘fast’ loading rate) are shown in Figs. 85 and 86 respectively. Both loading rates had remarkably similar fracture surfaces, so they will be described together. The ligament B-D was predominated by small ductile dimples, roughly 1 $\upmu \hbox {m}$ in diameter. In addition, there were relatively flat patches $\sim$50–100 $\upmu \hbox {m}$ in diameter on the fracture surface. In these flat patches, there were very few dimples, and the material had a smeared appearance somewhat reminiscent of a wear surface presumably associated with shear failure. This smeared zone has an appearance somewhat reminiscent of “slickenlines” associated with the shear fracture of geologic structures. Ligament D-E had similar features, although there was also a single rather large smeared flat patch 300–500 $\upmu \hbox {m}$ in diameter with a cluster of very large 10–20 $\upmu \hbox {m}$ diameter dimples on one side of the smear. These large dimples are thought to be associated with stable microvoid coalescence and the finer dimples are thought to be associated with fast fracture. While the large dimples and associated large smear patch was most evident in ligament D–E, it was also possible to find similar, albeit less pronounced, features in ligament B–D. The final rupture ligament, E-A, also had very pronounced cluster of large dimples as well as an even larger smear patch. In all cases, the dimples were not perfectly equiaxed as would be expected in a tensile failure, but had some degree of directionality consistent with a shear failure.

Fig. 85

Sample 11: example fractography of the slow rate loading condition. Images taken from ‘bottom’ half of broken specimen

Fig. 86

Sample 27: example fractography of the fast-rate loading condition. Images taken from ‘top’ half of broken specimen

Fig. 87

Fracture surface of ligament A–C from Sample 30

Sample 30 was the only exception that failed by path A–C–F. The fracture surface of the A–C ligament that failed apparently prematurely (at a lower COD1 than any other sample) is shown in Fig. 87. This ligament, A–C, should have nominally been loaded in pure tension. Therefore, it is reasonable to compare this ligament to the tensile fractures observed in the tensile bars provided for material calibration, specifically Fig. 3e. There are important differences that suggest that Sample 30 could have exhibited anomalously low ductility. Firstly, unlike the tensile bar the outer shape of the ligament A–C shows very little curvature suggestive of limited necking. Secondly, the center of the fracture surface shows marked differences. This central zone is typically called the ‘fibrous zone’ in tensile cup-and-cone failure, and it is surrounded by ‘shear lips’. The fibrous zone where fracture originates is typically flat, with only microscale perturbations from the mode-I crack path. In the tensile test fracture, Fig. 3e, this central fibrous zone is indeed reasonably flat with only minor ridges running horizontally in the image indicative of the lamellar microstructure developed during rolling. However, in Sample 30’s A–C ligament fracture surface, these ridges are markedly more pronounced and faceted indicating a much coarser and perhaps less uniform underlying crystallographic texture. In fact in Sample 30 there is no nominal mode-I crack plane and the entire central fibrous zone appears more like alternating shear lips. Inspection of the secondary crack ligament, C–F also revealed a pronounced ridge that deviated from the expected mode-I crack plane. This unusual fracture morphology raises suspicion that Sample 30 was not a nominal failure. This apparently anomalous behavior is discussed further in Sect. 3.3

1.3 Post-challenge experimental observations from the Ravi-Chandar Lab at University of Texas at Austin

The University of Texas volunteered to perform additional tests after the predictions had been made in order to produce a complimentary set of data to those already compiled by the two Sandia laboratories. Experiments were performed on three samples; 2, 5, and 31. These samples were obtained from the same manufacturing lot as the samples tested at Sandia National Laboratories. Due to the limited number of samples, only experiments with the slow loading rate were performed.

Fig. 88

The experimental setup used in the University of Texas lab. Specimen is shown mounted in the grips and being viewed with a DSLR camera for DIC based COD measurements, two angled cameras for 3D-DIC, and a high speed camera to resolve the cracking sequence

Fig. 89

Comparison of the Load-COD curves measured in the University of Texas tests with the data obtained from the Sandia Structural Mechanics Laboratory tests (grey lines). The COD1 in the UT tests was obtained from 2D DIC measurements rather than clip gages. Specimen S02 had coarse temporal sampling for COD measurements and is estimated to have failed at a COD1 of 2.9 mm. S31 was not loaded to failure; the test was interrupted and preserved for microscopic characterization

Fig. 90

High speed images of sample 2 during failure of the first two ligaments with overlaid vertical displacement fields from DIC (positive displacement is down): a Both ligaments are intact; b ligament DE has broken but BD remains intact; and c ligament BD has also failed

The experimental setup used in the University of Texas laboratory can be seen in Fig. 88. The experiments utilized a 100-kN Instron electromechanical load frame, with a 100-kN load cell ($\pm$0.25 % uncertainty of the measured value) at ambient temperature. The level of noise in the load signal was measured to be 2 N. The crosshead rate was maintained at 0.0254 mm/s, as prescribed in the challenge. Two universal joints were placed, one each at the upper and lower grips in order to minimize the effect of loading misalignments. In addition, the same clevises used by the Sandia laboratories were used. Instead of using COD gages to measure the displacements at the notch mouths, a digital single-lens reflex (DSLR) camera was used to view the entire specimen to allow the COD measurement to be made using DIC. Two additional cameras focused on the region between the notches were used to perform 3D-DIC and to obtain the kinematic fields in the regions of highest deformation and eventual failure. A high-speed video camera, with high frame rate capability, was positioned to view the ligaments B-D and D-E and resolve the sequence of failure; the camera was post-triggered with the falling signal from the load drop associated with specimen failure. Further details of the experimental methods, sensitivity, resolution, and results are described by Gross and Ravi-Chandar (2016).

Confirmation of the load-COD1 results produced at both of the Sandia laboratories is shown in Fig. 89. All three samples indicated the same crack path (B–D–E–A); failure occurred in ligaments B–D and D–E, although the loading on sample 31 was halted just after localization occurred in these ligaments, but before they failed. Follow up microscopy on this sample is presented in Gross and Ravi-Chandar (2016). For the two samples loaded until failure, fast fracture occurred in ligaments B-D and D-E nearly simultaneously. To resolve which ligament failed first, sample 2 was imaged at 20,000 fps and sample 5 was imaged at 40,000 fps. An image sequence showing three subsequent frames captured at 50-$\upmu \hbox {s}$ intervals by the high speed camera at the time of failure for sample 2 is shown in Fig. 90. The overlaid color contours are of the vertical displacement field (relative to the trigger point) calculated with DIC from the high speed images. The first image shows the state of the sample just before cracking of any ligament, the second image shows ligament BD intact with ligament DE completely severed by a crack and the final image shows both ligaments fully cracked. Identification of cracking in the second image is made by observing a displacement field consistent with the elastic recovery expected after external loading is released from the ligament by the presence of a crack. A high speed video with more frames for this sample and without DIC processing is included as Supplementary Information for this article. Despite increasing the framing rate for sample 5, only three subsequent frames capture the same behavior observed for sample 2. Sufficient temporal resolution to determine the location of crack initiation in each ligament was not pursued. Thus, the greatest specificity that can be given for the cracking sequence of these two specimens is that fracture initiates in the ligament D–E, the associated unloading and the subsequent fracture of the ligament B–D occur within the next 100 $\upmu \hbox {s}$, suggesting a very dynamic process of fracture. After continued loading ligament E–A is expected to fail as observed in the experiments performed by the Sandia laboratories.